Abstract
To simulate the current climate, a 20-year integration of a non-hydrostatic regional climate model (NHRCM) with grid spacing of 5 and 2 km (NHRCM05 and NHRCM02, respectively) was nested within the AGCM. The three models did a similarly good job of simulating surface air temperature, and the spatial horizontal resolution did not affect these statistics. NHRCM02 did a good job of reproducing seasonal variations in surface air temperature. NHRCM05 overestimated annual mean precipitation in the western part of Panama and eastern part of the Pacific Ocean. NHRCM05 is responsible for this overestimation because it is not seen in MRI-AGCM. NHRCM02 simulated annual mean precipitation better than NHRCM05, probably due to a convection-permitting model without a convection scheme, such as the Kain and Fritsch scheme. Therefore, the finer horizontal resolution of NHRCM02 did a better job of replicating the current climatological mean geographical distributions and seasonal changes of surface air temperature and precipitation.
1. Introduction
Scientists and policymakers alike are requesting high-resolution estimates of global warming and its consequences in order to map out the changes and consequences in greater detail. Dynamical downscaling of global climate models is a valuable strategy for generating comprehensive estimates of regional climate changes owing to global warming [,]. As an example, previous works projected the future climate in and around Panama with a global climate model (GCM) with grid spacing of 20 km [,,,,].
Even with fine grid spacing, however, this model did not adequately replicate extreme events and did not resolve the main mountain ranges or river basins, all of which must be depicted if climate projections are to be relevant for water resource and flood planning, agriculture, and other applications. To overcome these issues, a non-hydrostatic regional climate model (NHRCM) was used in order to simulate current climate in Panama.
Only a few studies on high-resolution models (e.g., [,,]) have been published in Central America. Climate change projections for Central America and Mexico were initially performed with a regional climate model []. Dynamical downscaling with horizonal resolution of 27, 9, and 3 km over Panama using the Weather Research and Forecasting (WRF) model was performed to forecast one-day precipitation with different physical parameterizations []. This is the only study on forecasting for Panama, but it is not a study on a climate time-scale. In this study, we nested our NHRCM within the results of AGCM’s current climate experiment, integrated it for all four seasons over a 20-year period from 1980 to 1999, and analyzed its performance to make the model useful for climate studies surrounding Panama.
2. Materials and Methods
2.1. Experiment Design
This study used a multiple nesting approach, as shown in Figure 1a. The lateral boundary data on the outskirts were derived from current climate simulations, employing an AGCM with a grid spacing of 20 km []. The AGCM is based on the Japan Meteorological Agency’s (JMA) previous operational model for numerical weather prediction []. The integration period was 1979 to 2003. This simulation was designed to perform dynamical downscaling with accurate current climate replication to avoid garbage-in-garbage-out, since coupled GCMs replicate current climate with distinct and/or systematic biases, especially at regional scale. The AGCM is externally forced with observation-based time series of sea surface temperature, sea ice concentration, greenhouse gas concentration, sulfate aerosol concentration, ozone gas concentration, and volcanic aerosol concentration. The AGCM does a good job of replicating the current climate in Central America [] and in most of the world [].
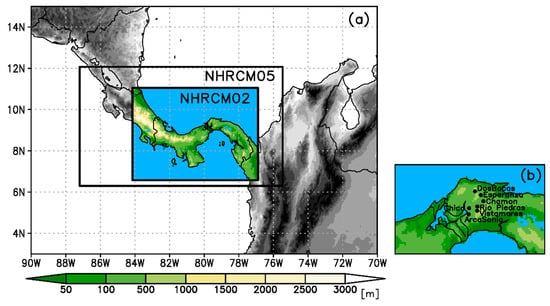
Figure 1.
(a) Target area for current climate simulations. Inner domain (colored) represents area for NHRCM02, outer domain (grayscale) represents area for NHRCM05. (b) Eight ground-based precipitations stations observed by Panama Canal Authority.
NHRCMs with grid spacing of 5 and 2 km (NHRCM05 and NHRCM02, respectively) were nested within the AGCM. The AGCM lacks cloud water, cloud ice, and other cloud characteristic variables, so both NHRCM05 and NHRCM02 were used to produce them for the lateral border of the two smaller domains with 5 and 2 km grid spacing. Calculations were simplified by skewing the inner domain, which still spans almost the entire Panama Isthmus. The setup of NHRCM employed in this study can be found in Table 1. NHRCM was externally forced with observation-based time series of sea surface temperature and greenhouse gas concentration. In this work, the time slice integration method was applied. Each integration took place between 1 December and 4 December of the following year. The first month of results was discarded in favor of spin-up. Since 1980, this cycle has repeatedly occurred 20 times. Comparisons of climate between NHRCM05 and NHRCM02 are the focus in this study; comparisons between NHRCMs and MRI-AGCM are provided in the Figure 1a.

Table 1.
Model specifications chosen in this study. Minimal details are given in main text, and full details are described in references.
2.2. Surface Air Temperature and CRU TS v4.05 Data
The The gridded Climatic Research Unit (CRU) Time-series (TS) data version 4.05 dataset was used, which is the fourth version of the gridded product established by the Climate Research Unit of the University of East Anglia []. It includes a number of variables (precipitation, surface air temperature, mean temperature, etc.) compiled in a global (excluding Antarctica) 0.5 × 0.5 grid (56 km) from 1901 to 2017, obtained by the interpolation of monthly data collected from the World Meteorological Organization’s archives.
2.3. Precipitation Data
For the observation dataset, we used GSMaP Gauge v.5 global satellite mapping of precipitation data [,] (https://sharaku.eorc.jaxa.jp/GSMaP/guide.html#09; accessed on 2 February 2020). Ground truth data are used to adjust the satellite data bias in this dataset. It has a time resolution of one hour and a spatial resolution of 0.1°. For the target season, this dataset is only accessible for the period from 2000 to 2010. There are differences in the reference period between the simulations and GSMaP. Monthly precipitation in CRU TS with a 0.5 × 0.5 grid was used to see if there was an issue with the reference period difference.
Eight ground-based precipitation stations observed by the Panama Canal Authority were also used (Figure 1b). The eight stations are located in and around the upper Chagres River Basin, a part of the Panama Canal Basin [], which is a very important area for water resources of canal operations; the coordinates of the observation stations range from 79.40° E to 79.51° E and from 9.19° N to 9.45° N, corresponding to about a single grid box of MRI-AGCM. The elevation ranges from 110 to 2100 m.
3. Results and Discussion
3.1. Surface Air Temperature
The models were validated by comparing the CRU to the simulations averaged over CRU grids on land. Figure 2 depicts the differences in annual mean climatological surface air temperature between the simulation and observations. Except for several grids, the bias of the surface air temperature simulated with NHRCM02 lies between −1 and 1 °C (Figure 2d). A large negative bias of −3 °C was found in the mountainous terrain of the western border. NHRCM05 did a good job of simulating surface air temperature, although the biases in NHRCM05 are large compared to those in NHRCM (Figure 2c).
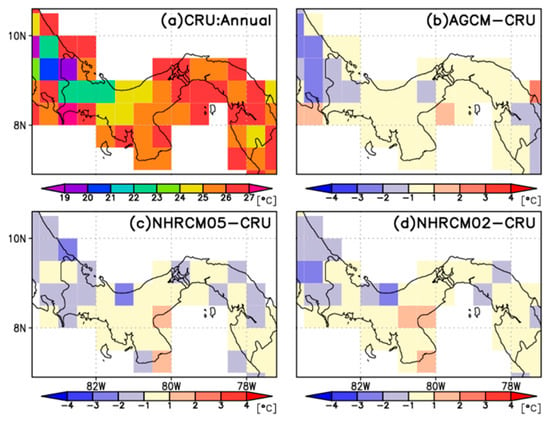
Figure 2.
Geographic evaluation of 20-year mean annual surface air temperature derived from (a) CRU (CRU_TS4.05), and biases in (b) MRI-AGCM, (c) NHRCM05, and (d) NHRCM02. Values in biases are difference between simulations and CRU observations. See Table 2 for quantitative evaluation.
As the grid size becomes finer, the NHRCMs have negative biases, opposite to those of MRI-AGCM. NHRCM02 has small biases that are geographically distributed in Panama, and the area average over the country is minimal (Table 2). For the 20-year mean annual surface air temperature, the spatial correlation between the NHRCMs and CRU was 0.90 and 0.92 for 5 and 2 km grid spacing, respectively. The root mean square errors (RMSEs) for NHRCMs are almost the same. Therefore, NHRCM02 has better performance in simulating surface air temperature, and the spatial horizontal resolution contributes slightly to the replicability of geographic distribution of surface air temperature.

Table 2.
Quantitative evaluation of 20-year mean annual surface air temperature averaged over Panama in three simulations against observation. See Figure 2 for geographic evaluation.
Table 2.
Quantitative evaluation of 20-year mean annual surface air temperature averaged over Panama in three simulations against observation. See Figure 2 for geographic evaluation.
| Bias (°C) | RMSE (°C) | Correlation | |
|---|---|---|---|
| AGCM | 0.55 | 1.05 | 0.93 |
| NHRCM05 | −0.66 | 1.09 | 0.90 |
| NHRCM02 | −0.51 | 1.08 | 0.92 |
NHRCM02 did a good job of reproducing seasonal variations in surface air temperature (see Figure 3). The NHRCMs had cool biases in the rainy season, from May to November, in comparison to CRU, whereas in the dry season, from January to March, the simulated surface air temperatures of NHRCMs were almost the same as those of CRU. All models accurately simulated maximum mean monthly surface air temperatures at the end of the dry season, but with a 1-month behind/advance maximum, while the minimum surface air temperature in NHRCMs occurred in October, with two months advance, in comparison to CRU.
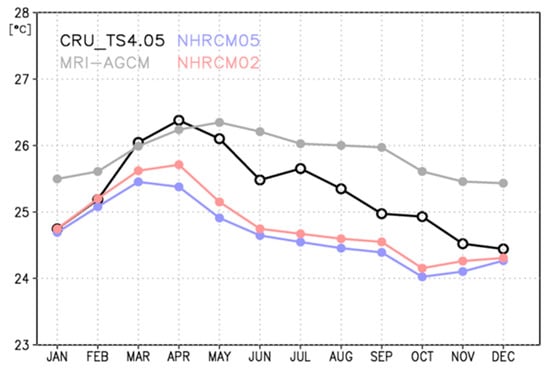
Figure 3.
Seasonal changes in 20-year mean monthly surface air temperatures averaged over grids with altitude below 1000 m. Black, gray, blue, and red lines represent observations, MRI-AGCM, NHRCM05, and NHRCM02, respectively.
For seasonal changes in 20-year mean surface air temperature, NHRCM02 had a smaller bias and RMSE and higher temporal correlation than NHRCM05 (Table 3). The correlation between model simulation and CRU was 0.74 and 0.83 for NHRCM05 and NHRCM02, respectively, and NHRCM02 did a better job at simulating seasonal changes than NHRCM05.

MRI-AGCM showed large negative biases in many grids, especially in the western border and the Caribbean Sea (Figure 2b). MRI-AGCM’s average annual mean surface air temperature biases over Panama were negative by 0.55 °C (Table 2). As the grid size becomes finer, NHRCMs have negative biases, opposite to MRI-AGCM. The three models show very small varieties ranging from 1.05 to 1.09 °C. The spatial correlation for MRI-AGCM was slightly high compared to NHRCM02. The range of monthly surface air temperature of NHRCMs was better than that of MRI-AGCM (Figure 3). MRI-AGCM had the best temporal correlation of seasonal changes in the three models (Table 3), although the difference in the correlation coefficients is not statistically significant. Therefore, the nested NHRCMs reproduced the spatial details of surface air temperature as well as MRI-AGCM did. Different horizontal resolutions of datasets of observations and models means different representative altitudes. The altitude–surface air temperature dependence may affect the biases.
3.2. Precipitation
The models were validated by comparing the GSMaP to the simulations averaged over the GSMaP grid. The differences in annual mean climatological precipitation between simulations and observations are provided in Figure 4. NHRCM05 overestimated annual mean precipitation in the western part of Panama and eastern part of the Pacific Ocean side. Very large biases, exceeding a ratio of 3, were seen in the western part of the Caribbean Sea. NHRCM05 was responsible for this overestimation, as it was not seen in MRI-AGCM. Precipitation in NHRCM05 is understood as high sensitivity to mountainous terrains []. NHRCM02 simulated annual mean precipitation better than NHRCM05, probably due to a convection-permitting model without a convection scheme, such as Kain and Fritsch’s scheme. The underestimation is seen in the eastern part of the Azuero Peninsula, the driest region in Panama.
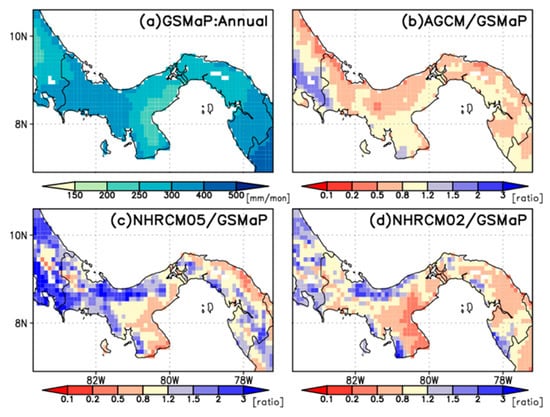
The finer version of NHRCM, NHRCM02, had smaller absolute bias and RMSE and higher spatial correlation than NHRCM05 (Table 4). These results are consistent with the fact that orographic precipitation is generally simulated in a model with a finer horizontal resolution.

Table 4.
Same as in Table 2 but for quantitative evaluation of 20-year mean annual precipitation. See Figure 4 for geographic evaluation.
| Bias (mm/Month) | RMSE (mm/Month) | Correlation | |
|---|---|---|---|
| AGCM | −44.9 | 95.8 | 0.40 |
| NHRCM05 | 127.5 | 253.1 | 0.33 |
| NHRCM02 | 4.0 | 131.5 | 0.38 |
Figure 5 shows the seasonal changes in precipitation in Panama. The two models simulated similar seasonal changes, except for the period October to February. There are three monthly precipitation stages: about 470 mm/month from May to August, about 410 mm/month from September to November, and dry conditions or less precipitation from December to April. The seasonal changes in Panama were fairly well represented by NHRCM02 (Figure 5), but the second stage was not. NHRCM05 overestimated precipitation, especially in the second and the first half of the second stages. NHRCM02 also overestimated precipitation in the same period because it used the lateral boundary simulated in NHRCM05.
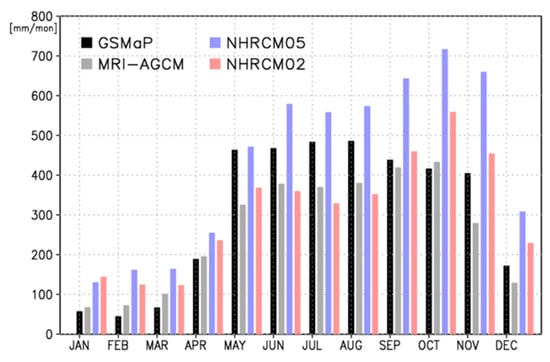
Figure 5.
Seasonal changes of 20-year mean monthly precipitation in three simulations against observations.
A quantitative evaluation of seasonal changes is tabulated in Table 5. The biases are the same as in Table 4, since they do not vary when spatial or temporal means are computed on an annual time scale. Although NHRCMs are nested in the lateral boundary conditions of MRI-AGCM, they have opposite signs in the biases. NHRCM05 has larger RMSE than NHRCM02. The temporal correlation between NHRCMs and CRU was 0.92 for NHRCM05 and 0.85 for NHRCM02.

Scatter plots of annual precipitation totals of the three models and GSMaP are depicted in Figure 6. The range of annual precipitation is confined between about 200 and 500 mm/month, while for NHRCM02 the range is widely distributed between 50 and 1000 mm/month. NHRCM05 only simulated about 1400 mm/month in the three grids. These values obviously seem to be overestimated, since the maximum simulated in NHRCM02 is about 1100 mm/month and that in GSMaP is about 480 mm/month. The seasonal variations of monthly climatological precipitation in NHRCM05 resemble those of the observations but with larger amounts. The time series of daily precipitation always show large amounts of precipitation, which contributes to the overestimations, but little event-specific heavy precipitation with outlier amounts is seen. The outlier of about 1400 mm/month in NHRCM05 is not an implausible value, and the so-called gridpoint storm on a sub-daily time scale [] may have affected the overestimations and is a challenging study relevant to extreme precipitation events. Therefore, the higher horizontal resolution of 2 km and the convection-permitting model without a convection scheme is responsible for the low maximum simulated in NHRCM02.
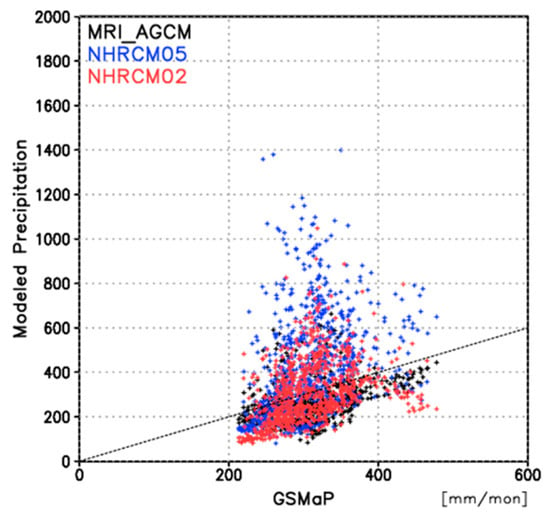
Figure 6.
Scatter plot showing 20-year mean annual precipitation amount of GSMaP and NHRCM02. Black dots represent values (in mm/month) for entire domains including oversea areas, and blue dots represent values for land areas only.
The area in and around the upper Chagres River Basin, a part of the Panama Canal Basin (Figure 1b), was selected to evaluate the capability of NHRCM02 to simulate precipitation over complex terrain, since it has complex topography with elevation ranging from 110 to 2100 m. NHRCM02 well simulated the spatial pattern of precipitation, while NHRCM05 did not (Figure 7). The spatial correlation coefficient of precipitation in NHRCM02 and NHRCM05 with ground-based stations is 0.76 and −0.95, respectively. The negative correlation coefficient of NHRCM05 suggests that less than 5 km scale topography strongly affects local precipitation there. The size of the basin corresponds to that of a grid box of MRI-AGCM, and MRI-AGCM cannot capture the spatial pattern of precipitation in the basin. GSMaP has a correlation of 0.4, but the absolute precipitation is almost the same at the eight stations due to 0.1° horizontal resolution. This shows the benefit of the high horizontal resolution of NHRCM02.
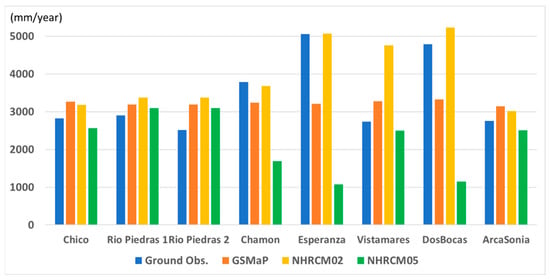
Figure 7.
Comparison of annual precipitation at eight stations in upper Chagres River Basin among four datasets: ground observations, GSMaP, NHRCM02, and NHRCM05.
Overestimation at Vistamares in NHRCM02 is probably due to the complexity of the topography, which cannot be represented even at 2 km since the maximum and minimum annual precipitation in the eight grids surrounding Vistamares varies from about 2900 to 5000 mm. It may be enhanced due to climatological time-scale gridpoint storms fixed with the complexity of the topography.
MRI-AGCM has a smaller bias than NHRCM05, although NHRCM05 has finer horizontal resolution and uses the lateral boundary conditions obtained from MRI-AGCM (Figure 4). MRI-AGCM’s annual precipitation biases averaged over Panama were negative at −44.9 mm/year and the smallest of the three models (Table 4). The spatial correlations of MRI-AGCM and NHRCM02 were similar and higher than that of NHRCM05. The seasonal changes in Panama in MRI-AGMC were similar to those in NHRCM02 (Figure 5). The temporal correlation between MRI-AGCM and CRU was 0.95 for AGCM, the highest of the three models (Table 5). The range of annual precipitation amount was smaller for MRI-AGCM than NHRCMs but larger than GSMaP (Figure 6). Only NHRCM02 replicated the small-scale precipitation distribution in the complex terrain (Figure 7). Therefore, NHRCM02 reproduced many characteristics of precipitation as well as MRI-AGCM did.
3.3. Uncertainty in Precipitation Dataset
There are uncertainties in various precipitation datasets []. The annual climatological precipitation in Panama varies from 2501 to 2924 mm/year []. GSMaP used in this study showed the largest annual climatological precipitation of 3185 mm/year. The range of annual precipitation is large, and the choice of dataset affects the reproducibility. The biases in NHRCMs become larger than those shown in Table 4 and Table 5 when another dataset is used.
The geographic distribution of precipitation seems too smooth (Figure 4a) when we consider the topography in Panama (Figure 1), because orographic precipitation produces small-scale distribution. This is primarily the horizontal resolution of GSMaP. The spatial correlation of NHRCMs will be higher than that of MRI-AGCM when a precipitation dataset with a horizontal resolution higher than GSMaP is used.
The range of annual precipitation of GSMaP at each grid is small in comparison with the ranges of the three models (Figure 6). This is also due to the insufficient horizontal resolution of GSMaP. The spatial variability of precipitation is distinct in a mountainous area of the Panama Canal catchment []. Therefore, the horizontal resolution of a precipitation dataset may affect the reportability of precipitation, especially for finer horizontal resolution of models such as NHRCMs.
Another uncertainty in precipitation datasets stems from the specific time period, since precipitation has large variabilities in time. NHRCMs and GSMaP have no overlap period; the former period is 1981 to 2000, while the latter period is 2001 to 2010. The mean climatological precipitation was compared between the two periods using precipitation in CRU TS. The ratio of annual precipitation of the former to the latter is 1.03. The maximum monthly precipitation ratio is 1.19 in November, while the minimum is 0.95 in October. These differences allow us to compare climatological precipitation between the two reference periods.
4. Conclusions
We used an inner nested grid with spacing of 2 and 5 km to run NHRCMs for a 20-year integration of the current climate. As the grid size becomes finer, NHRCMs have smaller biases. NHRCM02 has small biases that are geographically distributed in Panama, and the area average over the country is minimal. NHRCM02 did a better job of simulating surface air temperature than NHRCM05, and the spatial horizontal resolution did not affect the biases and RMSE, but did affect the spatial correlation.
NHRCM02 simulated annual mean precipitation better than NHRCM05, probably due to a convection-permitting model without a convection scheme, such as the Kain and Fritsch scheme. The spatial correlations of NHRCM02 were slightly higher than those of NHRCM05. The seasonal changes of precipitation were well simulated in both models.
MRI-AGCM had good replicability of precipitation similar to NHRCM02 and outperformed NHRCM05. This suggests that 5 km horizontal resolution is not suitable for simulating climate in Panama and 2 km is required for correct simulation. The difference between NHRCM02 and NHRCM05 is whether it is a convection-permitting model or not, or, in other words, whether the convection scheme is switched on or not, which may play an important role in replicability. The range of annual precipitation in GSMaP at each grid is small compared with the three models. Therefore, the horizontal resolution of a precipitation dataset may affect the reportability of precipitation, especially for models with finer horizontal resolution such as NHRCMs. NHRCMs tend to simulate geographic precipitation too finely to compare with GSMaP. Therefore, the horizontal resolution of a precipitation dataset may affect the reportability of precipitation, especially for models with finer horizontal orientation such as NHRCMs.
There are many challenging topics for simulation of the current climate with a regional climate model in Panama as well as all over the world []. For example, the climatological aspect of the diurnal cycle in the tropics is a key phenomenon to be replicated in regional climate models []. The replicability of extreme events [,,,,] in the current climate is an important feature in climate modeling, along with the replicability of climates. We expect impact assessment researchers and decisionmakers to make use of the NHRCM to analyze the details of projected global warming and related climate changes around Panama.
Author Contributions
Conceptualization, R.P. and T.N.; methodology, R.P., N.N.I., H.S. and T.N.; software, N.N.I. and H.S.; validation, R.P., N.N.I., H.S. and T.N.; resources, R.P. and T.N.; writing—original draft preparation R.P. and T.N.; writing—review and editing, R.P., N.N.I., H.S. and T.N.; visualization, N.N.I. All authors have read and agreed to the published version of the manuscript.
Funding
R.P. had scientific support from SENACYT through projects FID-2016-275 and EIE-2018-16, and through the Sistema Nacional de Investigación (SNI) of SENACYT. R.P. visited MRI with support from the Exchange Program for Research Institutions in Developing Countries of the Japanese Ministry of Land, Infrastructure, Transport and Tourism. T.N. received funds and support from the JSPS KAKENHI Grant Numbers-in-Aid for Specially Promoted Research (grant numbers 20K12154, 16H06291, and 21H05002) and support from Theme C of the TOUGOU program (JPMXD0717935498), funded by the Japanese Ministry of Education, Culture, Sports, Science and Technology.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author for. The data are not publicly available due to the size of data produced under ongoing research program.
Acknowledgments
The authors acknowledge administrative support provided by the Universidad Tecnológica de Panamá. We thank the editor and reviewers for their time and constructive comments, which have helped improve our manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sasaki, H.; Kurihara, K.; Takayabu, I.; Uchiyama, T. Preliminary experiments of reproducing the present climate using the non-hydrostatic regional climate model. SOLA 2008, 4, 25–28. [Google Scholar] [CrossRef]
- Sasaki, H.; Murata, A.; Hanafusa, M.; Oh’izumi, M.; Kurihara, K. Reproducibility of present climate in a non-hydrostatic regional climate model nested within an atmosphere general circulation model. SOLA 2011, 7, 173–176. [Google Scholar] [CrossRef]
- Fábrega, J.; Nakaegawa, T.; Pinzón, R.; Nakayama, K.; Arakawa, O.; SOUSEI Theme-C Modeling Group. Hydroclimate projections for Panama in the 21st century. Hydrol. Res. Lett. 2013, 7, 23–29. [Google Scholar] [CrossRef]
- Nakaegawa, T.; Kitoh, A.; Kusunoki, S.; Murakami, H.; Arakawa, O. Hydroclimate change over central America and the Caribbean in a global warming climate projected with 20-km and 60-km mesh MRI atmospheric general circulation models. Pap. Meteorol. Geophys. 2014, 65, 15–33. [Google Scholar] [CrossRef][Green Version]
- Nakaegawa, T.; Kitoh, A.; Murakami, H.; Kusunoki, S. Maximum 5-day rainfall total and the maximum number of consecutive dry days over central America in the future climate projected by an atmospheric general circulation model with three different horizontal resolutions. Theor. Appl. Climatol. 2014, 116, 155–168. [Google Scholar] [CrossRef]
- Pinzón, R.E.; Hibino, K.; Takayabu, I.; Nakaegawa, T. Virtual experiencing future climate changes in Central America with MRI-AGCM: Climate analogues study. Hydrol. Res. Lett. 2017, 11, 106–113. [Google Scholar] [CrossRef]
- Kusunoki, S.; Nakaegawa, T.; Pinzón, R.; Sanchez-Galan, J.E.; Fábrega, J.R. Future precipitation changes over Panama projected with the atmospheric global model MRI-AGCM3.2. Clim. Dyn. 2019, 53, 5019–5034. [Google Scholar] [CrossRef]
- Karmalkar, A.V.; Bradley, R.S.; Diaz, H.F. Climate change in Central America and Mexico: Regional climate model validation and climate change projections. Clim. Dyn. 2011, 37, 605–629. [Google Scholar] [CrossRef]
- Poleo, D.; Vindas, C.; Stoltz, W. Comparación y evaluación de diferentes esquemas de parametrización de cúmulos con WRF EMS aplicadas al caso del huracán otto. Tóp. Meteorol. Oceanogr. 2017, 16, 28–40. [Google Scholar] [CrossRef][Green Version]
- Sierra-Lorenzo, M.; Bezanilla-Morlot, A.; Centella-Artola, A.; León-Marcos, A.; Borrajero-Montejo, I.; Ferrer-Hernández, A.; Salazar-Gaitán, J.; Lau-Melo, A.; Picado-Traña, F.; Pérez-Fernández, J. Assessment of different WRF configurations performance for a rain event over Panama. Atmos. Clim. Sci. 2020, 10, 280–297. [Google Scholar] [CrossRef]
- Kitoh, A.; Ose, T.; Kurihara, K.; Kusunoki, S.; Sugi, M.; KAKUSHIN Team-3 Modeling Group. Projection of changes in future weather extremes using super-high resolution global and regional atmospheric models in the KAKUSHIN Pro- gram: Results of preliminary experiments. Hydrol. Res. Lett. 2009, 3, 49–53. [Google Scholar] [CrossRef]
- Mizuta, R.; Oouhi, K.; Yoshimura, H.; Noda, A.; Katayama, K.; Yukimoto, S.; Hosaka, M.; Kusunoki, S.; Kawai, H.; Nakagawa, M. 20 km-mesh global climate simulations using JMA-GSM model—Mean climate state. J. Meteorol. Soc. Jpn. 2006, 84, 165–185. [Google Scholar] [CrossRef]
- Ito, R.; Nakaegawa, T.; Takayabu, I. Comparison of regional characteristics of land precipitation climatology projected by an MRI-AGCM multi-cumulus scheme and multi-SST ensemble with CMIP5 multi-model ensemble projections. Prog. Earth Planet. Sci. 2020, 7, 77. [Google Scholar] [CrossRef]
- Yoshimura, H.; Mizuta, R.; Murakami, H. A spectral cumulus parameterization scheme interpolating between two convective updrafts with semi-Lagrangian calculation of transport by compensatory subsidence. Mon. Weather Rev. 2015, 143, 597–621. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. A one-dimensional entraining/detraining plume model and its application in convective parameterization. J. Atmos. Sci. 1990, 47, 2784–2802. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. A hierarchy of turbulence closure models for planetary boundary layers. J. Atmos. Sci. 1974, 31, 1791–1806. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. An improved Mellor–Yamada level-3 model with condensation physics: Its design and verification. Bound. Layer Meteorol. 2004, 112, 1–31. [Google Scholar] [CrossRef]
- JMA. Outline of the Operational Numerical Weather Prediction at the Japan Meteorological Agency. March 2007. Available online: http://www.jma.go.jp/jma/jma-eng/jma-center/nwp/outline2007-nwp/index.htm (accessed on 10 November 2021).
- Yabu, S.; Murai, S.; Kitagawa, H. Clear-sky radiation scheme. Rep. Numer. Predict. Div. 2005, 51, 53–64. (In Japanese) [Google Scholar]
- Kitagawa, H. Radiation processes. Rep. Numer. Predict. Div. 2000, 46, 16–31. (In Japanese) [Google Scholar]
- Hirai, M.; Sakashita, T.; Kitagawa, H.; Tsuyuki, T.; Hosaka, M.; Oh’izumi, M. Development and validation of a new land surface model for JMA’s operational global model using the CEOP observation dataset. J. Meteorol. Soc. Jpn. 2007, 85, 1–24. [Google Scholar] [CrossRef]
- Hirai, M.; Oh’izumi, M. Development of a new land-surface model for JMA-GSM. In Extended Abstract of 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction; American Meteorological Society: Tokyo, Japan, 2004; Available online: https://ams.confex.com/ams/84Annual/webprogram/Paper68652.html (accessed on 10 November 2021).
- Ishii, M.; Shouji, A.; Sugimoto, S.; Matsumoto, T. Objective analyses of sea-surface temperature and marine meteorological variables for the 20th century using ICOADS and the Kobe collection. Int. J. Climatol. 2005, 25, 865–879. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef] [PubMed]
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Nakagawa, K.; Iwanami, K.; et al. Global precipitation map using satellite-borne microwave radiometers by the GSMaP project: Production and validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Kubota, T.; Aonashi, K.; Ushio, K.; Shige, S.; Takayabu, Y.N.; Kachi, M.; Arai, Y.; Tashima, T.; Masaki, T.; Kawamoto, N.; et al. Global satellite mapping of precipitation (GSMaP) products in the GPM era. In Satellite Precipitation Measurement; Levizzani, V., Kidd, C., Kirschbaum, D.B., Kummerow, C.D., Nakamura, K., Turk, K.J., Eds.; Springer: Berlin, Germany, 2020. [Google Scholar] [CrossRef]
- Nakaegawa, T.; Pinzon, R.; Fabrega, J.; Cuevas, J.A.; De Lima, H.A.; Cordoba, E.; Nakayama, K.; Lao, J.I.B.; Melo, A.L.; Gonzalez, D.A.; et al. Seasonal changes of the diurnal variation of precipitation in the upper Río Chagres basin, Panamá. PLoS ONE 2019, 14, e0224662. [Google Scholar] [CrossRef] [PubMed]
- Takayabu, I.; Ishizaki, N.N.; Nakaegawa, T.; Sasaki, H.; Wongseree, W. Potential of representing the diurnal cycle of local-scale precipitation in northeastern Thailand using 5-km and 2-km grid regional climate models. Hydrol. Res. Lett. 2021, 15, 1–8. [Google Scholar] [CrossRef]
- Chan, S.C.; Kendon, E.J.; Fowler, H.J.; Blenkinsop, S.; Roberts, N.M.; Ferro, C.A.T. The value of high-resolution met office regional climate models in the simulation of multihourly precipitation extremes. J. Clim. 2014, 27, 6155–6174. [Google Scholar] [CrossRef]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of near-real-time precipitation estimates from satellite observations and numerical models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Nakaegawa, T.; Arakawa, O.; Kamiguchi, K. Investigation of climatological onset and withdrawal of the rainy season in panama based on a daily gridded precipitation dataset with a high horizontal resolution. J. Clim. 2015, 28, 2745–2763. [Google Scholar] [CrossRef]
- Prein, A.F.; Rasmussen, R.; Stephens, G. Challenges and advances in convection-permitting climate modeling. Bull. Am. Meteorol. Soc. 2017, 98, 1027–1030. [Google Scholar] [CrossRef]
- Croce, P.; Formichi, P.; Landi, F. Evaluation of current trends of climatic actions in Europe based on observations and regional reanalysis. Remote Sens. 2021, 13, 2025. [Google Scholar] [CrossRef]
- Forzieri, G.; Bianchi, A.; E Silva, F.B.; Herrera, M.A.M.; Leblois, A.; LaValle, C.; Aerts, J.C.; Feyen, L. Escalating impacts of climate extremes on critical infrastructures in Europe. Glob. Environ. Chang. 2018, 48, 97–107. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).