A Gaussian Process Method with Uncertainty Quantification for Air Quality Monitoring
Abstract
:1. Introduction
2. Background Knowledge
2.1. Gaussian Processes
2.2. Neumann Series Approximation
3. Uncertainty Quantification in Gaussian Processes
3.1. Uncertainty in Measurements
3.2. Uncertainty in Hyperparameters
3.3. Derivatives Approximation with Neumann Series
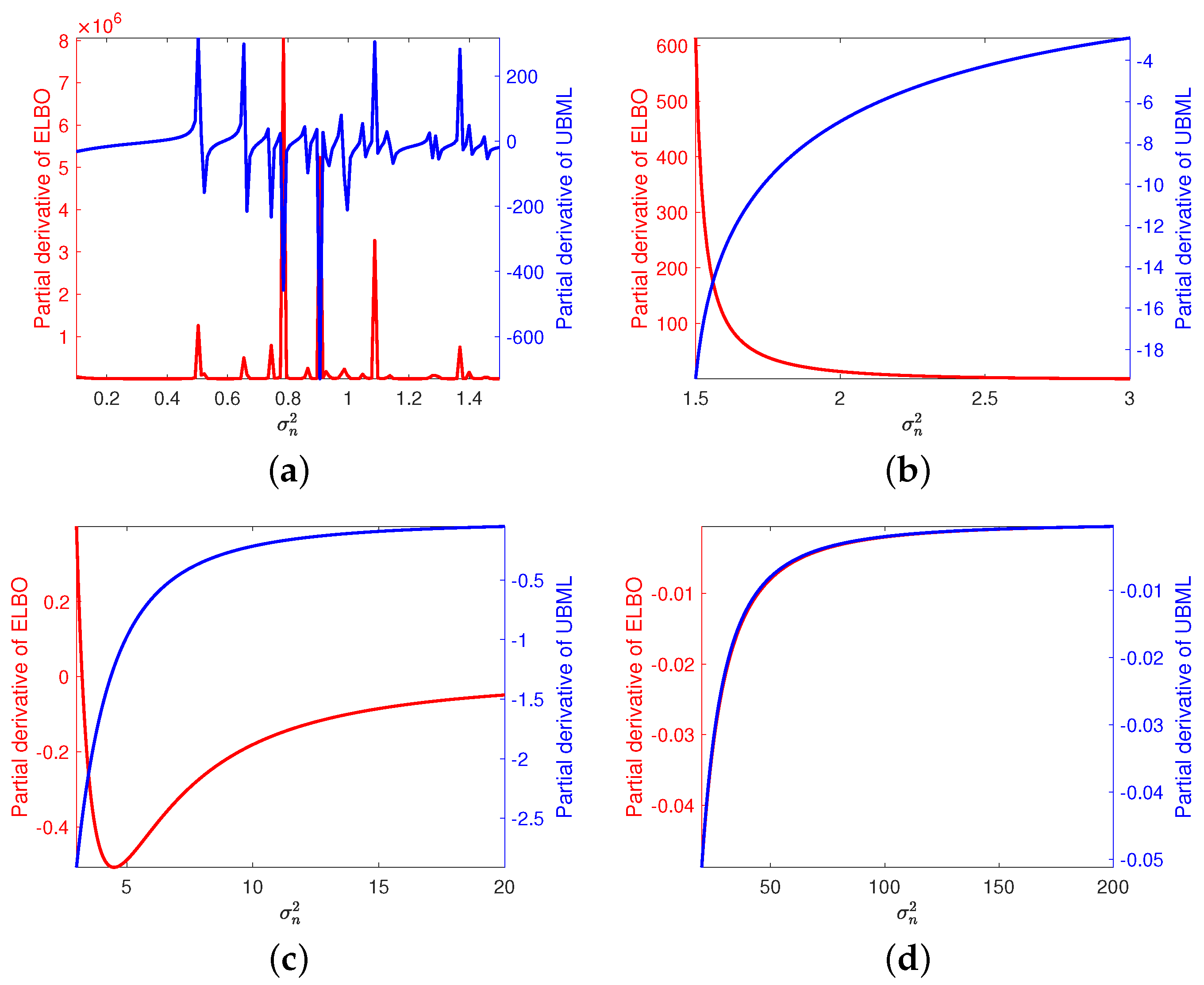
3.4. Impacts of Noise Level and Hyperparameters on ELBO and UBML
4. Experiments and Analysis
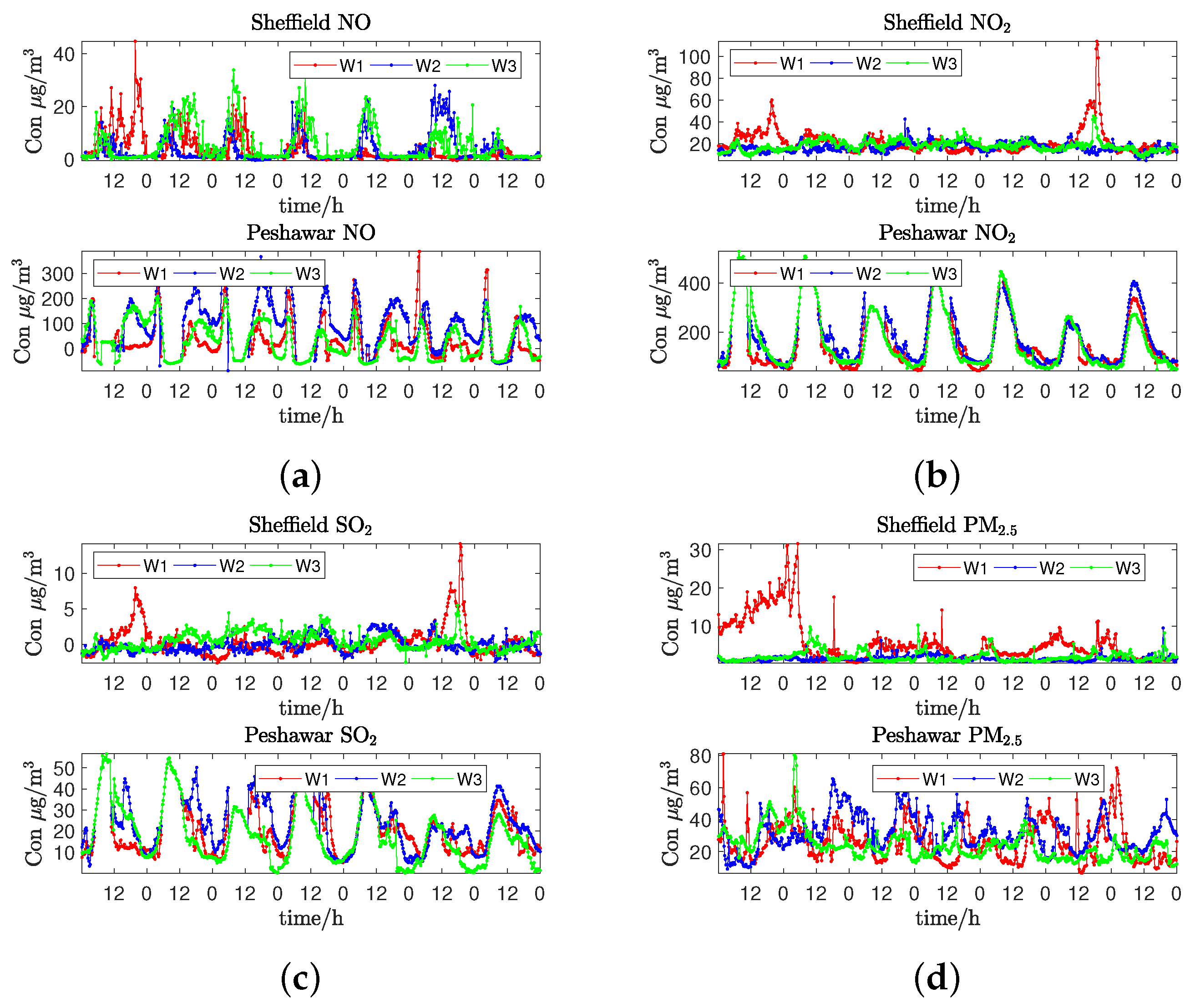
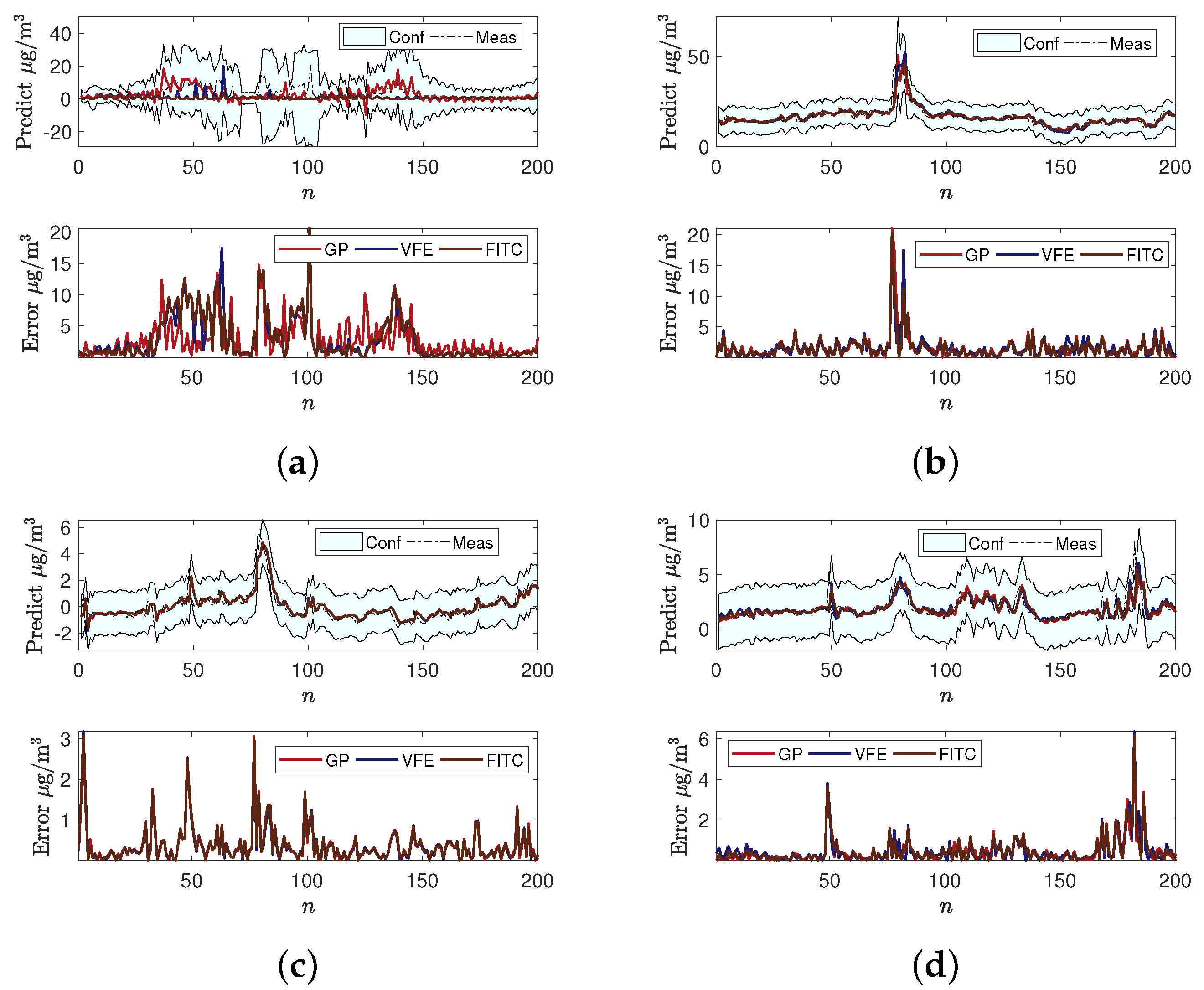
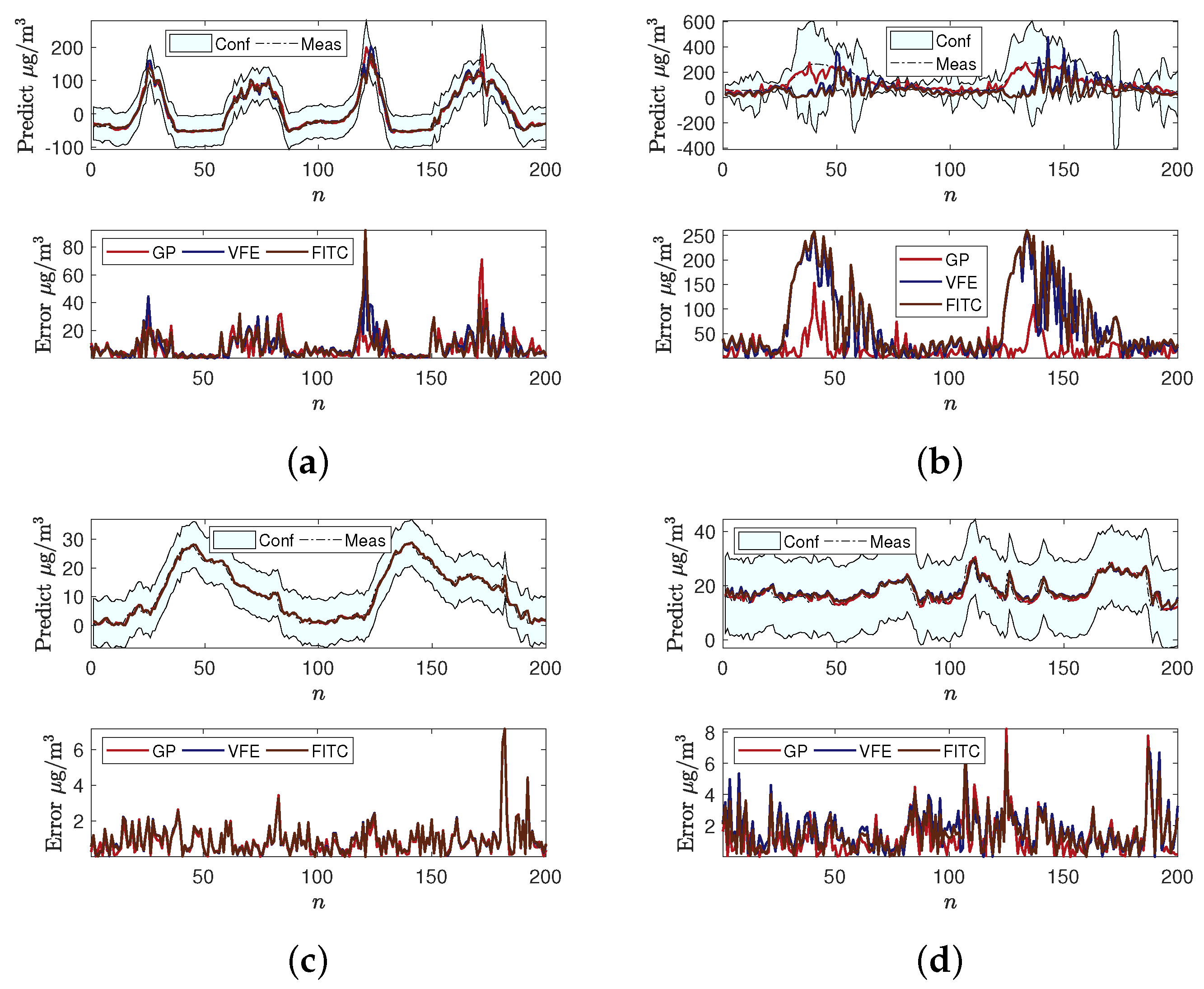
4.1. Air Quality Prediction
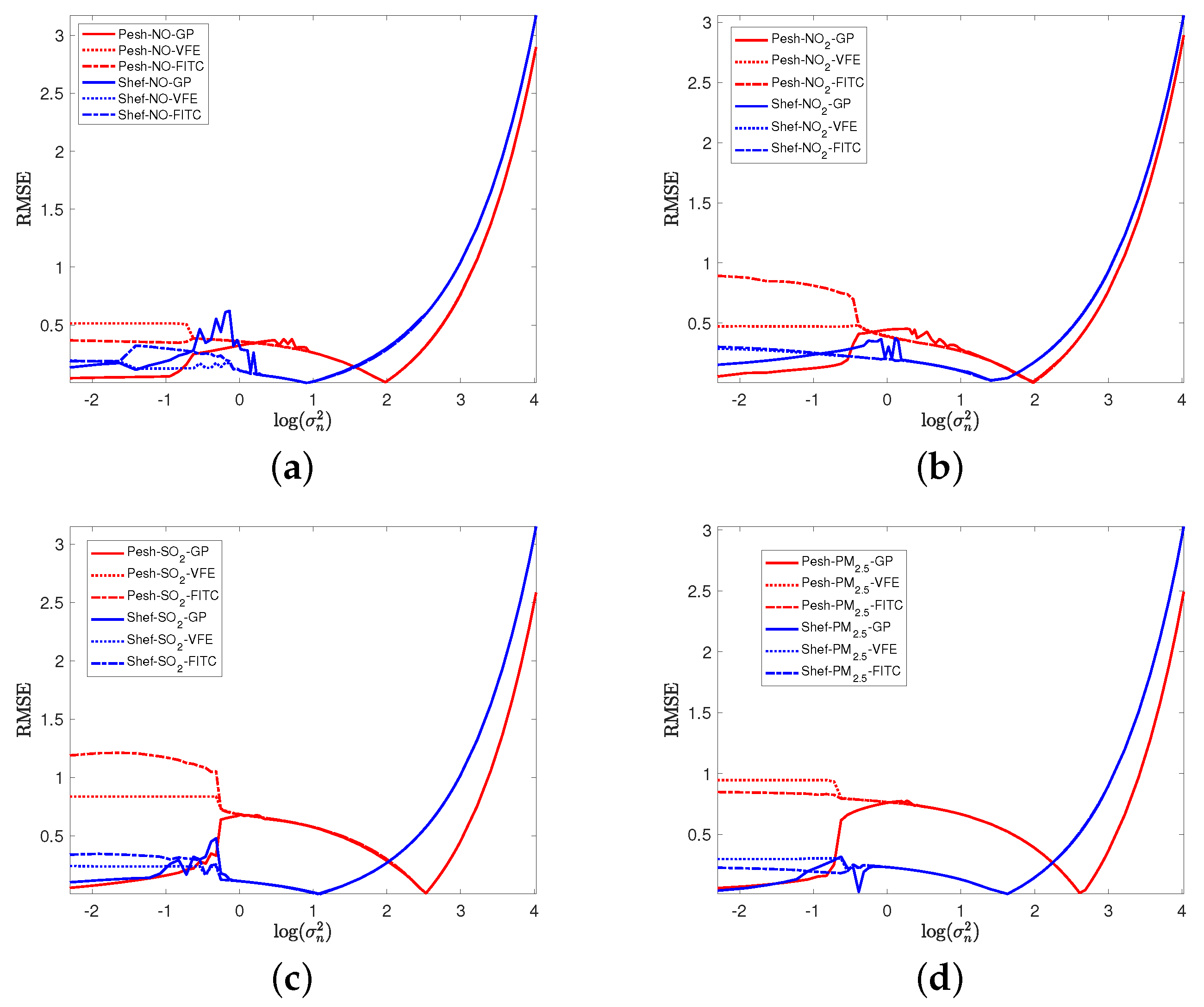
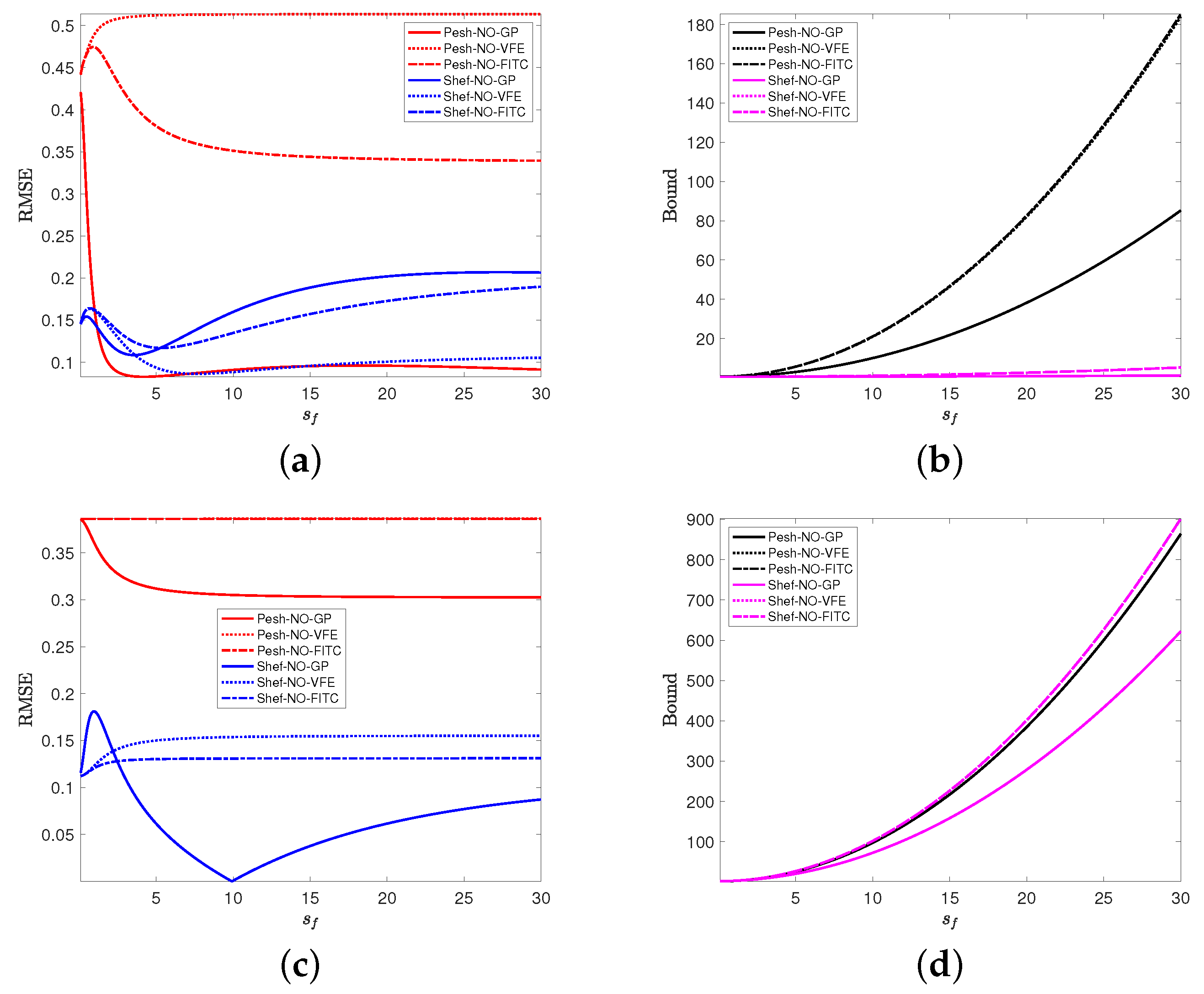
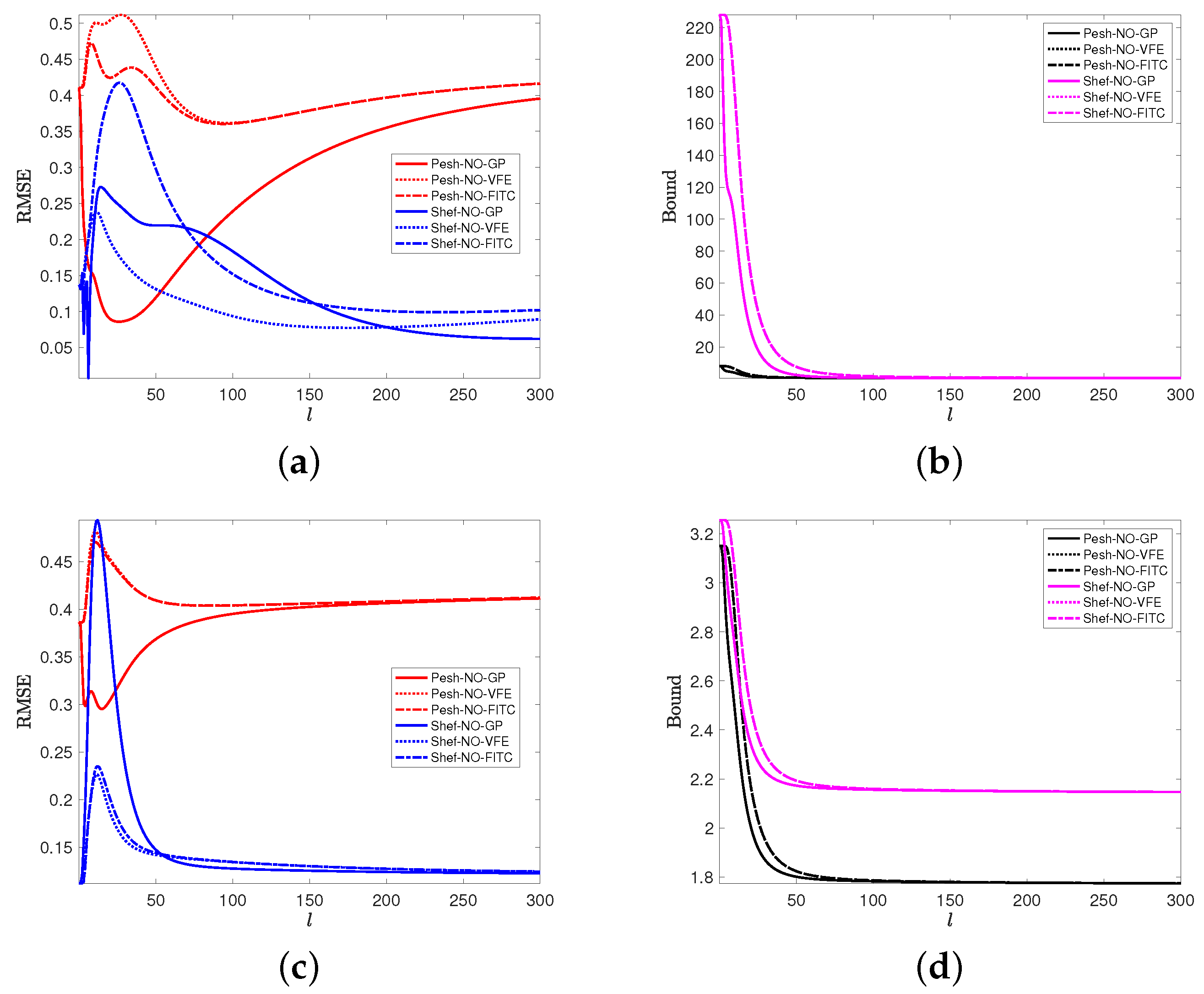
4.2. Impacts of Measurement Noise Level and Hyperparameters
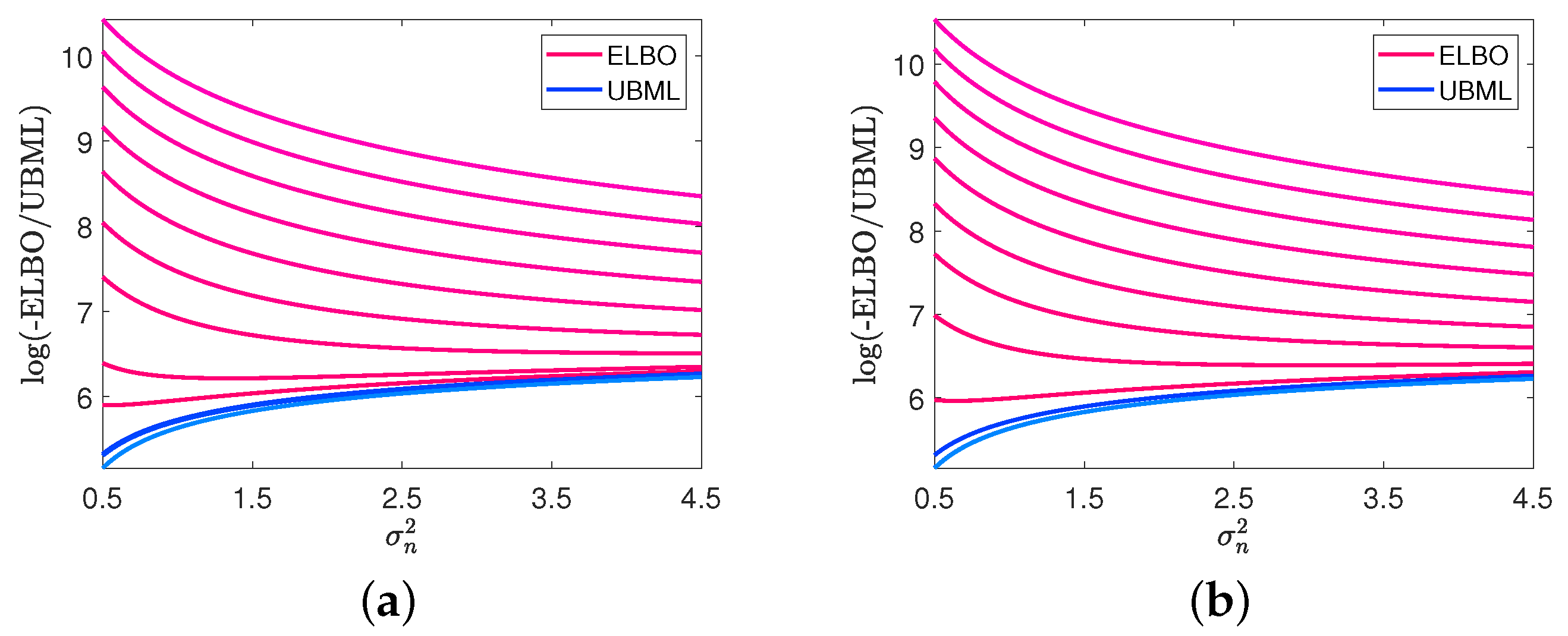
4.3. Impacts of Noise Level on ELBO and UBML
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Data Collection
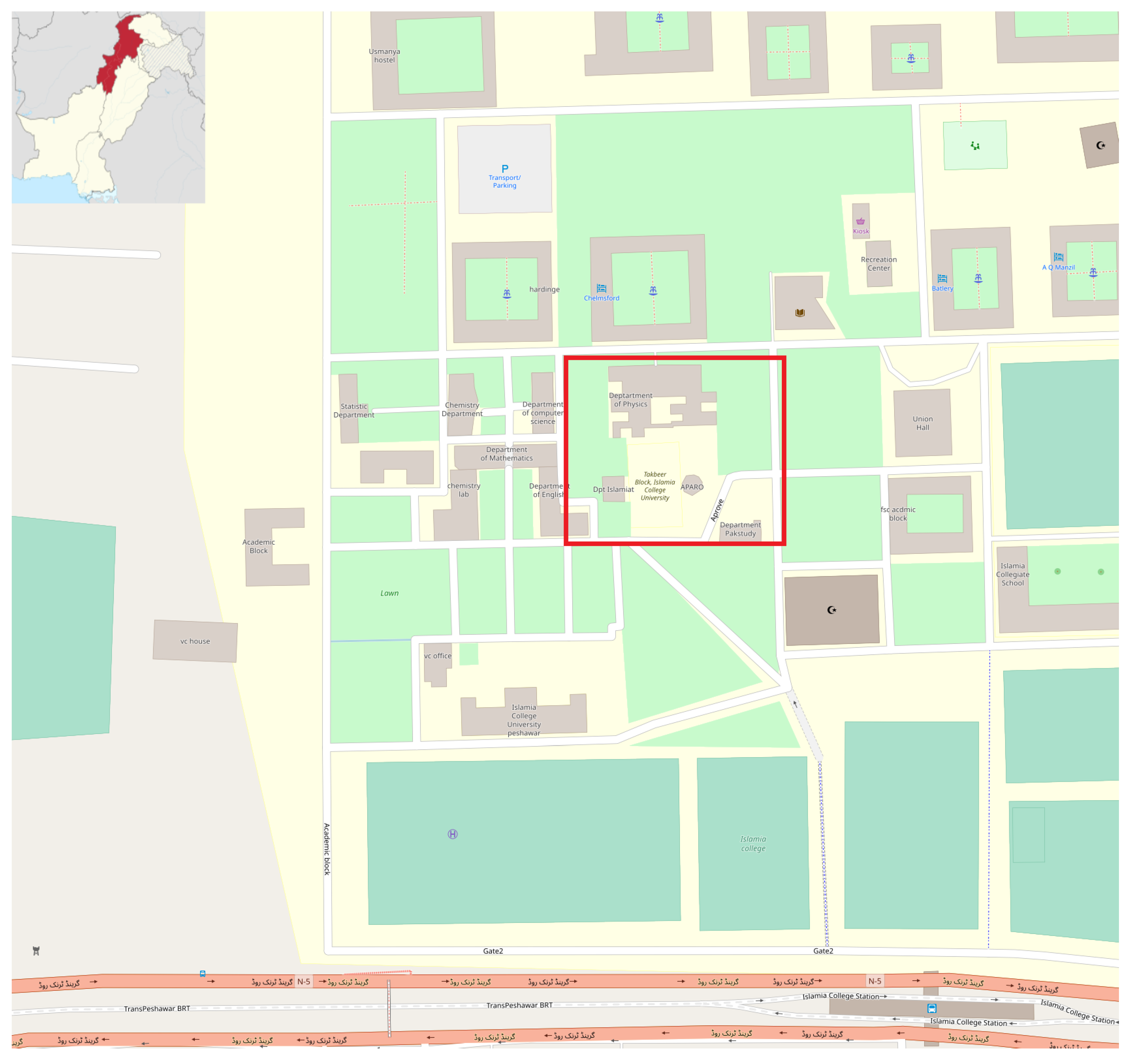
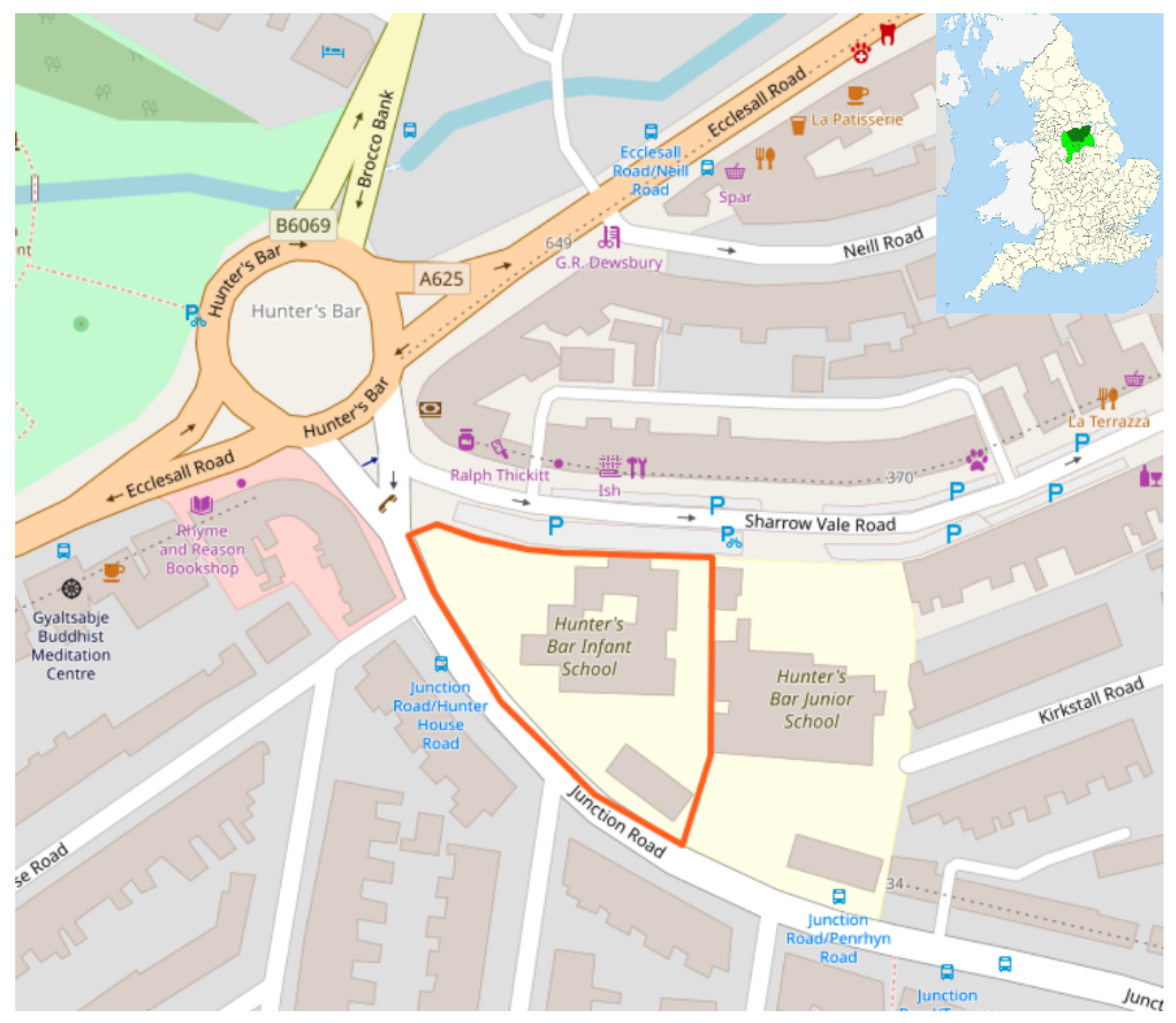
Appendix B. The WHO Concentration Criteria for Pollutants
- WHO
| Nitrogen Dioxide | Annual Mean | 1-h Mean |
|---|---|---|
- WHO
| Sulfur Dioxide | 24-h Mean | 10-min Mean |
|---|---|---|
- WHO and
| Particulate Matter | Annual Mean | 24-h Mean |
|---|---|---|
- WHO
| Ozone | 8-h Mean |
|---|---|
Appendix C. Approximated Derivatives of SE Kernel
References
- WHO. WHO Global Ambient Air Quality Database (Update 2018); World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Landrigan, P.J. Air pollution and health. Lancet Public Health 2017, 2, e4–e5. [Google Scholar] [CrossRef] [Green Version]
- WHO. Health Effects of Particulate Matter: Policy Implications for Countries in Eastern Europe, Caucasus and Central Asia (2013); World Health Organization Regional Office for Europe: Copenhagen, Denmark, 2013. [Google Scholar]
- Chen, H.; Kwong, J.C.; Copes, R.; Tu, K.; Villeneuve, P.J.; Van Donkelaar, A.; Hystad, P.; Martin, R.V.; Murray, B.J.; Jessiman, B.; et al. Living near major roads and the incidence of dementia, Parkinson’s disease, and multiple sclerosis: A population-based cohort study. Lancet 2017, 389, 718–726. [Google Scholar] [CrossRef]
- Khreis, H.; de Hoogh, K.; Nieuwenhuijsen, M.J. Full-chain health impact assessment of traffic-related air pollution and childhood asthma. Environ. Int. 2018, 114, 365–375. [Google Scholar] [CrossRef] [PubMed]
- Improving Air Quality in the Tackling Nitrogen Dioxide in Our Towns and Cities; UK Overview Document; Department for Environment, Food & Rural Affairs and Department for Transport: London, UK, 2017.
- Rai, A.C.; Kumar, P.; Pilla, F.; Skouloudis, A.N.; Di Sabatino, S.; Ratti, C.; Yasar, A.; Rickerby, D. End-user perspective of low-cost sensors for outdoor air pollution monitoring. Sci. Total Environ. 2017, 607, 691–705. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, T.; Bergin, M.H.; Sutaria, R.; Tripathi, S.N.; Caldow, R.; Carlson, D.E. Gaussian process regression model for dynamically calibrating and surveilling a wireless low-cost particulate matter sensor network in Delhi. Atmos. Meas. Tech. 2019, 12, 5161–5181. [Google Scholar] [CrossRef] [Green Version]
- Shen, J. PM2.5 concentration prediction using times series based data mining. City 2012, 2013, 2014–2020. [Google Scholar]
- Silibello, C.; D’Allura, A.; Finardi, S.; Bolignano, A.; Sozzi, R. Application of bias adjustment techniques to improve air quality forecasts. Atmos. Pollut. Res. 2015, 6, 928–938. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Lin, K.; Pai, P.; Yang, S. Forecasting concentrations of air pollutants by logarithm support vector regression with immune algorithms. Appl. Math. Comput. 2011, 217, 5318–5327. [Google Scholar] [CrossRef]
- Mao, Y.; Lee, S. Deep Convolutional Neural Network for Air Quality Prediction. J. Phys. Conf. Ser. 2019, 1302, 032046. [Google Scholar] [CrossRef]
- Garriga-Alonso, A.; Rasmussen, C.E.; Aitchison, L. Deep convolutional networks as shallow gaussian processes. arXiv 2018, arXiv:1808.05587. [Google Scholar]
- Bai, L.; Wang, J.; Ma, X.; Lu, H. Air pollution forecasts: An overview. Int. J. Environ. Res. Public Health 2018, 15, 780. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, P.; Mihaylova, L.; Munir, S.; Chakraborty, R.; Wang, J.; Mayfield, M.; Alam, K.; Khokhar, M.F.; Coca, D. A computationally efficient symmetric diagonally dominant matrix projection-based Gaussian process approach. Signal Process. 2021, 183, 108034. [Google Scholar] [CrossRef]
- Burt, D.R.; Rasmussen, C.E.; Van Der Wilk, M. Rates of Convergence for Sparse Variational Gaussian Process Regression. arXiv 2019, arXiv:1903.03571. [Google Scholar]
- Liu, H.; Ong, Y.S.; Shen, X.; Cai, J. When Gaussian process meets big data: A review of scalable GPs. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4405–4423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; Number 3; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Wu, M.; Yin, B.; Wang, G.; Dick, C.; Cavallaro, J.R.; Studer, C. Large-scale MIMO detection for 3GPP LTE: Algorithms and FPGA implementations. IEEE J. Sel. Top. Signal Process. 2014, 8, 916–929. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Wang, B. How priors of initial hyperparameters affect Gaussian process regression models. Neurocomputing 2018, 275, 1702–1710. [Google Scholar] [CrossRef] [Green Version]
- Zhu, D.; Li, B.; Liang, P. On the matrix inversion approximation based on Neumann series in massive MIMO systems. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 1763–1769. [Google Scholar]
- Titsias, M. Variational learning of inducing variables in sparse Gaussian processes. In Proceedings of the Artificial Intelligence and Statistics, Clearwater Beach, FL, USA, 16–18 April 2009; pp. 567–574. [Google Scholar]
- Snelson, E.; Ghahramani, Z. Sparse Gaussian processes using pseudo-inputs. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, Canada, 4–9 December 2006; pp. 1257–1264. [Google Scholar]
- WHO. Air Quality Guidelines for Particulate Matter, Ozone, Nitrogen Dioxide and Sulphur Dioxide. Global Update 2005; World Health Organization: Geneva, Switzerland, 2006. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Mihaylova, L.; Chakraborty, R.; Munir, S.; Mayfield, M.; Alam, K.; Khokhar, M.F.; Zheng, Z.; Jiang, C.; Fang, H. A Gaussian Process Method with Uncertainty Quantification for Air Quality Monitoring. Atmosphere 2021, 12, 1344. https://doi.org/10.3390/atmos12101344
Wang P, Mihaylova L, Chakraborty R, Munir S, Mayfield M, Alam K, Khokhar MF, Zheng Z, Jiang C, Fang H. A Gaussian Process Method with Uncertainty Quantification for Air Quality Monitoring. Atmosphere. 2021; 12(10):1344. https://doi.org/10.3390/atmos12101344
Chicago/Turabian StyleWang, Peng, Lyudmila Mihaylova, Rohit Chakraborty, Said Munir, Martin Mayfield, Khan Alam, Muhammad Fahim Khokhar, Zhengkai Zheng, Chengxi Jiang, and Hui Fang. 2021. "A Gaussian Process Method with Uncertainty Quantification for Air Quality Monitoring" Atmosphere 12, no. 10: 1344. https://doi.org/10.3390/atmos12101344
APA StyleWang, P., Mihaylova, L., Chakraborty, R., Munir, S., Mayfield, M., Alam, K., Khokhar, M. F., Zheng, Z., Jiang, C., & Fang, H. (2021). A Gaussian Process Method with Uncertainty Quantification for Air Quality Monitoring. Atmosphere, 12(10), 1344. https://doi.org/10.3390/atmos12101344












