Abstract
Continued developments in instrumentation and modeling have driven progress in monitoring methane (CH4) emissions at a range of spatial scales. The sites that emit CH4 such as landfills, oil and gas extraction or storage infrastructure, intensive livestock farms account for a large share of global emissions, and need to be monitored on a continuous basis to verify the effectiveness of reductions policies. Low cost sensors are valuable to monitor methane (CH4) around such facilities because they can be deployed in a large number to sample atmospheric plumes and retrieve emission rates using dispersion models. Here we present two tests of three different versions of Figaro® TGS tin-oxide sensors for estimating CH4 concentrations variations, at levels similar to current atmospheric values, with a sought accuracy of 0.1 to 0.2 ppm. In the first test, we characterize the variation of the resistance of the tin-oxide semi-conducting sensors to controlled levels of CH4, H2O and CO in the laboratory, to analyze cross-sensitivities. In the second test, we reconstruct observed CH4 variations in a room, that ranged from 1.9 and 2.4 ppm during a three month experiment from observed time series of resistances and other variables. To do so, a machine learning model is trained against true CH4 recorded by a high precision instrument. The machine-learning model using 30% of the data for training reconstructs CH4 within the target accuracy of 0.1 ppm only if training variables are representative of conditions during the testing period. The model-derived sensitivities of the sensors resistance to H2O compared to CH4 are larger than those observed under controlled conditions, which deserves further characterization of all the factors influencing the resistance of the sensors.
1. Introduction
Anthropogenic CH4 emissions comprise 30% of the global source of this greenhouse gas, and are from various economic sectors [1]. Oil, gas and coal sector sources are localized in space, going from point scale (e.g., a single well, a compressor) to area sources (e.g., a refinery, a gas extraction field). The waste sector has area sources for waste-water treatment plants and landfills, although within a site there can be leaky equipment forming point sources.
Numerous campaigns estimated emissions from point and area sources using atmospheric measurements by deploying local dense networks of CH4 instruments at fixed points and using mobile ground-based platforms and aircraft [2,3,4]. The signal from a source in terms of CH4 concentration at a nearby atmospheric measurement location depends on the magnitude of this source, on the wind speed, on the atmospheric turbulence and on the sampling distance. An excess of CH4 mixing ratio going from a few tenth parts per billion (ppb) [5,6] up to several parts per million (ppm) [7] is typically recorded at a downwind distance from the source.
Research class CH4 analyzers such as Cavity Ring Down Spectrometers (CRDS) used for background air monitoring have a precision higher than 1 ppb [8,9] but they are expensive. Such precision is needed to monitor the small CH4 gradients between background stations, on the order of 10 to 50 ppb, that are used as an input of atmospheric inversion models to diagnose large-scale emissions [10]. The deployment of multiple CRDS instruments in the vicinity of an industrial site for detecting and/or estimating its emissions is however a too costly option on a routine basis, especially when needing a very dense network to ensure precise location and quantification of a fugitive source. This has prompted research to develop low-cost sensors with a precision sufficient to characterize the signal of atmospheric plumes from industrial sites. From typical plume signals that are on the order of more than a ppm, a precision of 0.1 to 0.2 ppm on instantaneous measurements can be deemed to be sufficient for a low cost CH4 sensors. Low cost sensors are more likely to drift with time than CRDS analyzers, but the atmospheric signal used to quantify the emission of an industrial site is the near instantaneous difference between upwind and downwind concentrations [7,11]. Therefore, constraining the drift of upwind and downwind sensors during a few hours to be less than 0.1 to 0.2 ppm would still be sufficient for monitoring CH4 emissions from an industrial site.
Here, we formulate a target precision requirement of 0.1 to 0.2 ppm over a time scale of one hour for CH4 low cost sensors to be deployed on dense networks around an emitting source. This requirement is suitable for detecting variations of CH4 in background air, which are on the order of 0.1 ppm on an hourly time scale, and characterize CH4 conditions upwind from an emitting source. We tested for this requirement solid-state tin-oxide (SnO2) sensors models TGS 2600, TGS 2611-C00 and TGS 2611-E00 manufactured by Figaro®. We performed measurements of room air where CH4 concentration varies from day to day by up to 0.5 ppm above a background value of 1950 ppb. The principle of those sensors is to measure changes in the tin-oxide resistance affected by electron donors in the air to which the tin-oxide is exposed. These sensors are cheap, with a unit cost of about 3 € to 25 € per sensor and they were shown to be sensitive to low CH4 concentrations, thus being potentially suitable for emissions monitoring with a good characterization of background variations and plume amplitudes even for modest sources [3]. On the other hand, low cost sensors are known to drift with time, to be sensitive to other reduced species than CH4 and to factors such as water vapor, pressure and temperature [12]. Therefore, cross sensitivities to these other species must be characterized in order to understand how they impact the retrieval of CH4 from measured variations of resistance.
The first research question addressed in this study is to characterize the cross sensitivities of Figaro® resistances to CH4 versus other factors known to influence the tin-oxide resistance: carbon monoxide (CO), water vapor, pressure and temperature [13]. To address this question, we characterized in a laboratory facility under controlled conditions the resistances of six Figaro® sensors for a range of CH4, CO, temperature and H2O, and examined covariance between their sensitivities, in a first step to diagnose cross-sensitivity effects from non-CH4 related variables.
The second research question is to test whether measurements of low-cost sensors resistance combined with other cross-sensitivity variables allow for the reconstruction of CH4 concentration and its variability to meet our precision requirement of 0.1 to 0.2 ppm, here in the case of CH4 variations around background values of up to 0.5 ppm. To address this second question, we analyzed time series of Figaro® resistances continuously recorded by six Figaro® sensors and CH4 measured with a high-precision CRDS analyzer for room air CH4 variations, during a period of 47 days. This study is the first step to assess the potential of Figaro® sensors for measuring CH4 concentrations close to current atmospheric levels; with small co-variations of water vapor and of a limited number of cross-sensitive species. On previous studies [12] and on initial tests showing that there is a non-linear relation between CH4, resistances and other variables affecting resistances such as temperature and H2O mole fraction, we chose to construct and apply a machine learning model to reconstruct the true CH4 concentration from the CRDS by using as predictors the resistances of the Figaro® sensors, as well as H2O mixing ratio, carbon monoxide, temperature and pressure recorded by other sensors. The model is trained to optimally reconstruct the true CH4 signal during a given period, and its results are evaluated against an independent subset of the data. The results are systematically evaluated varying the training and test periods, the number of ambient variables, and the addition of more than one type of Figaro® sensor resistance to reconstruct the true CH4 time series.
2. Experimental Set-Up
2.1. Measurement of Low-Cost Sensors Sensitivities to CH4, CO and H2O
The cross sensitivities of the resistance of Figaro® sensors types TGS 2600, TGS 2611-C00, and TGS 2611-E00 were measured in the laboratory (measurements conducted at LSCE, Saclay, France). The sensors were incorporated into a low-cost sensor logger that featured a Raspberry Pi 3B+ single-board computer and Raspbian operating system, using bespoke software (coded in Python). Figaro resistances for types TGS 2600, TGS 2611-C00 and TGS 2611-E00 were measured as voltages using a voltage divider [14,15] with precision resistor (5 kΩ, tolerance, temp coeff), and measured as single-ended voltages using an A/D board (ADCPiPlus, ABElectronics) with 17-bit resolution across the 5.06 V range. Air temperature and relative humidity were measured using a Sensirion SHT75 digital sensor which has an accuracy of ±0.3 °C and ±1.8%RH respectively and a repeatability of ±0.1 °C and ±0.1 %RH respectively. Air pressure was measured using a digital Bosch BMP180 pressure sensor (Adafruit, BMP180 breakout module), which has an accuracy of ±0.12% across the range 950-1050 hPa. All sensors were mounted in a 120 mL stainless steel/glass sealed chamber (EIF 3S1NRGL), which provided a gas inlet and outlet and an air-tight port for the sensor cable (see Figure 1a). All measurements were made at 0.5 Hz and stored on the Raspberry Pi’s SD card.
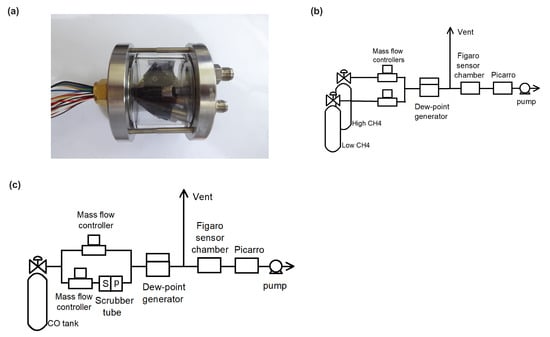
Figure 1.
(a) Picture showing the sealed chamber with six Figaro® sensors of different types, and temperature and pressure sensors. (b) Scheme of the CH4 and H2O cross-sensitivity measurement set up. (c) Scheme of the CO and H2O cross-sensitivity measurement set up.
To assess the sensitivities of the sensor resistances to CH4 and H2O, we used air from two high pressure dry air cylinders, with a high CH4 mole fraction of 8.999 ppm CH4 and 0.08 ppm CO, and a low CH4 mole fraction of 1.900 ppm CH4 and 0.11 ppm CO, respectively. Air from the two cylinders was mixed using two mass flow controllers (see Figure 1b) to create six levels of CH4 of 1.9, 2.985, 4.04, 6.17, 7.58 and 8.985 ppm in dry air. This range covers CH4 mole fractions recorded in the atmosphere from background sites up to typical excess found in plumes from industrial sites [16]. The air with different CH4 concentration was humidified by a dew-point generator (Licor, LI-610) in order to get four H2O mixing ratios of 0.65, 1, 1.5 and 2.5% at stable atmospheric pressure and temperature. The experiment set up is illustrated in Figure 1b.
In the experiment, the dew point generator was set to one of the four H2O mixing ratios. At each change of H2O mixing ratio, the Figaro® reading was given 40 or more minutes to stabilize at the lowest CH4 level, before CH4 was increased in steps at 20 min intervals. Only the last 5 min’ data of each step was used. Data from the sensors and the Picarro CRDS were merged and converted to one-minute medians.
The Figaro® sensors’ sensitivity to CO and H2O was measured in a similar manner, using a single high pressure dry air cylinder containing 1.5 ppm CO and 2 ppm CH4. The sample line was split into two branches, one equipped with Sofnocat 514, a hydrophobic CO oxidizing agent, to remove CO without changing the humidity. The air from the two lines was combined in different ratios thanks to dedicated mass flow controllers in order to produce CO mole fractions of 0, 0.07, 0.14, 0.29, 0.57, 0.87, 1.17 and 1.50 ppm, at H2O mixing ratios of 0, 1.0 and 2.3% thanks to a dew point generator (Licor, LI-610) operated at constant temperature and pressure. The experimental configuration is shown in Figure 1c. The logging equipment and sampling procedure were the same as for the first experiment.
In this experiment, a Picarro G2401 CRDS was used as a reference high-precision instrument for CH4, CO2, CO and H2O mole fraction. The CH4 precision of a Picarro CRDS analyzer in dry air is below 1 ppb [6,17] at instrument data acquisition rate (0.3 Hz) within the atmospheric range. CRDS calibration drift over time is usually better than 1 ppb CH4 per month [6].
2.2. Measurements of Room Air with Low Cost Sensors and CRDS
The resistances of six Figaro® sensors exposed to CH4 variability in indoor air were monitored during 47 days (from 27 April to 12 June of 2018) in an air-conditioned room, with three versions of Figaro® sensors: TGS 2600, TGS 2611-C00 and TGS 2611-E00. Details of the data acquisition are as described in the previous section. Reference data was again provided by a Picarro G2401 gas analyzer. Air temperature and relative humidity was measured using a DHT22 digital sensor (Aosong Electronics) which has an accuracy of ±0.5 °C and ±0.5% RH respectively. The sensors were installed in a semi-open enclosure from which the Picarro CRDS took its intake, thus sampling the same air that the Figaro® sensors.
3. Modeling CH4 from Figaro Resistances and Other Predictors
Low-cost sensors, generally, present a non-linear dependency on environmental variables causing cross-sensitivities [3]. There is no mathematical model of the relationship between the resistances and CH4, given the dependency of resistances on other environmental variables (CO, H2O, pressure and temperature). The analytical problem thus remains nonlinear and multi-dimensional. Therefore, an Artificial Neural Network model (ANN) was chosen to reconstruct CH4 from observed time series of resistances, CO, H2O, pressure and temperature. We chose a Multi Layer Perceptron (MLP) which is a classical supervised-based algorithm [18]. MLP models are generally considered to be the reference among machine learning methods because several theoretical results prove their ability as a universal approximator [19,20], capable of learning from examples. For our problem, the advantages of a machine learning model such as MLP are the following: (i) it does not require any prior knowledge about I/O dependencies, (ii) it is able to construct arbitrary functions from noisy data [21], it makes no assumption on the distribution of data [22], and (iii) could produce reasonable outputs from entries that are not present in the learning set, i.e., generalization [23]. Over the past decade, deep networks such as MLP have demonstrated superior performance over a wide variety of tasks, including function approximation. Recently, MLP have been proven to be more efficient than inverse linear methods in reconstructing the signals of trace gas species from low-cost sensors [24].
In a MLP model, unknown parameters (i.e., architecture and connection weights) are adjusted in order to obtain the best match between a dataset of model inputs (Figaro resistances, H2O, CO, Temperature and Pressure) and corresponding outputs (Figaro CH4). The connection weights are adjusted by using iterative learning processes such as the backpropagation [18] or several algorithms that have been developed in order to achieve a good learning of the model (i.e., Stochastic gradient descent, Adam, etc., [25]). In our study, we chose to use a quasi-Newton method, the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm, which provide the optimal MLP weights in a limited number of iterations (300) due to its relatively fast convergence [23]. For our study, the architecture of the MLP producing the best results was found to be a four-layer network with 5 units in the input layer, 14 and 19 units with tanh activation function in the hidden layer and 1 unit with a linear activation function in the output layer. All models were constructed using the library scikit-learn [26] on python 3.6.
The generalization error, also called test error, is the expected value of the error produced by new inputs [27]. This error is obtained from the performance of the MLP to match an independent test dataset. A central challenge of function approximation by MLPs is the risk of underfitting and overfitting [27]. Underfitting is referred to a high training error when, because of an inconvenient architecture or because of training inputs that are not explanatory enough for example, the MLP does not manage to efficiently fit the training data set. In our case, the risk of underfitting is mitigated by using a sufficiently complex model. Overfitting happens when the MLP learns features from the training data set, e.g., noise or biases, that are not relevant and do not generalize well to a different data set. To reduce the risk of overfitting we used the weight decay regularizer or L2 Norm that drives excess weights (weights of the network that does have little or no influence in the model) to values close to zero [23]. We use also an early stopping technique that constantly monitors the error produced by the model with respect to an independent validation data set (validation error) during the learning process. When the validation error starts increasing, the training process is stopped in order to moderate the generalization error [21,27]. The best MLP model was selected as the one producing the lowest validation error from the results of many tests in which the number of neurons of the hidden layer were varied (see Section 4.4).
4. Results
4.1. Sensitivities of Low-Cost Sensors
To account for the systematic error of the Figaro® resistances sensitivities to CH4 and H2O, caused by the different CO levels in the two CH4 target tanks, the sensors’ sensitivities to CO and H2O were separately measured and used to correct the data. In Figure 2, for each Figaro® type, the upper plot shows the measured voltage across the load resistor for changing CO mole fraction, at each of the three humidity levels 0, 1 and 2.3% mole fraction. The lower plot shows how much the Figaro® voltages increased above the baseline voltage, where the baseline is the voltage at zero CO and is a function of the humidity.
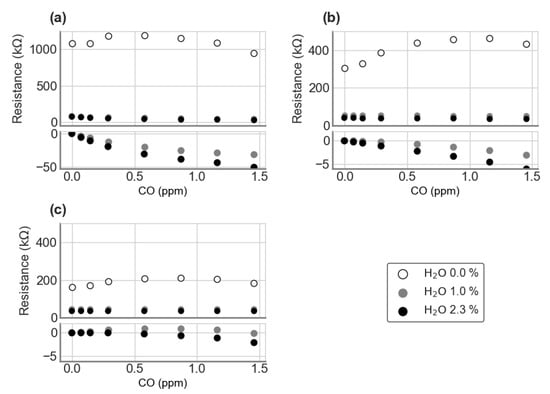
Figure 2.
Measured sensitivity of Figaro® sensors (a) TGS 2600, (b) TGS 2611-C00 and (c) TGS 2611-E00 to CO, at different humidity levels. Upper plots show the measured resistance, while lower plots show the contribution to the resistance due to CO.
For each sensor type, these data were fitted with a multivariate quadratic model of the form:
The voltage contribution due to CO was calculated as , where f is the fitted value. This model was used to correct the CH4-H2O voltage data to zero CO by subtracting the CO contribution from each point. These corrected values are show in Figure 3, converted to resistances.
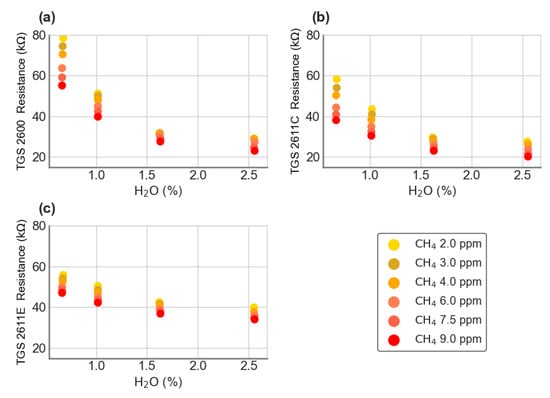
Figure 3.
Resistances of Figaro® sensors (a) TGS 2600, (b) TGS 2611-C00 and (c) TGS 2611-E00 calculated from load voltages corrected for the cross-sensitivity to CO.
The range of CH4 mole fraction was 2 to 9 ppm, thus being larger than in the room air experiment where CH4 varied only from 1.95 to 2.5 ppm. The range of H2O mole fraction was from 0.5% to 2.5%, which is comparable to that of the room air experiment. In general, the sensors resistance presents a strong sensitivity to H2O and a small sensitivity to CH4. The TGS 2611-C00 is slightly the most sensitive sensor to CH4, with a slope of −1.85 kΩ/ppm CH4 at 1% H2O.
4.2. Data Pre-Processing for MLP Model
The data pre-processing scheme for the MLP model is summarized in Figure 4. We filtered the input and output data by removing NaN values and observations by an unknown source in the room that resulted in clear spikes of the TGS resistances. This resulted in 49,103 observations at a resolution of 1-min or 34 days of measurements. For each of the independent input variables, a low pass Savitzky-Golay Filter has been applied to remove high frequencies corresponding to fluctuations of sensor measurements (1 min variations) and a median filter has been used to remove the effect produced by the low pass filter on gaps [28]. These filters have been not applied to the output data because the CH4 observations provided by the Picarro are not characterized by high frequency variations and because we wanted to keep the output data used for the training of the MLP as close as possible to the original data set. Figure A1 shows a comparison between the raw signal and the filtered signal for one day of data. Because input variables have different units and scales that could affect the relative sensitivities of the MLP with respect to each variable, they were normalized with a robust scaler which considers the statistical dispersion of the observations by, removing the median and scaling the data according to a quantile range [29]. We used this scaler in order to prevent that outliers could affect the relative importance of each variable in the model, with that filtered dataset, we created two sub-sets of data to train and evaluate the MLP model. A training set always contained 70% of the entire dataset, the remaining 30% being the cross-validation dataset.
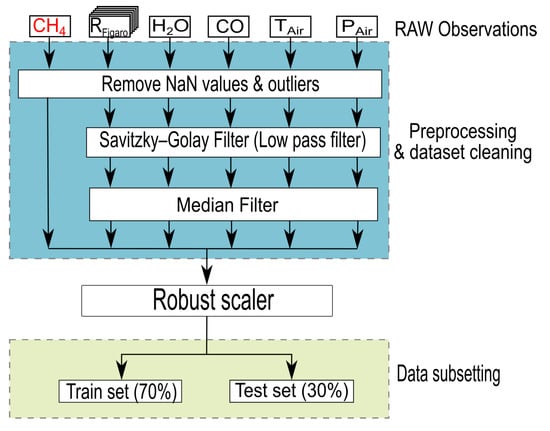
Figure 4.
Data preprocessing and sub setting for the training and cross-validation of the Multi-Layer Perceptron model.
4.3. Room Air Measurements
In Figure 5 are shown the smoothed time series on a time step of 1 min after a low pass filtering (see Section 4.2) of room CH4 from the CRDS analyzer, resistances from each Figaro® CO from CRDS, room temperature of the DHT22 sensor, and pressure of the BMP180 sensor. H2O mole fraction (in %) was computed from relative humidity and temperature of the DHT22 sensor and atmospheric pressure of the BMP180 sensor using Rankine’s formula:
where RH is the relative humidity in %, P the atmospheric pressure in Pa and T the temperature in °C.
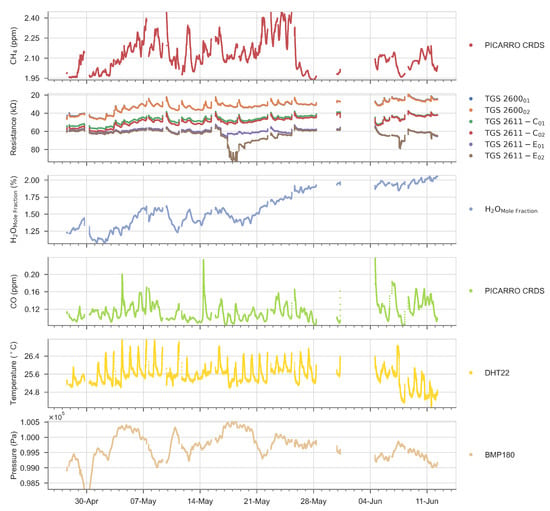
Figure 5.
Time series of gas mole fractions, Figaro® sensors’ resistances, temperature and pressure in room air during the room air experiment. The data was filtered as explained in Section 4.2.
The large spikes in the variations of temperature is due to the room air conditioning regulation system. Table 1 summarizes the principal statistics of the dataset.

Table 1.
Summary of the statistics for each variable in the dataset.
Before applying MLP models to reconstruct the (CRDS) reference CH4 time series, we analyzed the partial correlations between resistances and other predictors. The correlation matrix is show in Figure 6. This first analysis of linear correlations does not capture non-linear sensitivities of Figaro® resistances to CH4 and other predictors, but it is performed in order to identify the most influential predictors of CH4 (i.e., those showing a higher positive or negative correlation with CH4), the sign of the sensitivities (i.e., the sign of the correlation coefficient) and how stable is the influence of different predictors on CH4 during the 47 days duration of the experiment (variability of correlations in time between 3-h intervals during the measurement period). The data in Figure 6 shows the upper triangular part the correlation matrix between variables, and in the lower triangular part the standard deviation of the correlation computed on bins of 3 days previously smoothed on 3-h intervals (the temporal resolution at which MLP is trained and applied). A stationary correlation would give a standard deviation close to zero. The Figaro® resistances presented weak partial correlations with CH4, the target variable, with r values of 0.25 and −0.27 for TGS 2600, 0.015 and −0.0098 for TGS 2611-C00, and −0.14 and 0.099 for TGS 2611-E00 types, respectively. Other variables also presented weak correlations with CH4 of −0.17 (H2O mole fraction), 0.16 (CO), 0.21 (T) and −0.18 (P), respectively. Correlations between of the resistances of two versions of sensors of the same type were strong for TGS 2600 (1) and TGS 2611-C00 (0.98) but not for TGS 2611-E00 (0.3). There were also appreciable strong correlations, positive and negative, between resistances of sensors from different types, in particular between TGS 2600 and TGS 2611-C00 types. The resistance of TGS 2611-E00 showed a weak correlation with TGS 2600 and a stronger one with TGS 2611-C00 (Figure 6). Again, as for the correlations with CH4, we found a clear difference in the correlations of resistances from TGS 2600 and TGS 2611-C00 types on one hand, and from TGS 2611-E00 on the other. The resistances of all sensors were negatively correlated with H2O on one version, with r values of. −0.31, −0.61 and −0.32 for version 2 of TGS 2600, TGS 2611-C00 and TGS 2611-E00 types, respectively. However, version 1 of the same sensors was instead positively correlated with H2O (Figure 6). We also found weak correlations of the resistances with CO, but still larger in absolute values than the correlations with CH4.
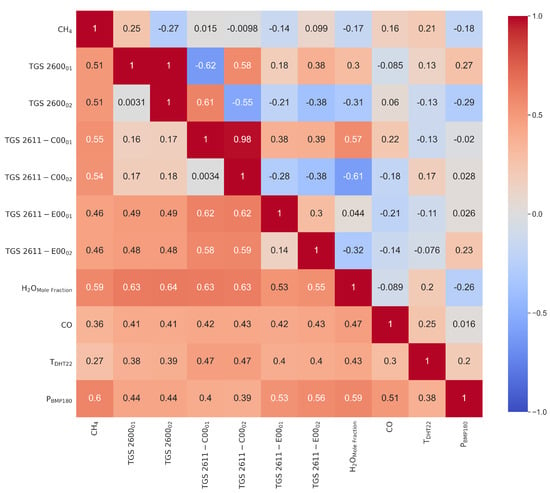
Figure 6.
Partial correlation (r) matrix (upper triangular) and standard deviation of correlation for bins of 3 days previously smoothed at 20 min scale on 3 consecutive hours (lower triangular).
From the stability analysis (see lower triangular in Figure 6) we observe that most of the r (correlation) values are under 0.5 meaning that most of the data are consistent during a window of 3 days. We also noted relatively high values of r on the two versions of the TGS 2611-E00 with the TGS 2611-C00 (0.59), the H2O with the two versions of TGS 2600 (0.64) and with the two versions of TGS 2611-C00 (0.63), high values are also present on the pressure with the CH4 (0.6) and with the H2O (0.59).
We conclude from this first analysis of correlations that, although there are correlations, between CH4 and the resistances of TGS 2600 and TGS 2611 sensors, such correlations are small and vary with time, which will make it challenging to reconstruct CH4 time series with linear models, and justifies a priori our choice of a MLP model. Same conclusions have been drawn from previous studies [3,24].
4.4. Evaluation of the MLP Model
To assess the influence of the choice of the training period in the performance of the MLP, we defined over the whole data set 50 sliding training periods which contain 70% of the observations. The corresponding test sets contain thus 30% of the observations and the results associated to the fits of the 50 MLPs are described in Figure 7.
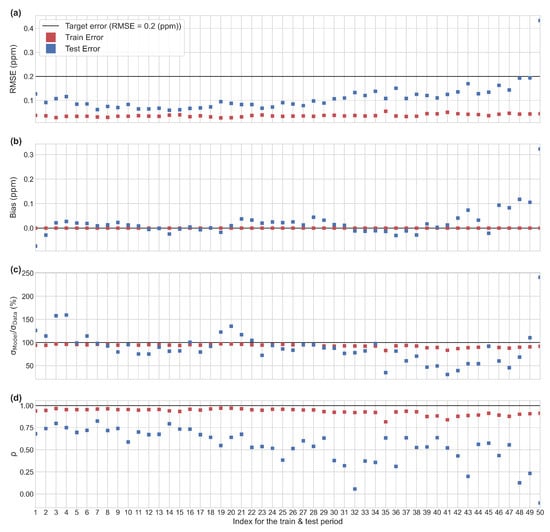
Figure 7.
Performance of the MLP model for the 50 training and test periods. (a) RMSE on hourly data. (b) Mean bias. (c) Ratio between the spread of the predicted outputs () and the spread of the true values (). (d) Correlation coefficient between the predicted outputs and the reference values.
The evaluation of the performance was based on 4 metrics: the RMSE on hourly data, the mean bias, the ratio between the spread of the predicted outputs from the model and the spread of the true values () and the correlation coefficient between the output of the model and the true values. On Figure 8 are presented two examples of the performance of the MLP with different test periods, selected to represents a bad (period 50) and a good test (period 7) performance.
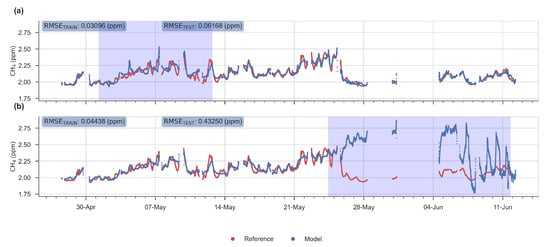
Figure 8.
Time series showing a good (a) and a bad (b) performance of the MLP model for the test period 7 and 50 respectively. In red, time series of the reference instrument, and in blue the reconstructed signal given by the MLP model. White background: observations used for the training stage. Blue background: observations used for the test stage.
In general, the RMSE, on the test set, was less than 0.2 ppm, except for one period in the end of the time series (50th). This value of RMSE meets our precision requirement target of 0.2 ppm posed in the introduction. The periods of lowest errors are periods 5 to 20 (from 30 April to 29 May), and we can observe that the worst case corresponds to a model learned only for low values of H2O and tested on a test set which contains much higher values of this input variable. Likewise, many low temperature values are observed in the test set, while these values are missing in the learning set. In the best case, on the contrary, the ranges of variation of the input variables are narrower in the test set than in the set used for learning. (see Figure A3 and Figure A4). A better performance in the model was observed when using the TGS 2611-C00 sensor. From the test periods 31 to 50 we observed a larger increase of the test error than in the previous periods, the worst case being test period 50 (RMSE > 0.4 ppm).
Misfits are mostly due to a wrong simulation by the MLPs of the variability and/or the phasing of the data. For the periods 2, 3, 19 to 21 and from 35 to the end of the series, the difference between the standard deviations of the data and the MLP can reach 50% which points out a incorrect reconstruction of the amplitudes of the test data sets by the corresponding MLPs. For all the periods, the MLPs face difficulties to reproduce the phasing of the test data sets: the mean correlation coefficient is indeed of 0.54 and from the periods 30 to the end of the series, the phasing between the MLP and the observations is notably deteriorated (r < 0.5). At the contrary, the MLPs simulate correctly the average values of the data: the mean bias is under 0.1 ppm which represents less than 1% of the average values of the data. This is likely explained by a tendency of the MLP to act as a low-pass filter of the data: during the process of learning, the weights are indeed adjusted in order to minimize the misfits, over the entire training data set, between the MLP outputs and the Picarro CH4 data which thus favors a correction of the misfits for the low frequencies.
In summary, the results of the MLP model point out to several critical aspects. In the first place, the selection of the training period affects the performance of the model to reconstruct CH4, in which the covering of the same range of values in the training and test set is traduced by good performance. The choice of a ‘good’ training period results in higher cross validation scores. In particular, the period of CH4 variation from 30 April to 29 May appears particularly critical and if it is not used for the training, the model cannot extrapolate the CH4 data well (RMSE > 0.4 ppm). An overlapping of the data distribution of the training set and the test set, in the sense of similar variations observed in both sets, increases the performance of the model (see Figure A3 and Figure A4). Secondly, we found that the model cannot reproduce well the magnitude of high frequency anomalies of CH4, but tends to better reproduce the low frequency component of the signal which is consistent with low-pass filter behavior of the MLP described above (see Figure A5).
4.5. Sensitivity of MLP Model to Input Variables
To understand the relative contribution of each input on the MLP model, the sensitivity to the number of inputs and to the number of TGS sensors were calculated and results are shown in Figure 9. For every case we compared the results with a reference model that has as inputs the Figaro TGS 2611-C00 resistance, H2O mole fraction, Air temperature and pressure, and CO, corresponding to our best case from the previous section. For every configuration we trained 50 models in the same way as described in Section 4.4. For all the tests we kept the same MLP architecture of 4 layers with the same number of units for the hidden layers, and compared their performance for training datasets using the root mean square error (RMSE) of hourly data. For an identical architecture, the number of input variables has consequences on the complexity of the model (total number of parameters of the model) and therefore on the overfitting effects already mentioned.
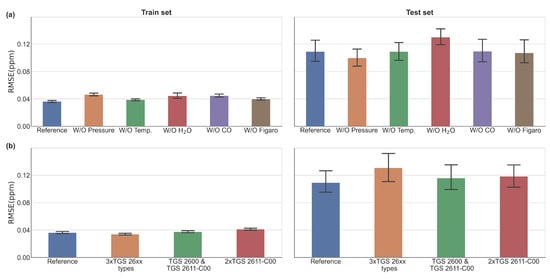
Figure 9.
(a) Comparison of 5 models in which one input has been removed at each time (denoted ‘W/O’) with the reference model that has been built with the resistance data of the Figaro TGS 2611-C00 and the 4 other types of data (Reference). (b) Effect of increasing the number of Figaro® sensors in the model with no modification of the ambient variables in the input. The bar plot represents the mean error for every configuration and the error bar on top is the range of variation over the 50 validation periods.
We observe in Figure 9a that omitting the air pressure results in a better performance on the test set compared with the omission of other variables. On the other hand, omitting H2O decreased the performance on the training periods RMSE increased from 0.036 to 0.046 ppm for the training set, and from 0.12 to 0.13 ppm for the test set. Omitting temperature gave a better performance on the test set, and omitting CO led to no appreciable differences. The Figure 9b shows the effect of increasing the number of Figaro® sensors in the MLP model. For this analysis, the four environmental variables (Temperature, pressure, CO, and water vapor mole fraction) and four different combinations of resistances data from the three types of Figaro® sensors were used to train the MLP with one combination corresponding to the reference model (blue bar). A decrease in the performance (RMSE ∼0.15 ppm) was found in the test set when using resistances from three types of Figaro sensor: the TGS 2600, the TGS 2611-E00 and the TGS 2611-C00, brown bar. Using two versions of the same sensor decreased the MLP performance in the test set (RMSE ∼0.133 ppm for a combination of two TGS 2600 and TGS 2611-C00 and RMSE ∼0.13 ppm for two versions of TGS 2611-C00) in relation to the reference MLP model. For the training set, we found a decrease on the training error when using 3 different types of sensor (RMSE = 0.034 ppm). We found that all the models of this sensitivity test are matching our requirement as presented on Table A1.
Several conclusions can be drawn from those tests using a reduced numbers of predictors. Firstly, the water vapor mole fraction affects significantly the predictive power of the model, and removing this variable produced a larger spread of the test error. This result is consistent with the large sensitivity of resistance to H2O shown in Figure 3 and indicates that this variable should be measured together with Figaro® resistances if using machine-learning models to reconstruct CH4. An interesting result was that when CO is removed from the model predictors, the MLP performance even slightly improved. Using three types of sensor data in the training of the model increased the spread of the test error, that affected the stability of the model, because of the inconsistent information from different sensors, in particular the different behavior of type TGS 2611-E00 compared to the two others. Using data resistances from two versions of the same type of sensor degrades as well the model performance.
In addition to testing the sensitivity of the MLP results to the choice of predictors and sensors type, we analyzed the partial dependence of the target variable CH4 to the marginal effect of each predictor in the reference model with 5 predictors included. The corresponding partial dependence plots were constructed using the scikit-learn package on python 3.6 [26]. The results for the type TGS 2611-C00 are show in Figure 10. In the case of the resistances of Figaro® sensors, we found a negative sensitivity of MLP-reconstructed CH4 to resistances. This result is in qualitative agreement with the negative sensitivities measured experimentally in Figure 3. We could not compare however the values of experimental sensitivities with those inferred by the MLP because the range of CH4 was much larger in the experiments (2 to 9 ppm) than in the room air dataset (2 to 2.5 ppm). Nevertheless, we noticed that the experimental sensitivity shown in Figure 3, ranging from −0.7 to −2.8 kΩ per ppm CH4 over a 7 ppm CH4 is much smaller (about twenty times less) than the sensitivity diagnosed from MLP partial dependence analysis in Figure 10. The reasons for this discrepancy may be due to sensors aging or to an over-estimation by the MLP model. The partial dependence of MLP-reconstructed CH4 to H2O showed a different behavior between ’good’ and the ’bad’ test datasets as seen in the data from Figure 10. For the good training period, the sensitivity to H2O was rather constant and even slightly positive for H2O values going from 1.2% to 1.6%, then a negative sensitivity was found until 1.9%. For the average of all training periods, the H2O sensitivity peaks and declines with a humped shape curve reaching a maximum at 1.6%. The positive sensitivity below 1.6% is consistent with experimental sensitivities of Figure 3, in which the resistance decreases for an increase of H2O and decreases when CH4 increases. Since some values are not or hardly represented in the training set for the worst case (see the comment in Section 4.4 for the variable H2O) the humped-shaped dependence of CH4 to H2O in Figure 10 may be linked to poor MLP learning in certain ranges of values. We found from the partial dependence analysis a positive sensitivity of reconstructed CH4 to CO. For temperature and the pressure, we found a quadratic shaped sensitivity for the worst case, with negative curvature for temperature and positive for pressure.
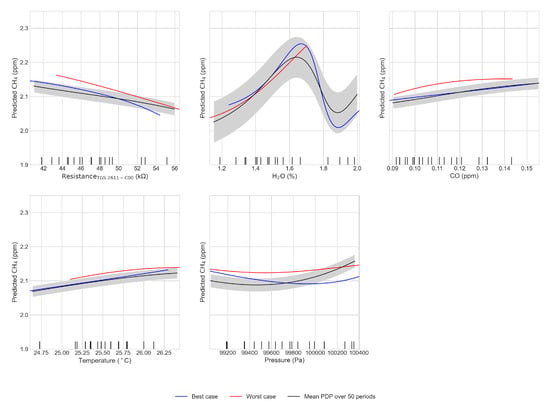
Figure 10.
Partial dependence plot for the best (blue) and worst (red) case and mean Partial dependence plot computed over the 50 periods (black), the shaded gray area is the uncertainty (1) for the 50 periods. The inputs of the model were the Figaro 2611-C00 resistance, water vapor mole fraction, CO, air temperature and pressure. Ticks on the x axes of the figures are the deciles of the input variables.
The bivariate partial dependence plots in Figure 11a show the dependence of the MLP-reconstructed CH4 on the joint values of resistance and the other variables for the best test case (see Figure 11b for the worst case). On this best case, we observe that there is a high dependence to resistance of the MLP-reconstructed CH4 for values of H2O under 1.6%, whereas for values between 1.6% and 1.8% the dependence flattens off. Considering CO and temperature, we found that the MLP model is highly dependent of resistances for values under 0.15 ppm of CO and temperature under 26.5 °C, for the best and the worst cases for CO. Finally, the model seems to be sensitive to pressure when the resistance varies over 48 kΩ and under 44 kΩ.
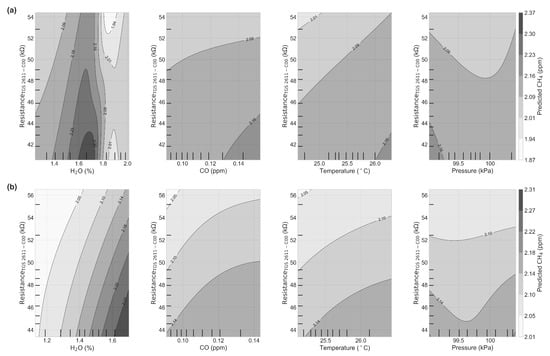
Figure 11.
Bivariate partial dependence plot for the TGS 2611-C00 sensor versus H2O mole fraction, CO, air temperature and pressure. (a) Partial Dependence Plot (PDP) for the model trained in the best case scenario and (b) Partial Dependence Plot (PDP) for the worst case scenario. Ticks on the x and y axes of the figures are the deciles of the input variables.
5. Discussion
Few studies have tried to use machine-learning models to reconstruct the variability and the concentration of greenhouse gases from low cost sensors [30]. In the work of [31,32,32]) several field calibration methods for low cost sensors were explored: Linear and multilinear regression and Artificial Neural Network (ANN), for five trace gases (O3, NO2, NO, CO and CO2) measured by metal oxide, electrochemical and miniaturized infrared sensors over five months. They concluded that the best calibration method was ANN and that the use of different types of sensors could help the ANN to solve the cross sensitivities. Here, we found that only using Figaro® TGS sensors, even from different types, it was not possible to make a good reconstruction of the signal without concurrent measurements of other environmental variables, because the sensors had a high cross sensitivity to water vapor, aggravated by differences on the distribution of the H2O density for the training and test set.
The study of Esposito et al. [33] compared the performance of feed forward neural networks (FFNN) with dynamical neural network (DNN) in the calibration of three trace gases (NOx, NO2 and O3) measured with low cost sensors over five weeks. They found that DNN was significantly more accurate than FFNN in the reconstruction of high variations of concentrations. As explained on Section 3, the high capacity problem in which the more complex models tend to overfit needs to be treated carefully, thus we tested a series of combinations of number of units and number of layers obtaining an architecture of 2 hidden layers the more adapted to this problem, our limited dataset also restraints a more complex model.
Cordero et al. [34] worked on a two-step calibration process of NO2, NO and O3 from low cost sensors. They applied a first multilinear regression considering all the predictors, then the error of the multilinear regression was introduced as an input, in addition to the others predictors, to a supervised machine learning algorithm (Support Vector Machine—SVM, random forest or ANN) to reconstruct the concentration of trace gases. They concluded that globally SVM and ANN performed well in the reconstruction of the concentrations in all the cases over a threshold (40 µg/m3. For data below that threshold, the random forest was the best model to reconstruct the signal. As a universal approximator, we decided to use MLP in our study for the reconstruction of small variations of CH4 measurements at levels around ambient air values, and we did not test the limits of this type of model in presence of high variations of our signal, such as CH4 spikes of several ppm encountered when measuring air at a point nearby an industrial site. This question remains open for a future study with a specific dataset of CH4 that contains spikes.
Casey et al. [24] compared the performance of direct linear models, inverse linear models and ANN models over three months of data of ambient air in a region influenced by oil and gas production. Their main results pointed that the ANN model, when applied to CH4 and CO observations, gave better performance (RMSE = 0.13 ppm over a month) than the direct and inverse linear models, due to the smaller dynamic range from their observations. For our study, a linear model could not be applied due to nonlinear relationships between predictors with the target CH4 signal. With a careful selection of the MLP model, our results indicate that the MLP model provided performances that meet our target requirement of an error of 0.1 to 0.2 ppm for hourly average CH4, except during periods when the distribution of training data was too different from the one of the test data (80% on the last test period of the cross validation). This illustrates the critical aspect for MLP and other machine learning models to use large datasets, with all the space of predictors being covered by training datasets, to reach good cross validation performance.
Eugster et al. [35] conducted a long term evaluation of the Figaro® TGS 2600 over seven years at Toolik Lake in Alaska; they proposed a multilinear model to calibrate the voltage signal from the sensor including other environmental variables such as air temperature and absolute humidity. The calibration methods were assessed under summer and winter conditions and compared their proposed model with an ANN. Eugster et al. [35] found satisfying agreement on 30 min average observations for the multilinear model (R2 = 0.424). They reported a more balanced performance of the ANN on cold conditions (winter), but they not find a substantial difference between their proposed model and the ANN. They concluded that ANN would outperform linear models if other driving variables were included to the model.
Riddick et al. [36] conducted an experiment to investigate the potential of Figaro® TGS 2600 to measure CH4 mixing ratios in ranges between 2 and 10 ppm, assess the long term measurements over 3 months and estimate the emissions from a natural gas point source. Calibration of the sensor was derived from a non linear relationship giving the best agreement with the reference measurements when computing the time averaged concentration with a uncertainty of ±0.01 ppm. The authors observed that reliably measurements of CH4 was in the range of 1.8 to 6 ppm and suggest that calibrations need to be derived for each individual sensor.
From the results of the sensitivity tests to removing predictors one at a time, and the partial dependence plots providing the sensitivities of the MLP modeled CH4 to individual predictors we could observe the importance of the water vapor as a critical input for the models. This is mainly due to the high sensitivity for the TGS sensors to H2O confirmed by our experimental data. Variations of H2O in the field are typically larger than the ones covered by our experiment and they have an important impact on the model’s performance. Refining models to further separate the H2O and CH4 signal will be needed to meet the target error when increasing the range of H2O and CH4 variations in future experiments. For the temperature, pressure and CO we found that those predictors have a lower influence on CH4 in our room air dataset, and for similar type of data, they could be ignored as concurrent measurements. The influence of CO on the model should be studied in depth as well as that of other cross-influencing compounds being electron donors such as ethane, hydrogen or H2S, whose concentrations in industrial environments are likely larger than the ones during our idealized experiments. This is the second critical topic that we should address in our following assessments of low-cost tin-oxide sensors.
6. Conclusions
The theoretical contribution of this study is to demonstrate the potential of Artificial Neural Networks models for the reconstruction of atmospheric CH4 variations based on tin-oxide sensors resistances, within a small CH4 variation range around mean levels similar to current atmospheric concentrations, achieving a target RMSE ≤ 0.2 ppm. The selection of the training and test periods was shown to be a critical factor to obtain good performance, because our dataset was relatively short and some training periods included predictor distributions that strongly differ from that of the test periods. The practical contribution of this study is a detailed characterization of CO and H2O cross influences on tin-oxide sensors resistances, from laboratory tests. We also found that adding different combinations of Figaro tin-oxide sensors versions did not produce better results. Using only the TGS 2611-C00 sensor version led to better results in regard to the others types.
Author Contributions
Conceptualization, R.R.M., D.S. and P.C.; Data curation, O.L. and F.C.; Formal analysis, R.R.M., D.S. and F.C.; Funding acquisition, C.B. and C.J.; Investigation, R.R.M., D.S. and O.L.; Methodology, R.R.M., D.S., C.M., M.R., C.C., G.B. and P.C.; Project administration, C.B., C.J. and P.C.; Resources, O.L. and F.C.; Software, R.R.M., D.S. and F.C.; Supervision, O.L., C.M., M.R., C.C., L.R., G.B., C.B., C.J. and P.C.; Validation, R.R.M., M.R., C.C., L.R., G.B. and P.C.; Visualization, R.R.M. and F.C.; Writing—original draft, R.R.M., C.M. and P.C.; Writing—review & editing, O.L., M.R., C.C., L.R., G.B., C.B., C.J. and P.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Chaire Industrielle Trace grant number ANR-17-CHIN-0004-01 and ICOS-France.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This study did not report any data.
Acknowledgments
This work was supported by the Chaire Industrielle Trace ANR-17-CHIN-0004-01 cofunded by the ANR French national research agency, SUEZ, TOTAL-Raffinage Chimie and THALES ALENIA SPACE and by the ICOS-France research infrastructure program.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
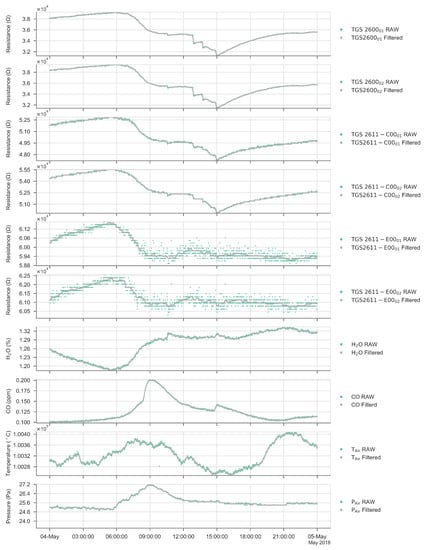
Figure A1.
Comparison between the raw (green) and the filtered signal (gray) over one day.
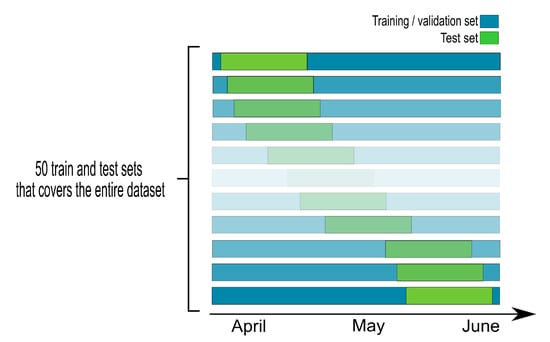
Figure A2.
Diagram showing the process of training and evaluation of the model with 50 training and test sets covering the entire time series.
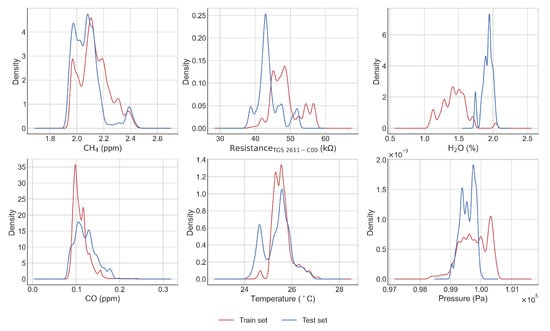
Figure A3.
Density distribution of the training (red) and test (blue) set for the worst case (50).
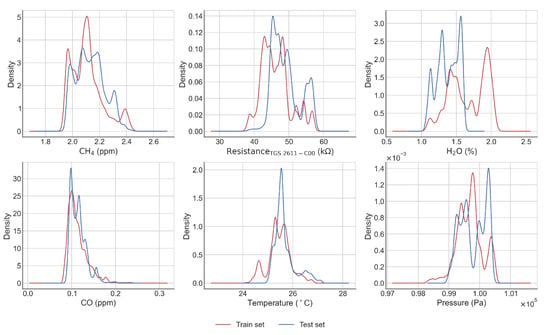
Figure A4.
Density distribution of the training (red) and test (blue) set for the best case (7).
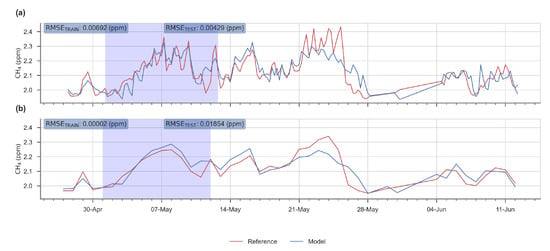
Figure A5.
Output of the model for a smoothed signal of 12 h (a) and 24 h (b).
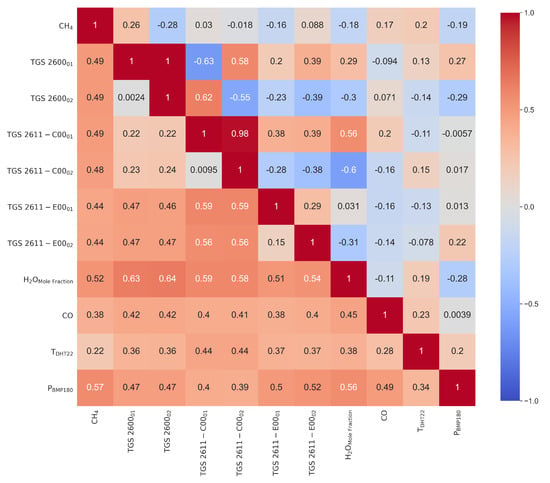
Figure A6.
Partial correlation (r) matrix (upper triangular) and standard deviation of correlation for bins of 3 days previously smoothed at an hourly scale (lower triangular).

Table A1.
Mean MSD and RMSE for the 50 training and test periods of the sensitivity test.
Table A1.
Mean MSD and RMSE for the 50 training and test periods of the sensitivity test.
| Mean MSD () | Mean RMSE (ppm) | ||
|---|---|---|---|
| Reference | 0.001352331 | 0.036774055 | |
| W/O Pressure | 0.002216097 | 0.047075444 | |
| W/O Temperature | 0.001535907 | 0.039190651 | |
| 0.002176811 | 0.046656307 | ||
| Training set | W/O CO | 0.002071878 | 0.045517882 |
| W/O Figaro | 0.001626768 | 0.040333216 | |
| 3xTGS 26xx types | 0.001183233 | 0.034398159 | |
| TGS 2600 & TGS 2611-C00 | 0.001441292 | 0.037964357 | |
| 2xTGS 2611-C00 | 0.001723121 | 0.04151049 | |
| Reference | 0.014911814 | 0.122113937 | |
| W/O Pressure | 0.012041034 | 0.109731645 | |
| W/O Temperature | 0.014275558 | 0.119480365 | |
| 0.018681443 | 0.136680075 | ||
| Test set | W/O CO | 0.015550217 | 0.124700508 |
| W/O Figaro | 0.015273629 | 0.123586523 | |
| 3xTGS 26xx types | 0.0224715 | 0.14990497 | |
| TGS 2600 & TGS 2611-C00 | 0.0178823 | 0.133724719 | |
| 2xTGS 2611-C00 | 0.01768717 | 0.132993119 |
References
- Saunois, M.; Bousquet, P.; Poulter, B.; Peregon, A.; Ciais, P.; Canadell, J.G.; Dlugokencky, E.J.; Etiope, G.; Bastviken, D.; Houweling, S.; et al. The global methane budget 2000–2012. Earth Syst. Sci. Data 2016, 8, 697–751. [Google Scholar] [CrossRef]
- Alvarez, R.A.; Zavala-Araiza, D.; Lyon, D.R.; Allen, D.T.; Barkley, Z.R.; Brandt, A.R.; Davis, K.J.; Herndon, S.C.; Jacob, D.J.; Karion, A.; et al. Assessment of methane emissions from the U.S. oil and gas supply chain. Science 2018, 361, 186–188. [Google Scholar] [CrossRef] [PubMed]
- Collier-Oxandale, A.; Gordon Casey, J.; Piedrahita, R.; Ortega, J.; Halliday, H.; Johnston, J.; Hannigan, M.P. Assessing a low-cost methane sensor quantification system for use in complex rural and urban environments. Atmos. Meas. Tech. 2018, 11, 3569–3594. [Google Scholar] [CrossRef]
- Duren, R.M.; Thorpe, A.K.; Foster, K.T.; Rafiq, T.; Hopkins, F.M.; Yadav, V.; Bue, B.D.; Thompson, D.R.; Conley, S.; Colombi, N.K.; et al. California’s methane super-emitters. Nature 2019, 575, 180–184. [Google Scholar] [CrossRef]
- Ars, S.; Broquet, G.; Kwok, C.Y.; Roustan, Y.; Wu, L.; Arzoumanian, E.; Bousquet, P. Statistical atmospheric inversion of local gas emissions by coupling the tracer release technique and local-scale transport modelling: A test case with controlled methane emissions. Atmos. Meas. Tech. 2017, 10, 5017–5037. [Google Scholar] [CrossRef]
- Yver Kwok, C.; Laurent, O.; Guemri, A.; Philippon, C.; Wastine, B.; Rella, C.W.; Vuillemin, C.; Truong, F.; Delmotte, M.; Kazan, V.; et al. Comprehensive laboratory and field testing of cavity ring-down spectroscopy analyzers measuring H2O, CO2, CH4 and CO. Atmos. Meas. Tech. 2015, 8, 3867–3892. [Google Scholar] [CrossRef]
- Feitz, A.; Schroder, I.; Phillips, F.; Coates, T.; Neghandhi, K.; Day, S.; Luhar, A.; Bhatia, S.; Edwards, G.; Hrabar, S.; et al. The Ginninderra CH4 and CO2 release experiment: An evaluation of gas detection and quantification techniques. Int. J. Greenh. Gas Control 2018, 70, 202–224. [Google Scholar] [CrossRef]
- Ayalneh Berhanu, T.; Satar, E.; Schanda, R.; Nyfeler, P.; Moret, H.; Brunner, D.; Oney, B.; Leuenberger, M. Measurements of greenhouse gases at Beromünster tall-tower station in Switzerland. Atmos. Meas. Tech. 2016, 9, 2603–2614. [Google Scholar] [CrossRef]
- Rella, C.W.; Chen, H.; Andrews, A.E.; Filges, A.; Gerbig, C.; Hatakka, J.; Karion, A.; Miles, N.L.; Richardson, S.J.; Steinbacher, M.; et al. High accuracy measurements of dry mole fractions of carbon dioxide and methane in humid air. Atmos. Meas. Tech. 2013, 6, 837–860. [Google Scholar] [CrossRef]
- Pison, I.; Berchet, A.; Saunois, M.; Bousquet, P.; Broquet, G.; Conil, S.; Delmotte, M.; Ganesan, A.; Laurent, O.; Martin, D.; et al. How a European network may help with estimating methane emissions on the French national scale. Atmos. Chem. Phys. 2018, 18, 3779–3798. [Google Scholar] [CrossRef]
- Kumar, P.; Feiz, A.A.; Singh, S.K.; Ngae, P.; Turbelin, G. Reconstruction of an atmospheric tracer source in an urban-like environment. J. Geophys. Res. 2015, 120, 12589–12604. [Google Scholar] [CrossRef]
- Collier-Oxandale, A.M.; Thorson, J.; Halliday, H.; Milford, J.; Hannigan, M. Understanding the ability of low-cost MOx sensors to quantify ambient VOCs. Atmos. Meas. Tech. 2019, 12, 1441–1460. [Google Scholar] [CrossRef]
- Chaiyboun, A.; Traute, R.; Haas, T.; Kiesewetter, O.; Doll, T. A logarithmic multi-parameter model using gas sensor main and cross sensitivities to estimate gas concentrations in a gas mixture for SnO2 gas sensors. Sens. Actuators B Chem. 2007, 123, 1064–1070. [Google Scholar] [CrossRef]
- Figaro TGS2600 (Air Quality Sensor). Available online: https://www.figaro.co.jp/en/product/entry/tgs2600.html (accessed on 10 February 2020).
- Figaro TGS2611-C00 (Methane Sensor). Available online: https://www.figaro.co.jp/en/product/entry/tgs2611-c00.html (accessed on 10 February 2020).
- Xueref-Remy, I.; Zazzeri, G.; Bréon, F.; Vogel, F.; Ciais, P.; Lowry, D.; Nisbet, E. Anthropogenic methane plume detection from point sources in the Paris megacity area and characterization of their δ13C signature. Atmos. Environ. 2019, 117055. [Google Scholar] [CrossRef]
- Picarro Inc. G2401 Analyzer for User’s Guide; Picarro Inc.: Santa Clara, CA, USA, 2017. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representation by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Bishop, C.; Bishop, P.; Hinton, G.; Press, O.U. Neural Networks for Pattern Recognition; Advanced Texts in Econometrics; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Haykin, S. Neural networks: A comprehensive foundation; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Casey, J.G.; Collier-Oxandale, A.; Hannigan, M. Performance of artificial neural networks and linear models to quantify 4 trace gas species in an oil and gas production region with low-cost sensors. Sens. Actuators B Chem. 2019, 283, 504–514. [Google Scholar] [CrossRef]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media: Bodega Avenue Sebastopol, CA, USA, 2019. [Google Scholar]
- Varoquaux, G.; Buitinck, L.; Louppe, G.; Grisel, O.; Pedregosa, F.; Mueller, A. Scikit-learn. Getmobile Mob. Comput. Commun. 2015, 19, 29–33. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 18 April 2020).
- Press, W.H.; Teukolsky, S.A. Savitzky-Golay Smoothing Filters. Comput. Phys. 1990, 4, 669. [Google Scholar] [CrossRef]
- Hagan, M.; Demuth, H.; Beale, M.; De Jesús, O. Neural Network Design; Martin Hagan: Pittsburgh, PA, USA, 2014. [Google Scholar]
- Shahid, A.; Choi, J.H.; Rana, A.U.H.S.; Kim, H.S. Least squares neural network-based wireless E-nose system using an SnO2 sensor array. Sensors 2018, 18, 1446. [Google Scholar] [CrossRef] [PubMed]
- Spinelle, L.; Gerboles, M.; Villani, M.G.; Aleixandre, M.; Bonavitacola, F. Field calibration of a cluster of low-cost available sensors for air quality monitoring. Part A: Ozone and nitrogen dioxide. Sens. Actuators B Chem. 2015, 215, 249–257. [Google Scholar] [CrossRef]
- Spinelle, L.; Gerboles, M.; Villani, M.G.; Aleixandre, M.; Bonavitacola, F. Field calibration of a cluster of low-cost commercially available sensors for air quality monitoring. Part B: NO, CO and CO2. Sens. Actuators B Chem. 2017, 238, 706–715. [Google Scholar] [CrossRef]
- Esposito, E.; De Vito, S.; Salvato, M.; Bright, V.; Jones, R.L.; Popoola, O. Dynamic neural network architectures for on field stochastic calibration of indicative low cost air quality sensing systems. Sens. Actuators B Chem. 2016, 231, 701–713. [Google Scholar] [CrossRef]
- Cordero, J.M.; Borge, R.; Narros, A. Using statistical methods to carry out in field calibrations of low cost air quality sensors. Sens. Actuators B Chem. 2018, 267, 245–254. [Google Scholar] [CrossRef]
- Eugster, W.; Laundre, J.; Eugster, J.; Kling, G.W. Long-term reliability of the Figaro TGS 2600 solid-state methane sensor under low-Arctic conditions at Toolik Lake, Alaska. Atmos. Meas. Tech. 2020, 13, 2681–2695. [Google Scholar] [CrossRef]
- Riddick, S.N.; Mauzerall, D.L.; Celia, M.; Allen, G.; Pitt, J.; Kang, M.; Riddick, J.C. The calibration and deployment of a low-cost methane sensor. Atmos. Environ. 2020, 230, 117440. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).