Resolution Dependence of Turbulent Structures in Convective Boundary Layer Simulations
Abstract
1. Introduction
2. Numerical Simulations
2.1. The Numerical Model
2.2. The Sub-Filter Model
2.3. The Convective Boundary Layer Simulations
3. Boundary Layer Characteristics
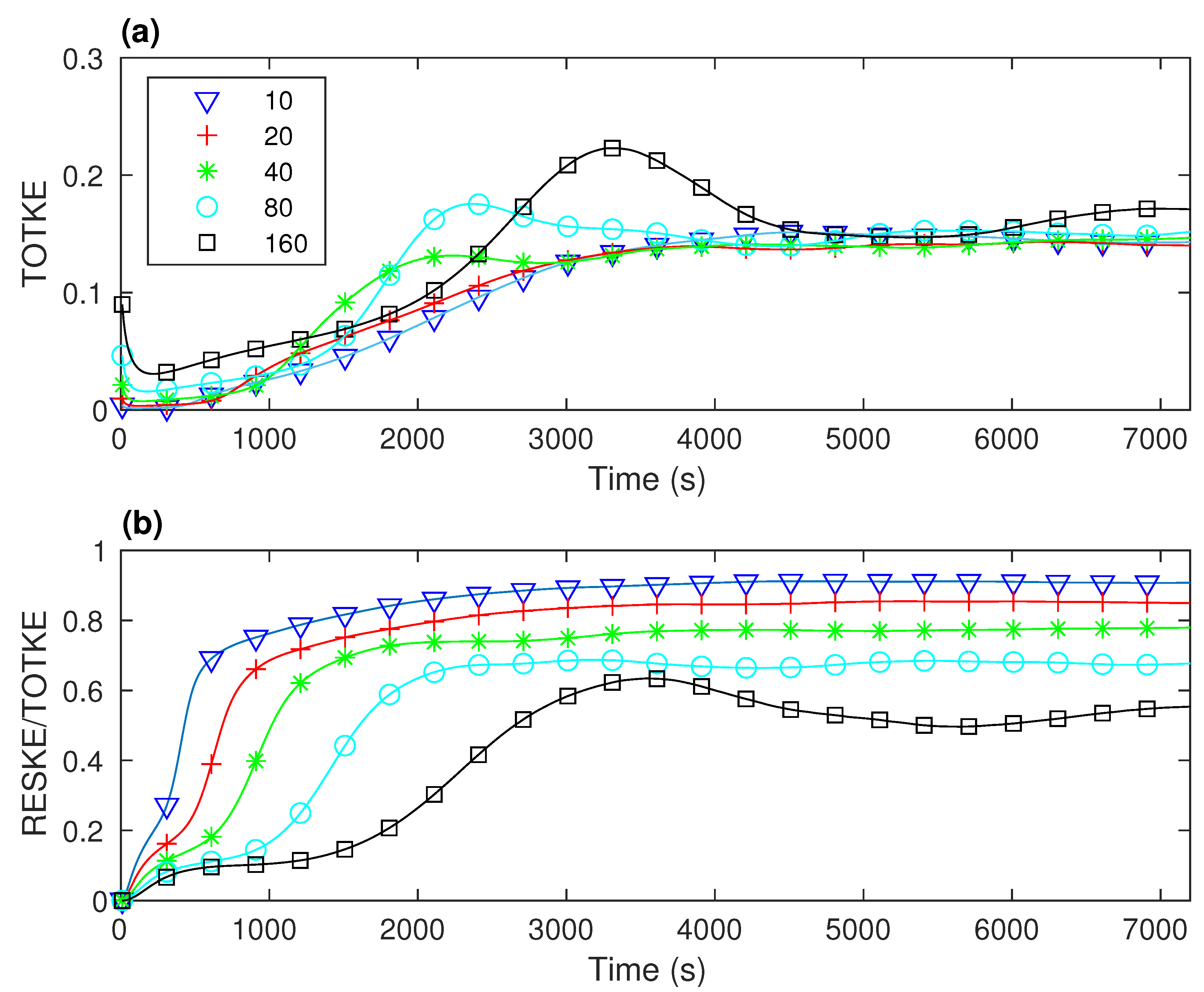
3.1. Turbulent Kinetic Energy
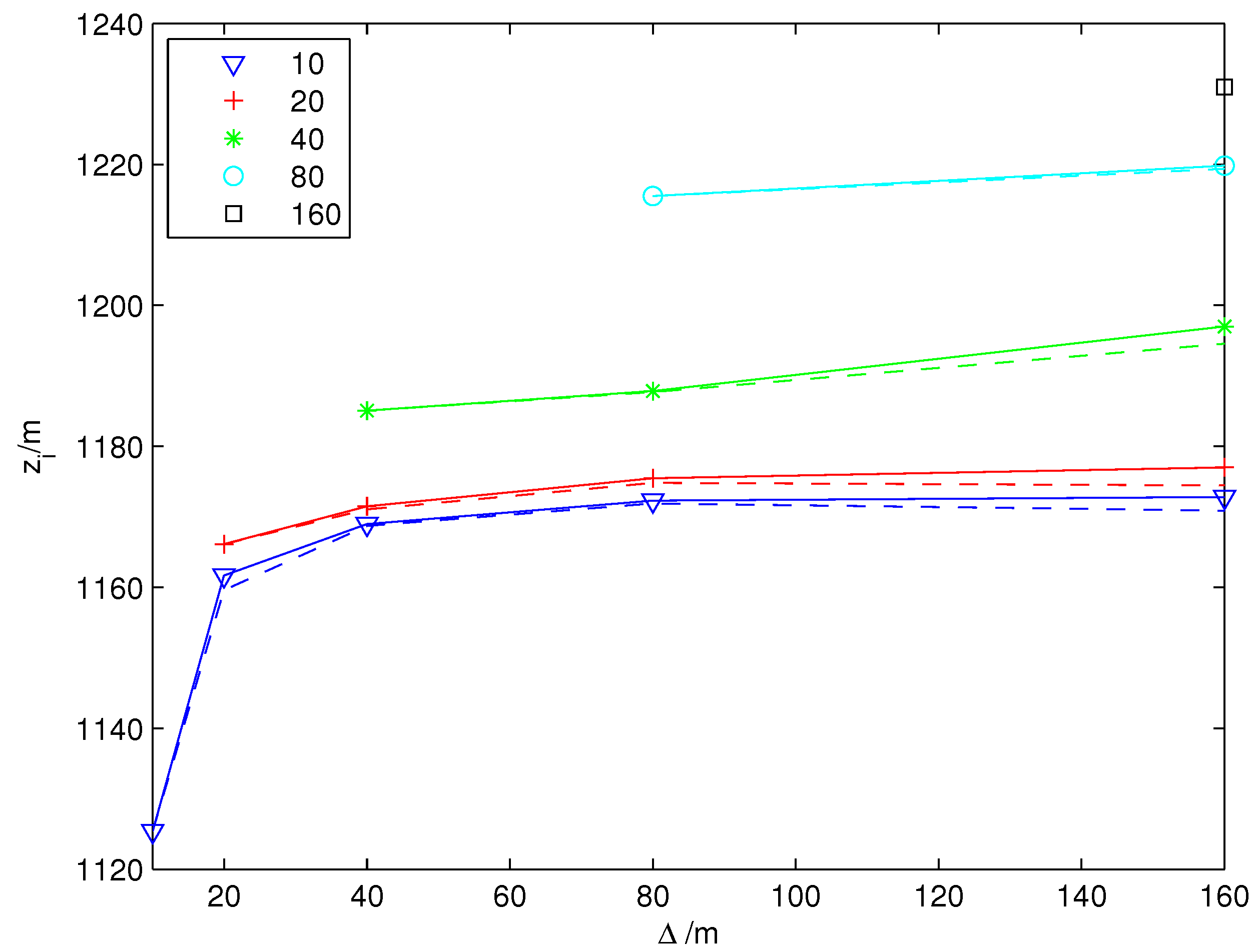
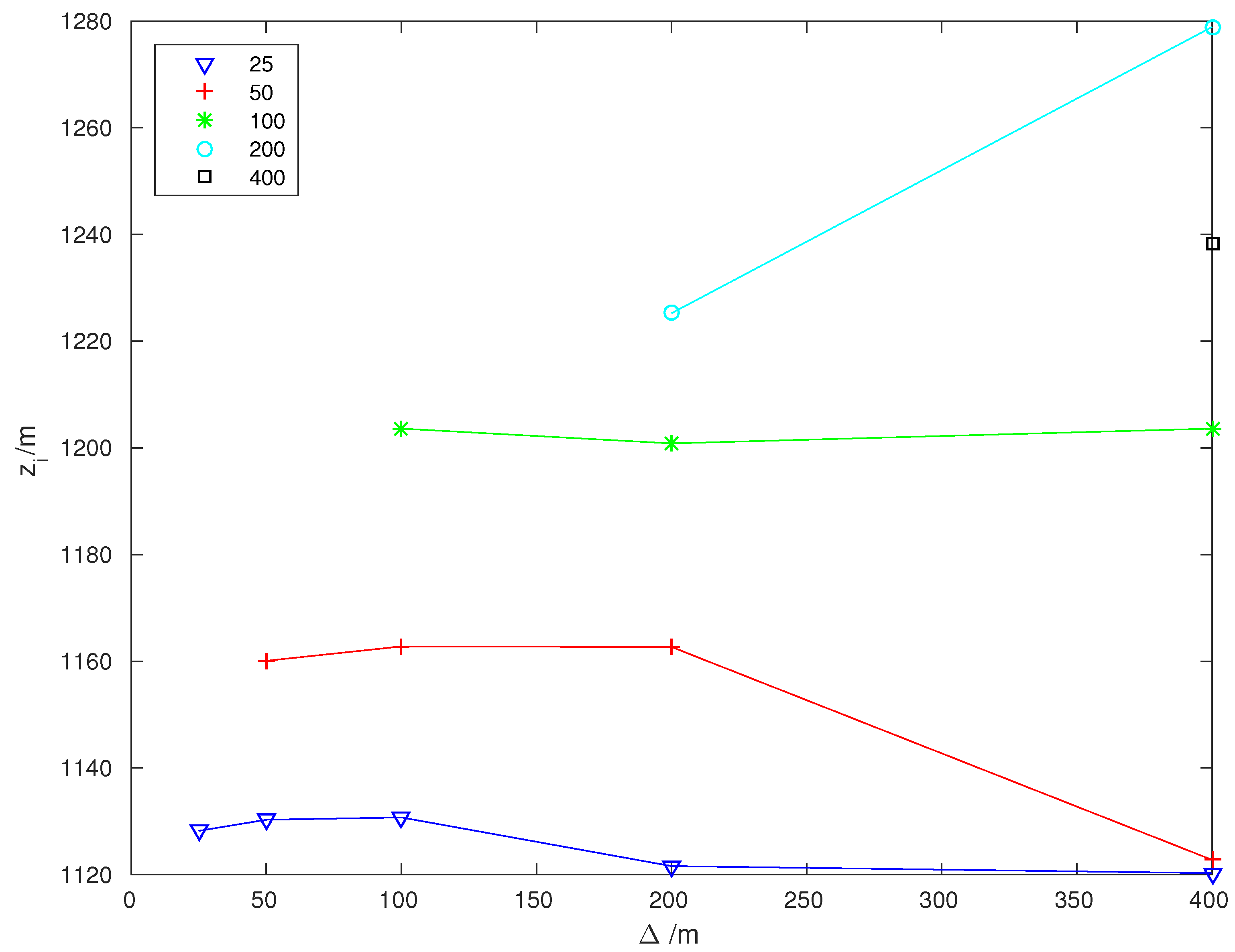
3.2. Boundary Layer Height
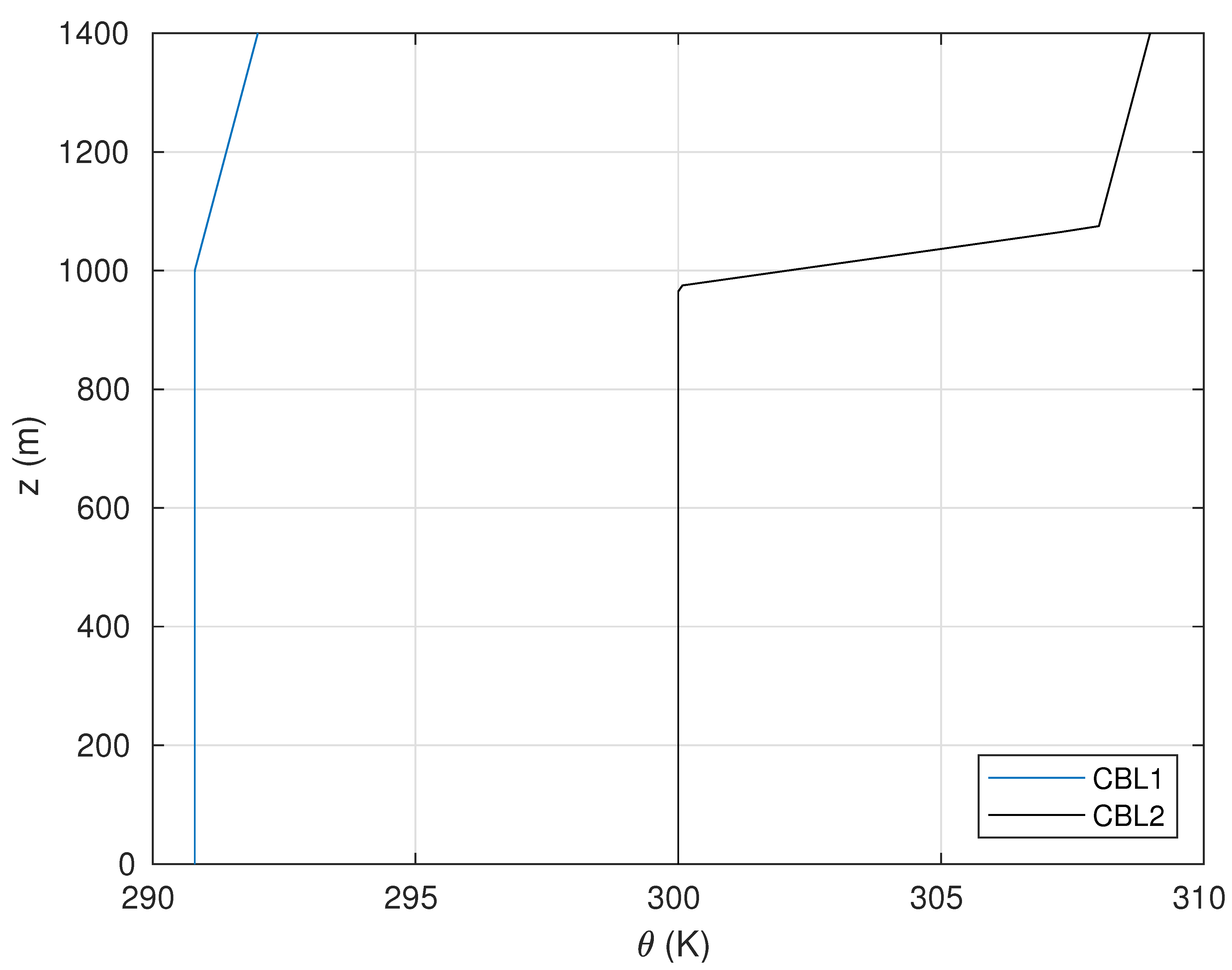
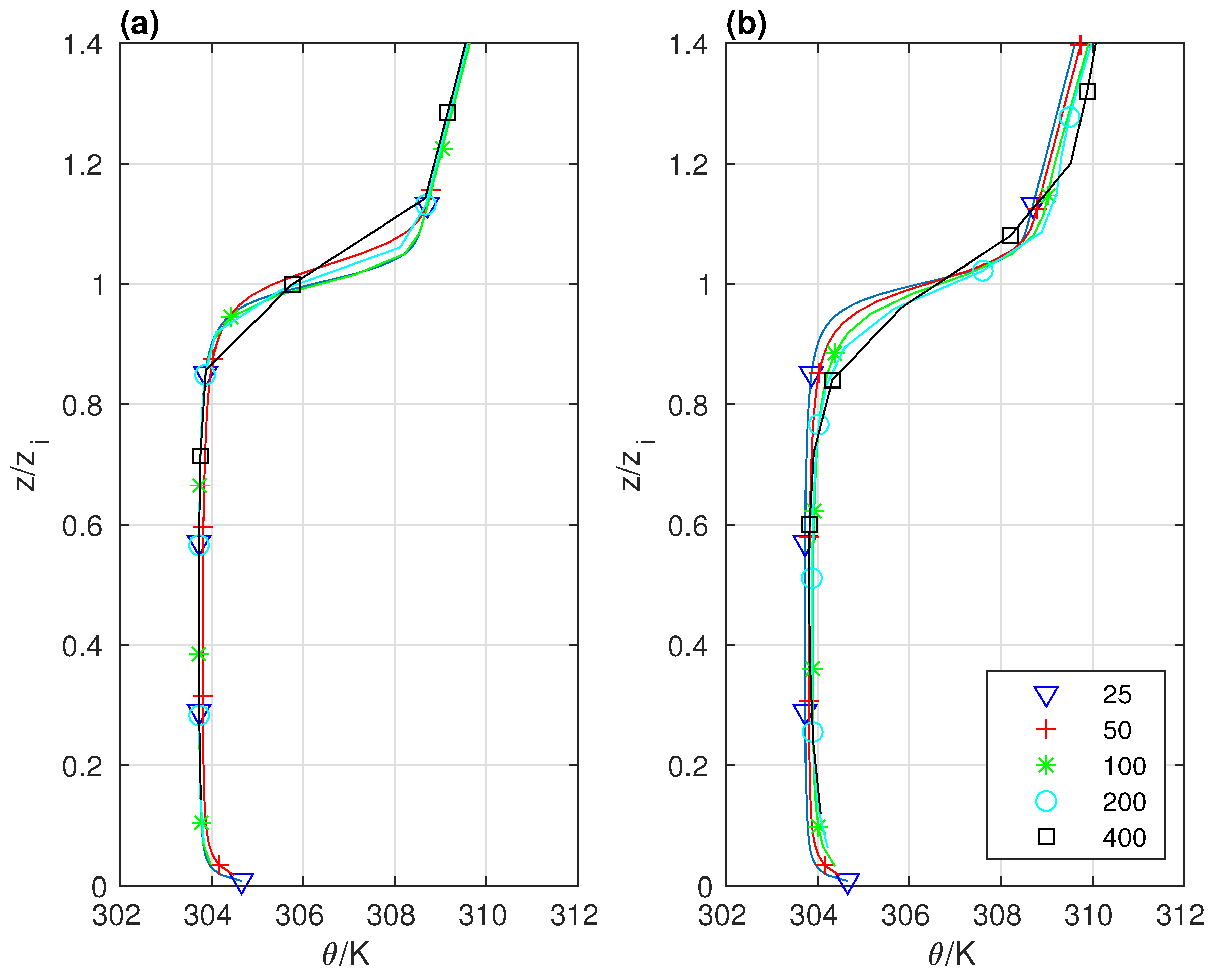
3.3. Temperature Profile
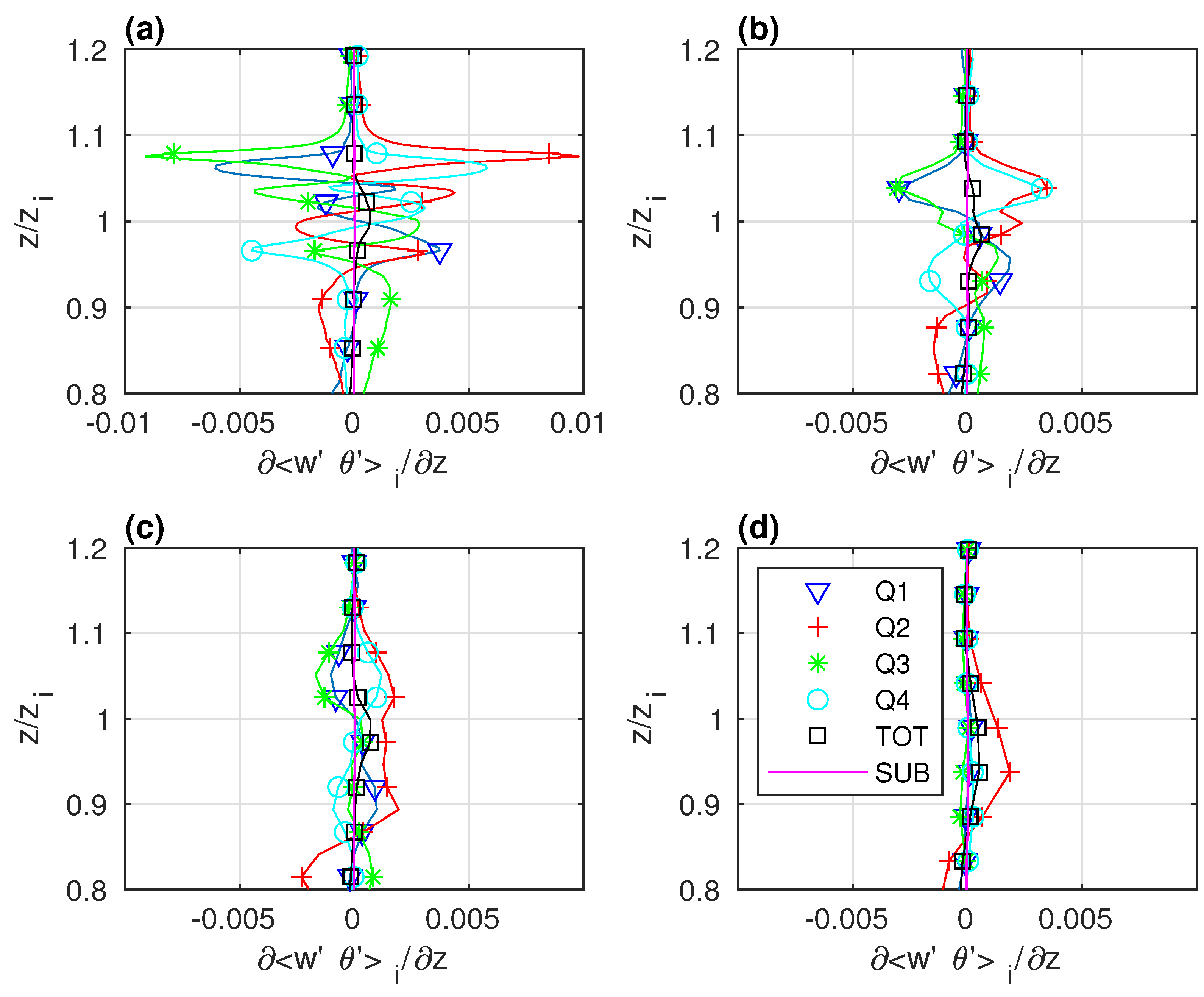
3.4. Heat Flux
4. The Role of Coherent Structures in Mixing Processes
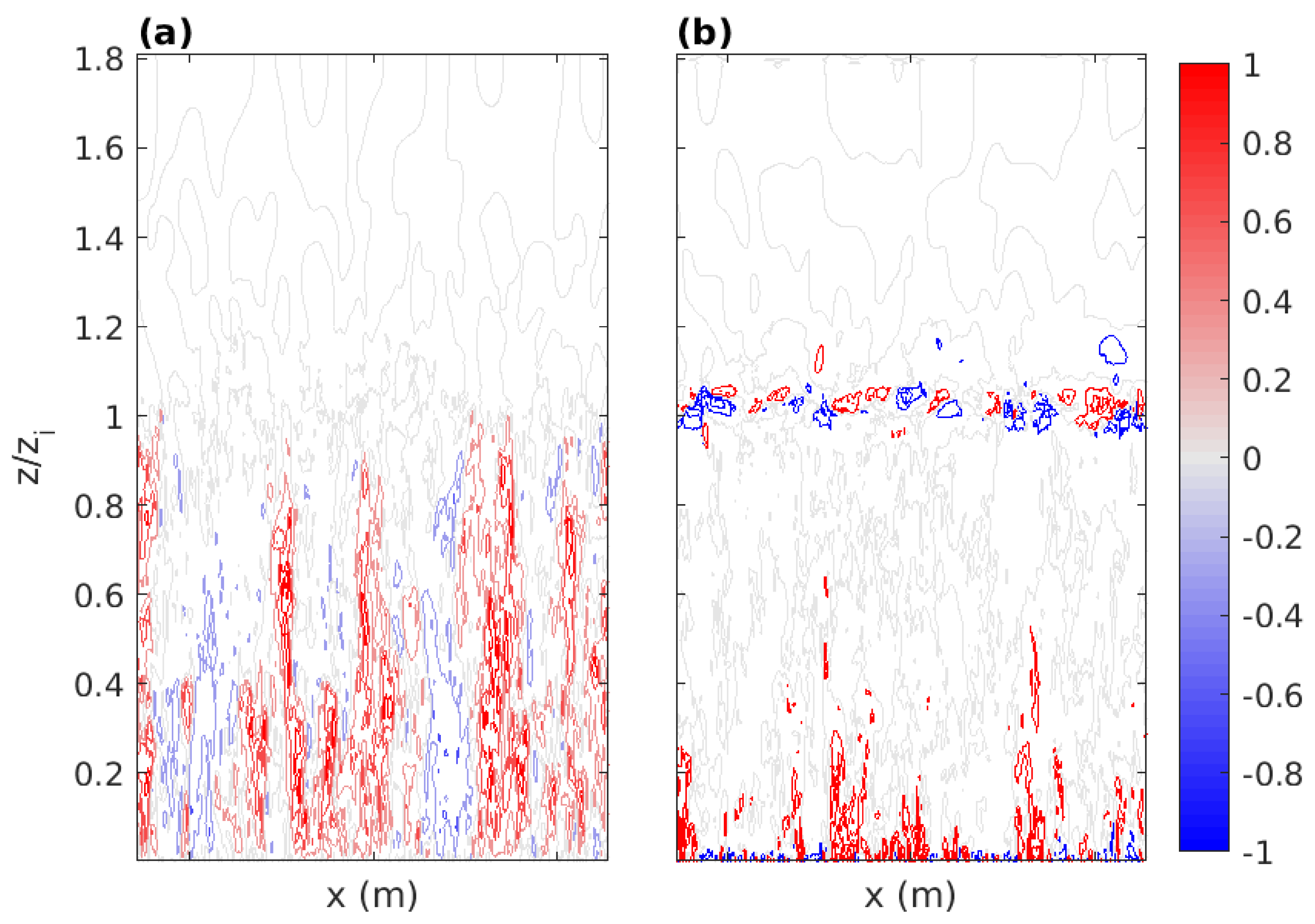
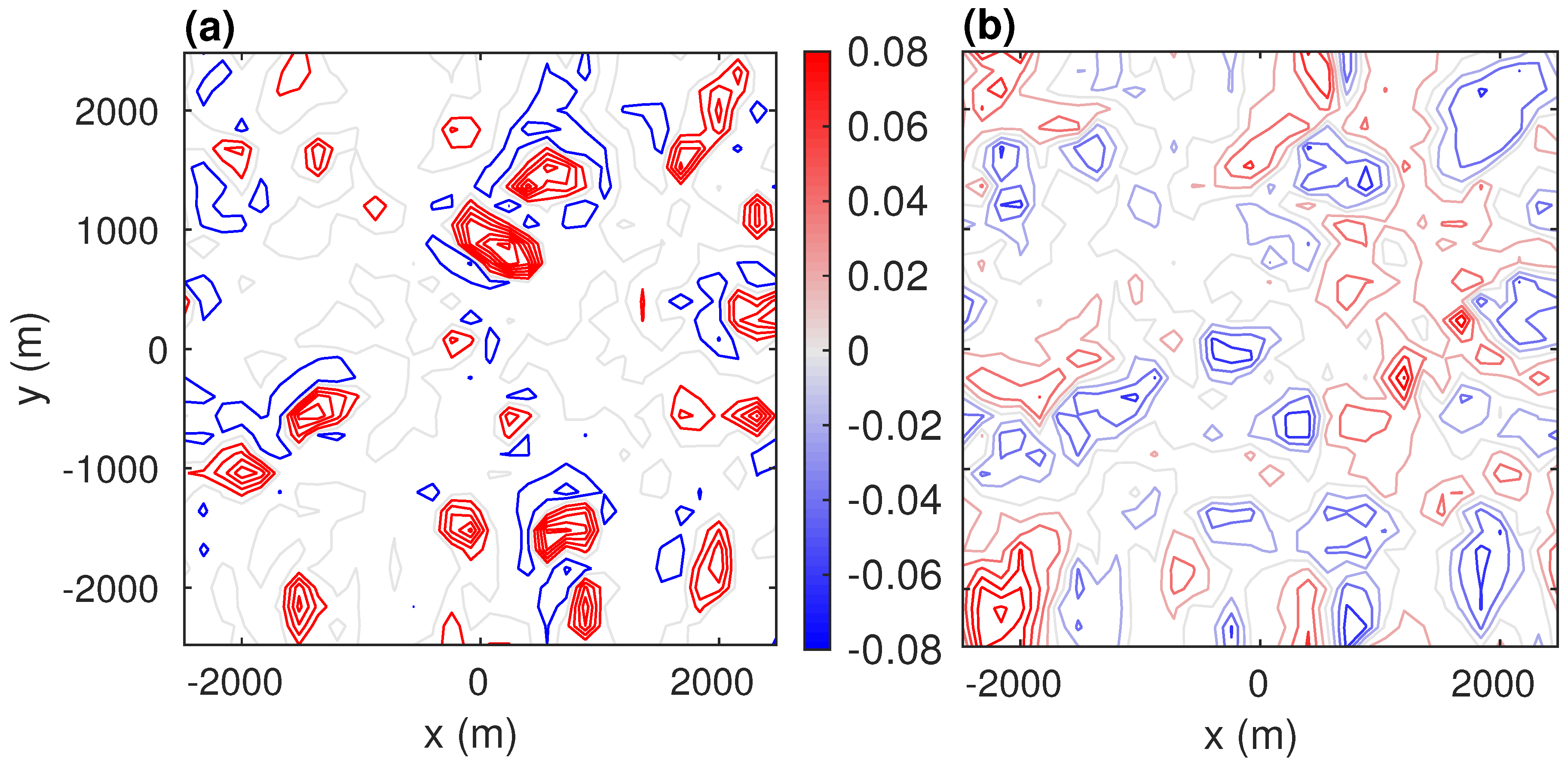
4.1. Flow Visualisation
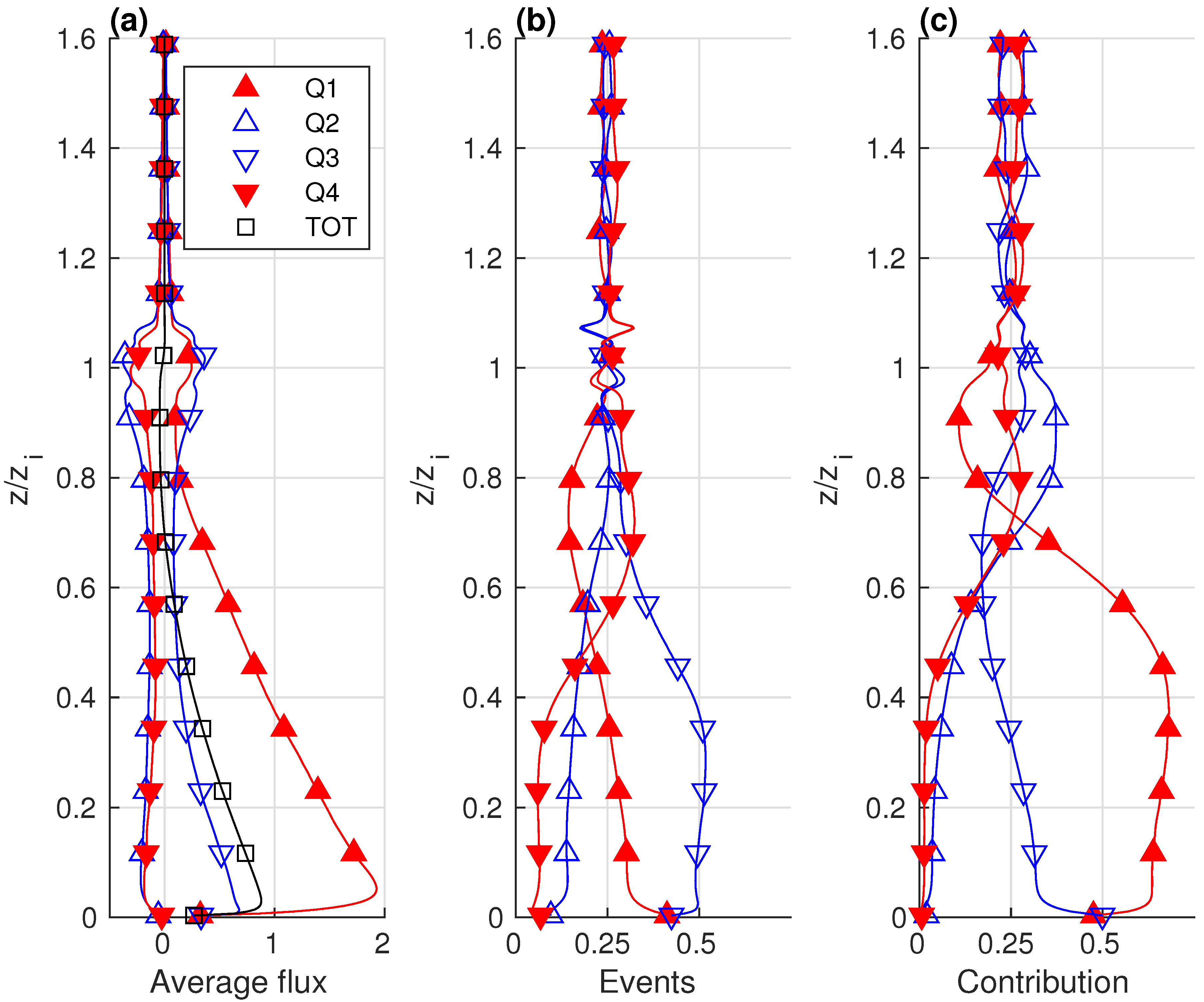
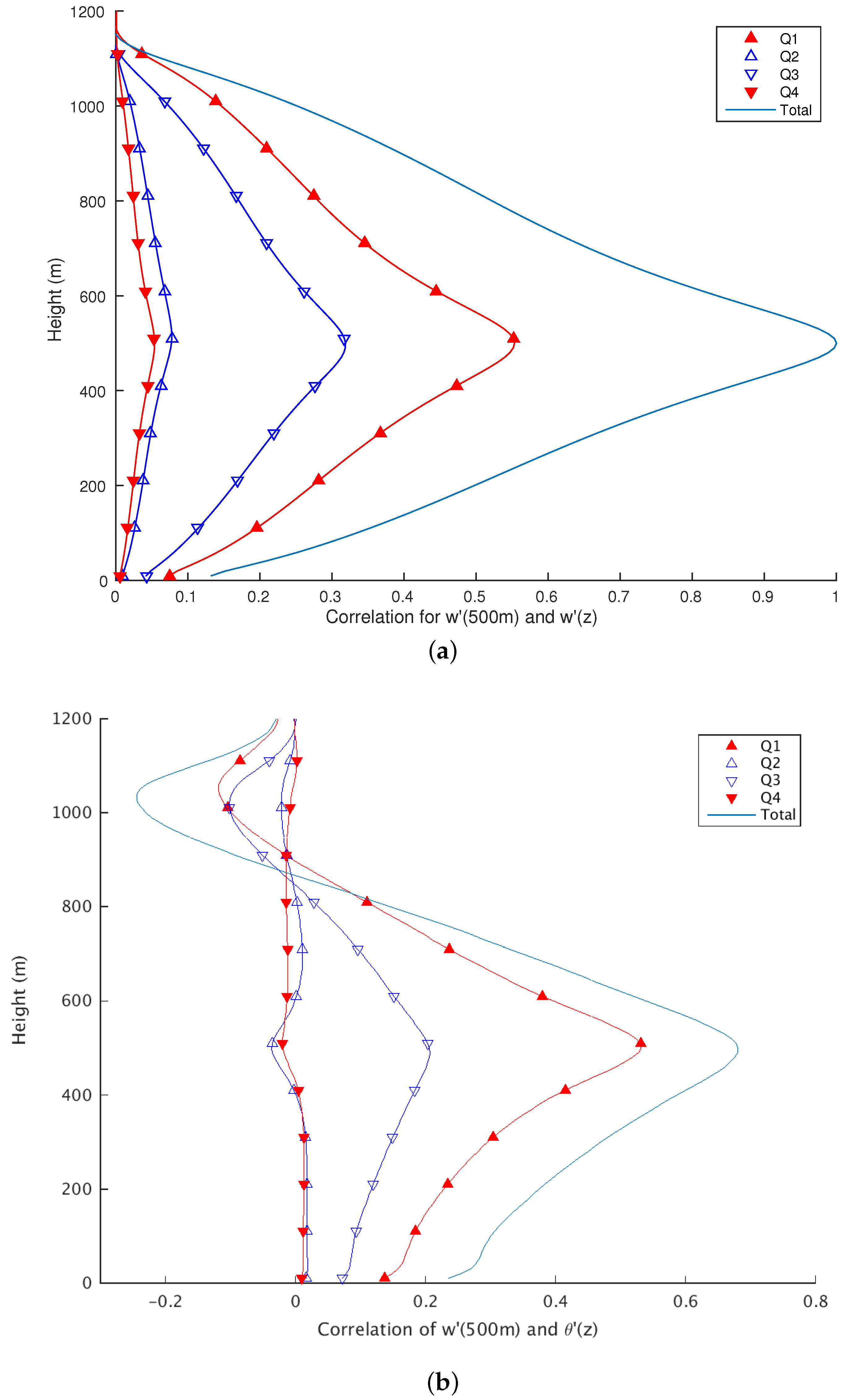
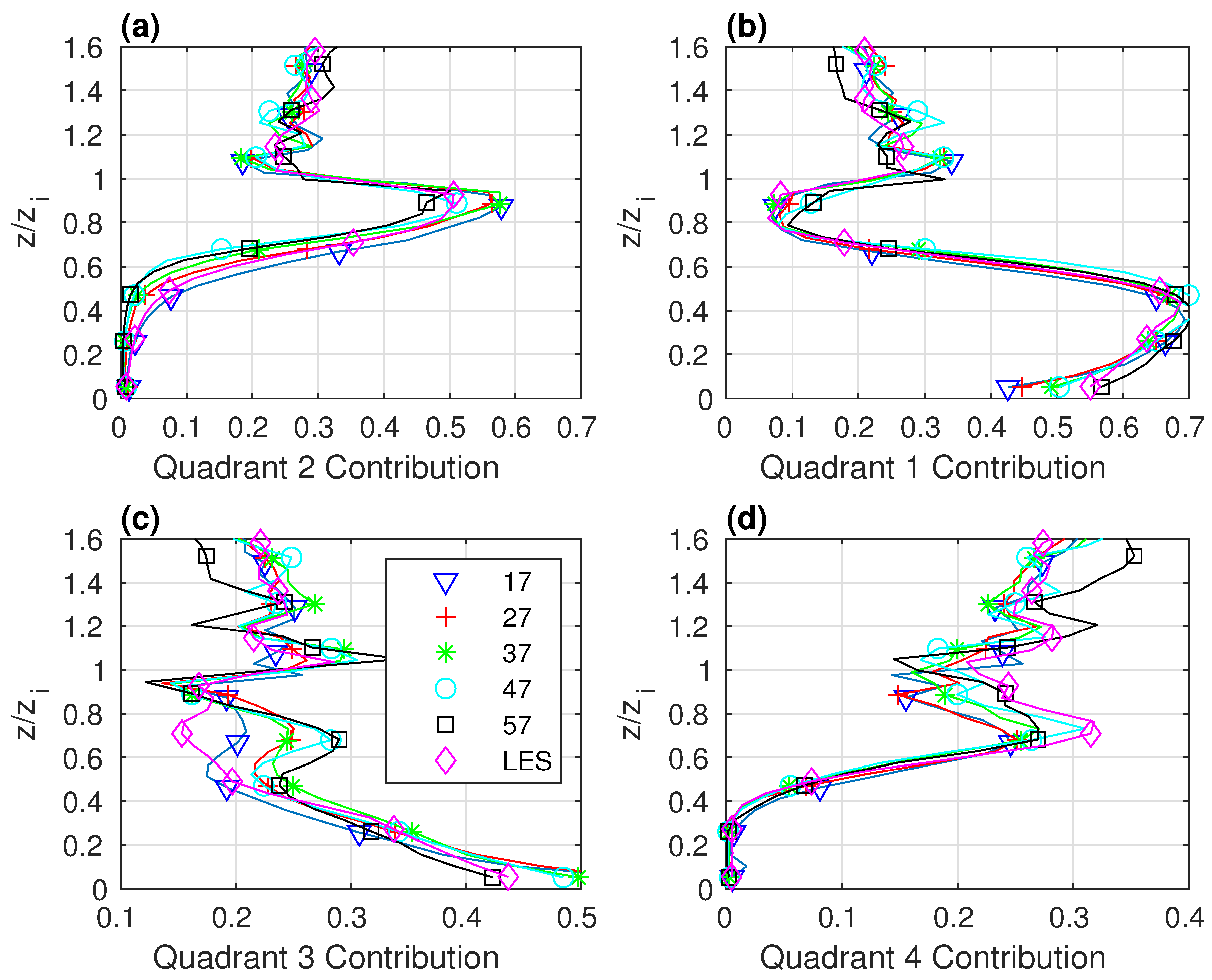
4.2. Quadrant Analysis Based on the “Truth Run”
- Q1: (warm air rising)
- Q2: (cold air rising)
- Q3: (cold air descending)
- Q4: (warm air descending)
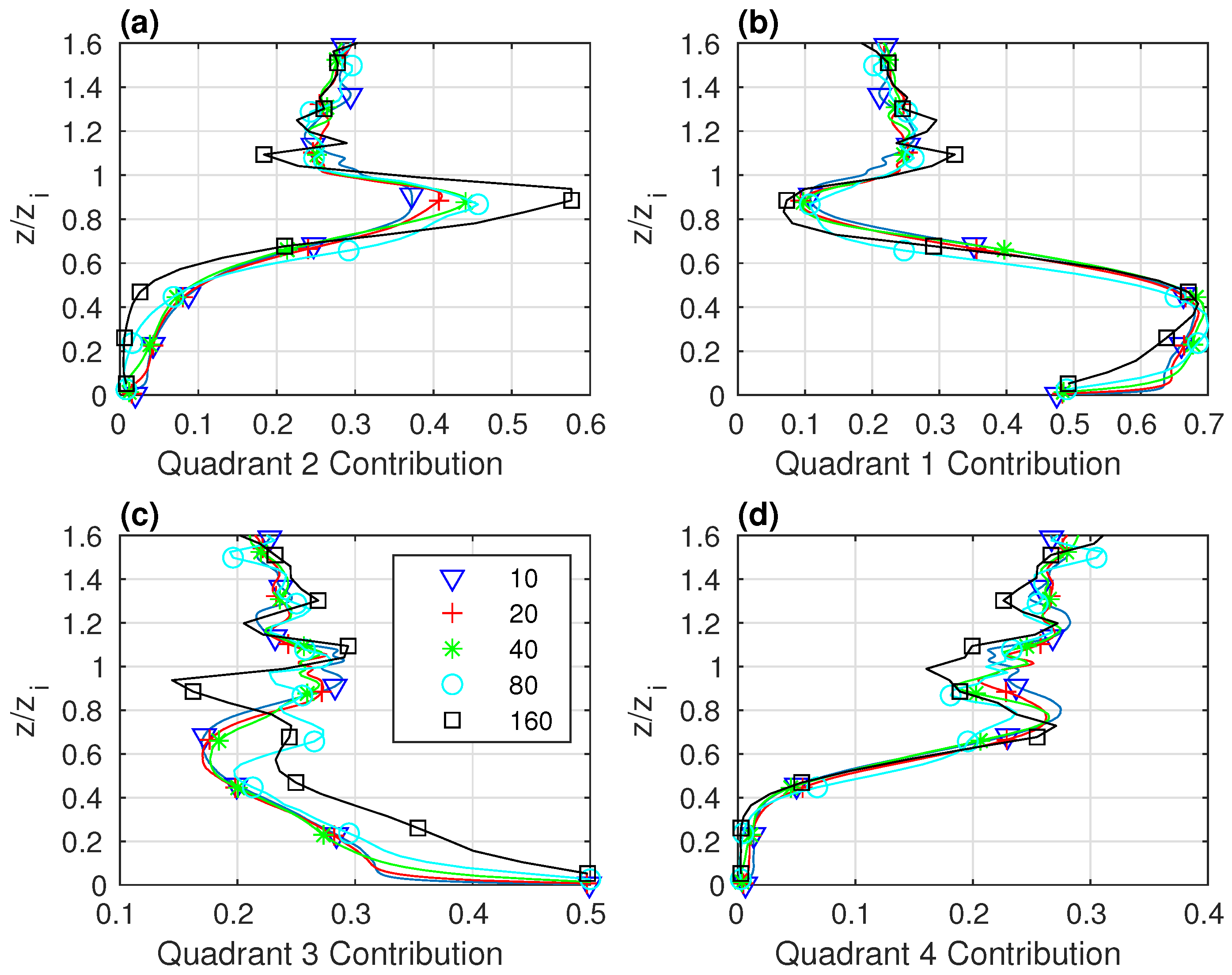
4.3. Resolution-Dependence of Quadrant Contributions to the Heat Flux
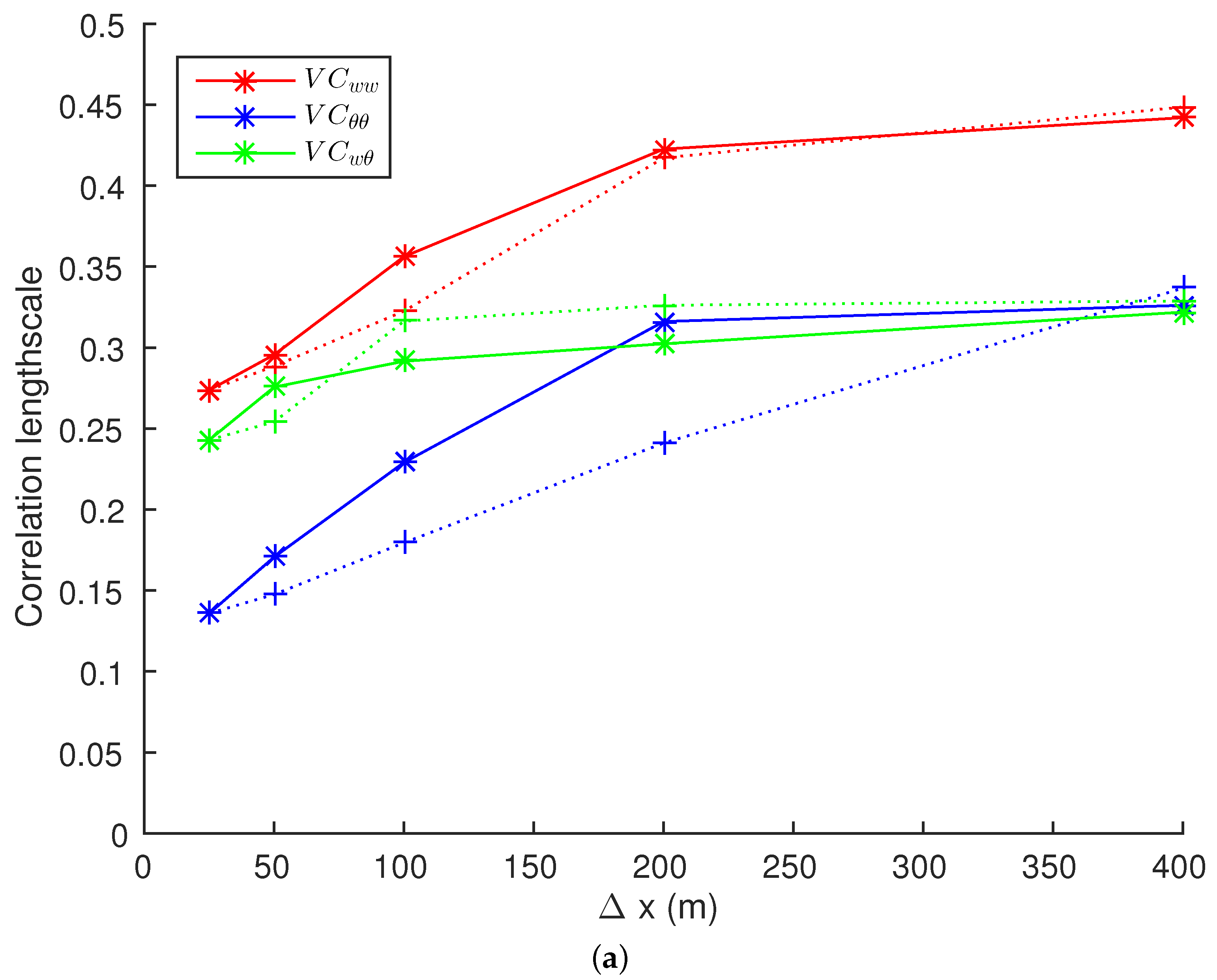
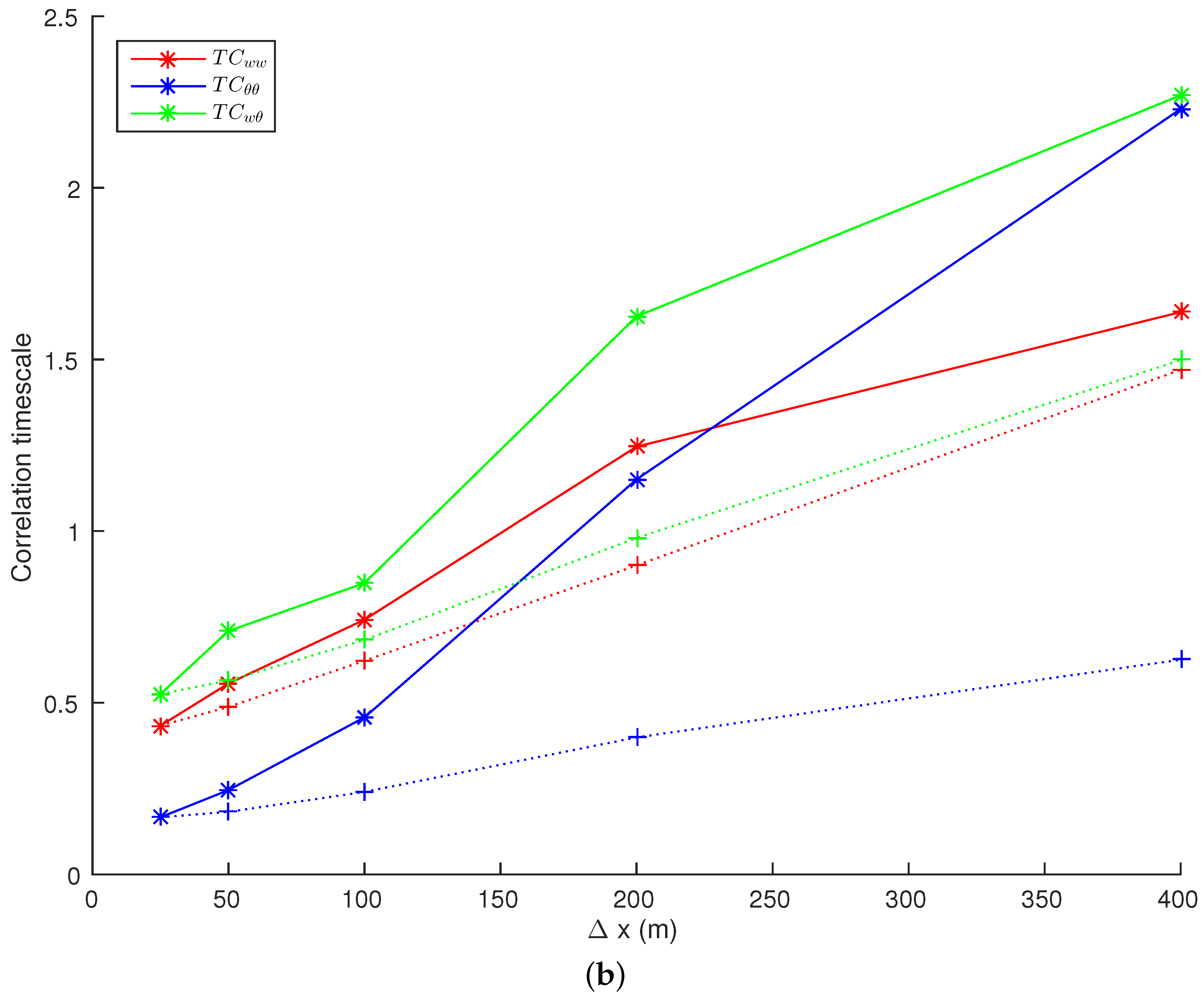
4.4. Resolution Dependence of Structure Length and Time Scales
5. Discussion
5.1. Temperature in the Boundary Layer
5.2. Increased Mixing
5.2.1. The Effect of Changing the Smagorinsky Constant
5.2.2. The Effect of Introducing Stochastic Backscatter
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bauer, P.; Thorpe, A.; Brunet, G. The quiet revolution of numerical weather prediction. Nature 2015, 525, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; p. 666. [Google Scholar]
- Honnert, R.; Masson, V.; Couvreux, F. A diagnostic for evaluating the representation of turbulence in atmospheric models at the kilometric scale. J. Atmos. Sci. 2011, 68, 3112–3131. [Google Scholar] [CrossRef]
- Hanley, K.E.; Plant, R.S.; Stein, T.H.M.; Hogan, R.J.; Lean, H.W.; Halliwell, C.; Clark, P.A. Mixing length controls on high resolution simulations of convective storms. Q. J. R. Meteorol. Soc. 2015, 141, 272–284. [Google Scholar] [CrossRef]
- Thurston, W.; Fawcett, R.J.B.; Tory, K.J.; Kepert, J.D. Simulating boundary layer rolls with a numerical weather prediction model. Q. J. R. Meteorol. Soc. 2016, 142, 211–223. [Google Scholar] [CrossRef]
- Doubrawa, P.; Muñoz-Esparza, D. Simulating Real Atmospheric Boundary Layers at Gray-Zone Resolutions: How Do Currently Available Turbulence Parameterizations Perform? Atmosphere 2020, 11, 345. [Google Scholar] [CrossRef]
- Wyngaard, J.C. Toward numerical modeling in the “terra incognita”. J. Atmos. Sci. 2004, 61, 1816–1826. [Google Scholar] [CrossRef]
- Honnert, R.; Efstathiou, G.A.; Beare, R.J.; Ito, J.; Lock, A.; Neggers, R.; Plant, R.S.; Shin, H.H.; Tomassini, L.; Zhou, B. The Atmospheric Boundary Layer and the “Gray Zone” of Turbulence: A critical review. J. Geophys. Res. Atmos. 2020, 125, 1. [Google Scholar] [CrossRef]
- Stoll, R.; Gibbs, J.A.; Salesky, S.T.; Anderson, W.; Calaf, M. Large-Eddy Simulation of the Atmospheric Boundary Layer. Bound. Layer Meteorol. 2020. [Google Scholar] [CrossRef]
- Wurps, W.; Steinfeld, G.; Heinz, S. Grid-Resolution Requirements for Large-Eddy Simulations of the Atmospheric Boundary Layer. Bound. Layer Meteorol. 2020, 175, 179–201. [Google Scholar] [CrossRef]
- Sullivan, P.P.; Patton, E.G. The effect of mesh resolution on convective boundary layer statistics and structures generated by Large-Eddy Simulation. J. Atmos. Sci. 2011, 68, 2395–2415. [Google Scholar] [CrossRef]
- Beare, R.J. A length scale defining partially-resolved boundary layer turbulence simulations. Bound. Layer Meteorol. 2014, 151, 39–55. [Google Scholar] [CrossRef][Green Version]
- Park, S.B.; Baik, J.J.; Han, B.S. Characteristics of Decaying Convective Boundary Layers Revealed by Large-Eddy Simulations. Atmosphere 2020, 11, 434. [Google Scholar] [CrossRef]
- Matheou, G.; Chung, D. Large-Eddy Simulation of Stratified Turbulence. Part II: Application of the Stretched-Vortex Model to the Atmospheric Boundary Layer. J. Atmos. Sci. 2014, 71, 4439–4460. [Google Scholar] [CrossRef]
- Matheou, G.; Chung, D.; Nuijens, L.; Stevens, B.; Teixeira, J. On the Fidelity of Large-Eddy Simulation of Shallow Precipitating Cumulus Convection. Mon. Weather Rev. 2011, 139, 2918–2939. [Google Scholar] [CrossRef]
- Moeng, C.H.; Sullivan, S.S. A comparison of shear- and buoyancy-driven planetary boundary layer flows. J. Atmos. Sci. 1994, 51, 999–1022. [Google Scholar] [CrossRef]
- Khanna, S.; Brasseur, J.G. Three-dimensional buoyancy- and shear-induced local structure of the atmospheric boundary layer. J. Atmos. Sci. 1998, 55, 710–743. [Google Scholar] [CrossRef]
- Pino, D.; Vila-Guerau de Arellano, J.; Duynkerke, P.G. The contribution of shear to the evolution of a convective boundary layer. J. Atmos. Sci. 2003, 60, 1913–1926. [Google Scholar] [CrossRef]
- Park, S.B.; Baik, J.J. Large-Eddy Simulations of convective boundary layers over flat and urbanlike surfaces. J. Atmos. Sci. 2014, 71, 1880–1892. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Wyngaard, J.C.; Haugen, D.A.; Coté, O.R.; Izumi, Y.; Caughey, S.J.; Readings, C.J. Turbulence structure in the convective boundary layer. J. Atmos. Sci. 1976, 33, 2152–2169. [Google Scholar] [CrossRef]
- Caughey, S.J.; Palmer, S.G. Some aspects of turbulence structure through the depth of the convective boundary layer. Q. J. R. Meteorol. Soc. 1979, 105, 811–827. [Google Scholar] [CrossRef]
- Moeng, C.H. A Large-Eddy-Simulation model for the study of planetary boundary layer turbulence. J. Atmos. Sci. 1984, 41, 2052–2062. [Google Scholar] [CrossRef]
- Garcia, J.R.; Mellado, J.P. The two-layer structure of the entrainment zone in the convective boundary layer. J. Atmos. Sci. 2014, 71, 1935–1955. [Google Scholar] [CrossRef]
- Sullivan, P.P.; Moeng, C.H.; Stevens, B.; Lenschow, D.H.; Mayor, S.D. Structure of the entrainment zone capping the convective atmospheric boundary layer. J. Atmos. Sci. 1998, 55, 3042–3064. [Google Scholar] [CrossRef]
- Catalano, F.; Moeng, C.H. Large-Eddy Simulation of the daytime boundary layer in an idealized valley using the Weather Research and Forecasting numerical model. Bound. Layer Meteorol. 2010, 137, 49–75. [Google Scholar] [CrossRef]
- Efstathiou, G.A.; Plant, R.S.; Bopape, M.J.M. Simulation of an Evolving Convective Boundary Layer Using a Scale-Dependent Dynamic Smagorinsky Model at Near-Gray-Zone Resolutions. J. Appl. Meteorol. Clim. 2018, 57, 2197–2214. [Google Scholar] [CrossRef]
- Boutle, I.A.; Eyre, J.E.J.; Lock, A.P. Seamless Stratocumulus Simulation across Turbulent Gray Zone. Mon. Weather Rev. 2014, 142, 1655–1668. [Google Scholar] [CrossRef]
- Shin, H.H.; Hong, S. Representation of the subgrid-scale turbulent transport in convective boundary layers at grey zone resolutions. Mon. Weather Rev. 2015, 142, 250–271. [Google Scholar] [CrossRef]
- Bou-Zeid, E.; Meneveau, C.; Parlange, M. A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 2005, 17, 025105. [Google Scholar] [CrossRef]
- Efstathiou, G.; Beare, R.; Osborne, S.; Lock, A. Grey zone simulations of the morning convective boundary layer development. J. Geophys. Res. Atmos. 2016, 121. [Google Scholar] [CrossRef]
- Mason, P.J. Large-eddy simulation: A critical review of the technique. Quart. J. R. Meteorol. Soc. 1994, 120, 1–26. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Lilly, D.K. On the computational stability of numerical solutions of time-dependent non-linear geophysical fluid dynamics problems. Mon. Weather Rev. 1965, 93, 11–25. [Google Scholar] [CrossRef]
- Mason, P.J.; Thomson, D.J. Stochastic backscatter in large eddy simulations of boundary layers. J. Fluid Mech. 1992, 242, 51–78. [Google Scholar] [CrossRef]
- Weinbrecht, S.; Mason, P.J. Stochastic backscatter for cloud-resolving models. Part I: Implementation and testing in a dry convective boundary layer. J. Atmos. Sci. 2008, 65, 123–139. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Meneveau, C.; Katz, J. Scale-invariance and turbulence models for large eddy simulation. Annu. Rev. Fluid Mech. 2000, 32, 1–32. [Google Scholar] [CrossRef]
- Shutts, G.J.; Gray, M.E.B. A numerical modelling study of the geostrophic adjustment process following deep convection. Quart. J. R. Meteorol. Soc. 1994, 120, 1145–1178. [Google Scholar] [CrossRef]
- Piacsek, S.A.; Williams, G.P. Conservation properties of convection difference schemes. J. Comput. Phys. 1970, 6, 392–405. [Google Scholar] [CrossRef]
- Brown, A.R.; Derbyshire, S.H.; Mason, P.J. Large-eddy simulation of stable atmospheric boundary layers with a revised stochastic subgrid model. Quart. J. R. Meteorol. Soc. 1994, 120, 1485–1512. [Google Scholar] [CrossRef]
- Lilly, D.K. On the Application of the Eddy Viscosity Concept in the Inertial Sub-Range of Turbulence; Technical Report 123; National Centre for Atmospheric Research: Boulder, CO, USA, 1966. [Google Scholar]
- Matheou, G. Numerical discretization and subgrid-scale model effects on large eddy simulations of a stable boundary layer. Quart. J. R. Meteorol. Soc. 2016, 142, 3050–3062. [Google Scholar] [CrossRef]
- Coceal, O.; Dobre, A.; Thomas, T.G.; Belcher, S.E. Structure of turbulent flow over regular arrays of cubical roughness. J. Fluid Mech. 2007, 598, 375–409. [Google Scholar] [CrossRef]




| (m) | (m) | (m) | Grid Points |
|---|---|---|---|
| 10 | 4 | 2.3 | 512 × 512 × 512 |
| 20 | 8 | 4.6 | 256 × 256 × 256 |
| 40 | 16 | 9.2 | 128 × 128 × 128 |
| 80 | 32 | 18.4 | 64 × 64 × 64 |
| 160 | 64 | 36.8 | 32 × 32 × 32 |
| (m) | (m) | (m) | Grid Points |
|---|---|---|---|
| 25 | 10 | 5.75 | 192 × 192 × 200 |
| 50 | 20 | 11.5 | 192 × 192 × 100 |
| 100 | 40 | 23 | 96 × 96 × 50 |
| 200 | 80 | 46 | 48 × 48 × 25 |
| 400 | 160 | 92 | 24 × 24 × 13 |
| 10 m | 20 m | 40 m | 80 m | 160 m | |
|---|---|---|---|---|---|
| RESKE | 0.1298 | 0.1191 | 0.1144 | 0.1054 | 0.0838 |
| SUBKE | 0.0132 | 0.0210 | 0.0323 | 0.0496 | 0.0749 |
| factor | — | 1.592 | 1.5400 | 1.5357 | 1.5084 |
| 25 m | 50 m | 100 m | 200 m | 400 m | |
|---|---|---|---|---|---|
| Z neg | 900 | 890 | 890 | 840 | 775 |
| Z zero | 1210 | 1200 | 1260 | 1240 | 1150 |
| Thickness | 310 | 310 | 370 | 400 | 375 |
| MinFlux | −0.15 | −0.22 | −0.21 | −0.19 | −0.11 |
| 160 m | m | 320 m | m | |
|---|---|---|---|---|
| TOTE | 0.1542 | 0.1838 | 0.1760 | 0.2146 |
| RESKE | 0.0793 | 0.1113 | 0.0669 | 0.1073 |
| SUBKE | 0.0750 | 0.0725 | 0.1091 | 0.1074 |
| 1267.3 | 1261.8 | 1280 | 1290.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bopape, M.-J.M.; Plant, R.S.; Coceal, O. Resolution Dependence of Turbulent Structures in Convective Boundary Layer Simulations. Atmosphere 2020, 11, 986. https://doi.org/10.3390/atmos11090986
Bopape M-JM, Plant RS, Coceal O. Resolution Dependence of Turbulent Structures in Convective Boundary Layer Simulations. Atmosphere. 2020; 11(9):986. https://doi.org/10.3390/atmos11090986
Chicago/Turabian StyleBopape, Mary-Jane M., Robert S. Plant, and Omduth Coceal. 2020. "Resolution Dependence of Turbulent Structures in Convective Boundary Layer Simulations" Atmosphere 11, no. 9: 986. https://doi.org/10.3390/atmos11090986
APA StyleBopape, M.-J. M., Plant, R. S., & Coceal, O. (2020). Resolution Dependence of Turbulent Structures in Convective Boundary Layer Simulations. Atmosphere, 11(9), 986. https://doi.org/10.3390/atmos11090986





