Changes in the Seasonality of Ethiopian Highlands Climate and Implications for Crop Growth
Abstract
1. Background
- 1.
- What temporal and spatial hydro-climate change has occurred in the 20th century and is projected for the 21st century?
- 2.
- How will changes in the hydro-climate affect the onset and cessation of the crop growing season?
2. Concepts and Methods
3. Results
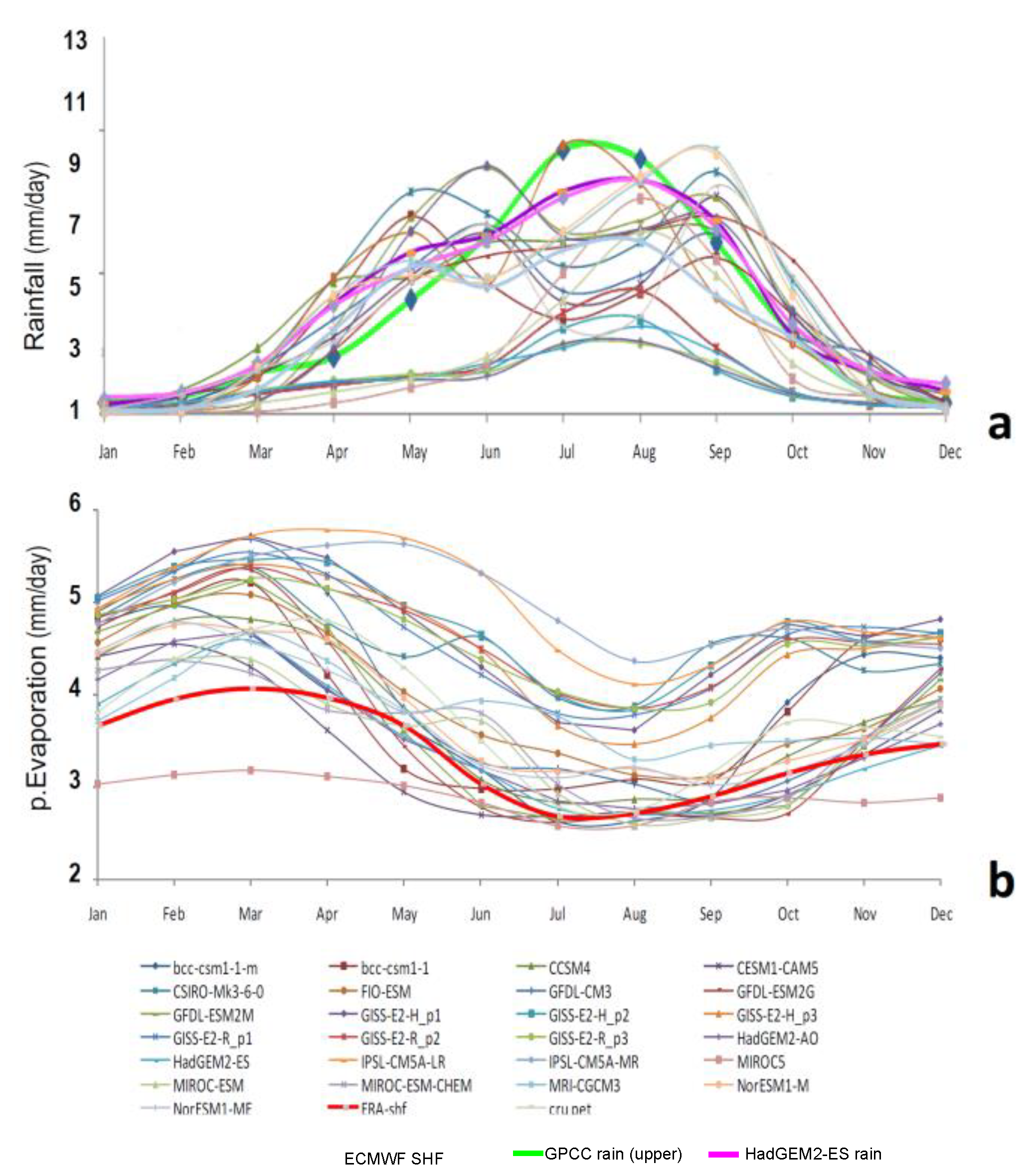
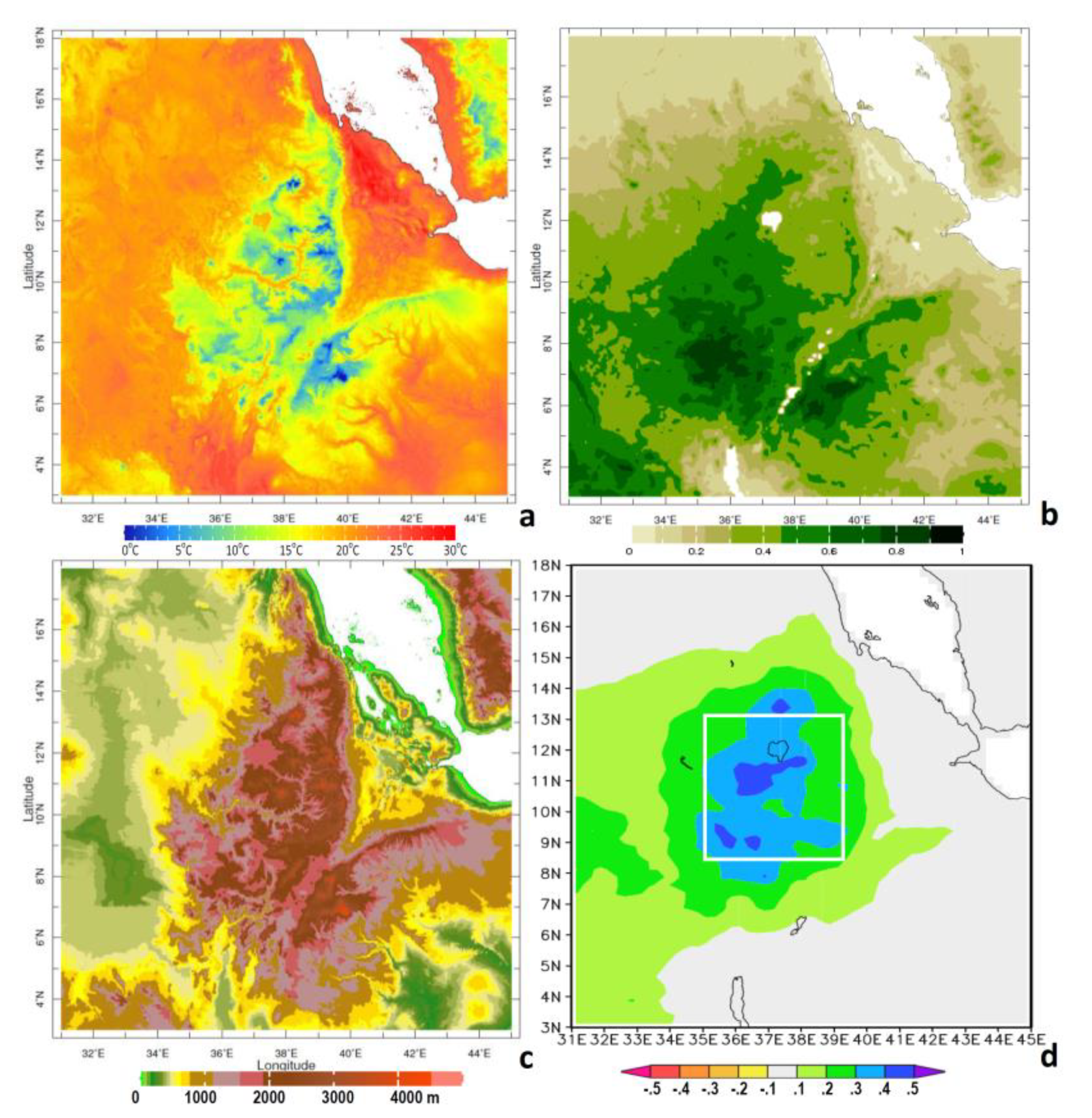
3.1. Historical Trends
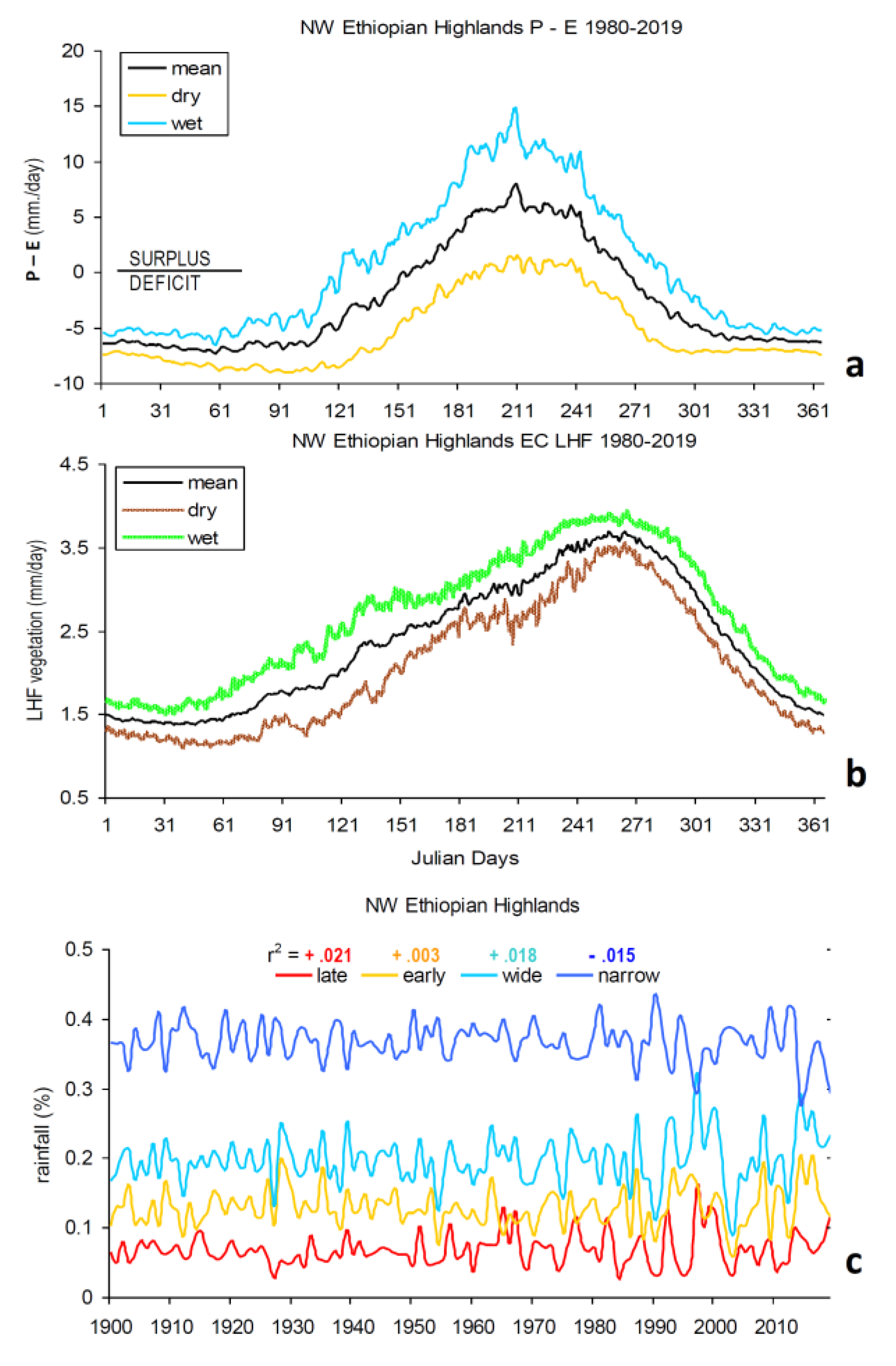
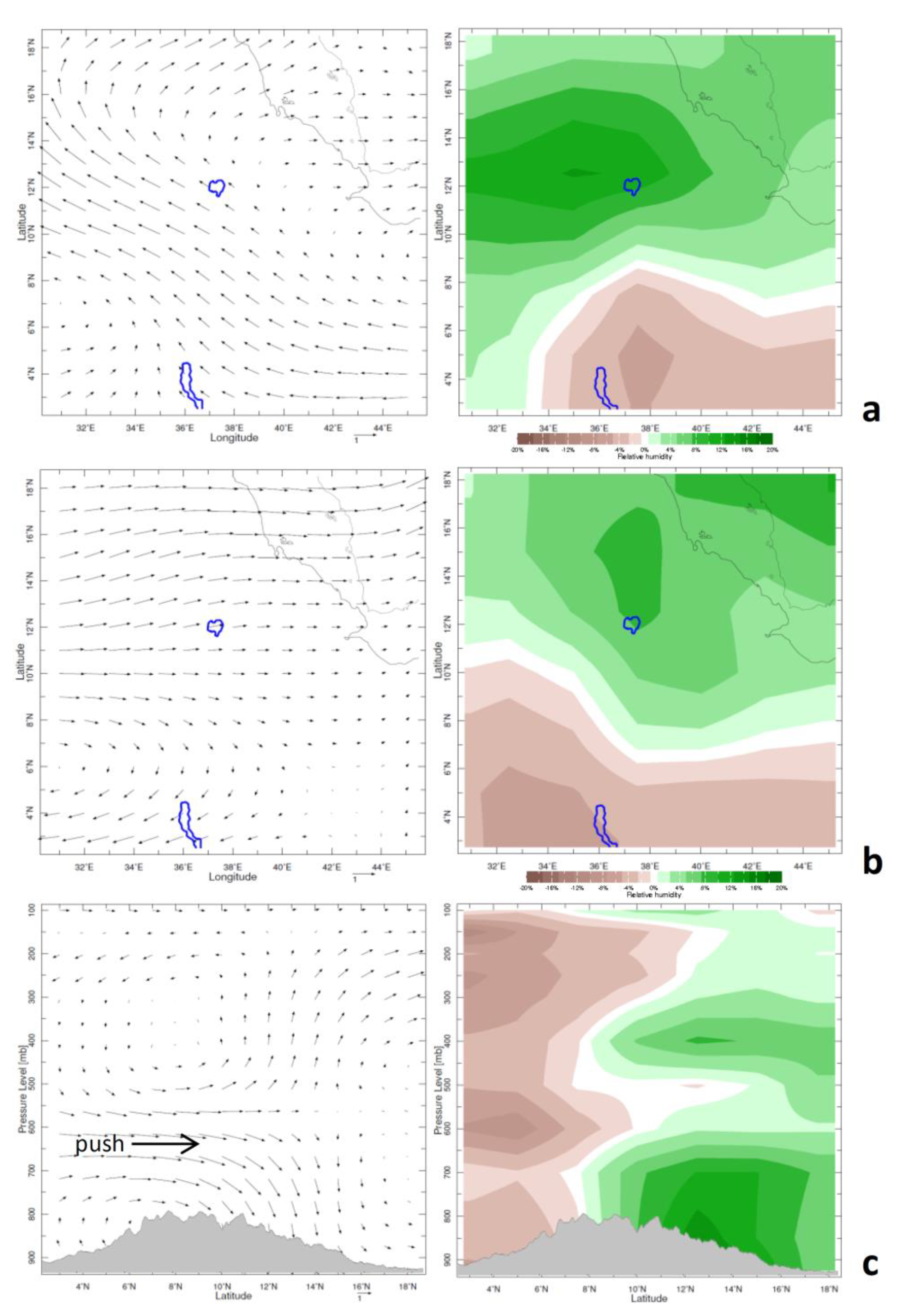
3.2. Composite Analysis
3.3. Annual Cycle
3.4. Hadley2 Projections
3.5. LGP Outcome
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Glossary
| cenTrends | centennial trends (precipitation) |
| Chirps2 | satellite-gauge blended rainfall product |
| CMIP5 | coupled model intercomparison project v5 |
| E | potential evaporation (p.Evap) |
| ECMWF | European community medium-range weather forecasts |
| EOF | Empirical Orthogonal Function |
| FLDAS | FEWS land data assimilation system |
| glowb | hydrological model (ISIMIP) |
| GRACE | gravity recovery climate experiment (satellite soil moisture) |
| Hadley2-rcp6 | Hadley v2 coupled model with +6 W/m2 scenario |
| ISIMIP | inter-sectoral impact hydrological model intercomparison project |
| LGP | length of (crop) growing period |
| LHF | latent heat flux (vegetation proxy) |
| NCEP2 | national lefts for environmental prediction reanalysis v2 |
| NDVI | normalized difference vegetation index (colour fraction) |
| NW | northwest |
| OLR | (net) outgoing long-wave radiation |
| P | precipitation |
| S | soil moisture (0–1 m) |
| SHF | sensible heat flux |
| T | temperature |
| watergap | hydrological model (ISIMIP) |
Appendix A
| No | Model | Rain Correlation | Jun.–Sep. Difference | Jul.–Aug. Value | Annual Cycle |
|---|---|---|---|---|---|
| 1 | bcc-csm1-1 | 0.65 | −3.2 | 3.8 | poor |
| 2 | bcc-csm1-1-m | 0.90 | −1.4 | 6.3 | poor |
| 3 | CCSM4 | 0.76 | −2.0 | 4.3 | poor |
| 4 | CESM1-CAM5 | 0.75 | −0.9 | 5.7 | poor |
| 5 | CSIRO-Mk3-6-0 | 0.91 | −1.1 | 8.8 | moderate |
| 6 | FIO-ESM | 0.80 | −2.1 | 4.6 | poor |
| 7 | GFDL-CM3 | 0.87 | −1.5 | 6.2 | poor |
| 8 | GFDL-ESM2G | 0.86 | −0.3 | 6.7 | moderate |
| 9 | GFDL-ESM2M | 0.87 | −0.5 | 6.4 | moderate |
| 10 | GISS-E2-H_p1 | 0.96 | −5.3 | 3.2 | poor |
| 11 | GISS-E2-H_p2 | 0.96 | −5.5 | 2.8 | poor |
| 12 | GISS-E2-H_p3 | 0.96 | −4.7 | 4.0 | poor |
| 13 | GISS-E2-R_p1 | 0.97 | −5.6 | 2.5 | poor |
| 14 | GISS-E2-R_p2 | 0.97 | −5.7 | 2.6 | poor |
| 15 | GISS-E2-R_p3 | 0.96 | −5.3 | 2.7 | poor |
| 16 | HadGEM2-AO | 0.96 | −0.4 | 8.1 | high |
| 17 | HadGEM2-ES | 0.97 | −0.5 | 8.0 | high |
| 18 | IPSL-CM5A-LR | 0.89 | −2.7 | 6.3 | poor |
| 19 | IPSL-CM5A-MR | 0.90 | −3.3 | 5.3 | poor |
| 20 | MIROC5 | 0.98 | 6.5 | 16.1 | poor |
| 21 | MIROC-ESM | 0.86 | −0.5 | 7.3 | high |
| 22 | MIROC-ESM-CHEM | 0.88 | −0.5 | 7.4 | high |
| 23 | MRI-CGCM3 | 0.93 | −2.5 | 6.0 | moderate |
| 24 | NorESM1-M | 0.66 | −2.7 | 3.4 | poor |
| 25 | NorESM1-ME | 0.62 | −2.3 | 3.3 | poor |
| No | Models | SHF Correlation | Feb.–Apr. Difference | Annual Cycle |
|---|---|---|---|---|
| 1 | bcc-csm1-1-m | 0.79 | 0.46 | moderate |
| 2 | bcc-csm1-1 | 0.73 | 0.72 | poor |
| 3 | CCSM4 | 0.96 | 0.63 | high |
| 4 | CESM1-CAM5 | 0.78 | 0.06 | moderate |
| 5 | CSIRO-Mk3-6-0 | 0.79 | 1.04 | poor |
| 6 | FIO-ESM | 0.95 | 0.81 | high |
| 7 | GFDL-CM3 | 0.92 | 1.26 | poor |
| 8 | GFDL-ESM2G | 0.9 | 0.92 | moderate |
| 9 | GFDL-ESM2M | 0.92 | 0.88 | moderate |
| 10 | GISS-E2-H_p1 | 0.95 | 1.48 | poor |
| 11 | GISS-E2-H_p2 | 0.96 | 1.32 | poor |
| 12 | GISS-E2-H_p3 | 0.97 | 1.21 | poor |
| 13 | GISS-E2-R_p1 | 0.95 | 1.29 | poor |
| 14 | GISS-E2-R_p2 | 0.97 | 1.11 | poor |
| 15 | GISS-E2-R_p3 | 0.97 | 1.04 | moderate |
| 16 | HadGEM2-AO | 0.93 | 0.34 | high |
| 17 | HadGEM2-ES | 0.96 | 0.24 | very high |
| 18 | IPSL-CM5A-LR | 0.87 | 1.52 | poor |
| 19 | IPSL-CM5A-MR | 0.74 | 1.34 | poor |
| 20 | MIROC5 | 0.95 | −0.95 | moderate |
| 21 | MIROC-ESM | 0.87 | 0.11 | moderate |
| 22 | MIROC-ESM-CHEM | 0.85 | 0.05 | moderate |
| 23 | MRI-CGCM3 | 0.8 | 0.31 | moderate |
| 24 | NorESM1-M | 0.95 | 0.58 | high |
| 25 | NorESM1-ME | 0.91 | 0.44 | high |
| N = 119 | Glowb | Watergap | ||
|---|---|---|---|---|
| Months | Time Cor. | p-Value | Time Cor. | p-Value |
| Jan | −0.25 | 0.01 | 0.12 | 0.18 |
| Feb | −0.28 | 0.00 | 0.12 | 0.19 |
| Mar | −0.19 | 0.03 | 0.12 | 0.21 |
| Apr | −0.06 | 0.49 | 0.14 | 0.12 |
| May | −0.08 | 0.38 | 0.12 | 0.21 |
| Jun | 0.13 | 0.17 | 0.36 | 0.00 |
| Jul | −0.43 | 0.00 | −0.07 | 0.42 |
| Aug | −0.19 | 0.03 | −0.42 | 0.00 |
| Sep | 0.15 | 0.11 | −0.10 | 0.26 |
| Oct | 0.17 | 0.06 | 0.05 | 0.57 |
| Nov | −0.27 | 0.00 | −0.02 | 0.82 |
| Dec | −0.23 | 0.01 | −0.03 | 0.77 |

References
- Adenew, B. Climate Change and Policy Process in Ethiopia: Preliminary Review Results; Ethiopian Economics Association: Addis Ababa, Ethiopia, 2010. [Google Scholar]
- Degefu, W.; Glantz, M. (Eds.) Some aspects of meteorological drought in Ethiopia. In Drought and Hunger in Africa: Denying Famine a Future; Cambridge University Press: Cambridge, UK, 1987; pp. 23–36. [Google Scholar]
- Davidson, O.; Halsnaes, K.; Huq, S.; Kok, M.; Metz, B.; Sokona, Y.; Verhagen, J. The development and climate nexus: The case of sub-Saharan Africa. Clim. Policy 2003, 3, S97–S113. [Google Scholar] [CrossRef]
- Adem, A.; Bewket, W. A Climate Change Country Assessment: Report for Ethiopia. Forum for Environment (ECSNCC); Epsilon International R&D: Addis Ababa, Ethiopia, 2011. [Google Scholar]
- Cheung, W.H.; Senay, G.B.; Singh, A. Trends and spatial distribution of annual and seasonal rainfall in Ethiopia. Int. J. Climatol. 2008, 28, 1723–1734. [Google Scholar] [CrossRef]
- Segele, Z.T.; Lamb, P.J. Characterization and variability of JJAS rainy season over Ethiopia. Meteorol. Atmos. Phys. 2005, 89, 153–180. [Google Scholar] [CrossRef]
- Bewket, W. Rainfall Variability and Crop Production in Ethiopia: Case Study in the Amhara Region. In Proceedings of the 16th International Conference of Ethiopian Studies, Norway, 2009. Available online: http://hpccc.gov.in/PDF/Agriculture/Rainfall%20Variability%20and%20Crop%20production%20in%20Ethiopia%20Case%20study%20in%20the%20Amhara%20Region.pdf (accessed on 16 June 2020).
- Ayalew, D.; Tesfaye, K.; Mamo, G.; Yitaferu, B.; Bayu, W. Variability of rainfall and its current trend in Amhara region, Ethiopia. Afr. J. Agric. Res. 2012, 7, 1475–1486. [Google Scholar] [CrossRef]
- Shi, L.; Hendon, H.; Alves, O.; Luo, J.-J.; Balmaseda, M.; Anderson, D.L.T. How Predictable is the Indian Ocean Dipole? Mon. Weather Rev. 2012, 140, 3867–3884. [Google Scholar] [CrossRef]
- Henricksen, B.L.; Durkin, J.W. Moisture Availability, Cropping Period and the Prospects for Early Warning of Famine in Ethiopia; ILCA: Addis Ababa, Ethiopia, 1987. [Google Scholar]
- Belay, S. Agroclimatic analysis in relation to crop production. In Proceedings of the Ethiopian Agricultural Research Organization of Ethiopia, Bahir Dar, Ethiopia, 23 January 2001. [Google Scholar]
- Mersha, E. Agroclimatic classification of Ethiopia. Ethiop. J. Nat. Resour. 2005, 2, 137–154. [Google Scholar]
- Tesfaye, M. Water Balance Applications in the Identification and Analysis of Agricultural Droughts in South Wollo Zone, Ethiopia. Ph.D. Thesis, Andhra University, Visakhapatnam, India, 2014. [Google Scholar]
- Funk, C.; Nicholson, S.; Landsfeld, M.; Klotter, D.; Peterson, P.; Harrison, L. The centennial trends greater horn of Africa precipitation dataset. Sci. Data 2015, 2, 150050. [Google Scholar] [CrossRef]
- Agnew, C.T.; Chappel, A. Drought in the Sahel. GeoJournal 1999, 48, 299–311. [Google Scholar] [CrossRef]
- Cherkos, T. Intensity–Duration–Frequency Relationships for Northern Ethiopia Rainfall. Master’s Thesis, Addis Ababa University, Addis Ababa, Ethiopia, 2002. [Google Scholar]
- Jain, S.K.; Kumar, V. Trend analysis of rainfall and temperature data for India. Curr. Sci. 2012, 102, 37–49. [Google Scholar]
- Hemerance, M.A. Addressing Climate Variability in Agricultural Land Evaluation. Case Study for Crop Production in Far North Cameroon. Master’s Thesis, Ghent University, Brussels, Belgium, 2013. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: A guideline for computing crop water requirements. In FAO Irrigation and Drainage Paper 56; FAO Water Resources, Development and Management Service: Rome, Italy, 1998; ISBN 92-5-104219-5. [Google Scholar]
- Kebede, B. Analysis of the Variability of Rainfall Distribution and Evapotranispiration over Eastern Amahara Region. Master’s Thesis, Arba Minch University, Arba Minch, Ethiopia, 2009. [Google Scholar]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Parinussa, R.; Dorigo, W.; de Jeu, R.; Wagner, W.; van Dijk, A.; McCabe, M.; Evans, J. Developing an improved soil moisture dataset by blending passive and active microwave satellite-based retrievals. Hydrol. Earth Sys. Sci. 2011, 15, 425–436. [Google Scholar] [CrossRef]
- Crippen, R.E. Calculating the vegetation index faster. Remote Sens. Environ. 1990, 34, 71–73. [Google Scholar] [CrossRef]
- Ji, L.; Peters, A.J. Assessing vegetation response to drought in the northern Great Plains using vegetation and drought indices. Remote Sens. Environ. 2003, 87, 85–98. [Google Scholar] [CrossRef]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.; Pak, E.W.; Mahoney, R.; Vermote, E.; Saleous, N. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
- Kaicun, W.K.; Pucai, W.; Zhanqing, L.; Cribb, M.; Michael, S. A simple method to estimate actual evapotranspiration from a combination of net radiation, vegetation index, and temperature. J. Geophys. Res. 2007, 112, D15107. [Google Scholar] [CrossRef]
- United Nations International Strategy for Disaster Reduction. Drought risk reduction framework and practices: Contributing to the implementation of the Kyoto framework for action. In International Strategy for Disaster Risk; UNISDR: Geneva, Switzerland, 2009. [Google Scholar]
- Mekuria, E. Spatial and Temporal Analysis of Recent Drought Years Using Vegetation Temperature Condition index, Case of Somali Regional State. Master’s Thesis, Arba Minch University, Arba Minch, Ethiopia, 2012. [Google Scholar]
- Yohannes, Z. Estimation of teff yield using remote sensing and GIS techniques in Tigray region, Northern Ethiopia. In Proceedings of the Research Application Summary, 3rd RU-Forum Biennial Meeting, Entebbe, Uganda, 24–28 September 2012. [Google Scholar]
- Tadesse, T.; Demisse, G.B.; Zaitchik, B.; Dinku, T. Satellite-based hybrid drought monitoring tool for prediction of vegetation condition in Eastern Africa: A case study for Ethiopia. Water Resour. Res. 2014, 50, 2176–2190. [Google Scholar] [CrossRef]
- Dodamani, B.M.; Anoop, R.; Mahajan, D.R. Agricultural drought modeling using remote sensing. Int. J Environ. Sci. Dev. 2015, 6, 326. [Google Scholar] [CrossRef]
- Hundera, H.; Berhan, B.; Bewuket, W. Remote sensing and GIS based agricultural drought risk assessment in east Shewa zone, central Rift Valley region of Ethiopia. J. Environ. Earth Sci. 2016, 6, 48–54. [Google Scholar]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP–DOE AMIP reanalysis R2. Bull. Am. Meteorol. Soc. 2002, 83, 1631–1644. [Google Scholar] [CrossRef]
- Oleson, K.W.; Niu, G.Y.; Yang, Z.L.; Lawrence, D.M.; Thornton, P.E.; Lawrence, P.J.; Stöckli, R.; Dickinson, R.E.; Bonan, G.B.; Levis, S.; et al. Improvements to the community land model and their impact on the hydrological cycle. J. Geophys. Res. 2008, 113, G01021. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. Roy. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- McNally, A.; Arsenault, K.; Kumar, S.; Shukla, S.; Peterson, P.; Wang, S.; Funk, C.; Peters-Lidard, C.D.; Verdin, J.P. A land data assimilation system for sub-Saharan Africa food and water security applications (FLDAS). Sci. Data 2017, 4, 170012. [Google Scholar] [CrossRef] [PubMed]
- Dinku, T.; Connor, S.J.; Ceccato, P.; Ropelewski, C.F. Comparison of global gridded precipitation products over a mountainous region of Africa. Int. J. Climatol. 2008, 28, 1627–1638. [Google Scholar] [CrossRef]
- Diro, G.T.; Black, E.; Grimes, D.I.F. Seasonal forecasting of Ethiopian spring rains. Meteorol. Appl. 2009, 15, 73–83. [Google Scholar] [CrossRef]
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pedreros, D.H.; Verdin, J.P.; Rowland, J.D.; Romero, B.E.; Husak, G.J.; Michaelsen, J.C.; Verdin, A.P. A quasi-global precipitation time series for drought monitoring. US Geological. Surv. Data Ser. 2014, 832, 1–4. [Google Scholar] [CrossRef]
- Masresha, E. Growing season belts of Ethiopia. In Proceedings of the National Workshop on Agrometeorology and GIS, EIAR, Addis Ababa, Ethiopia, 7–11 July 2003; pp. 35–36. [Google Scholar]
- Araya, S.D.; Keesstra, L.; Stroosnijder, L. A new agro-climatic classification for crop suitability zoning in northern semi-arid Ethiopia. Agricul. For. Meteorol. 2010, 150, 1057–1064. [Google Scholar] [CrossRef]
- Yemenu, F.; Chemeda, D. Climate resources analysis for use of planning in crop production and rainfall water management in the central highlands of Ethiopia, the case of Bishoftu district, Oromia region, Hydrol. Earth Syst. Sci. Discuss 2010, 7, 3733–3763. [Google Scholar] [CrossRef]
- Dereje, G.; Eshetu, A. Crops and Agro-Ecological Zones of Ethiopia; Ethiopian Institute of Agricultural Research: Addis Ababa, Ethiopia, 2011.
- Gebremichael, A.; Quraishi, S.; Mamo, G. Analysis of seasonal rainfall variability for agricultural water resource management in southern region, Ethiopia. J. Nat. Sci. Res. 2014, 4, 2224–3186. [Google Scholar]
- Sawa, B.A.; Adebayo, A.A.; Bwala, A.A. Dynamics of hydrological growing aeason at Kano as evidence of climate change. Asian J. Agric. Sci. 2014, 62, 75–78. [Google Scholar] [CrossRef]
- Thornton, P.K.; Jones, P.G.; Owiyo, T. Mapping Climate Vulnerability and Poverty in Africa, Report to the Department of International Development; UN: Nairobi, Kenya, 2006; 171p. [Google Scholar]
- Ati, O.F.; Stigter, C.J.; Olandipo, E.O. A Comparison of methods to determine the onset of the growing season in northern Nigeria. Int. J. Climatol. 2002, 22, 732–742. [Google Scholar] [CrossRef]
- Nata, T. Surface water potential of the Hantebet Basin, Tigray, Northern Ethiopia. Agric. Eng. Int. CIGRE J. 2006, 8, 5–10. [Google Scholar]
- Kebede, K.; Bekelle, E. Tillage effect on soil water storage and wheat yield on the vertisols of north central highlands of Ethiopia. Ethiop. J. Environ. Stud. Manag. 2008, 1, 49–55. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Met. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. Climate Change 2014: Synthesis Report. Contribution of Working Group I Fifth Assessment Report; Pachauri, M., Ed.; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Bhattacharjee, P.S.; Zaitchik, B.F. Perspectives on CMIP5 model performance in the Nile River head waters regions. Int. J. Climatol. 2015, 35, 4262–4275. [Google Scholar] [CrossRef]
- Jones, C.; Hughes, J.K.; Bellouin, N.; Hardiman, S.C.; Jones, G.S.; Knight, J.; Liddicoat, S.; O’connor, F.M.; Andres, R.J.; Bell, C.; et al. The HadGEM2-ES implementation of CMIP5 centennial simulations. Geosci. Model Dev. 2011, 4, 543–570. [Google Scholar] [CrossRef]
- Frieler, K.; Lange, S.; Piontek, F.; Reyer, C.P.; Schewe, J.; Warszawski, L.; Zhao, F.; Chini, L.; Denvil, S.; Emanuel, K.; et al. Assessing the impacts of 1.5 °C global warming—Simulation protocol of the Inter-Sectoral Impact Model Intercomparison Project ISIMIP2b. Geosci. Model Dev. 2018, 10, 4321–4345. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Reda, D.T.; Engida, A.N.; Asfaw, D.H.; Hamdi, R. Analysis of precipitation based on ensembles of regional climate model simulations and observational databases over Ethiopia for the period 1989–2008. Int. J. Climatol. 2015, 35, 948–971. [Google Scholar] [CrossRef]
- Byrne, M.P.; Pendergrass, A.G.; Rapp, A.D.; Wodzicki, K.R. Response of the intertropical convergence zone to climate change: Location, width, and strength. Curr. Clim. Chang. Rep. 2018, 4, 355–370. [Google Scholar] [CrossRef]
- Shanko, D.; Chamberlain, P. The effects of the southwest Indian ocean tropical cyclones on Ethiopian drought. Int. J. Climatol. 1998, 18, 1373–1388. [Google Scholar] [CrossRef]
- Seleshi, Y.; Zanke, U. Recent changes in rainfall and rainy days in Ethiopia. Int. J. Climatol. 2004, 24, 973–983. [Google Scholar] [CrossRef]
- Conway, D.; Schipper, E.L.F. Adaptation to climate change in Africa: Challenges and opportunities. Glob. Environ. Chang. 2011, 21, 227–237. [Google Scholar] [CrossRef]
- Jury, M.R. Ethiopian highlands crop-climate prediction 1979–2009. J. Appl. Meteorol. Climatol. 2013, 52, 1116–1126. [Google Scholar] [CrossRef]
- Jury, M.R. Statistical evaluation of CMIP5 climate change model simulations for the Ethiopian highlands. Int. J. Climatol. 2015, 35, 37–44. [Google Scholar] [CrossRef]
- Ethiopian Panel on Climate Change (EPCC). First Assessment Report, Working Group I Physical Science Basis; Ethiopian Academy of Sciences: Addis Ababa, Ethiopia, 2015. [Google Scholar]
- Jury, M.R.; Funk, C. Climatic trends over Ethiopia: Regional signals and drivers. Int. J. Climatol. 2013, 33, 1924–1935. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations the CRU4 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
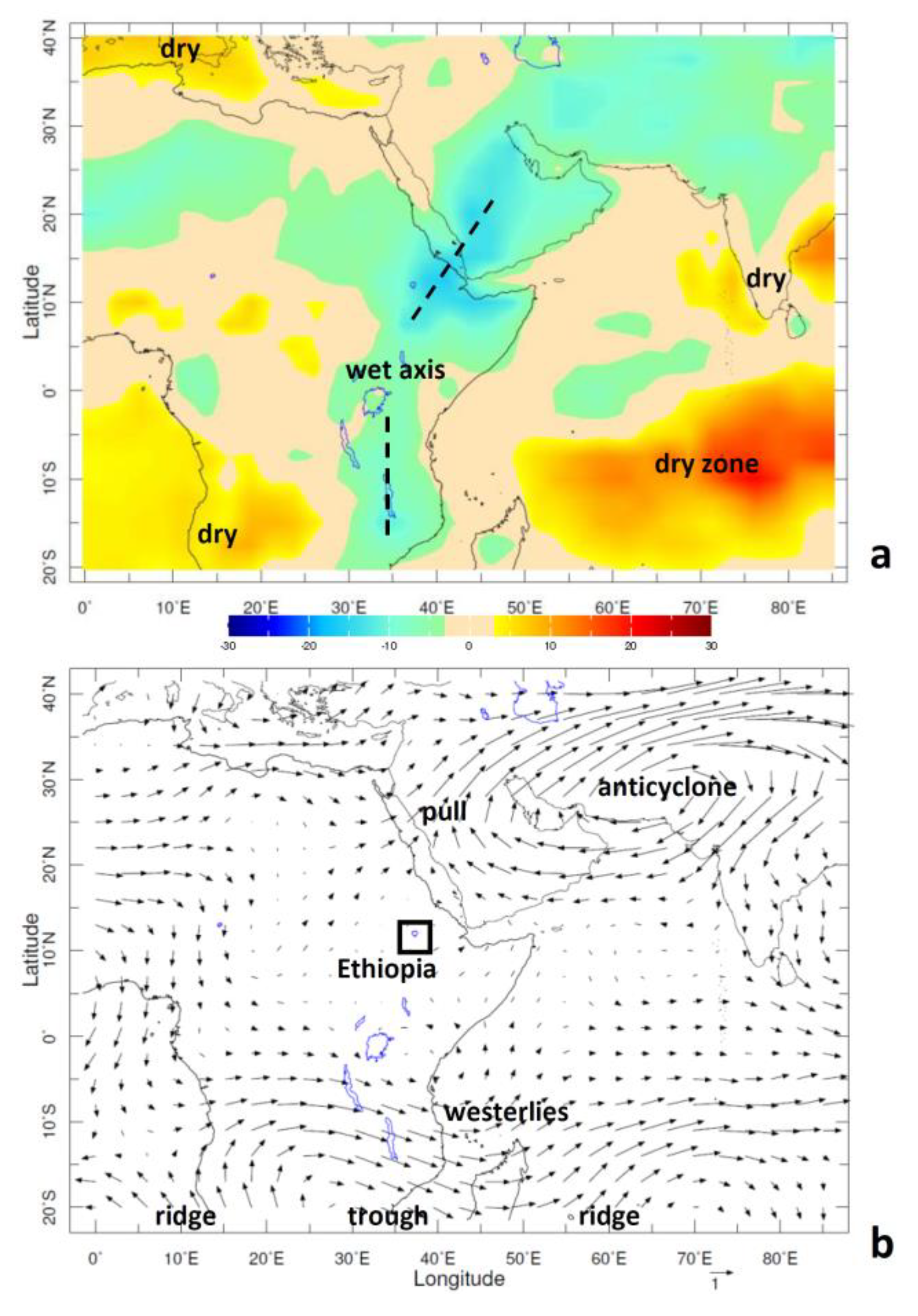
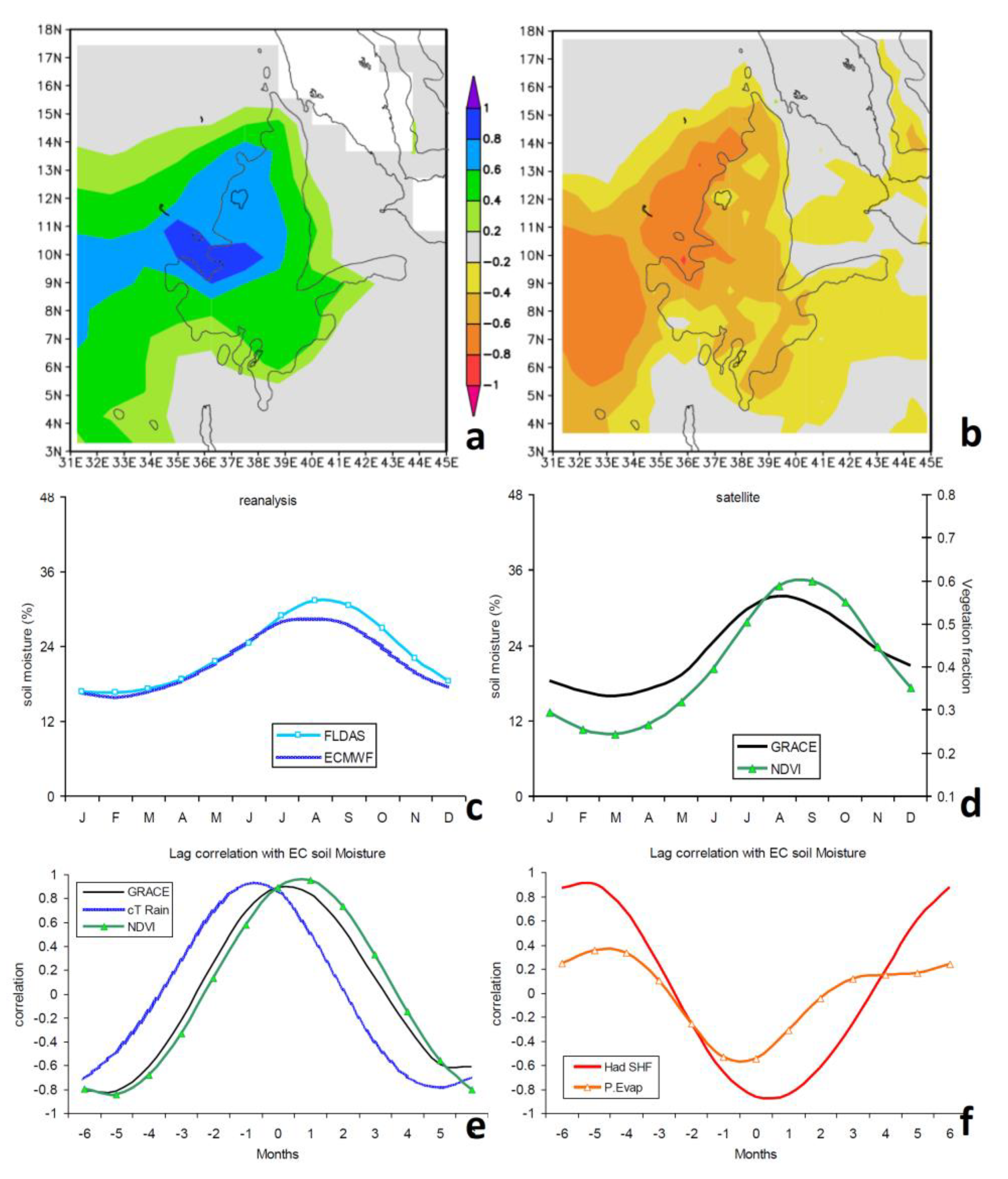
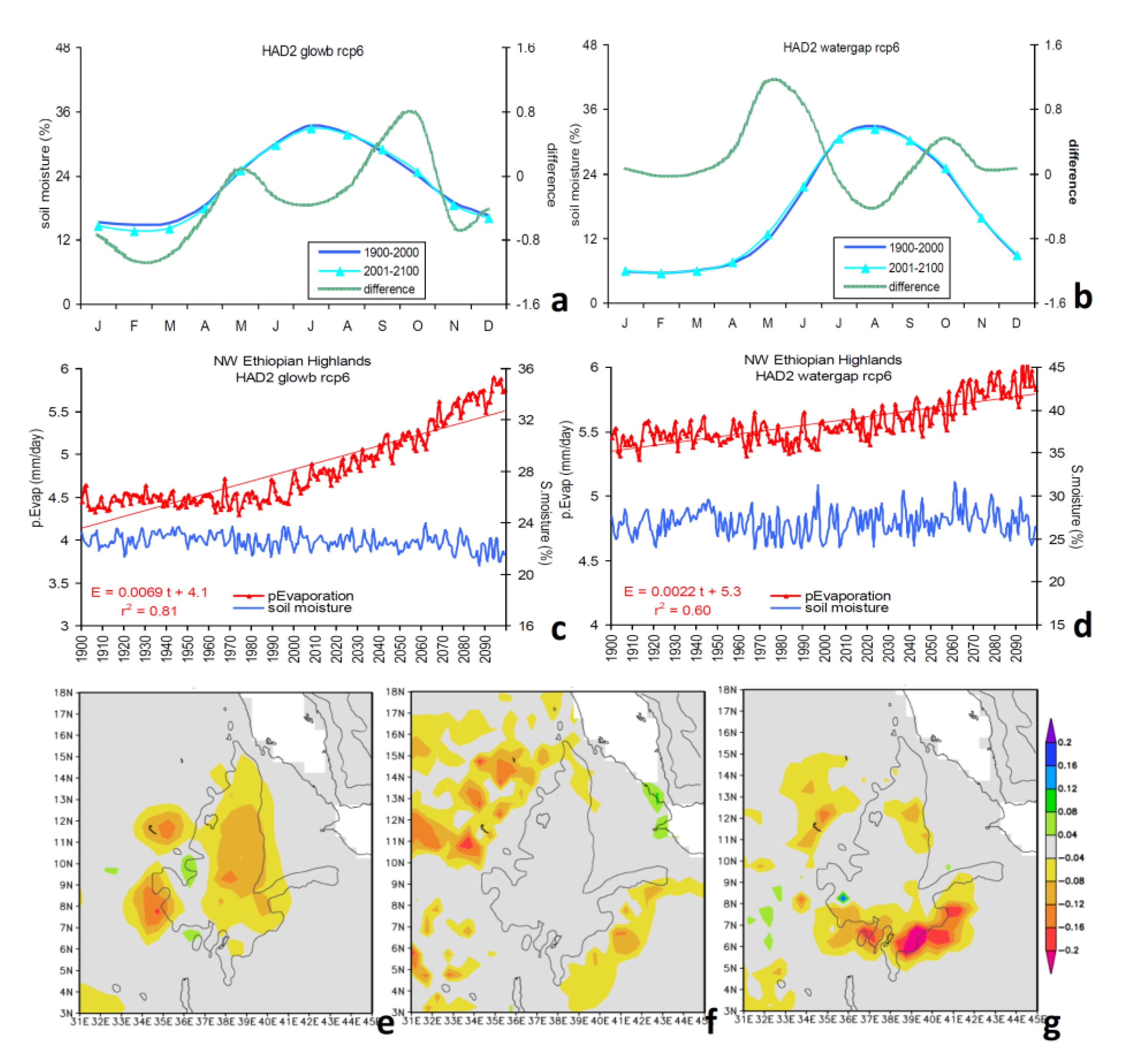
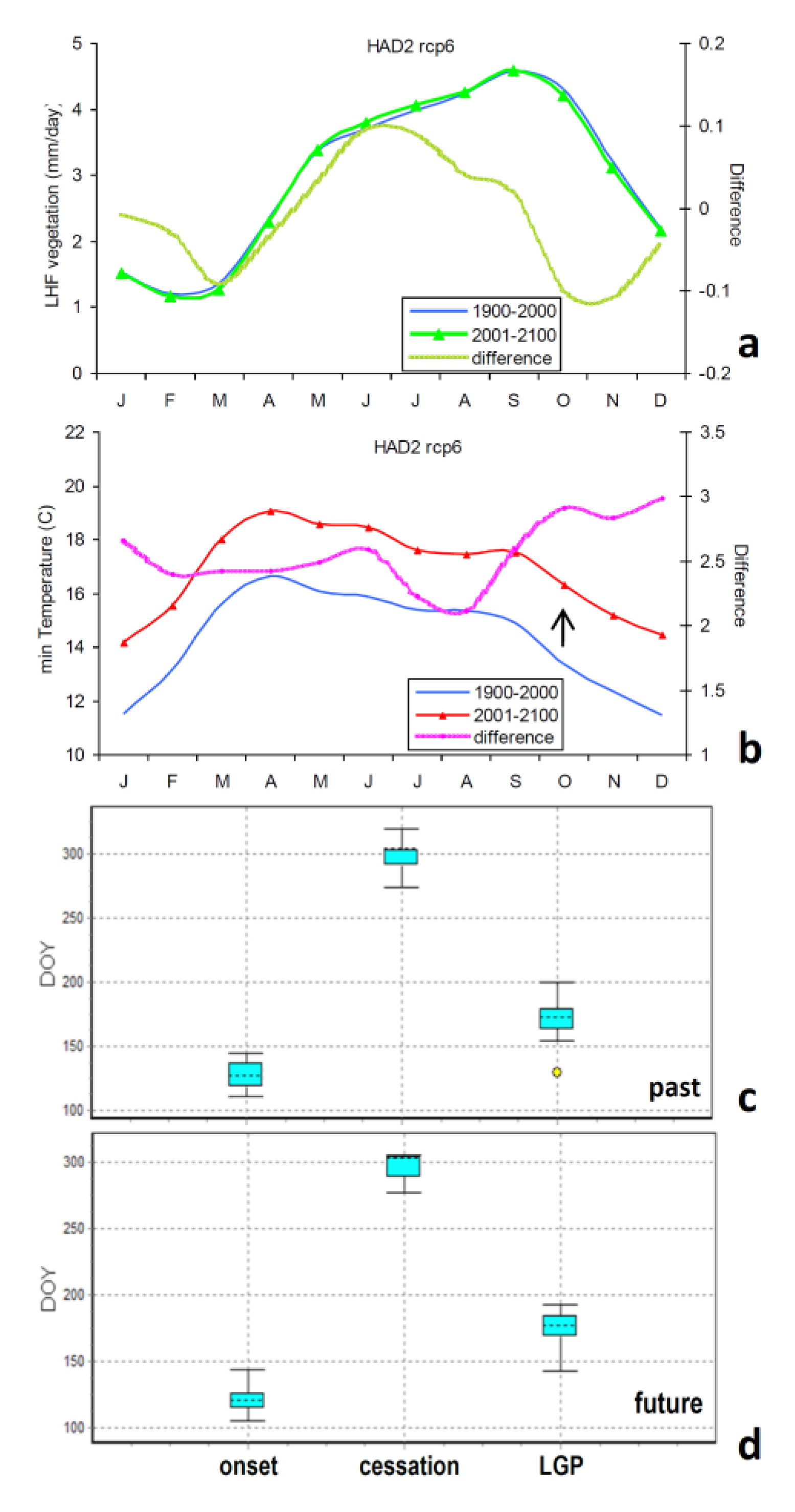
| Scope | Methods and Variables | |
|---|---|---|
| 1 | Determination of homogenous study area | EOF cluster analysis of cenTrends precipitation (P): 8.5–13 N, 35–39.5 E |
| 2 | Evaluate potential evaporation (E) | Comparison of observed, reanalysis, model-simulated sensible heat flux (SHF) |
| 3 | CMIP5 model validation and selection | Apply criteria to determine annual cycle bias in P, SHF as proxy for E |
| 4 | Soil moisture fraction (S) | Compare P–E, latent heat flux (LHF) and NDVI with S |
| 5 | Collection of optimal time series | Area-average NW Ethiopian highlands: P, E, S, T; 8.5–13 N, 35–39.5 E |
| 6 | Characterization of annual cycle | Calculate annual cycle and percentiles for P, E, S, T, LHF; determine shift/width |
| 7 | Meteorological forcing of annual cycle | Composite analysis of reanalysis fields for early-late, wide-narrow LGP |
| 8 | Analysis of climate trends | Statistical regression slope and significance; seasonal changes for P, E, S |
| 9 | Assess LGP and impact of climate change | Onset and cessation in past (1900–2000) and future (2001–2100) |
| LEAST | Early | LEAST | Late | LEAST | Wide | LEAST | Narrow |
|---|---|---|---|---|---|---|---|
| 2003 | 0.06 | 1984 | 0.03 | 2003 | 0.09 | 2014 | 0.38 |
| 1990 | 0.08 | 1995 | 0.03 | 1990 | 0.11 | 1997 | 0.39 |
| 2002 | 0.08 | 1990 | 0.03 | 2002 | 0.12 | 2019 | 0.39 |
| 2009 | 0.08 | 2003 | 0.03 | 2012 | 0.13 | 2015 | 0.40 |
| 1988 | 0.09 | 1991 | 0.04 | 1986 | 0.14 | 1987 | 0.41 |
| 2012 | 0.09 | 2010 | 0.04 | 1991 | 0.15 | 1993 | 0.42 |
| Apr.–May | Oct.–Nov. | Early + late | Jul.–Aug. | ||||
| 1996 | 0.18 | 1982 | 0.11 | 2008 | 0.26 | 1994 | 0.50 |
| 1993 | 0.19 | 2019 | 0.12 | 1987 | 0.26 | 2013 | 0.51 |
| 1987 | 0.19 | 2000 | 0.12 | 2016 | 0.27 | 2009 | 0.52 |
| 2008 | 0.19 | 1992 | 0.13 | 2000 | 0.27 | 2012 | 0.52 |
| 2016 | 0.20 | 1999 | 0.13 | 2014 | 0.29 | 1981 | 0.52 |
| 2014 | 0.20 | 1997 | 0.16 | 1997 | 0.32 | 1990 | 0.54 |
| MOST | early | MOST | late | MOST | wide | MOST | narrow |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarkegn, G.B.; Jury, M.R. Changes in the Seasonality of Ethiopian Highlands Climate and Implications for Crop Growth. Atmosphere 2020, 11, 892. https://doi.org/10.3390/atmos11090892
Tarkegn GB, Jury MR. Changes in the Seasonality of Ethiopian Highlands Climate and Implications for Crop Growth. Atmosphere. 2020; 11(9):892. https://doi.org/10.3390/atmos11090892
Chicago/Turabian StyleTarkegn, Gashaw Bimrew, and Mark R. Jury. 2020. "Changes in the Seasonality of Ethiopian Highlands Climate and Implications for Crop Growth" Atmosphere 11, no. 9: 892. https://doi.org/10.3390/atmos11090892
APA StyleTarkegn, G. B., & Jury, M. R. (2020). Changes in the Seasonality of Ethiopian Highlands Climate and Implications for Crop Growth. Atmosphere, 11(9), 892. https://doi.org/10.3390/atmos11090892





