Analysis of Extreme Temperature Events over the Iberian Peninsula during the 21st Century Using Dynamic Climate Projections Chosen Using Max-Stable Processes
Abstract
1. Introduction
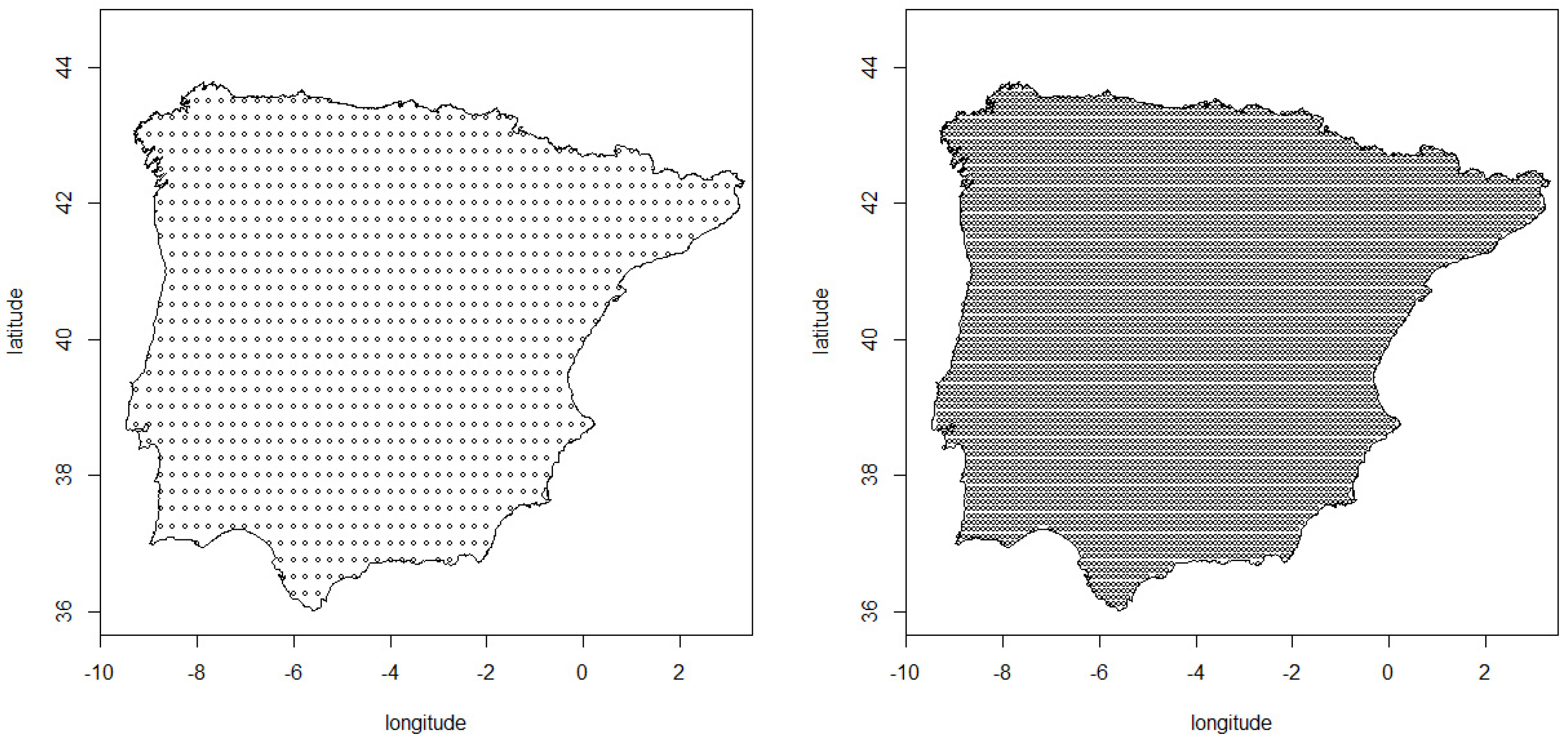
2. Dataset
3. Methodology
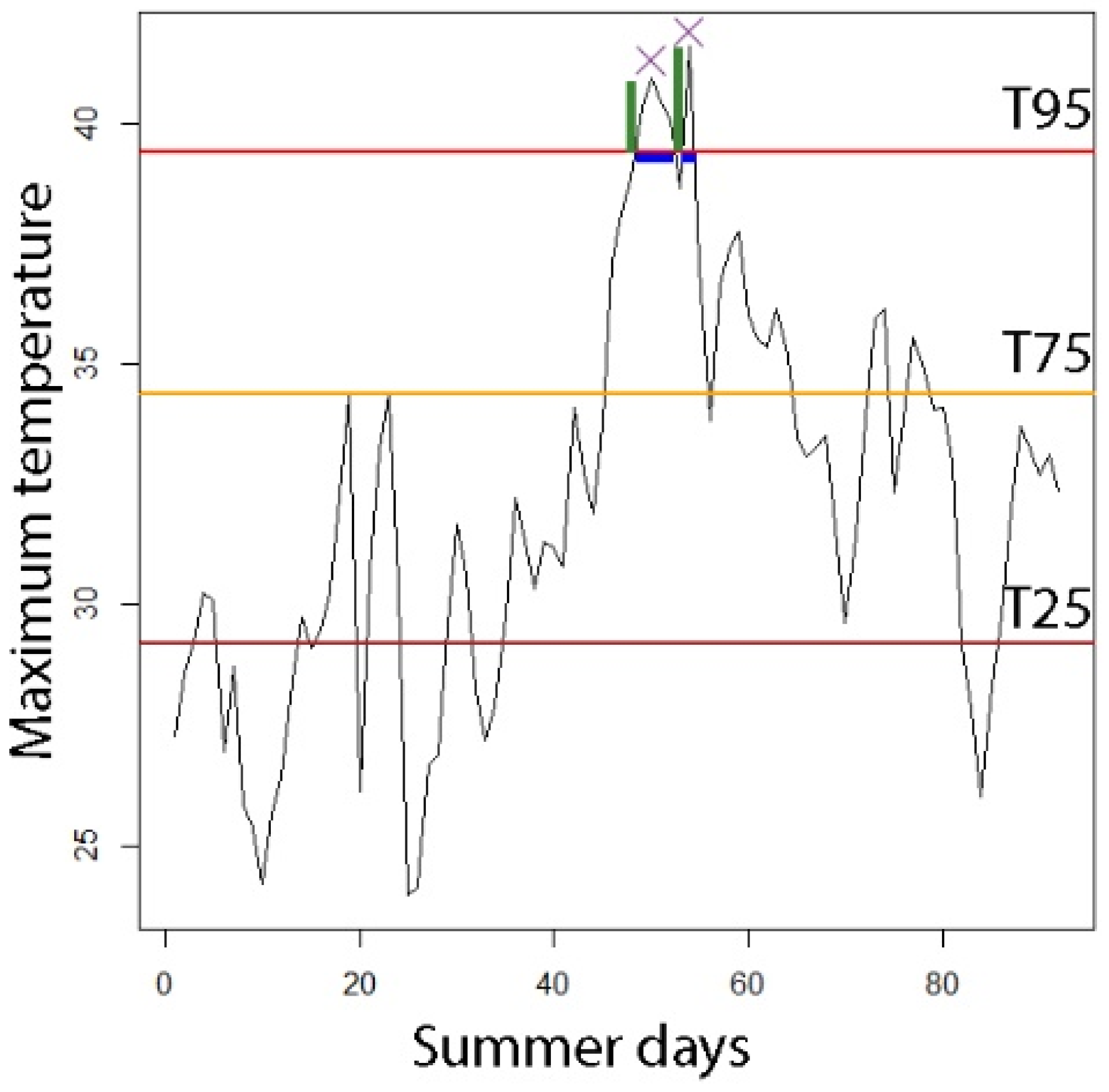
3.1. Definition of Extreme Temperature Events
3.2. Identification of Trends
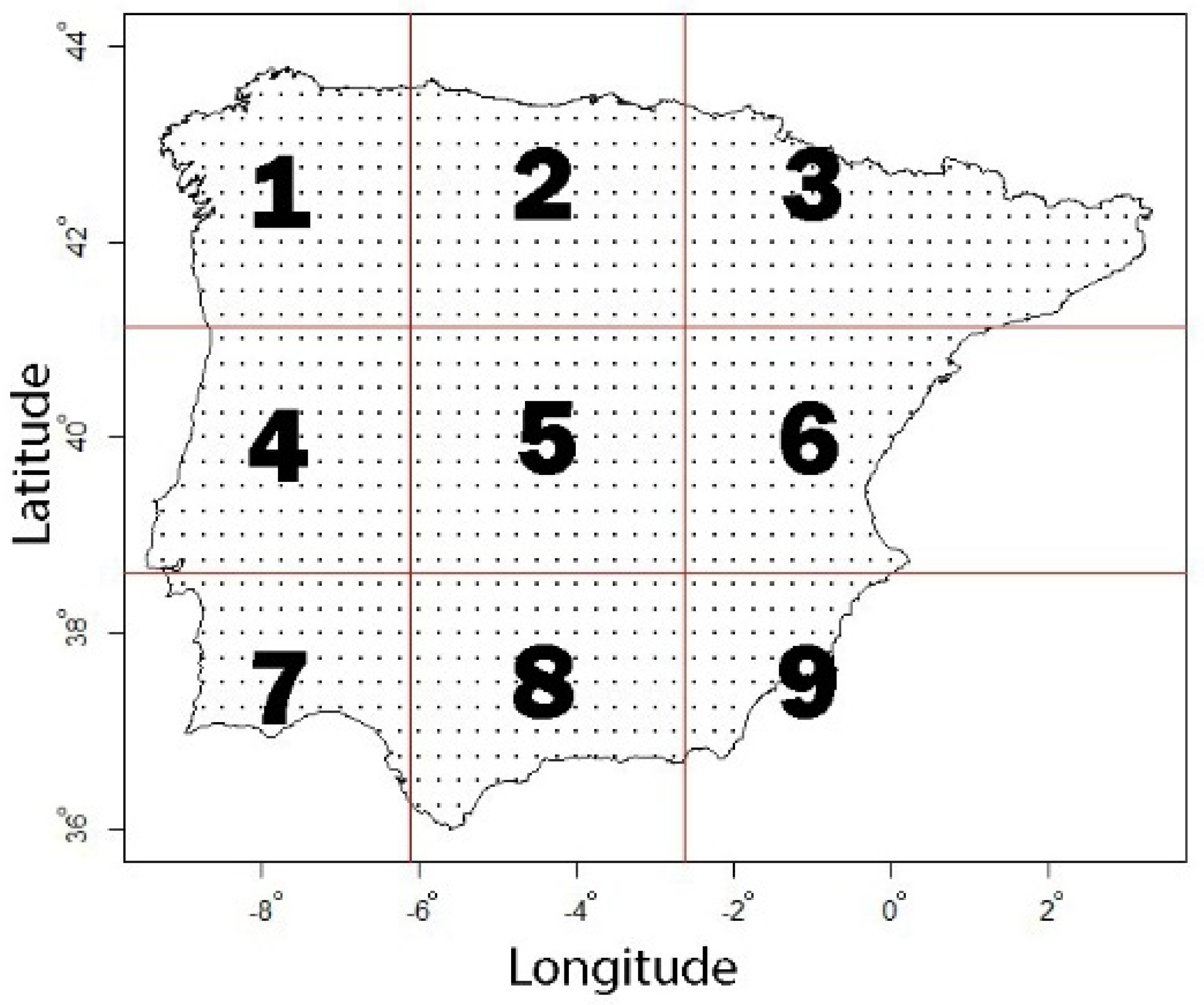
3.3. Spatial Dependence
4. Results
4.1. Comparison Period
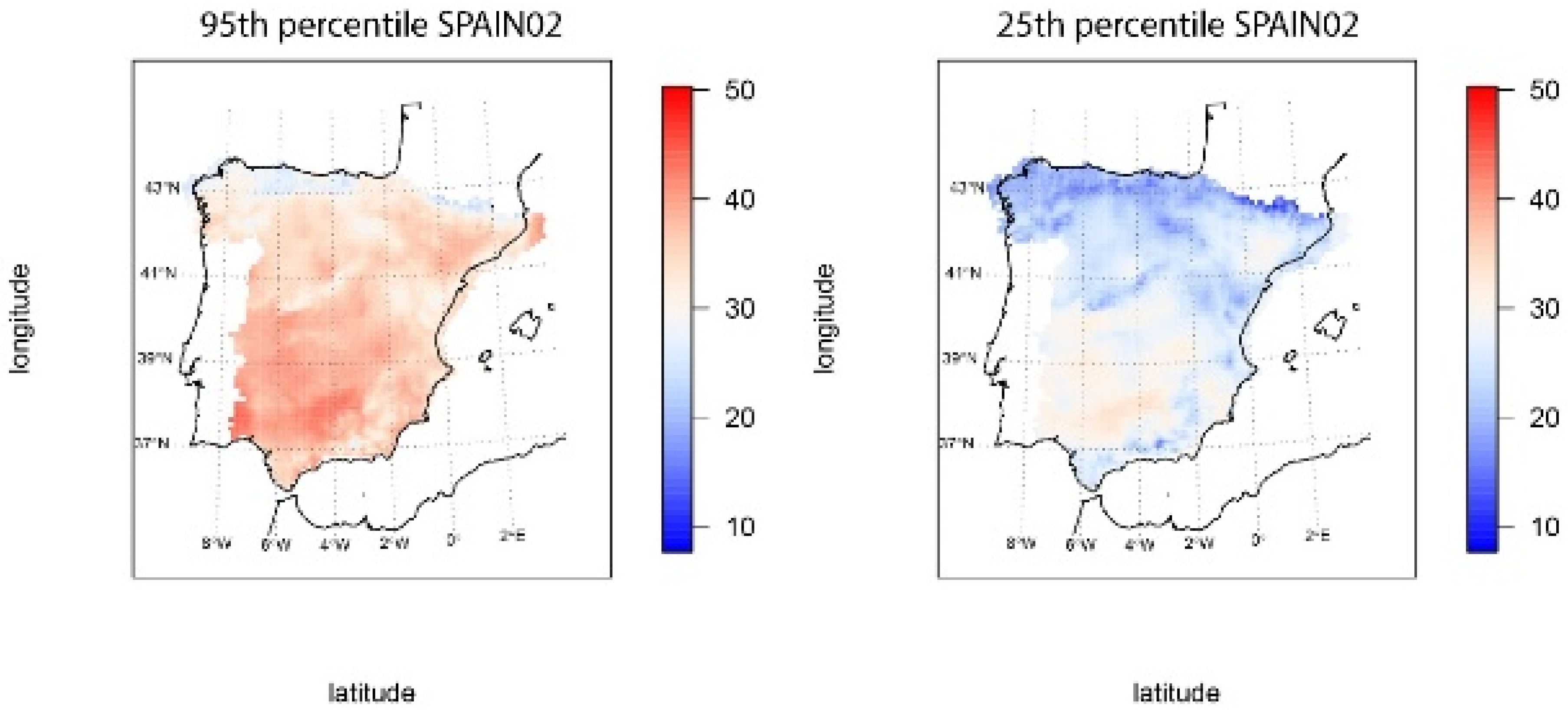
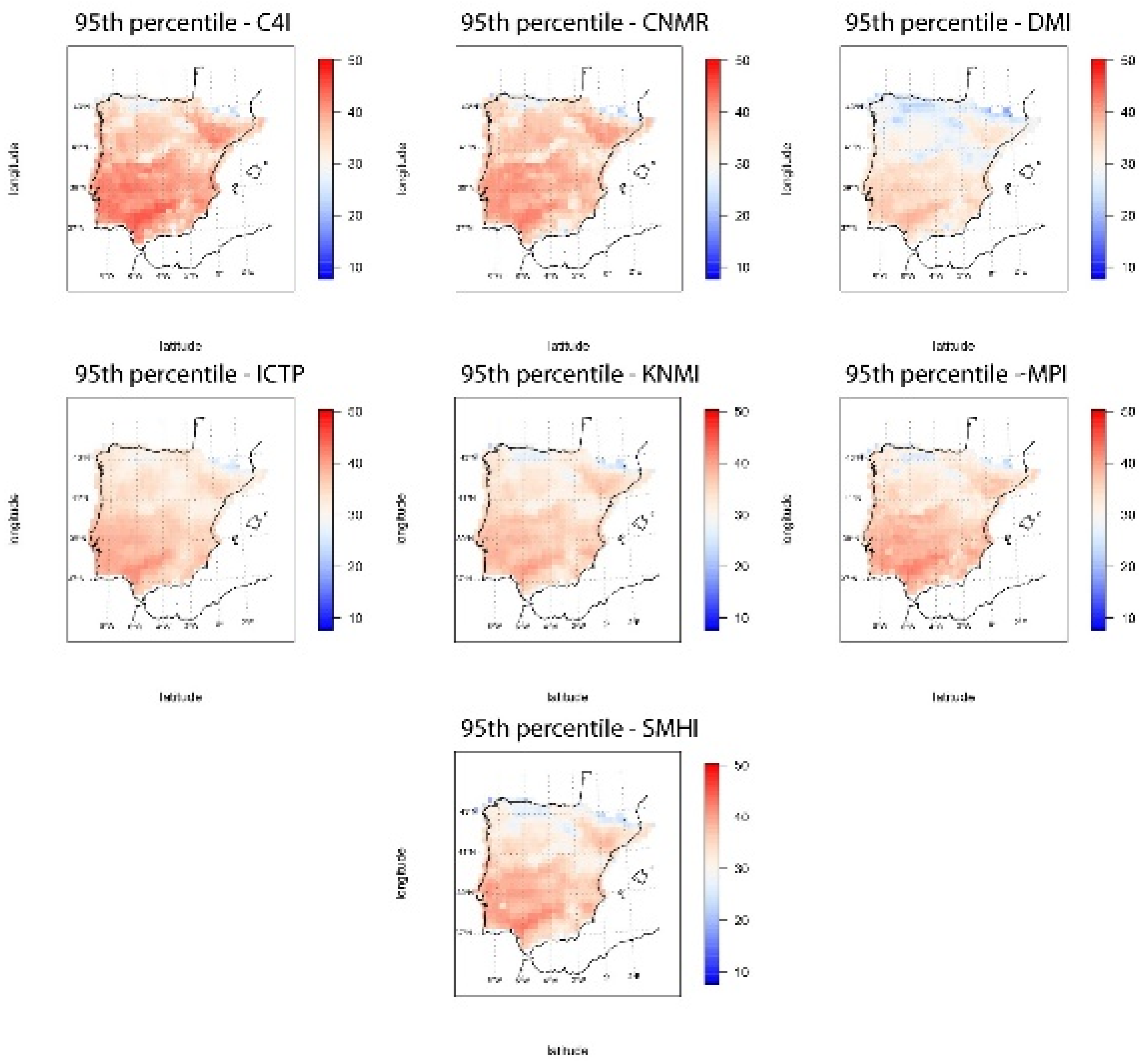
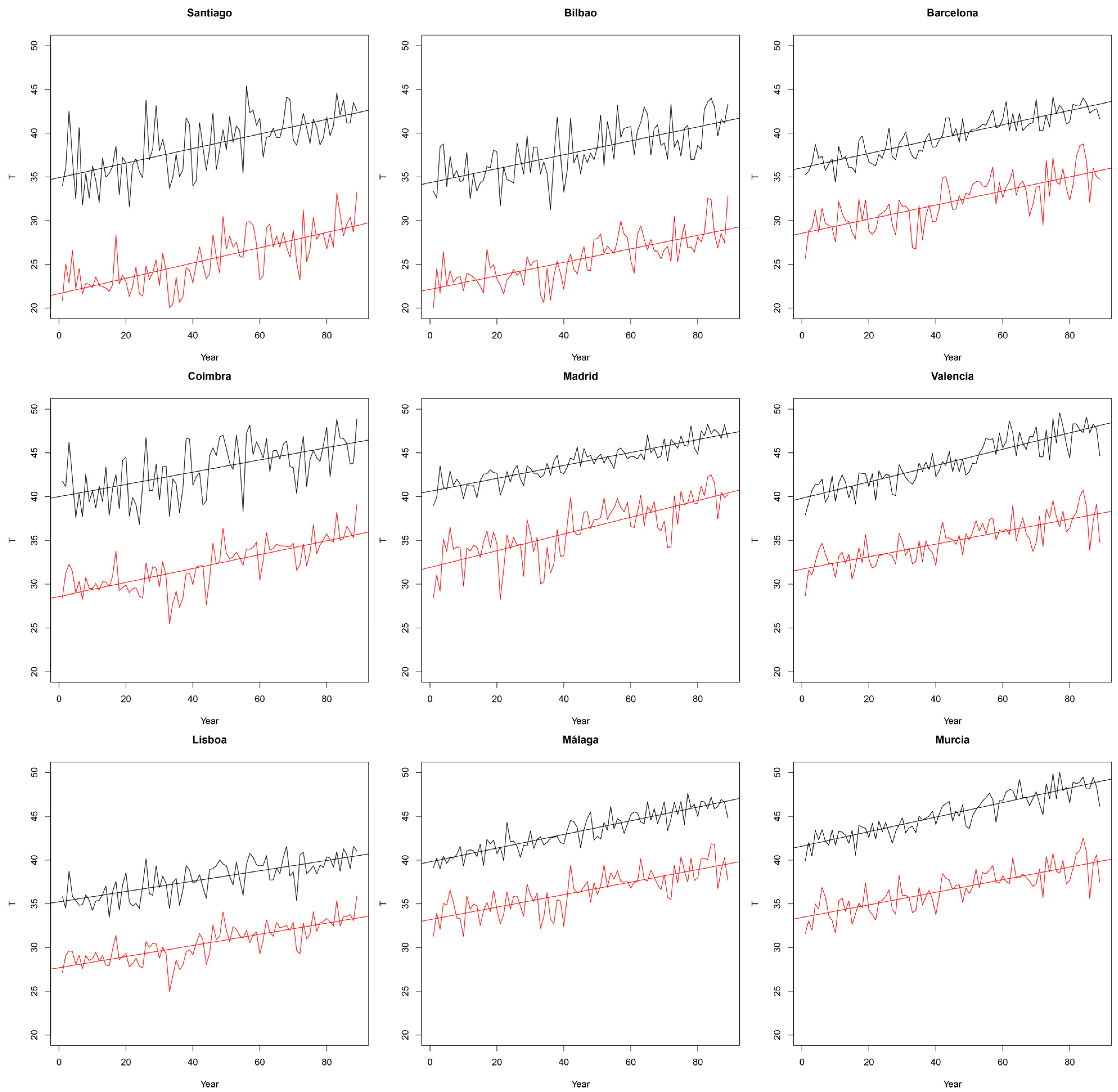
4.1.1. Threshold Distribution
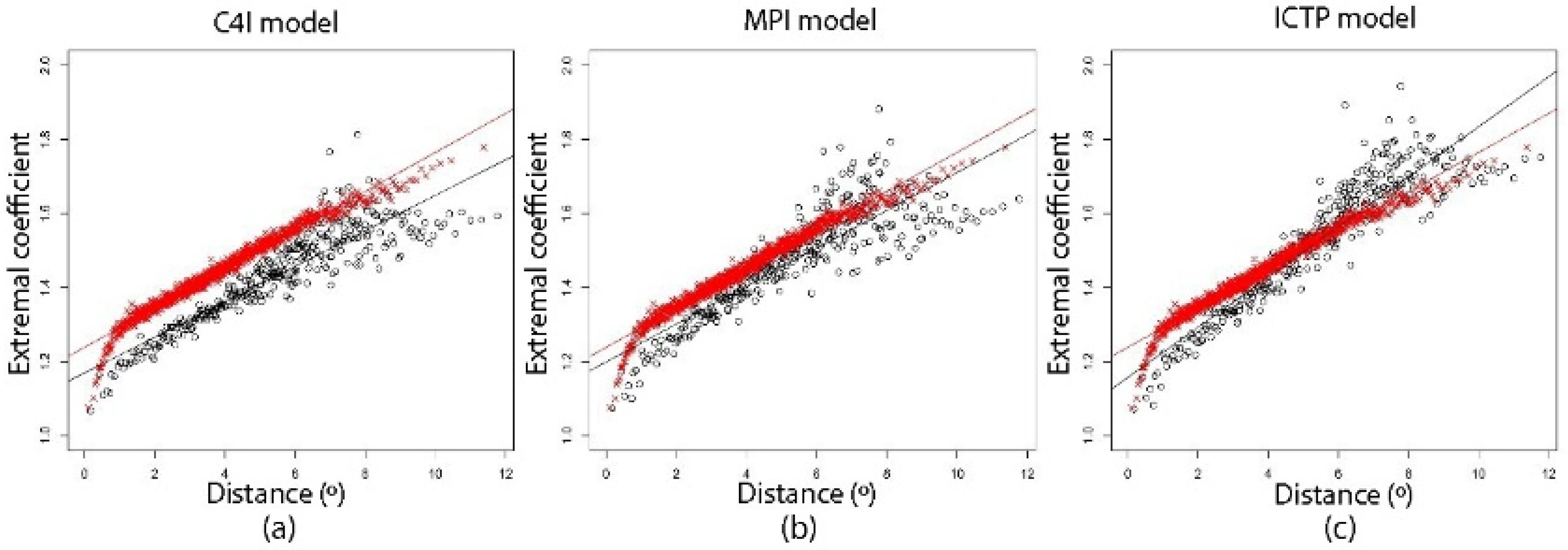
4.1.2. Spatial Dependence
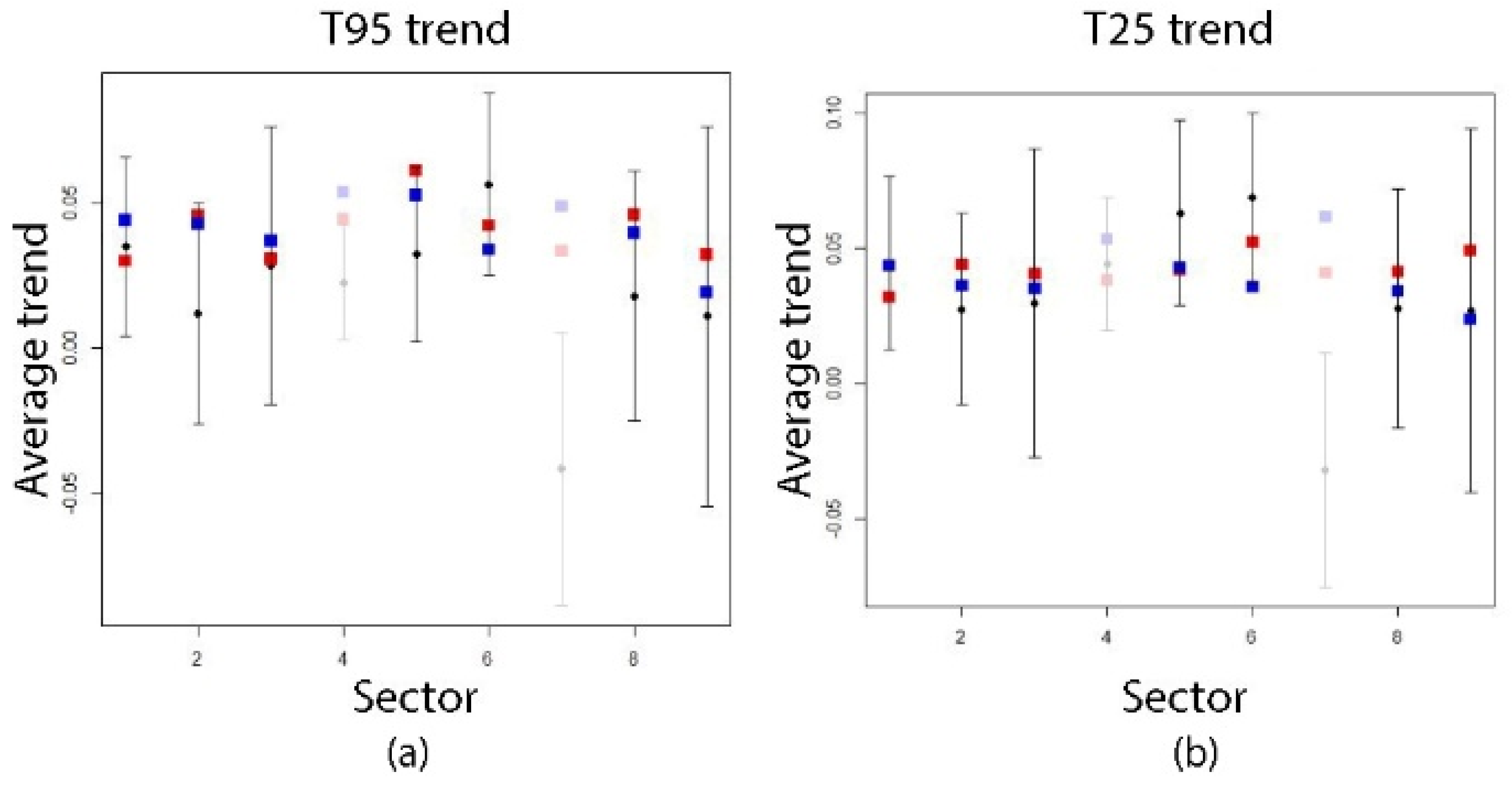
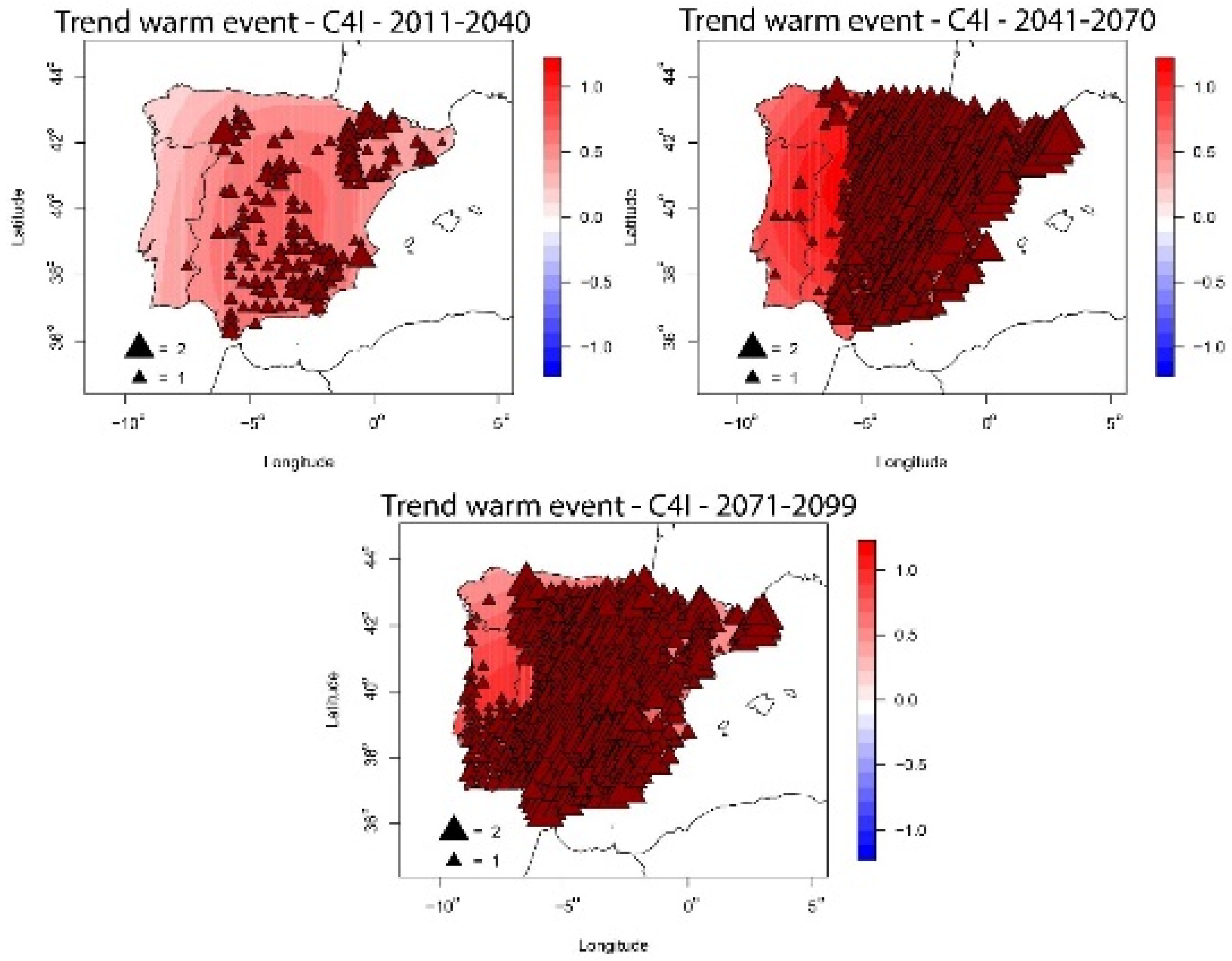
4.1.3. Percentile Trend
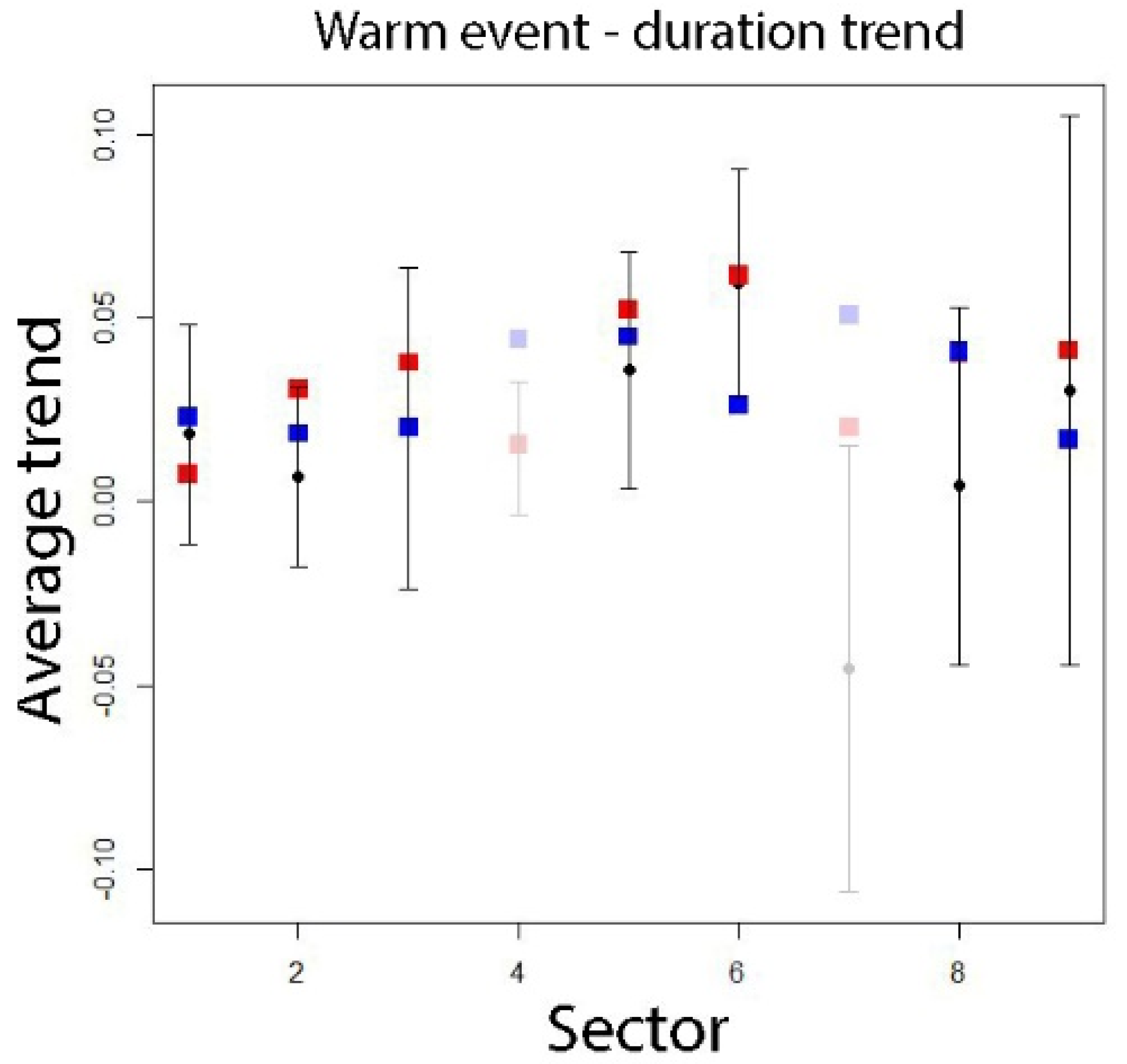
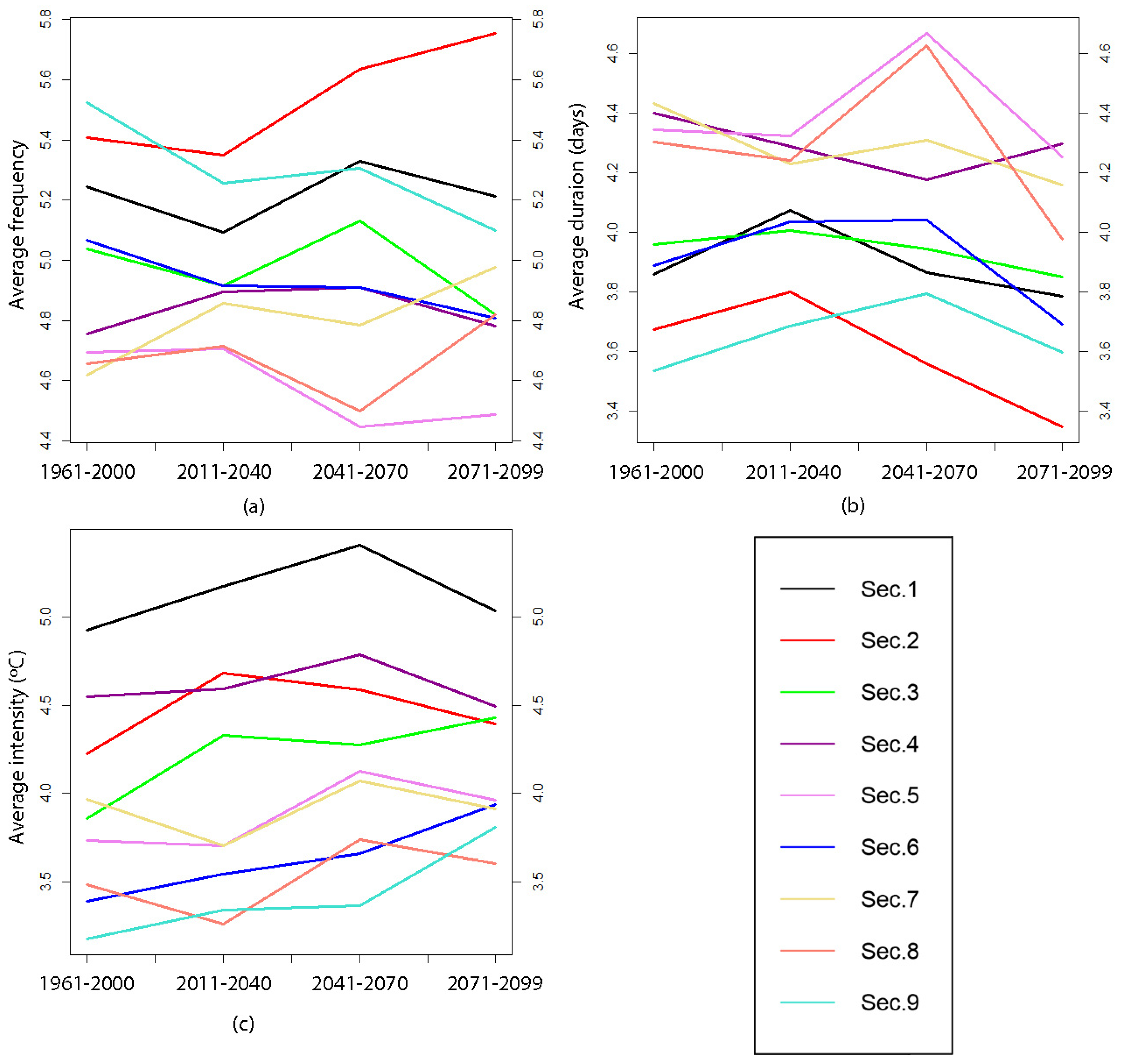
4.1.4. Trends in Warm Events Characteristics
4.1.5. Trends in Heat Waves Characteristics
4.2. Future Period
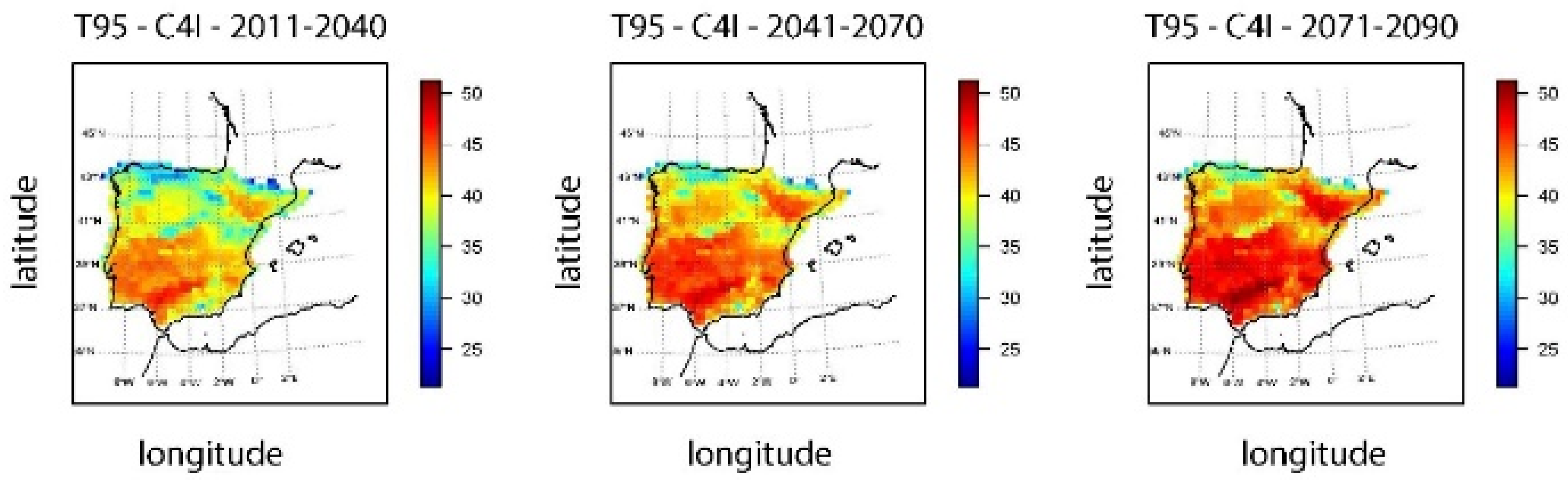
4.2.1. Threshold Distribution
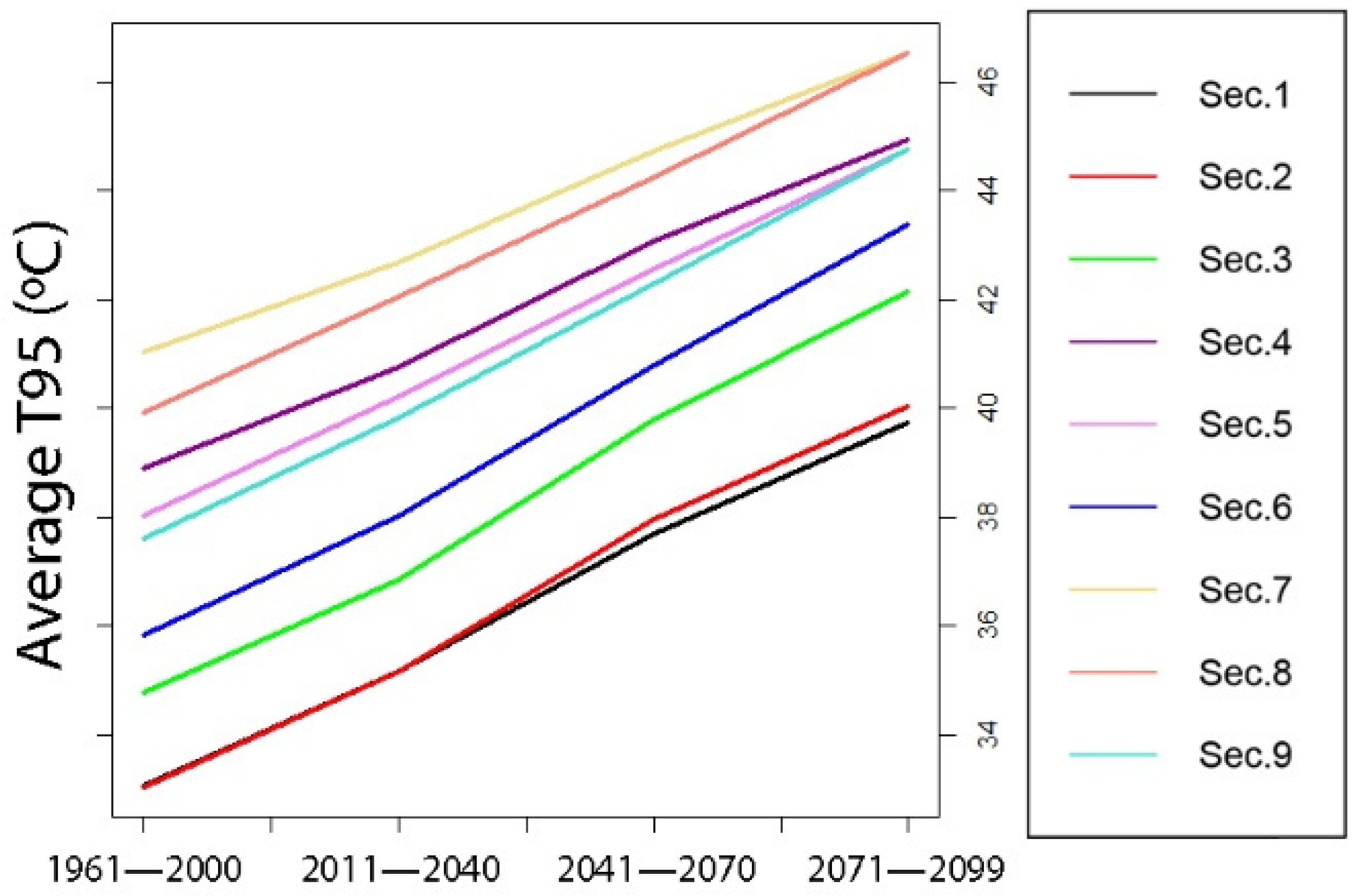
4.2.2. Percentile Trend
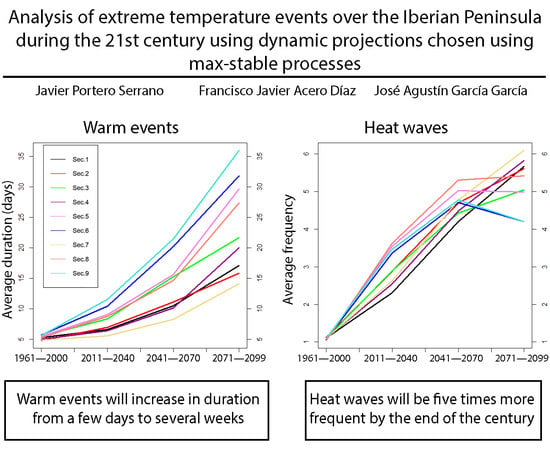
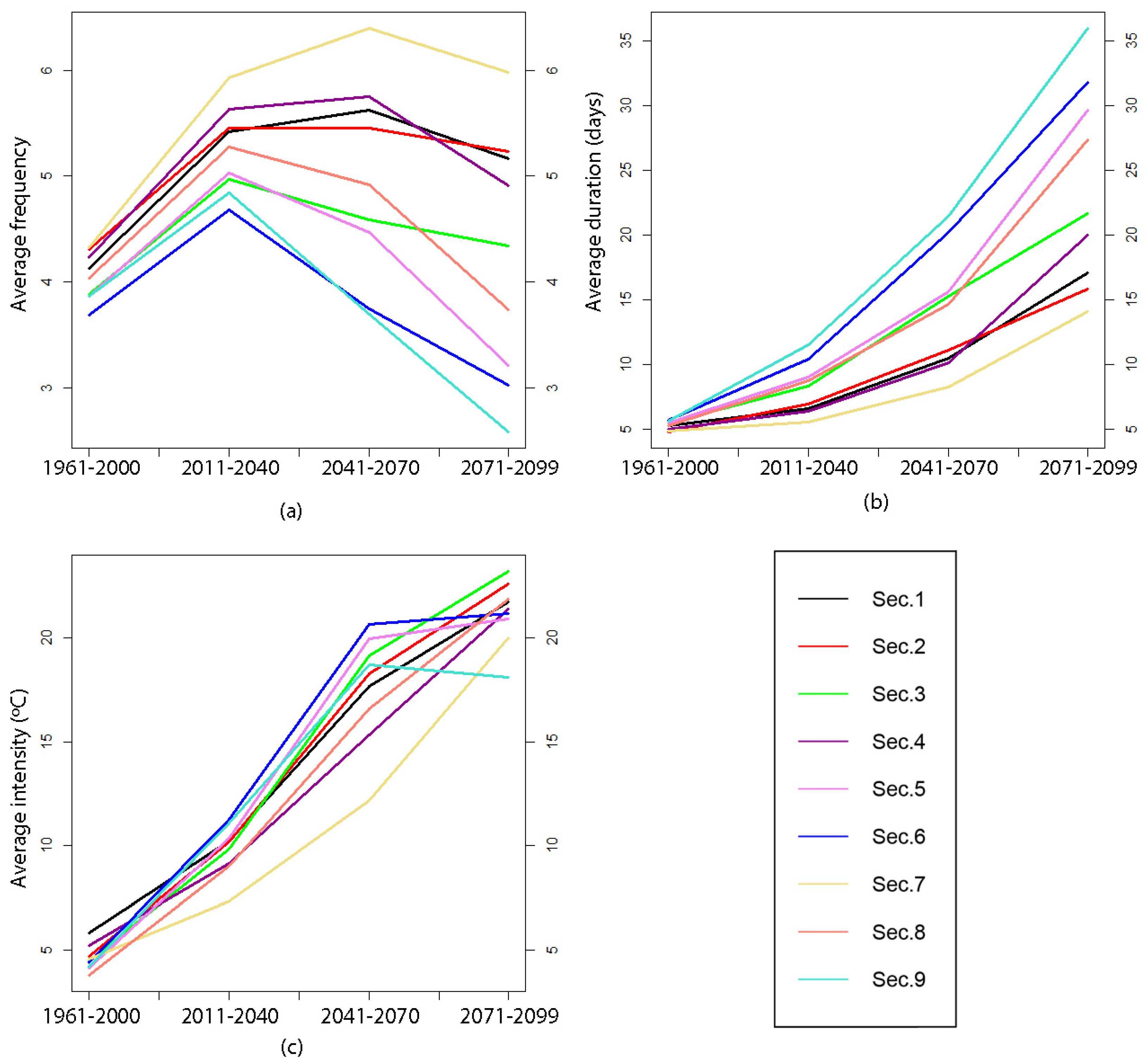
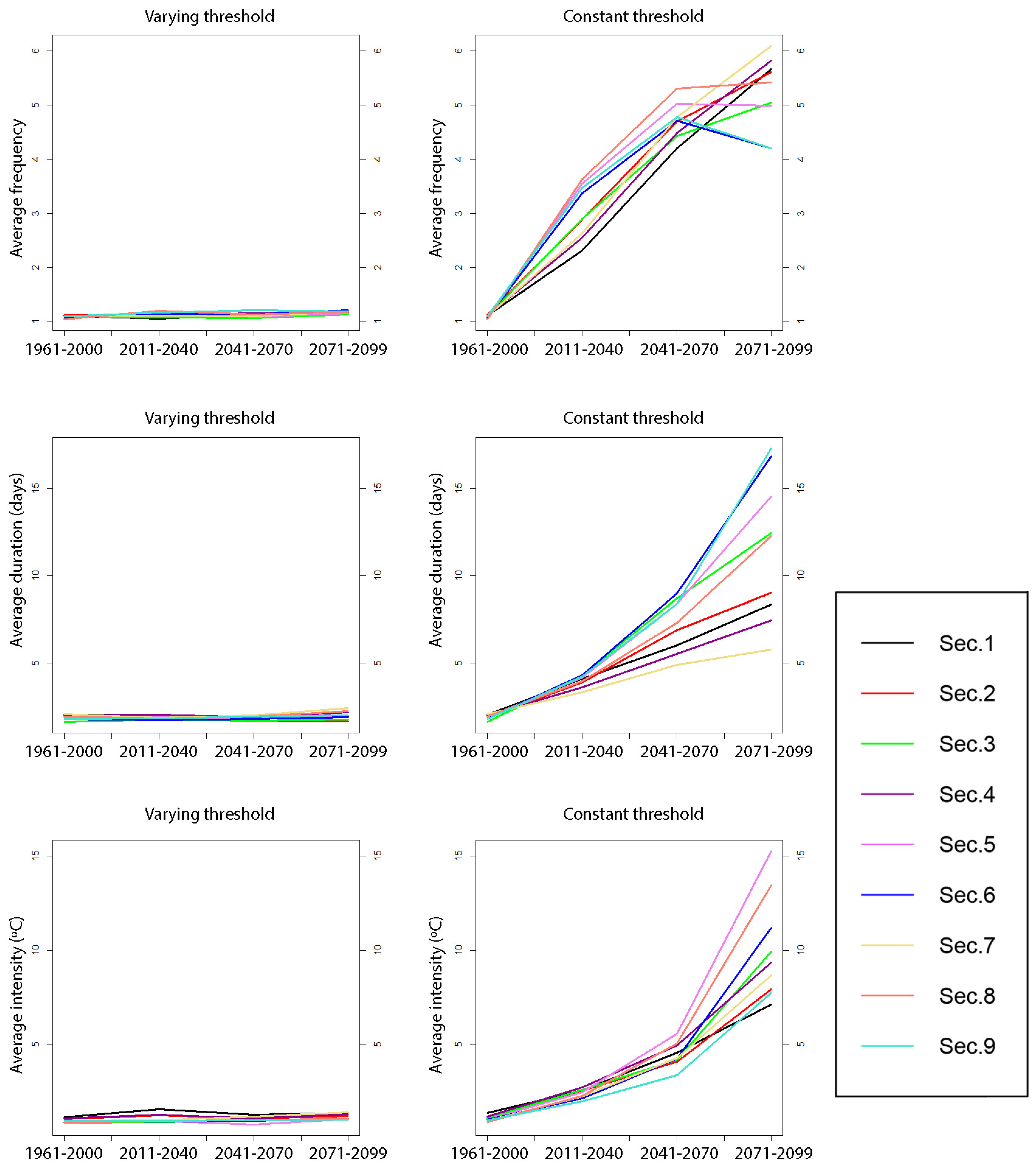
4.2.3. Trend in Future Warm Events Characteristics
4.2.4. Trends in Future Heat Waves Characteristics
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.-O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; IPCC: Geneva, Switzerland, 2018. [Google Scholar]
- Mínguez, M.I. Agriculture in Spain and the Climate Change Issue; Research Center for the Management of Agricultural and Environmental Risks of the Technical University of Madrid (CEIGRAM): Madrid, Spain, 2016. [Google Scholar]
- Brunet, M.; Jones, P.D.; Sigró, J.; Saladié, O.; Aguilar, E.; Moberg, A.; Della-Marta, P.M.; Lister, D.; Walther, A.; López, D. Temporal and spatial temperature variability and change over Spain during 1850–2005. J. Geophys. Res. 2007, 112, D12117. [Google Scholar] [CrossRef]
- Piñol, J.; Terradas, J.; Lloret, F. Climate Warming, Wildlife Hazard, and Wildfire Occurrence in Coastal Eastern Spain. Clim. Chang. 1998, 38, 345–357. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; Esteve, M.A. A critical view of the desertification debate in southeastern Spain. Land Degrad. Dev. 2005, 16, 529–539. [Google Scholar] [CrossRef]
- Fischer, E.M. Autopsy of two mega-heatwaves. Nat. Geosci. 2014, 7, 332–333. [Google Scholar] [CrossRef]
- Bador, M.; Terray, L.; Boé, J.; Somot, S.; Alias, A.; Gibelin, A.; Dubuisson, B. Future summer mega-heatwave and record-breaking temperatures in a warmer France climate. Environ. Res. Lett. 2017, 12, 074025. [Google Scholar] [CrossRef]
- Meehl, G.A.; Tebaldi, C. More intense, more frequent, and more longer lasting heat waves in the 21st Century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef]
- Guerreiro, S.B.; Dawson, R.J.; Kilsby, C.; Lewis, E.; Ford, A. Future heat-waves, droughts and floods in 571 European cities. Environ. Res. Lett. 2018, 13, 034009. [Google Scholar] [CrossRef]
- Olesen, J.E.; Bindi, M. Consequences of climate change for European agricultural productivity, land use and policy. Eur. J. Agron. 2002, 16, 239–262. [Google Scholar] [CrossRef]
- Murgueitio, E.; Chará, J.; Barahona, R.; Cuartas, C.; Naranjo, J. Los sistemas silvopastoriles intensivos (SSPI), herramienta de mitigación y adaptación al cambio climático. Trop. Subtrop. Agroecosyst. 2014, 17, 501–507. [Google Scholar]
- Estrela, T.; Pérez-Martin, M.A.; Vargas, E. Impacts of climate change on wáter resources in Spain. Hydrol. Sci. J. 2012, 57, 1154–1167. [Google Scholar] [CrossRef]
- De Sario, M.; Katsouyanni, K.; Michelozzi, P. Climate change, extreme weather events, air pollution and respiratory health in Europe. Eur. Respir. J. 2013, 42, 826–843. [Google Scholar] [CrossRef] [PubMed]
- Acero, F.J.; Fernández-Fernández, M.I.; Sánchez Carrasco, V.M.; Parey, S.; Huong Hoang, T.T.; Dacunha-Castelle, D.; García, J.A. Changes in heat wave characteristics over Extremadura (SW Spain). Theor. Appl. Climatol. 2018, 133, 605–617. [Google Scholar] [CrossRef]
- Beniston, M.; Stephenson, D.B. Extreme climatic events and their evolution under changing climatic conditions. Glob. Planet. Chang. 2004, 44, 1–9. [Google Scholar] [CrossRef]
- Sari Kovats, R.; Ebi, K.L. Heatwaves and public health in Europe. Eur. J. Public Health 2006, 16, 592–599. [Google Scholar] [CrossRef] [PubMed]
- Meehl, G.A.; Zwiers, F.; Evans, J.; Knutson, T.; Mearns, L.; Whetton, P. Trends in Extreme weather and climate events: Issues related to modeling extremes in projections of future climate change. Bull. Am. Meteorol. Soc. 2000, 81, 3. [Google Scholar] [CrossRef]
- Hughes, L. Climate change and Australia: Trends, projections and impacts. Aust. Ecol. 2003, 28, 423–443. [Google Scholar] [CrossRef]
- Boo, K.-O.; Kwon, W.-T.; Baek, H.-J. Change of extreme events of temperature and precipitation over Korea using regional projection of future climate change. Geophys. Res. Lett. 2006, 33, L01701. [Google Scholar] [CrossRef]
- Pielke, R.A., Sr.; Wilby, R.L. Regional climate downscaling. What’s the point? Eos Trans. Am. Geophys. Union 2012, 93, 52–53. [Google Scholar] [CrossRef]
- Nikulin, G.; Kjellstro, E.; Hansson, U.; Strandberg, G.; Ullerstig, A. Evaluation and future projections of temperature, precipitation and wind extremes over Europe in an ensemble of regional climate simulations. Tellus A Dyn. Meteorol. Oceanogr. 2009, 63, 41–55. [Google Scholar] [CrossRef]
- Yang, T.; Wang, X.; Zhao, C.; Chen, X.; Yu, Z.; Shao, Q.; Xu, C.-Y.; Xia, J.; Wang, W. Changes of climate extremes in a typical arid zone: Observations and multimodel ensemble projections. J. Geophys. Res. 2011, 116, D19. [Google Scholar] [CrossRef]
- Forzieri, G.; Feyen, L.; Rojas, R.; Flörke, M.; Wimmer, F.; Bianchi, A. Emsemble projections of future streamflow droughts in Europe. Hydrol. Earth Syst. Sci. 2014, 18, 85–108. [Google Scholar] [CrossRef]
- Herrera, S.; Fernández, J.; Gutiérrez, J.M. Update of the Spain02 gridded observational dataset for EURO-CORDEX evaluation: Assessing the effect of the interpolation methodology. Int. J. Climatol. 2016, 36, 900–908. [Google Scholar] [CrossRef]
- Tang, J.; Niu, X.; Wang, S.; Gao, H.; Wang, X.; Wu, J. Statistical downscaling and dynamical downscaling of regional climate in China: Present climate evaluations and future climate projections. J. Geophys. Res. Atmos. 2016, 121, 2110–2129. [Google Scholar] [CrossRef]
- Reich, B.J.; Shaby, B.A. A hierarchical max-stable spatial model for extreme precipitation. Ann. Appl. Stat. 2012, 6, 1430–1451. [Google Scholar] [CrossRef]
- Coles, S.G. Regional Modelling of Extreme Storms Via Max-Stable Processes. J. R. Stat. Soc. 1993, 55, 797–816. [Google Scholar] [CrossRef]
- Ribatet, M. Spatial extremes: Max-stable processes at work. J. Société Française Stat. 2013, 154, 156–177. [Google Scholar]
- Giorgi, F.; Gutowski, W.J., Jr. Regional Dynamical Downscaling and the CORDEX Initiative. Annu. Rev. Environ. Resour. 2015, 40, 467–490. [Google Scholar] [CrossRef]
- Gordon, C.; Cooper, C.; Senior, C.A.; Banks, H.; Gregory, J.M.; Johns, T.C.; Mitchell, J.F.B.; Wood, R.A. The simulation of SST, sea ice extents and ocean heat transports in a version of the Hadley Centre coupled model without flux adjustments. Clim. Dyn. 2000, 16, 147–168. [Google Scholar] [CrossRef]
- Samuelsson, P.; Jones, C.G.; Willén, U.; Ullerstig, A.; Gollvik, S.; Hansson, U.; Jansson, C.; Kjellström, E.; Nikulin, G.; Wyser, K. The Rossby Centre Regional Climate model RCA3: Model description and performance. Tellus A Dyn. Meteorol. Oceanogr. 2011, 63, 4–23. [Google Scholar] [CrossRef]
- Li, S.; Jarvis, A. Long run surface temperature dynamics of an A-OGCM: The HadCM3 4xCO2 forcing experiment revisited. Clim. Dyn. 2009, 33, 817–825. [Google Scholar] [CrossRef]
- Déqué, M.; Dreveton, C.; Braun, A.; Cariolle, D. The ARPEGE/IFS atmosphere model: A contribution to the French community climate modelling. Clim. Dyn. 1994, 10, 249–266. [Google Scholar] [CrossRef]
- Dosio, A. Bias Corrected High Resolution Temperature and Precipitation Projection for Europe in Daily Temporal Resolution from the CNRM RM5 Regional Climate Model Driven by Boundary Conditions from the ARPEGE Global Circulation Model According to SRES A1B Scenario, 1961–2099 (ENSEMBLES); European Commision: Brussels, Belgium; Joint Research Centre (JRC): Ispra, Italy, 2015. [Google Scholar]
- Timbal, B.; Royer, J.F.; Mahfouf, J.F.; Déqué, M. Sensitivity Parameters of the Meteo-France Climate Models: Emeraude and Arpege. In Climate Sensitivity to Radiative Perturbations: Physical Mechanisms and Their Validation; Springer: New York, NY, USA, 1996; pp. 203–212. ISBN 9783642610530. [Google Scholar]
- Christensen, O.B.; Drews, M.; Christensen, J.H.; Dethloff, K.; Ketelsen, K.; Hebestadt, I.; Rinke, A. The HIRHAM Regional Climate Model. Version 5; Technical Report 06-17; Danish Climate Center, Danish Meteorological Institute: Copenhagen, Denmark, 2007; ISSN 1399-1388. [Google Scholar]
- Roeckner, E.; Bäuml, G.; Bonaventura, L.; Brokopf, R.; Esch, M.; Giorgetta, M.; Hagemann, S.; Kirchner, I.; Kornblueh, L.; Manzini, E.; et al. The Atmospheric General Circulation Model ECHAM5. Part 1; Report Nº 349; Max Planck Institute for Meteorology: Hamburg, Germany, 2003; ISSN 0937-1060. [Google Scholar]
- Andrews, T.; Gregory, J.M.; Webb, M.J.; Taylor, K.E. Forcing, feedbacks and climate sensitivity in CMIP5 coupled atmosphere-ocean climate models. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Rockel, B.; Geyer, B. The performance of the regional climate model CLM in different climate regions, based on the example of precipitation. Meteorol. Z. 2008, 17, 487–498. [Google Scholar] [CrossRef]
- Hadley Centre for Climate Prediction and Research. UKCP09: Met Office Hadley Centre Regional Climate Model (HadRM3-PPE) Data; NCAS British Atmospheric Data Centre, Date of Citation; Hadley Centre for Climate Prediction and Research: Exeter Devon, UK, 2008. [Google Scholar]
- Pal, J.S.; Giorgi, F.; Bi, X.; Elguindi, N. Regional climate modelling for the developing world: The ICTP RegCM3 and RegCNET. Bull. Am. Meteorol. Soc. 2007, 88, 1395–1409. [Google Scholar] [CrossRef]
- Van Meijgaard, E.; Van Ulft, L.H.; Van de Berg, W.J.; Bosveld, F.C.; Van den Hurk, B.J.J.M.; Lenderink, G.; Siebesma, A.P. The KNMI Regional Atmospheric Climate Model RACMO Version 2.1; Technical Report TR-302; KNMI: De Bilt, The Netherlands, 2008. [Google Scholar]
- Remo-RCM The REMO Model. Available online: https://www.remo-rcm.de/059966/index.php.en (accessed on 12 April 2020).
- Tijiputra, J.F.; Assman, K.; Bentsen, M.; Bethke, I.; Ottera, O.H.; Sturm, C.; Heine, C. Bergen Earth system model (BCM-C): Model description and regional climate-carbon cycle feedback assessment. Geosci. Model Dev. 2010, 3, 123–141. [Google Scholar] [CrossRef]
- Uppala, S.M.; Kallberg, P.W.; Simmons, A.J.; Andrae, U.; Da Costa Bechtold, V.; Fiorino, M.; Gibson, J.K.; Haseler, J.; Hernandez, A.; Kelly, G.A.; et al. The ERA-40 re-analysis. Q. J. R. Meteorol. Soc. 2005, 131, 2961–3012. [Google Scholar] [CrossRef]
- van der Linden, P.; Mitchell, J.F.B. (Eds.) ENSEMBLES: Climate Change and Its Impacts: Summary of Research and Results from the ENSEMBLES Project; Met Office Hadley Centre: Exeter, UK, 2009; p. 160.
- Nakicenovic, N.; Davidson, O.; Davis, G.; Grübler, A.; Kram, T.; La Rovere, E.L.; Metz, B.; Morita, T.; Pepper, W.; Pitcher, H.; et al. Emissions Scenarios; IPCC Special Report; IPCC: Geneva, Switzerland, 2000; ISBN 92-9169-113-5. [Google Scholar]
- Le Quéré, C.; Raupach, M.R.; Canadell, J.; Marland, G.; Bopp, L.; Ciais, P.; Conway, T.J.; Doney, S.C.; Feely, R.A.; Foster, P.; et al. Trends in the sources and sinks of carbon dioxide. Nat. Geosci. 2009, 2, 831–836. [Google Scholar] [CrossRef]
- Hewitt, C.D. ENSEMBLES-providing ensemble-based predictions of climate changes and their impacts. Parliam. Mag. 2005, 11, 57. [Google Scholar]
- Giannakopoulos, C.; Kostopoulou, E.; Varotsos, K.V.; Tziotziou, K.; Plitharas, A. An integrated assessment of climate change impacts for Greece in the near future. Reg. Environ. Chang. 2011, 11, 829–843. [Google Scholar] [CrossRef]
- Thompson, D.W.J.; Barnes, E.A.; Deser, C.; Fouest, W.E.; Phillips, A.S. Quantifying the Role of Internal Climate Variability in Future Climate Trends. Am. Meteorol. Soc. 2015, 28, 6443–6456. [Google Scholar] [CrossRef]
- Deser, C.; Philips, A.; Bourdette, V.; Teng, H. Uncertainty in climate change projections: Te role of internal variability. Clim. Dyn. 2012, 38, 527–546. [Google Scholar] [CrossRef]
- Fischer, E.M.; Sedlácek, J.; Hawkins, E.; Knutti, R. Models agree on forced response pattern of precipitation and temperatures extremes. Geophys. Res. Lett. 2014, 41, 8554–8562. [Google Scholar] [CrossRef]
- Suarez-Gutierrez, L.; Li, C.; Müller, W.A.; Marotzke, J. Internal Variability in European summer temperatures at 1.5 °C and 2 °C of global warming. Environ. Res. Lett. 2018, 13, 064026. [Google Scholar] [CrossRef]
- Tong, S.; Wang, X.Y.; Barnett, A.G. Assessment of Heat-Related Health Impacts in Brisbane, Australia: Comparison of Different Heatwave Definitions. PLoS ONE 2010, 5, e12155. [Google Scholar] [CrossRef] [PubMed]
- Acero, F.J.; García, J.A.; Gallego, M.C.; Parey, S.; Dacunha-Castelle, D. Trends in summer extreme temperatures over the Iberian Peninsula using nonurban station data. J. Geophys. Res. Atmos. 2013, 119, 39–53. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1369–1379. [Google Scholar] [CrossRef]
- Kendall, S. Time Series; Oxford University Press: New York, NY, USA, 1976. [Google Scholar]
- Gallego, M.C.; García, J.A.; Vaquero, J.M.; Mateos, V.L. Changes in frequency and intensity of daily precipitation over the Iberian Peninsula. J. Geophys. Res. 2006, 111, D24105. [Google Scholar] [CrossRef]
- Wilcox, R.R. Introduction to Robust Estimation and Hypothesis Testing; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Ribatet, M.; Dombry, C.; Oesting, M. Spatial Extremes and max-stable processes. In Extreme Value Modelling and Risk Analysis: Methods and Applications; Dey, D., Yan, J., Eds.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015; pp. 176–194. [Google Scholar]
- Alves, M.I.F.; Neves, C. Extreme Value Distribution. 2010. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.631.1233&rep=rep1&type=pdf (accessed on 10 May 2020).
- Ribatet, M.; Mohammed, S. Extreme copulas and max-stables processes. J. Soc. Française Stat. 2013, 154, 138–150. [Google Scholar]
- Schlather, M.; Tawn, J.A. A dependence measure for multivariate and spatial extreme values: Properties and inference. Biometrika 2003, 90, 139–156. [Google Scholar] [CrossRef]
- Bernard, E.; Naveau, P.; Vrac, M. Clustering of Maxima: Dependencies among Heavy Rainfall in France. Bull. Am. Meteorol. Soc. 2013, 26, 7929–7937. [Google Scholar] [CrossRef]
- Von Trentini, F.; Aalbers, E.E.; Fischer, E.M.; Ludwig, R. Comparing internal variabilities in three regional single model initial-condition large ensembles (SMILE) over Europe. In Proceedings of the American Geophysical Union, Fall Meeting 2019, San Francisco, CA, USA, 9–13 December 2019. GC31G-1259. [Google Scholar]
- Dombry, C.; Engelke, S.; Oesting, M. Exact simulation of max-stable processes. Biometrika 2016, 103, 303–317. [Google Scholar] [CrossRef]
- Turkman, K.F.; Amaral Turkman, M.A.; Pereira, J.M. Asymptotic models and inference for extremes of spatio-temporal data. Extremes 2010, 13, 375–397. [Google Scholar] [CrossRef]
- Schnr, C.; Videla, P.L.; Lüthi, D.; Frei, C.; Häberli, C.; Liniger, M.A.; Appenzeller, C. The role of increasing temperature variability in European summer heatwaves. Nature 2004, 427, 332–336. [Google Scholar]
- Fischer, E.M.; Rajczak, J.; Schär, C. Changes in European summer temperature variability revisited. Geophys. Res. Lett. 2012, 39, L19702. [Google Scholar] [CrossRef]
- Donat, M.; Pitman, A.J.; Seneviratne, S.I. Regional warming of hot extremes accelerated by surface energy fluxes. Geophys. Res. Lett. 2017, 44, 7011–7019. [Google Scholar] [CrossRef]

| Acronym | Institute | General Circulation Model | Regional Climate Model | Equilibrium Climate Sensitivity (K) |
|---|---|---|---|---|
| C4I | Swedish Meteorological and Hydrological Institute (Sweden) | HadCM3Q16 [30] | RCA3.0 [31] | 4.62 [32] |
| CNRM | Météo-France (France) | ARPEGE [33] | RM5.1 [34] | 2 [35] |
| DMI | Danish Meteorological Institute (Denmark) | ARPEGE | HIRHAM5 [36] | 2 |
| ECHAM5 [37] | HIRHAM5 | 3.65 [38] | ||
| ETHZ | Swiss Institute of Technology (Switzerland) | HadCM3Q0 [30] | CLM2.4.6 [39] | 4.62 |
| HC | Hadley Centre for Climate Prediction and Research (United Kingdom) | HadCM3Q0 | HadRM3Q0 [40] | 4.62 |
| HadCM3Q3 [30] | HadRM3Q3 [40] | 4.62 | ||
| HadCM3Q16 | HadRM3Q16 [40] | 4.62 | ||
| ICTP | The Abdus Salam International Centre for Theoretical Physics (Italy) | ECHAM5 | REGCM3 [41] | 3.65 |
| KNMI | The Royal Netherlands Meteorological Institute (Netherlands) | ECHAM5 | RACMO2.1 [42] | 3.65 |
| MPI | Max Planck Institute for Meteorology (Germany) | ECHAM5 | REMO5.7 [43] | 3.65 |
| SMHI | Swedish Meteorological and Hydrological Institute (Sweden) | BCM [44] | RCA3.0 | 2 [44] |
| SMHI | Swedish Meteorological and Hydrological Institute (Sweden) | ECHAM5 | RCA3.0 | 3.65 |
| SMHI | Swedish Meteorological and Hydrological Institute (Sweden) | HadCM3Q3 | RCA3.0 | 4.62 |
| Model | Slope | Intercept | Slope Error (%) | Intercept Error (%) |
|---|---|---|---|---|
| C4I | 0.050 | 1.169 | 5.109 | 5.581 |
| CNMR | 0.062 | 1.180 | 18.130 | 4.685 |
| DMI | 0.068 | 1.157 | 28.641 | 6.582 |
| ICTP | 0.046 | 1.228 | 12.142 | 0.890 |
| KNMI | 0.061 | 1.137 | 16.358 | 8.191 |
| MPI | 0.051 | 1.199 | 2.821 | 3.196 |
| SMHI | 0.059 | 1.161 | 12.847 | 6.259 |
| SPAIN02 | 0.053 | 1.239 | 0.000 | 0.000 |
| Sectors | Slope T95 | Slope T25 |
|---|---|---|
| Sector 1 | 0.08323 | 0.08748 |
| Sector 2 | 0.07970 | 0.07723 |
| Sector 3 | 0.08193 | 0.08053 |
| Sector 4 | 0.06999 | 0.07936 |
| Sector 5 | 0.07386 | 0.09556 |
| Sector 6 | 0.09350 | 0.07165 |
| Sector 7 | 0.05913 | 0.06377 |
| Sector 8 | 0.07821 | 0.07158 |
| Sector 9 | 0.08303 | 0.07200 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Portero Serrano, J.; Acero Díaz, F.J.; García García, J.A. Analysis of Extreme Temperature Events over the Iberian Peninsula during the 21st Century Using Dynamic Climate Projections Chosen Using Max-Stable Processes. Atmosphere 2020, 11, 506. https://doi.org/10.3390/atmos11050506
Portero Serrano J, Acero Díaz FJ, García García JA. Analysis of Extreme Temperature Events over the Iberian Peninsula during the 21st Century Using Dynamic Climate Projections Chosen Using Max-Stable Processes. Atmosphere. 2020; 11(5):506. https://doi.org/10.3390/atmos11050506
Chicago/Turabian StylePortero Serrano, Javier, Francisco Javier Acero Díaz, and José Agustín García García. 2020. "Analysis of Extreme Temperature Events over the Iberian Peninsula during the 21st Century Using Dynamic Climate Projections Chosen Using Max-Stable Processes" Atmosphere 11, no. 5: 506. https://doi.org/10.3390/atmos11050506
APA StylePortero Serrano, J., Acero Díaz, F. J., & García García, J. A. (2020). Analysis of Extreme Temperature Events over the Iberian Peninsula during the 21st Century Using Dynamic Climate Projections Chosen Using Max-Stable Processes. Atmosphere, 11(5), 506. https://doi.org/10.3390/atmos11050506