Time Series Analysis and Forecasting Using a Novel Hybrid LSTM Data-Driven Model Based on Empirical Wavelet Transform Applied to Total Column of Ozone at Buenos Aires, Argentina (1966–2017)
Abstract
1. Introduction
2. Materials and Methods
2.1. Total Column Ozone
2.2. Mann-Kendal
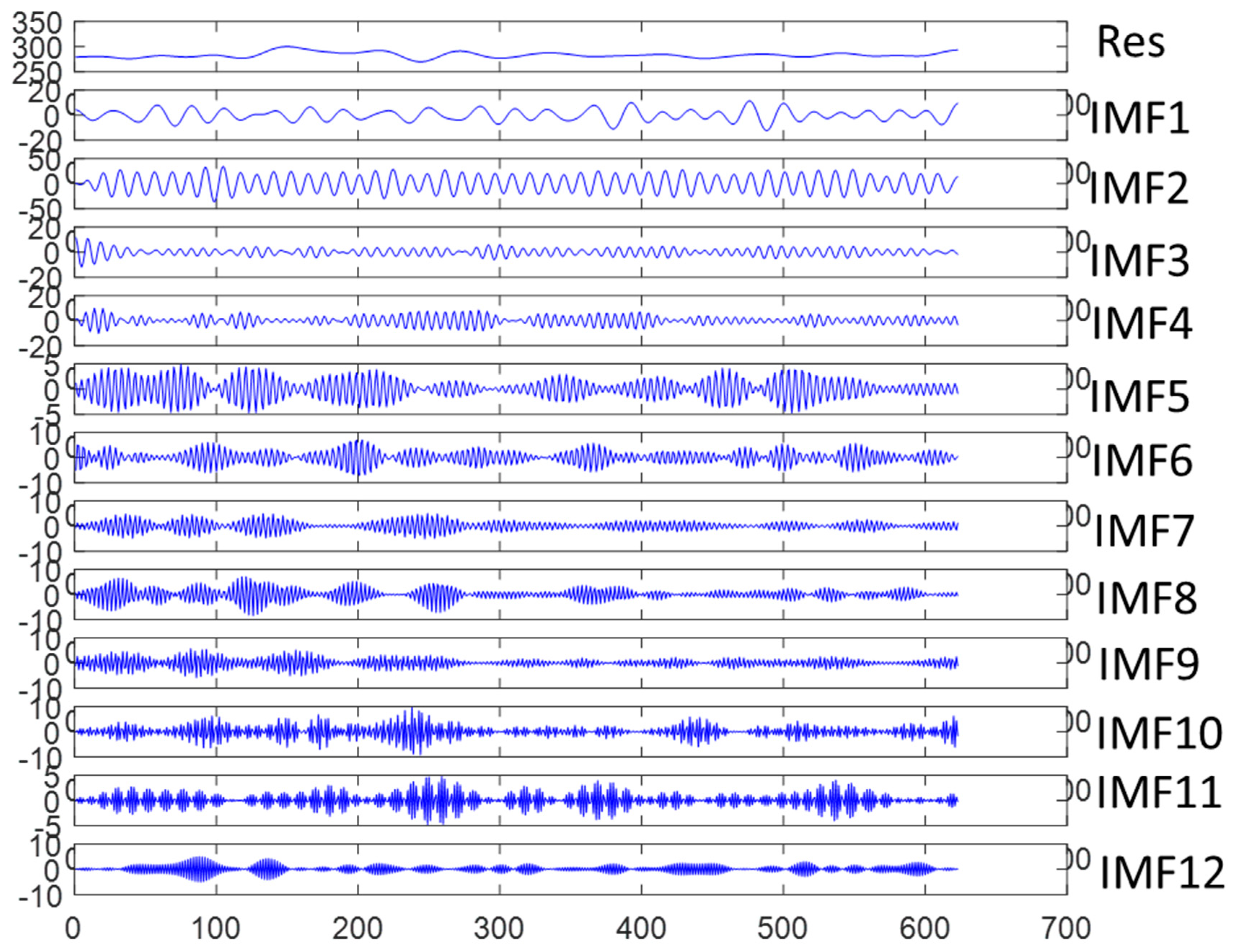
2.3. Empirical Mode Decomposition (EMD)
2.4. Empirical Wavelet Tranform
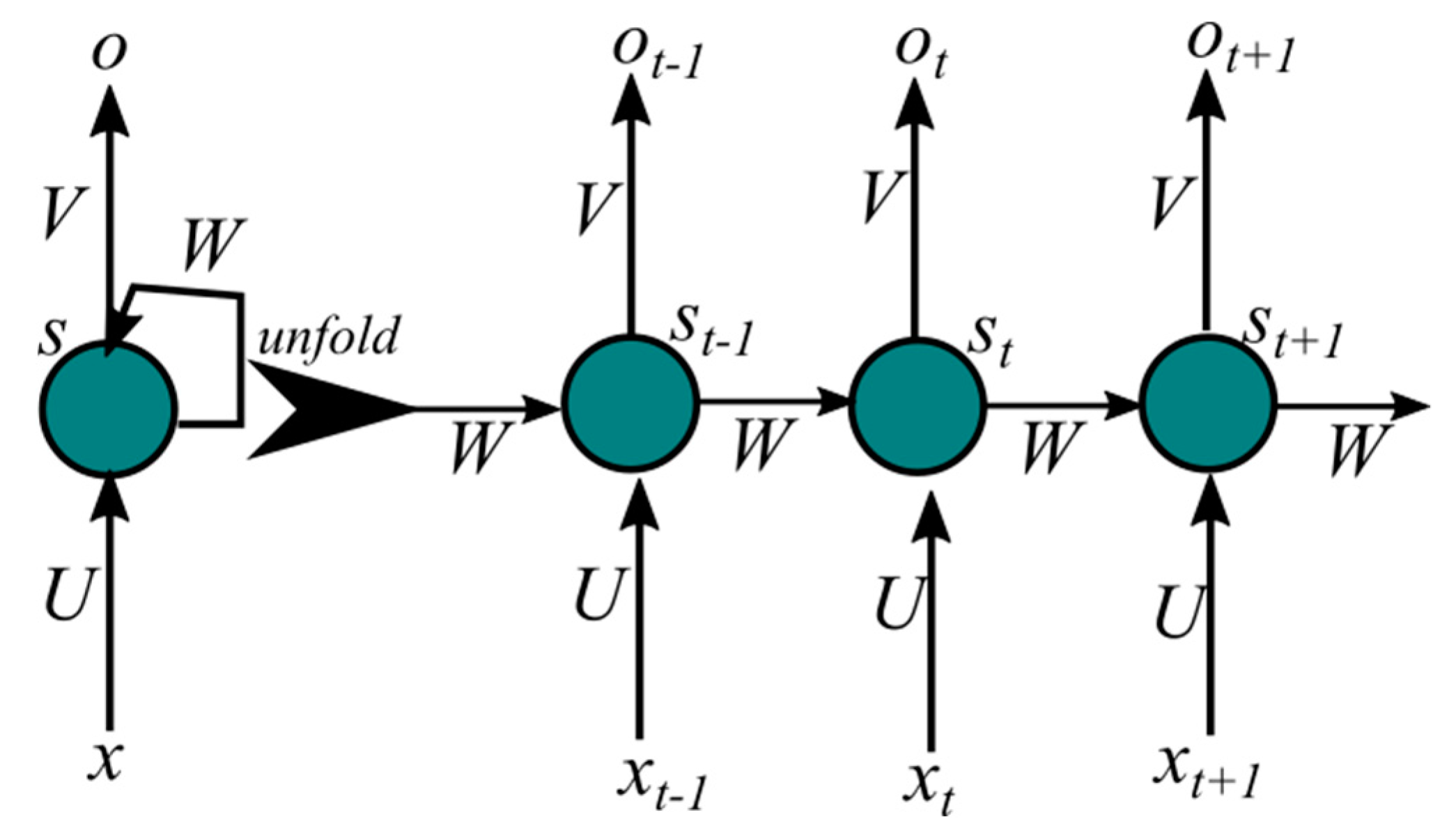
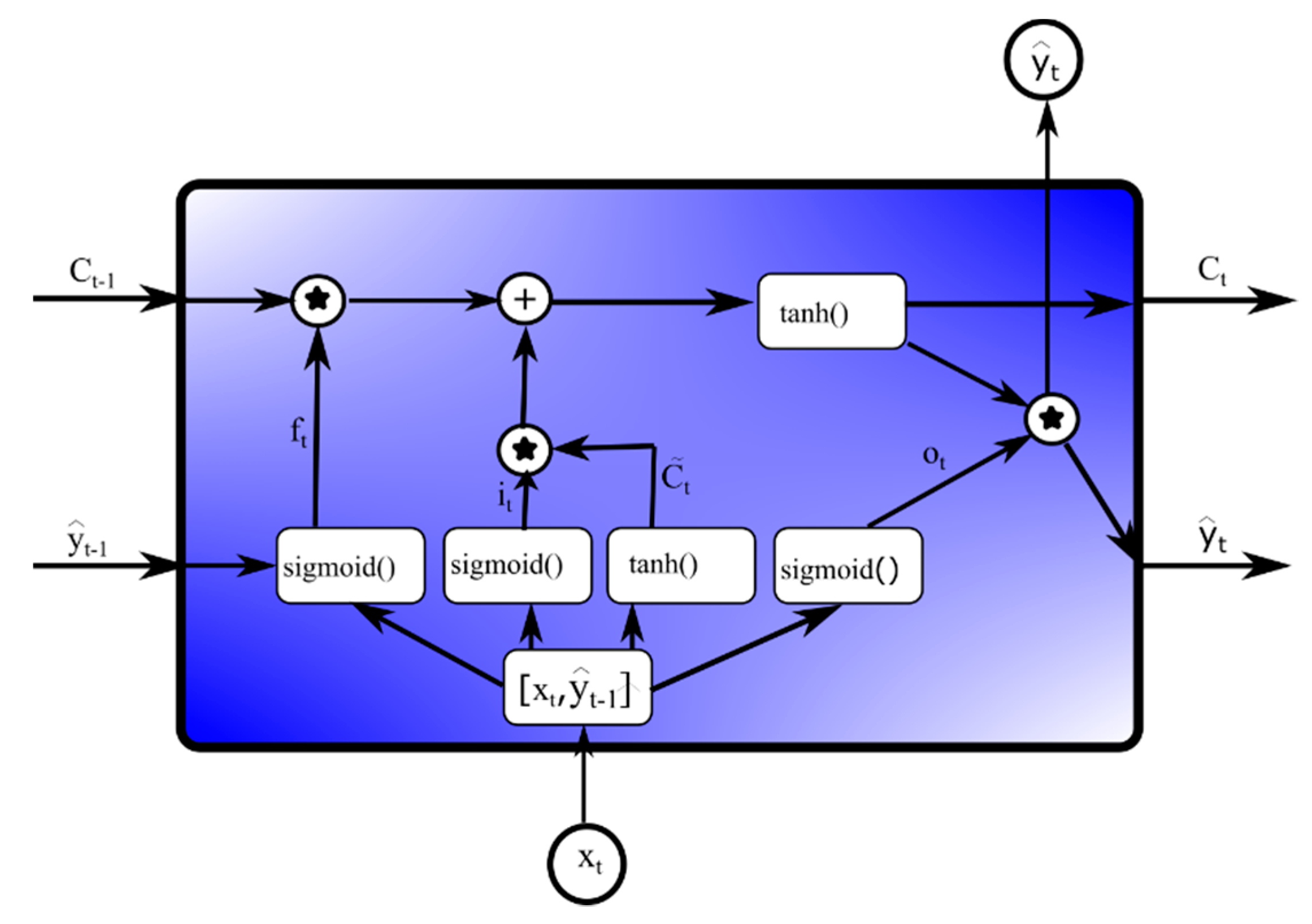
2.5. Long Short-Term Memory (LSTM)
2.6. Novel Hybrid Model Design
2.7. Model Performance
3. Results and Discussion
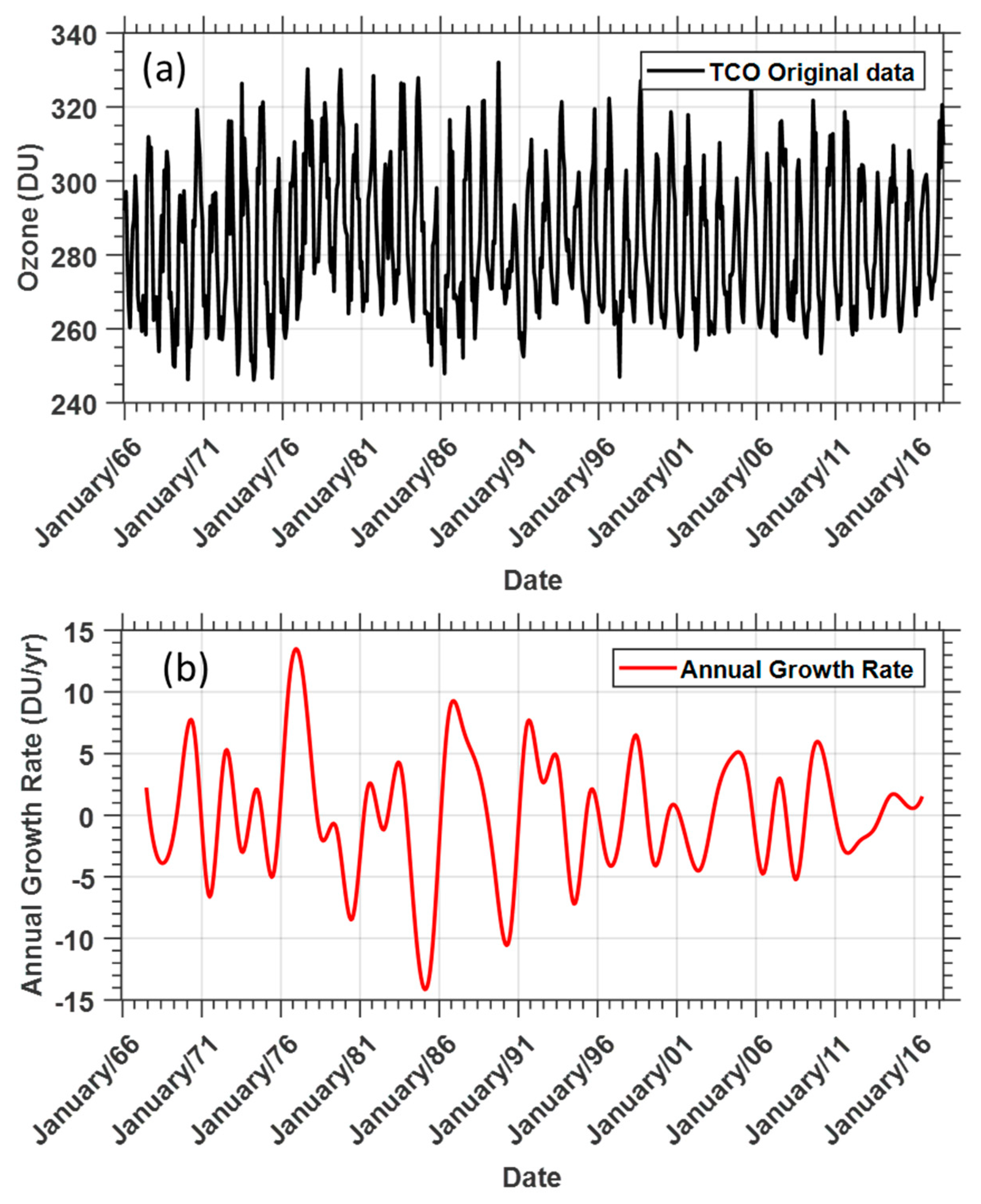
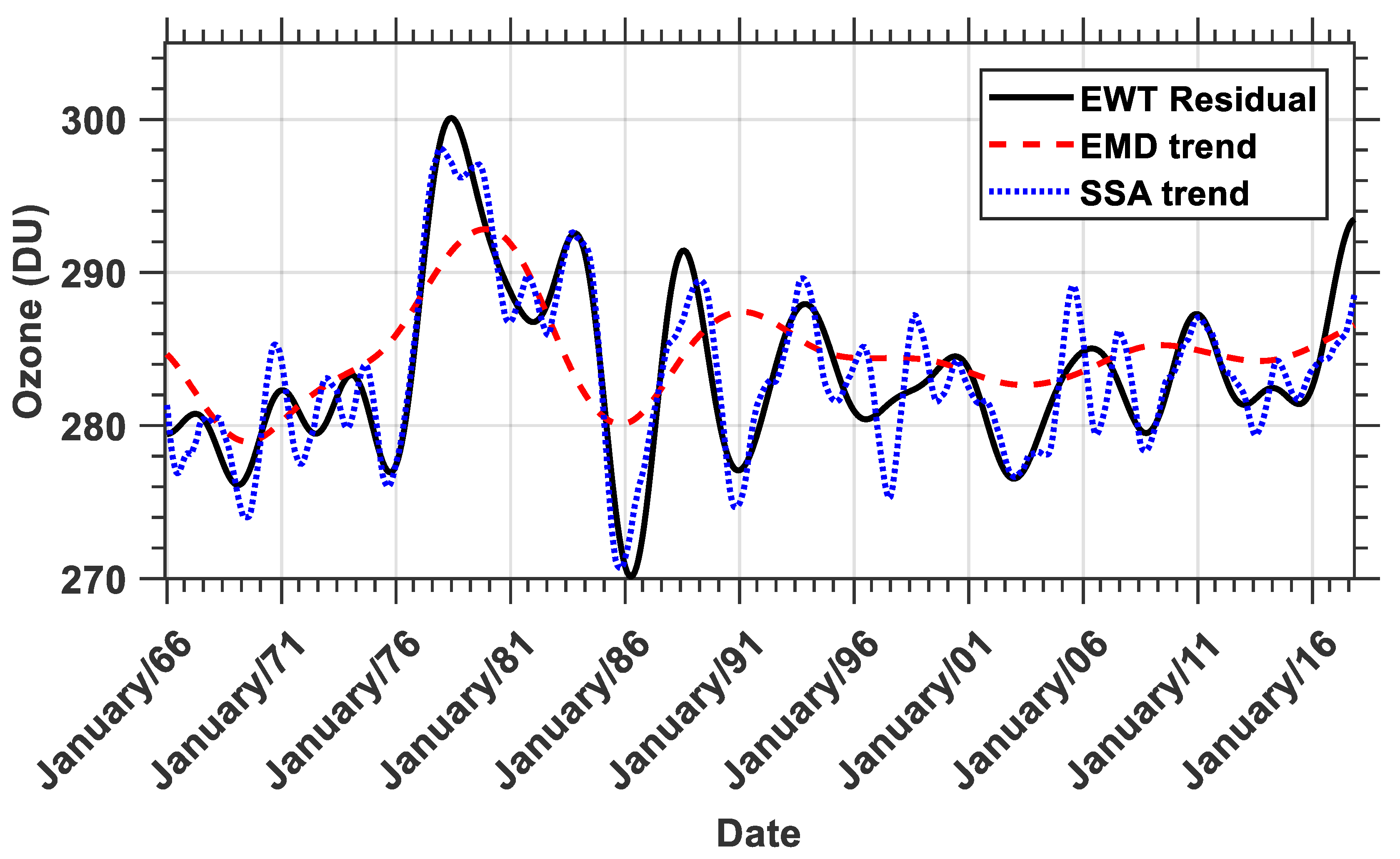
3.1. TCO Data Series and Trends
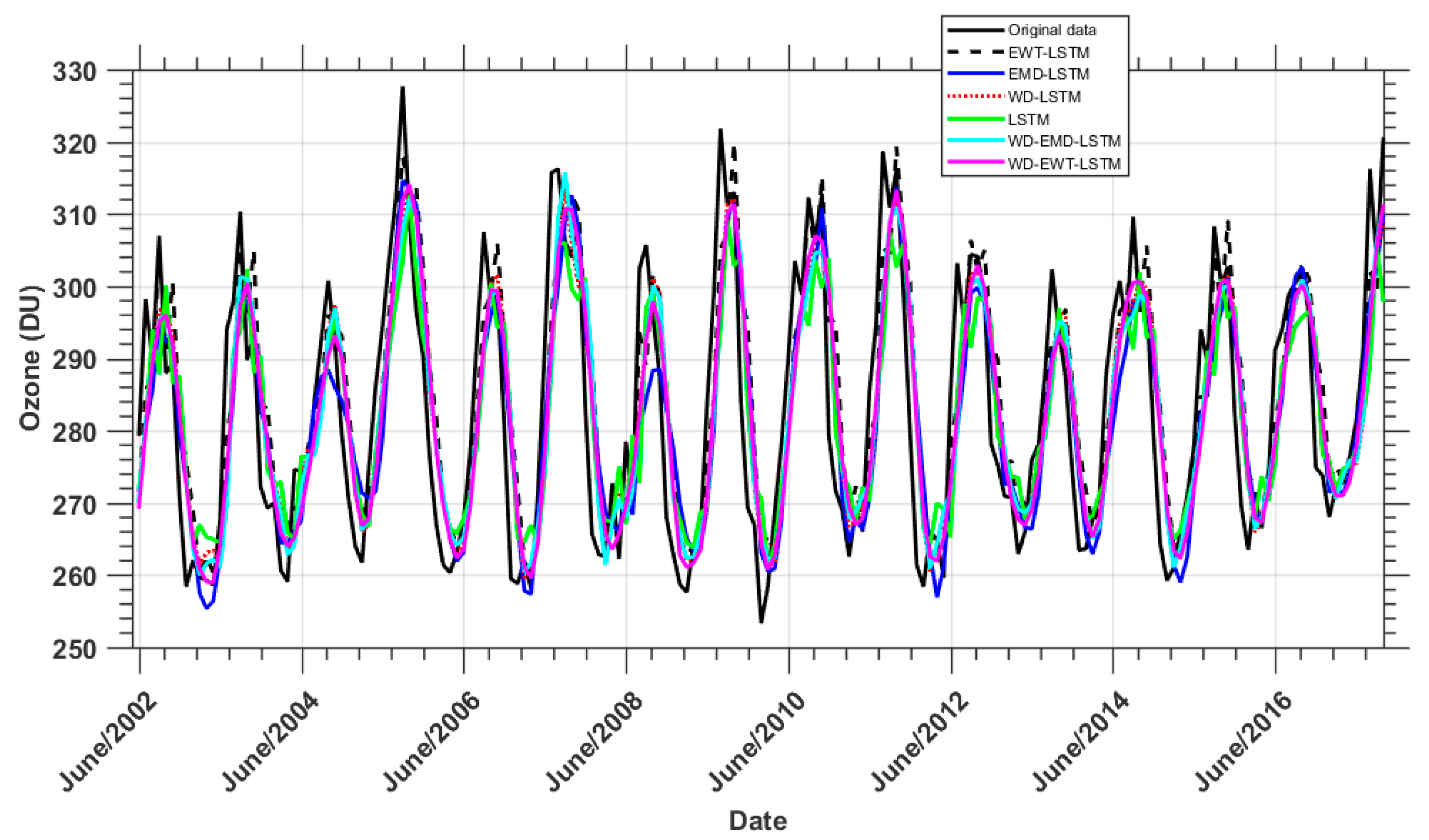
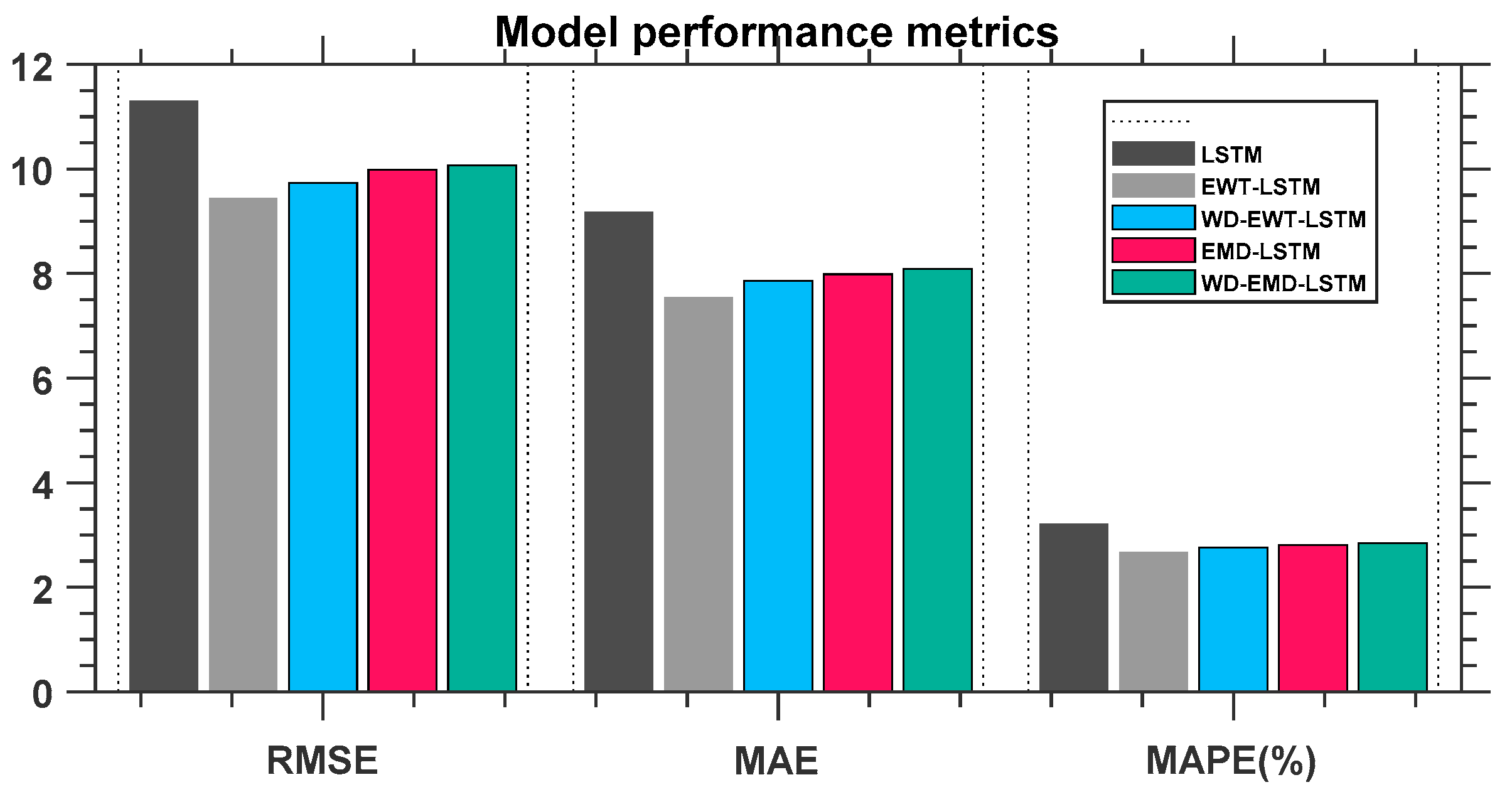
3.2. Empirical Models Results and Its Performance
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Weber, M.; Coldewey-Egbers, M.; Fioletov, V.E.; Frith, S.M.; Wild, J.D.; Burrows, J.P.; Long, C.S.; Loyola, D. Total ozone trends from 1979 to 2016 derived from five merged observational datasets – the emergence into ozone recovery. Atmos. Chem. Phys. 2018, 18, 2097–2117. [Google Scholar] [CrossRef]
- Farman, J.C.; Gardiner, B.G.; Shanklin, J.D. Large losses of total ozone in Antarctica reveal seasonal ClO x/NO x interaction. Nature 1985, 315, 207–210. [Google Scholar] [CrossRef]
- Solomon, S.; Garcia, R.R.; Rowland, F.S.; Wuebbles, D.J. On the depletion of Antarctic ozone. Nature 1986, 321, 755–758. [Google Scholar] [CrossRef]
- Rigby, M.; Park, S.; Saito, T.; Western, L.M.; Redington, A.L.; Fang, X.; Henne, S.; Manning, A.J.; Prinn, R.G.; Dutton, G.S. Increase in CFC-11 emissions from eastern China based on atmospheric observations. Nature 2019, 569, 546–550. [Google Scholar] [CrossRef] [PubMed]
- Ball, W.T.; Alsing, J.; Mortlock, D.J.; Staehelin, J.; Haigh, J.D.; Peter, T.; Tummon, F.; Stübi, R.; Stenke, A.; Anderson, J.; et al. Evidence for a continuous decline in lower stratospheric ozone offsetting ozone layer recovery. Atmos. Chem. Phys. 2018, 18, 1379–1394. [Google Scholar] [CrossRef]
- Braesicke, P.; Neu, J.; Fioletov, V.; Godin-Beekmann, S.; Hubert, D.; Petropavlovskikh, I.; Shiotani, M.; Sinnhuber, B.-M. Update on Global Ozone: Past, Present, and Future. In Scientific Assessment of Ozone Depletion: 2018; Global Ozone Research and Monitoring Project–Report No. 58; World Meteorological Organization: Geneva, Switzerland, 2018; Chapter 3. [Google Scholar]
- Pawson, S.; Steinbrecht, W.; Charlton-Perez, A.J.; Fujiwara, M.; Karpechko, A.Y.; Petropavlovskikh, I.; Urban, J.; Weber, M.; Aquila, V.; Chehade, W. Update on global ozone: Past, present, and future. In Scientific Assessment of Ozone Depletion: 2014; Global Ozone Research and Monitoring Project–Report No. 55; World Meteorological Organization: Geneva, Switzerland, 2014; Chapter 3. [Google Scholar]
- Chehade, W.; Weber, M.; Burrows, J.P. Total ozone trends and variability during 1979–2012 from merged data sets of various satellites. Atmos. Chem. Phys. 2014, 14, 7059–7074. [Google Scholar] [CrossRef][Green Version]
- Ball, W.T.; Alsing, J.; Staehelin, J.; Davis, S.M.; Froidevaux, L.; Peter, T. Stratospheric ozone trends for 1985–2018: Sensitivity to recent large variability. Atmos. Chem. Phys. 2019, 19, 12731–12748. [Google Scholar] [CrossRef]
- Lei, M.; Shiyan, L.; Chuanwen, J.; Hongling, L.; Yan, Z. A review on the forecasting of wind speed and generated power. Renew. Sust. Energ. Rev. 2009, 13, 915–920. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Q.; Zhang, G.; Nie, Z.; Gui, Z.; Que, H. A Novel Hybrid Data-Driven Model for Daily Land Surface Temperature Forecasting Using Long Short-Term Memory Neural Network Based on Ensemble Empirical Mode Decomposition. Int. J. Environ. Res. Public. Health. 2018, 15, 1032. [Google Scholar] [CrossRef]
- Zhang, G.P.; Qi, M. Neural network forecasting for seasonal and trend time series. Eur. J. Oper. Res. 2005, 160, 501–514. [Google Scholar] [CrossRef]
- Tealab, A. Time series forecasting using artificial neural networks methodologies: A systematic review. future computing inform. j. 2018, 3, 334–340. [Google Scholar] [CrossRef]
- Tian, C.; Hao, Y.; Hu, J. A novel wind speed forecasting system based on hybrid data preprocessing and multi-objective optimization. Applied Energy 2018, 231, 301–319. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Khandelwal, I.; Adhikari, R.; Verma, G. Time Series Forecasting Using Hybrid ARIMA and ANN Models Based on DWT Decomposition. Procedia Comput. Sci. 2015, 48, 173–179. [Google Scholar] [CrossRef]
- Zhou, J.; Peng, T.; Zhang, C.; Sun, N. Data Pre-Analysis and Ensemble of Various Artificial Neural Networks for Monthly Streamflow Forecasting. Water 2018, 10, 628. [Google Scholar] [CrossRef]
- Altan, A.; Karasu, S.; Bekiros, S. Digital currency forecasting with chaotic meta-heuristic bio-inspired signal processing techniques. Chaos Soliton. Fract. 2019, 126, 325–336. [Google Scholar] [CrossRef]
- Liu, Y.; Guan, L.; Hou, C.; Han, H.; Liu, Z.; Sun, Y.; Zheng, M. Wind Power Short-Term Prediction Based on LSTM and Discrete Wavelet Transform. Appl. Sci. 2019, 9, 1108. [Google Scholar] [CrossRef]
- Li, Y.; Wu, H.; Liu, H. Multi-step wind speed forecasting using EWT decomposition, LSTM principal computing, RELM subordinate computing and IEWT reconstruction. Energy Convers. Manag. 2018, 167, 203–219. [Google Scholar] [CrossRef]
- Nazir, H.M.; Hussain, I.; Faisal, M.; Shoukry, A.M.; Gani, S.; Ahmad, I. Development of Multidecomposition Hybrid Model for Hydrological Time Series Analysis. Complexity 2019, 2019, 1–14. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal. Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Computation 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- World Ozone and Ultraviolet Radiation Data Centre website. Available online: https://woudc.org/home.php (accessed on 30 June 2018).
- Dobson, G.M.B.; Harrison, D.N.; Lindemann, F.A. Measurements of the amount of ozone in the earth’s atmosphere and its relation to other geophysical conditions. P. R. Soc. A-Math. Phy. 1926, 110, 660–693. [Google Scholar] [CrossRef]
- Stolarki, R.S.; Krueger, A.J.; Schoeberl, M.R.; McPeters, R.D.; Newman, P.A.; Alpert, J.C. Nimbus 7 SBUV/TOMS measurements of the springtime Antarctic ozone hole. Nature 1986, 322, 808–811. [Google Scholar] [CrossRef]
- Grant, W.B. Ozone Measuring Instruments for the Stratosphere; Collection Work in Optics; Optical Society of Amer: Washington DC, USA, 1989. [Google Scholar]
- Mbatha, N.; Xulu, S. Time Series Analysis of MODIS-Derived NDVI for the Hluhluwe-Imfolozi Park, South Africa: Impact of Recent Intense Drought. Climate 2018, 6, 95. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Sneyers, R. On the statistical analysis of series of observations; Technical Note 143; World Metrological Organization, : Geneva, Switzerland, 1991. [Google Scholar]
- Pohlert, T. Trend: Non-Parametric Trend Tests and Change-Point Detection. Available online: https://cran.r-project.org/web/packages/trend/index.html (accessed on 6 August 2018).
- Schaber, J. Pheno: Auxiliary Functions for Phenological Data Analysis. Available online: https://cran.r-project.org/web/packages/pheno/index.html (accessed on 6 August 2018).
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Bangkok, Thailand, 1992. [Google Scholar]
- Giles, C.L.; Lawrence, S.; Tsoi, A.C. Noisy Time Series Prediction using Recurrent Neural Networks and Grammatical Inference. Mach. Learn. 2001, 44, 161–183. [Google Scholar] [CrossRef]
- Miniconda—Conda documentation. Available online: https://docs.conda.io/en/latest/miniconda.html (accessed on 1 May 2019).
- Xu, Y.; Yang, W.; Wang, J. Air quality early-warning system for cities in China. Atmos. Environ. 2017, 148, 239–257. [Google Scholar] [CrossRef]
- Thoning, K.W.; Tans, P.P.; Komhyr, W.D. Atmospheric carbon dioxide at Mauna Loa Observatory: 2. Analysis of the NOAA GMCC data, 1974–1985. J. Geophys. Res: Atmos. 1989, 94, 8549–8565. [Google Scholar] [CrossRef]
- Apadula, F.; Cassardo, C.; Ferrarese, S.; Heltai, D.; Lanza, A. Thirty Years of Atmospheric CO2 Observations at the Plateau Rosa Station, Italy. Atmosphere 2019, 10, 418. [Google Scholar] [CrossRef]
- Fioletov, V.E. Ozone climatology, trends, and substances that control ozone. Atmos. Ocean. 2008, 46, 39–67. [Google Scholar] [CrossRef][Green Version]
- Toihir, A.M.; Portafaix, T.; Sivakumar, V.; Bencherif, H.; Pazmino, A.; Bègue, N. Variability and trend in ozone over the southern tropics and subtropics. Ann. Geophys. 2018, 36, 381–404. [Google Scholar] [CrossRef]
- NASA Ozone Watch: Latest status of ozone. Available online: https://ozonewatch.gsfc.nasa.gov/ (accessed on 2 February 2020).
- Harmouche, J.; Fourer, D.; Auger, F.; Borgnat, P.; Flandrin, P. The sliding singular spectrum analysis: A data-driven nonstationary signal decomposition tool. IEEE Trans. Signal. Process. 2017, 66, 251–263. [Google Scholar] [CrossRef]
- Moghtaderi, A.; Borgnat, P.; Flandrin, P. Trend filtering: Empirical mode decompositions versus ℓ1 and Hodrick–Prescott. Adv. Adapt. Data Anal. 2011, 3, 41–61. [Google Scholar] [CrossRef]
- Geetikaverma, V.S. Empirical Wavelet Transform & its Comparison with Empirical Mode Decomposition: A review. Int. J. Appl. Eng. 2016, 4, 5. [Google Scholar]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. P. R. Soc. A-Math. Phy. 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Sang, Y.-F.; Wang, Z.; Liu, C. Comparison of the MK test and EMD method for trend identification in hydrological time series. J. Hydrol. 2014, 510, 293–298. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Bègue, N.; Vignelles, D.; Berthet, G.; Portafaix, T.; Payen, G.; Jégou, F.; Benchérif, H.; Jumelet, J.; Vernier, J.-P.; Lurton, T.; et al. Long-range transport of stratospheric aerosols in the Southern Hemisphere following the 2015 Calbuco eruption. Atmos. Chem. Phys. 2017, 17, 15019–15036. [Google Scholar] [CrossRef]
- Bègue, N.; Shikwambana, L.; Bencherif, H.; Pallotta, J.; Sivakumar, V.; Wolfram, E.; Mbatha, N.; Orte, F.; Du Preez, J.; Ranaivombola, M.; et al. Statistical analysis of the long-range transport of the 2015 Calbuco volcanic eruption from ground-based and space-borne observations. Ann. Geophys. 2020, 38, 395–420. [Google Scholar]




| Metric | Definition | Formula |
|---|---|---|
| MAE | Mean absolute error | |
| RMSE | Root mean square error | |
| MAPE | Mean absolute percentage error |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mbatha, N.; Bencherif, H. Time Series Analysis and Forecasting Using a Novel Hybrid LSTM Data-Driven Model Based on Empirical Wavelet Transform Applied to Total Column of Ozone at Buenos Aires, Argentina (1966–2017). Atmosphere 2020, 11, 457. https://doi.org/10.3390/atmos11050457
Mbatha N, Bencherif H. Time Series Analysis and Forecasting Using a Novel Hybrid LSTM Data-Driven Model Based on Empirical Wavelet Transform Applied to Total Column of Ozone at Buenos Aires, Argentina (1966–2017). Atmosphere. 2020; 11(5):457. https://doi.org/10.3390/atmos11050457
Chicago/Turabian StyleMbatha, Nkanyiso, and Hassan Bencherif. 2020. "Time Series Analysis and Forecasting Using a Novel Hybrid LSTM Data-Driven Model Based on Empirical Wavelet Transform Applied to Total Column of Ozone at Buenos Aires, Argentina (1966–2017)" Atmosphere 11, no. 5: 457. https://doi.org/10.3390/atmos11050457
APA StyleMbatha, N., & Bencherif, H. (2020). Time Series Analysis and Forecasting Using a Novel Hybrid LSTM Data-Driven Model Based on Empirical Wavelet Transform Applied to Total Column of Ozone at Buenos Aires, Argentina (1966–2017). Atmosphere, 11(5), 457. https://doi.org/10.3390/atmos11050457






