Abstract
Record-breaking precipitation events have been frequent in Japan in recent years. To investigate the statistical characteristics of the frequency of record-breaking events, observations can be compared with the values derived from sampling theory with a stationary state. This study counted the number of record-breaking daily and 3-day total precipitation events at 58 rain-gauge stations in Japan between 1901 and 2018. The average number of record-breaking events over the 118-year period was 5.9 for daily total precipitation, which is larger than the theoretical value of 5.4 derived using the assumption that the climate system over the same period was stationary. Sampling theory was used to incorporate the influence of the long-term temperature trend from the Clausius–Clapeyron relation associated with the saturation vapor pressure. In theory, the long-term temperature trend gives a similar number of observed record-breaking events when the long-term temperature trend is approximately 0.5 Kelvin/100 years.
1. Introduction
Severe flood events have become frequent in many parts of Japan, particularly since 2014. Between 28 June 2018 and 8 July 2018, torrential rainfall exceeding 1000 mm associated with the Baiu front caused floods and landslides that killed 237 people; 8 people are still missing [1]. According to the Japan Meteorological Agency (JMA), this record-breaking heavy rainfall event could have been related to increases in both temperature and water vapor associated with climate change [2].
In the context of global warming, system energy has increased due to ocean warming. Based on land- and ocean-surface data, average global temperatures increased linearly by 0.85 Kelvin from 1880 to 2012 [3], and the period from 1983 to 2012 which was the warmest 30-year period in the Northern Hemisphere in the last 1400 years. Global temperatures are expected to increase by approximately 1.0 Kelvin, and probably by as much as 1.5 Kelvin, between 2030 and 2052 [4], Rising temperatures have likely increased precipitation since 1951, and possibly since 1901 [3].
Extreme precipitation events provide valuable information about the effects of climate change [5,6,7,8]. Changes in precipitation intensity can be categorized using thermodynamic and dynamic components [9]. Thermodynamic changes in the saturation vapor pressure, the so-called Clausius–Clapeyron relation, can be assessed using climate models and observational approaches (e.g., [5,10]). Some studies have shown that short-term precipitation follows the Clausius–Clapeyron-like relationship in Japan [11,12]. Yamada et al. (2014) [13] analyzed radiosonde and rain-gauge data for the Sapporo area of Hokkaido, the northernmost island of Japan, and suggested that, when sufficient samples are obtained, the 99th percentile hourly water vapor and precipitation values both follow the Clausius–Clapeyron relation up to certain temperatures.
Under the assumption that climate follows a steady state, the numbers of record-breaking events can be obtained using sampling theory [14,15]. Studies have investigated the number of extreme warm events [16,17,18,19,20,21]. For example, Benestad [16] suggested that record-warm events are more frequent than for a stationary series. Therefore, it is possible to compare the theoretical and observed numbers of record-breaking events given a sufficiently long observation period. Lehmann and Frieler (2015) [22] analyzed HadEX2 [23], which is available for 1901–2010 for 3.75° × 2.5° grid cells, and showed that over the last three decades, the number of record-breaking events has increased significantly over the global mean. They suggested that, although the number of record-breaking rainfall events was related to natural multi-decadal variability over the period 1901–1980, the observed record-breaking rainfall events increased significantly after 1980, consistent with rising temperatures.
In Japan, daily measurements from 58 rain gauges have been obtained since 1901. We determined the amount of new records for annual maximum daily and 3-day total precipitation and compared the results with theoretical values based on the predicted occurrence of new records given a steady state. In Japan, large river basins generally adopt 1 to 3-day total precipitation for river planning. Following [22], the theoretical value includes the influence of the long-term trend in temperature, which represents thermodynamics. We explored the long-term trend in temperature that conformed to the actual number of new records for annual maximum daily precipitation and 3-day total precipitation for the 58 rain gauges. Section 2 introduces the study methodology, and the results are provided in Section 3. We summarize this paper in Section 4.
2. Methodology
2.1. Data
Since 1901, 58 observation stations in Japan operated by the JMA have measured daily precipitation, from Hokkaido Prefecture in the north to Okinawa Prefecture in the south (Figure 1). These rain gauges are located at elevations between 0.5 and 200 m above sea level, except for five in central Japan at above 201 m. Note that there is no missing data for the all rain gauges during the whole period.
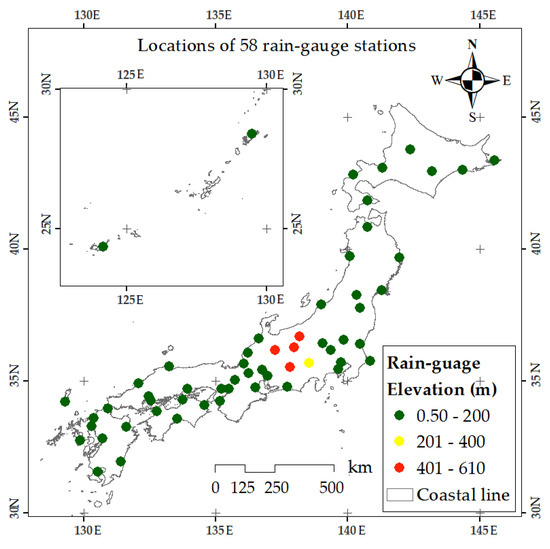
Figure 1.
Locations of 58 rain-gauge stations. Colors indicate the elevation of each rain gauge.
2.2. Sampling Number Theory
Here, a new record for the annual maximum daily precipitation is followed by a sequence of events , in which each value in the sequence is followed by a random independent variable with an identical distribution. If precipitation is not affected by any systematic trend, such as a drift in climate (e.g., the long-term trend in sea-surface temperature), the annual maximum precipitation over the 118 years would follow an independent identical continuous distribution with the assumption that extreme precipitation occurs in a stationary climate [16,23].
We consider that precipitation data exist from an arbitrary year and focus only on annual maximum precipitation days. The annual maximum precipitation day in the first year is treated as a new record. If annual maximum precipitation is not affected by systematic trends and follows the same continuous distribution, the probability of a new record for the annual maximum precipitation intensity in the ith year becomes 1/i. Two important factors affect this: the probability of having a new record, Pr, and the number of new records in a specific period, Rn. First, the probabilistic variable is defined as yi, which has a value of 1 for year i when it is a new record and 0 otherwise. These are independent of each other, and and . The expectation and variance are given by Equations (1) and (2), respectively.
Here, as shown in Figure 2 as an example, the number of new records in a specific period Rn can be calculated simply as the sum of the occurrences of record-breaking events, which is the maximum precipitation compared with previous years, as denoted by
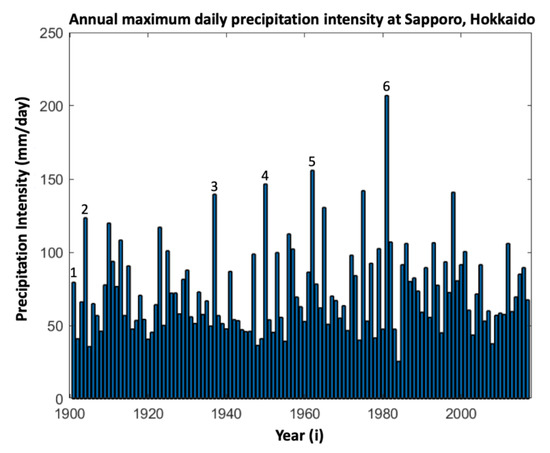
Figure 2.
An example of annual maximum daily precipitation at a single rain-gauge station (Sapporo, Hokkaido, northern island of Japan). Number of new records are plotted on the figure.
Then, the expectation and variance of are
When a new record is expected to occur too often, the record number can be obtained by the harmonic sum of the estimated records number , where is the Euler constant.
Next, we estimate the probability distribution of the number of new records . If we assume
the event is expressed as the summation of two exclusive events such as and , the following relationships hold.
Note that
In the following section, the theoretical number of new records is numerically obtained by solving the recurrence relation for Equations (7) and (8).
2.3. Number of New Records with Long-Term Temperature Trend
As we introduced in the previous subsection, the number of new records under a steady-state condition is obtained theoretically. According to [3], the global temperature increased by approximately 0.85 Kelvin between 1880 and 2012. Following [22], the influence of the climate-drift term associated with temperature change is included in the new-record theory. If extreme precipitation is affected by systematic trends, such as a drift in climate (e.g., global warming), and the annual maximum precipitation for all years follows an identical continuous distribution, the random variable x needs to be updated. This term is replaced by Pr, i.e., the reconstructed precipitation in the time series in this new-record theory associated with the temperature trend. The global mean temperature is given as follows (Equation (10)):
where indicates the global mean temperature in the first year. Note that the temperature is in Kelvin. The value of this constant (i.e., c = 0.01) defines a temperature trend increase of 1 Kelvin/100 years. From this assumption, the water vapor change can be obtained from the Clausius–Clapeyron relation, which reflects a water moisture content increase of 7%/Kelvin. This ideal condition defines the long-term change in the ideal temperature (climate drift). The Clausius–Clapeyron Equation is then used in Equation (11).
In Equation (11), indicates the freezing point temperature. If the global mean climatological temperature is expressed as , the water vapor rate of change, , between the saturated water vapor of surface temperature and that of the mean surface temperature is estimated in Equation (12).
The reconstructed precipitation data are given by Equation (13), which formulates the new reproduced precipitation using the rate change of water vapor plus a variation term, which is the detrended inter-annual variability of annual maximum precipitation represented as a stochastic term , and includes is the climatological mean precipitation time series.
The parameter c in Equation (10) affects the number of new records because of the long-term trend in temperature in Equation (13).
3. Results
Figure 3 shows the geographical distribution of the amount of new records for the annual maximum daily precipitation (Figure 3a) and 3-day total precipitation (Figure 3b). For both, the amounts of new records vary between 3 and 10 for all 58 rain-gauge stations. The values tend to be greater in central and western Japan than in eastern and northern Japan.
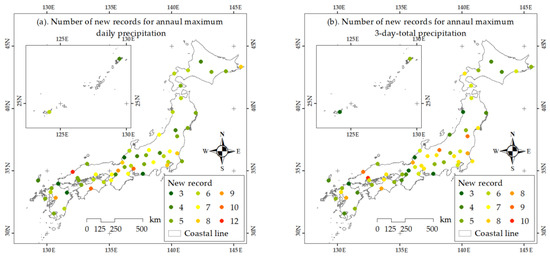
Figure 3.
Amount of new records for annual maximum (a) daily precipitation and (b) 3-day total precipitation of the 58 rain gauges in Japan. Colors indicate the numbers of new records for annual maximum daily and 3-day total precipitation, respectively.
Figure 4a shows the numbers of new records each year starting in 1901. The black line is the mean for all 58 stations, and the standard deviation is plotted with dotted line. The values calculated from sampling theory with the steady-state assumption are shown with the solid blue line, with standard deviations shown by dashed lines. The number of new records from the 58 stations was approximately 5.9 over the first 118 years, compared with the theoretical value of 5.4 based on the steady-state assumption. Therefore, the actual number of new records exceeded the predicted number by 0.5, although it fell within the standard deviation of 1.9.

Figure 4.
Comparison of the theoretical values without the temperature trend (blue solid line) with the average values of new records among the 58 rain gauges in Japan (black solid line) for annual maximum (a) daily and (b) 3-day total precipitation. The standard deviation is plotted with the black dashed lines. The theoretical values incorporating the temperature trend are plotted with the red solid line.
Using sampling theory with the long-term temperature trend, the actual number of new records is plotted with the solid red line. Using a long-term temperature trend of 0.5 Kelvin/100 years, the theoretical value is similar to the observed number of new records. A 0.5-Kelvin increase over 100 years is slightly smaller than the value of 0.85 Kelvin reported [3] for the period 1880–2012 (this corresponds to 0.63 Kelvin/100 years), although the values are comparable. Figure 4b shows a similar figure for 3-day total precipitation, using similar notation. For the 58 stations, the average number of new records was 5.7, which is 0.3 higher than the theoretical value with the steady-state assumption. In this case, the use of a long-term temperature trend gives a better fit with the observations when we adopt the 0.5 Kelvin/100 years estimate.
4. Summary
This study investigated the number of annual maximum daily and 3-day total precipitation records for 58 rain gauges in Japan between 1901 and 2018. There were 5.9 new daily precipitation records per station during the 118 years, and 5.4 new records for 3-day total precipitation. In both cases, the number of new records exceeded the theoretical value derived using sampling theory. We incorporated the influence of the long-term temperature trend into sampling theory. The use of a long-term temperature trend gave a better fit with the observations when we adopt the 0.5 Kelvin/100 years estimate even though this was slightly smaller than the reported long-term temperature trend of 0.63 Kelvin/100 years [3]. The precipitation change is affected by thermodynamic and dynamic parameters. Incorporation of the long-term temperature trend adds a thermodynamic parameter that affects precipitation change. For cases when the fitted long-term temperature trend is not comparable to observations, dynamic effect (e.g., change of general circulation or shift of climate zone) may affect the change of precipitation in addition to thermodynamic effect which we focus in this study. The use of long-term precipitation data to investigate the frequency of extreme precipitation events in terms of steady and unsteady climate systems associated with temperature trends could be useful when discussing future climate conditions.
Author Contributions
Conceptualization, T.J.Y.; data curation, C.N.S.; formal analysis, T.J.Y. and C.N.S.; funding acquisition, T.J.Y.; investigation, T.J.Y. and C.N.S.; methodology, T.J.Y.; supervision, T.J.Y.; validation, T.H.; visualization, C.N.S.; writing—original draft, T.J.Y. and C.N.S.; writing—review and editing, T.J.Y. and T.H. All authors have read and agreed to the published version of the manuscript.
Funding
This study was partially supported by MEXT/SI-CAT, ADAP-T(SATREPS)/JICA-JST, and KAKENHI (19H0224109, 17KT006607).
Acknowledgments
We thank two anonymous reviewers for the comments that help improve the quality of the paper substantially.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ministry of Land, Infrastructure, Transport, and Tourism (MLIT). Water Disaster Report. Available online: https://www.mlit.go.jp/river/pamphlet_jirei/pdf/suigai2018.pdf (accessed on 15 February 2020).
- Japan Meteorological Agency (JMA). Available online: https://www.jma.go.jp/jma/press/1808/10c/h30goukouon20180810.html (accessed on 15 February 2020).
- AR5 Synthesis Report: Climate Change 2014; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2014.
- Summary for Policymakers. Global warming of 1.5 °C; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2018. [Google Scholar]
- Pall, P.; Stone, D.A. Testing the Clausius-Clapeyron constraint on changes in extreme precipitation under CO2 warming. Clim. Dyn. 2007, 28, 351–363. [Google Scholar] [CrossRef]
- Zhang, X.; Zwiers, F.W.; Hegerl, G.C.; Lambert, F.H.; Gillett, N.P.; Solomon, S.; Stott, P.A.; Nozawa, T. Detection of human influence on twentieth-century precipitation trends. Nature 2007, 448, 461–465. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wan, H.; Zwiers, F.W.; Hegerl, G.C.; Min, S.-K. Attributing intensification of precipitation extremes to human influence. Geophys. Res. Lett. 2013, 40, 5252–5257. [Google Scholar] [CrossRef]
- Min, S.-K.; Zhang, X.; Zwiers, F.W.; Hegerl, G.C. Human contribution to more-intense precipitation extremes. Nature 2011, 470, 378–381. [Google Scholar] [CrossRef] [PubMed]
- Emori, S.; Brown, S.J. Dynamic and thermodynamic changes in mean and extreme precipitation under changed climate. Geophys. Res. Lett. 2005, 32, L17706. [Google Scholar] [CrossRef]
- Allen, M.; Ingram, W. Constraints on future changes in climate and the hydrologic cycle. Nature 2002, 419, 224–232. [Google Scholar] [CrossRef] [PubMed]
- Utsumi, N.; Seto, S.; Kanae, S.; Eiji Maeda, E.; Oki, T. Does higher surface temperature intensity extreme precipitation? Geophys. Res. Lett. 2011, 38, L16708. [Google Scholar] [CrossRef]
- Fujibe, F. Clausius-Clapeyron-like relationship in multidecadal changes of extreme short-term precipitation and temperature in Japan. Atmos. Sci. Lett. 2013, 14, 127–132. [Google Scholar] [CrossRef]
- Yamada, T.J.; Farukh, M.A.; Fukushima, T.; Inatsu, M.; Sato, T.; Pokhrel, Y.N.; Oki, T. Extreme precipitation intensity in future climates associated with the Clausius-Clapeyron-like relationship. Hydrol. Res. Lett. 2014, 8, 108–113. [Google Scholar] [CrossRef]
- Glick, N. Breaking Records and Breaking Boards. Am. Math. Mon. 1978, 85, 2–26. [Google Scholar] [CrossRef]
- Galambos, J. Asymptotic Theory of Extreme Order Statistics; Wiley Series in Probability and Mathematical Statistics; John Wiley and Sons: Hoboken, NJ, USA, 1978. [Google Scholar]
- Benestad, R.E. How often can we expect a record event? Clim. Res. 2003, 25, 3–13. [Google Scholar] [CrossRef]
- Benestad, R.E. Record-values, non-stationarity tests and extreme value distributions. Glob. Planet. Chang. 2004, 44, 11–26. [Google Scholar] [CrossRef]
- Redner, S.; Petersen, M.R. Role of global warming on the statistics of record-breaking temperatures. Phys. Rev. E 2006, 74, 061114. [Google Scholar] [CrossRef] [PubMed]
- Meehl, G.A.; Tebaldi, C.; Walton, G.; Easterling, D.; McDaniel, L. Relative increase of record high maximum temperatures compared to record low minimum temperatures in the U.S. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Anderson, A.; Kostinski, A. Evolution and distribution of record-breaking high and low monthly mean temperatures. J. Appl. Meteorol. Climatol. 2011, 50, 1859–1871. [Google Scholar] [CrossRef]
- Coumou, D.; Robinson, A.; Rahmstorf, S. Global increase in record-breaking monthly-mean temperatures. Clim. Chang. 2013, 118, 771–782. [Google Scholar] [CrossRef]
- Lehmann, J.; Coumou, D.; Frieler, K. Increased record-breaking precipitation events under global warming. Clim. Chang. 2015, 132, 501–515. [Google Scholar] [CrossRef]
- Donat, M.G. Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: The HadEX2 dataset. J. Geophys. Res. 2013, 118, 2098–2118. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).