Decadal-to-Multidecadal Variability of Seasonal Land Precipitation in Northern Hemisphere in Observation and CMIP6 Historical Simulations
Abstract
1. Introduction
2. Data and Methodology
2.1. Data
2.2. Methods
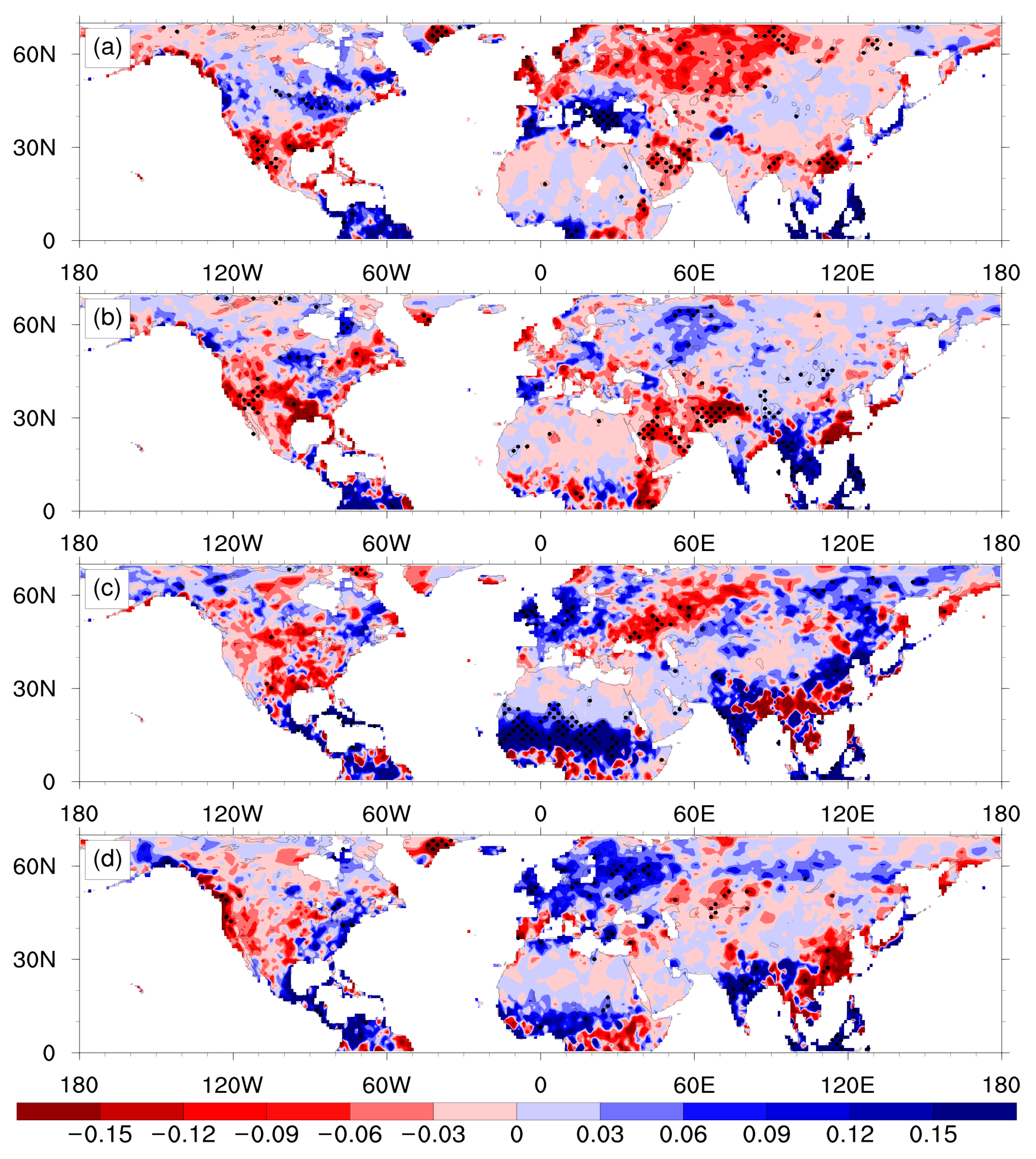
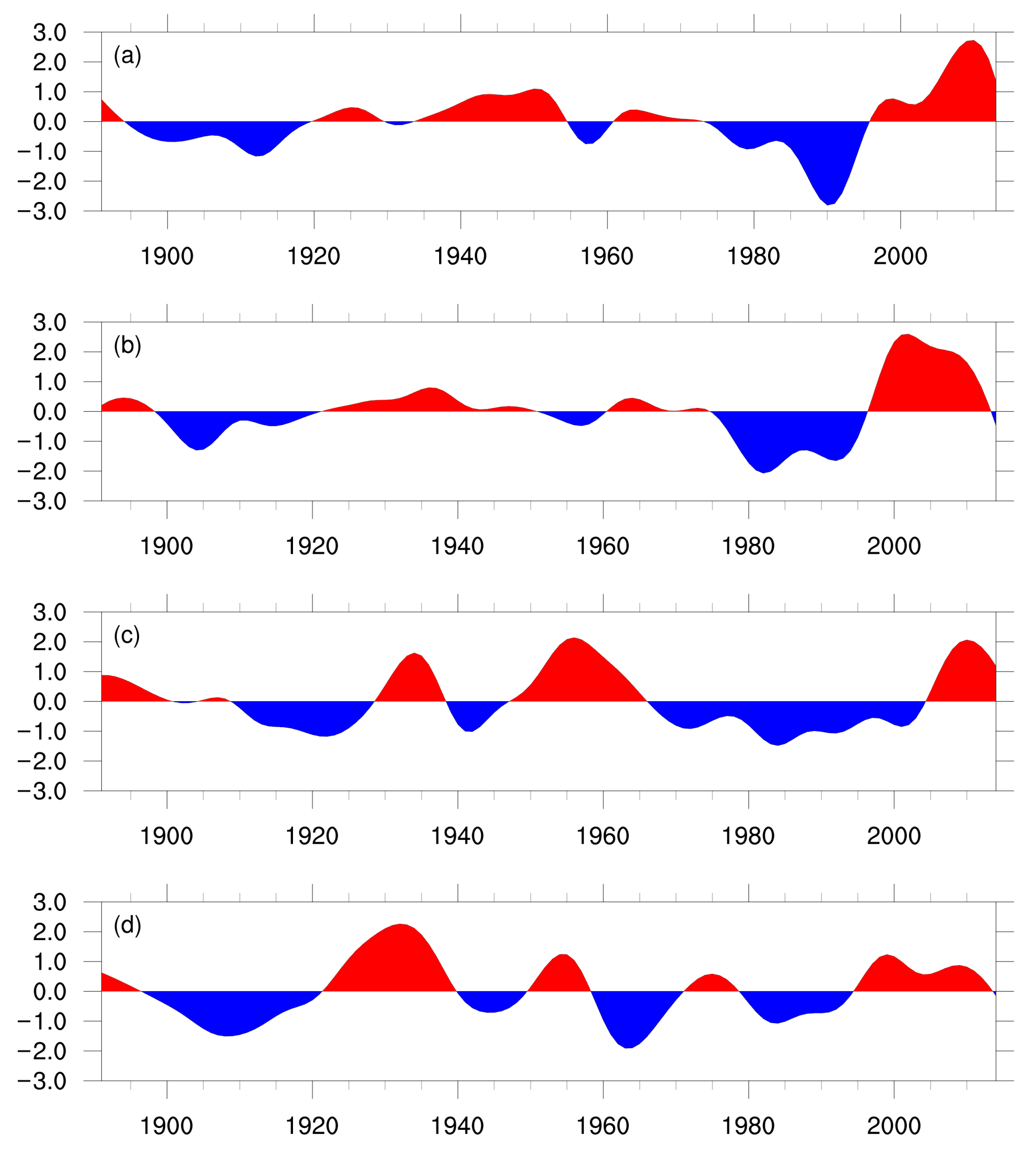
3. Spatial and Temporal Features of the DMVLP in GPCC
3.1. Winter
3.2. Spring
3.3. Summer
3.4. Autumn
3.5. Summary
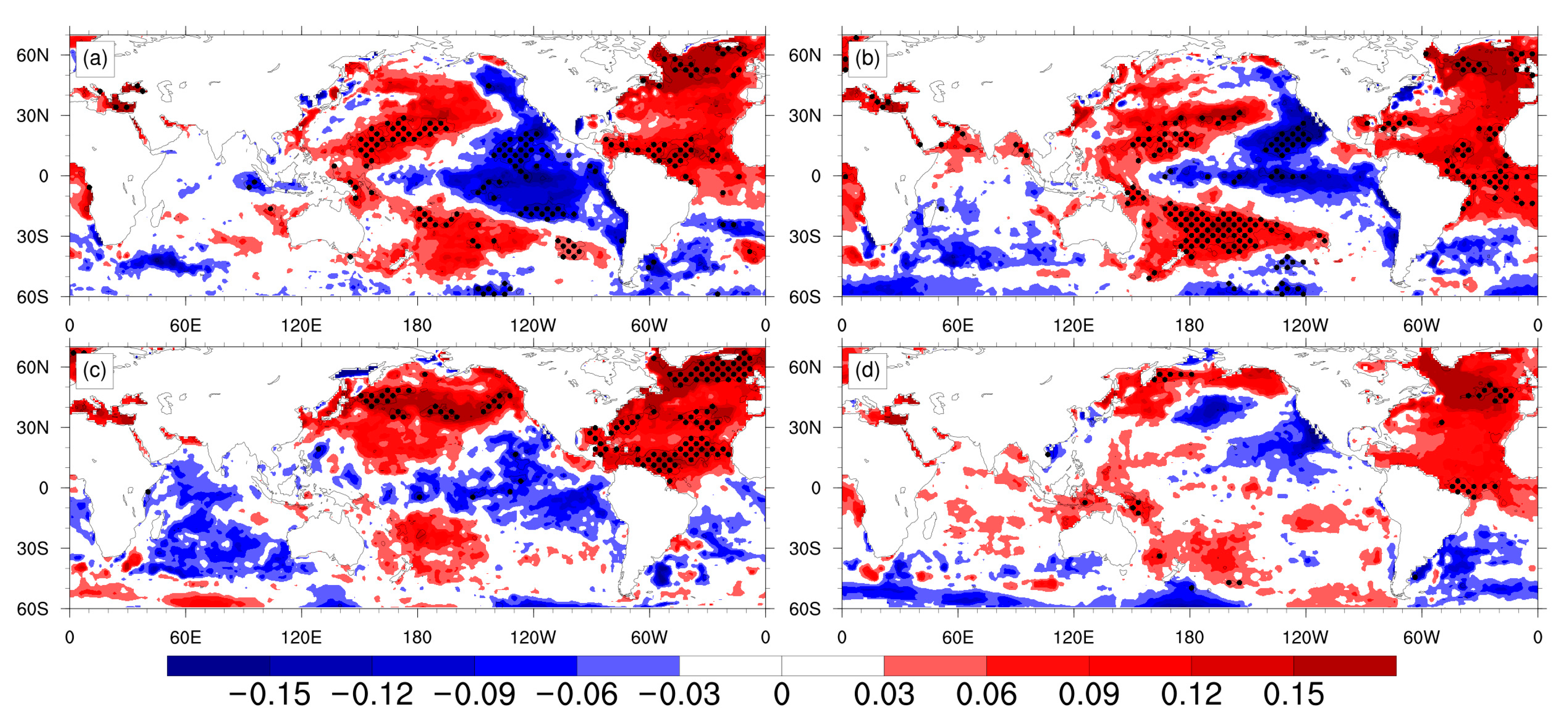
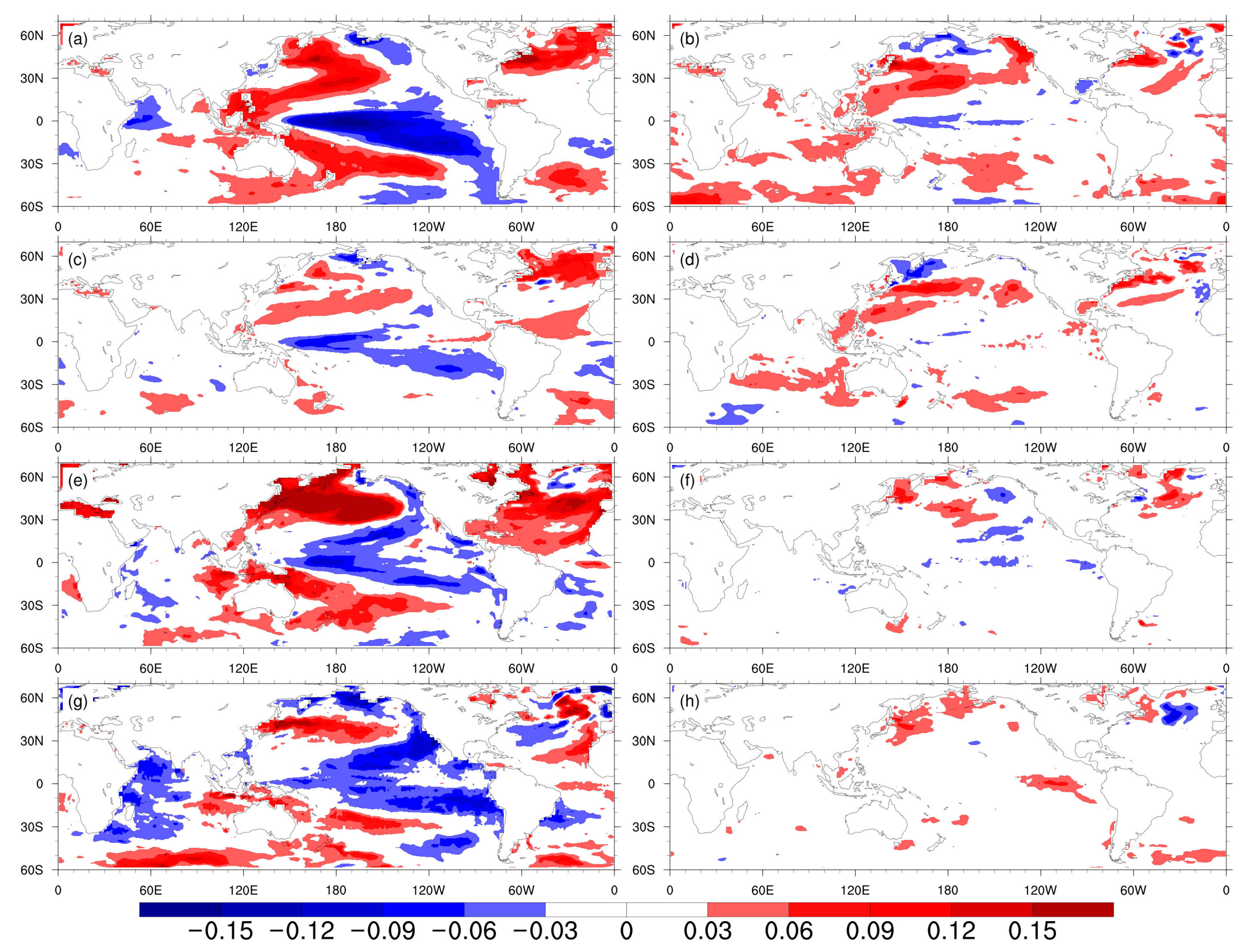
4. Oceanic Signals
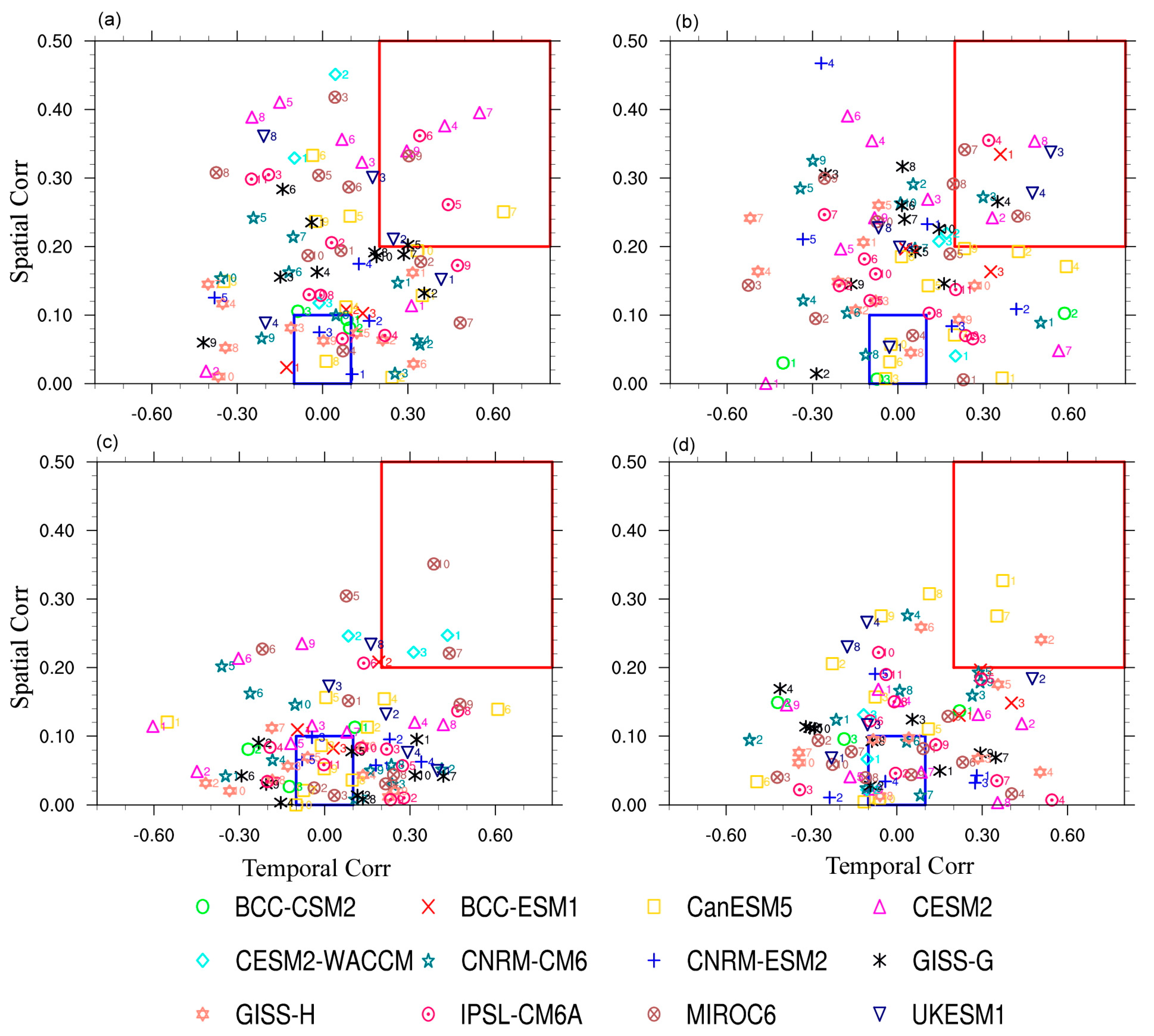
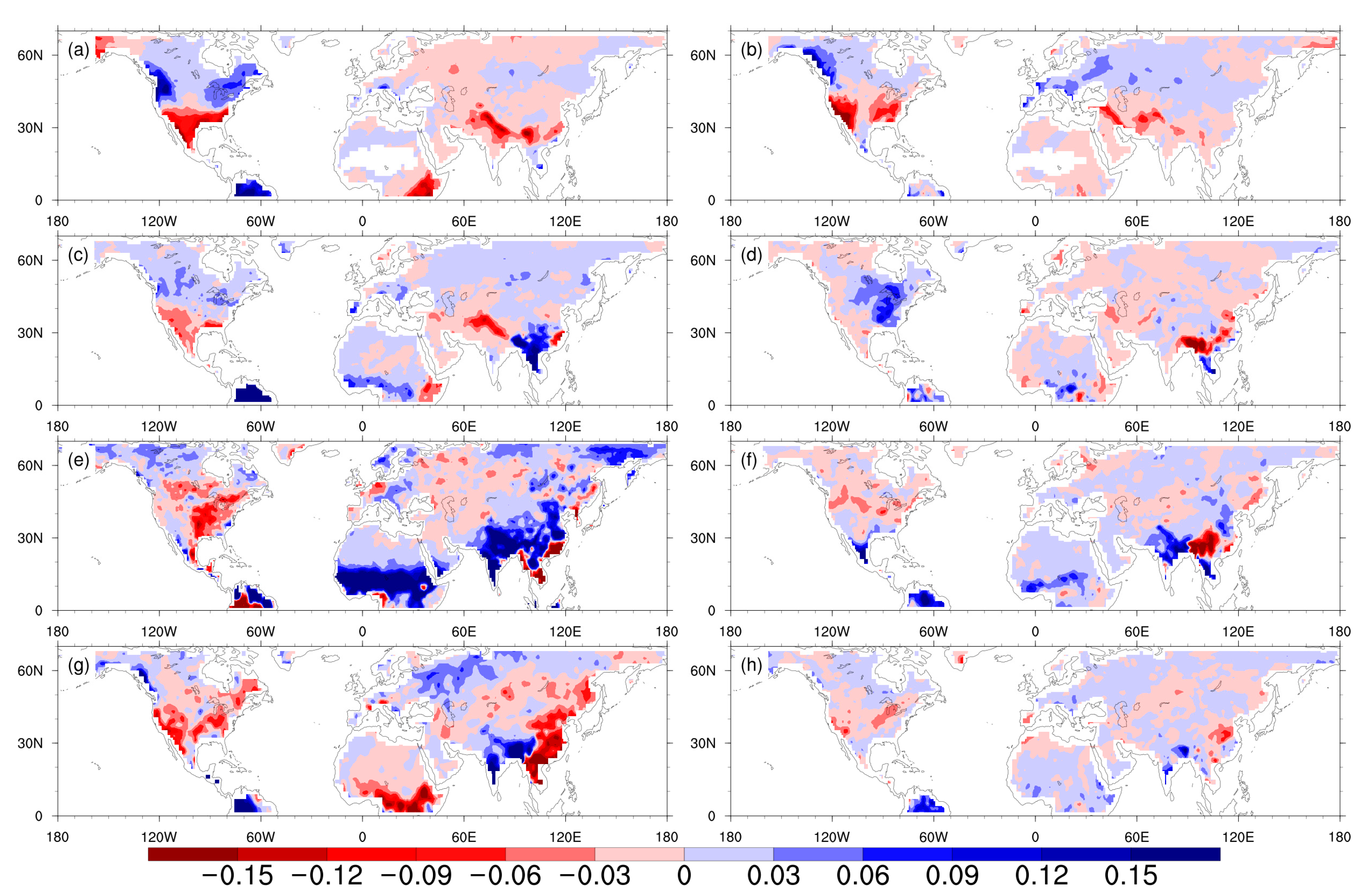
5. DMVLP in CMIP6 Simulations
Regressions of SSTA
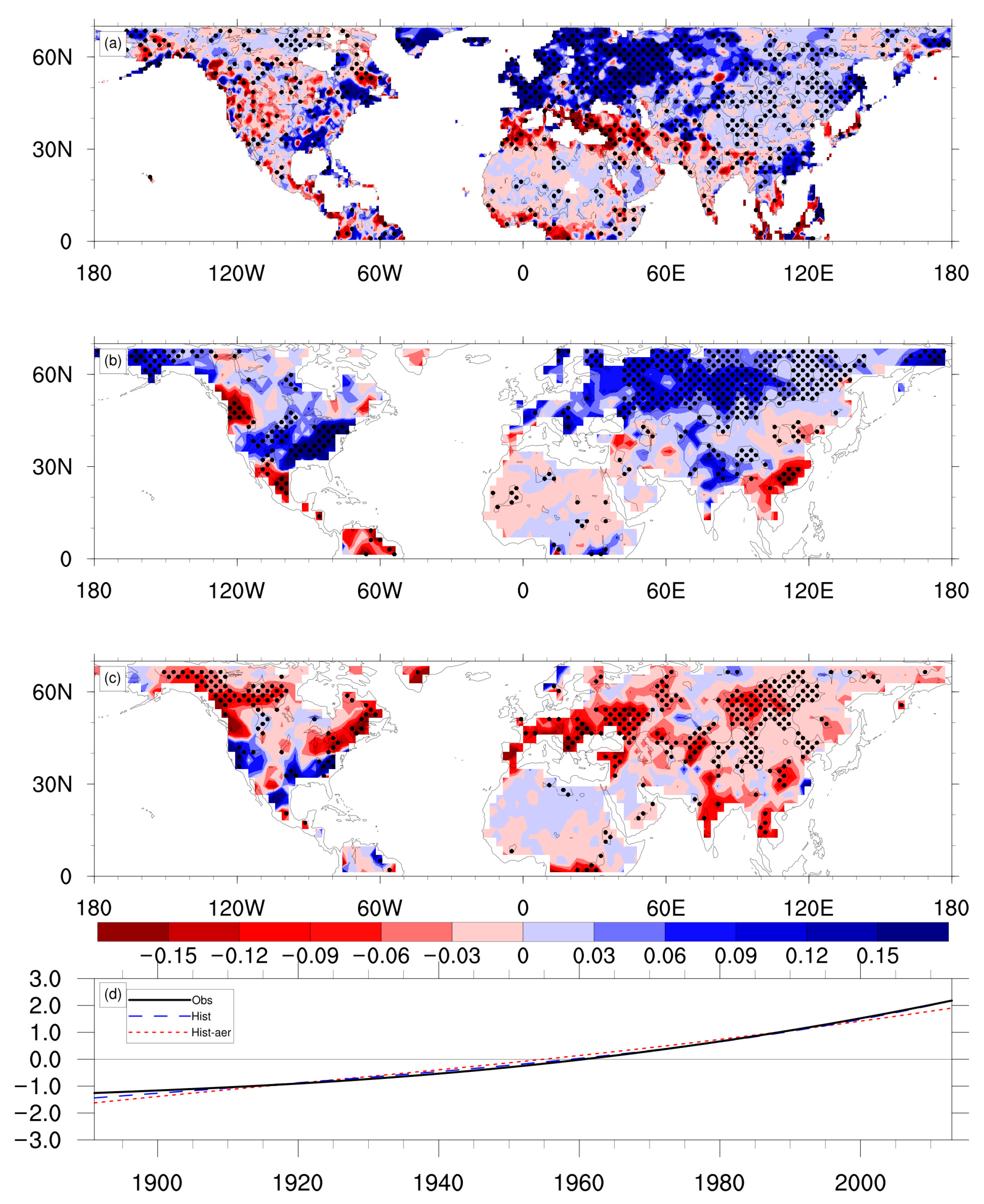
6. Summary and Discussion
6.1. Summary
6.2. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nicholson, S.E.; Tucker, C.J.; Ba, M.B. Desertification, drought, and surface vegetation: An example from the West African Sahel. Bull. Am. Meteorol. Soc. 1998, 79, 815–829. [Google Scholar] [CrossRef]
- Dai, A.; Trenberth, K.E.; Qian, T. A global dataset of palmer drought severity index for 1870–2002: Relationship with soil moisture and effects of surface warming. J. Hydrometeorol. 2004, 5, 1117–1130. [Google Scholar] [CrossRef]
- Shi, N.; Chen, L.; Fen, G.; Gao, H.; Ling, Z.; Guo, L. Climate characters and change in global land precipitation field from 1920 to 2000. Plateau Meteorol. 2004, 23, 435–443. [Google Scholar]
- Wang, B.; Ding, Q. Changes in global monsoon precipitation over the past 56 years. Geophys. Res. Lett. 2006, 33, 272–288. [Google Scholar] [CrossRef]
- Ma, Z.; Fu, C. Global aridification in the second half of the 20th century and its relationship to large-scale climate background. Sci. China Ser. D Earth Sci. 2007, 50, 776–788. [Google Scholar] [CrossRef]
- Narisma, G.T.; Foley, J.A.; Licker, R.; Ramankutty, N. Abrupt changes in rainfall during the twentieth century. Geophys. Res. Lett. 2007, 34, L06710. [Google Scholar] [CrossRef]
- Trenberth, K.E. Changes in precipitation with climate change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef]
- Haren, R.V.; Oldenborgh, G.J.V.; Lenderink, G.; Collins, M.; Hazeleger, W. SST and circulation trend biases cause an underestimation of European precipitation trends. Clim. Dyn. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Wen, G.; Huang, G.; Hu, K.; Qu, X.; Tao, W.; Gong, H. Changes in the characteristics of precipitation over northern Eurasia. Theor. Appl. Clim. 2015, 119, 653–665. [Google Scholar] [CrossRef]
- Gu, G.; Adler, R.F.; Huffman, G.J. Long-term changes/trends in surface temperature and precipitation during the satellite era (1979–2012). Clim. Dyn. 2016, 46, 1091–1105. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Andsager, K.; Easterling, D.R. Long-term trends in extreme precipitation events over the conterminous United States and Canada. J. Clim. 1999, 12, 2515–2527. [Google Scholar] [CrossRef]
- Xu, B.; Yang, Q.; Ma, Z. Decadal characteristics of global land annual precipitation variation on multiple spatial scales. Chin. J. Atmos. Sci. 2017, 41, 593–602. [Google Scholar]
- Mauget, S.A. Intra-to Multidecadal Climate Variability over the Continental United States: 1932–1999. J. Clim. 2003, 16, 2215–2231. [Google Scholar] [CrossRef]
- Ault, T.R.; George, S.S. The magnitude of decadal and multidecadal variability in North American precipitation. J. Clim. 2010, 23, 842–850. [Google Scholar] [CrossRef]
- Dieppois, B.; Pohl, B.; Rouault, M.; New, M.; Lawler, D.; Keenlyside, N. Interannual to interdecadal variability of winter and summer southern African rainfall, and their teleconnections. J. Geophys. Res. 2016, 121, 6215–6239. [Google Scholar] [CrossRef]
- Fu, C.; Jiang, Z.; Guan, Z.; He, J.; Guo, W. Regional Climate Studies of China; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Hu, P.; Qiao, S.; Feng, G. Interdecadal variation of precipitation pattern and preliminary studies during the summer of late-1990s in East Asia. Acta Phys. Sin. 2014, 63, 209204. [Google Scholar]
- Zhang, R.; Delworth, T.L. Impact of Atlantic Multidecadal Oscillations on India/Sahel Rainfall and Atlantic Hurricanes. Geophys. Res. Lett. 2006, 33, L17712. [Google Scholar] [CrossRef]
- Wang, B.; Liu, J.; Kim, H.-J.; Webster, P.J.; Yim, S.-Y. Recent changes of the global monsoon precipitation (1979–2008). Clim. Dyn. 2012, 39, 1123–1135. [Google Scholar] [CrossRef]
- Wang, B.; Liu, J.; Kim, H.-J.; Webster, P.J.; Yim, S.-Y.; Xiang, B. Northern Hemisphere summer monsoon intensified by mega-El Niño/Southern Oscillation and Atlantic multidecadal oscillation. Proc. Natl. Acad. Sci. USA 2013, 110, 4347–5352. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, X.; Yang, X. Understanding the interdecadal variability of East Asian summer monsoon precipitation: Joint influence of three oceanic signals. J. Clim. 2018, 31, 5485–5506. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, T. Amplified contiguous United States summer rainfall variability induced by East Asian monsoon interdecadal change. Clim. Dyn. 2018, 50, 3523–3536. [Google Scholar] [CrossRef]
- Dai, A. The influence of the inter-decadal Pacific oscillation on US precipitation during 1923–2010. Clim. Dyn. 2013, 41, 633–646. [Google Scholar] [CrossRef]
- Dong, B.; Dai, A. The influence of the interdecadal Pacific oscillation on temperature and precipitation over the globe. Clim. Dyn. 2015, 45, 2667–2681. [Google Scholar] [CrossRef]
- Qian, C.; Zhou, T. Multidecadal variability of North China aridity and its relationship to PDO during 1900–2010. J. Clim. 2013, 27, 1210–1222. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, A. How would the twenty-first-century warming influence Pacific decadal variability and its connection to North American rainfall: Assessment based on a revised procedure for the IPO/PDO. J. Clim. 2018, 31, 1547–1563. [Google Scholar] [CrossRef]
- Enfield, D.B.; Mestas-Nunes, A.M.; Trimble, P.J. The Atlantic multidecadal oscillation and its relation to rainfall and river flows in the continental U.S. Geophys. Res. Lett. 2001, 28, 2077–2080. [Google Scholar] [CrossRef]
- Wang, H.; Fu, R.; Kumar, A.; Li, W. Intensification of summer rainfall variability in the Southeastern United States during recent decades. J. Hydrometeorol. 2010, 11, 1007–1018. [Google Scholar] [CrossRef]
- Hu, Q.; Feng, S.; Oglesby, R.J. Variations in North American summer precipitation driven by the Atlantic Multidecadal Oscillation. J. Clim. 2011, 24, 5555–5570. [Google Scholar] [CrossRef]
- Goswami, B.N.; Madhusoodanan, M.S.; Neema, C.P.; Sengupta, D. A Physical Mechanism for North Atlantic SST Influence on the Indian Summer Monsoon. Geophys. Res. Lett. 2006, 33, L02706. [Google Scholar] [CrossRef]
- Sun, C.; Li, J.; Zhao, S. Remote influence of Atlantic multidecadal variability on Siberian warm season precipitation. Sci. Rep. 2015, 5, 16853. [Google Scholar] [CrossRef]
- Gu, G.; Adler, R.F. Spatial patterns of global precipitation change and variability during 1901–2010. J. Clim. 2015, 28, 4431–4453. [Google Scholar] [CrossRef]
- Luo, F.F.; Li, S.; Furevik, T. Weaker connection between the Atlantic Multidecadal Oscillation and Indian summer rainfall since the mid-1990s. Atmos. Ocean. Sci. Lett. 2018, 11, 37–43. [Google Scholar] [CrossRef]
- Kumar, S.; Merwade, V.; Kinter, J.L.; Niyogi, D. Evaluation of temperature and precipitation trends and long-term persistence in CMIP5 twentieth-century climate simulations. J. Clim. 2013, 26, 4168–4185. [Google Scholar] [CrossRef]
- Purich, A.; Cowan, T.; Min, S.K.; Cai, W. Autumn Precipitation trends over southern hemisphere midlatitudes as simulated by CMIP5 models. J. Clim. 2013, 26, 8341–8356. [Google Scholar] [CrossRef]
- Ren, L.; Arkin, P.; Smith, T.M.; Shen, S.S.P. Global precipitation trends in 1900–2005 from a reconstruction and coupled model simulations. J. Geophys. Res. 2013, 118, 1679–1689. [Google Scholar] [CrossRef]
- Ault, T.R.; Cole, J.E.; George, S.S. The amplitude of decadal to multidecadal variability in precipitation simulated by state-of-the-art climate models. Geophys. Res. Lett. 2012, 39, L21705. [Google Scholar] [CrossRef]
- Gaetani, M.; Mohino, E. Decadal prediction of the Sahelian precipitation in CMIP5 simulations. J. Clim. 2013, 26, 7708–7719. [Google Scholar] [CrossRef]
- Hirota, N.; Takayabu, Y.N.; Hamada, A. Reproducibility of summer precipitation over northern Eurasia in CMIP5 multiclimate models. J. Clim. 2016, 29, 3317–3337. [Google Scholar] [CrossRef]
- Lyu, K.; Yu, J.Y. Climate impacts of the Atlantic Multidecadal Oscillation simulated in the CMIP5 models: A re-evaluation based on a revised index. Geophys. Res. Lett. 2017, 44, 3867–3876. [Google Scholar] [CrossRef]
- Joshi, M.K.; Kucharski, F. Impact of Interdecadal Pacific Oscillation on Indian summer monsoon rainfall: An assessment from CMIP5 climate models. Clim. Dyn. 2017, 48, 2375–2391. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Rayner, N.A.; Parker, D.E.; Horton, E.B.; Folland, C.K.; Alexander, L.V.; Rowell, D.P. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. 2003, 108, 1063–1082. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M. GPCC Full Data Monthly Product Version 2018 at 1.0°: Monthly Land-Surface Precipitation from Rain-Gauges Built on GTS-Based and Historic Data; Global Precipitation Climatology Centre: Berlin, Germany, 2018. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Widmann, M.; Dymnikov, V.P.; Wallace, J.M.; Bladé, I. The effective number of spatial degrees of freedom of a time-varying field. J. Clim. 1999, 12, 1990–2009. [Google Scholar] [CrossRef]
- Trenberth, K.E. Recent observed interdecadal climate changes in the northern hemisphere. Bull. Am. Meteorol. Soc. 1990, 71, 988–993. [Google Scholar] [CrossRef]
- Huang, H.P.; Seager, R.; Kushnir, Y. The 1976/77 transition in precipitation over the Americas and the influence of tropical sea surface temperature. Clim. Dyn. 2005, 24, 721–740. [Google Scholar] [CrossRef]
- McCabe, G.J.; Palecki, M.A.; Betancourt, J.L. Pacific and Atlantic Ocean influences on multidecadal drought frequency in the United States. Proc. Natl. Acad. Sci. USA 2004, 101, 4136–4141. [Google Scholar] [CrossRef]
- Si, D.; Ding, Y. Oceanic forcings of the interdecadal variability in East Asian summer rainfall. J. Clim. 2016, 29, 7633–7649. [Google Scholar] [CrossRef]
- Chikamoto, Y.; Timmermann, A.; Luo, J.; Mochizuki, T.; Kimoto, M.; Watanabe, M.; Ishii, M.; Xie, S.-P.; Jin, F.-F. Skilful multi-year predictions of tropical trans-basin climate variability. Nat. Commun. 2015, 6, 6869. [Google Scholar] [CrossRef]
- Li, X.; Xie, S.-P.; Gille, S.T.; Yoo, C. Atlantic-induced pan-tropical climate change over the past three-decades. Nat. Clim. Chang. 2016, 6, 275–279. [Google Scholar] [CrossRef]
- Kamae, Y.; Li, X.; Xie, S.-P.; Ueda, H. Atlantic effects on recent decadal trends in global monsoon. Clim. Dyn. 2017, 49, 3443–3455. [Google Scholar] [CrossRef]
- Smith, D.M.; Booth, B.B.B.; Dunstone, N.J.; Eade, R.; Hermanson, L.; Jones, G.S.; Scaife, A.A.; Sheen, K.L.; Thompson, V. Role of volcanic and anthropogenic aerosols in recent global surface warming slowdown. Nat. Clim. Chang. 2016, 6, 936–940. [Google Scholar] [CrossRef]

| Models | No. of Ensemble Members |
|---|---|
| CanESM5 | 10 |
| CNRM-CM6-1 | 10 |
| GISS-E2-1-G | 10 |
| GISS-E2-1-H | 10 |
| IPSL-CM6A-LR | 10 |
| MIROC6 | 10 |
| CESM2 | 9 |
| CNRM-ESM2-1 | 5 |
| UKESM1-0-LL | 5 |
| BCC-CSM2-MR | 3 |
| BCC-ESM1 | 3 |
| CESM2-WACCM | 3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Xu, Z. Decadal-to-Multidecadal Variability of Seasonal Land Precipitation in Northern Hemisphere in Observation and CMIP6 Historical Simulations. Atmosphere 2020, 11, 195. https://doi.org/10.3390/atmos11020195
Chen H, Xu Z. Decadal-to-Multidecadal Variability of Seasonal Land Precipitation in Northern Hemisphere in Observation and CMIP6 Historical Simulations. Atmosphere. 2020; 11(2):195. https://doi.org/10.3390/atmos11020195
Chicago/Turabian StyleChen, Hua, and Zhenchen Xu. 2020. "Decadal-to-Multidecadal Variability of Seasonal Land Precipitation in Northern Hemisphere in Observation and CMIP6 Historical Simulations" Atmosphere 11, no. 2: 195. https://doi.org/10.3390/atmos11020195
APA StyleChen, H., & Xu, Z. (2020). Decadal-to-Multidecadal Variability of Seasonal Land Precipitation in Northern Hemisphere in Observation and CMIP6 Historical Simulations. Atmosphere, 11(2), 195. https://doi.org/10.3390/atmos11020195




