Abstract
The existence of several gridded precipitation products (GPP) has facilitated studies related to climate change, climate modeling, as well as a better understanding of the physical processes underpinning this key variable. Due to complexities in estimating rainfall, gridded datasets exhibit different levels of accuracy across regions, even when they are developed at relatively high resolution or using sophisticated procedures. The performance of 16 GPP are evaluated over the Caribbean region, which includes the Caribbean Islands, and portions of Central South America. Monthly data for sixty weather stations are used as a reference for the period 1983–2010. The 16 GPP include six products based on station data only, two that combine ground station and satellite information, two merging station and reanalysis information, four based on reanalysis, and two using multisource information. The temporal resolution of the GPP ranged between daily and monthly and spatial resolution from 0.033° to 0.5°. The methodological approach employed combined a comparison of regional and sub-regional precipitation annual cycles, the Kling–Gupta efficiency (KGE) index, as well as several metrics derived from the standardized precipitation index (SPI). Overall, the best performances were obtained from GPCC025 and MSWEP2, likely reflecting the positive impact of the large number of station data utilized in their development. It is also demonstrated that a higher spatial resolution does not always mean better accuracy. There is a need for this kind of assessment when undertaking climate studies in regions like the Caribbean where resolution is a significant consideration. ERA5 performed best among the reanalyses analyzed and has the potential to be used to develop regionally based GPP by applying bias correction or downscaling techniques. The methodological approach employed provides a comprehensive and robust evaluation of the relative strengths and weaknesses of GPP in the Caribbean region.
1. Introduction
Precipitation is one of the most important climatic variables and it is included in a large number of studies of weather and climate. Precipitation datasets in the form of a regular grid (herein, gridded precipitation products (GPP)) have particular importance for various applications related to climate change detection [1], climate model evaluation [2], and the parameterization of stochastic generators [3,4]. GPP are also useful for understanding the interactions between climate and terrain, as well as hydrological and biogeochemical processes [5,6,7].
The adequate representation of the spatial and temporal variations of precipitation is difficult, mainly because it is significantly affected by the availability and quality of observed data. Although the rain gauges are the most suitable ways to estimate precipitation [8], stations are often sparsely located, and present errors that arise from instrumental and non-instrumental problems (e.g., wind influences) which limit the quality of the observed data [9,10]. Also, despite the notable advances in estimating precipitation from satellite data, this option is limited by temporal sampling and algorithm errors [11]. Additionally, the spatial distribution of precipitation is also affected by complex topography [12].
In recent years, many GPP have been developed, covering different periods, and temporal and spatial scales. These datasets were created, not only using ground-based measurements [13,14] or satellite data [15] but also by combining different sources of precipitation data [16,17,18]. The accuracy of those GPP has been assessed at different spatial and temporal scales using disparate methodologies, showing the advantages and limitations of each product. Most of these assessments were conducted on global or regional scales [18,19], such as in Africa [20,21], Europe [22], Asia [23], and North America [24]. In Latin America, most evaluation studies are concentrated in portions of South America [25,26,27]. In general, these studies suggest different pictures of the best GPP datasets at global and/or regional scales and reinforce the need to evaluate the accuracy of a particular GPP in a region. This problem is especially critical for insular regions such as the Caribbean Islands.
For the Caribbean region, where small scattered countries are dominant and a sparse land-based observational precipitation network exists, there are very few studies evaluating the accuracy of GPP. An intercomparison study using several GPP, including various models from the Coupled Model Intercomparison Project phase 3 (CMIP3) [28], highlights differences in representing the spatial pattern of rainfall in the eastern half of the Caribbean Islands. Ref. [28] concluded that no single GPP was without its discrepancy and that the high-resolution satellite products examined were reasonably representative notwithstanding their short time span (five years at the time of the study). Many of the GPP examined in that study have since been updated to incorporate more observations, improved interpolation techniques, and/or a finer resolution, suggesting the need for re-evaluation. Other studies have compared different GPP when evaluating the spatial and temporal variability of rainfall across the Caribbean [29] and the performance of climate models [30,31]. However, these studies start with the premise that the GPP offer either the best available or the most reasonable representation of the regional climate and thereafter use the GPP as the reference for analysis being undertaken. Recently, ref. [32] produced a very high-resolution monthly dataset (0.033° × 0.033°) that, along with other climate variables, includes precipitation. The authors prove a better accuracy of their downscaled precipitation product, as compared with the original low-resolution (1° × 1°) Global Precipitation Climatology Centre (GPCC) version 7 [14].
As suggested by Jones et al. (2016) [29], many studies have investigated the dynamical drivers of precipitation variability in the Caribbean, aiming to improve the skill of weather and climate forecasting. Most of these studies used different GPP without a comprehensive evaluation of their abilities to represent the main features of precipitation in the Caribbean, and/or conclude that their results were limited to the large-scale because the datasets employed do not have a horizontal resolution appropriate for the Caribbean islands. An accurate description of the temporal and spatial variations of precipitation in the Caribbean requires products that are capable of reproducing regional features at the appropriate spatial resolution. Theoretically, higher resolution GPP could best fulfill this requirement, as compared with lower resolution ones. However, since higher resolution does not necessarily mean a better representation of the observed climate features, it is critical to always evaluate the GPP performance.
This work aims to: (1) assess the ability of 16 GPP in representing the characteristics of precipitation in the Caribbean as compared to surface stations, and (2) determine which products perform best over the region using common statistical metrics. To do so, we conduct a comprehensive evaluation and intercomparison of several GPP across the Caribbean, including the latest versions of some previously evaluated for the region and others that have not yet been evaluated for the Caribbean. Results from this work might be used as a reference to select the most appropriate GPP (e.g., for model evaluation and climate change studies), based on their advantages and limitations. This paper is organized as follows. Section 2 presents the study domain, the data, and methods used in this work. In Section 3, we describe the results, while Section 4 provides the conclusions of the study.
2. Data and Methods
2.1. Study Area
As in [29,33,34], our study domain is located between 10–24° N, and 90–59° W, which includes the Caribbean Islands, and portions of Central and South America (Figure 1). Precipitation seasonality in the Caribbean generally has two main seasons: a dry season from November to April, and a wet season from May to October [33]. An exception is the Eastern Caribbean, where the rainy season extends until November. An important feature of the rainfall annual cycle is a relatively drier period that occurs within the wet season (more commonly in July), called the mid-summer drought (MSD) [35], which is more prominent in the Western Caribbean than in the Eastern Caribbean. Because of the differences in precipitation between the Western and Eastern Caribbean, the study area was subdivided into two sub-regions (see Figure 1b,c).
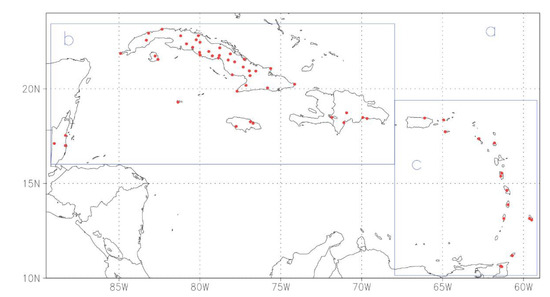
Figure 1.
Study area and the location of the rain-gauge network. (a) Caribbean region, (b) the western Caribbean sub-region, and (c) the eastern Caribbean sub-region.
2.2. Datasets
We use monthly precipitation data from 60 rain-gauges spatially distributed across the study area (Figure 1 and Table A1). Data from Belize and Cuba were supplied by the respective Meteorological Services from each country, while data from the Dominican Republic are homogenized series from [36]. Station data for the rest of the study domain were those used by [34].
We use fifteen global and one regional monthly GPP (Table 1). These datasets vary in their spatial and temporal resolutions, as well as in the methods used to develop them. The 16 GPP includes 6 products based on station data only, 2 that combine ground station information and satellite, 2 merging station and reanalysis, 4 based on reanalysis, and 2 using multisource (i.e., a combination of data sources) information. The GPP were selected based on their prior use in the region as well as on their availability and accessibility for the period 1983–2010 (28 years) which overlapped with the available station data. It is difficult to consider a longer time-interval due to, for example, limitations such as surface station data availability, completeness and inhomogeneities. However, as suggested by previous studies, this is a common constraint for most countries in the Caribbean [34,37].

Table 1.
Information on GPP used in this study. The abbreviations in column 3 are defined as follow: G, gauges; S, satellite; and R, reanalysis. The term land in the column 5 means the dataset is limited to land areas only. A detailed description of each GPP is provided as Supplementary Information.
2.3. Methodology
We followed a point-to-grid approach by extracting the GPP grid cell over the underlying weather stations, which produces similar results as the neighborhood interpolation method. Features of precipitation at both point and spatial scale are analyzed over the subregions shown in Figure 1. We evaluate the GPP following 2 steps. First, we assess the ability of each GPP to represent the main features of the rainfall annual cycle in our study domain, including the presence of the MSD. Secondly, we use indicators of performance such as the modified efficiency index of Kling-Gupta (KGE) [47] and the standardized precipitation index (SPI) at 3, 6, and 12 months [48,49,50]. Since the KGE index integrates other statistical metrics such as the bias and correlation coefficients, we also use these metrics in our evaluation. The KGE is calculated for every location (station/grid point) using monthly precipitation during the dry (November–April) and wet (May–October) periods and annually with the following equation:
where n is the number of observations, Oi and Si are the observed and estimated data, respectively, in month i; O and S are the average values of the observations and the estimates, respectively.
The optimal value of the KGE index and its components (R, B, and V) is equal to one. R is the linear correlation between observations and precipitation estimates; B is the bias, which reflects when the estimated values are greater or lower than observations, while V is similar to the bias but for variability.
We calculate SPIs for 3, 6, and 12 months to explore how each GPP represents the observed statistics of drought and pluvial conditions (SPI ≤ −1.0 and SPI ≥ 1.0, respectively) [48] in the Caribbean. The evaluation considers both the drought statistics as well as the number of grid points within the region with different SPI categories. We evaluate drought statistics such as the frequency of dry months (DF) and the number of drought events (DE). We define a drought considering the experiences from the Meteorological Service of Cuba, in which a drought occurs when the SPI value of a single or sequence of months falls below the −0.5 threshold (herein SPI-0.5). A dry interval ends when the SPI becomes greater than −0.5. Similarly, an SPI value of −1.5 (SPI-1.5) is also used to examine severe droughts. The number of the grid points either under pluvial or drought conditions is determined by creating a time series of the number of stations or GPP grid cells affected by each category. Since this time series is an indicator of the pluvial/drought area, we called it the SPI Areal Assessment (SPIAA). We use the CARiDRO system [51] to derive most of the hydroclimate statistics and calculations.
3. Results and Discussion
3.1. The Mean Annual Cycle of Precipitation
The mean precipitation annual cycle from the GPP (Figure 2a–c) reveals a high correspondence with observations for the subregions defined in Figure 1. For the western sub-region and the Caribbean as a whole, the GPP represent well the bimodal pattern of the rainfall, including the MSD (Figure 2a,b). There is strong coincidence between the GPP that overestimate or underestimate observations in the western Caribbean and the Caribbean as a whole. This may reflect the fact that the larger proportion of stations fall in the western Caribbean (45 out of the 60 stations). In the Eastern Caribbean (Figure 2c), where the MSD is absent and the land masses are smaller, the GPP similarly capture the main features of the observed annual variation pattern including the occurrence of the maximum in November. However, differences from the observations tend to be greater than for the western Caribbean and some GPP a such as PERSIANNCDR, CFSR, and CHELSA are even displaying a displaying the opposite sign in total precipitation particularly in the wet season months (not show). The implication is that a GPP that does well at capturing mean climate in the western Caribbean or the Caribbean as a whole may not necessarily be equally good in the eastern Caribbean.
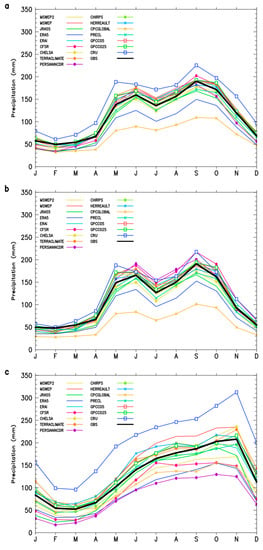
Figure 2.
Annual cycle of observations and GPP, averaged over the region (a), western subregion (b) and eastern subregion (c) defined in Figure 1.
For the eastern sub-region, four gauge only/gauge-based GPP (CHIRPS, PRECL, GPCC025, and GPCC05) are among the best performers, having the lowest absolute differences. In comparison, the reanalysis products tend to underestimate the monthly mean precipitation, with ERAi producing the best representation of observations (smallest monthly deviations). GPP with largest deviations are CPCGLOBAL, ERA5, PERSIANNCDR and MSWEP2 (underestimates) and CRU, MSWEP and HERREAULT (overestimates). These GPP use different methodologies in their development and different sources of data; for example, whereas CPCGLOBAL and CRU use only rain-gauges, PERSIANNCDR and CHIRPS merge rain-gauges and satellite information, while ERA5 is a reanalysis product. We suggest that the relatively poorer performance of most of the GPP over the eastern Caribbean may result from: (i) the scarcity of rain-gauges in this subregion, and (ii) the poor representation by the reanalysis-based GPP of the precipitation processes that occur in the small islands (e.g., with areas ≤ 1500 km2).
The GPP’ performance is significantly better in the western Caribbean, though substantial departures exist between observations and some GPP e.g., CPCGLOBAL and ERA5. We note that the better performance by some GPP with respect to the entire domain reflect their ability to minimize differences with ground stations in both subregions. Over the entire domain, GPCC025, GPCC05, CHIRPS, and CHELSA stand out as the better performing GPP with respect to the annual precipitation cycle features in the Caribbean.
3.2. Evaluation of GPP Based on the Modified Efficiency Index of Kling-Gupta
Figure 3 shows the results from the modified KGE analysis and its components (Bias, Correlation and Variability). The five GPP with highest KGE median values are the two versions of GPCC (GPCC025 and GPCC05), the two MSWEP products (MSWEP and MSWEP2) (all greater than 0.7) and the CHELSA product (median score of 0.68). The GPP with the lowest median KGE was CPCGLOBAL (<0.4) which also had large deviations from observations in the climatological analysis. The same GPP emerge as the best performers with respect to median KGE for the wet and dry seasons (Figure 4), though their relative rankings shift depending on season. Across the two seasons, CPCGLOBAL remains the worst performer. The five best GPP generally perform well across the entire Caribbean, with high values of KGE distributed across the region (Figure 5). The inclusion of a higher number of rain gauges and other improvements in the 8th version of GPCC [40] might explain the good skill of GPCC025 and GPCC05. The MSWEP and MSWEP2 products likely also perform well because of the use of a high-resolution dataset based on surface stations. Furthermore, since CHELSA uses a similar downscaling procedure as GPCC025, it shares similarities with GPCC in our study region.
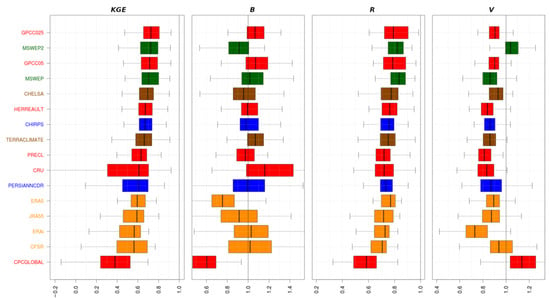
Figure 3.
Boxplot of the KGE index and its components B (bias), R (correlation) and V (variability). The names of the GPP are colored according to data source considered in its development (red: stations; brown: stations and reanalysis; blue: stations and satellites; orange: reanalysis and green: multisources). The GPP have been sorted according to the median value of KGE index. In all the cases the optimal value is 1.0.
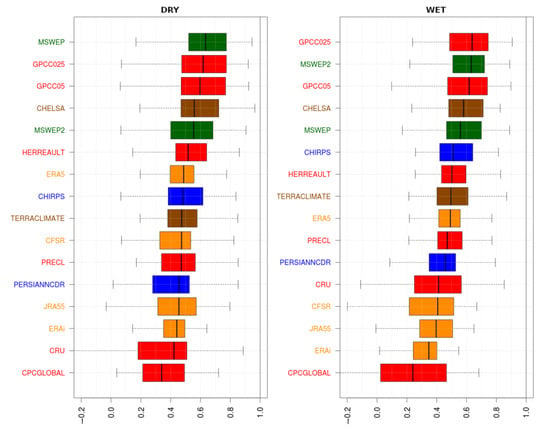
Figure 4.
As in Figure 3 but just for KGE index for dry (left) and wet (right) seasons.
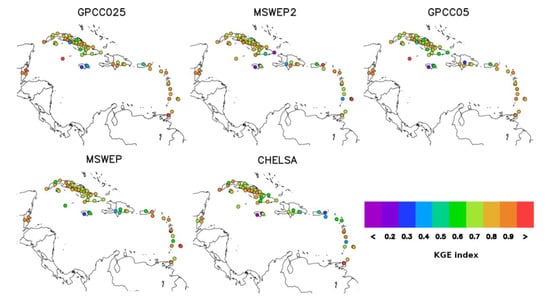
Figure 5.
Spatial distribution of KGE scores for GPCC025, MSWEP2, GPCC05, MSWEP, and CHELSA. Colors for KGE range from violet to red, representing very poor to optimum skill respectively. Diagrams ordered according to median annual performance (see Figure 3).
Figure 3 also shows the annual KGE component scores for each GPP. Relative performance with respect to correlation generally matches that for the overall KGE score suggesting the strong influence of the latter in the calculation of the former. It is noted that the five best GPP and the worst GPP with respect to median KGE also emerge as the GPP with highest correlation values (ranging from 0.752 to 0.841) and lowest value (0.582) respectively. A similar result was found by [24] when evaluating various daily precipitation datasets over the conterminous US. As in [24], we confirm that correlation has a dominant influence on KGE scores. For GPP to have a better representation of observations, then, improving this statistic, without degrading the information content, should be a priority. When the analysis is done by season (not shown), the median values of temporal correlations are comparable, ranging from 0.5 to 0.8 (0.45 to 0.75) for the dry (wet) season. Almost all GPP underestimate the rainfall variability in the region (median values from 0.7 to 0.95), except for CPCGLOBAL and MSWEP2, which are the only products that overestimate it. Across individual seasons MSWEP2 also shows the best results for variability (not shown).
Table 2 presents the mean scores across all GPP for the median KGE’s components. Table 2 highlights the poor performance of correlation in general, which greatly influences the final KGE scores. Table 2 also suggests that the variability component should also be taken into account to improve the GPP performance in the wet season.

Table 2.
Mean median KGE components scores. Bias, Correlation and Variability are expressed as |B − 1|, | R− 1| and |V − 1|, respectively (see Equation (1)).
We also note the following based on the calculated scores for KGE and its components:
- Based on the KGE index, GPCC025 and GPCC05 (gauge only), MSWEP and MSWEP2 (gauge, satellite, and reanalysis), and CHELSA (gauge and reanalysis) display an overall good performance, including for each season and the whole year. Of the two datasets that merge rain-gauge and satellite information, we find that, at least in our study domain, PERSIANNCDR performs worse than CHIRPS. We suggest that the use of a coarse precipitation dataset (2.5°) such as GPCP [16], possibly reduces the skill of PERSIANNCDR to adequately represent precipitation features in the Caribbean.
- CRU and PRECL datasets are among the station-based products with the lowest performance in representing precipitation variability across the Caribbean. This is likely due to the lower number of surface station taken into account in their development, as compared with other station based GPP such as GPCC025, GPCC05, and HERREAULT.
- Although we expected similar performance for HERREAULT as GPCC, considering the former was built upon a GPCC product [32], this was not observed. In this regard, we found significant differences between the GPCC version 7 (used in HERREAULT) and version 8 (evaluated here), as shown by their low correlations over our study domain (Figure 6). This could in part explain the differences in the performance between HERREAULT and the GPCC products used in this paper. Nevertheless, further investigation should be carried out due to the potential to generate a more accurate regional high-resolution product (such as HERREAULT) based on the GPCC full data version 8.
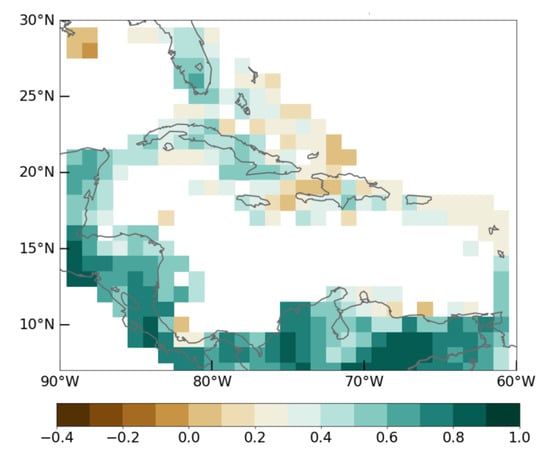 Figure 6. Correlation between full data GPCCversion 8 and version 7 over the period 1983–2000. The products were used with a native spatial resolution of 1° × 1°.
Figure 6. Correlation between full data GPCCversion 8 and version 7 over the period 1983–2000. The products were used with a native spatial resolution of 1° × 1°.
- The lowest KGE scores, suggesting a relatively poor performance, correspond to most reanalyses (except for ERA5) and consistently CPCGLOBAL. The reanalysis products are among the GPP with the lowest performance, which reflects the limitations of the current atmospheric models to represent the fine-scale precipitation processes. This might be due to limitations in representing sub-grid convection and land-surface parameterization schemes. This result also reveals a constraint related to the spatial resolution needed to adequately represent the small islands of the Lesser Antilles. A possible solution to this limitation could be the incorporation of high-resolution, non-hydrostatic, regional models [52].
- Although ERA5 significantly underestimates precipitation across the Caribbean, it is the reanalysis product with the best performance based on the KGE scores. This is seen in the better correlation and variability scores with ground stations. This suggests its potential for use in the development of new GPP products for the Caribbean especially with bias correction techniques employed—which may prove easier than trying to improve the linear correlations [27]. For example, it is hypothesized that the CHELSA product, which was developed based on ERA-Interim [44], may perform even better over the region if using ERA5 instead, which is currently the primary reanalysis model from the ECMWF.
3.3. GPP Evaluation Based on SPI
The results for selected drought statistics determined using SPI-0.5 and SPI-1.5 are presented in Figure 7 for SPI 3, 6, and 12. Overall, most of the GPP fail in representing accurately the SPI-0.5 statistics (Figure 7a,c), having different ratings for different statistics. The GPP with best performance were MSWEP, MSWEP2, ERA5, and CHELSA. For SPI-1.5 (Figure 7b,d), the GPP better resemble the observations with a discernible distinction between the worst and best performers, and a tendency to overestimate the maximum consecutive months with drought and the number of drought events. In general, products such as MSWEP2, ERA5, CHELSA, and MSWEP were the most accurate. The best performing products across both SPI statistics are the same as those with highest correlations in the KGE analysis (see Figure 3). We note, however, that care must be exercised when assessing GPP performance on the basis of an individual drought statistic, as it only offers a limited perspective while not capturing the overall ability of the GPP across SPI’s of different intensity and length. For instance, following the methodology used by [23], who only consider DF in the evaluation of GPP, we would conclude that CRU or TERRACLIMATE are among the best GPP for SPI-0.5. Conversely, if we take into account the DE statistics, the performance of those GPP is not as good. Similarly, we find that PRECL is among the GPP with best skill in representing DE statistics for SPI-0.5, but not DF for SPI-0.5.
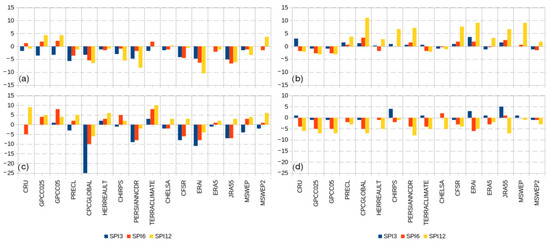
Figure 7.
Differences between observation and the GPP for drought statistics derived from SPI-0.5 (left column) and SPI-1.5 (right column). Drought Frequency (DF) and Number of Drought Events (DE) are shown in panels (a,b), and (c,d), respectively. Bars show values for SPI3 (blue), SPI6 SPI6 (red) and SPI12 (yellow). In the case of DF (a,b) the differences are represented as percentage. (red) and SPI12 (yellow). In the case of DF (a,b) the differences are represented as percentage.
In conducting the SPIAA analysis, we compared the SPIAA time series from observations against the GPP for SPI 3, 6, and 12. To do so, we selected −0.5 and 0.5 as SPI thresholds to identify droughts and pluvial events. Figure 8 presents the results of SPIAA using SPI12. (Though SPI3 and SPI6 are not shown they indicate similar results). For drought conditions, the GPP have different performances across the drought categories, with correlations ranging from 0.3 to 0.8, and temporal variability greater than observations. The results are better for areas with SPI lower than −0.5 (Figure 8a) and worse when moderate and severe drought categories are considered (Figure 8b,c). MSWEP, CHIRPS, and GPCC025 show the best skill overall across SPI categories, although their accuracy for severe dry category is very low. On the other hand, it is also noted that some GPP show noticeable better skill for pluvial conditions, as reflected by a lower dispersion within each category, higher correlation scores, and standard deviation values closer to the observations (Figure 8d–f). In this regard, the GPCC025, GPCC05, and MSWEP2 products display the best performance.
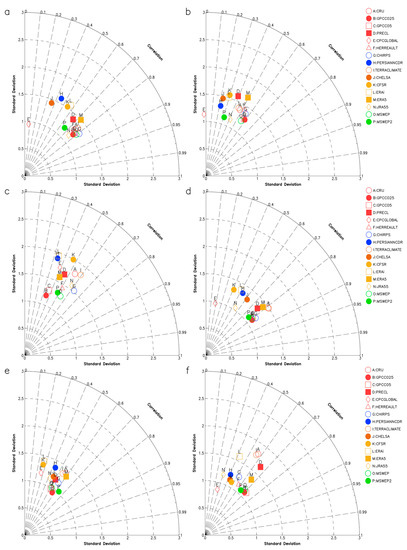
Figure 8.
Taylor diagrams for the areas with SPI lower than −0.5 (a), moderate and severe droughts (b,c, respectively). SPI greater than 0.5 as well as moderate and severe wet conditions are shown in (d–f), respectively.
The aforementioned results suggest the following about the use of SPI as a performance measure. Firstly, the use of drought statistics offers only a general idea about the GPP performance, without reflecting possible differences in the temporal occurrence of drought events between observations and GPP. Secondly, GPP skills are seemingly better for pluvial conditions than for drought ones, at least for the time period considered in this study. Thirdly, the assessment based on SPI suggests that MSWEP2, MSWEP, and GPCC025 are among the best overall performers, even when other GPP products show a better ability for individual SPI indicators. This suggests, once again, that GPP products based on a larger number of station data have a better ability to reproduce the behavior of rainfall in the Caribbean. Finally, the combination of drought statistics with other indicators that represent temporal variations of drought (such our SPIAA) offers a better approach to evaluate the GPP by avoiding possible bias in the interpretation of the results.
4. Conclusions
To our knowledge, this is the first study that objectively evaluates the performance of GPP across the entire Caribbean. We evaluated the strengths and weaknesses of sixteen gridded monthly precipitation products for the period 1983–2010, by comparing them to 60 weather stations across the Caribbean. The evaluation was limited to 28-year period due to data availability and data quality. The evaluation was carried out by analyzing the differences in the representation of the rainfall annual cycle and by employing different statistical metrics such as the KGE as well as others derived from SPIs which characterize various features for drought and pluvial conditions. We summarize the main findings of this work as follows:
- With respect to the applied methodological approach, we conclude that:
- The combined analysis of the annual precipitation cycle and KGE and SPI metrics, provide a robust and comprehensive understanding of the performance of the considered precipitation products for the Caribbean. While the comparison of the annual precipitation cycles between GPP and observations provided useful preliminary information about the best and worst GPP, the KGE index added a global and objective picture of the GPP abilities by integrating correlation, bias, and variability. At the same time, SPIs gave insights about the GPP skill with respect to other important features of precipitation. For instance, ERA5 was the worst reanalysis product in representing the annual precipitation cycle for the Caribbean, underestimating the total monthly precipitation. However, it performed better than other GPP in the SPI analysis, mainly because of its higher correlation with observations. Similarly, GPP, such as CHELSA or TERRACLIMATE, were among the best for some individual performance indicators (e.g., DF and DE statistics) but did not show similar ability in other ones (e.g., SPIAA moderate and severe (Figure 8b,c)).
- With respect to the annual cycle analysis, we conclude that:
- The analysis of the annual precipitation cycle revealed a high correspondence between GPP and observations across the Caribbean as whole, as well as for the two sub-regions analysed. Features such as the MSD and the maximum of rainfall during November were well represented for the Western and Eastern sub-regions respectively. There was a better performance for the majority of the GPP over the Western Caribbean when compared with the eastern side. This might either be due to the low station density used in the development of these GPP, especially over the Eastern Caribbean, or the inability of the reanalysis products to properly represent the small territories and the precipitation processes that happen on these small land areas. Considering this analysis, we suggest that the best performing products for the whole Caribbean and the sub-regions were the gauge-based GPCC025 and GPCC05 and the gauge and satellite-based CHIRPS.
- With respect to the evaluation based on the KGE index we highlight the following:
- Although correlation has a strong influence in the KGE scoring, it was the worst component captured by the GPP. We suggest that for further improvement or development of GPP for use in the Caribbean, improving correlation should be a primary goal.
- Generally speaking, the reanalysis products were among the lowest-performing GPP group, although some of them performed better than PERSIANCDR (gauge and satellite) and CPCGLOBAL (gauge, satellite, and reanalysis). The lower representativeness of reanalysis suggests deficiencies of atmospheric models to reproduce the small-scale precipitation processes. In this group, ERA5 had the best performance, despite its significant precipitation underestimation. This result calls the attention of the potential users of ERA5 to develop new regional precipitation products by using bias correction or downscaling techniques.
- On the basis of the KGE analysis, GPCC025, GPCC05, MSWEP, and MSWEP2 yielded better results for both annual and seasonal time scales. We suggest that the use of higher surface station density in these GPP highly influenced this outcome, notwithstanding that their development methodologies are different.
- With respect to the evaluation based on SPI, we observe the following:
- Overall, the GPP fail in representing accurately the SPI-0.5 statistics, having different ratings for different statistics. The GPP with best performance were MSWEP, MSWEP2, ERA5, and CHELSA. For SPI-1.5, the GPP better resemble the observations with a discernible distinction between the worst and best performers, and a tendency to overestimate the maximum consecutive months with drought and the number of drought events. In general, products such as MSWEP2, ERA5, CHELSA, and MSWEP were the most accurate.
- Considering the areas affected by different SPI categories, all GPP perform better for pluvial conditions than for drought for all SPI lengths. For wet periods, the correlations were higher, and the amplitudes were greater but closer to the observations. The GPCC025, MSWEP, MSWEP2, CHIRPS, and HERREAULT products had the best performance.
- The strategy to explore GPP performance across varying SPI statistics as well as using the temporal variations of the areas affected by pluvial and drought conditions are complementary. This provides a more robust evaluation of the GPP and avoids potential bias in the interpretation of results.
In general, we conclude that GPCC025 and MSWEP2 appear to be the best performers for the whole study domain and each sub-region as they were always among the better performing GPP across the range of metrics and evaluation methods examined.
It is not a surprise that the GPP that use a greater number of ground stations in their development have a better representation of precipitation as compared to others GPP that uses much less observations. For example, in the development of GPP such GPCC, the number of stations used within our study region is relatively high, even though the number of stations has decreased in recent decades. In addition, GPCC uses many of the 60 stations we used to evaluate all GPP in this work. This fact might explain the better performance of GPCC over other station-based products.
GPCC025 offers the opportunity to develop climate studies over longer time intervals because of its temporal span (1891–2017) and relatively high spatial resolution. MSWEP2 offers the possibility for studies that requires a very high spatial resolution (0.1°) over the last three decades. The use of other products will generally depend on the aim and particularities of their application. For example, multivariate datasets, such as TERRACLIMATE or CRU, can be considered when different climate variables are needed to calculate derived parameters, especially for very long-term assessments. At the same time, caution is recommended when employing a GPP with a relatively low performance, even if it has a high spatial resolution or shows good accuracy at global scale. As indicated earlier, whereas higher resolution is a key consideration for the Caribbean region with its small islands, it does not necessarily mean better performance, and it is still necessary to evaluate the products.
A similar strategy to the methodology applied in this study can be used when assessing climate model outputs against observations, i.e., extending the analysis beyond just bias or annual cycles. Our results also indicate that revisiting previous evaluations of model performance over the region could produce new interpretations about accuracy, at least in the case of precipitation. For example, the conclusions reached by [30,31,46] on the accuracy of regional climate models to reproduce the observed precipitation may potentially be modified if GPCC025 is used as a reference observational dataset, instead of CRU, particularly for the Eastern Caribbean.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4433/11/12/1334/s1.
Author Contributions
Conceptualization, A.C.-A., A.B.-M., M.A.T., and D.A.H.; methodology A.C.-A., A.B.M., D.A.H., D.M.-C., M.A.T., and C.F.; software, A.B.-M., M.S.-L., and A.C.-A.; formal analysis, A.C.-A., D.M.-C., I.G., D.A.H., M.A.T., T.S., and J.C.; data curation and validation, A.C.-A., A.B.-M., C.F., and A.V.-L.; writing—original draft preparation, A.C.-A., M.A.T., D.A.H., D.M.-C., I.G., T.S., and A.B.-M.; writing—review and editing, A.C.-A., M.A.T., D.A.H., D.M.-C., I.G., T.S., J.C., C.F., A.V.-L., M.A., and A.B.-M.; visualization, A.B.-M., A.C.-A., A.V.-L., and C.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Ministry of Science, Technology and Environment of Cuba through the SUPERCLIMA project executed under the Cuban National Research Program “Climate Change in Cuba: Impacts, Mitigation and Adaptation”.
Acknowledgments
We would like to thank the institutions responsible for the development of the gridded precipitation products. We thank them for making them available for use in this study. We also say thank the Princeton Climate Analysis group for their particular interest in allowing the use of the MSWEPv2 dataset. Special thanks to the Caribbean Institute for Meteorology and Hydrology for making available station data for the eastern Caribbean islands and the Caribbean Climate Change Center for providing the funds to finance this publication.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Rain-gauges used in the study. The stations are organized from the western to the eastern Caribbean.
Table A1.
Rain-gauges used in the study. The stations are organized from the western to the eastern Caribbean.
| No. | Station Name | Country | Latitude | Longitude | No. | Station Name | Country | Latitude | Longitude |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Central Farm (CAYO) | Belize | 17.1 | −89.0 | 31 | Nuevitas | Cuba | 21.6 | −77.2 |
| 2 | Melinda (STANN Creek) | Belize | 17.0 | −88.3 | 32 | Manzanillo | Cuba | 20.2 | −77.2 |
| 3 | Phillip Goldson International Airport | Belize | 17.5 | −88.3 | 33 | Las Tunas | Cuba | 20.9 | −76.9 |
| 4 | Cabo San Antonio | Cuba | 21.9 | −85.0 | 34 | Jucarito | Cuba | 20.7 | −76.9 |
| 5 | Paso Real de San Diego | Cuba | 22.6 | −83.3 | 35 | Orange | Jamaica | ||
| 6 | Bahía Honda | Cuba | 22.9 | −83.2 | 36 | WorthyPark2 | Jamaica | ||
| 7 | La Fe | Cuba | 21.7 | −82.8 | 37 | La Jíquima | Cuba | 20.9 | −76.5 |
| 8 | Punta del Este | Cuba | 21.6 | −82.5 | 38 | Universidad | Cuba | 20.0 | −75.8 |
| 9 | Casablanca | Cuba | 23.1 | −82.3 | 39 | Punta Lucrecia | Cuba | 21.1 | −75.6 |
| 10 | Owen Robert A. Georgetown | Cayman | 19.3 | −81.4 | 40 | Maisí | Cuba | 20.2 | −74.1 |
| 11 | Jovellanos | Cuba | 22.8 | −81.2 | 41 | Jimaní | Dominican Republic | 18.3 | −71.5 |
| 12 | Aguada de Pasajeros | Cuba | 22.4 | −80.8 | 42 | Barahona | Dominican Republic | 18.2 | −71.1 |
| 13 | Cienfuegos | Cuba | 22.2 | −80.4 | 43 | Padre Las Casas | Dominican Republic | 18.7 | −70.9 |
| 14 | Santo Domingo | Cuba | 22.6 | −80.2 | 44 | Santo Domingo | Dominican Republic | −69.5 | |
| 15 | Sagua la Grande | Cuba | 22.8 | −80.1 | 45 | Las Americas | Dominican Republic | 18.3 | −69.4 |
| 16 | Topes de Collante | Cuba | 21.9 | −80.0 | 46 | San Juan | Puerto Rico | 18.5 | −66.1 |
| 17 | Yabú | Cuba | 22.5 | −80.0 | 47 | St. Thomas | Virgin Islands | 18.3 | −65.0 |
| 18 | Trinidad | Cuba | 21.8 | −80.0 | 48 | St. Croix | Virgin Islands | 17.7 | −64.8 |
| 19 | Sancti Spíritus | Cuba | 22.0 | −79.4 | 49 | National Agricultural Station | St. Kitts | 17.3 | −62.7 |
| 20 | Jibaro | Cuba | 21.7 | −79.2 | 50 | V.C. Bird International Airport | Antigua | 17.1 | −61.5 |
| 21 | Júcaro | Cuba | 21.6 | −78.9 | 51 | St. Augustine | Trinidad & Tobago | 10.6 | −61.4 |
| 22 | Venezuela | Cuba | 21.8 | −78.8 | 52 | Canefield Airport | Dominica | 15.2 | −61.3 |
| 23 | Camilo Cienfuegos | Cuba | 22.2 | −78.8 | 53 | Melville Hall Airport | Dominica | 15.3 | −61.3 |
| 24 | Florida | Cuba | 21.5 | −78.3 | 54 | Piarco | Trinidad & Tobago | 10.6 | −61.3 |
| 25 | Esmeralda | Cuba | 21.8 | −78.1 | 55 | Arnosvale/E.T. Joshua Airport | St. Vincent | 13.1 | −61.2 |
| 26 | Santa Cruz del Sur | Cuba | 20.7 | −78.0 | 56 | Lamentin | Martinique | 14.6 | −61.0 |
| 27 | Camagüey | Cuba | 21.4 | −77.8 | 57 | Hewanorra | St. Lucia | 13.7 | −60.9 |
| 28 | Bsavannah | Jamaica | 58 | Crown Point | Trinidad & Tobago | 11.2 | −60.8 | ||
| 29 | Cabo Cruz | Cuba | 19.8 | −77.7 | 59 | Caribbean Institute for Meteorology and Hidrology | Barbados | 13.2 | −59.6 |
| 30 | Palo Seco | Cuba | 21.1 | −77.3 | 60 | Grantley Adams Airport | Barbados | 13.1 | −59.5 |
References
- Barnett, T.; Zwiers, F.; Hengerl, G.; Allen, M.; Crowly, T.; Gillett, N.; Hasselmann, K.; Jones, P.; Santer, B.; Schnur, R.; et al. Detecting and Attributing External Influences on the Climate System: A Review of Recent Advances. J. Clim. 2005, 18, 1291–1314. [Google Scholar] [CrossRef]
- Ryu, J.H.; Hayhoe, K. Understanding the sources of Caribbean precipitation biases in CMIP3 and CMIP5 simulations. Clim. Dyn. 2014, 42, 3233–3252. [Google Scholar] [CrossRef]
- Hutchinson, M.F. Stochastic space-time weather models from ground-based data. Agric. For. Meteorol. 1995, 73, 237–264. [Google Scholar] [CrossRef]
- Keller, D.E.; Fisher, A.M.; Frei, C.; Liniger, M.A.; Appenzeller, C.; Knutti, R. Stochastic modelling of spatially andtemporally consistent daily precipitationtime-series over complex topography. Hydrol. Earth Syst. Sci. Discuss. 2014, 11, 8737–8777. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Shen, S.S.; Dzikowski, P.; Li, G.; Griffith, D. Interpolation of 1961–97 Daily Temperature and Precipitation Data onto Alberta Polygons of Ecodistrict and Soil Landscapes of Canada. J. Appl. Meteorol. 2001, 40, 2162–2177. [Google Scholar] [CrossRef]
- Scholze, M.; Knorr, W.; Arnell, N.W.; Prentice, I.C. A climate-change risk analysis for world ecosystems. Proc. Natl. Acad. Sci. USA 2006, 103, 13116–13120. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J.; et al. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104–105, 70–97. [Google Scholar] [CrossRef]
- Adam, J.C.; Lettenmaier, D.P. Adjustment of global gridded precipitation for systematic bias. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Villarini, G.; Krajewski, W.F. Sensitivity Studies of the Models of Radar-Rainfall Uncertainties. J. Appl. Meteorol. Climatol. 2010, 49, 288–309. [Google Scholar] [CrossRef]
- Gebremichael, M.; Krajewski, W.F. Modeling distribution of temporal sampling errors in area-time-averaged rainfall estimates. Atmos. Res. 2005, 73, 243–259. [Google Scholar] [CrossRef]
- New, M.; Hulme, M.; Jones, P. Representing Twentieth-Century Space–Time Climate Variability. Part I: Development of a 1961–90 Mean Monthly Terrestrial Climatology. J. Clim. 1999, 12, 829–856. [Google Scholar] [CrossRef]
- Harris, I.C.; Jones, P.D. (2017): CRU TS4.01: Climatic Research Unit (CRU) Time-Series (TS) version 4.01 of high-resolution gridded data of month-by-month variation in climate (Jan. 1901–Dec. 2016). Cent. Environ. Data Anal. 2017. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christofferet, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2. [Google Scholar] [CrossRef]
- Beck, H.E.; Van Dijk, A.I.; Levizzani, V.; Schellekens, J.; Gonzalez Miralles, D.; Martens, B.; De Roo, A. MSWEP: 3-hourly 0.25° global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21. [Google Scholar] [CrossRef]
- Sapiano, M.R.P.; Arkin, P.A. An Intercomparison and Validation of High-Resolution Satellite Precipitation Estimates with 3-Hourly Gauge Data. J. Hydrometeorol. 2009, 10, 149–166. [Google Scholar] [CrossRef]
- Negrón Juárez, R.I.; Li, W.; Fu, R.; Fernandes, K.; de Oliveira Cardoso, A. Comparison of precipitation data sets over the tropical South American and African continents. J. Hydrometeorol. 2009, 10, 289–299. [Google Scholar] [CrossRef]
- Cattani, E.; Merino, A.; Levizzani, V. Evaluation of Monthly Satellite-Derived Precipitation Products over East Africa. J. Hydrometeorol. 2016, 17, 2555–2573. [Google Scholar] [CrossRef]
- Kidd, C.; Bauer, P.; Turk, J.; Huffman, G.J.; Joyce, R.; Hsu, K.L.; Braithwaite, D. Intercomparison of High-Resolution Precipitation Products over Northwest Europe. J. Hydrometeorol. 2012, 13, 67–83. [Google Scholar] [CrossRef]
- Faiz, M.A.; Liu, D.; Fu, Q.; Sun, Q.; Li, M.; Baig, F.; Li, T.; Cui, S. How accurate are the performances of gridded precipitation data products over Northeast China? Atmos. Res. 2018, 211, 12–20. [Google Scholar] [CrossRef]
- Beck, H.E.; Wood, E.F.; Pan, M.; Fisher, C.K.; Miralles, D.G.; Van Dijk, A.I.J.M.; McVicar, T.R.; Adler, R.F. MSWep v2 Global 3-hourly 0.1° precipitation: Methodology and quantitative assessment. Bull. Am. Meteorol. Soc. 2019, 100, 473–500. [Google Scholar] [CrossRef]
- Vila, D.A.; De Goncalves, L.G.G.; Toll, D.L.; Rozante, J.R. Statistical Evaluation of Combined Daily Gauge Observations and Rainfall Satellite Estimates over Continental South America. J. Hydrometeorol. 2009, 10, 533–543. [Google Scholar] [CrossRef]
- Scheel, M.L.M.; Rohrer, M.; Huggel, C.; Villar, D.S.; Silvestre, E.; Huffman, G.J. Evaluation of TRMM Multi-satellite Precipitation Analysis (TMPA) performance in the Central Andes region and its dependency on spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2011, 15, 2649–2663. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Nauditt, A.; Birkel, C.; Verbist, K.; Ribbe, L. Temporal and spatial evaluation of satellite-based rainfall estimates across the complex topographical and climatic gradients of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 1295–1320. [Google Scholar] [CrossRef]
- Jury, M.R. An Intercomparison of Observational, Reanalysis, Satellite, and Coupled Model Data on Mean Rainfall in the Caribbean. J. Hydrometeorol. 2009, 10, 413–430. [Google Scholar] [CrossRef]
- Jones, P.D.; Harpham, C.; Harris, I.; Goodess, C.M.; Burton, A.; Centella-Artola, A.; Taylor, M.A.; Bezanilla-Morlot, A.; Campbell, J.D.; Stephenson, T.S.; et al. Long-term trends in precipitation and temperature across the Caribbean. Int. J. Climatol. 2016, 36, 3314–3333. [Google Scholar] [CrossRef]
- Campbell, J.D.; Taylor, M.A.; Stephenson, T.S.; Watson, R.A.; Whyte, F.S. Future climate of the Caribbean from a regional climate model. Int. J. Clim. 2011, 31, 1866–1878. [Google Scholar] [CrossRef]
- Centella-Artola, A.; Taylor, M.A.; Bezanilla-Morlot, A.; Martinez-Castro, D.; Campbell, J.D.; Stephenson, T.S.; Vichot, A. Assessing the effect of domain size over the Caribbean region using the PRECIS regional climate model. Clim. Dyn. 2015, 44, 1901–1918. [Google Scholar] [CrossRef]
- Herrera, D.; Ault, T. Insights from a new high-resolution drought Atlas for the Caribbean spanning 1950–2016. J. Clim. 2017, 30, 7801–7825. [Google Scholar] [CrossRef]
- Taylor, M.A.; Enfield, D.B.; Chen, A.A. Influence of the tropical Atlantic versus the tropical Pacific on Caribbean rainfall. J. Geophys. Res. Ocean. 2002, 107, 10–14. [Google Scholar] [CrossRef]
- Stennett-Brown, R.K.; Stephenson, T.S.; Taylor, M.A. Caribbean climate change vulnerability: Lessons from an aggregate index approach. PLoS ONE 2019, 14, e0219250. [Google Scholar] [CrossRef] [PubMed]
- Magaña, V.; Amador, J.A.; Medina, S. The Midsummer Drought over Mexico and Central America. J. Clim. 1999, 12, 1577–1588. [Google Scholar] [CrossRef]
- Izzo, M. Analisi del clima e delle dinamiche climatiche nella Repubblica Dominicana e delle relative influenze sul territorio. Ph.D. Thesis, University of Molise, Campobasso, Italy, 2011; 162p. [Google Scholar]
- Stennett-Brown, R.K.; Jones, J.J.; Stephenson, T.S.; Taylor, M.A. Future Caribbean temperature and rainfall extremes from statistical downscaling. Int. J. Clim. 2017, 37, 4828–4845. [Google Scholar] [CrossRef]
- Xie, P.; Chen, M.; Shi, W. CPC global unified gauge-based analysis of daily precipitation. In Proceedings of the 24th Conference on Hydrology, Atlanta, GA, USA, 16–21 January 2010. [Google Scholar]
- Chen, M.; Xie, P.; Janowiak, J.E.; Arkin, P.A. Global land precipitation: A 50-yr monthly analysis based on gauge observations. J. Hydrometeorol. 2002, 3, 249–266. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M. GPCC Full Data Monthly Product Version 7.0 at 0.5°: Monthly Land-Surface Precipitation from Rain-Gauges built on GTS-based and Historic Data. Offenbach/GERMANY. Glob. Precip. Climatol. Cent. 2015. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958–2015. Sci. Data 2018, 5, 170191. [Google Scholar] [CrossRef]
- Karger, D.N.; Conrad, O.; Böhner, J.; Kawohl, T.; Kreft, H.; Soria-Auza, R.W.; Zimmermann, N.E.; Linder, H.P.; Kessler, M. Climatologies at high resolution for the earth’s land surface areas. Sci. Data 2017, 4, 170122. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.Y.; Iredell, M.; et al. The NCEP Climate Forecast System Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorological. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service (C3S). ERA5: Fifth Generation of ECMWF Atmospheric Reanalyses of the Global Climate. Copernicus Climate Change Service Climate Data Store (CDS). 2017. Available online: https://cds.climate.copernicus.eu/cdsapp#!/home (accessed on 4 December 2019).
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General specifications and basic characteristics. J. Meteor. Soc. 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the Eighth Conference on Applied Climatology. Am. Meteorol. Soc. 1993, 17, 179–184. [Google Scholar]
- Edwards, D.C.; McKee, T.B. Characteristics of 20th Century Drought in the United States at Multiple Time Scales. 1997. Available online: http://hdl.handle.net/10217/170176 (accessed on 5 June 2020).
- WMO. Stantardized Precipitation Index. User Guide. Geneva, Switzerland 2012. Available online: https://public.wmo.int/en/resources/library/standardized-precipitation-index-user-guide (accessed on 5 June 2020).
- Centella, A.; Bezanilla, A.; Vichot, A.; Silva, M. CARiDRO the Caribbean Assessment Regional Drought Tool: Case Study Report 1 of the CARIWIG Project. 2017. Available online: https://cdkn.org/wp-content/uploads/2013/01/Cariwig-case-study-final-report-caridro-drought.pdf (accessed on 9 March 2020).
- Kendon, E.J.; Roberts, N.M.; Senior, C.A.; Roberts, M.J. Realism of Rainfall in a Very High-Resolution Regional Climate Model. J. Clim. 2012, 25, 5791–5806. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).