Examination of WRF-ARW Experiments Using Different Planetary Boundary Layer Parameterizations to Study the Rapid Intensification and Trajectory of Hurricane Otto (2016)
Abstract
1. Introduction
1.1. Previous Rapid Intensification Cases over the Atlantic Basin
1.2. Rapid Intensification, Storm Track and Boundary Layer in Regional Models
2. Data, Methods and Experimental Design
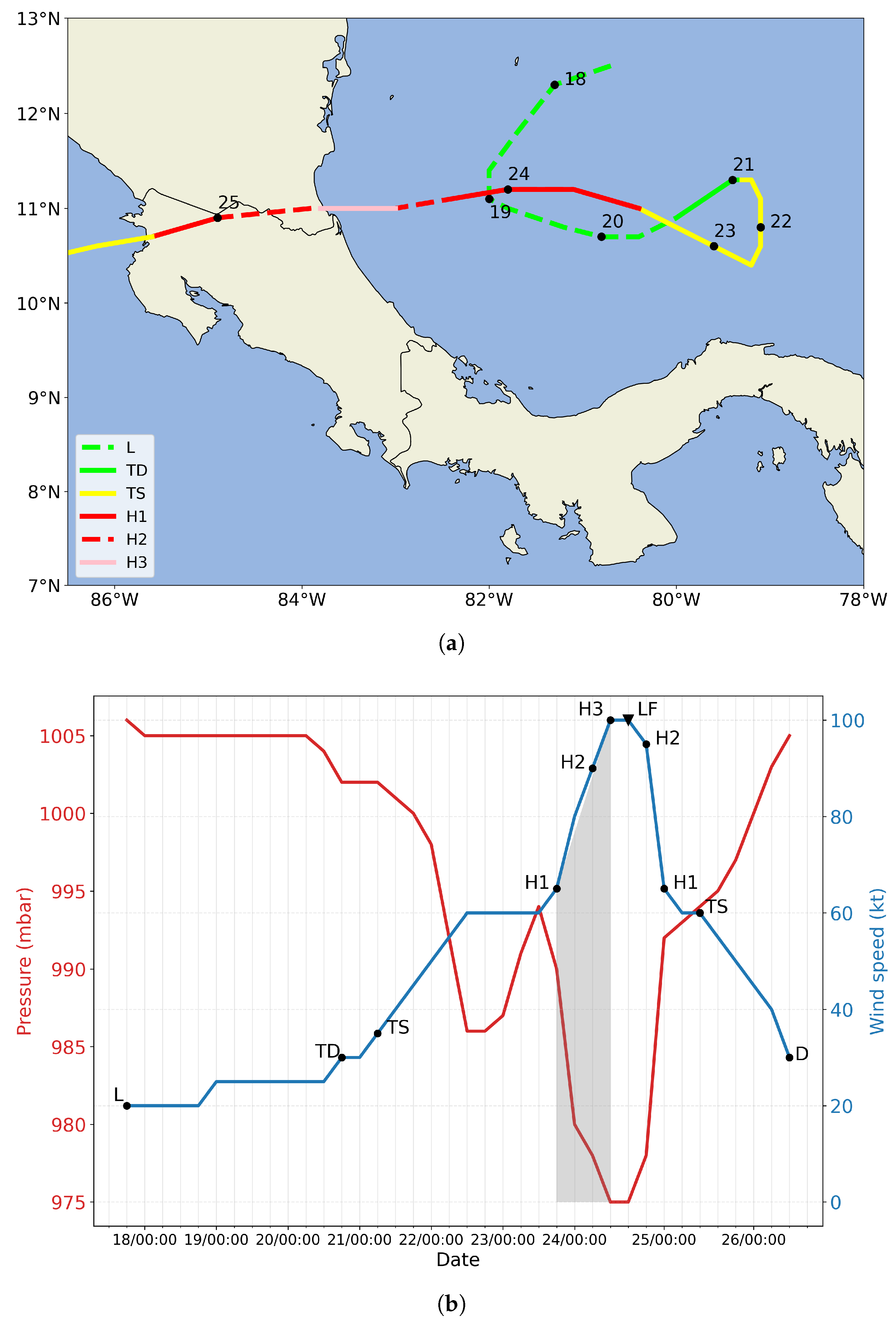
2.1. Observations
2.2. Detecting Rapid Intensification and Tropical Storm Track
- The relative vorticity at 850 hPa must be greater than s.
- There must be a closed pressure minimum within the radius of 100 km. This minimum pressure is then defined as the centre of the cyclone. Note that use of a 100 km radius improves the TC distribution near the coasts.
- The minimum surface pressure satisfying the above criteria is at least 2 hPa lower than the averaged surface pressure over the surrounding grid boxes, each with a resolution of 105 km.
- The 10-m surface wind speed must exceed 17.5 m s.
- The total tropospheric temperature anomaly calculated by the sum of temperature anomalies at 700, 500 and 300 hPa around the centre of the cyclone must be greater than zero.
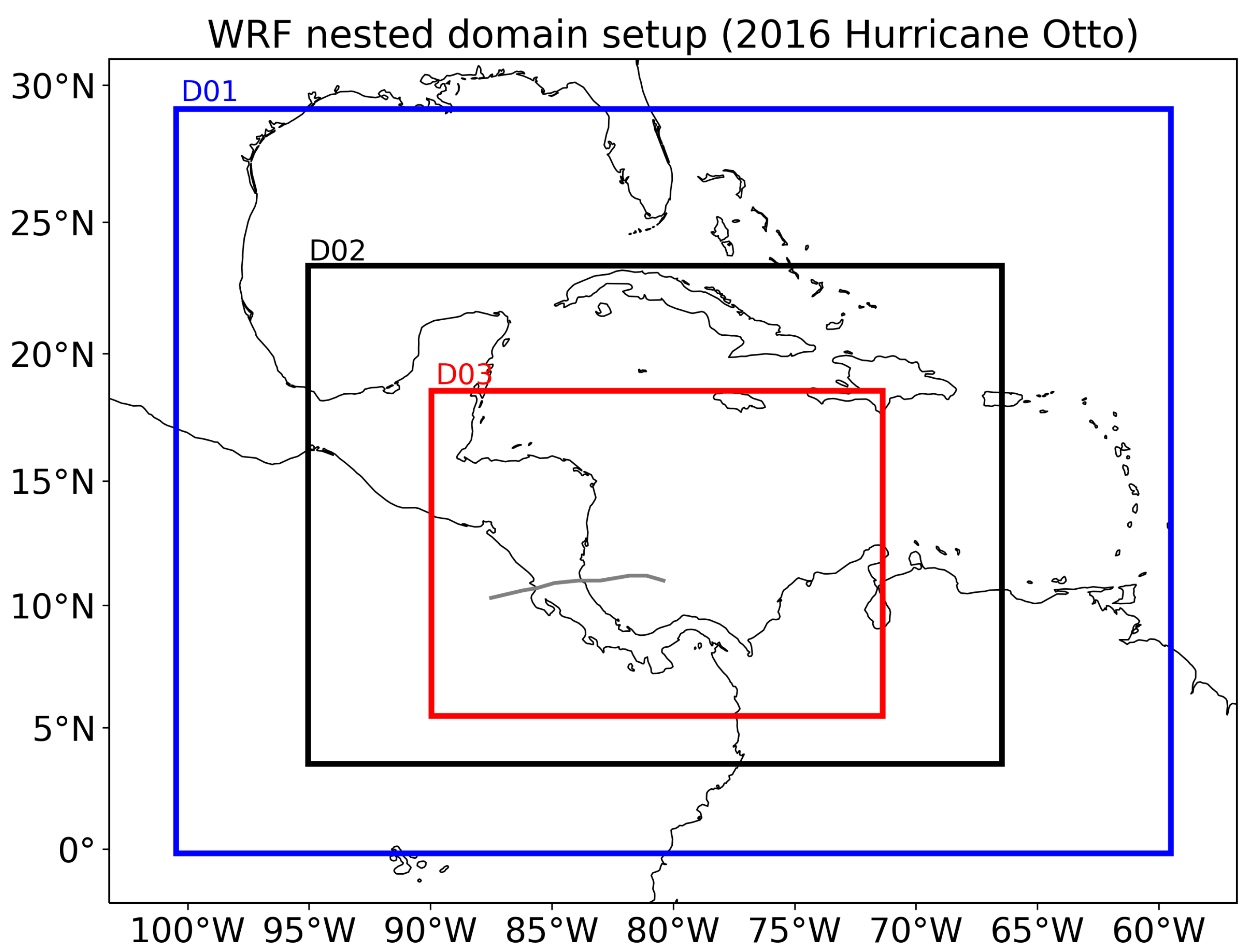
2.3. Experimental Design
PBL Parameterizations in WRF
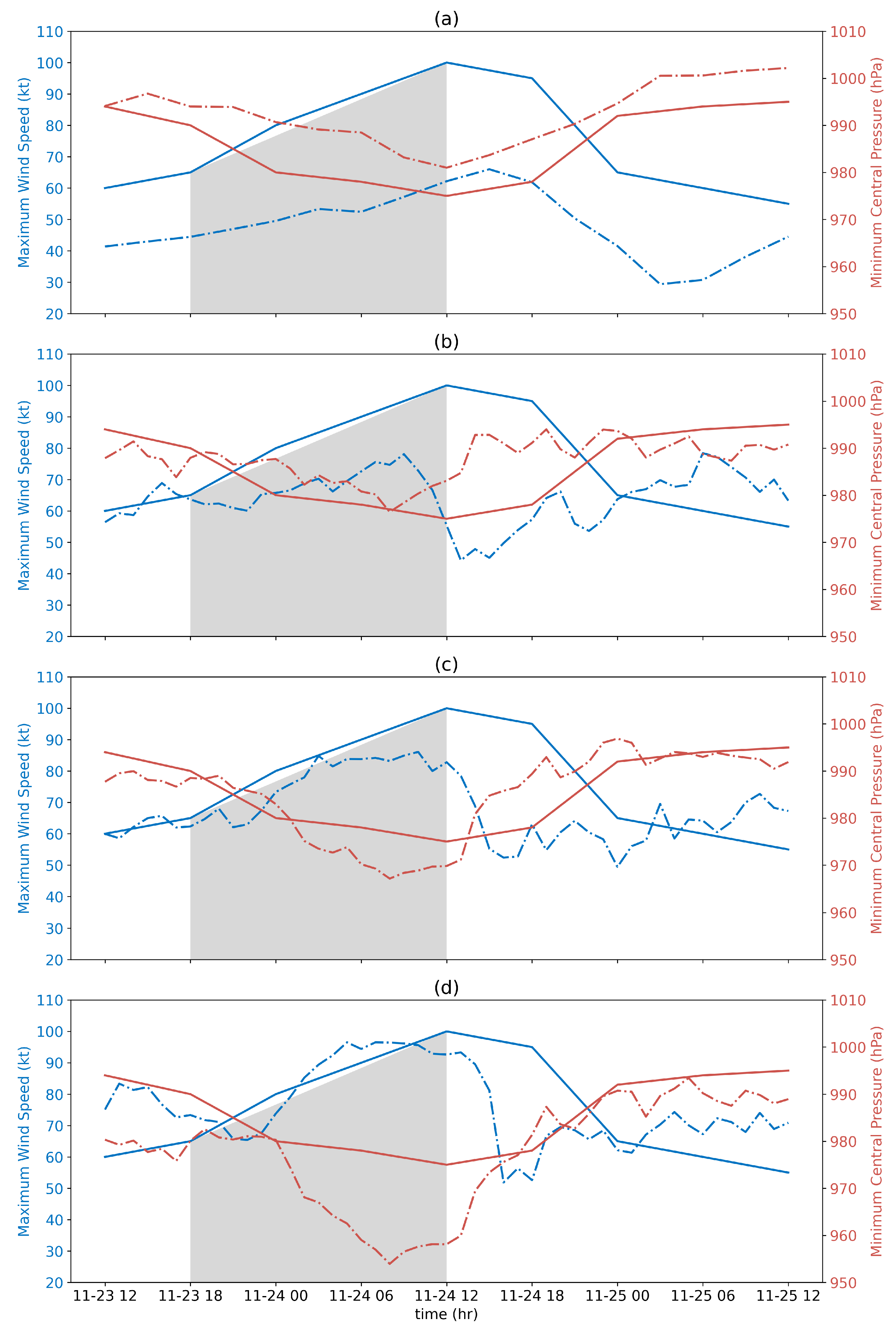
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peña, M.; Douglas, M.W. Characteristics of Wet and Dry Spells over the Pacific Side of Central America during the Rainy Season. Mon. Weather Rev. 2002, 130, 3054–3073. [Google Scholar] [CrossRef]
- Hidalgo, H.G.; Alfaro, E.J.; Hernández-Castro, F.; Pérez-Briceño, P.M. Identification of Tropical Cyclones’ Critical Positions Associated with Extreme Precipitation Events in Central America. Atmosphere 2020, 11, 1123. [Google Scholar] [CrossRef]
- Brown, D.P. Hurricane Otto (AL162016, EP22016): 20–26 November 2016; Technical Report; National Hurricane Center: Miami, FL, USA, 2017.
- Simpson, R.H.; Hope, J.R. Atlantic Hurricane Season of 1971. Mon. Weather Rev. 1972, 100, 256–267. [Google Scholar] [CrossRef]
- Díaz-Bolaños, R.E. La tormenta tropical de 1887 y su paso por las fuentes históricas costarricenses. Estudios 2004, 39–56. [Google Scholar] [CrossRef]
- Simpson, R.H.; Sugg, A.L. The Atlantic hurricane season of 1969. Mon. Weather Rev. 1970, 98, 293–306. [Google Scholar] [CrossRef]
- Kaplan, J.; DeMaria, M. Large-Scale Characteristics of Rapidly Intensifying Tropical Cyclones in the North Atlantic Basin. Weather Forecast. 2003, 18, 1093–1108. [Google Scholar] [CrossRef]
- Arce-Fernández, D.; Amador, J.A. Actividad eléctrica asociada al huracán Otto (2016) en el Mar Caribe y en el Corredor Seco Centroamericano. Rev. Bras. Meteorol. 2020, 35. in press. [Google Scholar]
- Knapp, K.R.; Kossin, J.P. New global tropical cyclone data set from ISCCP B1 geostationary satellite observations. J. Appl. Remote Sens. 2007, 1, 013505. [Google Scholar] [CrossRef]
- Amador, J.A.; Hidalgo, H.G.; Alfaro, E.J.; Durán-Quesada, A.M.; Calderón, B.; Mora, N.; Arce, D. Central America [in “State of the Climate in 2016”]. Butt. Am. Meteorol. Soc. 2017, 98, Si-S280. [Google Scholar] [CrossRef]
- IMN. Huracán Otto: Informe Técnico; Technical Report; Instituto Meteorógico Nacional: San José, Costa Rica, 2017. [Google Scholar]
- Chinchilla-Ramírez, M.G. Resumen Meteorológico Noviembre 2016; Technical Report; Instituto Meteorógico Nacional: San José, Costa Rica, 2016. [Google Scholar]
- Alfaro, E.J.; Hidalgo, H.G.; Maldonado, T.; Pérez-Briceño, P.M.; Mora, N.P. A Tri-dimensional Approach to Climate Sciences. Caribb. Q. 2018, 64, 26–56. [Google Scholar] [CrossRef]
- Quesada-Román, A.; Fallas-López, B.; Hernández-Espinoza, K.; Stoffel, M.; Ballesteros-Cánovas, J.A. Relationships between earthquakes, hurricanes, and landslides in Costa Rica. Landslides 2019, 16, 1539–1550. [Google Scholar] [CrossRef]
- Quesada-Román, A.; Villalobos-Chacón, A. Flash flood impacts of Hurricane Otto and hydrometeorological risk mapping in Costa Rica. Geogr. Tidsskr. 2020, 1–14. [Google Scholar] [CrossRef]
- Poleo, D.C.V.; Stoltz, W. Comparación y evaluación de diferentes esquemas de parametrización de cúmulus con el WRF EMS aplicadas al huracán Otto. Top. Meteorol. Oceanogr. 2017, 16, 28–40. [Google Scholar]
- Grell, G.A.; Freitas, S.R. A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmos. Chem. Phys. 2014, 14, 5233–5250. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR Tech. Note NCAR/TN-475+ STR; NCAR: Boulder, CO, USA, 2008. [Google Scholar]
- Kaplan, J.; DeMaria, M.; Knaff, J.A. A Revised Tropical Cyclone Rapid Intensification Index for the Atlantic and Eastern North Pacific Basins. Weather Forecast. 2010, 25, 220–241. [Google Scholar] [CrossRef]
- Klotzbach, P.J. El Niño-Southern Oscillation, the Madden-Julian Oscillation and Atlantic basin tropical cyclone rapid intensification. J. Geophys. Res.-Atmos. 2012, 117, D14104. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.; Weisberg, R.H.; Black, M.L. Variability of tropical cyclone rapid intensification in the North Atlantic and its relationship with climate variations. Clim. Dynam. 2017, 49, 3627–3645. [Google Scholar] [CrossRef]
- Knabb, R.D.; Rhome, J.R.; Brown, D.P. Hurricane Katrina (AL122005): 23–30 August 2005; Technical Report; National Hurricane Center: Miami, FL, USA, 2005.
- McTaggart-Cowan, R.; Bosart, L.F.; Gyakum, J.R.; Atallah, E.H. Hurricane Katrina (2005). Part I: Complex Life Cycle of an Intense Tropical Cyclone. Mon. Weather Rev. 2007, 135, 3905–3926. [Google Scholar] [CrossRef]
- Pasch, R.J.; Penny, A.B.; Berg, R. Hurricane María (AL 152017), 16–30 September 2017; Technical Report; National Hurricane Center: Miami, FL, USA, 2018.
- Klotzbach, P.J.; Carl, J.; Schreck, C.J., III; Collins, J.M.; Bell, M.M.; Blake, E.S.; Roache, D. The Extremely Active 2017 North Atlantic Hurricane Season. Mon. Weather Rev. 2018, 146, 3425–3443. [Google Scholar] [CrossRef]
- Charney, J.G.; Eliassen, A. On the Growth of the Hurricane Depression. J. Atmos. Sci. 1964, 21, 68–75. [Google Scholar] [CrossRef]
- Ogura, Y. Frictionally Controlled, Thermally Driven Circulations in a Circular Vortex with Application to Tropical Cyclones. J. Atmos. Sci. 1964, 21, 610–621. [Google Scholar] [CrossRef][Green Version]
- Ooyama, K. Numerical Simulation of the Life Cycle of Tropical Cyclones. J. Atmos. Sci. 1969, 26, 3–40. [Google Scholar] [CrossRef]
- Emanuel, K.A. An Air-Sea Interaction Theory for Tropical Cyclones. Part I: Steady-State Maintenance. J. Atmos. Sci. 1986, 43, 585–605. [Google Scholar] [CrossRef]
- Emanuel, K.A. The Behavior of a Simple Hurricane Model Using a Convective Scheme Based on Subcloud-Layer Entropy Equilibrium. J. Atmos. Sci. 1995, 52, 3960–3968. [Google Scholar] [CrossRef]
- Emanuel, K.A. Some Aspects of Hurricane Inner-Core Dynamics and Energetics. J. Atmos. Sci. 1997, 54, 1014–1026. [Google Scholar] [CrossRef]
- Smith, R.K.; Montgomery, M.T.; Vogl, S. A critique of Emanuel’s hurricane model and potential intensity theory. Q. J. R. Meteorol. Soc. 2008, 134, 551–561. [Google Scholar] [CrossRef]
- Zhang, J.A.; Nolan, D.S.; Rogers, R.F.; Tallapragada, V. Evaluating the Impact of Improvements in the Boundary Layer Parameterization on Hurricane Intensity and Structure Forecasts in HWRF. Mon. Weather Rev. 2015, 143, 3136–3155. [Google Scholar] [CrossRef]
- Kilroy, G.; Smith, R.K. The effects of initial vortex size on tropical cyclogenesis and intensification. Q. J. R. Meteorol. Soc. 2017, 143, 2832–2845. [Google Scholar] [CrossRef]
- Zhang, J.A.; Rogers, R.F.; Tallapragada, V. Impact of Parameterized Boundary Layer Structure on Tropical Cyclone Rapid Intensification Forecasts in HWRF. Mon. Weather Rev. 2017, 145, 1413–1426. [Google Scholar] [CrossRef]
- Diro, G.T.; Giorgi, F.; Fuentes-Franco, R.; Walsh, K.J.E.; Giuliani, G.; Coppola, E. Tropical cyclones in a regional climate change projection with RegCM4 over the CORDEX Central America domain. Clim. Chang. 2014, 125, 79–94. [Google Scholar] [CrossRef]
- Biswas, M.K.; Carson, L.; Newman, K.; Bernardet, L.; Kalina, E.; Grell, E.; Frimel, J. Available online: https://dtcenter.org/sites/default/files/community-code/hwrf/HWRF_v3.9a_UG.pdf (accessed on 26 November 2020).
- Li, X.; Pu, Z. Sensitivity of Numerical Simulation of Early Rapid Intensification of Hurricane Emily (2005) to Cloud Microphysical and Planetary Boundary Layer Parameterizations. Mon. Weather Rev. 2008, 136, 4819–4838. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, D.L.; Carton, J.; Atlas, R. On the Rapid Intensification of Hurricane Wilma (2005). Part I: Model Prediction and Structural Changes. Weather Forecast. 2011, 26, 885–901. [Google Scholar] [CrossRef]
- Kilroy, G.; Smith, R.K.; Montgomery, M.T. A unified view of tropical cyclogenesis and intensification. Q. J. R. Meteorol. Soc. 2016, 143, 450–462. [Google Scholar] [CrossRef]
- Kilroy, G.; Montgomery, M.T.; Smith, R.K. The role of boundary-layer friction on tropical cyclogenesis and subsequent intensification. Q. J. R. Meteorol. Soc. 2017, 143, 2524–2536. [Google Scholar] [CrossRef]
- Kilroy, G.; Smith, R.K.; Montgomery, M.T. The role of heating and cooling associated with ice processes on tropical cyclogenesis and intensification. Q. J. R. Meteorol. Soc. 2018, 144, 99–114. [Google Scholar] [CrossRef]
- Rogers, E.; Black, T.; Ferrier, B.; Lin, Y.; Parrish, D.; DiMego, G. National Oceanic and Atmospheric Administration Changes to the NCEP Meso Eta Analysis and Forecast System: Increase in resolution, new cloud microphysics, modified precipitation assimilation, modified 3DVAR analysis. NWS Tech. Proced. Bull. 2001, 488, 1–15. [Google Scholar]
- Dudhia, J. Numerical Study of Convection Observed during the Winter Monsoon Experiment Using a Mesoscale Two-Dimensional Model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res.-Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Tewari, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.A.; Mitchell, K.; Ek, M.; Gayno, G.; Wegiel, J.; Cuenca, R.H. Implementation and verification of the unified NOAH land surface model in the WRF model (Formerly Paper Number 17.5). In Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction, Seattle, WA, USA, 14 January 2004; pp. 11–15. [Google Scholar]
- Kain, J.S. The Kain–Fritsch Convective Parameterization: An Update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Grell, G.A.; Dudhia, J.; Stauffer, D.R. A Description of the Fifth-Generation Penn State/NCAR Mesoscale Model (MM5); University Corporation for Atmospheric Research: Boulder, CO, USA, 1994. [Google Scholar]
- Janjić, Z.I. The Step-Mountain Eta Coordinate Model: Further Developments of the Convection, Viscous Sublayer, and Turbulence Closure Schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A Revised Scheme for the WRF Surface Layer Formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Hong, S.Y.; Pan, H.L. Nonlocal Boundary Layer Vertical Diffusion in a Medium-Range Forecast Model. Mon. Weather Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef]
- Troen, I.B.; Mahrt, L. A simple model of the atmospheric boundary layer: Sensitivity to surface evaporation. Bound.-Layer Meteorol. 1986, 37, 129–148. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Noh, Y.; Cheon, W.G.; Hong, S.Y.; Raasch, S. Improvement of the K-profile Model for the Planetary Boundary Layer based on Large Eddy Simulation Data. Bound.-Lay. Meteorol. 2003, 107, 401–427. [Google Scholar] [CrossRef]
- Fang, J.; Tang, J.; Wu, R. The effect of surface friction on the development of tropical cyclones. Adv. Atmos. Sci. 2009, 26, 1146–1156. [Google Scholar] [CrossRef]
- Wong, M.L.M.; Chan, J.C.L. Tropical Cyclone Motion in Response to Land Surface Friction. J. Atmos. Sci. 2006, 63, 1324–1337. [Google Scholar] [CrossRef]
- Yuan, J.; Huang, Y.; Liu, C.; Wan, Q. A simulation study of the influence of land friction on landfall tropical cyclone track and intensity. J. Trop. Meteorol. 2008, 14, 53–56. [Google Scholar]
- Shin, H.H.; Hong, S.Y. Intercomparison of Planetary Boundary-Layer Parametrizations in the WRF Model for a Single Day from CASES-99. Bound.-Layer Meteorol. 2011, 139, 261–281. [Google Scholar] [CrossRef]
- Lee, J.; Shin, H.H.; Hong, S.Y.; Jiménez, P.A.; Dudhia, J.; Hong, J. Impacts of subgrid-scale orography parameterization on simulated surface layer wind and monsoonal precipitation in the high-resolution WRF model. J. Geophys. Res. Atmos. 2015, 120, 644–653. [Google Scholar] [CrossRef]
- Wang, C.; Qian, Y.; Duan, Q.; Huang, M.; Berg, L.K.; Shin, H.H.; Feng, Z.; Yang, B.; Quan, J.; Hong, S.; et al. Assessing the sensitivity of land-atmosphere coupling strength to boundary and surface layer parameters in the WRF model over Amazon. Atmos. Res. 2020, 234, 104738. [Google Scholar] [CrossRef]

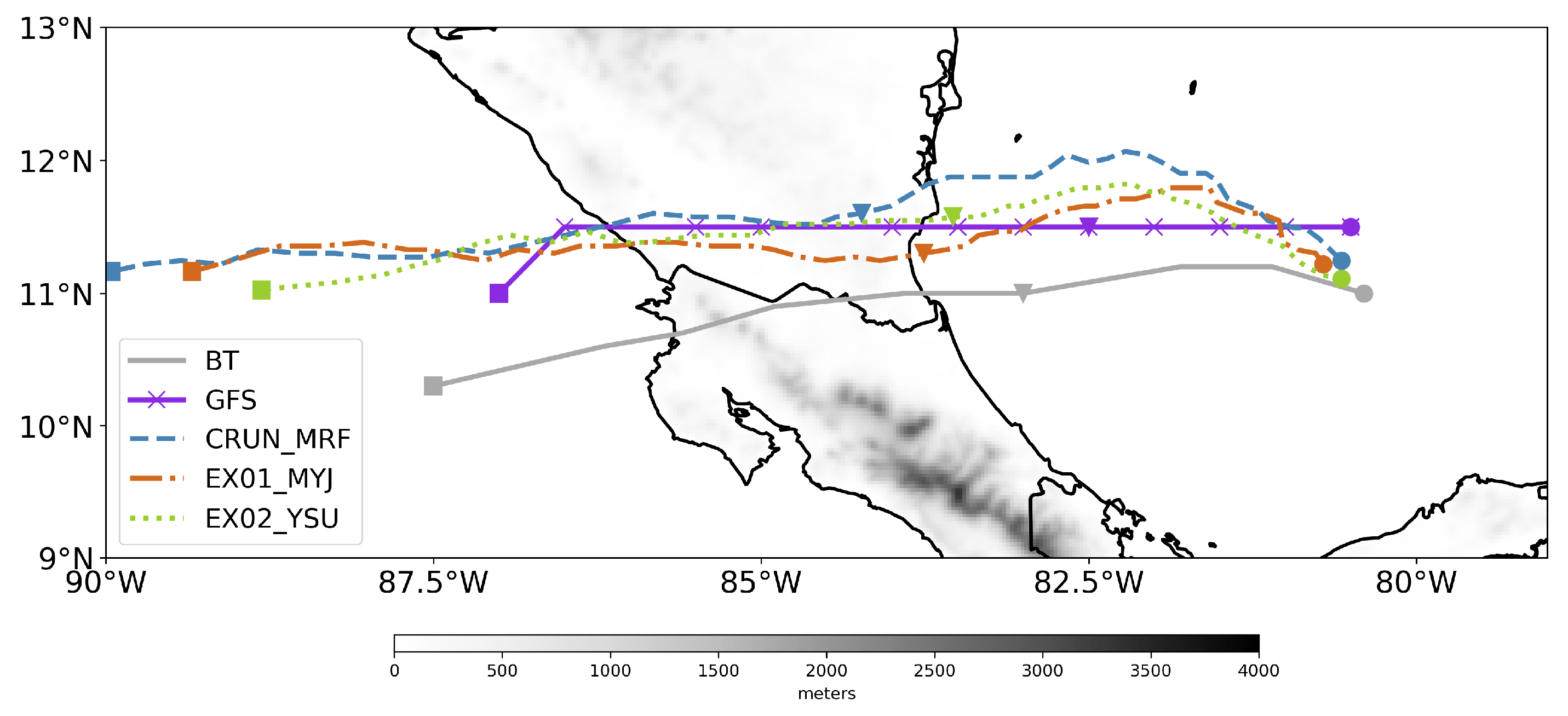
| Experiment | Spinup | PBL | SL | Mean Distance () | Forward Speed (m s) |
|---|---|---|---|---|---|
| GFS | 0.7 | 4.8 | |||
| CRUN_MRF | 1-day | MRF | Similarity | 1.4 | 6.4 |
| EX01_MYJ | 1-day | MYJ | Monin-Obukov | 0.9 | 5.9 |
| EX02_YSU | 1-day | YSU | revised MM5 | 0.8 | 5.5 |
| Data | Lon. | Lat. | DFOL | FS | T | P | MWS | Cat. |
|---|---|---|---|---|---|---|---|---|
| Obs. | −83.7 | 11.0 | 8.3 | 16:42 | 975 | 50 | 3 | |
| GFS | −83.8 | 11.5 | 0.5 | 5.4 | 23:05 | 993 | 22 | TS |
| CRUN_MRF | −83.7 | 11.8 | 0.8 | 5.3 | 09:51 | 980 | 37 | 1 |
| EX01_MYJ | −83.9 | 11.3 | 0.4 | 5.3 | 13:40 | 978 | 36 | 1 |
| EX02_YSU | −83.8 | 11.6 | 0.6 | 5.8 | 23:11 | 971 | 44 | 2 |
| Data | Date | Lon. | Lat. | WS | Cat. | PER | D200 | SHRD | |
|---|---|---|---|---|---|---|---|---|---|
| Obs. | 2016-11-24 12:00:00 | −83.0 | 11 | 52 | 3 | 40 | 10 | ||
| GFS | 2016-11-24 15:00:00 | −83.0 | 11.5 | 33 | 1 | 22 | 6 | ||
| CRUN_MRF | 2016-11-24 12:00:00 | −82.4 | 12 | 33 | TS | −1 | −5 | 1 | 11 |
| EX01_MYJ | 2016-11-24 12:00:00 | −83.6 | 11.3 | 42 | 1 | 23 | 5 | 8 | 8 |
| EX02_YSU | 2016-11-24 12:00:00 | −83.4 | 11.6 | 46 | 2 | 16 | 9 | 9 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maldonado, T.; Amador, J.A.; Rivera, E.R.; Hidalgo, H.G.; Alfaro, E.J. Examination of WRF-ARW Experiments Using Different Planetary Boundary Layer Parameterizations to Study the Rapid Intensification and Trajectory of Hurricane Otto (2016). Atmosphere 2020, 11, 1317. https://doi.org/10.3390/atmos11121317
Maldonado T, Amador JA, Rivera ER, Hidalgo HG, Alfaro EJ. Examination of WRF-ARW Experiments Using Different Planetary Boundary Layer Parameterizations to Study the Rapid Intensification and Trajectory of Hurricane Otto (2016). Atmosphere. 2020; 11(12):1317. https://doi.org/10.3390/atmos11121317
Chicago/Turabian StyleMaldonado, Tito, Jorge A. Amador, Erick R. Rivera, Hugo G. Hidalgo, and Eric J. Alfaro. 2020. "Examination of WRF-ARW Experiments Using Different Planetary Boundary Layer Parameterizations to Study the Rapid Intensification and Trajectory of Hurricane Otto (2016)" Atmosphere 11, no. 12: 1317. https://doi.org/10.3390/atmos11121317
APA StyleMaldonado, T., Amador, J. A., Rivera, E. R., Hidalgo, H. G., & Alfaro, E. J. (2020). Examination of WRF-ARW Experiments Using Different Planetary Boundary Layer Parameterizations to Study the Rapid Intensification and Trajectory of Hurricane Otto (2016). Atmosphere, 11(12), 1317. https://doi.org/10.3390/atmos11121317







