Inter-Comparison of Gauge-Based Gridded Data, Reanalysis and Satellite Precipitation Product with an Emphasis on Hydrological Modeling
Abstract
1. Introduction
2. Material and Methods
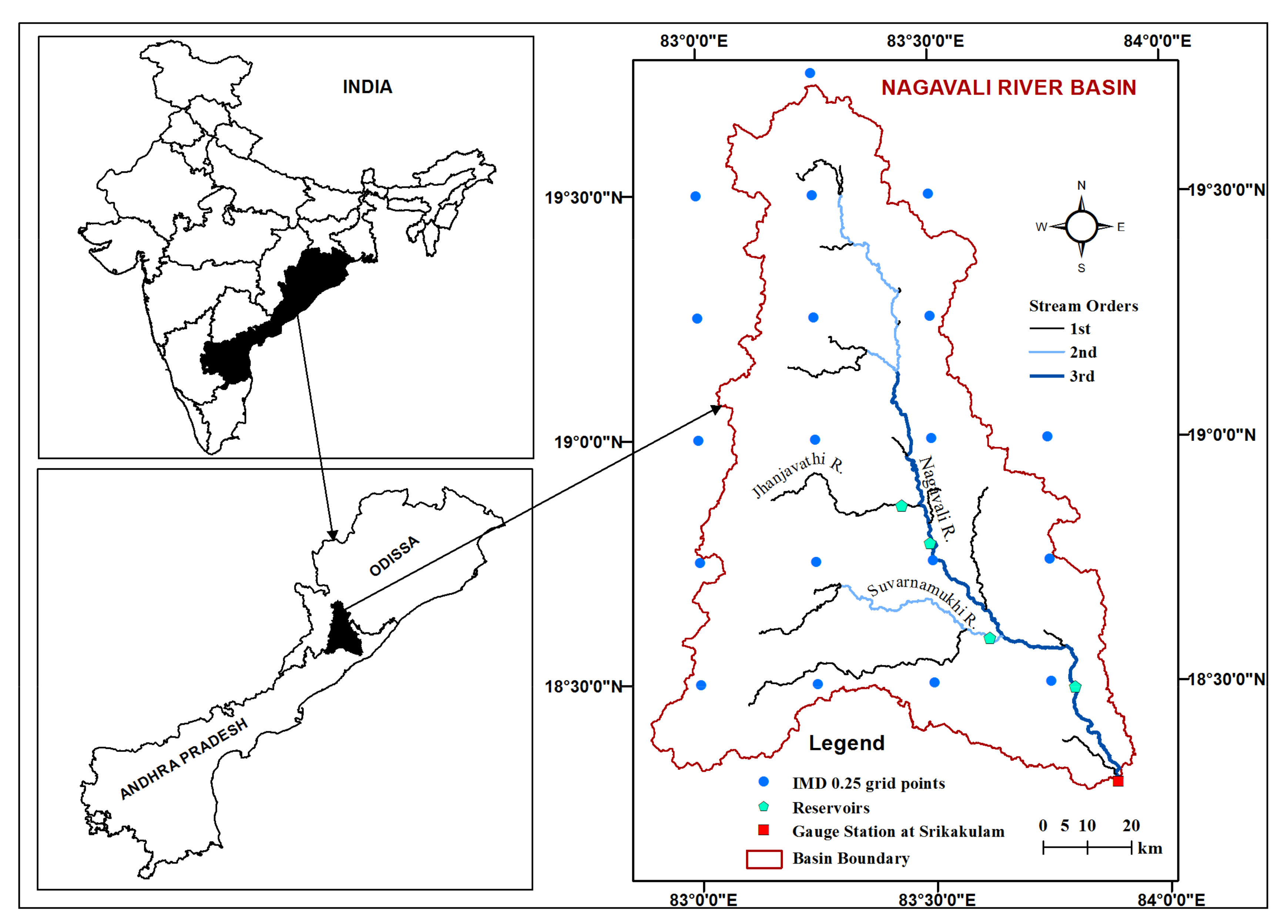
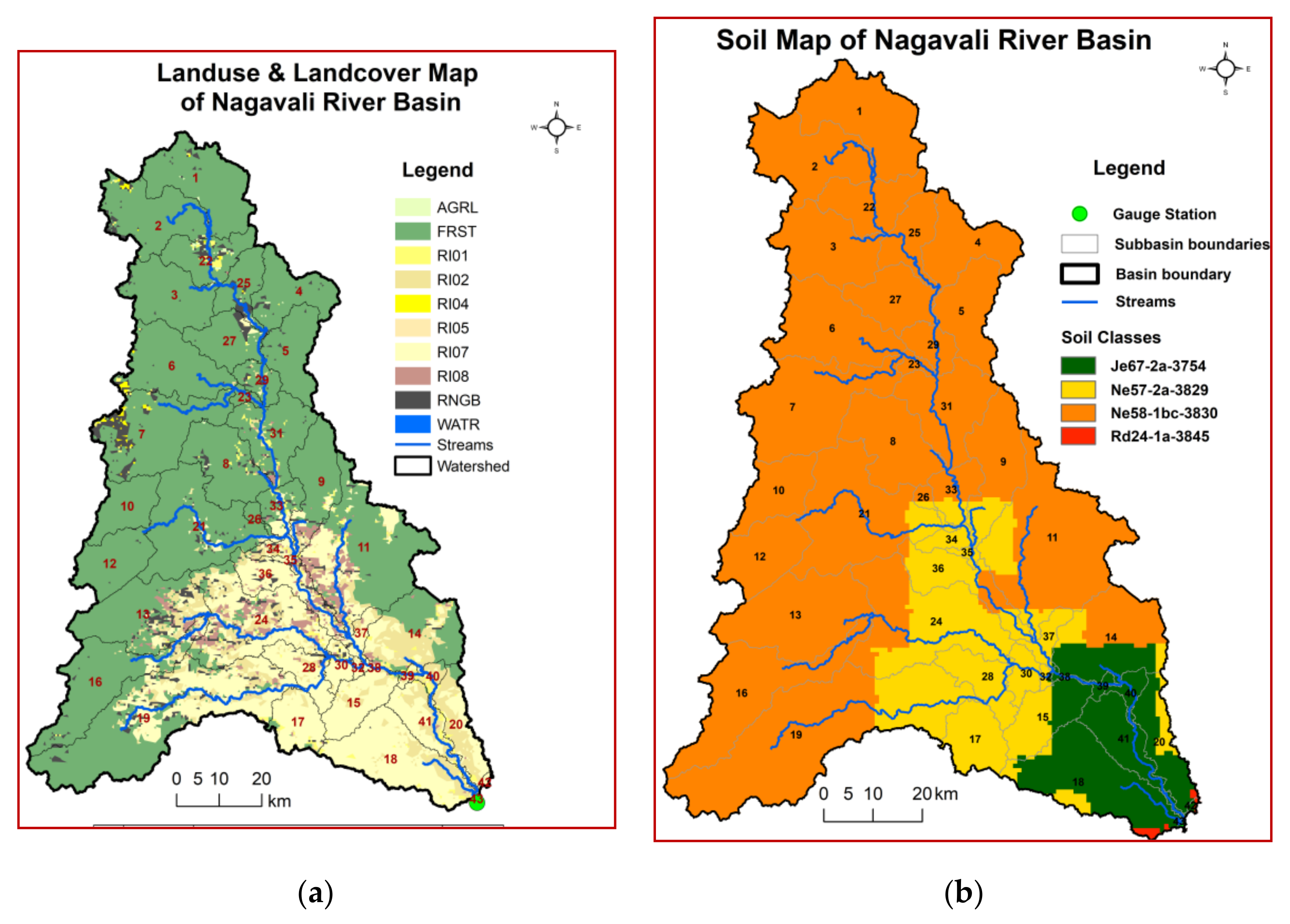
2.1. Study Area
2.2. Datasets
2.3. Verification Strategy
2.4. Hydrological Model
3. Model Development and Evaluation
4. Results and Discussion
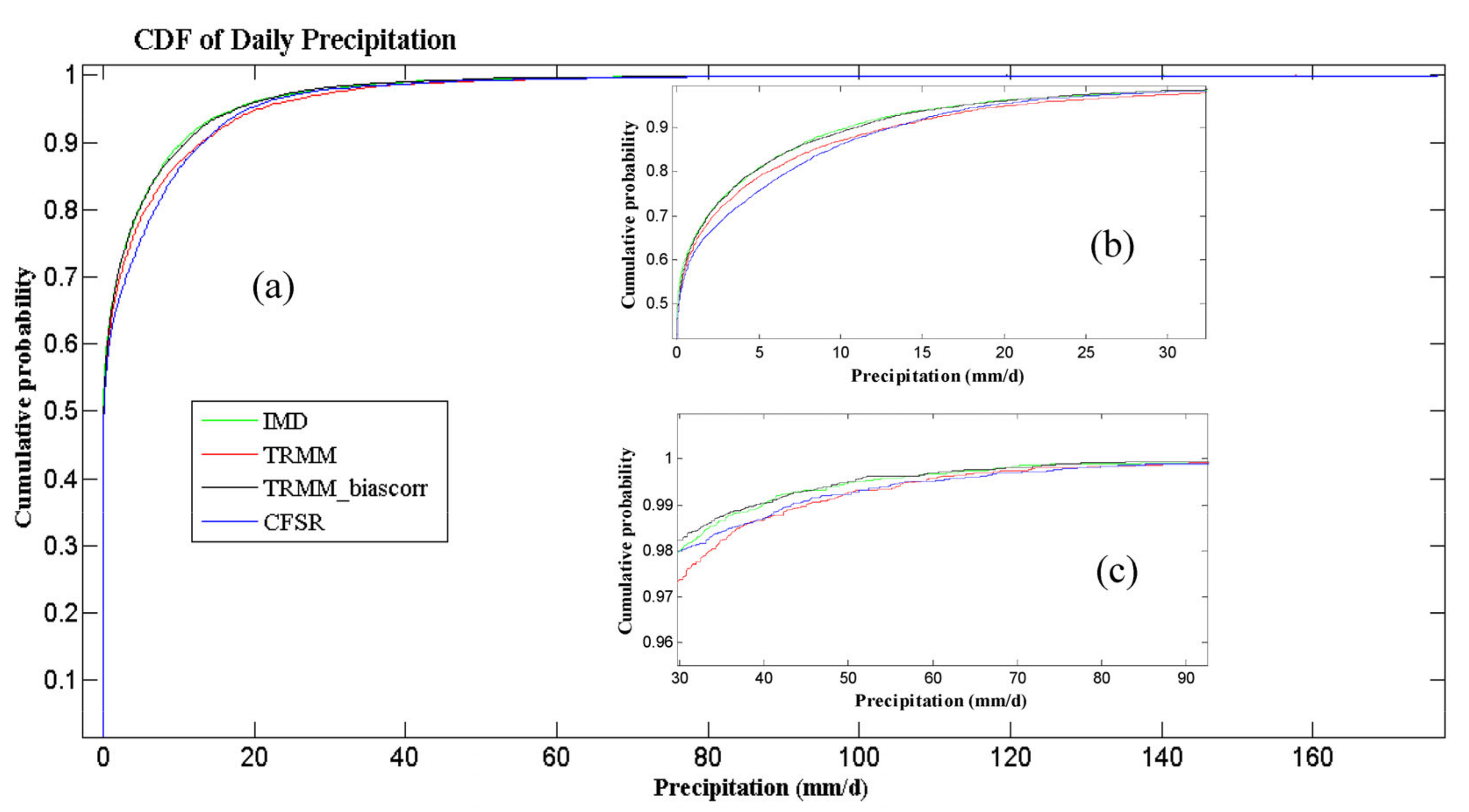
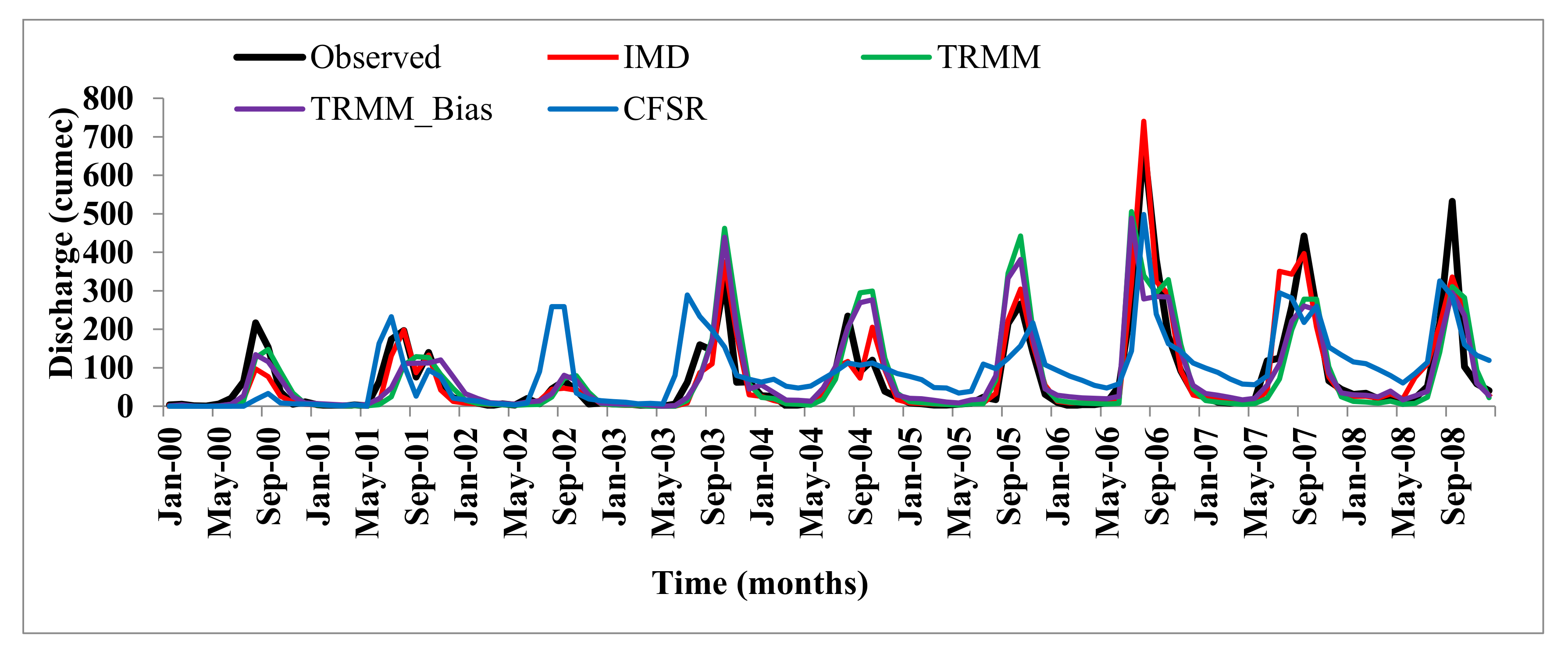
4.1. Comparison of Satellite Data and Reanalysis Data with Ground-Based IMD Data
4.2. Hydrological Model-Based Evaluation of the Precipitation Products
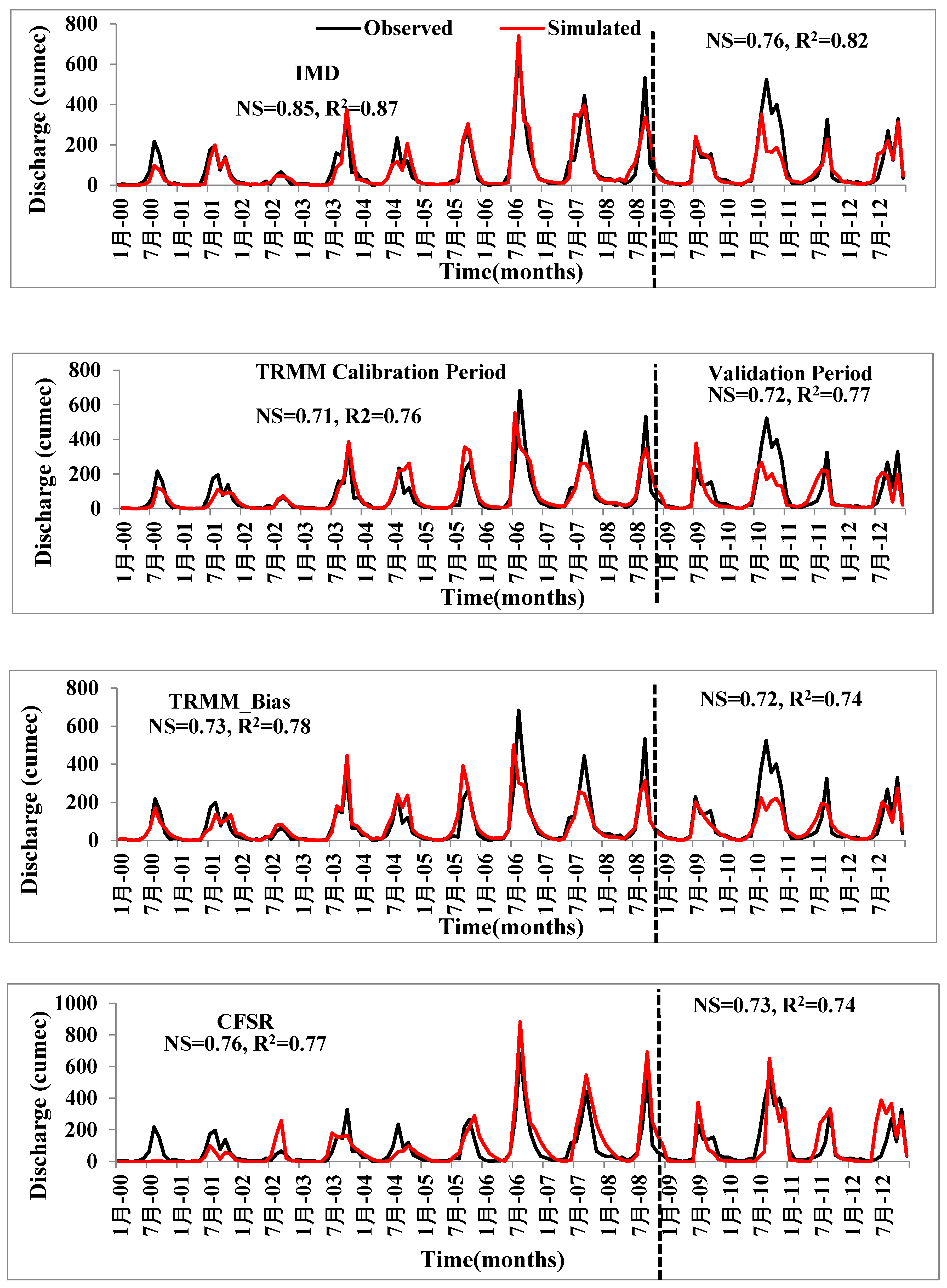
4.2.1. Scenario A: SWAT Model Calibrated with IMD Data
4.2.2. Calibration of the SWAT Model with IMD Data
4.2.3. Scenario B: SWAT Model Calibrated Individually with Precipitation Products
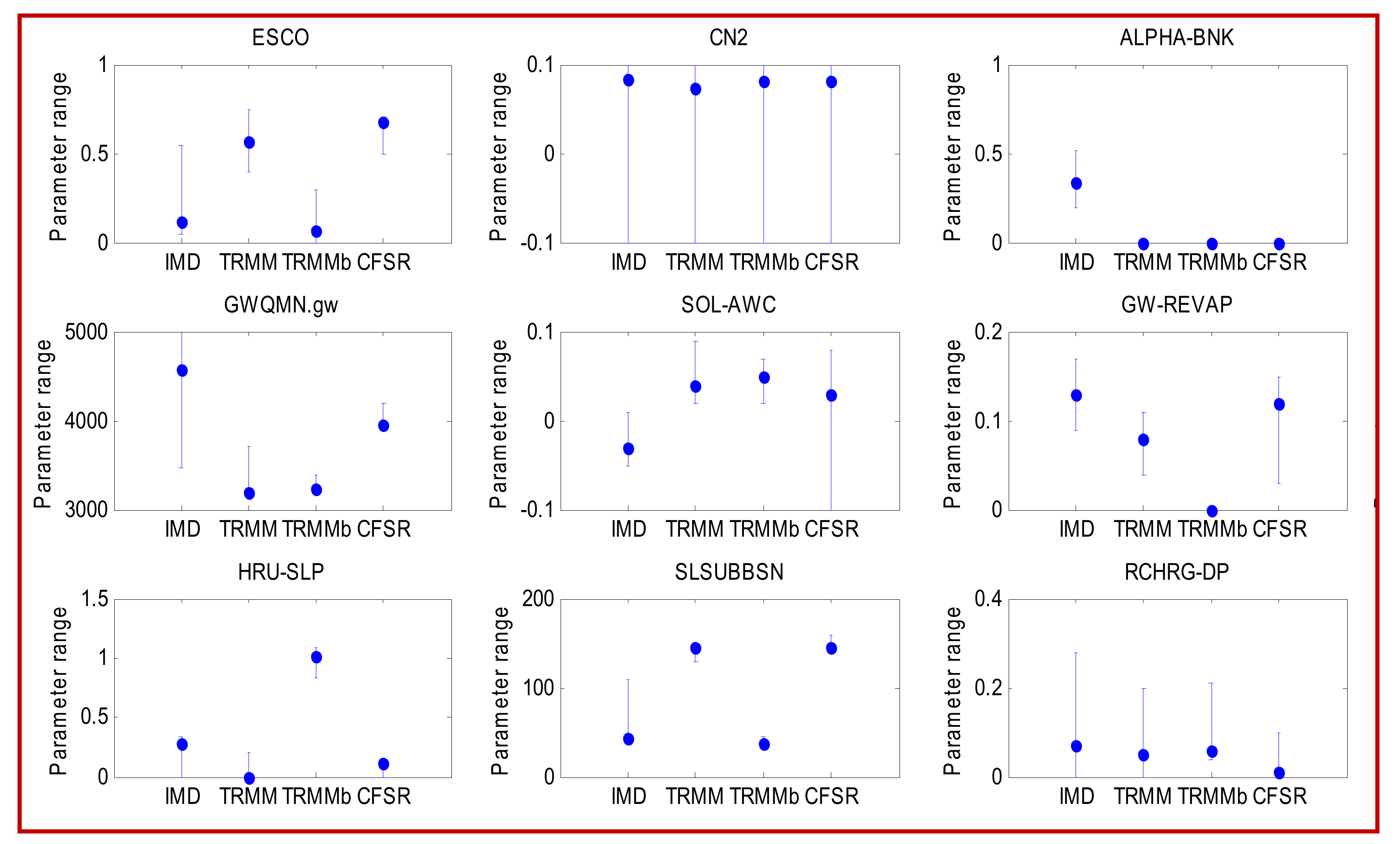
4.2.4. Sensitive Parameters
4.2.5. Model Calibration
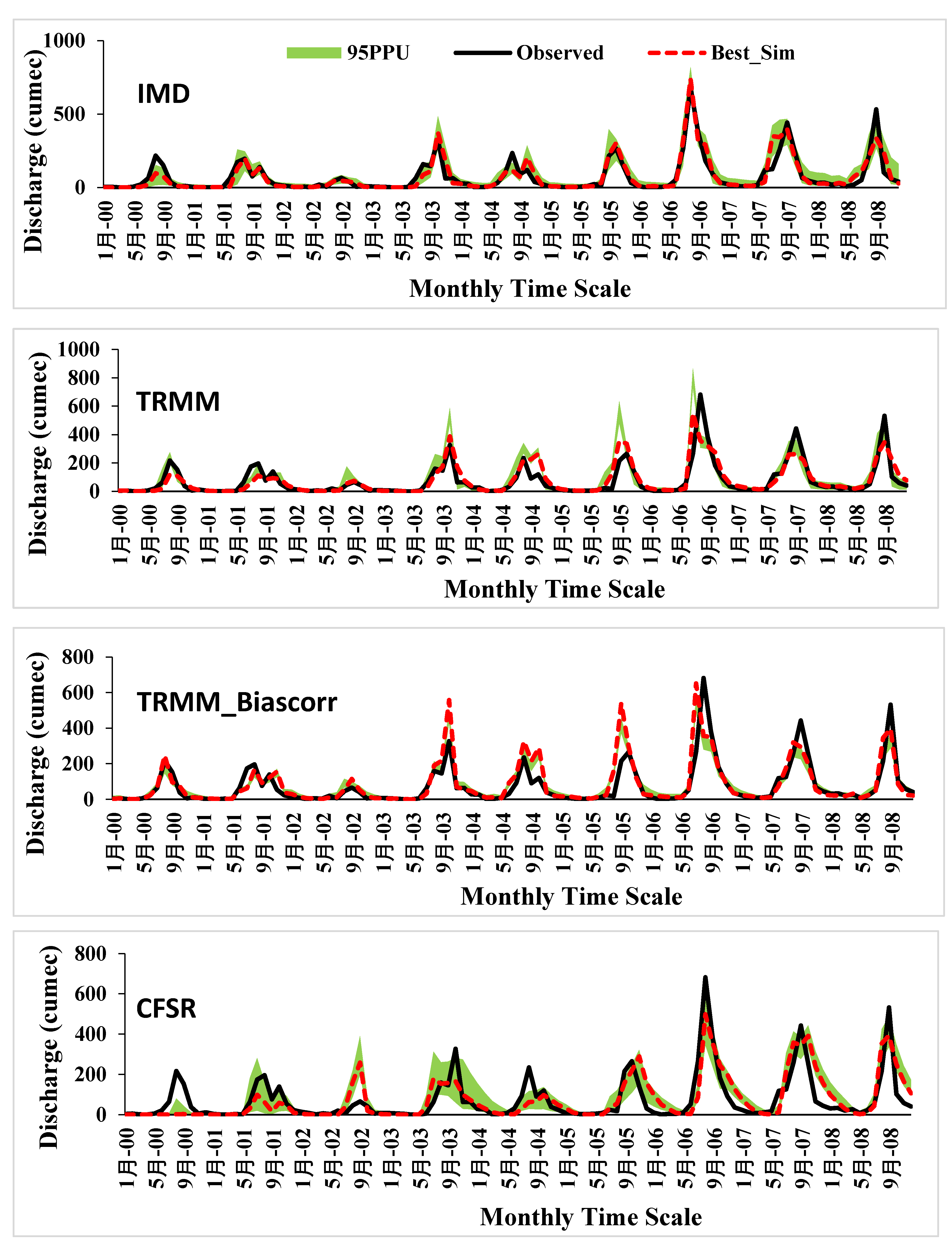
4.2.6. Parameter Uncertainty
4.2.7. Uncertainty in Streamflow Simulation
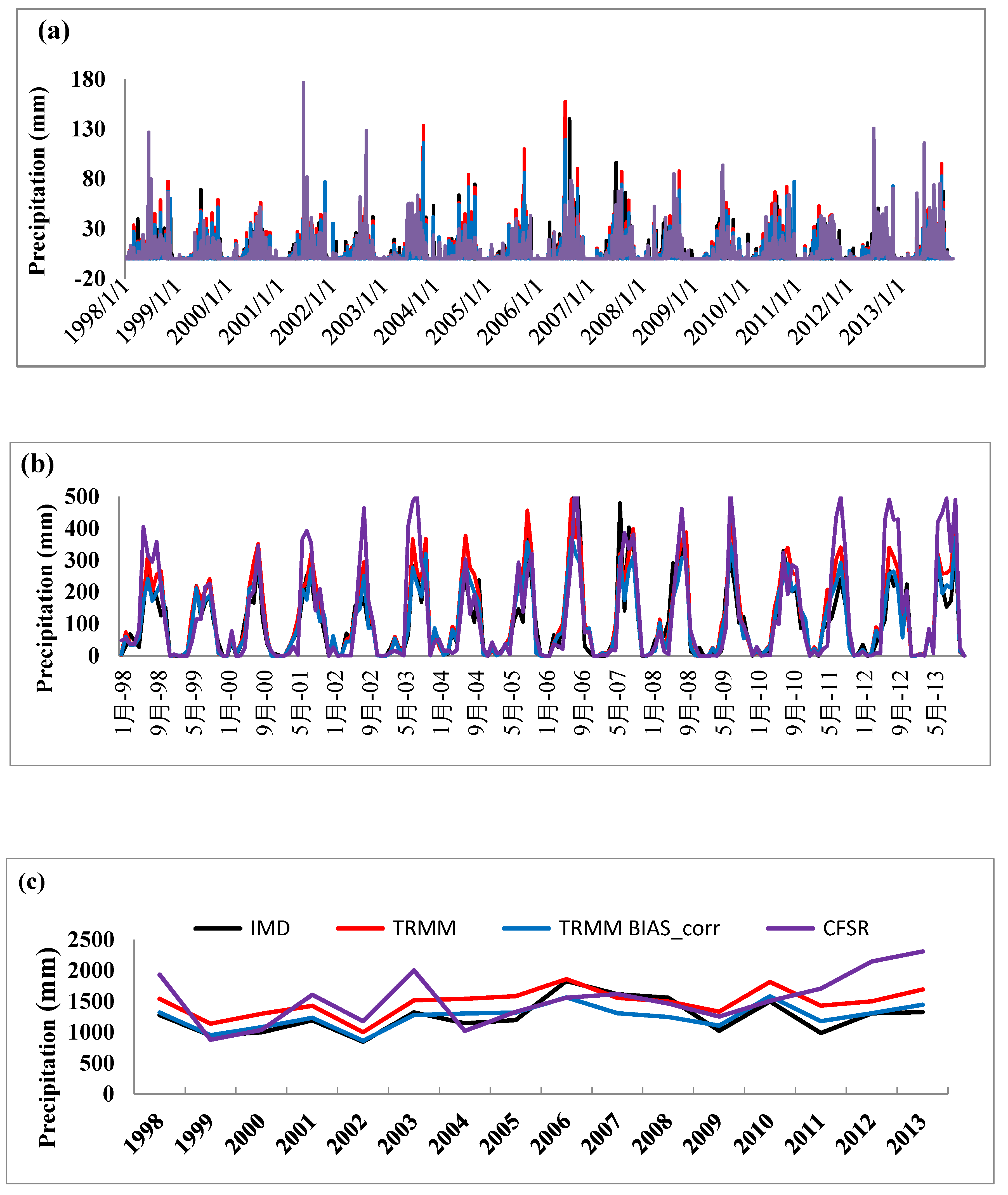
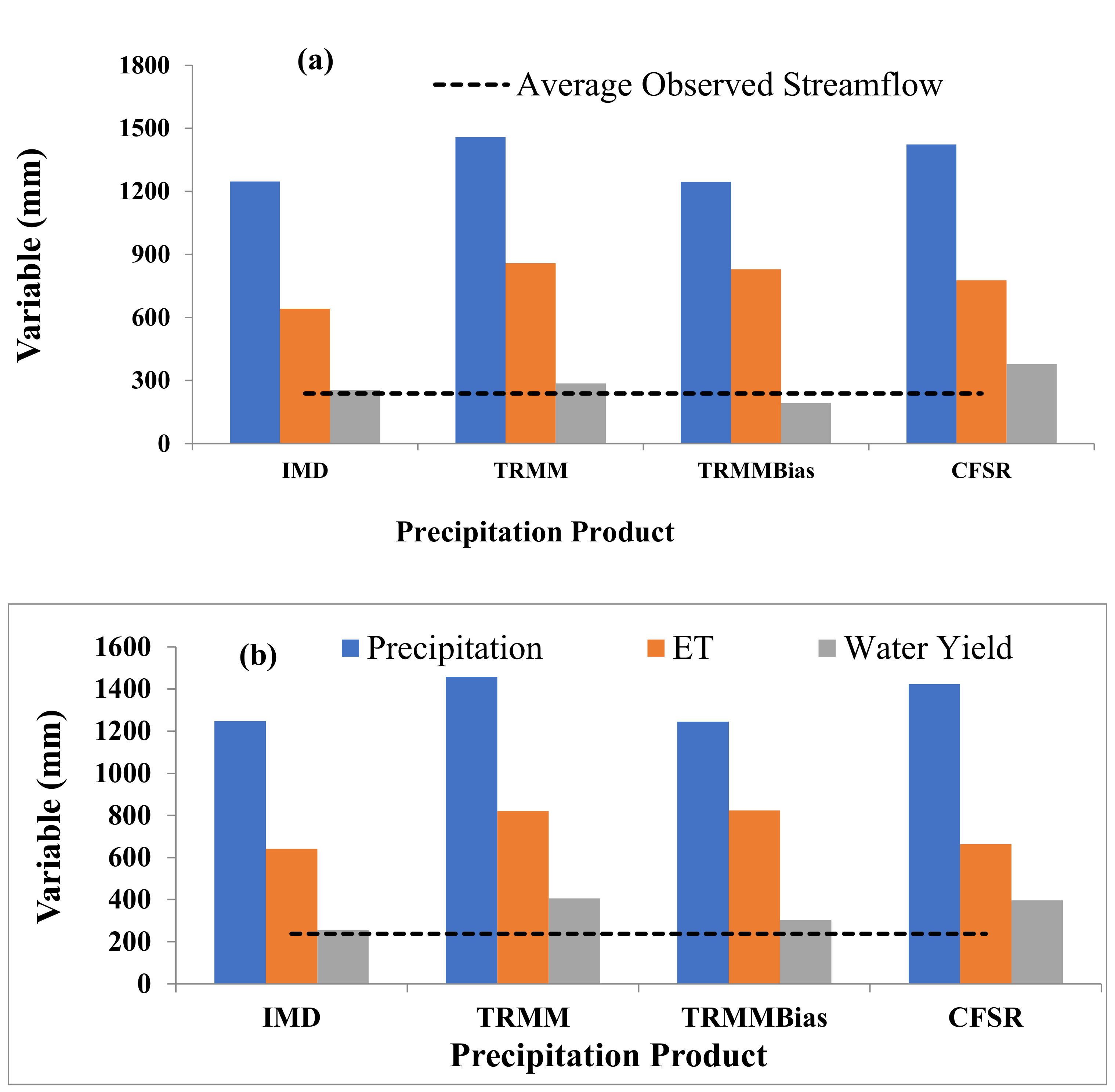
4.3. Comparison of the Annual Water Balance
4.3.1. Precipitation
4.3.2. Streamflow
4.3.3. Evapotranspiration
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Tuo, Y.; Marcolini, G.; Disse, M.; Chiogna, G. A multi-objective approach to improve SWAT model calibration in alpine catchments. J. Hydrol. 2018, 559, 347–360. [Google Scholar] [CrossRef]
- Agarwal, A.; Marwan, N.; Maheswaran, R.; Ozturk, U.; Kurths, J.; Merz, B. Optimal Design of Hydrometric Station Networks Based on Complex Network Analysis. J. Hydrol. Earth Syst. Sci. 2020, 24, 2235–2251. [Google Scholar] [CrossRef]
- Dile, Y.T.; Srinivasan, R. Evaluation of CFSR climate data for hydrologic prediction in data-scarce watersheds: An application in the Blue Nile River Basin. J. Am. Water Resour. Assoc. (JAWRA) 2014, 50, 1226–1241. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Woollen, J. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.E.A.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.L.; Sorooshian, S.; Gao, X.G. Precipitation estimation from remotely sensed imagery using an artificial neural network cloud classification system. J. Appl. Meteorol. 2004, 43, 1834–1852. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Peterson, S.; Shukla, S.; Davenport, F.; Michaelsen, J.; Knapp, K.R.; Landsfeld, M.; Husak, G.; Harrison, L.; et al. A High-Resolution 1983–2016 T max Climate Data Record Based on Infrared Temperatures and Stations by the Climate Hazard Center. J. Clim. 2019, 32, 5639–5658. [Google Scholar] [CrossRef]
- Hou, A.; Jackson, G.S.; Kummerow, C.; Shepherd, J.M. Global precipitation measurement. In Precipitation: Advances in Measurement, Estimation, and Prediction; Michaelides, S., Ed.; Springer: Berlin, Germany, 2008; pp. 131–170. [Google Scholar]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Hamada, A.; Arakawa, O.; Yatagai, A. An automated quality control method for daily rain-gauge data. Glob. Environ. Res. 2011, 15, 165–172. [Google Scholar]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Pai, D.S.; Sridhar, L.; Rajeevan, M.; Sreejith, O.P.; Satbhai, N.S.; Mukhopadhyay, B. (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region. Mausam 2014, 1, 1–18. [Google Scholar]
- Li, D.; Christakos, G.; Ding, X.; Wu, J. Adequacy of TRMM satellite rainfall data in driving the SWAT modeling of Tiaoxi catchment (Taihu lake basin, China). J. Hydrol. 2018, 556, 1139–1152. [Google Scholar] [CrossRef]
- Wang, A.; Zeng, X. Evaluation of multireanalysis products with in situ observations over the Tibetan Plateau. J. Geophys. Res. Atmos. 2012, 117, 1–12. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I. Evaluation of remote-sensing-based rainfall products through predictive capability in hydrological runoff modelling. Hydrol. Process. 2010, 24, 879–891. [Google Scholar] [CrossRef]
- Skinner, C.J.; Coulthard, T.J.; Parsons, D.R.; Ramirez, J.A.; Mullen, L.; Manson, S. Simulating tidal and storm surge hydraulics with a simple 2D inertia based model, in the Humber Estuary, U.K. Estuar. Coast. Shelf Sci. 2015, 155, 126–136. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, X.; McCarty, G.W.; Sadeghi, A.M.; Cosh, M.H.; Zeng, X.; Gao, F.; Daughtry, C.S.; Huang, C.; Lang, M.W.; et al. Assessing the performance of a physically-based soil moisture module integrated within the Soil and Water Assessment Tool. J. Environ. Model. Softw. 2018, 109, 329–341. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, J.; Cheng, F.; Deng, H.; Chen, S. Drought monitoring in Yunnan Province based on a TRMM precipitation product. J. Nat. Hazards 2020, 104, 2369–2387. [Google Scholar] [CrossRef]
- Tuo, Y.; Duan, Z.; Disse, M.; Chiogna, G. Evaluation of precipitation input for SWAT modeling in Alpine catchment: A case study in the Adige river basin (Italy). Sci. Total Environ. 2016, 573, 66–82. [Google Scholar] [CrossRef]
- Fuka, D.R.; Walter, M.T.; MacAlister, C.; Degaetano, A.T.; Steenhuis, T.S.; Easton, Z.M. Using the climate forecast system reanalysis as weather input data for watershed models. Hydrol. Process. 2013, 28, 5613–5623. [Google Scholar] [CrossRef]
- Wang, J.; Hong, Y.; Li, L.; Gourley, J.J.; Khan, S.I.; Yilmaz, K.K.; Limaye, A.S. The coupled routing and excess storage (CREST) distributed hydrological model. Hydrol. Sci. J. 2011, 56, 84–98. [Google Scholar] [CrossRef]
- Roth, V.; Lemann, T. Comparing CFSR and conventional weather data for discharge and soil loss modelling with SWAT in small catchments in the Ethiopian highlands. Hydrol. Earth Syst. Sci. 2016, 20, 921–934. [Google Scholar] [CrossRef]
- Tolera, M.B.; Chung, I.M.; Chang, S.W. Evaluation of the climate forecast system reanalysis weather data for watershed modeling in Upper Awash basin, Ethiopia. Water 2018, 10, 725. [Google Scholar] [CrossRef]
- Zhu, D.; Ren, Q. Hydrological evaluation of hourly merged satellite—Station precipitation product in the mountainous basin of China using a distributed hydrological model. Meteorol. Appl. 2020, 27, e1909. [Google Scholar] [CrossRef]
- Ma, M.; Wang, H.; Jia, P.; Tang, G.; Wang, D.; Ma, Z.; Yan, H. Application of the GPM-IMERG Products in Flash Flood Warning: A Case Study in Yunnan, China. Remote Sens. 2020, 12, 1954. [Google Scholar] [CrossRef]
- Yeditha, P.K.; Venkatesh, K.; Maheswaran, R.; Ankit, A. Forecasting of extreme flood events using different satellite precipitation products and wavelet-based machine learning methods. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 063115. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Evaluation of satellite rainfall products through hydrologic simulation in a fully distributed hydrologic model. Water Resour. Res. 2011, 47, 1–11. [Google Scholar] [CrossRef]
- Vu, M.T.T.; Raghavan, S.V.; Liong, S.Y.Y. SWAT use of gridded observations for simulating runoff—A Vietnam river basin study. Hydrol. Earth Syst. Sci. 2012, 16, 2801–2811. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and hydrological comparisons between TRMM and GPM Level-3 products over a midlatitude Basin: Is day-1 IMERG a good successor for TMPA 3B42V7? J. Hydrometeorol. 2016, 17, 121–137. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Y.; Huang, Y.; Li, Y.; Hou, C.; Shi, X. Evaluation and hydrological application of satellite-based precipitation datasets in driving hydrological models over the Huifa river basin in Northeast China. J. Atmos. Res. 2018, 207, 28–41. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Leng, G.; Huang, Q. Integrated index for drought assessment based on variable fuzzy set theory: A case study in the Yellow River basin, China. J. Hydrol. 2015, 527, 608–618. [Google Scholar] [CrossRef]
- Sun, R.; Yuan, H.; Liu, X.; Jiang, X. Evaluation of the latest satellite-gauge precipitation products and their hydrologic applications over the Huaihe River basin. J. Hydrol. 2016, 536, 302–319. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the GPM IMERG satellite-based precipitation products and the hydrological utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Hogue, T.S.; Hsu, K.L.; Sorooshian, S.; Gupta, H.V.; Wagener, T. Intercomparison of rain gauge, radar, and satellite-based precipitation estimates with emphasis on hydrologic forecasting. J. Hydrometeorol. 2005, 6, 497–517. [Google Scholar] [CrossRef]
- Su, F.; Hong, Y.; Lettenmaier, D.P. Evaluation of TRMM multisatellite precipitation analysis (TMPA) and its utility in hydrologic prediction in the La Plata Basin. J. Hydrometeorol. 2008, 9, 622–640. [Google Scholar] [CrossRef]
- Gao, Z.; Long, D.; Tang, G.; Zeng, C.; Huang, J.; Hong, Y. Assessing the potential of satellite-based precipitation estimates for flood frequency analysis in ungauged or poorly gauged tributaries of China’s Yangtze River basin. J. Hydrol. 2017, 550, 478–496. [Google Scholar] [CrossRef]
- Maggioni, V.; Massari, C. On the performance of satellite precipitation products in riverine flood modeling: A review. J. Hydrol. 2018, 558, 214–224. [Google Scholar] [CrossRef]
- Jiang, L.; Bauer-Gottwein, P. How do GPM IMERG precipitation estimates perform as hydrological model forcing? Evaluation for 300 catchments across Mainland China. J. Hydrol. 2019, 572, 486–500. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, J.; Huang, Y.; Chen, X.; Chen, S.; Duan, Z. Hydrologic evaluation of TRMM and GPM IMERG satellite-based precipitation in a humid basin of China. Remote Sens. 2019, 11, 431. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, K. The role of satellite-based remote sensing in improving simulated streamflow: A review. Water 2019, 11, 1615. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Soe, K.M.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Applications of TRMM- and GPM-era multiple- satellite precipitation products for flood simulations at sub-daily scales in a sparsely gauged watershed in Myanmar. Remote Sens. 2019, 11, 140. [Google Scholar] [CrossRef]
- Grassotti, C.; Hoffman, R.N.; Vivoni, E.R.; Entekhabi, D. Multiple-timescale intercomparison of two radar products and rain gauge observations over the Arkansas—Red River basin. J. Weather Forecast. 2003, 18, 1207–1229. [Google Scholar] [CrossRef][Green Version]
- Yang, F.; Zhang, G.L.; Yang, J.L.; Li, D.C.; Zhao, Y.G.; Liu, F.; Yang, R.M.; Yang, F. Organic matter controls of soil water retention in an alpine grassland and its significance for hydrological processes. J. Hydrol. 2014, 519, 3010–3027. [Google Scholar] [CrossRef]
- Le, M.H.; Lakshmi, V.; Bolten, J.; Du Bui, D. Adequacy of Satellite-derived Precipitation Estimate for Hydrological modeling in Vietnam Basins. J. Hydrol. 2020, 586, 124820. [Google Scholar] [CrossRef]
- Guo, D.; Wang, H.; Zhang, X.; Liu, G. Evaluation and analysis of grid precipitation fusion products in Jinsha river basin based on China meteorological assimilation datasets for the SWAT model. Water 2019, 11, 253. [Google Scholar] [CrossRef]
- Jiang, L.; Madsen, H.; Bauer-Gottwein, P. Simultaneous calibration of multiple hydrodynamic model parameters using satellite altimetry observations of water surface elevation in the Songhua River. Remote Sens. Environ. 2019, 225, 229–247. [Google Scholar] [CrossRef]
- Harris, A.; Rahman, S.; Hossain, F.; Yarborough, L.; Bagtzoglou, A.C.; Easson, G. Satellite-based flood modeling using TRMM-based rainfall products. J. Sens. 2007, 7, 3416–3427. [Google Scholar] [CrossRef]
- Su, J.; Lü, H.; Zhu, Y.; Cui, Y.; Wang, X. Evaluating the hydrological utility of latest IMERG products over the Upper Huaihe River Basin, China. J. Atmos. Res. 2019, 225, 17–29. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, W.; Wen, J.; Qiu, C.; Sun, W.; Fang, Q.; Xu, M.; Tan, J. Accuracy evaluation of two high-resolution satellite-based rainfall products: TRMM 3B42V7 and CMORPH in Shanghai. Water 2018, 10, 40. [Google Scholar] [CrossRef]
- Shukla, R.; Agarwal, A.; Gornott, C.; Sachdeva, K.; Joshi, P.K. Farmer typology to understand differentiated climate change adaptation in Himalaya. Sci. Rep. 2019, 9, 20375. [Google Scholar] [CrossRef] [PubMed]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Sridhar, V. Tracking the influence of irrigation on land surface fluxes and boundary layer climatology. J. Contemp. Water Res. Educ. 2013, 152, 79–93. [Google Scholar] [CrossRef]
- Setti, S.; Rathinasamy, M.; Chandramouli, S. Assessment of water balance for a forest dominated coastal river basin in India using a semi distributed hydrological model. Model. Earth Syst. Environ. 2017, 4, 127–140. [Google Scholar] [CrossRef]
- Haerter, J.O.; Hagemann, S.; Moseley, C.; Piani, C. Climate model bias correction and the role of timescales. Hydrol. Earth Syst. Sci. 2011, 15, 1065–1079. [Google Scholar] [CrossRef]
- Sridhar, V.; Wedin, D.A. Hydrological behavior of Grasslands of the Sandhills: Water and Energy Balance Assessment from Measurements, Treatments and Modeling. Ecohydrology 2009, 2, 195–212. [Google Scholar] [CrossRef]
- Guntu, R.K.; Rathinasamy, M.; Agarwal, A.; Sivakumar, B. Spatiotemporal variability of Indian rainfall using multiscale entropy. J. Hydrol. 2020, 587, 124916. [Google Scholar] [CrossRef]
- Guntu, R.K.; Maheswaran, R.; Agarwal, A.; Singh, V.P. Accounting for temporal variability for improved precipitation regionalization based on self-organizing map coupled with information theory. J. Hydrol. 2020, 590, 125236. [Google Scholar] [CrossRef]
- Agarwal, A. Unraveling Spatio-Temporal Climatic Patterns via Multi-Scale Complex Networks. PhD Thesis, Universität Potsdam, Potsdam, Germany, 2019. [Google Scholar]
- Kurths, J.; Agarwal, A.; Marwan, N.; Rathinasamy, M.; Caesar, L.; Krishnan, R.; Merz, B. Unraveling the spatial diversity of Indian precipitation teleconnections via nonlinear multi-scale approach. Nonlinear Process. Geophys. 2019, 26, 251–266. [Google Scholar] [CrossRef]
- Yeggina, S.; Teegavarapu, R.S.; Muddu, S. Evaluation and bias corrections of gridded precipitation data for hydrologic modelling support in Kabini River basin, India. Theor. Appl. Climatol. 2020, 140, 1495–1513. [Google Scholar] [CrossRef]
- Setti, S.; Maheswaran, R.; Radha, D.; Sridhar, V.; Asce, M.; Barik, K.K.; Narasimham, M.L. Attribution of Hydrologic Changes in a Tropical River Basin to Rainfall Variability and Land-Use Change: Case Study from India. J. Hydrol. Eng. 2020, 25, 1–15. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Mehran, A. Extended contingency table: Performance metrics for satellite observations and climate model simulations. Water Resour. Res. 2013, 49, 7144–7149. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I- A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic Calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. J. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Griensven, V.; Liew, V. DigitalCommons@University of Nebraska-Lincoln SWAT: Model use, calibration, and validation. Biol. Syst. Eng. Pap. Publ. 2012. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Kang, H.; Sridhar, V. Combined statistical and spatially distributed hydrological model for evaluating future drought indices in Virginia. J. Hydrol. Reg. Stud. 2017, 12, 253–272. [Google Scholar] [CrossRef]
- Kang, H.; Sridhar, V. Improved drought prediction using near real-time climate forecasts and simulated hydrologic conditions. Sustainability 2018, 10, 1799. [Google Scholar] [CrossRef]
- Sehgal, V.; Sridhar, V.; Juran, L.; Ogejo, J. Integrating Climate Forecasts with the Soil and Water Assessment Tool (SWAT) for High-Resolution Hydrologic Simulation and Forecasts in the Southeastern USS. Sustainability 2018, 10, 3079. [Google Scholar] [CrossRef]
- Sridhar, V.; Kang, H.; Ali, S.A. Human-induced alterations to land use and climate and their responses on hydrology and water management in the Mekong River basin. Water 2019, 11, 1307. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R. Soil & Water Assessment Tool: Input/Output Documentation; Version 2012. TR-439; Texas Water Resources Institute: College Station, TX, USA, 2012. [Google Scholar]
- Arnold, J.G.; Williams, J.R.; Maidment, D.R. Continuous-time water and sediment-routing model for large basins. J. Hydraul. Eng. 1995, 121, 171–183. [Google Scholar] [CrossRef]
- Mosbahi, M.; Benabdallah, S. Assessment of land management practices on soil erosion using SWAT model in a Tunisian semi-arid catchment. J. Soils Sediments 2020, 1129–1139. [Google Scholar] [CrossRef]
- CWC (Central Water Commission). Stream Flow Discharge Data for the Period 1985–2012. 2018. Available online: http://cwc.gov.in/water-resources-information-system-wris (accessed on 22 March 2018).
- Abbaspour, K.C. SWAT-CUP: SWAT Calibration and Uncertainty Programs—A User Manual. 2015. Available online: http://swat.tamu.edu/software/swatcup/ (accessed on 10 August 2016).
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- World Meteorological Organization. Observation of present and past weather state of the ground. In Guide to Meteorological Instruments and Methods of Observation; Chapter 14; WMO: Geneva, Switzerland, 2012; pp. 14–19. [Google Scholar]
- Abbaspour, K.C.; Johnson, C.A.; van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]

| Name and Type | Spatial Resolution/Coverage | Temporal Resolution/Period | Remarks, References and Data Sources |
|---|---|---|---|
| IMD (gridded rainfall dataset) | 0.25°/Pan India | Daily/1901–2013 | The gridded data were generated from the observed data of 6995 gauging stations across India using spatial interpolation for the period 1901–2013 [14] Details about these data can be obtained from http://imd.gov.in (homepage/rainfall information). |
| TRMM 3B42V7 (satellite product) | 0.25°/Global (50 N-S) | Daily/1998–2014 | Joint mission between the National Aeronautics and Space Administration (NASA) and the Japan Aerospace Exploration Agency (JAXA) to monitor tropical precipitation [6] one type of the TRMM multi-satellite precipitation analysis (TMPA) products) https://giovanni.gsfc.nasa.gov |
| Bias-corrected TRMM (satellite product) | 0.25°/Global (50 N-S) | Daily/1998–2014) | The bias of TRMM rainfall was corrected by applying monthly multiplicative correction coefficients (MCC) of IMD rainfall [56] https://giovanni.gsfc.nasa.gov |
| CFSR (reanalysis dataset) | 0.31°/Global (50 N-S) | Daily/1979–2014 | Global, high resolution, coupled atmosphere–ocean–land surface-sea ice system started in 1979 by the National Centers for Environmental Prediction [22] https://globalweather.tamu.edu/ |
| S. No | Statistical Metrics | Equation | Description |
|---|---|---|---|
| 1 | Probability of detection (POD) | POD = H/(H + M) | It represents the detected rainfall events correctly by satellite out of rainfall events by reference data. Its ranges from 0 to 1 (1 is the best value) |
| 2 | False alarm ratio (FAR) | FAR = F/(F + H) | It represents the false, detected as rainfall event by satellite when reference data showed no rainfall. Its ranges from 0 to 1 (0 is the best value) |
| 3 | Critical success index (CSI) | CSI = H/(H + M + F) | It is more accurate when correct negative values are not considered. Its ranges from 0 to 1 (1 is the perfect value) |
| Data Type | Scale | Source |
|---|---|---|
| Digital elevation model (DEM) | 30 m × 30 m | Shuttle radar topography mission (SRTM) of USGS (https://earthexplorer.usgs.gov/) |
| Land use/land cover (LULC) | 500 m | GIAM-IWMI (http://www.iwmi.cgiar.org) |
| Soil | 1:1,500,000 | http://www.fao.org/soils-portal/soil-survey/soil-maps-and-databases/faounesco-soil-map-of-the-world/en/ Food and Agriculture Organization (FAO) |
| Rainfall, temperature | 0.25° (~32 km) | http://imdpune.gov.in/Clim_Pred_LRF_New/Grided_Data_Download.html Indian Metrological Department (IMD), PUNE |
| Solar radiation, relative humidity, wind speed | 0.31° (~38 km) | https://rda.ucar.edu/datasets/ds093.1/ Climate Forecast System Reanalysis (CFSR) |
| Hydrological data | Daily | https://indiawris.gov.in/wris, (Central Water Commission (CWC)_ |
| Statistical Measures | IMD | TRMM | Bias Corrected TRMM | CFSR |
|---|---|---|---|---|
| Minimum rainfall (mm) | 2.5 | 2.5 | 2.5 | 2.5 |
| Maximum rainfall (mm) | 140.2 | 157.7 | 119.4 | 176.4 |
| Mean rainfall (mm) | 11.9 | 13.3 | 11.9 | 12.6 |
| Standard deviation(mm) | 12.7 | 13.7 | 11.9 | 13.1 |
| Skewness | 3.8 | 3.4 | 3.2 | 4.3 |
| Event | IMD | Observed Event | TRMM | Bias Corrected TRMM | CFSR |
|---|---|---|---|---|---|
| Rainy days | 1591 | Hit (H) | 978 | 932 | 1161 |
| Miss (M) | 613 | 659 | 430 | ||
| Non-rainy days | 4253 | False alarm (F) | 718 | 658 | 712 |
| Correct negative | 3535 | 3595 | 3541 |
| Statistical Metrics | TRMM | Bias Corrected TRMM | CFSR | |
|---|---|---|---|---|
| Probability of detection | POD | 0.61 | 0.69 | 0.73 |
| False alarm ratio | FAR | 0.42 | 0.39 | 0.38 |
| Critical success index | CSI | 0.42 | 0.45 | 0.50 |
| Statistical Metrics | Performance of Different Datasets under Scenario A | |||
|---|---|---|---|---|
| IMD | TRMM | Bias Corrected TRMM | CFSR | |
| R2 | 0.87 | 0.60 | 0.68 | 0.54 |
| NS | 0.85 | 0.55 | 0.62 | 0.52 |
| PBIAS | −5.5 | −15.3 | −7.4 | −16.2 |
| P-factor | 0.83 | 0.65 | 0.8 | 0.65 |
| r-factor | 0.67 | 0.48 | 0.63 | 0.91 |
| S. No | Parameter | Description | Min | Max |
|---|---|---|---|---|
| 1 | CN2.mgt * | SCS runoff curve number for moisture condition II, which controls the surface runoff | −0.1 | 0.1 |
| 2 | ALPHA_BF.gw | Baseflow alpha factor for groundwater flow response to changes in recharge | 0 | 1 |
| 3 | GW_DELAY.gw | Groundwater delay represents the time taken by water move from the bottom soil layer to the upper shallow aquifer (days) | 30 | 450 |
| 4 | GWQMN.gw | Threshold depth of water in the shallow aquifer required for return flow to occur. If it is decreased, baseflow will be decreased (in mm) | 0 | 5000 |
| 5 | GW_REVAP.gw | Groundwater “revap” coefficient (Water movement from shallow aquifer to vegetation roots). If it is close to zero, the movement of water is restricted; if it approaches 1, the rate of water approaches the rate of evapotranspiration | 0.02 | 0.2 |
| 6 | RCHRG_DP.gw | Deep aquifer percolation fraction from the root zone which recharges in a deep aquifer | 0 | 1 |
| 7 | REVAPMN.gw | Threshold depth of water in the shallow aquifer for “revap” to occur (mm). Controls the water movement from a shallow aquifer to a deep aquifer | 0 | 1000 |
| 8 | SLSUBBSN.hru | Average slope length | 10 | 150 |
| 9 | HRU_SLP.hru | Average slope steepness (m/m) | 0 | 1 |
| 10 | OV_N.hru | Manning’s “n” value for overland flow | 0.01 | 30 |
| 11 | LAT_TTIME.hru | Lateral flow travel time (days) | 0 | 180 |
| 12 | ESCO.hru | Soil evaporation compensation factor (represents the process of evapotranspiration from soil moisture to atmosphere, if the ESCO is reduced, the evaporation is increased) | 0 | 1 |
| 13 | EPCO.hru | Plant uptake compensation factor (The amount of water uptake by a plant for transpiration, If EPCO value is 1, the model allows more of the water uptake demand) | 0 | 1 |
| 14 | SURLAG.bsn | Surface runoff lags time (days). It controls the fraction of water to allow to the reach on the day | 0.05 | 24 |
| 15 | SOL_AWC().sol | Available water capacity of the soil layer | 0 | 1 |
| 16 | SOL_K().sol | Saturated hydraulic conductivity (mm/h). This relates to soil water flow rate to the hydraulic gradient. | 0 | 2000 |
| 17 | CH_K2.rte | Effective hydraulic conductivity in main channel alluvium (mm/h). If streams have continuous groundwater contribution, the effective conductivity will be zero. | 0.1 | 500 |
| 18 | ALPHA_BNK.rte | Baseflow alpha factor for bank storage (Contributes flow to the reach within the subbasin) | 0 | 1 |
| S. No | Parameter | IMD | TRMM | Bias Corrected TRMM | CFSR |
|---|---|---|---|---|---|
| 1 | r__CN2.mgt | 6 | 1 | 2 | 1 |
| 2 | v__ALPHA_BF.gw | 18 | 18 | 17 | 14 |
| 3 | v__GW_DELAY.gw | 12 | 13 | 15 | 10 |
| 4 | v__GWQMN.gw | 3 | 6 | 8 | 3 |
| 5 | v__GW_REVAP.gw | 5 | 8 | 14 | 5 |
| 6 | v__RCHRG_DP.gw | 1 | 2 | 3 | 2 |
| 7 | v__REVAPMN.gw | 13 | 10 | 10 | 15 |
| 8 | v__SLSUBBSN.hru | 7 | 4 | 4 | 6 |
| 9 | v__HRU_SLP.hru | 8 | 5 | 6 | 7 |
| 10 | v__OV_N.hru | 16 | 11 | 12 | 11 |
| 11 | v__LAT_TTIME.hru | 17 | 7 | 7 | 9 |
| 12 | v__ESCO.hru | 2 | 3 | 1 | 4 |
| 13 | v__EPCO.hru | 11 | 12 | 11 | 17 |
| 14 | v__SURLAG.bsn | 15 | 16 | 18 | 18 |
| 15 | r__SOL_AWC().sol | 9 | 9 | 5 | 8 |
| 16 | r__SOL_K().sol | 14 | 14 | 9 | 13 |
| 17 | v__CH_K2.rte | 10 | 17 | 16 | 12 |
| 18 | v__ALPHA_BNK.rte | 4 | 15 | 13 | 16 |
| Statistical Results during the Calibration and Validation Period | ||||||||
|---|---|---|---|---|---|---|---|---|
| Statistical Metrics | Calibration | Validation | ||||||
| IMD | TRMM | TRMM-Bias | CFSR | IMD | TRMM | Bias Corrected TRMM | CFSR | |
| R2 | 0.87 | 0.76 | 0.78 | 0.77 | 0.82 | 0.77 | 0.74 | 0.74 |
| NS | 0.85 | 0.71 | 0.74 | 0.76 | 0.79 | 0.72 | 0.72 | 0.73 |
| PBIAS | −5.5 | −13.4 | −7.2 | −14.3 | −6.2 | −15.2 | −8.1 | −17.2 |
| P-factor | 0.83 | 0.68 | 0.72 | 0.64 | 0.85 | 0.67 | 0.69 | 0.61 |
| r-factor | 0.67 | 0.46 | 0.59 | 0.40 | 0.79 | 0.44 | 0.61 | 0.41 |
| S. No | Parameter | IMD | TRMM | Bias Corrected TRMM | CFSR |
|---|---|---|---|---|---|
| 1 | v__ESCO.hru | 0.11 | 0.56 | 0.06 | 0.67 |
| 2 | v__SLSUBBSN.hru | 42.59 | 145.7 | 36.7 | 145.6 |
| 3 | v__HRU_SLP.hru | 0.28 | 0.06 | 1.0 | 0.11 |
| 4 | r__SOL_AWC().sol | −0.03 | 0.037 | 0.054 | 0.03 |
| 5 | r__CH_K2.rte | 367.1 | X | X | X |
| 6 | r__CN2.mgt | −0.152 | −0.09 | -0.15 | −0.19 |
| 7 | V__ALPHA_BNK.rte | 0.33 | X | X | X |
| 8 | V__RCHRG_DP.gw | 0.073 | 0.047 | 0.06 | 0.011 |
| 9 | V__GW_REVAP.gw | 0.13 | 0.079 | X | 0.115 |
| 10 | V__GWQMN.gw | 4577 | 3196 | 3234 | 3942 |
| 11 | V__OV_N.hru | X | 13.47 | X | 21.1 |
| 12 | V__LAT_TTIME.hru | X | 85 | 47 | 28.8 |
| 13 | V__GW_DELAY.gw | X | X | X | 72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Setti, S.; Maheswaran, R.; Sridhar, V.; Barik, K.K.; Merz, B.; Agarwal, A. Inter-Comparison of Gauge-Based Gridded Data, Reanalysis and Satellite Precipitation Product with an Emphasis on Hydrological Modeling. Atmosphere 2020, 11, 1252. https://doi.org/10.3390/atmos11111252
Setti S, Maheswaran R, Sridhar V, Barik KK, Merz B, Agarwal A. Inter-Comparison of Gauge-Based Gridded Data, Reanalysis and Satellite Precipitation Product with an Emphasis on Hydrological Modeling. Atmosphere. 2020; 11(11):1252. https://doi.org/10.3390/atmos11111252
Chicago/Turabian StyleSetti, Sridhara, Rathinasamy Maheswaran, Venkataramana Sridhar, Kamal Kumar Barik, Bruno Merz, and Ankit Agarwal. 2020. "Inter-Comparison of Gauge-Based Gridded Data, Reanalysis and Satellite Precipitation Product with an Emphasis on Hydrological Modeling" Atmosphere 11, no. 11: 1252. https://doi.org/10.3390/atmos11111252
APA StyleSetti, S., Maheswaran, R., Sridhar, V., Barik, K. K., Merz, B., & Agarwal, A. (2020). Inter-Comparison of Gauge-Based Gridded Data, Reanalysis and Satellite Precipitation Product with an Emphasis on Hydrological Modeling. Atmosphere, 11(11), 1252. https://doi.org/10.3390/atmos11111252








