Comparing Simulations of Umbrella-Cloud Growth and Ash Transport with Observations from Pinatubo, Kelud, and Calbuco Volcanoes
Abstract
1. Introduction
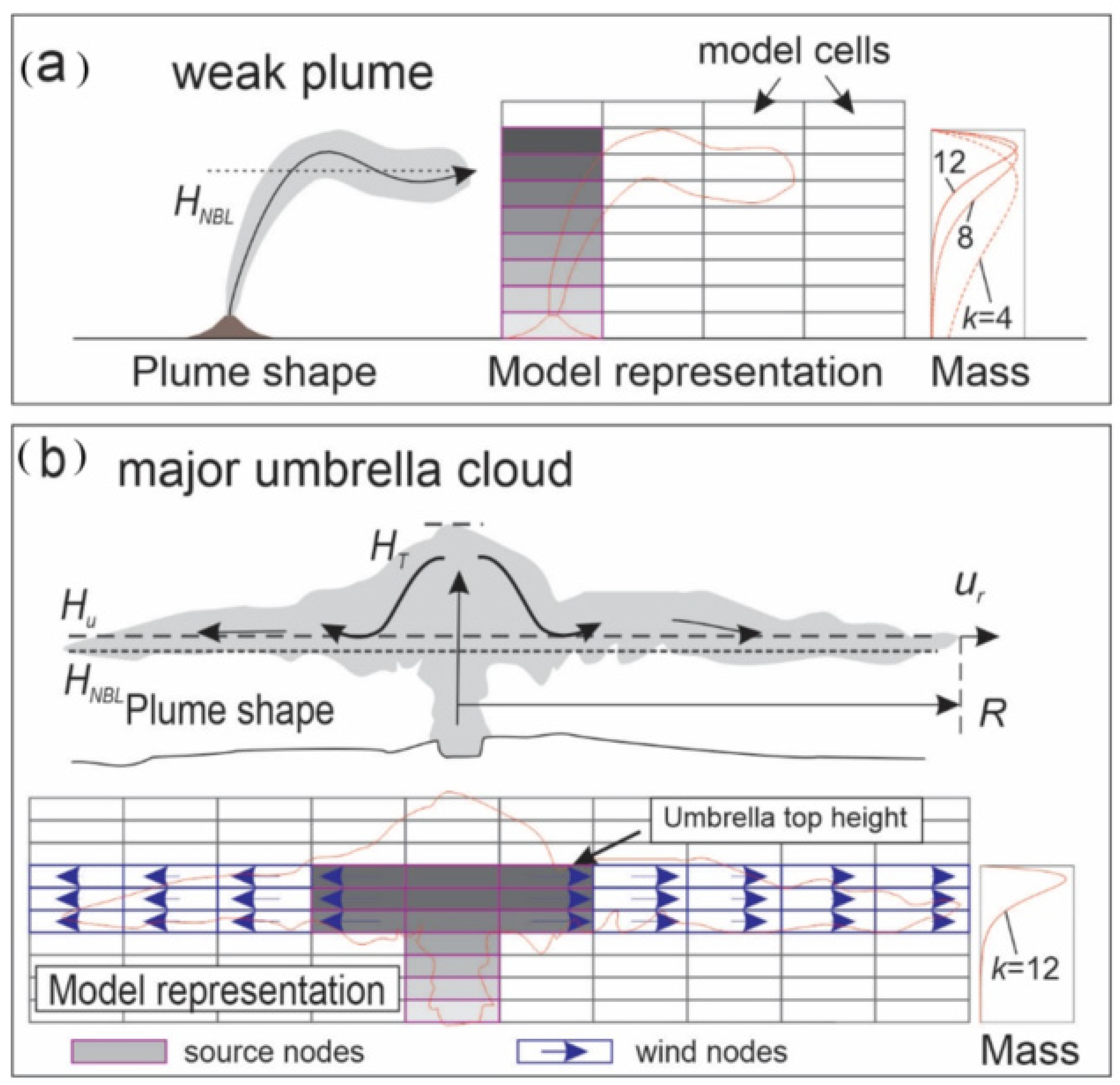
2. Dynamics of Umbrella Growth
3. Model Implementation
4. Application to Eruptions
4.1. Pinatubo 15 June 1991
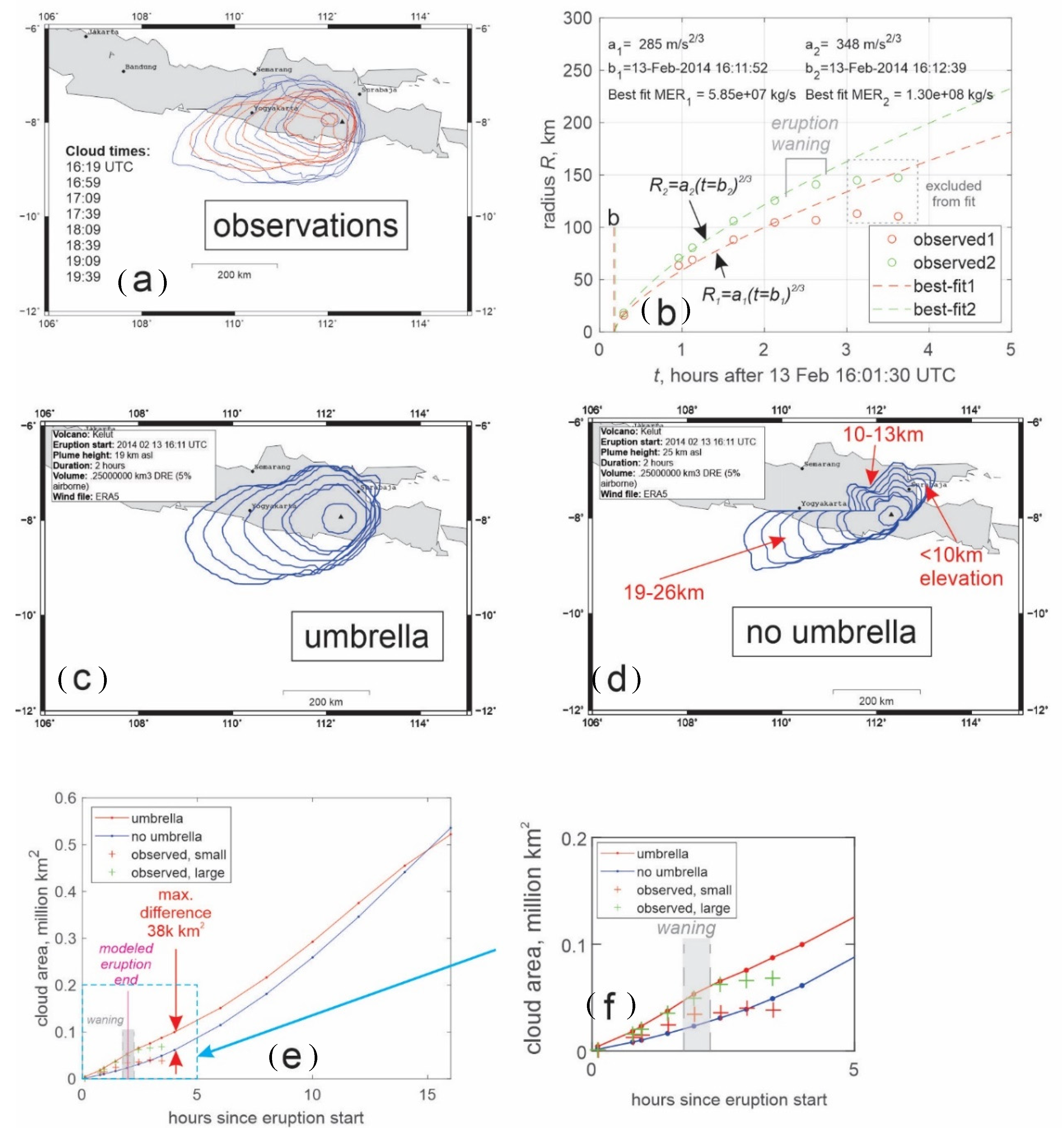
4.2. Kelud, 13 February 2014
4.3. Calbuco, 22–23 April 2015
Calbuco Deposit
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Newhall, C.G.; Self, S. The volcanic explosivity index/VEI/- An estimate of explosive magnitude for historical volcanism. J. Geophys. Res. 1982, 87. [Google Scholar] [CrossRef]
- Webster, H.N.; Devenish, B.J.; Mastin, L.G.; Thomson, D.J.; Van Eaton, A.R. Operational Modelling of Umbrella Cloud Growth in a Lagrangian Volcanic Ash Transport and Dispersion Model. Atmosphere 2020, 11, 200. [Google Scholar] [CrossRef]
- Costa, A.; Folch, A.; Macedonio, G. Density-driven transport in the umbrella region of volcanic clouds: Implications for tephra dispersion models. Geophys. Res. Lett. 2013, 40, 4823–4827. [Google Scholar] [CrossRef]
- Mastin, L.G.; Van Eaton, A.R.; Lowenstern, J.B. Modeling ash fall distribution from a Yellowstone supereruption. Geochem. Geophy. Geosy. 2014, 15, 3459–3475. [Google Scholar] [CrossRef]
- Costa, A.; Smith, V.; Macedonio, G.; Matthews, N. The magnitude and impact of the Youngest Toba Tuff super-eruption. Front. Earth SC-Switz 2014, 2. [Google Scholar] [CrossRef]
- Koyaguchi, T.; Tokuno, M. Origin of the giant eruption cloud of Pinatubo, June 15, 1991. J. Volcanol. Geoth. Res. 1993, 55, 85–96. [Google Scholar] [CrossRef]
- Holasek, R.E.; Self, S.; Woods, A.W. Satellite observations and interpretation of the 1991 Mount Pinatubo eruption plumes. J. Geophys. Res. 1996, 101, 27635–27656. [Google Scholar] [CrossRef]
- Kristiansen, N.I.; Prata, A.J.; Stohl, A.; Carn, S.A. Stratospheric volcanic ash emissions from the 13 February 2014 Kelut eruption. Geophys. Res. Lett. 2015, 42, 588–596. [Google Scholar] [CrossRef]
- Van Eaton, A.R.; Amigo, Á.; Bertin, D.; Mastin, L.G.; Giacosa, R.E.; González, J.; Valderrama, O.; Fontijn, K.; Behnke, S.A. Volcanic lightning and plume behavior reveal evolving hazards during the April 2015 eruption of Calbuco volcano, Chile. Geophys. Res. Lett. 2016, 43, 3563–3571. [Google Scholar] [CrossRef]
- Romero, J.E.; Morgavi, D.; Arzilli, F.; Daga, R.; Caselli, A.; Reckziegel, F.; Viramonte, J.; Díaz-Alvarado, J.; Polacci, M.; Burton, M.; et al. Eruption dynamics of the 22–23 April 2015 Calbuco Volcano (Southern Chile): Analyses of tephra fall deposits. J. Volcanol. Geoth. Res. 2016, 317, 15–29. [Google Scholar] [CrossRef]
- Sparks, R.S.J.; Bursik, M.I.; Carey, S.N.; Gilbert, J.S.; Glaze, L.S.; Sigurdsson, H.; Woods, A.W. Volcanic Plumes; John Wiley & Sons: Chichester, UK, 1997; p. 574. [Google Scholar]
- Rooney, G.G.; Devenish, B.J. Plume rise and spread in a linearly stratified environment. Geophys. Astro. Fluid. 2014, 108, 168–190. [Google Scholar] [CrossRef]
- Pouget, S.; Bursik, M.; Johnson, C.G.; Hogg, A.J.; Phillips, J.C.; Sparks, R.S.J. Interpretation of umbrella cloud growth and morphology: Implications for flow regimes of short-lived and long-lived eruptions. B. Volcanol. 2015, 78. [Google Scholar] [CrossRef]
- Sparks, R.S.J.; Moore, J.G.; Rice, C.J. The initial giant umbrella cloud of the May 18th, 1980, explosive eruption of Mount St. Helens. J. Volcanol. Geoth. Res. 1986, 28, 257–274. [Google Scholar] [CrossRef]
- Woods, A.W.; Kienle, J. The dynamics and thermodynamics of volcanic clouds: Theory and observations from the april 15 and april 21, 1990 eruptions of redoubt volcano, Alaska. J. Volcanol. Geoth. Res. 1994, 62, 273–299. [Google Scholar] [CrossRef]
- Hargie, K.A.; Van Eaton, A.R.; Mastin, L.G.; Holzworth, R.H.; Ewert, J.W.; Pavolonis, M. Globally detected volcanic lightning and umbrella dynamics during the 2014 eruption of Kelud, Indonesia. J. Volcanol. Geoth. Res. 2019, 382, 81–91. [Google Scholar] [CrossRef]
- Suzuki, Y.J.; Koyaguchi, T. A three-dimensional numerical simulation of spreading umbrella clouds. J. Geophys. Res-Sol. Ea. 2009, 114, B03209. [Google Scholar] [CrossRef]
- Barker, S.J.; Van Eaton, A.R.; Mastin, L.G.; Wilson, C.J.N.; Thompson, M.A.; Wilson, T.M.; Davis, C.; Renwick, J.A. Modeling Ash Dispersal From Future Eruptions of Taupo Supervolcano. Geochem. Geophy. Geosy. 2019, 20, 3375–3401. [Google Scholar] [CrossRef]
- Schwaiger, H.; Denlinger, R.; Mastin, L.G. Ash3d: A finite-volume, conservative numerical model for ash transport and tephra deposition. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Suzuki, T. A Theoretical model for dispersion of tephra. In Arc Volcanism: Physics and Tectonics; Shimozuru, D., Yokoyama, I., Eds.; Terra Scientific Publishing Company: Tokyo, Japan, 1983; pp. 95–113. [Google Scholar]
- Mastin, L.G.; Van Eaton, A.R.; Durant, A.J. Adjusting particle-size distributions to account for aggregation in tephra-deposit model forecasts. Atmos. Chem. Phys. 2016, 16, 9399–9420. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service (C3S). ERA5: Fifth Generation of ECMWF Atmospheric Reanalyses of the Global Climate. Copernicus Climate Change Service Climate Data Store (CDS). Available online: https://cds.climate.copernicus.eu/cdsapp#!/home (accessed on 1 May 2020).
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Matson, M. The 1982 El Chichón Volcano eruptions—A satellite perspective. J. Volcanol. Geoth. Res. 1984, 23, 1–10. [Google Scholar] [CrossRef]
- Koyaguchi, T. Grain-size variations of the tephra derived from umbrella clouds. B. Volcanol. 1994, 56, 1–9. [Google Scholar] [CrossRef]
- Koyaguchi, T.; Ohno, M. Reconstruction of eruption column dynamics on the basis of grain size of tephra fall deposits: 2. Application to the Pinatubo 1991 eruption. J. Geophys. Res-Sol. Ea. 2001, 106, 6513–6533. [Google Scholar] [CrossRef]
- Pouget, S.; Bursik, M.; Webley, P.; Dehn, J.; Pavolonis, M. Estimation of eruption source parameters from umbrella cloud or downwind plume growth rate. J. Volcanol. Geoth. Res. 2013, 258, 100–112. [Google Scholar] [CrossRef]
- Guffanti, M.; Casadevall, T.J.; Budding, K. Encounters of Aircraft with Volcanic Ash Clouds: A Compilation of Known Incidents, 1953–2009. In U.S. Geological Survey Data Series 545; U.S. Government Printing Office: Washington, DC, USA, 2010; p. 16. [Google Scholar]
- Christmann, C.; Nunes, R.R.; Schmitt, A.R.; Guffanti, M. Flying into Volcanic Ash Clouds: An Evaluation of Hazard Potential. In Proceedings of the STO-MP-AVT-272: Impact of Volcanic Ash Clouds on Military Operations, Vilnius, Lithuania, 17 May 2017. [Google Scholar]
- Hoblitt, R.P.; Wolfe, E.W.; Scott, W.E.; Couchman, M.R.; Pallister, J.S.; Javier, D. The Preclimactic eruptions of Mount Pinatubo, June 1991. In Fire and Mud: Eruptions and Lahars of Mount Pinatubo, Philippines; Newhall, C.G., Punongbayan, R.S., Eds.; University of Washington Press: Seattle, WA, USA, 1996; pp. 457–511. [Google Scholar]
- Wolfe, E.W.; Hoblitt, R.P. Overview of the Eruptions. In Fire and Mud: Eruptions and Lahars of Mount Pinatubo, Philipines; University of Washington Press: Seattle, WA, USA, 1996; pp. 3–20. [Google Scholar]
- Mastin, L.G.; Guffanti, M.; Servranckx, R.; Webley, P.; Barsotti, S.; Dean, K.; Durant, A.; Ewert, J.W.; Neri, A.; Rose, W.I.; et al. A multidisciplinary effort to assign realistic source parameters to models of volcanic ash-cloud transport and dispersion during eruptions. J. Volcanol. Geoth. Res. 2009, 186, 10–21. [Google Scholar] [CrossRef]
- Dacre, H.F.; Grant, A.L.M.; Hogan, R.J.; Belcher, S.E.; Thomson, D.J.; Devenish, B.; Marenco, F.; Haywood, J.; Ansmann, A.; Mattis, I. Evaluating the structure and magnitude of the ash plume during the initial phase of the Eyjafjallajökull eruption, evaluated using lidar observations and NAME simulations. J. Geophys. Res. 2011, 116, D00U03. [Google Scholar] [CrossRef]
- Wilson, L.; Huang, T.C. The influence of shape on the atmospheric settling velocity of volcanic ash particles. Earth Planet. Sc. Lett. 1979, 44, 311–324. [Google Scholar] [CrossRef]
- Fero, J.; Carey, S.N.; Merrill, J.T. Simulating the dispersal of tephra from the 1991 Pinatubo eruption: Implications for the formation of widespread ash layers. J. Volcanol. Geoth. Res. 2009, 186, 120–131. [Google Scholar] [CrossRef]
- Zen, M.T.; Hadikusumo, D. The future danger of Mt. Kelut (eastern Java-Indonesia). B. Volcanol. 1965, 28, 275–282. [Google Scholar] [CrossRef]
- Cassidy, M.; Ebmeier, S.K.; Helo, C.; Watt, S.F.L.; Caudron, C.; Odell, A.; Spaans, K.; Kristianto, P.; Triastuty, H.; Gunawan, H.; et al. Explosive Eruptions With Little Warning: Experimental Petrology and Volcano Monitoring Observations From the 2014 Eruption of Kelud, Indonesia. Geochem. Geophy. Geosy. 2019, 20, 4218–4247. [Google Scholar] [CrossRef]
- Nakashima, Y.; Heki, K.; Takeo, A.; Cahyadi, M.N.; Aditiya, A.; Yoshizawa, K. Atmospheric resonant oscillations by the 2014 eruption of the Kelud volcano, Indonesia, observed with the ionospheric total electron contents and seismic signals. Earth Planet. Sc. Lett. 2016, 434, 112–116. [Google Scholar] [CrossRef]
- Goode, L.R.; Handley, H.K.; Cronin, S.J.; Abdurrachman, M. Insights into eruption dynamics from the 2014 pyroclastic deposits of Kelut volcano, Java, Indonesia, and implications for future hazards. J. Volcanol. Geoth. Res. 2019, 382, 6–23. [Google Scholar] [CrossRef]
- Suzuki, Y.J.; Iguchi, M. Determination of the mass eruption rate for the 2014 Mount Kelud eruption using three-dimensional numerical simulations of volcanic plumes. J. Volcanol. Geoth. Res. 2017. [Google Scholar] [CrossRef]
- Global Volcanism Program. Report on Calbuco (Chile). In Weekly Volcanic Activity Report, 22 April–28 April 2015; Sennert, S.K., Ed.; Smithsonian Institution; U.S. Geological Survey: Reston, VA, USA, 2015. [Google Scholar]
- Poffo, D.A.; Caranti, G.M.; Comes, R.A.; Rodriguez, A. A new ash concentration estimation method using polarimetric data: The RMA observation of the 2015 Calbuco eruption. Remote Sens. Appl. Soc. Environ. 2018. [Google Scholar] [CrossRef]
- Hayes, J.L.; Calderón B., R.; Deligne, N.I.; Jenkins, S.F.; Leonard, G.S.; McSporran, A.M.; Williams, G.T.; Wilson, T.M. Timber-framed building damage from tephra fall and lahar: 2015 Calbuco eruption, Chile. J. Volcanol. Geoth. Res. 2019, 374, 142–159. [Google Scholar] [CrossRef]
- Hayes, J.L.; Wilson, T.M.; Stewart, C.; Villarosa, G.; Salgado, P.; Beigt, D.; Outes, V.; Deligne, N.I.; Leonard, G.S. Tephra clean-up after the 2015 eruption of Calbuco volcano, Chile: A quantitative geospatial assessment in four communities. J. Appl. Volcanol. 2019, 8, 7. [Google Scholar] [CrossRef]
- Mastin, L.G. Testing the accuracy of a 1-D volcanic plume model in estimating mass eruption rate. J. Geophys. Res-Atmos. 2014, 119. [Google Scholar] [CrossRef]
- Castruccio, A.; Clavero, J.; Segura, A.; Samaniego, P.; Roche, O.; Le Pennec, J.-L.; Droguett, B. Eruptive parameters and dynamics of the April 2015 sub-Plinian eruptions of Calbuco volcano (southern Chile). B. Volcanol. 2016, 78, 62. [Google Scholar] [CrossRef]
- Sarna-Wojcicki, A.M.; Shipley, S.; Waitt, R.; Dzurisin, D.; Wood, S.H. Areal distribution, thickness, mass, volume, and grain size of air-fall ash from the six major eruptions of 1980. In The 1980 Eruptions of Mount St. Helens, Washington; U.S. Geological Survey Professional Paper 1250; Lipman, P.W., Christiansen, R.L., Eds.; U.S. Government Printing Office: Washington, DC, USA, 1981; pp. 577–601. [Google Scholar]
- Folch, A.; Costa, A.; Durant, A.; Macedonio, G. A model for wet aggregation of ash particles in volcanic plumes and clouds: 2. Model application. J. Geophys. Res. 2010, 115, B09202. [Google Scholar] [CrossRef]
- Kristiansen, N.I.; Stohl, A.; Prata, A.J.; Bukowiecki, N.; Dacre, H.; Eckhardt, S.; Henne, S.; Hort, M.C.; Johnson, B.T.; Marenco, F.; et al. Performance assessment of a volcanic ash transport model mini-ensemble used for inverse modeling of the 2010 Eyjafjallajökull eruption. J. Geophys. Res. 2012, 117, D00U11. [Google Scholar] [CrossRef]
- Moxnes, E.D.; Kristiansen, N.I.; Stohl, A.; Clarisse, L.; Durant, A.; Weber, K.; Vogel, A. Separation of ash and sulfur dioxide during the 2011 Grímsvötn eruption. J. Geophys. Res-Atmos. 2014. [Google Scholar] [CrossRef]
- Zidikheri, M.J.; Lucas, C.; Potts, R.J. Estimation of optimal dispersion model source parameters using satellite detections of volcanic ash. J. Geophys. Res-Atmos. 2017, 122, 8207–8232. [Google Scholar] [CrossRef]
- Hort, M. VAAC Operational Dispersion Model Configuration Snap Shot: Version 3. Available online: https://www.wmo.int/aemp/sites/default/files/VAAC_Modelling_OperationalModelConfiguration-2018.pdf (accessed on 26 May 2020).
- Costa, A.; Suzuki, Y.J.; Cerminara, M.; Devenish, B.J.; Ongaro, T.E.; Herzog, M.; Van Eaton, A.R.; Denby, L.C.; Bursik, M.; de’ Michieli Vitturi, M.; et al. Results of the eruptive column model inter-comparison study. J. Volcanol. Geoth. Res. 2016, 326, 2–25. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Eruption start (UTC) | 15 June 1991, 05:30 UTC * |
| vent latitude | 15.133° N |
| vent longitude | 120.350° E |
| Eruption duration (hrs) | 9:00 |
| max. plume height (km asl) | 35 † |
| erupted volume (km3 DRE) | 8 * |
| erupted mass (kg) ** | 2 × 1013 |
| umbrella cloud-top height (km asl) | 25 † |
| k (no umbrella) | 8 |
| k (with umbrella) | 12 |
| Diffusivity (K, m2 s−1) | 0 †† |
| horizontal nodal spacing (deg.) | 0.2 |
| vertical nodal spacing (km) | 2 |
| Grain size, shape, density‡ | single particle size, 0.01 mm, density = 2000 kg m−3, F = 0.44 |
| C (m3 kg−3/4 s−3/2) | 430 |
| N (s−1) | 0.02 ‡‡ |
| λ | 0.2 ‡‡ |
| Meteorological model used | European Centre for Medium-range Weather Forecasts (ECMWF) ERA5 model |
| Parameter | Value |
|---|---|
| Eruption start (UTC) | 13 February 2014, 16:12 UTC * |
| vent longitude | 112.308° E |
| vent latitude | −7.903° N |
| Eruption duration (hrs) | 2:00 |
| max. plume height (km asl) | 25 ** |
| erupted volume (km3 DRE) | 0.25 † |
| erupted mass (kg) | 6.3 × 1011 |
| umbrella cloud-top height (km asl) | 19 ** |
| k (no umbrella) | 8 |
| k (with umbrella) | 12 |
| Diffusivity (K, m2 s−1) | 0 |
| horizontal nodal spacing (deg.) | 0.2 |
| vertical nodal spacing (km) | 2 |
| Total grain-size distribution | single particle size, 0.01 mm, density = 2000 kg m−3, shape factor F = 0.44 |
| C (m3 kg−3/4 s−3/2) | 430 |
| N (s−1) | 0.02 †† |
| λ | 0.2 |
| Meteorological model used to provide the wind field | ECMWF ERA5 |
| Phase 1 | Phase 2 | |
|---|---|---|
| Eruption start (UTC) | 22 April, 21:04 | 23 April, 04:01 |
| vent latitude | −41.326N | same |
| vent longitude | −72.614E | same |
| Eruption duration | 1:31 | 6:14 |
| max. plume height (km asl) | 25 | 25 |
| erupted volume (km3 DRE) | 0.033 * | 0.12 * |
| erupted mass (kg) | 8 × 1010 | 3 × 1011 |
| umbrella cloud height (km asl) | 16 | 16 |
| k (no umbrella) | 8 | 8 |
| k (with umbrella) | 12 | 12 |
| Diffusivity (K, m2 s−1) | 0 | 0 |
| horizontal nodal spacing (deg.) | 0.05 | 0.05 |
| vertical nodal spacing (km) | 2 | 2 |
| TGSD for cloud simulations | single particle 0.01 mm, density = 2000 kg m−3 shape factor F = 0.44 | same |
| TGSD for deposit simulations | see Table 4 † | see Table 4 † |
| C (m3 kg−3/4 s−3/2) | 870 | 870 |
| N (s−1) | 0.02 ** | 0.02 ** |
| λ | 0.1 | 0.1 |
| Meteorological model used to provide the wind field | ECMWF ERA5 | ECMWF ERA5 |
| Diameter mm | Mass Fraction | Density kg m−3 | Shape Factor F |
|---|---|---|---|
| 2 | 0.0611 | 800 | 0.44 |
| 1 | 0.07098 | 1040 | 0.44 |
| 0.5 | 0.22701 | 1280 | 0.44 |
| 0.25 | 0.21868 | 1520 | 0.44 |
| 0.1768 | 0.05326 | 1640 | 0.44 |
| 0.125 | 0.04039 | 1760 | 0.44 |
| 0.088 | 0.02814 | 1880 | 0.44 |
| 0.2176 | 0.018 | 600 | 1.0 |
| 0.2031 | 0.072 | 600 | 1.0 |
| 0.1895 | 0.12 | 600 | 1.0 |
| 0.1768 | 0.072 | 600 | 1.0 |
| 0.1649 | 0.018 | 600 | 1.0 |
| Pinatubo | Kelud | Calbuco Phase 2 | |||||||
| MER | ~6 × 108 kg s−1 | 6–13 × 107 kg s−1 | 9–16 × 107 kg s−1 | ||||||
| Volume | ~8 km3 DRE | ~0.25 km3 DRE | ~0.15 km3 DRE | ||||||
| Cloud Areas, thousand km2 | |||||||||
| Umb | None | Obs | Umb | None | Obs | Umb | None | Obs | |
| Eruption end | 851 | 385 | 883 | 53.2 | 23.3 | 34–49 | 100 | 64 | 60–77 |
| After 24 h | 2336 | 1887 | N/A | 565 | 589 | N/A | 530 | 533 | N/A |
| Performance | better | slightly better | slightly worse | ||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mastin, L.G.; Van Eaton, A.R. Comparing Simulations of Umbrella-Cloud Growth and Ash Transport with Observations from Pinatubo, Kelud, and Calbuco Volcanoes. Atmosphere 2020, 11, 1038. https://doi.org/10.3390/atmos11101038
Mastin LG, Van Eaton AR. Comparing Simulations of Umbrella-Cloud Growth and Ash Transport with Observations from Pinatubo, Kelud, and Calbuco Volcanoes. Atmosphere. 2020; 11(10):1038. https://doi.org/10.3390/atmos11101038
Chicago/Turabian StyleMastin, Larry G., and Alexa R. Van Eaton. 2020. "Comparing Simulations of Umbrella-Cloud Growth and Ash Transport with Observations from Pinatubo, Kelud, and Calbuco Volcanoes" Atmosphere 11, no. 10: 1038. https://doi.org/10.3390/atmos11101038
APA StyleMastin, L. G., & Van Eaton, A. R. (2020). Comparing Simulations of Umbrella-Cloud Growth and Ash Transport with Observations from Pinatubo, Kelud, and Calbuco Volcanoes. Atmosphere, 11(10), 1038. https://doi.org/10.3390/atmos11101038







