Abstract
The processes removing aerosols from the atmosphere during rainfall are generically referred to as scavenging. Scavenging influences aerosol distributions in the atmosphere, with consequent effects on cloud properties, radiative forcing, and human health. In this study, we investigated the below-cloud scavenging process, specifically focusing on the scavenging of 0.2 to 2 µm-sized microbial aerosols by populations of water drops with average diameters of 3.0 and 3.6 mm. Rainfall was simulated in convective boundary layer air masses by dispensing the water drops from a 55 m bridge and collecting them at ground level. Particles and microbial cells scavenged by the water drops were visualized, enumerated, and sized using scanning electron and epifluorescence microscopy. Aerosolized particles and DNA-containing microbial cells of 2 µm diameter were scavenged at efficiencies similar to those reported previously in empirical studies; however, the efficiencies derived for smaller aerosols were significantly higher (one to three orders of magnitude) than those predicted by microphysical modeling. Application of the derived scavenging efficiencies to cell data from rainfall implies that, on average, approximately 50 to 70% of the 1 µm microbial cells in the precipitation originated from within the cloud. Further study of submicron to micron-sized aerosol scavenging over a broader raindrop size distribution would improve fundamental understanding of the scavenging process and the capacity to estimate (bio)aerosol abundances in the source cloud through analysis of rainfall.
1. Introduction
Particles aerosolized from natural and anthropogenic sources are transported horizontally and vertically in the atmosphere, where they can have direct effects on the formation of clouds and precipitation by serving as cloud condensation and ice nuclei, respectively [1]. In-cloud water droplets that form around aerosols (i.e., in the wet phase) are deposited in precipitation together with aerosols that are scavenged by rain drops as they descend through the atmosphere. In fact, the scavenging of aerosols by rain drops is the major process of particle deposition from the troposphere [2]. As such, knowledge of wet deposition processes is vital for understanding its consequences on global distributions and concentrations of aerosols in the atmosphere.
Multiple mechanisms are involved in aerosol scavenging by rain drops, including inertial impaction, Brownian diffusion, and interception [1,3]. Aerosol scavenging simulations that consider these mechanisms are generally in good agreement with empirical observations for the scavenging of particles <0.1 and >1 µm in diameter [4]. However, the predictive value of existing models is limited because they significantly underestimate scavenging efficiencies for particles that are within the “scavenging gap” (0.1–1 µm in diameter) [5,6,7]. The scavenging gap paradox is specifically related to particles of this size because their diameters are too small to experience inertial impaction and too large to be subject to Brownian diffusion [5]. Based on these assumptions, models considering scavenging gap-sized aerosols infer interception to be the primary mode of scavenging by drops [3]. In this process, the particle impacts the surface of the drop after following streamlines of a distance equal to the particle’s radius [8]. Additional mechanisms expected to affect the scavenging process include thermo-, electro-, and diffusio-phoresis, whereby differences in temperature, charge, and presence of a gas concentration gradient, respectively, induce particle motion [9,10,11].
An improved understanding of the scavenging gap phenomenon is highly relevant to aerobiology since the majority of microbial aerosols are within or near this size range [12,13,14]. In addition to the role of wet deposition in dissemination of microbiota, there is evidence that certain bioaerosols may play roles in the formation of precipitation by serving as efficient ice nucleating particles [15,16,17,18]. Since logistical challenges have limited opportunities to study microorganisms in cloud water droplets, the characterization of microbes in precipitation is often used as a proxy for cloud water compositions [19]. However, experimental data support that bacteria and fungi are scavenged from the atmosphere during precipitation events [20,21], complicating efforts to infer cloud water compositions from rainfall. The wet deposition process for bacterial-sized aerosols is poorly constrained by empirical data, and to our knowledge, scavenging of micron-to sub-micron- sized aerosols has not been experimentally examined for drop diameters outside of the 2–2.6 mm range. Therefore, new data are necessary to validate the veracity of predictions by scavenging models for the range of bioaerosol sizes observed in the atmosphere [22].
This study examined the efficiency at which two water drop sizes captured 0.2 to 2 µm aerosols while descending through the atmosphere, with the specific objective of deriving data relevant for understanding wet deposition processes of microorganisms and similarly sized particles. The drop sizes (average equivalent diameters of 3.0 and 3.6 mm) used in these experiments are similar to those typically observed in thunderstorms that form from melting ice particles [2]. The scavenging efficiencies we derived provide the first empirical observations for aerosol sizes that are typical for most bacteria [14] and fall within the “scavenging gap” [5]. We discuss the implications of our findings for understanding wet scavenging of microbial bioaerosols in the atmosphere and how inverse modeling may be used to estimate bioaerosol abundances in precipitating source clouds.
2. Materials and Methods
2.1. Site Description
The field site for this study is located at the Virginia Tech Transportation Institute Smart Road Bridge (SRB) in Blacksburg, VA (USA). The location on the SRB where experiments were performed is 55 m above ground level. Further detail on the site is provided in Hanlon et al. [20].
2.2. Simulated Rain Events
Eight simulated rain events (SREs) were generated using two commercially available ~10 L watering cans (Gardener’s Supply, # 06-341). The cans have interchangeable stainless-steel rose heads, which were modified so that two size populations of water drops could be generated (the holes were 1.65 ± 0.02 mm and 1.04 ± 0.02 mm in diameter). Each watering can was cleaned using detergent and rinsed thoroughly with deionized water. Prior to each experiment, the watering cans were flushed with 2 L of 0.22 µm-filtered deionized water to reduce contributions of contaminating cells and particles to the measurements.
Six liters of 0.22 µm-filtered deionized water was poured from the watering cans during each experiment, and a total of ~1 L of each sample was successfully recovered ~2 m above ground in three 117 L galvanized cans (Home Depot, cat #001223296) that were lined with sterile polypropylene bags (Fisher #01-830E, 122 cm × 94 cm). Each SRE was approximately the same duration (mean of 41 s). After collection, the water was transferred to sterile 1-L Nalgene bottles (Nalgene #2187-0032) and chilled on ice. Immediately after return to the laboratory (~4 h), the water samples were fixed by the addition of formalin to a final concentration of 4% (v/v), stored at 4 °C, and processed within 30 days of collection.
To determine the mean volumes of the drop populations, two of the SREs (7 and 8, watering cans with 1.65 ± 0.02 mm and 1.04 ± 0.02 mm diameter holes, respectively) were collected in a dewar containing liquid nitrogen [23] and processed as described previously [20]. Briefly, the frozen water drops collected in the liquid nitrogen were recovered and placed into individual microcentrifuge tubes. These drops were then thawed and their volume was determined using a micropipette [23].
Procedural blanks were prepared for each SRE and analyzed in parallel to assess the level of background microbe and particle contamination associated with the measurements. The controls used the same water source as the SREs but were poured directly into a bag-lined galvanized can, collected, and analyzed.
2.3. Measurement of Ambient Particulate Matter
Two Plantower PMS7003 particle sensors and two Nova Fitness SD021 particle sensors were positioned adjacent to where the SREs were deployed from the top of the bridge. Both sensors measure particulate matter between 0.3 and 10 µm in diameter. Data were continuously collected during the experiments, with the Plantower PMS7003 measuring ambient particulate matter (PM) ≤1, ≤2.5, and ≤10 µm in diameter, and the Nova Fitness SD021 measuring PM ≤ 2.5, and ≤10 µm. The particulate matter data are expressed by weight (µg m−3).
2.4. Characterization of Microbial Cells and Particles
To enumerate DNA-containing cells, triplicate 10 mL samples from each SRE and control were stained with a final concentration of 25× SYBRTM Gold (Life Technologies Corp., cat. no. S-11494) in the dark for 15 min. The samples were then filtered onto black, 25 mm diameter 0.22 μm polycarbonate Isopore™ filters (Millipore, cat. no. GTTP04700). A 4 μL drop of antifade (1:1 solution of glycerol and PBS, 0.1% phenylenediamine) was added to each of the filters before coverslips were mounted. A Nikon ECLIPSE Ni epifluorescence microscope was used to visualize and enumerate the DNA-containing microbial cells in sixty random fields of view (FOV, area of 1.8 × 104 μm2) on each filter. NIS-Elements Advanced Research software (Nikon, Inc., Tokyo, Japan) was used to automatically trace and measure the cells in each FOV. Cells that were present as aggregates were not individually counted; each aggregate was sized and considered a single particle [24].
For particle characterization, triplicate 10 mL samples from eight SREs and controls were filtered onto white, 25 mm diameter 0.22 µm polycarbonate filters (GE Water & Process Technologies, cat. no. K02CP02500) and sputter coated with gold palladium for 1.5 min [12]. Particles were visualized using a Hitachi SU5000 Schottky Field-Emission scanning electron microscope under high vacuum mode. Sixty random FOVs (69 μm2 each) from each filter were imaged at a voltage of 11–12 kV and the particle area was traced and analyzed using ImageJ software [12,25]. Particles that appeared aggregated were counted as a single particle [24].
Particle and cell area was used to calculate equivalent diameters according to the following formula [24]:
Equivalent diameter = √(4 × area/π)
Particle and cell concentration per SRE sample was calculated based on the average number of objects per FOV, filtration area (226.9 mm2), and sample volume (10 mL). Particles and cells with equivalent diameters of 0.2 to 2 µm were binned into 10 categories of 0.2 µm increments. For each size bin where the sample and control concentrations were significantly different, the mean number of objects (particles or cells) per FOV in the controls were subtracted from the mean number of objects per FOV in the samples. The binned number concentrations were used to estimate particle and cell mass by assuming a particle density of 1.0 g cm−3 and cell density of 1.1 g cm−3 [26,27].
2.5. Ambient Particulate Size Distribution
The size distribution of ambient aerosols 0.2 to 2 µm in diameter was estimated by Equation (2) [28]:
where n is the number of particles cm−3 of radius r (µm) and Φ is the volume of particles per unit volume of air sampled. This equation is based on Junge’s power law [29] and creates size distribution curves that have been shown to agree well with empirical measurements of aerosols with radii >0.05 µm [24,28,29]. PM10 measurements taken during each SRE (W) and the particle density estimated per unit volume (ρ) were utilized in the calculation of Φ (Φ = W/ρ; [28]). The mass concentration distribution of ambient particles was inferred from the number concentration distribution and assuming a density of 1.0 g cm−3 [27]. Cell mass and number distribution was estimated from the ambient particle distribution, the cell to particle ratio observed by bin in the 3.6 mm drops (Tables S1 and S2), and assuming a cell density of 1.1 g cm−3 [26].
n(r) = 0.05 × Φ × r−4
2.6. Calculation of Scavenging Efficiencies
The efficiency of drop scavenging was calculated according to Equation (3) [11]:
where E is the scavenging efficiency for a drop of diameter D, [PM]drop is mass concentration (µg m−3) for particles of diameter d in the drop, H is the fall height of the drop, and [PM]air is the mass concentration (µg m−3) of particulate matter of diameter d in the ambient air (Equation (2)).
E = (2 × D × [PM]drop)/(3 × H × [PM]air)
2.7. Application of the Scavenging Efficiencies to Rain Data
The capture cross-section of a droplet, namely E × π × D2/4 [21], was used to estimate the volume of air scavenged by a drop (V) falling from a cloud-base height of B (in meters). This was calculated according to Equation (4):
V = (π × D2)/(4 × E × B)
The number of particles or cells removed from the air column below the cloud by a single drop was estimated by multiplication of V by the number of ambient particles or cells m−3.
To assess the contribution of scavenging to the microbes deposited in rain at the surface, the fraction of cells scavenged and that originated from the precipitating cloud was estimated using select events from a two-year record of rainfall data from Baton Rouge, Louisiana [30]. Following Marshall and Palmer’s [31] drop-size distributions derived from rain rates, 13 rain events were chosen for the scavenging calculations, representing end members of rain rates (mean 2.8 mm h−1, n = 7; and 14.5 mm h−1, n = 6) that would be expected to contain drop sizes relevant to this study (average equivalent diameter of 3.0 and 3.6 mm). The cloud-base heights for both subsets of storms ranged from 100 to 1160 m above ground level, and the cell concentrations in the rain samples ranged from 8.45 × 104 to 1.3 × 106 cells L−1 [30]. Using Equation (2), the number of 1 µm bioaerosols (in cells m−3) for each rain event was estimated based on the 24-h average PM10 records for Baton Rouge (US Environmental Protection Agency daily records, https://www.epa.gov/outdoor-air-quality-data). The estimated number of cells scavenged by each rain drop size was based on the cloud-base height for each rain event, the capture cross-section of each raindrop, and the concentration of 1 µm bioaerosols (Equation (4)). The difference between the number of scavenged cells per liter of drops and the cell density in each rain sample provides an estimate for the number of cells that originated from the cloud (As compared to below-cloud).
2.8. Statistical Analyses
R Software Version 3.5.1 [32] was used for all statistical analyses. Differences between concentration, volume, and efficiencies were determined using Student’s t-tests (base R). Analysis of variance (ANOVA) was utilized to test the differences between measured and calculated ambient particle concentrations. Scavenging efficiency models were produced and plotted with the ggplot2 package [33]. The models were fit with the stat_smooth function using the linear model method and the y = x + x2 formula [34].
3. Results
3.1. Water Drop Volumes
Hundreds of drops generated from two dispensing cans with different hole sizes (1.04- and 1.65-mm diameter) were recovered in liquid nitrogen from SRE 7 and 8 (Table 1). From these populations, the volume of randomly selected drops from SRE 7 (n = 56) and SRE 8 (n = 52) was measured. Mean drop volumes of 14.6 ± 1.6 μL and 25.0 ± 1.9 μL (± standard error of the mean) from the small and large holes, respectively, in the dispensing cans were significantly different (t-test, p < 0.001). Assuming a sphere, the drop volumes correspond to equivalent diameters of 3.0 ± 1.5 mm and 3.6 ± 1.5 mm (Figure 1).

Table 1.
Total particle, cell, and environmental data from simulated rain events. The total particles and cells scavenged (0.2 to 2 µm in diameter) are average concentrations ± standard error of the mean, n = 3. (EDT: Eastern Daylight Time).
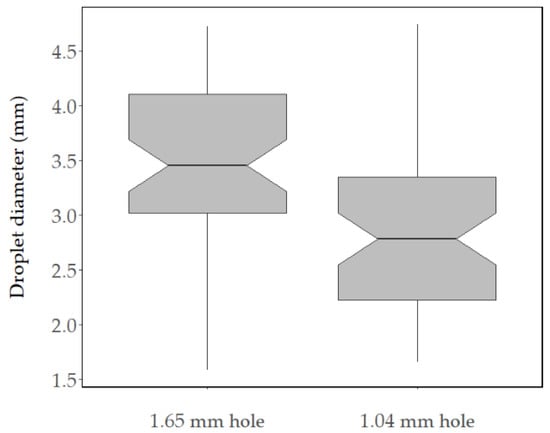
Figure 1.
The diameter of sampled drop populations, inferred by volume, based on the size (1.65 or 1.04 mm) of the holes in the rose head. Boxes represent the interquartile range, with the middle horizontal line indicating the median, and whiskers represent the minimum and maximum values.
3.2. Ambient Particulate Size Distribution
Ambient PM10 concentrations measured during the experiments were not statistically different (t-test, p > 0.05) and averaged 22 ± 4 μg m−3. Using this value and Equation (2), the number distribution of particles m−3 was determined (Figure 2). The concentration of ambient particles and cells were estimated from this distribution as described in Section 2.5 (Figure 2).
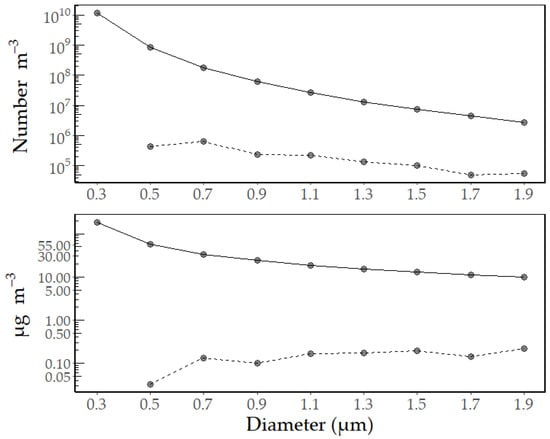
Figure 2.
Inferred size distribution of the number and mass concentration of total ambient particulates (solid line) and microbial cells (dashed line). Standard error of the mean = ±10%, n = 4.
The PM10 mass concentration distribution (Figure 2) in the sampled air masses are consistent with the Environmental Protection Agency Air Quality Index category “Good” and indicative of relatively low anthropogenic emissions. Inferred biomass was highly similar across the size bins, but inferred cell concentrations were highest for cells <1 µm in diameter. The estimated µg m−3 distribution (Figure 2) was not statistically different (ANOVA, p = 0.99) from measured values of PM10, PM2.5, and PM1 sampled during the SREs (Figure S1). Based on these results, the calculated µg m−3 distribution was used in the scavenging efficiency calculations.
3.3. Cell and Particle Scavenging
Based on data from the procedural controls and a limit of detection at 3-sigma, our method allowed detection of 9.0 × 102 cells and 6.5 × 105 particles mL−1. The concentrations of particles (raw mean 1.0 ± 0.18 × 106 mL−1) and cells (raw mean 2.0 ± 0.049 × 104 mL−1) in samples for the 3.6 mm drops were above the level of detection and significantly different (t-test, p < 0.001) from the procedural controls (background average 2.1 ± 1.1 × 102 cells and 3.5 ± 0.70 × 105 particles mL−1). For samples of the 3.0 mm drops, the raw concentrations of cells (raw mean 1.3 ± 0.18 × 103 cells mL−1) were also above the level of detection and significantly different from the background concentrations; however, the particle data (raw mean 5.8 ± 1.1 × 105 particles mL−1) were only above the level of detection in the 0.6 to 0.8 and 1.4 to 1.6 µm diameter size bins. Background concentrations were subtracted from the raw sample concentrations for all size bins that were above the level of detection (Figure 3).
Figure 3.
Total particles (triangle) and DNA-containing cells (circle) scavenged per mL of 3.6 (blue) or 3.0 (red) mm drops. The data are binned by particle/cell diameter (µm), as described in Section 2.5. Error bars indicate standard error of the mean, n = 4.
Particle abundance between individual size bins was significantly different based on drop size (t-test, p < 0.01). The concentrations of 0.2 to 2 µm particles collected by the 3.0-and 3.6-mm drops averaged 1.4 ± 0.42 × 105 and 7.3 ± 1.4 × 105 particles mL−1, respectively (Figure 3, Tables S1 and S2). This equates to 1.0 ± 0.29 × 104 and 3.0 ± 0.55 × 104 particles scavenged per 3.0-or 3.6-mm drop (Table 1), respectively, while descending 53 m in the atmosphere. Bulk samples of the 3.0-and 3.6-mm drops contained 0.4 to 2 µm cells at average concentrations of 9.9 ± 2.7 × 102 and 1.8 ± 0.42 × 103 cells mL−1, respectively (Figure 3, Tables S1 and S2). This corresponds to 68 ± 18 and 73 ± 17 cells scavenged per 3.0-or 3.6-mm drop, respectively, during the experiments.
The scavenging efficiencies of particles and cells collected by the 3.6 mm drops showed an identical trend, with minimum values observed for the smallest particle and cell diameters (Figure 4, Tables S1 and S2). The scavenging efficiencies of 3.6 mm drops for cells and particles with mean diameters 0.5 to 1.9 µm were not significantly different (p > 0.05) (Tables S1 and S2). Similarly, scavenging efficiencies of 3.0 mm drops were not significantly different between cells and particles within the 0.6 to 0.8 and 1.4 to 1.6 µm bins (p > 0.05) (Tables S1 and S2). Therefore, the particle and cell data were combined and fitted to quadratic models to examine the difference in scavenging efficiencies between the 3.0-and 3.6-mm drops (Figure 4). The highest scavenging efficiencies for both drop sizes were for the largest (2 µm) particles, and the efficiency decreased exponentially with particle size. The efficiency at which 3.6 mm drops scavenged particles in the 0.4 to 2 µm size range was ~twofold higher than the 3.0 mm drops.
Figure 4.
Scavenging collection efficiencies (all technical replicates from eight SREs) derived for particles and cells collected by 3.6 mm and 3.0 mm drops. The data were fitted to quadratic models (solid lines) and are provided in supplemental Tables S1 and S2. The grey shaded regions indicate 95% confidence intervals.
To explore the contribution of scavenged bioaerosols to cell concentrations in precipitation, we used select events from a published precipitation dataset collected in Louisiana [30]. We assumed the majority of bacterial-sized aerosols were 1 µm in diameter and used the corresponding modelled scavenging efficiencies for 3.0-and 3.6-mm drops to infer source contributions from scavenging versus the precipitating cloud (Table 2). Low intensity rain events are associated with smaller drops (1 to 2 mm), whereas moderate to heavy rainfalls can produce larger drops (1 to 4 mm) [2]. Our analysis implies higher scavenging of cell sizes within the scavenging gap range for larger drop sizes and rainfall intensities. For example, calculations based on the lowest intensity rainfalls (2.8 mm h−1) suggest 27% of cells in precipitation were scavenged by drops below the cloud, whereas higher intensity rainfalls (14.5 mm h−1) had higher rates of scavenging (45%; Table 2). Nevertheless, our data and related calculations imply that the majority of cells in these rain samples originated from the source cloud.

Table 2.
Effect of drop size and rain intensity on cell scavenging. The proportion of cells in Louisiana rain samples that were scavenged below-cloud (%S) or originated from the cloud (%C) were estimated using the scavenging efficiencies in Figure 4. Rain data are from [29].
4. Discussion
A number of phoretic forces are known to affect scavenging of particles within the scavenging gap range. The negative surface charge possessed by bacterial cells could potentially influence drop scavenging through electrophoresis [6]. Nonetheless, we observed no significant differences in drop scavenging of microbial cells and particles with mean equivalent diameters of 0.5 to 1.9 µm (Figure 4). Diffusiophoresis can occur during drop evaporation, with a higher concentration of water vapor nearest the evaporating drop resulting in particle motion away from the drop [1]. Thermophoresis is also possible if there is a temperature gradient between the drop and the surrounding air. For example, aerosols may be attracted toward an evaporating drop that becomes colder at its surface. However, phoretic effects are generally thought to be negligible unless there is a steep temperature or gas gradient (e.g., >1 °C difference between the drop surface and air temperature) [1,35]. Brownian diffusion may also effect scavenging by bringing a particle into contact with a drop, and this random motion is important for the scavenging of particles <0.2 µm in diameter [1]. For aerosol particles >2 µm in diameter, chemical composition may affect scavenging rates; however, its effects may be negligible for the particle sizes examined in this study [36]. Considering this, the most relevant scavenging mechanism applicable to particles with equivalent diameters of 0.2 to 2 μm is interception.
Drop scavenging of particles in the scavenging gap size range (Figure 4) occurs at much higher efficiencies than the model predictions of Quérel et al. [22] and Slinn [3] (Figure S2). The scavenging efficiencies derived for the 3.0 and 3.6 mm drops were at least an order of magnitude greater than those predicted in the DESCAM model (Figure S2; DEtailed SCavening Model, [11,22]). For example, the DESCAM model efficiency for 0.81 µm diameter particles is 9.30 × 10−4 for 3.25 mm drops, whereas observed efficiencies for 3.0 and 3.6 mm drops are 2 × 10−2 and 4 × 10−2, respectively (Figure S2) [22]. The empirically derived drop scavenging efficiencies are also ~600-fold higher than those for 3.6 mm drops using the interception term from the Slinn model (Figure S2) [37]. This is consistent with previous studies that have observed scavenging efficiencies for particles within the scavenging gap one to five orders of magnitude greater than efficiencies predicted using the Slinn model [7,10,37,38]. Volken and Schumann [39] and Chate and Pranesha [10] suggest that some of the mechanisms neglected in current models (e.g., phoretic forces and the growth of hygroscopic aerosol particles) may explain the discrepancies. Nevertheless, attempts to incorporate parameters that may be relevant (i.e., thermophoresis, diffusiophoresis, and electric forces) have not improved the predictive value of models for particles within the scavenging gap [10].
Rain drops in many precipitation events are 1 to 3 mm in diameter, with larger drops typically forming from melting ice particles produced by convective storms [2,31]. The drop diameters (3.0 and 3.6 mm) examined in this study are relevant for low to moderately intense rainfall rates in the range of 2.5–25 mm h−1 [31,40]. There have been few empirical data available on scavenging within the scavenging gap by drops of known diameters. For example, our results generally agree with those measured during natural rainfall events [6,7]; however, the lack of drop diameter data makes direct comparisons difficult. Also notable is the work of Pranesha and Kamra [41], who examined large water drops (3.6, 4.2, and 4.8 mm diameter) and the scavenging of particles 1.9 to 6.4 µm diameter. The scavenging efficiency they found for 3.6 mm drops of 1.9 µm diameter particles (~3 × 10−1) is similar to our estimate (2 × 10−1; Figure S2). Although below-cloud scavenging of bacterial and fungal bioaerosols has been studied previously [20], there have been no measurements of drop scavenging efficiencies for particles that are representative of bacterial cell sizes <2 μm.
Based on the drop population sizes tested in this study, scavenging efficiency increases with drop diameter (Figure 4). This relationship has been observed previously [42,43,44], but it is not consistent with all studies. For example, Pranesha and Kamra [41] observed a decrease in collection efficiency of particle diameters 1.9 to 6.4 µm with increasing drop size (3.6–4.8 mm). The Slinn model also predicts a decrease in collection efficiency with increasing drop size [37]. However, Hampl et al. [44] found that collection efficiency increased with increasing drop diameter (1.44 to 5.08 mm) for silver chloride aerosols with average diameters of 0.366 µm. The experimental data of Beard et al. [42] for scavenging of 0.38 to 4.4 µm particles by 0.28 to 1.24 mm drops also demonstrated increased efficiency with drop size. Furthermore, there were no discernable differences in the experimental collection efficiencies measured by Quérel et al. [22] for 2.0 to 2.62 mm drops, suggesting little to no difference between drop sizes. This collection of contrary results, generated under a variety of experimental conditions (e.g., temperature, relative humidity, drop charge, aerosol composition and diameter), makes clear the complexity of this phenomenon and need for future studies that examine scavenging under controlled experimental conditions [4,38].
In addition to improving understanding of bioaerosol removal by descending rain drops in the atmosphere, information about the scavenging process can be used to assess the fraction of particles in rain that originated from the source cloud. We used data on microbial cell concentrations from Louisiana rain [30] and the scavenging behaviors documented in this study to infer that the majority (55% to 73%) of 1 µm microbes in low to moderate rainfall intensity events originated from within the cloud (Table 2). When compared to low intensity rainfall, moderately intense rainfall produces larger drop sizes, which tend to be more efficient at scavenging below-cloud aerosols (Figure 4). Our results are consistent with recent observations showing the fungal composition of rain correlated with lower altitude characteristics of storms, whereas the smaller-sized bacteria assemblages correlated with macroscale drivers that implied nonlocal sources [45]. It should be noted our calculations have ignored the contribution of microbial aerosols within the cloud that are subject to scavenging as drops descend through the cloud. As such, we are likely overestimating the fraction of aerosols that are sourced from the wet phase of a cloud. Furthermore, since we did not consider the progressive reduction of aerosol concentration during each storm, the total aerosols scavenged per rain event are likely overestimated.
Various studies have leveraged the scavenging gap in attempts to estimate the concentration of particles and microbial cells in cloud water based on precipitation data [19,30,46]. If, however, the contribution of below-cloud scavenging is much larger than currently appreciated, then the cloud contribution of particles and cells will be overestimated [19,46] and assumptions inherent to aerosol transport models [14,47] may be flawed. For example, the particle transport model utilized by Burrows et al. [48] incorporated Slinn model scavenging efficiencies on microbial-sized particles [49], which are roughly three orders of magnitude lower than the values we obtained (Figure S2). Hence, improved understanding of droplet scavenging efficiency for particles with diameters of 0.2 to 2 μm would allow atmospheric residence time estimates for microbial aerosols to be constrained with greater confidence.
5. Conclusions
Although we did not determine the composition of microorganisms or particles present in the air masses sampled, our results (Figure 4) indicate that microbial aerosol composition was less important than their equivalent diameter. Therefore, we speculate that altering the microbial species that compose the bioaerosols would not have a perceptible effect on scavenging. These experimental results are consistent with the limited number of data available from empirical studies (e.g., [41]), documenting order of magnitude discrepancies between experimentally-derived scavenging efficiencies and those widely used in simulation models [22,37]. Intrinsically, the assumptions on which a number of microphysical models are based severely underestimate PM2.5 deposition flux for wet processes. New observations of rain scavenging over a broader range of drop diameters would improve understanding of how precipitation that deposits microorganisms entrained in cloud water droplets affects aerosol distributions in the air masses underlying precipitating clouds, and controls removal of atmospheric particles that have important consequences on public health. To our knowledge, no studies have considered scavenging processes for submicron aerosols over the entire range of drop diameters found in rain (0.5–5 mm) [2]. Future investigations that examine the effect of environmental conditions (e.g., temperature and relative humidity), aerosol composition, and a wider range of drop sizes could lend valuable insight into the wet deposition process for aerosol sizes within the scavenging gap.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4433/11/1/80/s1, Figure S1: Comparison of measured (particle sensor data) with computed (Equation (2)) PM1, PM2.5-1, and PM10-2.5 values across all SREs, Figure S2: Comparison of the scavenging efficiencies derived in this study with published and modeled values, Table S1: Drop volumes, Table S2: Scavenging efficiencies from all replicates.
Author Contributions
B.C.C. and R.A.M. designed the research; R.A.M. assisted in field collections, collected/analyzed particle and cell data and led the writing of the manuscript. B.C.C., D.G.S.III., and R.H. coordinated and assisted in field collections. C.P. collected particulate matter data. All authors have read and agreed to the published version of the manuscript
Funding
This work was supported by the National Science Foundation [grant number DEB-1241068 and 1643288]. Any opinions, findings, and conclusions or recommendations expressed are from the authors and do not necessarily reflect the views of the NSF.
Acknowledgments
The authors thank K. Aho, K. Failor, H. Grothe, R. Joyce, and R. Pietsch for assistance with sample collection in the field.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Pruppacher, H.; Klett, J. Microphysics of Clouds and Precipitation, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-0-7923-4211-3. [Google Scholar]
- Slinn, W.G.N. Precipitation Scavenging; Division of Biomedical Environmental Research; U.S. Department of Energy: Washington, DC, USA, 1983.
- Santachiara, G.; Prodi, F.; Belosi, F. A Review of Termo- and Diffusio-Phoresis in the Atmospheric Aerosol Scavenging Process. Part 1: Drop Scavenging. Atmos. Clim. Sci. 2012, 2, 148–158. [Google Scholar] [CrossRef]
- Greenfield, S.M. Rain Scavenging of Radioactive Particulate Matter from the Atmosphere. J. Meteorol. 1957, 14, 115–125. [Google Scholar] [CrossRef]
- Chate, D.M. Study of scavenging of submicron-sized aerosol particles by thunderstorm rain events. Atmos. Environ. 2005, 39, 6608–6619. [Google Scholar] [CrossRef]
- Radke, L.F.; Hobbs, P.V.; Eltgroth, M.W. Scavenging of Aerosol Particles by Precipitation. J. Appl. Meteorol. 1980, 19, 715–722. [Google Scholar] [CrossRef]
- Ardon-Dryer, K.; Huang, Y.W.; Cziczo, D.J. Laboratory studies of collection efficiency of sub-micrometer aerosol particles by cloud droplets on a single-droplet basis. Atmos. Chem. Phys. 2015, 15, 9159–9171. [Google Scholar] [CrossRef]
- Tinsley, B.A.; Rohrbaugh, R.P.; Hei, M.; Beard, K.V. Effects of Image Charges on the Scavenging of Aerosol Particles by Cloud Droplets and on Droplet Charging and Possible Ice Nucleation Processes. J. Atmos. Sci. 2000, 57, 2118–2134. [Google Scholar] [CrossRef]
- Chate, D.M.; Pranesha, T.S. Field studies of scavenging of aerosols by rain events. J. Aerosol Sci. 2004, 35, 695–706. [Google Scholar] [CrossRef]
- Lemaitre, P.; Querel, A.; Monier, M.; Menard, T.; Porcheron, E.; Flossmann, A.I. Experimental evidence of the rear capture of aerosol particles by raindrops. Atmos. Chem. Phys. 2017, 17, 4159–4176. [Google Scholar] [CrossRef]
- Bryan, N.C.; Stewart, M.; Granger, D.; Guzik, T.G.; Christner, B.C. A method for sampling microbial aerosols using high altitude balloons. J. Microbiol. Methods 2014, 107, 161–168. [Google Scholar] [CrossRef]
- Després, V.; Huffman, J.; Burrows, S.M.; Hoose, C.; Safatov, A.; Buryak, G.; Fröhlich-Nowoisky, J.; Elbert, W.; Andreae, M.; Pöschl, U.; et al. Primary biological aerosol particles in the atmosphere: A review. Tellus B Chem. Phys. Meteorol. 2012, 64, 15598. [Google Scholar] [CrossRef]
- Burrows, S.M.; Elbert, W.; Lawrence, M.G.; Pöschl, U. Bacteria in the global atmosphere—Part 1: Review and synthesis of literature data for different ecosystems. Atmos. Chem. Phys. 2009, 9, 9263–9280. [Google Scholar] [CrossRef]
- Schnell, R.C.; Vali, G. Atmospheric Ice Nuclei from Decomposing Vegetation. Nature 1972, 236, 163–165. [Google Scholar] [CrossRef]
- Christner, B.C.; Morris, C.E.; Foreman, C.M.; Cai, R.; Sands, D.C. Ubiquity of biological ice nucleators in snowfall. Science 2008, 319, 1214. [Google Scholar] [CrossRef] [PubMed]
- Morris, C.E.; Georgakopoulos, D.G.; Sands, D.C. Ice nucleation active bacteria and their potential role in precipitation. J. Phys. IV (Proc.) 2004, 121, 87–103. [Google Scholar] [CrossRef]
- Möhler, O.; Demott, P.J.; Vali, G.; Levin, Z. Microbiology and Atmospheric Processes: The Role of Biological Particles in Cloud Physics. Biogeosci. Discuss. 2007, 4, 2559–2591. [Google Scholar] [CrossRef]
- Petters, M.D.; Wright, T.P. Revisiting ice nucleation from precipitation samples. Geophys. Res. Lett. 2015, 42, 8758–8766. [Google Scholar] [CrossRef]
- Hanlon, R.; Powers, C.; Failor, K.; Monteil, C.L.; Vinatzer, B.A.; Schmale, D.G. Microbial ice nucleators scavenged from the atmosphere during simulated rain events. Atmos. Environ. 2017, 163, 182–189. [Google Scholar] [CrossRef]
- McDonald, J.E. Collection and Washout of Airborne Pollens and Spores by Raindrops. Science 1962, 135, 435–437. [Google Scholar] [CrossRef]
- Quérel, A.; Monier, M.; Flossmann, A.I.; Lemaitre, P.; Porcheron, E. The importance of new collection efficiency values including the effect of rear capture for the below-cloud scavenging of aerosol particles. Atmos. Res. 2014, 142, 57–66. [Google Scholar] [CrossRef]
- Garcia, E.B.; Hanlon, R.; Makris, M.R.; Powers, C.W.; Jimenez-Sanchez, C.; Karatum, O.; Marr, L.C.; Sands, D.C.; Schmale, D.G. Microbial diversity of individual raindrops collected from simulated and natural precipitation events. Atmos. Environ. 2019, 209, 102–111. [Google Scholar] [CrossRef]
- Hinds, W.C. Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Bratbak, G.; Dundas, I. Bacterial dry matter content and biomass estimations. Appl. Environ. Microbiol. 1984, 48, 755–757. [Google Scholar] [CrossRef] [PubMed]
- Huffman, J.A.; Sinha, B.; Garland, R.M.; Snee-Pollmann, A.; Gunthe, S.S.; Artaxo, P.; Martin, S.T.; Andreae, M.O.; Pöschl, U. Size distributions and temporal variations of biological aerosol particles in the Amazon rainforest characterized by microscopy and real-time UV-APS fluorescence techniques during AMAZE-08. Atmos. Chem. Phys. 2012, 12, 11997–12019. [Google Scholar] [CrossRef]
- Clark, W.E.; Whitby, K.T. Concentration and Size Distribution Measurements of Atmospheric Aerosols and a Test of the Theory of Self-Preserving Size Distributions. J. Atmos. Sci. 1967, 24, 677–687. [Google Scholar] [CrossRef][Green Version]
- Junge, C.E. Air Chemistry and Radioactivity; Academic Press: Cambridge, MA, USA, 1963. [Google Scholar]
- Joyce, R.; Lavender, H.; Farrar, J.; Werth, J.T.; Weber, C.F.; D’Andrilli, J.; Vaitilingom, M.; Christner, B.C. Biological Ice-Nucleating Particles Deposited Year-Round in Subtropical Precipitation. Appl. Environ. Microbiol. 2019, 85, 1–21. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing 2018. R Foundation for Statistical Computing, Vienna, Austria. Available online: https://www.r-project.org/ (accessed on 4 January 2020).
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016; ISBN 978-3-319-24277-4. [Google Scholar]
- Cleveland, W.S.; Grosse, E.; Shyu, W.M. Local regression models. In Statistical Models in S; Springer: New York, NY, USA, 1992. [Google Scholar]
- Bae, S.Y.; Jung, C.H.; Kim, Y.P. Relative contributions of individual phoretic effect in the below-cloud scavenging process. J. Aerosol Sci. 2009, 40, 621–632. [Google Scholar] [CrossRef]
- Chate, D.M.; Devara, P.C.S. Parametric study of scavenging of atmospheric aerosols of various chemical species during thunderstorm and nonthunderstorm rain events. J. Geophys. Res. 2005, 110, D23208. [Google Scholar] [CrossRef]
- Slinn, W.G.N. Some approximations for the wet and dry removal of particles and gases from the atmosphere. Water Air Soil Pollut. 1977, 7, 513–543. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, L.; Moran, M.D. Uncertainty assessment of current size-resolved parameterizations for below-cloud particle scavenging by rain. Atmos. Chem. Phys. 2010, 10, 5685–5705. [Google Scholar] [CrossRef]
- Volken, M.; Schumann, T. A Critical review of below-cloud aerosol scavenging results on Mt. Rigi. Water Air Soil Pollut. 1993, 68, 15–28. [Google Scholar] [CrossRef]
- Houghton, D.D. Handbook of Applied Meteorology; John Wiley & Sons. Inc.: New York, NY, USA, 1985; ISBN 978-0-471-08404-4. [Google Scholar]
- Pranesha, T.S.; Kamra, A.K. Scavenging of aerosol particles by large water drops: 1. Neutral case. J. Geophys. Res. Atmos. 1996, 101, 23373–23380. [Google Scholar] [CrossRef]
- Beard, K.V.; Grover, S.N. Numerical Collision Efficiencies for Small Raindrops Colliding with Micron Size Particles. J. Atmos. Sci. 1974, 31, 543–550. [Google Scholar] [CrossRef][Green Version]
- Beard, K.V. Experimental and Numerical Collision Efficiencies for Submicron Particles Scavenged by Small Raindrops. J. Atmos. Sci. 1974, 31, 1595–1603. [Google Scholar] [CrossRef][Green Version]
- Hampl, V.; Kerker, M.; Cooke, D.D.; Matijevic, E. Scavenging of Aerosol Particles by a Falling Water Droplet. J. Atmos. Sci. 1971, 28, 1211–1221. [Google Scholar] [CrossRef]
- Aho, K.; Weber, C.F.; Christner, B.C.; Vinatzer, B.A.; Morris, C.E.; Joyce, R.; Failor, K.; Werth, J.T.; Bayless-Edwards, A.L.H.; Schmale III, D.G. Spatiotemporal patterns of microbial composition and diversity in precipitation. Ecol. Monogr. 2019, in press. [Google Scholar] [CrossRef]
- Failor, K.C.; Schmale, D.G.; Vinatzer, B.A.; Monteil, C.L. Ice nucleation active bacteria in precipitation are genetically diverse and nucleate ice by employing different mechanisms. ISME J. 2017, 11, 2740–2753. [Google Scholar] [CrossRef]
- Loosmore, G.A.; Cederwall, R.T. Precipitation scavenging of atmospheric aerosols for emergency response applications: Testing an updated model with new real-time data. Atmos. Environ. 2004, 38, 993–1003. [Google Scholar] [CrossRef]
- Burrows, S.M.; Butler, T.; Jöckel, P.; Tost, H.; Kerkweg, A.; Pöschl, U.; Lawrence, M.G. Bacteria in the global atmosphere—Part 2: Modeling of emissions and transport between different ecosystems. Atmos. Chem. Phys. 2009, 9, 9281–9297. [Google Scholar] [CrossRef]
- Tost, H.; Jöckel, P.; Kerkweg, A.; Sander, R.; Lelieveld, J. A New Comprehensive SCAVenging Submodel for Global Atmospheric Chemistry Modelling. Atmos. Chem. Phys. 2006, 6, 565–574. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).