Abstract
By means of direct numerical simulations (DNS), we study the impact of an imposed uniform magnetic field on precessing magnetohydrodynamic homogeneous turbulence with a unit magnetic Prandtl number. The base flow which can trigger the precessional instability consists of the superposition of a solid-body rotation around the vertical ( axis (with rate and a plane shear (with rate viewed in a frame rotating (with rate about an axis normal to the plane of shear and to the solid-body rotation axis and under an imposed magnetic field that aligns with the solid-body rotation axis ( While rotation rate and Poincaré number are fixed, and the B intensity was varied, , and so that the Elsasser number is about and respectively. At the final computational dimensionless time, the Rossby number Ro is about characterizing rapidly rotating flow. It is shown that the total (kinetic + magnetic) energy , production rate due the basic flow and dissipation rate ( occur in two main phases associated with different flow topologies: (i) an exponential growth and (ii) nonlinear saturation during which these global quantities remain almost time independent with The impact of a "strong" imposed magnetic field on large scale structures at the saturation stage is reflected by the formation of structures that look like filaments and there is no dominance of horizontal motion over the vertical (along the solid-rotation axis) one. The comparison between the spectra of kinetic energy and at the saturation stage reveals that, at large horizontal scales, the major contribution to does not come only from the mode but also from the mode which is the most energetic. Only at very large horizontal scales at which the flow is almost two-dimensional. In the wavenumbers range the spectra and respectively follow the scaling and Unlike the velocity field the magnetic field remains strongly three-dimensional for all scales since At the saturation stage, the Alfvén ratio between kinetic and magnetic energies behaves like for
1. Introduction
Rotating flows are omnipresent in several geophysical and astrophysical systems (oceans, Earth’s atmosphere [1], gaseous planets, stars [2]). The role of the Coriolis force, however, is not as dominant in the dynamics of the Earth’s atmosphere as it is in the atmosphere of giant planets, regarding its impact on zonal flows (e.g., see Galperin [3]). This relative weakness of the Coriolis force in Earth’s atmosphere is illustrated by the different interpretations proposed for the Nastrom et al. spectra [4]: according to Cho and Lindborg [5], the stratification frequency is privileged in the prefactor of their scalings; on the other hand, this scaling was revisited by Galperin and Sukoriansky [6] with system rotation, from the evidence that this prefactor depends on the latitude.
Rotating flows combine inertial waves and a possible geostrophic vortex component, in a very complex, fully nonlinear, way. In addition to relevant quasi-linear analyses [7], a wealth of direct numerical simulations (DNS) studies were developed at significant Reynolds number. The simplest were pseudo-spectral DNS’s in tri-periodic boxes. In these DNS studies for purely rotating flows, large-scale energy, and sometime helicity, is often forced by a stochastic process, whereas high-Reynolds rotating turbulence can be modeled by statistical triadic theories, often without forcing [8,9]. On the other hand, additional effects, even weak, via linear operators, can produce energy and anisotropy. It is suggested that some universality is found, especially for the scaling of the inertial range, in turbulence dominated by rotation, be the forcing stochastic or “physical”. This question of universality will be addressed in our paper, in line with [10], as a part of a nonlinear approach to precessional instability, for the physical process. This process is generally induced by an interaction between the system rotation and a mean shear, or a mean buoyancy gradient, not to mention magnetohydrodynamics (MHD) if other planetary atmospheres, or Earth’s core, are considered. All these mechanisms generate instabilities, from exponential to algebraic, that produce energy, mainly in the largest scales: energy growth is then attenuated or saturated, depending on nonlinear cascades and eventual dissipation.
The physical mechanism addressed in this article for sustaining energy and anisotropy in rotating turbulence is the effect of precession, neglecting explicit boundaries. Precession can arise when there is a continuous change of the orientation of the rotation axis [7,11,12]. Here, we will consider the misaligment of the main vorticity with the system vorticity in a rotating frame. This effect is known as equinoxial precession and is characterized by the very small parameter Poincaré number [13], ratio of system precessional vorticity to main vorticity, in the Earth. Of course, other cases of precession with larger Poincaré number are relevant, both for theoretical understanding and from experiments [14,15,16,17,18] and various physical aspects are of interest, as follows: in the geophysical context, the problem of precession of the Earth’s liquid outer core has been widely studied because of its potential to drive the geodynamo (see, e.g., [14,19]). In the astrophysical context, precession may trigger instabilities leading to the formation of vortex tangles and generate turbulence as in superfluid neutron star interiors [20].
The case of precessing rotational flow offers an example of elliptical instability [21,22] in which the ellipticity of mean trajectories results from an additional mean shear. In our simplified context of extensional mean flow and homogeneity restricted to fluctuations [23], the additional shear is induced by the gyroscopic torque, which results from the misalignment of the main “rapid” angular velocity and the precessional one, treated as an external Coriolis force. Accordingly, the related instability results from the resonant growth of two inertial waves when the difference in their frequencies coincides with one of the “distortion” frequencies of the base flow [11,21,22]. Accordingly, the base-flow, called Mahalov solution [24] is chosen in this study. It consists of the superposition of a solid-body rotation around the vertical ( axis (with rate and a plane shear (with rate viewed in a frame rotating (with rate about an axis normal to the plane of shear and to the solid-body rotation axis, so that,
where denotes the physical coordinate. We indicate that the vorticity vector of the plane shear balances the gyroscopic torque created by the misalignment of and The additional plane shear, which results from the precession, was found in previous experimental studies (see, e.g., [25]).
Mahalov [24] considered an infinite cylinder in which a tilted (sheared) streamline solution can exist under precession. From that study, Salhi and Cambon [23] have derived the solution (1) and called it as Mahalov’s solution. A similar solution to (1) was derived by Kerswell [11] from the Poincaré’s solution for a precessing oblate spheroid [13]: for the Mahalov’s solution the velocity vector of plane shear aligns with the solid rotation axis while for the Kerswell’s solution is normal to the solid-body rotation axis but for the two solutions the absolute vorticity is the same, The limit case corresponds to the case of rotating turbulence that was widely addressed in the literature to characterize the role of the Coriolis force (see, e.g., [8,26]).
Mahalov’s solution corresponds to an extensional flow, characterized by space-uniform vector fields (vorticity field, magnetic field) and/or space-uniform velocity gradients (shear, strain). Disturbances (or fluctuations) to that base flow are expanded in terms of Fourier modes with a (periodic) time-dependent wave vector. This is for the viewpoint of conventional stability analysis: in this context, a single disturbance mode cannot interact with itself, in purely incompressible turbulence (e.g., see [27]), so that the whole base flow plus the disturbance flow can be seen as an exact solution of Navier–Stokes equation in an unbounded domain, provided that some admissibility conditions be fulfilled. Regarding more realistic flow cases, linear spectral theory (LST), also called rapid distortion theory (RDT), for homogeneous turbulence can have the same starting point as the previous stability analysis but initial data can consist of a superposition of many individual Fourier modes, with a dense spectrum. As an advantage with respect to stability analysis, very large Reynolds numbers can be reached only with the particular choice of initial dense spectra. In counterpart, the linear dynamics from given initial data are only valid in a “rapid” time of evolution.
The third aspect investigated in this article is the interplay with MHD, that is relevant for the study of some magnetized planetary atmospheres. In addition to details found in [11,23,24] without MHD, new instability tongues are presented in Salhi et al. [28] for magnetized precessing flow (see also [8]). The aim of the present study is to provide new DNS results for explicit nonlinear dynamics on magnetized precessing rotating flows including stability analysis and related LST.
For the Mahalov’s solution (1), the wave-vector component along the solid-body rotation axis, remains time-independent while the other two components are periodic in time with period This makes it possible at any time t to compare DNS results characterizing the precessing turbulence dynamics at the planes with those in forced rotating turbulence (see later). In counterpart, for the Kerswell’s solution, is periodic in time with period (see [11,23,29,30]).
In rapidly rotating turbulence (i.e., the Rossby number is small) the emergence of large-scale vortices characterizes a quasi-two-dimensional (2D) state perpendicular to the fixed rotation axis [26,31], and, at increasing rotation rate, energy accumulates in the vicinity of the so-called “spectral buffer layer“ around [26]. The Rossby number where l is a characteristic length scale and is the associated velocity, measures the ratio of the advection term on the Coriolis force in the Navier–Stokes equations, also a small value of Ro means a dynamics mainly driven by rotation. Typical large-scale planetary flows are characterized by [32]. At the inertial wave frequency vanishes. The separation between the dynamics of velocity modes with non zero and zero inertial wave frequencies, or equivalently, with (wave modes) and (vortex modes) was discussed and observed in previous studies of rotating flows [33,34,35,36].
In the astrophysical context, Barker [30] used the Kerswell’s solution and studied, by means of DNS, the effect of nonlinear interactions on the precessional instability for several values of the Poincaré number ( while rotation rate was fixed, He found that the instability led to turbulence and the formation of columnar vortices similar to those observed in rapidly rotating turbulence. The similarity between the observed elongated structures in the two flow cases (precessing and rotating) was investigated in more detail in the study by Khlifi et al. [10]. In that study, the Mahalov’s solution (Equation (1)) was considered and DNS was performed for several values of the couple It is shown that the time development of the kinetic energy occurs in two main phases associated with different flow topologies: (i) an exponential growth characterizing three-dimensional turbulence dynamics and (ii) nonlinear saturation during which the kinetic energy remains almost time independent, the flow becoming quasi-2D-dimensional. The latter stage, wherein the development of kinetic energy remains insensitive to the initial state, shares an important common feature with other quasi-two-dimensional rotating flows such as rotating Rayleigh-Bénard convection [37,38], or the large atmospheric scales [9,39,40,41]: in the plane the kinetic energy spectrum scales as for where and are the Zeman “precessional” and “rotational” wavenumbers, respectively (defined by Equation (29)). In addition, an inverse cascade develops for and the spherically averaged kinetic energy spectrum exhibits a inertial scaling for
Some DNS results for explicit nonlinear dynamics on magnetized precessing rotating flows [30] indicate that, in the presence of even a weak magnetic field, the properties of the precessing flow are significantly altered and the formation of the columnar structures (observed in precessing hydrodynamic turbulence, hereinafter, PHT) is inhibited. In the present DNS study, we analyze the impact of an imposed magnetic field on turbulence dynamics by investigating various spectra for kinetic and magnetic energies. For the Mahalov’s solution the imposed magnetic field must align with the solid-body rotation axis to satisfy the admissibility conditions [27]. Denoting by B the associated Alfvén velocity vector. We perform DNS for which rotation rate and Poincaré’s number are fixed, and while the magnetic field intensity is varied, and so that and respectively. The value can be seen as a “strong” intensity. Initially (at the Rossby number is about and reaches at the final computational time In addition, we perform DNS for the case of PHT with and and for the case of rotating MHD turbulence (hereinafter, RMHDT) with and
Note that RMHDT with was investigated in recent studies [42,43,44,45,46]. For instance, it is found that, at large scales, the equipartition between magnetic and kinetic energies observed in the case of non-rotating MHD turbulence in a weak turbulence regime ( is broken by the dynamics of inertial waves, so that, the Alfvén ratio between kinetic and magnetic energies behaves like for at [42,45]. A similar behavior is found for the staturation stage of precessing MHD turbulence (hereinafter, PMHDT), as shown in the present study.
The paper is organized as follows. Model equations are given in Section 2 in physical space, for base (mean) flow and disturbance (fluctuating) one, with additional relationship for statistics and energetics. Section 3 is devoted to their spectral counterpart, mainly in a continuous unbounded domain, with time-dependent wave-vector. Some results from the linear stability analysis of precessing MHD flows by Salhi et al. [28] are reported in this section. Numerical results from DNS are given and discussed in Section 4. Concluding remarks are offered in Section 5.
2. Model Equations
2.1. Incompressible MHD Equations
We consider a precessing homogeneous turbulence of an incompressible electrically conducting fluid in the presence of a uniform background magnetic field. In the following, mean and fluctuating magnetic fields are scaled using Alfvén velocity units i.e., they are divided by where and are the constant density and the magnetic permeability. Incompressible MHD equations provide the simplest theoretical framework for studying large-scale turbulent motion of an electrically conducting fluid. Accordingly, the equations for the instantaneous velocity and magnetic field are [47]
where is the pressure (including the magnetic part and the centrifugal potential), is the kinematic viscosity and is the magnetic diffusivity. We choose , so that the magnetic Prandtl number is . In the momentum conservation Equation (2a), is the inertial term and and are the Coriolis and Lorentz forces per unit mass, respectively. In the induction Equation (2b), and respectively represent the advection and stretching of magnetic field.
Instantaneous velocity and magnetic fields are decomposed into base (or mean) flow and disturbances (or fluctuations), and As indicated previously, the base flow considered in the present study (see Equation (1) and Figure 1) corresponds to a vertical solid-body rotation viewed in a rotating frame about the axis, ( with additional plane shear, in an external uniform magnetic field where the matrix is given by (1). Obviously, the base flow (1) is an admissible solution, i.e., a solution of Equation (2) [23,28]. This ensures consistency with statistical homogeneity [8].
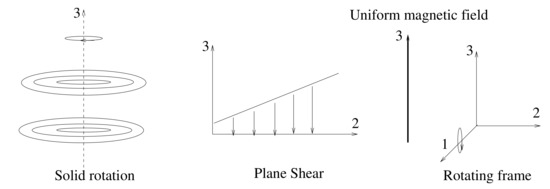
Figure 1.
Sheck of base flow which corresponds to a superposition of a solid-body rotation about the vertical axis with rate and a plane shear in with rate in a rotating frame about the axis with rate under a uniform magnetic field along the vertical ( axis.
2.2. Equations for the Kinetic and Magnetic Energies
The resulting MHD equations for the fluctuating velovity and magnetic field can be written as follows:
in which denotes the fluctuating modified pressure.
We assume that the turbulence is statistically homogeneous, so that the resulting equations for the kinetic and magnetic energies per unit mass and where denotes ensemble (statistical) averaging, are
in which denotes the turbulent kinetic energy production which is proportional to the Reynolds stress component while denotes the turbulent magnetic energy production which is proportional to the Maxwell stress component Both and are due to the background shear with rate Note that rotation produces no energy. Here, and denote respectively the viscous and magnetic (or Joule) dissipation rates per unit mass and
represents the energy exchanges between magnetic and kinetic energies due to the imposed magnetic field. Note that the term has no explicit contribution on the total (kinetic + magnetic, energy evolution,
where and
3. Equations for Fourier Amplitudes
3.1. Time-Dependent Wave Vector
Fourier space representation is useful to quantify the energy contents at various scales. Therefore, we represent the fluctuating fields as the superposition of Fourier modes using the Fourier transforms
where is a time-dependent wave vector. In order to remove the explicit dependence on x in the resulting equations for the Fourier amplitudes and one has to ensure that varies in time according to (i.e., the eikonal equation),
This amounts to following characteristic lines of the mean flows, although expressed in spectral variables (details in Ref. [23,28]). Accordingly, the wave-vector components evolve as
where with is the initial wave vector component. Therefore, the wave-vector trajectories are circles with sheared centers, as their counterparts in physical space, since We note that both the wavenumbers
are time-independent.
3.2. Equations for the Fourier Amplitudes
The resulting equations for the Fourier coefficients and are
where is the spectral counterpart of the linear part of pressure fluctuations. Here, is the time derivative. The two terms and are bilinear operators for the kinetic and magnetic energy transfers, written as [48]
where is the projection operator and is the Kronecker delta.
In the direct numerical simulation approach used here, the fully nonlinear equations of motion (11) are solved using a modified version of the Fourier spectral code Snoopy by [49]. Note that in this entire paper, as for the basic nonlinearity seen as a convolution product in 3D Fourier space, according to previous equations, both the physical space of coordinates and the spectral space are considered as continuous. Consequently, integrals are used, and this description will prevail for the definition of statistical quantities, such as averaged energy spectra, single-point statistics, etc., obtained by integration of 3D basic spectra. On the other hand, the calculation of terms connected to nonlinearity in DNS follows the classical pseudo-spectral procedure inherited from Orszag and Patterson [50]: a regular mesh is used in a triple-periodic box, with related discretization and the convolution product is evaluated from its physical counterpart by inverse fast Fourier transform (FFT). More details can be found at the beginning of Section 4. In addition, we use here a less classical, modified, version of the Snoopy code [49] for DNS in the presence of mean distortion: as for SLT, the equations are solved using the comoving system of coordinates; this is equivalent to following mean (elliptical here) trajectories as characteristic lines in physical space and to using time-dependent wave vectors in Fourier space. Finally, the classical pseudo-spectral procedure for nonlinear terms is applied to an initial grid or an initial vector , as in Equation (9).
3.3. Linear Stability Analysis
In the inviscid ( and ideal ( linear limit, the differential system (11) reduces to a seventh order Floquet system
The use of the constraints and allows us to eliminate the Fourier amplitude of fluctuating pressure
and to reduce the latter seventh order differential system to a fourth order one. The rank of the differential system can be reduced using new variables, corresponding to solenoidal modes, that are individually divergence-free in physical space, or normal to the wavevector in Fourier space. The three Fourier components of the velocity field reduce to only two components, denoted and related to a poloidal/toroidal divergence-free decomposition (see [8] for details). The same holds for the magnetic field, with and components. In terms of these variables [28]
The resulting fourth order Floquet system takes the form
where The elements are not reported here for the sake of brevity (see [28]). We denote by the fundamental matrix solution of the Floquet system (16), with where is the unit matrix and by the Floquet multiplier matrix [51,52]. Because
it is found that and hence [28,53]. This implies that the product of the eigenvalues of is unity, say or equivalently, since the general solution of the Floquet system (16) is a linear superposition of Floquet modes, where is periodic with period [51]. A necessary condition for the onset of linear instability is a resonance where two Floquet multipliers coincide (if an eigenvalue is at the onset of instability, it must have multiplicity 2 or higher). In the stable case, all the eigenvalues lie on the unit circle [52].
The resonant cases for are characterized by the condition where ℓ is an integer and ( denotes the frequency (normalized by associated with the eigenvalue of the matrix solution
Here, is a local Lehnert number [54],
The first two frequencies ( correspond to hydrodynamic modes or fast modes, while the second two ( refer to magnetic modes [52], slow modes [55], or magnetostrophic modes [44] since they vanish in the purely hydrodynamic case ( Previous studies for magneto-inertial wave turbulence indicate that the equipartition between kinetic and magnetic energy due to Alfvén waves is broken by inertial waves for [43,45].
The stability analysis at first-order in by Salhi et al. [28] shows that there are three subharmonic instabilities associated to (hydrodynamic modes), (mixed modes), and (magnetic modes). The analytical results for the maximal growth rate of the three subharmonic instabilities normalized by versus the local Lehner number are displayed in the right panel of Figure 2. Note that the magnetic modes instability occurs only for As it can be seen, for the magnetic modes instability increases with approaching at while for the hydrodynamic modes instability which takes the value at decreases with approaching at In counterpart, for the mixed modes instability, approaches zero at Nonlinear interactions act to saturate the linear precessional instability since the time evolution of the turbulent (magnetic) energy exhibits two important stages: an exponential growth stage during which the energy grows exponentially with time followed by a saturation stage where the energy remains almost constant (see Section 4, see also [10]). The present simulations indicate that, at the quasi-equipartition between kinetic and magnetic energies observed in non-rotating MHD turbulence is broken while, at the magnetic energy slightly exceeds the kinetic energy (see later).
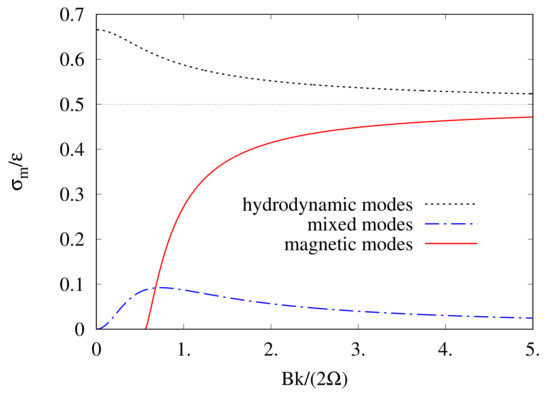
Figure 2.
Variation of the maximal growth rate versus the local Lehner number for the precessing magnetohydrodynamics (MHD) instability, where and are the frequencies of Alfvén and inertial waves, respectively. Hydrodynamic modes: where Mixed modes: Magnetic modes: where (see Salhi et al. [28]).
3.4. Spectral Density of Energy
The resulting equation for the spectral density of kinetic energy and that for the spectral magnetic energy density , where stands for complex conjugate, are
where
denote the spectral density of kinetic and magnetic energy production, respectively, and
again characterizes the energy exchange between the kinetic and magnetic components due to the background magnetic field B. Here, , and are transfer-like terms that involve triple velocity and magnetic fluctuation correlations and are such that and The energy exchange between kinetic and magnetic component due to nonlinear interactions is characterized by both terms and
At the inviscid linear solution shows that there is no linear instability: the vertical mode remains identical to its initial value, as in the pure rotating case ( while the horizontal mode ( performs a precessing motion (with period induced by the vertical mode,
where Obviously, at the nonlinear interactions can generate a coupling between vertical and horizontal modes as shown by the equation for the horizontal and vertical spectral density of energies,
(the same notation is used for the fluctuating magnetic fields),
in which the subscript refers to the mode, for example, where is the Dirac delta function and
4. DNS Results and Discussions
4.1. Initial Conditions
We initialize direct numerical simulations from homogeneous isotropic hydrodynamic turbulence generated by a separate simulation started from random initial conditions with the initial energy spectrum [56] where is a normalization constant, is a characteristic length scale ( and is the initial kinetic energy. In order to let the turbulence develop a significant inertial zone as well as nonlinear transfer, an isotropic precomputation [10,57] is done before applying the mean flow (1). Only during this pre computation, a large-scale forcing is applied until a statistical steady state, with a Taylor-microscale-based Reynolds number This state holds for a new initial one before starting the effect of the mean flow; the procedure is not sufficient to reach a developed Kolmogorov-like energy spectrum but the trend is satisfactory. In all the runs, the magnetic fluctuations are initially zero. Note that in the case of PHT, it is found that the saturation stage, during which the turbulent kinetic energy remains almost time independent, is insensitive to the initial Reynolds number independently of the initial conditions (precomputed initial isotropic or solenoidal random noise) [10].
The domain is a periodic cube with edge length with grid points to a side. Aliasing errors are removed using the dealiasing rule and as a result the minimum and maximum wavenumbers are and respectively. We also limit the effects of periodic boundary conditions, by computing all integral scales
in the ( directions, and imposing that (no sum over subscript j). By this, we control numerical confinement, even if one integral length scale grows faster due to precessional instability.
In our simulations, the initial value of Rossby number is defined as follows
where characterizes rather a case of rapidly rotating turbulence, which is known to mimic some of the features of the 2D turbulence. Here, is a characteristic length scale, is the associated velocity, and E and D respectively denote the total (kinetic+magnetic) energy and dissipation rate. Typical large-scale planetary flows are characterized by [32], as already indicated, and the liquid metals in the Earth’s outer core are strongly affected by rotation with [58]. For a giant planet like Jupiter, it is believed that the Rossby number may even be smaller [59], whereas for the solar convective region (where the magnetic field is believed to be enhanced) [44]. The present simulations show that, at the saturation stage (see below), the Rossby number can reach the value (see the inset of Figure 3).
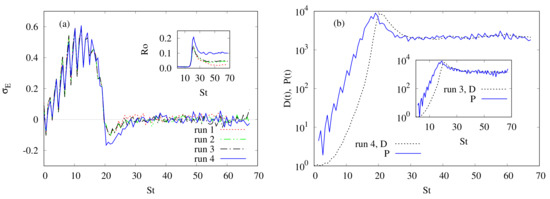
Figure 3.
(a) Time development of the growth rate of total (kinetic + magnetic) energy (see Equation (27)) in the precessing hydrodynamic turbulence (PHT) case (run 1) and the precessing MHD turbulence (PMHDT cases) (runs 3–4). The inset shows the time development of the Rossby number Ro (see Equation (25)) for the same runs. (b) Time development of total (kinetic + magnetic) dissipation rate, and total production rate, in the precessing MHD turbulence (PMHDT) case with (run 4). The results reported in the inset characterize the case where (run 3).
The value of the Poincaré parameter considered in the present study is about so that, the value of the shear rate is In addition to the case of PHT, we consider three values for the strength of the imposed magnetic field in the case of MHD precessing turbulence, namely, The respective values of the Elsasser number, which characterizes the relative strengths of the Lorentz and Coriolis forces,
are and (see Table 1). We also consider the case of RMHDT ( with so that and B is parallel to the solid-body rotation axis. Note that the Elsasser number is commonly employed as a measure of the strong field dynamo, which is synonymous with the magnetostrophic balance (i.e., the pressure gradient, the Coriolis force, and the Lorentz force are balanced). It is believed that the Elsasser number of the Earth’s core is about unity [59]. All the runs are run up to a maximum computational dimensionless time

Table 1.
Summary of the parameters for the different runs performed: precessing hydrodynamic turbulence (PHT), precessing MHD turbulence (PMHDT), rotating MHD turbulence (RMHDT).
4.2. Time Evolution of Global Quantities
In this section, we study the temporal behavior of several global quantities to characterize the precessing MHD flow dynamics and the influence of the strength of the imposed magnetic field on it.
The present simulations indicate that the time evolution of total (kinetic+magnetic) energy, exhibits two important stages: (i) an exponential growth of followed by (ii) a saturation stage at during which remains almost constant. This is also clear when observing the evolution of the energy growth rate,
which slightly fluctuates about zero during the saturation stage for all runs, as shown by Figure 3a. Recall that (respectively, is the kinetic (magnetic) production rate and (respectively, denotes the kinetic (magnetic) dissipation rate. For the runs 2–4 (PMHDT cases), a similar behavior is found for the total dissipation rate, and the total production rate where they become slowly balanced such that at the saturation stage (see Figure 3b). Indicate that the Rossby number Ro is about for the runs 3 and 4 and about for the run 2 (see the inset of Figure 3a).
For the run 1 (PHT case), both and exhibit an exponential growth at and decay with time at the saturation stage during which they become slowly balanced such that (see also Khlifi et al. [10]).
At the exponential growth stage, the kinetic quantities and are approximately insensitive to the B intensity as illustrated by Figure 4a and its inset displaying the time evolution of and In counterpart, the generation of large and small scales magnetic fluctuations during the exponential growth stage is sensitive to the B intensity as shown by Figure 4b and its inset displaying and respectively. Recall that our simulations start from homogeneous isotropic hydrodynamic turbulence, so that, the initial magnetic energy and dissipation rate (or Joule dissipation) are zero. From Figure 4b, it clearly appears that for both the runs 2 and 3 (for which and respectively) the magnetic energy increases with time even at the saturation stage while for the run 4 (for which it remains almost constant at the saturation stage. As for the behavior of the magnetic (or Joule) dissipation rate at the saturation stage, we observe that remains almost constant for the three runs (2–4, see the inset of Figure 4b). In the following, we analyze the dynamics of the saturation stage and comment about the exponential growth stage when relevant.
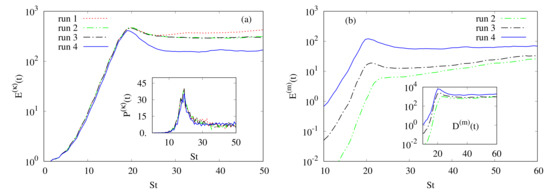
Figure 4.
(a) Time development of kinetic energy normalized by its initial value in the PHT case (run 1) and the PMHDT cases (runs 3–4). The inset shows the time development of kinetic production rate for the same runs. (b) Time development of magnetic energy normalized by in the PMHDT cases (runs 2–4). The inset shows the time development of magnetic dissipation rate normalized by for the same runs.
For non-rotating MHD flows in the weak turbulence regime ( the Alfvén ratio between kinetic and magnetic energies, is equal to one, thus characterizing an equipartition between kinetic and magnetic energies. However, For non-rotating MHD flows in the strong turbulence regime ( this ratio is slightly smaller than one, indicating the presence of non-Alfvénic fluctuations [60]. For RMHDT ( inertial waves have an important impact on the dynamics of large scales since the equipartition between kinetic and magnetic energies is broken. At large scales such that the generation of magnetic fluctuations is reduced more and more by the inertial waves as the rotation rate increases (whereas the B intensity remains constant). This leads to an increase of the Alfvén ratio with rotation rate [42,43]. In addition, it was shown that, scale by scale, the Alfvén ratio behaves like for and is about one for ([45], see also the next section).
In Figure 5a we plot the time evolution of the Alfvén ratio for the three runs 2–4 (i.e., PMHDT cases). We observe that, at the saturation stage, the Alfvén ratio decreases as the B intensity increases (whereas rotation rate remains constant). For both the runs 2 (for which ) and 3 (for which ), decreases with time reaching the value at the final computational time. In counterpart, for the run 4 (for which the Alfvén ratio and also the ratio are almost constant (at the saturation stage), and (see Figure 5a and its left inset), while the ratio oscillates around (see the right inset of Figure 5a). Indicate that for the same value of the Elsasser number ( the contribution to total (kinetic + magnetic) energy coming from the magnetic component is more important in the case of PMHDT than in the case of RMHDT. Indeed, from Figure 5b displaying the behavior of versus the dimensionless time for the runs 4 and 5, we can see that in the later case (run 5) is approximately six times larger than in the former case (run 4).
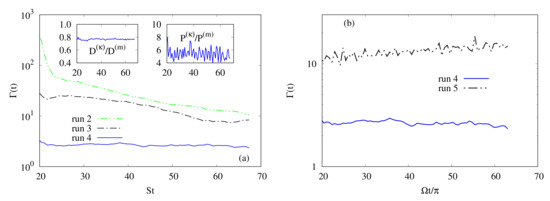
Figure 5.
(a) Time development of Alfvén ratio in the PMHDT cases (runs 2–4) at the saturation stage. The left (respectively, right) inset shows the time development of the ratio (respectively, ) for the run 4. (b) Variation of the Alfvén ratio, versus the dimensionless time in PMHTD case (run 4) and in RMHDT case (run 5). For both cases, the Elsasser number is about
In order to see if the dominance of the horizontal motion (over the vertical one) observed in the case of PHT [45] or in the case of rapidly rotating turbulence [26,31] is altered or not in PMHDT we examine the behavior of the ratio of horizontal to vertical kinetic energies and the ratio of associated integral length scales. Here, the horizontal and vertical kinetic energies are defined as and We consider only the integral length scales in the direction parallel to the solid-body rotation axis, defined by Equation (24), or equivalently,
since increases due to rotation (see e.g., [45,61]). Figure 6 shows the time development of and for the runs 1–4. Note that in isotropic turbulence, one has and With respect to the PHT case (run 1), the ratios and are strongly reduced at the saturation stage only for the PMHDT case with (run 4). Therefore, we may conclude that the dominance of the horizontal motion (over the vertical one) observed in the PHT case (run 1) is prevented in the presence of a “strong” imposed magnetic field. The visualizations of the vertical vorticity field for both the runs 1 and 4 corroborates such a conclusion (see Figure 7). Indeed, the left panel of Figure 7 related to the PHT case (run 1) indicates the presence of columnar structures along the solid-body rotation which are indicative of a quasi-2D state of turbulence (e.g., see [26]). The recent numerical study by Goto et al. [62] of an incompressible fluid confined in precessing containers (sphere, spheroid, and cylinder) indicates that a pair of twisted large-scale vortices appears in the developed turbulence ( and shear flow around these vortices stretches and amplifies the small-scale turbulent eddies (the mechanism of small-scale turbulent vortices is consistent with the experimental results for the precessing sphere [18]).
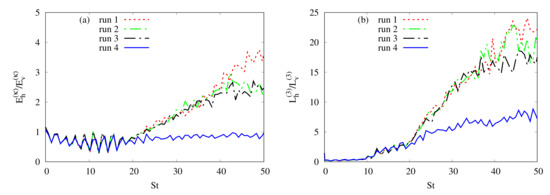
Figure 6.
Time evolution of the ratios between horizontal and vertical (a) kinetic energies, and (b) integral length scales in the vertical ( direction for the runs 1 (PHT case) and 2–4 (PMHDT cases).
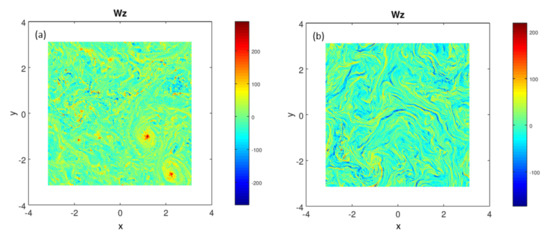
Figure 7.
Horizontal cut of vertical vorticity in PHT and PMHDT cases (runs 1 and 4) at . The elongated structures along the rotation axis observed in PHT case (left panel) are affected by the mean magnetic field: they are inhibited or distorted by the magnetic field (right panel) but their intensity is not strongly reduced. The flow structures look like filaments.
From the right panel of Figure 7 related to the run 4, we observe structures which look like filaments. Note that the inhibition of the formation of columnar structures in PMHDT was also observed in the DNS by Barker [30] as already indicated. On the other hand, in their review of interstellar turbulence (observations and processes), Elmegreen and Scalo [63] indicated that magnetism can slow collapsing cores and remove angular momentum on large and small scales, and it may contribute to filamentary structures that control the accretion rate of gas onto protostars. According to the DNS study by Bigot et al. [60], the formation of filaments is reported within current and vorticity sheets in strongly magnetized flows.
4.3. Spectra for Kinetic and Magnetic Energies
In this section, we analyze some spectra of kinetic and magnetic energies since they provide information about the distribution of energy at different scales. A first simple dimensional analysis suggests to delineate the range of anisotropic scales using a single threshold wavenumbers based on shear rate or on rotation rate and on kinetic dissipation rate
as proposed by Corrsin [64] and Zeman [65] for shear flows and rotating flows, respectively. The corresponding threshold length scales would then be and For rotating flows, the wavenumber identifies a scale at which turbulence eddy turnover time is commensurate with the time scale of system rotation. It characterizes scalewise strength of the effect of rotation: it is strong on scales where and weak on scales where (isotropy is restored for wavenumbers larger than [66,67]). The present simulations indicate that, at the saturation stage, the precessional and rotational numbers are about 4 and respectively (see also [10]).
In the light of the analysis presented in Section 4.2, we principally consider the runs 1 (PHT) and 4 (PMHDT with .
4.3.1. Radial Spectra
The radial spectrum of kinetic energy is defined as follows
where is a spherical coordinates system for the wave vector k such that and Similar definitions hold for other radial spectra. Theoretical arguments for forced rapidly rotating flows suggest that for the intermediate wave numbers where denotes the forcing wavenumber, behaves like where [65]. This scaling is also observed in a DNS study of a rotating turbulence under precessionlike perturbation generated by a change of the rotation axis at a fixed time instant [68].
Figure 8a shows the radial (spherically averaged) spectrum of total energy at different times, and as well as the average over the time window for the run 4. The time development of the kinetic energy spectrum and its average over the same time window is reported in the inset. As it can be seen, there are no noticeable differences between the spectra and their time average indicating a statistical steady state of turbulence at the saturation stage. Hereinafter, we use the notation instead of for the sake of clarity. The same notation holds for the other spectra.
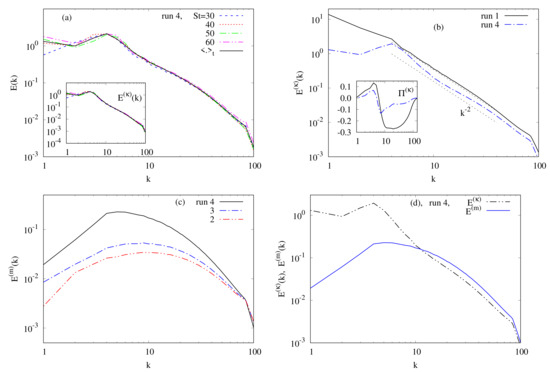
Figure 8.
(a) Radial spectra of total (kinetic + magnetic) energy at different dimensionless time and their average over the time window for run 4. The development of kinetic energy at these different times and its average over the same time window is reported in the inset. (b) Radial spectrum for runs 1 and 4. The inset shows the spectral energy flux normalized by the kinetic energy for the same runs. In Figure 8b the dashed straight line, which indicates the scaling, delimits the range (c) Radial spectra of magnetic energy for runs 2–4. (d) Comparison between and for run 4.
Figure 8b displays for both the runs 1 (PHT) and 4 (PMHDT case with or On the basis of the case of PHT, the kinetic energy is strongly reduced at even if it also reduced at the other scales, and the wavenumbers range at which is compatible with the scaling is also reduced. For the PHT, well follows the scaling at In Figure 8c we plot the radial spectrum of magnetic energy, for the runs 2–4. It is clear that, at almost all scales, increases as the intensity of the applied magnetic field is increased. Recall that our simulations start from isotropic hydrodynamic turbulence with zero magnetic fluctuations. Moreover, at increases like where for run 3 and for run 4. Otherwise, for the three runs (2–4), the amplitude of the magnetic energy is much smaller than that of the kinetic energy in the large scales but of the same order in the small scales as shown by Figure 8d. This is essential for the presence of the 2D-inverse cascade for the kinetic energy since if the magnetic field fluctuations were strong enough in the large scales the flow would behave as a 2D-MHD flow with a direct cascade [69]. The spectral energy flux
which is reduced when compared to the PHT case (see the inset of Figure 8b) is positive for indicating an inverse energy cascade. Negative energy flux corresponds to a forward cascade (e.g., see [68]).
4.3.2. The Role of the Mode and Its Nearest Neighbors Modes
In rapidly rotating (or precessing) hydrodynamic turbulence, energy accumulates in the vicinity of the so-called “spectral buffer layer” around [10,26]. This physical phenomenon corresponds to the emergence of large-scale vortices and characterizes a quasi-2D state perpendicular to the fixed rotation axis [31], as already indicated. In Figure 9a we plot the spectrum of the 2D kinetic energy at the plane
for the runs 1 and 4. It can be seen that for run 4 (PMHDT with is reduced, especially at large scales, when compared to run 1 (PHT). It is rather the horizontal motion that is strongly affected in the presence of a “strong” imposed magnetic field (see Figure 9b) since the vertical kinetic energy is almost the same as its counterpart in PHT (see the inset of Figure 9b). This may be explained as follows. The equation for and is deduced from Equations (23a) and (23b)
where is the 2D horizontal production term (the 2D vertical one is zero). At there is no linear precessional instability (see § III.4) and the coupling between horizontal and vertical kinetic energies are only due to the nonlinear transfers which are strongly reduced by rotation (e.g., see [8]). In counterpart, the 2D horizontal kinetic energy is reduced (see the top inset) due to the diminution of the production term when compared to the PHT case (not shown).
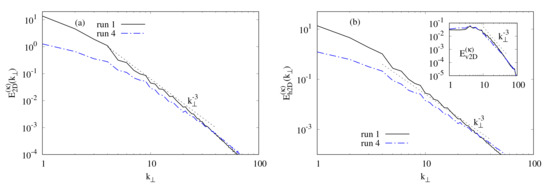
Figure 9.
Kinetic energy spectra of runs 1 and 4. (a) displays the 2D kinetic energy associated to the mode. (b) and its inset respectively show the 2D horizontal and vertical kinetic energies. The dashed straight lines, which indicate the scaling, delimit the range
Even if the dynamics of the spectral buffer layer around [26] may not be completely captured by simulations due to discretization between the planes and similarities between the dynamics of this spectral buffer layer and the dynamics of its near-neighbor 3D modes can be drawn. Figure 10a,b compares the following kinetic energy spectra
and
for the runs 1 et 4. Note that characterizes the dynamics of the 3D modes.
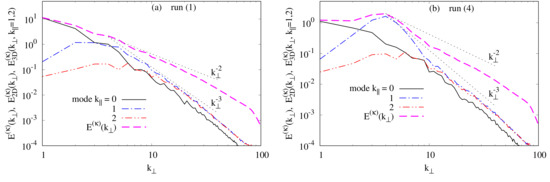
Figure 10.
Kinetic energy spectra. (a,b) compare the spectra and for runs 1 and 4, respectively. The dashed straight lines, which indicate the and scaling, delimit the range
For run 1 (PHT), it is the that is the most energetic one, at least for since We note that, at the behavior of well follows the scaling whereas the behavior of and is compatible with the scaling and the three modes ( have substantially the same contribution to kinetic energy (see Figure 11a). Comparing the saturation stage of PHT with other quasi-2D flows, the spectrum was observed in “isotropically” forced rotating turbulence [36,70,71,72,73] and in rapidly rotating Rayleigh-Bénard convection [37,38].
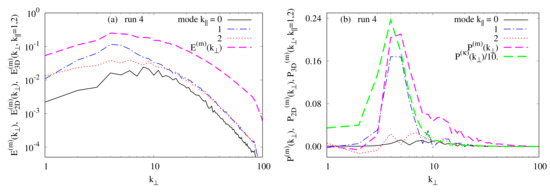
Figure 11.
Spectra of magnetic energy and production due to the background shear for run 4. (a) compares , and (b) shows , and
For the PMHDT case with a “strong” imposed magnetic field (run 4), the contribution to coming from is dominant only in the very thin layer around while the contribution coming from is dominant for (see Figure 10b). For instance, for at which reaches its maximum. We note that the spectra and are respectively compatible with the scaling and only for the range Therefore, we may conclude that for run 4 (PMHDT with the major contribution to kinetic energy does not come only from the mode but also from the mode which is the most energetic one. Thus the velocity field in run 4 is quasi-2D only for a very thin layer around otherwise, it is three-dimensional.
Figure 11a compares the magnetic energy spectra , and at the saturation stage of PMHDT (run 4). Unlike the velocity field the magnetic field remains strongly three-dimensional for all scales since Moreover, one has for all scales and the contribution to coming from the mode is more important than those of the modes and This is mainly due to the fact that (i.e., the spectrum of the magnetic production at the plane, see Equation (20)) is significantly larger than and does not strongly differ from (see Figure 12b). We indicate that at large scales, the main contribution to the spectrum which characterizes the energy exchange between kinetic and magnetic energies (see Equation (21), comes from the mode (not shown). The maximum value of is approximately the same as the one of which is 10 times lower than the maximal value of the kinetic production These maximum values are reached at
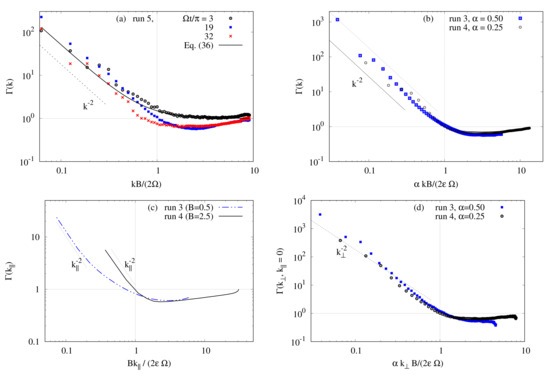
Figure 12.
Alfvén ratio between kinetic and magnetic energies versus local Lehnert’s number. (a) versus at the dimensionless time for the case of RMHDT (run 5, which is a freely decaying turbulence). (b) versus at the saturation stage of PMHDT (runs 3 and 4). The coefficient depends on the B intensity, for (run 3) and for (run 4). (c) versus for the runs 3 and 4. (d) versus for the runs 3 and 4.
4.3.3. Alfvén Ratio between Kinetic and Magnetic Energies
As indicated previously, for the case of rotating MHD weak wave turbulence ( linear theory shows that, scale by scale, the Alfvén ratio between kinetic and magnetic energies behaves like
so that, for large scales and indicating equipartion between kinetic and magnetic energies for small scales (see Salhi et al. [45]). The present DNS results for the case of freely decaying rotating MHD turbulence (run 5) are in agreement with LST predictions as shown by Figure 12a displaying versus for , and A similar behavior is found for the saturation stage of precessing MHD turbulence (PMHDT) as it clearly appears from Figure 12b displaying versus where the coefficient depends on the B intensity: for (run 3) and for (run 4). Indeed, behaves like for and is sligtly less than one for
Because the frequency of Alfvén (respectively, inertial) waves is proportional to the parallel wavenumber, (respectively, it appears relevant to also investigate the variation of the Alfvén ratio versus local Lehnert’s number defined as Here, is the one-dimensional spectrum of kinetic energy along the direction parallel to rotation axis,
in which and Note that the Wronskian of the transformation is unity.
In Figure 12c we plot versus for the runs 3 and 4. We observe that is about one for for both the flow cases. At is greater than unity and behaves like while, at it is slightly smaller than one. The variation of the Alfvén ratio at the plane versus is shown in Figure 12d for runs 3 and 4. It can be seen that, at decreases with slope slightly steeper than This is mainly due to the fact that the smallest contribution of the modes to the magnetic energy corresponds to that of the mode (see Figure 11a). Recall that the energy exchanges between kinetic and magnetic energies due to the imposed magnetic field vanish at and the contribution of that mode to the magnetic production due to the background shear is small (see Figure 11b).
5. Concluding Remarks
By means of direct numerical simulations (DNS), we studied the impact of an imposed uniform magnetic field on precessing magnetohydrodynamic turbulence with a unit magnetic Prandtl number. Our simulations start from homogeneous isotropic hydrodynamic turbulence, so that the initial magnetic energy and dissipation rate (or Joule dissipation) are zero. Since our main goal is to study the impact of an imposed magnetic field on the dynamics of large scales and intermediate scales, we have limited ourselves to a resolution of grid points. The mean flow, which can trigger precessional instability, corresponds to the so-called Mahalov solution (see Equation (1)). Disturbances to that base flow are expanded in terms of Fourier modes with a time-dependent wave vector. For instance, the component ( along the rotation axis is time-independent while the other two components of the wave vector are periodic in time. In the background of a linear stability analysis, the mode at which both the dispersion frequency ( of Alfvén waves and the one of inertial waves vanish, is stable. For there is a parametric (precessional) instability resulting from the resonant growth of two magneto-inertial waves when the difference in their frequencies coincides with one of the ”distortion” frequencies of the basic flow [28]. At large local Lehnert’s number the maximal growth rate of instability due to the resonance of slow waves, i.e., those characterized by the frequency approaches the one of instability due the resonance of fast waves, i.e., those characterized by the frequency The instability acts to enhance turbulence until nonlinear interactions (of that turbulence) saturate it. In other words, the energy production due to the background shear, feeds the nonlinear interactions and in turn they saturate the instability even in the presence of a “strong” imposed magnetic field, so at the saturation stage, the dissipation () and production rates become slowly balanced ( Therefore, at the saturation stage, the turbulence behaves as being forced at large scales by the energy production (rather by kinetic energy production since it is 10 times higher than the magnetic one, see Figure 11b). At the saturation stage, total (kinetic + magnetic) energy, dissipation, and production rates are almost time independent (see Figure 3).
For precessing hydrodynamic turbulence (PHT), similarities between large scale structures of the saturation stage and those occurring in rapidly rotating turbulence were drawn in previous studies [10,30]. The impact of a “strong” imposed magnetic field on large scale structures of the saturation stage is traduced by the formation of structures that look like filaments (see Figure 7). In strongly magnetized non-rotating flows the formation of filaments is reported within current and vorticity sheets [60]. The dominance of the horizontal motion (the motion in the plane perpendicular to the solid-body rotation axis) over the vertical one observed in PHT is altered in the presence of a “strong” imposed magnetic field. Indeed, for PMHDT, it is found that the ratio of horizontal to vertical kinetic energies is about one at the saturation stage (see Figure 6a). It is rather the horizontal motion that is most affected in the presence of a “strong” magnetic field especially at large scales (Figure 9b illustrates this).
At the exponential growth stage, the development of kinetic energy, dissipation, and production rates is not sensitive to the B intensity ( while their magnetic counterparts increase as B is increased (see Figure 5a). At the saturation stage, the Alfvén ratio between kinetic and magnetic energies decreases as B is increased and for fixed B the contribution to total energy coming from the magnetic fluctuations are more important in the presence of precession than without precession ( see Figure 5b).
The dynamics of the mode and its nearest neighbors modes ( were investigated in detail in addition to radial (spherically averaged) spectra of kinetic and magnetic energies for all the runs presented in the present study. In fact, the state of turbulence at the saturation stage of PHT is 2D–3C (C for componality) as in rapidly rotating nonmagnetized flows and is mainly due to the dynamics of the spectral buffer layer around [26].
The radial spectrum of kinetic energy at the saturation stage of PHT follows the scaling for k ranging between the precessional and rotational Zeman’s wavenumbers and there is an inverse cascade of energy at (see Figure 8b). For the case of PMHDT, the kinetic energy is reduced at all scales especially at large ones, and the wavenumbers range at which is compatible with the scaling is also reduced when compared to the case of PHT. The amplitude of the magnetic energy is much smaller than the one of kinetic energy in the large scales but of the same order in the small scales (see Figure 8d).
The comparison between the spectra , and at the saturation stage of PMHDT under a “strong” imposed magnetic field reveals that, at large horizontal scales, the major contribution to does not come only from the mode but also from the mode which is the most energetic. Only at very large horizontal scales at which the flow is almost two-dimensional (see Figure 10b). Unlike the velocity field the magnetic field remains strongly three-dimensional for all scales since (see Figure 11a). Note that the wavenumbers range at which the spectra and respectively follow the scaling and is reduced when compared to the PHT case.
The behavior, scale by scale, of the Alfvén ratio between kinetic and magnetic energies is also investigated. For the case of RMHDT, the DNS results are in agreement with the linear theory solution: where This is so that behaves like for large scales. A similar behavior is found for versus and also for versus
Author Contributions
Conceptualization, writing-original draft preparation A.S.; data curation, A.K.; supervision, C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pedlowsky, J. Geophysical Fluid Dynamics; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Maeder, A. Physics, Formation and Evolution of Rotating Stars; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Galperin, B.; Read, P.L. Zonal Jets Phenomenology, Genesis, and Physics; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Nastrom, G.D.; Gage, K.S. A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 1985, 42, 950–960. [Google Scholar] [CrossRef]
- Cho, J.Y.N.; Lindborg, E. Horizontal velocity structure functions in the upper troposphere and lower stratosphere 1. Observations. J. Geophys. Res. 2001, 106, 10223–10232. [Google Scholar] [CrossRef]
- Galperin, B.; Sukoriansky, S. Turbulence in rotating fluids and the Nastrom & Gage spectrum. In Proceedings of the Sixth International Conference Turbulence Mixing and Beyond, ICTP, Trieste, Italy, 14–18 August 2017; pp. 14–18. [Google Scholar]
- Greenspan, H.P. The Theory of Rotating Fluids; Cambridge University Press: Cambridge, UK, 1968. [Google Scholar]
- Sagaut, P.; Cambon, C. Homogeneous Turbulence Dynamics; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Sukoriansky, S.; Galperin, B. QNSE theory of turbulence anisotropization and onset of the inverse energy cascade by solid-body rotation. J. Fluid Mech. 2016, 805, 384–421. [Google Scholar] [CrossRef]
- Khlifi, A.; Salhi, A.; Nasraoui, S.; Godeferd, F.; Cambon, C. Spectral energy scaling in precessing turbulence. Phys. Rev. E 2018, 98, 011102. [Google Scholar] [CrossRef]
- Kerswell, R.R. The instability of precessing flow. Geophys. Astrophys. Fluid Dyn. 1993, 72, 107–144. [Google Scholar] [CrossRef]
- Hollerbach, R.; Kerswell, R.R. Oscillatory internal shear layers in rotating and precessing flows. J. Fluid Mech. 1995, 298, 327–339. [Google Scholar] [CrossRef]
- Poincaré, H. Sur la précession des corps déformables. Bull. Astron. 1910, 27, 321–356. [Google Scholar]
- Malkus, W.V.R. Precession of the Earth as the cause of geomagnetism: Experiments lend support to the proposal that precessional torques drive the Earth’s dynamo. Science 1968, 160, 259–264. [Google Scholar] [CrossRef]
- Noir, J.; Cardin, P.; Jault, D.; Masson, J.-P. Experimental evidence of nonlinear resonance effects between retrograde precession and the tilt-over mode within a spheroid. Geophys. J. Int. 2003, 154, 407–416. [Google Scholar] [CrossRef]
- Herault, J.; Gundrum, T.; Giesecke, A.; Stefani, F. Subcritical transition to turbulence of a precessing flow in a cylindrical vessel. Phys. Fluids 2015, 27, 124102. [Google Scholar] [CrossRef]
- Horimoto, Y.; Goto, S. Sustaining mechanism of small-scale turbulent eddies in a precessing sphere. Phys. Rev. Fluids 2017, 2, 114603. [Google Scholar] [CrossRef]
- Horimoto, Y.; Simonet-Davin, G.; Katayama, A.; Goto, S. Impact of a small ellipticity on the sustainability condition of developed turbulence in a precessing spheroid. Phys. Rev. Fluids 2018, 3, 044603. [Google Scholar] [CrossRef]
- Wu, C.C.; Roberts, P.H. On a dynamo driven by topographic precession. Geophys. Astrophys. Fluid Dyn. 2009, 103, 467–501. [Google Scholar] [CrossRef]
- Glampedakis, K.; Andersson, N.; Jones, D.I. On the stability of precessing superfluid neutron stars. Phys. Rev. Lett. 2008, 100, 081101. [Google Scholar] [CrossRef] [PubMed]
- Bayly, B.J. Three-dimensional instability of elliptical flow. Phys. Rev. Lett. 1986, 57, 2160–2163. [Google Scholar] [CrossRef] [PubMed]
- Kerswell, R.R. Elliptical instability. Annu. Rev. Fluid Mech. 2002, 34, 83–113. [Google Scholar] [CrossRef]
- Salhi, A.; Cambon, C. Precessing rotating flows with additional shear: Stability analysis. Phys. Rev. E 2009, 79, 036303. [Google Scholar] [CrossRef] [PubMed]
- Mahalov, A. The instability of rotating fluid columns subjected to a weak external Coriolis force. Phys. Fluids 1993, 5, 891–900. [Google Scholar] [CrossRef]
- Wiener, R.J.; Hammer, P.W.; Swanson, C.E.; Donnelly, R.J. Stability of Taylor-Couette Flow Subject to an External Coriolis Force. Phys. Rev. Lett. 1990, 64, 1115–1118. [Google Scholar] [CrossRef]
- Biferale, L.; Bonaccorso, F.; Mazzitelli, I.M.; van Hinsberg, M.A.T.; Lanotte, A.S.; Musacchio, S.; Perlekar, P.; Toschi, F. Coherent Structures and Extreme Events in Rotating Multiphase Turbulent Flows. Phys. Rev. X 2016, 6, 041036. [Google Scholar] [CrossRef]
- Craik, A.D.D.; Criminale, W.O. Evolution of wavelike disturbances in shear flows: A class of exact solutions of the Navier-Stokes equations. Proc. R. Soc. Lond. A 1986, 406, 13–26. [Google Scholar] [CrossRef]
- Salhi, A.; Lehner, T.; Cambon, C. Magnetohydrodynamic instabilities in rotating and precessing sheared flows: An asymptotic analysis. Phys. Rev. E 2010, 82, 016315. [Google Scholar] [CrossRef] [PubMed]
- Mason, R.M.; Kerswell, R.R. Chaotic dynamics in a strained rotating flow: A precessing plane fluid layer. J. Fluid Mech. 2002, 471, 71–106. [Google Scholar] [CrossRef]
- Barker, A.J. On turbulence driven by axial precession and tidal evolution of the spin-orbit angle of close-in giant planets. Mon. Not. R. Astron. Soc. 2016, 460, 2339–2350. [Google Scholar] [CrossRef]
- Godeferd, F.S.; Moisy, F. Structure and Dynamics of Rotating Turbulence: A Review of Recent Experimental and Numerical Results. Appl. Mech. Rev. 2015, 67, 030802. [Google Scholar] [CrossRef]
- Shirley, J.H.; Fairbridge, R.W. Encyclopedia of Planetary Sciences; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Babin, A.; Mahalov, A.; Nicolaenko, B. Global regularity of 3d rotating Navier-Stokes equations for resonant domains. Appl. Maths Lett. 2000, 13, 51–57. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, S.; Eyink, G.L.; Holm, D.D. Resonant interactions in rotating homogeneous three-dimensional turbulence. J. Fluid Mech. 2005, 542, 139–164. [Google Scholar] [CrossRef]
- Thiele, M.; Muller, W.-C. Structure and decay of rotating homogeneous turbulence. J. Fluid Mech. 2009, 637, 425–442. [Google Scholar] [CrossRef]
- Bourouiba, L.; Straub, D.N.; Waite, M.L. Non-local energy transfers in rotating turbulence at intermediate Rossby number. J. Fluid Mech. 2012, 690, 129–147. [Google Scholar] [CrossRef]
- Julien, K.; Rubio, A.M.; Grooms, I.; Knobloch, E. Statistical and physical balances in low Rossby number Rayleigh-Bénard convection. Geophys. Astrophys. Fluid Dyn. 2012, 106, 392–428. [Google Scholar] [CrossRef]
- Rubio, A.M.; Julien, K.; Knobloch, E.; Jeffrey, B.W. Upscale Energy Transfer in three-dimensional rapidly rotating turbulent convection. Phys. Rev. Lett. 2014, 112, 144501. [Google Scholar] [CrossRef] [PubMed]
- Nastrom, G.; Jasperson, W.; Gage, K. Kinetic energy spectrum of large and mesoscale atmospheric processes. Nature 1984, 310, 36–38. [Google Scholar] [CrossRef]
- Byrne, D.; Zhang, J.A. Height-dependent transition from 3-D to 2-D turbulence in the hurricane boundary layer. Geophys. Res. Lett. 2013, 40, 1439–1442. [Google Scholar] [CrossRef]
- Sahoo, G.; Alexakis, A.; Biferale, L. Discontinuous transition from direct to inverse cascade in three-dimensional turbulence. Phys. Rev. Lett. 2017, 118, 164501. [Google Scholar] [CrossRef] [PubMed]
- Baklouti, F.S.; Khlifi, A.; Salhi, A.; Godeferd, G.; Cambon, C.; Lehner, T. Kinetic magnetic energy exchanges in rotating magnetohydrodynamic turbulence. J. Turbulence 2019, 20, 263–284. [Google Scholar] [CrossRef]
- Favier, B.; Godeferd, F.; Cambon, C. On the effect of rotation on magnetohydrodynamic turbulence at high magnetic Reynolds number. Geophys. Astrophys. Fluid Dyn. 2012, 106, 89–111. [Google Scholar] [CrossRef][Green Version]
- Galtier, S. Weak turbulence theory for rotating magnetohydrodynamics and planetary dynamos. J. Fluid Mech. 2014, 757, 114–154. [Google Scholar] [CrossRef]
- Salhi, A.; Baklouti, F.S.; Godeferd, F.; Lehner, T.; Cambon, C. Energy partition, scale by scale, in magnetic Archimedes Coriolis weak wave turbulence. Phys. Rev. E. 2017, 95, 023112. [Google Scholar] [CrossRef]
- Menu, M.D.; Galtier, S.; Petitdemange, L. Inverse cascade of hybrid helicity in BΩ-MHD turbulence. Phys. Rev. Fluids 2019, 4, 073701. [Google Scholar] [CrossRef]
- Biskamp, D. Nonlinear Magnetohydrodynamics; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Baerenzung, J.; Politano, H.; Ponty, Y.; Pouquet, A. Spectral Modeling of Magnetohydrodynamic Turbulent Flows. Phys. Rev. E 2008, 78, 026310. [Google Scholar] [CrossRef]
- Lesur, G.; Longaretti, P.-Y. Impact of dimensionless numbers on the efficiency of magnetorotational instability induced turbulent transport. Mon. Not. R. Astron. Soc. 2007, 378, 1471–1480. [Google Scholar] [CrossRef]
- Orszag, S.A.; Patterson, G.S. Numerical Simulation of Three-Dimensional Homogeneous Isotropic Turbulence. Phys. Rev. Lett. 1972, 28, 76–79. [Google Scholar] [CrossRef]
- Yakubovich, V.A.; Starzhinskii, V.M. Linear Differential Equations with Periodic Coefficients; Wiley: New York, NY, USA, 1975; Volume 1. [Google Scholar]
- Lebovitz, N.R.; Zweibel, E. Magnetoelliptic instabilities. Astrophys. J. 2004, 609, 301–312. [Google Scholar] [CrossRef]
- Salhi, A.; Cambon, C. Stability of rotating stratified shear flow: An analytical study. Phys. Rev. E 2010, 81, 026302. [Google Scholar] [CrossRef] [PubMed]
- Lehnert, B. The decay of magnetoturbulence in the presence of a magnetic field and Coriolis force. Q. Appl. Math. 1955, 12, 321–341. [Google Scholar] [CrossRef][Green Version]
- Nornberg, M.D.; Ji, H.; Schartman, E.; Roach, A.; Goodman, J. Observation of Magnetocoriolis Waves in a Liquid Metal Taylor- Couette Experiment. Phys. Rev. Lett. 2010, 104, 074501. [Google Scholar] [CrossRef] [PubMed]
- Rogallo, R.S. Numerical Experiments in Homogeneous Turbulence; NASA Ames Research Center: Moffett Field, CA, USA, 1981. [Google Scholar]
- Salhi, A.; Jacobitz, F.G.; Schneider, K.; Cambon, C. Nonlinear dynamics and anisotropic structure of rotating sheared turbulence. Phys. Rev. E. 2014, 89, 013020. [Google Scholar] [CrossRef] [PubMed]
- Roberts, P.H.; King, E.M. On the genesis of the Earth’s magnetism. Rep. Prog. Phys. 2013, 76, 096801. [Google Scholar] [CrossRef] [PubMed]
- Jones, C. Planetary magnetic fields and fluid dynamos. Annu. Rev. Fluid Mech. 2011, 43, 583–614. [Google Scholar] [CrossRef]
- Bigot, B.; Galtier, S.; Politano, H. Development of anisotropy in incompressible magnetohydrodynamic turbulence. Phys. Rev. E 2008, 78, 066301. [Google Scholar] [CrossRef]
- Cambon, C.; Rubinstein, R.; Godeferd, F. Advances in wave turbulence: Rapidly rotating flows. New J. Phys. 2004, 6, 1–30. [Google Scholar] [CrossRef]
- Goto, S.; Komoda, K.; Kanki, J. Turbulence in precessing containers. In Proceedings of the 11th International Symposium on Turbulence and Shear Flow Phenomena (TSFP11), Southampton, UK, 30 July–2 August 2019. [Google Scholar]
- Elmegreen, B.G.; Scalo, J. Interstellar Turbulence I: Observations and Processes. Ann. Rev. Astron. Astrophys. 2004, 42, 211–273. [Google Scholar] [CrossRef]
- Corrsin, S. On Local Isotropy in Turbulent Shear Flow; Technical Report 58B11; NACA R & M: Washington, DC, USA, 1958. [Google Scholar]
- Zeman, O. A note on the spectra and decay of rotating homogeneous turbulence. Phys. Fluids 1994, 6, 3221–3223. [Google Scholar] [CrossRef]
- Mininni, P.D.; Rosenberg, D.; Pouquet, A. Isotropisation at small scales of rotating helically driven turbulence. J. Fluid Mech. 2012, 699, 263–279. [Google Scholar] [CrossRef]
- Delache, A.; Cambon, C.; Godeferd, F. Scale by scale anisotropy in freely decaying rotating turbulence. Phys. Fluids 2014, 26, 025104. [Google Scholar] [CrossRef]
- Iyer, K.P.; Mazzitelli, I.; Bonaccorso, F.; Pouquet, A.; Biferale, L. Rotating turbulence under “precession-like” perturbation. Eur. Phys. J. E 2015, 38, 128–134. [Google Scholar] [CrossRef][Green Version]
- Alexakis, A. On the 2D behavior of 3D MHD with a strong guiding field. Phys. Rev. E 2011, 84, 056330. [Google Scholar] [CrossRef]
- Smith, L.M.; Chasnov, J.R.; Waleffe, F. Crossover from two- to three-dimensional turbulence. Phys. Rev. Lett. 1996, 77, 2467–2470. [Google Scholar] [CrossRef]
- Smith, L.M.; Lee, Y. On near resonances and symmetry breaking in forced rotating flows at moderate Rossby number. J. Fluid Mech. 2005, 535, 111–142. [Google Scholar] [CrossRef]
- Sen, A.; Mininni, P.D.; Rosenberg, D.; Pouquet, A. Anisotropy and nonuniversality in scaling laws of the large-scale energy spectrum in rotating turbulence. Phys. Rev. E 2012, 86, 036319. [Google Scholar] [CrossRef]
- Pouquet, A.; Sen, A.; Rosenberg, D.; Mininni, P.D.; Baerenzung, J. Inverse cascades in turbulence and the case of rotating flows. Phys. Scr. 2013, 2013, 014032. [Google Scholar] [CrossRef][Green Version]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).