Large-Eddy Simulations with an Immersed Boundary Method: Pollutant Dispersion over Urban Terrain
Abstract
1. Introduction
2. The Immersed Boundary Method in Meso-NH
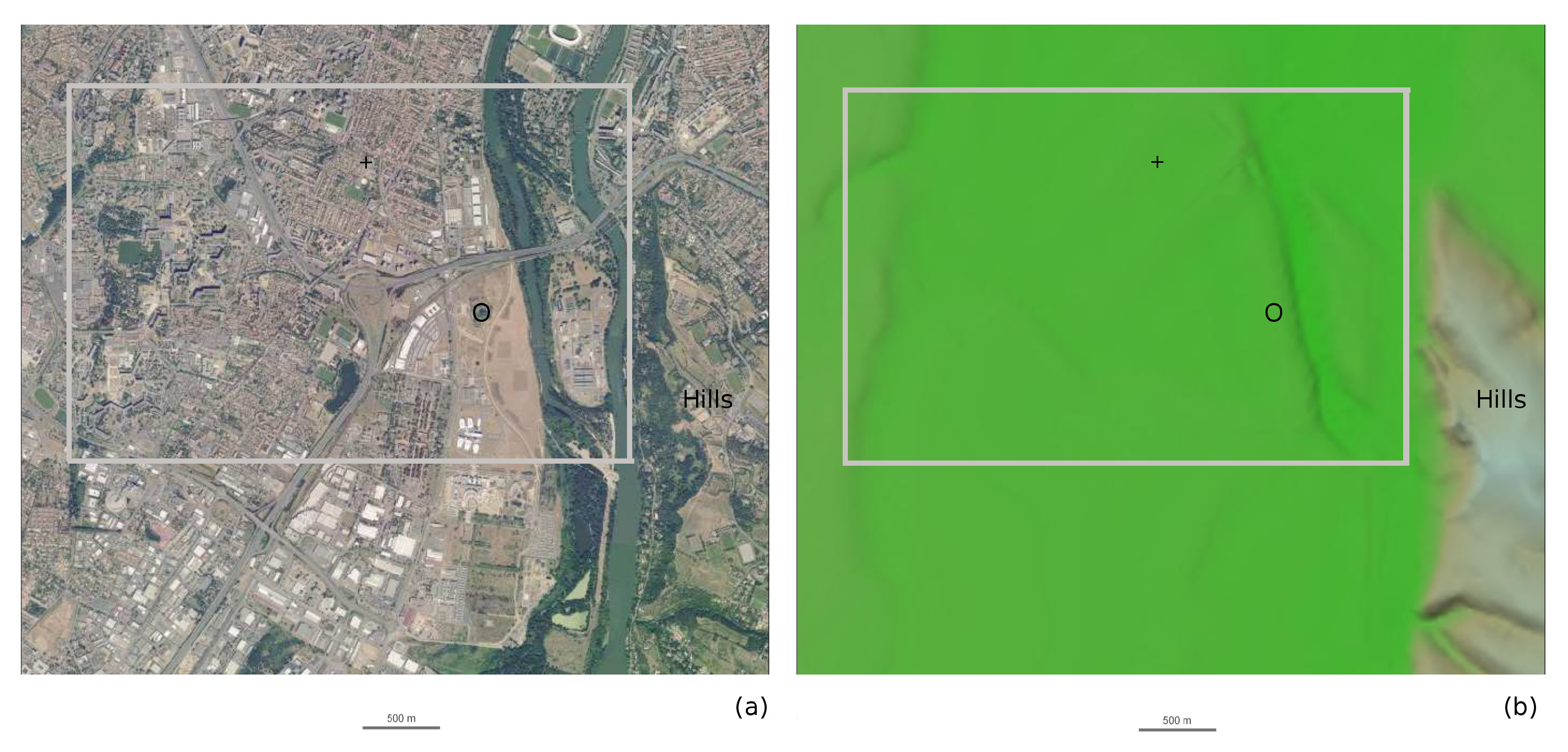
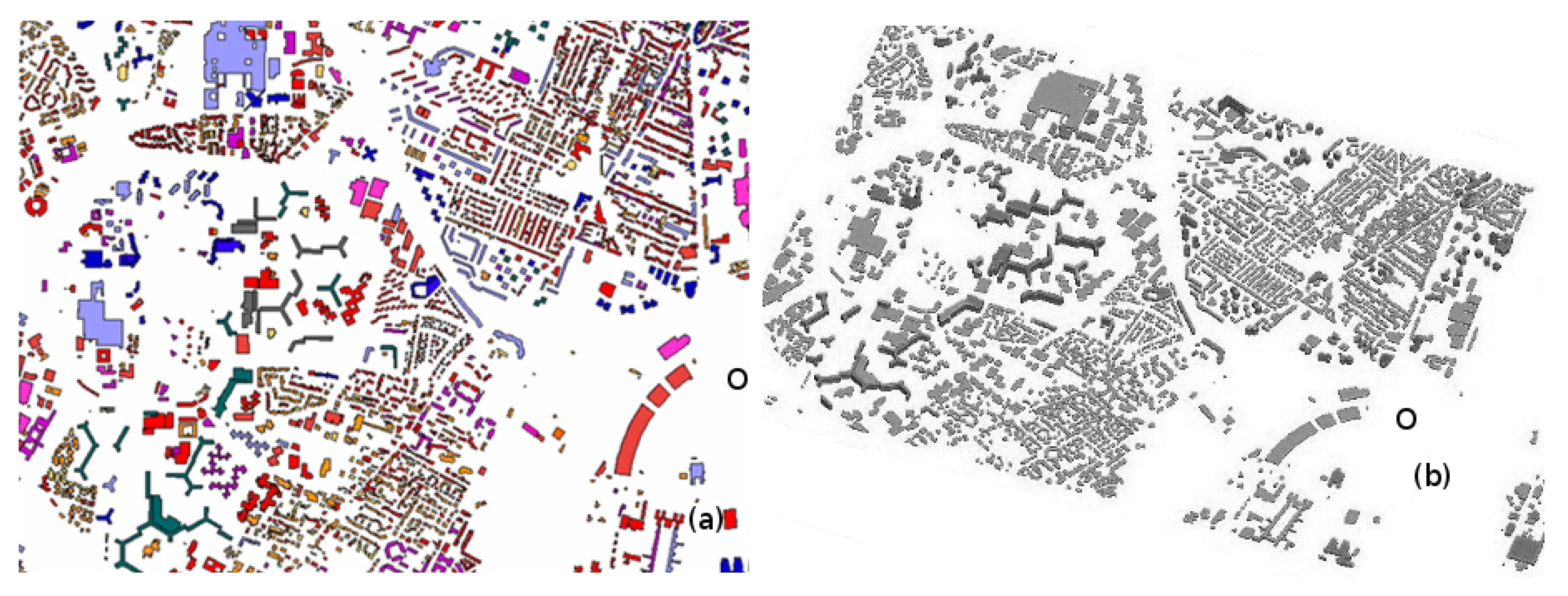
3. The AZF Case
4. Presentation of the AZF Case Simulation
5. Simulations of the AZF Case
5.1. Sensitivity to Different Numerical Schemes
5.2. Nitrogen Dioxide Dispersion
6. Discussion on Population Exposure
6.1. The Initial Plume Structure
- Barthélémy et al. [21] mentioned an explosion of 1010 kg of ammonium nitrate. The maximum produced NO mass can be evaluated assuming that oxidation was complete and that all the nitrogen atoms formed the nitrogen dioxide. Assuming [4:8] dozen of tons of detonated ammonium nitrate [20], a plume with a volume of 5.10 m and an uniform NO distribution results in a mean concentration approaching [1:2] g m.
- Considering the ORAMIP measurement at the Jacquier Station, the passive sampler used for the measurement provides a NO value mean over 15 min which gives a dose estimate. Knowing the experimental value of 350 g m (the difference of the observed concentrations at Jacquier between 0830 and 0815 UTC), considering the plume dilution to be well–modelled by MNH-IBM and following the numerical results for (Figure 7b), the range of the presumed initial NO concentration is estimated to [10:30] mg m with a more likely value of 20 mg m 10 ppm (ratio defined by the mole fraction).
- Deedi [22] reported several concentration values from a study of the plume opacity. The few pictures of the initial plume lead to a 1010mg m NO concentration range.
6.2. The Population Exposure
7. Conclusions and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AZF | Azote de France |
| BL | Boundary Layer |
| CCT | Cut-Cell Technique |
| DFT | Discrete Fourier Transform |
| ERK | Explicit Runge-Kutta scheme |
| GCT | Ghost-Cell Technique |
| IBM | Immersed Boundary Method |
| LES | Large Eddy Simulation |
| MNH-IBM | IBM adapted to the Meso-NH model |
| MUST | Mock Urban Setting Test |
| ORAMIP | Observatoire Régional de l’Air en Midi-Pyrénées |
| PPM | Piecewise Parabolic Method |
| SSF | Surface State Function |
| SSI | Surface State Index |
| WENO | Weight-Essential-Non-Oscillatory |
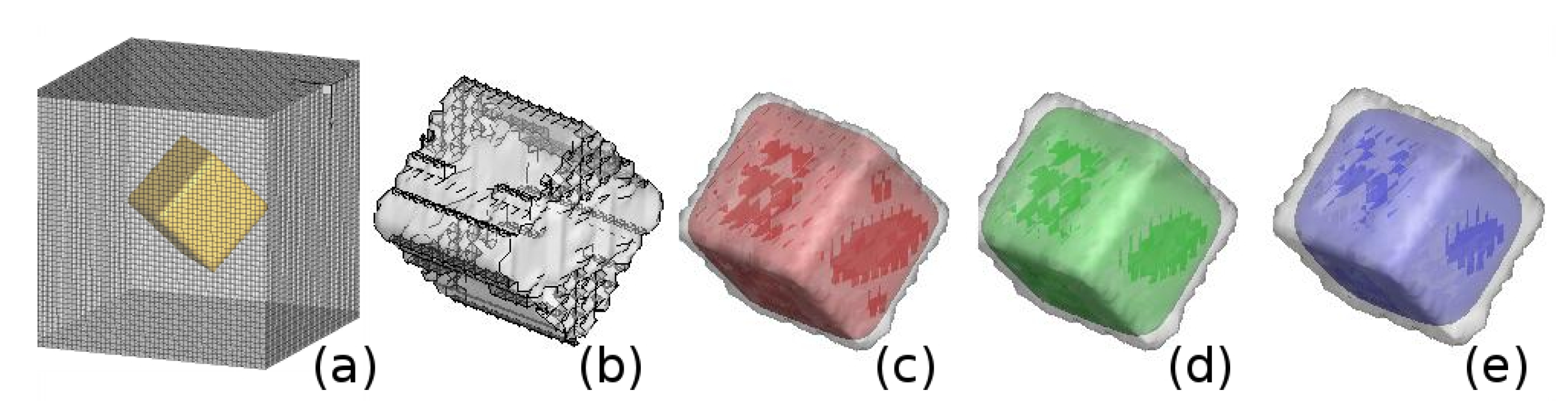
Appendix A. Surface State and LevelSet Function
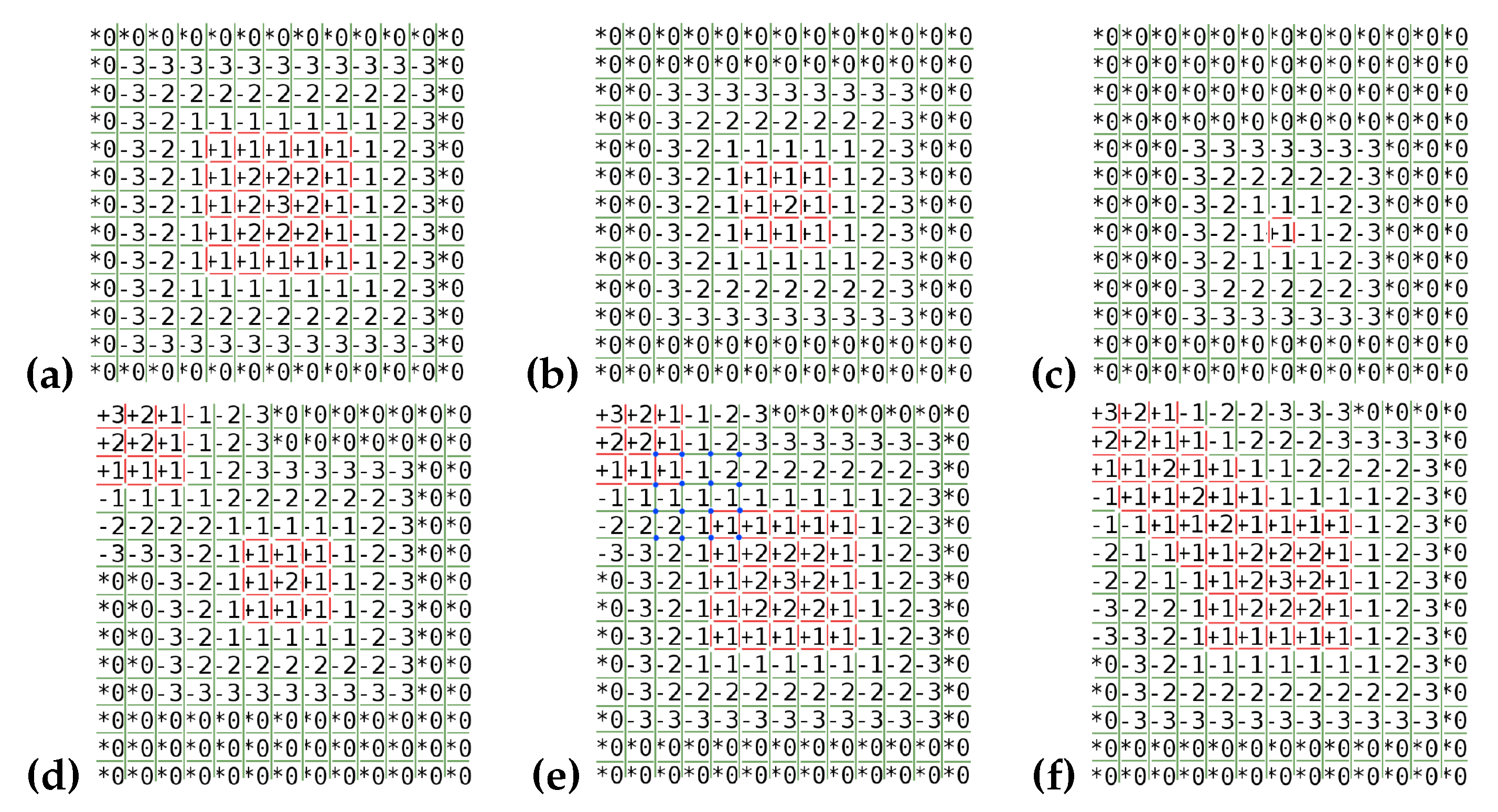
- P1: If , no process is expected (Figure A1a).
- P3: If and , the ‘filtering’ process is activated. The obstacle shown in Figure A1c disappears.
- P4: The proximity of the obstacles (or spacings) can induce a ‘merging’ process testing = ±1 and (opposite sign). This is performed once in all grid directions and a second time only in the diagonal directions to limit the ‘stair-step shaped edges’ effect (Figure A1d–f). Figure A1d shows a small obstacle in the domain centre and another obstacle in the top-left corner. The ’increasing’ process (P2) is activated and the obstacle in the centre is extended. The first step of the ’merging’ process (P4) affects the median height of the two obstacles for cells detected at the blue points (Figure A1e). The second ’merging pass’ softens the border of the merged blue region (Figure A1f).
| Process | Class | Direction | Local | Surrounding |
|---|---|---|---|---|
| P1 | Nothing | All | . | |
| P2 | Increasing | All | ||
| P3 | Filtering | All | ||
| P4 | Merging | All |
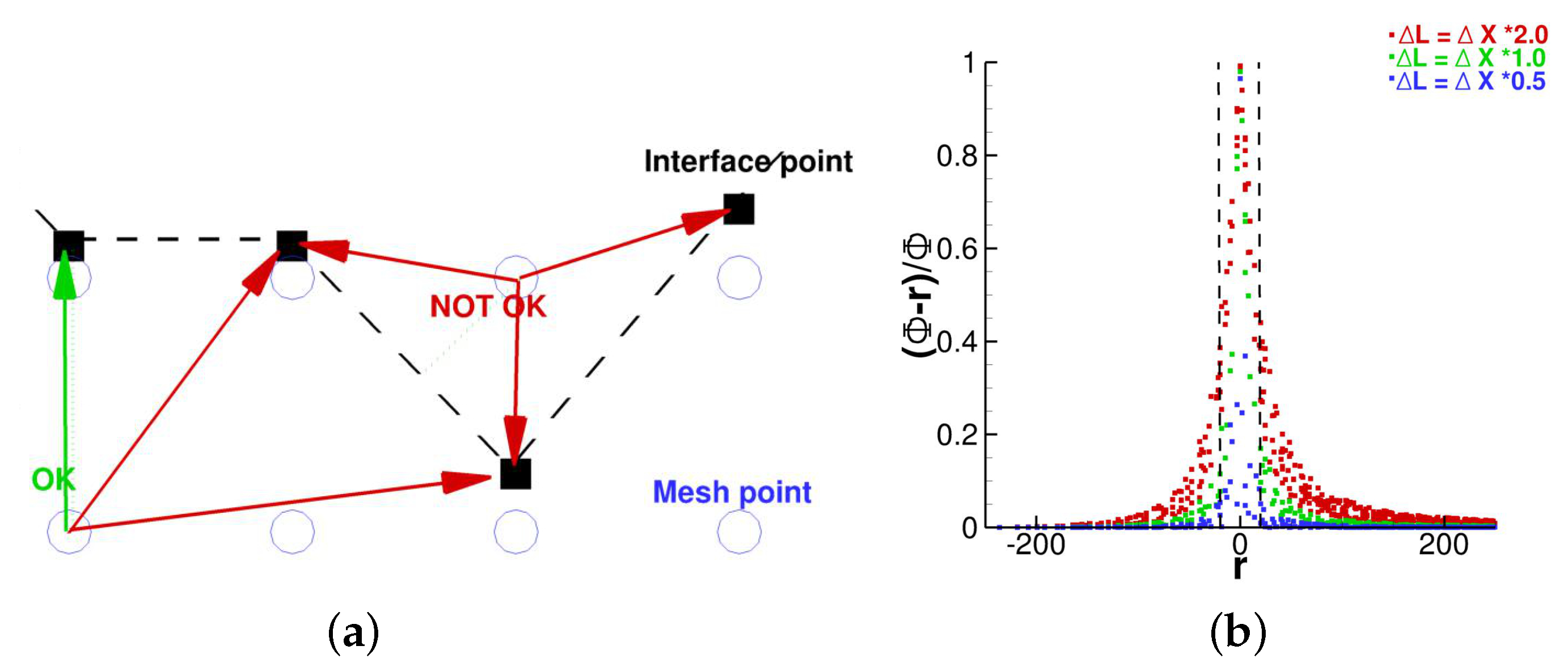
Appendix B. Smoothing Technique and LevelSet Function
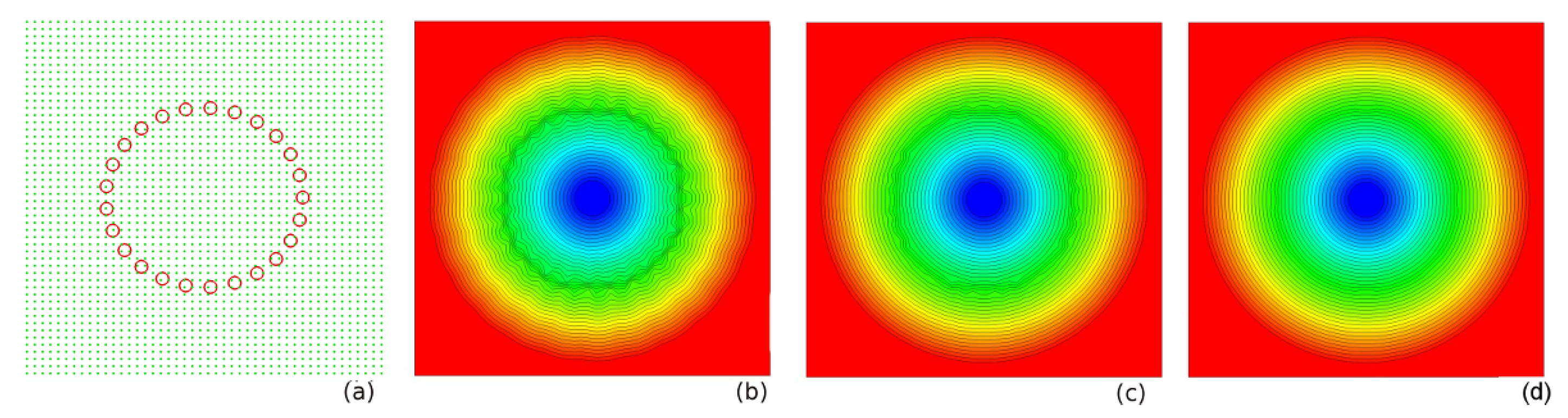
Appendix C. Geometric Properties and LevelSet Function
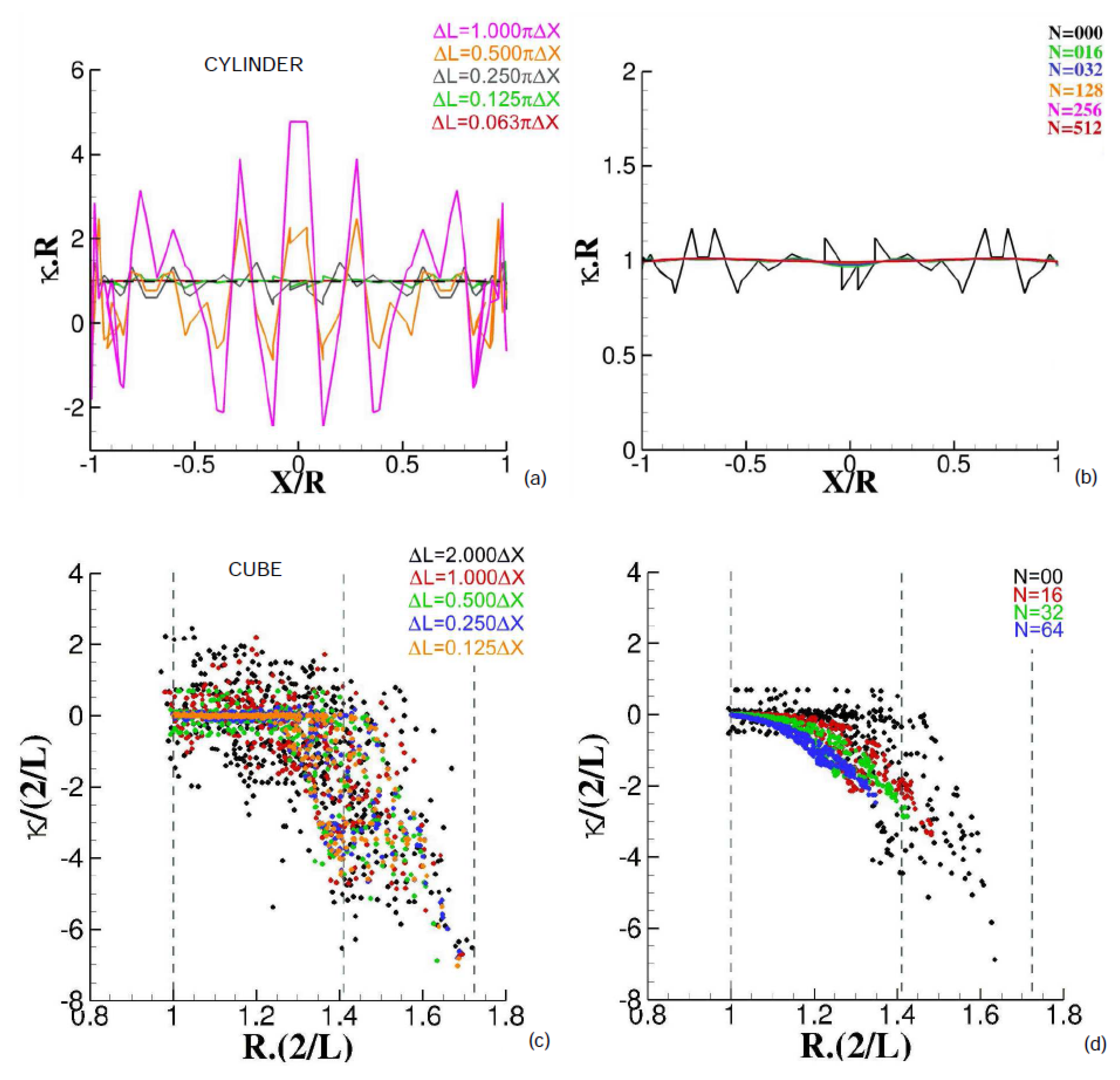

References
- Santiago, J.; Dejoan, A.; Martilli, A.; Martin, F.; Pinelli, A. Comparison between large-eddy simulation and Reynolds-averaged Navier–Stokes computations for the MUST field experiment. Part I: Study of the flow for an incident wind directed perpendicularly to the front array of containers. Bound.-Layer Meteorol. 2010, 135, 109–132. [Google Scholar] [CrossRef]
- Milliez, M.; Carissimo, B. Numerical simulations of pollutant dispersion in an idealized urban area, for different meteorological conditions. Bound.-Layer Meteorol. 2007, 122, 321–342. [Google Scholar] [CrossRef]
- Onodera, N.; Aoki, T.; Shimokawabe, T.; Kobayashi, H. Large-scale LES wind simulation using lattice Boltzmann method for a 10 km × 10 km area in metropolitan Tokyo. TSUBAME E-Sci. J. Glob. Sci. Inf. Comput. Cent. 2013, 9, 2–8. [Google Scholar]
- Bergot, T.; Escobar, J.; Masson, V. Effect of small scale surface heterogeneities and buildings on radiation fog: Large-Eddy Simulation study at Paris-Charles de Gaulle airport. Q. J. R. Meteorol. Soc. 2015, 141, 285–298. [Google Scholar] [CrossRef]
- Mittal, R.; Iaccarino, G. Immersed boundary methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef]
- Aumond, P.; Masson, V.; Lac, C.; Gauvreau, B.; Dupont, S.; Bérengier, M. Including the drag effects of canopies: Real case large-eddy simulation studies. Bound.-Layer Meteorol. 2013, 146, 65–80. [Google Scholar] [CrossRef]
- Tseng, Y.H.; Ferziger, J.H. A ghost-cell immersed boundary method for flow in complex geometry. J. Comput. Phys. 2003, 192, 593–623. [Google Scholar] [CrossRef]
- Lundquist, K.A.; Chow, F.K.; Lundquist, J.K. An immersed boundary method for the weather research and forecasting model. Mon. Weather Rev. 2010, 138, 796–817. [Google Scholar] [CrossRef]
- Lundquist, K.A.; Chow, F.K.; Lundquist, J.K. An immersed boundary method enabling large-eddy simulations of flow over complex terrain in the WRF Model. Mon. Weather Rev. 2012, 140, 3936–3955. [Google Scholar] [CrossRef]
- Arthur, R.S.; Lundquist, K.A.; Mirocha, J.D.; Chow, F.K. Topographic effects on radiation in the WRF Model with the immersed boundary method: Implementation, validation, and application to complex terrain. Mon. Weather Rev. 2018, 146, 3277–3292. [Google Scholar] [CrossRef]
- Auguste, F.; Réa, G.; Paoli, R.; Lac, C.; Masson, V.; Cariolle, D. Implementation of an immersed boundary method in the Meso-NH V5.2 model: Applications to an idealized urban environment. Geosci. Model Dev. 2019, 12, 2607–2633. [Google Scholar] [CrossRef]
- Lac, C.; Chaboureau, J.P.; Masson, V.; Pinty, J.P.; Tulet, P.; Escobar, J.; Leriche, M.; Barthe, C.; Aouizerats, B.; Augros, C.; et al. Overview of the Meso-NH model version 5.4 and its applications. Geosci. Model Dev. 2018, 11, 1929–1969. [Google Scholar] [CrossRef]
- Lafore, J.P.; Stein, J.; Asencio, N.; Bougeault, P.; Ducrocq, V.; Duron, J.; Fischer, C.; Héreil, P.; Mascart, P.; Masson, V.; et al. The Meso-NH Atmospheric Simulation System. Part I: Adiabatic formulation and control simulations. Scientific objectives and experimental design. Ann. Geophys. 1998, 16, 90–109. [Google Scholar] [CrossRef]
- Masson, V.; Lion, Y.; Peter, A.; Pigeon, G.; Buyck, J.; Brun, E. Grand Paris: Regional landscape change to adapt city to climate warming. Clim. Chang. 2013, 117, 769–782. [Google Scholar] [CrossRef]
- Yang, G.; Causon, D.; Ingram, D.; Saunders, R.; Battent, P. A Cartesian cut cell method for compressible flows. Part A: Static body problems. Aeronaut. J. 1997, 101, 47–56. [Google Scholar]
- Piomelli, U.; Balaras, E. Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 2002, 34, 349–374. [Google Scholar] [CrossRef]
- Bernardet, P. The pressure term in the anelastic model: A symmetric elliptic solver for an Arakawa C grid in generalized coordinates. Mon. Weather Rev. 1995, 123, 2474–2490. [Google Scholar] [CrossRef][Green Version]
- Cuxart, J.; Bougeault, P.; Redelsperger, J.L. A turbulence scheme allowing for mesoscale and large-eddy simulations. Q. J. R. Meteorol. Soc. 2000, 126, 1–30. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Cassadou, S.; Ricoux, C.; Gourier-Fréry, C.; Schwoebel, V.; Guinard, A. Conséquences Sanitaires de l’explosion Survenue à l’usine AZF de Toulouse le 21 Sept. 2001 (Expositions Environnementales); Technical Report, Rapport du DRASS Midi-Pyrénées; Institute de Veille Sanitaire: Saint-Maurice, France, 2003.
- Barthélémy, F.; Hornus, H.; Roussot, J.; Hufschmitt, J.P.; Raffoux, J.F. Usine de la Société Grande Paroisse Toulouse—Accident du 21 Septembre 2001; Technical Report, Rapport de l’Inspection Générale de l’Environnement; Ministère de l’Aménagement du Territoire et de l’Environnement: Paris, France, 2001.
- Deedi. Management of Oxides of Nitrogen in Open Cut Blasting; Technical Report, Queensland Guidance Note, QGN 20, v3; Department of Employment, Economic Development, and Innovation: Barcaldine, Australia, 1999.
- Tissot, S.; Lafon, D. Seuils de toxicité aiguë utilisés lors d’émissions atmosphériques accidentelles de produits chimiques. Archives des Maladies Professionnelles et de l’Environnement 2006, 67, 870–876. [Google Scholar] [CrossRef]
- Lunet, T.; Lac, C.; Auguste, F.; Visentin, F.; Masson, V.; Escobar, J. Combination of WENO and Explicit Runge-Kutta methods for wind transport in Meso-NH model. Mon. Weather Rev. 2017, 145, 3817–3838. [Google Scholar] [CrossRef]
- Colella, P.; Woodward, P.R. The piecewise parabolic method (PPM) for gas-dynamical simulations. J. Comput. Phys. 1984, 54, 174–201. [Google Scholar] [CrossRef]
- Carpenter, K.M. Note on the paper ‘Radiation conditions for lateral boundaries of limited area numerical models’. Q. J. R. Meteorol. Soc. 1982, 110, 717–719. [Google Scholar] [CrossRef]
- Skamarock, W.C. Evaluating mesoscale NWP models using kinetic energy spectra. Mon. Weather Rev. 2004, 132, 3019–3032. [Google Scholar] [CrossRef]
- Ricard, D.; Lac, C.; Riette, S.; Legrand, R.; Mary, A. Kinetic energy spectra characteristics of two convection-permitting limited-area models AROME and Meso-NH. Q. J. R. Meteorol. Soc. 2013, 139, 1327–1341. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Hadjadj, A.; Chinnayya, A. On the use of immersed boundary methods for shock and obstacle interactions. J. Comput. Phys. 2011, 230, 1731–1748. [Google Scholar] [CrossRef]

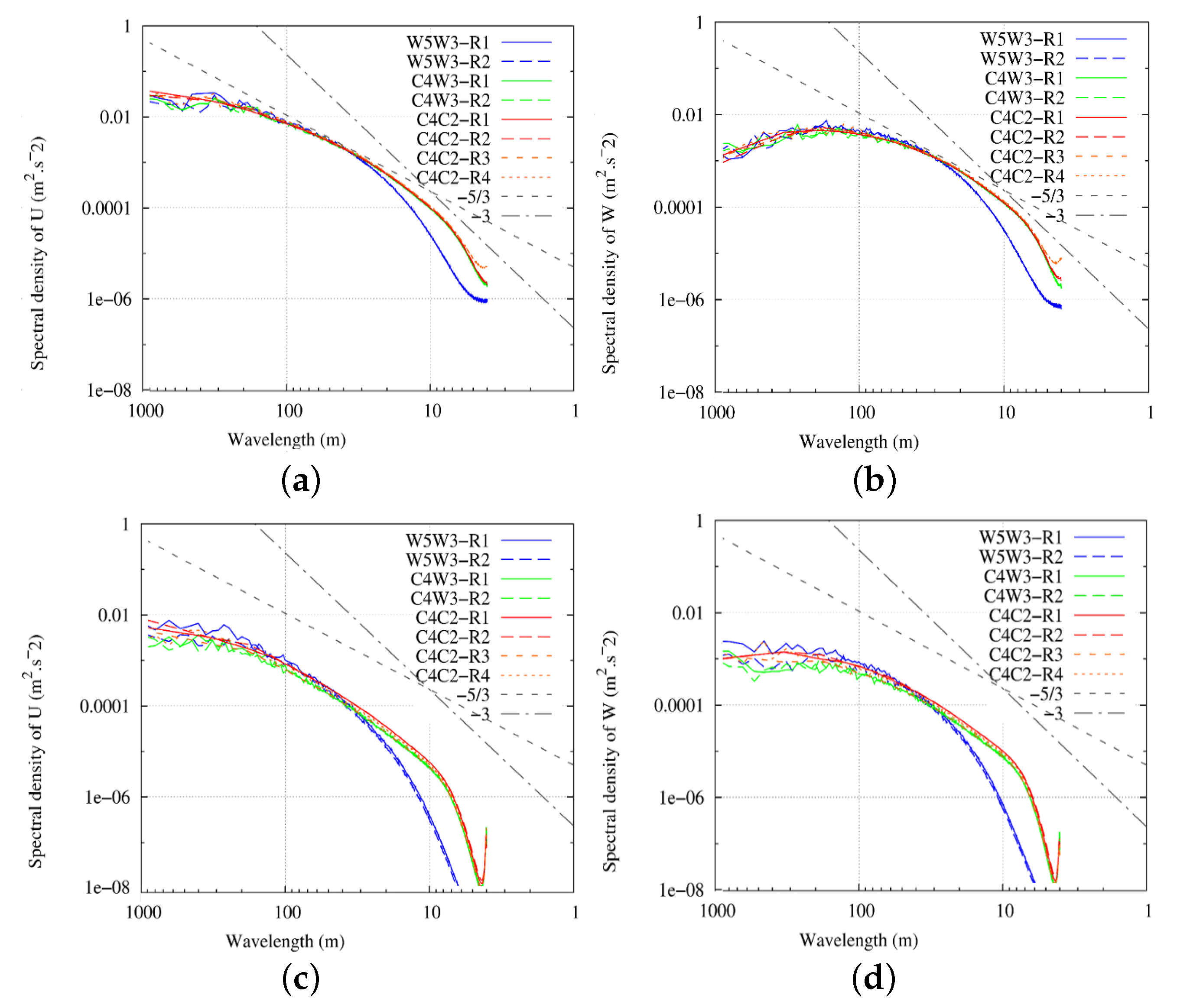

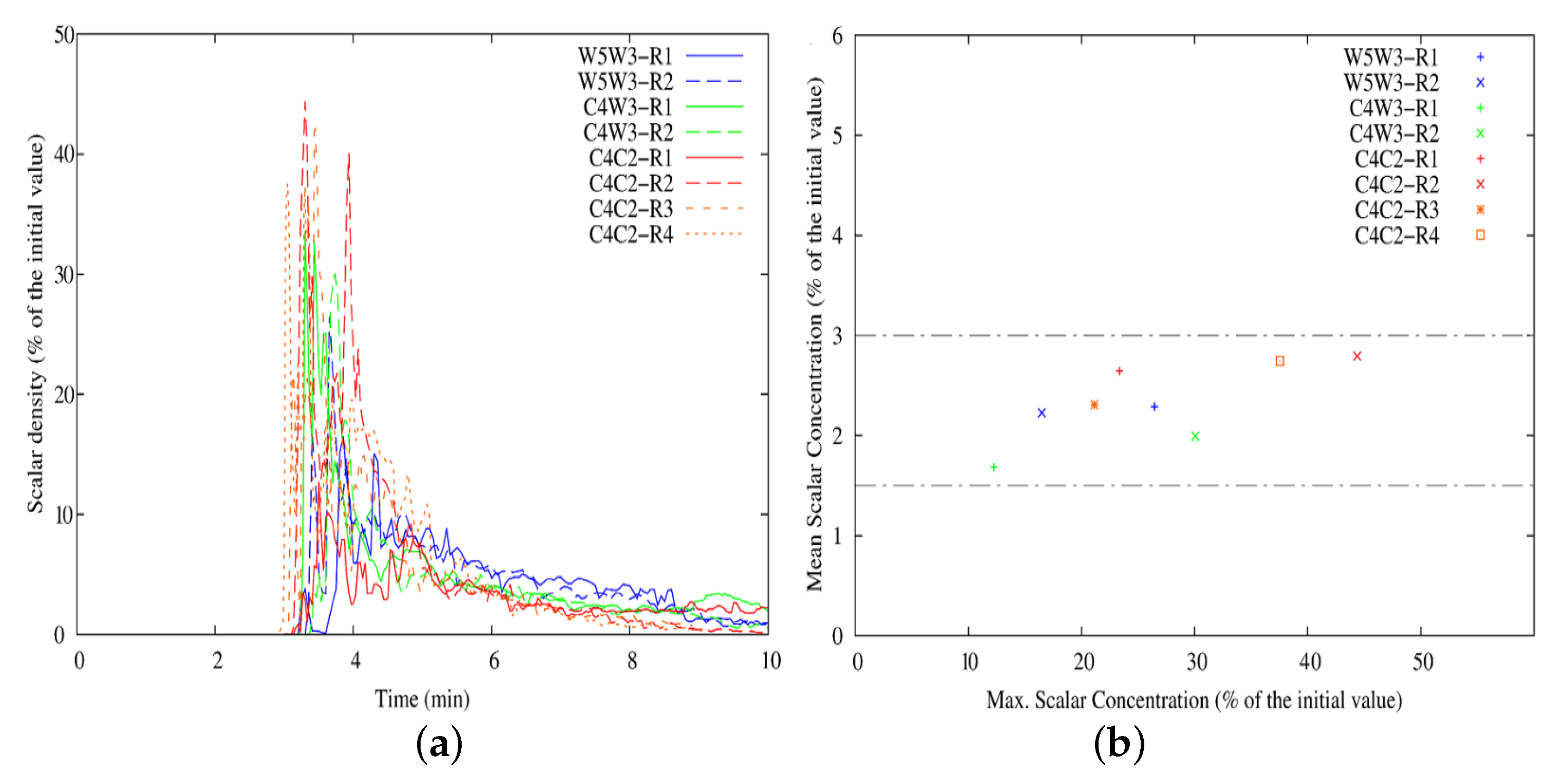
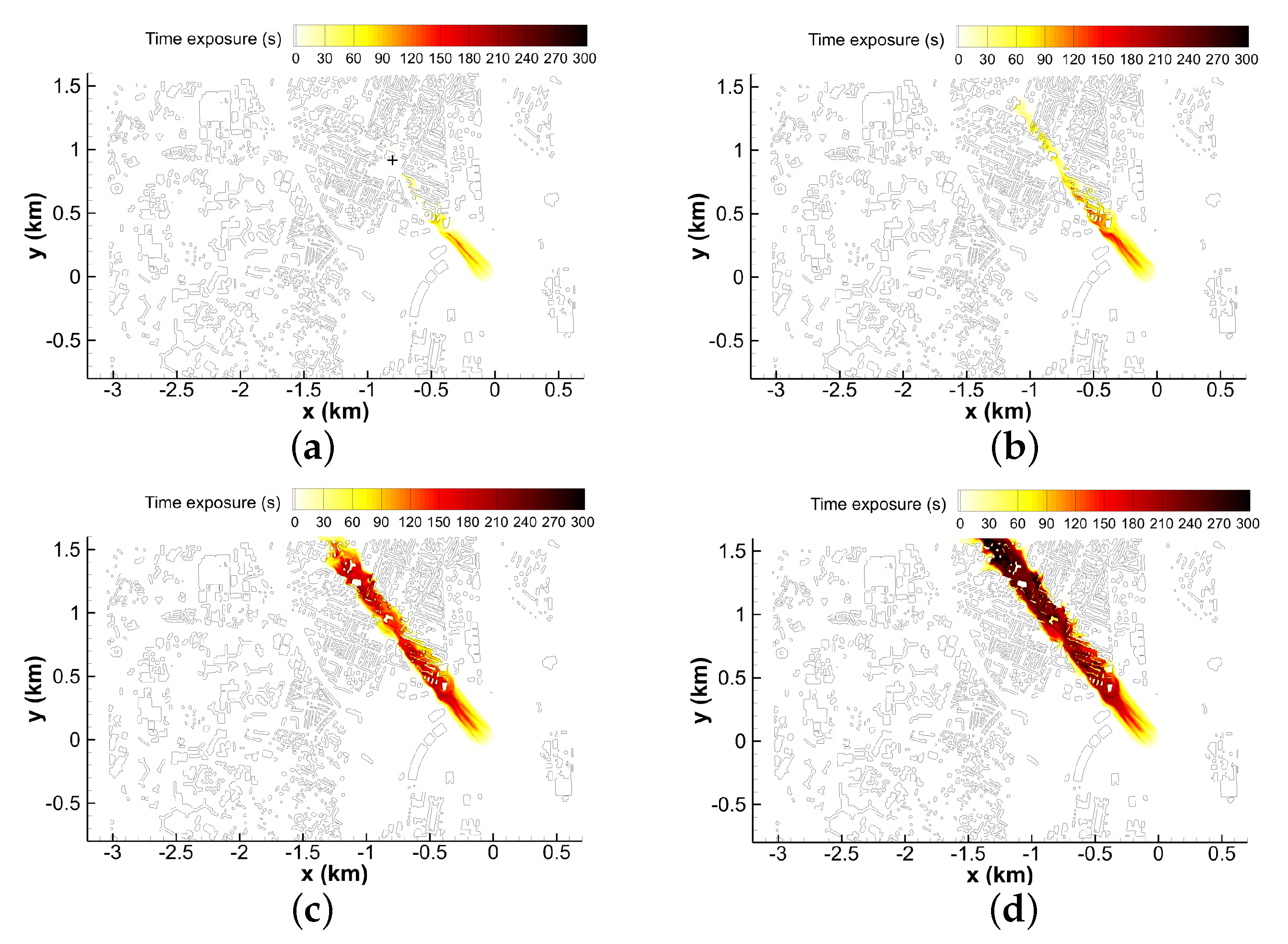
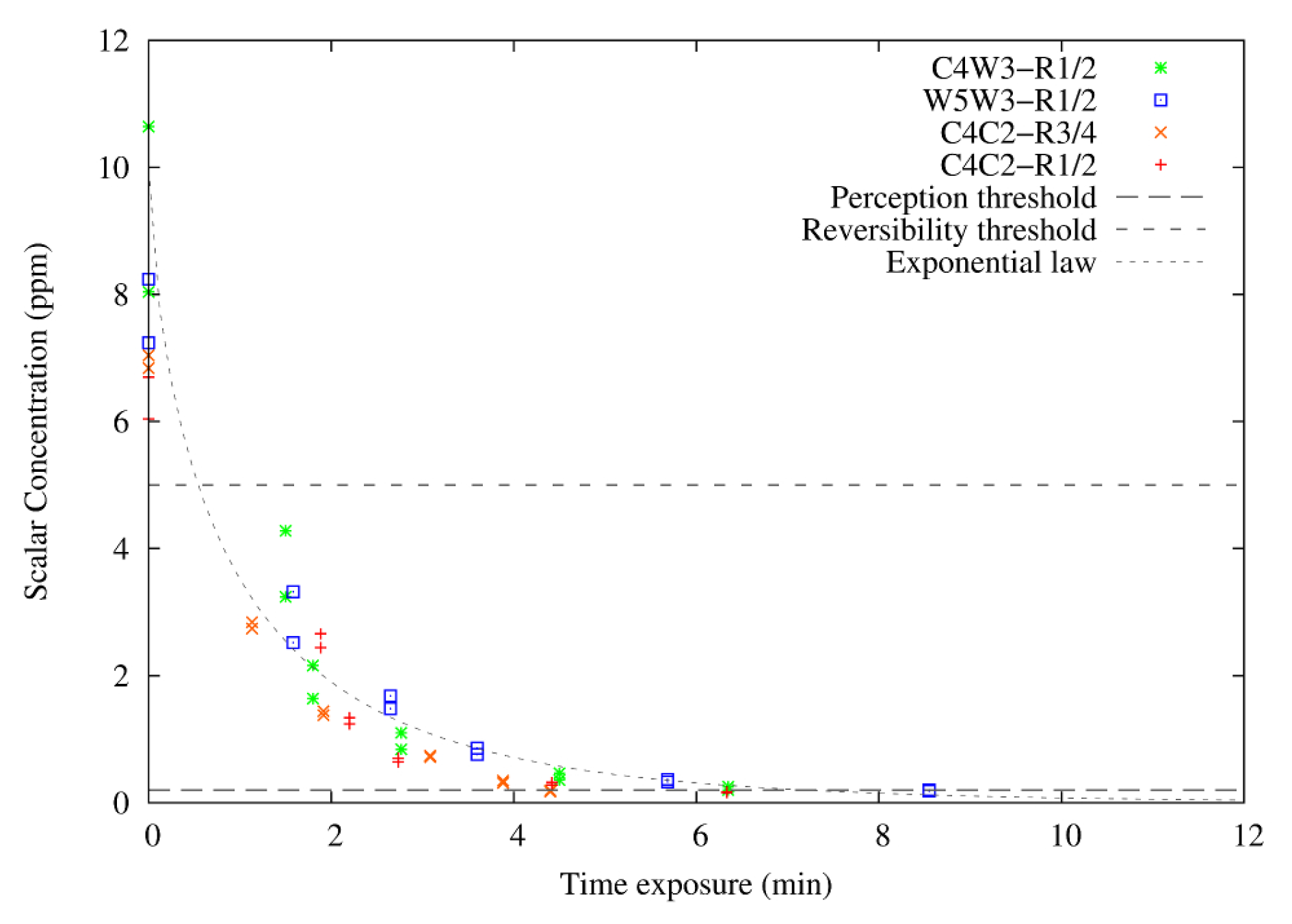
| Notation | Definition |
|---|---|
| f | Local and instantaneous variable |
| Gaussian distribution near the ground | |
| 15 min integration |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Auguste, F.; Lac, C.; Masson, V.; Cariolle, D. Large-Eddy Simulations with an Immersed Boundary Method: Pollutant Dispersion over Urban Terrain. Atmosphere 2020, 11, 113. https://doi.org/10.3390/atmos11010113
Auguste F, Lac C, Masson V, Cariolle D. Large-Eddy Simulations with an Immersed Boundary Method: Pollutant Dispersion over Urban Terrain. Atmosphere. 2020; 11(1):113. https://doi.org/10.3390/atmos11010113
Chicago/Turabian StyleAuguste, Franck, Christine Lac, Valery Masson, and Daniel Cariolle. 2020. "Large-Eddy Simulations with an Immersed Boundary Method: Pollutant Dispersion over Urban Terrain" Atmosphere 11, no. 1: 113. https://doi.org/10.3390/atmos11010113
APA StyleAuguste, F., Lac, C., Masson, V., & Cariolle, D. (2020). Large-Eddy Simulations with an Immersed Boundary Method: Pollutant Dispersion over Urban Terrain. Atmosphere, 11(1), 113. https://doi.org/10.3390/atmos11010113






