Assessment of a Real-Time Prediction Method for High Clothing Thermal Insulation Using a Thermoregulation Model and an Infrared Camera
Abstract
1. Introduction
2. Methods for Evaluating Clo Level
2.1. Standard Method Using a Thermal Manikin
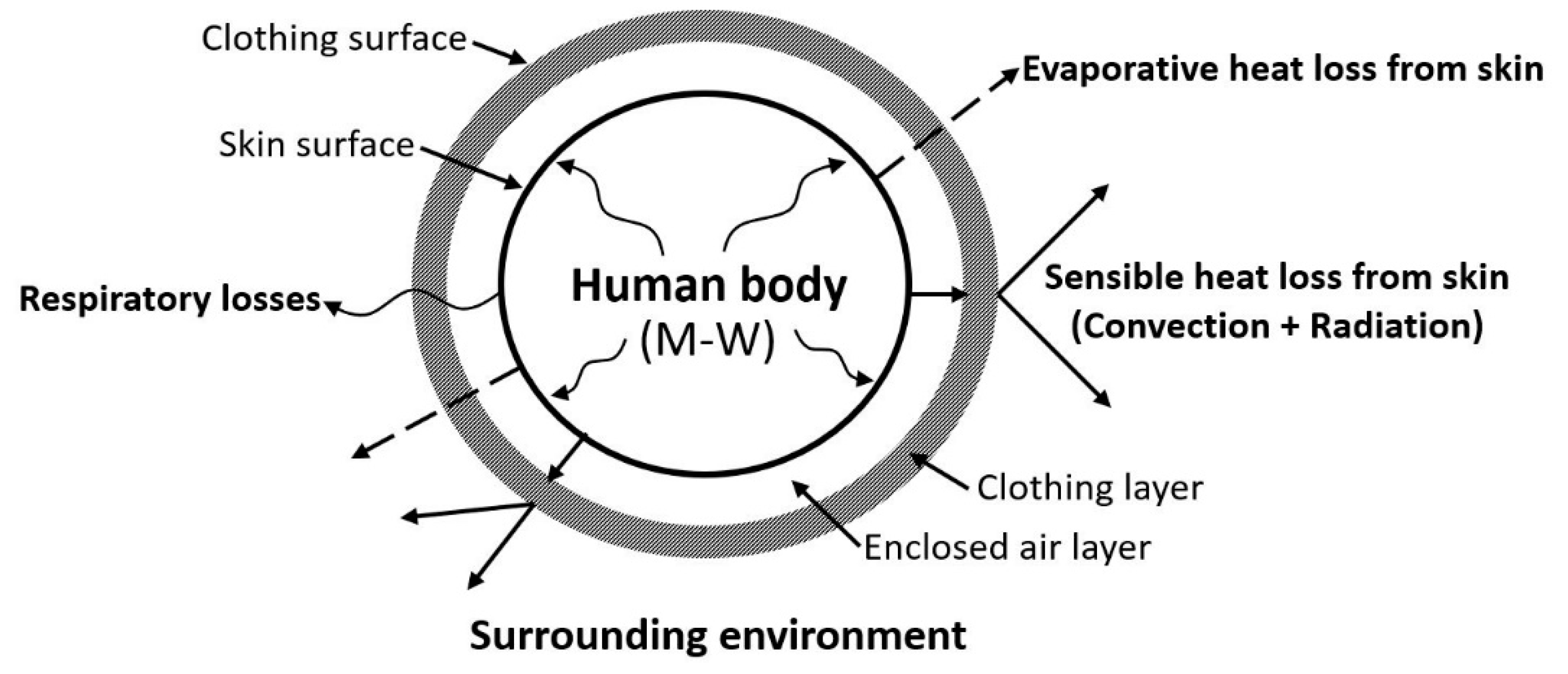
2.2. Evaluation Method Using a Human Thermoregulation Model
2.3. Multi-Node Human Thermoregulation Model
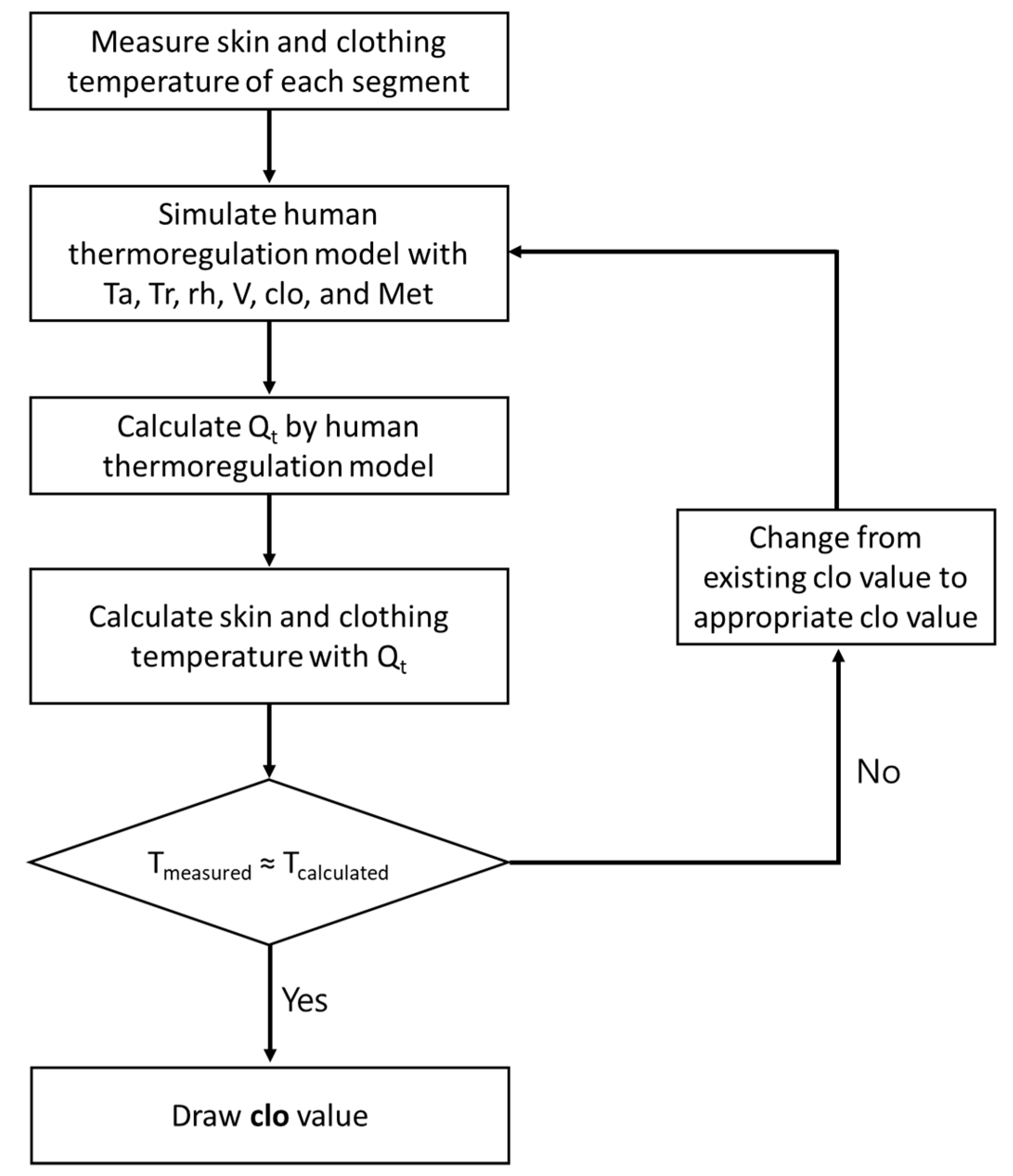
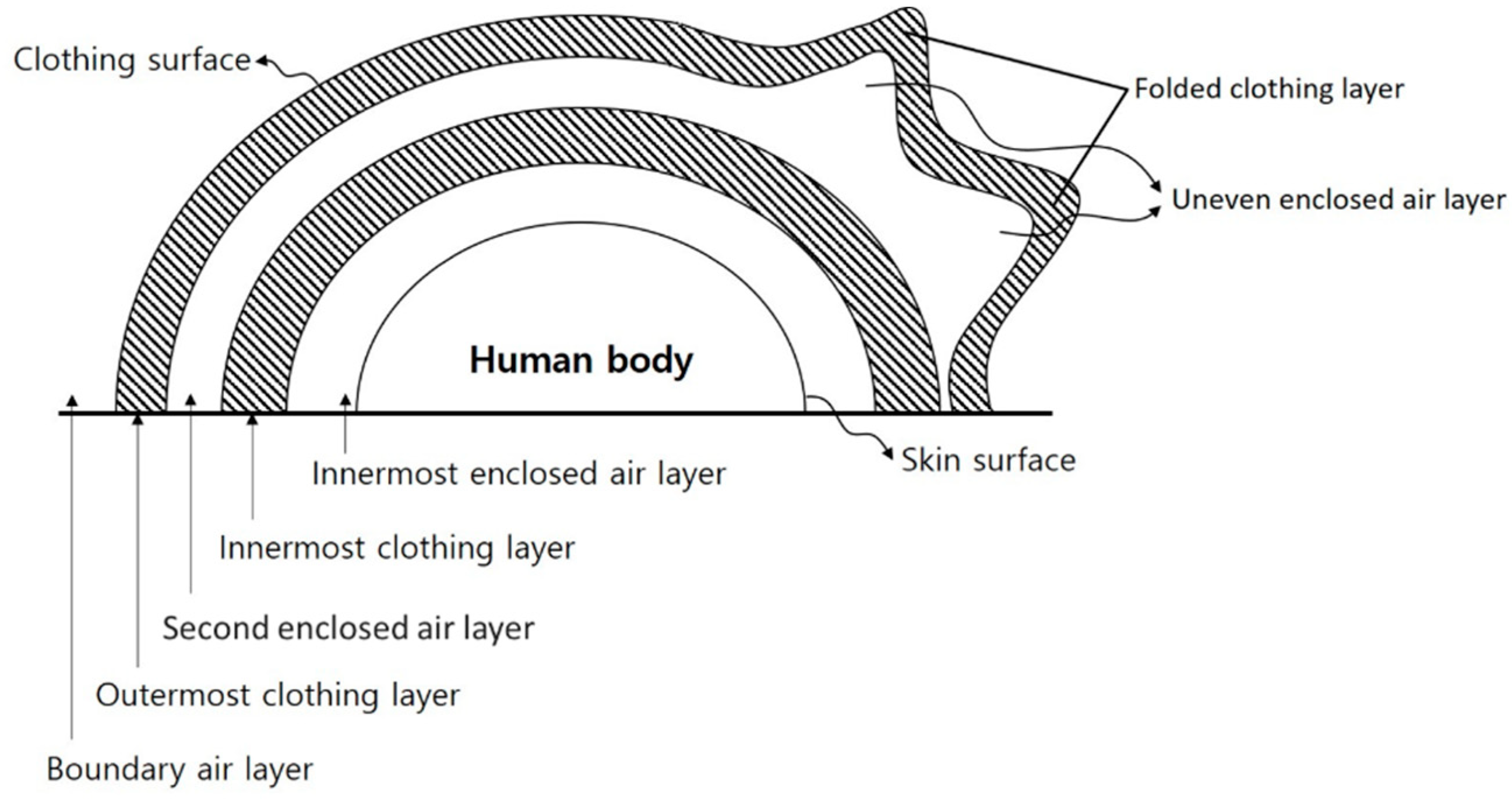
2.4. Calculation of Clothing Insulation Using a Human Thermoregulation Model and an IR Camera
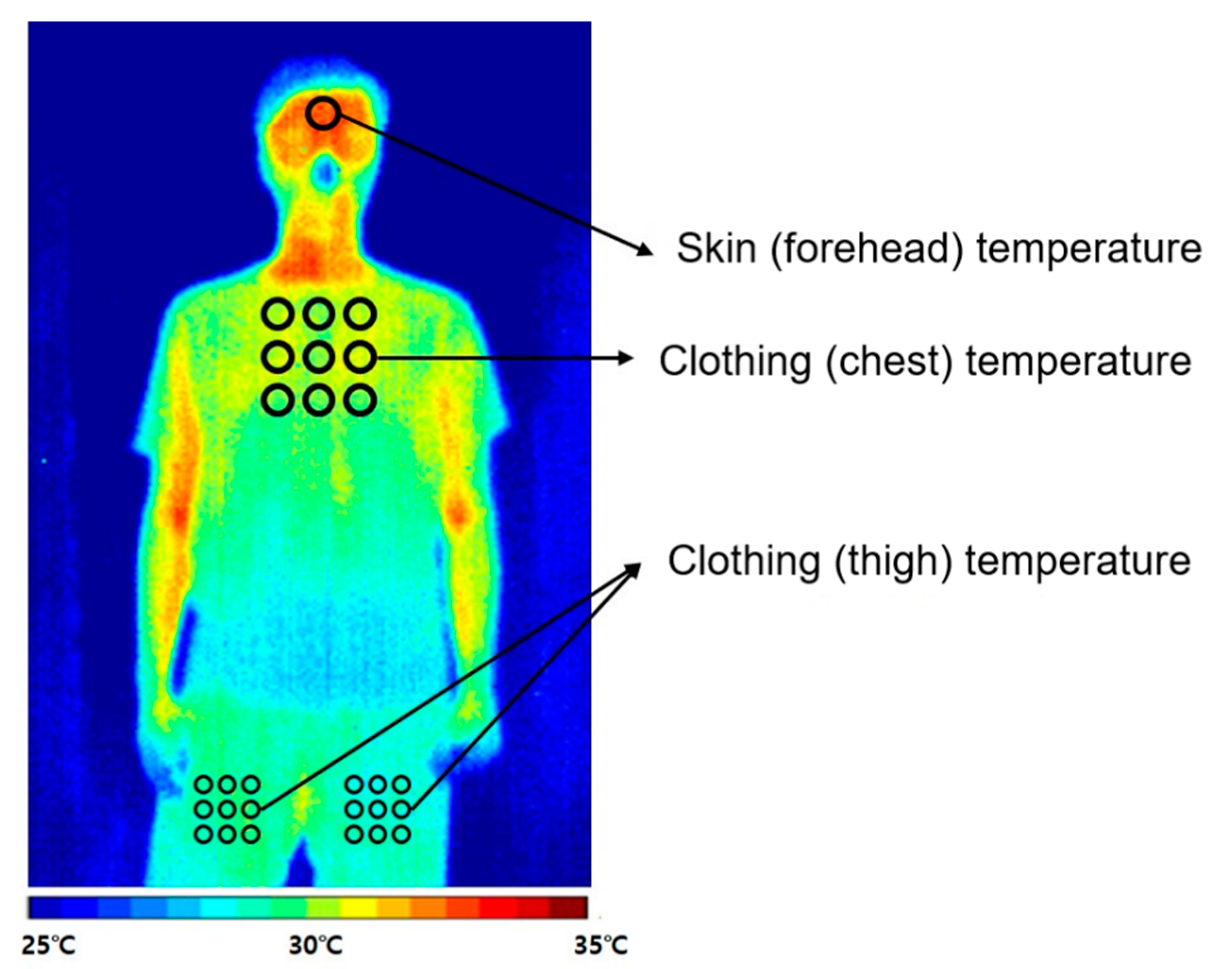
- To determine the temperatures of the skin and clothing surface, the temperature of the human body was measured using an IR camera. Theoretically, to calculate the thermoregulation model, we only need to know the temperatures of several parts of the human body. Therefore, we measured the skin temperature at the forehead, the top clothing temperature at the chest, and the bottom clothing temperature at the thigh. These measurements were easily performed using the IR camera, and it was easy to extract stable values from the experiment. The skin temperature inside the clothing was predicted using the human thermoregulation model.
- The human thermoregulation model was simulated using Ta, MRT, RH, V, the assumed clo, and Met.
- The human thermoregulation model was used to calculate the sensible heat loss from the skin. In the Fanger model, the sensible heat loss from the skin ( in Equation (4)) was calculated using the method specified in Annex D of ISO 7730. In the Tanabe model, the sensible heat loss from the skin ( in Equation (5)) of each body part was calculated.
- In each prediction model, the skin and clothing temperatures of each part were calculated using the sensible heat loss from the skin.
- The calculated skin and clothing temperatures of each part were compared with the measured temperature from step a. If a difference was found between the two temperatures, the clo level from step b was modified, and the calculation was performed again.
- The calculations of steps b–e were repeated to determine the clo level at which the predicted skin temperature and measured temperature of each part were equal. The identified clo levels were those evaluated using the Fanger and Tanabe models.
3. Experiments for Evaluating Clothing Insulation
3.1. Outline
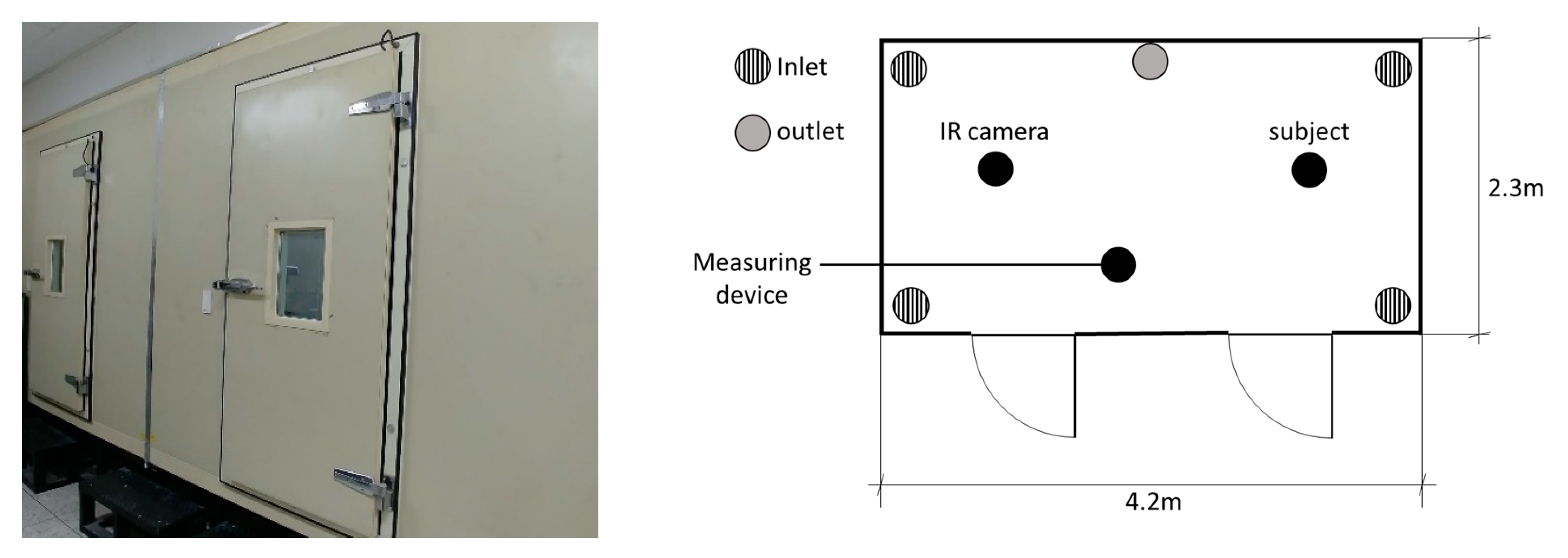
3.1.1. Climate Chamber
3.1.2. Experimental Equipment
3.1.3. Evaluation of Clo Level for Clothes Used in Experiment According to ASTM F1291
3.1.4. Experimental Procedure
- The subject wore winter clothing in the climate chamber and was given 10 min to adapt to the winter conditions.
- After the 10 min of adaptation, the subject assumed a standing posture and relaxed for 20 min while looking at the front of the IR camera.
- The temperatures of the skin (forehead) and clothing surface (chest and thigh) were measured using the IR camera.
3.2. Prediction Models for Evaluating Clothing Insulation
4. Results and Discussion
4.1. Results of Experiments
4.2. Four Clo Prediction Models
5. Discussion
6. Conclusions
- (1)
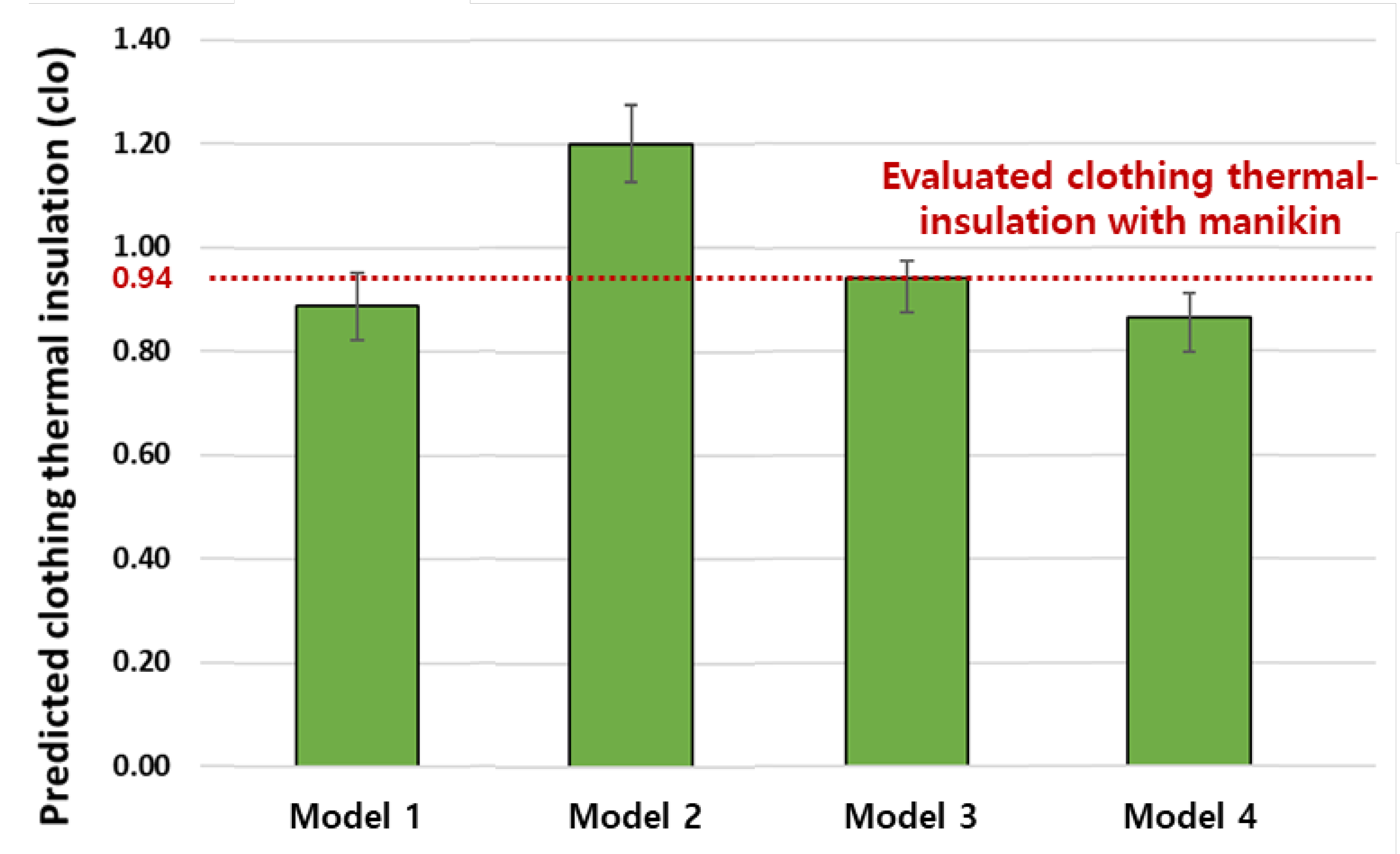
- When skin temperature and top clothing temperature were used as input data, Model 3 predicted clo level better than Model 1. Model 4 also predicted clo level better than Model 2 when skin temperature and top and bottom clothing temperatures were used. As shown in the comparison results of two models, the clo levels predicted by the Tanabe model were closer to the manikin measurements than the Fanger models. Thus, the Tanabe model exhibited better prediction results than the Fanger model. The multi-node thermoregulation model (Tanabe model) was superior for predicting the sensible heat loss from the skin of each body part.
- (2)
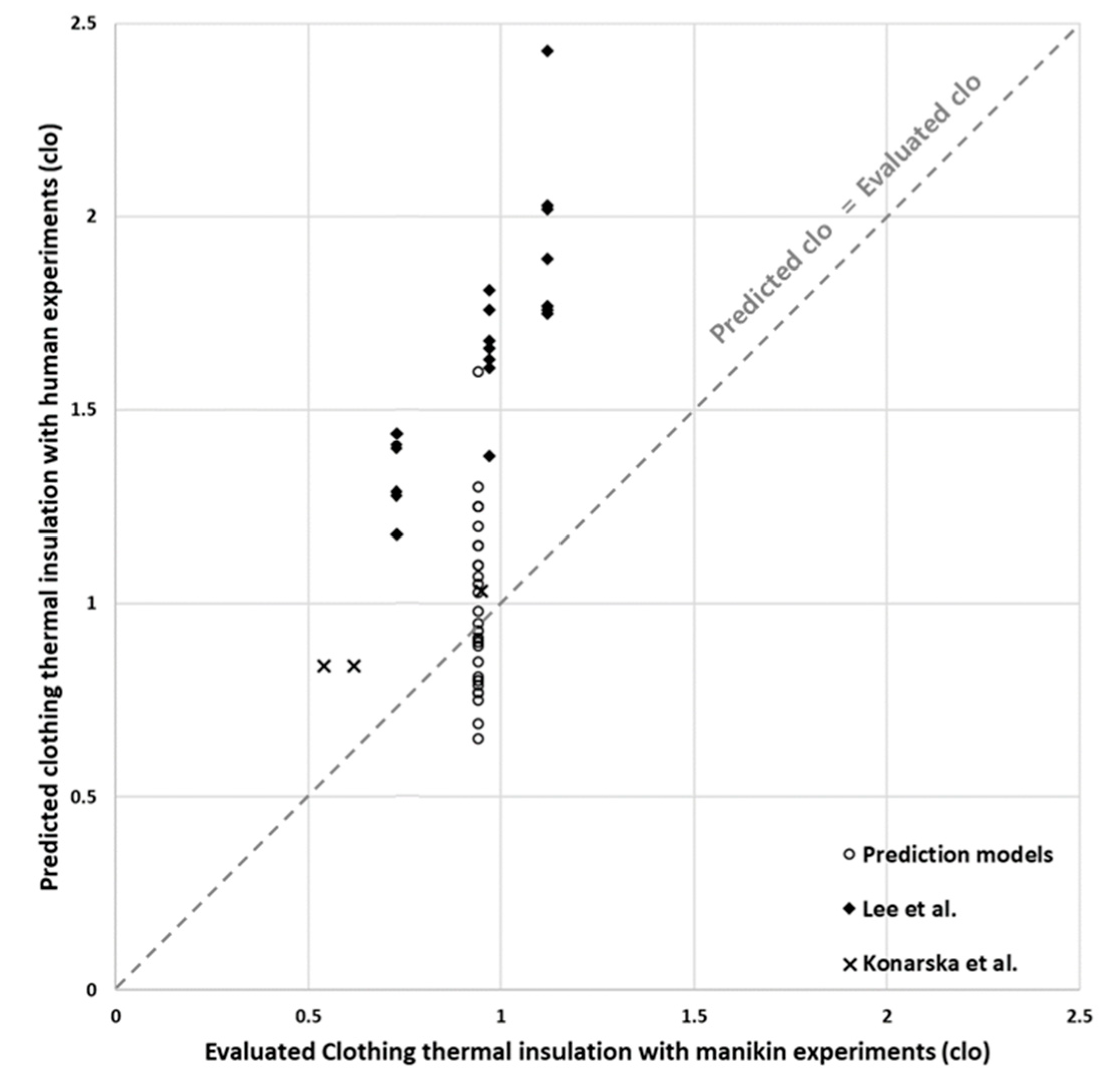
- Regardless of the thermoregulation model used, the high clo level for winter clothing was well predicted. In particular, the predicted values of Model 3 using the Tanabe model were similar to measurement values obtained using a mannequin. In addition, prediction models yielded somewhat higher clo levels than traditional methods.
Author Contributions
Funding
Conflicts of Interest
References
- Dounis, A.I.; Caraiscos, C. Advanced control systems engineering for energy and comfort management in a building environment—A review. Renew. Sustain. Energy Rev. 2009, 13, 1246–1261. [Google Scholar] [CrossRef]
- Ashrae Standard. Standard 55-2017—Thermal Environmental Conditions for Human Occupancy; ASHRAE Inc.: Tullie Circle, NE, USA, 2017; pp. 9–11. [Google Scholar]
- Iso, E. Ergonomics of the thermal Environment-Analytical determination and interpretation of thermal comfort using calculation of the PMV and PPD indices and local thermal comfort criteria. Management 2005, 3, e615. [Google Scholar]
- Newsham, G.R. Clothing as a thermal comfort moderator and the effect on energy consumption. Energy Build. 1997, 26, 283–291. [Google Scholar] [CrossRef]
- Lee, K.; Schiavon, S. Influence of three dynamic predictive clothing insulation models on building energy use, HVAC sizing and thermal comfort. Energies 2014, 7, 1917–1934. [Google Scholar] [CrossRef]
- Konarska, M.; Sołtynski, K.; Sudoł-Szopińska, I.; Chojnacka, A. Comparative evaluation of clothing thermal insulation measured in a thermal manikin and on volunteers. Fibres Text. East. Eur. 2007, 15, 73–79. [Google Scholar]
- Olesen, B.; Nielsen, R. Thermal insulation of clothing measured on a movable thermal manikin and on human subjects. ECSC Programme Res. 1983, 7206, 914. [Google Scholar]
- McCullough, E.A.; Jones, B.W.; Huck, J. A comprehensive data base for estimating clothing insulation. ASHRAE Trans. 1985, 91, 29–47. [Google Scholar]
- De Carli, M.; Olesen, B.W.; Zarrella, A.; Zecchin, R. People’s clothing behaviour according to external weather and indoor environment. Build. Environ. 2007, 42, 3965–3973. [Google Scholar] [CrossRef]
- Schiavon, S.; Lee, K.H. Dynamic predictive clothing insulation models based on outdoor air and indoor operative temperatures. Build. Environ. 2013, 59, 250–260. [Google Scholar] [CrossRef]
- Matsumoto, H.; Iwai, Y.; Ishiguro, H. Estimation of Thermal Comfort by Measuring Clo Value without Contact. In Proceedings of the MVA2011 IAPR Conference on Machine Vision Applications, Nara, Japan, 13–15 June 2011; pp. 491–494. [Google Scholar]
- Lee, J.H.; Kim, Y.K.; Kim, K.S.; Kim, S. Estimating clothing thermal insulation using an infrared camera. Sensors 2016, 16, 341. [Google Scholar] [CrossRef]
- Fanger, P.O. Thermal Comfort: Analysis and Applications in Environmental Engineering; Danish Technical Press: Copenhagen, Denmark, 1970; p. 244. [Google Scholar]
- Tanabe, S.I.; Kobayashi, K.; Nakano, J.; Ozeki, Y.; Konishi, M. Evaluation of thermal comfort using combined multi-node thermoregulation (65MN) and radiation models and computational fluid dynamics (CFD). Energy Build. 2002, 34, 637–646. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO15831:2004 Clothing—Physiological Effects—Measurement of Thermal Insulation by Means of a Thermal Manikin; ISO. Vernier: Geneva, Switzerland, 2004. [Google Scholar]
- American Society of Testing and Materials International (ASTM). Standard Test Method for Measuring the Thermal Insulation of Clothing Using a Heated Manikin; Standard, F1291-10; ASTM International: West Conshohocken, PA, USA, 2010. [Google Scholar]
- Havenith, G.; Holmér, I.; Parsons, K. Personal factors in thermal comfort assessment: Clothing properties and metabolic heat production. Energy Build. 2002, 34, 581–591. [Google Scholar] [CrossRef]
- Fanger, P. Calculation of thermal comfort, Introduction of a basic comfort equation. ASHRAE Trans. 1967, 73, III4.1–III4.20. [Google Scholar]
- ASHRAE. Chapter 9 Thermal Comfort. ASHRAE Handbook-Fundamentals; ASHRAE Inc.: Atlanta, GA, USA, 2017. [Google Scholar]
- Givoni, B.; Goldman, R.F. Predicting metabolic energy cost. J. Appl. Physiol. 1971, 30, 429–433. [Google Scholar] [CrossRef]
- Gagge, A.P.; Stolwijk, J.A.J.; Nishi, Y. Effective temperature scale based on a simple model of human physiological regulatory response. ASHRAE Trans. 2017, 77, 247–263. [Google Scholar]
- Gagge, A.P. A two node model of human temperature regulation in FORTRAN. In Bioastronautics Data, 2nd ed.; Parker, J.F., Jr., West, V.R., Eds.; NASA Special Publication: Washington, DC, USA, 1973; pp. 142–148. [Google Scholar]
- Jones, B. Transient interaction between the human and the thermal environment. ASHRAE Trans. 1992, 98, 189–195. [Google Scholar]
- Takada, S.; Kobayashi, H.; Matsushita, T. Thermal model of human body fitted with individual characteristics of body temperature regulation. Build. Environ. 2009, 44, 463–470. [Google Scholar] [CrossRef]
- Cheng, Y.; Niu, J.; Gao, N. Thermal comfort models: A review and numerical investigation. Build. Environ. 2012, 47, 13–22. [Google Scholar] [CrossRef]
- Huizenga, C.; Hui, Z.; Arens, E. A model of human physiology and comfort for assessing complex thermal environments. Build. Environ. 2001, 36, 691–699. [Google Scholar] [CrossRef]
- Fiala, D.; Lomas, K.J.; Stohrer, M. A computer model of human thermoregulation for a wide range of environmental conditions: The passive system. J. Appl. Physiol. 1999, 87, 1957–1972. [Google Scholar] [CrossRef]
- Fiala, D.; Lomas, K.J.; Stohrer, M. Computer prediction of human thermoregulatory and temperature responses to a wide range of environmental conditions. Int. J. Biometeorol. 2001, 45, 143–159. [Google Scholar] [CrossRef] [PubMed]
- Stolwijk, J.A. A Mathematical Model of Physiological Temperature Regulation in Man; NASA: Washington, DC, USA, 1971. [Google Scholar]
- Salloum, M.; Ghaddar, N.; Ghali, K. A new transient bioheat model of the human body and its integration to clothing models. Int. J. Therm. Sci. 2007, 46, 371–384. [Google Scholar] [CrossRef]
- Li, D.; Menassa, C.C.; Kamat, V.R. Non-intrusive interpretation of human thermal comfort through analysis of facial infrared thermography. Energy Build. 2018, 176, 246–261. [Google Scholar] [CrossRef]
- Cosma, A.C.; Simha, R. Thermal comfort modeling in transient conditions using real-time local body temperature extraction with a thermographic camera. Build. Environ. 2018, 143, 36–47. [Google Scholar] [CrossRef]
- Metzmacher, H.; Wölki, D.; Schmidt, C.; Frisch, J.; van Treeck, C. Real-time human skin temperature analysis using thermal image recognition for thermal comfort assessment. Energy Build. 2018, 158, 1063–1078. [Google Scholar] [CrossRef]
- Cosma, A.C.; Simha, R. Machine learning method for real-time non-invasive prediction of individual thermal preference in transient conditions. Build. Environ. 2019, 148, 372–383. [Google Scholar] [CrossRef]
- Ning, H.; Wang, Z.; Ji, Y. Thermal history and adaptation: Does a long-term indoor thermal exposure impact human thermal adaptability? Appl. Energy 2016, 183, 22–30. [Google Scholar] [CrossRef]
- Bae, C.; Chun, C. Research on seasonal indoor thermal environment and residents’ control behavior of cooling and heating systems in Korea. Build. Environ. 2009, 44, 2300–2307. [Google Scholar] [CrossRef]
- Choi, J.H.; Yeom, D. Development of the data-driven thermal satisfaction prediction model as a function of human physiological responses in a built environment. Build. Environ. 2019, 150, 206–218. [Google Scholar] [CrossRef]
- Choi, J.H.; Yeom, D. Investigation of the relationships between thermal sensations of local body areas and the whole body in an indoor built environment. Energy Build. 2017, 149, 204–215. [Google Scholar] [CrossRef]
- Lee, K.; Choi, H.; Choi, J.H.; Kim, T. Development of a Data-Driven Predictive Model of Clothing Thermal Insulation Estimation by Using Advanced Computational Approaches. Sustainability 2019, 11, 5702. [Google Scholar] [CrossRef]
- Marins, J.C.B.; Moreira, D.G.; Cano, S.P.; Quintana, M.S.; Soares, D.D.; de Andrade Fernandes, A.; da Silva, F.S.; Costa, C.M.A.; dos Santos Amorim, P.R. Time required to stabilize thermographic images at rest. Infrared Phys. Technol. 2014, 65, 30–35. [Google Scholar] [CrossRef]
- Bach, A.J.E.; Stewart, I.B.; Disher, A.E.; Costello, J.T. A comparison between conductive and infrared devices for measuring mean skin temperature at rest, during exercise in the heat, and recovery. PLoS ONE 2015, 10, e0117907. [Google Scholar] [CrossRef]
- Buono, M.J.; Jechort, A.; Marques, R.; Smith, C.; Welch, J. Comparison of infrared versus contact thermometry for measuring skin temperature during exercise in the heat. Physiol. Meas. 2007, 28, 855–859. [Google Scholar] [CrossRef] [PubMed]
- Mert, E.; Psikuta, A.; Bueno, M.-A.; Rossi, R.M. Effect of heterogenous and homogenous air gaps on dry heat loss through the garment. Int. J. Biometeorol. 2015, 59, 1701–1710. [Google Scholar] [CrossRef] [PubMed]
- Frackiewicz-Kaczmarek, J. Determination of the Air Gap Thickness and the Contact Area Under Wearing Conditions. Ph.D. Thesis, Université de Haute Alsace-Mulhouse, Mulhouse, France, 2013. [Google Scholar]
- Li, X.; Wang, Y.; Lu, Y. Effects of body postures on clothing air gap in protective clothing. J. Fiber Bioeng. Informat. 2011, 4, 277–283. [Google Scholar]
- Steketee, J. Spectral emissivity of skin and pericardium. Phys. Med. Biol. 1973, 18, 686. [Google Scholar] [CrossRef]
- Anand, S.; Horrocks, A.R. Handbook of Technical Textiles; CRC Press/Woodhead Pub: Boca Raton, FL, USA, 2000. [Google Scholar]
- Schleimann-Jensen, A.; Forsberg, K. New test method for determination of emissivity and reflection properties of protective materials exposed to radiant heat. In Performance of Protective Clothing; ASTM International: West Conshohocken, PA, USA, 1986; pp. 376–386. [Google Scholar]



| Parameter | Measuring Device | Specifications |
|---|---|---|
| Air temperature | Testo 480 (thermal-flow probe) | 0.5 |
| MRT | Testo 480 (globe probe) | 1.5 |
| RH | Testo 480 (thermal-flow probe) | (1.8% RH + 0.7% of measured value) |
| Wind speed | Testo 480 (thermal-flow probe) | (0.03 m/s + 4% of measured value) |
| Skin and clothing temperatures | TE-Q1 (IR camera) | Scene range temperature: –10 to 150 Accuracy: ±3% at ambient temperature Thermal sensitivity <0.08 Resolution: 384 × 288 (17 µm pitch) Emissivity factor: 0.98 |
| Sex | Number of Subjects | Age | Height (cm) | Weight (kg) |
|---|---|---|---|---|
| Male | 8 | 24.3 ± 1.58 | 171.6 ± 4.27 | 64.7 ± 7.94 |
| Subject No. | RH (%) | Air Velocity (m/s) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 22.1 | 22.0 | 44.4 | 0.08 | 33.6 | 27.4 | 25.8 |
| 2 | 22.3 | 22.7 | 44.1 | 0.08 | 32.6 | 27.3 | 26.7 |
| 3 | 21.9 | 22.8 | 46.0 | 0.08 | 33.4 | 26.7 | 24.7 |
| 4 | 22.0 | 22.7 | 46.3 | 0.08 | 34.1 | 26.6 | 25.7 |
| 5 | 21.9 | 22.9 | 47.1 | 0.08 | 34.1 | 27.4 | 25.7 |
| 6 | 21.9 | 22.9 | 46.7 | 0.08 | 34.1 | 27.9 | 25.1 |
| 7 | 21.9 | 22.3 | 46.3 | 0.10 | 33.3 | 27.9 | 25.1 |
| 8 | 21.9 | 22.6 | 45.2 | 0.08 | 33.4 | 27.7 | 25.3 |
| Mean | 22.0 | 22.4 | 45.8 | 0.08 | 33.6 | 27.4 | 25.5 |
| SD | 0.13 | 0.19 | 1.07 | 0.01 | 0.54 | 0.52 | 0.62 |
| Prediction Model | Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|---|
| Error | 0.05 clo | 0.26 clo | 0.00 clo | 0.08 clo |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, K.; Choi, H.; Kim, H.; Kim, D.D.; Kim, T. Assessment of a Real-Time Prediction Method for High Clothing Thermal Insulation Using a Thermoregulation Model and an Infrared Camera. Atmosphere 2020, 11, 106. https://doi.org/10.3390/atmos11010106
Lee K, Choi H, Kim H, Kim DD, Kim T. Assessment of a Real-Time Prediction Method for High Clothing Thermal Insulation Using a Thermoregulation Model and an Infrared Camera. Atmosphere. 2020; 11(1):106. https://doi.org/10.3390/atmos11010106
Chicago/Turabian StyleLee, Kyungsoo, Haneul Choi, Hyungkeun Kim, Daeung Danny Kim, and Taeyeon Kim. 2020. "Assessment of a Real-Time Prediction Method for High Clothing Thermal Insulation Using a Thermoregulation Model and an Infrared Camera" Atmosphere 11, no. 1: 106. https://doi.org/10.3390/atmos11010106
APA StyleLee, K., Choi, H., Kim, H., Kim, D. D., & Kim, T. (2020). Assessment of a Real-Time Prediction Method for High Clothing Thermal Insulation Using a Thermoregulation Model and an Infrared Camera. Atmosphere, 11(1), 106. https://doi.org/10.3390/atmos11010106





