The Effect of the Surface Wind Field Representation in the Operational Storm Surge Model of the National Hurricane Center

Abstract

The Sea, Lake, and Overland Surges from Hurricanes (SLOSH) model is the operational storm surge model of the National Hurricane Center (NHC). Previous studies have found that the SLOSH model estimates storm surges with an accuracy of ±20%. In this study, through hindcasts of historical storms, we assess the accuracy of the SLOSH model for four coastal regions in the Northeastern United States. We investigate the potential to improve this accuracy through modification of the wind field representation. We modify the surface background wind field, the parametric wind profile, and the maximum wind speed based on empirical, physical, and observational data. We find that on average the SLOSH model underestimates maximum storm surge heights by 22%. The modifications to the surface background wind field and the parametric wind profile have minor impacts; however, the effect of the modification to maximum wind speed is significant—it increases the variance in the SLOSH model estimates of maximum storm surges, but improves its accuracy overall. We recommend that observed values of maximum wind speed be used in SLOSH model simulations when possible.

1. Introduction

Storm surges, i.e., coastal floods, pose the greatest threat to life and property loss during severe hurricanes in the United States [1,2,3,4]. The prediction of these hazards is vital for preventing casualties and property damage. The extent of storm surge is dependent on many factors, including the topography of the coastline, the slope of the continental shelf, and the bottom friction of the coastal ocean floor [5,6,7,8,9]. The shallow water equations, which consist of continuity and momentum equations, can be developed and solved numerically for a region of interest to quantify these dependencies and model the storm surges with great accuracy (see e.g., [10,11,12]). However, one of the primary sources of uncertainty in storm surge modeling is the atmospheric forcing, i.e., the hurricane itself. When storm surges are hindcasted using detailed hydrodynamic models and accurate representations of the surface wind field, the simulated hydrodynamics are effectively replicated (e.g., [10,13,14,15,16]). However, for operational forecasting, measurements of the full surface wind field are unavailable [17], and hurricane wind fields are often represented parametrically, using a small number of storm characteristics that can be more readily obtained. Furthermore, many storm surge simulations are often desired to capture and communicate uncertainty. Minimal computational cost of the numerical storm surge model is requisite to produce these ensemble forecasts regularly, and in time for coastal residents to evacuate to areas of safety; the use of very detailed hydrodynamic models is currently not feasible for this purpose.

To this end, the Sea, Lake, and Overland Surges from Hurricanes (SLOSH) model was developed by the National Weather Service (NWS) in the 1970s, and remains the operational storm surge model of the National Hurricane Center (NHC) today [17]. Finite difference schemes are used to discretize two-dimensional shallow water equations in both space and time. Standardized discretizations of the spatial domains used in the model are called basins, and range in resolution from hundreds to thousands of meters. Polar, elliptical, or hyperbolic grids are used to allow increased resolution near coastlines, bays, and estuaries. The basins are defined using topographic and bathymetric data that are averaged across each grid cell. This data is obtained from the U.S. Geological Survey (USGS) and the National Oceanic and Atmospheric Administration (NOAA) National Geophysical Data Center, respectively, and updates are incorporated into the basins every several years. Currently, the operational version of the SLOSH model does not include wave setup, wave runup, or freshwater flooding. Initially, NWS forecasters opted to also exclude tides so that they could be added based on the predicted time of landfall [18]. In the version of the SLOSH model used for this study, astronomical tides are not included; however, the model has recently been updated to include them.

The SLOSH model has been used to develop two composite products, the Maximum Envelope of Water (MEOW), and the Maximum of MEOWs (MOM). The MEOW products are the maximum storm surge heights attained at each point in the model domain when modeling thousands of synthetic storms with identical storm parameters but different, parallel tracks. The MOM products are the maximum storm surge heights attained by combining all the MEOW surge results from storms of the same category on the Saffir-Simpson scale. Additionally, the SLOSH model has been used to develop probabilistic storm surge (P-surge) forecasts. These forecasts are developed from an ensemble of forecasts obtained by sampling from a normal distribution of uncertain storm parameters (track, size, forward speed, and intensity). The surge ensembles are then used to compute exceedance probabilities, which are used by the NHC and emergency managers to assess risk of both real-time guidance and long-term planning [18,19]. Due to its extreme computational efficiency, the SLOSH model is often used in a similar manner for other probabilistic assessments of risk [20,21,22].

The SLOSH model implements a parametric wind model to represent the surface wind field used to approximate the surface wind stresses in the momentum equations. In general, parametric wind models approximate the surface wind field as the sum of the background wind speed of the atmosphere, $V_b$, and the axisymmetric wind speed, V, of the storm. The definition used for each of these components differentiates various parametric wind field models that have been developed, e.g., [13,16,23,24]. In the SLOSH model, the background wind field is modeled as a radially variable fraction of the storm’s translational speed, $V_s$, and the axisymmetric wind profile is modeled as a radially variable fraction of the storm’s maximum wind speed, $V_{max}$. Both fractions increase from zero in the eye of the storm to a maximum value at the radius of maximum wind speed, $R_{max}$, and then decrease toward the storm’s outer radius. Previous studies have shown that storm surges simulated by the SLOSH model have errors ranging from 0–20% [17,19]; however, the sensitivity of this error to various model components is not well understood. Specifically, it is not clear whether the SLOSH model can be improved by improving the wind field representation.

In this work, we investigate the effect of the surface wind field representation on storm surge predictions of the SLOSH model. We focus on four regions along the North Atlantic coast of the United States, which will likely see increasing numbers of hurricanes and storm surges over the coming decades [20,21,25]. We hindcast the storm surges of several historical hurricanes, and assess the impacts of three changes to the parametric wind field model currently implemented in the SLOSH model. First, we change the background wind field from a variable factor of the forward speed of the storm to a constant, rotated factor empirically derived in [26]. Second, we change the axisymmetric wind profile from that which was empirically formulated for the SLOSH model to a theoretical model developed in [27]. Finally, we remove the iterative process currently used in the SLOSH model to calculate the maximum velocity of a storm from the pressure deficit, and instead allow this value to be input to the model explicitly. We investigate both the individual and combined effects of these changes.

2. Materials and Methods

2.1. Surface Background Wind

The translational movement of a tropical cyclone is due to advection by the background wind in the free troposphere. Thus, the translational velocity of a hurricane, $V_s$, and the background wind velocity of the atmosphere, $V_b$, are related. However, they are not identical, as surface friction causes deviations in both the magnitude and direction of the two velocities [28]. The background wind speed can generally be expressed as a rotated fraction of $V_s$. In many parametric wind models, the rotation of $V_s$ is assumed to be negligible, and the fraction ranges from zero (i.e., background wind is not included at all) to 1.0 [21,29,30,31,32,33].

In the SLOSH model, the degree of rotation is considered negligible, and $V_b$ is modeled as a variable fraction of the storm’s translational speed,

$$V_b\left(r\right)=\frac{R_{max}r}{R_{max}^2+r^2}\left|V_s\right|,$$

(1)

where r is the radial distance from the center of the storm. This formula was empirically derived, and though it has been described as “potentially faulty” for fast-moving, weak storms, it has been shown to be adequate for storms of moderate to extreme intensity [17].

In [26], the observed surface wind fields of tropical cyclones in the Atlantic that occurred between 1998–2009 were analyzed. A pronounced deceleration and rotation from $V_s$ to $V_b$ was found, indicating that neither deceleration nor rotation should be neglected for the accurate approximation of the surface background wind field. Specifically, it was shown that the incorrect specification of either resulted in errors as high as 33% in simulations of storm surges near New York City. It was determined that $V_b$ should be approximated as a constant factor, 0.55, of $|V_s|$, rotated 20${}^{\circ }$ counter-clockwise. In this work, we implement this finding in place of the unrotated, radially variable factor currently used in the SLOSH model (1), i.e.,

$$V_b\left(r\right)=0.55\left|V_s\right|,\mathrm{rotated}{20}^{\circ }\mathrm{counter}-\mathrm{clockwise}.$$

(2)

2.2. Parametric Wind Profile

In a study of synthetic, high impact, low frequency events in Tampa Bay, FL [26], it was determined that although the choice of the axisymmetric wind profile, $V\left(r\right)$, had only a moderate effect on the values of peak winds, its impact on associated storm surges was more substantial. There are several prominent descriptions of $V\left(r\right)$ (e.g., [27,34,35,36,37]). In the SLOSH model, the wind field is modeled as

$$V\left(r\right)=\frac{2R_{max}r}{R_{max}^2+r^2}{V}_{max}.$$

(3)

This description was originally developed in the 1960s for storms with $R_{max}$ between 10 and 50 miles [38], and values of $V_{max}$ near 100 mph [39]. The wind model was described as an “arbitrary choice to form a simple algebraic formulation of the wind speed,” and was designed to reduce the sensitivity of modeled storm surges to errors in the wind field.

Several studies have shown that the SLOSH model sufficiently represents hurricane wind fields [40,41,42]; however, it is expected that the wind profile can be better approximated by including some of the known physical mechanisms that occur in the storm. Different mechanisms define the winds in the inner and outer regions of the storm. Here, the inner region of the storm describes the region near the eyewall, and the outer region describes the regions at radii farther away. In [37], asymptotic solutions of the equations describing the profile in each of these regions were merged. The inner region profile was then improved in [27], and the asymptotic solution of the full profile has been approximated as

$$V\left(r\right)=\frac{2(R_{max}{V}_{max}+\frac{1}{2}f{R}_{max}^2)r}{R_{max}^2+r^2}-\frac{fr}{2},$$

(4)

where f is the Coriolis parameter. Note that if Coriolis effects are neglected, this profile is by coincidence identically equal to that used in the SLOSH model. The physical assumptions used to develop this profile can be violated in the outer region of the storm, and thus the model is presumably less accurate in this region. (In [36], the model representing the outer region was improved, but the improved model is too complex to be readily incorporated into the SLOSH model.) Additionally, the profile is not ideally described near the center of the storm, as it does not account for radial diffusion in the eye. However, the profile is extremely accurate near $R_{max}$, the region which most significantly affects maximum storm surges. Here we implement this model in place of (3).

2.3. Maximum Wind Speed

As seen in Section 2.2, parametric wind profiles commonly describe the axisymmetric wind field as a function of $V_{max}$, one of the few storm parameters that directly impacts the magnitude and extent of storm surges. Unfortunately, this value is not always available; in [38] it was described as a “distressingly difficult parameter to measure or observe,” and even for the most recent tropical cyclone events, maximum wind speeds are rarely directly measured [43]. Central pressure is correlated with $V_{max}$, and the SLOSH model was developed to use an iterative procedure to estimate $V_{max}$ from the more readily available storm parameter, $\Delta P$, the pressure deficit (i.e., the difference in atmospheric pressure between the storm center and the environment), and $R_{max}$. However, the pressure-wind relationship has significant variability and the effects of this estimation on storm surge modeling are not well studied. In this work, we modify the SLOSH model to directly read values of $V_{max}$, observed or estimated from improved methods.

2.4. Hindcasts

We study the impacts of the wind field representation by hindcasting tropical cyclones that occurred between 1988 and 2012 and affected four regions along the North Atlantic coast: Narragansett Bay, Rhode Island; Jamaica Bay, New York; Atlantic City, New Jersey; and Norfolk, Virginia. These regions are chosen for study as they were identified as increasingly geographically, socially, and economically vulnerable to storm surges and used as the study sites for the project, Structures of Coastal Resilience [25], which complemented the North Atlantic Coast Comprehensive Study of the U.S. Army Corps of Engineers. In the end, we simulate 11 storms for Narragansett Bay, 9 storms for Jamaica Bay, 12 storms for Atlantic City, and 23 storms for Norfolk. Several storms affected more than one study site, and are thus represented more than once in the total set of 55 simulations. These tropical cyclones are listed in

Table 1. Historical tropical cyclones simulated for each study site.

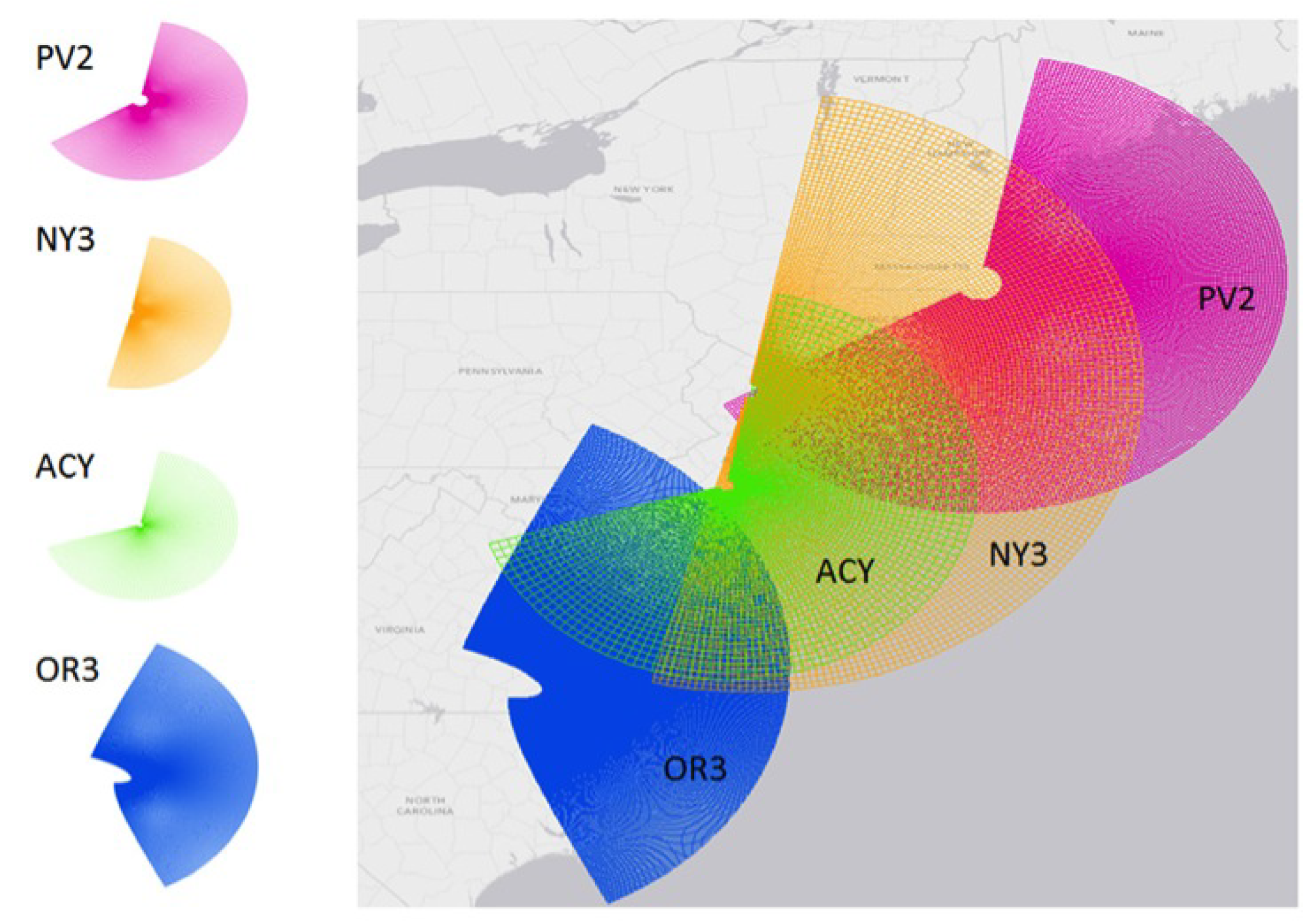
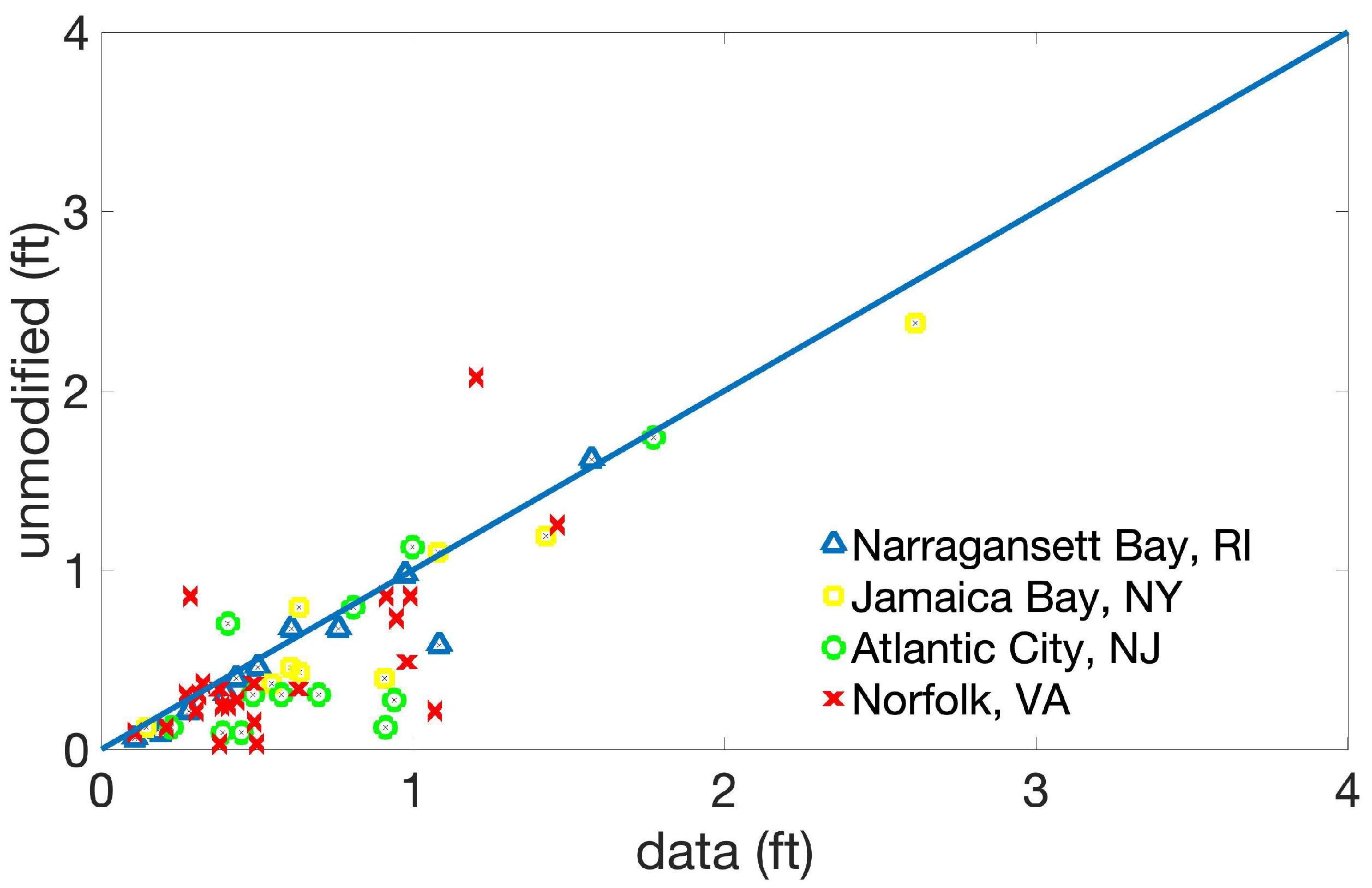
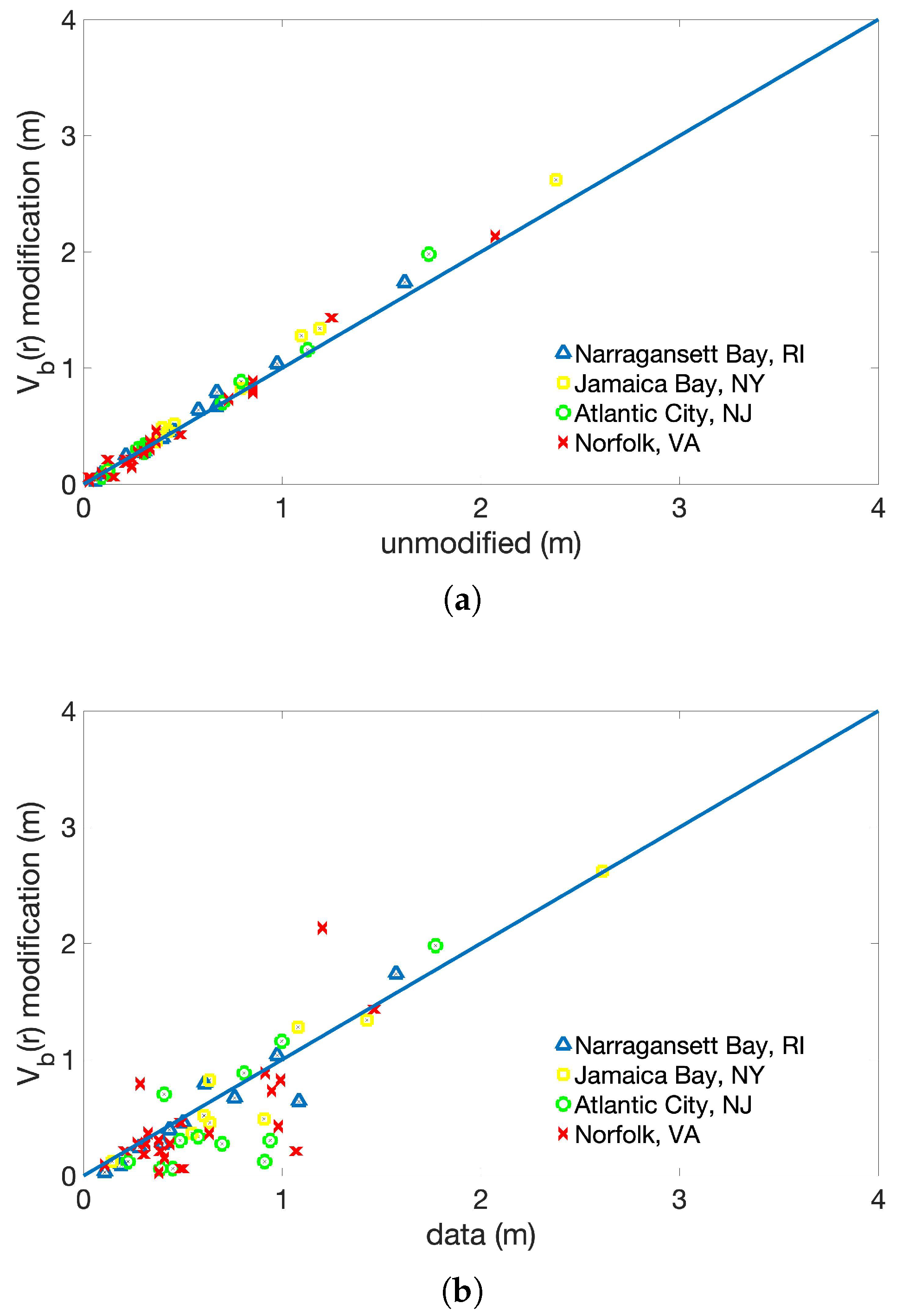
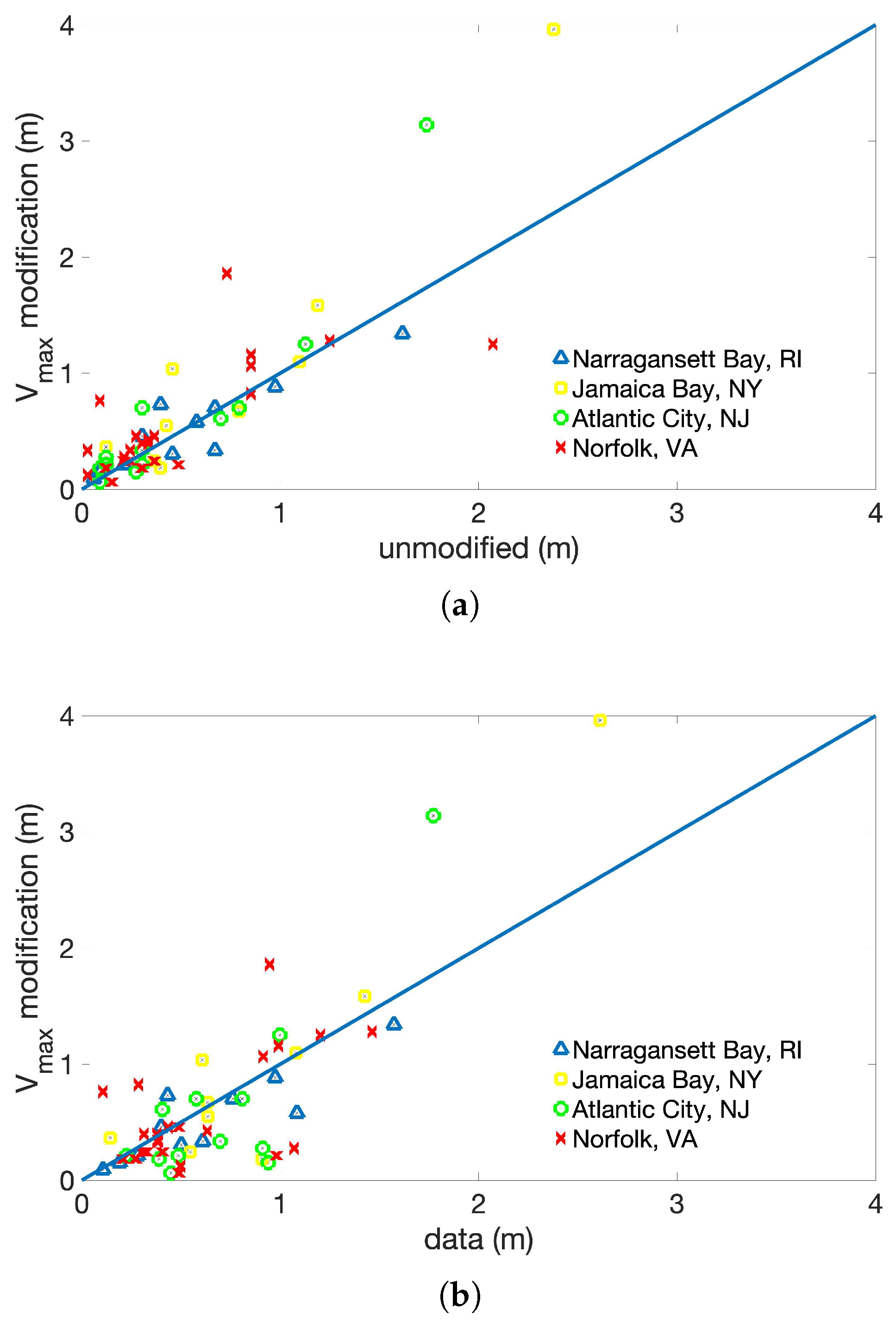
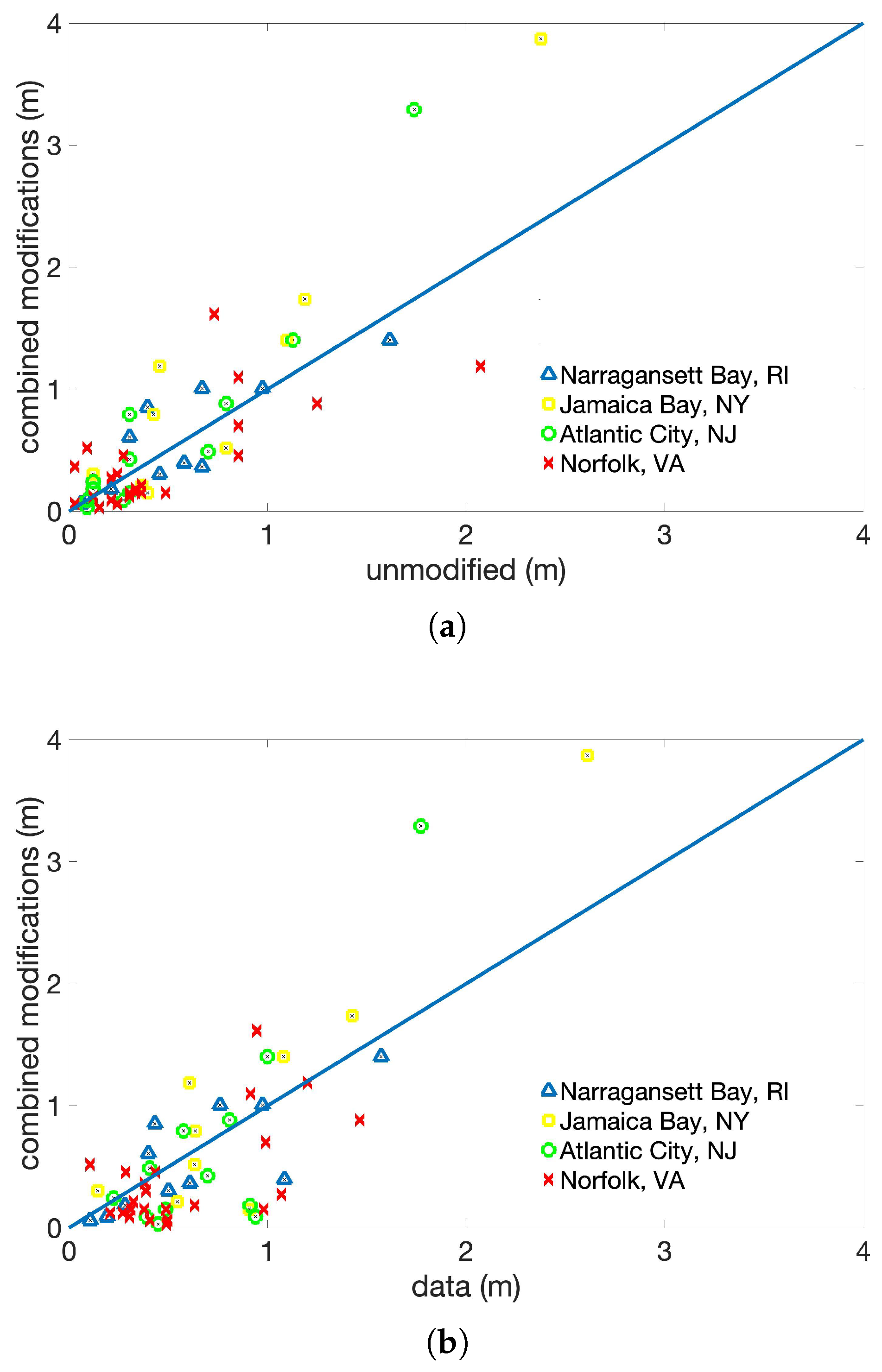
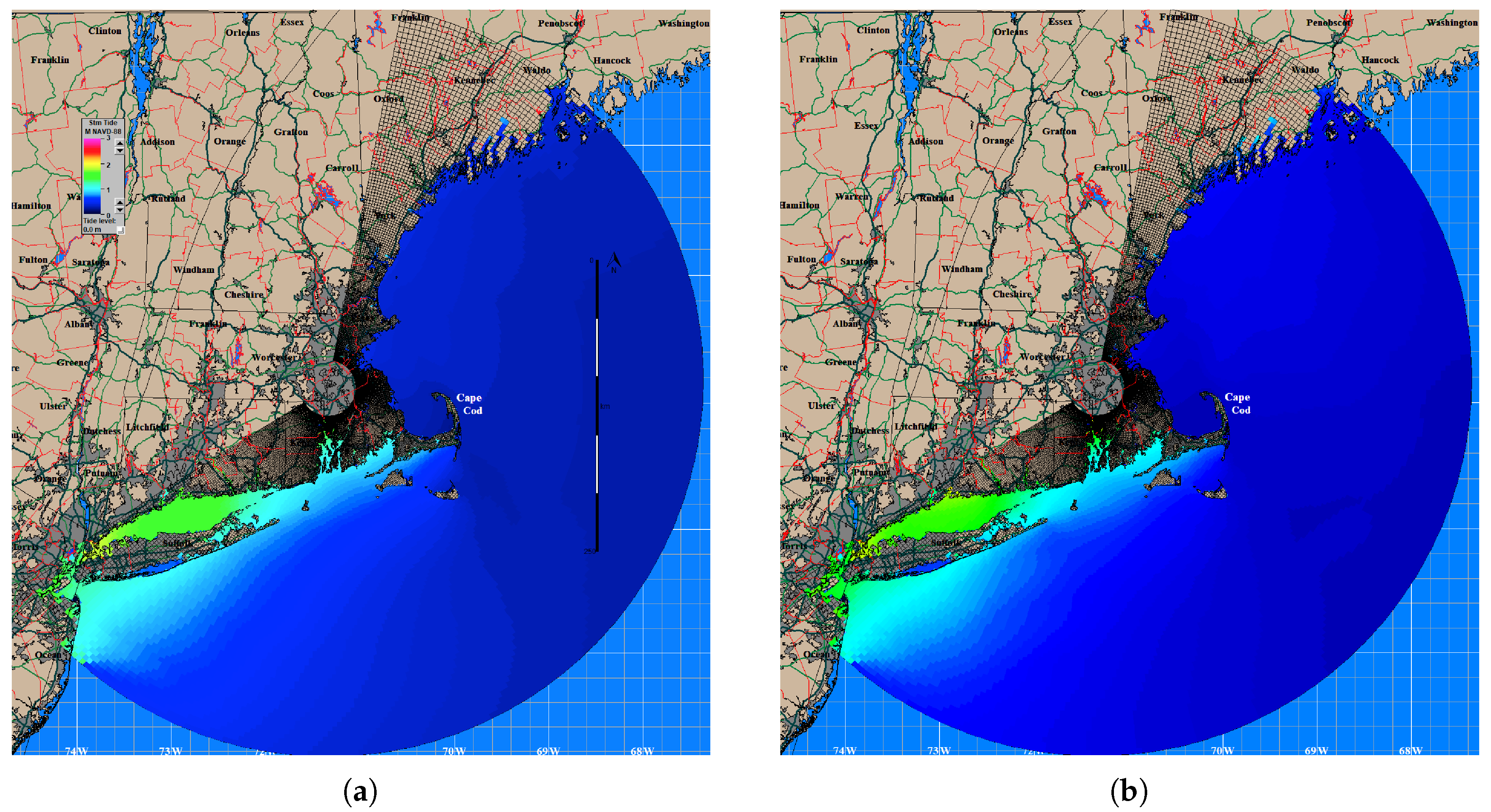
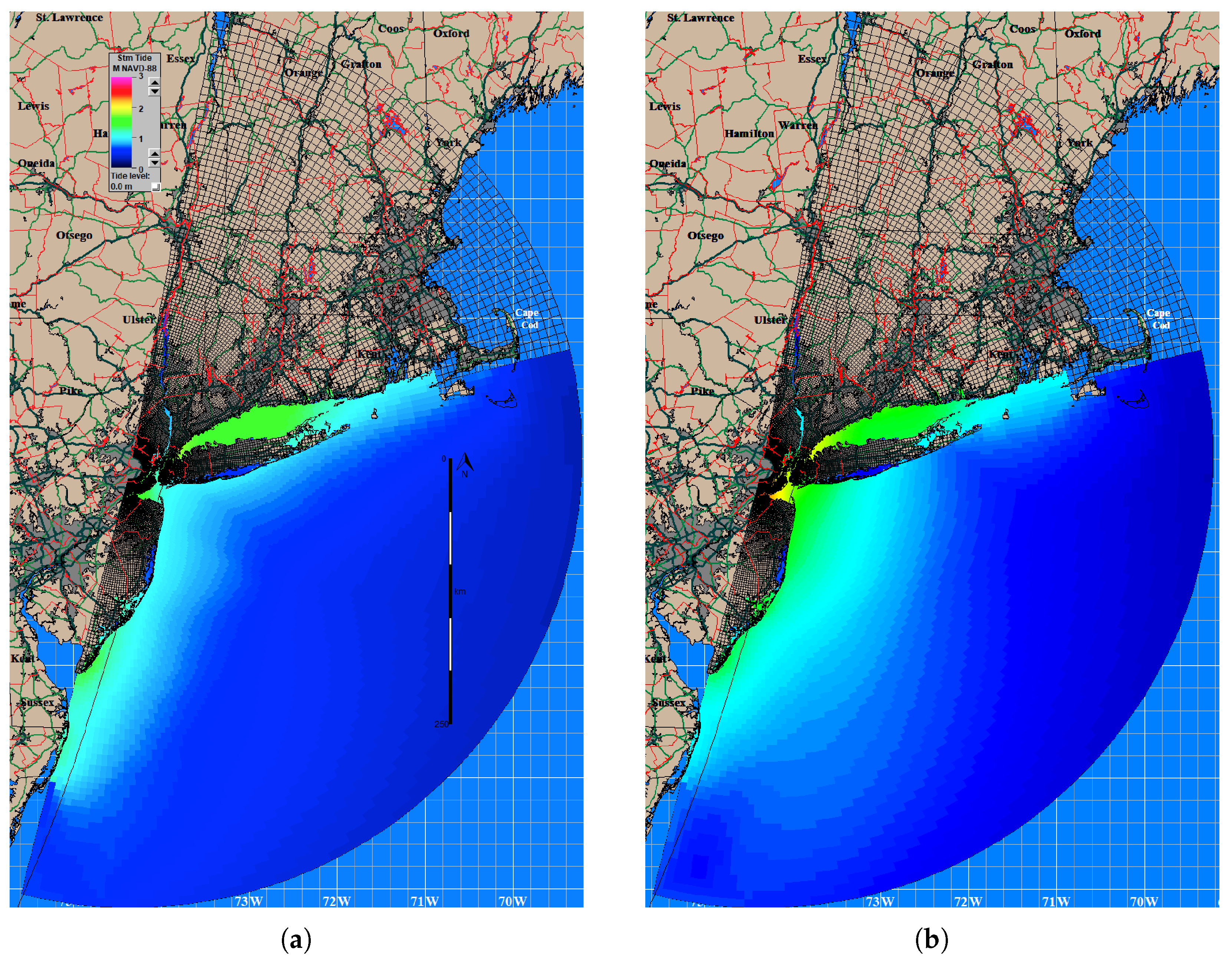
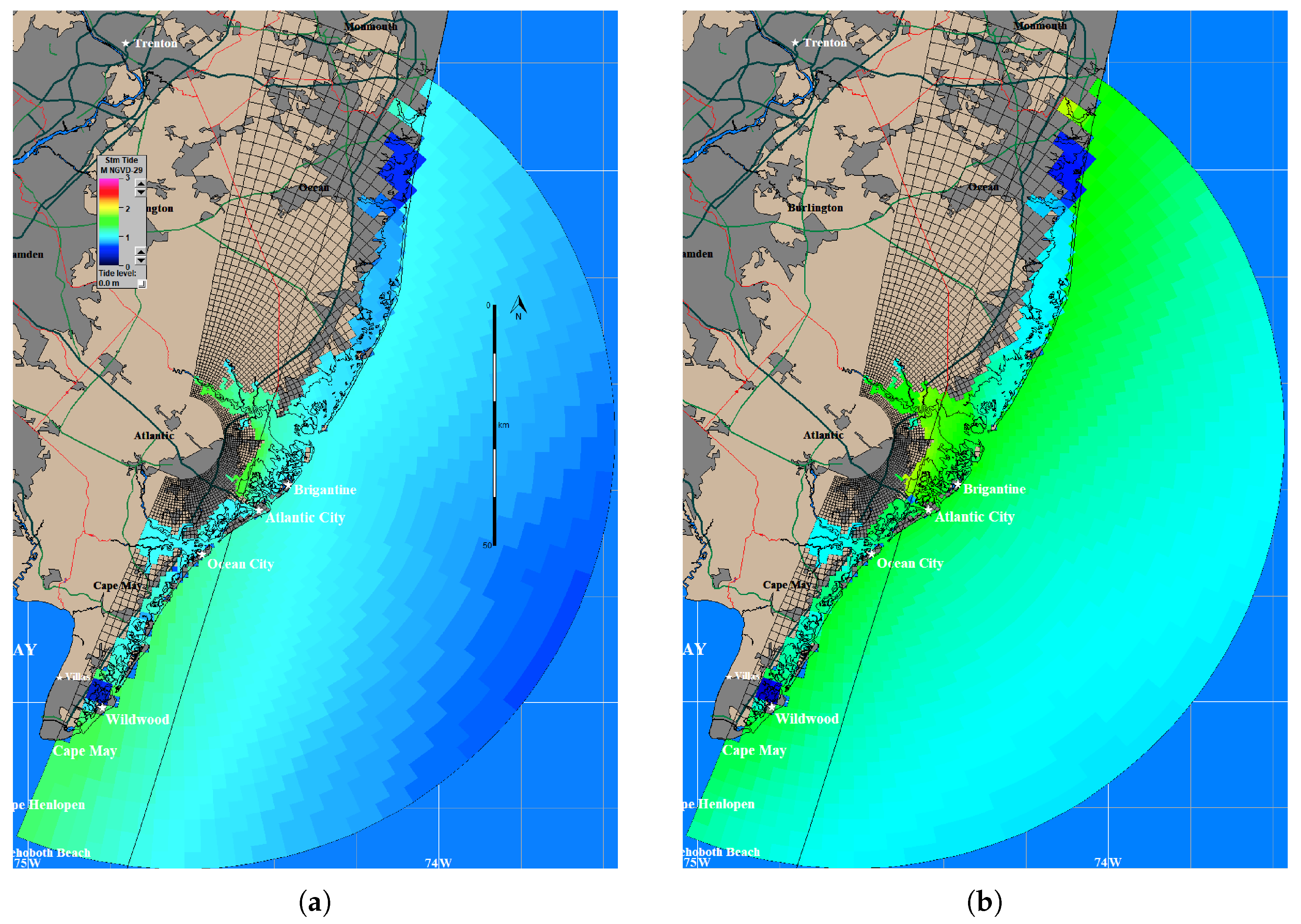
Name	Date	Category at Peak Intensity	Maximum Storm Surge Calculated from NOAA Tide Gauge Data (m)
Narragansett Bay, Rhode Island
Bob	08/1991	3	1.57
Grace	10/1991	2	1.09
Bertha	07/1996	3	0.43
Edouard	08/1996	4	0.28
Josephine	10/1996	TS	0.61
Danny	07/1997	1	0.11
Floyd	09/1999	4	0.76
Ophelia	09/2005	1	0.19
Hanna	09/2008	1	0.40
Earl	09/2010	4	0.50
Irene	08/2011	3	0.98
Jamaica Bay, New York
Bob	08/1991	3	0.63
Bertha	07/1996	3	0.61
Josephine	10/1996	TS	0.91
Floyd	09/1999	4	1.08
Allison	06/2001	TS	0.14
Barry	06/2007	1	0.55
Hanna	09/2008	1	0.64
Irene	08/2011	3	1.43
Sandy	10/2012	3	2.61
Atlantic City, New Jersey
Bob	08/1991	3	0.41
Bertha	07/1996	3	0.58
Josephine	10/1996	TS	0.94
Danny	07/1997	1	0.45
Floyd	09/1999	4	0.81
Helene	09/2000	TS	0.39
Allison	06/2001	TS	0.23
Ernesto	08/2006	1	0.91
Barry	06/2007	1	0.49
Hanna	09/2008	1	0.70
Irene	08/2011	3	1.00
Sandy	10/2012	3	1.77 *
Norfolk, Virginia
Bob	08/1991	3	0.29
Emily	08/1993	3	0.99
Allison	06/1995	1	0.27
Bertha	07/1996	3	0.44
Fran	09/1996	3	0.49
Josephine	10/1996	TS	0.98
Danny	07/1997	1	0.49
Bonnie	08/1998	3	0.95
Earl	09/1998	2	0.39
Dennis	09/1999	2	0.63
Floyd	09/1999	4	0.91
Helene	09/2000	1	0.38
Gustav	09/2002	2	0.38
Kyle	10/2002	1	0.50
Isabel	09/2003	5	1.46
Alex	09/2004	3	0.41
Ophelia	09/2005	1	0.31
Ernesto	08/2006	TS	1.07
Barry	06/2007	TS	0.32
Cristobal	07/2008	TS	0.11
Hanna	09/2008	1	0.21
Irene	08/2011	3	1.20
Beryl	05/2012	TS	0.30

* tide gauge failed to measure water levels for the entire duration of this storm.

. We have excluded a small number of storms for which the SLOSH model develops numerical instabilities.

To hindcast the storms, we use Extended Best Track datasets [44], developed by supplementing NOAA HURricane DATabases (HURDAT), to create “.trk” files, SLOSH model input files that define hurricane parameters. Maximum wind speed data is added to the standard .trk files for the simulations where this value is to be input directly. Five versions of the SLOSH model (the original version, three versions incorporating each of the three modifications individually, and one version incorporating the combination of all three) are used to simulate the resulting storm surges on the most appropriate SLOSH model basin for the study site: pv2 for Narragansett Bay, ny3 for Jamaica Bay, acy for Atlantic City, and or3 for Norfolk (Figure 1).

For each simulation, the SLOSH model produces a “.rex” file, a binary output file containing a time series of the storm surges computed on each grid cell in the respective SLOSH basin. Maximum storm surge data is extracted from these files for the basin grid cells corresponding to locations of interest. Here, we choose locations corresponding to four NOAA tide gauge stations near each study site, Stations 8452660, 8531680, 8534720, and 8638863 for Narragansett Bay, Jamaica Bay, Atlantic City, and Norfolk, respectively (

Table 2. NOAA tide gauge stations used to estimate maximum storm surges.

Location	Station ID	Latitude	Longitude
Narragansett Bay, Rhode Island	8452660	4130.2${}^{\prime }$ N	7119.6${}^{\prime }$ W
Jamaica Bay, New York	8531680	4028${}^{\prime }$ N	740.6${}^{\prime }$ W
Atlantic City, New Jersey	8534720	3921.4${}^{\prime }$ N	7425.1${}^{\prime }$ W
Norfolk, Virginia	8638863	3658${}^{\prime }$ N	766.8${}^{\prime }$ W

).

2.5. Storm Surge Data

Hurricane storm surge data is generally sparse, spatially discontinuous, and lacks time history (e.g., in the case of high-water marks). Here we compare modeled storm surge heights to storm surge residuals calculated from NOAA tide gauge data. For each study site, we use data from the NOAA tide gauge in closest proximity, with the most reliable data (i.e., gauges positioned along open coastlines rather than deep within back bays or channels). We subtract predictions of astronomical tides from water elevations (storm tides) measured during hurricanes to estimate storm surges. The data is measured relative to the North American Vertical Datum of 1988 (NAVD 88). We compare the maximum storm surge values attained over the duration of the storm to those estimated by each version of the SLOSH model. Note that we consequently neglect wind-driven waves, and the data may thus overestimate storm surge levels. We also neglect nonlinear tide-surge interactions, perhaps underestimating (or overestimating) surges that occur at high (or low) tide [7].

While small storm surges can be hazardous, storm surges above 0.91 m (3.0 ft) pose a significant threat to life and property. The NWS currently uses this value as a threshold for its newly implemented storm surge warnings [45,46]. For this reason, we analyze the subset of surge events that reach 0.91 m according to the computed storm surge residuals. In total, this occurs for 16 of the 55 simulations (Table 1; the Norfolk, VA simulation of Hurricane Floyd produces a surge of slightly more than 0.91 m). In other words, the hindcasts conducted in this study are for storms that mostly had low to moderate impacts at the study sites. It is also deserving of note that for small storm surges, data is subject to noise and measurement error. While this does not affect our assessment of the general impacts of the modifications to the wind field, it has implications for our assessment of the SLOSH model accuracy. Further investigation of additional data sources, e.g., Federal Emergency Management Agency (FEMA) high-water marks and USGS temporary storm surge sensors, will be useful in better understanding the results presented here.

3. Results

3.1. Baseline Case

Previous studies have shown that the SLOSH model estimates storm surges within ±20% of observed data at most locations [17,19]. The model was designed for operational use for a wide range of storms in various locations, and thus undetermined model coefficients have not been used to calibrate the model for specific storm events. Rather, the model has been developed to produce sufficient results for all storms in all regions, and reasonable model results on average are preferable to ideal results for a particular event [17]. Here, we modify the wind field with the goal of improving the average accuracy of modeled maximum storm surges at the study sites. We establish a baseline by simulating the maximum surges of the storms listed in Table 1 with the original, unmodified version of the SLOSH model (Figure 2).

The SLOSH model underestimates 44 of the 55 maximum storm surge heights. On average, the underestimation has a magnitude of 0.23 m. The largest underestimation is 0.86 m (80.1%) for Hurricane Ernesto in the Norfolk, VA simulation. This storm also impacts the Atlantic City area, and a similar underestimation of 0.79 m (86.6%) is observed for this simulation. The SLOSH model overestimates 11 of the 55 maximum storm surge heights by an average of 0.20 m. The largest overestimation is 0.87 m (72.3%) during the Norfolk, VA simulation of Hurricane Irene. Hurricane Irene impacts the three other regions of the study, and this overestimation of the maximum storm surge is not observed for the other simulations. Overall, the average error of the SLOSH model when computing the maximum storm surge at each site for each relevant storm is −0.14 m (−22.2%). To be consistent with the literature, we present the SLOSH model accuracy in terms of the average percent error of each simulation relative to the respective NOAA tide gauge data; however, as noted in Section 2.5, for these simulations, most of the maximum storm surges are less than 0.91 m (3.0 ft). Large percent errors may overstate absolute errors. The mean absolute error of all the simulations is 0.22 m and the root mean square error is 0.31 m.

For “large” storm surges, i.e., those greater than or equal to 0.91 m (3.0 ft), the SLOSH model performs similarly. Of the 55 simulations, the storm surge residuals computed at the NOAA tide gauges are large for 16 of them. Of these, 11 are underestimated by an average of 0.33 m. Five are overestimated by an average of 0.21 m. Overall, the average error in the SLOSH model is −0.16 m (−15.2%) for large storm surges. The mean absolute error is 0.30 m and the root mean square error is 0.41 m.

3.2. Surface Background Wind Modification

The modification to the surface background wind field has varying effects on the simulated maximum storm surge heights. There is a general tendency for the modification to cause the predicted storm surges to increase, particularly for storm surges originally simulated as greater than 0.91 m (3.0 ft). With this change, the maximum storm surges at the NOAA tide gauge locations increase for 24 (of the 55) simulations, decrease for 15 of the simulations, and do not change for 16 of the simulations (Figure 3). The impacts are moderate, with an average increase of 0.09 m (17.7%) and an average decrease of 0.04 m (20.9%) of the maximum storm surge height. For storms with observed maximum storm surge levels greater than or equal to 0.91 m, the maximum storm surges increase for 12 of the 16 simulations and decrease for two. The mean increase is 0.12 m (9.4%) and the mean decrease is 0.05 m (8.0%).

After the modification to the surface background wind field, on average the model underestimates the maximum storm surges by 0.11 m (20.9%) when compared to the computed storm surge residuals. This is a modest improvement from the average underestimation of 22.2% observed in the baseline case. However, the mean absolute error and the root mean square error do not improve. They remain 0.22 m and 0.31 m, respectively. For storms with observed maximum storm surge levels greater than or equal to 0.91 m, the model underestimates the maximum storm surges by an average of 0.08 m (9.7%). The mean absolute error and the root mean square error also remain 0.30 m and 0.41 m, respectively.

3.3. Parametric Wind Profile Modification

Implementing the parametric wind profile (4) generally results in a decrease of the maximum storm surge heights (Figure 4). With the change, 39 of the 55 maximum storm surges decrease compared to ten that increase. This modification has larger impacts than the change to the background wind; however, the impact is still relatively minor. The mean increase in maximum storm surge height is 0.06 m (23.1%) and the mean decrease is 0.12 m (29.2%). For storms with observed maximum storm surge levels greater than or equal to 0.91 m (3.0 ft), the maximum storm surges increase for two of the 16 simulations and decrease for 12. The mean increase is 0.08 m (6.7%) and the mean decrease is 0.15 m (15.7%).

After the modification to the parametric wind profile, on average the model underestimates the maximum storm surges by 0.21 m (36.1%) when compared to the data. This is a degradation in the performance of the original, unmodified model. The mean absolute error and the root mean square error increase to 0.26 m and 0.34 m, respectively. For storms with observed maximum storm surge levels greater than or equal to 0.91 m, the model underestimates the maximum storm surges by 0.27 m (23.7%) on average. The mean absolute error and the root mean square error are 0.37 m and 0.47 m, respectively.

3.4. Maximum Wind Speed Modification

The magnitude of storm surge is most affected by the winds that occur near the eye of the storm, and as a result changes to $V_{max}$, which occurs within the eyewall, are expected to significantly impact maximum storm surge heights. Our results confirm this (Figure 5). On average, the maximum storm surge heights change in absolute value by 79.4%. This contrasts with the more modest changes of 13.3% and 24.9% that result from the modifications to the surface background wind and the parametric wind profile, respectively. The tendency is for the maximum storm surge heights to increase; 33 of the 55 simulations result in higher maximum storm surges compared to 18 which decrease the maximum storm surges. The changes are significant, with an average increase of 114.8% and an average decrease of 32.1% of the original maximum storm surge height. For storms with observed maximum storm surge levels greater than or equal to 0.91 m (3.0 ft), the maximum storm surges increase for nine of the 16 simulations and decrease for five. The mean increase is 0.58 m (48.6%) and the mean decrease is 0.32 m (33.4%).

After the modification to maximum wind speed, on average the model underestimates the maximum storm surges by 0.03 m (3.8%) when compared to the data. This is a significant improvement in percent error from the average underestimation of 22.2% in the baseline case. However, the mean absolute error and the root mean square error again increase, here to 0.29 m and 0.43 m, respectively. For storms with observed maximum storm surge levels greater than or equal to 0.91 m, the model underestimates the maximum storm surges by an average of 0.07 m (1.2%). The mean absolute error and the root mean square error increase to 0.49 m and 0.66 m, respectively.

3.5. Combined Modifications

Finally, we implement each of the above changes jointly (Figure 6). Twenty-five of the maximum storm surges increase by an average of 0.39 m (128.5%), and 26 of them decrease by an average of 0.22 m (46.7%). The changes have significant impacts. For storms with observed maximum storm surge levels greater than or equal to 0.91 m (3.0 ft), the maximum storm surges increase for nine of the 16 simulations and decrease for seven. The mean increase is 0.60 m (48.0%) and the mean decrease is 0.33 m (38.6%).

Compared to the data, after all the modifications are implemented, on average the model underestimates the maximum storm surges by 0.07 m (11.1%), reducing the error of the baseline case by a factor of two. However, the mean absolute error and the root mean square error increase compared with the baseline from 0.22 m and 0.31 m to 0.34 m and 0.46 m, respectively. For storms with observed maximum storm surge levels greater than or equal to 0.91 m, the model underestimates the maximum storm surges by an average of 0.03 m (4.6%), reducing the error of the baseline case. The mean absolute error and the root mean square error increase to 0.56 m and 0.69 m, respectively. A summary of these results is provided in

Table 3. Summary of errors produced by SLOSH model hindcasts.

	Average (Percent) Error (m)	Mean Absolute Error (m)	Root Mean Square Error (m)
Baseline Case
all surges	−0.14 (−22.2%)	0.22	0.31
large surges	−0.16 (−15.2%)	0.30	0.41
Surface Background Wind Modification
all surges	−0.11 (−20.9%)	0.22	0.31
large surges	−0.08 (−9.7%)	0.30	0.41
Parametric Wind Profile Modification
all surges	−0.21 (−36.1%)	0.26	0.34
large surges	−0.27 (−23.7%)	0.37	0.47
Maximum Wind Speed Modification
all surges	−0.03 (−3.8%)	0.29	0.43
large surges	−0.07 (−1.2%)	0.49	0.66
Combined Modifications
all surges	−0.07 (−11.1%)	0.34	0.46
large surges	−0.03 (−4.6%)	0.56	0.69

.

3.6. Case Studies

Four major hurricanes impacted all four study sites, Hurricane Bob (1991), Hurricane Bertha (1996), Hurricane Floyd (1999), and Hurricane Irene (2011). Each of these hurricanes had similar tracks, approaching the Caribbean Islands from the southeast, and then traversing along the east coast. Hurricane Bob is the only storm that did not make landfall in North Carolina, and thus it continued to intensify in the vicinity of this region, while the other three storms weakened here. The performance of the SLOSH model with and without modifications to the wind field varies; results are not consistent across storms or locations.

Hurricane Bob was a category three storm that originated in the Caribbean, and reached its maximum intensity east of North Carolina. It made landfall as a category two storm in Rhode Island. Hindcasts using the original SLOSH model overestimate the maximum storm surge heights at all study sites relative to the storm surge residuals computed from NOAA tide gauge data. The magnitude of the overestimation relative to the storm surges increases southward. It is overestimated by 3%, 25%, 73%, and 198%, for Narragansett Bay, Jamaica Bay, Atlantic City, and Norfolk, respectively. The combined modifications to the wind field representation reduce the simulated maximum storm surges, and improve the results at all sites except Narragansett Bay. The (signed) percent errors are reduced to −10%, −18%, 20%, and 60% (i.e., the maximum storm surges are underestimated at Jamaica Bay and Narragansett Bay).

Hurricane Bertha was a category three storm. It originated in the central Atlantic Ocean and reached its maximum intensity early, north of the Dominican Republic, before making landfall in North Carolina. It decreased to a tropical storm, and moved along the North Atlantic coastline. The SLOSH model originally underestimates the maximum storm surge heights at all four of the study sites. Maximum storm surge is underestimated by −8%, −25%, −47%, and −37% for Narragansett Bay, Jamaica Bay, Atlantic City, and Norfolk, respectively. The modifications to the wind field representation result in increases in the simulated maximum storm surges. The results are improved at Atlantic City (37%) and Norfolk (5%) but made worse at Narragansett Bay (97%) and Jamaica Bay (96%).

Hurricane Floyd was a very large, category four storm. It first made landfall in the U.S. in North Carolina as a category two storm, re-entered the Atlantic Ocean, and made a second U.S. landfall on Long Island before transitioning into an extratropical storm in Maine. The SLOSH model underestimates the maximum storm surge heights at all locations except Jamaica Bay; however, errors in the original SLOSH simulations are small. They are between −12% and 2% for the four sites. The modifications to the wind field representation increase the maximum storm surge heights, but degrade these results. All modified simulations overestimate the maximum storm surges by 32%, 30%, 9%, and 20% for Narragansett Bay, Jamaica Bay, Atlantic City, and Norfolk, respectively.

Hurricane Irene was a category three storm. It made landfall in the U.S. as a category one storm, first in North Carolina, and then again in southeastern New Jersey. The original, unmodified version of the SLOSH model accurately simulates the maximum storm surges of this storm at three of the sites, with errors of 0.0%, −16.7%, 12.9% and 72.3% at Narragansett Bay, Jamaica Bay, Atlantic City, and Norfolk, respectively. The modifications to the wind field representation increase the maximum storm surge heights at all sites except Norfolk. Norfolk is also the only location where the modifications to the wind field improve the magnitude of the relative error. With the changes, the errors in the maximum storm surges become 3.2%, 21.8%, 40.4%, and −1.2% (Figure 7, Figure 8, Figure 9 and Figure 10). The modifications degrade the results at all other sites, overestimating the surge by an average of 0.25 m (21.8%).

To summarize, the SLOSH model overestimates the storm surge caused by Hurricane Bob at all sites, and modifying the wind field decreases the storm surges, improving the estimates at all sites except Narragansett Bay. For Hurricane Bertha, the SLOSH model underestimates the storm surge at all sites, and the modifications increase the storm surges, improving the results at Atlantic City and Norfolk. For Hurricane Floyd, the SLOSH model slightly underestimates the storm surges at three sites, and the modifications to the wind field increase the storm surges too much and do not improve the results. For Hurricane Irene, the SLOSH model overestimates the storm surges at two of the sites, and the modifications only improve the results at Norfolk. In other words, results at Norfolk are improved with the modifications for each storm except Hurricane Floyd, and the number of simulations that are improved for each region decreases northward; the modifications do not improve the results at Naragannsett Bay for any of the storms.

4. Discussion

Relative to storm surge residuals computed from tide gauge data, the SLOSH model baseline simulations produce estimates of maximum storm surge heights with accuracy comparable to that commonly reported in the literature. At the tide gauge locations, the average error of all simulations is less than 0.15 m in absolute value, and the average relative error is −22.2%. The simulations reveal bias in the SLOSH model at the study sites. The model underestimates 80% of the maximum storm surges simulated, although less (relative) bias is observed for large storm surges. As expected, the wind field representation significantly impacts the maximum storm surge heights simulated by the SLOSH model, though the specific impacts observed are not obvious a priori.

The modification to the surface background wind increases nearly one half of the maximum storm surge heights. In the original, unmodified SLOSH model, the magnitude of the radially variable factor used in the background wind (1) has a maximum value of 0.5 at $R_{max}$, and decreases toward the core and outer radius of the storm. Increasing the factor to a constant value of 0.55 predictably increases most storm surge heights. We expect this modification to improve the underestimation of the maximum storm surges seen in the baseline case, and while the average error does slightly decrease, the mean absolute error and the root mean square error are essentially unchanged. This modification does not have a significant impact on the average error of the SLOSH model, perhaps due to the relatively slow translational speed of tropical cyclones.

The modification to the parametric wind profile generally decreases the simulated maximum storm surge heights, which does not improve the underestimation of the maximum storm surges seen in the baseline case. In [36], it is discussed that the modified profile significantly underestimates the outer radius of the storm. The winds near the core of the storm most significantly impact the generation of maximum storm surges; however, this result indicates that the winds at larger radii play a significant role as well. This can be explored through additional study of wind profiles (e.g., [36]) that better approximate the outer regions of the storm. Also, hurricanes often undergo an extratropical transition as they move through the higher latitudes of the study region. When this occurs, the hurricane structure evolves and the wind profiles explored here, which were intended to represent traditional hurricane structures, may fail to accurately represent the structure of a given storm. Further study of wind profiles of transitioning tropical cyclones is needed.

The direct implementation of $V_{max}$ has the greatest influence on the maximum storm surge heights. In general, it increases these values, indicating that the iterative procedure in the unmodified version of the SLOSH model used to estimate $V_{max}$ causes an underestimation of the storm surge. With the modification, the average error in the storm surge significantly decreases. However, the mean absolute error and the root mean square error are made worse. In other words, the bias is improved, but at the expense of larger variance in the estimates of maximum storm surges. The iterative procedure in the original, unmodified version of the SLOSH model was implemented to reduce model sensitivity to errors in $V_{max}$. Implementing $V_{max}$ directly increases sensitivity to this value, and as a result the variance in $V_{max}$ is reflected in the variance of the maximum storm surge heights. The uncertainty in estimates of maximum storm surge heights computed by the SLOSH model is increased.

The three modifications interact nonlinearly, with the effect of the direct implementation of $V_{max}$ dominating. When each of the changes is implemented jointly, the bias is reduced, though not to the low values seen with the $V_{max}$ modification alone. The mean absolute error and the root mean square error increase to values larger than any of those obtained from any of the modifications in isolation.

The four storms that impacted all the sites allow a more careful assessment of the impact of the combined modifications across several regions, across several storms. In general, the original, unmodified SLOSH model accurately estimates the maximum storm surges at Narragansett Bay. These results are difficult to improve, and the wind field modifications prove to be detrimental. On the other hand, the maximum storm surges simulated using the original model have considerable error at Norfolk, and the modifications do improve the results. This suggests that for major storms, the incorporated physics and data may play less of a role at higher latitudes.

Additionally, the original model generally overestimates storm surges produced by Hurricane Bob and Hurricane Irene, and underestimates those of Hurricane Bertha and Hurricane Floyd. For this subset of major hurricanes, there is no consistent trend in the errors. After the incorporation of the wind field modifications, the storm surges are generally adjusted in the correct direction; however, sometimes they are adjusted too much. The modifications improve the simulated storm surges from Hurricane Bob, which did not make landfall and maintained its structure as it approached the U.S. North Atlantic coast. The modifications did not improve the simulated storm surges of Hurricane Floyd, which was very large and asymmetric. The incorporated physics and data used in the wind field modifications may better represent smaller storms that do not make landfall; however, further study is needed to understand the broader implications of these four cases.

It should be noted that in this work, we specifically focus on coastal regions in the Northeastern United States. Further study is needed to investigate the applicability of the results to broader regions.

5. Conclusions

The surface wind stress is one of the most important components of hurricane storm surge modeling, and there are many methods of representing the surface wind field used in its approximation. In this study, we have assessed the impact of a wind field representation developed based on empirical, physical, and observational data on SLOSH model performance at four vulnerable locations in the Northeastern United States. Specifically, we have implemented an empirically derived representation of the background wind field, a physically based parametric wind profile, and the direct use of observed maximum wind speeds. We have assessed the impacts of these changes individually and collectively on the simulation of maximum storm surge heights for a broad range of historical storms that impacted the study region.

The original, unmodified SLOSH model sufficiently estimates maximum storm surges at the study sites. However, there is a potential model bias that frequently produces underestimation. While overestimation of storm surge can have detrimental social consequences such as distrust of scientific experts and authorities [47], underestimation of storm surge can be deadly, especially for regions in low-lying, coastal terrain, such as those included in this study. For both real-time forecasting and long-term planning and risk assessment, it is desirable to eliminate this model bias. Here we find that the wind field representation can play a significant role in this effort.

Modifying the background wind field representation generally increases maximum storm surge heights and is thus beneficial, although the change to simulated maximum storm surge heights is not dramatic. The impact of the parametric wind profile is also relatively minor; however the modification generally decreases maximum storm surge heights, which does not improve the systematic underestimation. Further investigation and development of wind profiles that better represent the storm’s outer region (e.g., [36]), particularly as storms undergo extratropical transition, are needed. Finally, the implementation of observed maximum wind speeds generally increases simulated maximum storm surge heights and significantly improves model accuracy; however, it also increases model uncertainty. The variance in the estimates of maximum storm surge heights increases with the change. The combination of modifications reveals that the changes interact nonlinearly, and the resulting model accuracy decreases compared to when the observed maximum wind speeds are implemented alone. Based on these results, the recommendation is the direct use of observed values of $V_{max}$, particularly when measurement errors and uncertainty in this value are small.

In practice, the SLOSH model is used to produce both deterministic and probabilistic storm surge forecasts. When a hurricane threatens the U.S. coastline, SLOSH model simulations are used to provide guidance to NHC forecasters, emergency managers, and other government officials through various products. The MEOW products are precomputed and provide a worst-case storm surge scenario when uncertainty lies in the position and landfall location of a storm. The MOM products are precomputed and provide a worst-case storm surge scenario if only the storm intensity is known. The P-surge products are real-time, probabilistic forecasts, developed by permuting uncertain storm parameters forecasted by the NHC (i.e., storm position, size, intensity, and forward speed) based on historical errors. The SLOSH model is also used to develop probabilistic information to guide design criteria [19,22,25]. Here, we have shown how the wind field representation can be improved to reduce errors in SLOSH simulations. This error reduction may be applied to the various SLOSH-based products to improve real-time forecasts as well as long-term risk analyses of storm surge.