Forecasting of Surface Ozone Concentration by Using Artificial Neural Networks in Rural and Urban Areas in Central Poland

Abstract

This paper presents the development of artificial neural network models for the prediction of the daily maximum hourly mean of surface ozone concentration for the next day at rural and urban locations in central Poland. The models were generated with six input variables: forecasted basic meteorological parameters and the maximum O₃ concentration recorded on the previous day and number of the month. The training data set covered the period from April 2015 to September 2015. An analogous data set of input variables, for the 2014 year, not used during the process of training the networks, was used as test data to examine the quality of these models. From the results of simulations for the year 2014, the average relative error values were equal to 15.3% and 15.7% for Belsk and Warsaw stations, respectively. The mean error (ME) value indicates a tendency to overestimate the predicted values by 4.8 µg/m³ for Belsk station and to underestimate the predicted values by 0.9 µg/m³ for Warsaw station. The analysis of days when the relative error value was >50% revealed that all predictions with extremely high relative error value were associated with relatively low daily maximum surface ozone concentration values that occurred suddenly due to a sharp drop in day-to-day ozone concentration values.

1. Introduction

Ozone is a naturally occurring component of the atmosphere. The primary source of ground-level ozone is production through a chain of photochemical reactions involving NO_x, CO and VOC (Volatile Organic Compounds) [1,2]. Another natural source is the flux of ozone from the stratosphere to troposphere [3]. The relative importance of the above-mentioned mechanisms changes according to spatial and temporal characteristics [4]. The largest influence of stratosphere–troposphere exchange is noted at mountain stations with a maximum value during the spring season [5,6], while photochemical ozone production dominates in urbanized and industrialized regions causing extensive spring–summer maximums. The concentration of surface ozone in a given area is determined by the combination of factors involved in its formation (photochemical reactions), destruction (dry deposition, chemical reactions) and transport (stratospheric intrusions, long-range transport). The relatively long life-time of the ozone molecule in the boundary layer (1–2 days) [7] enables it to be transported for long distances feeding the budget of areas located far from the source region. Additionally, the lack of mechanisms that deplete ozone contribute to usually higher surface ozone concentrations at rural stations than at urban or suburban stations [8,9].

Ozone is a primary component of photochemical smog [10], with extensively documented negative effects on human health, vegetation and materials [11,12,13]; further, it is an important greenhouse gas with radiative forcing 0.40 ± 0.20 W/m² [14]. Photochemistry of ozone plays a significant role in the troposphere. The process of photolysis of ozone (λ < 320) is the dominant source of hydroxyl radicals (OH), the primary atmospheric oxidant, thus removing significant amounts of halocarbons, CO and CH₄ [5,15]. Because of the important role of ground-level ozone in the atmosphere, it is necessary to understand the temporal-spatial variability of surface ozone concentration and to develop methods of forecasting high ozone concentrations and information systems, especially in populated areas.

Surface ozone concentration values can be predicted using both deterministic and statistical methods [16]. Deterministic models are based on mathematical equations that describe chemical and physical processes in the atmosphere [17] and work on the principle of cause and effect. The use of deterministic models requires detailed information about air pollutants (especially “ozone precursors”) as well as numerous meteorological parameters, otherwise, the modeling process is not effective. Statistical models, used in empirical research methods, are based on the statistical relationship between input data as predictors and output data as the explained variable. The most commonly used models are multiple linear regression (MLR) [18,19,20] and classification and regression trees [21,22]. Although these methods have been widely applied in the prediction of surface ozone concentration values, they have several limitations. The processes of surface ozone formation (involving VOC, NO_x, and incoming solar radiation) are strongly nonlinear. Additionally, they depend on many factors such as meteorological parameters (temperature, relative humidity, etc.), processes of atmospheric transport and mixing or concentration of chemical compounds in the atmosphere. Because of these issues, the prediction of ozone peak levels using existing statistical models has become problematic and inefficient. One of the most effective statistical approaches is the artificial neural network tool—mathematical structures that imitate the biological nervous system with a strong ability to fit data to present and learn complicated, nonlinear relationships.

Neural networks are a relatively recent technique of modeling. The first publication on this subject was the article by McCulloch and Pitts in 1943 [23]. Since then, neural networks have been widely used in many fields of science. The use of neural networks in air quality modeling started in the 1990s. Because of the ability to recognize highly complex and nonlinear relationships between ozone and their precursors, artificial neural networks are widely used for both approximation and forecasting of surface ozone time series. The most frequently used type of neural network is a multilayer perceptron (MLP). This type of artificial neural network is characterized by the best estimation performance and functionality [21]. Usually, neural networks are characterized by a set of input variables, including meteorological parameters and concentrations of individual air pollutants as precursors to ozone formation [24,25]. Comparisons of the predictions of neural models and linear regression or ARMA (Autoregressive-moving-average model) models indicate that neural networks perform more efficiently than other methods [26,27,28]. Yi and Prybutok [29] predicted the maximum surface ozone concentration values in an industrialized region of southern United States, by using the neural network model (MLP) with nine predictor variables, including both chemical (NO, NO₂, NO_x, CO₂ and O₃ at 9:00 a.m.) and meteorological (temperature, wind speed and wind direction) compounds. The results of the models’ performance compared with those of the traditional regression model and ARIMA (Autoregressive-integrated-moving-average model) indicate the superiority of MLP models over the other two models. Chaloulakou et al. [30] predicted the maximum surface ozone concentration for the next day in Athens, Greece. The input data set included 11 variables (eight meteorological parameters and maximum O₃ from the previous three days). Detailed statistical analysis comparing the results of neural network models with MLR models showed that neural network models better forecast high ozone concentration values. The threshold ozone value of 180 µg/m³ was well predicted in >70% of cases on average. Inal [31] predicted the maximum surface ozone concentration in Istanbul, Turkey by using a neural network model that included 18 input predictors (nine meteorological parameters and nine air pollutant concentrations). Sensitivity analysis and further statistical analysis indicated that only nine of these predictors (maximum and average O₃ concentration, NO, PM₁₀, maximum and average temperature, sunshine time, solar radiation and wind direction) were crucial for the quality of the model. Hadjiiski and Hopke [32] used an expanded input set (almost 60 chemical components and a set of meteorological parameters) and concluded that the most important input variables were nitrogen oxides, 5 of the 53 hydrocarbons, temperature and solar radiation. Subsequently Faris et al. [33] developed neural network models (MLP-ANN: Multilayer perceptron and RBF-ANN: Radial basis function) for short-term forecasts of surface ozone concentrations based on only three variables (temperature, relative humidity and nitrogen dioxide concentration). The results indicate good prediction of measured O₃ data and better forecast capability of the MLP model than that of the RBF model. Whereas, according to Comrie [34], the use of the surface ozone concentration on the previous day as an input variable significantly improved the quality of the model. One of the main issues related to creating neural models refers to the size of the input data set, used especially for the training subset, and their representativeness. In the training subset has only a small number of cases, may be insufficient to present all possible situations to the neural network to enable it to learn the correct prediction of extreme values of surface ozone concentrations.

The major aim of this study was to investigate the possibility of using an artificial neural network to predict the daily maximum hourly mean concentration of surface ozone for the next day in rural and urban locations in central Poland by using several basic input variables (mainly meteorological parameters) with chemical parameters limited to the ozone concentration from the previous day.

2. Data

Information on forecasted meteorological parameters was obtained from the Department of Physics of the Atmosphere, Institute of Geophysics, Polish Academy of Sciences. Forecasts were performed using the WRF-ARW model (global numerical model of weather prediction) [35]. Data from 1 April to 30 September 2015 were used for the development of forecast models, while data from 1 April to 30 September 2014 were used for testing the efficiency of the models. Data on the daily maximum hourly concentration of surface ozone were obtained from the Chief Inspectorate for Environmental Protection. The ozone analyzers at both stations use the standard method of measurement–absorption of UV radiation by ozone particles, with reference to the norm PN-EN 14625. The analyzers were calibrated on a regular basis against certified transfer ozone standards in accordance with routine quality assurance procedures. The selected period of the forecast included months when the highest surface ozone concentration occurs, including the exceedances of acceptable levels (April–September).

Both stations selected for the analysis are located in Masovian Voivodeship in the central part of Poland (Figure 1). Belsk (51°50′ N, 20°47′ E; 176 m a.s.l.), representing rural background conditions is located in the Nature Reserve Modrzewina area, approximately 60 km south of Warsaw. The station is surrounded by orchards and a coniferous forest. The second station, namely, Warsaw (52°09′ N, 21°02′ E; 102 m a.s.l.) represents urban background conditions. This station is located in the commercial service zone in the south of the city.

3. Methods

The processes leading to photochemical ozone formation are complex and strongly nonlinear. The surface ozone concentration in a given area is associated with the availability of chemical precursors of ozone as well as the prevailing meteorological conditions that can promote or inhibit the process of ozone formation. Hence, the prediction of the maximum 1-h surface ozone concentration was performed using artificial neural networks (regression analysis method) that can capture complicated, nonlinear dependencies between predictors as input variables of the model (which are usually dependent on each other) and the expected output value. The creation of artificial neural networks to predict the maximum 1-h surface ozone concentration for the next day was realized in the following steps:

(1)

Determination of the forecast value of basic meteorological parameters for the period April–September 2014 and April–September 2015 by using the global numerical weather forecast model WRF-ARW. The predicted values (for the next day) included the following parameters: temperature of the air (°C; T), solar radiation (W/m²; SR), wind speed (m/s; WS), and relative humidity (%; RH). These meteorological parameters were predicted with a frequency of 3 h (for 2014) and with a frequency of 1 h (for 2015).

(2)

Creation of a data set containing the daily maximum 1-h value of meteorological parameters during the day.

(3)

Adding 2 additional variables to the existing data set:

• the number of the month for which surface ozone prediction was carried out (April, 4; May, 5; etc.)
• the maximum hourly mean value of surface ozone concentration within 24 h on the day preceding the forecast

(4)

Implementing a complete data set in the Neural Networks package of the Statistica 10 Program. The input variables of the model were the six selected parameters, while the values of these variables for each day of the analyzed period were the cases of the model.

(5)

Division of the entire data set into training (70% of cases), test (15%), and validation (15%) subsets.

This was done to avoid losing the network generalization skills. As the error value is minimized only in the training subset, 2 other subsets, which were not presented during the training process, were extracted. Observations of the error values in all groups avoided overfitting of the neural network. Assignment of all cases to individual subsets was carried out randomly. The number of cases in the training subset was equal to 112 and 110 at Belsk and Warsaw stations, respectively, while these cases in test and validation subsets were equal to 23.

By using the Statistica 10 “Automatic Neural Network” Program and automatic network designer function, the set of best-performing networks for each station was generated. Then, the best neural networks were tuned by testing three-layer MLP neural networks with different numbers of neurons in the hidden layer and a different activation function. In accordance with the rule suggested by Goethals et al [36], the number of neurons in the hidden layers was conditioned by the number of inputs and outputs of the network. This rule (2 × In+1, where In is the number of input variables) limited the maximum number of neurons in the hidden layer of the analyzed networks to 13.

The quasi-Newton BFGS (Broyden–Fletcher–Goldfarb–Shanno) algorithm belonging to the group of gradient methods was used for the network learning process. The weights were initiated randomly and during the learning processes their reduction was not applied.

The choice of the optimal model was made on the basis of the following factors:

(1)

Prediction error values for each subset. Most attention was paid to errors in the validation and testing subsets as they were independent and not participating in the learning process.

(2)

Correlation coefficient values for measured values of surface ozone concentration from the neural network and reality.

4. Results

All neural networks selected for forecasting were characterized by six neurons in the input layer (as there were six input variables) and one neuron in the output layer (as there is one output variable O₃ forecast) (

Table 1. Characteristics of the selected neural networks.

1-h Max	Kind of Network	Architecture of the Network	Correlation Coefficient			Prediction Error			Activation Function
			Training	Test	Validation	Training	Test	Validation	Hidden Layer	Output Layer
Belsk	MLP	6-6-1	0.92	0.87	0.88	57.9	55.9	48.6	Tanh	Linear
Warsaw	MLP	6-4-1	0.93	0.93	0.85	48.3	66.0	66.5	Tanh	Logistic

MLP-Multilayer perceptron.

).

The optimal neural network for the Belsk station had six neurons in the hidden layer. The prediction errors (calculated as the average of squares of residuals divided by 2) for individual subsets were equal to 57.9, 55.9, and 48.6 for the training, test, and validation subsets, respectively. Correlation coefficient values ranged from 0.87 (test subset) to 0.92 (training subset).

The best neural network for the Warsaw station had four neurons in the hidden layer. Prediction error values were equal to 48.3, 66.0, and 66.5, while correlation coefficient values were equal to 0.93, 0.93, and 0.85 for the training, test, and validation subsets, respectively.

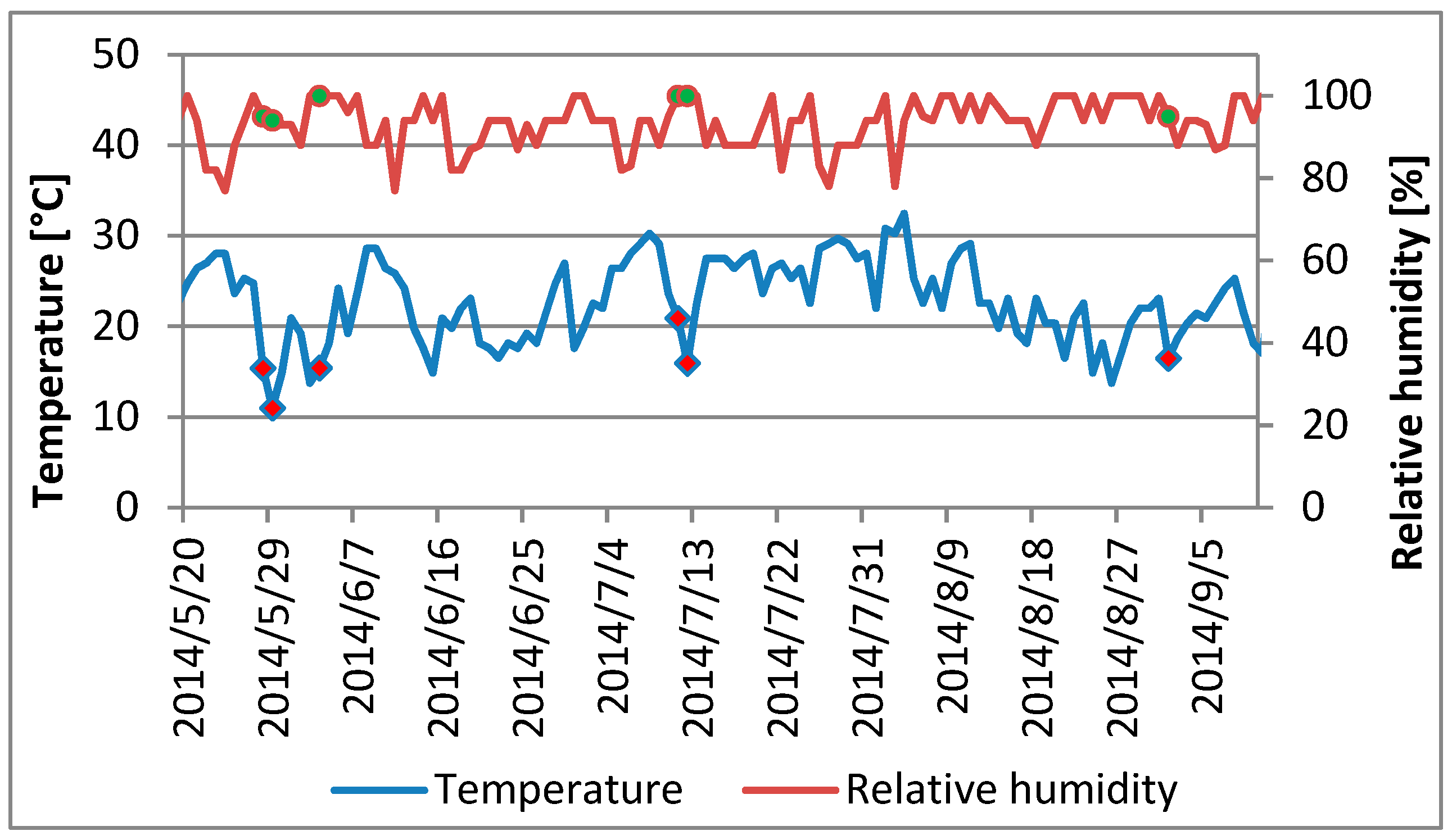
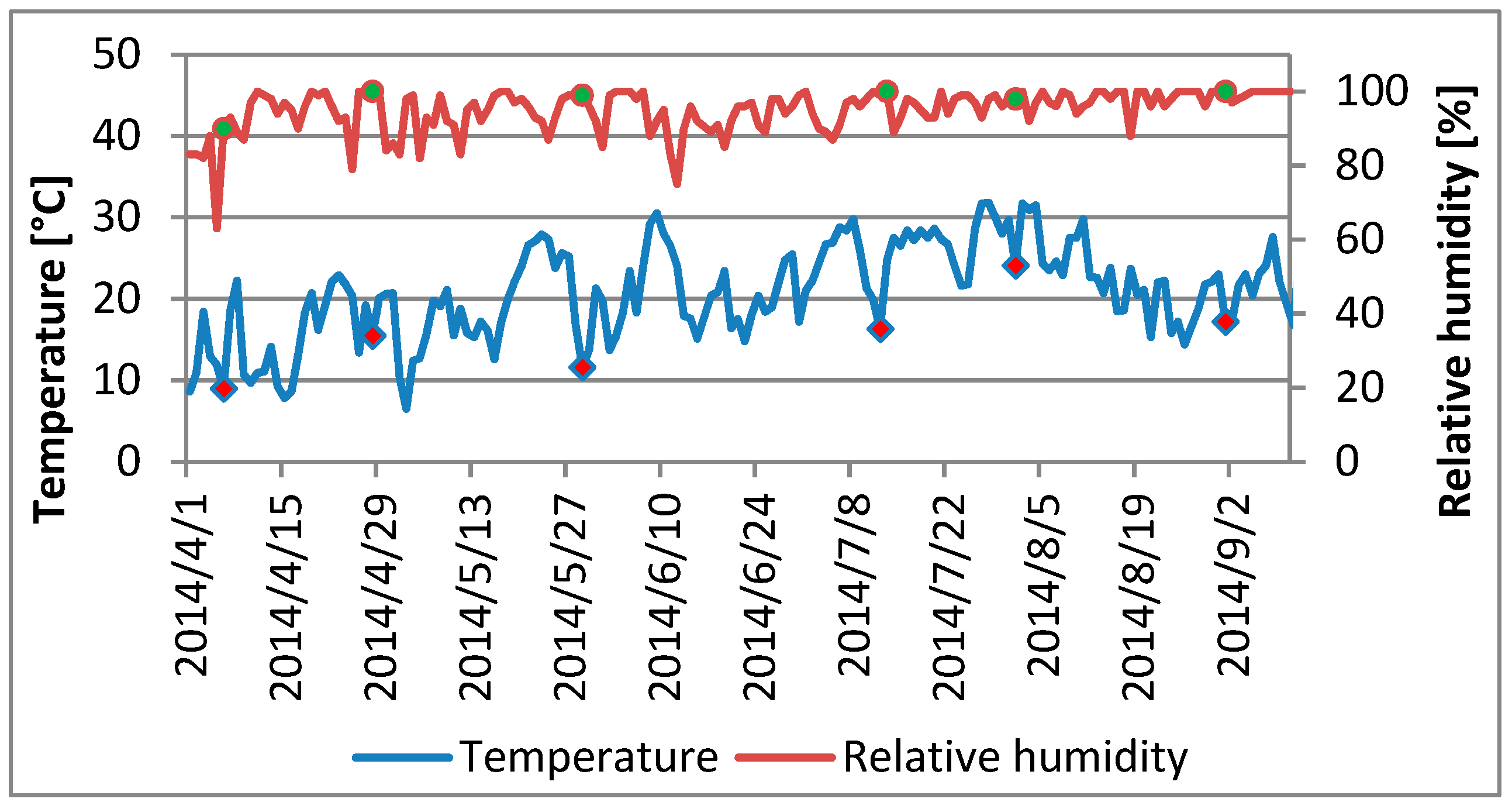
4.1. Global Sensitivity Analysis

The global sensitivity analysis (

Table 2. The results of global sensitivity analysis.

1-h Max	Temperature		Solar Radiation		Month		Ozone 1 Day before		Relative Humidity		Wind Speed
	Quotient	Rank	Quotient	Rank	Quotient	Rank	Quotient	Rank	Quotient	Rank	Quotient	Rank
Belsk	5.32	1	1.53	3	2.67	2	1.25	4	1.13	5	1.04	6
Warsaw	5.84	1	1.68	2	1.47	3	1.35	4	1.14	6	1.16	5

) allows checking of the appropriateness of using certain variables in the model and also checks the importance of individual variables for the quality of maximum surface ozone prediction. Higher quotient values indicate the greater ability of a specific variable to yield good results for the model.

The error quotient value (in Table 2) in all cases was above 1, which indicated a good choice of all parameters as input model variables and their significance in the network learning process. The most important predictor was the air temperature. Solar radiation and the number of the month were the next two most important predictors, followed by the maximum ozone concentration on the previous day, and finally, wind speed and relative humidity. Theoretically, only variables with an error quotient above 1 are crucial in the process of creating an effective network. Because input variables usually are not completely independent, we should be careful while removing individual variables (with quotients below 1) to avoid losing any important information resulting from the coexistence of relevant variables.

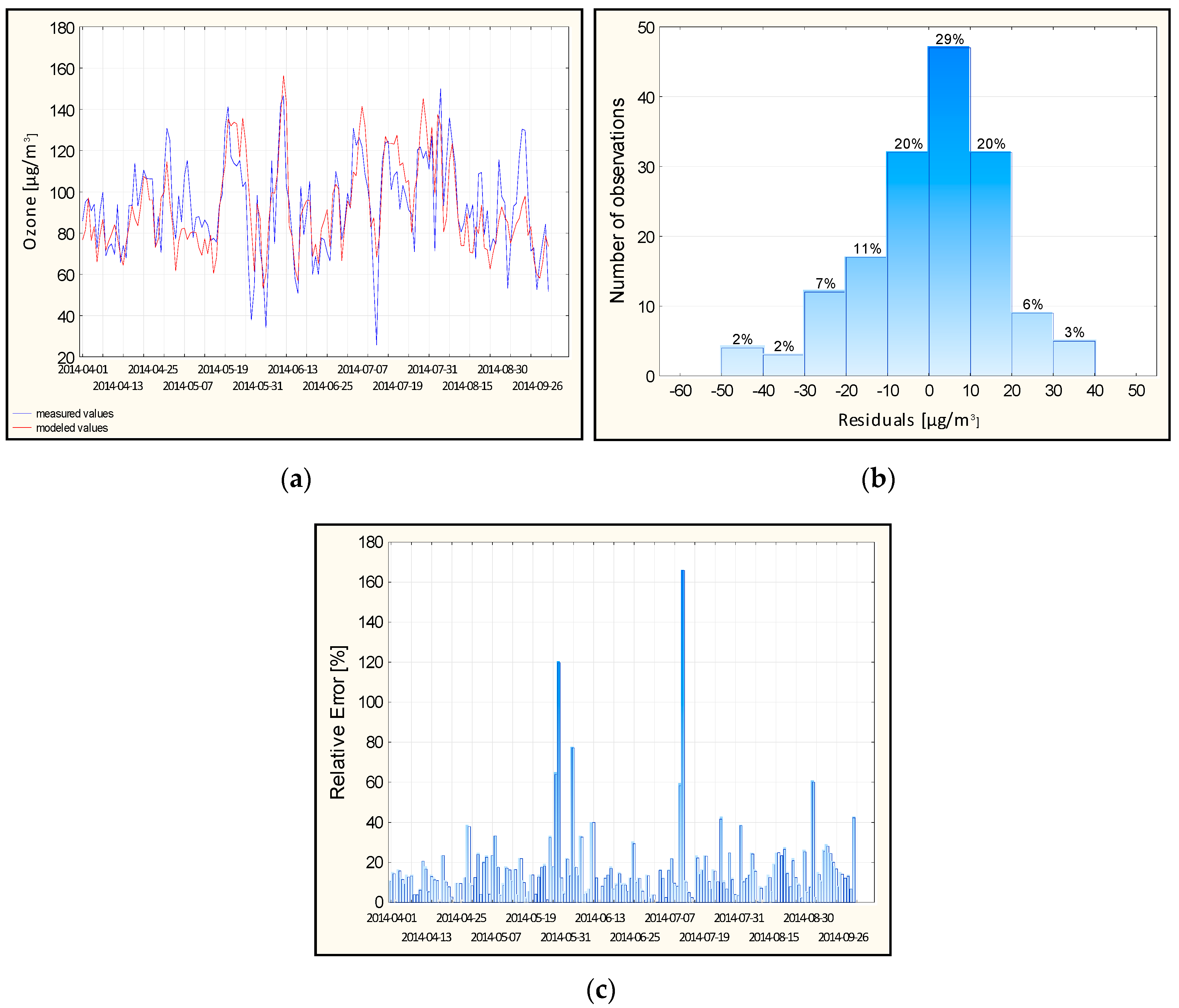
4.2. Quality Assessment of Generated Neural Prognostic Models

The graphic analysis of the quality of prognostic neural models was estimated on the basis of the analysis of graphs of differences between forecasted and measured surface ozone concentration values and graphs of relative error values calculated according to Formula (1):

δ = (|X_m − X_c|)/X_m × 100%

(1)

where X_m is the measured value and X_c is the calculated value.

An additional criterion of the quality of prognostic neural networks is the value of errors as a measure of deviations of calculated ozone concentration values from the measured values. The performance statistics for Belsk and Warsaw stations are summarized in

Table 3. Statistical performance of the neural network models for data set from 2015. $\stackrel{-}{\mathrm{O}}$ and $\stackrel{-}{\mathrm{A}}$-mean maximum observed and predicted concentration (µg/m³), respectively; So and Sa—standard deviation of observed and predicted concentration (µg/m³), respectively; R²—coefficient of determination; MBE—mean bias error (µg/m³); MAE—mean absolute error (µg/m³); RMSE—root mean square error (µg/m³); d₂—index of agreement.

Station/Measure.	$\stackrel{-}{\mathrm{O}}$ [µg/m3]	$\stackrel{-}{\mathrm{A}}$ [µg/m3]	So [µg/m3]	Sa [µg/m3]	R2	MBE [µg/m3]	MAE [µg/m3]	RMSE [µg/m3]	d2
Belsk	91.2	92.6	19.6	20.8	0.78	−1.3	8.6	9.9	0.94
Warsaw	97.2	95.7	20.9	20.7	0.72	1.4	8.9	11.5	0.92

. According to Legates and McCabe [37], a sufficient set of model performance assessments should contain at least one relative error measure (e.g., index of agreement) and absolute error measure (e.g., root mean square error) with complementary measures (e.g., standard deviation). Furthermore, after the analysis of studies by Fox [38], Willmott [39], and Gardner and Dorling [23], Table 3 includes the following measures: $\stackrel{-}{\mathrm{O}}$, mean observed concentration (µg/m³); $\stackrel{-}{\mathrm{A}}$, mean predicted concentration (µg/m³); So, standard deviation of observations (µg/m³); Sa, standard deviation of predictions (µg/m³); MBE, mean bias error (µg/m³); MAE, mean absolute error (µg/m³); RMSE, root mean square error (µg/m³); R², coefficient of determination; and d₂, index of agreement.

MBE determines the difference between the mean forecasted concentration and the mean observed concentration. It allows assessment of whether forecast values are underestimated or overestimated.

The most commonly used statistical measures of residual error are MAE and RMSE. Both summarize the mean difference between observed and forecasted concentrations, although RMSE is more sensitive to extreme residual values than MAE. Large differences between RMSE and MAE indicate the occurrence of large residuals values. A general rule is that RMSE is higher than MAE and the value by which RMSE exceeds MAE indicates the extent to which extreme values occur in the data set.

Two dimensionless measures used in this paper are: coefficient of correlation (R²) and index of agreement (d₂). They are intended to ensure a relative estimation of model performance. The coefficient of determination (R²), one of the most widely used measures of model performance assessment, indicates the proportion of variability of the observed data that is predictable by the model. The index of agreement (d₂) is a standardized measure of the degree of model error value. The values of R² and d₂ ranged from 0 to 1, where the value of 1 indicates the best model performance. The fact that they are bounded means that they can be applied to future comparison between models.

An important feature of neural network models is the ability to generalize the knowledge acquired during the learning process and correct forecasting based on new data, and not data that has been presented before. Therefore, in this paper, we will present the results only for validation subset.

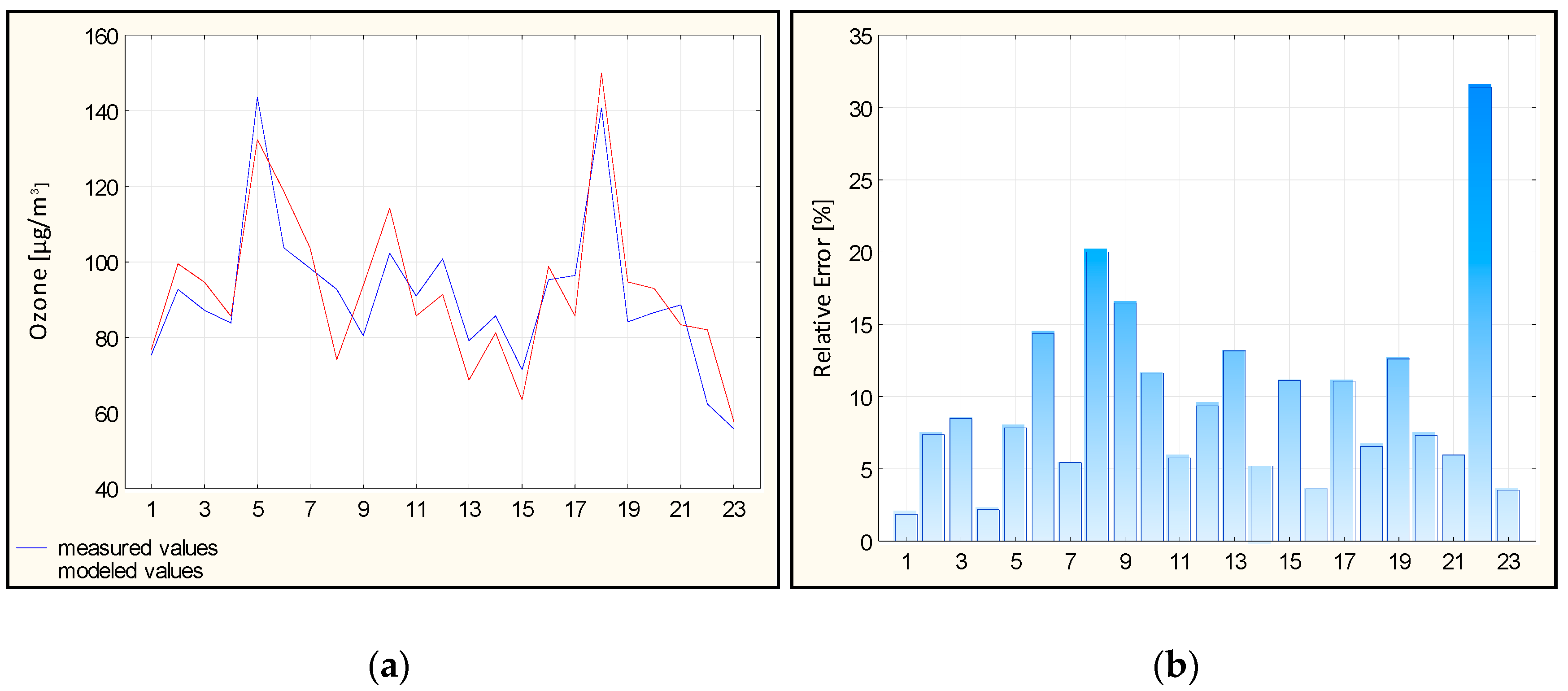
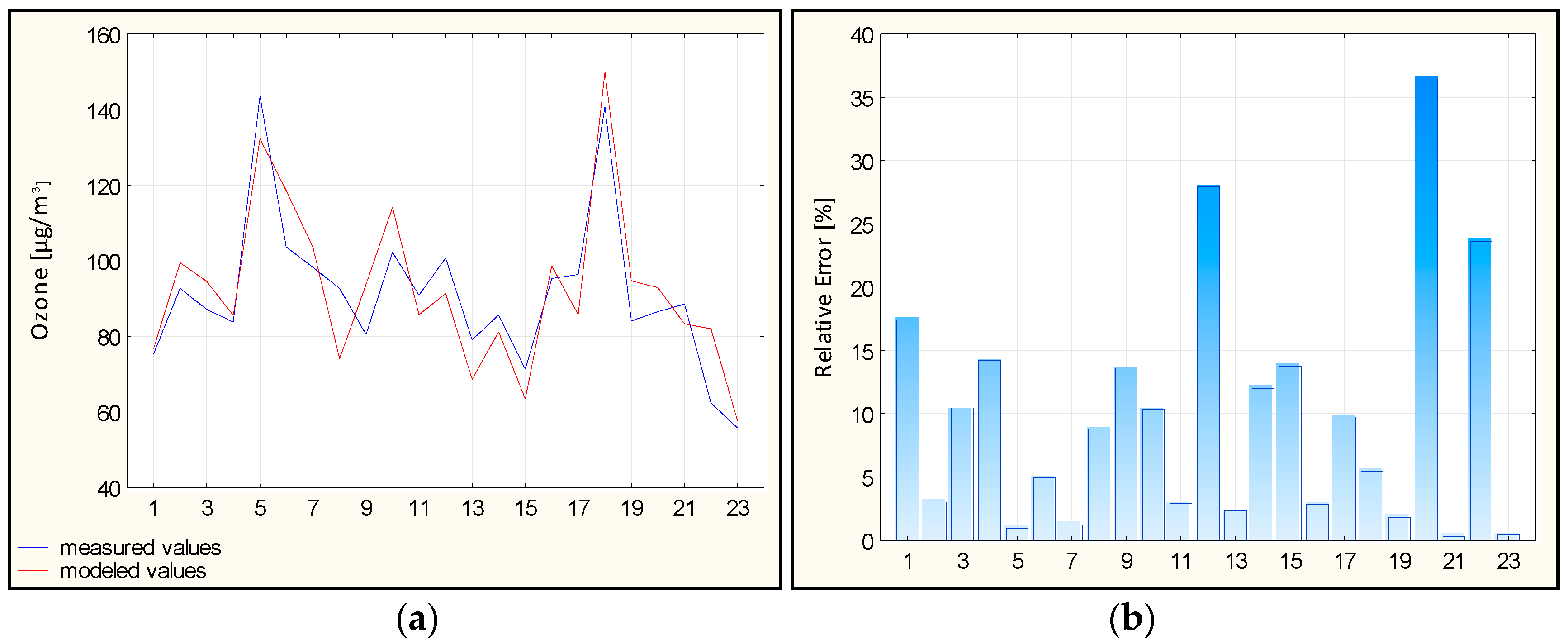
4.3. Results of Ozone Concentration Prediction for Belsk and Warsaw Stations

Measured and modeled values of surface ozone concentration at Belsk station are shown in Figure 2. The relative error values ranged between 1.9% and 31.4%. The highest error value was noted at the end of September for relatively low maximum ozone concentration values (62.4 µg/m³). The average relative error was equal to 9.7%. In 61% of cases the values estimated by the model were obtained with relative error value below 10% and in 91% of cases the relative error values were below 20%.

Measured and modeled values of surface ozone concentration at Warsaw station are shown in Figure 3. Relative error value for the validation subset ranged from 0.3% to 36.5%. The highest error value was noted at the beginning of September for relatively low 1-h maximum surface ozone concentration (58.7 µg/m³). The average relative error value was 9.8%, wherein 56% of ozone concentration values were characterized by relative error value below 10% and 87% of ozone concentration values by relative error value below 20%.

Analysis of Table 3 reveals that the means of maximum of observed surface ozone concentrations are higher at Warsaw station (97.2 µg/m³) than at Belsk station (91.2 µg/m³). The difference is equal to 6 µg/m³ and is not statistically significant; however, it reflects the dominant role of higher levels of ozone precursors in the urban area that can lead to more effective surface ozone formation. This situation is in contrast with the generally higher daily means (averaged for the whole day) of surface ozone concentration noted at Belsk and other rural background stations compared to urban background stations. The predicted surface ozone data for both stations did not differ significantly from observed means, and differences are slightly above 1 µg/m³.

Standard deviations of the observed and estimated ozone data are similar for both stations and are approximately 20 µ/m³. The differences between observed and predicted standard deviations values (So and Sa) are relatively small (up to 1.2 µg/m³ of absolute value); this indicates that concentrations predicted by the model have comparable variability with the observed data and shows the ability of the neural network model to capture the variability of the observed data set.

The MBE values at both sites are comparable and generally small (up to 1.4 µg/m³ of absolute value), but exhibit a difference in terms of sign of the value. In Belsk, the MBE value is negative indicating a tendency for a slight overestimation, while in Warsaw, the MBE value is positive indicating a tendency for underestimation of ozone concentrations by the model.

RMSE values are equal to 9.9 µg/m³ and 11.5 µg/m³, while the MAE values are equal to 8.6 µg/m³ and 8.9 µg/m³ for Belsk and Warsaw stations, respectively. For both sites, in accordance with the applicable rule, the RMSE value is higher than the MAE.

The d² and R² are relatively high for both sites, indicating a reasonably good performance of the models used; for Belsk station both measures are slightly higher (0.94 and 0.78, respectively) than for Warsaw (0.92 and 0.72, respectively). In terms of R², the model can reproduce more than 70% of the variability in the original, observed data set in both Belsk and Warsaw stations.

By summarizing Table 3, it can be stated that the chosen models have good generalization performance, with a slightly better forecast potential for Belsk station. Analysis of appropriate measures proves that the dependence of surface ozone on meteorological conditions can be quite accurately reflected using several, basic meteorological parameters.

Further statistical analysis to determine whether the differences between O₃ concentration values in the modeled and observed data sets are significantly different included the following:

• performing the test of normality of the data sets to determine whether the data are well characterized by a normal distribution (Shapiro–Wilk test, available in STATISTICA)
• performing the test of statistical significance (parametric or non-parametric) to determine whether the differences in the two analyzed groups are statistically significant. If the conditions for the existence of a normal distribution and homogeneity of the variances in the analyzed data sets are met, we can use parametric tests (t-test). In the case when the assumptions regarding the applicability of the parametric test are not met, we can perform nonparametric tests that do not depend on the shape of distribution.

Table 3 presents the results of Shapiro–Wilk tests for both stations. The results of this test were interpreted by comparing the right probability value p with the given level of significance at which the test was performed (α = 0.05). The condition for stating that the analyzed population has a normal distribution is a p value of less than or equal to 0.05 in each data set.

The analysis of the data given in

Table 4. Results of the Shapiro–Wilk test together with the right values of probability for Belsk and Warsaw stations for 2015.

Station/Measure	Observation		Model
	Shapiro–Wilk Test	p	Shapiro–Wilk Test	p
Belsk	0.8845	0.012	0.9387	0.168
Warsaw	0.9225	0.075	0.9106	0.042

reveals that both stations (Belsk and Warsaw) do not show a normal distribution. This is the basis for using one of the non-parametric tests to determine the significance of differences between model results and the observed values of surface ozone. In this study, we used the Mann–Whitney test (

Table 5. Results of the Mann–Whitney test together with the right values of probability for Belsk and Warsaw stations for 2015.

Station/Measure	Mann–Whitney Test	p
Belsk	−0.1318	0.895
Warsaw	0.2855	0.775

). Based on the assumed level α = 0.05 and statistics of the Mann–Whitney test, we can assume that there are no statistically significant differences between the values of surface ozone generated by the neural network model and the observed values.

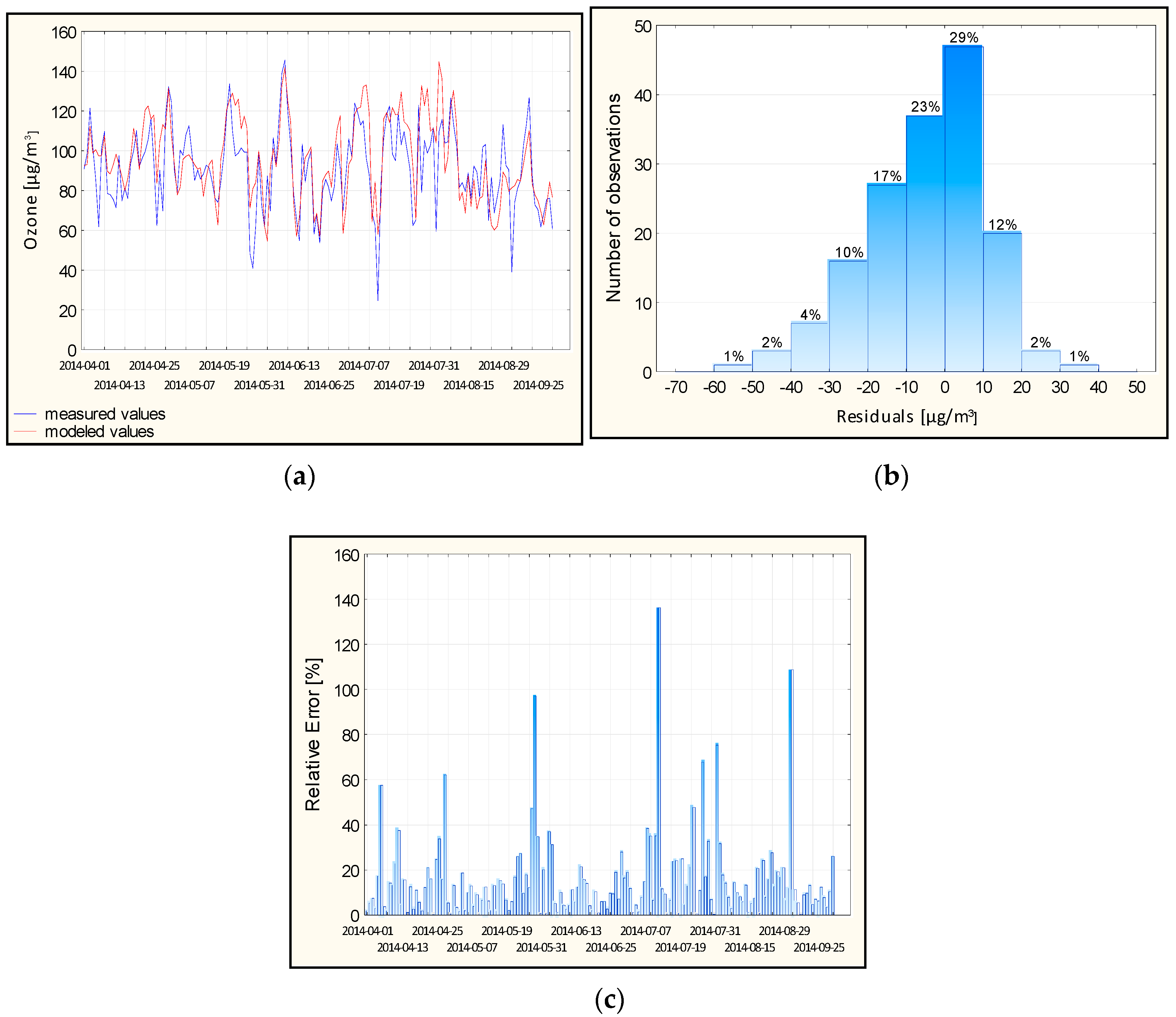
4.4. Prediction of the Maximum 1-h Surface Ozone Concentration Value for 2014

The main purpose of this study was to create simple, neural prognostic models as a tool to predict the maximum 1-h surface ozone concentration for the next day with an ability to generalize the acquired knowledge for new, unknown data. To evaluate the forecast potential of the constructed models, new forecasts for independent test data for 2014 (with the same input data as that for 2015) were performed. The new 1-h maximum surface ozone predictions covered the period from April to September 2014. The results of the forecasts performed for April–September 2014 are shown in Figure 4 and Figure 5.

Table 6. Statistical performance of the neural network models for data set from 2014. $\stackrel{-}{\mathrm{O}}$ and $\stackrel{-}{\mathrm{A}}$―mean maximum observed and predicted concentration (µg/m³), respectively; So and Sa―standard deviation of observed and predicted concentration (µg/m³), respectively; R²―coefficient of determination; MBE―mean bias error (µg/m³); MAE―mean absolute error (µg/m³); RMSE―root mean square error (µg/m³); d²―index of agreement.

Station/Measure	$\stackrel{-}{\mathrm{O}}$	$\stackrel{-}{\mathrm{A}}$	So	Sa	R2	MBE	MAE	RMSE	d2
Belsk	91.3	96.0	20.4	20.6	0.53	−4.8	12.1	15.9	0.83
Warsaw	93.0	92.1	22.9	22.0	0.55	0.9	13.0	16.3	0.86

summarizes the results of the forecasting models.

The results of the artificial neural model for Belsk station are presented in Figure 4. Based on the time course chart (Figure 4a), the actual course of ozone concentrations is reproduced by the model quite well. The exception is the first half of April when the model slightly overestimated relative low ozone concentrations and the turn of July and August when the model underestimated high ozone concentration values. During the analyzed period, the maximum surface ozone concentration was equal to 145.4 µg/m³, while the appropriate value for this day, as estimated by the model, was 141.5 µg/m³. The range of residuals (Figure 4b) was from −60 µg/m³ to +40 µg/m³, wherein variations from real values for 52% of cases ranged between −10 µg/m³ and +10 µg/m³, for 81% of cases between −20 µg/m³ and +20 µg/m³, for 93% of cases between −30 µg/m³ and +30 µg/m³ and for 98% of all cases between −40 µg/m³ and +40 µg/m³. The maximum residual value (associated with underestimation) was equal to 53.6 µg/m³. The average individual relative error value (Figure 4c) was equal to 15.3%, while 67% of cases were modeled with an error value below 15.3%.

The results of the artificial neural network model for Warsaw station are presented in Figure 5. The time course chart (Figure 5a) indicates good compatibility between observation and the output data for all analyzed time periods, except for two periods: the first half of May and the turn of August and September. In both cases, the model underestimated relatively high ozone concentration values. The maximum 1-h ozone concentration value was equal to 150 µg/m³ (July 2014) and was underestimated by the neural network model by 18 µg/m³. The values of residuals (Figure 5b) were in the range from −50 µg/m³ to +40 µg/m³. For 49% of cases, residuals values were between −10 µg/m³ and +10 µg/m³, for 80% of cases between −20 µg/m³ and +20 µg/m³, for 93% of cases between −30 µg/m³ and +30 µg/m³ and for 98% of cases between −40 µg/m³ and +40 µg/m³. The maximum residual value was equal to 45.3 µg/m³ and was associated with very low real surface ozone concentration value (May 2014: 37.8 µg/m³). The average relative error (Figure 5c) value was 15.7%, wherein 67% of predicted cases were characterized by error value below 15.7%.

Table 6 presents the values of the statistical parameters of the result of forecasting of surface ozone concentrations for Belsk and Warsaw stations with the 2014 data set. The characteristic of variability in the examination set for 2014 was similar to the data set for 2015. As noted in the previous case, the mean of the maximum observed concentration values at the urban background station is slightly higher than that at the rural background station. The differences between observed and estimated means of the maximums are equal to only 4.7 µg/m³ and 0.8 µg/m³ of absolute value, respectively, for Belsk and Warsaw stations.

Standard deviation values for observed and predicted data sets are approximately 20 µg/m³ and 22 µg/m³ for Belsk and Warsaw stations, respectively. The discrepancy between observed and estimated data sets is very small (<1 µg/m³), indicating the ability of the model to capture the primary variability in the modeled data.

In terms of R², the model could explain >50% of the original variance. The d₂ has a high value for both stations, reaching values above 0.8 for both stations.

The MBE values indicate the same tendency as that in 2015. For the Belsk station, the model overestimated concentrations of ozone by 4.8 µg/m³, and for the Warsaw station, it underestimated the value by 0.9 µg/m³.

The absolute error measures of MAE and RMSE were approximately 12–13 µg/m³ and 16 µg/m³, respectively.

Analysis of the statistical significance of differences between the modeled values and the observed values for data sets from 2014 was performed according to the same procedure as that for 2015 (see Section 4.3). Analysis of the results of the Shapiro–Wilk test is presented in

Table 7. Results of the Shapiro–Wilk test together with the right values of probability for Belsk and Warsaw stations for 2014.

Station/Measure	Observation		Model
	Shapiro–Wilk Test	p	Shapiro–Wilk Test	p
Belsk	0.9955	0.912	0.9836	0.052
Warsaw	0.9946	0.825	0.9442	0.000

; the results reveal that for Belsk station, the p-value in both data sets was higher than the assumed significance level (α = 0.05). For Warsaw station, only for the observed concentrations of O₃ was a dependence of p > α noted. Thus, this shows that the data set for Belsk station has a normal distribution, while the data set for Warsaw station does not have a normal distribution.

Therefore, the significance tests performed for Belsk and Warsaw stations were different. For Belsk station, the conditions of normality of distribution and homogeneity of variance (Levene’s test;

Table 8. Results of the Levene test and t-test together with the right values of probability for Belsk station for 2014.

Station/Measure	Levene’s Test	p	t-Test	p
Belsk	0.2903	0.590	−2.0855	0.037

) were met, which allowed the parametric t-test to be conducted.

The results indicate that differences between modeled and measured surface ozone concentration values are statistically significant (because p = 0.038, which is less than the given significance level α = 0.05). For Warsaw station, where the condition of normality of distribution was not met, the nonparametric Mann–Whitney test was performed (

Table 9. Results of the Mann–Whitney test together with the right values of probability for Warsaw station for 2014.

Station/Measure	Mann–Whitney Test	p
Warsaw	0.92782	0.35350

).

In this case the probability value p is higher than the given significance level, thus indicating no statistically significant differences between the modeled and measured concentrations of surface ozone.

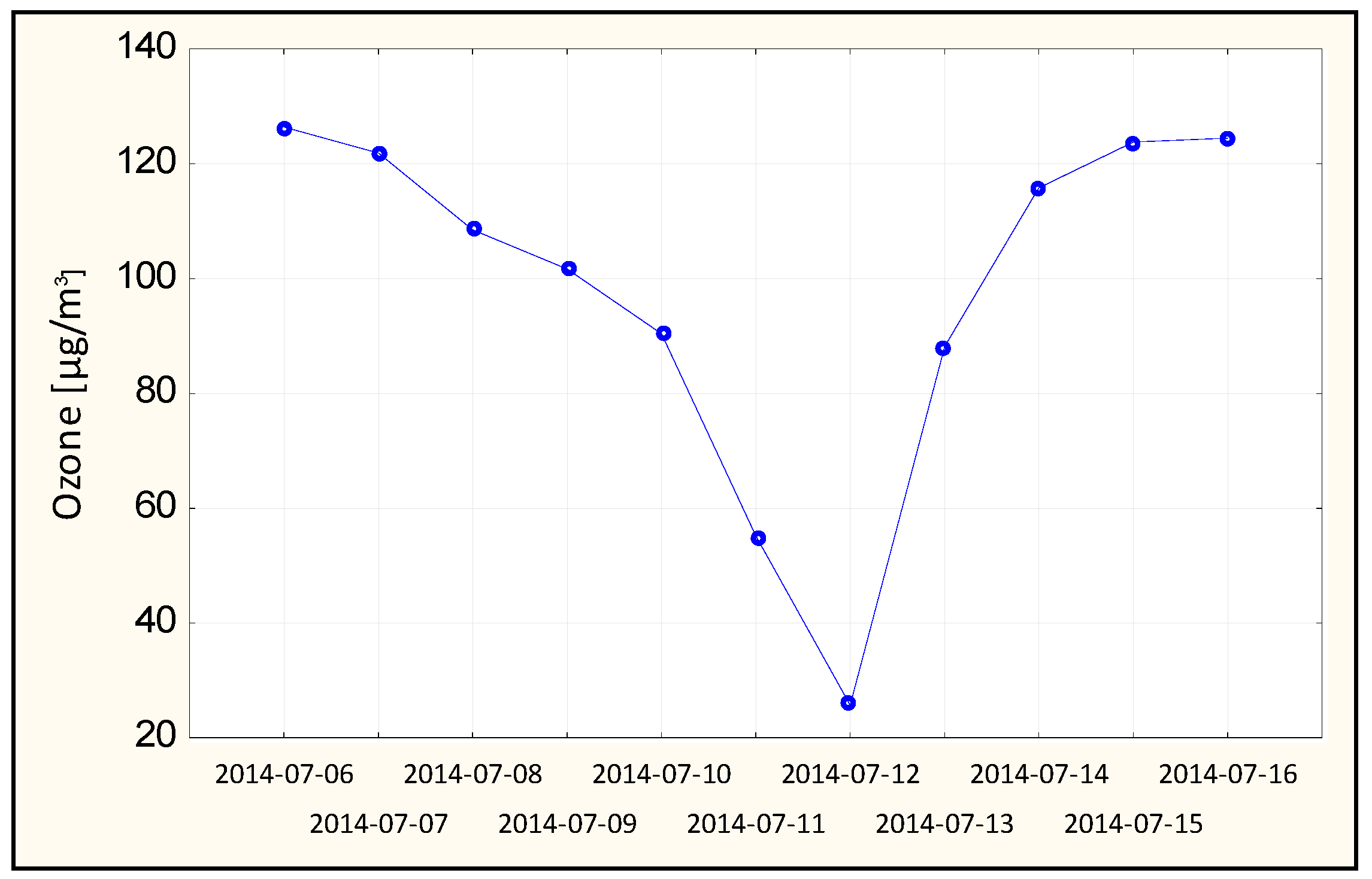
4.5. Analysis of Days with Extremely Bad Forecasts

Some of the forecasts performed for April–September 2014 were characterized by especially high differences (with relative error value above 50%) between the measured and predicted maximum 1-h surface ozone concentration values. These predictions were selected for further examination to define the potential reason of inefficiency of the neural network model. The adopted criterion (50%) is related to Directive 2008/50/EC [40]. According to this directive, the deviations from the observed value for at least 90% of the forecasts should be below 50%. Days with especially high values of difference between observed and modeled concentrations were noted at both locations: at Belsk station—6 days; at Warsaw station—6 days. For both stations, the number of forecasts with deviations below 50% met the criteria of the directive and was equal to approximately 96%. Analysis of

Table 10. Comparison of the results of two predictions using forecasted meteorological parameters as input variables (Forecast 1) and using real meteorological parameters as input variables (Forecast 2) performed for the days with relative error value >50%.

Date	Measured Values [µg/m3]	Forecast 1		Forecast 2
		Forecast [µg/m3]	Relative Error [%]	Forecast [µg/m3]	Relative Error [%]
Belsk
2014-04-06	61.8	97.4	57.6	96.1	55.4
2014-04-28	69.8	113.2	62.1	86.9	24.4
2014-05-29	41.1	81.0	97.1	67.6	64.4
2014-07-12	24.6	58.2	136.4	54.5	121.6
2014-08-01	59.4	104.2	75.4	81.0	36.4
2014-09-01	39.0	81.4	108.8	73.2	87.7
Warsaw
2014-05-28	63.1	103.4	63.8	69.9	10.9
2014-05-29	37.8	83.1	119.9	57.1	51.0
2014-06-03	34.0	60.3	77.2	54.0	58.8
2014-07-11	55.2	87.4	58.4	76.4	38.5
2014-07-12	25.7	68.4	166.0	52.3	103.3
2014-09-01	53.2	85.2	60.1	58.2	9.4

reveals that the values of relative error are associated with relatively low maximum surface ozone concentration values (for Belsk, from 24.6 to 69.8 µg/m³, for Warsaw, from 25.7 to 63.1 µg/m³).

It is important that, in each case, the model overestimated the real ozone concentration values, which was usually connected with a sharp drop in ozone concentration. A good example is a situation from 12 July 2014, presented in Figure 6, which shows an extremely low maximum 1-h surface ozone concentration values together with 6 days before and 4 days after at the Warsaw station. During a 2-day period, the maximum ozone concentration value decreased by 70 µg/m³, and on the next day, it increased again by more than 60 µg/m³. The generated neural model correctly detected the direction of changes, but it did not manage to predict such a low ozone concentration value.

One of the main possible reasons for the inability of the model to correctly predict relatively low 1-h maximum ozone concentrations could be the lack of precise forecasts of input meteorological variables. To verify this hypothesis, a new analogous prediction of 1-h maximum surface ozone concentration but using real, observed meteorological input data was done. Results of the new simulation revealed that:

• for Belsk: for all six cases, the relative error value decreased, wherein for two cases, the predicted values were characterized by relative error values below 50%.
• for Warsaw: for all six cases, the relative error value decreased, wherein for three cases, the value decreased below 50%.

It is important that in the case of Warsaw station the biggest percentage decreases in the relative error (>80%) were recorded on 28 May 2014 and 1 September 2014, when the differences between forecast and measured values of the temperature (as the most important predictor) were the highest (7.6 °C and 5.5 °C, respectively).

These results indicate that a better quality of forecasts of input variables should significantly improve the quality of 1-h maximum surface ozone prediction.

Besides performing a new simulation using real data, an analysis of the meteorological situation (on the basis of temperature, relative humidity and precipitation) for the days with especially bad surface ozone forecasts was performed. Figure 7 and Figure 8 present the time courses of temperature and relative humidity during the whole period when the relative error value was >50%.

The values of maximum temperature and relative humidity that were measured during the days with a bad quality of the prediction are marked as colored indicators. The analysis of these figures reveals that extremely bad O₃ forecasts were connected with weather deterioration characterized by drop of temperature, increased cloudiness and rain falling. In the case of the Warsaw station, the maximum temperatures during the day were relatively low. Almost in all cases it did not exceed 17 °C. Only on one day (11 July 2014) did the temperature reached a value of almost 20 °C. Simultaneously, the values of relative humidity (whose increase is inversely proportional to the concentration of surface ozone) were high and usually >90%. Additionally, during three days rain fall was noted. The occurrence of precipitation usually means a full cloudy sky, no solar radiation, and, in effect, the lack of processes of ozone formation. In the case of Belsk station, the situation was similar to that at Warsaw station. Usually the temperature did not exceed 18 °C while the values of the relative humidity in most cases were equal to 100%. During four days, rain fall was noted.

5. Conclusions

The main objective of this work was to generate a simple artificial neural model with a small number of input variables to forecast the daily maximum surface ozone concentration values for the next day. The forecast included the period from April to September 2015 as a time of the highest surface ozone concentration and a real risk of exceedances of the acceptable level of surface ozone concentration. Neural networks were generated using six input variables, four of which were basic meteorological parameters forecasted using the WRF-ARW model. As the created models were examined to perform forecasts of surface ozone concentration for the next day (not approximation of time series), they can be used as a significant, effective tool to support the prediction of extreme levels of air pollution. From the process of generation and examination of efficiency of the generated artificial neural models, the following important conclusions can be made:

• The artificial neural network models developed for forecasting of surface ozone concentration present good statistical compatibility with the measured data in both rural and urban conditions.
• In accordance with the global sensitivity analysis, the most important input variable is the air temperature followed by the number of the month, solar radiation, and the maximum ozone concentration value on the previous day.
• The majority of the highest deviations (with relative error value >50%) from the measured ozone concentration values noted at both Belsk and Warsaw stations (6 and 6 days, respectively) resulted from overestimation of relatively low surface ozone concentrations. Usually, they were associated with a sudden, significant drop of surface ozone concentration values from day to day. In most cases, the direction of the prediction was correct, but the network did not manage the forecast of such low values.
• The forecasts of the high values of surface ozone concentration (approximately 150 µg/m³) present very good statistical compliance with the measured data.
• Possible reasons of overestimation of the lowest surface ozone concentration values could be associated with the quality of forecasts of the input variables, or a training subset that is too small to present all possible variations.