Performance Assessment of a Low-Cost PM2.5 Sensor for a near Four-Month Period in Oslo, Norway
Abstract
:1. Introduction
2. Materials and Methods
2.1. Nova PM Sensor SDS011
2.2. Sensors Co-Location and Its Measurement Site Description
2.3. Data Preparation
2.4. Data Analysis
3. Results and Discussion
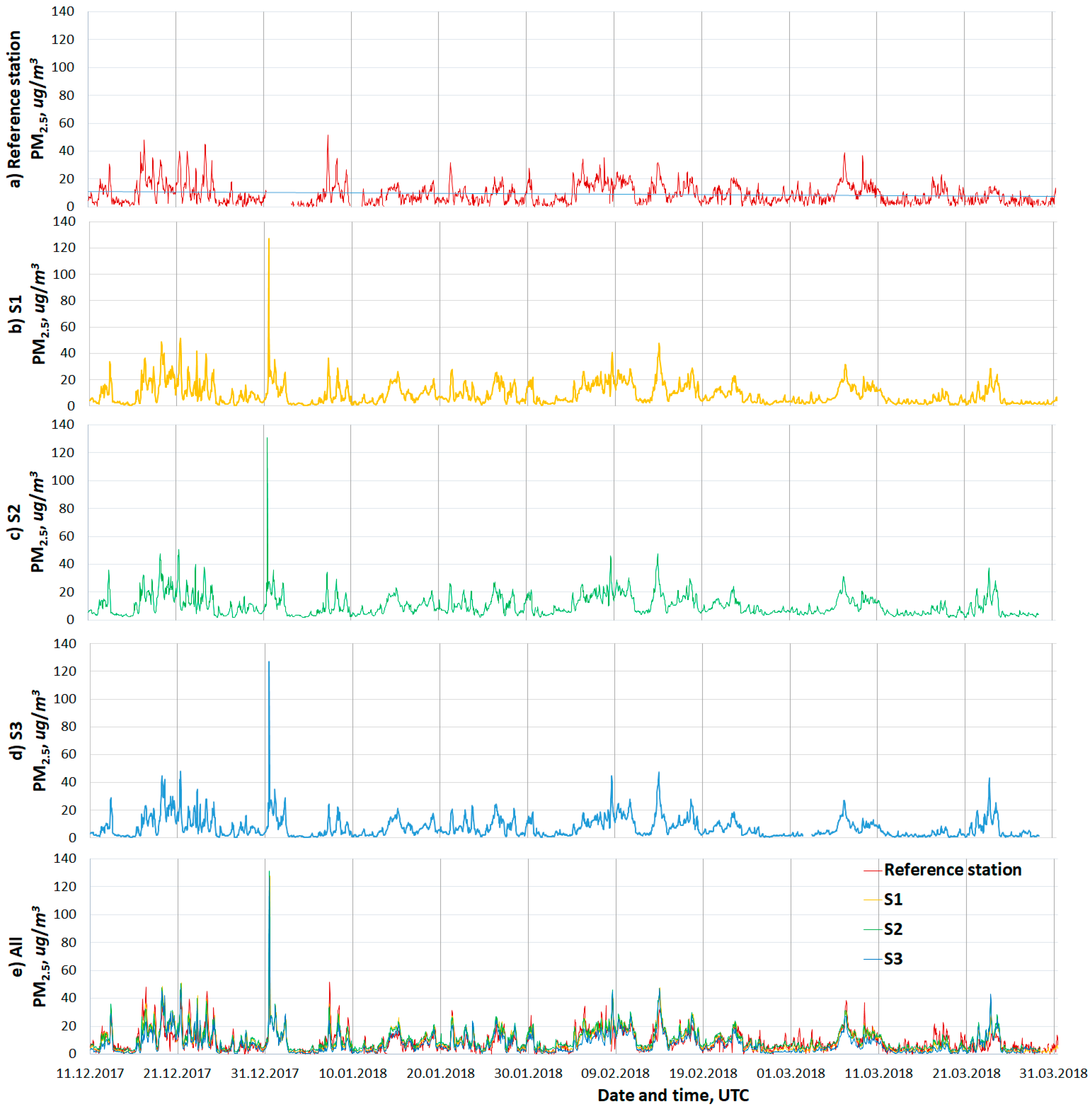
3.1. Sensors and Reference Instrument Operational Data Coverage
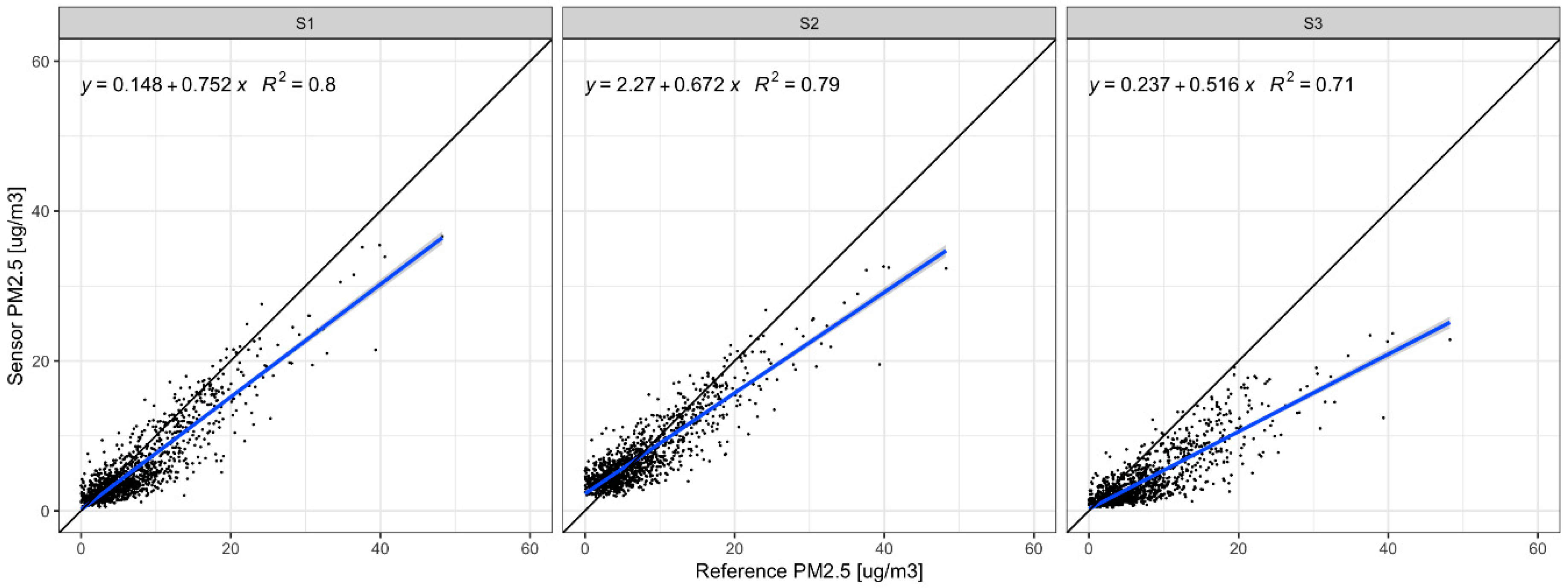
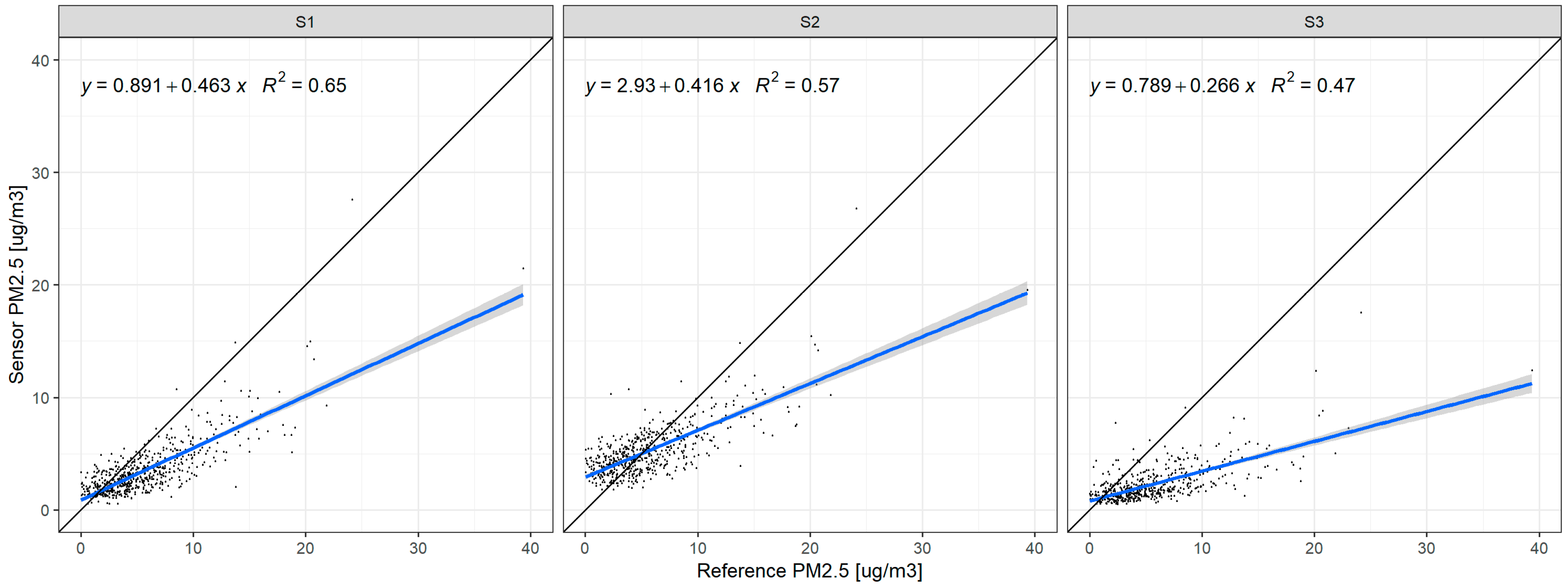
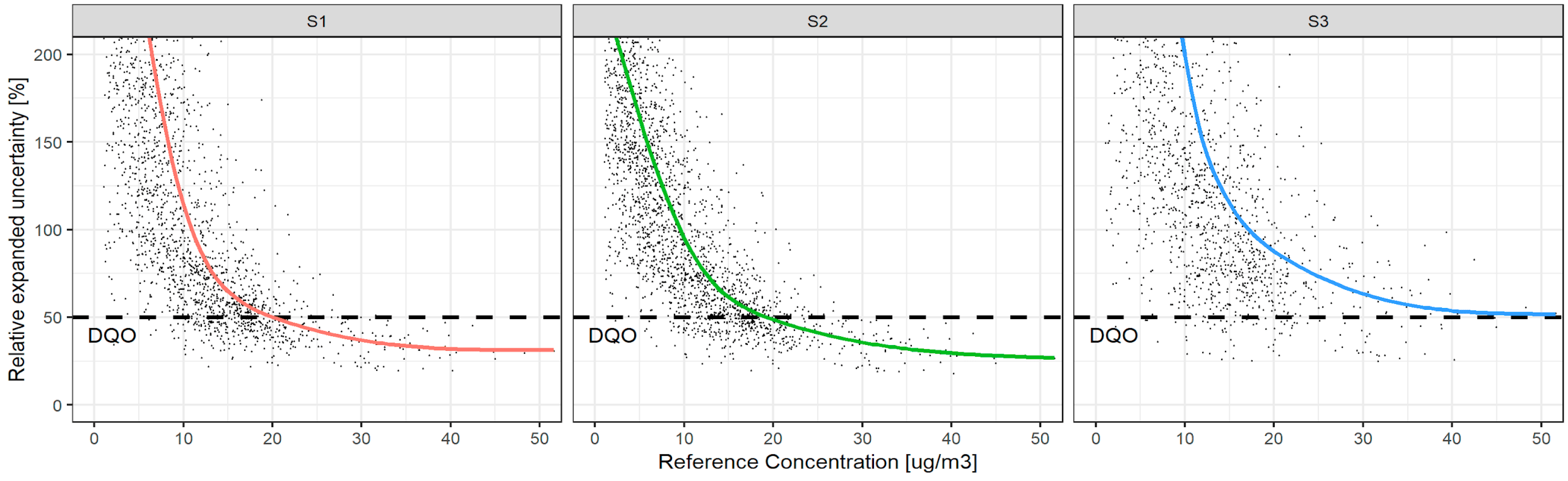
3.2. Linearity of the Response and Accuracy
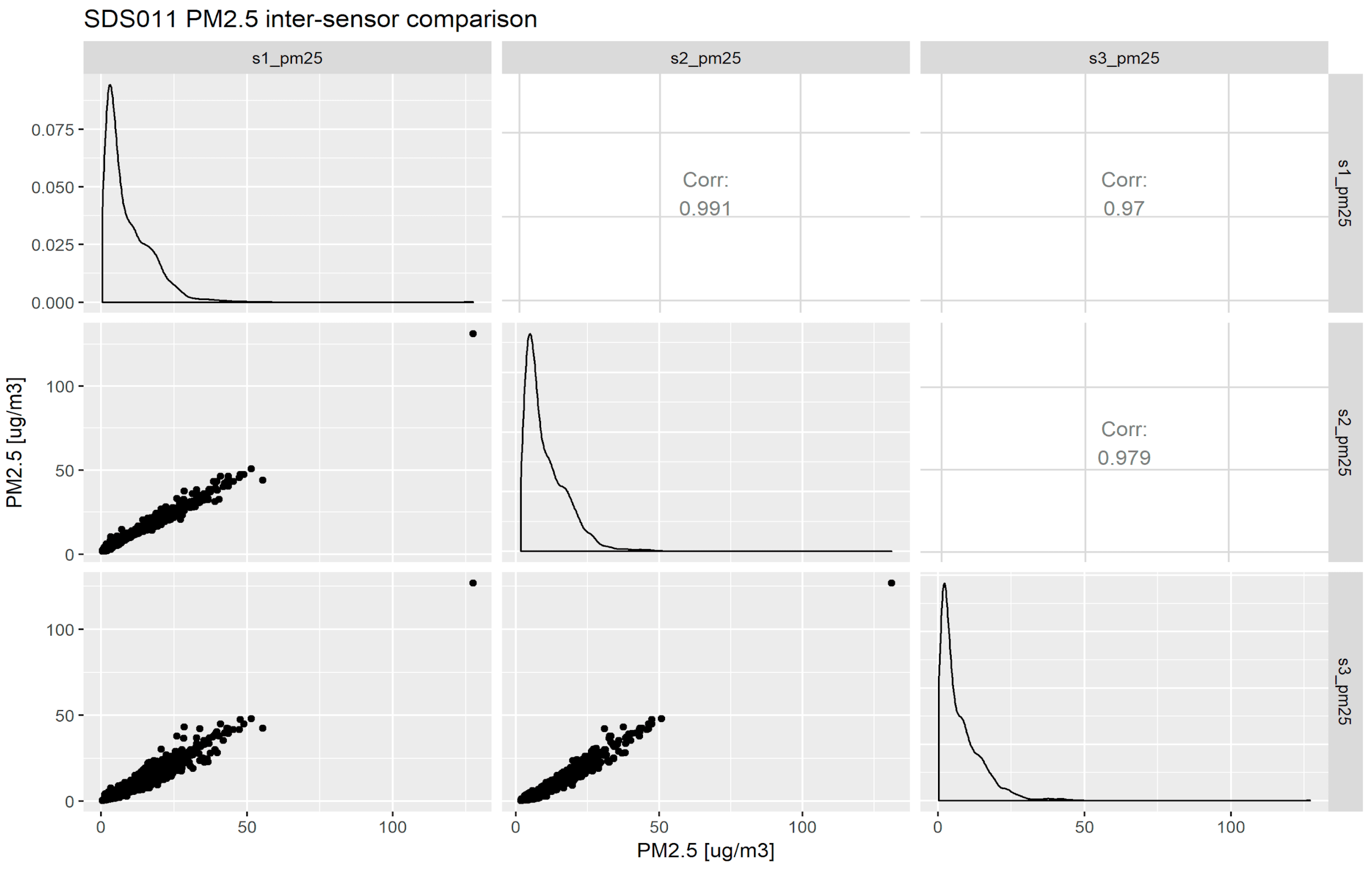
3.3. Intersensor Variability
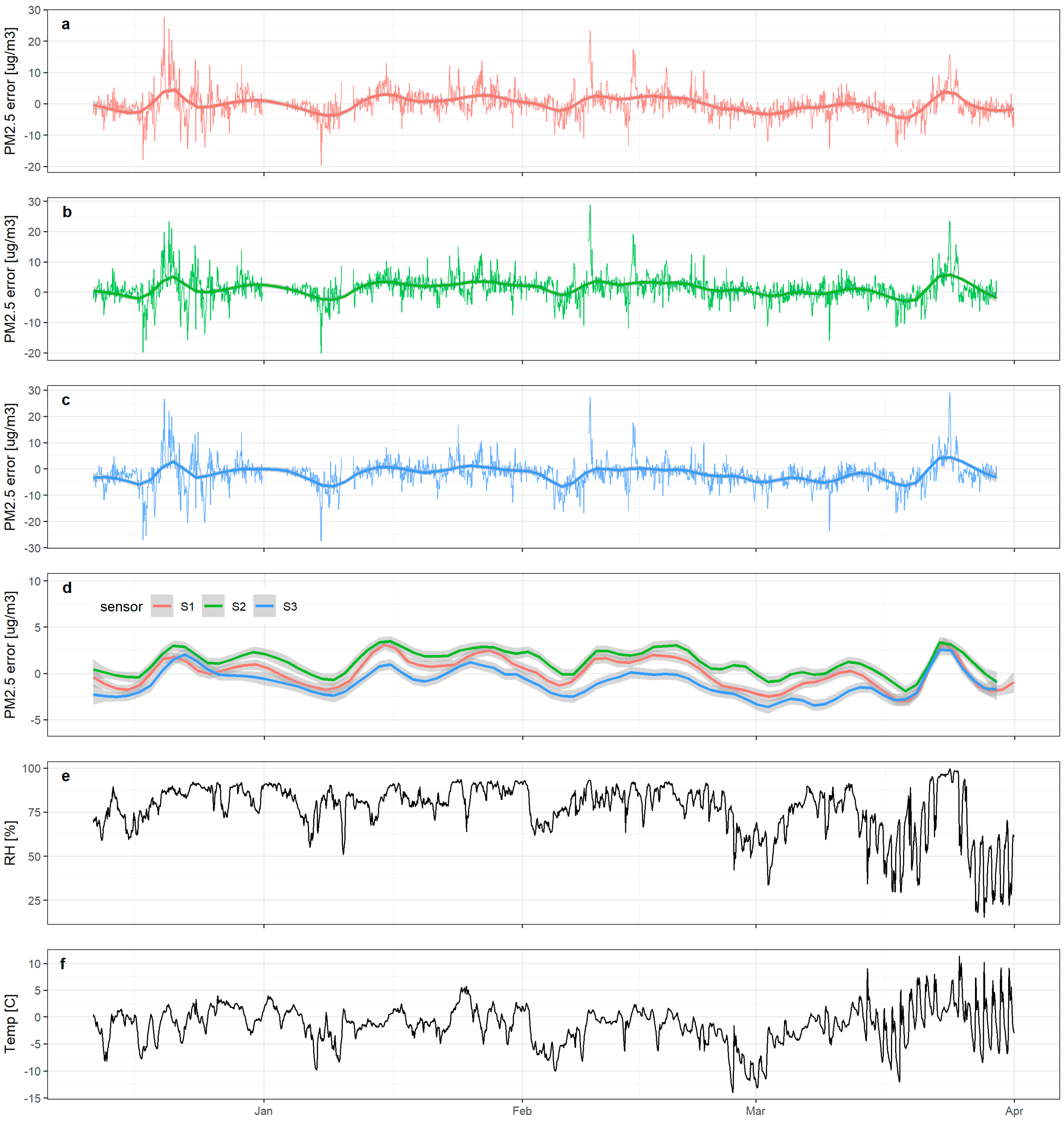
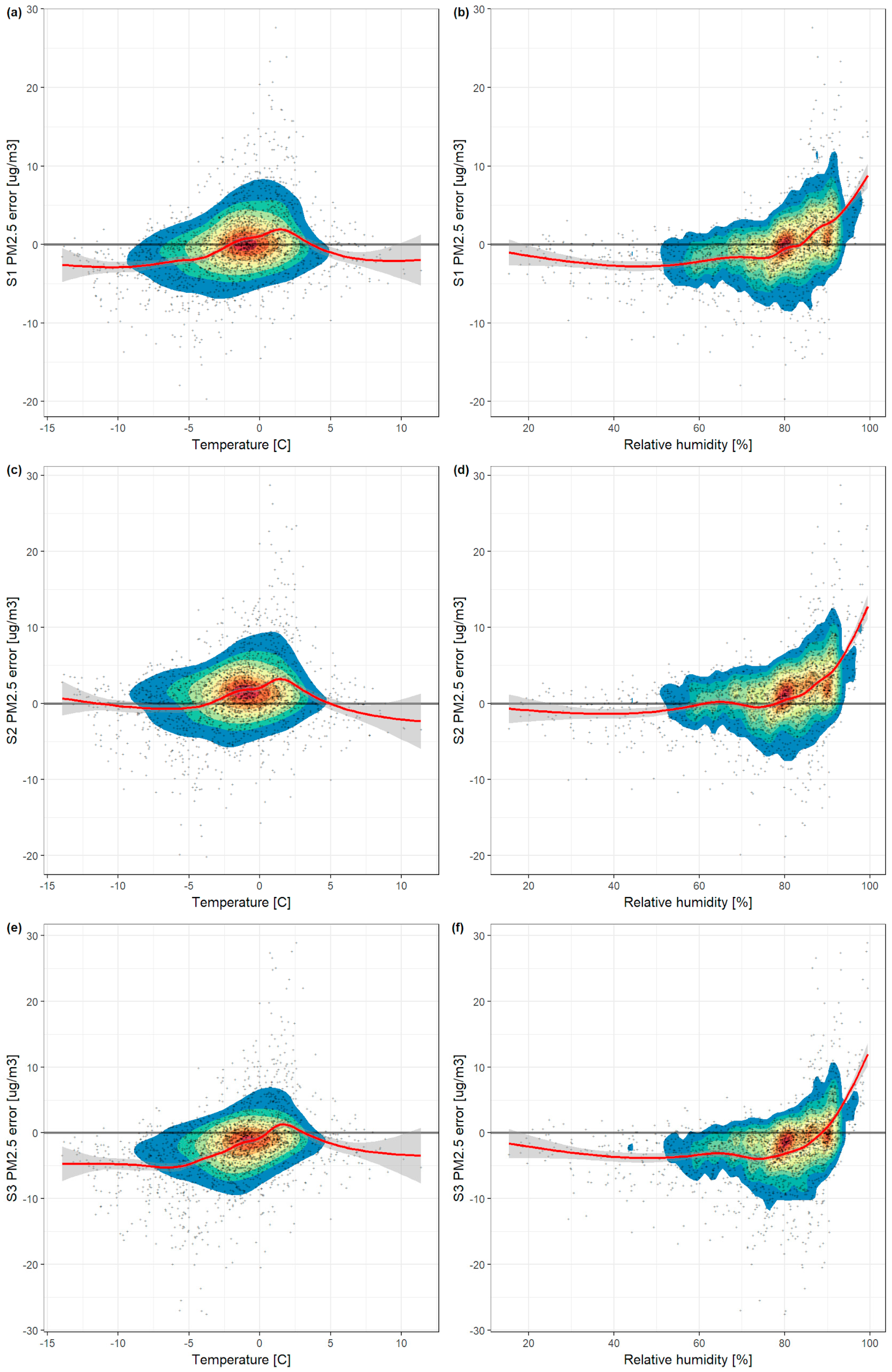
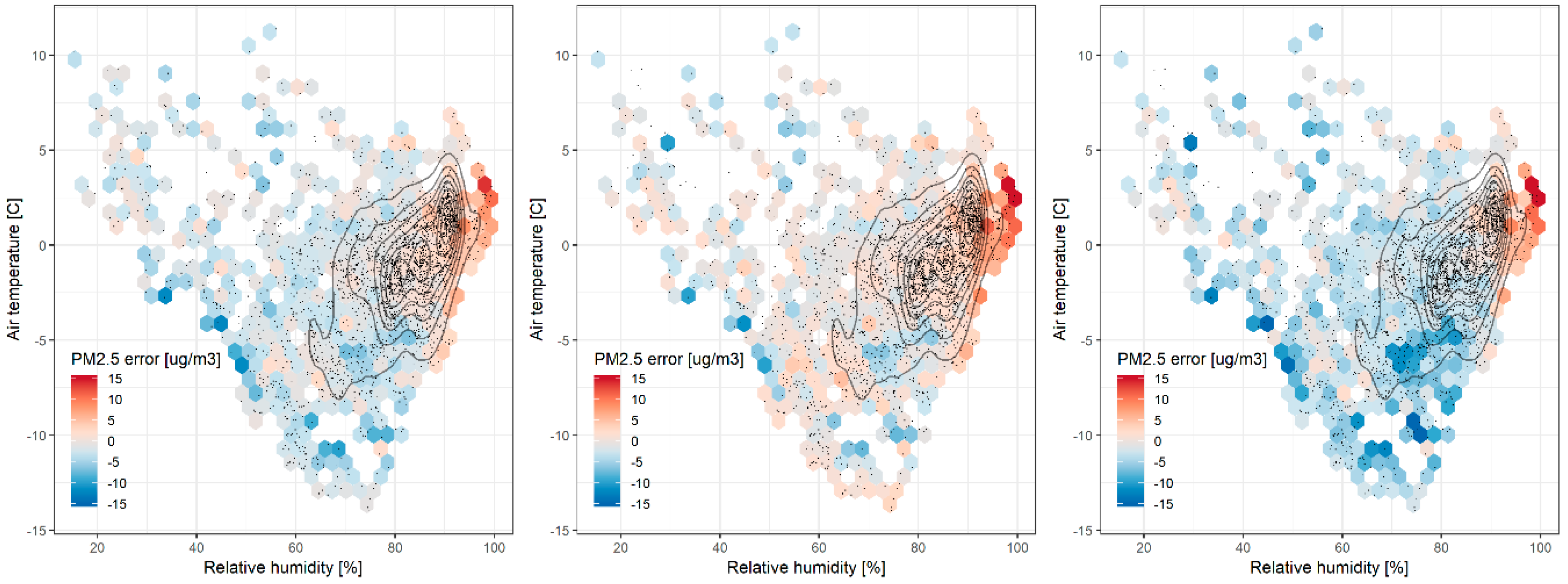
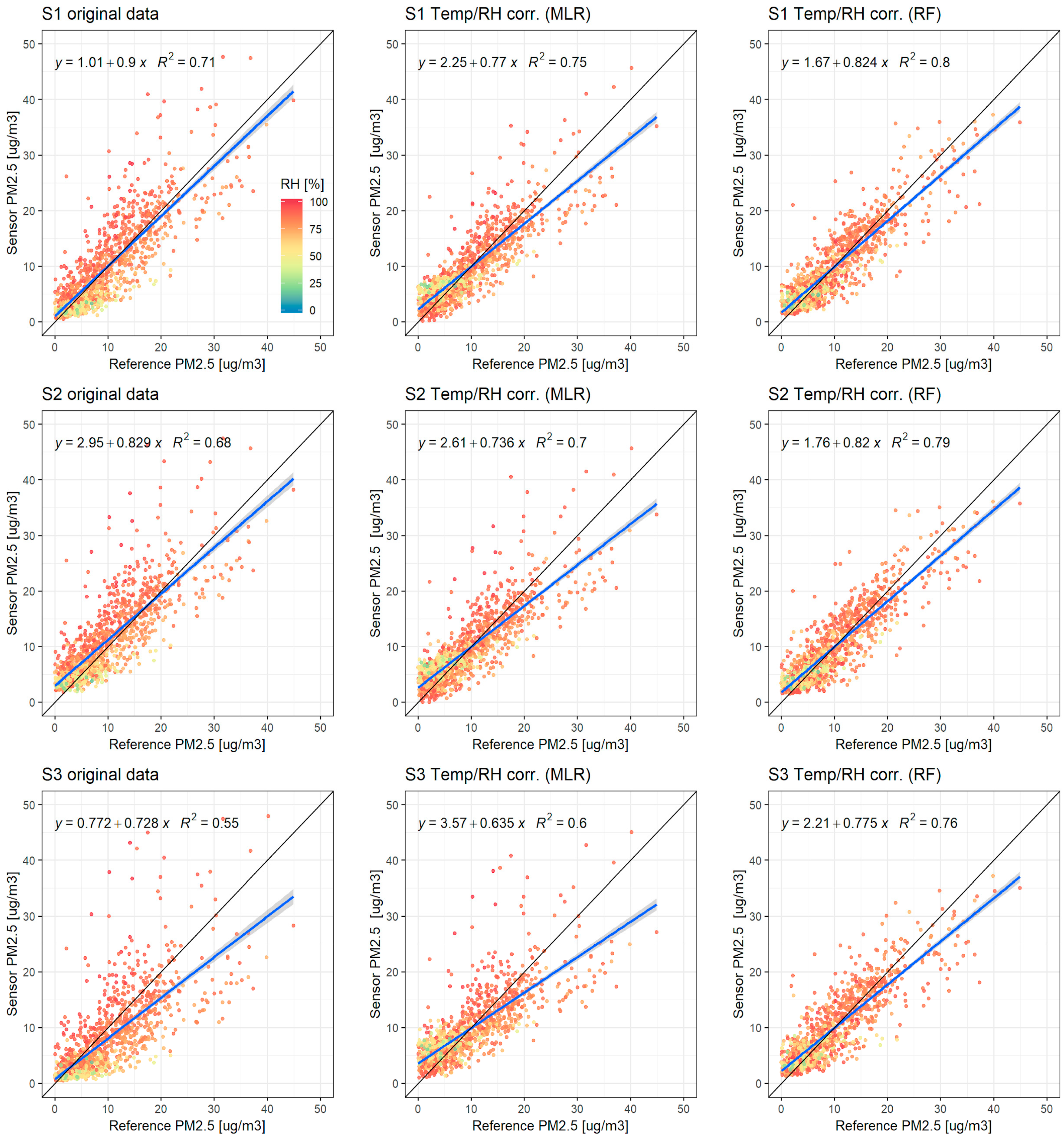
3.4. Influence of Relative Humidity and Air Temperature
3.5. Correction for Temperature and Humidity Effects
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European Environmental Agency (EEA). Air Quality in Europe—2017 Report; Publications Office of the European Union: Luxembourg, 2017; pp. 30–65. ISBN 978-92-9213-920-9. [Google Scholar]
- Liu, H.-Y.; Dunea, D.; Iordache, S.; Pohoata, A. A Review of Airborne Particulate Matter Effects on Young Children’s Respiratory Symptoms and Diseases. Atmosphere 2018, 9, 150. [Google Scholar] [CrossRef]
- Liu, H.-Y.; Bartonova, A.; Schindler, M.; Sharma, M.; Behera, S.N.; Katiyar, K.; Dikshit, O. Respiratory Disease in Relation to Outdoor Air Pollution in Kanpur, India. Arch. Environ. Occup. Health 2013, 68, 204–217. [Google Scholar] [CrossRef] [PubMed]
- Dockery, D.W.; Stone, P.H. Cardiovascular risks from fine particulate air pollution. N. Engl. J. Med. 2007, 356, 511–513. [Google Scholar] [CrossRef] [PubMed]
- Pérez, L.; Medina-Ramón, M.; Künzli, N.; Alastuey, A.; Pey, J.; Pérez, N.; García, R.; Tobías, A.; Querol, X.; Sunyer, J. Size fractionate particulate matter, vehicle traffic, and case-specific daily mortality in Barcelona (Spain). Environ. Sci. Technol. 2009, 43, 4707–4714. [Google Scholar] [CrossRef] [PubMed]
- IARC: Outdoor Air Pollution a Leading Environmental Cause of Cancer Deaths. Available online: https://www.iarc.fr/en/media-centre/iarcnews/pdf/pr221_E.pdf (accessed on 5 April 2018).
- EEA: Europe Air Pollution Causes 467,000 Early Deaths a Year: Report. Available online: https://phys.org/news/2016-11-europe-air-pollution-early-deaths.html (accessed on 7 May 2018).
- Directive 2008/50/EC of the European Parliament and the Council of 21 May 2008 on Ambient Air Quality and Cleaner Air for Europe. Available online: https://eur-lex.europa.eu/legal-content/en/ALL/?uri=CELEX:32008L0050 (accessed on 16 October 2018).
- Breslow, N.E.; Lin, X. Bias correction in generalised linear mixed models with a single component of dispersion. Biometrika 1995, 82, 81–91. [Google Scholar] [CrossRef]
- Gibson, M.D.; Kundu, S.; Satish, M. Dispersion model evaluation of PM2.5, NOx and SO2 from point and major line sources in Nova Scotia, Canada using AERMOD Gaussian plume air dispersion model. Atmos. Pollut. Res. 2013, 4, 157–167. [Google Scholar] [CrossRef]
- Schneider, P.; Castell, N.; Vogt, M.; Dauge, F.R.; Lahoz, W.A.; Bartonova, A. Mapping urban air quality in near real-time using observations from low-cost sensors and model information. Environ. Int. 2017, 106, 234–247. [Google Scholar] [CrossRef]
- Schneider, P.; Castell, N.; Dauge, F.R.; Vogt, M.; Lahoz, W.A.; Bartonova, A. A Network of Low-Cost Air Quality Sensors and Its Use for Mapping Urban Air Quality. In Mobile Information Systems Leveraging Volunteered Geographic Information for Earth Observation; Bordogna, G., Carrara, P., Eds.; Springer International Publishing: Cham, Switzerland, 2017; Volume 4, pp. 93–110. ISBN 978-3-319-70878-2. [Google Scholar]
- Castell, N.; Schneider, P.; Grossberndt, S.; Fredriksen, M.F.; Sousa-Santos, G.; Vogt, M.; Bartonova, A. Localized real-time information on outdoor air quality at kindergartens in Oslo, Norway using low-cost sensor nodes. Environ. Res. 2018, 165, 410–419. [Google Scholar] [CrossRef]
- Castell, N.; Dauge, F.R.; Schneider, P.; Vogt, M.; Lerner, U.; Fishbain, B.; Broday, D.; Bartonova, A. Can commercial low-cost sensor platforms contribute to air quality monitoring and exposure estimates? Environ. Int. 2017, 99, 293–302. [Google Scholar] [CrossRef]
- Liu, H.-Y.; Skjetne, E.; Kobernus, M. Mobile phone tracking: In support of modelling traffic-related air pollution contribution to individual exposure and its implications for public health impact assessment. Environ. Health 2013, 12, 93. [Google Scholar] [CrossRef]
- Skjetne, E.; Liu, H.-Y. Traffic maps and smartphone trajectories to model air pollution, exposure and health impact. J. Environ. Prot. 2017, 8, 1372–1392. [Google Scholar] [CrossRef]
- GP2Y1010AU0F: Compact Optical Dust Sensor. Available online: https://www.sparkfun.com/datasheets/Sensors/gp2y1010au_e.pdf (accessed on 21 May 2018).
- Shinyei PPD42 Particle Sensor. Available online: https://github.com/mozilla-sensorweb/sensorweb-wiki/wiki/Shinyei-PPD42-Particle-Sensor (accessed on 21 May 2018).
- Digital Universal Particle Concentration Sensor. Available online: http://www.aqmd.gov/docs/default-source/aq-spec/resources-page/plantower-pms1003-manual_v2-5.pdf (accessed on 21 May 2018).
- PA-II Dual Laser Air Quality Sensor. Available online: https://www.purpleair.com/sensors (accessed on 21 May 2018).
- Laser PM2.5 Sensor Specification Product Model: SDS011, Version: V1.3. Available online: https://nettigo.pl/attachments/398 (accessed on 21 May 2018).
- AirBeam Technical Specifications, Operation & Performance. Available online: http://www.takingspace.org/airbeam-technical-specifications-operation-performance/ (accessed on 22 May 2018).
- Alphasense Air Sensors for Air Quality Networks—Particulates. Available online: http://www.alphasense.com/index.php/products/optical-particle-counter/ (accessed on 22 May 2018).
- Wuhan Cubic Optoelectronics Co., Ltd. Dust Sensor for Automotive Applications PM3007. Available online: http://www.directindustry.com/prod/wuhan-cubic-optoelectronics-co-ltd/product-54752-1844530.html (accessed on 17 October 2018).
- Hahn, D.W. Light Scattering Theory; University of Florida: Gainesville, FL, USA, 2009. [Google Scholar]
- Zikova, N.; Masiol, M.; Chalupa, D.C.; Rich, D.Q.; Ferro, A.R.; Hopke, P.K. Estimating Hourly Concentrations of PM2.5 across a Metropolitan Area Using Low-Cost Particle Monitors. Sensors 2017, 17, 1922. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, A.; Stanton, L.G.; Graham, A.R.; Roberts, P.T. Assessing the utility of low-cost particulate matter sensors over a 12-week period in the Guyama Valley of California. Sensors 2017, 17, 1805. [Google Scholar] [CrossRef]
- Zheng, T.; Bergin, M.H.; Johnson, K.K.; Tripathi, S.N.; Shirodkar, S.; Landis, M.S.; Sutaria, R.; Carlson, D.E. Field evaluation of low-cost particulate matter sensors in high and low concentration environments. Atmos. Meas. Tech. 2018, 11, 4823–4846. [Google Scholar] [CrossRef]
- Genikomsakis, K.N.; Galatoulas, F.K.; Dallas, P.I.; Ibarra, L.M.C.; Margaritis, D.; Ioakimidis, C. Development and On-Field Testing of Low-Cost Portable System for Monitoring PM2.5 Concentrations. Sensors 2018, 18, 1056. [Google Scholar] [CrossRef] [PubMed]
- Badura, M.; Batog, P.; Drzeniecka-Osiadacz, A.; Modzel, P. Evaluation of Low-Cost Sensors for Ambient PM2.5 Monitoring. J. Sens. 2018, 2018, 5096540. [Google Scholar] [CrossRef]
- Kosmidis, E.; Syropoulou, P.; Tekes, S.; Schneider, P.; Spyromitros-Xioufis, E.; Riga, M.; Charitidis, P.; Moumtzidou, A.; Papadopoulos, S.; Vrochidis, S.; et al. hackAIR: Towards Raising Awareness about Air Quality in Europe by Developing a Collective Online Platform. ISPRS Int. J. Geo-Inf. 2018, 7, 187. [Google Scholar] [CrossRef]
- Measure Air Quality Yourself. Available online: https://luftdaten.info/en/home-en/ (accessed on 21 May 2018).
- Thermo Scientific™—1405-F TEOM™ Continuous Air Monitor. Available online: https://www.thermofisher.com/order/catalog/product/TEOM1405F (accessed on 22 June 2018).
- Polidori, A.; Papapostolou, V.; Zhang, H. Laboratory Evaluation of Low-Cost Air Quality Sensors—Laboratory Setup and Testing Protocol. Available online: http://www.aqmd.gov/docs/default-source/aq-spec/protocols/sensors-lab-testing-protocol6087afefc2b66f27bf6fff00004a91a9.pdf (accessed on 13 December 2018).
- Papapostolou, V.; Zhang, H.; Feenstra, B.J.; Polidori, A. Development of an environmental chamber for evaluating the performance of low-cost air quality sensors under controlled conditions. Atmos. Environ. 2017, 171, 82–90. [Google Scholar] [CrossRef]
- Cleveland, W.S.; Devlin, S.J. Locally Weighted Regression: An Approach to Regression Analysis by Local Fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Freedman, D.A. Statistical Models: Theory and Practice, 1st ed.; Cambridge University Press: Cambridge, UK, 2009; p. 26. ISBN 978-0-521-74385-3. [Google Scholar]
- Ho, T.K. Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; pp. 278–282. [Google Scholar]
- The R Project for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 21 May 2018).
- Cleveland, W.S. Robust Locally Weighted Regression and Smoothing Scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Jayaratne, R.; Liu, X.; Thai, P.; Dunbabin, M.; Morawska, L. The influence of humidity on the performance of a low-cost air particle mass sensor and the effect of atmospheric fog. Atmos. Meas. Tech. 2018, 11, 4883–4890. [Google Scholar] [CrossRef]
- Hojaiji, H.; Kalantarian, H.; Bui, A.A.T.; King, C.E.; Sarrafzadeh, M. Temperature and Humidity Calibration of a Low-Cost Wireless Dust Sensor for Real-Time Monitoring. In Proceedings of the 2017 IEEE Sensors Applications Symposium (SAS), Glassboro, NJ, USA, 13–15 March 2017. [Google Scholar]
- Spinelle, L.; Gerboles, M.; Gabriella Villani, M.; Aleixandre, M.; Bonavitacola, F. Field calibration of a cluster of low-cost available sensors for air quality monitoring. Part A: Ozone and nitrogen dioxide. Sens. Actuators B Chem. 2015, 215, 249–257. [Google Scholar] [CrossRef]
- Bureau International des Poids et Mesures(BIPM); International Electrotechnical Commission (IEC); International Federation of Clinical Chemistry(IFCC); International Laboratory Accreditation Cooperation (ILAC); International Organization for Standardization (ISO); International Union of Pure and Applied Chemistry (IUPAC); International Union of Pure and Applied Physics (IUPAP); International Organization of Legal Metrology (OIML). Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement, 1st ed.; JCGM (Joint Committee for Guides in Metrology): Sèvres, France, 2008. [Google Scholar]
- International Organization for Standardization (ISO). Air Quality—Guidelines for Estimating Measurement Uncertainty, 1st ed.; ISO 20988:2007 (E); ISO: Geneva, Switzerland, 2007. [Google Scholar]

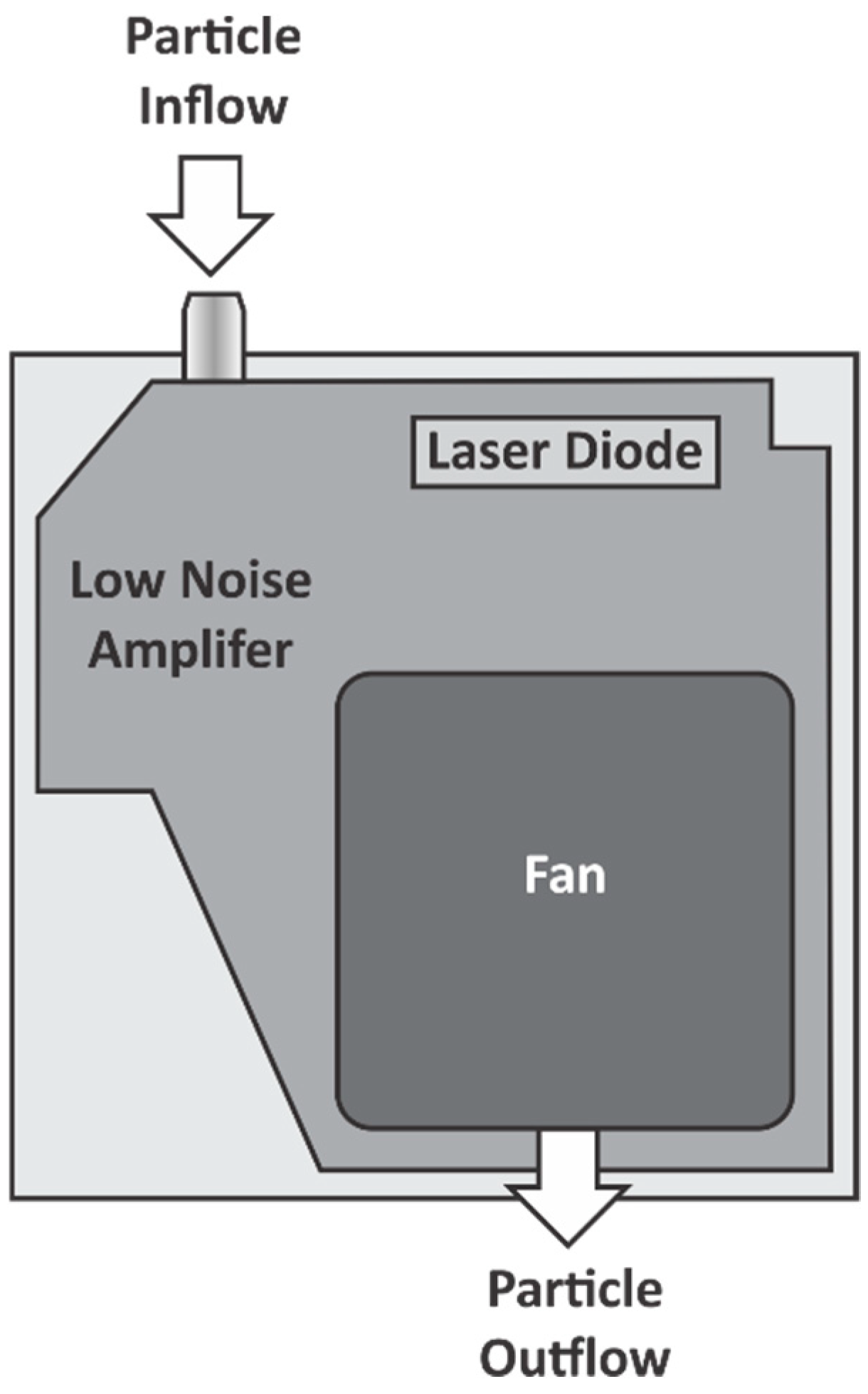
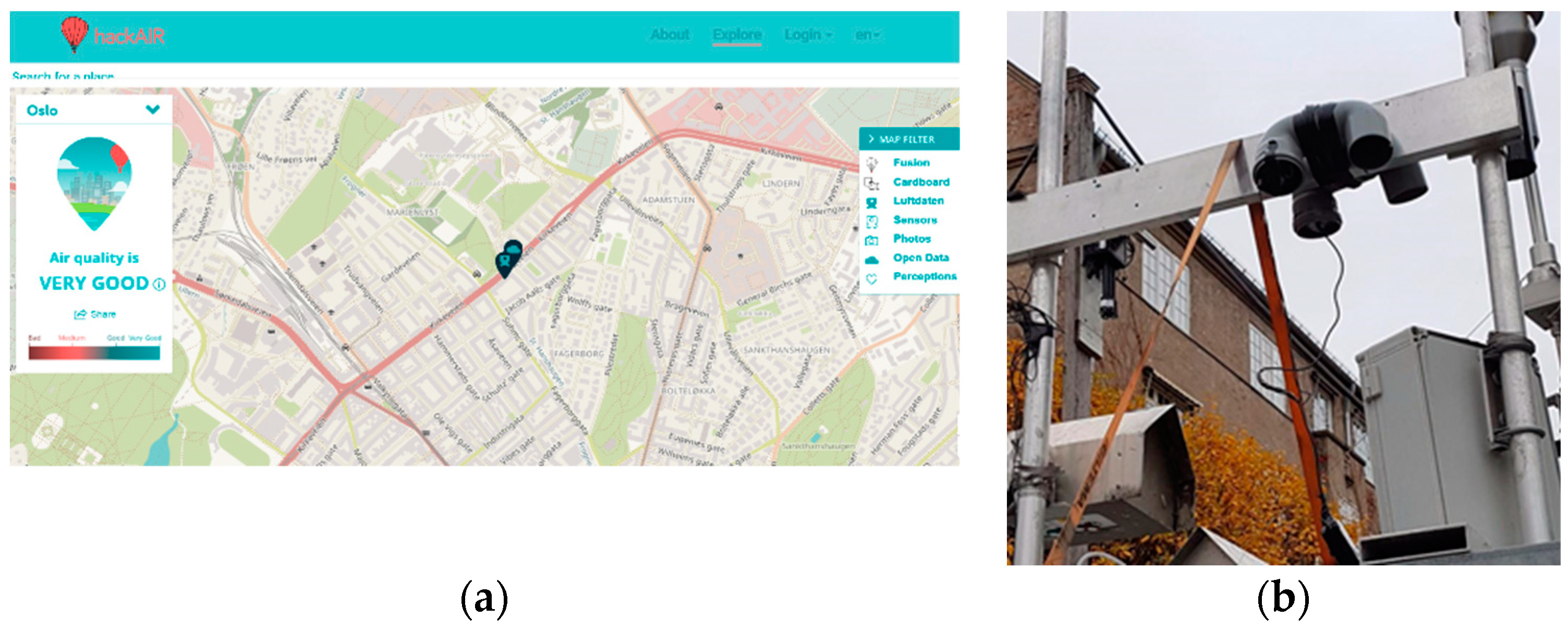

| Item | Specification |
|---|---|
| Measurement parameters | PM2.5, PM10 |
| Measuring range | 0.0–999.9 μg/m3 |
| Input voltage | 5 V |
| Related current | 70 mA ± 10 mA |
| Sleep current | < 4 mA (lase and fan sleep) |
| Response time | 1 s |
| Serial data output frequency | 1 Hz (1 time/s) |
| Minimum resolution of particle | 0.3 μm |
| Counting yield | 70% @ 0.3 μm; 98% @ 0. n5 μm |
| Relative error | Maximum of ± 15% and ±10 μg/m3 |
| Temperature range | Storage environment: −20–+60 °C; work environment: −10–+50 °C |
| Humidity range | Storage environment: max. 90%; work environment: max. 70% |
| Air pressure | 86 KPa–110 KPa |
| Product Size | L × W × H = 71 × 70 × 23 mm |
| Appropriate price | €16/piece |
| Appropriate weight | 50 g |
| Service life | Up to 8000 h |
| Certification | CE/FCC/RoHS |
| Variable | S1 | S2 | S3 |
|---|---|---|---|
| Mean error | −0.04 | 1.25 | −1.87 |
| SD | 4.21 | 4.31 | 5.12 |
| MAE | 2.97 | 3.18 | 3.84 |
| RMSE | 4.21 | 4.49 | 5.45 |
| Intercept | 0.97 | 2.97 | 0.87 |
| Slope | 0.89 | 0.82 | 0.71 |
| R2 | 0.71 | 0.68 | 0.55 |
| Sensor Model | Sensor Mean (μg/m3) | Official Reference Station Mean (μg/m3) | Accuracy (%) |
|---|---|---|---|
| S1 | 9.08 | 9.25 | 98.16 |
| S2 | 10.47 | 9.25 | 86.82 |
| S3 | 7.47 | 9.25 | 80.76 |
| Sensor Model | Mean (μg/m3) | Median (μg/m3) | Min (μg/m3) | Max (μg/m3) | Range (μg/m3) | SD (μg/m3) | Variance (μg/m3)2 |
|---|---|---|---|---|---|---|---|
| S1 | 9.08 | 6.28 | 0.43 | 127.50 | 127.07 | 8.11 | 65.75 |
| S2 | 10.47 | 7.93 | 1.73 | 131.03 | 129.30 | 7.69 | 59.11 |
| S3 | 7.47 | 4.19 | 0.39 | 126.93 | 126.54 | 7.48 | 55.97 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.-Y.; Schneider, P.; Haugen, R.; Vogt, M. Performance Assessment of a Low-Cost PM2.5 Sensor for a near Four-Month Period in Oslo, Norway. Atmosphere 2019, 10, 41. https://doi.org/10.3390/atmos10020041
Liu H-Y, Schneider P, Haugen R, Vogt M. Performance Assessment of a Low-Cost PM2.5 Sensor for a near Four-Month Period in Oslo, Norway. Atmosphere. 2019; 10(2):41. https://doi.org/10.3390/atmos10020041
Chicago/Turabian StyleLiu, Hai-Ying, Philipp Schneider, Rolf Haugen, and Matthias Vogt. 2019. "Performance Assessment of a Low-Cost PM2.5 Sensor for a near Four-Month Period in Oslo, Norway" Atmosphere 10, no. 2: 41. https://doi.org/10.3390/atmos10020041
APA StyleLiu, H.-Y., Schneider, P., Haugen, R., & Vogt, M. (2019). Performance Assessment of a Low-Cost PM2.5 Sensor for a near Four-Month Period in Oslo, Norway. Atmosphere, 10(2), 41. https://doi.org/10.3390/atmos10020041




