Inversion Models for the Retrieval of Total and Tropospheric NO2 Columns
Abstract
:1. Introduction
2. Regularization Methods
2.1. Tikhonov Regularization
- the relative X-convergence test [28], when the iterates converge, and/or
2.2. Iteratively Regularized Gauss–Newton Method
- the regularization parameters are the terms of a decreasing (geometric) sequence, i.e., , with ;
- the iterative process is stopped according to the discrepancy principle (15) instead of requiring the convergence of iterates.
3. Total NO2 Column Retrieval
- the differential radiance model with internal closure (DRMI), relying on the solution of the nonlinear equationfor the state vector , whereis the differential measured spectrum andis the differential simulated spectrum, and
- the differential radiance model with external closure (DRME), relying on the solution of the nonlinear equationfor the state vector .
- in DRMI, we fit the differential measured and simulated spectra, while in DRME we fit the differential measured spectrum with a simulated spectrum from which we extract its smooth component;
- in DRMI, the dimension of the state vector is smaller, and possible correlations between the components of the state vector can be avoided; however, the computational complexity is higher because the partial derivative of with respect to needs to be computed.
4. Tropospheric NO2 Column Retrieval
4.1. Nonlinear Model
- the nonlinear equation of DRMIfor the state vector , and
- the nonlinear equation of DRMEfor the state vector .
4.2. Linear Model
- Step 1.
- Step 2.
- In both models, we compute in the pre-processing step the total columns of all gases and the amplitudes of the correction spectra by means of DRMI or DRME.
- In the nonlinear model, we compute the tropospheric column of gas by using and determined in the pre-processing step and by solving a nonlinear equation corresponding to DRMI or DRME. The accuracy in computing is affected by the accuracy in computing and .
5. DOAS Model
5.1. Total Column Retrieval
- It is not hard to see that the DOAS model with the as in Equation (48) is in some sense equivalent with the first iteration step of DRME. Indeed, in this case, we consider a linearization of around the a priori as in Equation (47). Hence, from Equations (21) and (23), we getwhereThus, the solution of the linearized Equation (53) for is equivalent with the solution of the DOAS Equation (54) for . Note that because is close to , is also close to .
5.2. Tropospheric Column Retrieval
6. Numerical Analysis
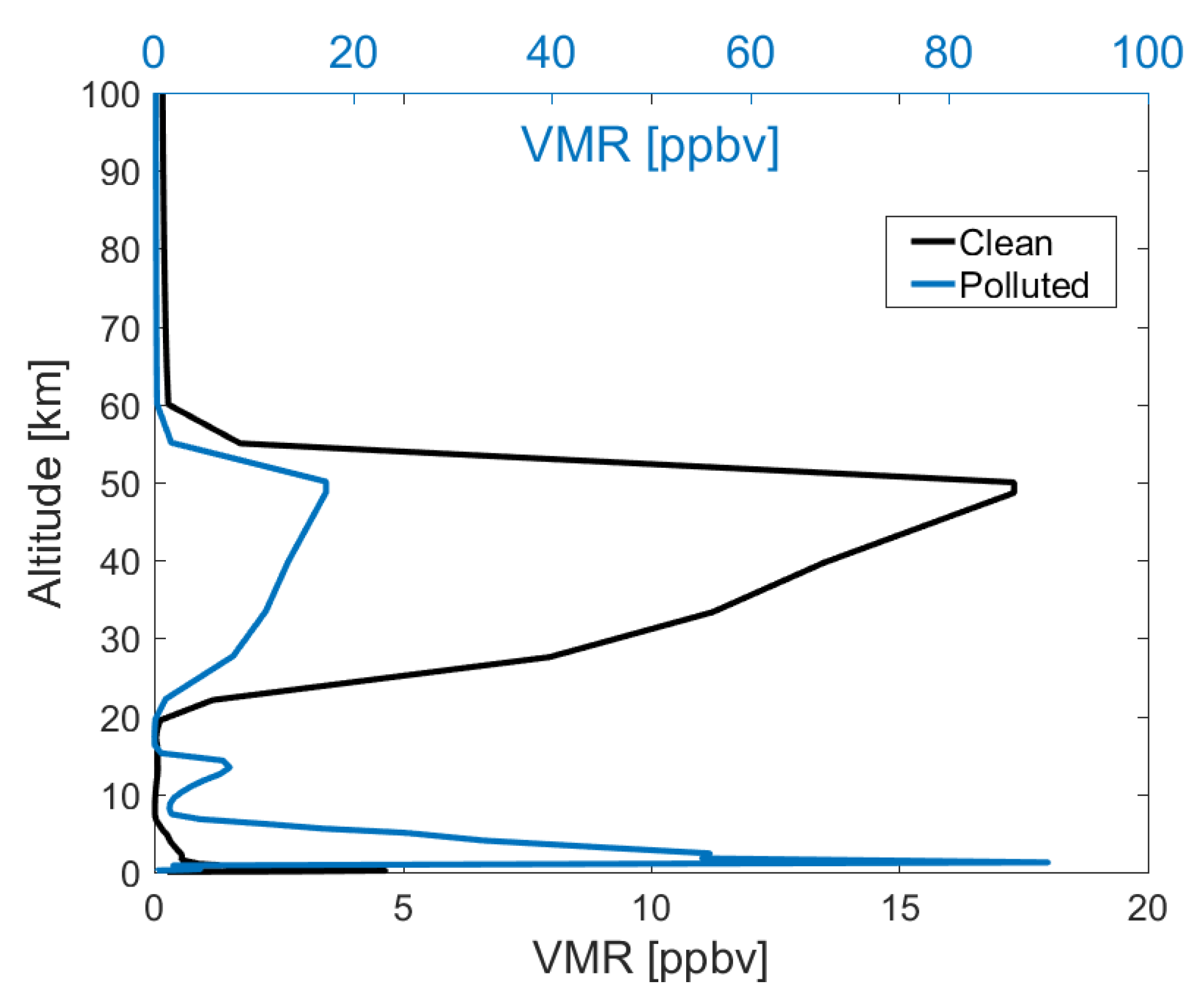
- we choose with and (if not stated otherwise) and compute , and ; thus, the exact total column to be retrieved is ;
- for , we compute by the radiative transfer model;
- we determine the coefficients of the smoothing polynomial by solving the least-squares problem (25);
- we compute , where are independent Gaussian random variables with zero mean and standard deviationand SNR is the signal-to-noise ratio;
- we choose , , and ;
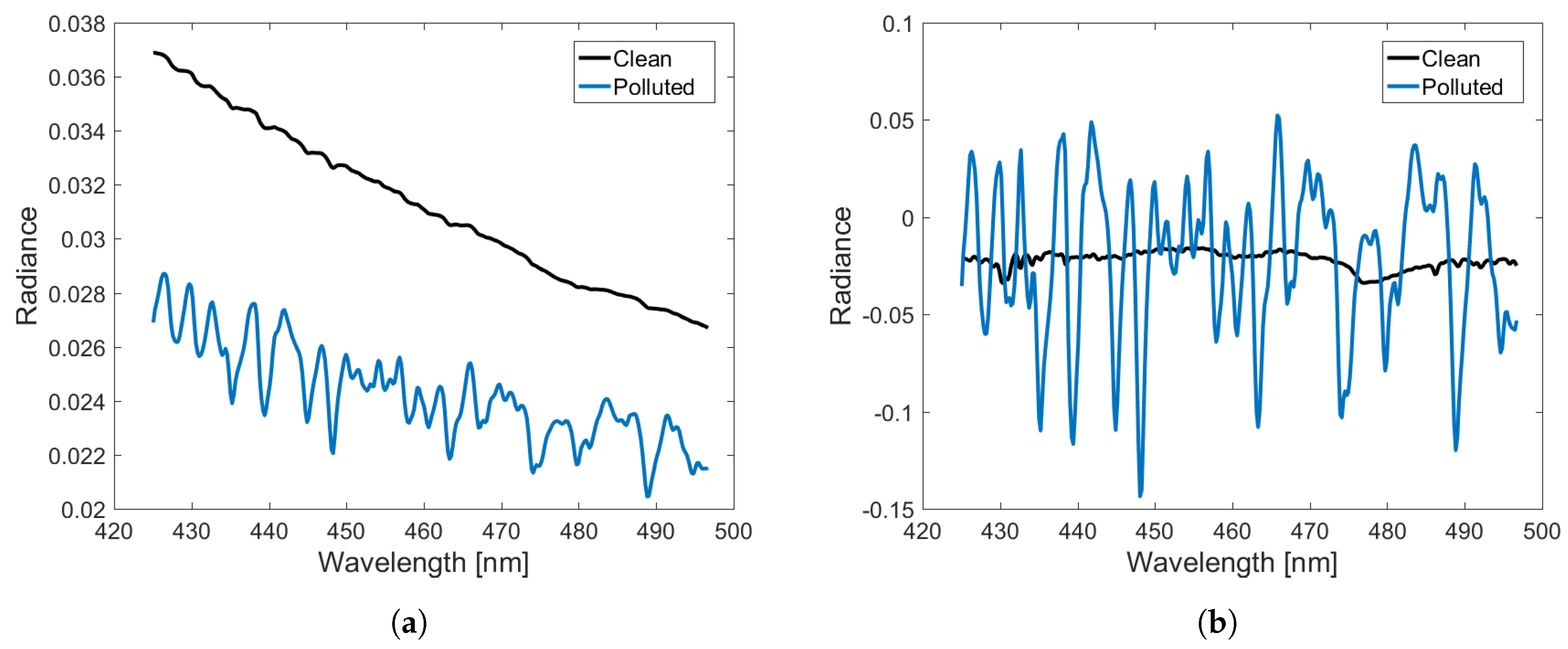
- for DRMI, we compute the kth component of the noisy data vector as
- for DRME, we choose and compute the kth component of the noisy data vector as
- As usual, the initial guess is taken to be equal to the a priori, i.e., .
- If not stated otherwise, the regularization parameter of the method of Tikhonov regularization is chosen as , while for the iteratively regularized Gauss–Newton method, the initial value of the regularization parameter is and the regularization strength is gradually decreased during the iterative process with a constant ratio . Because the iteratively regularized Gauss–Newton method is less sensitive to the overestimation of the regularization parameter, the choice of should guarantee that the method is able to capture the optimal value of the regularization parameter, i.e., .
- The control parameter in the discrepancy principle Equation (15) is .
6.1. Total Column Retrieval
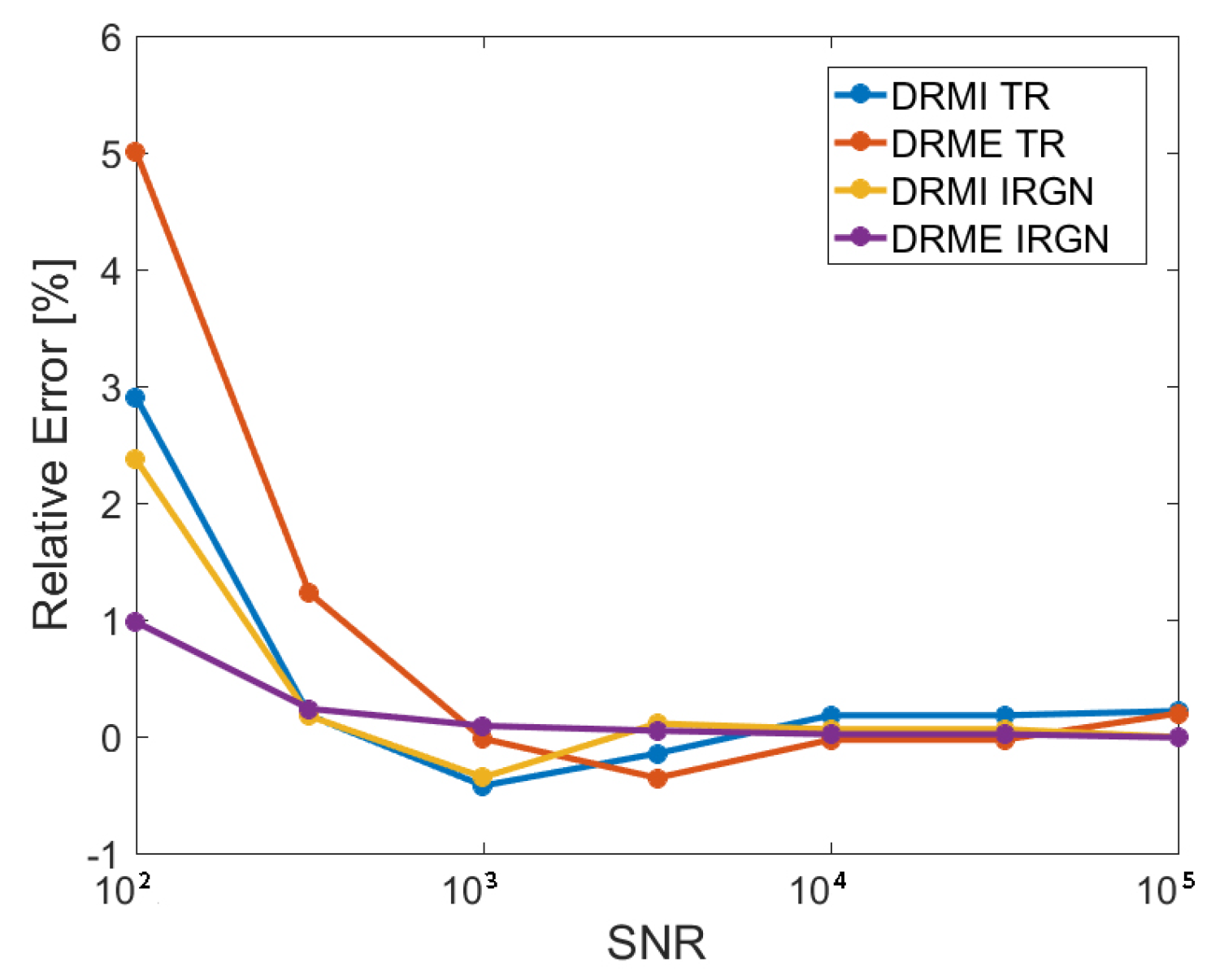
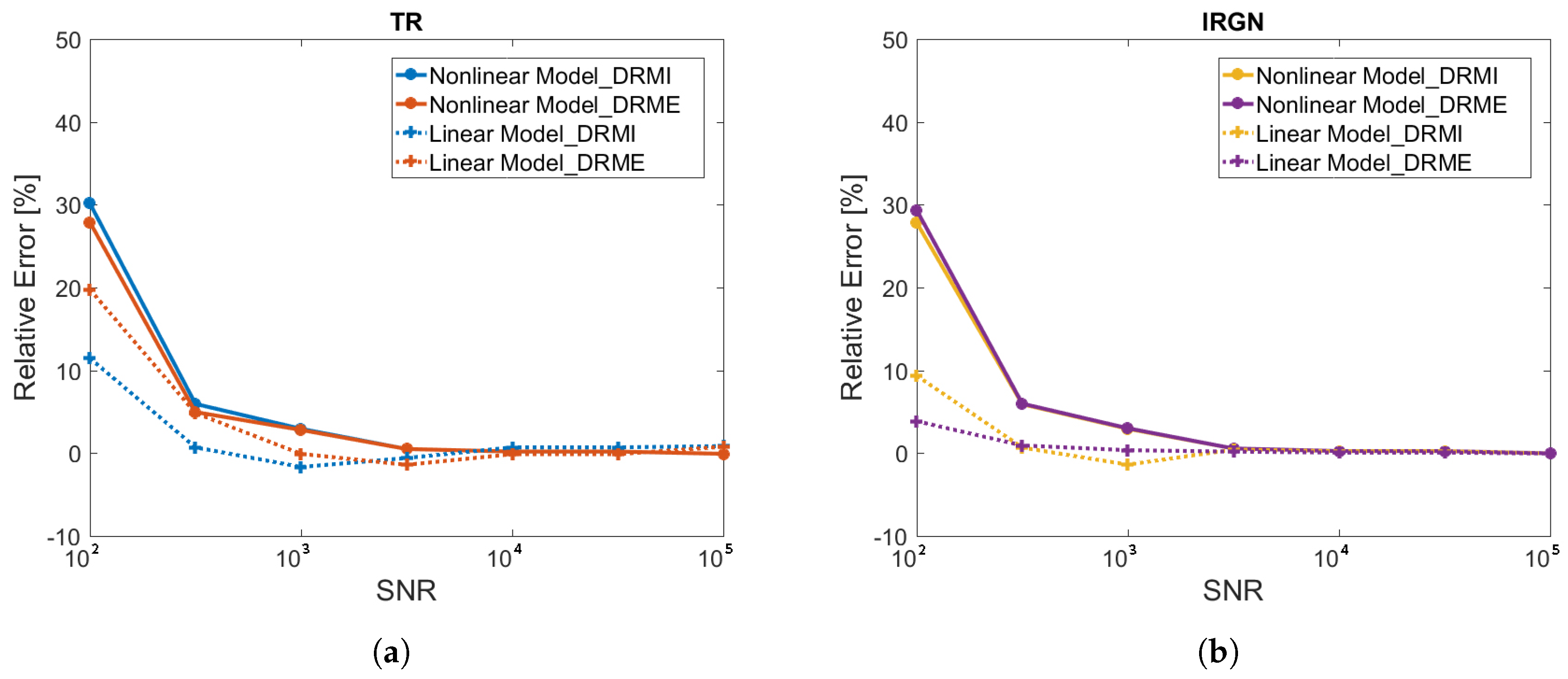
- The relative errors decrease with the increasing signal-to-noise ratio.
- In general, for small values of the signal-to-noise ratio (), the relative errors obtained by the iteratively regularized Gauss–Newton method are smaller than those delivered by the method of Tikhonov regularization. Note that for the clean scenario with (where the signal is very low and the noise level is relatively high), the retrieval error is dominated by the noise error rather than the smoothing error.
- For small values of the signal-to-noise ratio (), DRMI equipped with the method of Tikhonov regularization delivers more reliable results than DRME; when the iteratively regularized Gauss–Newton method is used as regularization method, the reverse situation occurs.
- For large values of the signal-to-noise ratio (), the relative errors are within for all inversion models and regularization methods.
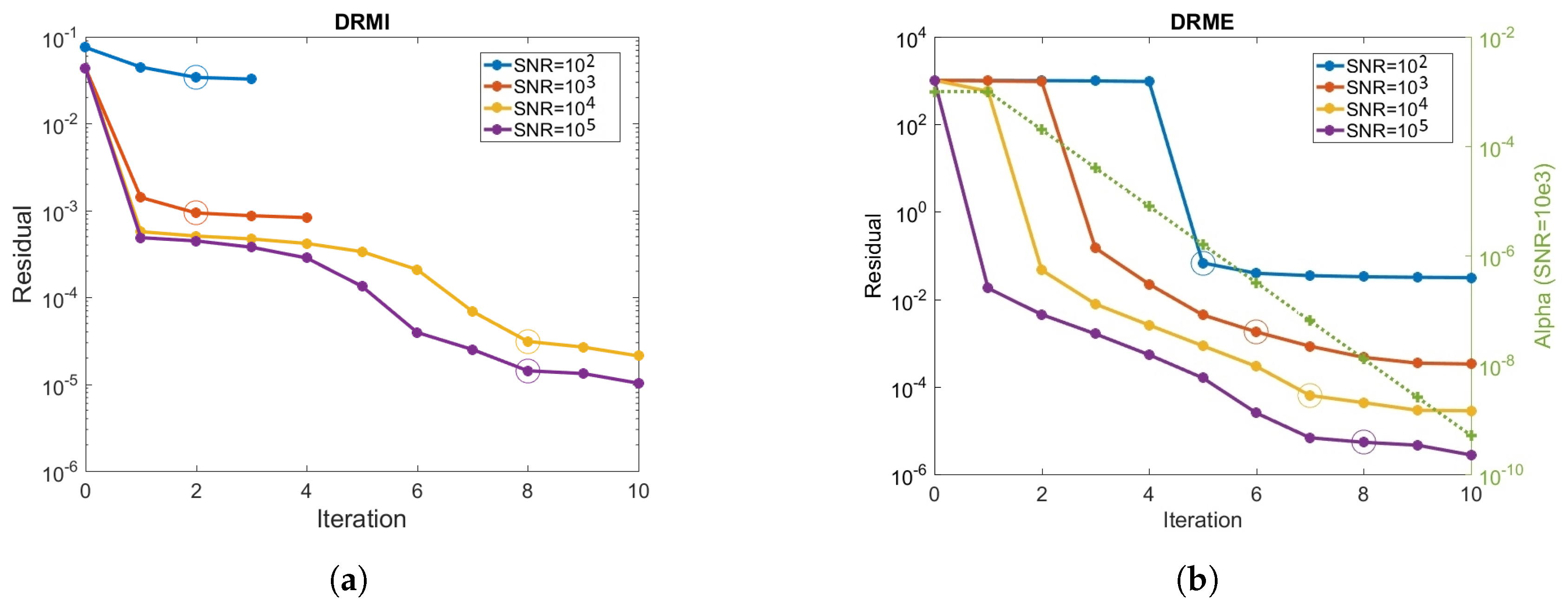
- The residuals attain a plateau, which is used for estimating the noise level. This plateau is more pronounced for small values of the signal-to-noise ratio and decreases when the signal-to-noise ratio increases.
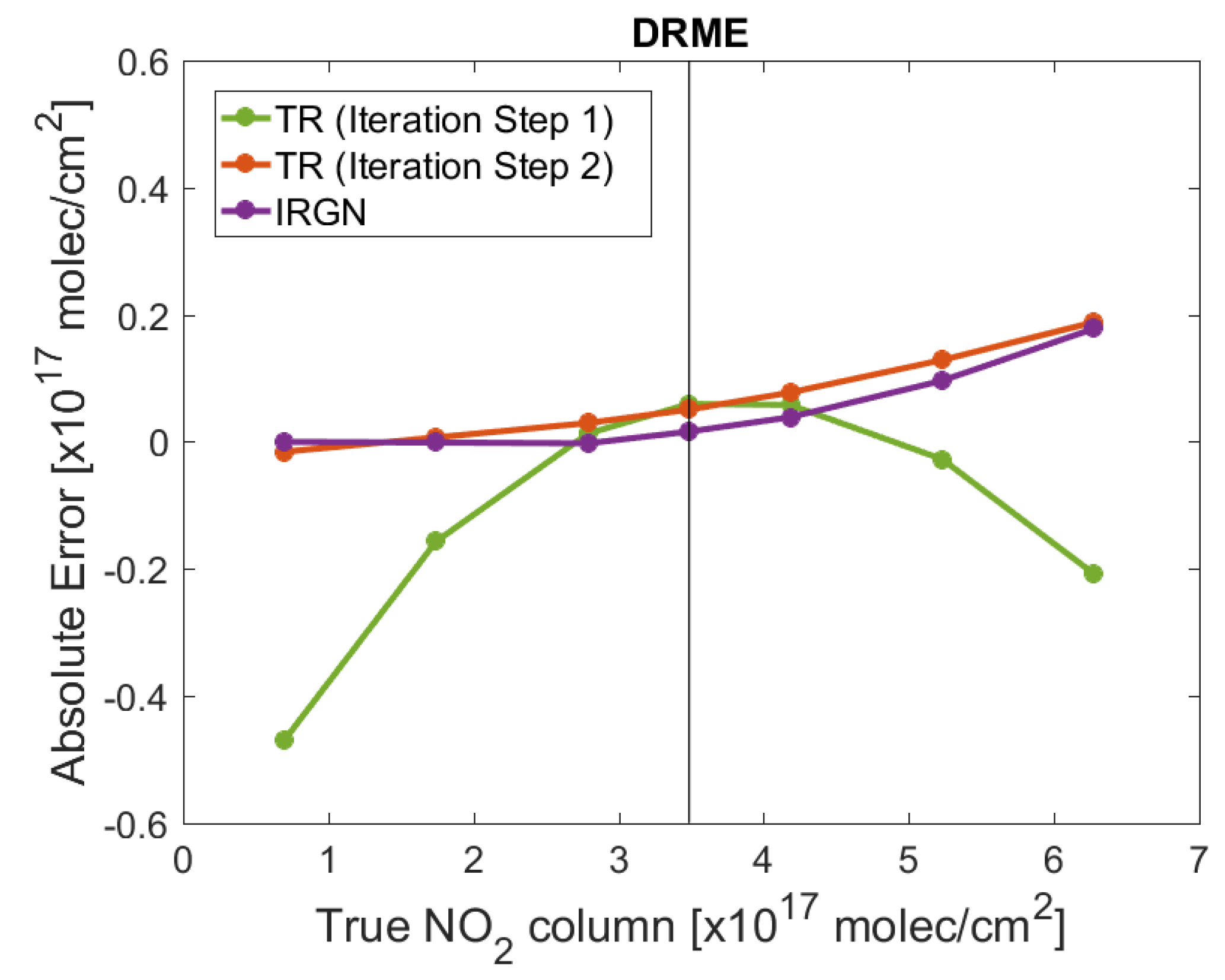
- At the initial guess, the residual corresponding to the DRMI model is much smaller than that corresponding to the DRME. The reason is that the discrepancies between the differential spectra are usually small. However, at the end of the iterative processes, the residuals are comparable.
- In DRMI, the residual decreases very fast at the first iteration step, while in DRME, there is a period of stagnation after which the residual decreases very rapidly.
- For small values of the signal-to-noise ratio (), the iterative process in DRMI terminates after 3–4 iterations, while 10 iteration steps are required in DRME. However, the final residual in DRMI is slightly larger than in DRME; this result explains the larger relative errors provided by DRMI.
- In DRME and for , the initial value of the regularization parameter is , while the final value, which is an estimate of the optimal value, is approximately equal to . Thus, the amount of regularization is small, and the solution coincides practically with the ordinary least-squares solution.
- The errors, obtained after one iteration step by the method of Tikhonov regularization, are large, and in particular when (i) the discrepancies between the values of the true and initial (a priori) total columns are significant, and (ii) the true values are lower than the initial values. However, the errors decrease significantly at the second iteration step, when they become comparable with the errors obtained by the iteratively regularized Gauss–Newton method. Recalling that the standard DOAS model is equivalent with the first iteration step of the DRME model (see Section 5), we conclude that the DOAS model can be used when the problem is not too nonlinear.
6.2. Tropospheric Column Retrieval
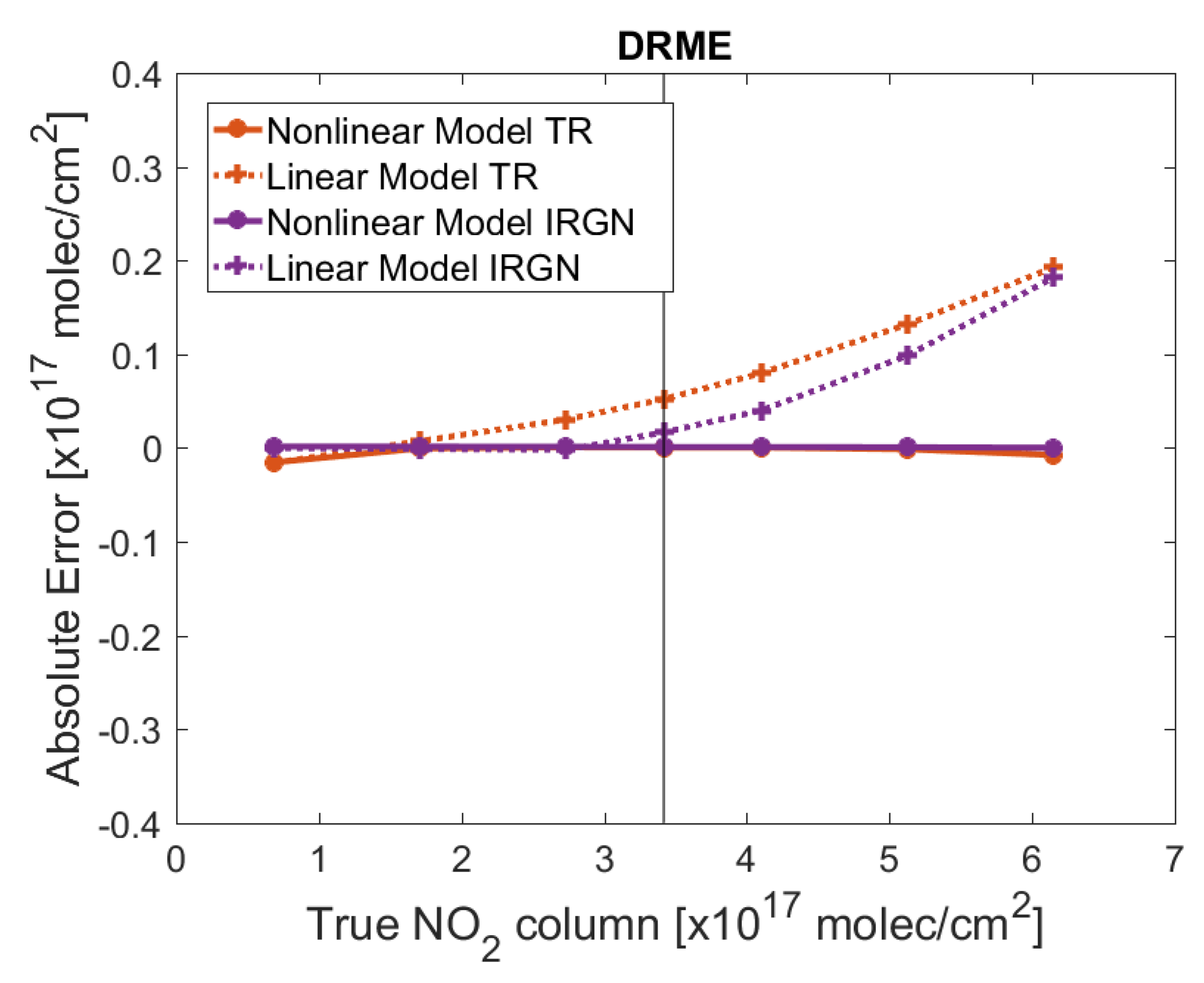
- The relative errors of the linear model are smaller than those of the nonlinear model. This means that in the pre-processing step, the columns of the auxiliary gases and the amplitudes of the correction spectra are not accurately retrieved, while the total column is.
- For the linear model, the relative errors corresponding to the total column delivered by the iteratively regularized Gauss–Newton method are smaller than those delivered by the method of Tikhonov regularization. This result is not surprising because the first method yields more accurate total column retrievals than the second one (see Figure 3).
- The linear model using DRME in the pre-processing step in conjunction with the iteratively regularized Gauss–Newton method has the best retrieval performance; the relative errors are less than for and less than for .
- In contrast to the clean scenario, the errors of the nonlinear model are smaller than those of the linear model. This means that the problem is nonlinear and that the linearizations (33) and (34) around the a priori do not describe the forward model accurately. Remember that the same conclusion has been drawn for the total column retrieval (see Figure 5).
- The corresponding errors of the nonlinear model are less than , regardless of the regularization method used in the pre-processing step.
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Solomon, S. Stratospheric ozone depletion: A review of concepts and history. Rev. Geophys. 1999, 37, 275–316. [Google Scholar] [CrossRef]
- Seinfeld, J.; Pandis, S. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 3rd ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Shindell, D.T.; Faluvegi, G.; Koch, D.M.; Schmidt, G.A.; Unger, N.; Bauer, S.E. Improved attribution of climate forcing to emissions. Science 2009, 326, 716–718. [Google Scholar] [CrossRef] [PubMed]
- Levelt, P.; Van den Oord, G.; Dobber, M.; Malkki, A.; Visser, H.; de Vries, J.; Stammes, P.; Lundell, J.; Saari, H. The Ozone Monitoring Instrument. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1093–1101. [Google Scholar] [CrossRef]
- Callies, J.; Corpaccioli, E.; Eisinger, M.; Hahne, A.; Lefebvre, A. GOME-2-Metop’s second-generation sensor for operational ozone monitoring. ESA Bull. 2000, 102, 28–36. [Google Scholar]
- Munro, R.; Lang, R.; Klaes, D.; Poli, G.; Retscher, C.; Lindstrot, R.; Huckle, R.; Lacan, A.; Grzegorski, M.; Holdak, A.; et al. The GOME-2 instrument on the Metop series of satellites: Instrument design, calibration, and level 1 data processing—An overview. Atmos. Meas. Tech. 2016, 9, 1279–1301. [Google Scholar] [CrossRef]
- Veefkind, J.; Aben, I.; McMullan, K.; Förster, H.; De Vries, J.; Otter, G.; Claas, J.; Eskes, H.; De Haan, J.; Kleipool, Q.; et al. TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the atmospheric composition for climate, air quality and ozone layer applications. Remote Sens. Environ. 2012, 120, 70–83. [Google Scholar] [CrossRef]
- Ingmann, P.; Veihelmann, B.; Langen, J.; Lamarre, D.; Stark, H.; Courrèges-Lacoste, G.B. Requirements for the GMES Atmosphere Service and ESA’s implementation concept: Sentinels-4/-5 and-5p. Remote Sens. Environ. 2012, 120, 58–69. [Google Scholar] [CrossRef]
- Lambert, J.; Granville, J.; Allaart, M.; Blumenstock, T.; Coosemans, T.; De Maziere, M.; Friess, U.; Gil, M.; Goutail, F.; Ionov, D.; et al. Ground-Based Comparisons of Early SCIAMACHY O3 and NO2 Columns. In ESA Special Publication; European Space Agency: Paris, France, 2003; Volume 531. [Google Scholar]
- Pinardi, G.; Van Roozendael, M.; Lambert, J.C.; Granville, J.; Hendrick, F.; Tack, F.; Yu, H.; Cede, A.; Kanaya, Y.; Irie, I.; et al. GOME-2 total and tropospheric NO2 validation based on zenith-sky, direct-sun and multi-axis DOAS network observations. In Proceedings of the 2014 EUMETSAT Meteorological Satellite Conference (EUMETSAT), Geneva, Swizerland, 22–26 September 2014. [Google Scholar]
- Pinardi, G.; Lambert, J.C.; Granville, J.; Yu, H.; De Smedt, I.; van Roozendael, M.; Valks, P. O3M-SAF Validation Report; Technical Report, SAF/O3M/IASB/VR/NO2/TN-IASB-GOME2-O3MSAF-NO2-2015; EUMETSAT: Darmstadt, Germany, 2015. [Google Scholar]
- Hilboll, A.; Richter, A.; Burrows, J. Long-term changes of tropospheric NO2 over megacities derived from multiple satellite instruments. Atmos. Chem. Phys. 2013, 13, 4145–4169. [Google Scholar] [CrossRef]
- Hilboll, A.; Richter, A.; Burrows, J.P. NO2 pollution over India observed from space—The impact of rapid economic growth, and a recent decline. Atmos. Chem. Phys. Discuss. 2017. [Google Scholar] [CrossRef]
- Zien, A.; Richter, A.; Hilboll, A.; Blechschmidt, A.M.; Burrows, J. Systematic analysis of tropospheric NO2 long-range transport events detected in GOME-2 satellite data. Atmos. Chem. Phys. 2014, 14, 7367–7396. [Google Scholar] [CrossRef]
- Ding, J.; Miyazaki, K.; van der A, R.J.; Mijling, B.; Kurokawa, J.I.; Cho, S.; Janssens-Maenhout, G.; Zhang, Q.; Liu, F.; Levelt, P.F. Intercomparison of NOx emission inventories over East Asia. Atmos. Chem. Phys. 2017, 17, 10125. [Google Scholar] [CrossRef]
- Visser, A.J.; Boersma, K.F.; Ganzeveld, L.N.; Krol, M.C. European NOx emissions in WRF-Chem derived from OMI: Impacts on summertime surface ozone. Atmos. Chem. Phys. 2019, 19, 11821–11841. [Google Scholar] [CrossRef]
- Safieddine, S.; Clerbaux, C.; George, M.; Hadji-Lazaro, J.; Hurtmans, D.; Coheur, P.F.; Wespes, C.; Loyola, D.; Valks, P.; Hao, N. Tropospheric ozone and nitrogen dioxide measurements in urban and rural regions as seen by IASI and GOME-2. J. Geophys. Res. Atmos. 2013, 118. [Google Scholar] [CrossRef]
- Varotsos, C.; Christodoulakis, J.; Tzanis, C.; Cracknell, A. Signature of tropospheric ozone and nitrogen dioxide from space: A case study for Athens, Greece. Atmos. Environ. 2014, 89, 721–730. [Google Scholar] [CrossRef]
- Platt, U.; Stutz, J. Differential Optical Absorption Spectroscopy; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Burrows, J.P.; Weber, M.; Buchwitz, M.; Rozanov, V.; Ladstätter-Weißenmayer, A.; Richter, A.; DeBeek, R.; Hoogen, R.; Bramstedt, K.; Eichmann, K.U.; et al. The global ozone monitoring experiment (GOME): Mission concept and first scientific results. J. Atmos. Sci. 1999, 56, 151–175. [Google Scholar] [CrossRef]
- Richter, A.; Burrows, J.P.; Nüß, H.; Granier, C.; Niemeier, U. Increase in tropospheric nitrogen dioxide over China observed from space. Nature 2005, 437, 129. [Google Scholar] [CrossRef]
- Valks, P.; Pinardi, G.; Richter, A.; Lambert, J.C.; Hao, N.; Loyola, D.; Van Roozendael, M.; Emmadi, S. Operational total and tropospheric NO2 column retrieval for GOME-2. Atmos. Meas. Tech. 2011, 4, 1491. [Google Scholar] [CrossRef]
- Van Geffen, J.; Boersma, K.; Van Roozendael, M.; Hendrick, F.; Mahieu, E.; De Smedt, I.; Sneep, M.; Veefkind, J. Improved spectral fitting of nitrogen dioxide from OMI in the 405–465 nm window. Atmos. Meas. Tech. 2015, 8, 1685–1699. [Google Scholar] [CrossRef]
- Van Geffen, J.; Boersma, K.; Eskes, H.; Maasakkers, J.; Veefkind, J. TROPOMI ATBD of the Total and Tropospheric NO2 Data Products; Technical Report, S5P-KNMI-L2-0005-RP issue 1.4.0; KNMI: De Bilt, The Netherlands, 2019. [Google Scholar]
- Liu, S.; Valks, P.; Pinardi, G.; De Smedt, I.; Yu, H.; Beirle, S.; Richter, A. An Improved Total and Tropospheric NO2 Column Retrieval for GOME-2. Atmos. Meas. Tech. 2019, 12, 1029–1057. [Google Scholar] [CrossRef]
- Doicu, A.; Trautmann, T.; Schreier, F. Numerical Regularization for Atmospheric Inverse Problems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Tikhonov, A.N. On the solution of ill-posed problems and the method of regularization. Dokl. Akad. Nauk SSSR 1963, 151, 501–504. [Google Scholar]
- Dennis, J.E., Jr.; Schnabel, R.B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1996; Volume 16. [Google Scholar]
- Gill, P.E.; Murray, W.; Wright, M.H. Practical Optimization; Academic Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Rodgers, C.D. Inverse Methods for Aatmospheric Sounding: Theory and Practice; World Scientific: Singapore, 2000; Volume 2. [Google Scholar]
- Carissimo, A.; De Feis, I.; Serio, C. The physical retrieval methodology for IASI: The δ-IASI code. Environ. Model. Softw. 2005, 20, 1111–1126. [Google Scholar] [CrossRef]
- Xu, J.; Schreier, F.; Doicu, A.; Trautmann, T. Assessment of Tikhonov-type regularization methods for solving atmospheric inverse problems. J. Quant. Spectrosc. Radiat. Transf. 2016, 184, 274–286. [Google Scholar] [CrossRef] [Green Version]
- Wahba, G. Practical approximate solutions to linear operator equations when the data are noisy. SIAM J. Numer. Anal. 1977, 14, 651–667. [Google Scholar] [CrossRef]
- Hansen, P.C. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 1992, 34, 561–580. [Google Scholar] [CrossRef]
- Bakushinskii, A.B. The problem of the convergence of the iteratively regularized Gauss–Newton method. Zhurnal Vychislitel’noi Mat. Mat. Fiz. 1992, 32, 1503–1509. [Google Scholar]
- Morozov, V.A. On the solution of functional equations by the method of regularization. Dokl. Akad. Nauk SSSR 1966, 167, 510–512. [Google Scholar]
- Huijnen, V.; Eskes, H.J.; Poupkou, A.; Elbern, H.; Boersma, K.F.; Foret, G.; Sofiev, M.; Valdebenito, A.; Flemming, J.; Stein, O.; et al. Comparison of OMI NO2 tropospheric columns with an ensemble of global and European regional air quality models. Atmos. Chem. Phys. 2010, 10, 3273–3296. [Google Scholar] [CrossRef]
- Richter, A.; Burrows, J. Tropospheric NO2 from GOME measurements. Adv. Space Res. 2002, 29, 1673–1683. [Google Scholar] [CrossRef]
- Bucsela, E.; Krotkov, N.; Celarier, E.; Lamsal, L.; Swartz, W.; Bhartia, P.; Boersma, K.; Veefkind, J.; Gleason, J.; Pickering, K. A new stratospheric and tropospheric NO2 retrieval algorithm for nadir-viewing satellite instruments: Applications to OMI. Atmos. Meas. Tech. 2013, 6, 2607. [Google Scholar] [CrossRef]
- Beirle, S.; Hörmann, C.; Jöckel, P.; Liu, S.; Penning de Vries, M.; Pozzer, A.; Sihler, H.; Valks, P.; Wagner, T. The STRatospheric Estimation Algorithm from Mainz (STREAM): Estimating stratospheric NO2 from nadir-viewing satellites by weighted convolution. Atmos. Meas. Tech. 2016, 9, 2753–2779. [Google Scholar] [CrossRef]
- Eskes, H.; Van Velthoven, P.; Valks, P.; Kelder, H. Assimilation of GOME total-ozone satellite observations in a three-dimensional tracer-transport model. Q. J. R. Meteorol. Soc. 2003, 129, 1663–1681. [Google Scholar] [CrossRef]
- Dirksen, R.J.; Boersma, K.F.; Eskes, H.J.; Ionov, D.V.; Bucsela, E.J.; Levelt, P.F.; Kelder, H.M. Evaluation of stratospheric NO2 retrieved from the Ozone Monitoring Instrument: Intercomparison, diurnal cycle, and trending. J. Geophys. Res. Atmos. 2011, 116, D08305. [Google Scholar] [CrossRef]
- Bucsela, E.J.; Celarier, E.A.; Wenig, M.O.; Gleason, J.F.; Veefkind, J.P.; Boersma, K.F.; Brinksma, E.J. Algorithm for NO2 vertical column retrieval from the ozone monitoring instrument. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1245–1258. [Google Scholar] [CrossRef]
- Rozanov, A.; Rozanov, V.; Buchwitz, M.; Kokhanovsky, A.; Burrows, J. SCIATRAN 2.0—A new radiative transfer model for geophysical applications in the 175–2400 nm spectral region. Adv. Space Res. 2005, 36, 1015–1019. [Google Scholar] [CrossRef]
- Doicu, A.; Trautmann, T. Discrete-ordinate method with matrix exponential for a pseudo-spherical atmosphere: Scalar case. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 146–158. [Google Scholar] [CrossRef]
- Doicu, A.; Trautmann, T. Discrete-ordinate method with matrix exponential for a pseudo-spherical atmosphere: Vector case. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 159–172. [Google Scholar] [CrossRef]
- Anderson, G.P.; Clough, S.A.; Kneizys, F.; Chetwynd, J.H.; Shettle, E.P. AFGL Atmospheric Constituent Profiles (0.120 km); Technical Report; Air Force Geophysics Lab.: Hanscom AFB, MA, USA, 1986. [Google Scholar]
- Marchenko, S.; Krotkov, N.; Lamsal, L.; Celarier, E.; Swartz, W.; Bucsela, E. Revising the slant column density retrieval of nitrogen dioxide observed by the Ozone Monitoring Instrument. J. Geophys. Res. Atmos. 2015, 120, 5670–5692. [Google Scholar] [CrossRef] [Green Version]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S. Inversion Models for the Retrieval of Total and Tropospheric NO2 Columns. Atmosphere 2019, 10, 607. https://doi.org/10.3390/atmos10100607
Liu S. Inversion Models for the Retrieval of Total and Tropospheric NO2 Columns. Atmosphere. 2019; 10(10):607. https://doi.org/10.3390/atmos10100607
Chicago/Turabian StyleLiu, Song. 2019. "Inversion Models for the Retrieval of Total and Tropospheric NO2 Columns" Atmosphere 10, no. 10: 607. https://doi.org/10.3390/atmos10100607



