Next Article in Journal
Magnitudes of Gravity Wave Pseudomomentum Flux Derived by Combining COSMIC Radio Occultation and ERA-Interim Reanalysis Data
Previous Article in Journal
Inter-Annual Variability of Boreal Summer Intra-Seasonal Oscillation Propagation from the Indian Ocean to the Western Pacific
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 10
Issue 10
10.3390/atmos10100597
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Assessment of CMIP5 Models Based on the Interdecadal Relationship between the PDO and Winter Temperature in China

by
Yifei Xu
1,
Te Li
2,
Shuanghe Shen
1,3,* and
Zhenghua Hu
1,3,*
1
School of Applied Meteorology, Nanjing University of Information Science & Technology, Nanjing 210044, China
2
School of Atmospheric Sciences and Institute for Climate and Global Change, Nanjing University, Nanjing 210023, China
3
Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters and Key Laboratory of Meteorological Disaster of Ministry of Education, Nanjing University of Information Science & Technology, Nanjing 210044, China
*
Authors to whom correspondence should be addressed.
Atmosphere 2019, 10(10), 597; https://doi.org/10.3390/atmos10100597
Submission received: 11 August 2019 / Revised: 26 September 2019 / Accepted: 27 September 2019 / Published: 2 October 2019
(This article belongs to the Section Meteorology)
Browse Figures
Versions Notes

Abstract

:
In this study, the impact of the Pacific Decadal Oscillation (PDO) on the China winter temperature (CWT) was assessed on an interdecadal timescale, and the capacities of the 35 models of the fifth Coupled Model Intercomparison Project (CMIP5) were assessed by simulating the PDO-CWT teleconnection. The Met Office Hadley Centre’s sea ice and sea surface temperature (HadISST) were used as the observational data, and Climatic Research Unit (CRU) datasets provided long-term temperature data for the 1901–2005 period. By calculating the spatial correlation coefficient between the PDO index and winter temperature in China, thirteen CMIP5 models close to the HadISST datasets were selected for this study. These models were averaged as the good multi-model ensemble (GOODMME), and the PDO-CWT spatial correlation between the GOODMME and the observations was 0.80. Overall, the correlation coefficient between the PDO index and atmospheric circulation suggests that the GOODMME produces the same excellent results as do the observations. The results also verify the GOODMME’s superiority in simulating the impact of the PDO on winter temperatures in China. The possible mechanisms underlying the impact of the different phases of the PDO on the CWT are also described.

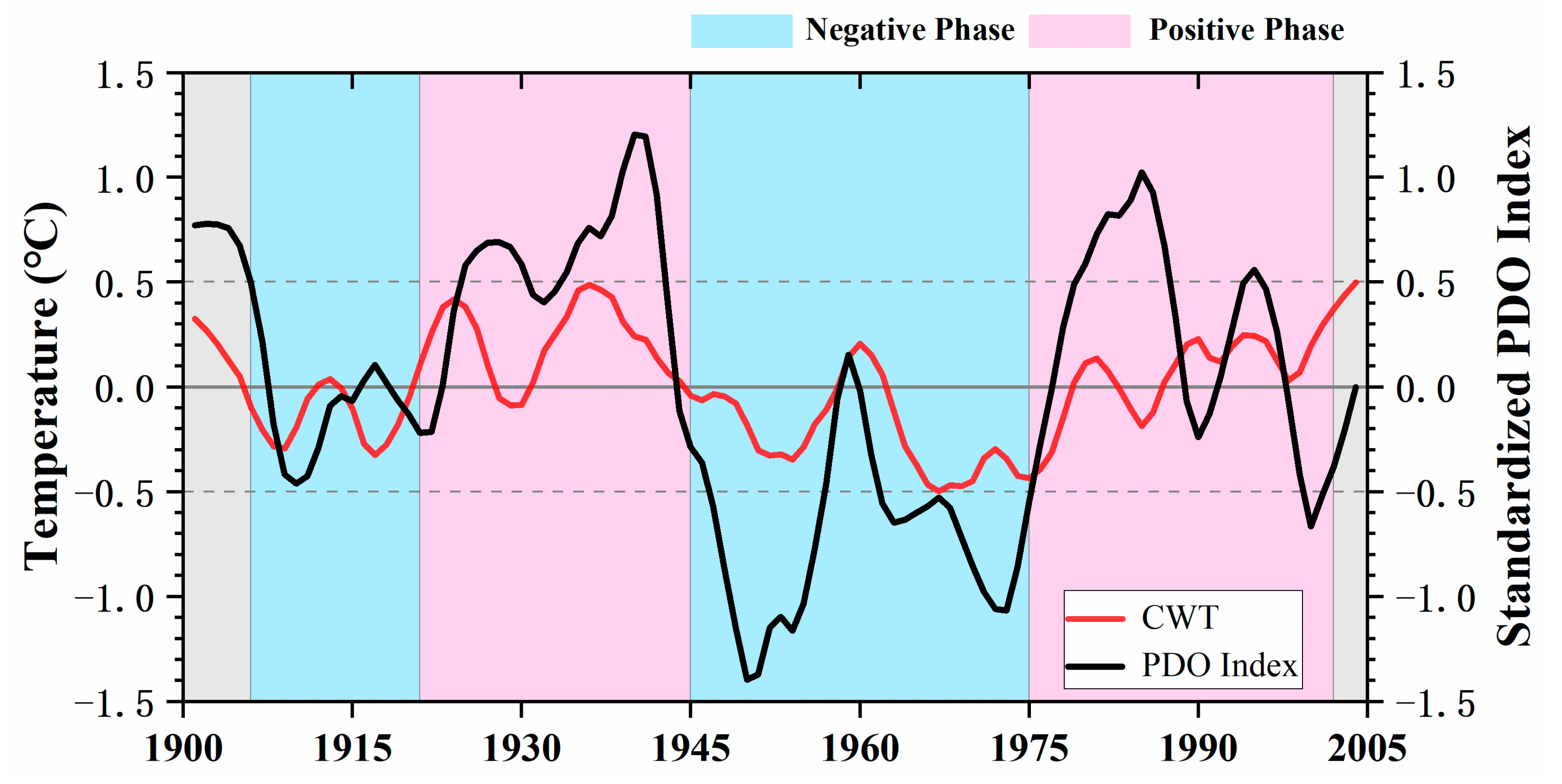
1. Introduction

The Pacific Decadal Oscillation (PDO) is one of the most dominant patterns affecting the sea surface temperature (SST) in the north Pacific on the decadal scale, and it is defined as the leading principal component of SST anomalies in the north Pacific. Previous studies [1,2,3,4,5,6,7] have indicated that the PDO influences the regional or even global climate. For example, the PDO affects the North American and East Asian climates [8,9]. The PDO also drives dry conditions during spring and summer in the United States [10], as well as precipitation anomalies in Australia [11].
The winter temperature in China (CWT) is strongly determined by the East Asian winter monsoon (EAWM), which comprises the East Asian trough in the troposphere, the Siberian high at the surface, and the jet stream in the upper troposphere [12]. Phase shifts in the PDO influence not only the interdecadal variability of the atmospheric circulation but also the EAWM intensity [13]. Ding et al. [14] noted that the CWT has experienced three stages of variation since in the 1950s, exhibiting coherent interdecadal variability with the PDO, and that when the PDO is in the negative phase, the EAWM is stronger and will lead to a colder temperature in China. Kenyon et al. [15] showed that the PDO has also substantially influenced temperature extremes in winter. The PDO provides a major source of decadal climate predictability [16]. Therefore, the impacts of the PDO on the climate are of great importance in decadal climate prediction. The interconnection between the PDO and CWT can offer opportunities to delineate the specific effects for use in meteorological forecasts and early warning for meteorological disasters such as winter extreme events.
The Coupled Model Intercomparison Project Phase 5 (CMIP5), along with general circulation models (CGCMs), not only has great potential for use in the study of the El Niño Southern Oscillation (ENSO) and PDO mechanisms, but has also been proven to be promising in predicting future global climate change [17,18]. Numerous researchers have focused on assessing the performance of CMIP5 models. For example, Roy [19] used the CMIP5 output to analyze the characteristics of the Indian summer monsoon and ENSO, while Zhang et al. [20] investigated the driving mechanism behind the observed changes that cause extreme summer droughts in northern China. Newman et al. [21] noted that the PDO time series output by the models was irregular because the time series of a model of unforced variability is random and arbitrary; however, some models can reproduce the PDO phase well. Joshi and Kucharski [22] simulated the observed teleconnection of the Interdecadal Pacific Oscillation (IPO) with the Indian Summer Monsoon Rainfall (ISMR), and they reported that approximately two-thirds of the 32 models could reproduce the IPO-ISMR relationship. Recent assessments have noted that 11 selected models could effectively reproduce the constructive interference between ENSO and PDO by analyzing their similar and different phases [23]. However, in these studies, the research duration of evaluating the capacity of the simulation was only approximately 50 years, since the PDO time series has a slowly varying component [3], and long-term changes cannot be adequately represented if short-term statistical information is used for reconstruction [24]. More importantly, a detailed systematic analysis of the PDO over a long simulation duration (over 100 years) using the CMIP5 models over China has not been previously performed.
In this paper, we have chosen 35 CMIP5 models to analyze the impact of the PDO on the CWT on an interdecadal timescale. A 105-year (1901–2005) ocean–atmosphere system dataset was used to analyze the differences between the simulation results and the observations. The remaining parts of this paper are organized as follows. In Section 2, the data and methodology are described, and the model comparison results are presented in Section 3. In Section 4, the possible mechanisms underlying the PDO and CWT are discussed, and the conclusions and recommendations are given in Section 5.

2. Data and Methodology

2.1. Data

To analyze the effect produced by the PDO, SST data over China during 1901–2005 from 35 CMIP5 models were employed. The CMIP5 simulations were available in the Earth System Grid Federation (ESGF) [25]. Table 1 provides a summary of the GCMs used in this study. Detailed information on CMIP5 with the respective GCMs can be found in Taylor et al. [26]. For each model, the first ensemble member (r1i1p1) run was carried out for the historical period 1901–2005.
To assess the capacity of the CMIP5 models, the Met Office Hadley Centre’s sea ice and SST dataset (HadISST) was used as the observation data for comparison with the simulation data [27]. HadISST data provide global SST data from 1870 to the present, with a resolution of 1° × 1°. The HadISST dataset details and analysis can be found in Rayner et al. [28]. To investigate the relationship between the PDO and CWT, monthly temperature data from the Climatic Research Unit (CRU TS3.22) were used. The data were retrieved from the University of East Anglia’s CRU [29].
A 6-year moving-average filter was employed to construct the PDO index to assess the PDO effect on the CWT. The data from the 20th century reanalysis for the sea level pressure (SLP) and geopotential height at 500 hPa and 200 hPa were used [30,31], which can be downloaded from NOAA Earth System Research Laboratory (ESRL) [32].

2.2. Methodology

Due to the varying model resolutions, all of the outputs were interpolated by natural neighborhood interpolation into a 1° × 1° grid over the 1901–2005 period for comparison. SSTs were used to calculate the annual sea surface temperature anomalies (SSTAs), and then the influence of global warming was removed by subtracting the monthly SSTA global average from each grid point per monthly SSTA. The PDO index was defined as the leading principal component (PC1) from the empirical orthogonal function (EOF) of the final SSTAs in the North Pacific (20° N–70° N, 130° E–90° W) [33]. A better assessment of the ability of models to simulate the PDO, known as the Taylor diagram [34], was used in this study. In this paper, the Pearson correlation coefficient [35] was used to calculate the correlation coefficient of the PDO and CWT.

3. Analysis of the PDO-CWT Simulation

3.1. Simulation of the PDO by the CMIP5 Models

The biases of the observed and CMIP5 model-simulated SSTs averaged over 1901–2005 during the wintertime (NDJFM) are displayed in Figure 1. The results were calculated by subtracting the observed SST field from the simulated SST field. The first picture shows the biases of the observation and the multi-model ensemble (MME), which is the average of the SSTs for 35 CMIP5 models. As shown in Figure 1, there are approximately −4–4 °C differences among the 35 CMIP5 models and observations. Most models overestimate the SSTs by 2–4 °C in the region to the north of 40° N and underestimate the SSTs by 1–3°C in the region of 0°–40° N. Some models show a region on the west coast of North America and South America where the SSTs are overestimated by 3–4 °C. In the equatorial region of the Pacific, some models exhibit a thin, narrow underestimated region, and the overestimated regions are symmetrically distributed on both sides of this region.
The models that produce fewer differences (|biases| ≤ 2 °C) from the observations in the North Pacific are as follows: CMCC-CM, CMCC-CMS, GFDL-ESM2G, GFDL-ESM2M, HadGEM2-ES, IPSL-CM5A-MR and MPI-ESM-LR. In contrast, the simulated SSTs in the northern Pacific based on CSIRO-MK3.6.0, GISS-E2-H-CC, GISS-E2-H, IPSL-CM5B-LR, INMCM4.0, MIROC5 and MRICGCM3 differ greatly from the observed results (|biases| ≥ 4 °C). A study carried out by Yim et al. [36] reported that the MME could capture the overall PDO features in the observations. However, the results of the MME SSTs in the northern Pacific are larger than the observation data, since some models that differ greatly from the observed SSTs were averaged in the MME, which means that different situations need to be analyzed specifically in the composition selection of the MME models.
Furthermore, to assess the abilities of the models to simulate SSTAs, the Taylor diagram was used. Figure 2 shows the Taylor diagram of the monthly SSTAs for 35 CMIP5 models and the MME over the 1901–2005 period. Monthly HadISST data are used as the reference data. As illustrated, except for IPSL-CM5B-LR, all models exhibited a correlation value greater than 0.9. The findings showed that CanESM2, BCC-CSM1.1, BCC-CMS1.1 (m), CNRM-CM5, FIO-ESM and FGOALS-g2 have smaller dispersions in comparison with the other models. Overall, the model results indicate that CanESM2, BCC-CSM1.1 (m), BCC-CSM1.1, and CNRM-CM5 are relatively closer to the observations than are the other models.
The EOF first spatial pattern of the SSTA can show the space-time evolution characteristics of the SST field. The EOF first spatial pattern of the SSTAs in the North Pacific (20° N–70° N, 130° E–90° W) was calculated (not shown). The EOF sign is arbitrary; therefore, some signs have been flipped such that all EOFs have the same sign as an anomaly in the Kuroshio-Oyashio extension (the index is multiplied by –1). Figure 3 is the PDO time series, and the correlation coefficients of the HadISST PDO index and CMIP5 model PDO index are represented by R. The models failed to simulate the PDO time series, as the PDO time series outputs were irregular [21]. However, some models in CMIP5 reproduce the PDO pattern well, such as GFDL-ESM2G, NorESM1-M and NorESM1-ME.

3.2. PDO-CWT Teleconnection

To assess the capacity of the CMIP5 models to represent the PDO-CWT teleconnection, we calculated the correlation coefficients between the annual winter-month (NDJFM) mean PDO time series and the annual winter temperature in China (Figure 4). The observed regression pattern depicts a positive correlation over most of China except for the southwestern region. This finding signifies that when the PDO is in a positive phase, the winter temperature over most of China will increase, whereas when the PDO is in a negative phase, the winter temperature over the southwest region will decrease, and vice versa. In terms of the simulations, most of the models presented negative correlations, including the MME. In particular, the models show that CSIRO-Mk3.6.0 and FIO-ESM exhibited the opposite correlation patterns from those of the observations. Only a few models could reproduce the correlation pattern. To compare the abilities of the models to reproduce the relationship between the PDO and CWT, the observed PDO-CWT correlation coefficient field and the individual CMIP5 model PDO-CWT correlation coefficient field were used to make a spatial correlation. Figure 5 shows a bar diagram that displays the spatial correlation coefficient of the individual models and the observation in describing the relationship between the PDO and CWT. In a previous study, Joshi et al. [22] compared the mean correlation coefficient between precipitation and the IPO according to observational data and CMIP5 data to find the best models. As China’s topography is varied, if only the correlation coefficient is averaged to compare the observational and CMIP5 data, spatial correlations may be neglected. Therefore, by calculating the correlation coefficient of the two related fields, the models with positive correlation coefficients show good spatial patterns of PDO-CWT teleconnection (shown as red bars). Hence, following this criterion, the models were categorized into two groups: (a) good models: ACCESS1.3, BCC-CSM1.1, CNRM-CM5, GFDL-ESM2G, GFDL-ESM2M, GISS-E2-H-CC, GISS-E2-H, HadCM3, HadGEM2-AO, INMCM4.0, MPI-ESM-LR, NorESM1-M and NorESM1-ME; and (b) poor models: ACCESS1.0, BCC-CSM1.1(m), CanESM2, CCSM4, CESM(WACCM), CESM1(BGC), CESM1(CAM5), CMCC-CM, CMCC-CMS, CSIRO-Mk3.6.0, EC-EARTH, FGOALS-g2, FIO-ESM, GISS-E2-R-CC, GISS-E2-R, HadGEM2-ES, IPSL-CM5A-LR, MPI-ESM-MR, IPSL-CM5B-LR, MIROC5, IPSL-CM5A-MR and MRICGCM3.
The GOODMME (good multi-model ensemble) is averaged in grid points from the good models, which show positive correlation patterns in Figure 5, as does the POORMME. The correlation between the observed PDO-CWT correlation field and the GOODMME/POORMME PDO-CWT correlation field is shown in Figure 6. The spatial correlation coefficient of the MME and the observed condition was −0.28, and that of POORMME was −0.69. The value for the GOODMME was 0.80 (not shown), indicating that the GOODMME was capable of simulating the spatial pattern of the PDO-CWT teleconnection. The spatial pattern of the GOODMME could reproduce the PDO-CWT correlation pattern, which closely resembles the observation in Figure 4 and shows a positive correlation over most parts of China. The POORMME exhibited the reverse pattern. Based on these findings, the GOODMME can efficiently simulate the PDO-CWT teleconnection, regardless of the spatial pattern distribution or the average correlation coefficient.

4. Possible Mechanisms Underlying the PDO and CWT

4.1. Relationship between the PDO and Atmospheric Circulation Systems

The interaction between the atmosphere and the ocean is extraordinarily complicated, and the PDO is also associated with atmospheric circulation. Therefore, to analyze the atmospheric circulation pattern associated with the PDO, the SLP, geopotential height at 500 hPa and zonal wind at 200 hPa are correlated with the PDO. Because the PDO signal is the strongest during the winter [4,21], the monthly winter (NDJFM) data of the PDO index and the atmospheric circulation systems are utilized.
The results in Figure 7a indicate that there were negative correlation centers at 30° N–70° N and in the north Pacific, and eastern Asia also showed weak negative correlations. There were positive correlative centers in the central Atlantic, Indian Ocean, and North Africa. These results are in agreement with those of Chen and Wallace (2016) [37]. Figure 7c shows the correlation between the 500 hPa geopotential height and the observed PDO. Negative correlation centers were observed in the North Pacific and eastern China, and positive correlation centers were found in North America and the Okhotsk Sea. In addition, there was a positive correlation in the tropical regions. The northern Pacific and North America show the Pacific-North-America (PNA) pattern [38]. The 200 hPa zonal wind can reflect the characteristics of the free atmosphere in the Northern Hemisphere during the winter period, and the wind clearly responds to the characteristics of the tropospheric circulation. Figure 7e depicts the spatial distribution of the correlation between the observed PDO index and the 200 hPa zonal wind. The PDO and the 200 hPa zonal wind speed are positively correlated in this region (15° N–30° N, 60° E–130° W) and negatively correlated in northern China and Japan (30° N–60° N, 60° E–160° E).
The results of the GOODMME were similar to the observations, although they underestimated the negative correlation centers in the middle Pacific and overestimated the negative correlation in eastern Asia between the SLP and PDO index (Figure 7b). The GOODMME can represent the correlation between the PDO and the 500 hPa geopotential height (Figure 7d) and 200 hPa zonal wind (Figure 7f), although the values are underestimated at mid-latitudes and overestimated at high latitudes in East Asia and the North Pacific. However, the POORMME completely failed to simulate the relationships between the PDO and atmospheric circulation systems, and the correlation coefficients were opposite to those of the GOODMME (not shown).

4.2. Variation of the Atmospheric Circulation Systems in Different Phases of the PDO

To study the changes of the atmospheric circulation during different phases of the PDO, the PDO phases were divided into two positive phases (1922–1945 and 1975–2002) and two negative phases (1906–1921 and 1946–1974) based on previous research [39,40]. Figure 8 shows that in the positive (negative) phase of the PDO, the CWT is higher (lower). The Siberian high dominates the East Asian region during winter [41]. Figure 9a,b exhibits the winter mean anomalies of the SLP during two PDO phases. The SLP anomalies during the positive phase were opposite to those during the negative phase. During the positive phase of the PDO, negative anomalies occurred over the East Asia and Pacific region to the north of 30° N, and positive anomalies occurred over the region to the south of 30° N. These findings suggested that when the PDO is in a positive (negative) phase, the SLP decreases (increases) in the mid-high latitudes of East Asia and the North Pacific and increases (decreases) in the tropical Pacific. Negative (positive) SLP anomalies (40°–70° N, 55°–140° E) will weaken (enhance) the strength of the Siberian high, producing a reduction (enhancement) of the EAWM strength, which will lead to a higher (lower) CWT [14]. Figure 9c,d depicts the 500 hPa geopotential height mean anomalies during different PDO phases over winter. The 500 hPa geopotential height anomalies in the region (20°–50° N, 125°–150° E) were positive during the positive phase of the PDO, which means that the East Asian trough will be relatively weak, and vice versa. The East Asian trough is a key factor related to the EAWM. The surface temperature in the East Asian region decreases due to the strong cold advection caused by strong northwesterlies, which are associated with the strength of the East Asian trough [42]. Figure 9e,f displays the 200 hPa zonal wind winter mean anomalies during different phases. During the positive phase of the PDO, the 200 hPa zonal wind anomalies have two positive regions (15°–30° N, 90°–140° E and 50°–70° N,90°–140° E) and one negative region (30°–50° N,90°–140° E) in East Asia (red box), and the same structures are observed in the negative phase but with the opposite sign. Li et al. (2010) [43] showed that the 200 hPa zonal wind over East Asia has three bands related to the EAWM, suggesting that when the 200 hPa zonal wind at 25°–40° N, 90°–170° E strengthens (weakens) and the zonal winds on both of its sides (10° S–15° N, 90°–170° E; 45°–60° N, 60°–180° E) weaken (strengthen), the surface northerly wind over East Asia becomes stronger (weaker), and the EAWM strengthens (weakens). In the positive PDO phase, upper level zonal winds are relatively weak in the midlatitudes of East Asia, leading to a weaker meridional temperature gradient, which is unfavorable for southward cold air invasion from high latitudes [42,44,45].

5. Conclusions and Discussion

The PDO plays a vital role in climate change, but the PDO index is arbitrarily based on the outputs of the CMIP5 models. To assess the capacity of the CMIP5 models to simulate the PDO, 35 models were collected for comparison with the observations. The spatial correlation coefficient was calculated to confirm the relationship between the PDO and CWT. According to this correlation, 13 models were used and averaged to produce the GOODMME. Finally, the possible mechanisms underlying the effects of different PDO phases on the CWT were researched. The results are as follows.
  • The HadISST and CMIP5 SST biases show that the wintertime average SST deviation is −4–4°C. Most models overestimate SSTs by 2–4 °C in the region north of 40° N and underestimate SSTs by 1–3 °C in the region of 40° N. Several CMIP5 models have a good effect in simulating the average SST over the northern Pacific region.
  • Zhang et al.’s [33] method was adopted to calculate the PDO index. The PDO time series of most models were irregular, but some models could reproduce the observed PDO phase. This indicates that the simulated annual average SST is good; however, the simulation of the SST change trends should be improved.
  • The CMIP5 models individually failed to represent the observed positive PDO-CWT relationship. To further study the capacities of the CMIP5 models for simulating the PDO-CWT teleconnection, the MME was considered. The 35 models were divided into two groups by calculating the spatial correlation coefficient. The 13 good models include ACCESS1.3, BCC-CSM1.1, CNRM-CM5, GFDL-ESM2G, GFDL-ESM2M, GISS-E2-H-CC, GISS-E2-H, HadCM3, HadGEM2-AO, INMCM4.0, MPI-ESM-LR, NorESM1-M and NorESM1-ME. The remaining models are defined as poor models. The PDO-CWT correlation spatial pattern for the GOODMME shows a positive correlation over most parts of China, which is consistent with the observational results. This result is better than the results of the individual models and the MME of all models.
  • The relationship between the observed PDO and atmospheric circulation shows that the PDO index is negatively correlated with the intensity of the Siberian high and positively correlated with the intensity of the Aleutian high. The correlation coefficient between the 500 hPa geopotential height and the PDO shows that negative correlation centers occurred in the North Pacific and eastern China, while positive correlation centers occurred in North America and the Okhotsk Sea. The PDO and 200 hPa zonal wind speed are positively correlated in southern China and negatively correlated in northern China and Japan. The results of the GOODMME were similar to the observations. The variation of the atmospheric circulation during different phases of the PDO shows that when the PDO is in the positive (negative) phase, the Siberian high weakens (strengthens), the East Asian trough weakens (strengthens), and the upper level zonal winds weaken (strengthen) over northern China and Japan. These changes will lead to a warmer (cooler) winter in China.
Previous studies have also shown that the Siberian high is associated with the upper level zonal winds in the midlatitudes of East Asia [42] and that the 200 hPa zonal winds in the northern China and Japan regions are positively correlated with the EAWM strength indices [45]. The PDO affects the CWT by influencing the atmospheric circulation. The results indicate that the GOODMME can also satisfactorily reproduce the relationship between the PDO and Siberian high and between the East Asian trough and upper level zonal winds, which are the main EAWM members. However, the POORMME failed to represent the PDO-CWT connection and PDO-atmospheric circulation relationship. Our findings suggest that by contrasting the spatial correlation coefficients between the PDO and CWT, sorting the CMIP5 models can aid in improving the capacity of simulating the PDO-CWT teleconnection. Because China’s topography is complicated, sorting the good models from the CMIP5 model is more effective than the method used by Joshi et al. [22]. By calculating the spatial correlation coefficient, the capacity for simulating the PDO-CWT relationship of ensemble models is significantly improved. However, uncertainties in the simulation output still exist [46,47]. We hope to find a better way to skillfully use this critical tool that will aid scholars in predicting winter temperatures over China. Moreover, the results are greatly affected by the data quality and PDO phase separation, and the data for the first half of the 20th century may contain certain errors. Research on interdecadal oscillation needs the support of accurate data collected over longer time periods.

Author Contributions

Conceptualization, Y.X.; Data curation, T.L.; Funding acquisition, S.S.; Project administration, S.S.; Supervision, Z.H.; Validation, Z.H.; Writing—original draft, Y.X.

Funding

This research was funded by China Special Fund for Meteorological Research in the Public Interest, grant number GYHY201506001 and the APC was funded by GYHY201506001.

Acknowledgments

Our cordial gratitude should be extended to the editor for his generous encouragement and great kindness for providing us an opportunity to improve the quality of this manuscript. We cordially thank anonymous reviewers for their professional comments and suggestions, which are greatly helpful for improvement of the quality of this manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Trenberth, K.E. Recent observed interdecadal climate changes in the Northern Hemisphere. Bull. Am. Meteorol. Soc. 1990, 71, 988–993. [Google Scholar] [CrossRef]
  2. Trenberth, K.E.; Hurrell, J.W. Decadal atmosphere-ocean variations in the Pacific. Clim. Dyn. 1994, 9, 303–319. [Google Scholar] [CrossRef]
  3. Deser, C.; Blackmon, M.L. On the relationship between tropical and North Pacific sea surface temperature variations. J. Clim. 1995, 8, 1677–1680. [Google Scholar] [CrossRef]
  4. Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1079. [Google Scholar] [CrossRef]
  5. Alexander, M.A.; Bladé, I.; Newman, M.; Lanzante, J.R.; Lau, N.; Scott, J.D. The atmospheric bridge: The influence of ENSO teleconnections on air–sea interaction over the global oceans. J. Clim. 2002, 15, 2205–2231. [Google Scholar] [CrossRef]
  6. Cai, W.; Van Rensch, P.; Borlace, S.; Cowan, T. Does the Southern Annular Mode contribute to the persistence of the multidecade-long drought over southwest Western Australia? Geophys. Res. Lett. 2011, 38, L144712. [Google Scholar] [CrossRef]
  7. Zhou, T.; Chen, X.; Dong, L.; Wu, B.; Man, W.; Zhang, L.; Lin, R.; Yao, J.; Song, F.; Zhao, C. Chinese contribution to CMIP5: An overview of five Chinese models’ performances. J. Meteorol. Res. 2014, 28, 481–509. [Google Scholar] [CrossRef]
  8. Maloney, E.D.; Camargo, S.J.; Chang, E.; Colle, B.; Fu, R.; Geil, K.L.; Hu, Q. North American climate in CMIP5 experiments: Part III: Assessment of twenty-first-century projections. J. Clim. 2014, 27, 2230–2270. [Google Scholar] [CrossRef]
  9. Yun, J.; Ha, K.J.; Jo, Y.H. Interdecadal changes in winter surface air temperature over East Asia and their possible causes. Clim. Dyn. 2018, 51, 1375–1390. [Google Scholar] [CrossRef]
  10. Zhao, S.; Deng, Y.; Black, R.X. Observed and Simulated Spring and Summer Dryness in the United States: The Impact of the Pacific Sea Surface Temperature and Beyond. J. Geophys. Res. Atmos. 2017, 122, 712–731. [Google Scholar] [CrossRef]
  11. Sun, C.; Li, J.; Feng, J.; Xie, F. A decadal-scale teleconnection between the North Atlantic Oscillation and subtropical eastern Australian rainfall. J. Clim. 2015, 28, 1074–1092. [Google Scholar] [CrossRef]
  12. Kim, J.W.; An, S.I.; Jun, S.Y.; Park, H.J.; Yeh, S.W. ENSO and East Asian winter monsoon relationship modulation associated with the anomalous northwest Pacific anticyclone. Clim. Dyn. 2017, 49, 1157–1179. [Google Scholar] [CrossRef]
  13. Ye, T.; Shen, Q.; Wang, K.; Zhang, Z.; Zhao, J. Interdecadal change of the northward jump time of the western Pacific subtropical high in association with the Pacific decadal oscillation. J. Meteorol. Res. 2015, 29, 59–71. [Google Scholar] [CrossRef]
  14. Ding, Y.; Liu, Y.; Liang, S.; Ma, X.; Zhang, Y.; Si, D.; Liang, P.; Song, Y.; Zhang, J. Interdecadal variability of the East Asian winter monsoon and its possible links to global climate change. J. Meteorol. Res. 2014, 28, 693–713. [Google Scholar] [CrossRef]
  15. Kenyon, J.; Hegerl, G.C. Influence of modes of climate variability on global temperature extremes. J. Clim. 2008, 21, 3872–3889. [Google Scholar] [CrossRef]
  16. Qin, M.; Li, D.; Dai, A.; Hua, W.; Ma, H. The influence of the Pacific Decadal Oscillation on North Central China precipitation during boreal autumn. Int. J. Climatol. 2018, 38, e821–e831. [Google Scholar] [CrossRef]
  17. Sperber, K.R.; Annamalai, H.; Kang, I.S.; Kitoh, A.; Moise, A.; Turner, A.; Wang, B.; Zhou, T. The Asian summer monsoon: An intercomparison of CMIP5 vs. CMIP3 simulations of the late 20th century. Clim. Dyn. 2013, 41, 2711–2744. [Google Scholar] [CrossRef]
  18. Wei, K.; Bao, Q. Projections of the East Asian winter monsoon under the IPCC AR5 scenarios using a coupled model: IAP_FGOALS. Adv. Atmos. Sci. 2012, 29, 1200–1214. [Google Scholar] [CrossRef]
  19. Roy, I. Indian Summer Monsoon and El Niño Southern Oscillation in CMIP5 Models: A Few Areas of Agreement and Disagreement. Atmosphere 2017, 8, 154. [Google Scholar] [CrossRef]
  20. Zhang, L.; Wu, P.; Zhou, T. Aerosol forcing of extreme summer drought over North China. Environ. Res. Lett. 2017, 12, 034020. [Google Scholar] [CrossRef]
  21. Newman, M.; Alexander, A.; Ault, R.; Cobb, K.; Deser, C.; Lorenzo, E.; Mantua, N.; Miller, A.; Minobe, S.; Nakamura, H.; et al. The Pacific Decadal Oscillation, Revisited. J. Clim. 2016, 29, 4399–4427. [Google Scholar] [CrossRef] [Green Version]
  22. Joshi, M.K.; Kucharski, F. Impact of Interdecadal Pacific Oscillation on Indian summer monsoon rainfall: An assessment from CMIP5 climate models. Clim. Dyn. 2017, 48, 2375–2391. [Google Scholar] [CrossRef]
  23. Fuentes-Franco, R.; Giorgi, F.; Coppola, E.; Kucharski, F. The role of ENSO and PDO in variability of winter precipitation over North America from twenty first century CMIP5 projections. Clim. Dyn. 2016, 46, 3259–3277. [Google Scholar] [CrossRef]
  24. Yasunaka, S.; Hanawa, K. Intercomparison of historical sea surface temperature datasets. Int. J. Climatol. 2011, 31, 1056–1073. [Google Scholar] [CrossRef]
  25. Lawrence Livermore National Laboratory Earth System Grid Federation Web Site. Available online: https://esgf-node.llnl.gov/projects/esgf-llnl/ (accessed on 29 September 2019).
  26. Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
  27. Hadley Centre Sea Ice and Sea Surface Temperature data set. Available online: https://www.metoffice.gov.uk/hadobs/hadisst/ (accessed on 29 September 2019).
  28. Rayner, N.A.; Parker, D.E.; Horton, E.B.; Folland, C.K.; Alexander, L.V.; Rowel, D.P.; Kent, E.C.; Kaplan, A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
  29. Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations-the CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
  30. Kanamitsu, M.; Alpert, J.C.; Campana, K.A.; Caplan, P.M.; Deaven, D.G.; Iredell, M.; Katz, B.; Pan, H.L.; Sela, J.; White, G.H. Recent changes implemented into the global forecast system at NMC. Weather Forecast. 1991, 6, 425–435. [Google Scholar] [CrossRef]
  31. Saha, S.; Nadiga, S.; Thiaw, C.; Wang, J.; Wang, W.; Zhang, Q.; Van den Dool, H.M.; Pan, H.L.; Moorthi, S.; Behringer, D.; et al. The NCEP climate forecast system. J. Clim. 2006, 19, 3483–3517. [Google Scholar] [CrossRef]
  32. Twentieth Century Reanalysis (V2) data. Available online: https://www.esrl.noaa.gov/psd/data/gridded/data.20thC_ReanV2.html (accessed on 29 September 2019).
  33. Zhang, Y.; Wallace, J.M.; Battisti, D.S. ENSO-like interdecadal variability: 1900–93. J. Clim. 1997, 10, 1004–1020. [Google Scholar] [CrossRef]
  34. Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
  35. Rider, P.R. On the distribution of the correlation coefficient in small samples. Biometrika 1932, 24, 382–403. [Google Scholar] [CrossRef]
  36. Yim, B.Y.; Kwon, M.H.; Min, H.S.; Kug, J.S. Pacific decadal oscillation and its relation to the extratropical atmospheric variation in CMIP5. Clim. Dyn. 2015, 44, 1521–1540. [Google Scholar] [CrossRef]
  37. Chen, X.; Wallace, M. Orthogonal PDO and ENSO indices. J. Clim. 2016, 29, 3883–3892. [Google Scholar] [CrossRef]
  38. Wallace, J.M.; Gutzler, D.S. Teleconnections in the geopotential height field during the Northern Hemisphere winter. Mon. Weather Rev. 1981, 109, 784–812. [Google Scholar] [CrossRef]
  39. Mantua, N.J.; Hare, S.R. The Pacific decadal oscillation. J. Oceanogr. 2002, 58, 35–44. [Google Scholar] [CrossRef]
  40. Qian, C.; Zhou, T. Multidecadal variability of North China aridity and its relationship to PDO during 1900–2010. J. Clim. 2014, 27, 1210–1222. [Google Scholar] [CrossRef]
  41. Ding, Y.; Krishnamurti, T.N. Heat budget of the Siberian high and the winter monsoon. Mon. Weather Rev. 1987, 115, 2428–2449. [Google Scholar] [CrossRef]
  42. Jhun, J.G.; Lee, E.J. A new East Asian winter monsoon index and associated characteristics of the winter monsoon. J. Clim. 2004, 17, 711–726. [Google Scholar] [CrossRef]
  43. Li, Y.; Yang, S. A dynamical index for the East Asian winter monsoon. J. Clim. 2010, 23, 4255–4262. [Google Scholar] [CrossRef]
  44. Zhu, Y. An index of East Asian winter monsoon applied to the description of China’s mainland winter temperature changes. J. Meteorol. Res. 2008, 22, 522–529. [Google Scholar]
  45. Wang, L.; Chen, W. How well do existing indices measure the strength of the East Asian winter monsoon? Adv. Atmos. Sci. 2010, 27, 855–870. [Google Scholar] [CrossRef]
  46. Chen, H.P. Projected change in extreme rainfall events in China by the end of the 21st century using CMIP5 models. Chin. Sci. Bull. 2013, 58, 1462–1472. [Google Scholar] [CrossRef] [Green Version]
  47. Yao, Y.; Luo, Y.; Huang, J.; Zhao, Z. Comparison of monthly temperature extremes simulated by CMIP3 and CMIP5 models. J. Clim. 2013, 26, 7692–7707. [Google Scholar] [CrossRef]
Atmosphere 10 00597 g001 550
Figure 1. Biases (°C) of the observed and simulated average sea surface temperatures (SSTs), including those produced by the MME (computed by averaging across all models) from 1901 to 2005 during winter (the model name is at the top of each figure, and the subsequent figures are labeled in the same way).
Figure 1. Biases (°C) of the observed and simulated average sea surface temperatures (SSTs), including those produced by the MME (computed by averaging across all models) from 1901 to 2005 during winter (the model name is at the top of each figure, and the subsequent figures are labeled in the same way).
Atmosphere 10 00597 g001
Atmosphere 10 00597 g002 550
Figure 2. Taylor diagram of the 1901–2005 monthly SSTA means simulated in 35 CMIP5 models over the northern Pacific region (20° N–70° N, 130° E–90° W). The reference data are HadISST data.
Figure 2. Taylor diagram of the 1901–2005 monthly SSTA means simulated in 35 CMIP5 models over the northern Pacific region (20° N–70° N, 130° E–90° W). The reference data are HadISST data.
Atmosphere 10 00597 g002
Atmosphere 10 00597 g003 550
Figure 3. PC1 time series in the observations and 35 model SSTAs, including those from the MME, for the period 1901–2005. The green line indicates a 6-year moving-average filter in the observation PC1 time series; the black line indicates a 6-year moving-average filter in the model PC1 time series; red shading indicates the positive phase; blue shading indicates the negative phase; and R represents the correlation coefficients of the simulation and observation.
Figure 3. PC1 time series in the observations and 35 model SSTAs, including those from the MME, for the period 1901–2005. The green line indicates a 6-year moving-average filter in the observation PC1 time series; the black line indicates a 6-year moving-average filter in the model PC1 time series; red shading indicates the positive phase; blue shading indicates the negative phase; and R represents the correlation coefficients of the simulation and observation.
Atmosphere 10 00597 g003
Atmosphere 10 00597 g004 550
Figure 4. Correlation map of the PDO with the moving filter and China winter temperature (CWT), including results from the MME for the winter period over 1901–2005. The black points indicate that the coefficient is statistically significant at the 90% level.
Figure 4. Correlation map of the PDO with the moving filter and China winter temperature (CWT), including results from the MME for the winter period over 1901–2005. The black points indicate that the coefficient is statistically significant at the 90% level.
Atmosphere 10 00597 g004
Atmosphere 10 00597 g005 550
Figure 5. Spatial correlation coefficients of the observation records and simulations over the historical period of 1901–2005 based on the correlation between the PDO and CWT.
Figure 5. Spatial correlation coefficients of the observation records and simulations over the historical period of 1901–2005 based on the correlation between the PDO and CWT.
Atmosphere 10 00597 g005
Atmosphere 10 00597 g006 550
Figure 6. Spatial correlation map of the PDO and CWT (same as in Figure 4). (a) GOODMME and (b) POORMME.
Figure 6. Spatial correlation map of the PDO and CWT (same as in Figure 4). (a) GOODMME and (b) POORMME.
Atmosphere 10 00597 g006
Atmosphere 10 00597 g007 550
Figure 7. Correlation maps of the monthly PDO and (a,b) the SLP, (c,d) the geopotential height at 500 hPa, and (e,f) the zonal wind at 200 hPa during winter over 1901–2005 (black points mean that the coefficient is statically significant at 90%; contours are the average values over 1901–2005; and the intervals are (a,b) 5 hPa, (c,d) 100 m, and (e,f) 10 m/s). (a), (c), and (e) correspond to HadISST and (b), (d), and (f) correspond to the GOODMME.
Figure 7. Correlation maps of the monthly PDO and (a,b) the SLP, (c,d) the geopotential height at 500 hPa, and (e,f) the zonal wind at 200 hPa during winter over 1901–2005 (black points mean that the coefficient is statically significant at 90%; contours are the average values over 1901–2005; and the intervals are (a,b) 5 hPa, (c,d) 100 m, and (e,f) 10 m/s). (a), (c), and (e) correspond to HadISST and (b), (d), and (f) correspond to the GOODMME.
Atmosphere 10 00597 g007
Atmosphere 10 00597 g008 550
Figure 8. Six-year moving average annual normalized PDO index and CWT. The pink and blue shading represent the positive and negative phases of the PDO, respectively. Grey shading is not classified due to incomplete stages.
Figure 8. Six-year moving average annual normalized PDO index and CWT. The pink and blue shading represent the positive and negative phases of the PDO, respectively. Grey shading is not classified due to incomplete stages.
Atmosphere 10 00597 g008
Atmosphere 10 00597 g009 550
Figure 9. Composite winter mean anomalies of the (a,b) SLP, (c,d) geopotential height at 500 hPa and (e,f) 200 hPa zonal wind during different phases of the PDO (the contours and interval are same as in Figure 7).
Figure 9. Composite winter mean anomalies of the (a,b) SLP, (c,d) geopotential height at 500 hPa and (e,f) 200 hPa zonal wind during different phases of the PDO (the contours and interval are same as in Figure 7).
Atmosphere 10 00597 g009
Table
Table 1. List of the fifth Coupled Model Intercomparison Project (CMIP5) models.
Table 1. List of the fifth Coupled Model Intercomparison Project (CMIP5) models.
ModelInstitutionResolution
ACCESS1.0Commonwealth Scientific and Industrial Research Organization/Bureau of Meteorology Australia300 × 360
ACCESS1.3Commonwealth Scientific and Industrial Research Organization/Bureau of Meteorology Australia300 × 360
BCC-CSM1.1Beijing Climate Center China232 × 360
BCC-CSM1.1 (m)Beijing Climate Center China232 × 360
CCSM4National Center for Atmospheric Research USA320 × 384
CESM1(WACCM)National Center for Atmospheric Research USA320 × 384
CESM1(BGC)National Center for Atmospheric Research USA320 × 384
CESM1(CAM5)National Center for Atmospheric Research USA320 × 384
CMCC-CMCentro Euro-Mediterraneo sui Cambiamenti Climatici Italy149 × 182
CMCC-CMSCentro Euro-Mediterraneo sui Cambiamenti Climatici Italy149 × 182
CNRM-CM5Centre National de Recherches Météorologiques, Centre Européen de Recherche et de Formation Avancéeen Calcul Scientifique France292 × 362
CSIRO-Mk3.6.0Commonwealth Scientific and Industrial Research Organization/Queensland Climate Change Centre of Excellence Australia189 × 192
CanESM2Canadian Centre for Climate Modelling and Analysis Canada192 × 256
EC-EARTHEC-EARTH consortium published at Irish Centre for High-End Computing Netherlands/Ireland292 × 362
FGOALS-g2Institute of Atmospheric Physics, Chinese Academy of Sciences China196 × 360
FIO-ESMThe First Institute of Oceanography, SOA China320 × 384
GFDL-ESM2GGeophysical Fluid Dynamics Laboratory USA210 × 360
GFDL-ESM2MGeophysical Fluid Dynamics Laboratory USA200 × 360
GISS-E2-HNASA/GISS (Goddard Institute for Space Studies) USA90 × 144
GISS-E2-H-CCNASA/GISS (Goddard Institute for Space Studies) USA90 × 144
GISS-E2-RNASA/GISS (Goddard Institute for Space Studies) USA90 × 144
GISS-E2-R-CCNASA/GISS (Goddard Institute for Space Studies) USA90 × 144
HadCM3Met Office Hadley Centre UK144 × 288
HadGEM2-AONational Institute of Meteorological Research, Korea Meteorological Administration South Korea216 × 360
HadGEM2-ESMet Office Hadley Centre UK216 × 360
INMCM4.0Russian Academy of Sciences, Russian Academy of Sciences, Institute of Numerical Mathematics Russia340 × 360
IPSL-CM5A-LRInstitut Pierre Simon Laplace France 149 × 182
IPSL-CM5A-MRInstitut Pierre Simon Laplace France 149 × 182
IPSL-CM5B-LRInstitut Pierre Simon Laplace France 149 × 182
MIROC5Atmosphere and Ocean Research Institute (The University of Tokyo), National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology Japan220 × 256
MPI-ESM-LRMax Planck Institute for Meteorology Germany220 × 256
MPI-ESM-MRMax Planck Institute for Meteorology Germany404 × 802
MRICGCM3Meteorological Research Institute Japan368 × 360
NorESM1-MBjerknes Centre for Climate Research, Norwegian Meteorological Institute Norway320 × 384
NorESM1-MEBjerknes Centre for Climate Research, Norwegian Meteorological Institute Norway320 × 384

Share and Cite

MDPI and ACS Style

Xu, Y.; Li, T.; Shen, S.; Hu, Z. Assessment of CMIP5 Models Based on the Interdecadal Relationship between the PDO and Winter Temperature in China. Atmosphere 2019, 10, 597. https://doi.org/10.3390/atmos10100597

AMA Style

Xu Y, Li T, Shen S, Hu Z. Assessment of CMIP5 Models Based on the Interdecadal Relationship between the PDO and Winter Temperature in China. Atmosphere. 2019; 10(10):597. https://doi.org/10.3390/atmos10100597

Chicago/Turabian Style

Xu, Yifei, Te Li, Shuanghe Shen, and Zhenghua Hu. 2019. "Assessment of CMIP5 Models Based on the Interdecadal Relationship between the PDO and Winter Temperature in China" Atmosphere 10, no. 10: 597. https://doi.org/10.3390/atmos10100597

APA Style

Xu, Y., Li, T., Shen, S., & Hu, Z. (2019). Assessment of CMIP5 Models Based on the Interdecadal Relationship between the PDO and Winter Temperature in China. Atmosphere, 10(10), 597. https://doi.org/10.3390/atmos10100597

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop