Validation of the IPSL Venus GCM Thermal Structure with Venus Express Data
Abstract
:1. Introduction
2. Data and Model
2.1. Visible and Infrared Thermal Imaging Spectrometer (VIRTIS) and Venus Express Radio Science Experiment (VeRa)
2.2. The Institut Pierre Simon Laplace (IPSL) Venus General Circulation Model (GCM)
3. Results and Discussion
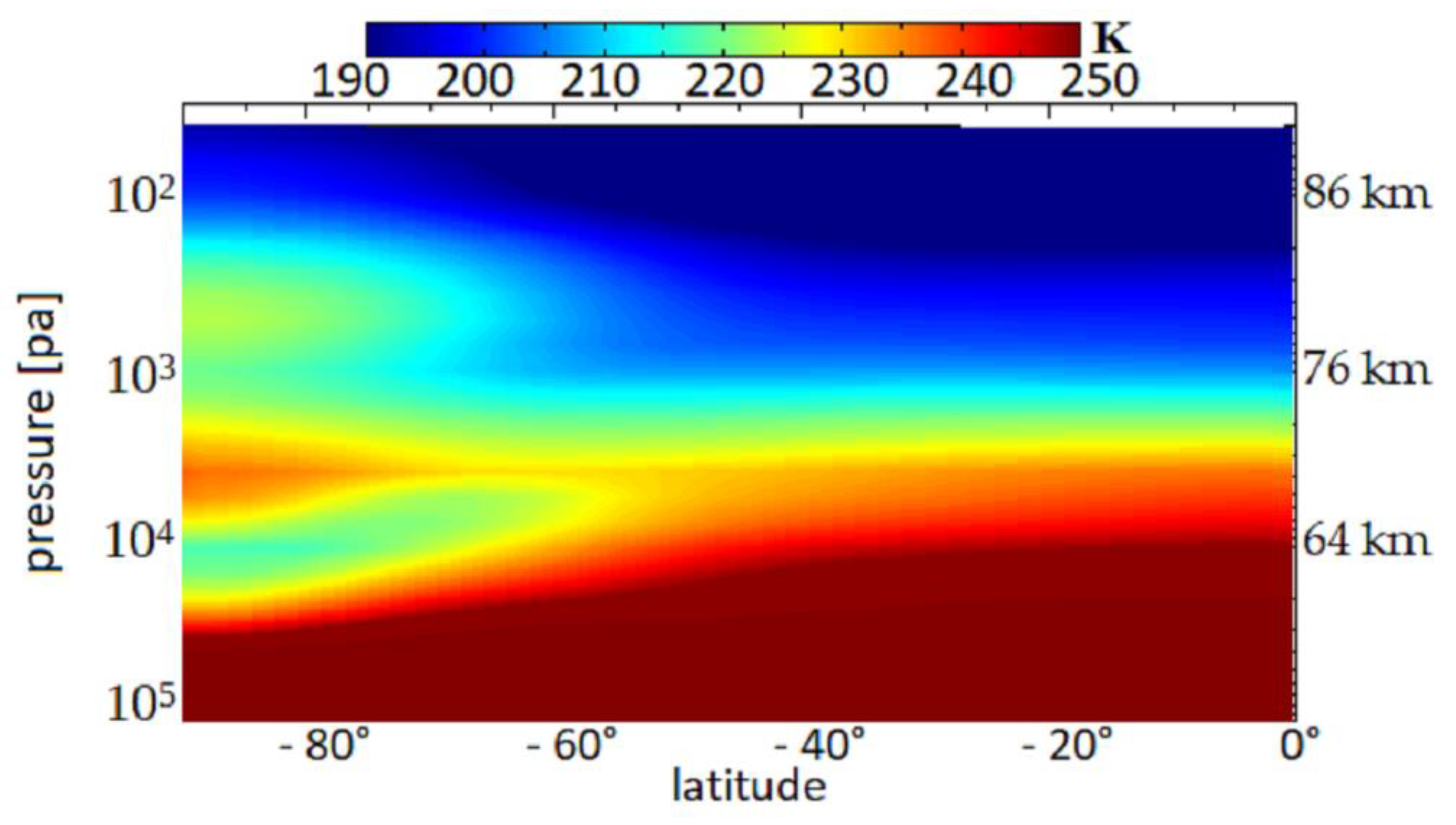
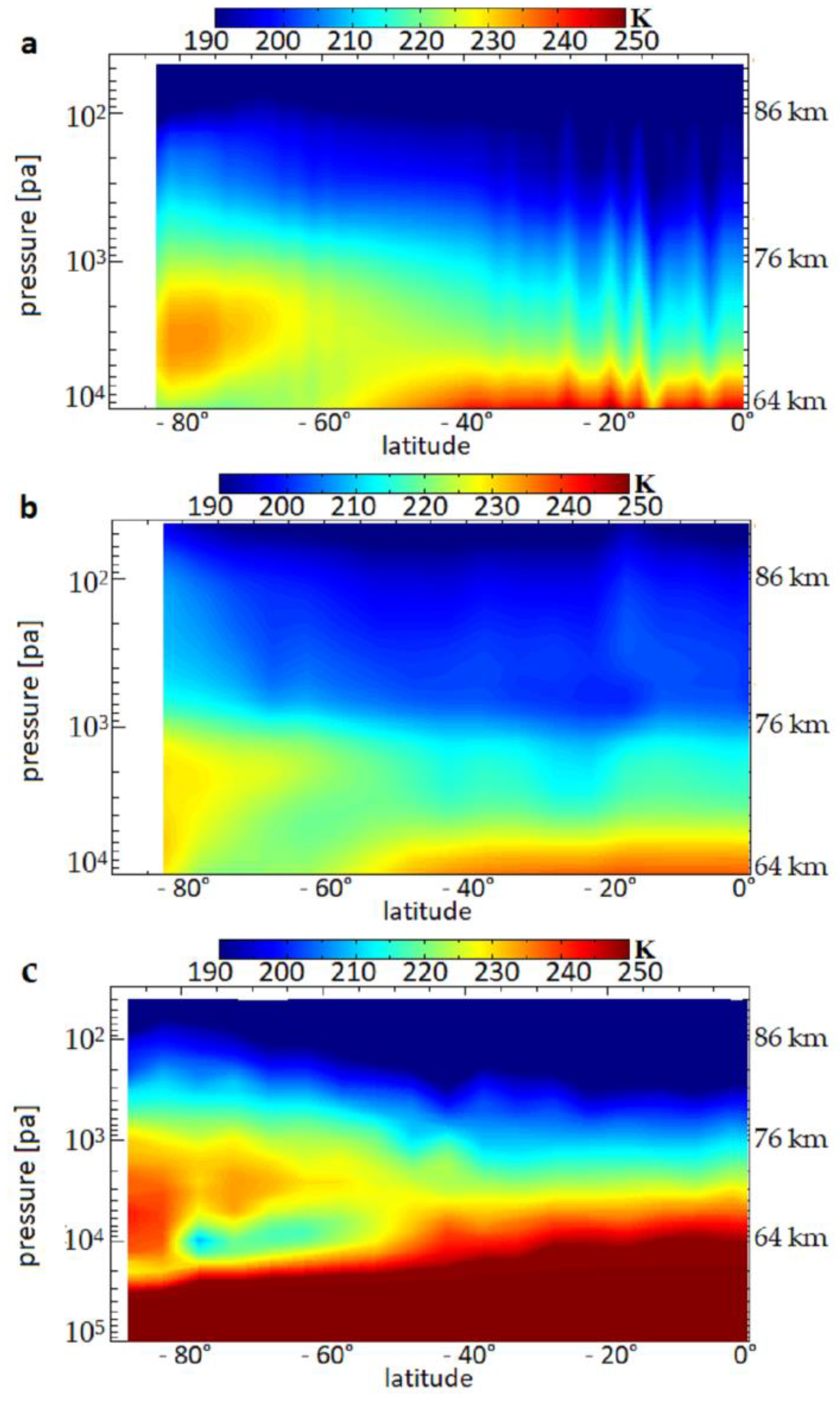
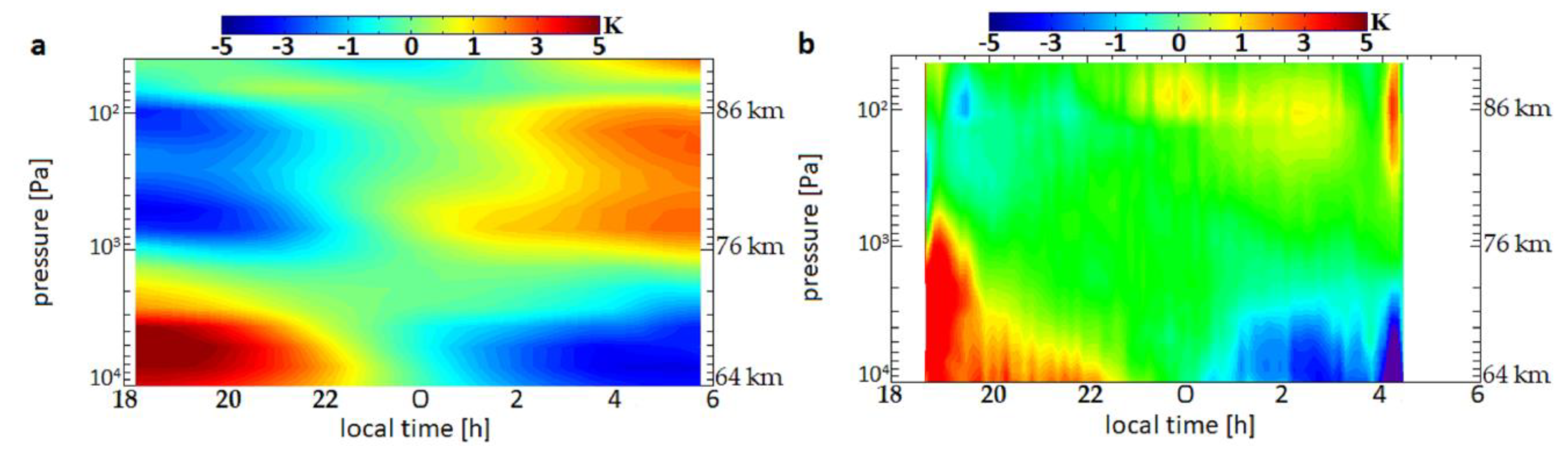
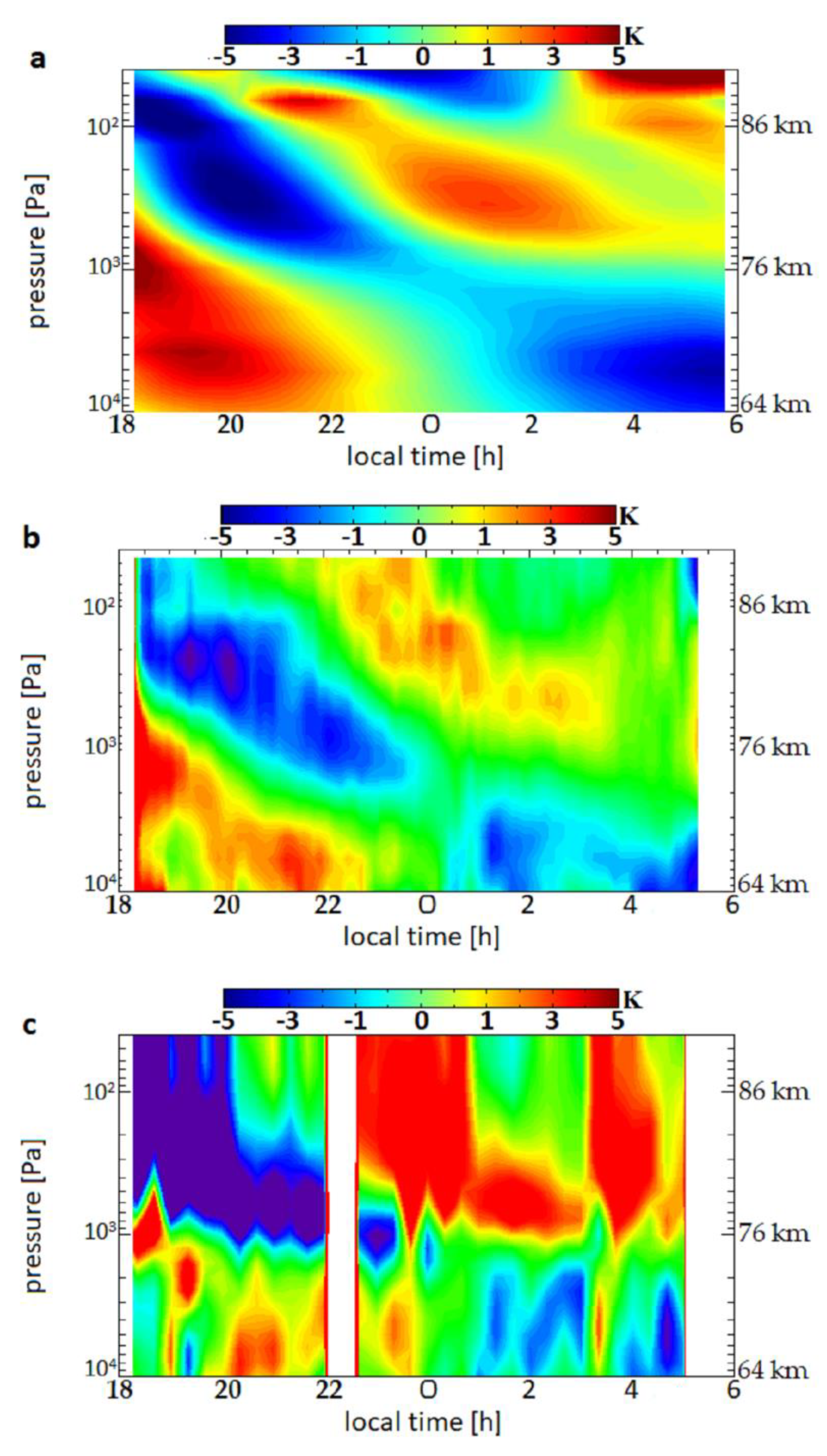
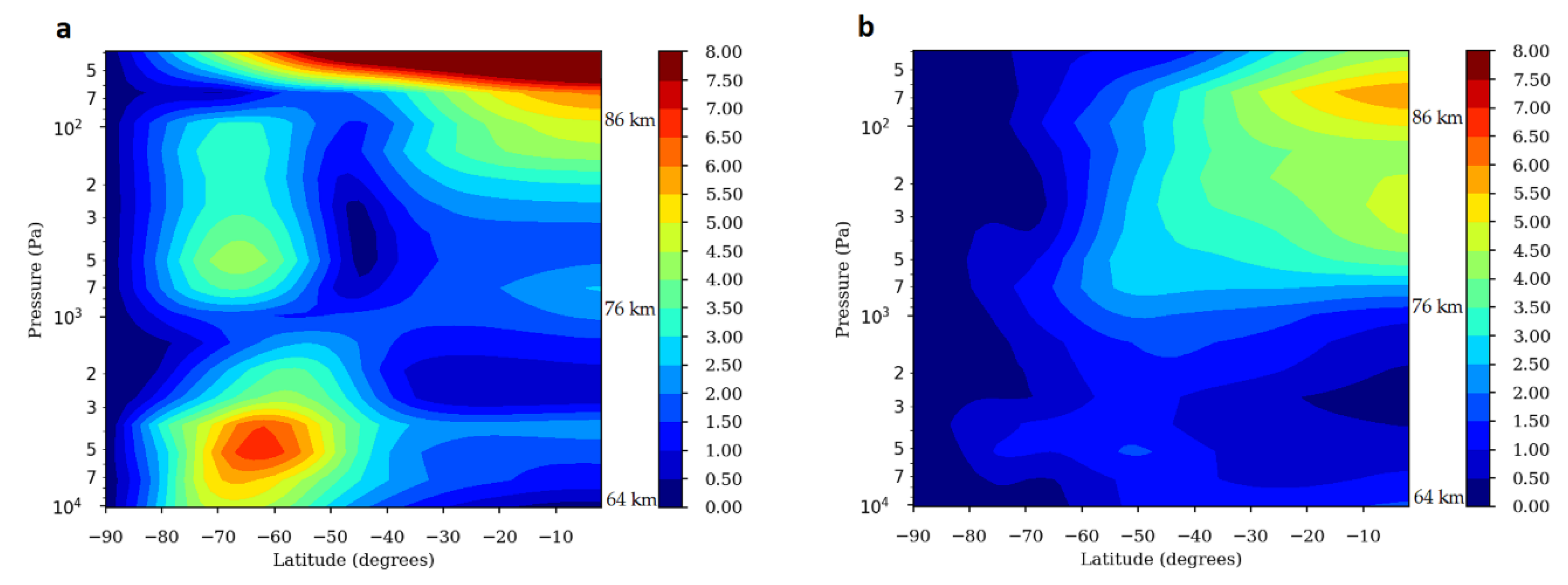
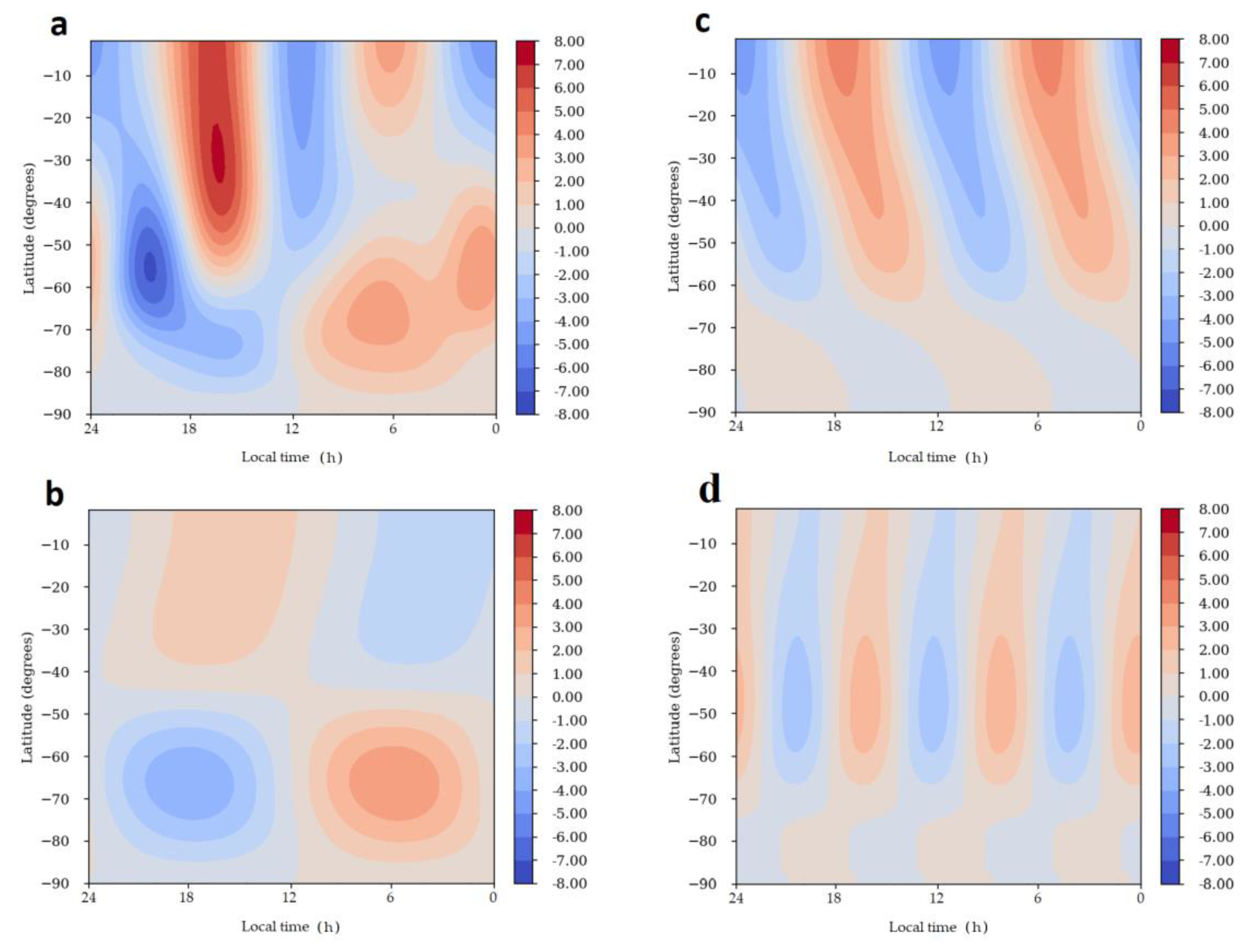
3.1. The Thermal Field
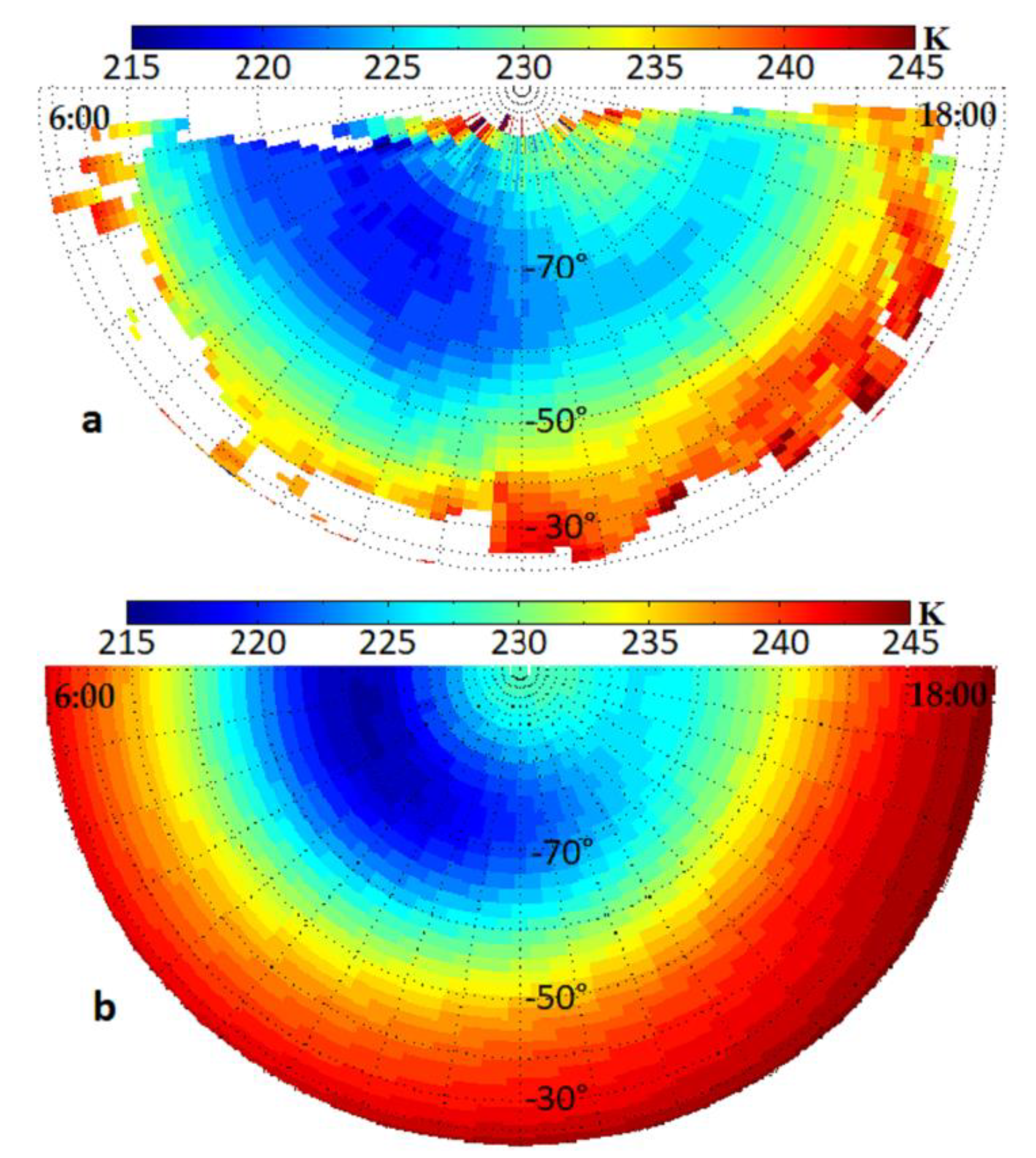
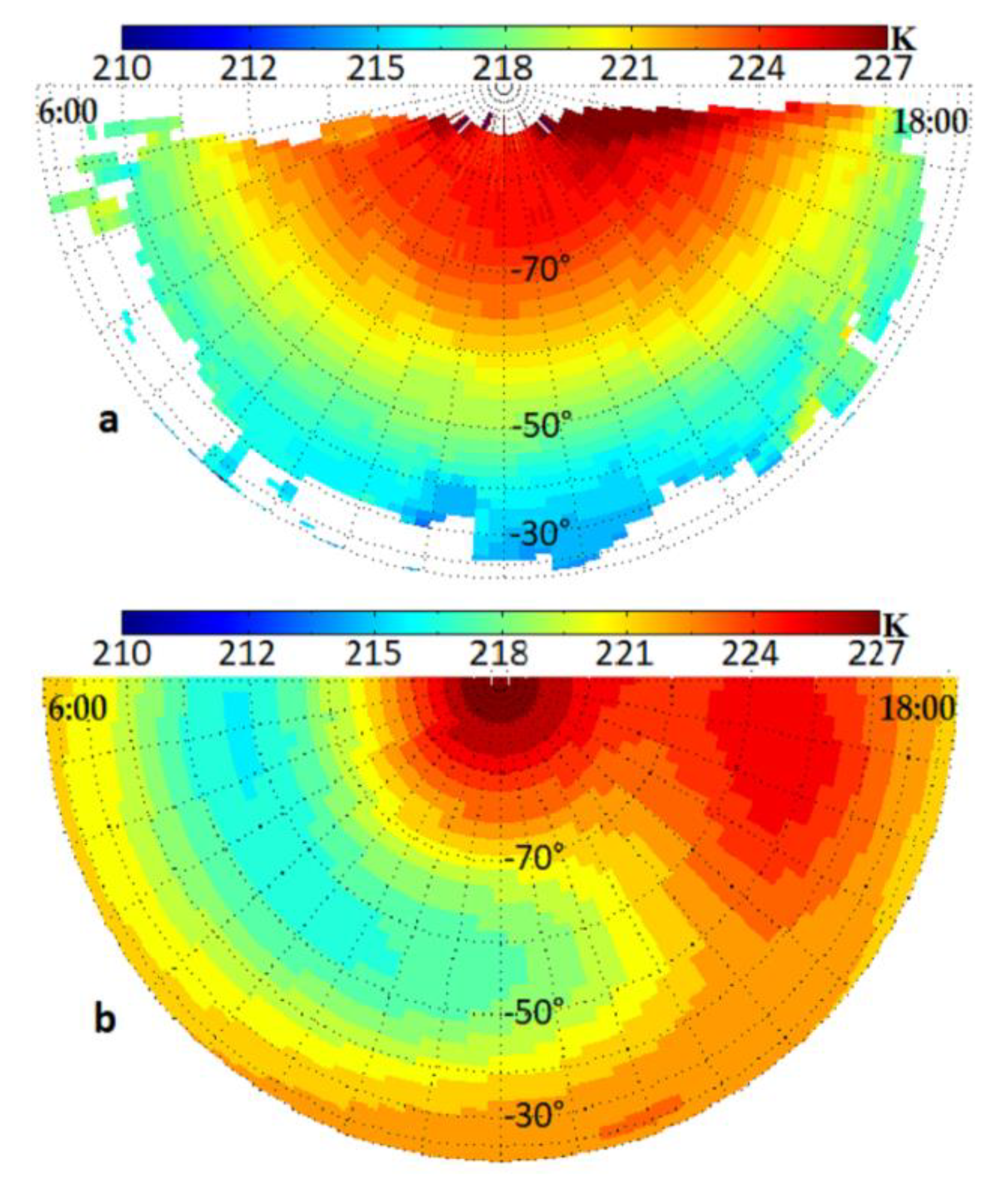
3.2. The Thermal Tides
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sonett, C.P. A Summary Review of the Scientific Findings of the Mariner Venus Mission. Space Sci. Rev. 1963, 2, 751–777. [Google Scholar] [CrossRef]
- Avduevskii, V.S.; Marov, M.I.; Kulikov, I.N.; Shari, V.P.; Gorbachevskii, A.I.; Uspenskii, G.R.; Cheremukhina, Z.P. Structure and Parameters of the Venus Atmosphere according to Venera Probe Data. In Venus; Hunten, D.M., Colin, L., Donahue, T.M., Moroz, V.I., Tucson, A.Z., Eds.; University of Arizona Press: Tucson, AZ, USA, 1983; pp. 280–298. [Google Scholar]
- Blamont, J.E. The VEGA Venus balloon experiment. Adv. Space Res. 1987, 7, 295–298. [Google Scholar] [CrossRef]
- Saunders, R.S.; Spear, A.J.; Allin, P.C.; Austin, R.S.; Berman, A.L.; Chandlee, R.C.; Clark, J.; deCharon, A.V.; De Jong, E.M.; Griffith, D.G.; et al. Magellan mission summary. J. Geophys. Res. 1992, 97, 13067–13090. [Google Scholar] [CrossRef]
- Svedhem, H.; Titov, D.V.; McCoy, D.; Lebreton, J.-P.; Barabash, S.; Bertaux, J.-L.; Drossart, P.; Formisano, V.; Häusler, B.; Korablev, O.; et al. Venus Express—The first European mission to Venus. Planet. Space Sci. 2007, 55, 1636–1652. [Google Scholar] [CrossRef]
- Nakamura, M.; Imamura, T.; Ishii, N.; Abe, T.; Satoh, T.; Suzuki, M.; Ueno, M.; Yamazaki, A.; Iwagami, N.; Watanabe, S.; et al. Overview of Venus orbiter, Akatsuki. Earth Planets Space 2011, 63, 443–457. [Google Scholar] [CrossRef] [Green Version]
- Read, P.L.; Lebonnois, S. Superrotation on Venus, on Titan, and Elsewhere. Annu. Rev. Earth Planet. Sci. 2018, 46, 175–202. [Google Scholar] [CrossRef]
- Yamamoto, M.; Takahashi, M. The Fully Developed Superrotation Simulated by a General Circulation Model of a Venus-like Atmosphere. J. Atmos. Sci. 2003, 60, 561–574. [Google Scholar] [CrossRef]
- Lee, C.; Lewis, S.R.; Read, P.L. Superrotation in a Venus general circulation model. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Sugimoto, N.; Takagi, M.; Matsuda, Y. Baroclinic instability in the Venus atmosphere simulated by GCM. J. Geophys. Res. Planets 2014, 11, 1950–1968. [Google Scholar] [CrossRef]
- Lebonnois, S.; Sugimoto, N.; Gilli, G. Wave analysis in the atmosphere of Venus below 100-km altitude, simulated by the LMD Venus GCM. Icarus 2016, 278, 38–51. [Google Scholar] [CrossRef] [Green Version]
- Takagi, M.; Matsuda, Y. Effects of thermal tides on the Venus atmospheric superrotation. J. Geophys. Res. 2007, 112, D09112. [Google Scholar] [CrossRef]
- Lebonnois, S.; Hourdin, F.; Eymet, V.; Crespin, A.; Fournier, R.; Forget, F. Superrotation of Venus’ atmosphere analyzed with a full general circulation model. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Sugimoto, N.; Takagi, M.; Matsuda, Y. Waves in a Venus general circulation model. Geophys. Res. Lett. 2014, 41, 7461–7467. [Google Scholar] [CrossRef]
- Piccioni, G.; Drossart, P.; Sanchez-Lavega, A.; Hueso, R.; Taylor, F.W.; Wilson, C.F.; Grassi, D.; Zasova, L.; Moriconi, M.; Adriani, A.; et al. South-polar features on Venus similar to those near the north pole. Nature 2007, 450, 637–640. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garate-Lopez, I.; Hueso, R.; Sánchez-Lavega, A.; Peralta, J.; Piccioni, G.; Drossart, P. A chaotic long-lived vortex at the southern pole of Venus. Nat. Geosci. 2013, 6, 254–257. [Google Scholar] [CrossRef]
- Luz, D.; Berry, D.L.; Piccioni, G.; Drossart, P.; Politi, R.; Wilson, C.F.; Erard, S.; Nuccilli, F. Venus’s Southern Polar Vortex Reveals Precessing Circulation. Science 2011, 332, 577–580. [Google Scholar] [CrossRef] [PubMed]
- Ando, H.; Sugimoto, N.; Takagi, M.; Kashimura, H.; Imamura, T.; Matsuda, Y. The puzzling Venusian polar atmospheric structure reproduced by a general circulation model. Nat. Commun. 2016, 7, 10398. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zasova, L.V.; Ignatiev, N.; Khatuntsev, I.; Linkin, V. Structure of the Venus atmosphere. Planet. Space Sci. 2007, 55, 1712–1728. [Google Scholar] [CrossRef]
- Tellmann, S.; Pätzold, M.; Häusler, B.; Bird, M.K.; Tyler, G.L. Structure of the Venus neutral atmosphere as observed by the Radio Science experiment VeRa on Venus Express. J. Geophys. Res. 2009, 114, E00B36. [Google Scholar] [CrossRef]
- Garate-Lopez, I.; Lebonnois, S. Latitudinal variation of clouds’ structure responsible for Venus’ cold collar. Icarus 2018, 314, 1–11. [Google Scholar] [CrossRef]
- Svedhem, H.; Titov, D.; Taylor, F.; Witasse, O. Venus Express mission. J. Geophys. Res. 2009, 114, E00B33. [Google Scholar] [CrossRef]
- Drossart, P.; Piccioni, G.; Adriani, A.; Angrilli, F.; Arnold, G.; Baines, K.H.; Bellucci, G.; Benkhoff, J.; Bézard, B.; Bibring, J.-P.; et al. Scientific goals for the observation of Venus by VIRTIS on ESA/Venus express mission. Planet. Space Sci. 2007, 55, 1653–1672. [Google Scholar] [CrossRef]
- Häusler, B.; Pätzold, M.; Tyler, G.L. Radio science investigations by VeRa onboard the Venus Express spacecraft. Planet. Space Sci. 2006, 54, 1315–1335. [Google Scholar] [CrossRef]
- Piccialli, A.; Montmessin, F.; Belyaev, D.; Mahieux, A.; Fedorova, A.; Marcq, E.; Bertaux, J.-L.; Tellmann, S.; Vandaele, A.C.; Korablev, O. Thermal structure of Venus nightside upper atmosphere measured by stellar occultations with SPICAV/Venus Express. Planet. Space Sci. 2015, 113, 321–335. [Google Scholar] [CrossRef]
- Grassi, D.; Politi, R.; Ignatiev, N.I.; Plainaki, C.; Lebonnois, S.; Wolkenberg, P.; Montabone, L.; Migliorini, A.; Piccioni, G.; Drossart, P. The Venus nighttime atmosphere as observed by the VIRTIS-M instrument. Average fields from the complete infrared data set. J. Geophys. Res. Planets 2014, 119, 837–849. [Google Scholar] [CrossRef]
- Migliorini, A.; Grassi, D.; Montabone, L.; Lebonnois, S.; Drossart, P.; Piccioni, G. Investigation of air temperature on the nightside of Venus derived from VIRTIS-H on board Venus-Express. Icarus 2012, 217, 640–647. [Google Scholar] [CrossRef]
- Pätzold, M.; Häusler, B.; Bird, M.K.; Tellmann, S.; Mattei, R.; Asmar, S.W.; Dehant, V.; Eidel, W.; Imamura, T.; Simpson, R.A.; et al. The structure of Venus’ middle atmosphere and ionosphere. Nature 2007, 450, 657–660. [Google Scholar] [CrossRef] [PubMed]
- Tellmann, S.; Häusler, B.; Pätzold, M.; Bird, M.; Tyler, G.L. The Structure of the Venus Neutral Atmosphere from the Radio Science Experiment VeRa on Venus Express. In Proceedings of the European Planetary Science Congress 2008, Münster, Germany, 21–25 September 2008; p. 44. [Google Scholar]
- Limaye, S.S.; Lebonnois, S.; Mahieux, A.; Pätzold, M.; Bougher, S.; Bruinsma, S.; Chamberlain, S.; Clancy, R.T.; Gérard, J.-C.; Gilli, G.; et al. The thermal structure of the Venus atmosphere: Intercomparison of Venus Express and ground based observations of vertical temperature and density profiles. Icarus 2017, 294, 124–155. [Google Scholar] [CrossRef]
- Hourdin, F.; Musat, I.; Bony, S.; Braconnot, P.; Codron, F.; Dufresne, J.-L.; Fairhead, L.; Filiberti, M.-A.; Friedlingstein, P.; Grandpeix, J.-Y.; et al. The LMDZ4 general circulation model: Climate performance and sensitivity to parametrized physics with emphasis on tropical convection. Clim. Dyn. 2006, 27, 787–813. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys. 1982, 20, 851–875. [Google Scholar] [CrossRef] [Green Version]
- Haus, R.; Kappel, D.; Arnold, G. Atmospheric thermal structure and cloud features in the southern hemisphere of Venus as retrieved from VIRTIS/VEX radiation measurements. Icarus 2014, 232, 232–248. [Google Scholar] [CrossRef] [Green Version]
- Haus, R.; Kappel, D.; Arnold, G. Lower atmosphere minor gas abundances as retrieved from Venus Express VIRTIS-M-IR data at 2.3 μm. Planet. Space Sci. 2015, 105, 159–174. [Google Scholar] [CrossRef]
- Eymet, V.; Fournier, R.; Dufresne, J.-L.; Lebonnois, S.; Hourdin, F.; Bullock, M.A. Net exchange parameterization of thermal infrared radiative transfer in Venus’ atmosphere. J. Geophys. Res. 2009, 11, E11008. [Google Scholar] [CrossRef]
- Lebonnois, S.; Eymet, V.; Lee, C.; Vatant d’Ollone, J. Analysis of the radiative budget of the Venusian atmosphere based on infrared Net Exchange Rate formalism. J. Geophys. Res. Planets 2015, 120, 1186–1200. [Google Scholar] [CrossRef] [Green Version]
- Seiff, A.; Schofield, J.T.; Kliore, A.J.; Taylor, F.W.; Limaye, S.S.; Revercomb, H.E.; Sromovsky, L.A.; Kerzhanovich, V.V.; Moroz, V.I.; Marov, M.Y. Models of the structure of the atmosphere of Venus from the surface to 100 kilometers altitude. Adv. Space Res. 1985, 5, 3–58. [Google Scholar] [CrossRef]
- Linkin, V.M.; Blamont, J.; Devyatkin, S.I.; Ignatova, S.P.; Kerzhanovich, V.V.; Lipatov, A.N.; Malique, C.; Stadnyk, B.I.; Sanotskij, Y.V.; Stolyarchuk, P.G.; et al. Thermal structure of the Venus atmosphere according to measurements with the Vega-2 lander. Kosm. Issled. 1987, 25, 659–672. [Google Scholar]
- Zasova, L.V.; Moroz, V.I.; Linkin, V.M.; Khatuntsev, I.V.; Maiorov, B.S. Structure of the Venusian atmosphere from surface up to 100 km. Cosm. Res. 2006, 44, 364–383. [Google Scholar] [CrossRef]
- Grassi, D.; Migliorini, A.; Montabone, L.; Lebonnois, S.; Cardesìn-Moinelo, A.; Piccioni, G.; Drossart, P.; Zasova, L.V.; et al. Thermal structure of Venusian nighttime mesosphere as observed by VIRTIS-Venus Express. J. Geophys. Res. 2010, 115, E09007. [Google Scholar] [CrossRef]
- Ando, H.; Imamura, T.; Sugimoto, N.; Takagi, M.; Kashimura, H.; Tellmann, S.; Pätzold, M.; Häusler, B.; Matsuda, Y. Vertical structure of the axi-asymmetric temperature disturbance in the Venusian polar atmosphere: Comparison between radio occultation measurements and GCM results. J. Geophys. Res. Planets 2017, 122, 1687–1703. [Google Scholar] [CrossRef]
- Ando, H.; Takagi, M.; Fukuhara, T.; Imamura, T.; Sugimoto, N.; Sagawa, H.; Noguchi, K.; Tellmann, S.; Pätzold, M.; Häusler, B.; et al. Local Time Dependence of the Thermal Structure in the Venusian Equatorial Upper Atmosphere: Comparison of Akatsuki Radio Occultation Measurements and GCM Results. J. Geophys. Res. Planets 2018, 123, 2270–2280. [Google Scholar] [CrossRef]
- Takagi, M.; Sugimoto, N.; Ando, H.; Matsuda, Y. Three-Dimensional Structures of Thermal Tides Simulated by a Venus GCM. J. Geophys. Res. Planets 2018, 123, 335–352. [Google Scholar] [CrossRef]
- Tomasko, M.G.; Doose, L.R.; Smith, P.H.; Odell, A.P. Measurements of the flux of sunlight in the atmosphere of Venus. J. Geophys. Res. 1980, 85, 8167–8186. [Google Scholar] [CrossRef]
- Crisp, D. Radiative forcing of the Venus mesosphere. I—Solar fluxes and heating rates. Icarus 1986, 76, 484–514. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scarica, P.; Garate-Lopez, I.; Lebonnois, S.; Piccioni, G.; Grassi, D.; Migliorini, A.; Tellmann, S. Validation of the IPSL Venus GCM Thermal Structure with Venus Express Data. Atmosphere 2019, 10, 584. https://doi.org/10.3390/atmos10100584
Scarica P, Garate-Lopez I, Lebonnois S, Piccioni G, Grassi D, Migliorini A, Tellmann S. Validation of the IPSL Venus GCM Thermal Structure with Venus Express Data. Atmosphere. 2019; 10(10):584. https://doi.org/10.3390/atmos10100584
Chicago/Turabian StyleScarica, Pietro, Itziar Garate-Lopez, Sebastien Lebonnois, Giuseppe Piccioni, Davide Grassi, Alessandra Migliorini, and Silvia Tellmann. 2019. "Validation of the IPSL Venus GCM Thermal Structure with Venus Express Data" Atmosphere 10, no. 10: 584. https://doi.org/10.3390/atmos10100584
APA StyleScarica, P., Garate-Lopez, I., Lebonnois, S., Piccioni, G., Grassi, D., Migliorini, A., & Tellmann, S. (2019). Validation of the IPSL Venus GCM Thermal Structure with Venus Express Data. Atmosphere, 10(10), 584. https://doi.org/10.3390/atmos10100584




