1. Introduction
Aging is a natural and undeniable process in the life of living organisms. This process is affected by various factors such as inheritance, environment, lifestyle and disease [
1]. The aging process alters the telomeres, gene expression and cellular structures in living organisms. By evaluating biomarkers, one can find out about the biological changes that occur in the body [
2]. Several biomarkers can be used for age predicton. One of the human age-related biomarkers is DNA methylation (DNAm), which is biologically and chemically more stable than biomarkers such as RNA messenger (mRNA) and proteins [
2], and among these biomarkers, it is also more correlated with age [
3].
DNAm, which often occurs in a CpG sequence, is an epigenetic sign and plays an important role in regulating cells to establish and maintain cellular identity. Various studies have shown that DNAm changes with age [
4,
5,
6,
7,
8]. This change in DNAm can be disclosed at specific CpG-sites in all individuals, although individual differences may affect the “speed” of this change [
6].
Various models for age prediction have been applied to DNAm data such as regression models including Linear regression [
9,
10], Multivariate linear regression [
2,
7], Multiple linear regression [
3,
11], or machine learning algorithms such as Support Vector Regression [
1], Random Forest Regression [
6], Artificial Neural Networks [
12,
13], and Gradient Boosting Regression [
4,
14]. In a vast majority of these studies, the mean absolute deviation (MAD) and the correlation between the actual value of age and DNAm (R
2) were reported to describe the model’s performance. Furthermore, most of these studies only used a simple statistical feature selection algorithm such as Pearson’s correlation to select age-related CpG-sites [
1,
4,
14]. In general, traditional feature selection algorithms are divided into three categories: filter, wrapper and embedded methods. Filter methods often use statistical functions, and therefore they are among the most rapid feature selection methods. Since these methods do not use a model to evaluate the selected features, they are not accurate enough, and additionally may select redundant features as they do not consider the interactions between features. As a consequence, many informative features may be ignored. For example, Naue et al. [
6] used the Mutual Information and Li et al. [
4] used the Pearson’s correlation to select a subset of features. In wrapper methods, in contrast to filter methods, a model is used to evaluate a subset of features, so as the data volume increases, the model accuracy and algorithm time complexity are both increase. For instance, Vidaki et al. [
12] used stepwise regression method to select 23 CpG-sites out of the 45 CpG-sites. The embedded methods combine the benefits of the two previous methods and select the subset of features during the modeling process with less computation time than wrapper methods. For example, Weidner et al. [
7] used an embedded methode, called Recursive Feature Elimination, in order to select five features to evaluate the multivariate linear regression model.
Nonetheless, a proper feature selection method should be used to select a subset of optimal features that are both informative alone and interact well with other selected features. Wrapper methods are a good choice regardless of their timing constraints. However, as the feature search space gets bigger, the runtime also increases by a wide margin. This is a serious problem in genomic data, where the number of features ranges from several tens to hundreds of thousands. There are several solutions for improving execution time of the complex wrapper methods for analyzing genomic data. In a series of studies, wrapper methods are used in combination with fast filter methodes [
15,
16,
17,
18]. In this approach, first, the dimensionality of the feature space is reduced from several thousand to several tens of features by taking advantage of a filter feature selection algorithm, and then a wrapper feature selection method is used to choose features from the remaining ones. However, in this way the previous problem still exists since many important features may be removed when reducing the data size from thousands to tens of features. Another set of studies used parallel computing to overcome the challenge of high execution time of feature selection methods. For example, Nieto et al. used the PSO algorithm in a parallel manner to select cancer-related genes in microarray data [
19]. In a similar work, Keco et al. used a type of parallel genetic algorithm to select features from microarray data for cancer classification task [
20], and Brahim et al. split the data into several partitions and executed feature selection algorithm on each partition independently. Finally, they combined the selected features from each partition and created their model [
21]. Islam et al. proposed a scalable parallel gene selection method using the Map Reduce programming model. They generated a predefined number of potential gene subsets of equal sizes, then calculated the classification accuracy of each subset using the KNN algorithm in parallel. Finally, they ranked features based on their existence in best gene subsets and select genes with highest rankings [
22].
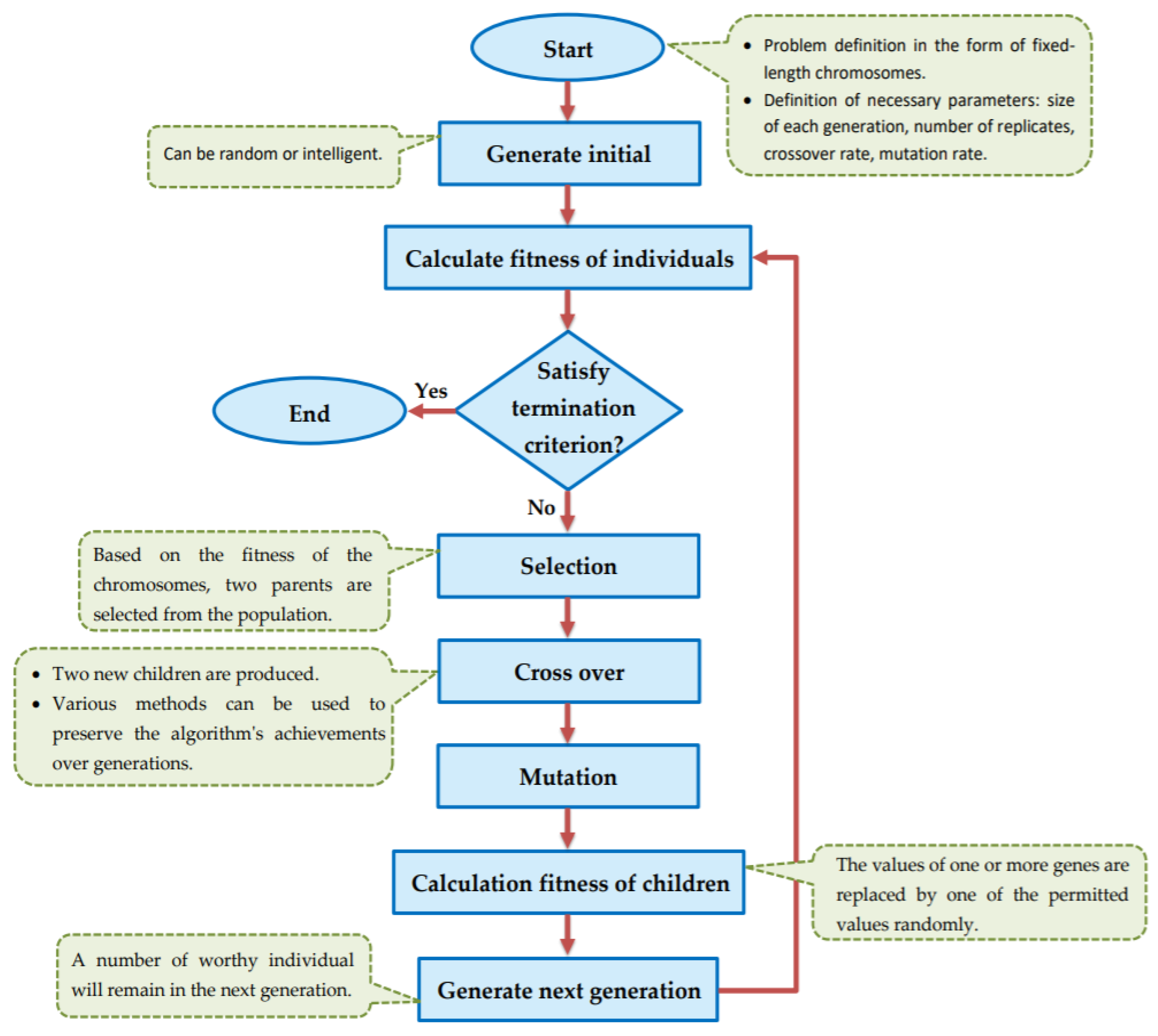
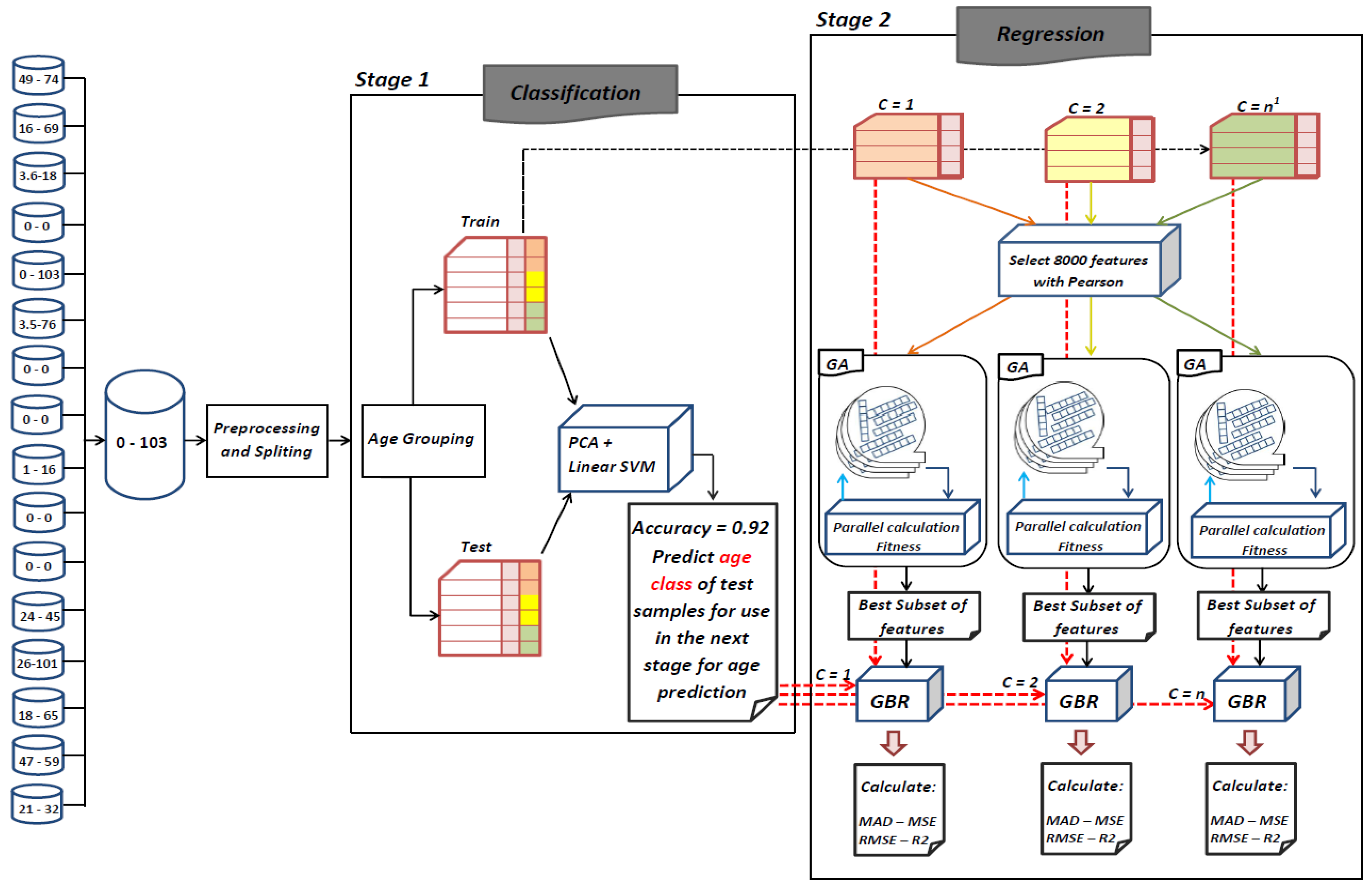
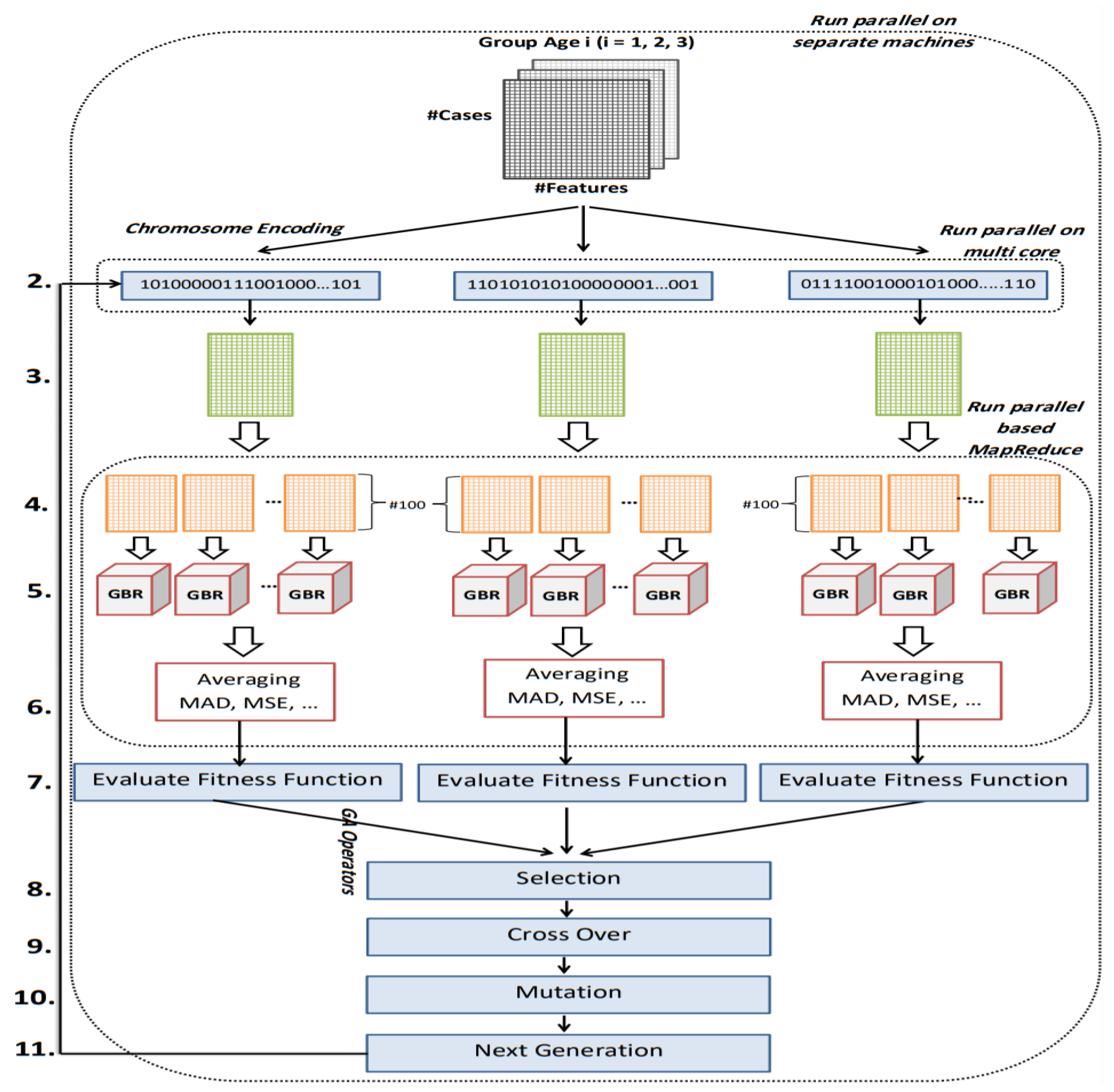
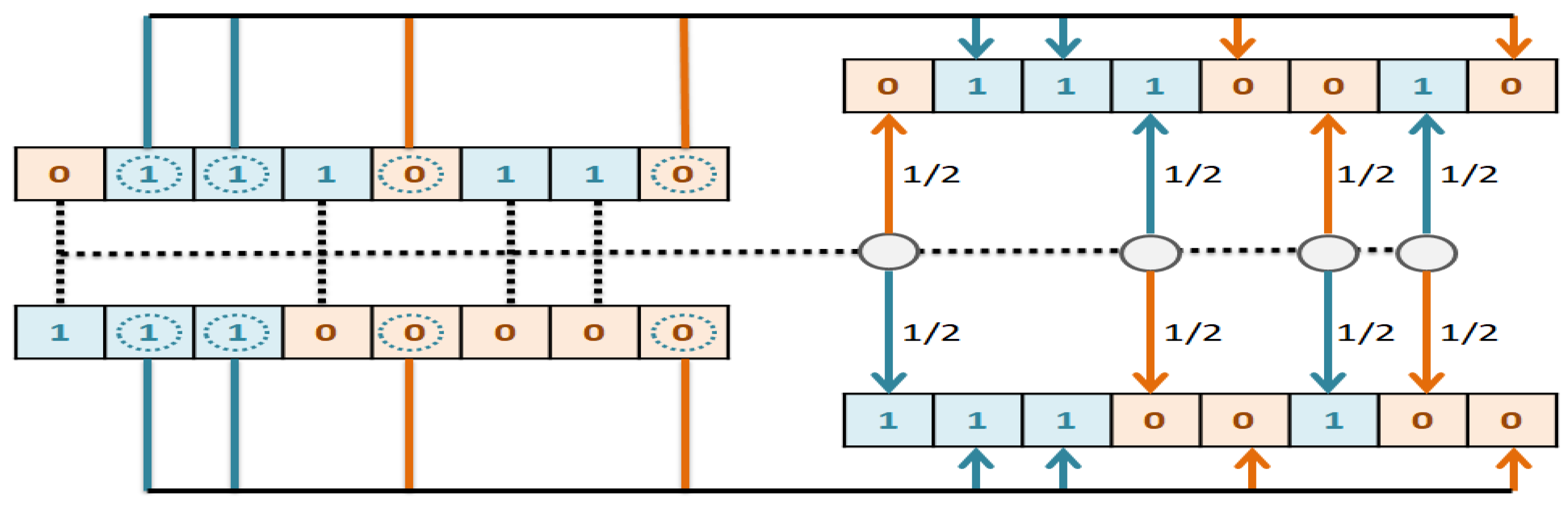
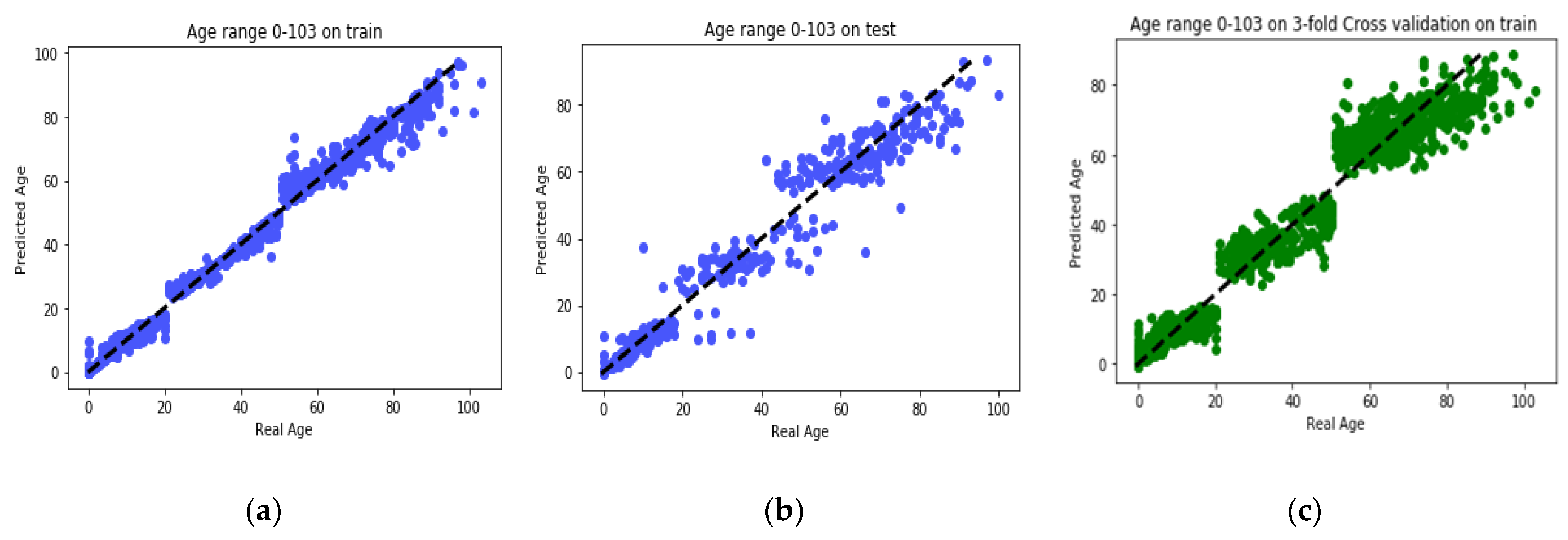
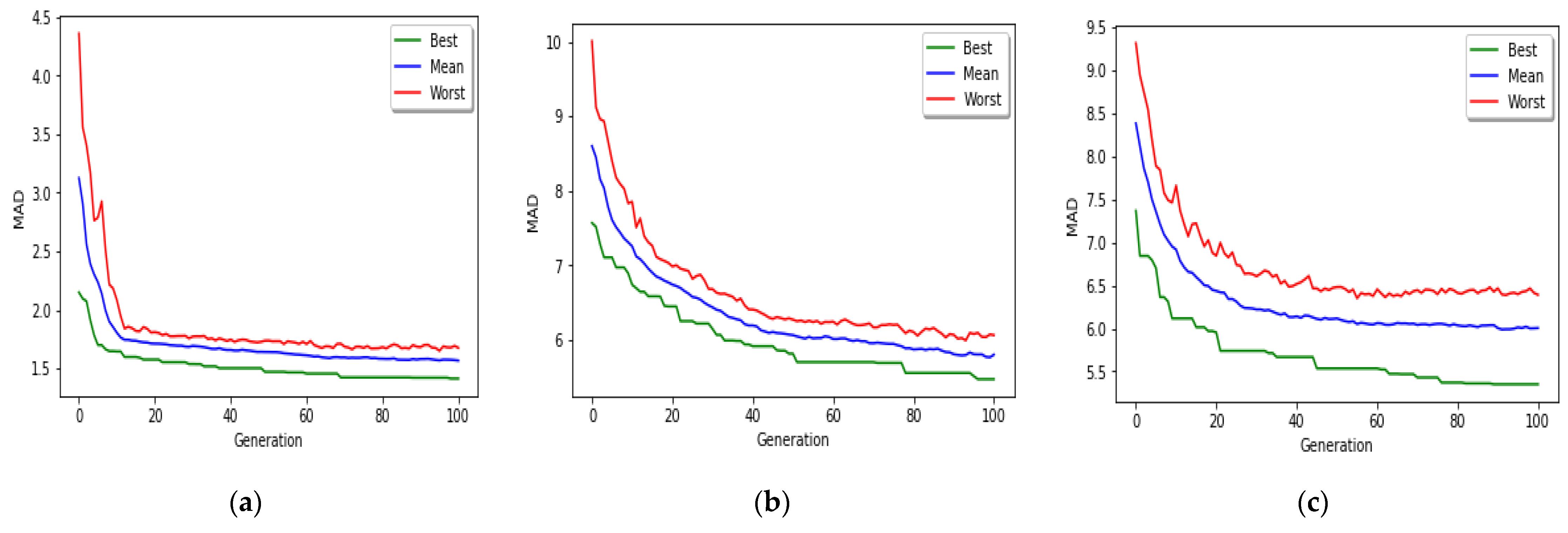
The goal of this study is to select the most important features in human age prediction using a rapid parallel framework. To achieve this goal, we first divide the training samples into three age groups based on similarity of their age change pattern to get better results. Second, we use the wrapper based genetic algorithm as feature selection method to find a set of features that optimize MAD of regression model for each age group. Third, we take advantage of parallel computing approaches in three parts of our proposed method and change some standard operators of genetic algorithm to lower the execution time. Finally, we evaluate our proposed method using 16 publicly available DNAm datasets, and obtain a MAD of 3.62 for the test data. We observe that the execution time of our proposed method is around 71.08 times lower compared to the sequential mode.
4. Discussion
Most studies in the age prediction field used a simple statistical filter-based feature selection method, such as Pearson correlation for age prediction [
1,
4,
14]. The reason behind selection of the mentioned feature selection method is its simplicity and also rapid operation. However, the problem is that, because they do not use modeling algorithms in their feature selection process, then they usually do not select an acceptable features set and lose many informative features. Another issue that is seen in the feature selection phase of previous studies is that they do not consider the interaction between the selected features set and give each gene a point individually. As a consequence, those approaches are unable to find the set of features that work best together. For these reasons, we used GA to find the best set of CpG-sites that are capable of optimizing MAD of GBR model from real ages. We found that MAD of MR-based PGA achieved superior results in comparison to recent research works.
Bekaert et al. [
37] and Alisch et al. [
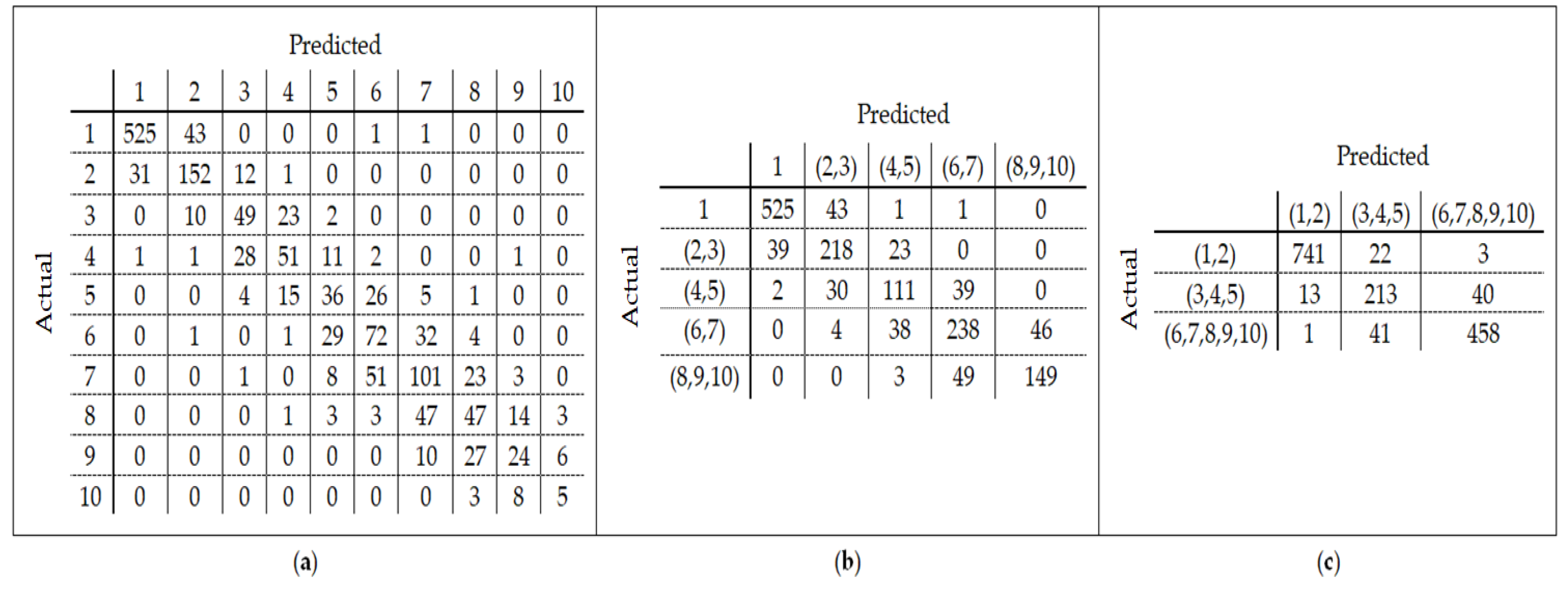
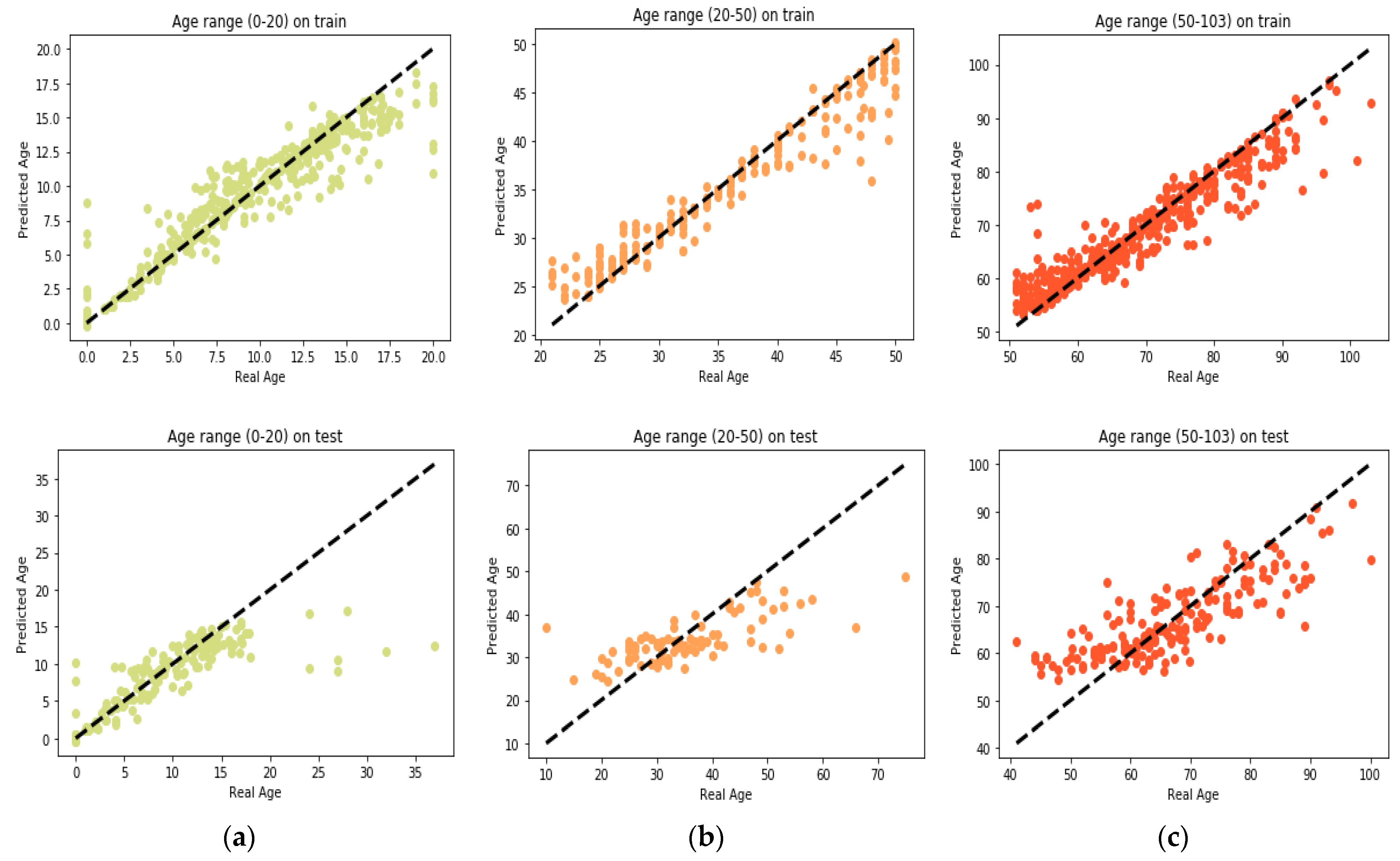
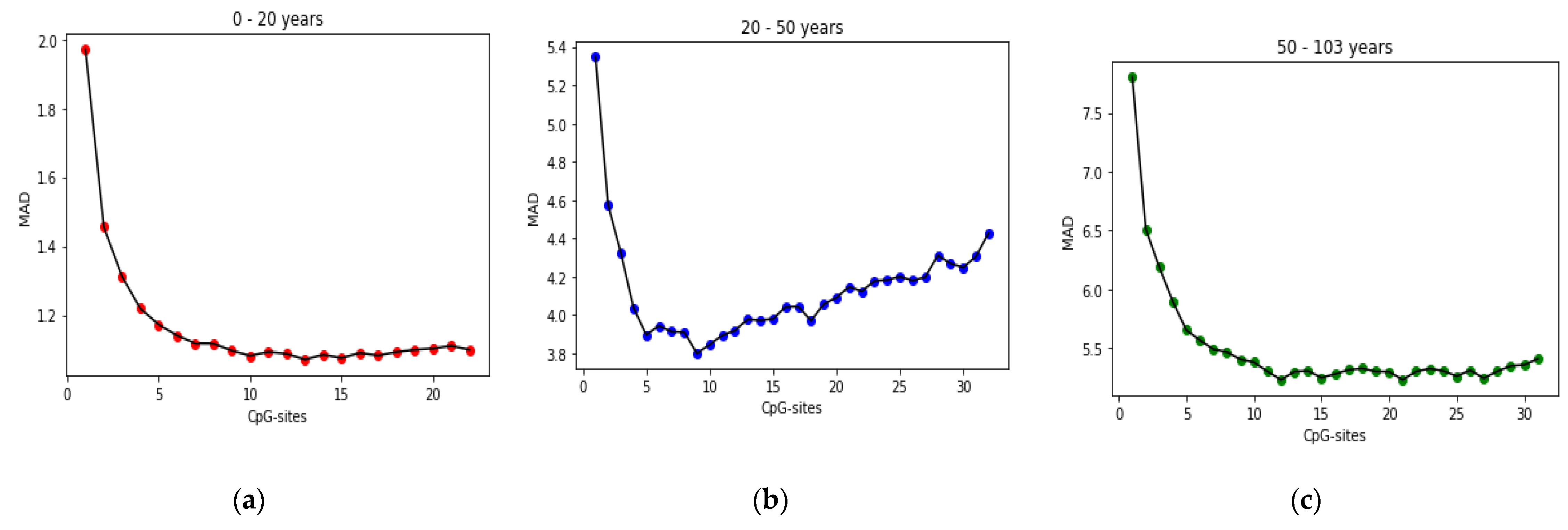
25] found that the relation between DNA methylation and age is not a straight line. Thus, we decided to put together samples where DNAm values change similar to each other, in a group, and build separate models on each group to get better results. Using the SVM classifier and by utilizing the confusion matrix, we divide the dataset to three age groups and consequently, we were able to obtain a better average MAD outcome than that of other previous studies. The results also show that aging pattern is more regular in young ages and very irregular in old ages. As it can be seen in the results of this paper, MAD in the age range of 0–20 years is 1.34 years (on test data) but in the age range of 50–103 is 5.53 years (on test data).
The implemented GA has hundred generations, and in each generation 100 GBR models are evolved for 100 chromosomes. Also, each chromosome has 8000 genes. Therefore, another major issue we faced was the long time it takes to run the feature selection process. The initial runtime of the algorithm took over than 100 h to complete. To solve this problem, we used parallel computing in our algorithm and implemented three parts of the algorithm in a parallel manner with the help of the MapReduce. We also changed some operators of the GA to reduce their execution time. For example, mutation operator in the GA works by generating a random number between [0, 1] for each gene, and the value of a gene changes if the random number was more than the specific threshold. However, running this operator consumes a lot of time for 8000 genes per chromosome. To overcome this issue, we modified the mutation operator to randomly select a fixed number of genes on each chromosome and change their values. Finally, by taking advantage of parallel computing and modifications in some genetic algorithm operators, we lowered the execution time of the algorithm to less than one hour.
Nevertheless, we acknowledge that our approach has some limitations. First, we did not consider the impact of gender on age prediction. Some studies have reported that age-related DNAm may be different in gender [
38,
39]. Second, we just studied blood tissue methylation patterns since DNAm data on other tissues are limited. Some studies have used DNAm data from teeth and saliva [
9,
13,
37]. If we can use DNAm datasets of different tissues of the body, we can build more complex models using integration methods and get better results on age prediction. Third, our results imply that the ages of samples at the boundaries of groups are poorly predicted. This problem occurred because samples were grouped using crisp age ranges. In future works, one can use fuzzy logic to group samples to get better results for samples at the boundaries of age ranges.