1. Introduction
Many biological processes rely on the spatiotemporal organization of proteins. Arguably one of the most elementary forms of such organization is cell polarization—the formation of a “cap” or spot of high protein concentration that determines a direction. Such a polarity axis then coordinates downstream processes including motility [
1,
2], cell division [
3], and directional growth [
4]. Cell polarization is an example for symmetry breaking [
5], as the orientational symmetry of the initially homogeneous protein distribution is broken by the formation of the polar cap.
Intracellular protein patterns arise from the interplay between protein interactions (chemical reactions) and protein transport. Diffusion in the cytosol serves as the most elementary means of transport. Pattern formation resulting from the interplay of reactions and diffusion has been widely studied since Turing’s seminal work [
6]. In addition to diffusion, proteins can be transported by fluid flows in the cytoplasm [
7,
8,
9] and along cytoskeletal structures (vesicle trafficking, cortical contractions) driven by molecular motors [
10,
11,
12]. These processes lead to advective transport of proteins.
Recently, it has been shown experimentally that advective transport (caused by cortical flows) induces polarization of the PAR system in the
C. elegans embryo [
13,
14,
15]. Furthermore, in vitro studies with the MinDE system of
E. coli, reconstituted in microfluidic chambers, have shown that the flow of the bulk fluid has a strong effect on the protein patterns that form on the membrane [
16,
17]. Increasing evidence shows that cortical and cytosolic flows (also called “cytoplasmic streaming”) are present in many cells [
18,
19,
20,
21,
22,
23]. In addition, cortical contractions can drive cell-shape deformations [
24], inducing flows in the incompressible cytosol [
8,
25]. However, the role of flows for protein-pattern formation remains elusive. This motivates to study the role of advective flow from a conceptual perspective, with a minimal model. The insights thus gained will help to understand the basic, principal effects of advective flow on pattern formation and reveal the underlying elementary mechanisms.
The basis of our study is a paradigmatic class of models for cell polarization that describe a single protein species which has a membrane-bound state and a cytosolic state. Such two-component mass-conserving reaction–diffusion (2cMcRD) systems serve as conceptual models for cell polarization [
7,
26,
27,
28,
29,
30,
31]. Specifically, they have been used to model Cdc42 polarization in budding yeast [
32] and PAR-protein polarity [
33]. 2cMcRD systems generically exhibit both spontaneous and stimulus-induced polarization [
5,
31,
33]. In the former case, a spatially uniform steady state is unstable against small spatial perturbations (“Turing instability” [
6]). Adjacent to the parameter regime of this lateral instability, a sufficiently strong, localized stimulus (e.g., an external signal) can induce the formation of a pattern starting from a stable spatially uniform state. The steady state patterns that form in two-component McRD systems are generally stationary (there are no traveling or standing waves). Moreover, the final stationary pattern has no characteristic wavelength. Instead, the peaks that grow initially from the fastest growing mode (“most unstable wavelength”) compete for mass until only a single peak remains (“winner takes all”) [
30,
34,
35]. The location of this peak can be controlled by external stimuli (e.g., spatial gradients in the reaction rates) [
34,
36].
Recently, a theoretical framework, termed local equilibria theory, has been developed to study these phenomena using a geometric analysis in the phase plane of the protein concentrations [
31,
37]. With this framework one can gain insight into the mechanisms underlying the dynamics of McRD systems both in the linear and in the strongly nonlinear regime, thereby bridging the gap between these two regimes.
Here, we show that cytosolic flow in two-component systems always induces upstream propagation of the membrane-bound pattern. In other words, the peak moves against the cytosolic flow direction. This propagation is driven by a higher protein influx on the upstream side of the membrane-concentration peak compared to its downstream side. Using this insight, we are able to explain why the propagation speed becomes maximal at intermediate flow speeds and vanishes when the rate of advective transport becomes fast compared to the rate of diffusive transport or compared to the reaction rates. We first study a uniform flow profile using periodic boundaries. This effectively represents a circular flow, which is observed in plant cells (where this phenomenon is called cytoplasmic streaming or cyclosis) [
38]. It also represents an in vitro system in a laterally large microfluidic chamber. We then study the effect of a spatially non-uniform flow profile in a system with reflective boundaries, as a minimal system for flows close to the membrane [
7,
13,
15], e.g., in the actin cortex. We show that a non-uniform flow profile redistributes the protein mass, which can trigger a regional lateral instability and thereby induce pattern formation from a stable homogeneous steady state.
The remainder of the paper is structured as follows. We first introduce the model in
Section 2. We then perform a linear stability analysis in
Section 3 to show how spatially uniform cytosolic flow influences the dynamics close to a homogeneous steady state. In
Section 4, we use numerical simulations to study the fully nonlinear long-term behavior of the system. Next, we show that upon increasing the cytosolic flow velocity, the pattern can qualitatively change from a mesa pattern to a peak pattern in
Section 5. Finally, in
Section 6, we study how a spatially non-uniform cytosolic flow can trigger a regional lateral instability and thus induce pattern formation. Implications of our findings and links to earlier literature are briefly discussed at the end of each section. We conclude with a brief outlook section.
2. Model
We consider a spatially one-dimensional system of length
L. The proteins can cycle between a membrane-bound state (concentration
) and a cytosolic state (concentration
), and diffuse with diffusion constants
and
, respectively (
Figure 1). In cells, the diffusion constant on the membrane is typically much smaller than the diffusion constant in the cytosol. In the cytosol, the proteins are assumed to be advected with a speed
, as indicated by the blue arrow in
Figure 1. Thus, the reaction-diffusion-advection equations for the cytosolic density and membrane density read
with either periodic or reflective boundary conditions. The nonlinear function
describes the reaction kinetics of the system. Attachment–detachment kinetics can generically be written in the form
where
and
denote the rate of attachment from the cytosol to the membrane and detachment from the membrane to the cytosol, respectively. The dynamics given by Equation (1) conserve the average total density
Here, we introduced the local total density .
For illustration purposes, we will use a specific realization of the reaction kinetics [
31],
describing attachment with a rate
, self-recruitment with a rate
, and enzyme-driven detachment with a rate
and the Michaelis–Menten constant
, respectively. However, our results do not depend on the specific choice of the reaction kinetics. Unless stated otherwise, we use the parameters:
.
4. Pattern Propagation in the Nonlinear Regime
So far we have analyzed how cytosolic flow affects the dynamics of the system in the vicinity of a homogeneous steady state, using linear stability analysis. However, patterns generically do not saturate at small amplitudes but continue to grow into the strongly nonlinear regime [
31] (see
Supplementary Materials Movie 1 for an example in which a small perturbation of the homogeneous steady state evolves into a large amplitude pattern in the presence of flow).
To study the long time behavior (steady state) far away from the spatially homogeneous steady state, we performed finite element simulations in Mathematica [
42]. To interpret the results of these numerical simulations, we will use local equilibria theory, building on the phase-space analysis introduced in Refs. [
31,
37].
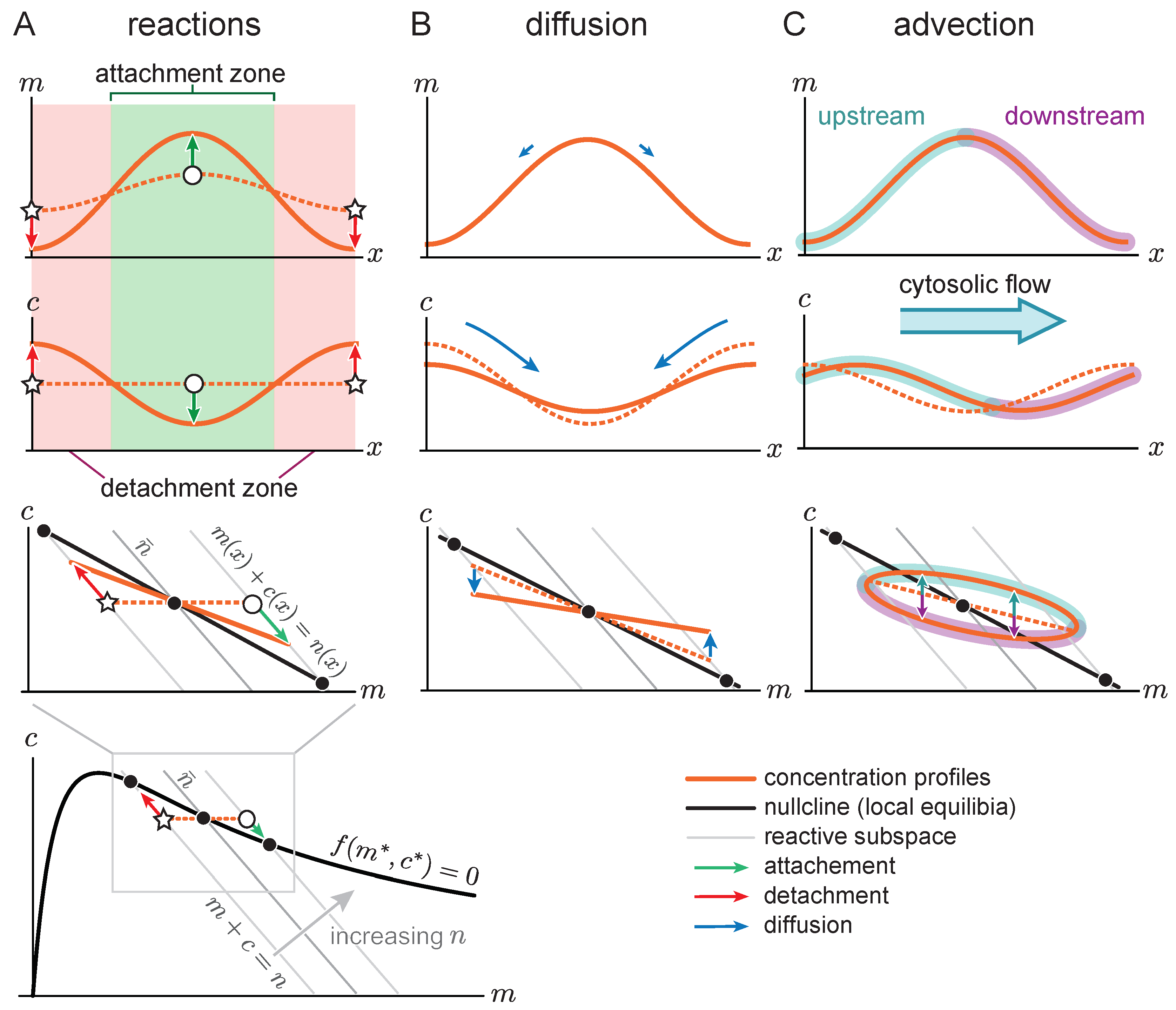
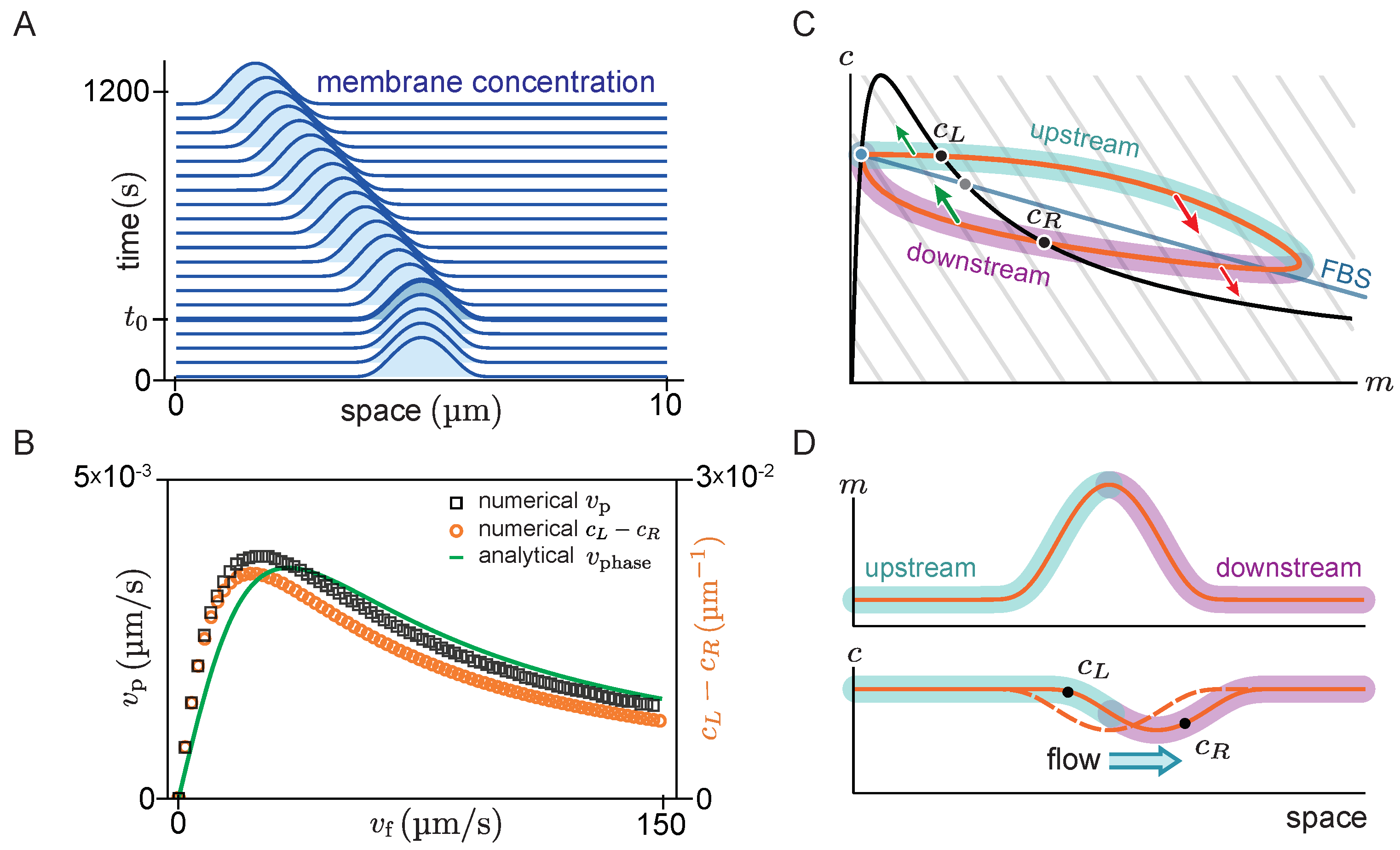
Figure 4A shows the space-time plot (kymograph) of a system where there is initially no flow (
), such that the system is in a stationary state with a single peak. For such a stationary steady state, diffusive fluxes on the membrane and in the cytosol have to balance exactly. This diffusive flux balance imposes the constraint that in the
-phase plane, the trajectory corresponding to the pattern lies on a straight line with slope
, called ‘flux-balance subspace’ (FBS) [
31] (see light blue line in
Figure 4C). At the plateaus and inflection points of the pattern, the net diffusive flow vanishes and attachment and detachment are balanced, i.e., the system is locally in reactive equilibrium (
). Hence, plateaus and inflection points of the spatial concentration profile correspond to intersection points between the reactive nullcline and the FBS in the
-phase plane (blue and green points in
Figure 4C). At the first intersection point (blue), the nullcline slope is larger than the FBS slope. Thus, by the slope criterion
for lateral instability, this point corresponds to a laterally stable state in the spatial domain—i.e., a plateau. Following a spatial perturbation, the concentrations will relax back towards the flat plateau.
At the second intersection point (green point in
Figure 4C), the nullcline slope is more negative than the FBS slope, indicating a laterally unstable state. This state corresponds to the inflection point of the pattern and the lateral instability there can be thought of as “spanning” the interfacial region of the pattern that connects the two plateaus. An in-depth analysis of stationary patterns based on these geometric relations in phase space can be found in Ref. [
31]. Here we ask how the phase portrait changes in the presence of flow.
At time
, a constant cytosolic flow in the positive
x-direction is switched on. Consistent with the expectation from linear stability analysis, we find that the peak propagates against the flow direction in the negative
x-direction (solid lines in
Figure 4A). The diffusive fluxes no longer balance for this propagating steady state, such that the phase-space trajectory is no longer embedded in the FBS. Instead, as advective flow shifts the cytosol concentration profile relative to the membrane profile, the phase-space trajectory becomes a loop (
Figure 4C). On the upstream side of the peak, the cytosolic density is increased, such that net attachment—which is proportional to the cytosolic density—is increased relative to net detachment. Conversely, the reactive balance is shifted towards detachment on the downstream side. As a result of the reactive flow is approximately proportional to the distance from the reactive nullcline in phase space, the asymmetry between net attachment and detachment on the upstream and downstream side of the peak can be estimated by the area enclosed by the loop-shaped trajectory in phase space.
To test whether the attachment–detachment asymmetry explains the propagation speed of the peak, we estimate the enclosed area in phase space by the difference in cytosolic concentrations at the points
and
(black dots in
Figure 4C,D) where the loop intersects the reactive nullcline (
black line
Figure 4C). At these points, the system is in a local reactive equilibrium. Indeed, we find that the propagation speed of the pattern obtained from numerical simulations (black open squares in
Figure 4B) is well approximated by the difference in cytosolic density (
) for all flow speeds (orange open circles in
Figure 4B). Furthermore, in the limit of slow and fast flow, the peak propagation speed is well approximated by the propagation speed of the unstable traveling mode with the longest wavelength, as obtained from linear stability analysis (The phase velocity depends on the mode’s wavelength. The relevant length scale for the peak’s propagation is its width, which is approximately given by
at the pattern’s inflection point [
31]. Thus, we infer the peak propagation speed from
at the inflection point of the stationary peak.). For small flow speeds, the pattern’s propagation speed
increases linearly with
(cf. Equation (
7)) and for large flow speeds the pattern speed is proportional to
(cf. Equation (
10)).
In summary, we found that the peak propagation speed in the slow and fast flow limits is well described by the propagation speed of the linearly unstable mode with the longest wavelength (i.e., the right edge of the band of unstable modes ). Moreover, we approximated the asymmetry of protein attachment by the area enclosed by the density distribution in phase space, and found that this is proportional to the peak speed for all flow speeds.
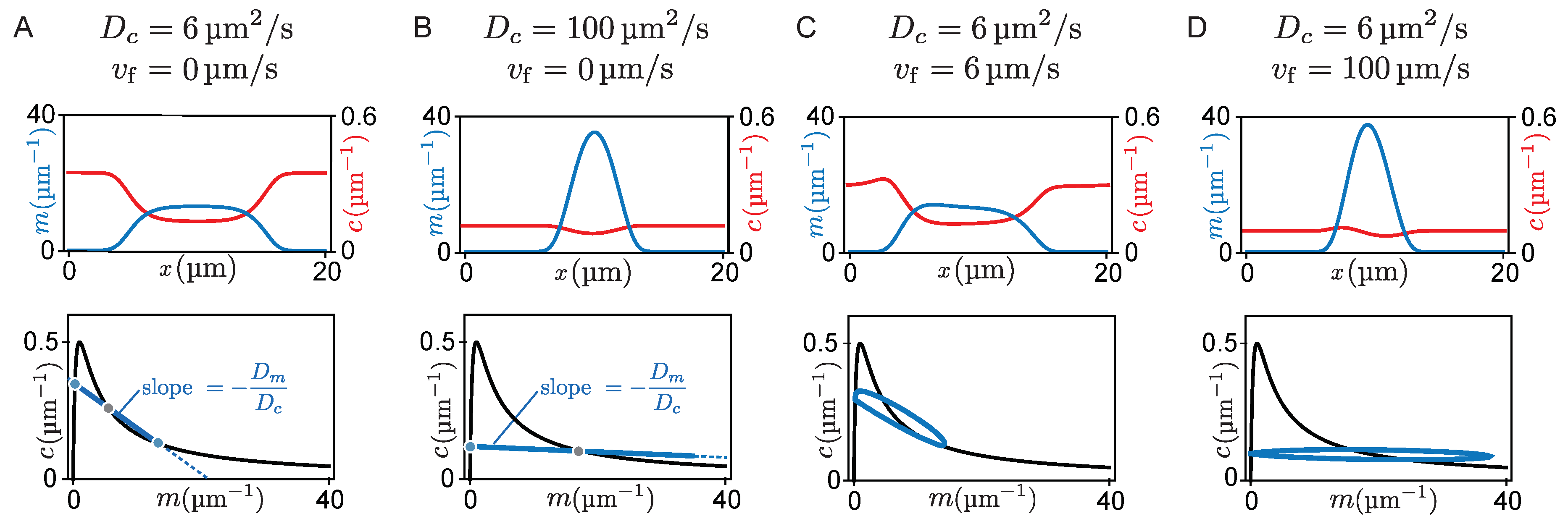
5. Flow-Induced Transition from Mesa to Peak Patterns
So far we have studied the propagation of patterns in response to cytosolic flow. Next, we will show how cytosolic flow can also drive the transition between qualitatively different pattern types. We distinguish two pattern types exhibited by McRD systems, peaks, and mesas [
30,
31]. Mesa patterns are composed of plateaus (low density and high density) connected by interfaces, while a peak can be pictured as two interfaces concatenated directly (cf.
Figure 5A). Mesa patterns form if protein attachment saturates in regions of high total density, forming a plateau there. As we argued above, the low- and high-density plateaus correspond to laterally stable steady states, marked—in the phase plane—by intersection points between the FBS and the reactive nullcline where the nullcline slope is larger than the FBS slope. Peaks form if the attachment rate does not saturate at high density, i.e., if the third intersection point between nullcline and FBS is not reached [
31]. Thus, while the amplitude of mesa patterns is determined by the attachment–detachment balance in the two plateaus, the amplitude (maximum concentration) of a peak is determined by the total mass available in the system [
31].
How does protein transport affect whether a peak or a mesa forms? As we argued above, a peak pattern forms if protein attachment in regions of high density does not saturate. In general, this will happen if attachment to the membrane depletes proteins from the cytosol slower than lateral transport can resupply proteins (see
Figure 5A). Let us first recap the situation without flow, where proteins are resupplied by diffusion from the detachment zone to the attachment zone across the pattern’s interface with width
. Thus, a peak pattern forms if the rate of transport by cytosolic diffusion is faster than the attachment rate (
). Further using that the interface width is given by a balance of membrane diffusion and local reactions (
), we obtain the condition
for the formation of peak patterns.
In terms of phase space geometry, this means that the slope
of the flux-balance subspace in phase space must be sufficiently shallow. For a steep slope
of the FBS, the membrane concentration saturates at the point where the FBS intersects with the reactive nullcline blue dots in
Figure 5A. There, attachment and detachment balance such that a mesa forms (
Figure 5A). For faster cytosol diffusion, the flux-balance subspace is shallower such that the third FBS-NC intersection point shifts to higher densities. Thus, for sufficiently fast cytosol diffusion a peak forms (
Figure 5B).
Adding slow cytosolic flow does not significantly contribute to the resupply of the cytosolic sink (i.e., attachment zone) and therefore does not alter the pattern type (
Figure 5C). In contrast, when cytosolic protein transport (by advection and/or diffusion) is fast compared to the reaction kinetics, the cytosolic sink gets resupplied quickly, leading to a flattening of the cytosolic concentration profile. Accordingly, the density distribution in phase space approaches a horizontal line, both for fast cytosolic diffusion (
Figure 5B) and for fast cytosolic flow (
Figure 5D). As a consequence, the point where the density distribution meets the nullcline shifts towards larger membrane concentrations, resulting in an increasing amplitude of the mesa pattern. Eventually, when the amplitude of the pattern can not grow any further due to limiting total mass, a peak pattern forms (
Figure 5B,D). Hence, an increased flow velocity can cause a transition from a mesa pattern to a peak pattern (see
Supplementary Materials Movie 4).
In summary, we found that cytosolic flow can qualitatively change the membrane-bound protein pattern from a small-amplitude, wide mesa pattern to a large-amplitude, narrow peak pattern. In cells, such flows could therefore promote the precise positioning of polarity patterns on the membrane. Furthermore, we hypothesize that flow can contribute to the selection of a single peak by accelerating the coarsening dynamics of the pattern via two distinct mechanisms. First, flow accelerates protein transport that drives coarsening. Second, as peak patterns coarsen faster than mesa patterns [
30,
43], flow can accelerate coarsening via the flow-driven mesa-to-peak transition. Such fast coarsening may be important for the selection of a single polarity axis, e.g., a single budding site in
S. cerevisiae [
4], for axon formation in neurons [
44], and to establish a distinct front and back in motile cells [
2,
45].
6. Flow-Induced Pattern Formation
So far we have studied how a uniform flow profile affects pattern formation on a domain with periodic boundary conditions, representing circular flows along the cell membrane and bulk flows in microfluidic in vitro setups. However, flows in the vicinity of the membrane can be non-uniform. For example, one (or more) components of the pattern forming system may be embedded in the cell cortex [
13,
15,
46] which is a contractile medium driven by myosin-motor activity. Furthermore, the incompressible cytosol can flow in the direction normal to the membrane, such that the 3D flow field of the cytosol is perceived as a compressible flow along the membrane [
9]. In this section, we will discuss how such non-uniform, uni-directional flows lead to pattern formation.
A non-uniform flow transports the proteins at different speeds along the membrane. Starting from a spatially homogeneous initial state, such a non-uniform flow leads to a redistribution of mass. It has been demonstrated in previous work that this non-uniform flow can induce pattern formation even if the homogeneous steady state is laterally stable (i.e., there is no spontaneous pattern formation) [
7,
13,
15]. Based on numerical simulations, a transition from flow-guided to self-organized dynamics has been reported [
15]. However, the physical mechanism underlying this transition, and what determines the transition point have remained unclear.
We address this question using the two-component model, which serves a conceptual model that mimics the qualitative behavior of the more complex PAR system [
33]. While flow in the PAR system is governed by the myosin concentration, we assume a stationary parabolic flow profile that vanishes at the system boundaries (
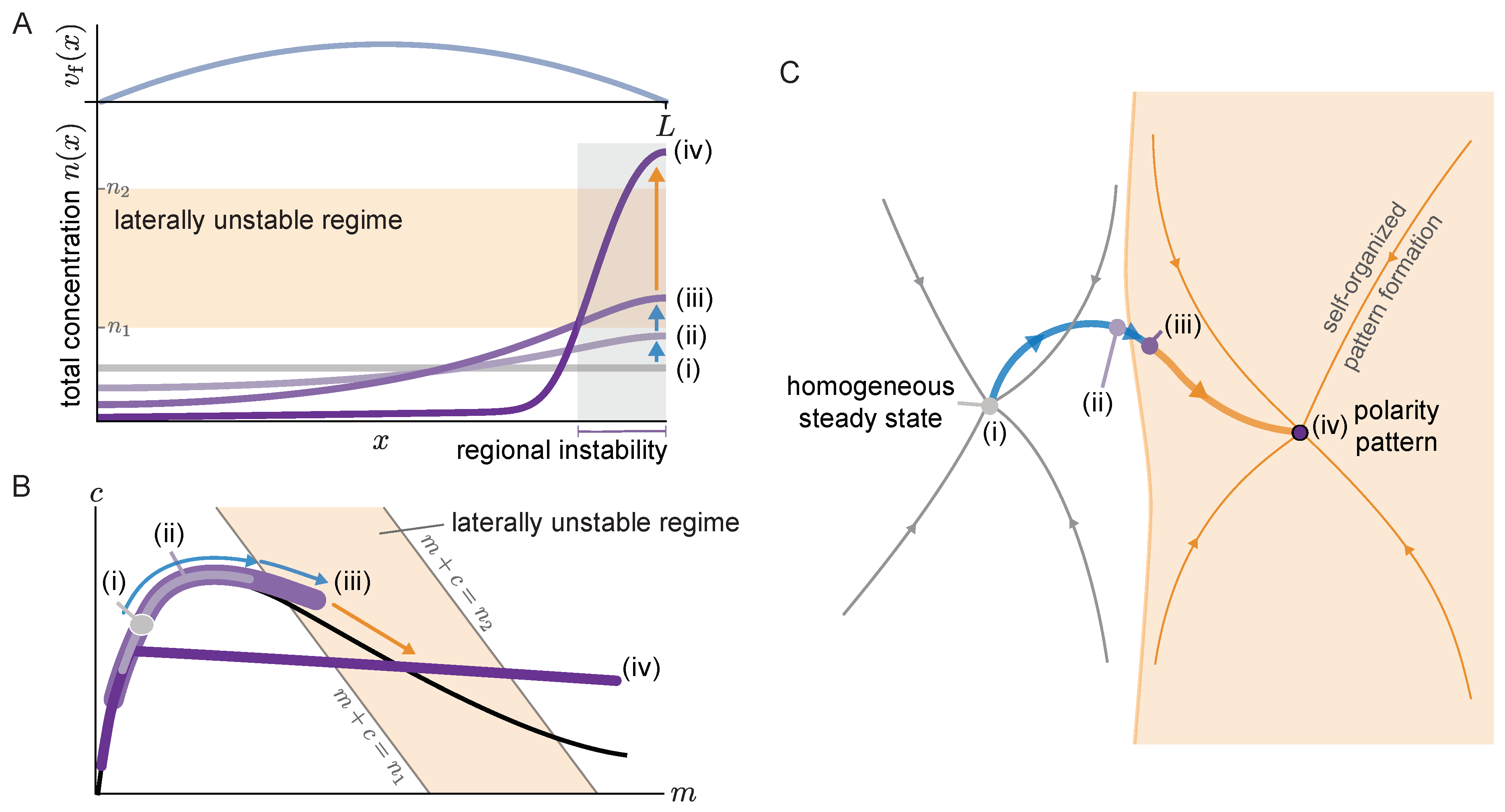
Figure 6A, top). We use a one-dimensional domain with no-flux boundary conditions that correspond to the symmetry axis of a rotationally symmetric flow profile. In the following, we describe the flow-induced dynamics starting from a spatially homogeneous steady state to the final polarity pattern observed in numerical simulations (see
Supplementary Materials Movie 5).
Figure 6 visualizes these dynamics in real space (A) and in the
-phase plane (B). To relate our findings to the previous study Ref. [
15], we also visualize the dynamics in an abstract representation of the state space (comprising all concentration profiles) used in this previous study. In this state space, steady states are points and the time evolution of the system is a trajectory (thick blue/orange line in
Figure 6C).
Starting from the homogeneous steady state (
i), the non-uniform advective flow redistributes mass in the cytosol (
ii). Due to this redistribution of mass, the local reactive equilibria shift as we have seen repeatedly here and in earlier studies of mass-conserving systems [
31,
47]. In fact, as long as the gradients of both the membrane and cytosol profiles are shallow, the concentrations remain close to the local equilibria, as evidenced by the density distribution in phase space spreading along the reactive nullcline (see profile (
ii) in
Figure 6A,B). As long as there is no laterally unstable region, the mass accumulation is limited by the counteracting diffusive flow in the cytosol. Eventually, the region where mass accumulates (here the right edge of the domain) enters the laterally unstable regime (see profile
iii). In this laterally unstable region, cytosol diffusion will enhance the accumulation of mass via the mass-redistribution instability, until it is limited by the much slower membrane diffusion. In the phase plane (
Figure 6B), the laterally unstable regime corresponds to the range of total densities
where the nullcline slope has a steeper negative value than the flux-balance subspace slope (
) (More precisely, the size of the laterally unstable region must be larger than the shortest unstable mode (corresponding to the right edge of the band of unstable modes in the dispersion relation (
Figure 2A))). The mass-redistribution instability in this region, based on the self-organized formation of attachment and detachment zones (cf.
Section 3.2) will lead to the formation of a polarity pattern there (
iv). Thus, the onset of a regional lateral instability marks the transition from flow-guided dynamics to self-organized dynamics.
In the abstract state space visualization (
Figure 6C) the area shaded in orange indicates the polarity pattern’s basin of attraction comprising all states (concentration profiles) where a spatial region in the system is laterally unstable. In the absence of flow, states that do not exhibit such a laterally unstable region return to the homogeneous steady state (thin gray lines). Non-uniform cytosolic flow induces mass-redistribution, that can drive an initially homogeneous system (
i) into the polarity pattern’s basin of attraction. From there on, self-organized pattern formation takes over, leading to the formation of a polarity pattern (
iv), essentially independently of the advective flow (orange trajectory). In future work, it would be interesting to make the abstract state space representation,
Figure 6C, more quantitative. For example, one could try to estimate the minimal flow velocity required to drive the system past the separatrix, i.e., into the basin of attraction of the polarity pattern. A promising approach is to use the fact that prior to the onset of regional lateral instability, the concentrations are slaved to the local equilibria that depend on the local total density. Thus, one can obtain an approximate, closed equation for the flow-driven evolution of the total density, similar to the “adiabatic scaffolding approximation” made in [
31]. Solving this equation would provide a criterion for when the total density exceeds the critical density for lateral instability in some spatial region that initiates the self-organized formation of a polarity pattern there.
Similar pattern forming mechanisms based on a regional instability have previously been shown to also underlie stimulus-induced pattern formation following a sufficiently strong initial perturbation [
31] and peak formation at a domain edge where the reaction kinetics abruptly change [
36]. Thus, an overarching principle for stimulus-induced pattern formation emerges: To trigger (polarity) pattern formation, the stimulus, be it advective flow or heterogeneous reaction kinetics, has to redistribute protein mass in a way such that a regional (lateral) instability is triggered.
It remains to be discussed what happens once the cytoplasmic flow is switched off after the polarity pattern has formed. In general, the polarity pattern will persist (see
Supplementary Materials Movie 5), since it is maintained by self-organized attachment and detachment zones, largely independent of the flow. However, as long as there is flow, the average mass on the right hand side of the system (downstream of the flow) is higher than on the left hand side. Hence, flow can maintain a polarity pattern even if the average mass in the system as a whole is too low to sustain polarity patterns in the absence of flow (see bifurcation analysis in Ref. [
31]). If this is the case, the peak disappears once the flow is switched off (see
Supplementary Materials Movie 6).
In summary, the redistribution of the protein mass is key to induce (polarity) pattern formation starting from a stable homogeneous state.
7. Conclusions and Outlook
Inside cells, proteins are transported via diffusion and fluid flows, which, in combination with reactions, can lead to the formation of protein patterns on the cell membrane. To characterize the role fluid flows play in pattern formation, we studied the effect of flow on the formation of a polarity pattern, using a generic two-component model. We found that flow leads to propagation of the polarity pattern against the flow direction with a speed that is maximal for intermediate flow speeds, i.e., when the rate of advective transport is comparable to either the reaction rates or to the rate diffusive transport in the cytosol. Using a phase-space analysis, we showed that the propagation of the pattern is driven by an asymmetric influx of protein mass to a self-organized protein-attachment zone. As a consequence, attachment is stronger on the upstream side of the pattern compared to the downstream side, leading to upstream propagation of the membrane bound pattern. Furthermore, we have shown that flow can qualitatively change the pattern from a wide mesa pattern (connecting two plateaus) to a narrow peak pattern. Finally, we have presented a phase-space analysis to elucidate the interplay between flow-guided dynamics and self-organized pattern formation. This interplay was previously studied numerically in the context of PAR-protein polarization [
13,
15]. Our analysis reveals the underlying cause for the transition from flow-guided to self-organized dynamics: the regional onset of a mass-redistribution instability.
We discussed implications of our results and links to earlier literature at the end of each section. Here, we conclude with a brief outlook. We expect that the insights obtained from the minimal two-component model studied here generalize to systems with more components and multiple protein species. For example, in vitro studies of the reconstituted MinDE system of
E. coli show that MinD and MinE spontaneously form dynamic membrane-bound patterns, including spiral waves [
48] and quasi-stationary patterns [
49]. These patterns emerge from the competition of MinD self-recruitment and MinE-mediated detachment of MinD [
50,
51]. In the presence of a bulk flow, the traveling waves were found to propagate upstream [
16]. Our analysis based on a simple conceptual model suggests that this upstream propagation is caused by a larger influx of the self-recruiting MinD on the upstream flanks compared to the downstream flanks of the traveling waves. However, the bulk flow also increases the resupply of MinE on the upstream flanks. As MinE mediates the detachment of MinD and therefore effectively antagonizes MinD’s self-recruitment, this may drive the membrane-bound patterns to propagate downstream instead of upstream. Which one of the two processes dominates—MinD-induced upstream propagation or MinE-induced downstream propagation—likely depends on the details of their interactions. This interplay will be the subject of future work.
A different route of generalization is to consider advective flows that depend on the protein concentrations. In cells, such coupling arises, for instance, from myosin-driven cortex contractions [
15,
52] and shape deformations [
8,
25]. Myosin-motors, in turn, may be advected by the flow and their activity is controlled by signaling proteins such as GTPases and kinases [
53]. This can give rise to feedback loops between flow and protein patterns. Previous studies show that such feedback loops can give rise to mechano-chemical instabilities [
54], drive pulsatile (standing-wave) patterns [
55,
56] or cause the breakup of traveling waves [
57]. We expect that our analysis based on phase-space geometry can provide insight into the mechanisms underlying these phenomena.