Inception Mechanisms of Tunneling Nanotubes
Abstract
1. Introduction
1.1. Early Experiments and Definitions
1.2. Bacterial TNTs
1.3. The role of TNTs in Spreading Pathogens
1.4. TNT Growth is Dependent on Case-Specific Regulatory Proteins
1.5. A General TNT Growth-Driving Mechanism?
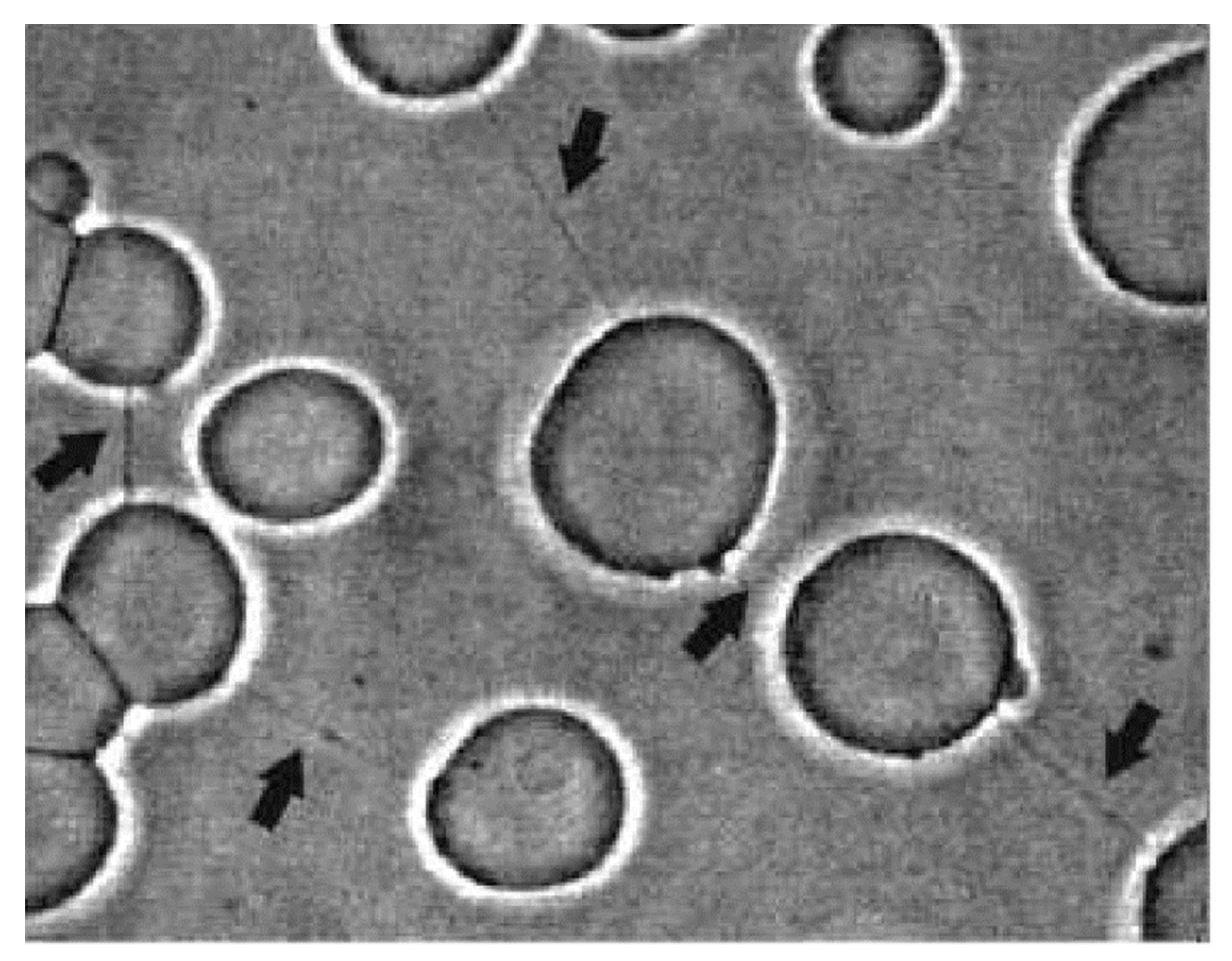
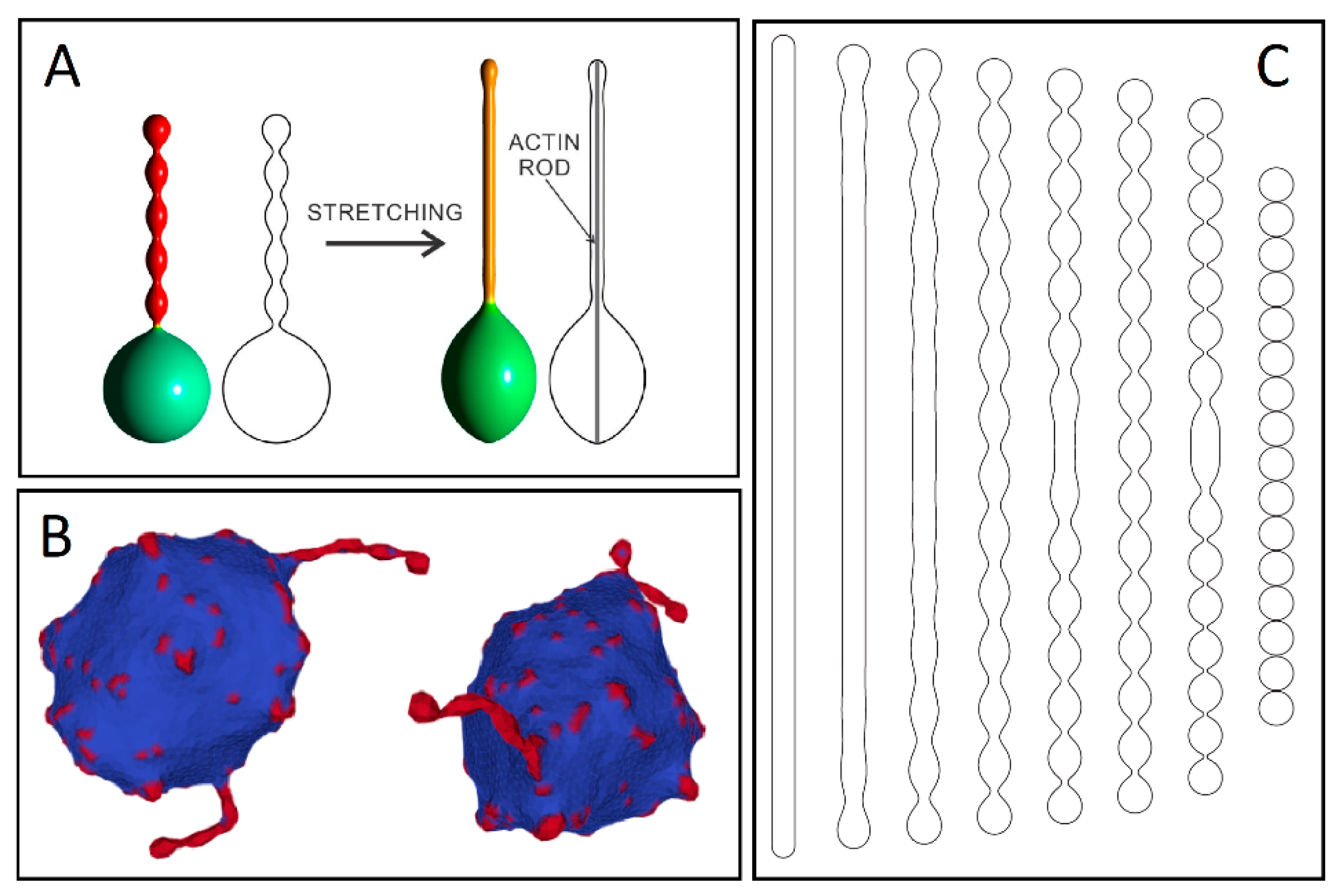
2. Stability of Membranous Tubular Structures
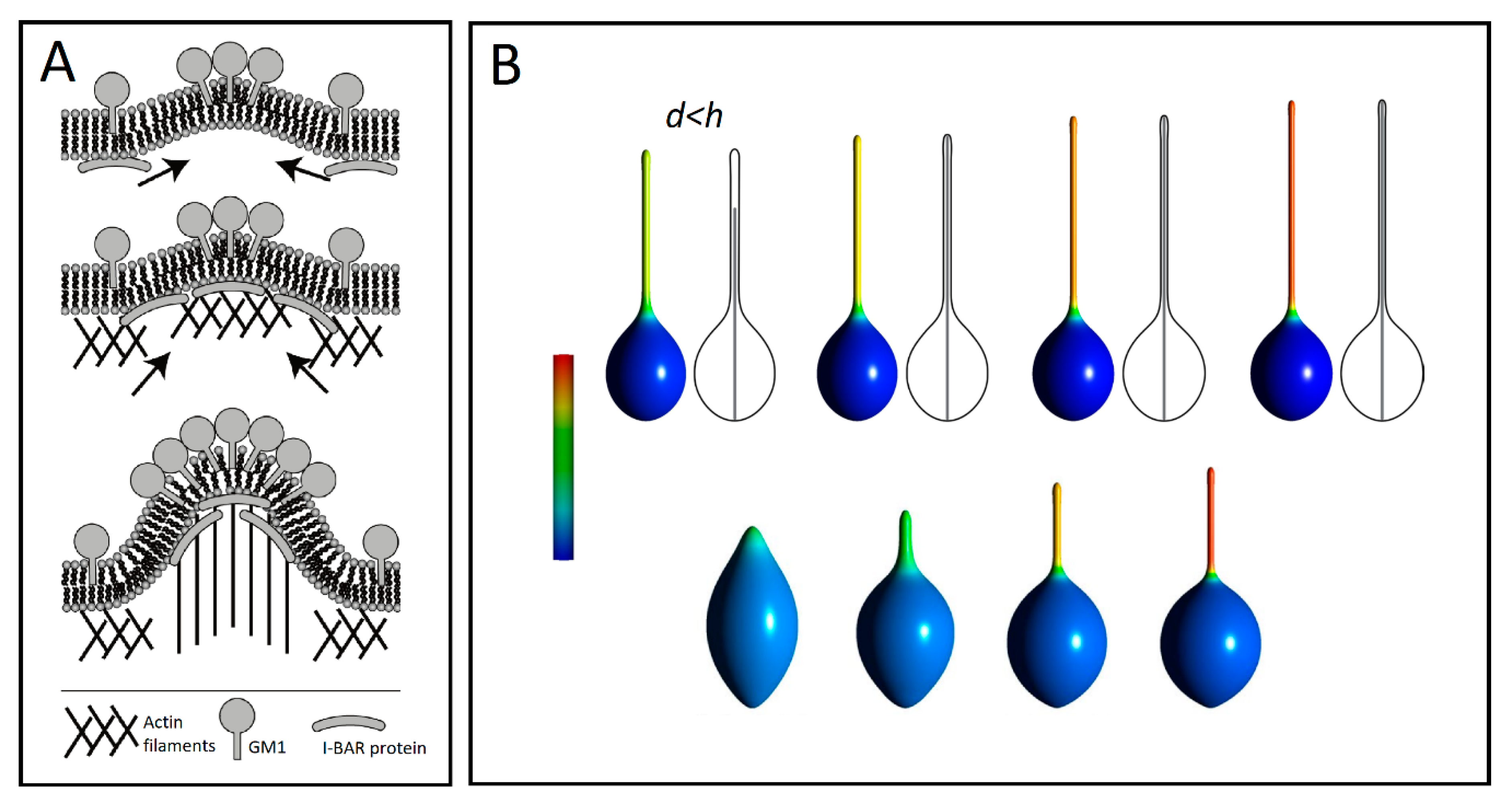
3. Membrane Protrusions Coupled with Local Curvature Changes
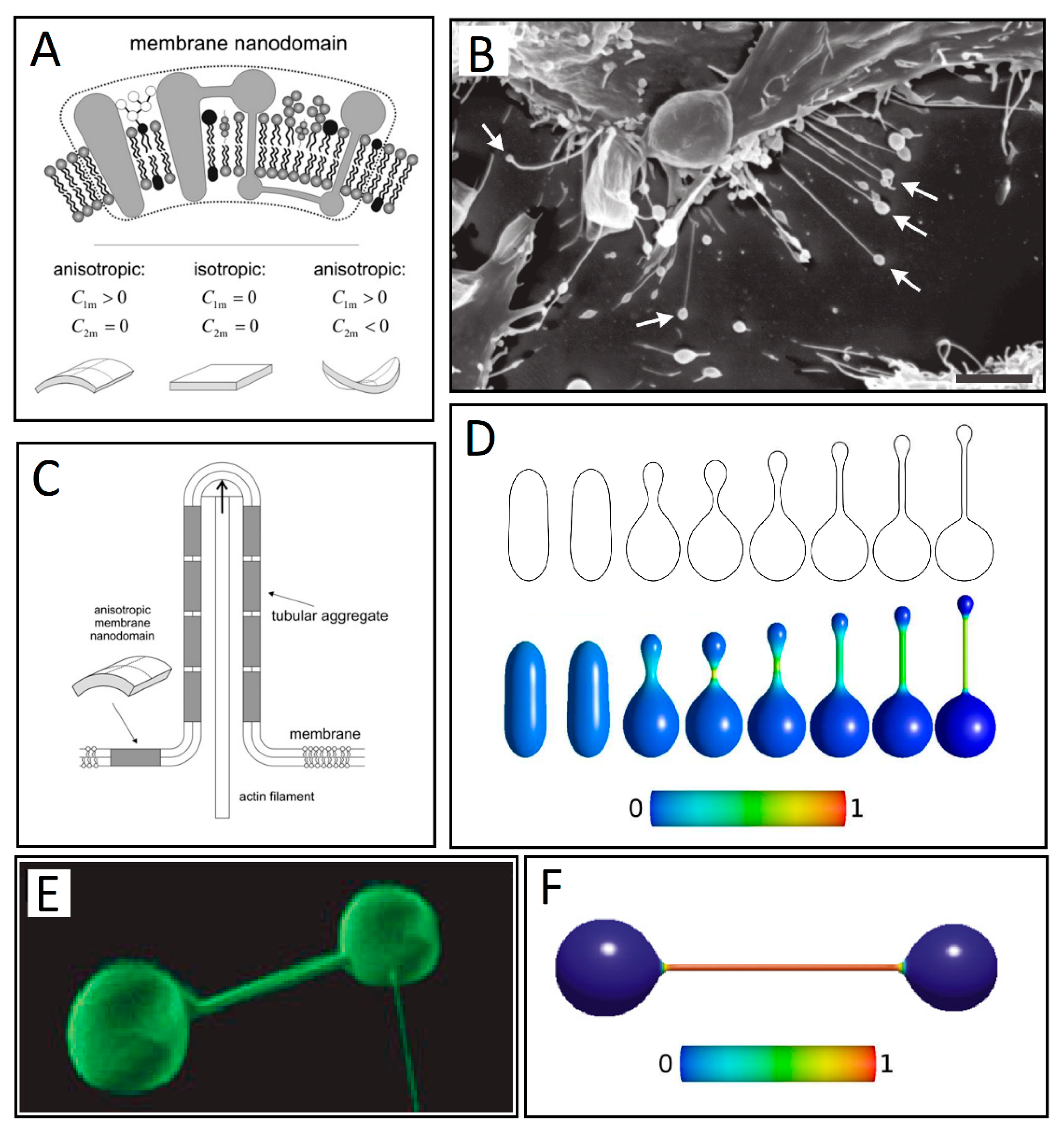
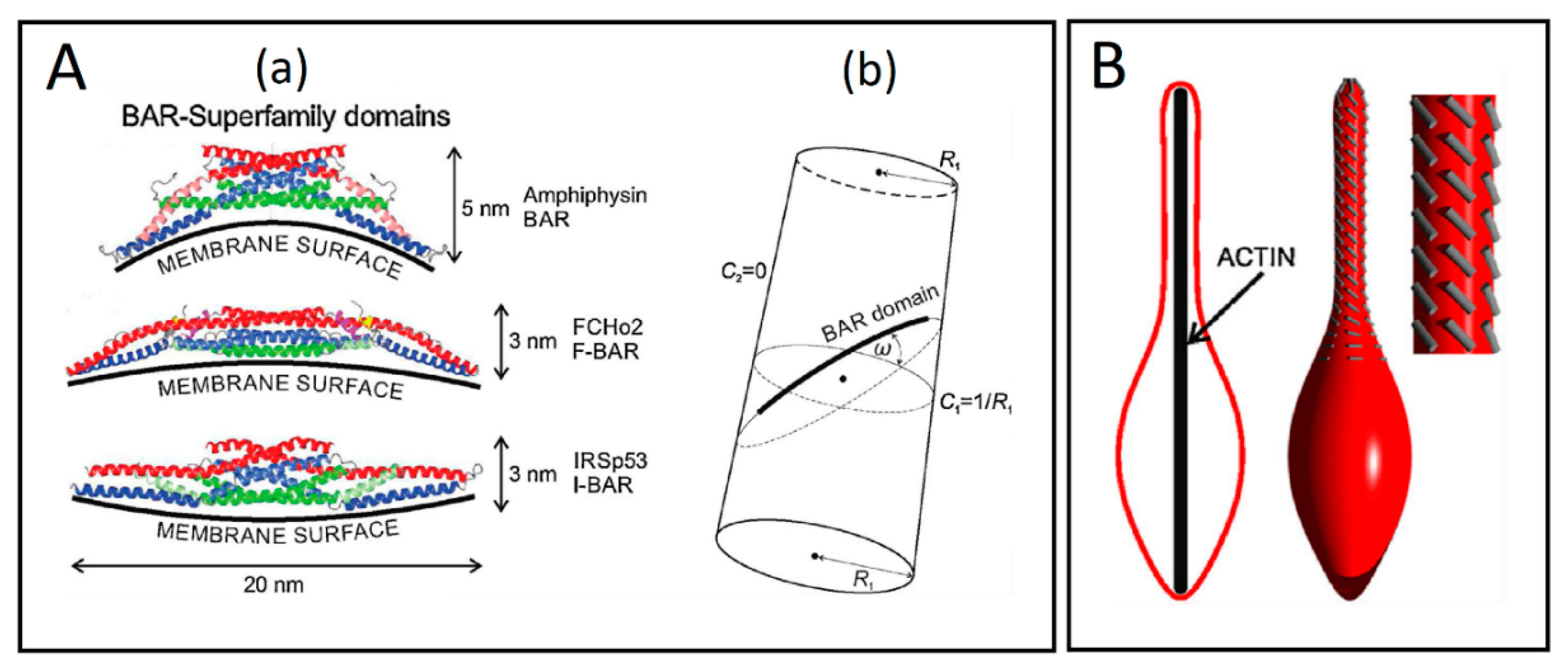
3.1. Curvature-Sensing Membrane Inclusions
3.2. Anisotropic Membrane Components Models
3.3. Alternate Theories: Protein Crowding
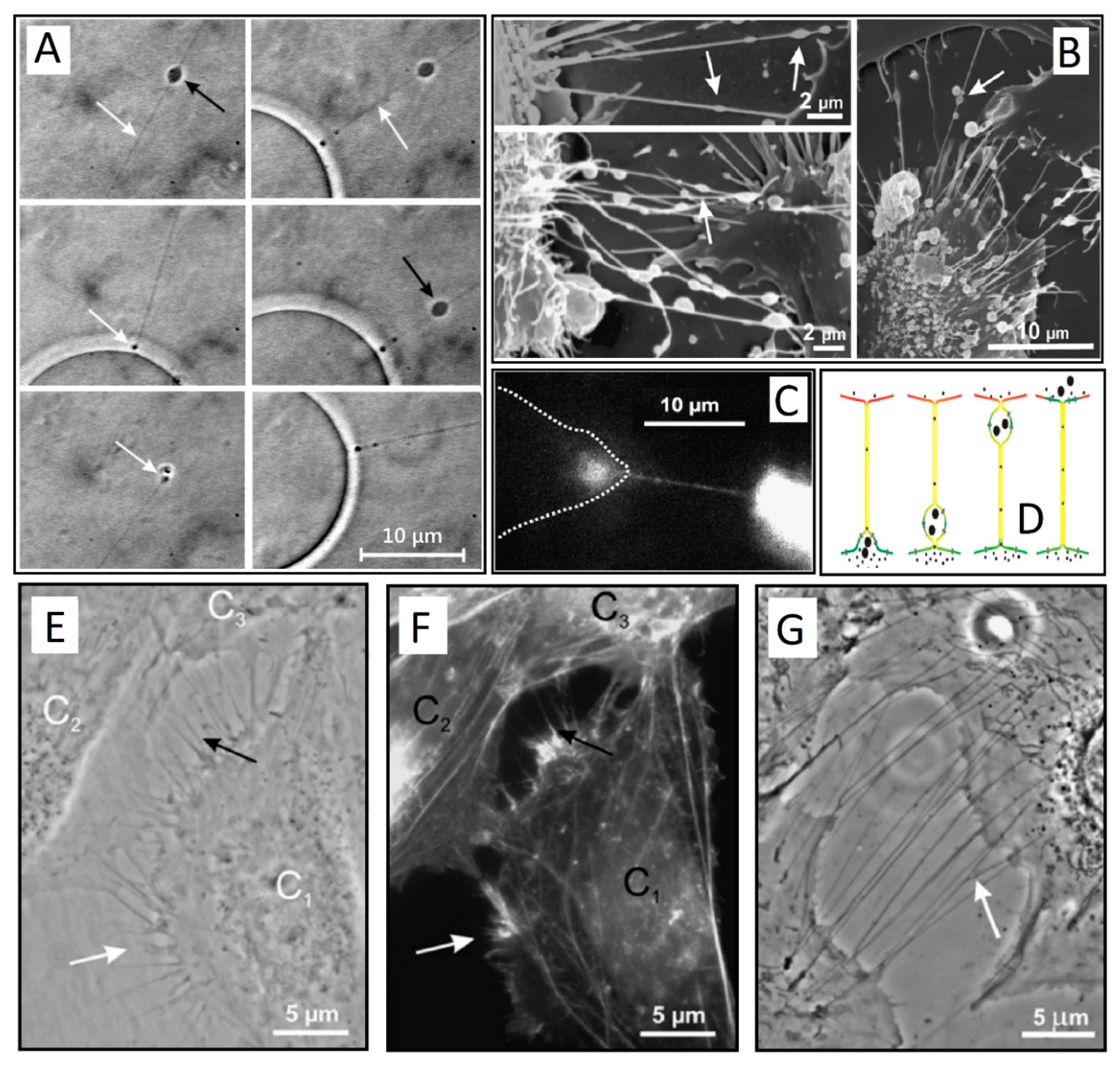
4. Membrane Protrusions Coupled with Cytoskeletal Forces
4.1. Membrane Deformation and Protrusive Forces: A Positive-Feedback Mechanism
4.2. Anisotropic Membrane Components Coupled with Protrusive Forces
4.3. Experimental Evidence of Membrane Clustering
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Arrigler, V.; Hägerstrand, H.; Kralj-Iglic, V.; Iglic, A.; Gomiscek, G.; Sevsek, F. Microtubes and nanotubes of a phospholipid bilayer membrane. J. Phys. A Math. Gen. 2002, 35, 1533–1549. [Google Scholar]
- Iglič, A.; Hägerstrand, H.; Bobrowska-Hägerstrand, M.; Arrigler, V.; Kralj-Iglič, V. Possible role of phospholipid nanotubes in directed transport of membrane vesicles. Phys. Lett. A 2003, 310, 493–497. [Google Scholar]
- Kralj-Iglič, V.; Iglič, A.; Bobrowska-Hägerstrand, M.; Hägerstrand, H. Tethers connecting daughter vesicles and parent red blood cell may be formed due to ordering of anisotropic membrane constituents. Colloids Surf. A Physicochem. Eng. Asp. 2001, 179, 57–64. [Google Scholar]
- Rustom, A.; Saffrich, R.; Walther, P.; Markovic, I.; Gerdes, H.-H. Nanotubular Highways for Intercellular Organelle Transport. Science 2004, 303, 1007–1010. [Google Scholar] [CrossRef] [PubMed]
- Lou, E.; Fujisawa, S.; Morozov, A.; Barlas, A.; Romin, Y.; Dogan, Y.; Gholami, S.; Moreira, A.L.; Manova-Todorova, K.; Moore, M.A.S. Tunneling Nanotubes Provide a Unique Conduit for Intercellular Transfer of Cellular Contents in Human Malignant Pleural Mesothelioma. PLoS ONE 2012, 7, 33093. [Google Scholar] [CrossRef]
- Rupp, I.; Sologub, L.; Williamson, K.C.; Scheuermayer, M.; Reininger, L.; Doerig, C.; Eksi, S.; Kombila, D.U.; Frank, M.; Pradel, G. Malaria parasites form filamentous cell-to-cell connections during reproduction in the mosquito midgut. Cell Res. 2011, 21, 683. [Google Scholar] [CrossRef] [PubMed]
- Önfelt, B.; Nedvetzki, S.; Benninger, R.K.P.; Purbhoo, M.A.; Sowinski, S.; Hume, A.N.; Seabra, M.C.; Neil, M.A.A.; French, P.M.W.; Davis, D.M. Structurally Distinct Membrane Nanotubes between Human Macrophages Support Long-Distance Vesicular Traffic or Surfing of Bacteria. J. Immunol. 2006, 177, 8476–8483. [Google Scholar] [CrossRef]
- Gurke, S.; Barroso, J.F.V.; Gerdes, H.-H. The art of cellular communication: tunneling nanotubes bridge the divide. Histochem. Cell Biol. 2008, 129, 539–550. [Google Scholar] [CrossRef]
- Sowinski, S.; Jolly, C.; Berninghausen, O.; Purbhoo, M.A.; Chauveau, A.; Köhler, K.; Oddos, S.; Eissmann, P.; Brodsky, F.M.; Hopkins, C.; et al. Membrane nanotubes physically connect T cells over long distances presenting a novel route for HIV-1 transmission. Nature 2008, 10, 211–219. [Google Scholar] [CrossRef]
- Kabaso, D.; Lokar, M.; Kralj-Iglič, V.; Veranič, P.; Iglič, A.; Iglic, A. Temperature and cholera toxin B are factors that influence formation of membrane nanotubes in RT4 and T24 urothelial cancer cell lines. Int. J. Nanomed. 2011, 6, 495–509. [Google Scholar] [CrossRef]
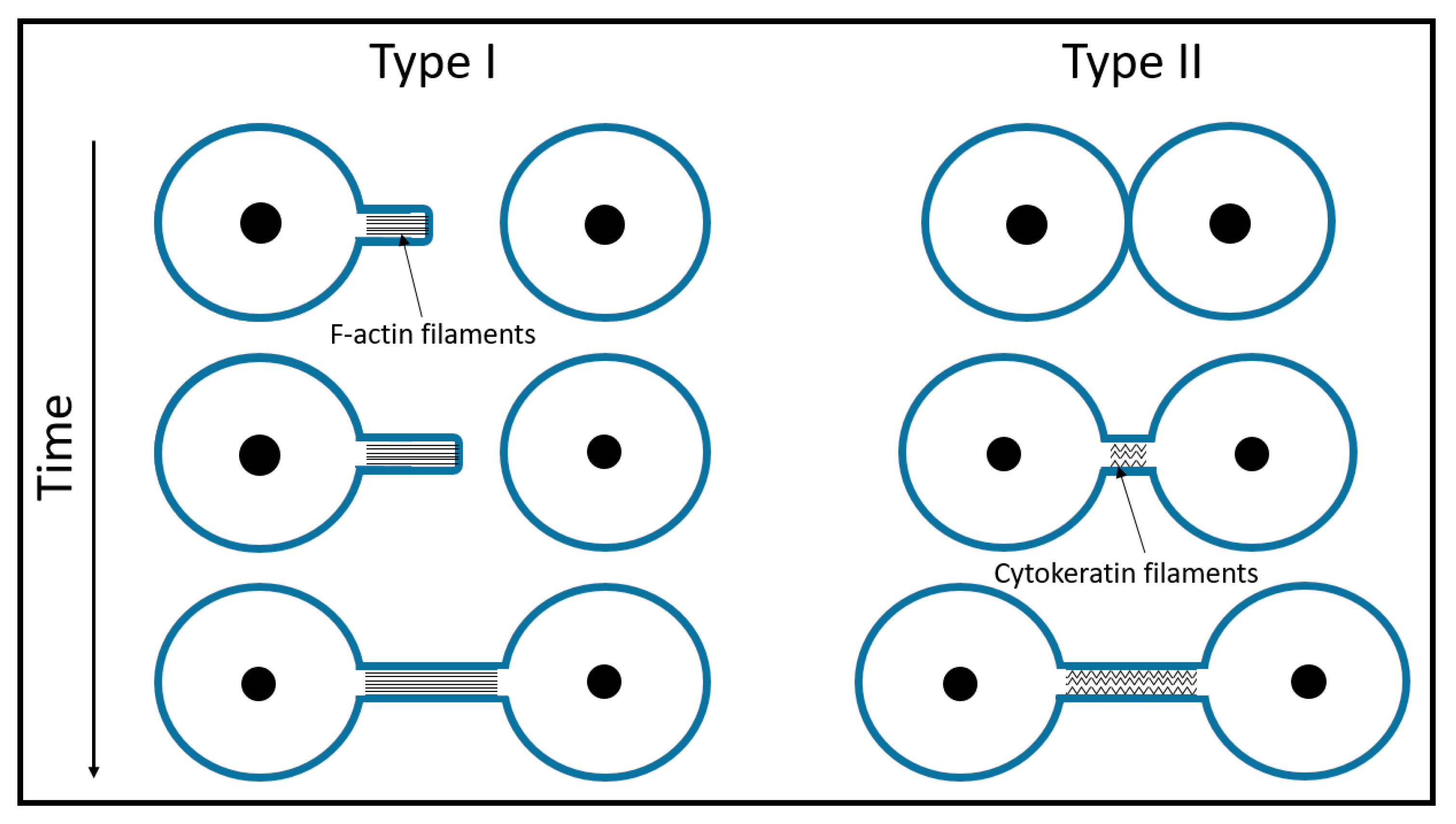
- Veranič, P.; Lokar, M.; Schütz, G.J.; Weghuber, J.; Wieser, S.; Hägerstrand, H.; Kralj-Iglič, V.; Iglič, A. Different Types of Cell-to-Cell Connections Mediated by Nanotubular Structures. Biophys. J. 2008, 95, 4416–4425. [Google Scholar] [CrossRef] [PubMed]
- Gerdes, H.-H.; Rustom, A.; Wang, X. Tunneling nanotubes, an emerging intercellular communication route in development. Mech. Dev. 2013, 130, 381–387. [Google Scholar] [CrossRef] [PubMed]
- Vignais, M.-L.; Caicedo, A.; Brondello, J.-M.; Jorgensen, C. Cell Connections by Tunneling Nanotubes: Effects of Mitochondrial Trafficking on Target Cell Metabolism, Homeostasis, and Response to Therapy. Stem Cells Int. 2017, 2017, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Austefjord, M.W.; Gerdes, H.H.; Wang, X. Tunneling nanotubes: Diversity in morphology and structure. Commun. Integr. Biol. 2014, 7, e27934. [Google Scholar] [CrossRef] [PubMed]
- Nawaz, M.; Fatima, F. Extracellular Vesicles, Tunneling Nanotubes, and Cellular Interplay: Synergies and Missing Links. Front. Mol. Biosci. 2017, 4, 50. [Google Scholar] [CrossRef] [PubMed]
- Dupont, M.; Souriant, S.; Lugo-Villarino, G.; Maridonneau-Parini, I.; Vérollet, C. Tunneling Nanotubes: Intimate Communication between Myeloid Cells. Front. Immunol. 2018, 9, 43. [Google Scholar] [CrossRef] [PubMed]
- Dubey, G.P.; Mohan, G.B.M.; Dubrovsky, A.; Amen, T.; Tsipshtein, S.; Rouvinski, A.; Rosenberg, A.; Kaganovich, D.; Sherman, E.; Medalia, O.; et al. Architecture and Characteristics of Bacterial Nanotubes. Dev. Cell 2016, 36, 453–461. [Google Scholar] [CrossRef]
- Dubey, G.P.; Ben-Yehuda, S. Intercellular Nanotubes Mediate Bacterial Communication. Cell 2011, 144, 590–600. [Google Scholar] [CrossRef]
- Ng, W.-L.; Bassler, B.L. Bacterial Quorum-Sensing Network Architectures. Annu. Rev. Genet. 2009, 43, 197–222. [Google Scholar] [CrossRef]
- Sretenovic, S.; Stojković, B.; Dogsa, I.; Kostanjšek, R.; Poberaj, I.; Stopar, D. An early mechanical coupling of planktonic bacteria in dilute suspensions. Nat. Commun. 2017, 8, 213. [Google Scholar] [CrossRef]
- Pande, S.; Shitut, S.; Freund, L.; Westermann, M.; Bertels, F.; Colesie, C.; Bischofs, I.B.; Kost, C. Metabolic cross-feeding via intercellular nanotubes among bacteria. Nat. Commun. 2015, 6, 6238. [Google Scholar] [CrossRef] [PubMed]
- Benomar, S.; Ranava, D.; Cárdenas, M.L.; Trably, E.; Rafrafi, Y.; Ducret, A.; Hamelin, J.; Lojou, É.; Steyer, J.-P.; Giudici-Orticoni, M.-T. Nutritional stress induces exchange of cell material and energetic coupling between bacterial species. Nat. Commun. 2015, 6, 6283. [Google Scholar] [CrossRef] [PubMed]
- Remis, J.P.; Wei, D.; Gorur, A.; Zemla, M.; Haraga, J.; Allen, S.; Witkowska, H.E.; Costerton, J.W.; Berleman, J.E.; Auer, M. Bacterial social networks: structure and composition of M yxococcus xanthus outer membrane vesicle chains. Environ. Microbiol. 2014, 16, 598–610. [Google Scholar] [CrossRef] [PubMed]
- Ducret, A.; Fleuchot, B.; Bergam, P.; Mignot, T.; Greenberg, P. Direct live imaging of cell–cell protein transfer by transient outer membrane fusion in Myxococcus xanthus. eLife 2013, 2, 00868. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Vassallo, C.N.; Pathak, D.T.; Wall, D. Myxobacteria Produce Outer Membrane-Enclosed Tubes in Unstructured Environments. J. Bacteriol. 2014, 196, 1807–1814. [Google Scholar] [CrossRef] [PubMed]
- Shetty, A.; Chen, S.; Tocheva, E.I.; Jensen, G.J.; Hickey, W.J. Nanopods: A New Bacterial Structure and Mechanism for Deployment of Outer Membrane Vesicles. PLoS ONE 2011, 6, e20725. [Google Scholar] [CrossRef] [PubMed]
- Pirbadian, S.; Barchinger, S.E.; Leung, K.M.; Byun, H.S.; Jangir, Y.; Bouhenni, R.A.; Reed, S.B.; Romine, M.F.; Saffarini, D.A.; Shi, L.; et al. Shewanella oneidensis MR-1 nanowires are outer membrane and periplasmic extensions of the extracellular electron transport components. Proc. Natl. Acad. Sci. USA 2014, 111, 12883–12888. [Google Scholar] [CrossRef]
- Osswald, M.; Jung, E.; Sahm, F.; Solecki, G.; Venkataramani, V.; Blaes, J.; Weil, S.; Horstmann, H.; Wiestler, B.; Syed, M.; et al. Brain tumour cells interconnect to a functional and resistant network. Nature 2015, 528, 93–98. [Google Scholar] [CrossRef]
- Panasiuk, M.; Rychłowski, M.; Derewońko, N.; Bieńkowska-Szewczyk, K. Tunneling Nanotubes as a Novel Route of Cell-to-Cell Spread of Herpesviruses. J. Virol. 2018, 92, e00090-18. [Google Scholar] [CrossRef]
- Delage, E.; Cervantes, D.C.; Pénard, E.; Schmitt, C.; Syan, S.; Disanza, A.; Scita, G.; Zurzolo, C. Differential identity of Filopodia and Tunneling Nanotubes revealed by the opposite functions of actin regulatory complexes. Sci. Rep. 2016, 6, 39632. [Google Scholar] [CrossRef]
- Gousset, K.; Schiff, E.; Langevin, C.; Marijanovic, Z.; Caputo, A.; Browman, D.T.; Chenouard, N.; De Chaumont, F.; Martino, A.; Enninga, J.; et al. Prions hijack tunnelling nanotubes for intercellular spread. Nature 2009, 11, 328–336. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Victoria, G.S.; Marzo, L.; Ghosh, R.; Zurzolo, C. Prion aggregates transfer through tunneling nanotubes in endocytic vesicles. Prion 2015, 9, 125–135. [Google Scholar] [CrossRef] [PubMed]
- Sowinski, S.; Alakoskela, J.-M.; Jolly, C.; Davis, D.M. Optimized methods for imaging membrane nanotubes between T cells and trafficking of HIV-1. Methods 2011, 53, 27–33. [Google Scholar] [CrossRef] [PubMed]
- Murooka, T.T.; Déruaz, M.; Marangoni, F.; Vrbanac, V.D.; Seung, E.; Von Andrian, U.H.; Tager, A.M.; Luster, A.D.; Mempel, T.R. HIV-infected T cells are migratory vehicles for viral dissemination. Nature 2012, 490, 283–287. [Google Scholar] [CrossRef] [PubMed]
- Malik, S.; Eugenin, E.A. Mechanisms of HIV neuropathogenesis: role of cellular communication systems. Curr. HIV Res. 2016, 14, 400–411. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, M.; Bhuyan, F.; Hiyoshi, M.; Noyori, O.; Nasser, H.; Miyazaki, M.; Saito, T.; Kondoh, Y.; Osada, H.; Kimura, S.; et al. Potential Role of the Formation of Tunneling Nanotubes in HIV-1 Spread in Macrophages. J. Immunol. 2016, 196, 1832–1841. [Google Scholar] [CrossRef] [PubMed]
- Hase, K.; Kimura, S.; Takatsu, H.; Ohmae, M.; Kawano, S.; Kitamura, H.; Ito, M.; Watarai, H.; Hazelett, C.C.; Yeaman, C.; et al. M-Sec promotes membrane nanotube formation by interacting with Ral and the exocyst complex. Nature 2009, 11, 1427–1432. [Google Scholar] [CrossRef] [PubMed]
- Davis, D.M.; Sowinski, S. Membrane nanotubes: dynamic long-distance connections between animal cells Daniel. Nat. Rev. Mol. Cell Biol. 2008, 9, 431–436. [Google Scholar] [CrossRef] [PubMed]
- Hurtig, J.; Chiu, D.T.; Önfelt, B. Intercellular nanotubes: Insights from imaging studies and beyond. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 2010, 2, 260–276. [Google Scholar] [CrossRef] [PubMed]
- McMahon, H.T.; Boucrot, E. Molecular mechanism and physiological functions of clathrin-mediated endocytosis. Nat. Rev. Mol. Cell Biol. 2011, 12, 517–533. [Google Scholar] [CrossRef]
- Liu, A.P.; Richmond, D.L.; Maibaum, L.; Pronk, S.; Geissler, P.L.; Fletcher, D.A. Membrane-induced bundling of actin filaments. Nat. Phys. 2008, 4, 789–793. [Google Scholar] [CrossRef] [PubMed]
- Jelerčič, U. Equilibrium shapes of tubular lipid membranes. Soft Matter 2017, 13, 3048–3052. [Google Scholar] [CrossRef] [PubMed]
- Mathivet, L.; Cribier, S.; Devaux, P. Shape change and physical properties of giant phospholipid vesicles prepared in the presence of an AC electric field. Biophys. J. 1996, 70, 1112–1121. [Google Scholar] [CrossRef]
- Angelova, M.; Soléau, S.; Méléard, P.; Faucon, F.; Bothorel, P. Preparation of giant vesicles by external AC electric fields. Kinetics and applications. In Trends in Colloid and Interface Science VI; Steinkopff: Darmstadt, Germany, 1992; pp. 127–131. [Google Scholar]
- Heinrich, V.; Waugh, R.E. A piconewton force transducer and its application to measurement of the bending stiffness of phospholipid membranes. Ann. Biomed. Eng. 1996, 24, 595–605. [Google Scholar] [CrossRef] [PubMed]
- Evans, E.; Bowman, H.; Leung, A.; Needham, D.; Tirrell, D. Biomembrane Templates for Nanoscale Conduits and Networks. Science 1996, 273, 933–935. [Google Scholar] [CrossRef] [PubMed]
- Waugh, R. Surface viscosity measurements from large bilayer vesicle tether formation. I. Analysis. Biophys. J. 1982, 38, 19–27. [Google Scholar] [CrossRef]
- Roux, A.; Cappello, G.; Cartaud, J.; Prost, J.; Goud, B.; Bassereau, P. A minimal system allowing tubulation with molecular motors pulling on giant liposomes. Proc. Natl. Acad. Sci. USA 2002, 99, 5394–5399. [Google Scholar] [CrossRef]
- Raucher, D.; Sheetz, M.P. Characteristics of a membrane reservoir buffering membrane tension. Biophys. J. 1999, 77, 1992–2002. [Google Scholar] [CrossRef]
- Perutková, Š.; Kralj-Iglič, V.; Frank, M.; Iglič, A. Mechanical stability of membrane nanotubular protrusions influenced by attachment of flexible rod-like proteins. J. Biomech. 2010, 43, 1612–1617. [Google Scholar] [CrossRef]
- Koster, G.; Cacciuto, A.; Derényi, I.; Frenkel, D.; Dogterom, M. Force Barriers for Membrane Tube Formation. Phys. Rev. Lett. 2005, 94, 16–19. [Google Scholar] [CrossRef]
- Rawicz, W.; Evans, E. Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys. Rev. Lett. 1990, 64, 2094–2097. [Google Scholar]
- Smith, A.-S.; Sackmann, E.; Seifert, U. Pulling Tethers from Adhered Vesicles. Phys. Rev. Lett. 2004, 92, 208101. [Google Scholar] [CrossRef] [PubMed]
- Derényi, I.; Jülicher, F.; Prost, J. Formation and Interaction of Membrane Tubes. Phys. Rev. Lett. 2002, 88, 238101. [Google Scholar]
- Li, Z.; Anvari, B.; Takashima, M.; Brecht, P.; Torres, J.H.; Brownell, W.E. Membrane Tether Formation from Outer Hair Cells with Optical Tweezers. Biophys. J. 2002, 82, 1386–1395. [Google Scholar] [CrossRef]
- Farsad, K.; De Camilli, P. Mechanisms of membrane deformation. Curr. Opin. Cell Biol. 2003, 15, 372–381. [Google Scholar] [CrossRef]
- Simons, K.; Ikonen, E. Functional rafts in cell membranes. Nature 1997, 387, 569–572. [Google Scholar] [CrossRef] [PubMed]
- Peter, B.J.; Kent, H.M.; Mills, I.G.; Vallis, Y.; Butler, P.J.G.; Evans, P.R.; McMahon, H.T. BAR Domains as Sensors of Membrane Curvature: The Amphiphysin BAR Structure. Science 2004, 303, 495–499. [Google Scholar] [CrossRef] [PubMed]
- Zimmerberg, J.; Kozlov, M.M. How proteins produce cellular membrane curvature. Nat Rev. Mol. Cell Biol. 2006, 7, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Veksler, A.; Gov, N.S. Phase Transitions of the Coupled Membrane-Cytoskeleton Modify Cellular Shape. Biophys. J. 2007, 93, 3798–3810. [Google Scholar] [CrossRef]
- Iglič, A.; Slivnik, T.; Kralj-Iglič, V. Elastic properties of biological membranes influenced by attached proteins. J. Biomech. 2007, 40, 2492–2500. [Google Scholar] [CrossRef]
- Kabaso, D.; Bobrovska, N.; Góźdź, W.; Gov, N.; Kralj-Iglič, V.; Veranič, P.; Iglič, A. On the role of membrane anisotropy and BAR proteins in the stability of tubular membrane structures. J. Biomech. 2012, 45, 231–238. [Google Scholar] [CrossRef] [PubMed]
- Powell, K. Cell biology: ahead of the curve. Nat. News 2009, 460, 318–320. [Google Scholar] [CrossRef] [PubMed]
- Tian, A.; Baumgart, T. Sorting of Lipids and Proteins in Membrane Curvature Gradients. Biophys. J. 2009, 96, 2676–2688. [Google Scholar] [CrossRef] [PubMed]
- Prevost, C.; Zhao, H.; Manzi, J.; Lemichez, E.; Lappalainen, P.; Callan-Jones, A.; Bassereau, P. IRSp53 senses negative membrane curvature and phase separates along membrane tubules. Nat. Commun. 2015, 6, 8529. [Google Scholar] [CrossRef] [PubMed]
- Shlomovitz, R.; Gov, N.S.; Roux, A. Membrane-mediated interactions and the dynamics of dynamin oligomers on membrane tubes. New J. Phys. 2011, 13, 65008. [Google Scholar] [CrossRef]
- Bobrovska, N.; Góźdź, W.; Kralj-Iglič, V.; Iglič, A. On the Role of Anisotropy of Membrane Components in Formation and Stabilization of Tubular Structures in Multicomponent Membranes. PLoS ONE 2013, 8, e73941. [Google Scholar] [CrossRef] [PubMed]
- Kralj-Iglič, V. Stability of membranous nanostructures: A possible key mechanism in cancer progression. Int. J. Nanomed. 2012, 7, 3579–3596. [Google Scholar] [CrossRef] [PubMed]
- Mesarec, L.; Góźdź, W.; Iglič, V.K.; Kralj, S.; Iglič, A. Closed membrane shapes with attached BAR domains subject to external force of actin filaments. Colloids Surf. B Biointerfaces 2016, 141, 132–140. [Google Scholar] [CrossRef] [PubMed]
- Kralj-Iglič, V.; Heinrich, V.; Svetina, S.; Žekš, B. Free energy of closed membrane with anisotropic inclusions. Europ. Phys. J. B 1999, 10, 5–8. [Google Scholar] [CrossRef]
- Kralj-Iglič, V.; Remskar, M.; Vidmar, G.; Fošnarič, M.; Iglič, A. Deviatoric elasticity as a possible physical mechanism explaining collapse of inorganic micro and nanotubes. Phys. Lett. A 2002, 296, 151–155. [Google Scholar] [CrossRef]
- Kralj-Iglic, V.; Remskar, M.; Iglic, A. Deviatoric elasticity as a mechanism describing stable shapes of nanotubes. Horiz. World Phys. 2004, 244, 111–156. [Google Scholar]
- Mesarec, L.; Iglič, A.; Kralj, S. In-Plane Membrane Ordering and Topological Defects. Nanomed. Nanotechnol. Open Access 2018, 3, 1–8. [Google Scholar]
- Drab, M.; Mesarec, L.; Imani, R.; Jeran, M.; Junkar, I.; Kralj-Iglič, V.; Kralj, S.; Iglič, A. The role of membrane vesiculation and encapsulation in cancer diagnosis and therapy. Adv. Biomembr. Lipid Self-Assem. 2019, 29, 159–199. [Google Scholar]
- Schara, K.; Janša, V.; Šuštar, V.; Dolinar, D.; Pavlič, J.I.; Lokar, M.; Kralj-Iglič, V.; Veranič, P.; Iglič, A. Mechanisms for the formation of membranous nanostructures in cell-to-cell communication. Cell. Mol. Biol. Lett. 2009, 14, 636–656. [Google Scholar] [CrossRef] [PubMed]
- Kabaso, D.; Bobrovska, N.; Góźdź, W.; Gongadze, E.; Kralj-Iglič, V.; Zorec, R.; Iglič, A. The transport along membrane nanotubes driven by the spontaneous curvature of membrane components. Bioelectrochemistry 2012, 87, 204–210. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Ladinsky, M.S.; Kirchhausen, T.; Linstedt, A. Cisternal Organization of the Endoplasmic Reticulum during Mitosis. Mol. Biol. Cell 2009, 20, 3471–3480. [Google Scholar] [CrossRef]
- Wu, M.; Huang, B.; Graham, M.; Raimondi, A.; Heuser, J.E.; Zhuang, X.; De Camilli, P. Coupling between clathrin-dependent endocytic budding and F-BAR-dependent tubulation in a cell-free system. Nature 2010, 12, 902–908. [Google Scholar]
- Dannhauser, P.N.; Ungewickell, E.J. Reconstitution of clathrin-coated bud and vesicle formation with minimal components. Nature 2012, 14, 634–639. [Google Scholar] [CrossRef]
- Stachowiak, J.C.; Schmid, E.M.; Ryan, C.J.; Ann, H.S.; Sasaki, D.Y.; Sherman, M.B.; Geissler, P.L.; Fletcher, D.A.; Hayden, C.C. Membrane bending by protein–protein crowding. Nature 2012, 14, 944–949. [Google Scholar] [CrossRef]
- Basquin, C.; Trichet, M.; Vihinen, H.; Malardé, V.; Lagache, T.; Ripoll, L.; Jokitalo, E.; Olivo-Marin, J.-C.; Gautreau, A.; Sauvonnet, N. Membrane protrusion powers clathrin-independent endocytosis of interleukin-2 receptor. EMBO J. 2015, 34, 2147–2161. [Google Scholar] [CrossRef]
- Dawson, J.C.; Legg, J.A.; Machesky, L.M. Bar domain proteins: a role in tubulation, scission and actin assembly in clathrin-mediated endocytosis. Trends Cell Biol. 2006, 16, 493–498. [Google Scholar] [CrossRef] [PubMed]
- Kaksonen, M.; Toret, C.P.; Drubin, D.G. Harnessing actin dynamics for clathrin-mediated endocytosis. Nat. Rev. Mol. Cell Biol. 2006, 7, 404–414. [Google Scholar] [CrossRef] [PubMed]
- Peleg, B.; Disanza, A.; Scita, G.; Gov, N. Propagating Cell-Membrane Waves Driven by Curved Activators of Actin Polymerization. PLoS ONE 2011, 6, 18635. [Google Scholar] [CrossRef] [PubMed]
- Gov, N.S.; Gopinathan, A. Dynamics of membranes driven by actin polymerization. Biophys. J. 2006, 90, 454–469. [Google Scholar] [CrossRef] [PubMed]
- Gov, N.S. Guided by curvature: shaping cells by coupling curved membrane proteins and cytoskeletal forces. Philos. Trans. R. Soc. B Biol. Sci. 2018, 373, 20170115. [Google Scholar] [CrossRef] [PubMed]
- Scita, G.; Confalonieri, S.; Lappalainen, P.; Suetsugu, S. IRSp53: crossing the road of membrane and actin dynamics in the formation of membrane protrusions. Trends Cell Biol. 2008, 18, 52–60. [Google Scholar] [CrossRef] [PubMed]
- Kast, D.J.; Yang, C.; Disanza, A.; Boczkowska, M.; Madasu, Y.; Scita, G.; Svitkina, T.; Domínguez, R. Mechanism of IRSp53 inhibition and combinatorial activation by Cdc42 and downstream effectors. Nat. Struct. Mol. Biol. 2014, 21, 413–422. [Google Scholar] [CrossRef] [PubMed]
- Disanza, A.; Bisi, S.; Winterhoff, M.; Milanesi, F.; Ushakov, D.S.; Kast, D.; Marighetti, P.; Müller, H.-M.; Nickel, W.; Linkner, J.; et al. CDC42 switches IRSp53 from inhibition of actin growth to elongation by clustering of VASP. EMBO J. 2013, 32, 2735–2750. [Google Scholar] [CrossRef] [PubMed]
- Kühn, S.; Erdmann, C.; Kage, F.; Block, J.; Schwenkmezger, L.; Steffen, A.; Rottner, K.; Geyer, M. The structure of FMNL2–Cdc42 yields insights into the mechanism of lamellipodia and filopodia formation. Nat. Commun. 2015, 6, 7088. [Google Scholar] [CrossRef]
- Sonnino, S.; Mauri, L.; Chigorno, V.; Prinetti, A. Gangliosides as components of lipid membrane domains. Glycobiology 2006, 17, 1R–13R. [Google Scholar] [CrossRef] [PubMed]
- Mesarec, L.; Góźdź, W.; Kralj, S.; Fošnarič, M.; Penič, S.; Kralj-Iglič, V.; Iglič, A. On the role of external force of actin filaments in the formation of tubular protrusions of closed membrane shapes with anisotropic membrane components. Eur. Biophys. J. 2017, 46, 705–718. [Google Scholar] [CrossRef] [PubMed]
- Kralj-Iglič, V.; Hägerstrand, H.; Veranič, P.; Jezernik, K.; Babnik, B.; Gauger, D.R.; Iglič, A. Amphiphile-induced tubular budding of the bilayer membrane. Eur. Biophys. J. 2005, 34, 1066–1070. [Google Scholar] [CrossRef] [PubMed]
- Fošnarič, M.; Penič, S.; Iglič, A.; Kralj-Iglič, V.; Drab, M.; Gov, N. Theoretical study of vesicle shapes driven by coupling curved proteins and active cytoskeletal forces. Soft Matter 2018, 1–12. [Google Scholar] [CrossRef]
- Iglič, A.; Kralj-Iglič, V.; Majhenc, J. Cylindrical shapes of closed lipid bilayer structures correspond to an extreme area difference between the two monolayers of the bilayer. J. Biomech. 1999, 32, 1343–1347. [Google Scholar] [CrossRef]
- Ziserman, L.; Mor, A.; Harries, D.; Danino, D. Curvature Instability in a Chiral Amphiphile Self-Assembly. Phys. Rev. Lett. 2011, 106, 238105. [Google Scholar] [CrossRef] [PubMed]
- Kralj-Iglič, V.; Iglič, A.; Hägerstrand, H.; Peterlin, P. Stable tubular microexovesicles of the erythrocyte membrane induced by dimeric amphiphiles. Phys. Rev. E 2000, 61, 4230. [Google Scholar]
- Góźdź, W.T. Spontaneous Curvature Induced Shape Transformations of Tubular Polymersomes. Langmuir 2004, 20, 7385–7391. [Google Scholar] [CrossRef] [PubMed]
- Saarikangas, J.; Kourdougli, N.; Senju, Y.; Chazal, G.; Segerstråle, M.; Minkeviciene, R.; Kuurne, J.; Mattila, P.K.; Garrett, L.; Hölter, S.M.; et al. MIM-Induced Membrane Bending Promotes Dendritic Spine Initiation. Dev. Cell 2015, 33, 644–659. [Google Scholar] [CrossRef]
- Ahmed, S.; Goh, W.I.; Bu, W. I-BAR domains, IRSp53 and filopodium formation. Semin. Cell Dev. Biol. 2010, 21, 350–356. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drab, M.; Stopar, D.; Kralj-Iglič, V.; Iglič, A. Inception Mechanisms of Tunneling Nanotubes. Cells 2019, 8, 626. https://doi.org/10.3390/cells8060626
Drab M, Stopar D, Kralj-Iglič V, Iglič A. Inception Mechanisms of Tunneling Nanotubes. Cells. 2019; 8(6):626. https://doi.org/10.3390/cells8060626
Chicago/Turabian StyleDrab, Mitja, David Stopar, Veronika Kralj-Iglič, and Aleš Iglič. 2019. "Inception Mechanisms of Tunneling Nanotubes" Cells 8, no. 6: 626. https://doi.org/10.3390/cells8060626
APA StyleDrab, M., Stopar, D., Kralj-Iglič, V., & Iglič, A. (2019). Inception Mechanisms of Tunneling Nanotubes. Cells, 8(6), 626. https://doi.org/10.3390/cells8060626






