SINFONIA: Scalable Identification of Spatially Variable Genes for Deciphering Spatial Domains
Abstract
1. Introduction
2. Materials and Methods
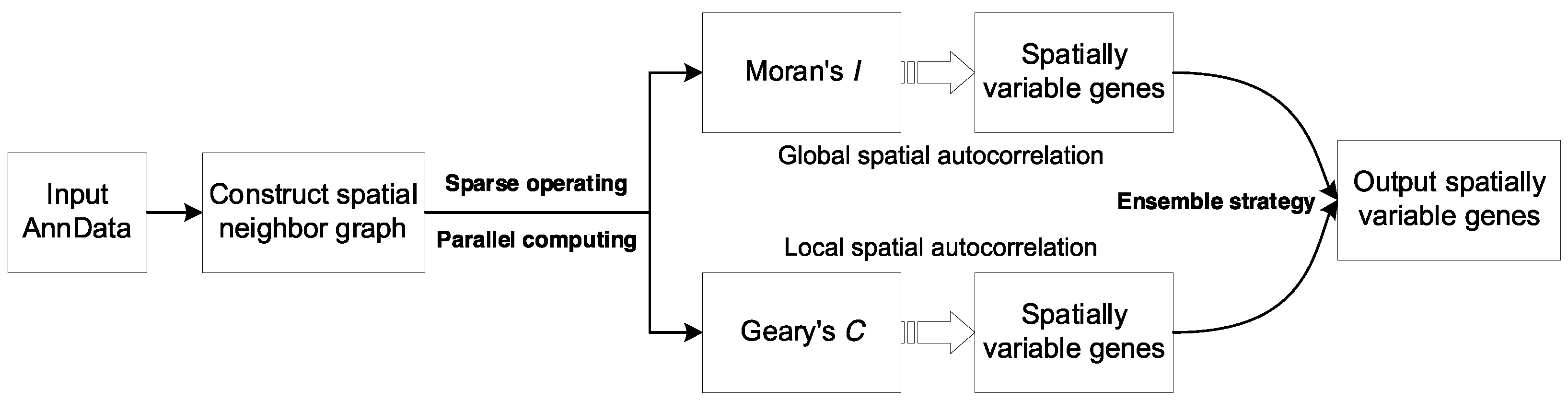
2.1. Construction of Spatial Neighbor Graph
2.2. Calculation of Spatial Autocorrelation Statistics
2.3. Identification of Spatially Variable Genes
2.4. Implementation and Usage of SINFONIA
2.5. Data Collection
2.6. Performance Evaluation
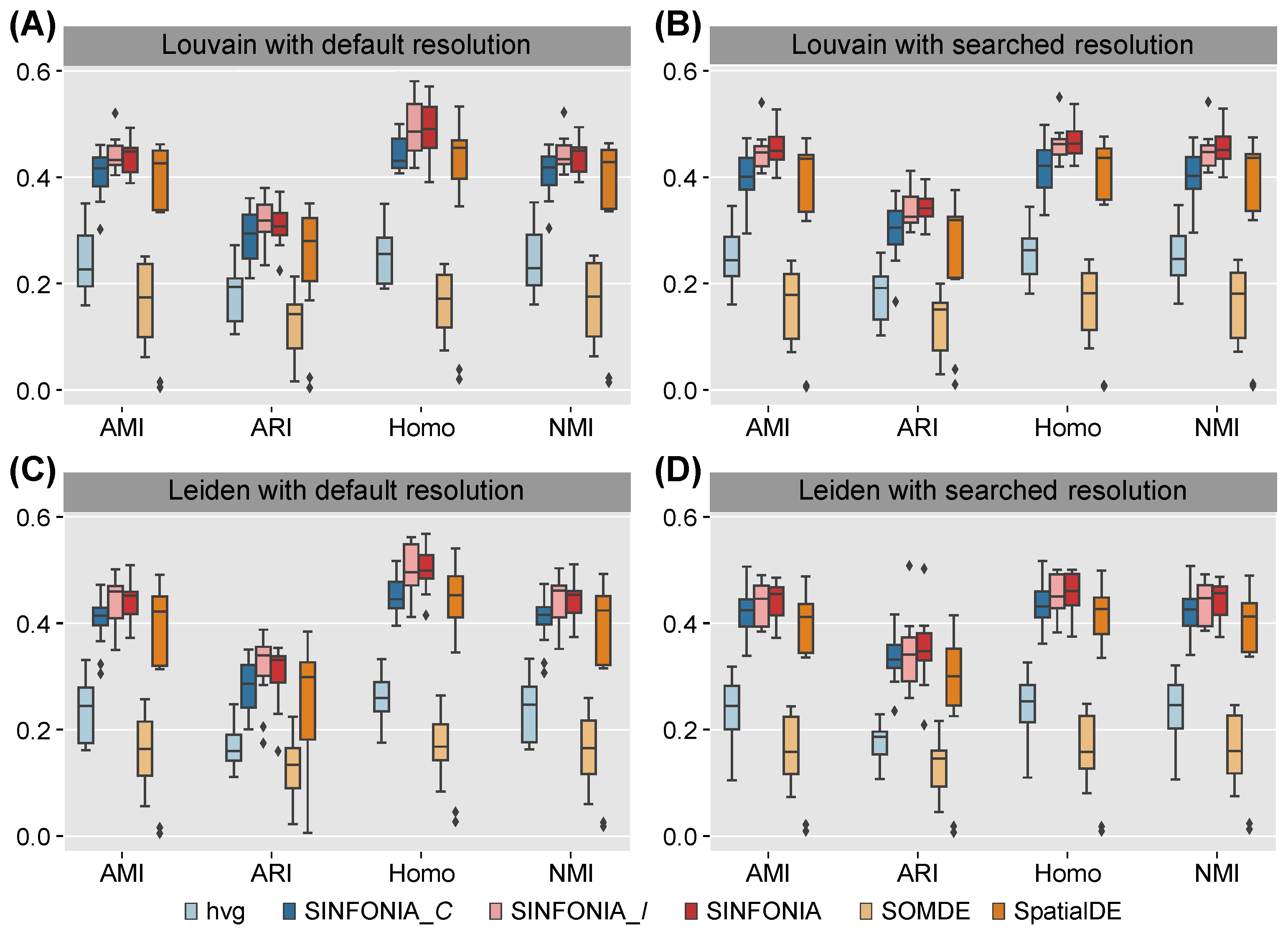
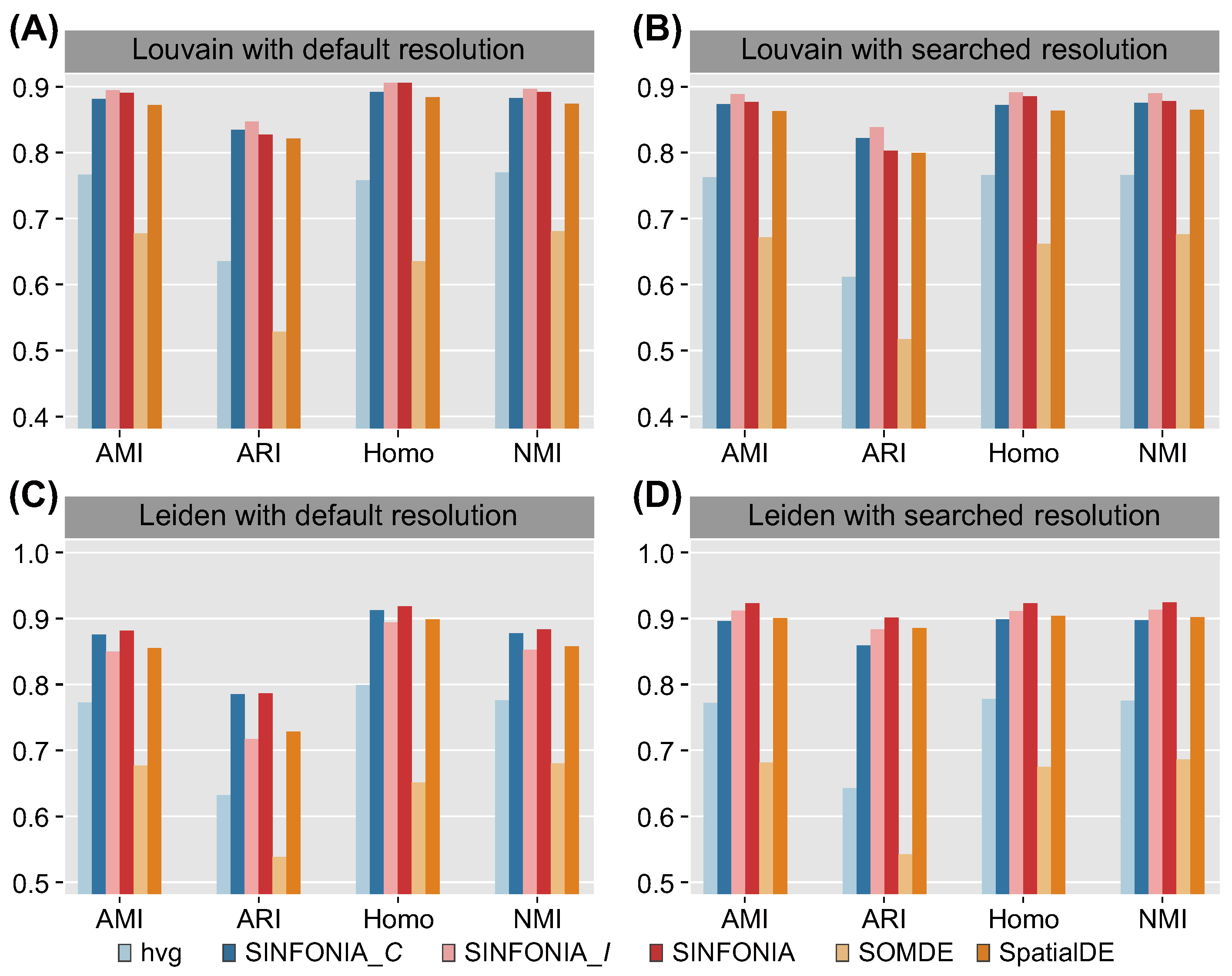
2.6.1. Spatial Clustering
2.6.2. Domain Resolution
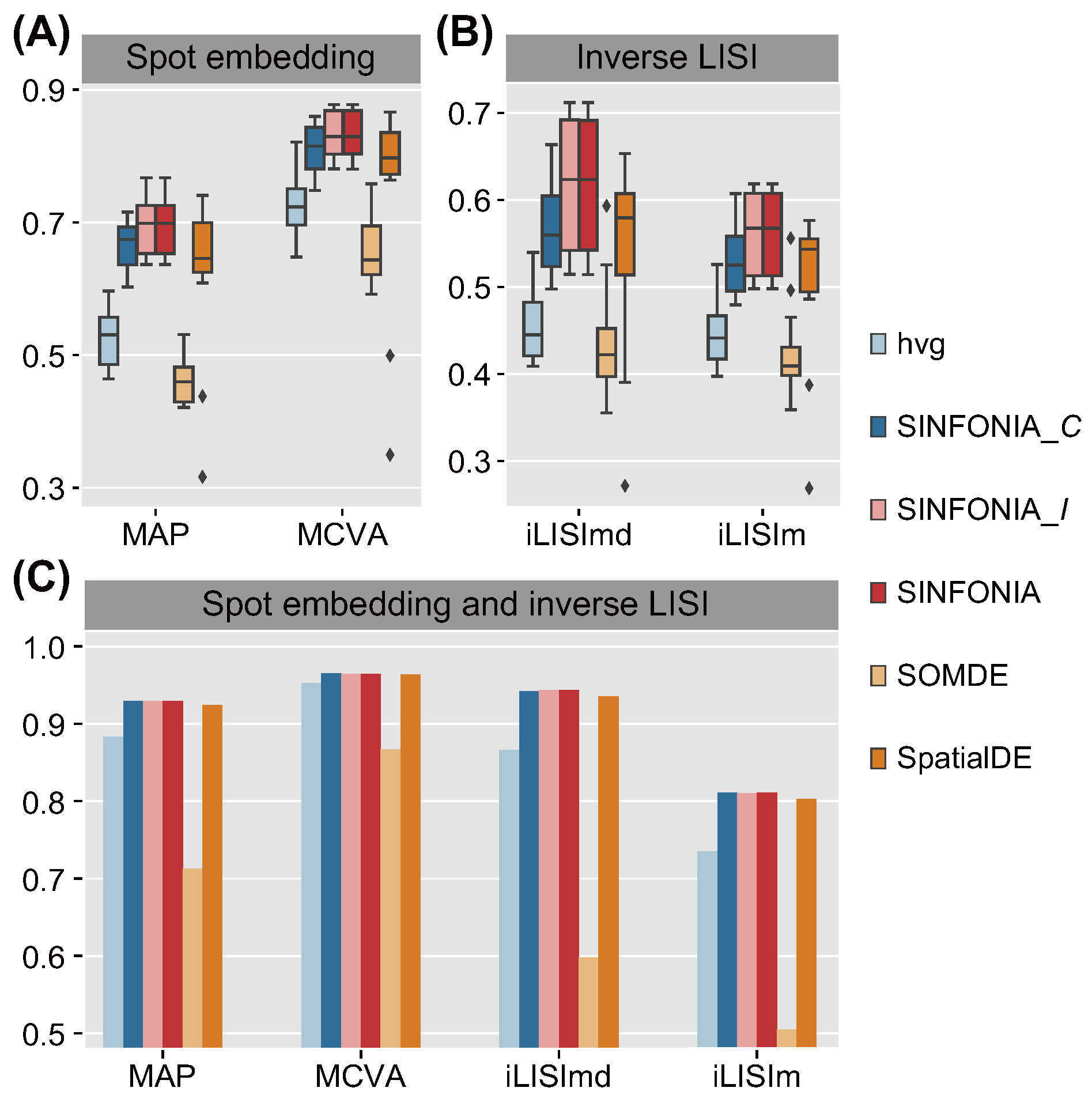
2.6.3. Latent Representation
2.6.4. Spot Visualization
2.6.5. Computational Efficiency
2.7. Baseline Methods
3. Results
3.1. SINFONIA Enables Accurate Spatial Clustering
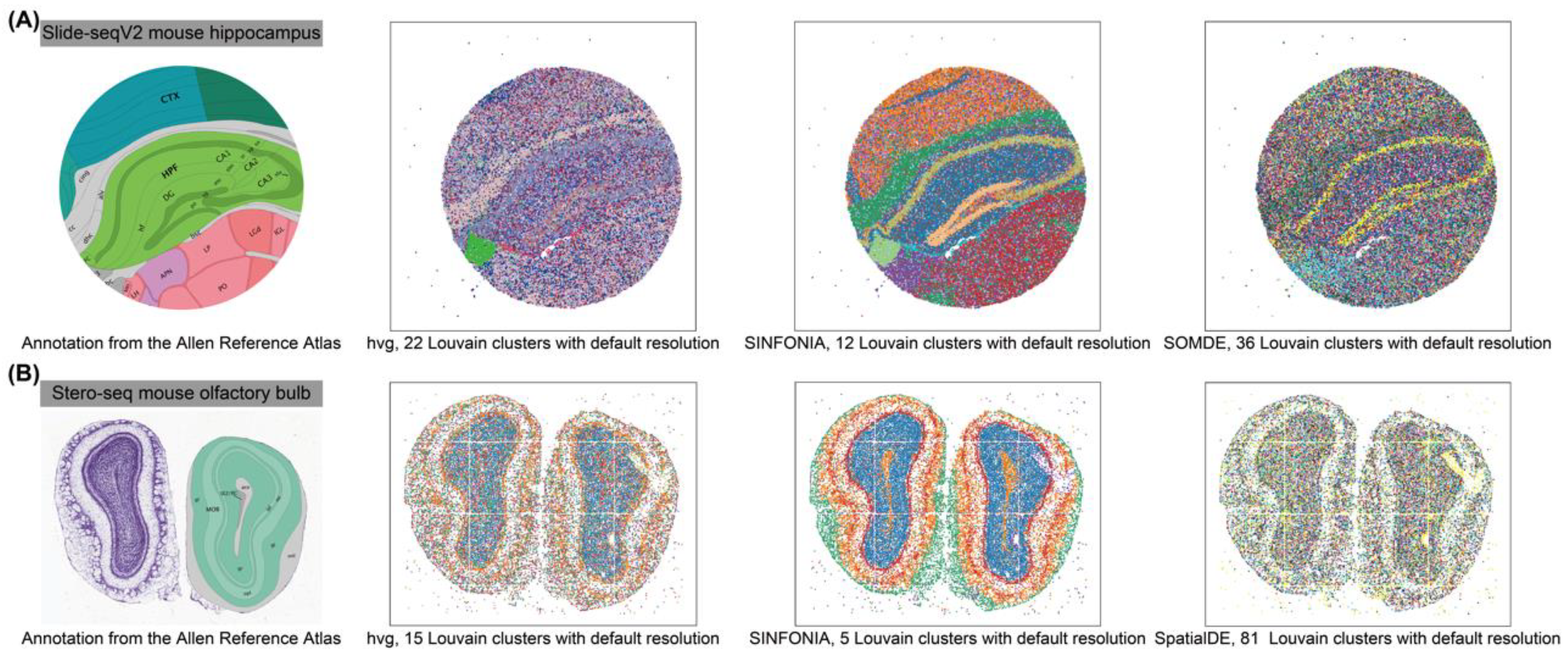
3.2. SINFONIA Effectively Characterizes Spatial Patterns
3.3. SINFONIA Facilitates Interpretable Spot Visualization
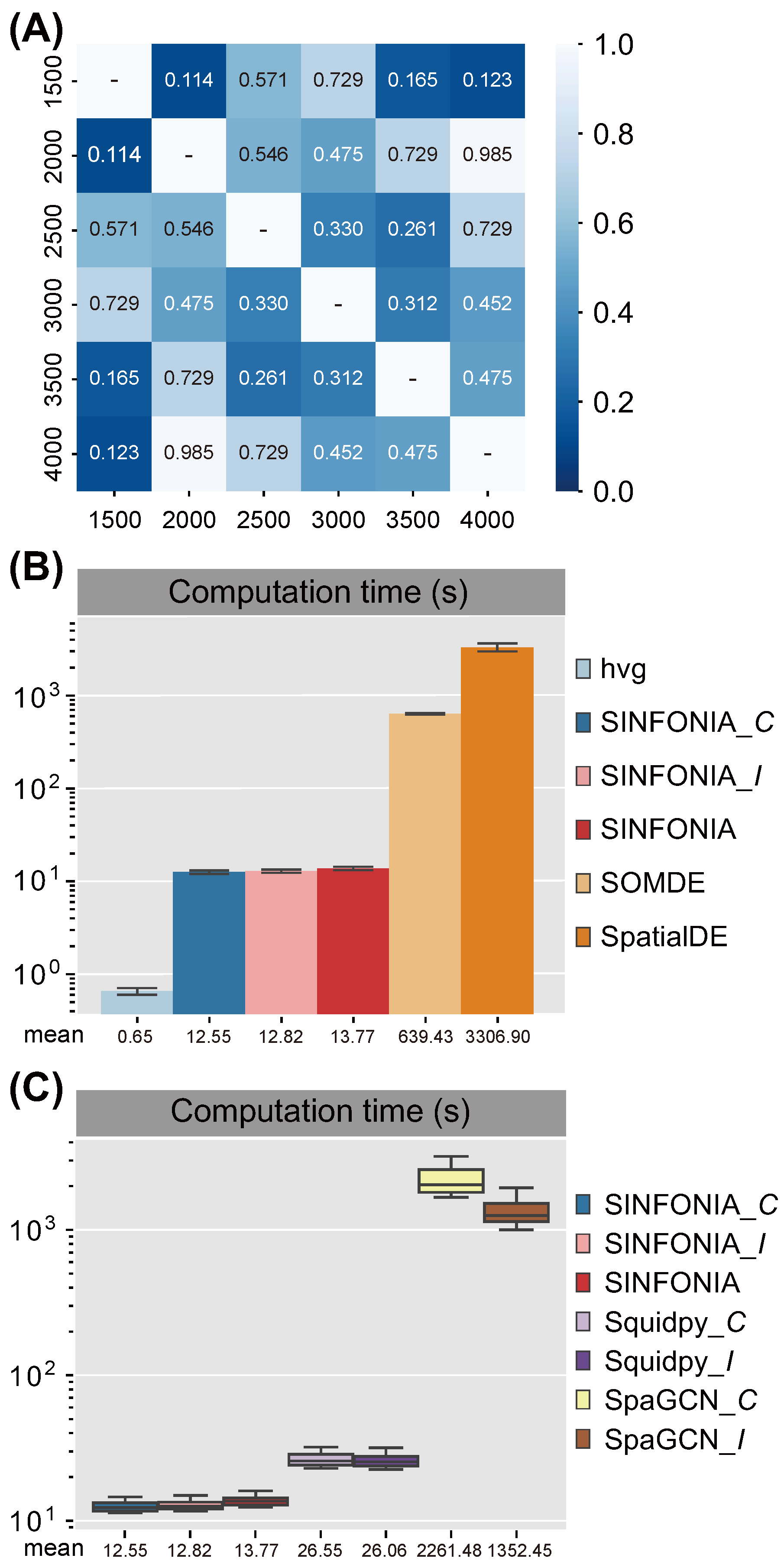
3.4. SINFONIA Is Robust and Computationally Efficient
3.5. SINFONIA Improves the Performance of Other Spatial Embedding Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Svensson, V.; Teichmann, S.A.; Stegle, O. SpatialDE: Identification of spatially variable genes. Nat. Methods 2018, 15, 343–346. [Google Scholar] [CrossRef] [PubMed]
- Hao, Y.; Hao, S.; Andersen-Nissen, E.; Mauck, W.M., III; Zheng, S.; Butler, A.; Lee, M.J.; Wilk, A.J.; Darby, C.; Zager, M.; et al. Integrated analysis of multimodal single-cell data. Cell 2021, 184, 3573–3587.e29. [Google Scholar] [CrossRef] [PubMed]
- Palla, G.; Spitzer, H.; Klein, M.; Fischer, D.; Schaar, A.C.; Kuemmerle, L.B.; Rybakov, S.; Ibarra, I.L.; Holmberg, O.; Virshup, I.; et al. Squidpy: A scalable framework for spatial omics analysis. Nat. Methods 2022, 19, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Abdelaal, T.; Mourragui, S.; Mahfouz, A.; Reinders, M.J.T. SpaGE: Spatial Gene Enhancement using scRNA-seq. Nucleic Acids Res. 2020, 48, E107. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Li, X.; Coleman, K.; Schroeder, A.; Ma, N.; Irwin, D.J.; Lee, E.B.; Shinohara, R.T.; Li, M. SpaGCN: Integrating gene expression, spatial location and histology to identify spatial domains and spatially variable genes by graph convolutional network. Nat. Methods 2021, 18, 1342–1351. [Google Scholar] [CrossRef]
- Li, K.; Yan, C.; Li, C.; Chen, L.; Zhao, J.; Zhang, Z.; Bao, S.; Sun, J.; Zhou, M. Computational elucidation of spatial gene expression variation from spatially resolved transcriptomics data. Mol. Ther. Nucleic Acids 2022, 27, 404–411. [Google Scholar] [CrossRef]
- Lu, L.; Welch, J.D. PyLiger: Scalable single-cell multi-omic data integration in Python. Bioinformatics 2022, 38, 2946–2948. [Google Scholar] [CrossRef]
- Wolf, F.A.; Angerer, P.; Theis, F.J. SCANPY: Large-scale single-cell gene expression data analysis. Genome Biol. 2018, 19, 15. [Google Scholar] [CrossRef]
- Gayoso, A.; Lopez, R.; Xing, G.; Boyeau, P.; Valiollah Pour Amiri, V.; Hong, J.; Wu, K.; Jayasuriya, M.; Mehlman, E.; Langevin, M.; et al. A Python library for probabilistic analysis of single-cell omics data. Nat. Biotechnol. 2022, 40, 163–166. [Google Scholar] [CrossRef]
- Bae, S.; Choi, H.; Lee, D.S. Discovery of molecular features underlying the morphological landscape by integrating spatial transcriptomic data with deep features of tissue images. Nucleic Acids Res. 2021, 49, e55. [Google Scholar] [CrossRef]
- BinTayyash, N.; Georgaka, S.; John, S.T.; Ahmed, S.; Boukouvalas, A.; Hensman, J.; Rattray, M. Non-parametric modelling of temporal and spatial counts data from RNA-seq experiments. Bioinformatics 2021, 37, 3788–3795. [Google Scholar] [CrossRef] [PubMed]
- Hao, M.; Hua, K.; Zhang, X. SOMDE: A scalable method for identifying spatially variable genes with self-organizing map. Bioinformatics 2021, 37, 4392–4398. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Shah, S.; Dries, R.; Cai, L.; Yuan, G.C. Identification of spatially associated subpopulations by combining scRNAseq and sequential fluorescence in situ hybridization data. Nat. Biotechnol. 2018, 36, 1183–1190. [Google Scholar] [CrossRef] [PubMed]
- Dong, K.; Zhang, S. Deciphering spatial domains from spatially resolved transcriptomics with an adaptive graph attention auto-encoder. Nat. Commun. 2022, 13, 1739. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, B.; Chen, X.; Zhang, X.; Jiang, R. stPlus: A reference-based method for the accurate enhancement of spatial transcriptomics. Bioinformatics 2021, 37, i299–i307. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, Y.; Li, Y.; Luo, Y. Statistical and machine learning methods for spatially resolved transcriptomics data analysis. Genome Biol. 2022, 23, 83. [Google Scholar] [CrossRef]
- Moran, P.A. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Geary, R.C. The Contiguity Ratio and Statistical Mapping. Inc. Stat. 1954, 5, 115–146. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Lahnemann, D.; Koster, J.; Szczurek, E.; McCarthy, D.J.; Hicks, S.C.; Robinson, M.D.; Vallejos, C.A.; Campbell, K.R.; Beerenwinkel, N.; Mahfouz, A.; et al. Eleven grand challenges in single-cell data science. Genome Biol 2020, 21, 31. [Google Scholar] [CrossRef]
- Pardo, B.; Spangler, A.; Weber, L.M.; Page, S.C.; Hicks, S.C.; Jaffe, A.E.; Martinowich, K.; Maynard, K.R.; Collado-Torres, L. spatialLIBD: An R/Bioconductor package to visualize spatially-resolved transcriptomics data. BMC Genom. 2022, 23, 434. [Google Scholar] [CrossRef] [PubMed]
- Maynard, K.R.; Collado-Torres, L.; Weber, L.M.; Uytingco, C.; Barry, B.K.; Williams, S.R.; Catallini, J.L., II; Tran, M.N.; Besich, Z.; Tippani, M.; et al. Transcriptome-scale spatial gene expression in the human dorsolateral prefrontal cortex. Nat. Neurosci. 2021, 24, 425–436. [Google Scholar] [CrossRef]
- 10XGenomics. Visium Spatial Gene Expression Reagent Kits User Guide. 2021. Available online: https://www.10xgenomics.com/support/spatial-gene-expression-fresh-frozen/documentation/steps/library-construction/visium-spatial-gene-expression-reagent-kits-user-guide (accessed on 17 July 2022).
- Sunkin, S.M.; Ng, L.; Lau, C.; Dolbeare, T.; Gilbert, T.L.; Thompson, C.L.; Hawrylycz, M.; Dang, C. Allen Brain Atlas: An integrated spatio-temporal portal for exploring the central nervous system. Nucleic Acids Res. 2013, 41, D996–D1008. [Google Scholar] [CrossRef] [PubMed]
- Gracia Villacampa, E.; Larsson, L.; Mirzazadeh, R.; Kvastad, L.; Andersson, A.; Mollbrink, A.; Kokaraki, G.; Monteil, V.; Schultz, N.; Appelberg, K.S.; et al. Genome-wide spatial expression profiling in formalin-fixed tissues. Cell Genom. 2021, 1, 100065. [Google Scholar] [CrossRef]
- Stickels, R.R.; Murray, E.; Kumar, P.; Li, J.; Marshall, J.L.; Di Bella, D.J.; Arlotta, P.; Macosko, E.Z.; Chen, F. Highly sensitive spatial transcriptomics at near-cellular resolution with Slide-seqV2. Nat. Biotechnol. 2021, 39, 313–319. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.; Liao, S.; Cheng, M.; Ma, K.; Wu, L.; Lai, Y.; Qiu, X.; Yang, J.; Xu, J.; Hao, S.; et al. Spatiotemporal transcriptomic atlas of mouse organogenesis using DNA nanoball-patterned arrays. Cell 2022, 185, 1777–1792.e1721. [Google Scholar] [CrossRef]
- Stuart, T.; Butler, A.; Hoffman, P.; Hafemeister, C.; Papalexi, E.; Mauck, W.M., 3rd; Hao, Y.; Stoeckius, M.; Smibert, P.; Satija, R. Comprehensive Integration of Single-Cell Data. Cell 2019, 177, 1888–1902.e21. [Google Scholar] [CrossRef]
- Chen, H.; Lareau, C.; Andreani, T.; Vinyard, M.E.; Garcia, S.P.; Clement, K.; Andrade-Navarro, M.A.; Buenrostro, J.D.; Pinello, L. Assessment of computational methods for the analysis of single-cell ATAC-seq data. Genome Biol. 2019, 20, 241. [Google Scholar] [CrossRef]
- Danese, A.; Richter, M.L.; Chaichoompu, K.; Fischer, D.S.; Theis, F.J.; Colome-Tatche, M. EpiScanpy: Integrated single-cell epigenomic analysis. Nat. Commun. 2021, 12, 5228. [Google Scholar] [CrossRef]
- Chen, S.; Wang, R.; Long, W.; Jiang, R. ASTER: Accurately estimating the number of cell types in single-cell chromatin accessibility data. Bioinformatics 2023, 39, btac842. [Google Scholar] [CrossRef]
- Chen, S.; Yan, G.; Zhang, W.; Li, J.; Jiang, R.; Lin, Z. RA3 is a reference-guided approach for epigenetic characterization of single cells. Nat. Commun. 2021, 12, 2177. [Google Scholar] [CrossRef] [PubMed]
- Vinh, N.X.; Epps, J.; Bailey, J. Information theoretic measures for clusterings comparison: Is a correction for chance necessary? In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 1073–1080. [Google Scholar]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Rosenberg, A.; Hirschberg, J. V-Measure: A Conditional Entropy-Based External Cluster Evaluation Measure. 2007, pp. 410–420. Available online: https://aclanthology.org/D07-1043.pdf (accessed on 17 July 2022).
- Strehl, A.; Ghosh, J. Cluster ensembles—A knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 2003, 3, 583–617. [Google Scholar] [CrossRef]
- Romano, S.; Vinh, N.X.; Bailey, J.; Verspoor, K. Adjusting for chance clustering comparison measures. J. Mach. Learn. Res. 2016, 17, 1–32. [Google Scholar]
- Cao, Z.-J.; Gao, G. Multi-omics single-cell data integration and regulatory inference with graph-linked embedding. Nat. Biotechnol. 2022, 40, 1458–1466. [Google Scholar] [CrossRef] [PubMed]
- Abdelaal, T.; Michielsen, L.; Cats, D.; Hoogduin, D.; Mei, H.; Reinders, M.J.T.; Mahfouz, A. A comparison of automatic cell identification methods for single-cell RNA sequencing data. Genome Biol. 2019, 20, 194. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Su, K.; Wu, H. Evaluation of some aspects in supervised cell type identification for single-cell RNA-seq: Classifier, feature selection, and reference construction. Genome Biol. 2021, 22, 264. [Google Scholar] [CrossRef] [PubMed]
- Korsunsky, I.; Millard, N.; Fan, J.; Slowikowski, K.; Zhang, F.; Wei, K.; Baglaenko, Y.; Brenner, M.; Loh, P.R.; Raychaudhuri, S. Fast, sensitive and accurate integration of single-cell data with Harmony. Nat. Methods 2019, 16, 1289–1296. [Google Scholar] [CrossRef]
- Shang, L.; Zhou, X. Spatially Aware Dimension Reduction for Spatial Transcriptomics. Nat. Commun. 2022, 13, 7203. [Google Scholar] [CrossRef]
- Mangul, S.; Martin, L.S.; Eskin, E.; Blekhman, R. Improving the usability and archival stability of bioinformatics software. Genome Biol. 2019, 20, 47. [Google Scholar] [CrossRef]

| Dataset | # of Spots | # of Genes | # of Domains | Sparsity | Protocol | Species | Reference |
|---|---|---|---|---|---|---|---|
| DLPFC_151507 | 4221 | 33,538 | 7 | 0.958 | 10X Visium | Homo sapiens | [22] |
| DLPFC_151508 | 4381 | 33,538 | 7 | 0.964 | 10X Visium | Homo sapiens | [22] |
| DLPFC_151509 | 4788 | 33,538 | 7 | 0.957 | 10X Visium | Homo sapiens | [22] |
| DLPFC_151510 | 4595 | 33,538 | 7 | 0.959 | 10X Visium | Homo sapiens | [22] |
| DLPFC_151669 | 3636 | 33,538 | 5 | 0.946 | 10X Visium | Homo sapiens | [22] |
| DLPFC_151670 | 3484 | 33,538 | 5 | 0.950 | 10X Visium | Homo sapiens | [22] |
| DLPFC_151671 | 4093 | 33,538 | 5 | 0.945 | 10X Visium | Homo sapiens | [22] |
| DLPFC_151672 | 3888 | 33,538 | 5 | 0.947 | 10X Visium | Homo sapiens | [22] |
| DLPFC_151673 | 3611 | 33,538 | 7 | 0.934 | 10X Visium | Homo sapiens | [22] |
| DLPFC_151674 | 3635 | 33,538 | 7 | 0.920 | 10X Visium | Homo sapiens | [22] |
| DLPFC_151675 | 3566 | 33,538 | 7 | 0.946 | 10X Visium | Homo sapiens | [22] |
| DLPFC_151676 | 3431 | 33,538 | 7 | 0.942 | 10X Visium | Homo sapiens | [22] |
| Brain coronal | 2800 | 32,285 | 15 | 0.870 | 10X Visium | Mus musculus | [23] |
| Hippocampus | 53,208 | 23,264 | - | 0.982 | Slide-seqV2 | Mus musculus | [26] |
| Olfactory bulb | 19,527 | 27,106 | - | 0.987 | Stereo-seq | Mus musculus | [27] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, R.; Li, Z.; Jia, Y.; Li, S.; Chen, S. SINFONIA: Scalable Identification of Spatially Variable Genes for Deciphering Spatial Domains. Cells 2023, 12, 604. https://doi.org/10.3390/cells12040604
Jiang R, Li Z, Jia Y, Li S, Chen S. SINFONIA: Scalable Identification of Spatially Variable Genes for Deciphering Spatial Domains. Cells. 2023; 12(4):604. https://doi.org/10.3390/cells12040604
Chicago/Turabian StyleJiang, Rui, Zhen Li, Yuhang Jia, Siyu Li, and Shengquan Chen. 2023. "SINFONIA: Scalable Identification of Spatially Variable Genes for Deciphering Spatial Domains" Cells 12, no. 4: 604. https://doi.org/10.3390/cells12040604
APA StyleJiang, R., Li, Z., Jia, Y., Li, S., & Chen, S. (2023). SINFONIA: Scalable Identification of Spatially Variable Genes for Deciphering Spatial Domains. Cells, 12(4), 604. https://doi.org/10.3390/cells12040604






