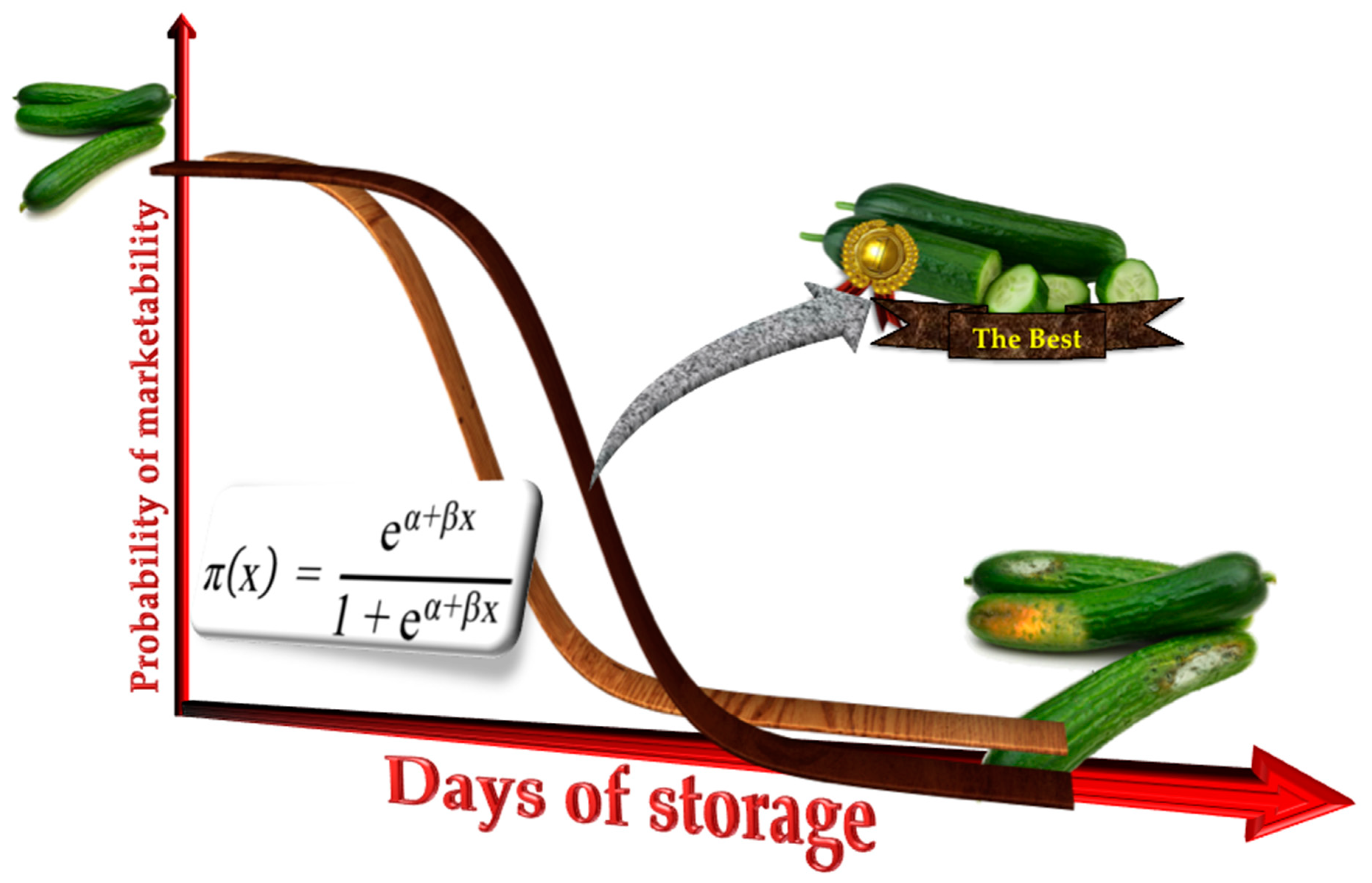
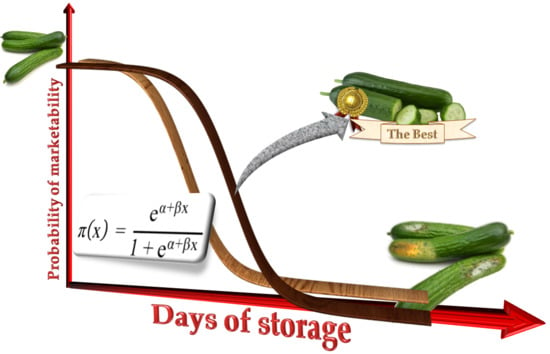
Figure 1.
Diagram of the interest in and practical application of the logistic regression model in comparative studies of cucumber cultivars to identify cultivars with the longest postharvest shelf life. In the figure, π (x) is the probability of marketability of a cucumber, “x” is the days of storage, “e” is Euler’s number, “α” is the intercept, and “β” is the slope. Source: Author’s elaboration based on Díaz-Pérez [
22].
Figure 1.
Diagram of the interest in and practical application of the logistic regression model in comparative studies of cucumber cultivars to identify cultivars with the longest postharvest shelf life. In the figure, π (x) is the probability of marketability of a cucumber, “x” is the days of storage, “e” is Euler’s number, “α” is the intercept, and “β” is the slope. Source: Author’s elaboration based on Díaz-Pérez [
22].
Figure 2.
Details of noncommercial cucumber fruits identified during the study. Apical wilt caused by fruit aging and water loss (a). Apical rot (b). Loss of green color (i.e., chlorophyll) with yellow development (c).
Figure 2.
Details of noncommercial cucumber fruits identified during the study. Apical wilt caused by fruit aging and water loss (a). Apical rot (b). Loss of green color (i.e., chlorophyll) with yellow development (c).
Figure 3.
Timeline of the probability of marketability of the LET cucumber cultivars. The results are obtained from the simple logistic model for each cultivar as a function of the days of storage.
Figure 3.
Timeline of the probability of marketability of the LET cucumber cultivars. The results are obtained from the simple logistic model for each cultivar as a function of the days of storage.
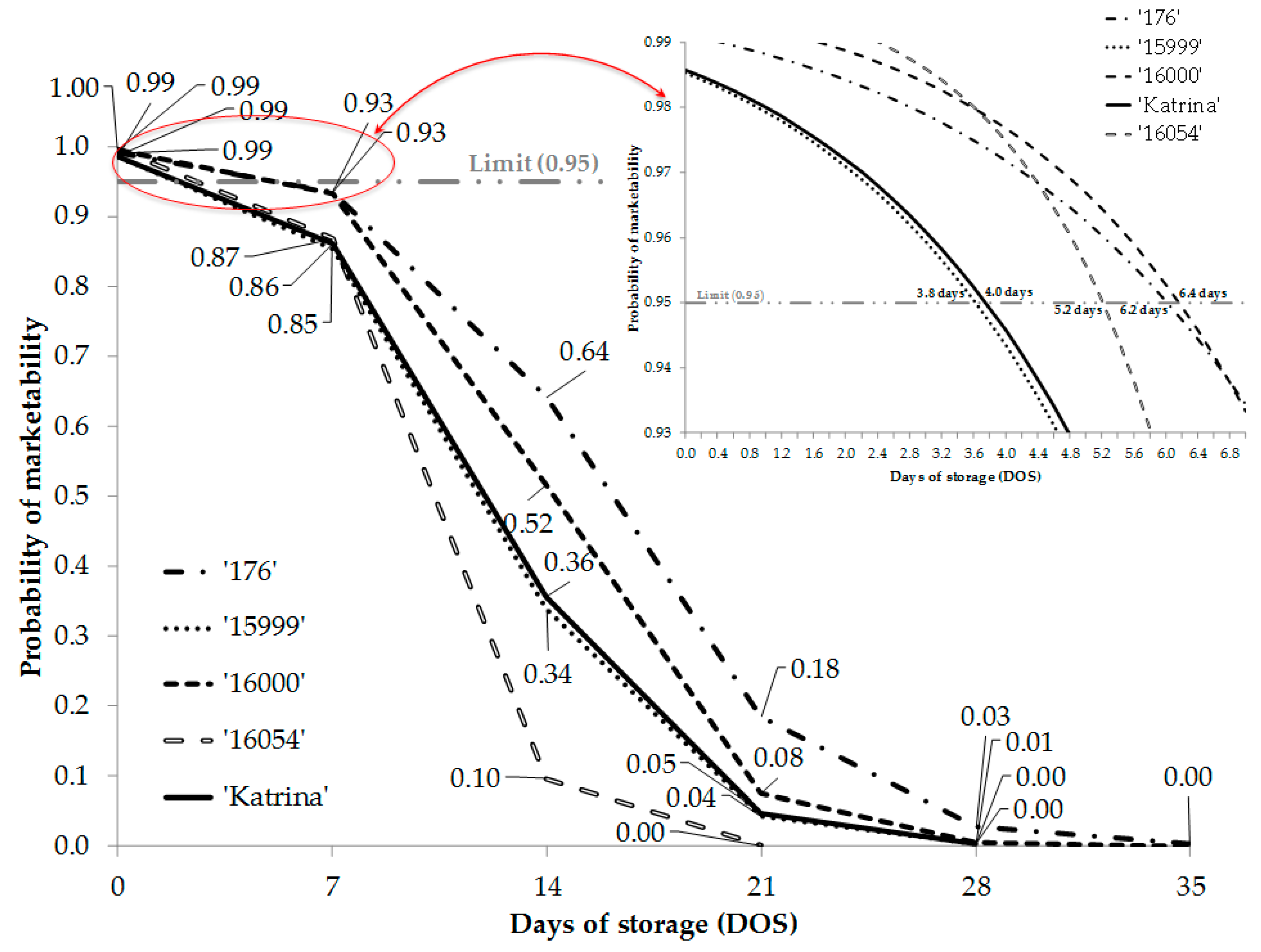
Figure 4.
Timeline of the probability of marketability in mini cucumber cultivars. The results are obtained from the simple logistic model for each cultivar, as a function of the days of storage.
Figure 4.
Timeline of the probability of marketability in mini cucumber cultivars. The results are obtained from the simple logistic model for each cultivar, as a function of the days of storage.
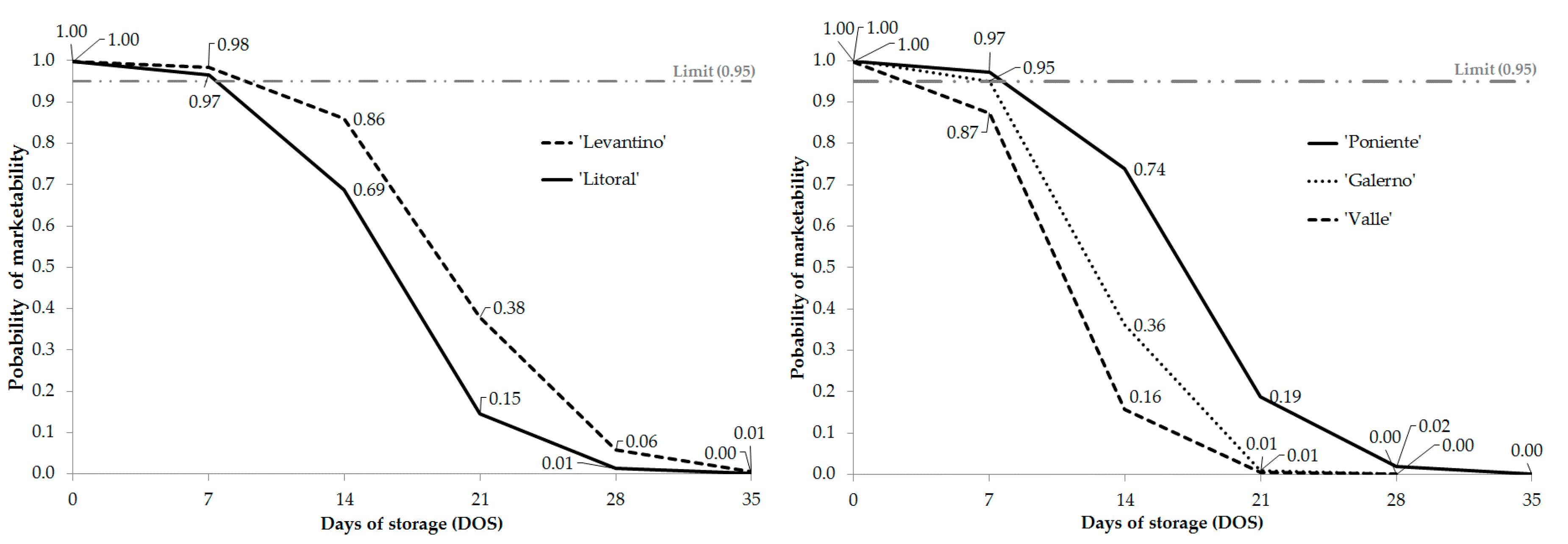
Figure 5.
Timeline of the probability of marketability as a function of the days of storage (DOS) for the Levantino and Litoral cucumber cultivars.
Figure 5.
Timeline of the probability of marketability as a function of the days of storage (DOS) for the Levantino and Litoral cucumber cultivars.
Figure 6.
Timeline of the probability of marketability as a function of the days of storage (DOS) for the Poniente, Galerno, and Valle cucumber cultivars.
Figure 6.
Timeline of the probability of marketability as a function of the days of storage (DOS) for the Poniente, Galerno, and Valle cucumber cultivars.
Figure 7.
Timeline of the probability of marketability as a function of the days of storage (DOS) for the mini-type cucumber cultivars.
Figure 7.
Timeline of the probability of marketability as a function of the days of storage (DOS) for the mini-type cucumber cultivars.
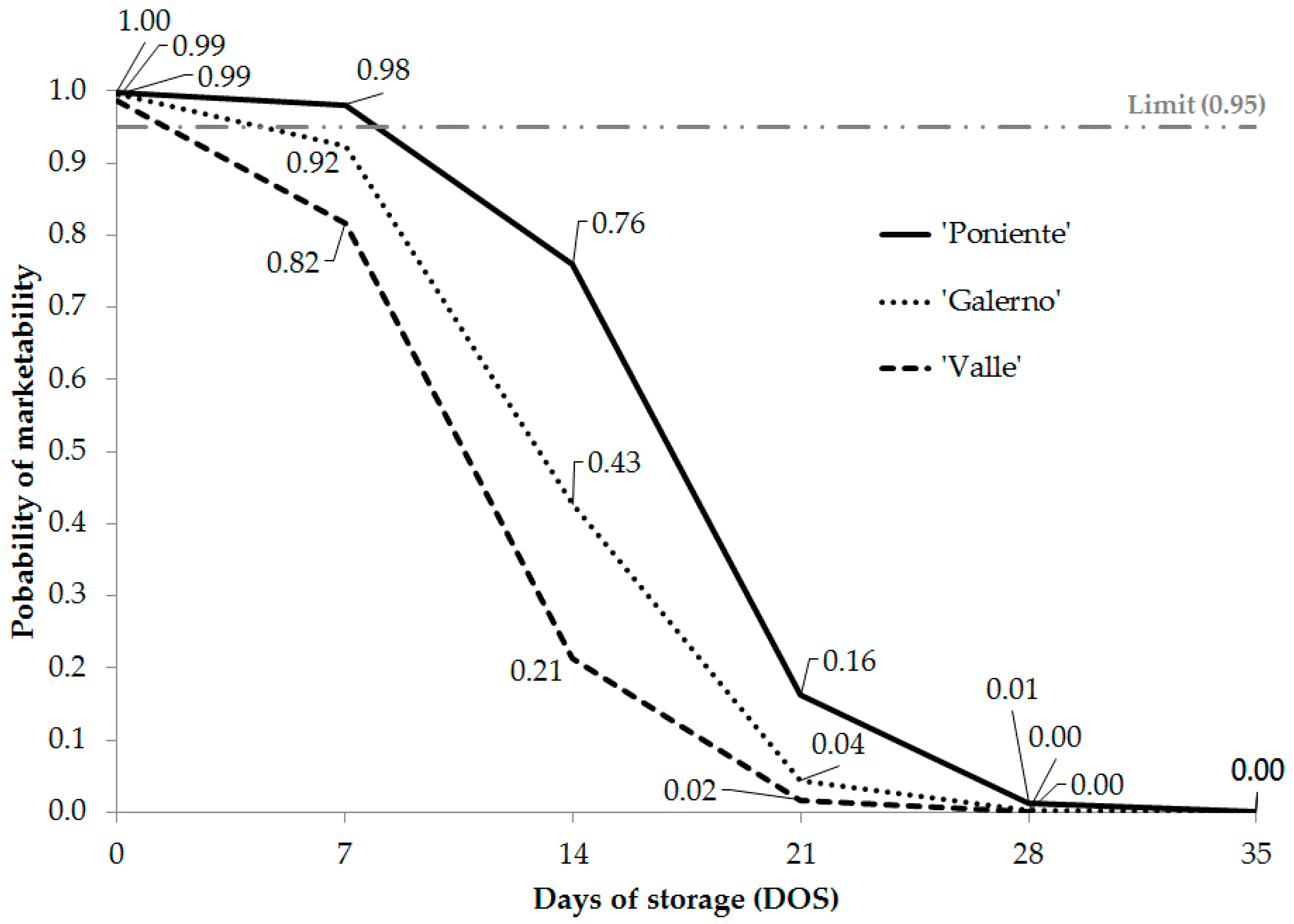
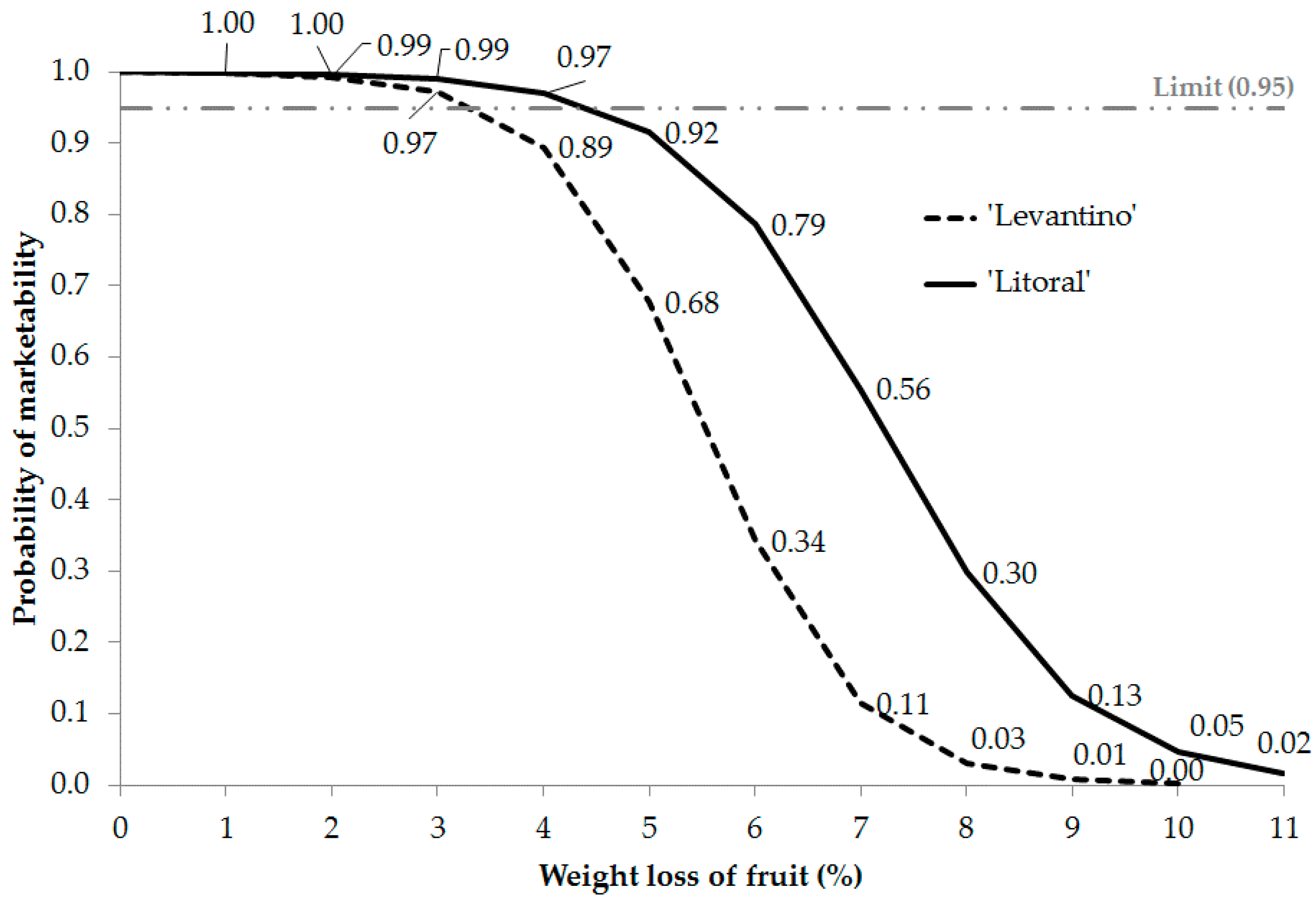
Figure 8.
Probability of marketability based on fruit loss percentage during storage for the Levantino and Litoral cultivars.
Figure 8.
Probability of marketability based on fruit loss percentage during storage for the Levantino and Litoral cultivars.
Figure 9.
Probability of marketability based on fruit loss percentage during storage for the Galerno, Poniente, and Valle cultivars.
Figure 9.
Probability of marketability based on fruit loss percentage during storage for the Galerno, Poniente, and Valle cultivars.
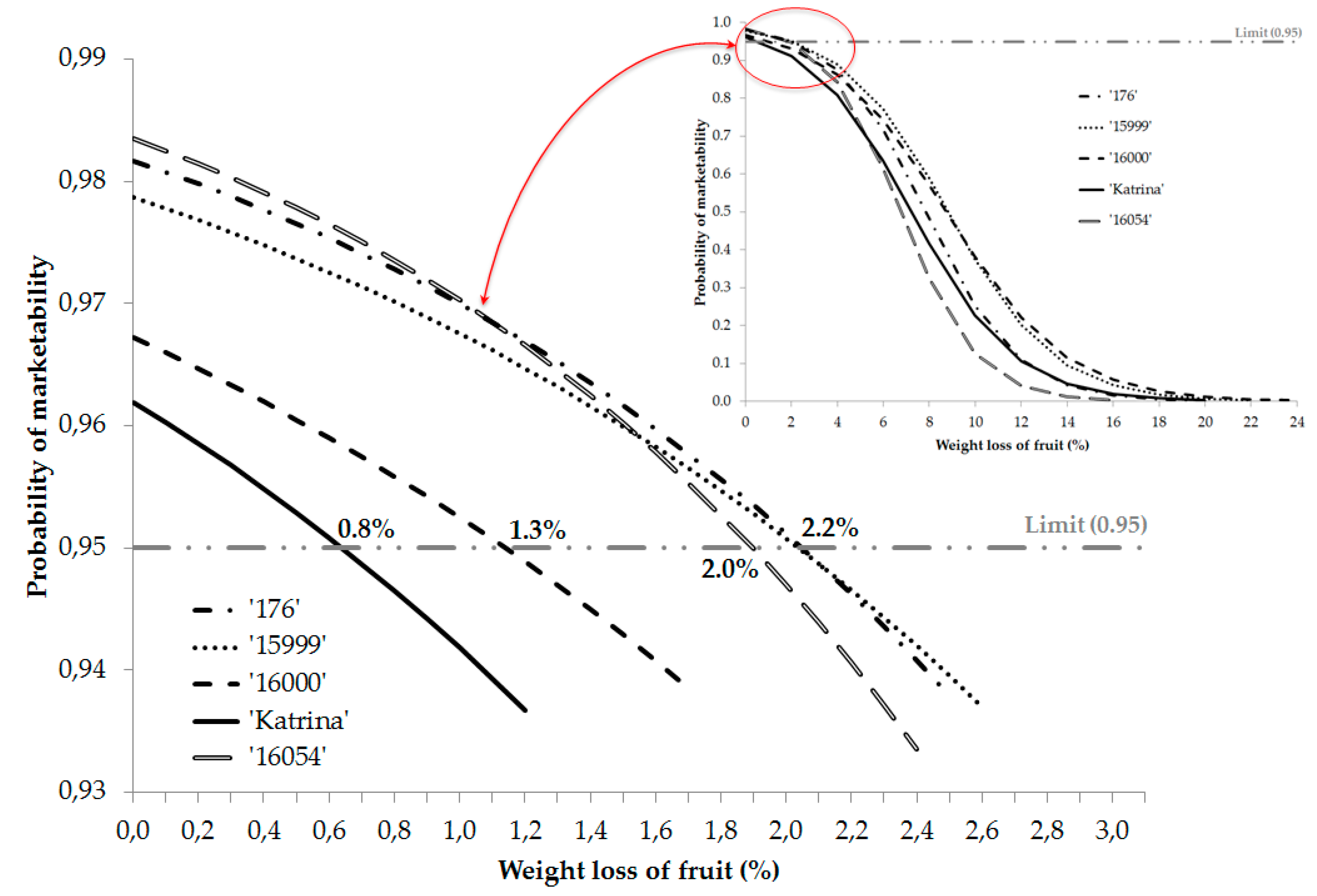
Figure 10.
Probability of marketability based on fruit weight loss of the mini-type cucumber cultivars studied. The results are obtained from the simple logistic model for each cultivar and based on fruit weight loss percentage (FWL %) during storage.
Figure 10.
Probability of marketability based on fruit weight loss of the mini-type cucumber cultivars studied. The results are obtained from the simple logistic model for each cultivar and based on fruit weight loss percentage (FWL %) during storage.
Table 1.
Sampling for each crop cycle and month of evaluation and days in which the samples of each cucumber cultivar were measured in the laboratory.
Table 1.
Sampling for each crop cycle and month of evaluation and days in which the samples of each cucumber cultivar were measured in the laboratory.
| | Evaluated Cycle | | Month of Evaluation/Cycle | DOS (a) |
|---|
| Cultivars | 14–15 | 16–17 | 17–18 | Nov. | Dec. | Jan. | Feb. | Mar. | 0 | 7 | 14 | 21 | 28 | 35 |
| LET | | | | | | | | | | | | | | |
| Litoral | | X | X | X | X | X | | | X | X | X | X | X | X |
| Levantino | | X | X | X | X | X | | | X | X | X | X | X | X |
| Galerno | X | X | X | | | | X | X | X | X | X | X | X | X |
| Poniente | X | X | X | | | | X | X | X | X | X | X | X | X |
| Valle | X | X | X | | | | X | X | X | X | X | X | X | X |
| Mini-type | | | | | | | | | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| Katrina | X | | | X | X | X | | | X | X | X | X | X | X | X | X |
| 176 | X | | | X | X | X | | | X | X | X | X | X | X | X | X |
| 15999 | X | | | X | X | X | | | X | X | X | X | X | X | X | X |
| 16000 | X | | | X | X | X | | | X | X | X | X | X | X | X | X |
| 16054 | X | | | X | X | X | | | X | X | X | X | X | X | X | X |
Table 2.
Estimated independent simple logistic regression parameters for each LET cucumber cultivar as a function of the days of storage (DOS), which is a factor influencing the probability of marketability.
Table 2.
Estimated independent simple logistic regression parameters for each LET cucumber cultivar as a function of the days of storage (DOS), which is a factor influencing the probability of marketability.
| Cultivar | | Coefficients | | | Odds Ratio | 95% CI for (Exp(β)) |
|---|
| Variable | (α, β) | Wald χ2 | p | (Exp(β)) | Lower | Upper |
|---|
| Period: November–January | | | | | |
| Levantino * | DOS | −0.330 | 193.198 | <0.000 | 0.719 | 0.687 | 0.753 |
| Constant | 6.430 | 192.484 | <0.000 | 619.996 | | |
| Litoral * | DOS | −0.366 | 180.054 | <0.000 | 0.694 | 0.658 | 0.732 |
| Constant | 5.910 | 171.565 | <0.000 | 368.591 | | |
| Period: February–March | | | | | |
| Galerno * | DOS | −0.585 | 15.730 | <0.000 | 0.557 | 0.417 | 0.744 |
| Constant | 7.620 | 15.470 | <0.000 | 2039.480 | | |
| Poniente * | DOS | −0.357 | 186.558 | <0.000 | 0.700 | 0.665 | 0.737 |
| Constant | 6.033 | 179.682 | <0.000 | 417.092 | | |
| Valle * | DOS | −0.514 | 66.923 | <0.000 | 0.598 | 0.529 | 0.676 |
| Constant | 5.521 | 57.952 | <0.000 | 249.885 | | |
Table 3.
Estimation of independent simple logistic regression parameters for each mini cucumber cultivar based on the days of storage (DOS), which is a factor influencing the probability of marketability.
Table 3.
Estimation of independent simple logistic regression parameters for each mini cucumber cultivar based on the days of storage (DOS), which is a factor influencing the probability of marketability.
| Cultivar | | Coefficients | | | Odds ratio | 95% CI for (Exp(β)) |
|---|
| Variable | (α, β) | Wald χ2 | p | (Exp(β)) | Lower | Upper |
|---|
| 176 * | DOS | −0.296 | 125.198 | <0.000 | 0.744 | 0.706 | 0.784 |
| Constant | 4.724 | 114.867 | <0.000 | 112.664 | | |
| 15999 * | DOS | −0.348 | 30.631 | <0.000 | 0.706 | 0.624 | 0.799 |
| Constant | 4.207 | 40.793 | <0.000 | 67.155 | | |
| 16000 * | DOS | −0.367 | 34.819 | <0.000 | 0.693 | 0.613 | 0.783 |
| Constant | 5.209 | 43.385 | <0.000 | 182.856 | | |
| 16054 * | DOS | −0.590 | 27.759 | <0.000 | 0.554 | 0.445 | 0.690 |
| Constant | 6.019 | 29.840 | <0.000 | 411.181 | | |
| Katrina * | DOS | −0.345 | 214.049 | <0.000 | 0.708 | 0.676 | 0.742 |
| Constant | 4.237 | 197.549 | <0.000 | 69.201 | | |
Table 4.
Estimation of the multiple logistic regression parameters for cultivars (Levantino and Litoral) and DOS as factors influencing the probability of marketability.
Table 4.
Estimation of the multiple logistic regression parameters for cultivars (Levantino and Litoral) and DOS as factors influencing the probability of marketability.
| Variables | Coefficients | Wald χ2 | p | Odds Ratio | 95% CI for (Exp(β)) |
|---|
| (α, β) | (Exp(β)) | Lower | Upper |
|---|
| Constant | 5.602 | 325.113 | <0.000 | 271.048 | | |
| DOS | −0.346 | 373.355 | <0.000 | 0.707 | 0.683 | 0.733 |
| Levantino | 1.144 | 39.917 | <0.000 | 3.140 | 2.202 | 4.477 |
| Litoral | | Reference | | | | |
Table 5.
Estimation of the multiple logistic regression parameters for cultivars (Galerno, Poniente, and Valle) and days of storage (DOS) as factors influencing the probability of marketability.
Table 5.
Estimation of the multiple logistic regression parameters for cultivars (Galerno, Poniente, and Valle) and days of storage (DOS) as factors influencing the probability of marketability.
| Variables | Coefficients | Wald χ2 | p | Odds Ratio | 95% CI for (Exp(β)) |
|---|
| (α, β) | (Exp(β)) | Lower | Upper |
|---|
| Constant | 4.272 | 160.644 | <0.000 | 71.692 | | |
| DOS | −0.398 | 266.725 | <0.000 | 0.671 | 0.640 | -0.398 |
| Galerno | 1.007 | 5.654 | 0.017 | 2.736 | 1.193 | 1.007 |
| Poniente | 2.447 | 72.483 | <0.000 | 11.558 | 6.580 | 2.447 |
| Valle | | Reference | | | | |
| Constant | 6.720 | 249.830 | <0.000 | 828.620 | | |
| DOS | −0.398 | 266.725 | <0.000 | 0.671 | 0.640 | 0.704 |
| Valle | −2.447 | 72.483 | <0.000 | 0.087 | 0.049 | 0.152 |
| Galerno | −1.441 | 12.835 | <0.000 | 0.237 | 0.108 | 0.521 |
| Poniente | | Reference | | | | |
| Constant | 5.279 | 125.272 | <0.000 | 196.184 | | |
| DOS | −0.398 | 266.725 | <0.000 | 0.671 | 0.640 | 0.704 |
| Poniente | 1.441 | 12.835 | <0.000 | 4.224 | 1.920 | 9.290 |
| Valle | −1.007 | 5.654 | 0.017 | 0.365 | 0.159 | 0.838 |
| Galerno | | Reference | | | | |
Table 6.
Estimation of the multiple logistic regression parameters for the mini-type cultivars and days of storage (DOS) as factors influencing the probability of marketability.
Table 6.
Estimation of the multiple logistic regression parameters for the mini-type cultivars and days of storage (DOS) as factors influencing the probability of marketability.
| Variables | Coefficients | Wald χ2 | p | Odds Ratio | 95% CI for (Exp(β)) |
|---|
| (α, β) | (Exp(β)) | Lower | Upper |
|---|
| Constant | 4.180 | 343.022 | <0.000 | 65.337 | | |
| DOS | −0.340 | 426.987 | <0.000 | 0.712 | 0.689 | 0.735 |
| 176 | 1.247 | 39.387 | <0.000 | 3.480 | 2.357 | 5.136 |
| 15999 | −0.054 | 0.035 | 0.851 | 0.947 | 0.537 | 1.670 |
| 16000 | 0.701 | 6.905 | 0.009 | 2.016 | 1.195 | 3.401 |
| 16054 | −0.491 | 3.170 | 0.075 | 0.612 | 0.357 | 1.051 |
| Katrina | | Reference | | | | |
| Constant | 3.689 | 164.413 | <0.000 | 40.000 | | |
| DOS | −0.340 | 426.987 | <0.000 | 0.712 | 0.689 | 0.735 |
| Katrina | 0.491 | 3.170 | 0.075 | 1.633 | 0.952 | 2.803 |
| 176 | 1.738 | 31.765 | <0.000 | 5.684 | 3.106 | 10.400 |
| 15999 | 0.437 | 1.469 | 0.225 | 1.547 | 0.764 | 3.134 |
| 16000 | 1.192 | 11.771 | 0.001 | 3.293 | 1.667 | 6.506 |
| 16054 | | Reference | | | | |
| Constant | 4.881 | 248.244 | <0.000 | 131.723 | | |
| DOS | −0.340 | 426.987 | <0.000 | 0.712 | 0.689 | 0.735 |
| 16054 | −1.192 | 11.771 | 0.001 | 0.304 | 0.154 | 0.600 |
| Katrina | −0.701 | 6.905 | 0.009 | 0.496 | 0.294 | 0.837 |
| 176 | 0.546 | 3.547 | 0.049 | 1.726 | 1.012 | 3.046 |
| 15999 | −0.755 | 4.444 | 0.035 | 0.470 | 0.233 | 0.948 |
| 16000 | | Reference | | | | |
| Constant | 4.125 | 181.986 | <0.000 | 61.891 | | |
| DOS | −0.340 | 426.987 | <0.000 | 0.712 | 0.689 | 0.735 |
| 16000 | 0.755 | 4.444 | 0.035 | 2.128 | 1.054 | 4.296 |
| 16054 | −0.437 | 1.469 | 0.225 | 0.646 | 0.319 | 1.309 |
| Katrina | 0.054 | 0.035 | 0.851 | 1.056 | 0.599 | 1.861 |
| 176 | 1.301 | 16.643 | <0.000 | 3.673 | 1.966 | 6.863 |
| 15999 | | Reference | | | | |
| Constant | 5.426 | 325.873 | <0.000 | 227.345 | | |
| DOS | −0.340 | 426.987 | <0.000 | 0.712 | 0.689 | 0.735 |
| 15999 | −1.301 | 16.643 | <0.000 | 0.272 | 0.146 | 0.509 |
| 16000 | −0.546 | 3.547 | 0.060 | 0.579 | 0.328 | 1.022 |
| 16054 | −1.738 | 31.765 | <0.000 | 0.176 | 0.096 | 0.322 |
| Katrina | −1.247 | 39.387 | <0.000 | 0.287 | 0.195 | 0.424 |
| 176 | | Reference | | | | |
Table 7.
Estimation of the multiple logistic regression parameters for cucumber cultivars (Levantino and Litoral) and FWL % during storage as factors influencing the probability of marketability.
Table 7.
Estimation of the multiple logistic regression parameters for cucumber cultivars (Levantino and Litoral) and FWL % during storage as factors influencing the probability of marketability.
| Variables | Coefficients | Wald χ2 | p | Odds Ratio | 95% CI for (Exp(β)) |
|---|
| (α, β) | (Exp(β)) | Lower | Upper |
|---|
| Constant | 7.718 | 227.008 | <0.000 | 2248.731 | | |
| FWL % | −1.395 | 236.828 | <0.000 | 0.248 | 0.207 | 0.296 |
| Litoral | 1.941 | 79.759 | <0.000 | 6.965 | 4.549 | 10.663 |
| Levantino | | Reference | | | | |
Table 8.
Estimation of multiple logistic regression parameters for cucumber cultivars (Galerno, Poniente, and Valle) and fruit weight loss percentage during storage as factors influencing the probability of marketability.
Table 8.
Estimation of multiple logistic regression parameters for cucumber cultivars (Galerno, Poniente, and Valle) and fruit weight loss percentage during storage as factors influencing the probability of marketability.
| Variables | Coefficients | Wald χ2 | p | Odds Ratio | 95% CI for (Exp(β)) |
|---|
| (α, β) | (Exp(β)) | Lower | Upper |
|---|
| Constant | 5.091 | 198.615 | <0.000 | 162.540 | | |
| FWL % | −1.069 | 273.219 | <0.000 | 0.343 | 0.302 | 0.390 |
| Galerno | −0.155 | 0.147 | 0.702 | 0.857 | 0.388 | 1.891 |
| Poniente | 1.351 | 29.928 | <0.000 | 3.861 | 2.380 | 6.265 |
| Valle | | Reference | | | | |
| Constant | 6.442 | 251.470 | <0.000 | 627.610 | | |
| FWL % | −1.069 | 273.219 | <0.000 | 0.343 | 0.302 | 0.390 |
| Valle | −1.351 | 29.928 | <0.000 | 0.259 | 0.160 | 0.420 |
| Galerno | −1.506 | 14.408 | <0.000 | 0.222 | 0.102 | 0.483 |
| Poniente | | Reference | | | | |
| Constant | 4.936 | 125.463 | <0.000 | 139.224 | | |
| FWL % | −1.069 | 273.219 | <0.000 | 0.343 | 0.302 | 0.390 |
| Poniente | 1.506 | 14.408 | <0.000 | 4.508 | 2.072 | 9.810 |
| Valle | 0.155 | 0.147 | 0.702 | 1.167 | 0.529 | 2.577 |
| Galerno | | Reference | | | | |
Table 9.
Estimation of the independent simple logistic regression parameters for each mini-type cucumber cultivar as a function of postharvest FWL % as a factor influencing the probability of marketability.
Table 9.
Estimation of the independent simple logistic regression parameters for each mini-type cucumber cultivar as a function of postharvest FWL % as a factor influencing the probability of marketability.
| cv. | Variable | Coefficients | Wald χ2 | p | Odds Ratio | 95% CI for (Exp(β)) |
|---|
| (α, β) | (Exp(β)) | Lower | Upper |
|---|
| 176 * | DOS | −0.507 | 116.197 | <0.000 | 0.603 | 0.550 | 0.661 |
| Constant | 3.983 | 116.870 | <0.000 | 53.696 | | |
| 15999 * | DOS | −0.434 | 30.836 | <0.000 | 0.648 | 0.556 | 0.755 |
| Constant | 3.829 | 44.146 | <0.000 | 46.005 | | |
| 16000 * | DOS | −0.387 | 35.562 | <0.000 | 0.679 | 0.598 | 0.771 |
| Constant | 3.385 | 63.741 | <0.000 | 29.505 | | |
| 16054 * | DOS | −0.603 | 27.788 | <0.000 | 0.547 | 0.437 | 0.685 |
| Constant | 4.089 | 33.558 | <0.000 | 59.709 | | |
| Katrina * | DOS | −0.446 | 207.820 | <0.000 | 0.640 | 0.603 | 0.680 |
| Constant | 3.230 | 197.323 | <0.000 | 25.277 | | |
Table 10.
Estimation of the multiple logistic regression parameters for the Levantino and Litoral cucumber cultivars.
Table 10.
Estimation of the multiple logistic regression parameters for the Levantino and Litoral cucumber cultivars.
| Variables | Coefficients | Wald χ2 | p | Odds Ratio | 95% CI for (Exp(β)) |
|---|
| (α, β) | (Exp(β)) | Lower | Upper |
|---|
| Constant | 10.561 | 262.608 | <0.000 | 38,613.016 | | |
| DOS | −0.259 | 108.555 | <0.000 | 0.772 | 0.735 | 0.810 |
| FWL % | −0.627 | 58.702 | <0.000 | 0.534 | 0.455 | 0.627 |
| Month | | | | | | |
| November | −2.809 | 79.297 | <0.000 | 0.060 | 0.032 | 0.112 |
| December | −2.246 | 60.086 | <0.000 | 0.106 | 0.060 | 0.187 |
| January | | Reference | | | | |
Table 11.
Estimation of the multiple logistic regression parameters for the Levantino and Litoral cucumber cultivars.
Table 11.
Estimation of the multiple logistic regression parameters for the Levantino and Litoral cucumber cultivars.
| Variables | Coefficients | Wald χ2 | p | Odds Ratio | 95% CI for (Exp(β)) |
|---|
| (α, β) | (Exp(β)) | Lower | Upper |
|---|
| Constant | 12.585 | 223.694 | <0.000 | 29,2001.831 | | |
| FWL % | −1.572 | 230.198 | <0.000 | 0.208 | 0.169 | 0.254 |
| Phenotype | | | | | | |
| Litoral | −2.239 | 88.104 | <0.000 | 0.107 | 0.067 | 0.170 |
| Levantino | | Reference | | | | |
| Month | | | | | | |
| November | −2.227 | 58.624 | <0.000 | 0.108 | 0.061 | 0.191 |
| December | −1.927 | 50.642 | <0.000 | 0.146 | 0.086 | 0.248 |
| January | | Reference | | | | |
Table 12.
Estimation of the multiple logistic regression parameters for the Galerno, Poniente, and Valle cucumber cultivars.
Table 12.
Estimation of the multiple logistic regression parameters for the Galerno, Poniente, and Valle cucumber cultivars.
| Variables | Coefficients | Wald χ2 | p | Odds Ratio | 95% CI for (Exp(β)) |
|---|
| (α, β) | (Exp(β)) | Lower | Upper |
|---|
| Constant | 6.964 | 251.516 | <0.000 | 1058.172 | | |
| Phenotype | | | | | | |
| Valle | −2.120 | 52.380 | <0.000 | 0.120 | 0.068 | 0.213 |
| Galerno | −1.581 | 15.203 | <0.000 | 0.206 | 0.093 | 0.456 |
| Poniente | | Reference | | | | |
| DOS | −0.248 | 38.792 | <0.000 | 0.781 | 0.722 | 0.844 |
| FWL % | −0.459 | 19.048 | <0.000 | 0.632 | 0.515 | 0.777 |
Table 13.
Estimation of multiple logistic regression parameters for the 176, 15999, 16000, 16054, and Katrina cucumber cultivars.
Table 13.
Estimation of multiple logistic regression parameters for the 176, 15999, 16000, 16054, and Katrina cucumber cultivars.
| Variables | Coefficients | Wald χ2 | p | Odds ratio | 95% CI for (Exp(β)) |
|---|
| (α, β) | (Exp(β)) | Lower | Upper |
|---|
| Constant | 5.563 | 259.041 | <0.000 | 260.574 | | |
| Phenotypes | | | | | | |
| 15999 | −1.515 | 20.334 | <0.000 | 0.220 | 0.114 | 0.425 |
| 16000 | −0.620 | 4.195 | 0.041 | 0.538 | 0.297 | 0.974 |
| 16054 | −1.852 | 31.323 | <0.000 | 0.157 | 0.082 | 0.300 |
| Katrina | −1.332 | 39.393 | <0.000 | 0.264 | 0.174 | 0.400 |
| 176 | | Reference | | | | |
| DOS | −0.303 | 179.599 | <0.000 | 0.738 | 0.706 | 0.772 |
| FWL % | −0.104 | 10.467 | 0.001 | 0.901 | 0.846 | 0.960 |
| Months | | | | | | |
| November | 1.162 | 30.793 | <0.000 | 3.197 | 2.121 | 4.819 |
| December | −0.389 | 3.939 | 0.047 | 0.678 | 0.462 | 0.995 |
| January | | Reference | | | | |