Development of Maize Canopy Architecture Indicators Through UAV Multi-Source Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Site and Design
2.2. Data Acquisition
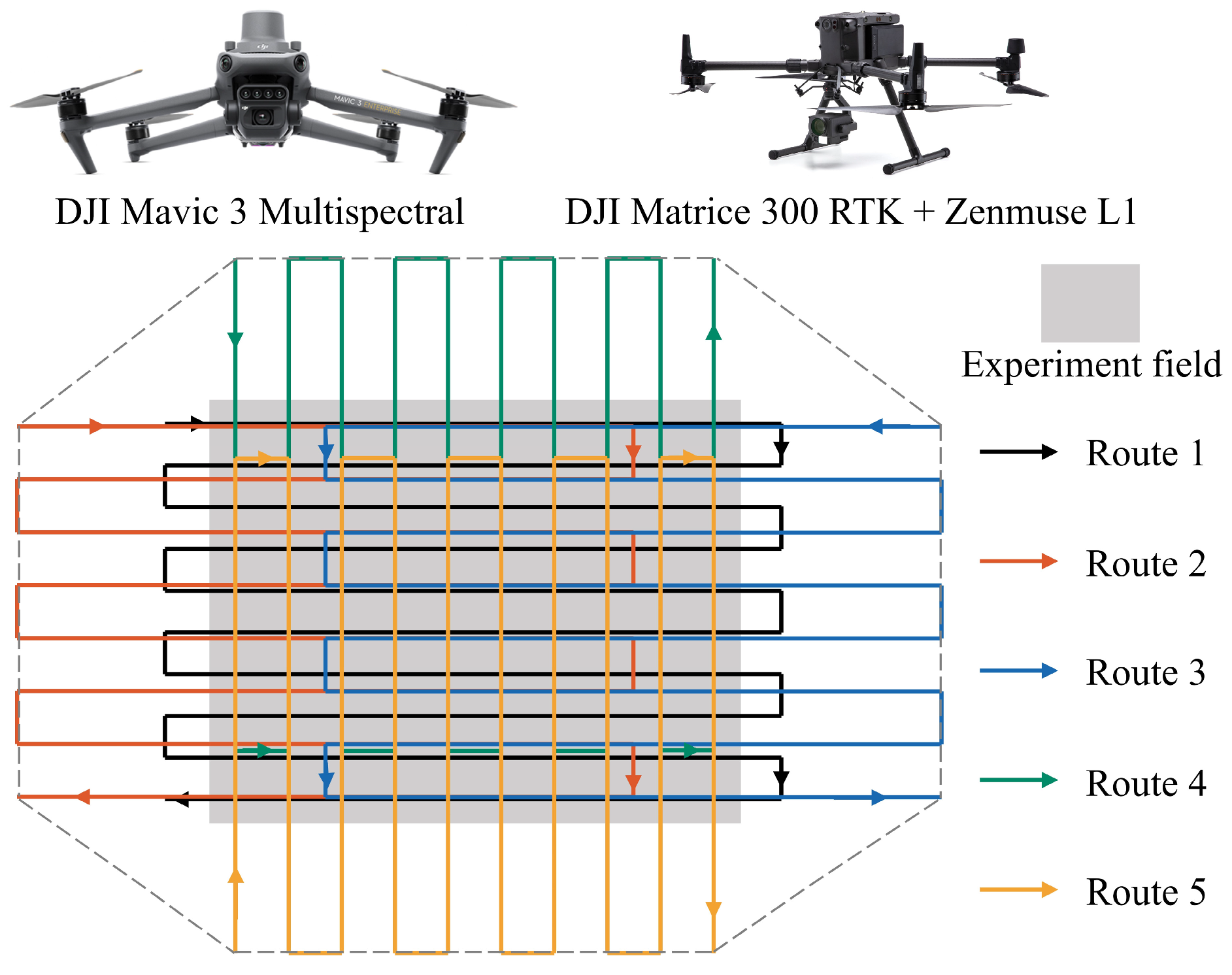
2.2.1. UAV Imagery Acquisition
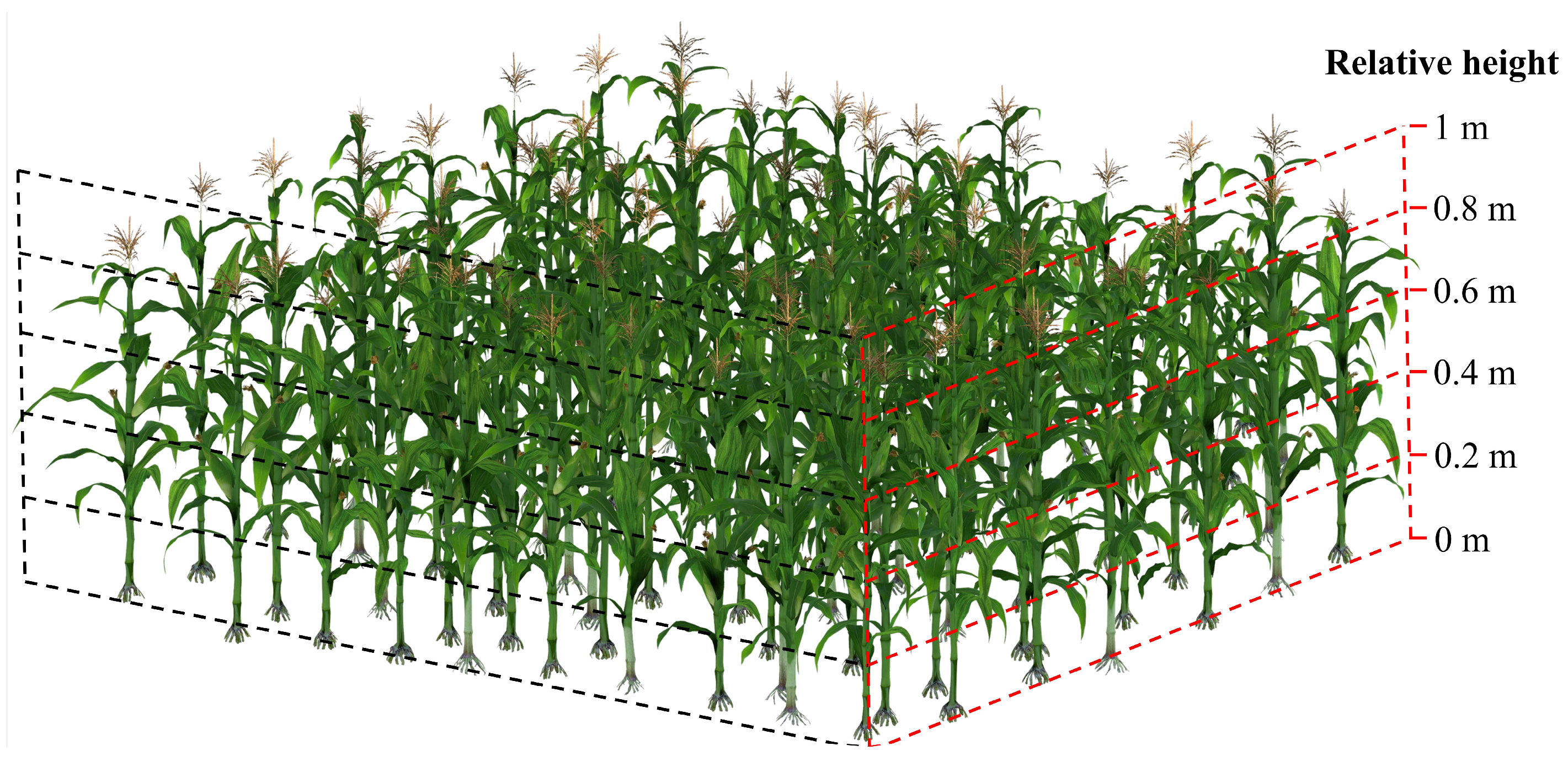
2.2.2. LAI Measurement and Processing
2.2.3. Yield
2.3. Imagery Processing
2.4. Features Extraction
2.4.1. Vegetation Indices
2.4.2. Texture Indices
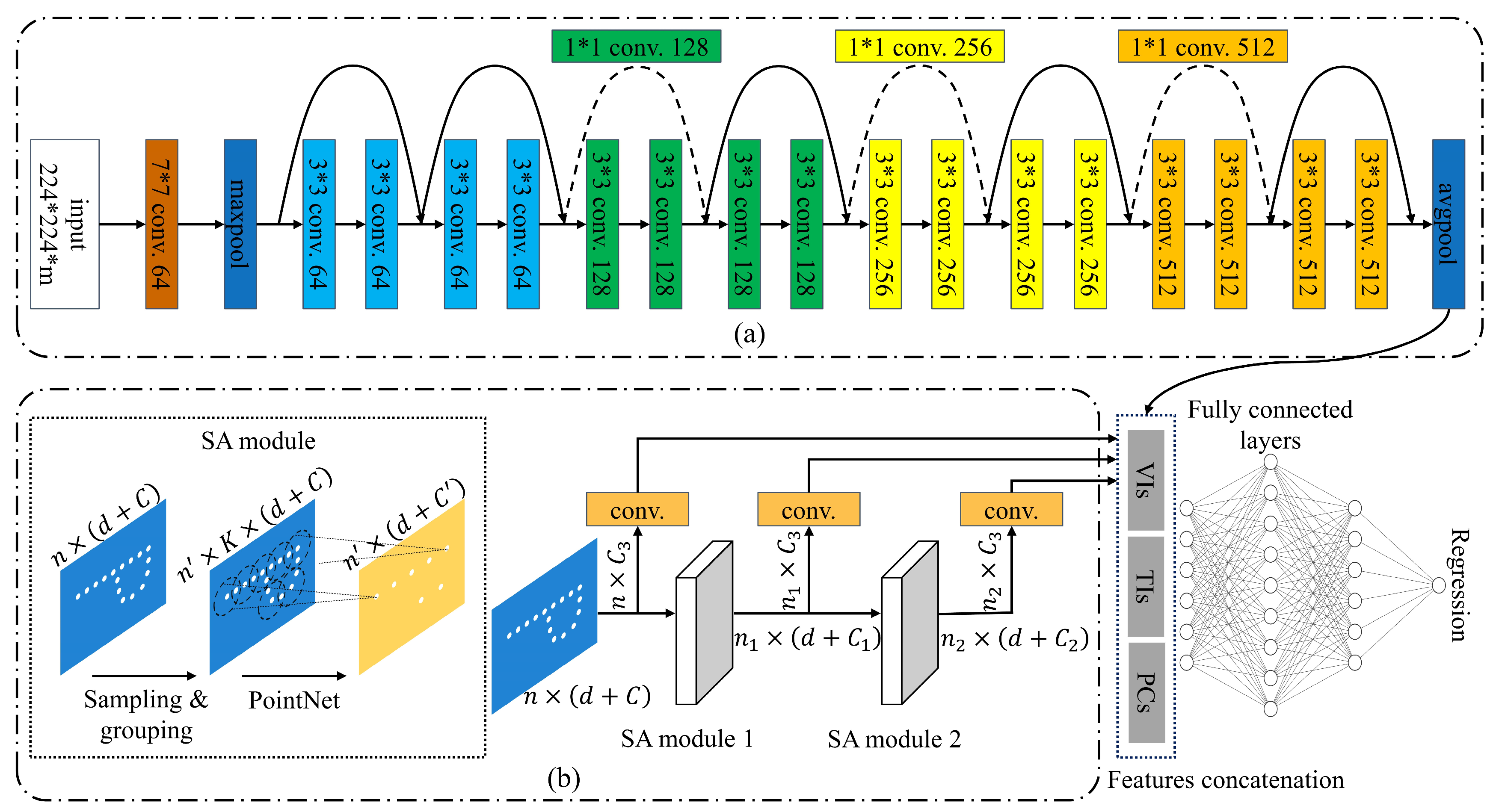
2.5. Construction of Deep Learning Model
2.6. Model Accuracy Evaluation
3. Results
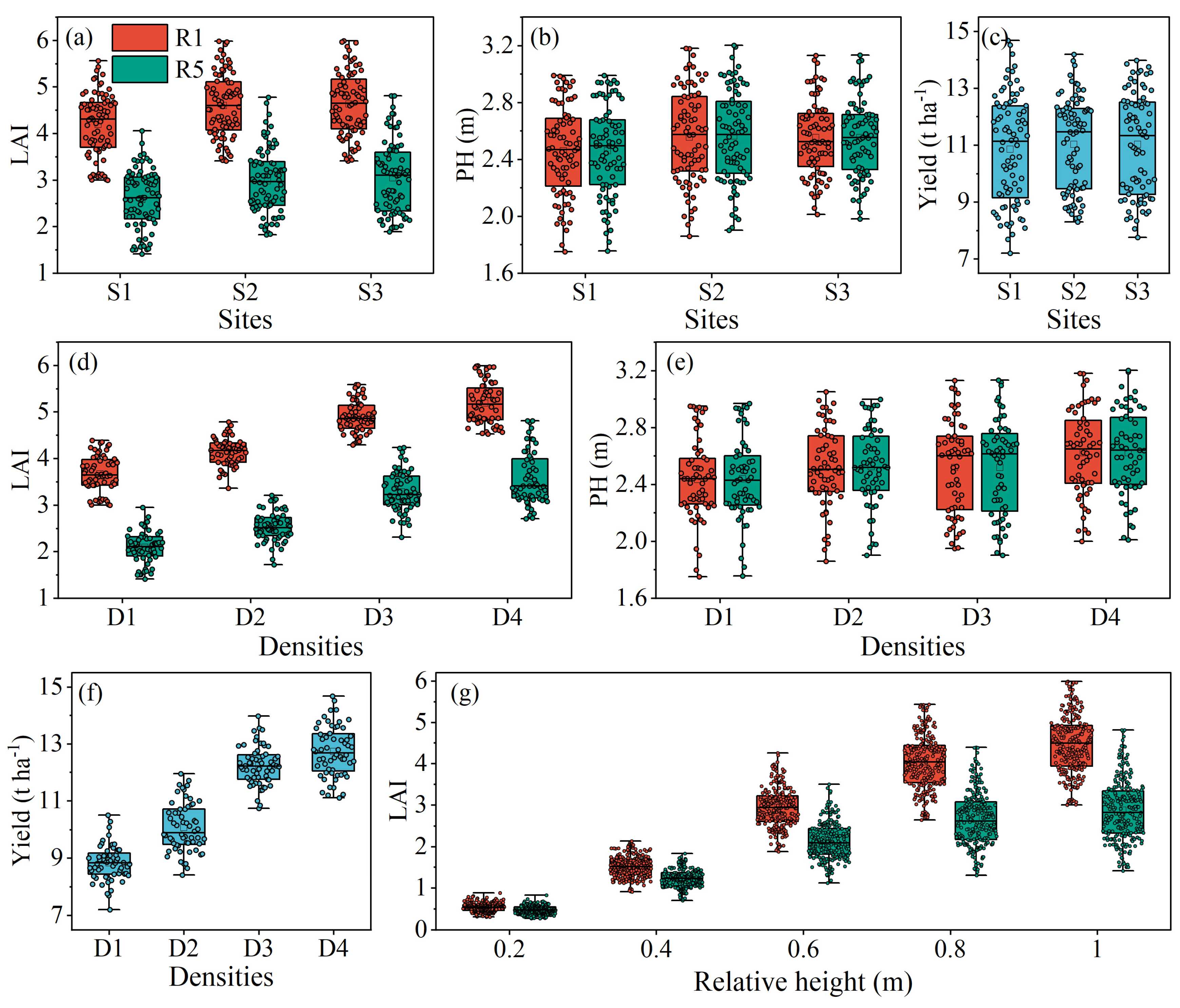
3.1. Descriptive Statistics
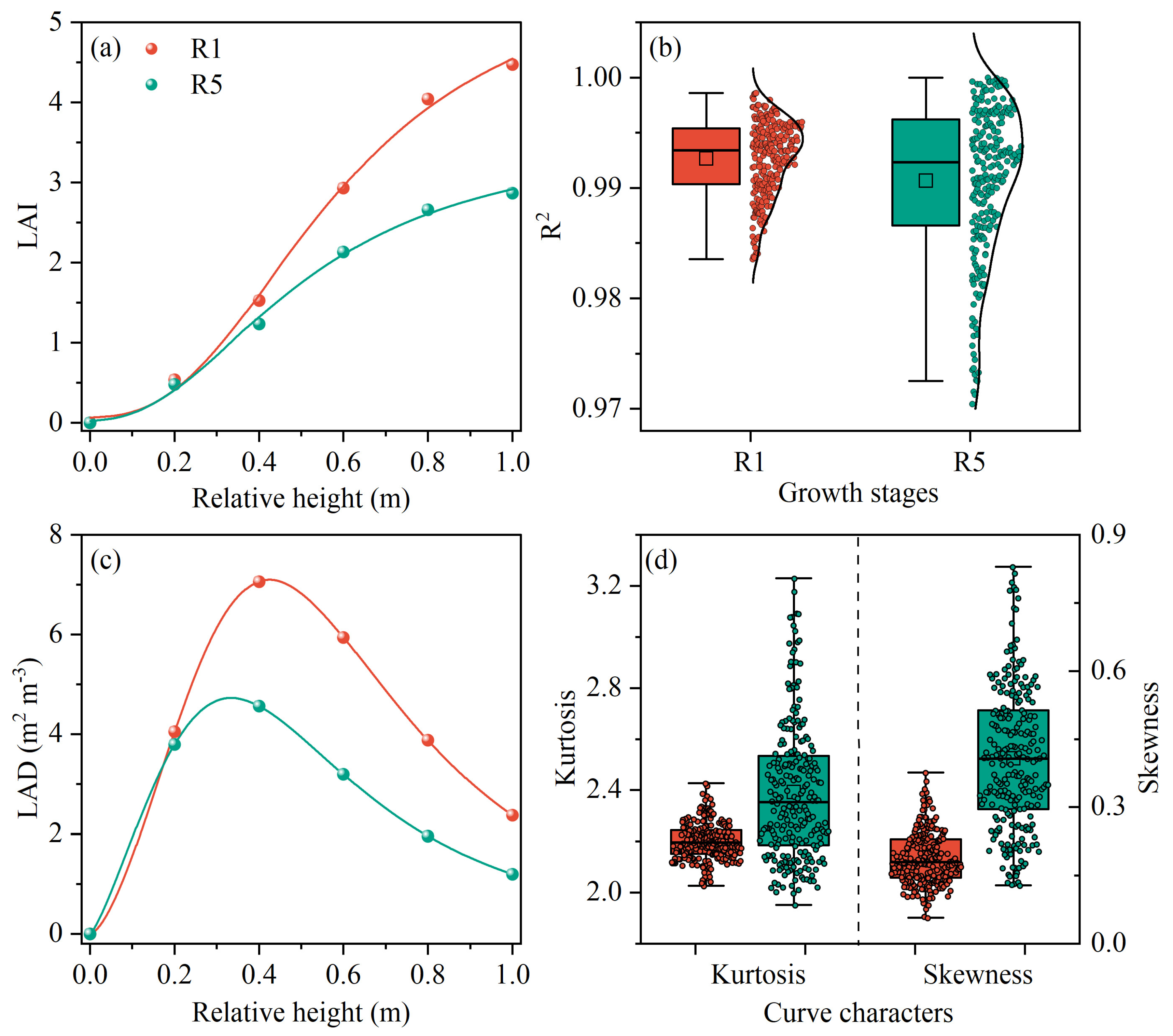
3.2. Construction of Canopy Architecture Indicators
3.3. Feasibility Analysis of Kurtosis and Skewness
3.3.1. Correlation Analysis
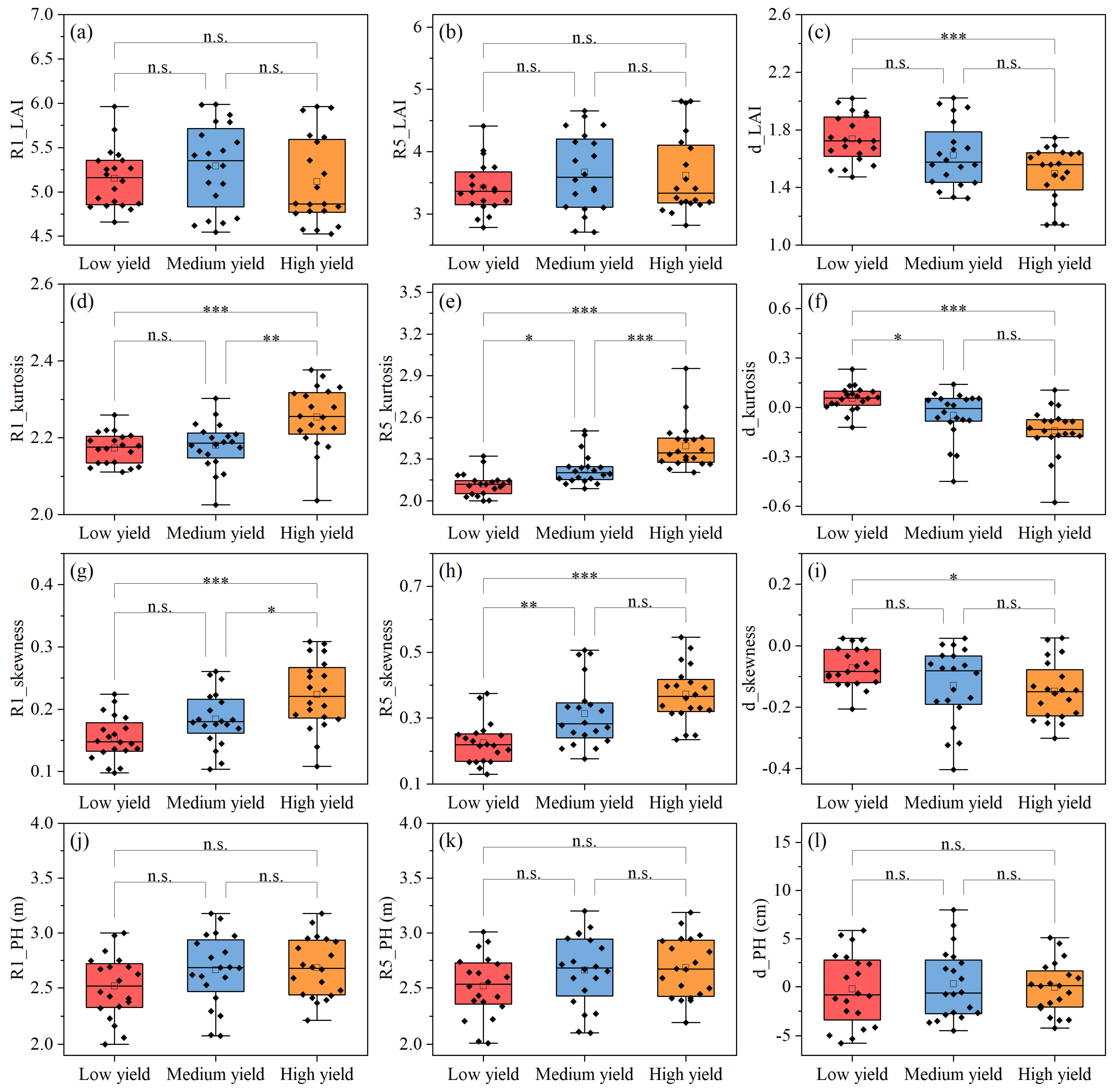
3.3.2. Yield Estimation
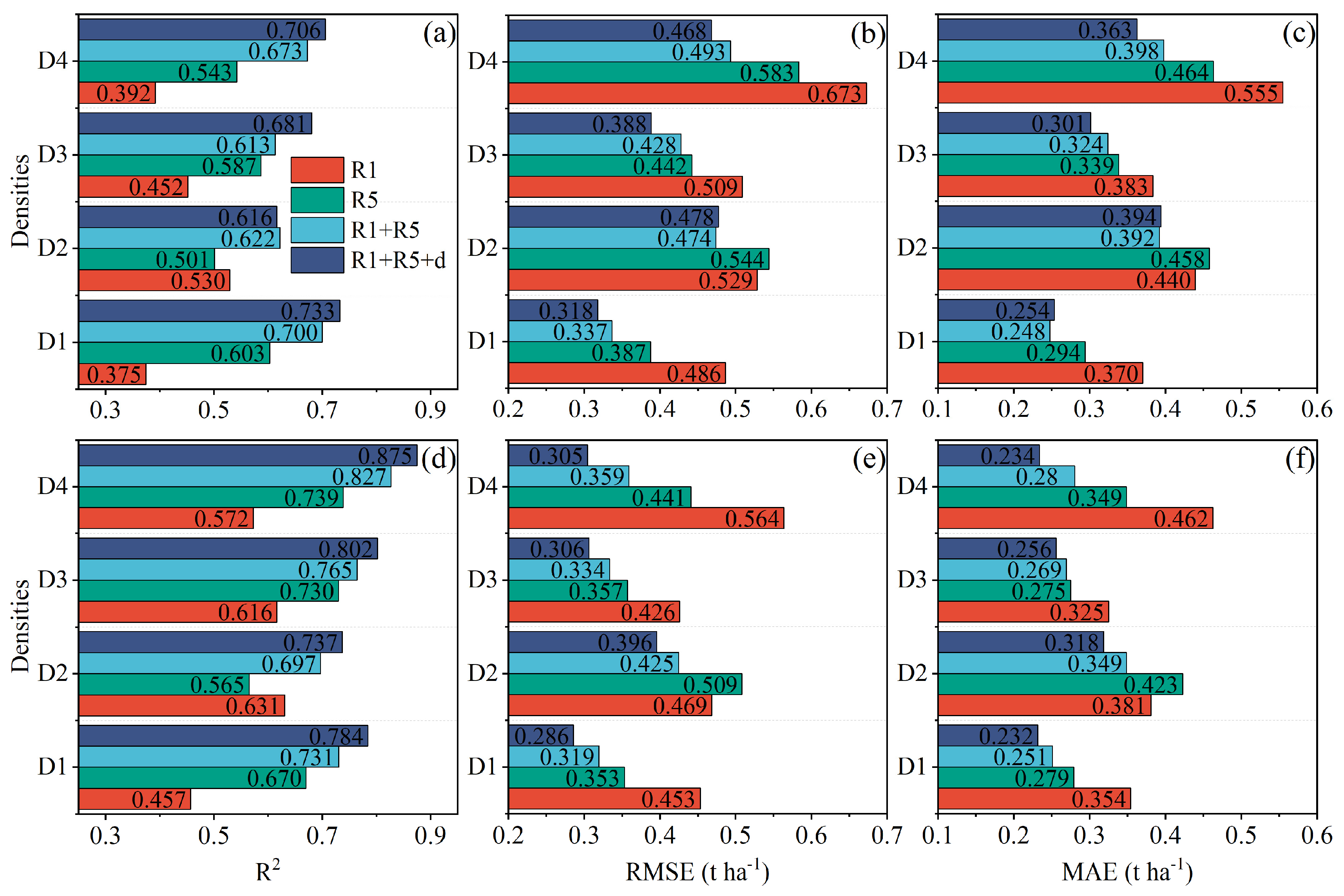
3.4. Canopy Indicator Estimation
3.4.1. Correlation Between VIs and Kurtosis and Skewness
3.4.2. Kurtosis and Skewness Estimation Results
4. Discussion
4.1. Vertical Distribution of Leaf Area in Maize Canopy
4.2. Effect of Canopy Architecture Indicators on Photosynthesis and Yield
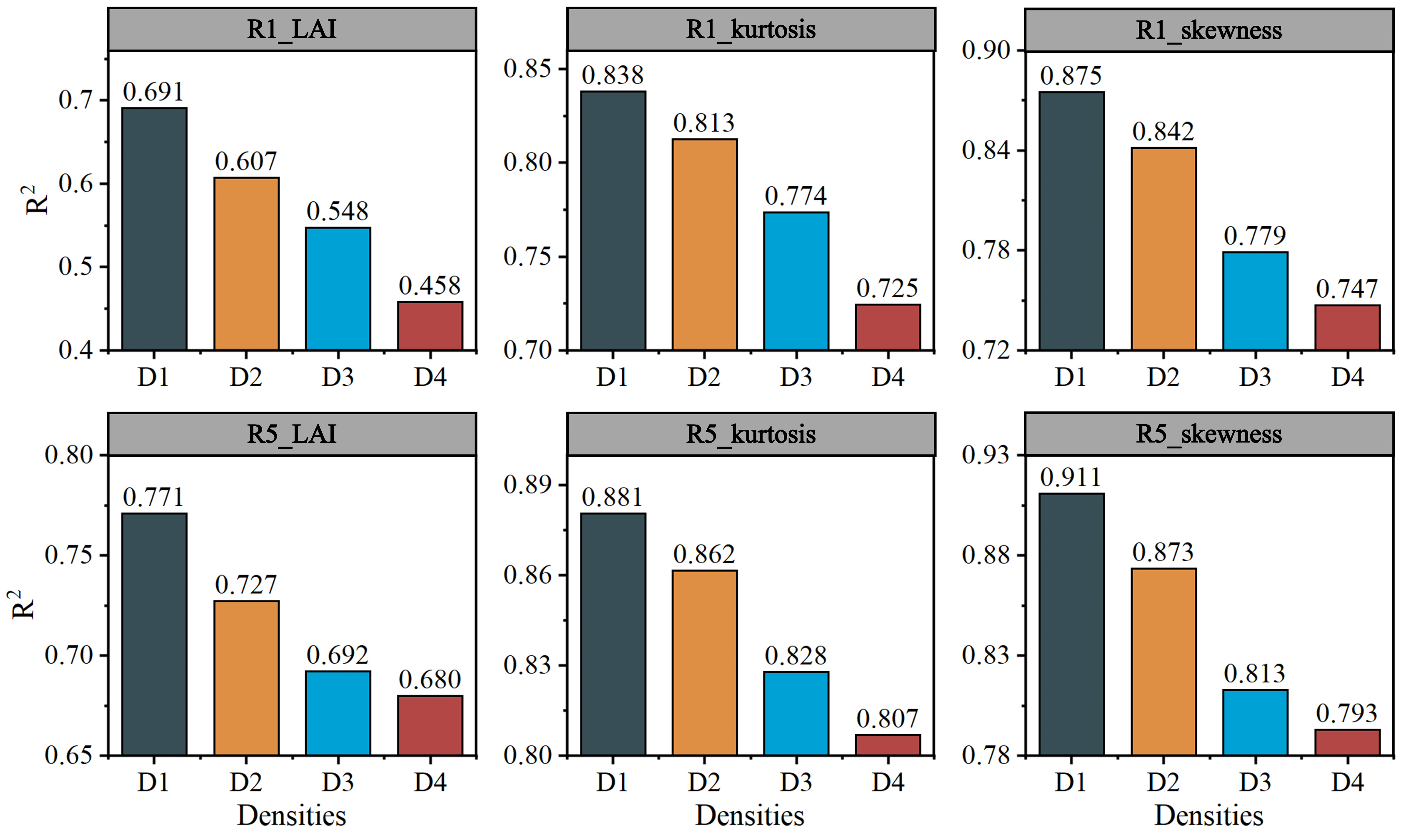
4.3. Effect of Planting Density on Photosynthesis and the Estimation Accuracy of Canopy Indicators
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CC | Canopy coverage |
| LAI | Leaf area index |
| PH | Plant height |
| LAD | Leaf area density |
| MS | Multispectral |
| LiDAR | Light detection and ranging |
| UAV | Unmanned aerial vehicle |
| M3M | Mavic 3 multispectral |
| R1 | Silking stage |
| R5 | Dent stage |
| R2 | Coefficient of determination |
| VIs | Vegetation indices |
| TIs | Texture indices |
| GLCM | Gray-level co-occurrence matrix |
| RMSE | Root-mean-square error |
| MAE | Mean absolute error |
References
- Feng, L.Y.; Raza, M.A.; Shi, J.Y.; Ansar, M.; Titriku, J.K.; Meraj, T.A.; Shah, G.A.; Ahmed, Z.; Saleem, A.; Liu, W.G.; et al. Delayed maize leaf senescence increases the land equivalent ratio of maize soybean relay intercropping system. Eur. J. Agron. 2020, 118, 126092. [Google Scholar] [CrossRef]
- Luo, N.; Meng, Q.; Feng, P.; Qu, Z.; Yu, Y.; Liu, D.L.; Müller, C.; Wang, P. China can be self-sufficient in maize production by 2030 with optimal crop management. Nat. Commun. 2023, 14, 2637. [Google Scholar] [CrossRef]
- Shafi, M.; Bakht, J.; Ali, S.; Khan, H.; Khan, M.A.; Sharif, M. Effect of planting density on phenology, growth and yield of maize (Zea mays L.). Pak. J. Bot. 2012, 44, 691–696. [Google Scholar]
- Li, R.F.; Zhang, G.Q.; Liu, G.Z.; Wang, K.R.; Xie, R.Z.; Hou, P.; Ming, B.; Wang, Z.G.; Li, S.K. Improving the yield potential in maize by constructing the ideal plant type and optimizing the maize canopy structure. Food Energy Secur. 2021, 10, e312. [Google Scholar] [CrossRef]
- Tian, J.G.; Wang, C.L.; Chen, F.Y.; Qin, W.C.; Yang, H.; Zhao, S.H.; Xia, J.L.; Du, X.; Zhu, Y.F.; Wu, L.S.; et al. Maize smart-canopy architecture enhances yield at high densities. Nature 2024, 632, 576–584. [Google Scholar] [CrossRef]
- Castro-Valdecantos, P.; Apolo-Apolo, O.E.; Pérez-Ruiz, M.; Egea, G. Leaf area index estimations by deep learning models using RGB images and data fusion in maize. Precis. Agric. 2022, 23, 1949–1966. [Google Scholar] [CrossRef]
- Gano, B.; Dembele, J.S.B.; Ndour, A.; Luquet, D.; Beurier, G.; Diouf, D.; Audebert, A. Using UAV borne, multi-spectral imaging for the field phenotyping of shoot biomass, leaf area index and height of West African sorghum varieties under two contrasted water conditions. Agronomy 2021, 11, 850. [Google Scholar] [CrossRef]
- Wang, Z.K.; Zhao, X.N.; Wu, P.T.; He, J.Q.; Chen, X.L.; Gao, Y.; Cao, X.C. Radiation interception and utilization by wheat/maize strip intercropping systems. Agric. For. Meteorol. 2015, 204, 58–66. [Google Scholar] [CrossRef]
- Fischer, K.S.; Edmeades, G.O.; Johnson, E.C. Recurrent selection for reduced tassel branch number and reduced leaf area density above the ear in tropical maize populations1. Crop Sci. 1987, 27, 1150–1156. [Google Scholar] [CrossRef]
- Ross, J.; Ross, V.; Koppel, A. Estimation of leaf area and its vertical distribution during growth period. Agric. For. Meteorol. 2000, 101, 237–246. [Google Scholar] [CrossRef]
- Chatterjee, S.; Baath, G.S.; Sapkota, B.R.; Flynn, K.C.; Smith, D.R. Enhancing LAI estimation using multispectral imagery and machine learning: A comparison between reflectance-based and vegetation indices-based approaches. Comput. Electron. Agric. 2025, 230, 109790. [Google Scholar] [CrossRef]
- Nguy-Robertson, A.L.; Peng, Y.; Gitelson, A.A.; Arkebauer, T.J.; Pimstein, A.; Herrmann, I.; Karnieli, A.; Rundquist, D.C.; Bonfil, D.J. Estimating green LAI in four crops: Potential of determining optimal spectral bands for a universal algorithm. Agric. For. Meteorol. 2014, 192, 140–148. [Google Scholar] [CrossRef]
- Zhao, D.; Yang, G.; Xu, T.; Yu, F.; Zhang, C.; Cheng, Z.; Ren, L.; Yang, H. Dynamic maize true leaf area index retrieval with KGCNN and TL and integrated 3D radiative transfer modeling for crop phenotyping. Plant Phenomics 2025, 7, 100004. [Google Scholar] [CrossRef]
- Savinelli, B.; Tagliabue, G.; Vignali, L.; Garzonio, R.; Gentili, R.; Panigada, C.; Rossini, M. Integrating drone-based LiDAR and multispectral data for tree monitoring. Drones 2024, 8, 744. [Google Scholar] [CrossRef]
- Nguyen, C.; Sagan, V.; Bhadra, S.; Moose, S. UAV multisensory data fusion and multi-task deep learning for high-throughput maize phenotyping. Sensors 2023, 23, 1827. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, W.; Yang, G.; Lei, L.; Han, S.; Xu, W.; Chen, R.; Zhang, C.; Yang, H. Maize ear height and ear–plant height ratio estimation with LiDAR data and vertical leaf area profile. Remote Sens. 2023, 15, 964. [Google Scholar] [CrossRef]
- Lei, L.; Qiu, C.X.; Li, Z.H.; Han, D.; Han, L.; Zhu, Y.H.; Wu, J.T.; Xu, B.; Feng, H.K.; Yang, H.; et al. Effect of leaf occlusion on leaf area index inversion of maize using UAV-LiDAR data. Remote Sens. 2019, 11, 1067. [Google Scholar] [CrossRef]
- Khun, K.; Tremblay, N.; Panneton, B.; Vigneault, P.; Lord, E.; Cavayas, F.; Codjia, C. Use of oblique RGB imagery and apparent surface area of plants for early estimation of above-ground corn biomass. Remote Sens. 2021, 13, 4032. [Google Scholar] [CrossRef]
- Che, Y.P.; Wang, Q.; Xie, Z.W.; Zhou, L.; Li, S.W.; Hui, F.; Wang, X.Q.; Li, B.G.; Ma, Y.T. Estimation of maize plant height and leaf area index dynamics using an unmanned aerial vehicle with oblique and nadir photography. Ann. Bot. 2020, 126, 765–773. [Google Scholar] [CrossRef]
- Wang, Y.; Wen, W.; Wu, S.; Wang, C.; Yu, Z.; Guo, X.; Zhao, C. Maize plant phenotyping: Comparing 3D laser scanning, multi-view stereo reconstruction, and 3D digitizing estimates. Remote Sens. 2018, 11, 63. [Google Scholar] [CrossRef]
- Liu, S.B.; Jin, X.L.; Nie, C.W.; Wang, S.Y.; Yu, X.; Cheng, M.H.; Shao, M.C.; Wang, Z.X.; Tuohuti, N.; Bai, Y.; et al. Estimating leaf area index using unmanned aerial vehicle data: Shallow vs. deep machine learning algorithms. Plant Physiol. 2021, 187, 1551–1576. [Google Scholar] [CrossRef]
- Yang, J.; Lu, Q. A study on mathematical models of canopy architecture for maize population. J. Shanxi Agric. Univ. 1996, 16, 347–349. [Google Scholar]
- Hirooka, Y.; Homma, K.; Shiraiwa, T.; Kuwada, M. Parameterization of leaf growth in rice (Oryza sativa L.) utilizing a plant canopy analyzer. Field Crops Res. 2016, 186, 117–123. [Google Scholar] [CrossRef]
- Main, R.; Cho, M.A.; Mathieu, R.; O’kennedy, M.M.; Ramoelo, A.; Koch, S. An investigation into robust spectral indices for leaf chlorophyll estimation. ISPRS J. Photogramm. Remote Sens. 2011, 66, 751–761. [Google Scholar] [CrossRef]
- Ahamed, T.; Tian, L.; Zhang, Y.; Ting, K.C. A review of remote sensing methods for biomass feedstock production. Biomass Bioenerg. 2011, 35, 2455–2469. [Google Scholar] [CrossRef]
- Datt, B. Remote sensing of water content in eucalyptus leaves. Aust. J. Bot. 1999, 47, 909–923. [Google Scholar] [CrossRef]
- Zhu, Y.; Yao, X.; Tian, Y.C.; Liu, X.J.; Cao, W.X. Analysis of common canopy vegetation indices for indicating leaf nitrogen accumulations in wheat and rice. Int. J. Appl. Earth Obs. 2008, 10, 1–10. [Google Scholar] [CrossRef]
- Tucker, C.J.; Elgin, J.H.; Iii, M.M.; Fan, C.J. Monitoring corn and soybean crop development with hand-held radiometer spectral data. Remote Sens. Environ. 1979, 8, 237–248. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.; Deering, D. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; National Aeronautics and Space Administration: Washington, DC, USA, 1973. [Google Scholar]
- Yang, C.; Everitt, J.H.; Bradford, J.M.; Murden, D. Airborne hyperspectral imagery and yield monitor data for mapping cotton yield variability. Precis. Agric. 2004, 5, 445–461. [Google Scholar] [CrossRef]
- Tian, Y.C.; Yao, X.; Yang, J.; Cao, W.X.; Hannaway, D.B.; Zhu, Y. Assessing newly developed and published vegetation indices for estimating rice leaf nitrogen concentration with ground- and space-based hyperspectral reflectance. Field Crops Res. 2011, 120, 299–310. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; De Colstoun, E.B.; Mcmurtrey, J.E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y. Non-destructive optical detection of pigment changes during leaf senescence and fruit ripening. Physiol. Plant. 1999, 106, 135–141. [Google Scholar] [CrossRef]
- Broge, N.H.; Mortensen, J.V. Deriving green crop area index and canopy chlorophyll density of winter wheat from spectral reflectance data. Remote Sens. Environ. 2002, 81, 45–57. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Hall-Beyer, M. Practical guidelines for choosing GLCM textures to use in landscape classification tasks over a range of moderate spatial scales. Int. J. Remote Sens. 2017, 38, 1312–1338. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Chica-Olmo, M.; Abarca-Hernandez, F.; Atkinson, P.M.; Jeganathan, C. Random forest classification of mediterranean land cover using multi-seasonal imagery and multi-seasonal texture. Remote Sens. Environ. 2012, 121, 93–107. [Google Scholar] [CrossRef]
- Zhao, K.; Xu, X.; Yuan, Y.; Zhang, H. Population structure and light distribution in maize fields. Acta Agron. Sin. 1963, 2, 321–332. [Google Scholar]
- Hirooka, Y.; Homma, K.; Shiraiwa, T. Parameterization of the vertical distribution of leaf area index (LAI) in rice (Oryza sativa L.) using a plant canopy analyzer. Sci. Rep. 2018, 8, 6387. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Fengler, K.A.; Van Hemert, J.L.; Gupta, R.; Mongar, N.; Sun, J.D.; Allen, W.B.; Wang, Y.; Weers, B.; Mo, H.; et al. Identification and characterization of a novel stay-green QTL that increases yield in maize. Plant Biotechnol. J. 2019, 17, 2272–2285. [Google Scholar] [CrossRef]
- Li, R.F.; Hu, D.D.; Ren, H.; Yang, Q.L.; Dong, S.T.; Zhang, J.W.; Zhao, B.; Liu, P. How delaying post-silking senescence in lower leaves of maize plants increases carbon and nitrogen accumulation and grain yield. Crop J. 2022, 10, 853–863. [Google Scholar] [CrossRef]
- Liu, N.; Li, L.; Li, H.T.; Liu, Z.M.; Lu, Y.; Shao, L.W. Selecting maize cultivars to regulate canopy structure and light interception for high yield. Agron. J. 2023, 115, 770–780. [Google Scholar] [CrossRef]
- Shapiro, C.A.; Wortmann, C.S. Corn response to nitrogen rate, row spacing, and plant density in eastern Nebraska. Agron. J. 2006, 98, 529–535. [Google Scholar] [CrossRef]
- Jafari, F.; Wang, B.B.; Wang, H.Y.; Zou, J.J. Breeding maize of ideal plant architecture for high-density planting tolerance through modulating shade avoidance response and beyond. J. Integr. Plant Biol. 2024, 66, 849–864. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.Z.; Ren, H.; Han, K.; Zhang, L.H.; Zhao, Y.L.; Liu, Y.E.; He, Q.J.; Li, G.; Zhang, J.W.; Zhao, B.; et al. Experimental assessment of the yield gap associated with maize production in the North China Plain. Field Crops Res. 2023, 295, 108897. [Google Scholar] [CrossRef]
- Niu, X.K.; Xie, R.Z.; Liu, X.; Zhang, F.L.; Li, S.K.; Gao, S.J. Maize yield gains in northeast China in the last six decades. J. Integr. Agric. 2013, 12, 630–637. [Google Scholar] [CrossRef]
- Gao, J.; Lei, M.; Yang, L.J.; Wang, P.; Tao, H.B.; Huang, S.B. Reduced row spacing improved yield by optimizing root distribution in maize. Eur. J. Agron. 2021, 127, 126291. [Google Scholar] [CrossRef]
- Liu, X.; Gu, S.H.; Wen, W.L.; Lu, X.J.; Jin, Y.; Zhang, Y.J.; Guo, X.Y. Disentangling the heterosis in biomass production and radiation use efficiency in maize: A phytomer-based 3D modelling approach. Plants 2023, 12, 1229. [Google Scholar] [CrossRef]

| Vegetation Indices | Formula | References |
|---|---|---|
| CARI (chlorophyll absorption ratio index) | [24] | |
| Cig (chlorophyll index—green) | [25] | |
| Datt | [26] | |
| DVI (difference vegetation index) | [27] | |
| GDVI (green difference vegetation index) | [28] | |
| MCARI (modified chlorophyll absorption in reflectance index) | [24] | |
| MTVI (modified triangular vegetation index) | [29] | |
| NDVI (normalized difference vegetation index) | [30] | |
| GNDVI (green normalized difference vegetation index) | [31] | |
| NDRE (normalized difference red-edge index) | [32] | |
| OSAVI (optimized soil-adjusted vegetation index) | [33] | |
| PSRI (plant senescence reflectance index) | [34] | |
| RVI (ratio vegetation index) | [35] | |
| TCARI (transformed chlorophyll absorption ratio) | [36] | |
| TVI (triangular vegetation index) | [24] |
| Texture Indices | Formula | References |
|---|---|---|
| Mean | [37] | |
| Variance | [37] | |
| Homogeneity | [37] | |
| Contrast | [37] | |
| Dissimilarity | [38] | |
| Entropy | [38] | |
| Second moment | [38] | |
| Correlation | [38] |
| Feature Type | Features | Kurtosis | Skewness | ||
|---|---|---|---|---|---|
| R1 Stage | R5 Stage | R1 Stage | R5 Stage | ||
| VIs | CARI | 0.392 *** | 0.420 *** | 0.374 *** | 0.445 *** |
| Cig | 0.383 *** | 0.117 | 0.461 *** | 0.259 *** | |
| Datt | −0.125 | −0.360 *** | −0.307 *** | −0.233 *** | |
| DVI | 0.389 *** | 0.543 *** | 0.195 ** | 0.476 *** | |
| GDVI | 0.457 *** | 0.579 *** | 0.233 *** | 0.537 *** | |
| MCARI | 0.255 *** | 0.441 *** | 0.336 *** | 0.562 *** | |
| MTVI | −0.175 ** | 0.429 *** | 0.167 ** | −0.196 ** | |
| NDVI | 0.425 *** | 0.487 *** | 0.130 * | 0.452 *** | |
| GNDVI | 0.340 *** | 0.386 *** | 0.103 | 0.363 *** | |
| NDRE | −0.210 ** | 0.493 *** | −0.146 * | 0.315 *** | |
| OSAVI | 0.481 *** | 0.239 *** | 0.264 *** | 0.131 * | |
| PSRI | 0.076 | −0.234 *** | 0.032 | −0.100 | |
| RVI | 0.398 *** | 0.525 *** | 0.358 *** | 0.518 *** | |
| TCARI | −0.332 *** | −0.468 *** | −0.220 *** | −0.341 *** | |
| TVI | 0.437 *** | 0.353 *** | 0.404 *** | 0.502 *** | |
| TIs | Mean | −0.130 | −0.078 | 0.152 * | −0.030 |
| Variance | 0.348 *** | 0.431 *** | 0.194 ** | 0.271 *** | |
| Homogeneity | −0.271 *** | −0.375 *** | −0.181 * | −0.298 *** | |
| Contrast | 0.294 *** | 0.453 *** | 0.148 * | 0.417 *** | |
| Dissimilarity | 0.261 *** | 0.359 *** | 0.128 | 0.115 | |
| Entropy | −0.178 * | 0.301 *** | 0.370 *** | 0.108 | |
| Second moment | 0.013 | −0.287 *** | 0.114 | −0.386 *** | |
| Correlation | 0.385 *** | 0.229 ** | 0.312 *** | 0.277 *** | |
| Canopy Indicators | Features | R1 Stage | R5 Stage | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | ||
| Kurtosis | VI images | 0.447 | 0.055 | 0.043 | 0.554 | 0.176 | 0.140 |
| TI images | 0.396 | 0.057 | 0.048 | 0.435 | 0.198 | 0.161 | |
| Point clouds | 0.694 | 0.041 | 0.034 | 0.798 | 0.119 | 0.098 | |
| All | 0.792 | 0.034 | 0.026 | 0.841 | 0.105 | 0.085 | |
| Skewness | VI images | 0.431 | 0.043 | 0.034 | 0.532 | 0.105 | 0.083 |
| TI images | 0.390 | 0.045 | 0.036 | 0.449 | 0.114 | 0.093 | |
| Point clouds | 0.747 | 0.029 | 0.023 | 0.809 | 0.067 | 0.054 | |
| All | 0.815 | 0.025 | 0.020 | 0.859 | 0.058 | 0.046 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, S.; Han, D.; Zhang, W.; Yang, T.; Yao, Z.; Liu, T.; Sun, C. Development of Maize Canopy Architecture Indicators Through UAV Multi-Source Data. Agronomy 2025, 15, 1991. https://doi.org/10.3390/agronomy15081991
Zhu S, Han D, Zhang W, Yang T, Yao Z, Liu T, Sun C. Development of Maize Canopy Architecture Indicators Through UAV Multi-Source Data. Agronomy. 2025; 15(8):1991. https://doi.org/10.3390/agronomy15081991
Chicago/Turabian StyleZhu, Shaolong, Dongwei Han, Weijun Zhang, Tianle Yang, Zhaosheng Yao, Tao Liu, and Chengming Sun. 2025. "Development of Maize Canopy Architecture Indicators Through UAV Multi-Source Data" Agronomy 15, no. 8: 1991. https://doi.org/10.3390/agronomy15081991
APA StyleZhu, S., Han, D., Zhang, W., Yang, T., Yao, Z., Liu, T., & Sun, C. (2025). Development of Maize Canopy Architecture Indicators Through UAV Multi-Source Data. Agronomy, 15(8), 1991. https://doi.org/10.3390/agronomy15081991






