Ensemble Learning-Driven and UAV Multispectral Analysis for Estimating the Leaf Nitrogen Content in Winter Wheat
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of the Experimental Area and Experimental Design
2.2. Data Handling
2.3. Image Preprocessing
2.4. Canopy Image Segmentation
2.4.1. Introduction to Image Algorithms
Random Forest (RF)
Support Vector Machine (SVM)
2.4.2. Image Segmentation Algorithm Specific Steps
Key Feature Extraction
Construction of Training Dataset
Classifier Construction and Biplot Generation
2.5. Vegetation Index Selection
2.6. Model Building
2.6.1. Random Forests
2.6.2. Ridge Regression
2.6.3. K-Nearest Neighbor
2.6.4. Support Vector Regression
2.6.5. Stacking Model
2.6.6. Voting Model
2.7. Modeling Evaluation
3. Results and Analysis
3.1. Variable Screening and Statistical Analysis
3.1.1. Descriptive Statistical Analysis
3.1.2. Z-Score Outlier Elimination
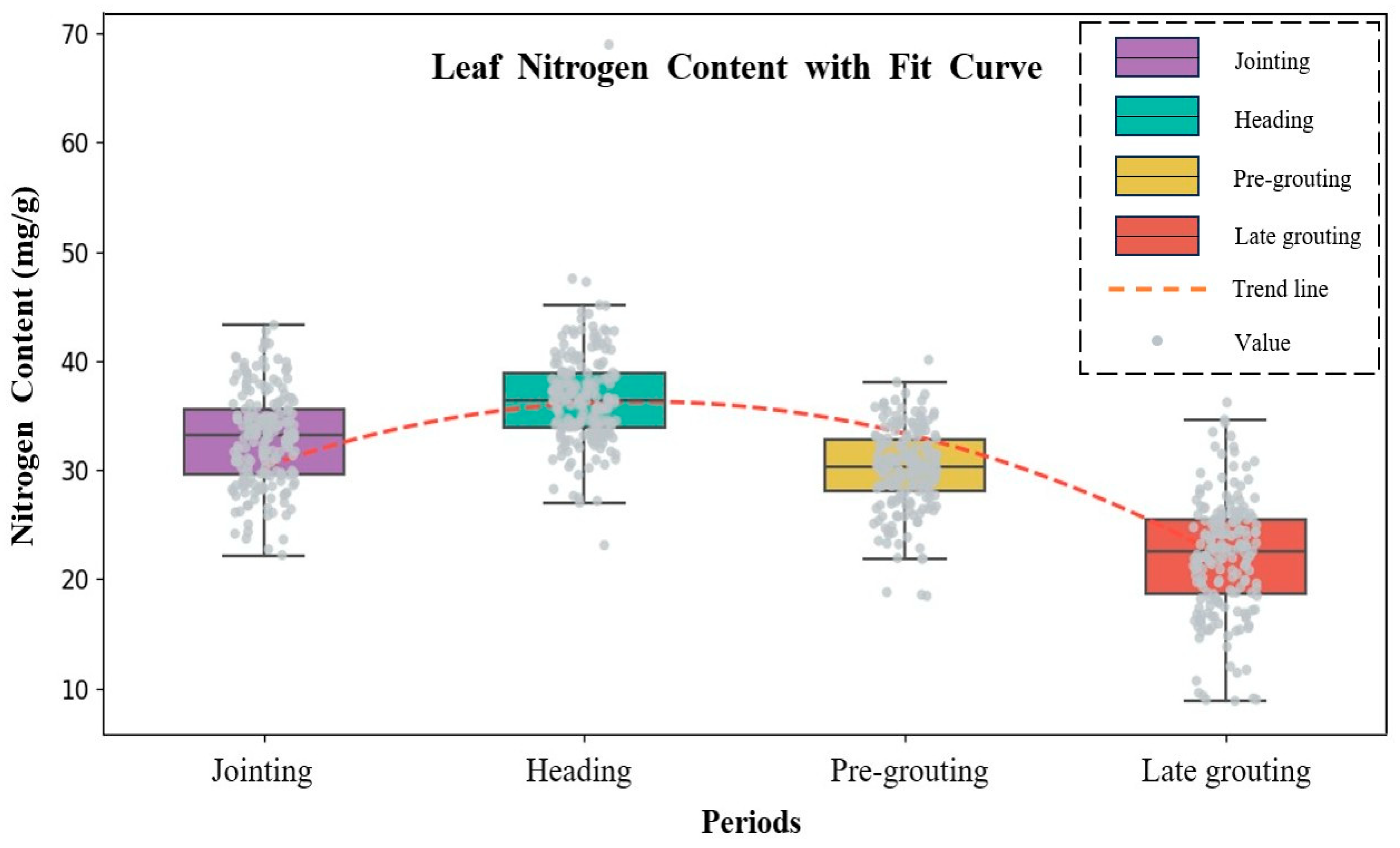
3.2. Analysis of Nitrogen Content in Winter Wheat Leaves at Different Periods
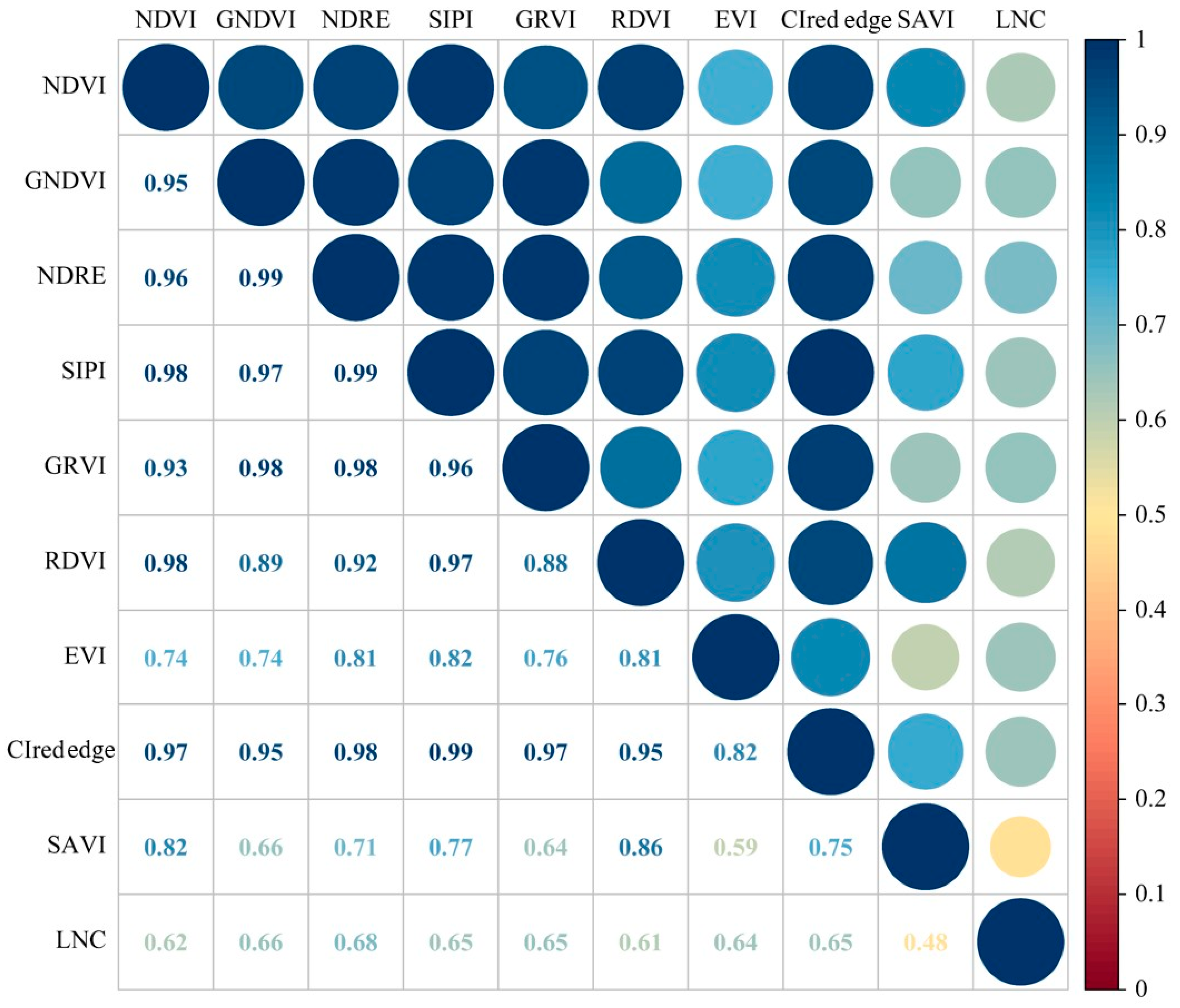
3.3. Correlation Between Vegetation Index and Nitrogen Content in Leaves
3.4. Estimation of Leaf Nitrogen Content Based on Vegetation Indices
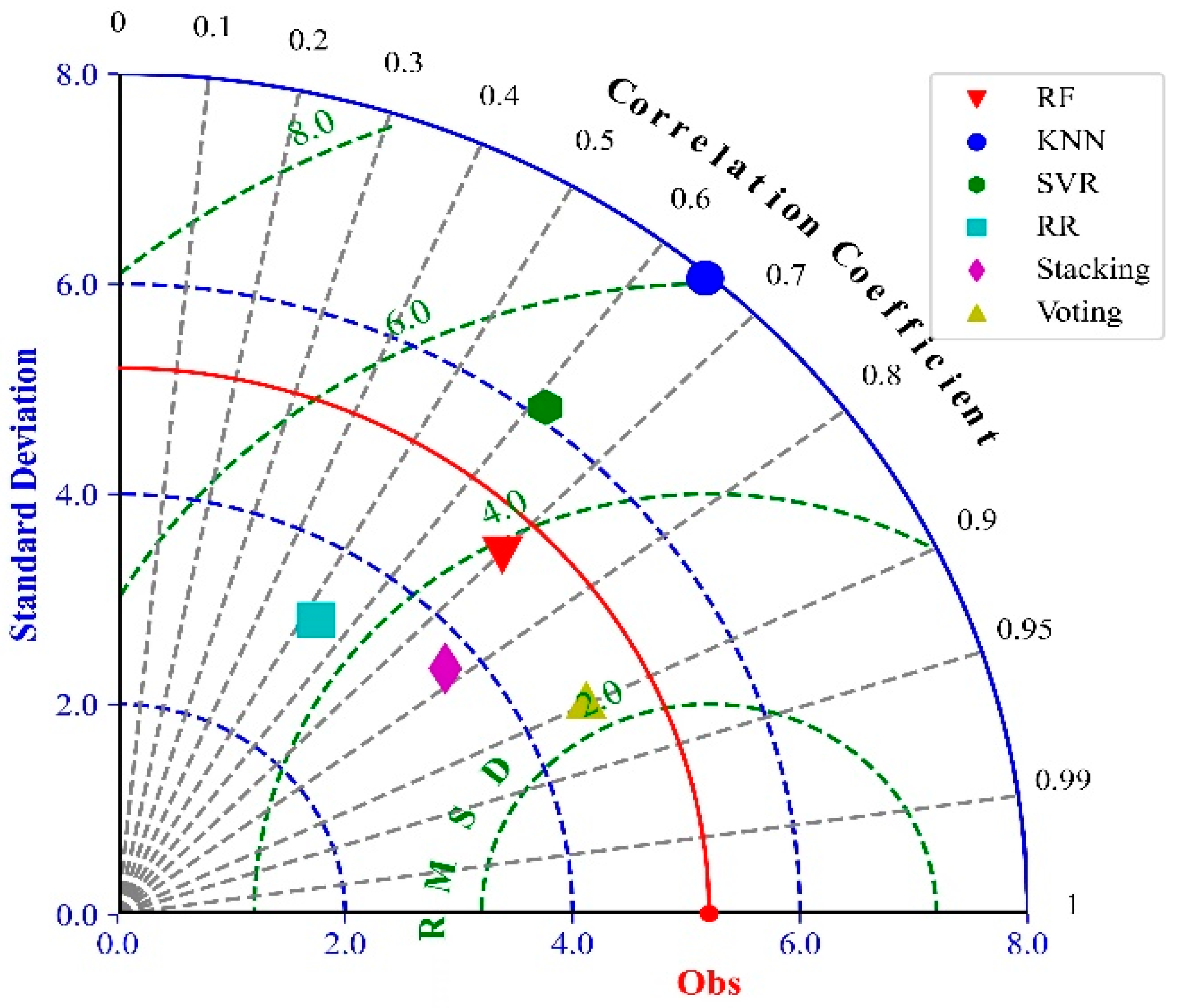
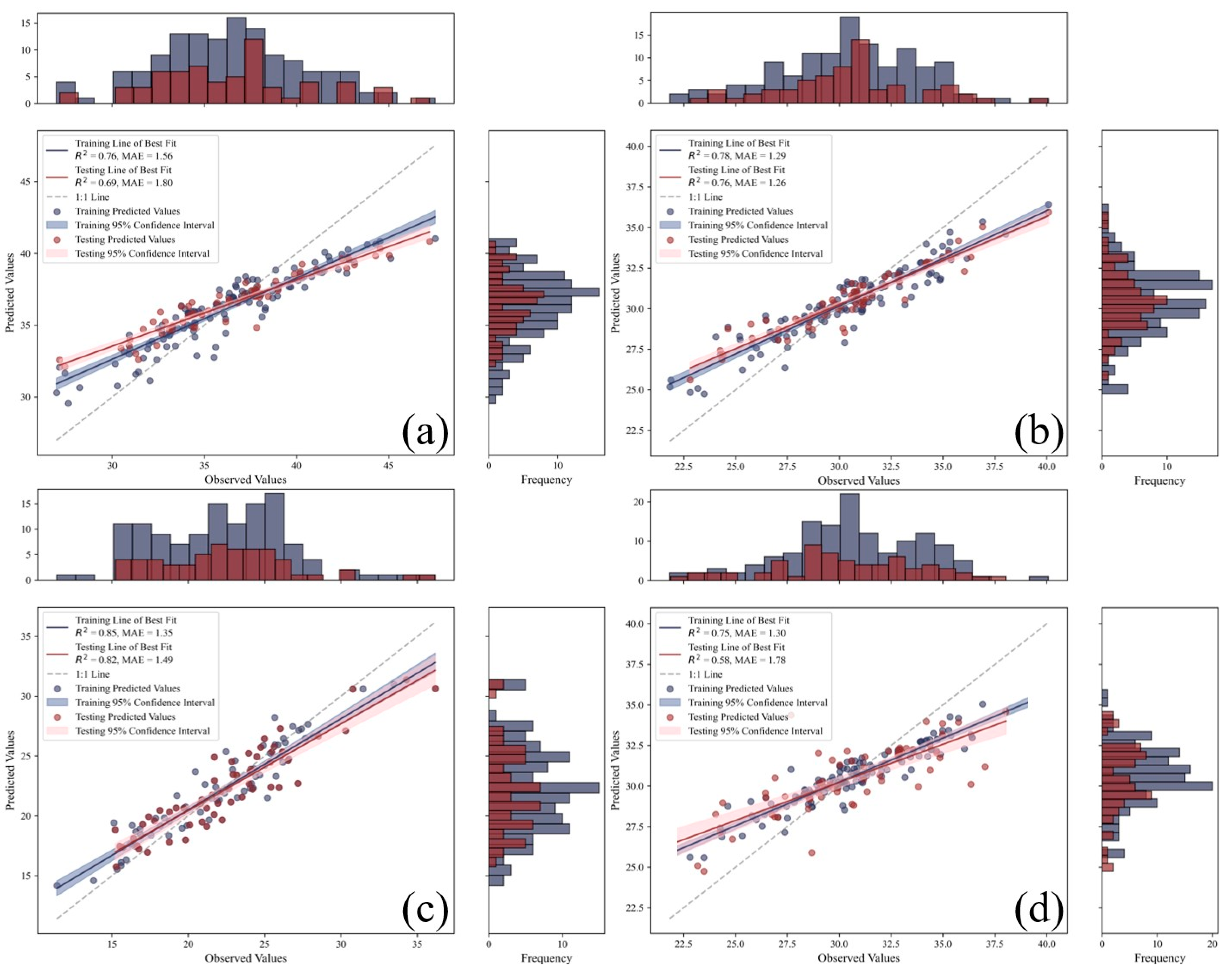
3.5. Model Construction and Inversion of Leaf Nitrogen Content Estimation Based on Vegetation Indices
4. Discussion
4.1. The Application Value of Multispectral Remote Sensing Images in Crop Canopy Segmentation
4.2. Performance Analysis of Winter Wheat Leaf Nitrogen Content Monitoring Using Vegetation Indices
4.3. Advantages of Estimating Nitrogen Content of Winter Wheat Leaves Based on Integrated Learning Models
4.4. Feasibility and Limitations of UAV-Based Multispectral Estimation for Winter Wheat LNC
5. Research Significance and Application Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CART | Classification and Regression Tree |
| CIred-edge | Chlorophyll Index Red-Edge |
| EVI | Enhanced Vegetation Index |
| GNDVI | Green Normalized Difference Vegetation Index |
| GRVI | Green-Red Vegetation Index |
| K-NN | K-Nearest Neighbors |
| LNC | Leaf Nitrogen Content |
| MSAVI | Modified Soil-Adjusted Vegetation Index |
| NDRE | Normalized Difference Red Edge Index |
| NDVI | Normalized Difference Vegetation Index |
| NIR | Near-Infrared |
| OLS | Ordinary Least Squares |
| PMS | Percentage of Missing Segmentation |
| PWS | Percentage of Wrong Split |
| RBF | Radial Basis Function |
| RDVI | Relative Difference Vegetation Index |
| RF | Random Forest |
| ROI | Support Vector Machine |
| RR | Ridge Regression |
| SAVI | Soil-Adjusted Vegetation Index |
| SIPI | Structure Insensitive Pigment Index |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| UAV | Unmanned Aerial Vehicle |
| VIs | Vegetation Indices |
References
- Yi, F.; Lyu, S.; Yang, L. More Power Generation, More Wheat Losses? Evidence from Wheat Productivity in North China. Environ. Resour. Econ. 2024, 87, 907–931. [Google Scholar] [CrossRef]
- Duan, B.; Fang, S.; Zhu, R.; Wu, X.; Wang, S.; Gong, Y.; Peng, Y. Remote estimation of rice yield with unmanned aerial vehicle (UAV) data and spectral mixture analysis. Front. Plant Sci. 2019, 10, 204. [Google Scholar] [CrossRef] [PubMed]
- Mgendi, G. Unlocking the potential of precision agriculture for sustainable farming. Discov. Agric. 2024, 2, 87. [Google Scholar] [CrossRef]
- ul Ain, N. Nitrogen Fertilization Strategies for Sustainable Winter Wheat Production in a Growing World. Int. J. Agric. Sustain. Dev. 2024, 6, 15–28. [Google Scholar]
- Xue, H.; Liu, J.; Oo, S.; Patterson, C.; Liu, W.; Li, Q.; Wang, G.; Li, L.; Zhang, Z.; Pan, X. Differential responses of wheat (Triticum aestivum L.) and cotton (Gossypium hirsutum L.) to nitrogen deficiency in the root morpho-physiological characteristics and potential microRNA-mediated mechanisms. Front. Plant Sci. 2022, 13, 928229. [Google Scholar] [CrossRef]
- Ali, A.; Jabeen, N.; Farruhbek, R.; Chachar, Z.; Laghari, A.A.; Chachar, S.; Ahmed, N.; Ahmed, S.; Yang, Z. Enhancing nitrogen use efficiency in agriculture by integrating agronomic practices and genetic advances. Front. Plant Sci. 2025, 16, 1543714. [Google Scholar] [CrossRef]
- Anas, M.; Liao, F.; Verma, K.K.; Sarwar, M.A.; Mahmood, A.; Chen, Z.-L.; Li, Q.; Zeng, X.-P.; Liu, Y.; Li, Y.-R. Fate of nitrogen in agriculture and environment: Agronomic, eco-physiological and molecular approaches to improve nitrogen use efficiency. Biol. Res. 2020, 53, 47. [Google Scholar] [CrossRef]
- Peron-Danaher, R.; Russell, B.; Cotrozzi, L.; Mohammadi, M.; Couture, J.J. Incorporating multi-scale, spectrally detected nitrogen concentrations into assessing nitrogen use efficiency for winter wheat breeding populations. Remote Sens. 2021, 13, 3991. [Google Scholar] [CrossRef]
- Hansen, P.; Schjoerring, J. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Li, D.; Chen, J.M.; Yan, Y.; Zheng, H.; Yao, X.; Zhu, Y.; Cao, W.; Cheng, T. Estimating leaf nitrogen content by coupling a nitrogen allocation model with canopy reflectance. Remote Sens. Environ. 2022, 283, 113314. [Google Scholar] [CrossRef]
- Schlemmer, M.; Gitelson, A.; Schepers, J.; Ferguson, R.; Peng, Y.; Shanahan, J.; Rundquist, D. Remote estimation of nitrogen and chlorophyll contents in maize at leaf and canopy levels. Int. J. Appl. Earth Obs. Geoinf. 2013, 25, 47–54. [Google Scholar] [CrossRef]
- Omia, E.; Bae, H.; Park, E.; Kim, M.S.; Baek, I.; Kabenge, I.; Cho, B.-K. Remote sensing in field crop monitoring: A comprehensive review of sensor systems, data analyses and recent advances. Remote Sens. 2023, 15, 354. [Google Scholar] [CrossRef]
- Jiang, J.; Wu, Y.; Liu, Q.; Liu, Y.; Cao, Q.; Tian, Y.; Zhu, Y.; Cao, W.; Liu, X. Developing an efficiency and energy-saving nitrogen management strategy for winter wheat based on the UAV multispectral imagery and machine learning algorithm. Precis. Agric. 2023, 24, 2019–2043. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Tian, T.; Yin, J. A review of unmanned aerial vehicle low-altitude remote sensing (UAV-LARS) use in agricultural monitoring in China. Remote Sens. 2021, 13, 1221. [Google Scholar] [CrossRef]
- Silva, D.C.; Madari, B.E.; Carvalho, M.d.C.S.; Ferreira, M.E. Optimizing nitrogen estimates in common bean canopies throughout key growth stages via spectral and textural data from unmanned aerial vehicle multispectral imagery. Eur. J. Agron. 2025, 169, 127697. [Google Scholar] [CrossRef]
- Peng, X.; Chen, D.; Zhou, Z.; Zhang, Z.; Xu, C.; Zha, Q.; Wang, F.; Hu, X. Prediction of the nitrogen, phosphorus and potassium contents in grape leaves at different growth stages based on UAV multispectral remote sensing. Remote Sens. 2022, 14, 2659. [Google Scholar] [CrossRef]
- Severtson, D.; Callow, N.; Flower, K.; Neuhaus, A.; Olejnik, M.; Nansen, C. Unmanned aerial vehicle canopy reflectance data detects potassium deficiency and green peach aphid susceptibility in canola. Precis. Agric. 2016, 17, 659–677. [Google Scholar] [CrossRef]
- Zhu, S.; Cui, N.; Zhou, J.; Xue, J.; Wang, Z.; Wu, Z.; Wang, M.; Deng, Q. Digital mapping of root-zone soil moisture using UAV-based multispectral data in a kiwifruit orchard of northwest China. Remote Sens. 2023, 15, 646. [Google Scholar] [CrossRef]
- Xia, F.; Quan, L.; Lou, Z.; Sun, D.; Li, H.; Lv, X. Identification and comprehensive evaluation of resistant weeds using unmanned aerial vehicle-based multispectral imagery. Front. Plant Sci. 2022, 13, 938604. [Google Scholar] [CrossRef]
- Wang, L.; Chen, S.; Li, D.; Wang, C.; Jiang, H.; Zheng, Q.; Peng, Z. Estimation of paddy rice nitrogen content and accumulation both at leaf and plant levels from UAV hyperspectral imagery. Remote Sens. 2021, 13, 2956. [Google Scholar] [CrossRef]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine learning approaches for crop yield prediction and nitrogen status estimation in precision agriculture: A review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Bharadiya, J.P.; Tzenios, N.T.; Reddy, M. Forecasting of crop yield using remote sensing data, agrarian factors and machine learning approaches. J. Eng. Res. Rep. 2023, 24, 29–44. [Google Scholar] [CrossRef]
- Mayer, S.; van Herwijnen, A.; Techel, F.; Schweizer, J. A random forest model to assess snow instability from simulated snow stratigraphy. Cryosphere 2022, 16, 4593–4615. [Google Scholar] [CrossRef]
- Sakamoto, T.; Sprague, D.S.; Okamoto, K.; Ishitsuka, N. Semi-automatic classification method for mapping the rice-planted areas of Japan using multi-temporal Landsat images. Remote Sens. Appl. Soc. Environ. 2018, 10, 7–17. [Google Scholar] [CrossRef]
- Meng, Z.; Yongnian, Z. Mapping paddy fields of Dongting Lake area by fusing Landsat and MODIS data. Trans. Chin. Soc. Agric. Eng. 2015, 31. [Google Scholar]
- Hu, H.; Bai, Y.-L.; Yang, L.-P.; Lu, Y.-L.; Wang, L.; Wang, H.; Wang, Z.-Y. Diagnosis of nitrogen nutrition in winter wheat (Triticum aestivum) via SPAD-502 and GreenSeeker. Chin. J. Eco-Agric. 2010, 18, 748–752. [Google Scholar] [CrossRef]
- Ali, M.; Al-Ani, A.; Eamus, D.; Tan, D.K. Leaf nitrogen determination using non-destructive techniques–A review. J. Plant Nutr. 2017, 40, 928–953. [Google Scholar] [CrossRef]
- Feng, H.; Li, Y.; Wu, F.; Zou, X. Estimating winter wheat nitrogen content using spad and hyperspectral vegetation indices with machine learning. Trans. Chin. Soc. Agric. Eng 2024, 40, 227–237. [Google Scholar]
- Deng, L.; Mao, Z.; Li, X.; Hu, Z.; Duan, F.; Yan, Y. UAV-based multispectral remote sensing for precision agriculture: A comparison between different cameras. ISPRS J. Photogramm. Remote Sens. 2018, 146, 124–136. [Google Scholar] [CrossRef]
- He, X.; Cai, Q.; Zou, X.; Li, H.; Feng, X.; Yin, W.; Qian, Y. Multi-modal late fusion rice seed variety classification based on an improved voting method. Agriculture 2023, 13, 597. [Google Scholar] [CrossRef]
- Burgos-Artizzu, X.P.; Ribeiro, A.; Guijarro, M.; Pajares, G. Real-time image processing for crop/weed discrimination in maize fields. Comput. Electron. Agric. 2011, 75, 337–346. [Google Scholar] [CrossRef]
- Chen, B.; Gu, S.; Huang, G.; Lu, X.; Chang, W.; Wang, G.; Guo, X. Improved estimation of nitrogen use efficiency in maize from the fusion of UAV multispectral imagery and LiDAR point cloud. Eur. J. Agron. 2025, 168, 127666. [Google Scholar] [CrossRef]
- Nyengere, J.; Okamoto, Y.; Funakawa, S.; Shinjo, H. Analysis of spatial heterogeneity of soil physicochemical properties in northern Malawi. Geoderma Reg. 2023, 35, e00733. [Google Scholar] [CrossRef]
- Adeluyi, O.; Harris, A.; Foster, T.; Clay, G.D. Exploiting centimetre resolution of drone-mounted sensors for estimating mid-late season above ground biomass in rice. Eur. J. Agron. 2022, 132, 126411. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Deering, D.W. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation. 1974. Available online: https://search.worldcat.org/title/Monitoring-the-vernal-advancement-and-retrogradation-(greenwave-effect)-of-natural-vegetation/oclc/67660194 (accessed on 4 May 2025).
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide dynamic range vegetation index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef]
- Penuelas, J.; Baret, F.; Filella, I. Semi-empirical indices to assess carotenoids/chlorophyll a ratio from leaf spectral reflectance. Photos Ynthetica 1995, 31, 221–230. [Google Scholar]
- Fitzgerald, P.B.; Huntsman, S.; Gunewardene, R. A randomized trial of low-frequency right-prefrontal-cortex transcranial magnetic stimulation as augmentation in treatment-resistant major depression. Int. J. Neuropsychopharmacol. 2006, 9, 655–666. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of leaf-area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Perach, O.; Solomon, N.; Avneri, A.; Ram, O.; Abbo, S.; Herrmann, I. Integrating Sentinel-2 imagery and meteorological data to estimate leaf area index and leaf water potential, with a leave-field-out validation strategy in chickpea fields. Eur. J. Agron. 2025, 168, 127632. [Google Scholar] [CrossRef]
- Vázquez-Veloso, A.; Caicoya, A.T.; Bravo, F.; Biber, P.; Uhl, E.; Pretzsch, H. Does machine learning outperform logistic regression in predicting individual tree mortality? Ecol. Inform. 2025, 88, 103140. [Google Scholar] [CrossRef]
- Lee, J.; Kim, J. Developing a convenience store product recommendation system through store-based collaborative filtering. Appl. Sci. 2023, 13, 11231. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble methods in machine learning. In International Workshop on Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar]
- Dharmaratne, P.; Salgadoe, A.; Rathnayake, W.; Weerasinghe, A. Investigation of Accuracy for Rice Crop Parameters Predicted Using UAV Multispectral Imagery. Trop. Agric. Res. 2025, 36, 82–98. [Google Scholar] [CrossRef]
- Cuaran, J.; Leon, J. Crop monitoring using unmanned aerial vehicles: A review. Agric. Rev. 2021, 42, 121–132. [Google Scholar] [CrossRef]
- Yubin, L.; Xiaoling, D.; Guoliang, Z. Advances in diagnosis of crop diseases, pests and weeds by UAV remote sensing. Smart Agric. 2019, 1, 1. [Google Scholar]
- Barbedo, J.G.A. Detection of nutrition deficiencies in plants using proximal images and machine learning: A review. Comput. Electron. Agric. 2019, 162, 482–492. [Google Scholar] [CrossRef]
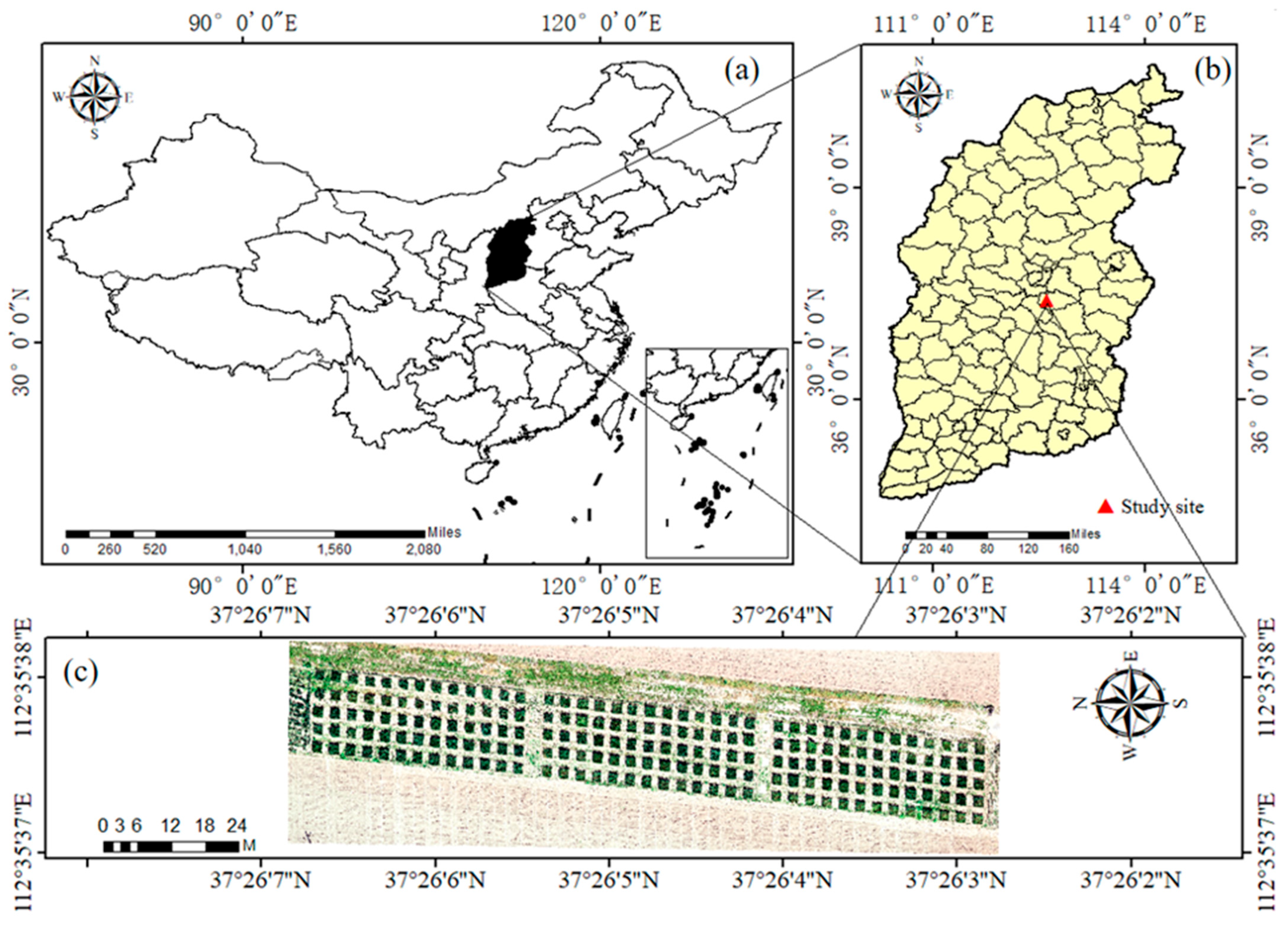



| Treatment | Fertilizer Rate (kg/hm2) | ||
|---|---|---|---|
| N | P2O5 | K2O | |
| N0 | 0 | 120 | 120 |
| N1 | 100 | 120 | 120 |
| N2 | 200 | 120 | 120 |
| Model | Threshold | Accuracy/% | PMS/% | PWS/% |
|---|---|---|---|---|
| RF | NDVI | 90.11 | 12.18 | 31.66 |
| EVI | 85.63 | 26.93 | 48.29 | |
| MSAVI | 87.45 | 22.87 | 29.65 | |
| SVM | NDVI | 86.29 | 17.28 | 57.96 |
| EVI | 81.79 | 28.34 | 50.42 | |
| MSAVI | 82.06 | 25.37 | 18.58 |
| Type of Vegetation Index | Calculation Formula | Source |
|---|---|---|
| NDVI | [26] | |
| GRVI | [27] | |
| SAVI | [28] | |
| GNDVI | [29] | |
| SIPI | [30] | |
| NDRE | [31] | |
| RDVI | [32] | |
| EVI | [33] | |
| CIred-edge | [34] |
| Period of Fertility | Datasets | Sample | Average | Kurtosis | Skewness | Minimum | Maximum |
|---|---|---|---|---|---|---|---|
| Jointing stage | Total | 195 | 32.870 | 0.624 | 0.357 | 22.174 | 43.278 |
| Train | 137 | 33.212 | 0.603 | 0.581 | 23.145 | 43.278 | |
| Test | 58 | 33.672 | 0.722 | 0.492 | 22.174 | 41.150 | |
| Heading stage | Total | 195 | 36.676 | 0.535 | 0.367 | 30.170 | 45.101 |
| Train | 137 | 38.302 | 0.501 | 0.604 | 34.332 | 45.101 | |
| Test | 58 | 32.832 | 0.493 | 0.680 | 30.170 | 34.327 | |
| Pre-grouting stage | Total | 195 | 30.692 | 0.706 | 0.272 | 25.065 | 36.914 |
| Train | 137 | 32.100 | 0.875 | 0.491 | 29.038 | 36.914 | |
| Test | 58 | 27.361 | 1.102 | 0.309 | 25.065 | 28.988 | |
| Late grouting stage | Total | 195 | 22.392 | 0.651 | 0.426 | 15.122 | 31.661 |
| Train | 137 | 24.447 | 0.812 | 0.646 | 20.148 | 31.661 | |
| Test | 58 | 17.531 | 1.186 | 0.583 | 15.122 | 20.100 |
| Model | Period of Fertility | R2 | RMSE | MAE |
|---|---|---|---|---|
| SVR | Jointing | 0.37 | 4.10 | 3.88 |
| Heading | 0.48 | 3.34 | 3.02 | |
| Pre-grouting | 0.43 | 3.69 | 3.45 | |
| Late grouting | 0.33 | 4.25 | 3.94 | |
| RF | Jointing | 0.58 | 2.97 | 2.76 |
| Heading | 0.72 | 2.08 | 1.73 | |
| Pre-grouting | 0.66 | 2.21 | 1.99 | |
| Late grouting | 0.68 | 2.14 | 1.91 | |
| RR | Jointing | 0.41 | 3.62 | 3.49 |
| Heading | 0.52 | 3.15 | 3.10 | |
| Pre-grouting | 0.47 | 3.47 | 3.13 | |
| Late grouting | 0.40 | 3.67 | 3.42 | |
| K-NN | Jointing | 051 | 3.20 | 3.23 |
| Heading | 0.66 | 2.13 | 1.86 | |
| Pre-grouting | 0.65 | 2.19 | 1.98 | |
| Late grouting | 0.63 | 2.39 | 2.01 | |
| Voting | Jointing | 0.69 | 1.98 | 1.80 |
| Heading | 0.76 | 1.88 | 1.26 | |
| Pre-grouting | 0.82 | 1.64 | 1.49 | |
| Late grouting | 0.58 | 2.79 | 2.51 | |
| Stacking | Jointing | 0.65 | 2.16 | 1.83 |
| Heading | 0.73 | 2.05 | 1.77 | |
| Pre-grouting | 0.80 | 1.77 | 1.15 | |
| Late grouting | 0.71 | 2.18 | 1.94 |
| Project/Indicator | UAV-Based Multispectral Method | Traditional Manual Sampling Method |
|---|---|---|
| Platform and sensors | DJI Phantom 4 Pro + RedEdge-MX | Manual sampling + laboratory chemical element analysis |
| Single job duration (this study area) | 5 min | 5–6 days |
| Data acquisition cost (estimated) | 150,000 RMB (unrestricted use) | 4000 RMB (single-use cost in this study, including sampling, labor, reagents, and elemental analysis) |
| Spatial resolution | 8 cm/pixel | None |
| Sampling method | Non-destructive sampling | Destructive sampling |
| Testing frequency | Every 7 days or more frequently | Long sampling and elemental analysis cycle |
| Data analysis and processing | Model-based prediction with near real-time output | Laboratory testing with longer turnaround time |
| Applicability | Scalable to large areas, multiple time points, and different regions | Limited to small-scale or controlled experiments |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Zhang, J.; Bai, Y.; Liang, Z.; Guo, X.; Zhao, Y.; Feng, M.; Xiao, L.; Song, X.; Zhang, M.; et al. Ensemble Learning-Driven and UAV Multispectral Analysis for Estimating the Leaf Nitrogen Content in Winter Wheat. Agronomy 2025, 15, 1621. https://doi.org/10.3390/agronomy15071621
Han Y, Zhang J, Bai Y, Liang Z, Guo X, Zhao Y, Feng M, Xiao L, Song X, Zhang M, et al. Ensemble Learning-Driven and UAV Multispectral Analysis for Estimating the Leaf Nitrogen Content in Winter Wheat. Agronomy. 2025; 15(7):1621. https://doi.org/10.3390/agronomy15071621
Chicago/Turabian StyleHan, Yu, Jiaxue Zhang, Yan Bai, Zihao Liang, Xinhui Guo, Yu Zhao, Meichen Feng, Lujie Xiao, Xiaoyan Song, Meijun Zhang, and et al. 2025. "Ensemble Learning-Driven and UAV Multispectral Analysis for Estimating the Leaf Nitrogen Content in Winter Wheat" Agronomy 15, no. 7: 1621. https://doi.org/10.3390/agronomy15071621
APA StyleHan, Y., Zhang, J., Bai, Y., Liang, Z., Guo, X., Zhao, Y., Feng, M., Xiao, L., Song, X., Zhang, M., Yang, W., Li, G., Yang, S., Qiao, X., & Wang, C. (2025). Ensemble Learning-Driven and UAV Multispectral Analysis for Estimating the Leaf Nitrogen Content in Winter Wheat. Agronomy, 15(7), 1621. https://doi.org/10.3390/agronomy15071621





