A Chemometric Analysis of Soil Health Indicators Derived from Mid-Infrared Spectra
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Field
2.2. Basic Soil Physicochemical Properties (Agrochemical DVs)
2.3. Soil Biology (Biological DVs)
2.4. Mid-Infrared Spectroscopy (Predictors Matrix, IVs)
2.5. Data Treatments
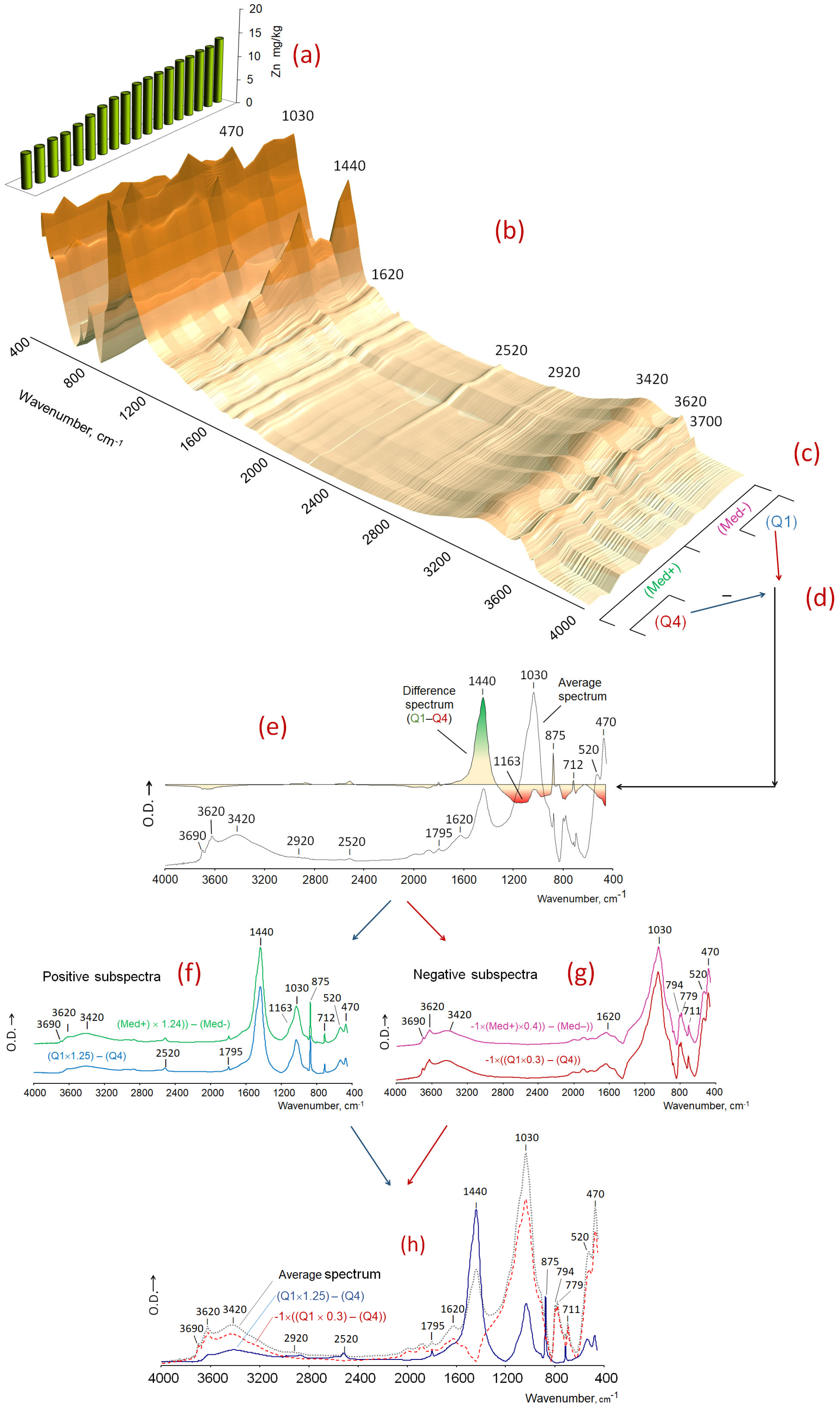
2.5.1. Management and Pretreatment of MIR Spectra Before PLS
- (a)
- The elimination of data points within the interval 2404–2363 cm−1, encompassing the range in which CO2 (an impurity derived from air) undergoes absorption (zero-filling followed by a moving average with the neighbouring baseline points).
- (b)
- The employment of digital smoothing through the implementation of the Savitzky–Golay algorithm. The algorithm is typically applied to spectra with n = 1000 points using a 2-point window.
- (c)
- The second derivative spectra were obtained in order to sharpen the peaks and minimise the differences between different spectrum at the baseline level [6].
- (d)
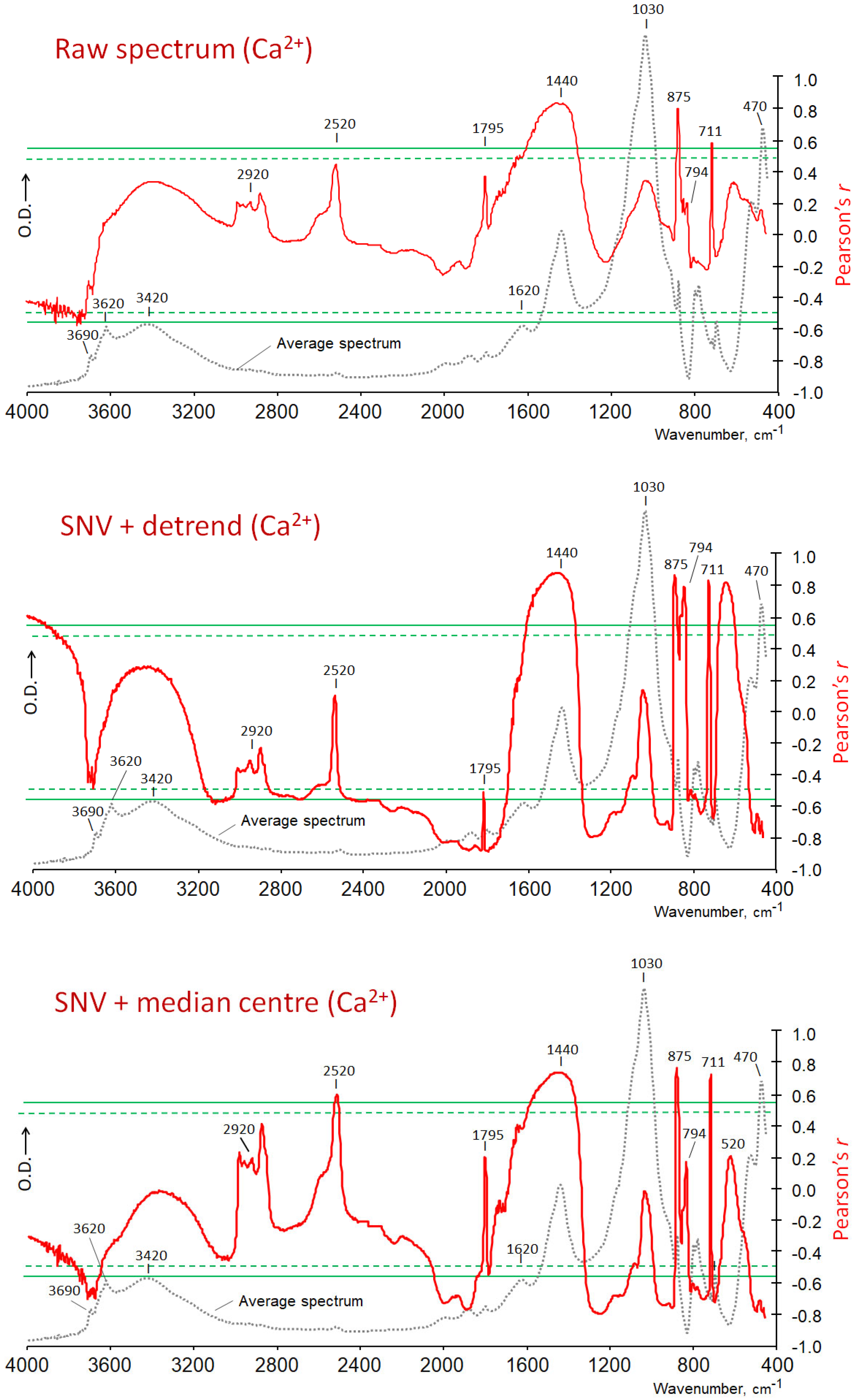
- The entire spectrum was processed with specific numeric pretreatments or transformations that are typical of chemometric studies [29]. The aforementioned treatments are outlined below: (i) Mean centring (MC), which entailed calculating the mean spectrum of the data set and subtracting it from each spectrum. (ii) The removal of baseline effects through multiplicative scatter correction (MSC), which entailed correcting the spectra to an ideal, average spectrum so that the baseline and amplification effects were at the same average level in every spectrum [30]. In models with a high degree of significance, where there are considerable differences between samples with low and high values, the impact of MSC was found to be negligible. However, MSC is recommended as it did not introduce artefacts in subtractions and was shown to enhance the quality of soil PLS models based on near- or MIR spectra [31]. (iii) With the standard normal variate (SNV) the centre of each spectrum was determined and each spectrum was scaled by its standard deviation. The resulting spectra thus possessed a mean value of 0 and a variance of 1, irrespective of the original values of the absorbance. (iv) Standard normal variates and detrending (SNV + DT), is a process which served to eliminate the multiplicative interference of scatter and particle size [32]. Each spectrum was then normalised to a mean of zero and a variance of one, followed by a detrending step. This process involved the fitting of a second-order polynomial to the SNV-transformed spectrum and the subsequent subtraction of this from the original spectrum in order to correct for wavelength-dependent scattering effects. Furthermore, the combination of the aforementioned pretreatment methods, such as SNV+MC, was also evaluated.
2.5.2. Forecasting Models
2.5.3. Extracting Information on Soil Chemistry and Biology from MIR Spectra
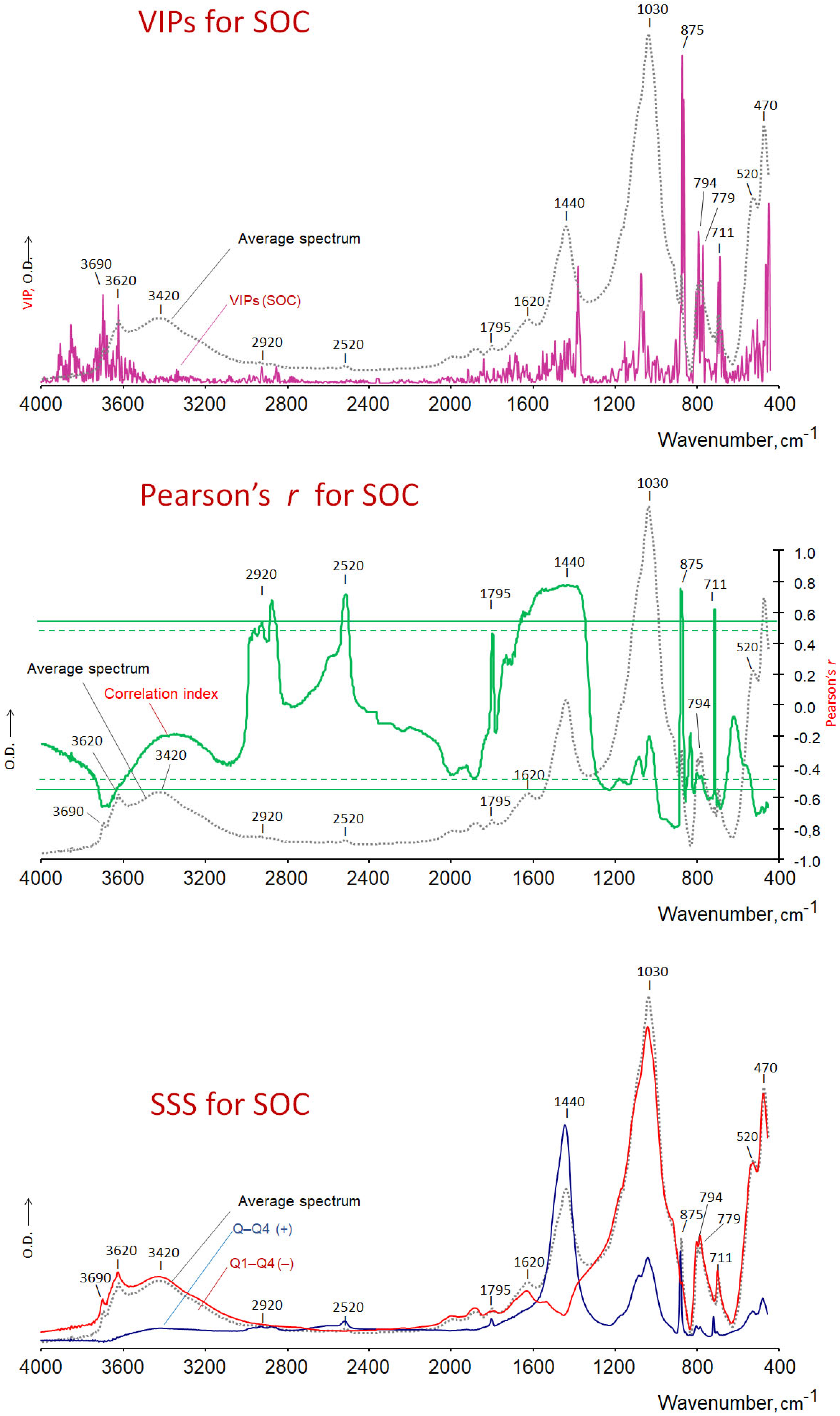
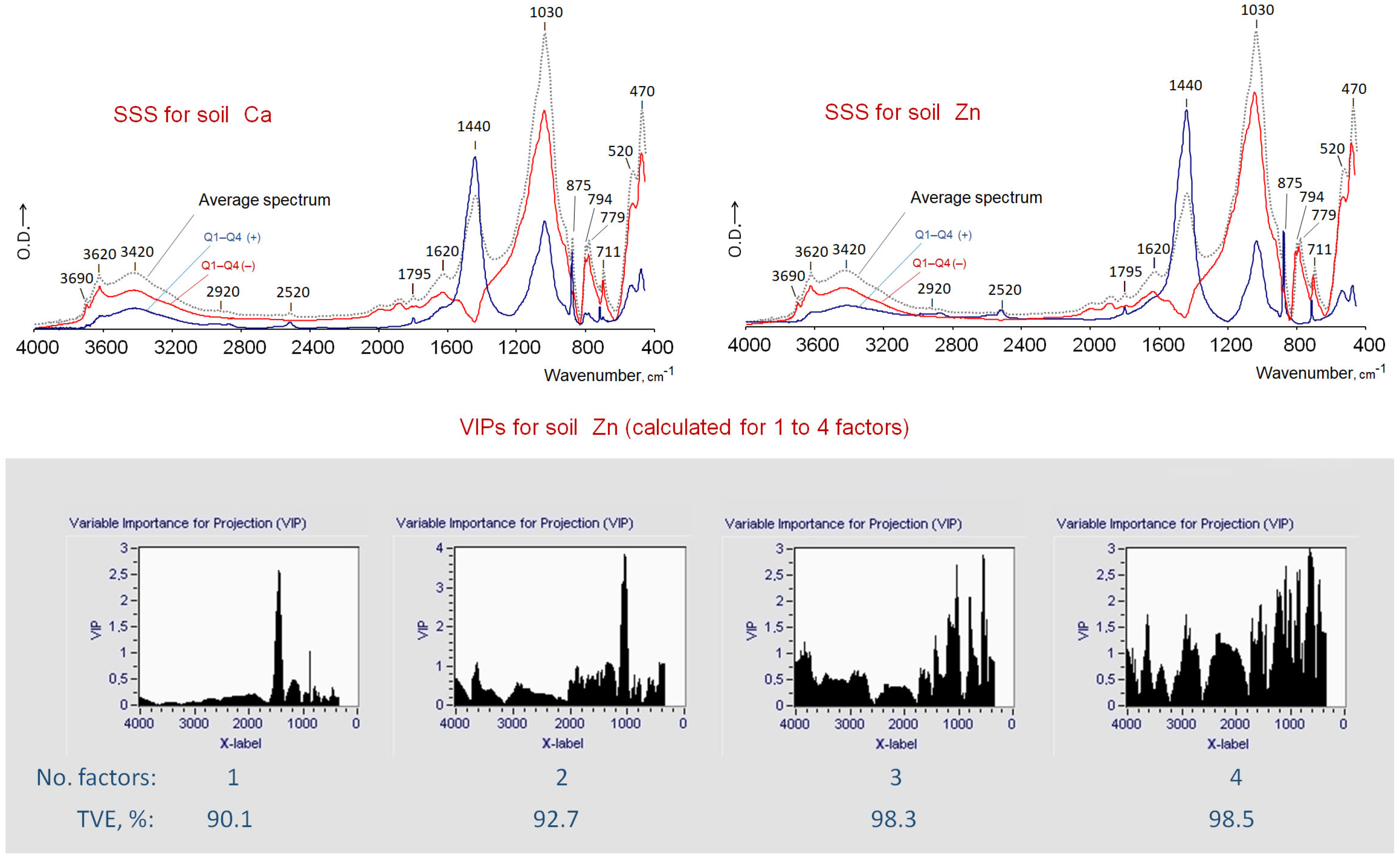
- (a)
- The VIPs calculated for the different significant PLS (p < 0.05) models,
- (b)
- The factor scores of the significant PLS models.
- (c)
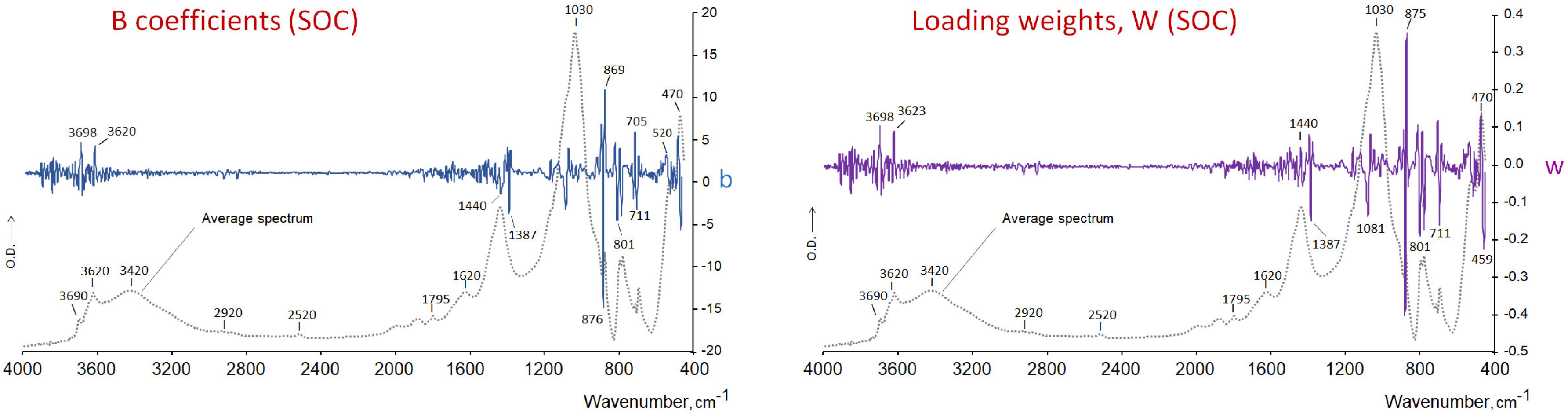
- The beta coefficients from the above PLS models (calibration equation coefficients showing the importance of spectral bands in the PLS calibration, i.e., representing the contribution of each IV to the model, with positive or negative signs [36]). The aforementioned indices were calculated with ParLes software [29].
- (d)
- Pearson’s correlation coefficients between the whole array of spectral data points and each DV, using authors’ programs [37].
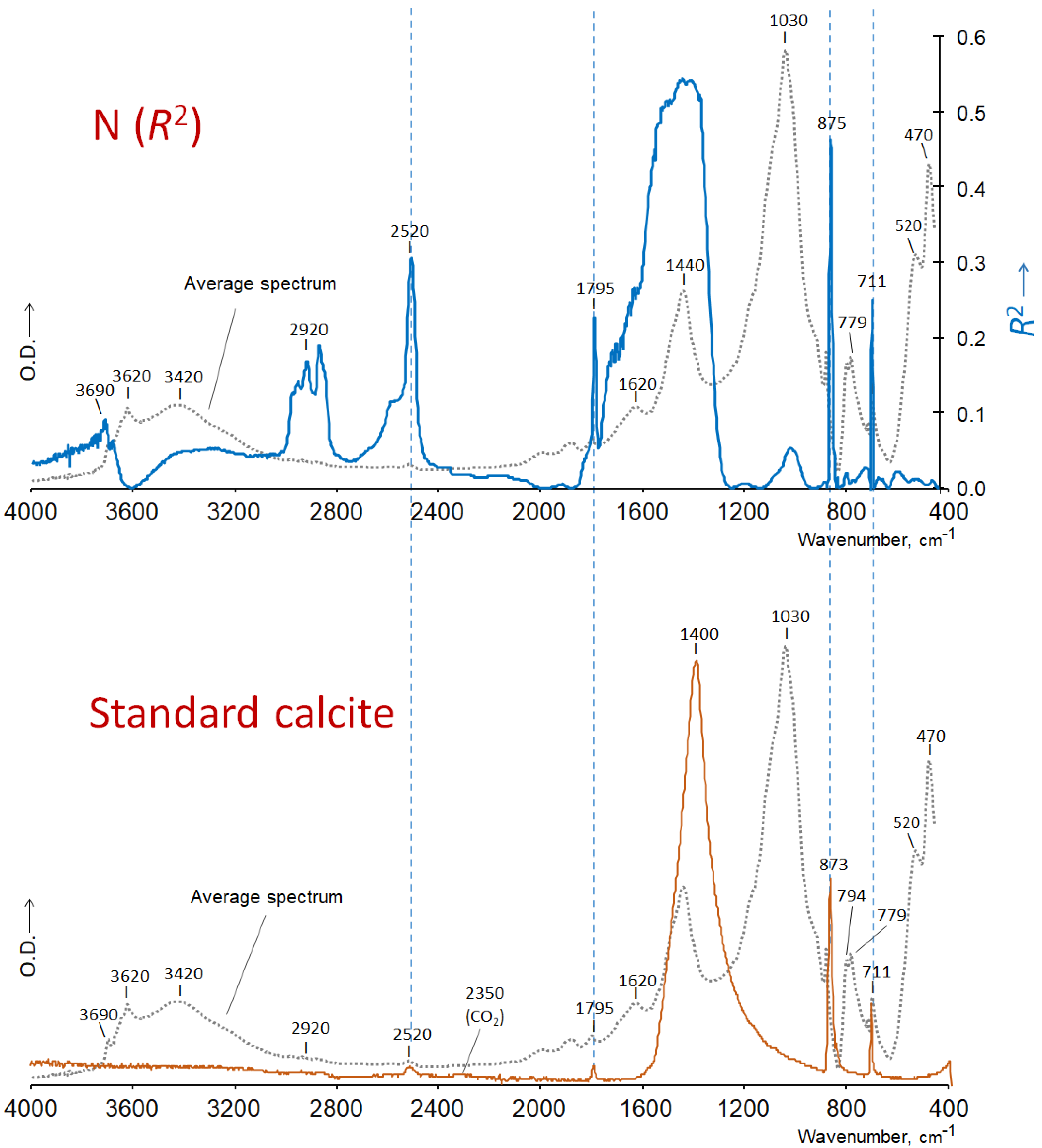
- (e)
- The coefficient of determination, R2, i.e., the square of the correlation coefficient.
- (f)
- The subtracted spectra.
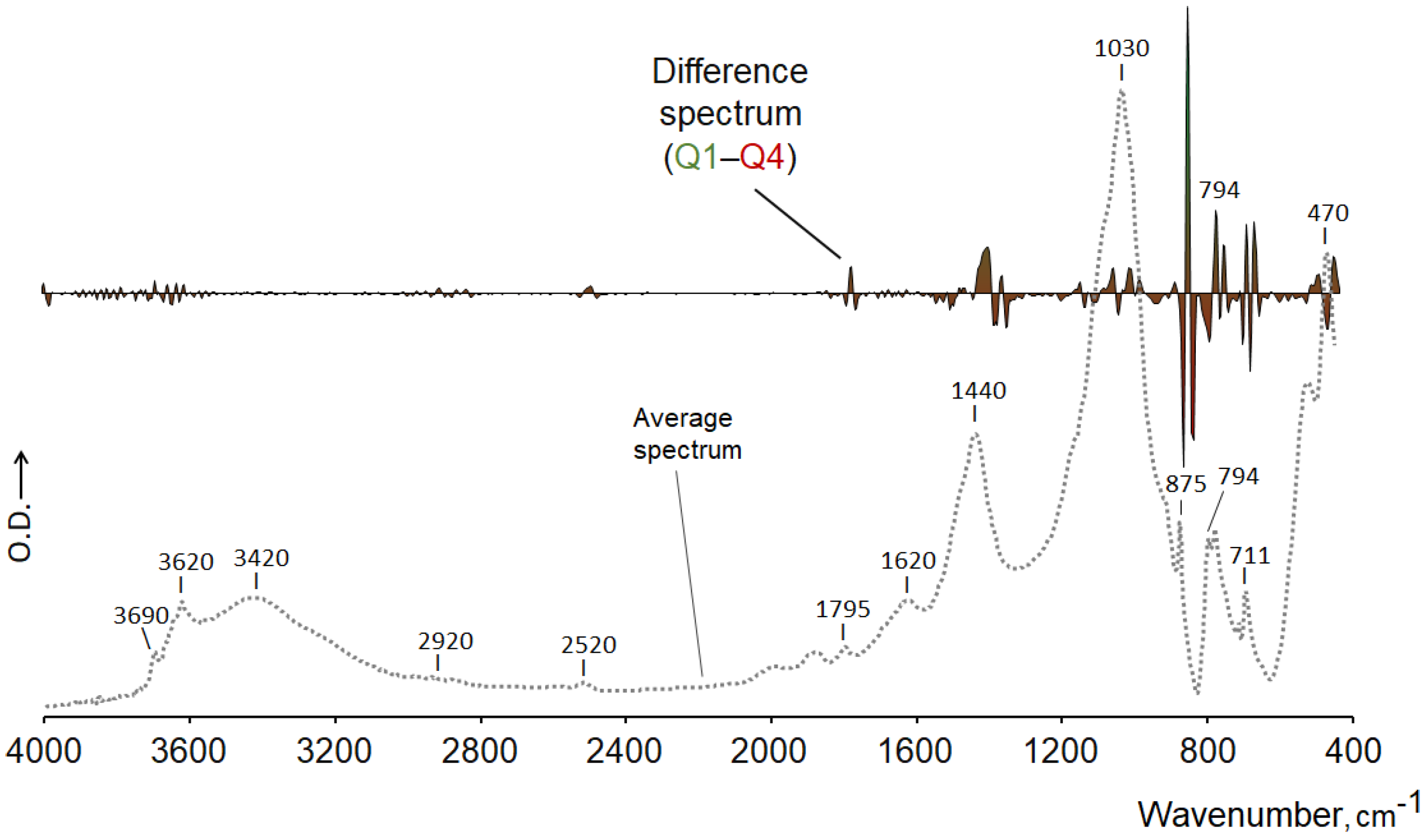
Subtracted Spectra
Scaled Subtraction Spectra (SSS)
3. Results
3.1. Forecasting Soil Agroecological Properties (Biological and Physicochemical) by PLS
3.1.1. Assessment of Basic Soil Physicochemical Properties by PLS
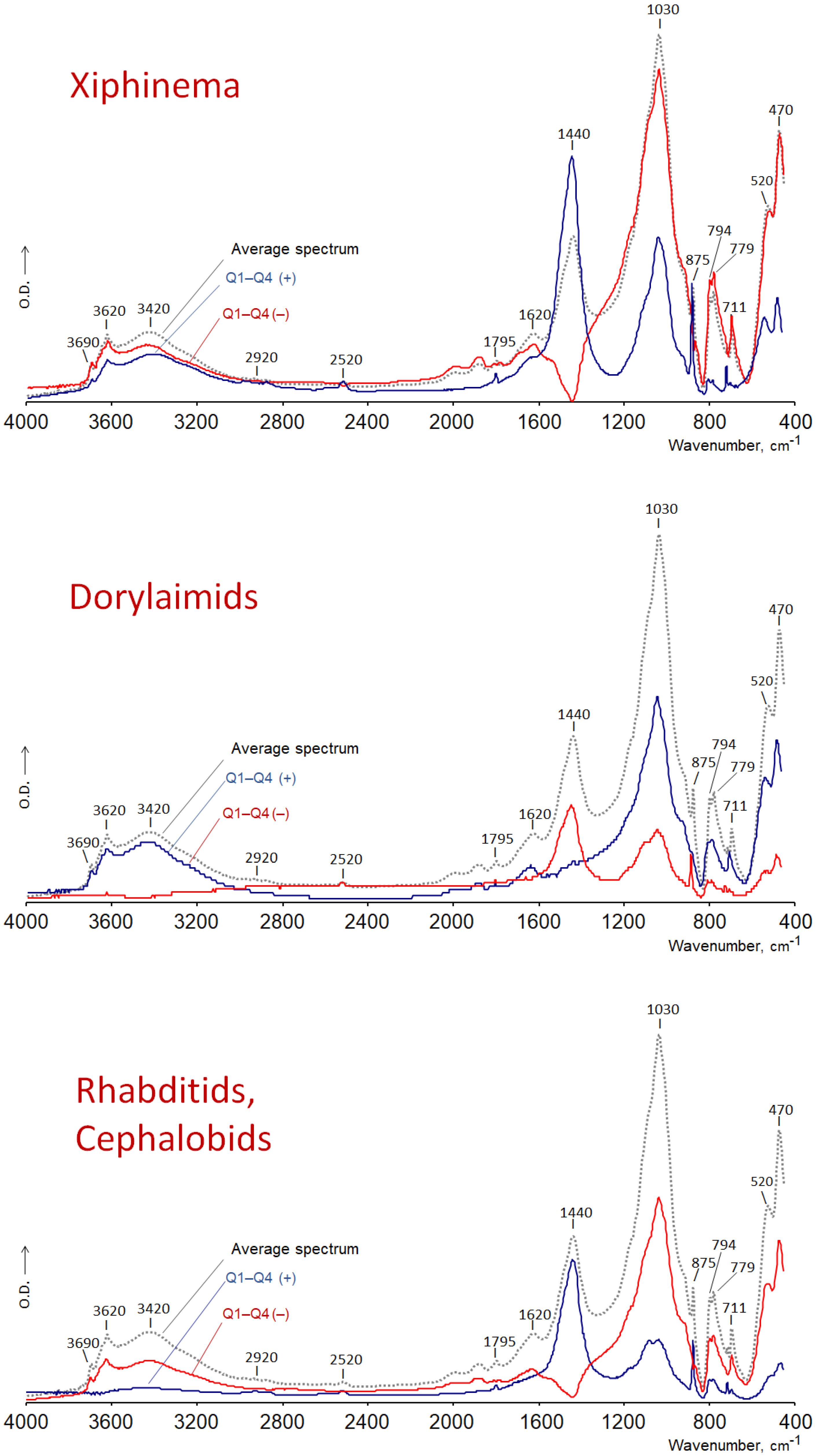
3.1.2. Soil Nematode Populations
4. Discussion
4.1. Optimisation of Partial Least Squares Models
4.2. A Comparative Analysis of the Utility of Spectral Traces Calculated by Uni- or Multivariate Data Treatments of MIR Spectra
4.2.1. Multivariate Treatments
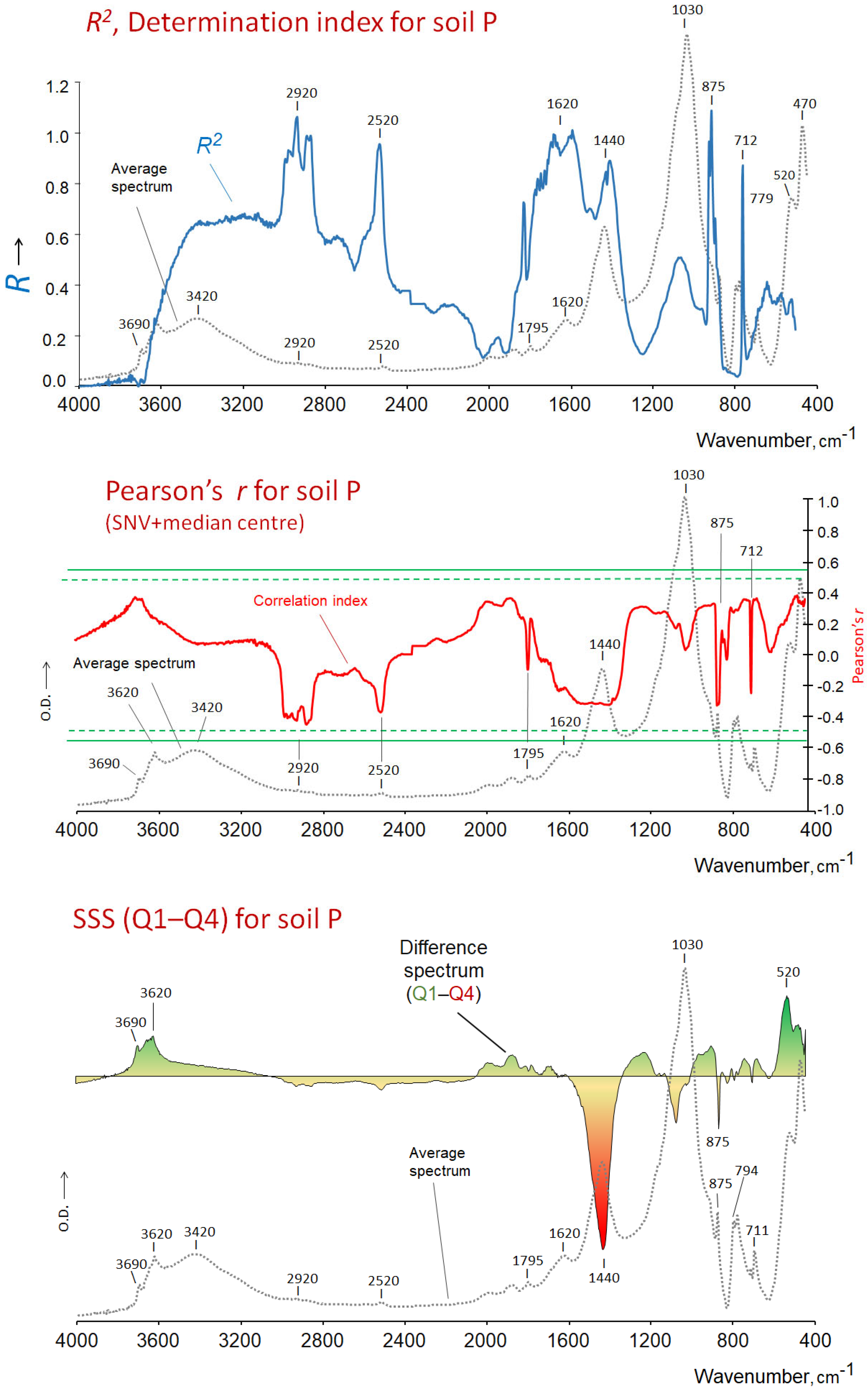
4.2.2. Traces Representing Pearson Coefficients (r) or Determination Coefficients (R2)
4.2.3. The Subtracted Spectra
4.2.4. The Scaled Subtraction Spectra
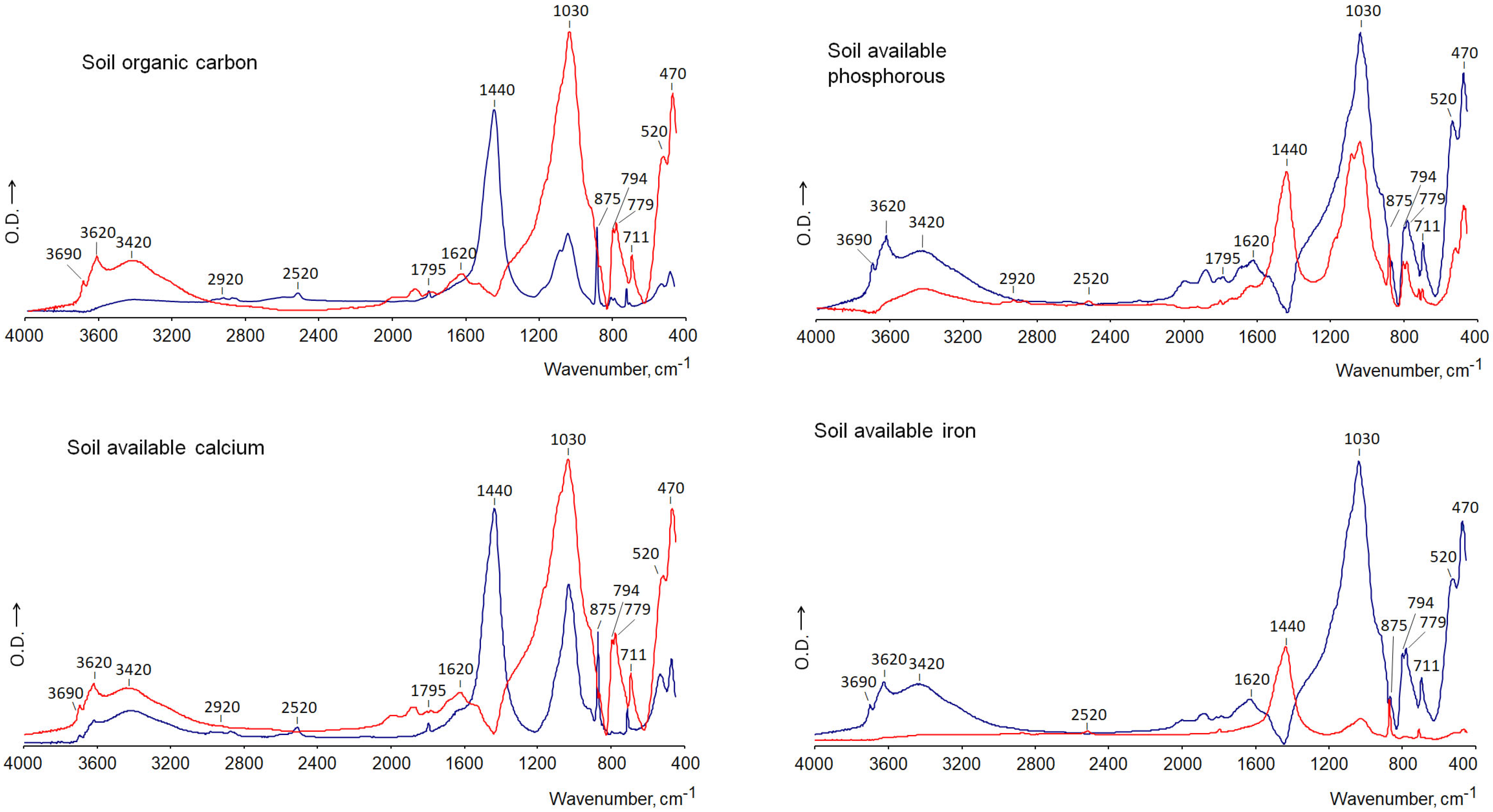
4.3. A Comparison of the Usefulness of the Different Traces in Order to Explain the Importance of the Different Spectral Regions in Terms of the Levels of the DV
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stepanov, I.S. Interpretation of infrared soil spectra. Sov. Soil Sci. 1974, 6, 354–368. [Google Scholar]
- van der Marel, H.W.; Beutelspacher, H. Atlas of Infrared Spectroscopy of Clay Minerals and Their Admixtures; Elsevier Scientific Pub. Co.: Amsterdam, The Netherlands, 1976; 396p. [Google Scholar]
- MacCarthy, P.; Rice, J.A. Spectroscopic methods (other than NMR) for determining functionality in humic substances. In Humic Substances in Soil, Sediment and Water; Aiken, G.R., McKnight, D.M., Wershaw, R.L., MacCarthy, P., Eds.; Wiley-Interscience: Hoboken, NJ, USA, 1985; pp. 527–559. [Google Scholar]
- Viscarra Rossel, R.A.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, Near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Cecillon, L.; Certini, G.; Lange, H.; Forte, C.; Strand, L.T. Spectral fingerprinting of soil organic matter composition. Org. Geochem. 2012, 46, 127–136. [Google Scholar] [CrossRef]
- Fernández-Getino, A.P.; Hernández, Z.; Piedra Buena, A.; Almendros, G. Exploratory analysis of the structural variability of forest soil humic acids based on multivariate processing of infrared spectral data. Eur. J. Soil Sci. 2013, 64, 66–79. [Google Scholar] [CrossRef]
- Liu, L.; Ji, M.; Buchroithner, M. Combining partial least squares and the gradient-boosting method for soil property retrieval using visible near-infrared shortwave infrared spectra. Remote Sens. 2017, 9, 1299. [Google Scholar] [CrossRef]
- Abbaszadeh, F.; Jalali, V.; Jafari, A. Feasibility study of PLS and bagging-PLS regressions in predicting some soil heavy metals by VIS to NIR and SWIR bands. Eurasian Soil Sci. 2023, 56, 1161–1171. [Google Scholar] [CrossRef]
- Janik, L.J.; Forrester, S.T.; Rawson, G. The prediction of soil chemical and physical properties from mid-infrared spectroscopy and combined partial least-squares regression and neural networks (PLS-NN) Analysis. Chemom. Intell. Lab. Syst. 2009, 97, 179–188. [Google Scholar] [CrossRef]
- Djuuna, I.A.F.; Abbott, L.; Russell, C. Determination and prediction of some soil properties using partial least square (PLS) calibration and mid-infra red (MIR) spectroscopy analysis. J. Trop. Soils 2011, 16, 93–98. Available online: https://journal.unila.ac.id/index.php/tropicalsoil/article/view/126 (accessed on 24 June 2025). [CrossRef]
- Janik, L.J.; Skjemstad, J.O. Characterization and analysis of soils using mid-infrared partial least- squares. II. Correlations with some laboratory data. Aust. J. Soil Res. 1995, 33, 637–650. [Google Scholar]
- D’Acqui, L.P.; Pucci, A.; Janik, L.J. Soil properties prediction of western Mediterranean islands with similar climatic environments by means of mid-infrared diffuse reflectance spectroscopy. Eur. J. Soil Sci. 2010, 61, 865–876. [Google Scholar] [CrossRef]
- Viscarra-Rossel, R.A.; Jeon, Y.S.; Odeh, I.O.A.; McBratney, A.B. Using a legacy soil sample to develop a mid-IR spectral library. Aust. J. Soil Res. 2008, 46, 1–16. [Google Scholar] [CrossRef]
- Yeates, G.W. Nematodes as soil indicators: Functional and biodiversity aspects. Biol. Fertil. Soils 2003, 37, 199–210. [Google Scholar] [CrossRef]
- Barthès, B.G.; Brunet, D.; Rabary, B.; Ba, O.; Villenave, C. Near infrared reflectance spectroscopy (NIRS) could be used for characterization of soil nematode community. Soil Biol. Biochem. 2011, 43, 1649–1659. [Google Scholar] [CrossRef]
- Hernández, Z.; Recio-Vázquez, L.; Pérez-Trujillo, J.P.; Sanz, J.; Álvarez, A.; Carral, P.; Almendros, G. Forecasting soil agrochemical properties from ATR-MIR spectroscopy and partial least-squares regression analysis. In Proceedings of the 4th International Congress of European Confederation of Soil Science Societies (ECSSS) EUROSOIL 2012, Bari, Italy, 2–6 July 2012; p. 1240. [Google Scholar]
- Luinge, H.J.; van der Maas, J.H.; Visser, T. Partial least squares regression as a multivariate tool for the interpretation of infrared spectra. Chemom. Intell. Lab. Syst. 1995, 28, 129–138. [Google Scholar] [CrossRef]
- Arias, M.; Fresno, J.; López-Pérez, J.A.; Escuer, M.; Arcos, S.C.; Bello, A. Nematodos, Virosis y Manejo del Viñedo en Castilla-La Mancha; CSIC-JCCM: Madrid, Spain, 1997; 117p. [Google Scholar]
- Hernández, Z.; López-Pérez, J.A.; González-López, M.R.; Díez-Rojo, M.A.; Piedra Buena, A.; Bello, A.; Almendros, G. Monitoring humic acid formation processes and soil physical properties in semiarid calcic soil treated with wine vinasses. Commun. Soil Sci. Plant Anal. 2010, 41, 1850–1862. [Google Scholar] [CrossRef]
- Carlevaris, J.J.; de la Horra, J.L.; Rodríguez, J.; Serrano, F. La Fertilidad de los Principales Suelos Agrícolas de la Zona Oriental de la Provincia de Ciudad Real: La Mancha y Campo de Montiel; CSIC & Junta de Comunidades de Castilla-La Mancha: Madrid, Spain, 1992; 293p. [Google Scholar]
- Soil Survey Staff. Keys to Soil Taxonomy, 10th ed.; Agricultural Handbook 436; U.S. Gov. Print Office: Washington, DC, USA, 2006. [Google Scholar]
- Nelson, D.W.; Sommers, L.E. Total carbon, organic carbon and organic matter. In Methods of Soil Analysis; Page, A.L., Ed.; Agronomy Monograph 9; American Society of Agronomy and Soil Science Society of America: Madison, WI, USA, 1982; pp. 539–579. [Google Scholar]
- Piper, C.S. Soil and Plant Analysis; The Hassell Press: Adelaide, Australia, 1950; 368p. [Google Scholar]
- Juo, A.S.R.; Ayanlaja, S.A.; Ogunwole, J.A. An evaluation of the cation exchange capacity measurements for soils in the tropics. Comm. Soil Sci. Plant Anal. 1976, 7, 751–761. [Google Scholar] [CrossRef]
- Lakanen, E.; Ervio, R. A comparison of eight extractants for the determination of plant available micronutrients in soils. Acta Agral. Fenn. 1971, 123, 223–232. [Google Scholar]
- Burriel, F.; Hernando, V. El fósforo en los suelos españoles. Contribución a la determinación colorimétrica del fósforo. An. Edafol. Agrobiol. 1950, 6, 543–582. [Google Scholar]
- Ferris, H.; Bongers, T. Nematode indicators of organic enrichment. J. Nematol. 2006, 38, 3–12. [Google Scholar]
- Flegg, J.J.M. Extraction of Xiphinema and Longidorus species from soil by a modification of Cobb’s decanting and sieving technique. Ann. Appl. Biol. 1967, 60, 429–437. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A. ParLeS: Software for chemometric analysis of spectroscopic data. Chemom. Intell. Lab. Syst. 2008, 90, 72–83. [Google Scholar] [CrossRef]
- Martens, H.; Stark, E. Extended multiplicative signal correction and spectral interference subtraction: New preprocessing methods for near infrared spectroscopy. J. Pharm. Biomed. Anal. 1991, 9, 625–635. [Google Scholar] [CrossRef]
- Madari, B.E.; Reeves III, J.B.; Machado, P.L.O.A.; Guimarães, C.M.; Torres, E.; McCarty, G.W. Mid- and near-infrared spectroscopic assessment of soil compositional parameters and structural indices in two Ferralsols. Geoderma 2006, 136, 245–259. [Google Scholar] [CrossRef]
- Barnes, R.J.; Dhanoa, M.S.; Lister, S.J. Standard normal variate transformation and de-trending of near-infrared diffuse reflectance spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Takahama, S.; Dillner, A.M. Model selection for partial least squares calibration and implications for analysis of atmospheric organic aerosol samples with mid-infrared spectroscopy. J. Chemom. 2015, 29, 659–668. [Google Scholar] [CrossRef]
- Haaland, D.M.; Thomas, E.V. Partial least-squares methods for spectral analyses. 1. Relation to other quantitative calibration methods and the extraction of qualitative information. Anal. Chem. 1988, 60, 1193–1202. [Google Scholar] [CrossRef]
- Almendros, G.; Fründ, R.; Martin, F.; González-Vila, F.J. Spectroscopic characteristics of derivatized humic acids from peat in relation to soil properties and plant growth. In Humic Substances in the Global Environment and Implications in Human Health; Senesi, N., Miano, T.M., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 1994; pp. 213–218. [Google Scholar]
- Janik, L.J.; Skjemstad, J.O.; Shepherd, K.D.; Spouncer, L.R. The prediction of soil carbon fractions using mid-infrared-partial least square analysis. Aust. J. Soil Res. 2007, 45, 73–81. [Google Scholar] [CrossRef]
- Zimmermann, M.; Leifeld, J.; Fuhrer, J. Quantifying soil organic carbon fractions by infrared-spectroscopy. Soil Biol. Biochem. 2007, 39, 224–231. [Google Scholar] [CrossRef]
- Xie, H.T.; Yang, X.M.; Drury, C.F.; Yang, J.Y.; Zhang, X.D. Predicting soil organic carbon and total nitrogen using mid- and near-infrared spectra for Brookston clay loam soil in Southwestern Ontario, Canada. Can. J. Soil Sci. 2011, 91, 53–63. [Google Scholar] [CrossRef]
- Omoike, A.; Chorover, J. Adsorption to goethite of extracellular polymeric substances from Bacillus subtilis. Langmuir 2004, 20, 11108–11114. [Google Scholar] [CrossRef] [PubMed]
- Zornoza, R.; Guerrero, C.; Mataix-Solera, J.; Scow, K.M.; Arcenegui, V.; Mataix-Beneyto, J. Near infrared spectroscopy for determination of various physical, chemical and biochemical properties in Mediterranean soils. Soil Biol. Biochem. 2008, 40, 1923–1930. [Google Scholar] [CrossRef] [PubMed]
- Viscarra Rossel, R.A.; Bui, E.N.; de Caritat, P.; McKenzie, N.J. Mapping iron oxides and the color of Australian soil using visible–near-infrared reflectance spectra. J. Geophys. Res. Earth Surf. 2010, 115, F04031. [Google Scholar] [CrossRef]
- Reyna-Bowen, J.L.; Vera Montenegro, L.; Delgado Moreira, M.I. Optimizing soil analysis in precision agriculture: Evaluating alternative methods for SOC prediction. J. Ecol. Eng. 2025, 26, 322–331. [Google Scholar] [CrossRef]
| Ref. | Tre. | SOC g/kg | pH | EC mS/cm | N g/kg | P2O5 g/kg | K+ g/kg | Ca2+ g/kg | Mg2+ g/kg | Na+ g/kg | Fe mg/kg | Mn g/kg | Cu mg/kg | Zn mg/kg | Xiph | Xind | Dor | Ench | Rha |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.3 | C | 4.43 | 8.15 | 0.19 | 0.45 | 0.02 | 0.26 | 3.91 | 0.22 | 0.01 | 15.55 | 90.98 | 1.36 | 12.50 | 0 | 0 | 105 | 0 | 5 |
| 3.4 | C | 4.24 | 8.11 | 0.18 | 0.36 | 0.05 | 0.18 | 3.61 | 0.18 | 0.01 | 12.56 | 74.16 | 1.13 | 12.56 | 10 | 0 | 100 | 15 | 10 |
| 5.5 | C | 2.39 | 8.17 | 0.11 | 0.21 | 0.16 | 0.19 | 1.97 | 0.17 | 0.01 | 15.15 | 99.76 | 1.05 | 6.91 | 5 | 5 | 40 | 15 | 0 |
| 5.7 | C | 2.03 | 7.94 | 0.10 | 0.18 | 0.20 | 0.19 | 1.43 | 0.16 | 0.01 | 20.07 | 95.62 | 1.22 | 6.43 | 20 | 0 | 40 | 65 | 0 |
| 6.1 | C | 2.39 | 8.04 | 0.16 | 0.36 | 0.01 | 0.25 | 4.35 | 0.23 | 0.01 | 13.29 | 96.35 | 1.24 | 11.29 | 10 | 0 | 115 | 0 | 5 |
| 6.3 | C | 3.50 | 8.07 | 0.14 | 0.28 | 0.05 | 0.21 | 4.01 | 0.20 | 0.00 | 14.68 | 103.47 | 1.19 | 10.74 | 40 | 0 | 115 | 5 | 5 |
| 1.5 | V | 4.93 | 7.93 | 0.23 | 0.48 | 0.02 | 0.32 | 3.57 | 0.18 | 0.01 | 11.35 | 55.97 | 2.00 | 13.55 | 40 | 5 | 110 | 15 | 40 |
| 1.7 | V | 4.20 | 8.10 | 0.27 | 0.52 | 0.04 | 0.32 | 3.89 | 0.19 | 0.01 | 9.81 | 49.36 | 1.23 | 11.42 | 10 | 0 | 160 | 20 | 10 |
| 1.8 | V | 4.01 | 8.04 | 0.20 | 0.42 | 0.06 | 0.29 | 3.73 | 0.19 | 0.01 | 11.37 | 62.10 | 1.67 | 11.42 | 5 | 0 | 70 | 15 | 5 |
| 2.1 | V | 4.56 | 8.04 | 0.21 | 0.52 | 0.01 | 0.32 | 3.77 | 0.24 | 0.01 | 12.93 | 88.11 | 1.59 | 10.86 | 20 | 0 | 100 | 10 | 25 |
| 2.2 | V | 4.20 | 8.05 | 0.28 | 0.42 | 0.06 | 0.39 | 3.70 | 0.20 | 0.01 | 12.00 | 80.54 | 1.42 | 11.03 | 0 | 0 | 145 | 25 | 15 |
| 2.3 | V | 4.56 | 7.66 | 0.75 | 0.58 | 0.16 | 0.54 | 3.67 | 0.17 | 0.01 | 11.92 | 71.83 | 1.37 | 12.08 | 15 | 0 | 20 | 10 | 15 |
| 2.4 | V | 4.56 | 7.57 | 0.76 | 0.52 | 0.06 | 0.45 | 3.80 | 0.17 | 0.01 | 10.55 | 57.98 | 1.59 | 12.72 | 10 | 0 | 85 | 20 | 25 |
| 3.7 | V | 2.37 | 8.25 | 0.18 | 0.24 | 0.01 | 0.34 | 2.95 | 0.20 | 0.01 | 9.81 | 72.01 | 1.29 | 8.34 | 10 | 0 | 45 | 15 | 0 |
| 3.8 | V | 3.28 | 8.16 | 0.17 | 0.29 | 0.03 | 0.31 | 3.01 | 0.21 | 0.01 | 11.34 | 65.70 | 1.17 | 7.73 | 5 | 0 | 25 | 5 | 0 |
| 4.1 | V | 3.47 | 8.15 | 0.20 | 0.38 | 0.04 | 0.34 | 3.64 | 0.22 | 0.01 | 13.67 | 108.49 | 1.48 | 9.90 | 20 | 0 | 105 | 0 | 0 |
| 4.2 | V | 3.47 | 8.14 | 0.18 | 0.40 | 0.01 | 0.29 | 3.67 | 0.21 | 0.01 | 12.00 | 95.69 | 1.32 | 10.73 | 5 | 0 | 30 | 15 | 0 |
| 4.4 | V | 3.65 | 7.72 | 0.58 | 0.43 | 0.07 | 0.40 | 3.61 | 0.18 | 0.01 | 10.56 | 84.50 | 1.44 | 11.12 | 0 | 0 | 5 | 0 | 0 |
| 2.7 | S | 3.47 | 8.20 | 0.23 | 0.41 | 0.03 | 0.40 | 3.06 | 0.20 | 0.01 | 12.11 | 70.43 | 1.89 | 9.50 | 0 | 0 | 130 | 50 | 5 |
| 4.7 | S | 2.79 | 8.33 | 0.29 | 0.37 | 0.09 | 0.86 | 1.86 | 0.16 | 0.07 | 13.04 | 84.34 | 0.79 | 7.03 | 0 | 0 | 60 | 0 | 25 |
| 4.8 | S | 3.61 | 8.17 | 0.24 | 0.39 | 0.01 | 0.60 | 2.39 | 0.18 | 0.04 | 12.98 | 77.36 | 0.85 | 9.13 | 10 | 0 | 175 | 5 | 15 |
| 5.1 | S | 4.43 | 8.22 | 0.37 | 0.50 | 0.01 | 0.91 | 3.54 | 0.19 | 0.05 | 11.91 | 89.76 | 1.32 | 12.07 | 0 | 0 | 145 | 10 | 165 |
| 5.2 | S | 4.43 | 8.24 | 0.32 | 0.52 | 0.01 | 0.92 | 3.44 | 0.19 | 0.05 | 12.18 | 81.05 | 1.30 | 12.18 | 0 | 0 | 65 | 0 | 55 |
| 5.3 | S | 3.61 | 8.26 | 0.23 | 0.41 | 0.03 | 0.55 | 3.40 | 0.20 | 0.01 | 10.60 | 85.32 | 1.13 | 10.74 | 40 | 0 | 105 | 5 | 5 |
| 5.4 | S | 3.61 | 8.50 | 0.35 | 0.44 | 0.06 | 1.06 | 3.99 | 0.19 | 0.06 | 13.64 | 103.09 | 0.84 | 9.84 | 0 | 0 | 45 | 20 | 5 |
| 6.5 | S | 2.30 | 8.42 | 0.18 | 0.24 | 0.10 | 0.50 | 1.30 | 0.18 | 0.01 | 13.14 | 106.16 | 0.90 | 6.92 | 0 | 0 | 60 | 5 | 5 |
| 6.6 | S | 1.97 | 8.35 | 0.16 | 0.23 | 0.07 | 0.54 | 1.05 | 0.15 | 0.01 | 13.38 | 93.88 | 1.03 | 6.38 | 0 | 0 | 125 | 10 | 25 |
| 6.7 | S | 2.46 | 8.32 | 0.31 | 0.32 | 0.05 | 0.74 | 1.74 | 0.20 | 0.06 | 19.06 | 108.77 | 0.80 | 7.52 | 0 | 0 | 200 | 5 | 45 |
| 6.8 | S | 2.79 | 8.19 | 0.17 | 0.25 | 0.04 | 0.45 | 1.73 | 0.17 | 0.01 | 13.73 | 84.58 | 0.91 | 6.55 | 0 | 0 | 145 | 0 | 15 |
| Av | 3.51 | 8.12 | 0.27 | 0.38 | 0.05 | 0.45 | 3.10 | 0.19 | 0.02 | 12.92 | 84.06 | 1.26 | 9.96 | 9 | 0.34 | 92 | 12 | 18 | |
| SD | 0.88 | 0.21 | 0.16 | 0.11 | 0.05 | 0.24 | 0.96 | 0.02 | 0.02 | 2.36 | 16.30 | 0.31 | 2.23 | 12 | 1.29 | 50 | 14 | 32 |
| DV | Differentiation | No. Factors | R2 | TVE % | RMSE | AIC | R2 Randomised |
|---|---|---|---|---|---|---|---|
| SOC | 2nd der | 2 | 0.483 | 94.48 | 0.118 | −35 | 0.049 |
| pH | n.s. | ||||||
| EC | 2nd der | 10 | 0.549 | 99.12 | 0.108 | −18 | 0.126 |
| N | 2nd der | 2 | 0.499 | 95.56 | 0.083 | −39 | 0.001 |
| P | 2nd der | 10 | 0.454 | 99.05 | 0.086 | −28 | 0.388 |
| Ca | 2nd der | 2 | 0.580 | 94.26 | 0.636 | −2 | 0.136 |
| Mg | No | 12 | 0.483 | 99.93 | 0.018 | −49 | 0.150 |
| K | No | 12 | 0.460 | 99.94 | 0.193 | −6 | 0.414 |
| Na | n.s. | ||||||
| Fe | n.s. | ||||||
| Mn | No | 8 | 0.548 | 99.46 | 12.130 | 57 | 0.031 |
| Cu | No | 6 | 0.451 | 99.56 | 0.248 | −12 | 0.220 |
| Zn | No | 2 | 0.823 | 90.08 | 0.967 | 4 | 0.108 |
| XIPH | 2nd der | 10 | 0.487 | 99.15 | 5.664 | 50 | 0.011 |
| XIPH | 2nd der | 11 | 0.696 | 99.94 | 4.635 | 50 | 0.094 |
| XIPH | 1st der | 11 | 0.619 | 99.55 | 4.819 | 50 | 0.199 |
| RHA | No | 11 | 0.523 | 99.93 | 5.166 | 51 | 0.376 |
| DOR | 2nd der | 11 | 0.642 | 99.20 | 13.013 | 68 | 0.126 |
| ENCH | n.s. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almendros, G.; López-Pérez, A.; Hernández, Z. A Chemometric Analysis of Soil Health Indicators Derived from Mid-Infrared Spectra. Agronomy 2025, 15, 1592. https://doi.org/10.3390/agronomy15071592
Almendros G, López-Pérez A, Hernández Z. A Chemometric Analysis of Soil Health Indicators Derived from Mid-Infrared Spectra. Agronomy. 2025; 15(7):1592. https://doi.org/10.3390/agronomy15071592
Chicago/Turabian StyleAlmendros, Gonzalo, Antonio López-Pérez, and Zulimar Hernández. 2025. "A Chemometric Analysis of Soil Health Indicators Derived from Mid-Infrared Spectra" Agronomy 15, no. 7: 1592. https://doi.org/10.3390/agronomy15071592
APA StyleAlmendros, G., López-Pérez, A., & Hernández, Z. (2025). A Chemometric Analysis of Soil Health Indicators Derived from Mid-Infrared Spectra. Agronomy, 15(7), 1592. https://doi.org/10.3390/agronomy15071592








