Next Article in Journal
Modeling of Droplet Deposition in Air-Assisted Spraying
Previous Article in Journal
Effects of Fertilizers and Soil Amendments on Soil Physicochemical Properties and Carbon Sequestration of Oat (Avena sativa L.) Planted in Saline–Alkaline Land
Previous Article in Special Issue
Bridging the Gap: Limitations of Machine Learning in Real-World Prediction of Heavy Metal Accumulation in Rice in Hunan Province
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Agronomy
Volume 15
Issue 7
10.3390/agronomy15071583
agronomy-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Photothermal Integration of Multi-Spectral Imaging Data via UAS Improves Prediction of Target Traits in Oat Breeding Trials

by
David Evershed
,
Jason Brook
,
Sandy Cowan
,
Irene Griffiths
,
Sara Tudor
,
Marc Loosley
,
John H. Doonan
* and
Catherine J. Howarth
National Plant Phenomics Centre, Institute of Biological, Environmental and Rural Sciences (IBERS), Aberystwyth University, Aberystwyth SY23 3EE, UK
*
Author to whom correspondence should be addressed.
Agronomy 2025, 15(7), 1583; https://doi.org/10.3390/agronomy15071583
Submission received: 28 May 2025 / Revised: 22 June 2025 / Accepted: 24 June 2025 / Published: 28 June 2025
(This article belongs to the Special Issue Application of Deep and Machine Learning in Crop Monitoring and Management)
Browse Figures
Versions Notes

Abstract

The modelling and prediction of important agronomic traits using remotely sensed data is an evolving science and an attractive concept for plant breeders, as manual crop phenotyping is both expensive and time consuming. Major limiting factors in creating robust prediction models include the appropriate integration of data across different years and sites, and the availability of sufficient genetic and phenotypic diversity. Variable weather patterns, especially at higher latitudes, add to the complexity of this integration. This study introduces a novel approach by using photothermal time units to align spectral data from unmanned aerial system images of spring, winter, and facultative oat (Avena sativa) trials conducted over different years at a trial site at Aberystwyth, on the western Atlantic seaboard of the UK. The resulting regression and classification models for various agronomic traits are of significant interest to oat breeding programmes. The potential applications of these findings include optimising breeding strategies, improving crop yield predictions, and enhancing the efficiency of resource allocation in breeding programmes.

1. Introduction

The progress within a traditional plant breeding programme relies on regular, detailed scoring of phenotypic traits. These measurements are key in accepting or rejecting new candidate genotypes, based on their profile of favourable versus unfavourable characteristics for a given crop, grower requirements or preferences, and intended end use [1]. Data collection is time consuming, expensive, and in many cases qualitative and difficult to standardise, meaning that its quality and availability can limit the throughput and efficacy of the programme.
Remote sensing for whole-plant and canopy/plot traits has the potential to reduce manual and/or destructive scoring in breeding programmes, thus addressing this “phenotyping bottleneck” [2,3,4]. Innovations in both sensors and the delivery of sensors to the plants (or vice versa) have been ubiquitous in recent years [5,6], making the approach scalable and therefore generally applicable to both research and breeding. However, high environmental variation in the field often confounds and/or degrades the signals in the data. This is a particular problem in highly variable oceanic climates such as found along the Atlantic seaboard of Western Europe, including the UK and Ireland. Exploiting on-going trials over several years with highly variable weather patterns, data was collected with a multi-spectral camera mounted on an unmanned aerial system (UAS) for the plot-scale prediction of numerous important phenotypic traits in oats (Avena sativa).
Oats are increasing in importance worldwide and recovering to a stable level of production following a significant decline throughout the 20th century [7,8]. Their positive nutritional and therapeutic characteristics, alongside apparent resilience in a changing climate, have made oats a key target for further improvement [9]. Improvement targets vary depending on the end uses, which are primarily as forage, feed, or human nutrition [10]. At IBERS, Aberystwyth University, the oat breeding programme focuses primarily on the development of new varieties of husked winter and spring oats for the milling industry. Important agronomic and grain quality traits for this end use in the context of UK agriculture and industry are given in Table 1 alongside their Crop Ontology Trait ID where available [11,12,13].
The accurate prediction of these traits from remote sensing is highly attractive for breeding programmes as well as for agronomy. The cost of both staff time and equipment for traditional phenotyping can be high. There are many examples of the successful prediction of the important traits of crops via multi-spectral UAS imaging, particularly with respect to biomass and grain yield, plant nitrogen, crop density and height as well as agronomic traits such as lodging. These models are generally effective for a given crop within a given growing season [14,15,16]. Existing models typically make use of transformed data from multi-spectral images of a plot or field in the form of various vegetation indices (VI’s), such as the normalised difference vegetation index (NDVI) [17]. More recently, through advances in machine learning techniques, applications are emerging that essentially skip this step and feed multi-dimensional raw (or lightly processed) sensor data into an algorithm such as a support vector machine (SVM) or random forest [18]. Deep learning techniques are increasingly used in crop research to integrate multi-temporal sensor data at a highly granular level (e.g., pixel by pixel) [19]. A variety of algorithms and architectures have proven effective for this type of modelling both independently and in combination, including convolutional neural networks (CNNs), Pyramid Scene Parsing Networks (PSPNets), Long Short-Term Memory networks (LSTMs), spatiotemporal transformers, and attention mechanisms [20,21,22,23,24,25]. These approaches enable the capture of both local and short-term variations between samples or plots, as well as broader, long-term changes. This makes them particularly well-suited for monitoring crops, where developmental changes over time drive corresponding changes in their measured spectral characteristics. However, the drawbacks of such models include their high computational cost, limited interpretability, and reliance on dense, high-quality training data [26,27]. Therefore, while deep learning techniques represent a powerful and increasingly prevalent approach for modelling multi-temporal sensor data, sparse historical datasets (such as the UAS data available for this study) may be better aligned with more traditional machine learning methods, which tend to be more robust under conditions of limited and heterogeneous data [28].
Despite the ability to capture large amounts of spectral data in a short time and to a tightly standardised protocol, UAS imaging has limitations. The current legislation in the UK requires specific training and qualification for the permitted operation of all but the smallest UASs, as well as various operational constraints relating to the safe use of UASs and the airspace [29]. These factors, plus in-house resource limitations, mean that the frequency of flights can be limited by several factors including the availability of sufficiently qualified staff or pooled resources (e.g., vehicles), appropriateness of weather conditions, and the safe availability of airspace above the crop.
These limiting factors, with the added complication of needing to align the sampling time of day (ideally around solar noon), make regular and uniformly spaced flights difficult to maintain in operational terms. Thus, flight data is usually mis-aligned across sites and seasons, both in terms of calendar and developmental time. This is further compounded when comparing winter versus spring-sown crops which have distinct developmental requirements for (and reactions to) colder weather, with the former also having an extended period of relative developmental quiescence over the winter. There is therefore a need for a robust method of aligning multi-year, multi-site flight data from both spring and winter oat trials with few common sampling points in such a way that it is possible to create models for the prediction of traits. Common developmental points (e.g., Feekes or Zadoks [30]) can be used for the comparison of sampling points, provided that the phenology does not differ significantly within or between trials, but many commercial trials do not routinely collect this information other than key dates such as emergence or flowering.
The effectiveness (and limitations) of photo and thermal time units for modelling in plant phenotyping is established [31,32,33] and there are examples of the use of, for example, Growth Degree Days and Photothermal Time in the alignment of phenotypic data from different years and sites [34,35,36]. These models tend to use a “snapshot” taken at an important developmental timepoint, rather than data from multiple timepoints. Multi-temporal spectral data has been identified as a key component of improved crop modelling by UASs but questions remain, for example, relating to the timing of flights and the equipment/spectral bands needed [37]. The implementation of such modelling would require sufficient training data, collected at common temporal or developmental timepoints and covering different growing seasons.
At IBERS, multi-spectral data for oat trials has been collected by UASs at as regular intervals as operationally possible since 2021 (with caveats as mentioned above). This data could produce strong retrospective standalone modelling for each individual trial, but attempts to combine over-year data are limited by the sparce incidence of sampling at these common temporal or developmental timepoints.
To address this problem, a statistical pipeline has been developed to align and scale UAS-collected plot-scale spectral data from different trials and seasons and synthesise spectral values for common timepoints via interpolation. Flights across three growing seasons between 2020 and 2023 covered several trials that included winter oats, facultative or autumn-sown spring oats and traditional spring oats. Given that the local weather conditions vary radically from season to season, the hypothesis under test is that one or more types of environmental data could be exploited to improve the developmental alignment between seasons, thus comparing similar phenologies at each timepoint, resulting in more accurate prediction models. A desirable outcome of this endeavour, from a breeding perspective, would be phenotypic trait estimates that were less dependent on season-to-season weather variation.
The key principles of the pipeline are outlined in Figure 1. Time-series UAS spectral data are scaled by various photothermal units and aligned (or “zeroed”) by key calendar or developmental dates. Data is then interpolated for timepoints in-between real flights to give estimates for sensor data at common timepoints for all trials across years and crops. This series of sensor data is then subjected to various supervised machine-learning algorithms for the creation of predictive models that can be applied to future trials.
By separately testing UAS data that has been scaled using environmental data, and aligned by calendar and developmental timepoints, data for both spring and winter sown oats can be combined into one training and test set. From this, LASSO regression and random forest models are created. The aim of these regression models is to assign a numerical value to a trait, but also explored in this study is within-trial classification based on the relative performance of that plot within each trial, which will be a useful outcome for the breeding programme as a phenotypic marker for post-harvest traits.

2. Materials and Methods

2.1. Oat Trials and Ground-Truth Data

The exact protocols for trials and associated ground-truth measurements varied slightly over the different trials and years, but the general methodology is given here alongside notes in the case of significant deviation from the standard methods. Ground truth and UAS data were collected from 7 oat trials grown between 2020 and 2023 at Gogerddan, Aberystwyth University. The trial details are given in Table 2. Trials were sown at a rate of 300 seeds/m2, in 5.2 m2 plots in a random block design. Trials and plant protection products and fertilisers were managed and applied in accordance with the AHDB trial protocol [38], apart from the trial sa_h21 which contained plots with a range of nitrogen applications from 0 to 300 kg/Ha.
DAF-zero (zero days after flowering) was used in this study to describe the start of the reproductive phase of the trial and is given as an estimation of the date at which the majority of the plots in the trial had advanced to gs59, by either the mean date of gs59 for that trial or, in the instances that gs59 was not scored, the mean date of gs51, plus the mean difference between gs51 and gs59 for all the other trials (+8 days, SD = 1.6 days). Plant height was taken with the plants at their full height, between gs69 and gs89, from between 3 and 5 random but representative plants within each plot, measured from the ground to the tip of the highest panicle and given as the mean height in cm. The grain yield, subsequent analysis of the grain quality traits specific weight, thousand grain weight (TGW), kernel content (KC), and hullability were determined as previously described [39]. To adjust for plot areas missing due to establishment issues or damage, the “adjusted grain yield” was calculated from the raw plot yield (t/Ha for the plot size as sown) and an estimation of the effective area of the plot by using the following equation:
Adjusted grain yield (t/Ha) = raw yield (t/Ha)/estimated plot cover (%)
The β-glucan, protein, and oil content of the groat were determined via near-infrared scanning spectroscopy on a NIRS6500 system (FOSS, Hillerød, Denmark) [39].

2.2. UAS Data Acquisition and Pre-Processing

UAS imaging was scheduled on an approximately fortnightly basis for all the trials. Operational limitations reduced this frequency. In total, across all the trials, there were 51 individual flights from which data was processable. The flight times for each individual trial are available in the supplementary data repository. The UAS used for imaging was a DJI M210 Version 2 (DJI, Shenzhen, China) fitted with a Slantrange 4p multi-spectral camera with a precision navigation module (Slantrange Inc., San Diego, CA, USA). Flights followed the same pre-programmed path at a height of 35 m above the surface level, with images taken at 80% overlap, implemented using DroneDeploy software (DroneDeploy Inc., San Fransisco, CA, USA). Images were captured in the following spectral bands: blue (470 nm centre, 120 nm width), green (550 nm centre, 100 nm width), red (620 nm centre, 110 nm width), red-narrow (650 nm centre, 40 nm width), red-edge (710 nm centre, 20 nm width), and near-infrared (850 nm centre, 100 nm width). Multi-spectral images were stitched using Agisoft Metashape software (Agisoft LLC, St. Petersburg, Russia). Supervised semi-automatic segmentation of plots from stitched images was carried out using the GRID python package [40] with a k value of 3. This returns one intensity value per spectral band (0–255) per plot, representing the mean intensity for all the segmented crop pixels.

2.3. Environmental Data and Photothermal Units

Local air temperature and rainfall data were collected by the Gogerddan Met Office surface station (longitude: −4.02, latitude: 52.43, altitude: 31 m) [41]. Growth Degree Days (GDD) were calculated by using the following equation:
GDD (° days) = ((TMAX − TMIN)/2) − TBASE
where TMAX and TMIN are the daily maximum and minimum air temperatures, respectively, at the crop level in °C, and TBASE is a constant describing the temperature below which plant development stops—for oats, TBASE was set as 0.0 °C [42]. If ((TMAX − TMIN)/2) < TBASE, GDD = TBASE [43].
For the same coordinates as the surface station, daily sunrise and sunset times for Gogerddan between 1 January 2020 and 31 December 2023 were downloaded from the U.S. Naval Observatory Astronomical Applications Department website [44]. The Photothermal Time (PTT) was calculated by using the formula:
PTT (° day hours) = GDD (° days) × Day Length (h)
where day length is the number of hours in decimal between sunrise and sunset [45].
The total daily Global Horizontal Irradiance (GHI) data for Gogerddan with a 1-day timestep between 1 January 2020 and 31 December 2023 were downloaded from the Copernicus Atmosphere Monitoring Service (CAMS) Atmosphere Data Store (ADS) [46,47,48,49,50]. Empirical conversion of GHI to Photosynthetically Active Radiation (PAR) (being the proportion of energy given by photons in the wavelength range 400–700 nm [51]) is non-trivial but can estimated by applying an accepted conversion factor of the total daily PAR being 45% of the total solar irradiance [52,53,54]. Daily Light Integral (DLI), the total amount of PAR received over a 24 h period (midnight to midnight), is therefore estimated by using the following equation:
DLI (mol/m2/day) = total GHI (Wh/m2/day) × 0.45 × 4.57 (µmol/J) × 3600 (J/Wh) × 10−6
where 0.45 = the estimated proportion of total solar radiation in the PAR waveband, 4.57 = photons per joule of PAR energy (µmol/J) [55,56], 3600 = number of joules per watt-hour and 10−6 for the conversion of µmol to mol. The Photothermal Integral (PTI), an experimental photothermal unit for temperate climate is given as:
PTI (° mol/m2) = GDD (° days) × DLI (mol/m2/day).

2.4. Statistical Analysis

Statistical analysis was carried out using R version 4.4.0 in the RStudio environment. Two interpolation methods within base-R were used to predict sensor data at timepoints between real measurements, the “approx” function for linear interpolation and “spline” function for curved or natural interpolation. Time units under the test were days, GDD, DLI, PTT, and PTI, as an accumulation since 1st January of the harvest year or “day of year” (DOY), since the date on which sowing was completed or “days after sowing” (DAS), and since the onset of flowering or “days after flowering” (DAF). For each unique combination of interpolation method, time unit, and alignment day, the sampling points at which to interpolate sensor data were determined as the four equidistant points with the largest common difference along the largest possible time unit overlap for all trials, with the 1st timepoint being the alignment day for DOY and DAS, and the 2nd timepoint for DAF. These parameters gave the best possible range of data in terms of covering common developmental and/or environmental timepoints between trials and years while minimising the occurrences of more than one interpolation point between real measurements. More than one interpolation point would give rise to strongly co-linear predictor variables in the training set, which is undesirable. Following interpolation, plots with intensity values for any of red, green, blue, red-edge, red-narrow, or NIR that were more than 1.5 times the inter-quartile range for that flight and sensor were removed as outliers. Interpolation methodology was tested using a leave-one-out validation for all flights (excluding the first and last flight for each trial), and R2 for the interpolated vs. real flight data were compared against both the timepoint of the interpolation within the growth of the trial as well as the size of the time gap within which the interpolation was made.
Plots were split randomly into training and test data at a ratio of 80:20 using the “createDataPartition” function of the “caret” package [57]. Each trait of interest was tested individually as a numeric outcome variable, with intensity data for each of the six sensors at four timepoints per sensor as the predictor variables (giving 24 predictor variables per test). Due to the potential for co-linearity, LASSO was chosen as a regression technique that mitigates this risk and reduces overfitting through the encouragement of sparse models. LASSO regression was implemented using the “glmnet” package, with λ selected as the largest value within one standard error of the minimum cross-validation error [58,59]. The same data was also tested using random forest regression which was implemented using the “randomForest” package [60]. The resulting regression models were compared to each other by normalising the test-set R2 and root mean square error (RMSE) across all the method combinations for each outcome variable, and then taking the mean normalised values for each method combination. The individual outcome variable model methods were compared by ranking test-set R2 (high–low) and RMSE (low–high), and adding the rankings with equal weighting, and dividing by 2 to give an overall rank. If two models have an equal rank following this process, then the model with the lowest RMSE receives the higher rank. Variable importance was calculated via the mean decrease in accuracy “importance” function in the “randomForest” package in R (an estimation of the % decrease in model accuracy should that variable be unavailable).
For within-trial classification, each outcome variable was ranked numerically within its own trial and partitioned as follows: equal to or less than the median value into “low” classification and greater than the median value into “high”. Three descriptive within-trial classes were also then created:
  • Milling quality, which was assigned “good” if that plot yielded grain with high classifications for both kernel content and hullability, and “poor” if both kernel content and hullability were classed as low. Any other combinations were classed as “intermediate”.
  • Physical quality, which was assigned “good” if both test weight and TGW classifications for the plot were high and screenings were low, and “poor” if both test weight and TGW were low and screenings high. Any other combinations were classed as “intermediate”.
  • Groat composition, which was assigned “good” if both groat protein and ß-glucan content classes were high and oil content class was low. Groat composition was classified as “poor” when both groat protein and β-glucan content classes were low and the oil content class was high. Any other combinations were classed as “intermediate”.
The same data as for the regression models was then used to train and test a random forest classification model for each combination of outcome variable class, interpolation method, timescale, and alignment timepoint. Implementation was with the “randomForest” package and tuned with the “tuneRF” function. To calculate the false positive rate and contextualise within the broad aims of the oat breeding programme, for plant height, oil content, and small grains/screenings, the positive class was set as “low”, while for all other traits, the positive class was “high”. The classification accuracy and false positive rate (FPR) were calculated as follows:
Accuracy = (TP + TN) / (TP + TN + FP + FN)
FPR = FP / (FP + TN)
where TP and TN are true positive and true negative classifications in the test set, and FP and FN are false positive and false negative.
Classification models were compared and ranked by their normalised accuracies and FPRs for each outcome variable. For the ranking, if two or more models shared an accuracy score, then the model with the lowest false positive rate was given the higher rank. The variable importance was calculated via the “importance” function in the “randomForest” package in R, using the same method as for the random forest regression.
To further investigate the importance of the sensor data, an ablation study was carried out separately for LASSO regression, random forest regression, and random forest classification. For all models, data from one sensor (either red, green, blue, red narrow, red edge, or NIR) was removed from the training set in turn, and the resulting drop in R2 (for regressions) or classification accuracy (for classifications) on the test set was measured. The differences in model performance were then evaluated using either a t-test (for normally distributed differences) or the Wilcoxon signed-rank test (for non-normally distributed differences). The null hypothesis in each case was that the mean (for t-tests) or median (for Wilcoxon tests) difference between the original and ablated models was zero. Resultant p-values were adjusted using the Bonferroni correction.

3. Results

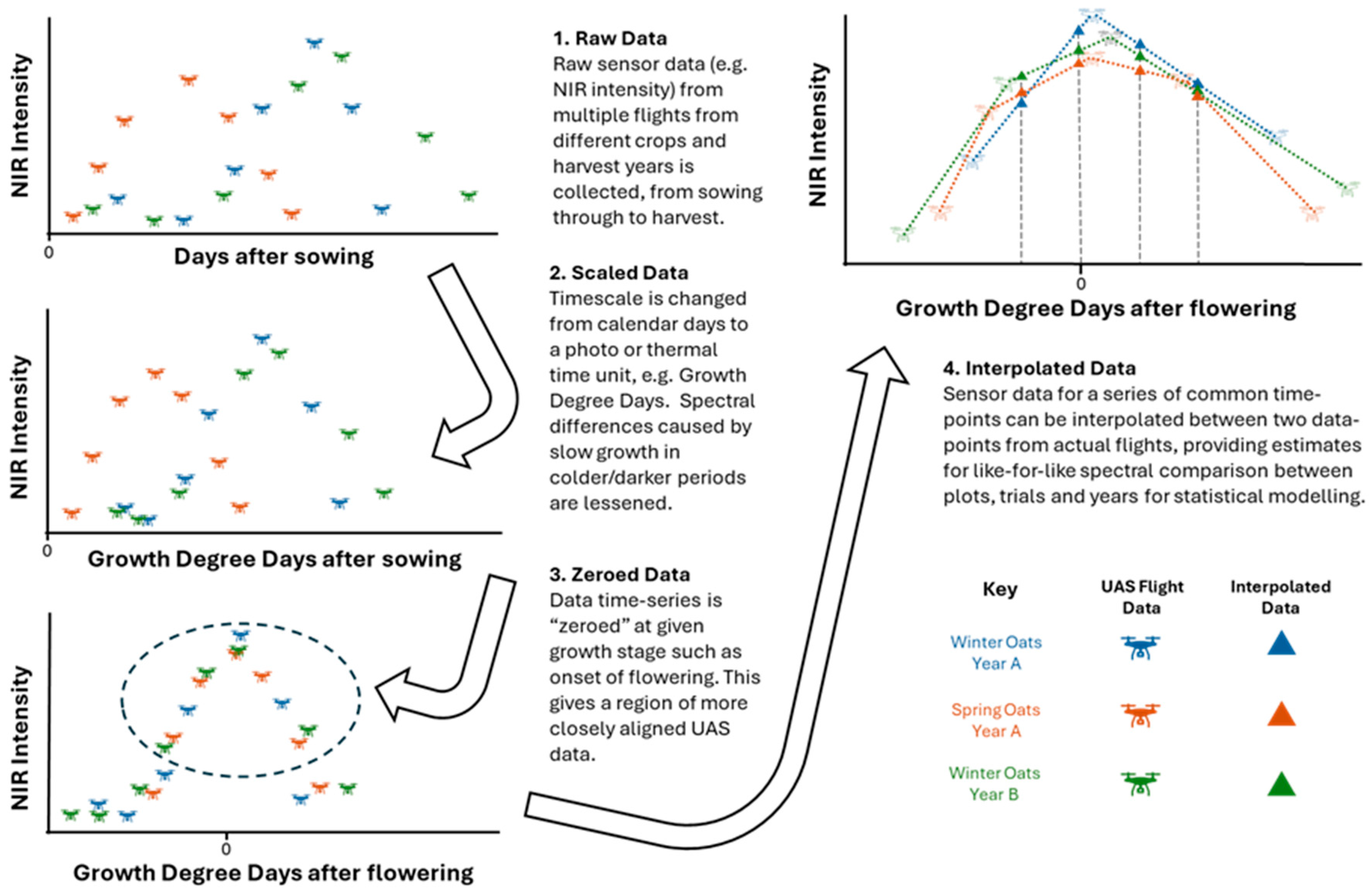
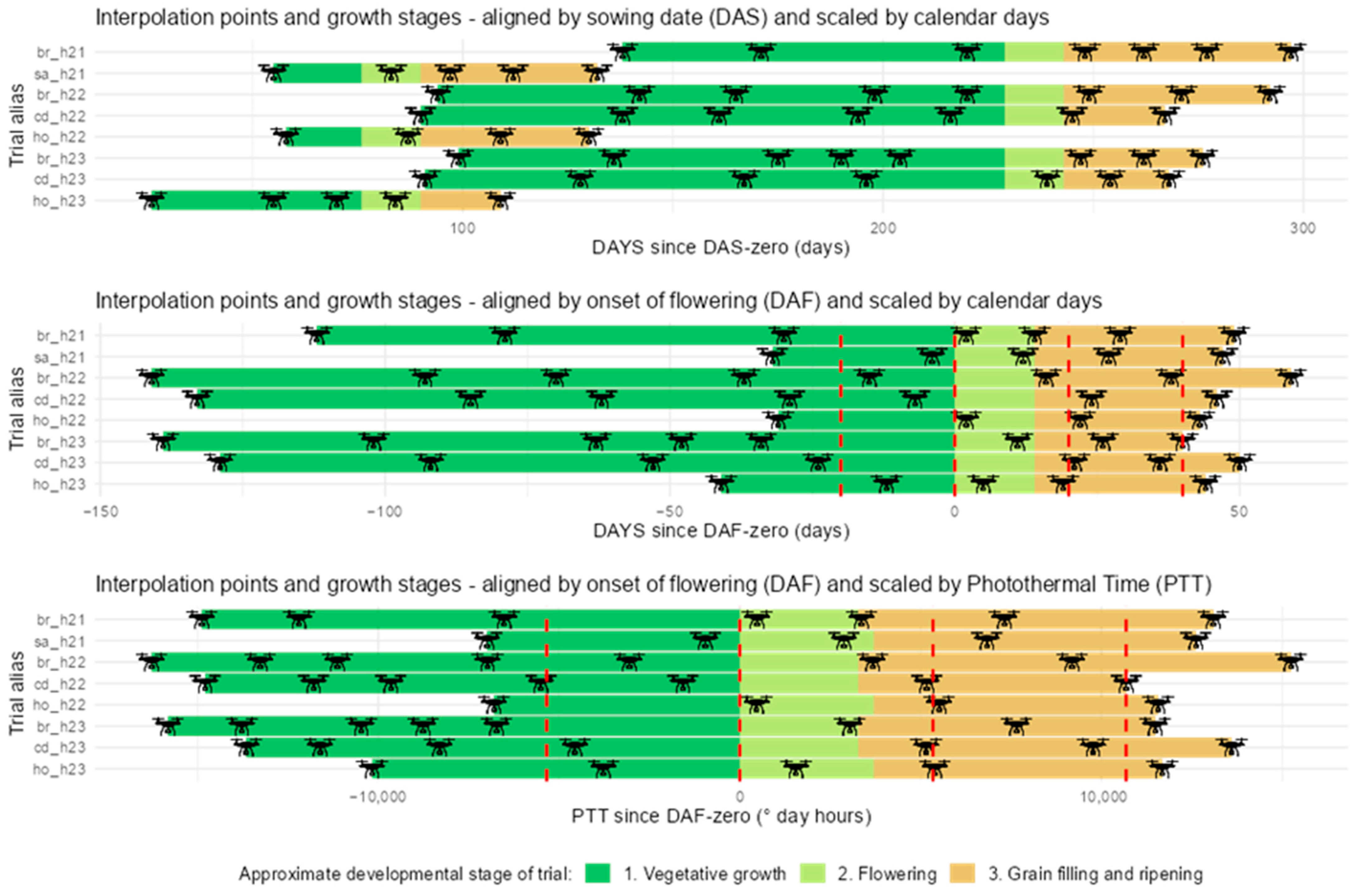
3.1. Data Interpolations

At each of the selected common timepoints, the spectral values for each plot were interpolated according to the values from real UAS flight data before and after the “artificial” point. This is essentially a form of synthesising data. Sometimes the synthetic data would be temporally very close to a “real” measurement and would therefore closely resemble that measurement, while at other times, there may have been several calendar days or the equivalent photothermal units between the interpolation point and the nearest real measurement. Figure S1, by showing the trends in mean R2 values from the leave-one-out validation, demonstrates that as the distance between points increases, data interpolated between those points becomes less likely to accurately portray a “real” measurement. R2 for interpolated vs. real data generally decreased as the timepoint increased, and an increase in the time gap between which interpolations are made was also associated with a decrease in R2. Complete leave-one-out validation data is available at the supplementary data repository. Figure 2 demonstrates how changing the alignment T-zero and/or timescale from calendar days to a photothermal unit creates overlapping sampling points and suitable points at which to interpolate.

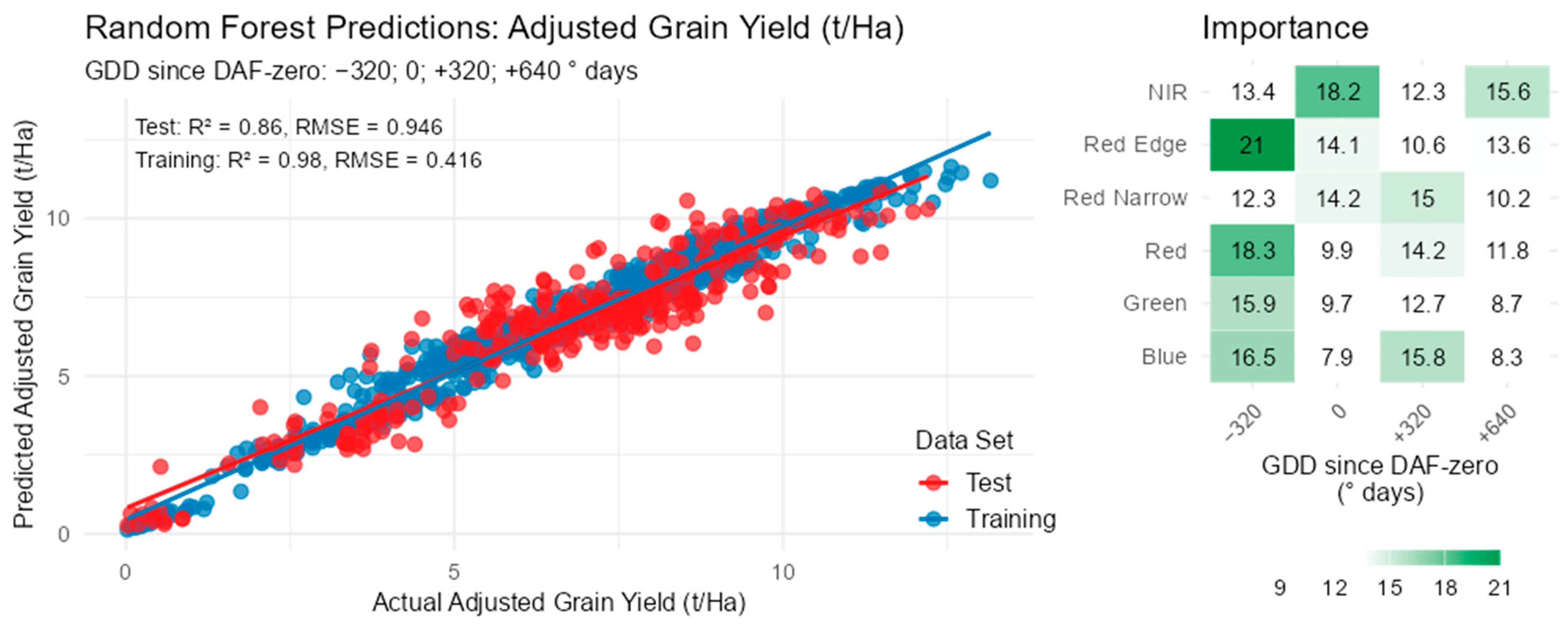
3.2. Regression Models

The regression models were trained to predict a continuous numerical outcome from the synthetic spectral data. Their performance (or potential usefulness) can be assessed by the R2 and RSME values of the predicted vs. ground truth data from the test data. Test data is the randomly selected portion of training data that is partitioned and not included in the model, so by presenting the test data to the model and comparing to the ground truth data (to which the model was blind), it is possible to estimate how the model will perform for future trials.
The detailed regression performance metrics are available at the supplementary data repository. The mean normalised R2 and RSME across all outcome variables for each method combination are shown in Figure S2. Generally, random forest regression models had a higher R2 and lower RMSE than their LASSO equivalent, and models using “day of year” as their alignment timepoint (or T-zero) had a higher R2 and lower RMSE. When looking across the normalised performance metrics, there was little evidence for a “strongest” combination of interpolation method or timescale. This finding suggests that each outcome variable is likely to have its own optimal set of interpolation method, timescale, and T-zero on which to build models. The individual outcome variables method combined rankings are given in Figure S3.
The data processing methods (combination of interpolation method, T-zero, and timescale) which yielded the top-ranked models for the regression methods are given in Figure S4.

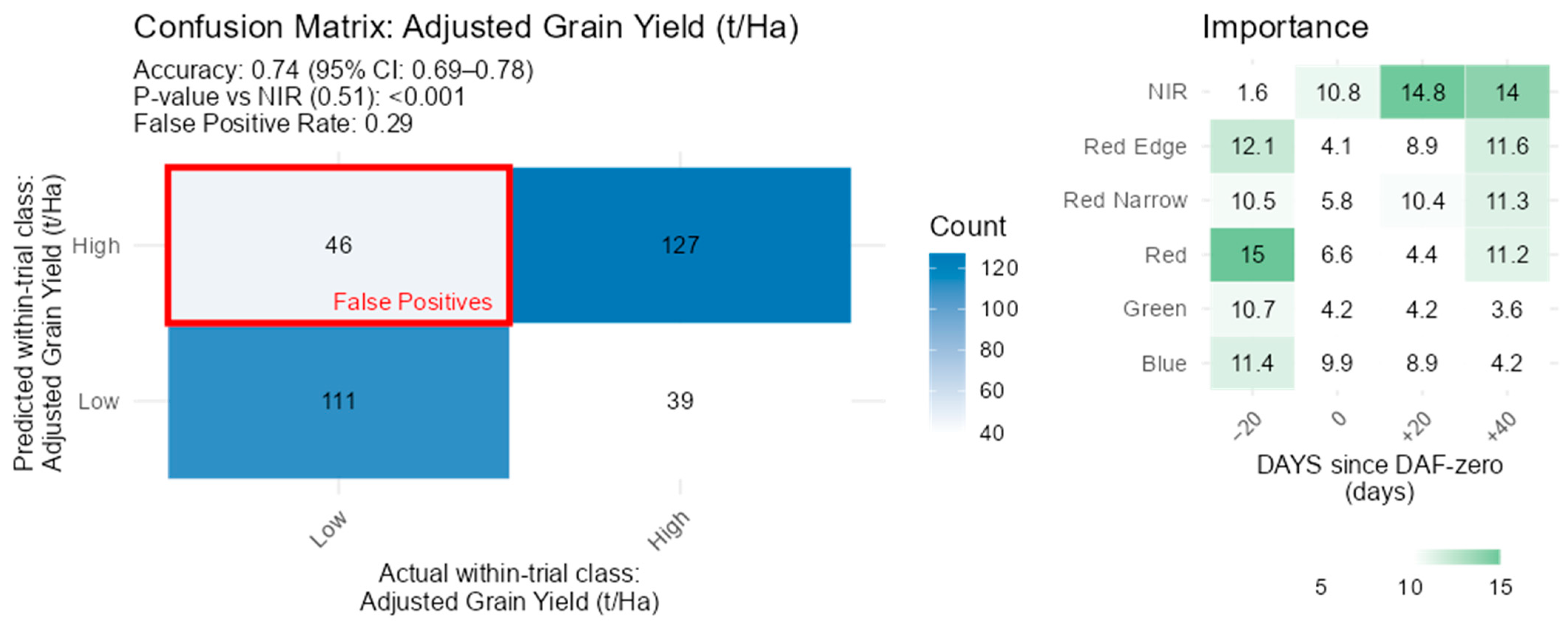
3.3. Classification Models

The classification models were designed to estimate the performance of a variety plots within each trial, relative to its peers, for some key target traits. This classification pipeline aimed to replicate what breeders are doing in variety trials, often making more qualitative assessments about which of the candidate varieties appear to be performing well in a given environment, without necessarily being concerned with the absolute number or score associated with that trait.
The detailed classification performance metrics are given in the supplementary data. The overall effectiveness of the different combinations of interpolation method, T-zero, and timescale are summarised in Figure S5 by reference to the means of the normalised accuracy and FPRs. None of the two interpolation methods, T-zeros, or timescales, provided a generally better classification performance across all the outcome variables. This again suggests that optimal data alignment and interpolation methods differ between outcome variables. The method accuracy ranks for each outcome variable are given in Figure S6, and the data pre-processing methods used for the highest ranked models are given in Figure S7.
Having ranked the models according to their performance for each individual trait, the highest ranked model was taken forward for further investigation. Along with the importance of variables, also measured was the advantage (if any) of the use of photothermal units over prediction models trained on data aligned by calendar days.

3.4. Grain Yield

The adjusted grain yield, being the principal measure against which breeding decisions are made, is preferred to raw yield data in the breeding programme, and therefore is the ground truth variable used for the description of the yield results. Adjusted yield performed slightly better than raw yield in general across the method combinations for both regression methods (mean R2 0.81 vs. 0.79) but fared slightly worse in the within-trial classification models (mean accuracy 69.2% vs. 69.6%). The strongest regression model used random forest with splined interpolations from DAF-alignment and GDD scaling (Figure 3). The strongest regression model that used calendar days as the timescale was ranked fifth. The strongest within-trial classification model for adjusted yield was trained using splined interpolations between timepoints measured in days, aligned by DAF (Figure 4).

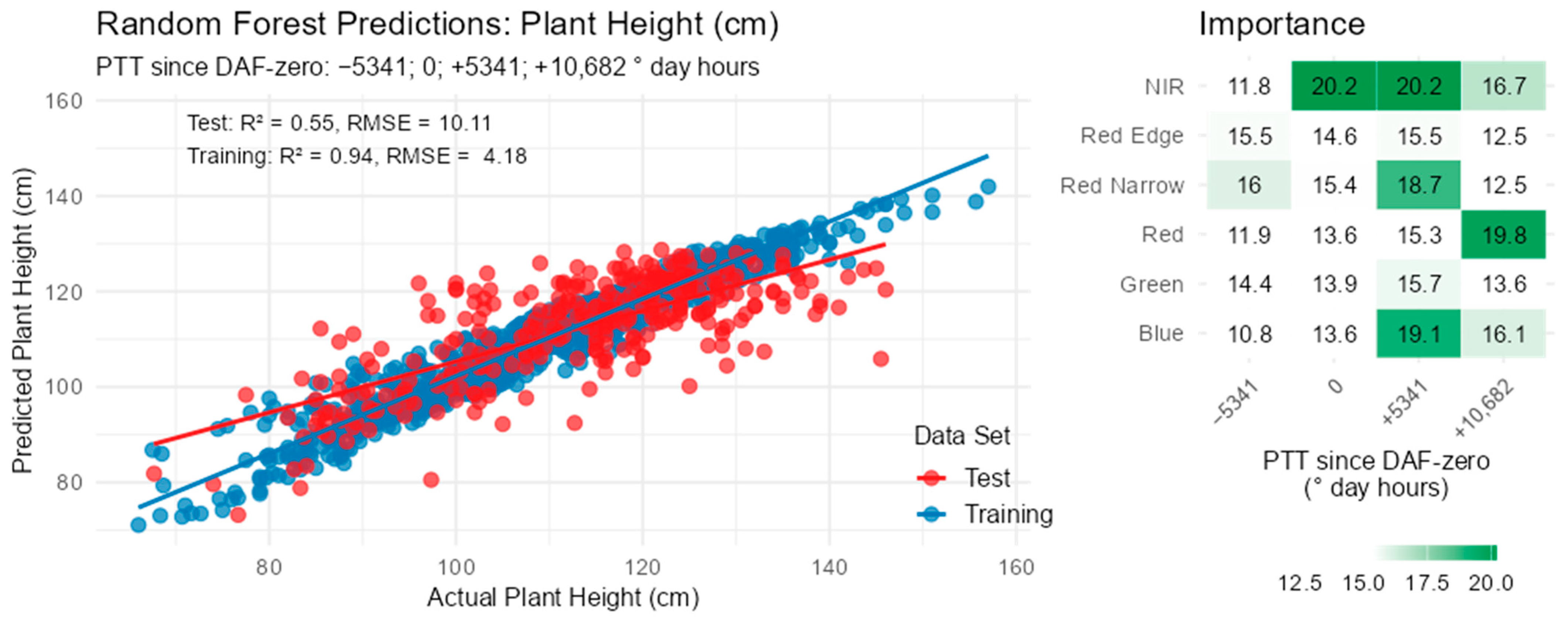
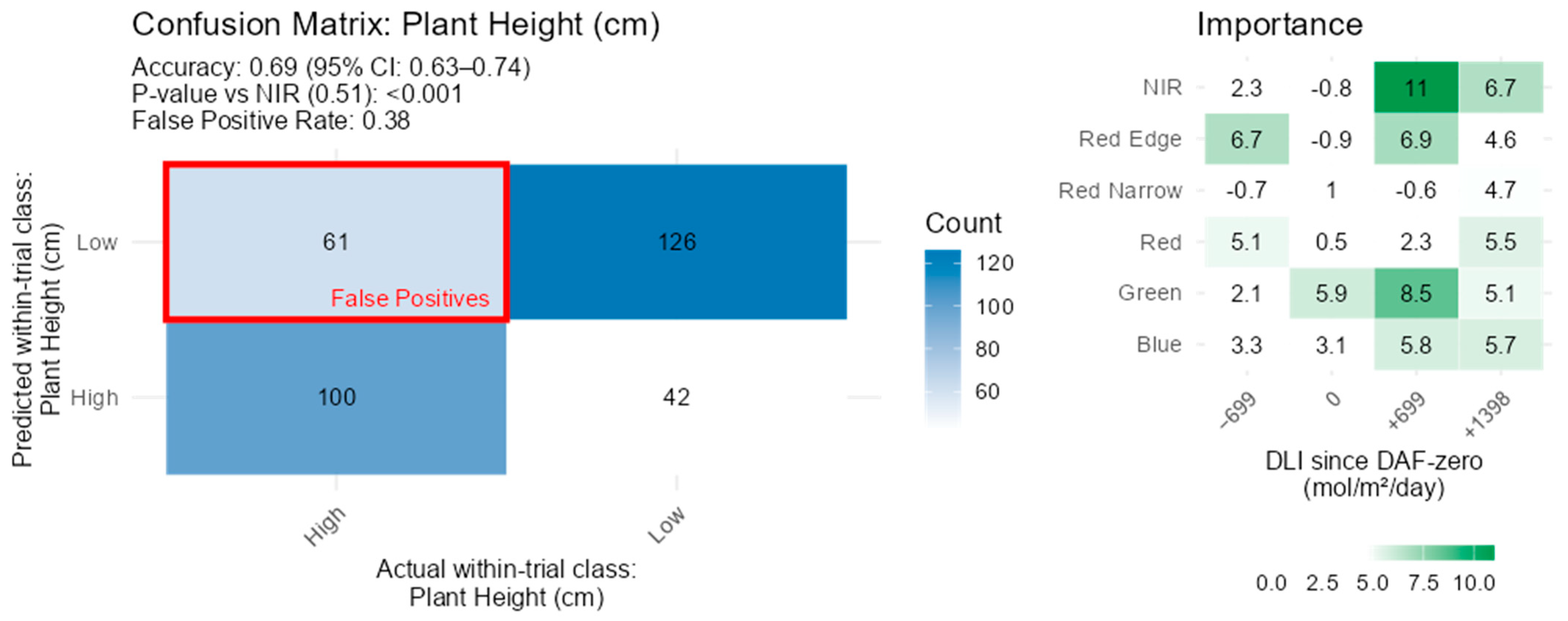
3.5. Plant Height

Random forest regression of splined interpolations from DAF-alignment and PTT scaling produced the strongest regression model for plant height (Figure 5). The strongest within-trial classification model for plant height was trained using linear interpolations between DLI timepoints, aligned by DAF (Figure 6).

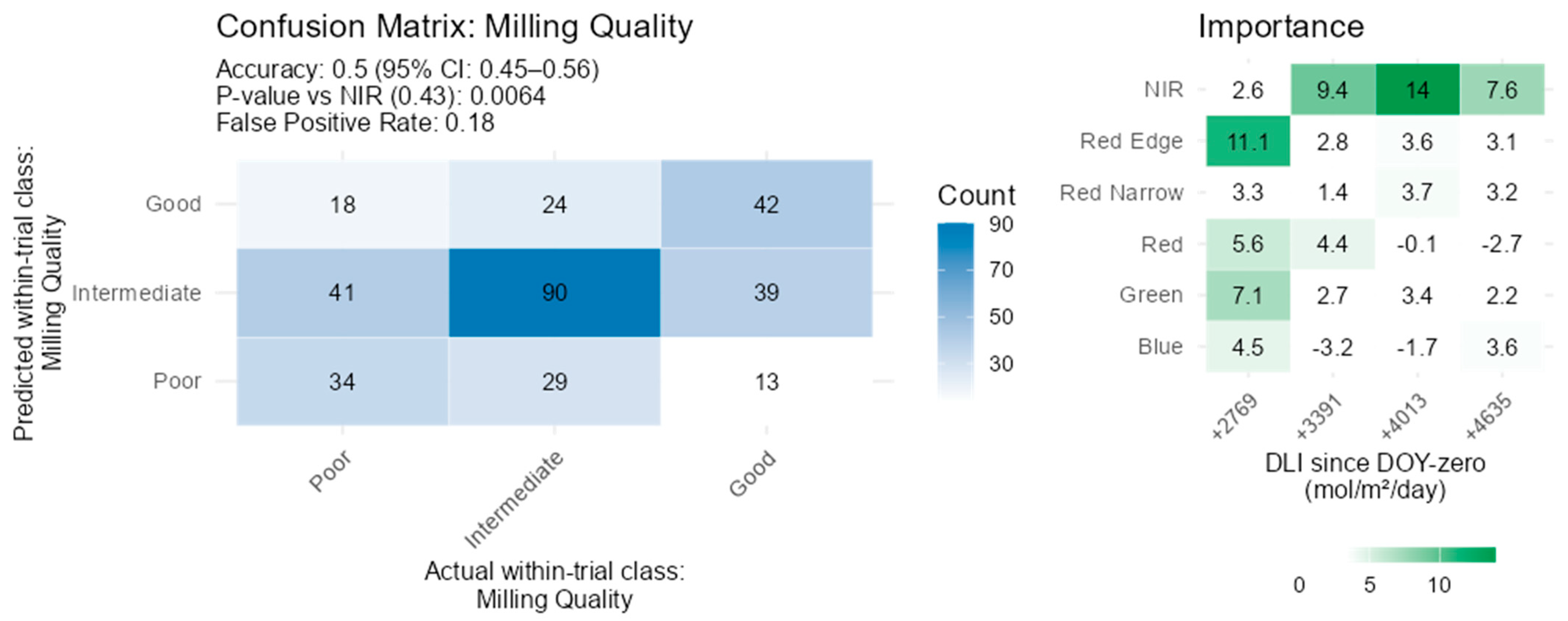
3.6. Milling Quality

Good milling quality is defined here as having a good kernel content and good hullability. Three models passed significance for within-trial classification of milling quality, the best of which used data from splined interpolations, DLI scaling, and DOY alignment and had a test accuracy of 50% (Figure 7).

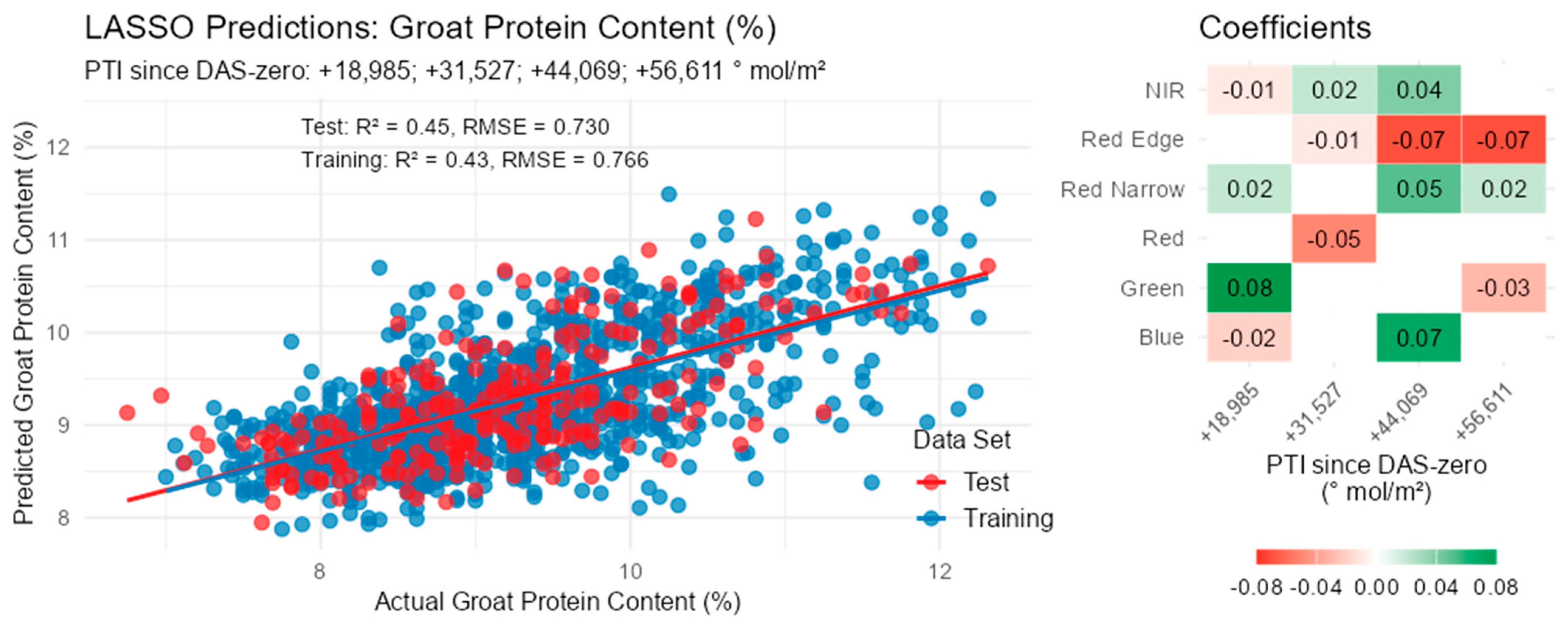
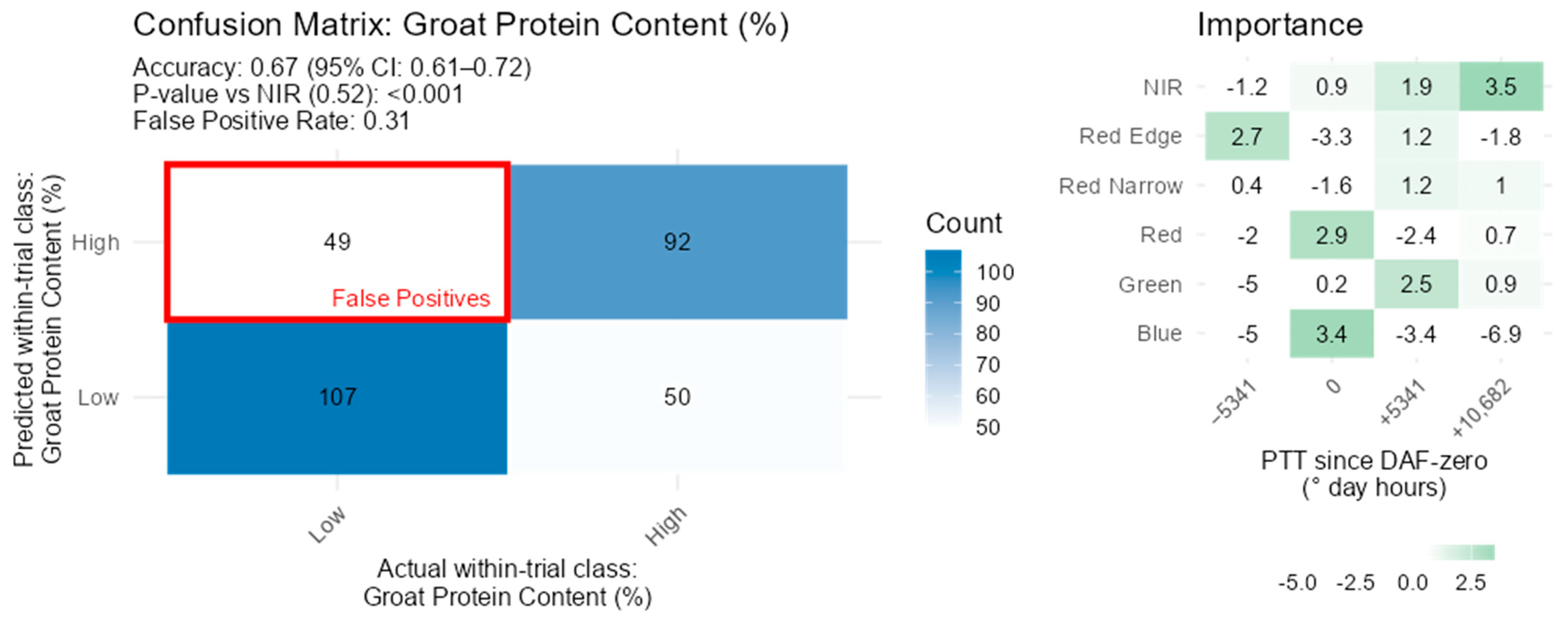
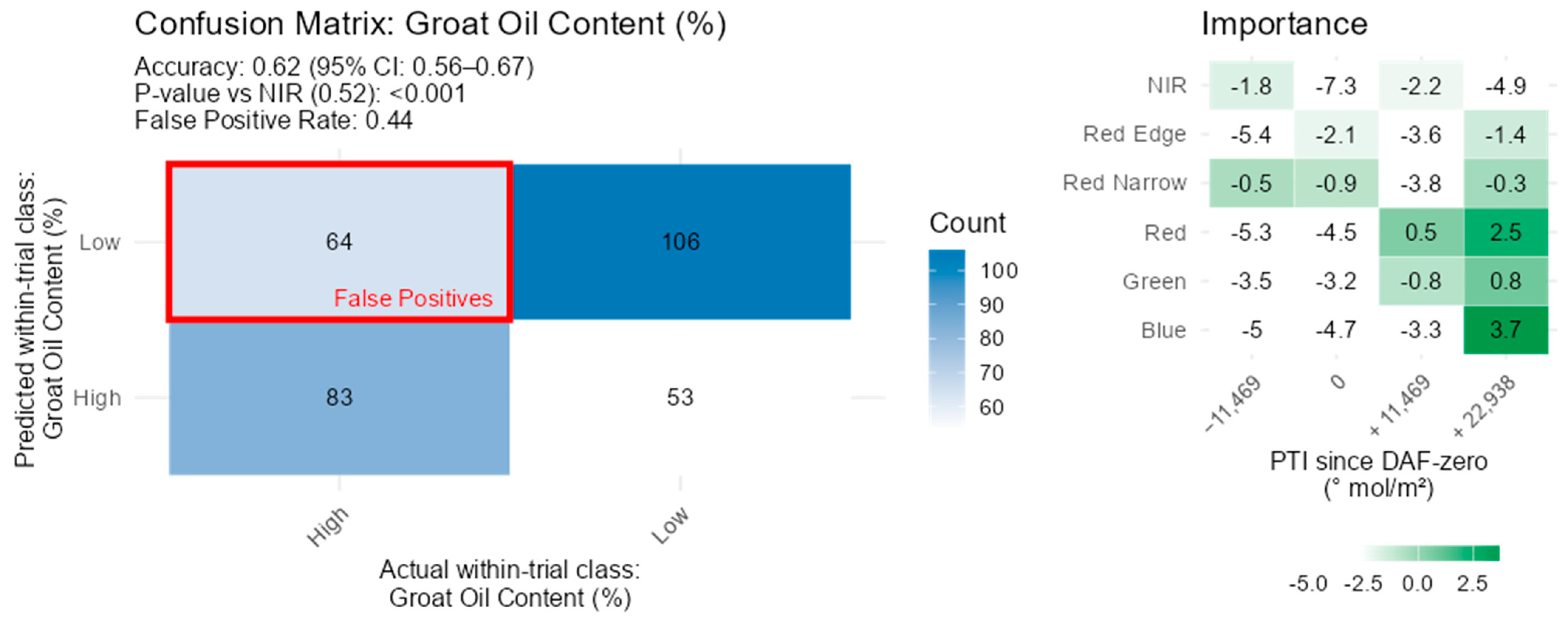
3.7. Groat Composition

None of the models produced were able to predict the composition class significantly better than the no-information rate. The groat oil and protein content were predicted with moderate success with a best R2 and RMSE of 0.45 and 0.73, from the LASSO regression using DAS alignment, PTI scale, and splined interpolations for protein (Figure 8), and a best R2 and RMSE of 0.70 and 0.61, from the random forest regression using DOY alignment and days timescale with splined interpolations for oil. The strongest within-trial classification for protein was made with splined interpolations from PTT-scaled and DAF-aligned data and had an accuracy of 67% (Figure 9), and for oil, the best classification model used DAF alignment, PTI scaling, and linear interpolations but gave an accuracy only slightly better than the NIR at 62% vs. 52% (Figure 10). The β-glucan content was the least successfully predicted component of groat composition for both regression and classification with a best R2 and RMSE of 0.33 and 0.26 (random forest regression using splined interpolations at DLI timepoints from DOY-zero) and a classification accuracy of 59% using the same pre-processing as for the regression.

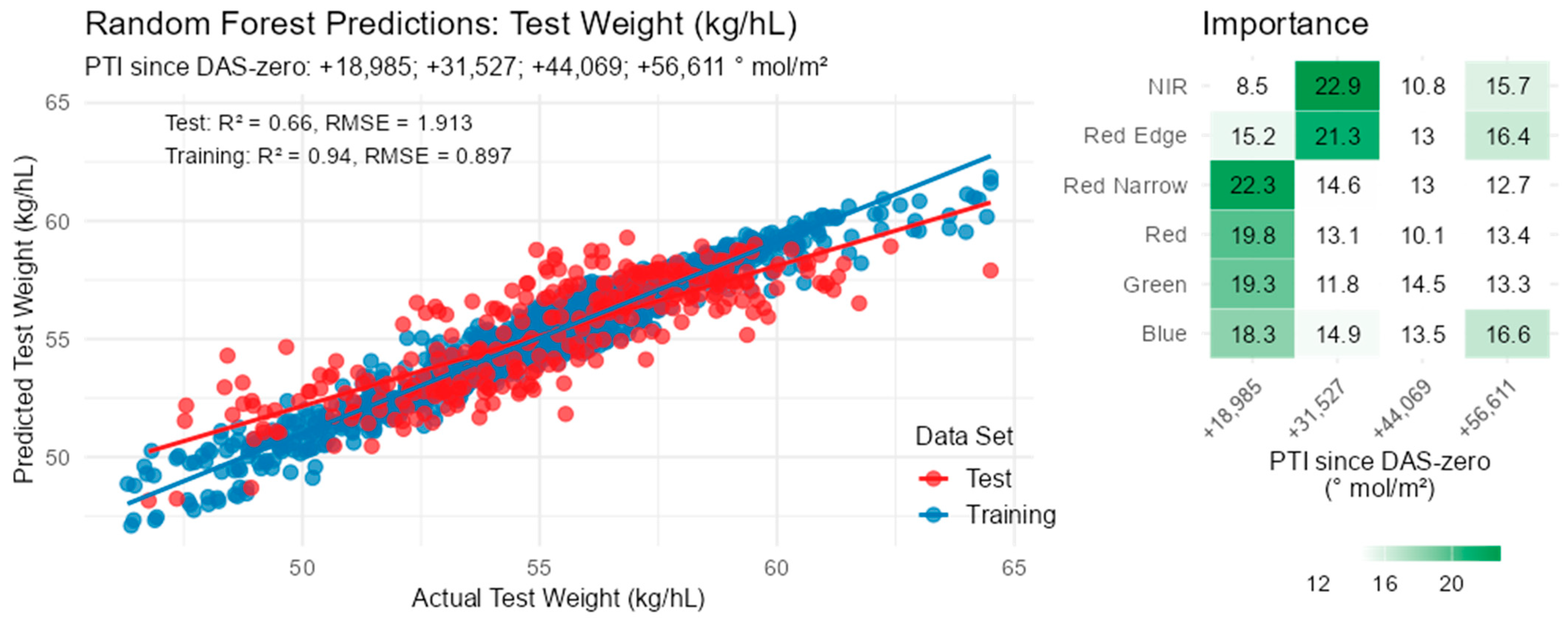
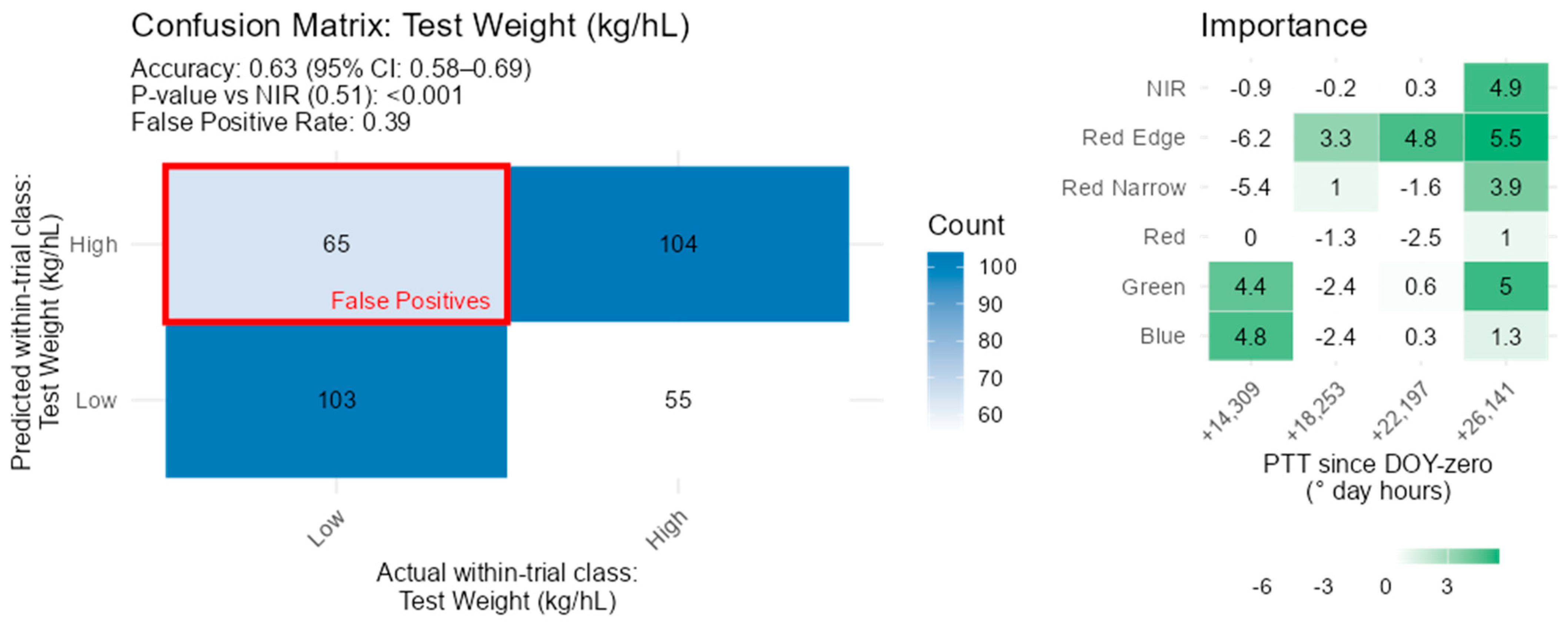
3.8. Physical Grain Quality

None of the models produced were able to predict the physical grain quality class significantly better than the no-information rate, but some individual components of physical quality were predicted with moderate success. The strongest regression model for test weight used linear interpolations at PTI timepoints, aligned by DAS and had an R2 of 0.66 and RMSE of 1.9 (Figure 11). The strongest within-trial classification model used linear interpolations at PTT timepoints from DOY-zero and had an accuracy of 63% (Figure 12). Regression models for screenings/small grains and TGW generally performed well for the training data but not for the test data; however, there were several within-trial classification models for both which passed significance.

3.9. Ablation Study

The results of the ablation study are given in Table 3. For LASSO regression, the removal of data from any one of the six sensors from the training set caused a small but significant average reduction in test R2. For random forest regression, the removal of the green channel did not significantly impact the test R2, but the removal of other sensor data each caused a small but significant average reduction in the test R2. For random forest classification, the removal of red, green, or red narrow data did not significantly affect the test accuracy of the models, but the removal of blue, reg edge, or NIR data caused a small but significant reduction in the model test accuracy.

4. Discussion

The overarching aim was to explore different modelling approaches to integrating UAS remote-sensed data collected from distinct oat crop-types, which also mitigate for radically different weather conditions between and during the different seasons. For a wide number of key traits in oat breeding, by measuring time as a function of the accumulation of key plant resources, light, and/or temperature, the models could be improved relative to measuring time in calendar days. Overall, for the 11 traits tested, photothermal units (either PTT or PTI) were used in the top three models 16 times, relative to 12 times for traditional thermal time or daily light integral, and 5 times for calendar days. So, despite the overall rankings not giving a clear indication of any one strongest timescale for modelling, it is reasonable to suggest that the strongest models tended to include the use of combined temperature and light data more often than temperature or light alone, and significantly more often than calendar days.
The resulting models are of interest for two main reasons. First, the training set contains data from a wide variety of oat varieties, landraces, and advanced breeding lines, also representing the two main UK oat crop types—spring oats and winter oats. Second, the data covers 3 years with very different weather patterns, both in terms of accumulated temperature and cloud cover. While the accumulated thermal time is widely used in agronomy for predicting crop productivity, in oceanic and some tropical climates, light quality can also have a significant impact. It is expected that the models could be applied to future growing seasons at Aberystwyth, where the model scores and classes will be used as a screen for potentially high-performing varieties. This screen will allow for the automatic progression of a selection of high performers without the need to wait for time-consuming laboratory analysis, thus reducing one of the key bottlenecks in the oat breeding programme.
While the current models were developed using data solely from Aberystwyth, the pipeline is designed for easy integration of training and environmental data from other sites. With sufficient additional data, the models are expected to generalise to regions with different climates. Predicting complex compositional traits such as groat protein and β-glucan remains challenging, and these models will require further refinement before being used in decision making. Except for milling quality, models of combined trait classes did not outperform a baseline assigning all plots to the majority “intermediate” class, highlighting an opportunity for improvement with more targeted training data.
Our methodology relies on several key assumptions. The first key assumption is that each of the spectral properties measured proceeds from timepoint to timepoint in a predictable way (i.e., that the true mean spectral value for a plot at an unmeasured timepoint is sufficiently close to its interpolated value)—which in turn relies on the assumption that in general, real flights were sufficiently close together, or close enough to each interpolation point, for that prediction to take place. The leave-one-out validation exercise demonstrated the sensitivity of the data synthesis pipeline to increased distances between measurements, but the best mean R2 for sensor data, around 0.4 for most combinations, was from interpolations over generally bigger distances than in the modelling itself. This finding gives confidence that the synthetic data provided acceptable estimates of spectral intensities for the non-existent UAS flights. Generally, vegetation indices display a predictable profile of change over time. For cereals, the indices relating to the abundance and health of green, photosynthesising tissue generally increase as the plants progress through vegetative growth and peak around the start of the reproductive phase, before a decline as the crop ripens [61,62]. However, stresses can cause deviations in these otherwise predictable profiles, such as extreme temperatures, both cold [63] and hot [64], drought [65], and biotic stresses [66]. After transformation to a vegetative index format, our multi-spectral data mostly conform to these expectations. This was consistent with the environmental data and disease scores, which indicated relatively low levels of both abiotic and biotic stresses for all the trials across all growing seasons. Therefore, based on these factors, we could also assume that the raw spectral values (the constituents of the vegetative indices) also progressed from timepoint to timepoint in a manner at least as predictable as shown in the leave-one-out validation (Figure S1). The general decline in average R2 in the leave-one-out validation for real sensor data vs. interpolated data as the plants developed and ripened is most likely explained by the fact that flights were generally further apart in both calendar days and especially photothermal units (which increased rapidly in summer) as the trial approached harvest ripeness.
The absence of any major abiotic plant stress allows for the reasonable assumption that increases in photothermal units positively advanced crop development, rather than harming it. It should be noted that our method does not discriminate between similar accumulations of photothermal units from, for example, several days of temperate weather with diffuse sunshine versus several days of cool weather followed by an extremely hot, bright day. Because the method uses a 24 h period as its standard unit of time, it may need further optimisation for highly unstable weather, for example reducing the time unit to provide more fine-grained modelling. Similar assumptions apply to resources beyond light and warmth, i.e., that water and nutrient availability are neither limiting nor excessive. Rainfall data (available at the supplementary data repository) generally supports this, and nutrient management was standardised to a reasonable degree by the trial husbandry, but for future trial material where this is not the case, again the modelling may perform differently.
The top-performing models for regression and classification used several different combinations of interpolation method, timescale, and T-zero but a large majority of the best models used a form of photothermal unit for scaling rather than calendar days. While splined interpolations gave more “natural” transitions between datapoints, the formulae for these curved interpolations are sensitive to noise, which can cause “overshooting”, especially with data towards the ends of the x-axis (for example in some instances reporting negative values for intensity). This is also evident in Figure S1, with the average R2 value for interpolated vs. real measurement against developmental time in the leave-one-out validation being often lower at the extremes of the x-axis for splined interpolation relative to linear. Other than at the extremes of the x-axis, sensor interpolations were similar between linear and splined methods in terms of the average R2.
Ablation testing helped clarify which sensors and wavelength bands contributed most to model performance. All six sensors showed statistically significant, though modest, importance in LASSO regression models; all except green were important in random forest regressions; and for classification, omitting the green, red, or red-narrow bands had little impact on accuracy. These findings suggest opportunities to simplify the pipeline by developing more lightweight models, while also highlighting the need for further investigation into why certain sensors consistently contribute more than others. The NIR sensor stood out as both the most accurately interpolated sensor in the leave-one-out validation and the most consistently important across all model types. Although more accurately interpolated sensor values (based on leave-one-out validation) tended to be more influential in modelling, this trend was not statistically significant (p = 0.08, 0.12, and 0.17 for LASSO, random forest regression, and classification, respectively). The blue sensor was a notable exception—despite being poorly interpolated, it remained among the most important predictors.
The next stages in the development of this methodology will be three-fold. Firstly, the models will be tested on UAS data from the 2025 growing season at Gogerddan, assessed, and refined for use as internal phenotypic markers. Secondly, data from oat trials in other locations (home and abroad) is needed to assess the extent to which the methodology is transferable within and beyond the mild maritime climate of West Wales. Finally, sensor technology is continuously evolving—the hardware used for the collection of spectral data in this study has been superseded, and while the core principles (and spectral bands) remain the same for now, each new combination of a UAS and sensor will need to be assessed as to whether training data from previous hardware can be used “as is” or require some sort of transformation.

5. Conclusions

Relative to calendar days as the timescale, the use of photothermal units can improve the alignment and scaling of UAS data for the purposes of multi-timepoint modelling and the subsequent prediction of oat traits. This approach also allowed for the combination of spring and winter-sown oat training sets. For the like-for-like comparison of different oat plot trials in different years, sensor data at common sampling points can be interpolated, negating the need for UAS flights to happen at exact developmental or temporal points for every trial. Caveats are principally that UAS flights must be sufficiently regular and close together for valid interpolations, and that the plants do not experience major stresses that cause physical and spectral noise or significant deviations from the “normal” profile of spectral changes over time. The resulting models from this study will be taken forward and incorporated into the oat breeding pipeline where, with new data for current and future growing seasons and additional trial locations, the efficacy of the models can be critically assed, and retrained and improved where necessary.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/agronomy15071583/s1, Figure S1; Mean R2 values for interpolated sensor values vs. real sensor values from the leave-one-out validation exercise. Shows R2 vs. the developmental time of the crop (as measured by the five different timescales under test), and vs. the total gap between neighbouring measurements. Line-of-best-fit is given in blue from LOESS regressions along with the 95% confidence intervals in light grey. Figure S2; Comparison heatmap of pre-processing methods for regression analysis by their resultant means of the R2 and RMSE values when normalised for each outcome variable. Figure S3; Rank heatmap of resultant regression models from each pre-processing method combination for each outcome variable. Figure S4; Heatmap showing the pre-processing method that yielded the highest rank regression model for each outcome variable, and that models’ associated metrics. Figure S5; Comparison heatmap of pre-processing methods for classification analysis by their resultant means of the accuracy and FPR values when normalised for each outcome variable. Figure S6; Rank heatmap of resultant classification models from each pre-processing method combination for each outcome variable. Where no rank is given, the corresponding model produced did not pass significance (p <0.05) for producing accuracy better than the no-information rate (NIR). Figure S7; Heatmap showing the pre-processing method that yielded the highest rank classification model for each outcome variable and that models’ associated metrics.

Author Contributions

Conceptualization, D.E., M.L. and J.B.; methodology, D.E., M.L. and J.B.; software, J.B. and M.L.; validation, C.J.H. and J.H.D.; formal analysis, D.E.; investigation, D.E.; resources, S.C., I.G., S.T. and M.L.; data curation, J.B., M.L., S.T. and C.J.H.; writing—original draft preparation, D.E.; writing—review and editing, D.E., J.H.D. and C.J.H.; visualization, D.E.; supervision, J.H.D. and C.J.H.; project administration, J.B., I.G., S.C. and C.J.H.; funding acquisition, J.H.D. and C.J.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by UKRI BBSRC FoodBioSystems Doctoral Training Partnership (DTP), grant number BB/T008776/1 to DE. C.J.H. and J.H.D. acknowledge support from UKRI grants BBS/E/IB/230001B, BBS/E/W/0012843 and EP/Y005430/1, from the Healthy Oats project, which has been part funded by the European Regional Development Fund through the Ireland Wales Programme. We also acknowledge funding from the European Union’s Horizon 2020 research and innovation programme for the project CropDiva under grant agreement No. 101000847 and from the Welsh Govt’s SMART Flexible Innovation Support Fund.

Data Availability Statement

Data are available from the Aberystwyth Data Repository: https://doi.org/10.20391/ec0863ab-3b5c-434b-837e-74bae4400387 (accessed on 23 June 2025).

Acknowledgments

This publication contains modified Copernicus Atmosphere Monitoring Service information (2025) (neither the European Commission nor ECMWF is responsible for any use that may be made of the Copernicus information or data that it contains).

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Brown, J.; Caligari, P.D.S.; Campos, H.A. Plant Breeding, 2nd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2014. [Google Scholar]
  2. Fiorani, F.; Schurr, U. Future scenarios for plant phenotyping. Annu. Rev. Plant Biol. 2013, 64, 267–291. [Google Scholar] [CrossRef] [PubMed]
  3. Pieruschka, R.; Schurr, U. Plant Phenotyping: Past, Present, and Future. Plant Phenomics 2019, 2019, 7507131. [Google Scholar] [CrossRef] [PubMed]
  4. Yang, W.; Feng, H.; Zhang, X.; Zhang, J.; Doonan, J.H.; Batchelor, W.D.; Xiong, L.; Yan, J. Crop Phenomics and High-Throughput Phenotyping: Past Decades, Current Challenges, and Future Perspectives. Mol. Plant 2020, 13, 187–214. [Google Scholar] [CrossRef] [PubMed]
  5. Atefi, A.; Ge, Y.; Pitla, S.; Schnable, J. Robotic Technologies for High-Throughput Plant Phenotyping: Contemporary Reviews and Future Perspectives. Front. Plant Sci. 2021, 12, 611940. [Google Scholar] [CrossRef]
  6. Shakoor, N.; Lee, S.; Mockler, T.C. High throughput phenotyping to accelerate crop breeding and monitoring of diseases in the field. Curr. Opin. Plant Biol. 2017, 38, 184–192. [Google Scholar] [CrossRef]
  7. Kris-Etherton, P.; Khoo, C.S.; Chu, Y.F. Introduction: Oat Nutrition, Health, and the Potential Threat of a Declining Production on Consumption. In Oats Nutrition and Technology; Wiley-Blackwell: Hoboken, NJ, USA, 2013; pp. 1–6. [Google Scholar] [CrossRef]
  8. Strychar, R. Chapter 1: World Oat Production, Trade, and Usage. In OATS: Chemistry and Technology; Cereals & Grains Association: Saint Paul, MN, USA, 2011; pp. 1–10. [Google Scholar] [CrossRef]
  9. Stewart, D.; McDougall, G. Oat agriculture, cultivation and breeding targets: Implications for human nutrition and health. Br. J. Nutr. 2014, 112 (Suppl. S2), S50–S57. [Google Scholar] [CrossRef]
  10. Gorash, A.; Armonienė, R.; Fetch, J.M.; Liatukas, Ž.; Danytė, V. Aspects in oat breeding: Nutrition quality, nakedness and disease resistance, challenges and perspectives. Ann. Appl. Biol. 2017, 171, 281–302. [Google Scholar] [CrossRef]
  11. Cooper, L.; Elser, J.; Laporte, M.A.; Arnaud, E.; Jaiswal, P. Planteome 2024 Update: Reference Ontologies and Knowledgebase for Plant Biology. Nucleic Acids Res. 2024, 52, D1548–D1555. [Google Scholar] [CrossRef]
  12. Cooper, L.; Meier, A.; Laporte, M.A.; Elser, J.L.; Mungall, C.; Sinn, B.T.; Cavaliere, D.; Carbon, S.; Dunn, N.A.; Smith, B.; et al. The Planteome database: An integrated resource for reference ontologies, plant genomics and phenomics. Nucleic Acids Res. 2018, 46, D1168–D1180. [Google Scholar] [CrossRef]
  13. Morales, N.; Ogbonna, A.C.; Ellerbrock, B.J.; Bauchet, G.J.; Tantikanjana, T.; Tecle, I.Y.; Powell, A.F.; Lyon, D.; Menda, N.; Simoes, C.C.; et al. Breedbase: A digital ecosystem for modern plant breeding. G3 Genes Genomes Genet. 2022, 12, jkac078. [Google Scholar] [CrossRef]
  14. Xie, C.; Yang, C. A review on plant high-throughput phenotyping traits using UAV-based sensors. Comput. Electron. Agric. 2020, 178, 105731. [Google Scholar] [CrossRef]
  15. Tanaka, T.S.T.; Wang, S.; Jørgensen, J.R.; Gentili, M.; Vidal, A.Z.; Mortensen, A.K.; Acharya, B.S.; Beck, B.D.; Gislum, R. Review of Crop Phenotyping in Field Plot Experiments Using UAV-Mounted Sensors and Algorithms. Drones 2024, 8, 212. [Google Scholar] [CrossRef]
  16. Yang, G.; Liu, J.; Zhao, C.; Li, Z.; Huang, Y.; Yu, H.; Xu, B.; Yang, X.; Zhu, D.; Zhang, X.; et al. Unmanned aerial vehicle remote sensing for field-based crop phenotyping: Current status and perspectives. Front. Plant Sci. 2017, 8, 1111. [Google Scholar] [CrossRef] [PubMed]
  17. Huang, S.; Tang, L.; Hupy, J.P.; Wang, Y.; Shao, G. A commentary review on the use of normalized difference vegetation index (NDVI) in the era of popular remote sensing. J. For. Res. 2021, 32, 1–6. [Google Scholar] [CrossRef]
  18. Farag, F.; Huggins, T.D.; Edwards, J.D.; McClung, A.M.; Hashem, A.A.; Causey, J.L.; Bellis, E.S. Manifold and spatiotemporal learning on multispectral unoccupied aerial system imagery for phenotype prediction. Plant Phenome J. 2024, 7, e70006. [Google Scholar] [CrossRef]
  19. Yuan, J.; Zhang, Y.; Zheng, Z.; Yao, W.; Wang, W.; Guo, L. Grain Crop Yield Prediction Using Machine Learning Based on UAV Remote Sensing: A Systematic Literature Review. Drones 2024, 8, 559. [Google Scholar] [CrossRef]
  20. Wei, L.; Yang, H.; Niu, Y.; Zhang, Y.; Xu, L.; Chai, X. Wheat biomass, yield, and straw-grain ratio estimation from multi-temporal UAV-based RGB and multispectral images. Biosyst. Eng. 2023, 234, 187–205. [Google Scholar] [CrossRef]
  21. Yu, J.; Cheng, T.; Cai, N.; Zhou, X.-G.; Diao, Z.; Wang, T.; Du, S.; Liang, D.; Zhang, D. Wheat Lodging Segmentation Based on Lstm_PSPNet Deep Learning Network. Drones 2023, 7, 143. [Google Scholar] [CrossRef]
  22. Wang, Y.; Feng, L.; Sun, W.; Wang, L.; Yang, G.; Chen, B. A lightweight CNN-Transformer network for pixel-based crop mapping using time-series Sentinel-2 imagery. Comput. Electron. Agric. 2024, 226, 109370. [Google Scholar] [CrossRef]
  23. Li, Z.; Chen, G.; Zhang, T. A CNN-Transformer Hybrid Approach for Crop Classification Using Multitemporal Multisensor Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 847–858. [Google Scholar] [CrossRef]
  24. Zhang, S.; Qi, X.; Duan, J.; Yuan, X.; Zhang, H.; Feng, W.; Guo, T.; He, L. Comparison of Attention Mechanism-Based Deep Learning and Transfer Strategies for Wheat Yield Estimation Using Multisource Temporal Drone Imagery. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4407723. [Google Scholar] [CrossRef]
  25. Yadav, S.A.; Zhang, X.; Wijewardane, N.K.; Feldman, M.; Qin, R.; Huang, Y.; Samiappan, S.; Young, W.; Tapia, F.G. Context-Aware Deep Learning Model for Yield Prediction in Potato Using Time-Series UAS Multispectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 6096–6115. [Google Scholar] [CrossRef]
  26. Pichler, M.; Hartig, F. Machine learning and deep learning—A review for ecologists. Methods Ecol. Evol. 2023, 14, 994–1016. [Google Scholar] [CrossRef]
  27. Ahmed, S.F.; Alam, M.S.B.; Hassan, M.; Rozbu, M.R.; Ishtiak, T.; Rafa, N.; Mofijur, M.; Ali, A.B.M.S.; Gandomi, A.H. Deep learning modelling techniques: Current progress, applications, advantages, and challenges. Artif. Intell. Rev. 2023, 56, 13521–13617. [Google Scholar] [CrossRef]
  28. Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
  29. Drones|UK Civil Aviation Authority. Available online: https://www.caa.co.uk/drones/ (accessed on 25 March 2025).
  30. The Growth Stages of Cereals|AHDB. Available online: https://ahdb.org.uk/knowledge-library/the-growth-stages-of-cereals (accessed on 9 May 2025).
  31. Parent, B.; Millet, E.J.; Tardieu, F. The use of thermal time in plant studies has a sound theoretical basis provided that confounding effects are avoided. J. Exp. Bot. 2019, 70, 2359–2370. [Google Scholar] [CrossRef]
  32. Schoving, C.; Stöckle, C.O.; Colombet, C.; Champolivier, L.; Debaeke, P.; Maury, P. Combining Simple Phenotyping and Photothermal Algorithm for the Prediction of Soybean Phenology: Application to a Range of Common Cultivars Grown in Europe. Front. Plant Sci. 2020, 10, 1755. [Google Scholar] [CrossRef]
  33. Poorter, H.; Fiorani, F.; Pieruschka, R.; Wojciechowski, T.; van der Putten, W.H.; Kleyer, M.; Schurr, U.; Postma, J. Pampered inside, pestered outside? Differences and similarities between plants growing in controlled conditions and in the field. New Phytol. 2016, 212, 838–855. [Google Scholar] [CrossRef]
  34. Segarra, J.; Rezzouk, F.Z.; Aparicio, N.; González-Torralba, J.; Aranjuelo, I.; Gracia-Romero, A.; Araus, J.L.; Kefauver, S.C. Multiscale assessment of ground, aerial and satellite spectral data for monitoring wheat grain nitrogen content. Inf. Process. Agric. 2023, 10, 504–522. [Google Scholar] [CrossRef]
  35. Li, Z.; Zhao, Y.; Taylor, J.; Gaulton, R.; Jin, X.; Song, X.; Li, Z.; Meng, Y.; Chen, P.; Feng, H.; et al. Comparison and transferability of thermal, temporal and phenological-based in-season predictions of above-ground biomass in wheat crops from proximal crop reflectance data. Remote Sens. Environ. 2022, 273, 112967. [Google Scholar] [CrossRef]
  36. Zeng, L.; Wardlow, B.D.; Wang, R.; Shan, J.; Tadesse, T.; Hayes, M.J.; Li, D. A hybrid approach for detecting corn and soybean phenology with time-series MODIS data. Remote Sens. Environ. 2016, 181, 237–250. [Google Scholar] [CrossRef]
  37. Prey, L.; Hanemann, A.; Ramgraber, L.; Seidl-Schulz, J.; Noack, P.O. UAV-Based Estimation of Grain Yield for Plant Breeding: Applied Strategies for Optimizing the Use of Sensors, Vegetation Indices, Growth Stages, and Machine Learning Algorithms. Remote Sens. 2022, 14, 6345. [Google Scholar] [CrossRef]
  38. AHDB Recommended Lists for Cereals and Oilseeds (2021–2026)|AHDB. Available online: https://ahdb.org.uk/ahdb-recommended-lists-for-cereals-and-oilseeds-2021-2026 (accessed on 9 April 2025).
  39. Howarth, C.J.; Martinez-Martin, P.M.J.; Cowan, A.A.; Griffiths, I.M.; Sanderson, R.; Lister, S.J.; Langdon, T.; Clarke, S.; Fradgley, N.; Marshall, A.H. Genotype and environment affect the grain quality and yield of winter oats (Avena sativa L.). Foods 2021, 10, 2356. [Google Scholar] [CrossRef]
  40. Chen, C.J.; Zhang, Z. GRID: A Python Package for Field Plot Phenotyping Using Aerial Images. Remote Sens. 2020, 12, 1697. [Google Scholar] [CrossRef]
  41. Met Office DataPoint—Met Office. Available online: https://www.metoffice.gov.uk/services/data/datapoint (accessed on 8 April 2025).
  42. McWilliam, S.C.; Sylvester-Bradley, R. Oat Growth Guide. 2019. Available online: https://www.hutton.ac.uk/sites/default/files/files/publications/Oat-Growth-Guide.pdf (accessed on 8 April 2025).
  43. McMaster, G.S.; Wilhelm, W.W. Growing degree-days: One equation, two interpretations. Agric. For. Meteorol. 1997, 87, 291–300. [Google Scholar] [CrossRef]
  44. Table of Sunrise/Sunset, Moonrise/Moonset, or Twilight Times for an Entire Year. Available online: https://aa.usno.navy.mil/data/RS_OneYear (accessed on 7 April 2025).
  45. Nandini, K.M.; Sridhara, S.; Kumar, K. Effect of different planting density on thermal time use efficiencies and productivity of guar genotypes under southern transition zone of Karnataka. J. Pharmacogn. Phytochem. 2019, 8, 2092–2097. Available online: https://www.phytojournal.com/archives/2019.v8.i1.7076/effect-of-different-planting-density-on-thermal-time-use-efficiencies-and-productivity-of-guar-genotypes-under-southern-transition-zone-of-karnataka (accessed on 8 April 2025).
  46. CAMS Solar Radiation Time-Series. Copernicus Atmosphere Monitoring Service (CAMS) Atmosphere Data Store (ADS). Available online: https://ads.atmosphere.copernicus.eu/datasets/cams-solar-radiation-timeseries?tab=overview (accessed on 7 April 2025).
  47. Schroedter-Homscheidt, M.; Azam, F.; Betcke, J.; Hanrieder, N.; Lefèvre, M.; Saboret, L.; Saint-Drenan, Y.-M. Surface solar irradiation retrieval from MSG/SEVIRI based on APOLLO Next Generation and HELIOSAT 4 methods. Meteorol. Z. 2022, 31, 455–476. [Google Scholar] [CrossRef]
  48. Qu, Z.; Oumbe, A.; Blanc, P.; Espinar, B.; Gesell, G.; Gschwind, B.; Klüser, L.; Lefèvre, M.; Saboret, L.; Schroedter-Homscheidt, M.; et al. Fast radiative transfer parameterisation for assessing the surface solar irradiance: The Heliosat 4 method. Meteorol. Z. 2017, 26, 33–57. [Google Scholar] [CrossRef]
  49. Gschwind, B.; Wald, L.; Blanc, P.; Lefèvre, M.; Schroedter-Homscheidt, M.; Arola, A. Improving the McClear model estimating the downwelling solar radiation at ground level in cloud-free conditions—McClear v3. Meteorol. Z. 2019, 28, 147–163. [Google Scholar] [CrossRef]
  50. Lefèvre, M.; Oumbe, A.; Blanc, P.; Espinar, B.; Gschwind, B.; Qu, Z.; Wald, L.; Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Arola, A.; et al. McClear: A new model estimating downwelling solar radiation at ground level in clear-sky conditions. Atmos. Meas. Tech. 2013, 6, 2403–2418. [Google Scholar] [CrossRef]
  51. McCree, K.J. The action spectrum, absorptance and quantum yield of photosynthesis in crop plants. Agric. Meteorol. 1971, 9, 191–216. [Google Scholar] [CrossRef]
  52. Spitters, C.J.T.; Toussaint, H.A.J.M.; Goudriaan, J. Separating the diffuse and direct component of global radiation and its implications for modeling canopy photosynthesis Part I. Components of incoming radiation. Agric. For. Meteorol. 1986, 38, 217–229. [Google Scholar] [CrossRef]
  53. Nyamsi, W.W.; Espinar, B.; Blanc, P.; Wald, L. Estimating the photosynthetically active radiation under clear skies by means of a new approach. Adv. Sci. Res. 2015, 12, 5–10. [Google Scholar] [CrossRef]
  54. García-Rodríguez, A.; García-Rodríguez, S.; Díez-Mediavilla, M.; Alonso-Tristán, C. Photosynthetic Active Radiation, Solar Irradiance and the CIE Standard Sky Classification. Appl. Sci. 2020, 10, 8007. [Google Scholar] [CrossRef]
  55. Thimijan, R.W.; Heins, R.D.; Thimijan, R.W.; Heins, R.D. Photometric, Radiometric, and Quantum Light Units of Measure: A Review of Procedures for Interconversion. HortScience 1983, 18, 818–822. [Google Scholar] [CrossRef]
  56. Sager, J.C.; McFarlane, J.C. Radiation. In NorthCentral Regional Research Publication; Iowa State University: Ames, IA, USA, 1997. [Google Scholar]
  57. Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
  58. Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
  59. Tay, J.K.; Narasimhan, B.; Hastie, T. Elastic Net Regularization Paths for All Generalized Linear Models. J. Stat. Softw. 2023, 106, 1–31. [Google Scholar] [CrossRef]
  60. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  61. Silva, M.L.; da Silva, A.R.A.; de Moura Neto, J.M.; Calou, V.B.C.; Fernandes, C.N.V.; Araújo, E.M. Enhanced Water Monitoring and Corn Yield Prediction Using Rpa-Derived Imagery. Eng. Agríc. 2025, 45, e20240092. [Google Scholar] [CrossRef]
  62. Choroś, T.; Oberski, T.; Kogut, T. UAV imaging at RGB for crop condition monitoring. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2020, 43, 1521–1525. [Google Scholar] [CrossRef]
  63. Thapa, S.; Rudd, J.C.; Xue, Q.; Bhandari, M.; Reddy, S.K.; Jessup, K.E.; Liu, S.; Devkota, R.N.; Baker, J.; Baker, S. Use of NDVI for characterizing winter wheat response to water stress in a semi-arid environment. J. Crop Improv. 2019, 33, 633–648. [Google Scholar] [CrossRef]
  64. Sharma, N.; Kumar, M.; Daetwyler, H.D.; Trethowan, R.M.; Hayden, M.; Kant, S. Phenotyping for heat stress tolerance in wheat population using physiological traits, multispectral imagery, and machine learning approaches. Plant Stress 2024, 14, 100593. [Google Scholar] [CrossRef]
  65. Descals, A.; Torres, K.; Verger, A.; Peñuelas, J. Evaluating Sentinel-2 for Monitoring Drought-Induced Crop Failure in Winter Cereals. Remote Sens. 2025, 17, 340. [Google Scholar] [CrossRef]
  66. Mahlein, A.K. Plant disease detection by imaging sensors—Parallels and specific demands for precision agriculture and plant phenotyping. Plant Dis. 2016, 100, 241–254. [Google Scholar] [CrossRef]
Agronomy 15 01583 g001
Figure 1. Schematic of the principles of the data pre-processing under test in this study.
Figure 1. Schematic of the principles of the data pre-processing under test in this study.
Agronomy 15 01583 g001
Agronomy 15 01583 g002
Figure 2. A visual example of 3 of the 15 alignment and scaling methods used. It shows progression of aligning and scaling allowing for the creation of overlapping sampling points. Black drone icons represent real flights, and red-dashed lines are the four calculated equidistant interpolation timepoints.
Figure 2. A visual example of 3 of the 15 alignment and scaling methods used. It shows progression of aligning and scaling allowing for the creation of overlapping sampling points. Black drone icons represent real flights, and red-dashed lines are the four calculated equidistant interpolation timepoints.
Agronomy 15 01583 g002
Agronomy 15 01583 g003
Figure 3. XY plot for the highest ranked random forest regression model for adjusted grain yield and heatmap of importance of each sensor and timepoint in the model.
Figure 3. XY plot for the highest ranked random forest regression model for adjusted grain yield and heatmap of importance of each sensor and timepoint in the model.
Agronomy 15 01583 g003
Agronomy 15 01583 g004
Figure 4. Confusion matrix representing the ground truth vs. predicted adjusted yield within-trial class from the highest ranked classification model, and heatmap showing the importance of each sensor value and interpolation timepoint.
Figure 4. Confusion matrix representing the ground truth vs. predicted adjusted yield within-trial class from the highest ranked classification model, and heatmap showing the importance of each sensor value and interpolation timepoint.
Agronomy 15 01583 g004
Agronomy 15 01583 g005
Figure 5. XY plot for the highest ranked random forest regression model for plant height and heatmap of importance of each sensor and timepoint in the model.
Figure 5. XY plot for the highest ranked random forest regression model for plant height and heatmap of importance of each sensor and timepoint in the model.
Agronomy 15 01583 g005
Agronomy 15 01583 g006
Figure 6. Confusion matrix representing the ground truth vs. predicted plant height within-trial class from the highest ranked classification model, and heatmap showing the importance of each sensor value and interpolation timepoint.
Figure 6. Confusion matrix representing the ground truth vs. predicted plant height within-trial class from the highest ranked classification model, and heatmap showing the importance of each sensor value and interpolation timepoint.
Agronomy 15 01583 g006
Agronomy 15 01583 g007
Figure 7. Confusion matrix representing the ground truth vs. predicted milling quality within-trial class from the highest ranked classification model, and heatmap showing the importance of each sensor value and interpolation timepoint.
Figure 7. Confusion matrix representing the ground truth vs. predicted milling quality within-trial class from the highest ranked classification model, and heatmap showing the importance of each sensor value and interpolation timepoint.
Agronomy 15 01583 g007
Agronomy 15 01583 g008
Figure 8. XY plot for the highest ranked regression model for groat protein content and heatmap showing the identity of the sensor and timepoint, and values of the non-zero coefficients. Groat protein content is the only outcome variable in this study for which LASSO regression outperformed random forest regression.
Figure 8. XY plot for the highest ranked regression model for groat protein content and heatmap showing the identity of the sensor and timepoint, and values of the non-zero coefficients. Groat protein content is the only outcome variable in this study for which LASSO regression outperformed random forest regression.
Agronomy 15 01583 g008
Agronomy 15 01583 g009
Figure 9. Confusion matrix representing the ground truth vs. predicted groat protein content within-trial class from the highest ranked classification model, and heatmap showing the importance of each sensor value and interpolation timepoint.
Figure 9. Confusion matrix representing the ground truth vs. predicted groat protein content within-trial class from the highest ranked classification model, and heatmap showing the importance of each sensor value and interpolation timepoint.
Agronomy 15 01583 g009
Agronomy 15 01583 g010
Figure 10. Confusion matrix representing the ground truth vs. predicted groat oil content within-trial class from the highest ranked classification model, and heatmap showing the importance of each sensor value and interpolation timepoint.
Figure 10. Confusion matrix representing the ground truth vs. predicted groat oil content within-trial class from the highest ranked classification model, and heatmap showing the importance of each sensor value and interpolation timepoint.
Agronomy 15 01583 g010
Agronomy 15 01583 g011
Figure 11. XY plot for the highest ranked regression model for test weight and heatmap showing the importance of each sensor value and interpolation timepoint.
Figure 11. XY plot for the highest ranked regression model for test weight and heatmap showing the importance of each sensor value and interpolation timepoint.
Agronomy 15 01583 g011
Agronomy 15 01583 g012
Figure 12. Confusion matrix representing the ground truth vs. predicted test weight within-trial class from the highest ranked classification model, and heatmap showing the importance of each sensor value and interpolation timepoint.
Figure 12. Confusion matrix representing the ground truth vs. predicted test weight within-trial class from the highest ranked classification model, and heatmap showing the importance of each sensor value and interpolation timepoint.
Agronomy 15 01583 g012
Table 1. Description of some of the key breeding targets for milling oats in the United Kingdom.
Table 1. Description of some of the key breeding targets for milling oats in the United Kingdom.
TraitCrop Ontology Trait IDDescriptionBreeding Target for UK Milling Oats
Plant Height (cm)CO_350:0000232Height of plant from the ground to tip of the panicleDecrease
(plants with short, stiff straw desirable)
Grain Yield (t/ha)CO_350:0000260Total weight of grains harvested per unit areaIncrease
Kernel Content (%)CO_350:0000162Percentage weight of harvested grain attributed to the valuable oat kernel/groat rather than the less valuable fibrous husk (which is removed during processing)Increase
Hullability (%)CO_350:0005066Weight of seed that is effectively dehulled via a standardised mechanical process as a percentage of the total weight of the sampleIncrease
Screenings (%)n/aPercentage weight of harvested grain that is less than 2.0 mm in widthDecrease
(plump, round, and uniformly sized grains desirable)
Specific Weight (kg/hL)CO_350:0000259Measurement of the weight of grain per unit volumeIncrease
Thousand Grain Weight (g, as-is)CO_350:0000251Weight of 1000 representative whole grainsIncrease
Beta-glucan Content (%)CO_350:0005065Amount of beta-glucan present in the groat expressed as a percentage of the entire groat weightIncrease
Protein Content (%)CO_350:0000164The amount of protein in the groat, expressed as a percentage of the groat weightIncrease
Oil Content (%)CO_350:0000163The amount of oil in the groat, expressed as a percentage of the groat weightDecrease
Table 2. Properties of the trials from which UAS and ground truth data was taken for this study.
Table 2. Properties of the trials from which UAS and ground truth data was taken for this study.
Trial AliasHarvest YearCropTrial TypeSowing DateTotal Plots
br_h212021Winter OatsCommercial advanced breeding linesWeek 41, 2020395
sa_h212021Spring OatsNitrogen response trial, commercial varietiesWeek 12, 202154
br_h222022Winter OatsCommercial advanced breeding linesWeek 40, 2021393
cd_h222022Facultative OatsMixed commercial varieties and advanced breeding linesWeek 41, 2021300
ho_h222022Spring OatsMixed commercial and heritage varietiesWeek 12, 202275
br_h232023Winter OatsCommercial crosses for breeding programmesWeek 41, 2022393
cd_h232023Facultative OatsMixed commercial varieties and advanced breeding linesWeek 42, 2022300
ho_h232023Spring OatsMixed commercial varieties and advanced breeding linesWeek 16, 202375
Table 3. Average differences from ablated models vs. models trained on data from all sensors, and the associated significance level from Bonferroni-adjusted p-values.
Table 3. Average differences from ablated models vs. models trained on data from all sensors, and the associated significance level from Bonferroni-adjusted p-values.
Removed SensorAverage Difference from Fully Trained Model
LASSO Regression
R2		Random Forest Regression
R2 		Random Forest Classification Accuracy (%)
Red−0.004 ***−0.002 ***−0.08 ns
Green−0.005 ***−0.001 ns0.05 ns
Blue−0.011 ***−0.009 ***−0.79 ***
Red Narrow−0.010 ***−0.004 ***−0.36 ns
Reg Edge−0.012 ***−0.002 ***−0.58 **
NIR−0.015 ***−0.013 ***−0.99 ***
t-test or Wilcoxon signed-rank test adjusted p-values ≤0.001 = ***, ≤0.01 = **, >0.05 = ns.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Evershed, D.; Brook, J.; Cowan, S.; Griffiths, I.; Tudor, S.; Loosley, M.; Doonan, J.H.; Howarth, C.J. Photothermal Integration of Multi-Spectral Imaging Data via UAS Improves Prediction of Target Traits in Oat Breeding Trials. Agronomy 2025, 15, 1583. https://doi.org/10.3390/agronomy15071583

AMA Style

Evershed D, Brook J, Cowan S, Griffiths I, Tudor S, Loosley M, Doonan JH, Howarth CJ. Photothermal Integration of Multi-Spectral Imaging Data via UAS Improves Prediction of Target Traits in Oat Breeding Trials. Agronomy. 2025; 15(7):1583. https://doi.org/10.3390/agronomy15071583

Chicago/Turabian Style

Evershed, David, Jason Brook, Sandy Cowan, Irene Griffiths, Sara Tudor, Marc Loosley, John H. Doonan, and Catherine J. Howarth. 2025. "Photothermal Integration of Multi-Spectral Imaging Data via UAS Improves Prediction of Target Traits in Oat Breeding Trials" Agronomy 15, no. 7: 1583. https://doi.org/10.3390/agronomy15071583

APA Style

Evershed, D., Brook, J., Cowan, S., Griffiths, I., Tudor, S., Loosley, M., Doonan, J. H., & Howarth, C. J. (2025). Photothermal Integration of Multi-Spectral Imaging Data via UAS Improves Prediction of Target Traits in Oat Breeding Trials. Agronomy, 15(7), 1583. https://doi.org/10.3390/agronomy15071583

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop