PSO-Based System Identification and Fuzzy-PID Control for EC Real-Time Regulation in Fertilizer Mixing System
Abstract
:1. Introduction
2. Materials and Methods
2.1. EC Control System
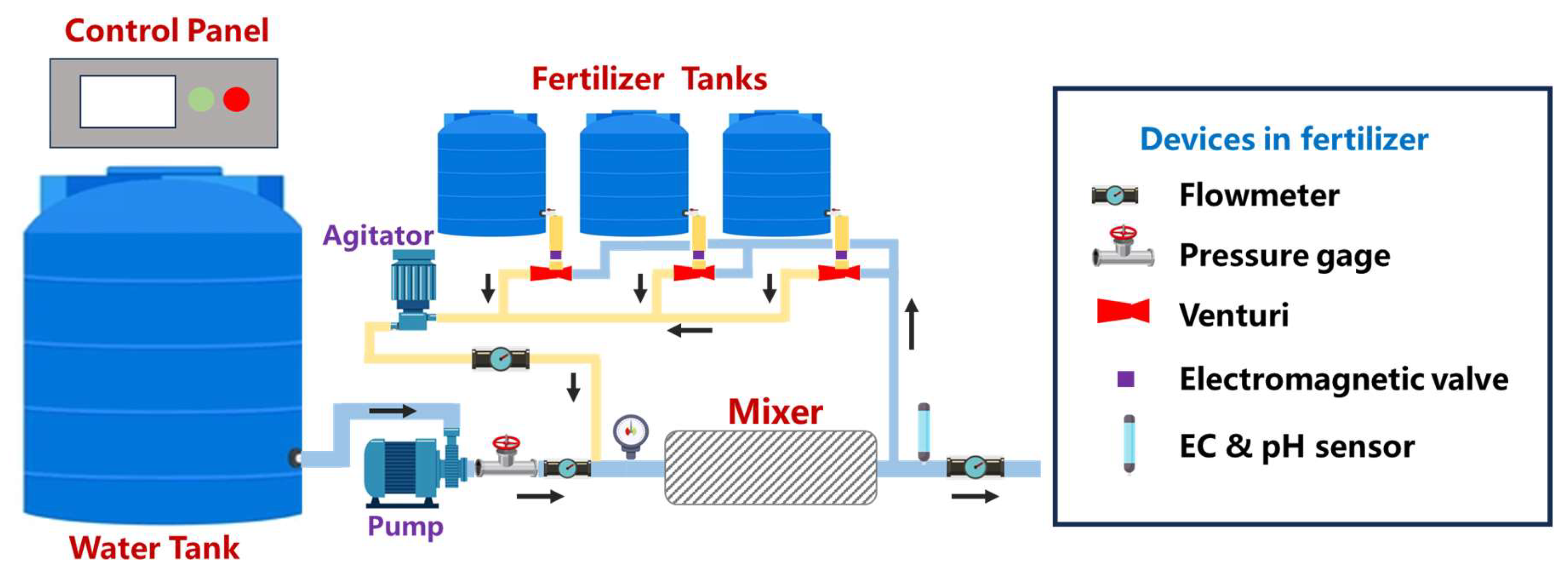
2.2. Description of the Fertigation System
2.3. System Identification of the Fertigation Process
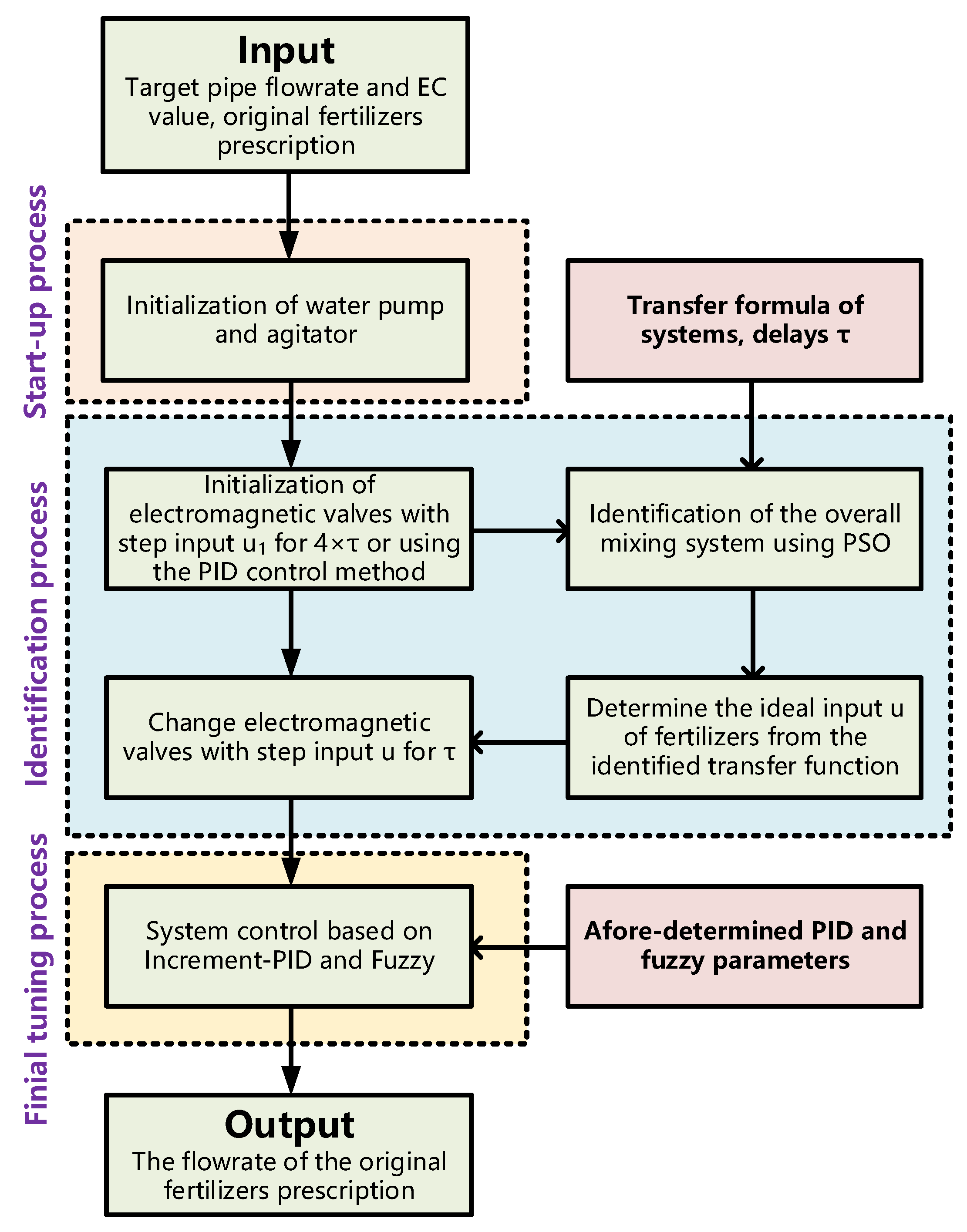
2.4. General Control Strategy of the Fertigation System
3. Results
3.1. Fertigation Performance and System Identification
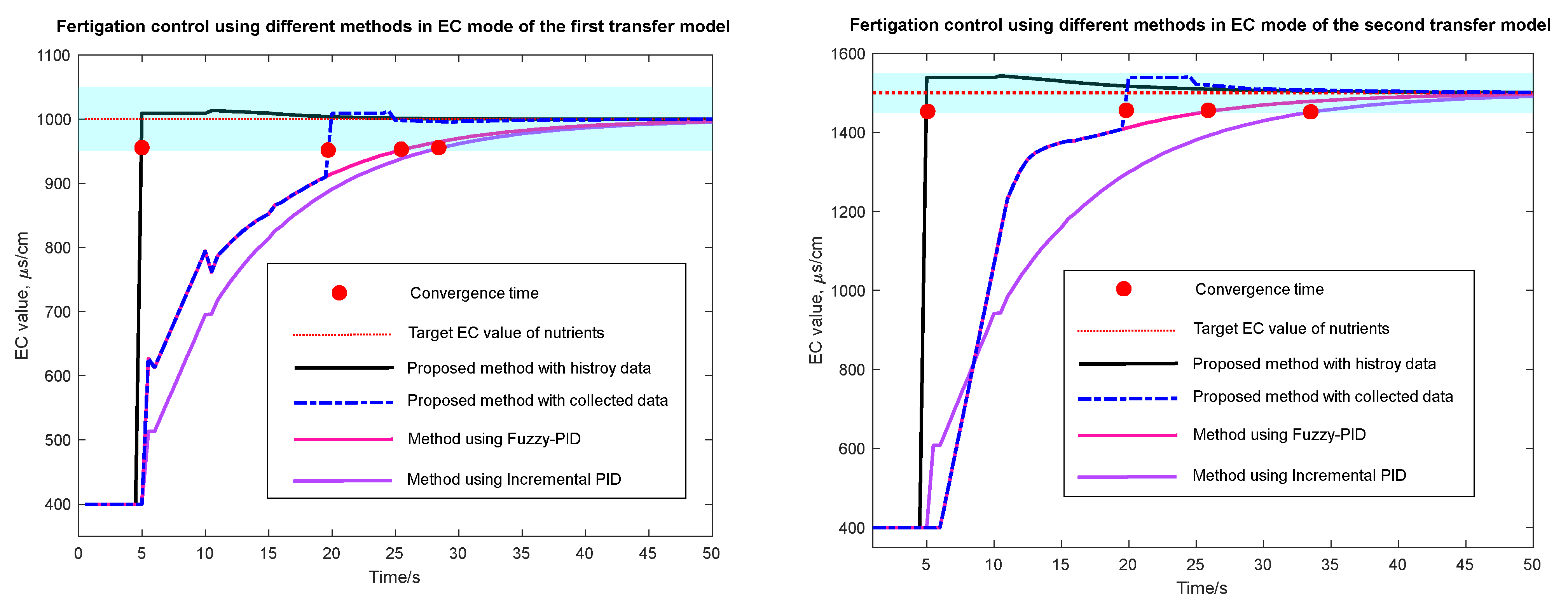
3.2. Simulation of Fertigation Control in EC Mode
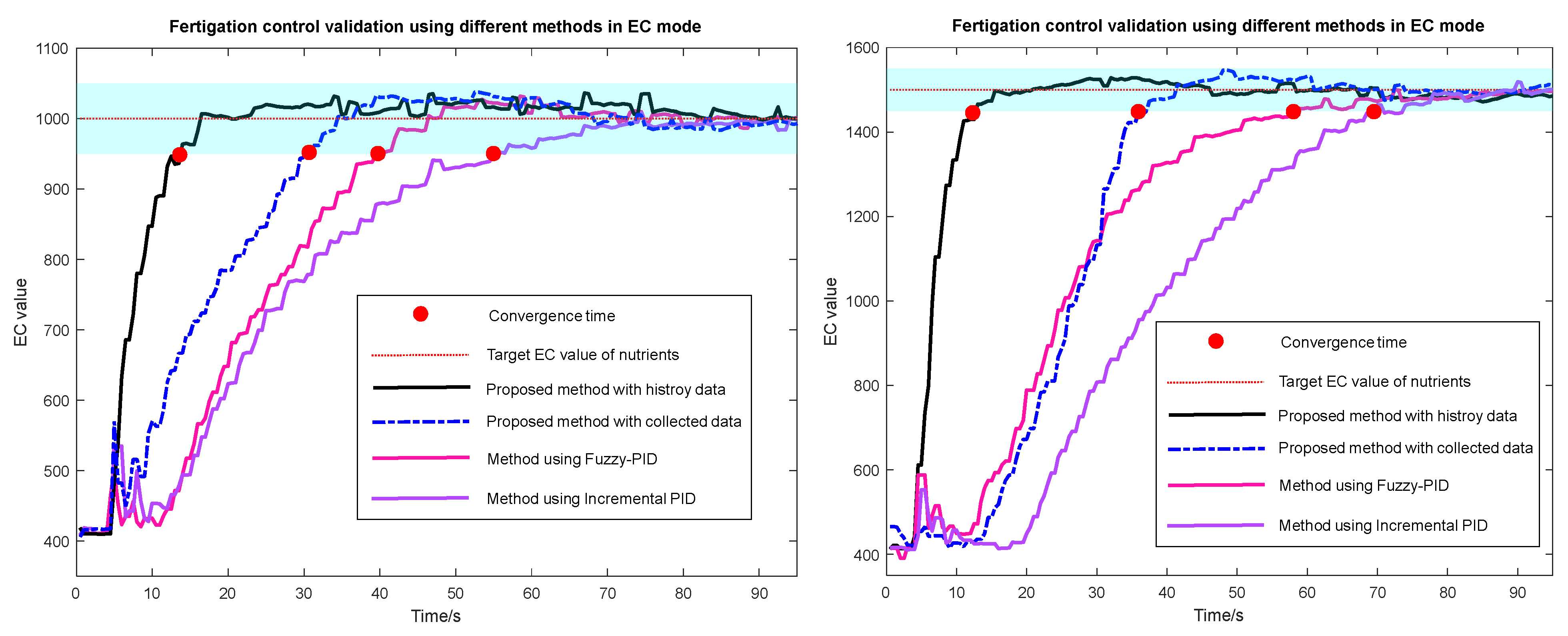
3.3. Test Validation of the Proposed EC Control Strategy
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Incrocci, L.; Massa, D.; Pardossi, A. New Trends in the Fertigation Management of Irrigated Vegetable Crops. Horticulturae 2017, 3, 37. [Google Scholar] [CrossRef]
- Rubio-Asensio, J.S.; Intrigliolo, D.S. Fertigation frequency is a useful tool for nitrate management in intensive open-field agriculture. Irrig. Sci. 2024, 42, 353–365. [Google Scholar] [CrossRef]
- He, J.; Wang, Y.; Liang, W.; Rasouli, F.; Li, L.; Bose, J.; Donovan-Mak, M.; Huda, S.; Jayasena, V.; Chen, Z.H.; et al. Optimised fertigation improves yield and quality of cucumbers for resource efficiency and economic return in high-tech greenhouses. J. Agric. Food Res. 2025, 19, 101699. [Google Scholar] [CrossRef]
- Howe, J.A.; McDonald, M.D.; Burke, J.; Robertson, I.; Coker, H.; Gentry, T.J.; Lewis, K.L. Influence of fertilizer and manure inputs on soil health: A review. Soil Secur. 2024, 16, 100155. [Google Scholar] [CrossRef]
- Kushwah, N.; Billore, V.; Sharma, O.P.; Singh, D.; Chauhan, A.P.S. Integrated Nutrient management for optimal plant health and crop yield. Plant Sci. Arch. 2023, 8, 10–12. [Google Scholar] [CrossRef]
- Singh, K.A.P.; Goutam, P.K.; Xaxa, S.; Nasima; Pandey, S.K.; Panotra, N.; Rajesh, G.M. The Role of Greenhouse Technology in Streamlining Crop Production. J. Exp. Agric. Int. 2024, 46, 776–798. [Google Scholar] [CrossRef]
- Dudala, S.; Dubey, S.K.; Goel, S. Microfluidic Soil Nutrient Detection System: Integrating Nitrite, pH, and Electrical Conductivity Detection. IEEE Sens. J. 2020, 20, 4504–4511. [Google Scholar] [CrossRef]
- Hutchinson, G.K.; Nguyen, L.X.; Rubio Ames, Z.; Nemali, K.; Ferrarezi, R.S. Sensor-controlled fertigation management for higher yield and quality in greenhouse hydroponic strawberries. Front. Plant Sci. 2025, 15, 1469434. [Google Scholar] [CrossRef] [PubMed]
- Maraveas, C.; Piromalis, D.; Arvanitis, K.G.; Bartzanas, T.; Loukatos, D. Applications of IoT for optimized greenhouse environment and resources management. Comput. Electron. Agric. 2022, 198, 106993. [Google Scholar] [CrossRef]
- Kayadibi, İ. An IoT-driven framework based on sensor technology for smart greenhouses and precision agriculture. Int. J. Smart Sens. Intell. Syst. 2025, 18, 1–13. [Google Scholar] [CrossRef]
- Sulaiman, H.; Yusof, A.A.; Mohamed Nor, M.K. Automated Hydroponic Nutrient Dosing System: A Scoping Review of pH and Electrical Conductivity Dosing Frameworks. AgriEngineering 2025, 7, 43. [Google Scholar] [CrossRef]
- Steidle Neto, A.J.; Zolnier, S.; de Carvalho Lopes, D. Development and evaluation of an automated system for fertigation control in soilless tomato production. Comput. Electron. Agric. 2014, 103, 17–25. [Google Scholar] [CrossRef]
- Giannoccaro, N.I.; Persico, G.; Strazzella, S.; Lay-Ekuakille, A.; Visconti, P. A System for Optimizing Fertilizer Dosing in Innovative Smart Fertigation Pipelines: Modeling, Construction, Testing and Control. Int. J. Precis. Eng. Manuf. 2020, 21, 1581–1596. [Google Scholar] [CrossRef]
- Wu, Y.; Li, L.; Li, S.; Wang, H.; Zhang, M.; Sun, H.; Sygrimis, N.; Li, M. Optimal control algorithm of fertigation system in greenhouse based on EC model. Int. J. Agric. Biol. Eng. 2019, 12, 118–125. [Google Scholar] [CrossRef]
- Zhou, R.; Zhang, L.; Fu, C.; Wang, H.; Meng, Z.; Du, C.; Shan, Y.; Bu, H. Fuzzy Neural Network PID Strategy Based on PSO Optimization for pH Control of Water and Fertilizer Integration. Appl. Sci. 2022, 12, 7383. [Google Scholar] [CrossRef]
- Dun, G.; Wu, X.; Ji, X.; Wei, Y. Design and Experiment of an Electric Control Spiral-Pushing Feed Mechanism for Field Fertilizer Applicator. Appl. Sci. 2023, 13, 12628. [Google Scholar] [CrossRef]
- Kyriakopoulos, G.L.; Huynh, H.X.; Tran, L.N.; Duong-Trung, N. Smart greenhouse construction and irrigation control system for optimal Brassica juncea development. PLoS ONE 2023, 18, e0292971. [Google Scholar] [CrossRef]
- Baha, V.; Piteľ, J.; Pavlenko, I. Analytical, Numerical, and Experimental Studies of the Working Process in a Pneumatic Abrasive Installation. Appl. Sci. 2024, 14, 11728. [Google Scholar] [CrossRef]
- Tang, P.; Zhang, Z. Structural Optimization Based on Response Surface Methodology for the Venturi Injector Used in Fertigation System. Horticulturae 2025, 11, 223. [Google Scholar] [CrossRef]
- aya Olalla, E.; Lopez Flores, A.; Zambrano, M.; Domínguez Limaico, M.; Diaz Iza, H.; Vasquez Ayala, C. Fuzzy Control Application to an Irrigation System of Hydroponic Crops under Greenhouse: Case Cultivation of Strawberries (Fragaria vesca). Sensors 2023, 23, 4088. [Google Scholar] [CrossRef]
- Zhou, W.; An, T.; Wang, J.; Fu, Q.; Wen, N.; Sun, X.; Wang, Q.; Liu, Z. Design and Experiment of a Targeted Variable Fertilization Control System for Deep Application of Liquid Fertilizer. Agronomy 2023, 13, 1687. [Google Scholar] [CrossRef]
- Mihalache, G.; Peres, C.I.; Bodale, I.; Achitei, V.; Gheorghitoaie, M.V.; Teliban, G.C.; Cojocaru, A.; Butnariu, M.; Muraru, V.; Stoleru, V. Tomato Crop Performances under Chemical Nutrients Monitored by Electric Signal. Agronomy 2020, 10, 1915. [Google Scholar] [CrossRef]
- Song, X.; Li, H.; Chen, C.; Xia, H.; Zhang, Z.; Tang, P. Design and Experimental Testing of a Control System for a Solid-Fertilizer-Dissolving Device Based on Fuzzy PID. Agriculture 2022, 12, 1382. [Google Scholar] [CrossRef]
- Fu, C.; Ma, X.; Zhang, L. Fuzzy-PID Strategy Based on PSO Optimization for pH Control in Water and Fertilizer Integration. IEEE Access 2022, 10, 4471–4482. [Google Scholar] [CrossRef]
- Jaiswal, S.; Ballal, M.S. Fuzzy inference based irrigation controller for agricultural demand side management. Comput. Electron. Agric. 2020, 175, 105537. [Google Scholar] [CrossRef]
- Shan, Y.; Zhang, L.; Ma, X.; Hu, X.; Hu, Z.; Li, H.; Du, C.; Meng, Z. Application of the Modified Fuzzy-PID-Smith Predictive Compensation Algorithm in a pH-Controlled Liquid Fertilizer System. Processes 2021, 9, 1506. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, L.; Wang, H.; Hu, X.; Zhao, J.; Zhu, F.; Wu, X. Research and Design of Improved Wild Horse Optimizer-Optimized Fuzzy Neural Network PID Control Strategy for EC Regulation of Cotton Field Water and Fertilizer Systems. Agriculture 2023, 13, 2176. [Google Scholar] [CrossRef]
- Mohindru, P. Review on PID, fuzzy and hybrid fuzzy PID controllers for controlling non-linear dynamic behaviour of chemical plants. Artif. Intell. Rev. 2024, 57, 97. [Google Scholar] [CrossRef]
- Kisi, O.; Parmar, K.S.; Yaseen, Z.M.; Kim, S. Modeling Wetting Front Redistribution of Drip Irrigation Systems Using a New Machine Learning Method: Adaptive Neuro-Fuzzy System Improved by Hybrid Particle Swarm Optimization–Gravity Search Algorithm. Agric. Water Manag. 2021, 256, 107067. [Google Scholar] [CrossRef]
- Heinen, M.; Marcelis, L.F.M.; Elings, A.; Figueroa, R. Effects of Ec and Fertigation Strategy on Water and Nutrient Uptake of Tomato Plants. Acta Hortic. 2002, 593, 101–107. [Google Scholar] [CrossRef]
- Ren, X.; Lu, N.; Xu, W.; Zhuang, Y.; Takagaki, M. Optimization of the Yield, Total Phenolic Content, and Antioxidant Capacity of Basil by Controlling the Electrical Conductivity of the Nutrient Solution. Horticulturae 2022, 8, 216. [Google Scholar] [CrossRef]
- Han, L.; Wang, Z.; He, X. Development of an Energy-Saving PWM Driving Method for Precision Pesticide Application Using Adjustable Frequency and Characterization of Spray. Comput. Electron. Agric. 2024, 217, 108634. [Google Scholar] [CrossRef]



| EC Error Change Rate | Difference Between the Measured and Target Value | ||||||
|---|---|---|---|---|---|---|---|
| NB | NM | NS | Z | PS | PM | PB | |
| NB | Z | Z | NM | NM | NM | NB | NB |
| NM | NS | Z | NS | NS | NM | NM | NB |
| NS | PS | PS | Z | NS | NS | NM | NM |
| Z | PM | PM | PS | Z | NS | NS | NM |
| PS | PM | PM | PM | PS | Z | NS | NS |
| PM | PB | PB | PM | PM | PS | Z | NS |
| PB | PB | PB | PM | PM | PS | Z | Z |
| PSO Number × Iteration | Time, s | RMSE, μs/cm | MAPE, % |
|---|---|---|---|
| 5 × 5 | 0.07 | 82.01 | 4.30 |
| 10 × 10 | 0.20 | 54.34 | 3.31 |
| 20 × 20 | 0.74 | 40.99 | 3.00 |
| 30 × 30 | 1.59 | 32.70 | 2.47 |
| 40 × 40 | 2.85 | 29.74 | 1.87 |
| 50 × 50 | 4.59 | 28.83 | 1.78 |
| PSO Number × Iteration | Time, s | RMSE, μs/cm | MAPE, % |
|---|---|---|---|
| 5 × 5 | 0.05 | 81.74 | 4.93 |
| 10 × 10 | 0.19 | 70.26 | 4.13 |
| 20 × 20 | 0.69 | 68.57 | 3.66 |
| 30 × 30 | 1.54 | 66.93 | 3.69 |
| 40 × 40 | 2.67 | 66.75 | 3.73 |
| 50 × 50 | 4.22 | 67.03 | 3.78 |
| Test Number/Time, s | ① | ② | ③ | ④ |
|---|---|---|---|---|
| 1 | 5 ± 1 | 20 ± 1 | 25 ± 1 | 28 ± 1 |
| 2 | 5 ± 1 | 20 ± 1 | 25 ± 1 | 32 ± 1 |
| Test Number/Time, s | ① | ② | ③ | ④ |
|---|---|---|---|---|
| 1 | 16 ± 1 | 34 ± 1 | 46 ± 1 | 74 ± 1 |
| 2 | 15 ± 1 | 41 ± 1 | 62 ± 1 | 77 ± 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Jin, Y.; Sun, Z.; Xue, X. PSO-Based System Identification and Fuzzy-PID Control for EC Real-Time Regulation in Fertilizer Mixing System. Agronomy 2025, 15, 1259. https://doi.org/10.3390/agronomy15051259
Xu Y, Jin Y, Sun Z, Xue X. PSO-Based System Identification and Fuzzy-PID Control for EC Real-Time Regulation in Fertilizer Mixing System. Agronomy. 2025; 15(5):1259. https://doi.org/10.3390/agronomy15051259
Chicago/Turabian StyleXu, Yang, Yongkui Jin, Zhu Sun, and Xinyu Xue. 2025. "PSO-Based System Identification and Fuzzy-PID Control for EC Real-Time Regulation in Fertilizer Mixing System" Agronomy 15, no. 5: 1259. https://doi.org/10.3390/agronomy15051259
APA StyleXu, Y., Jin, Y., Sun, Z., & Xue, X. (2025). PSO-Based System Identification and Fuzzy-PID Control for EC Real-Time Regulation in Fertilizer Mixing System. Agronomy, 15(5), 1259. https://doi.org/10.3390/agronomy15051259






