Estimation of Reference Crop Evapotranspiration in the Yellow River Basin Based on Machine Learning and Its Regional and Drought Adaptability Analysis
Abstract
1. Introduction
2. Material and Methods
2.1. Study Area Overview
2.2. Data Acquisition and Preprocessing
2.2.1. Meteorological Data
2.2.2. Climatic Zonation
2.2.3. Drought Year Identification
2.3. ET0 Calculation Method
2.3.1. Penman–Monteith Equation
2.3.2. Priestley–Taylor and Hargreaves Equation
2.3.3. Machine Learning Models
2.4. Data Analysis and Model Evaluation
2.4.1. Data Analysis
2.4.2. Model Evaluation
3. Results
3.1. Trends in ET0 and Its Influencing Factors in the Yellow River Basin
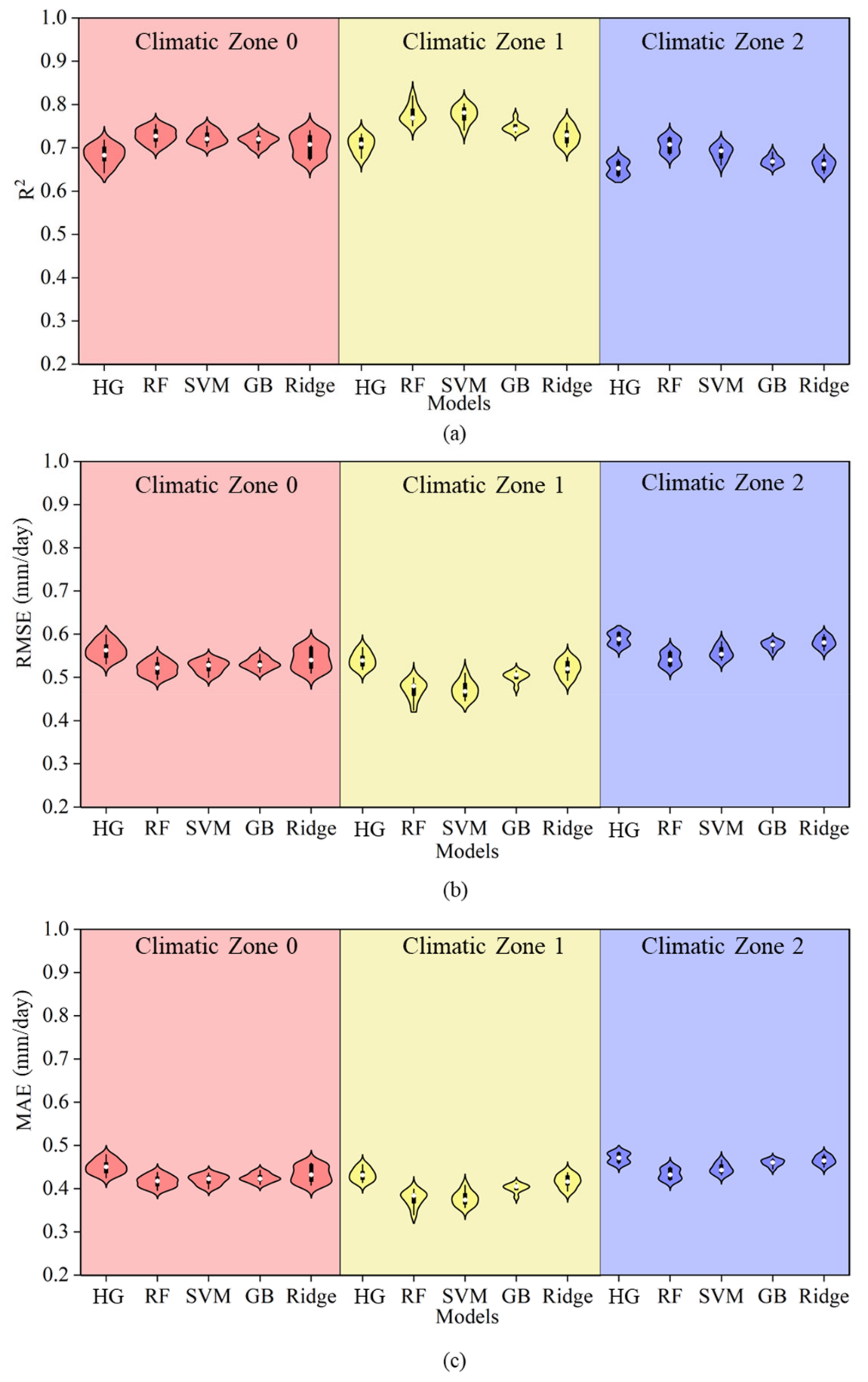
3.2. Comparison of Machine Learning Models and PT Equation
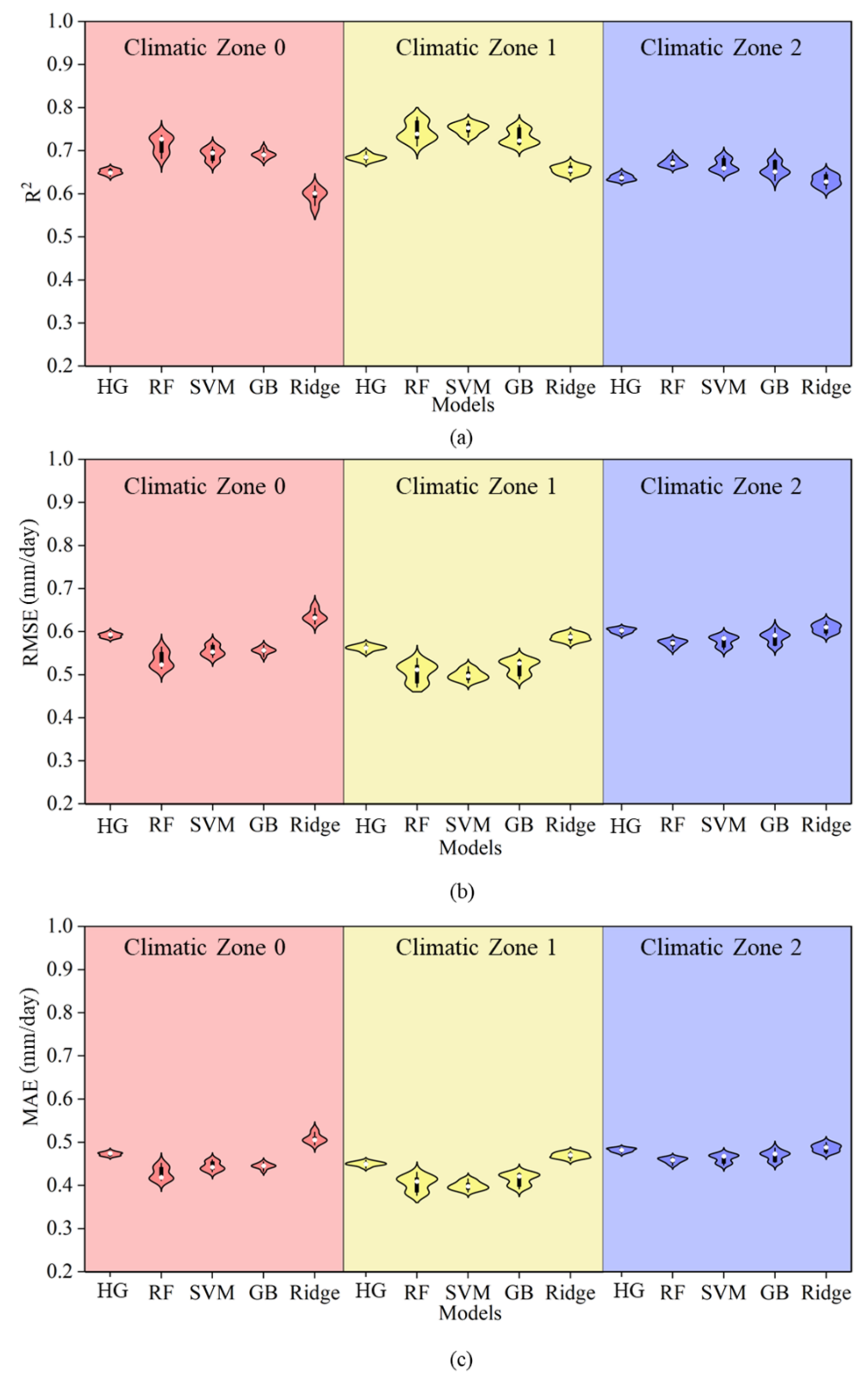
3.3. Comparison of Machine Learning Models and the HG Equation
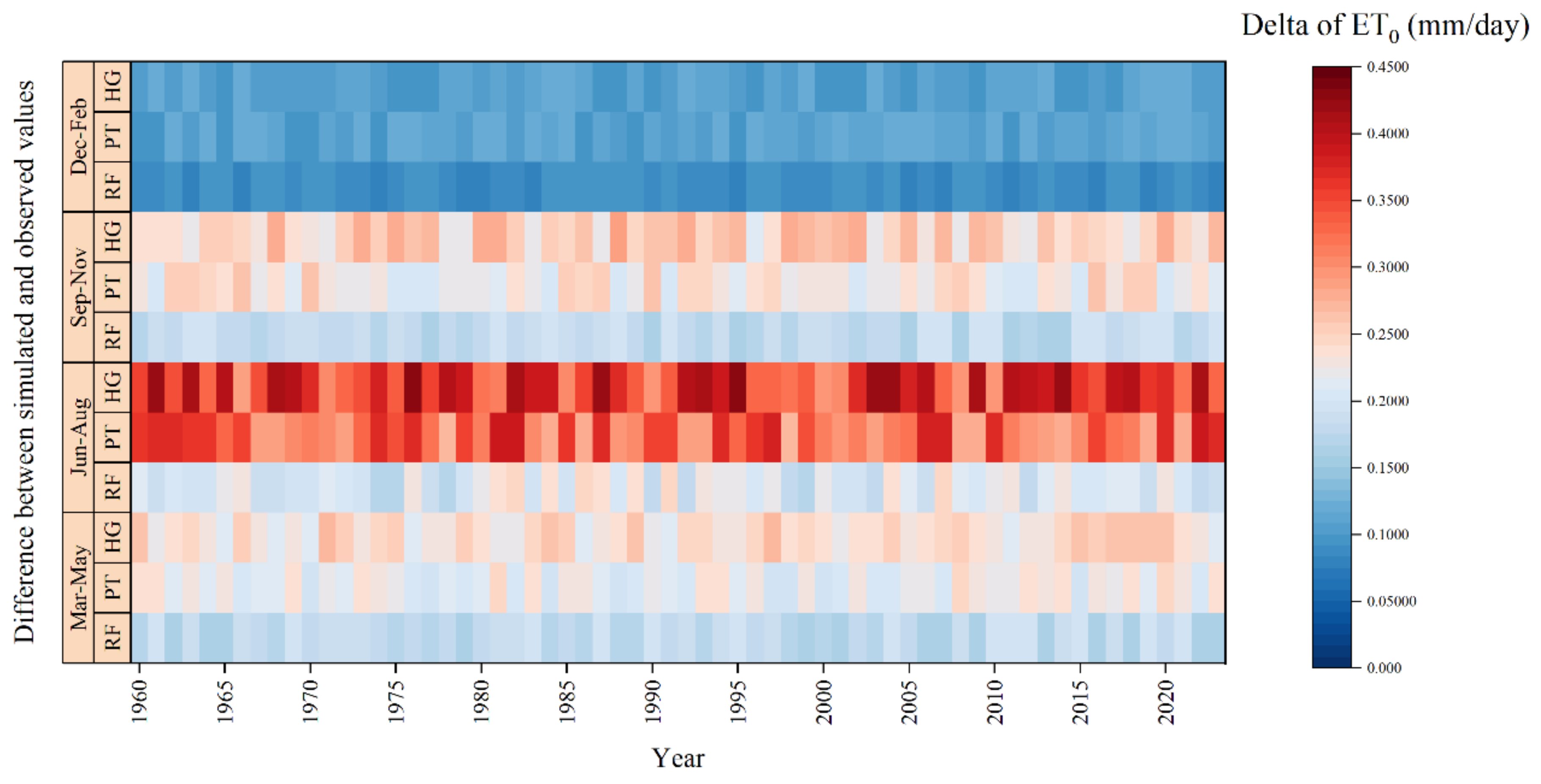
3.4. Error Between Simulated and Observed Values
4. Discussion
4.1. Comparison of ET0 Estimation Accuracy Under Strategy 1
4.2. Impact of Drought Stress on Model Accuracy in ET0 Estimation
4.3. Uncertainty and Perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, L.; Liu, J.; Peng, Q.; Wang, X.; Xu, J.; Cai, H. Propagation process-based agricultural drought typology and its copula-based risk. Irrig. Drain. 2024, 73, 1496–1519. [Google Scholar] [CrossRef]
- Qin, C.; Guo, W.; Liu, Y.; Liu, Z.; Qiu, J.; Peng, J. A novel electrochemical sensor based on graphene oxide decorated with silver nanoparticles–molecular imprinted polymers for determination of sunset yellow in soft drinks. Food Anal. Methods 2017, 10, 2293–2301. [Google Scholar] [CrossRef]
- Kenawy, A.E.; Al-Awadhi, T.; Abdullah, M.; Ostermann, F.O.; Abulibdeh, A. A Multidecadal Assessment of Drought Intensification in the Middle East and North Africa: The Role of Global Warming and Rainfall Deficit. Earth Syst. Environ. 2025, 1–20. [Google Scholar] [CrossRef]
- Yang, Z.; Solangi, Y.A. Analyzing the relationship between natural resource management, environmental protection, and agricultural economics for sustainable development in China. J. Clean. Prod. 2024, 450, 141862. [Google Scholar] [CrossRef]
- Yan, H.; Acquah, S.J.; Zhang, J.; Wang, G.; Zhang, C.; Darko, R.O. Overview of modelling techniques for greenhouse microclimate environment and evapotranspiration. Int. J. Agric. Biol. Eng. 2021, 14, 1–8. [Google Scholar] [CrossRef]
- Zhang, C.; Li, L.; Yan, H.; Ou, M.; Akhlaq, M.; Zhang, W.; Huang, S. Calibration and validation of three evapotranspiration models in a tea field in the humid region of south-east China. Irrig. Drain. 2022, 71, 1254–1267. [Google Scholar] [CrossRef]
- Ippolito, M.; De Caro, D.; Cannarozzo, M.; Provenzano, G.; Ciraolo, G. Evaluation of daily crop reference evapotranspiration and sensitivity analysis of FAO Penman-Monteith equation using ERA5-Land reanalysis database in Sicily, Italy. Agric. Water Manag. 2024, 295, 108732. [Google Scholar] [CrossRef]
- Allen, R.G.; Pruitt, W.O.; Wright, J.L.; Howell, T.A.; Ventura, F.; Snyder, R.; Itenfisu, D.; Steduto, P.; Berengena, J.; Yrisarry, J.B. A recommendation on standardized surface resistance for hourly calculation of reference ETo by the FAO56 Penman-Monteith method. Agric. Water Manag. 2006, 81, 1–22. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Proc. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar]
- Sentelhas, P.C.; Gillespie, T.J.; Santos, E.A. Evaluation of FAO Penman–Monteith and alternative methods for estimating reference evapotranspiration with missing data in Southern Ontario, Canada. Agric. Water Manag. 2010, 97, 635–644. [Google Scholar] [CrossRef]
- Córdova, M.; Carrillo-Rojas, G.; Crespo, P.; Wilcox, B.; Célleri, R. Evaluation of the Penman-Monteith (FAO 56 PM) method for calculating reference evapotranspiration using limited data. Mt. Res. Dev. 2015, 35, 230–239. [Google Scholar] [CrossRef]
- Vakili, M.; Sabbagh-Yazdi, S.R.; Khosrojerdi, S.; Kalhor, K. Evaluating the effect of particulate matter pollution on estimation of daily global solar radiation using artificial neural network modeling based on meteorological data. J. Clean. Prod. 2017, 141, 1275–1285. [Google Scholar] [CrossRef]
- Utset, A.; Farre, I.; Martínez-Cob, A.; Cavero, J. Comparing Penman–Monteith and Priestley–Taylor approaches as reference-evapotranspiration inputs for modeling maize water-use under Mediterranean conditions. Agric. Water Manag. 2004, 66, 205–219. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, X.; Xue, X.; Feng, F.; Zheng, W.; Chen, L. Analyzing Evapotranspiration in Greenhouses: A Lysimeter-Based Calculation and Evaluation Approach. Agronomy 2023, 13, 3059. [Google Scholar] [CrossRef]
- Valiantzas, J.D. Temperature-and humidity-based simplified Penman’s ET0 formulae. Comparisons with temperature-based Hargreaves-Samani and other methodologies. Agric. Water Manag. 2018, 208, 326–334. [Google Scholar] [CrossRef]
- Bishop, K.; Shanley, J.B.; Riscassi, A.; de Wit, H.A.; Eklöf, K.; Meng, B.; Mitchell, C.; Osterwalder, S.; Schuster, P.F.; Webster, J. Recent advances in understanding and measurement of mercury in the environment: Terrestrial Hg cycling. Sci. Total Environ. 2020, 721, 137647. [Google Scholar] [CrossRef]
- Sun, M.; Yuan, W.; Liu, N.; Jia, L.; Wu, F.; Huang, J.-H.; Wang, X.; Feng, X. Combined Impacts of Climate and Tree Physiology on Mercury Accumulation in Tropical and Subtropical Foliage and Robust Model Parametrization. Environ. Sci. Technol. 2025, 59, 1661–1672. [Google Scholar] [CrossRef]
- Dong, C.; Zhu, H.; Wang, J.; Yuan, H.; Zhao, J.; Chen, Q. Prediction of black tea fermentation quality indices using NIRS and nonlinear tools. Food Sci. Biotechnol. 2017, 26, 853–860. [Google Scholar] [CrossRef]
- Han, F.; Huang, X.; Teye, E. Novel prediction of heavy metal residues in fish using a low-cost optical electronic tongue system based on colorimetric sensors array. J. Food Process Eng. 2019, 42, e12983. [Google Scholar] [CrossRef]
- Sládek, D.; Marková, L.; Talhofer, V. Towards Sustainable Urban Mobility: Leveraging Machine Learning Methods for QA of Meteorological Measurements in the Urban Area. Sustainability 2024, 16, 5713. [Google Scholar] [CrossRef]
- Yong, S.L.S.; Ng, J.L.; Huang, Y.F.; Ang, C.K. Estimation of reference crop evapotranspiration with three different machine learning models and limited meteorological variables. Agronomy 2023, 13, 1048. [Google Scholar] [CrossRef]
- Wang, G.; Yang, Y. Quantitative evaluation of digital economy policy in Heilongjiang Province of China based on the PMC-AE index model. Sage Open 2024, 14, 21582440241234435. [Google Scholar] [CrossRef]
- Shi, H.; Luo, G.; Hellwich, O.; Xie, M.; Zhang, C.; Zhang, Y.; Wang, Y.; Yuan, X.; Ma, X.; Zhang, W. Evaluation of water flux predictive models developed using eddy-covariance observations and machine learning: A meta-analysis. Hydrol. Earth Syst. Sci. 2022, 26, 4603–4618. [Google Scholar] [CrossRef]
- Available online: http://data.cma.cn (accessed on 11 November 2024).
- Huan, J.; Cao, W.; Liu, X. A dissolved oxygen prediction method based on k-means clustering and the elm neural network: A case study of the Changdang Lake, China. Appl. Eng. Agric. 2017, 33, 461–469. [Google Scholar] [CrossRef]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef]
- Available online: https://developers.google.com/earth-engine/datasets (accessed on 11 November 2024).
- Lin, H.; Xu, P.T.; Sun, L.; Bi, X.k.; Zhao, J.w.; Cai, J.r. Identification of eggshell crack using multiple vibration sensors and correlative information analysis. J. Food Process Eng. 2018, 41, e12894. [Google Scholar] [CrossRef]
- Allen, R.G. Using the FAO-56 dual crop coefficient method over an irrigated region as part of an evapotranspiration intercomparison study. J. Hydrol. 2000, 229, 27–41. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Calder, I.R. Has the Priestley-Taylor equation any relevance to forest evaporation? J. Appl. Meteorol. Climatol. 1979, 18, 639–646. [Google Scholar] [CrossRef]
- Talebmorad, H.; Ahmadnejad, A.; Eslamian, S.; Ostad-Ali-Askari, K.; Singh, V.P. Evaluation of uncertainty in evapotranspiration values by FAO56-Penman-Monteith and Hargreaves-Samani methods. Int. J. Hydrol. Sci. Technol. 2020, 10, 135–147. [Google Scholar] [CrossRef]
- Iranzad, R.; Liu, X. A review of random forest-based feature selection methods for data science education and applications. Int. J. Data Sci. Anal. 2024, 1–15. [Google Scholar] [CrossRef]
- Yu, S.; Ren, Y.; Wu, X.; Guo, P.; Li, Y. Dynamic pruning-based Bayesian support vector regression for reliability analysis. Reliab. Eng. Syst. Saf. 2024, 244, 109922. [Google Scholar] [CrossRef]
- Wijayanti, E.B.; Setiadi, D.R.I.M.; Setyoko, B.H. Dataset analysis and feature characteristics to predict rice production based on eXtreme gradient boosting. J. Comput. Theor. Appl. 2024, 1, 299–310. [Google Scholar] [CrossRef]
- Kelly, H.R.; Sreekumar, S.; Manee, V.; Cuomo, A.E.; Newhouse, T.R.; Batista, V.S.; Buono, F. Ligand-Based Principal Component Analysis Followed by Ridge Regression: Application to an Asymmetric Negishi Reaction. ACS Catal. 2024, 14, 5027–5038. [Google Scholar] [CrossRef]
- Cheng, J.; Sun, J.; Yao, K.; Dai, C. Generalized and hetero two-dimensional correlation analysis of hyperspectral imaging combined with three-dimensional convolutional neural network for evaluating lipid oxidation in pork. Food Control 2023, 153, 109940. [Google Scholar] [CrossRef]
- McLeod, A.I. Kendall rank correlation and Mann-Kendall trend test. R Package Kendall 2005, 602, 1–10. [Google Scholar]
- Ouyang, Q.; Zhao, J.; Pan, W.; Chen, Q. Real-time monitoring of process parameters in rice wine fermentation by a portable spectral analytical system combined with multivariate analysis. Food Chem. 2016, 190, 135–141. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, Z.; Xiong, Z.; Shi, Y.; Saha, S.; Zhu, X.X. Beyond Grid Data: Exploring graph neural networks for Earth observation. IEEE Geosci. Remote Sens. Mag. 2024, 13, 175–208. [Google Scholar] [CrossRef]
- Niranjan, S.; Nandagiri, L. Effect of local calibration on the performance of the Hargreaves reference crop evapotranspiration equation. J. Water Clim. Change 2021, 12, 2654–2673. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Zhao, L.; Hu, X.; Gong, D. Comparison of ELM, GANN, WNN and empirical models for estimating reference evapotranspiration in humid region of Southwest China. J. Hydrol. 2016, 536, 376–383. [Google Scholar] [CrossRef]
- Tabari, H.; Kisi, O.; Ezani, A.; Talaee, P.H. SVM, ANFIS, regression and climate based models for reference evapotranspiration modeling using limited climatic data in a semi-arid highland environment. J. Hydrol. 2012, 444, 78–89. [Google Scholar] [CrossRef]
- Rajput, J.; Singh, M.; Lal, K.; Khanna, M.; Sarangi, A.; Mukherjee, J.; Singh, S. Data-driven reference evapotranspiration (ET0) estimation: A comparative study of regression and machine learning techniques. Environ. Dev. Sustain. 2024, 26, 12679–12706. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, Z.; Jiang, H.; Sun, S. Estimating daily reference evapotranspiration based on limited meteorological data using deep learning and classical machine learning methods. J. Hydrol. 2020, 591, 125286. [Google Scholar] [CrossRef]
- Katul, G.G.; Oren, R.; Manzoni, S.; Higgins, C.; Parlange, M.B. Evapotranspiration: A process driving mass transport and energy exchange in the soil-plant-atmosphere-climate system. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Haider, S.T.; Ge, W.; Li, J.; Rehman, S.U.; Imran, A.; Sharaf, M.; Haider, S.M. An Ensemble Machine Learning Framework for Cotton Crop Yield Prediction Using Weather Parameters: A Case Study of Pakistan. IEEE Access 2024, 12, 124045–124061. [Google Scholar] [CrossRef]
- Bariş, M.; Tombul, M. A review on models, products and techniques for evapotranspiration measurement, estimation, and validation. Environ. Qual. Manag. 2024, 34, e22250. [Google Scholar] [CrossRef]
- Nandgude, N.; Singh, T.; Nandgude, S.; Tiwari, M. Drought prediction: A comprehensive review of different drought prediction models and adopted technologies. Sustainability 2023, 15, 11684. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P.; Xia, Y. Seasonal drought prediction: Advances, challenges, and future prospects. Rev. Geophys. 2018, 56, 108–141. [Google Scholar] [CrossRef]
- Fridley, J.D.; Vandermast, D.B.; Kuppinger, D.M.; Manthey, M.; Peet, R.K. Co-occurrence based assessment of habitat generalists and specialists: A new approach for the measurement of niche width. J. Ecol. 2007, 95, 707–722. [Google Scholar] [CrossRef]
- Shen, C.; Appling, A.P.; Gentine, P.; Bandai, T.; Gupta, H.; Tartakovsky, A.; Baity-Jesi, M.; Fenicia, F.; Kifer, D.; Li, L. Differentiable modelling to unify machine learning and physical models for geosciences. Nat. Rev. Earth Environ. 2023, 4, 552–567. [Google Scholar] [CrossRef]
- Briceno-Mena, L.A.; Arges, C.G.; Romagnoli, J.A. Machine learning-based surrogate models and transfer learning for derivative free optimization of HT-PEM fuel cells. Comput. Chem. Eng. 2023, 171, 108159. [Google Scholar] [CrossRef]
- Tan, L.; Zheng, K.; Zhao, Q.; Wu, Y. Evapotranspiration estimation using remote sensing technology based on a SEBAL model in the upper reaches of the Huaihe river basin. Atmosphere 2021, 12, 1599. [Google Scholar] [CrossRef]
- Shahid, M.; Khalid, S.; Bibi, I.; Bundschuh, J.; Niazi, N.K.; Dumat, C. A critical review of mercury speciation, bioavailability, toxicity and detoxification in soil-plant environment: Ecotoxicology and health risk assessment. Sci. Total Environ. 2020, 711, 134749. [Google Scholar]
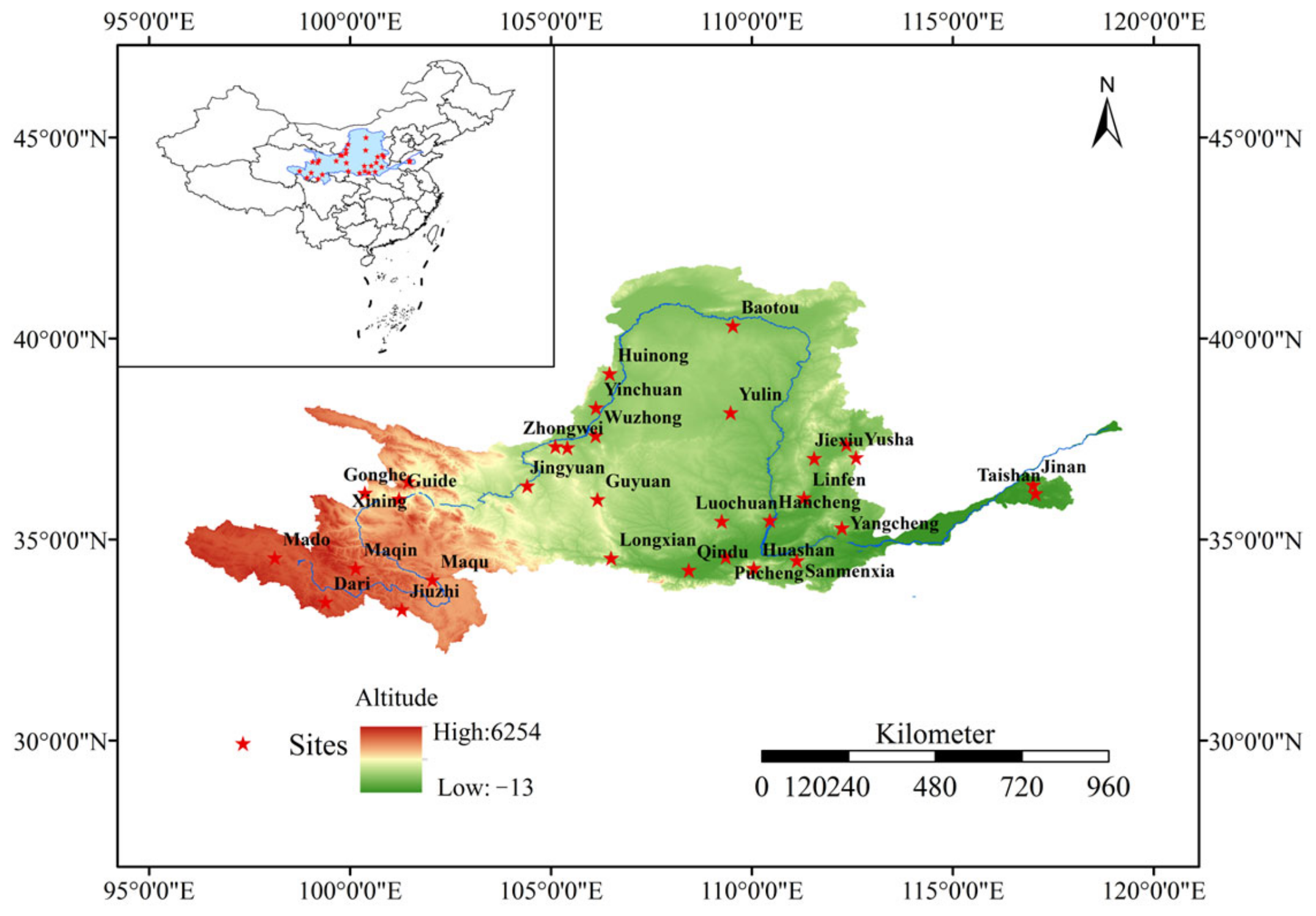
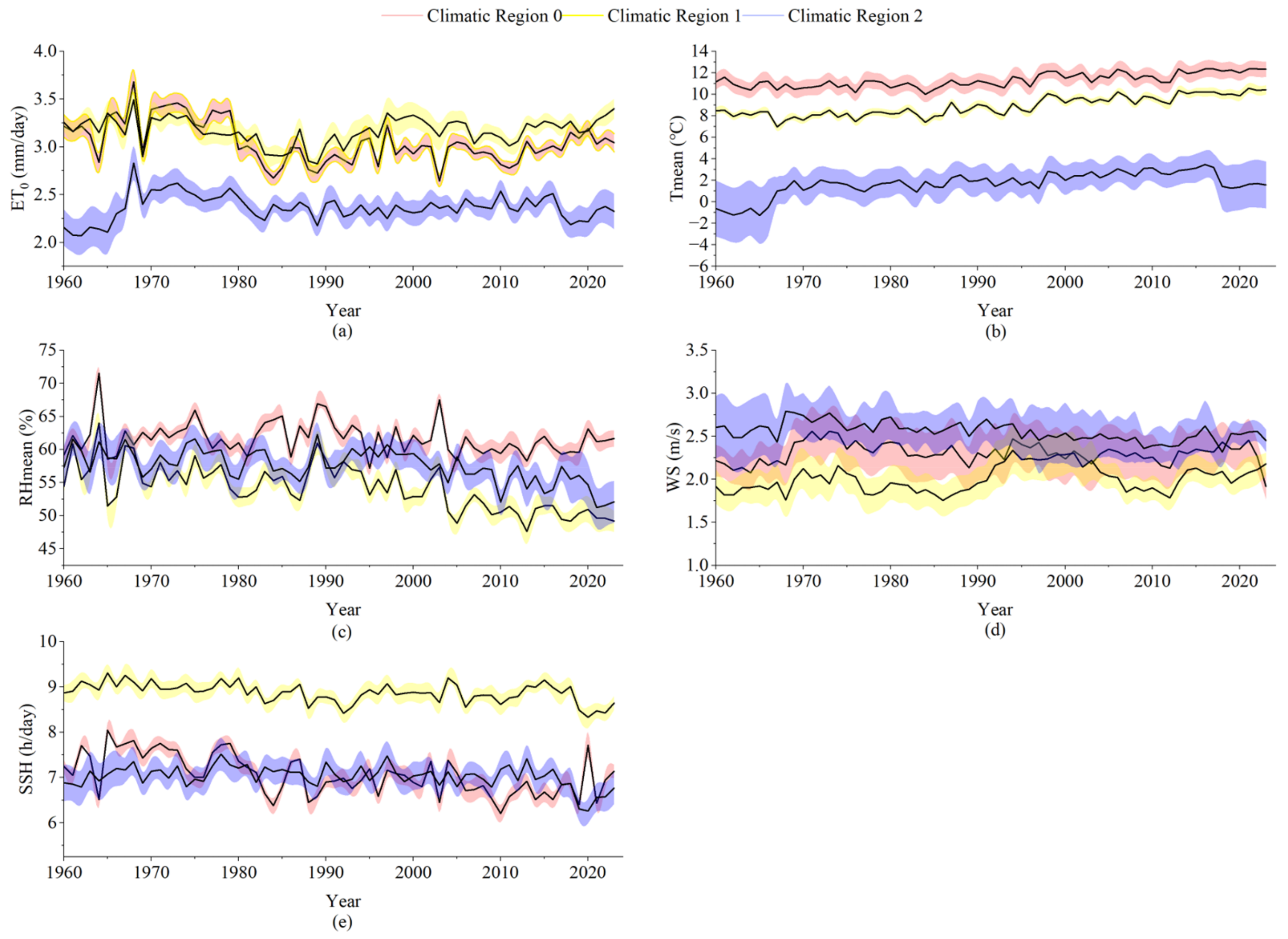
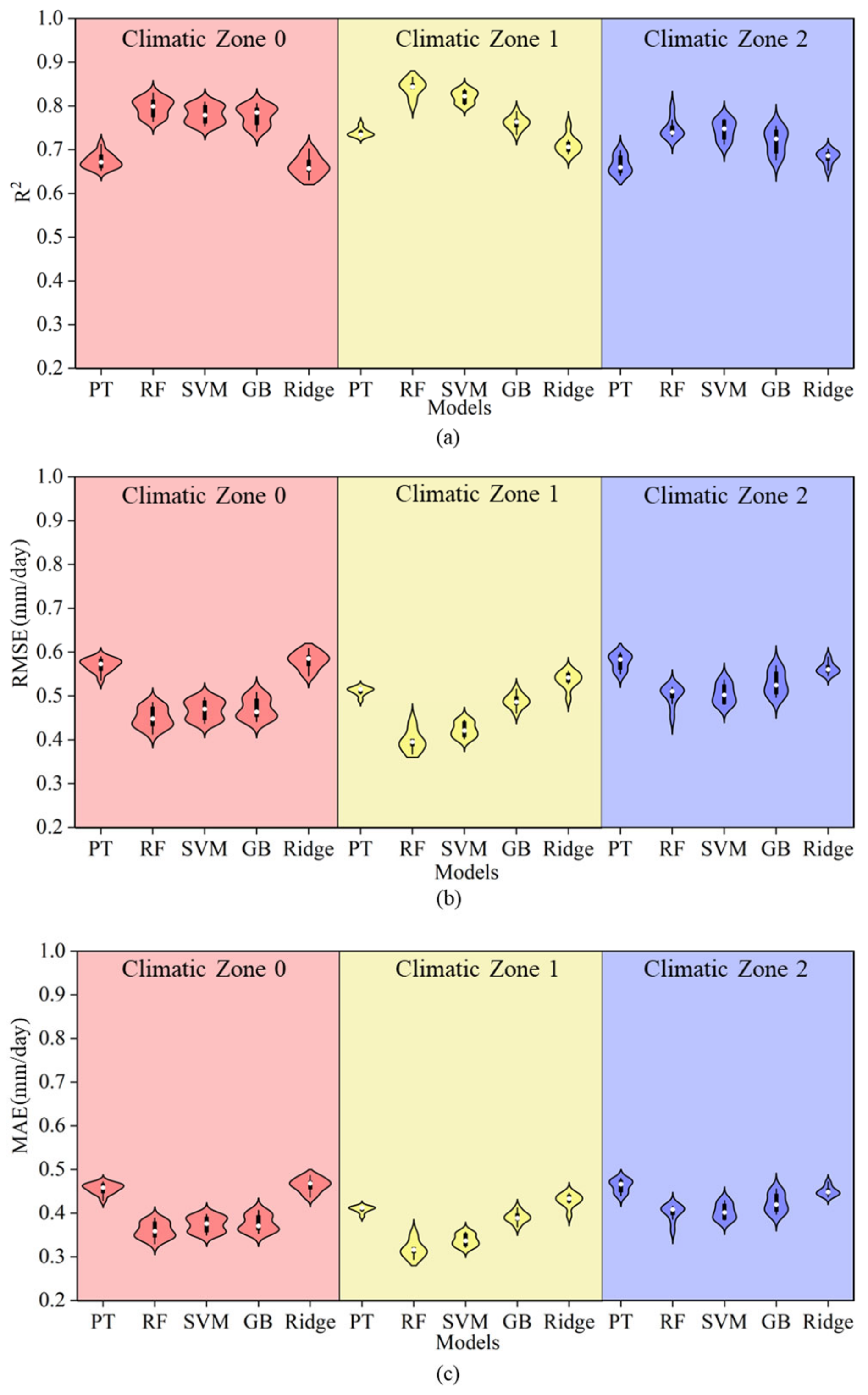
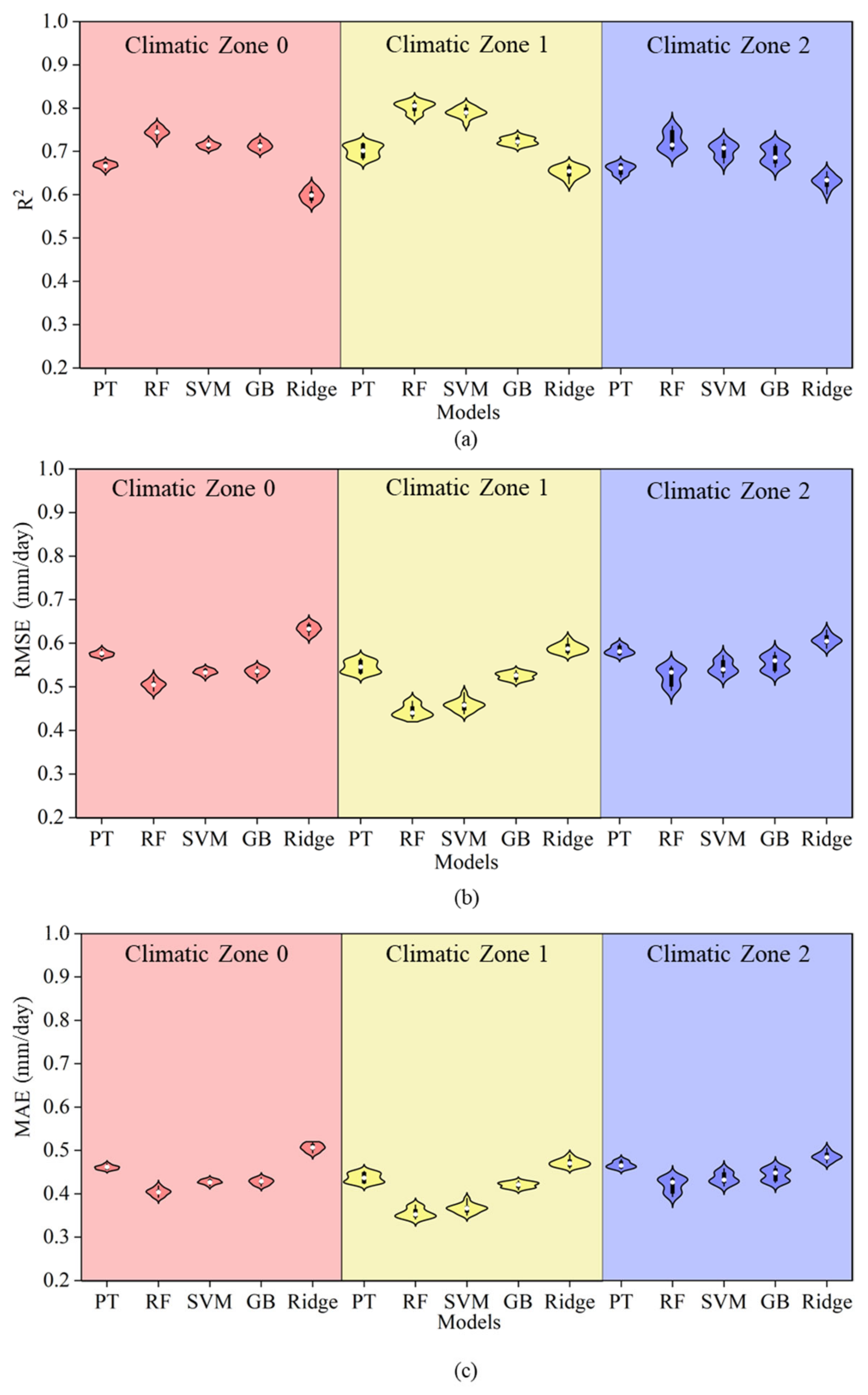
| Station ID | Station | Longitude (°) | Latitude (°) | Elevation (m) | Climatic Zone |
|---|---|---|---|---|---|
| 53772 | Taiyuan | 112.35 | 37.37 | 778.3 | 0 |
| 53787 | Yushe | 112.59 | 37.04 | 1041.4 | 0 |
| 53863 | Jiexiu | 111.55 | 37.02 | 743.9 | 0 |
| 53868 | Linfen | 111.3 | 36.04 | 449.5 | 0 |
| 53942 | Luocheng | 109.25 | 35.46 | 1159.8 | 0 |
| 53948 | Pucheng | 109.35 | 34.57 | 499.2 | 0 |
| 53955 | Hancheng | 110.45 | 35.48 | 458.1 | 0 |
| 53975 | Yangcheng | 112.24 | 35.29 | 659.5 | 0 |
| 54823 | Jinan | 117 | 36.36 | 170.3 | 0 |
| 54826 | Taishan | 117.06 | 36.15 | 1533.7 | 0 |
| 57003 | Longxian | 106.5 | 34.54 | 924.2 | 0 |
| 57046 | Huashan | 110.05 | 34.29 | 2064.9 | 0 |
| 57048 | Qindu | 108.43 | 34.24 | 472.8 | 0 |
| 57051 | Sanmenxia | 111.12 | 34.48 | 409.9 | 0 |
| 52895 | Jingyuan | 104.41 | 36.34 | 1398.2 | 1 |
| 53446 | Baotou | 109.53 | 40.32 | 1067.2 | 1 |
| 53519 | Huinong | 106.46 | 39.13 | 1092.5 | 1 |
| 53612 | Wuzhong | 106.11 | 37.59 | 1128.8 | 1 |
| 53614 | Yinchuan | 106.12 | 38.28 | 1110.9 | 1 |
| 53646 | Yulin | 109.47 | 38.16 | 1157 | 1 |
| 53704 | Zhongwei | 105.11 | 37.32 | 1225.7 | 1 |
| 53705 | Zhongning | 105.41 | 37.29 | 1183.4 | 1 |
| 53817 | Guyuan | 106.16 | 36 | 1753 | 1 |
| 52866 | Xining | 101.45 | 36.44 | 2295.2 | 2 |
| 52868 | Guide | 101.22 | 36.01 | 2237.1 | 2 |
| 52856 | Gonghe | 100.37 | 36.16 | 2835 | 2 |
| 56033 | Maduo | 98.13 | 34.55 | 4272.3 | 2 |
| 56043 | Maqin | 100.14 | 34.29 | 3719 | 2 |
| 56046 | Dari | 99.39 | 33.45 | 3967.5 | 2 |
| 56067 | Jiuzhi | 101.29 | 33.26 | 3628.5 | 2 |
| 56074 | Maqu | 102.05 | 34 | 3471.4 | 2 |
| Years | Climatic Zone | SPEI |
|---|---|---|
| 1963 | 2 | −1.79 |
| 1966 | 0, 1, 2 | −2.09, −1.15, −1.52 |
| 1970 | 1 | −1.16 |
| 1973 | 0 | −1.67 |
| 1981 | 2 | −1.83 |
| 1983 | 1 | −1.80 |
| 1987 | 0, 1 | −1.97, −1.52 |
| 1988 | 1, 2 | −1.32, −1.16 |
| 1992 | 1, 2 | −1.62, −2.15 |
| 1996 | 1 | −1.29 |
| 1998 | 0, 1, 2 | −2.19, −2.34, −1.32 |
| 2000 | 0 | −1.73 |
| 2001 | 1 | −1.89 |
| 2002 | 0, 2 | −1.99, −1.43 |
| 2003 | 0, 2 | −1.03, −1.07 |
| 2005 | 1, 2 | −1.71, −1.00 |
| 2006 | 0, 1 | −1.63, −1.89 |
| 2007 | 0, 1 | −1.40, −1.97 |
| 2009 | 1 | −2.00 |
| 2010 | 1 | −1.79 |
| 2014 | 2 | −1.84 |
| 2016 | 1 | −1.13 |
| 2017 | 2 | −1.12 |
| Climatic Zone | Variable | Z-Value |
|---|---|---|
| 0 | ET0 | −2.39 *** |
| Tmean | 6.10 *** | |
| RH | −1.62 * | |
| WS | 0.17 | |
| SSH | −4.85 *** | |
| 1 | ET0 | 0.18 |
| Tmean | 7.34 *** | |
| RH | −5.90 *** | |
| WS | 2.71 *** | |
| SSH | −3.81 *** | |
| 2 | ET0 | −0.53 |
| Tmean | 5.96 *** | |
| RH | −4.63 *** | |
| WS | −4.81 *** | |
| SSH | −2.18 ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Zhong, H.; Wang, C. Estimation of Reference Crop Evapotranspiration in the Yellow River Basin Based on Machine Learning and Its Regional and Drought Adaptability Analysis. Agronomy 2025, 15, 1237. https://doi.org/10.3390/agronomy15051237
Zhao J, Zhong H, Wang C. Estimation of Reference Crop Evapotranspiration in the Yellow River Basin Based on Machine Learning and Its Regional and Drought Adaptability Analysis. Agronomy. 2025; 15(5):1237. https://doi.org/10.3390/agronomy15051237
Chicago/Turabian StyleZhao, Jun, Huayu Zhong, and Congfeng Wang. 2025. "Estimation of Reference Crop Evapotranspiration in the Yellow River Basin Based on Machine Learning and Its Regional and Drought Adaptability Analysis" Agronomy 15, no. 5: 1237. https://doi.org/10.3390/agronomy15051237
APA StyleZhao, J., Zhong, H., & Wang, C. (2025). Estimation of Reference Crop Evapotranspiration in the Yellow River Basin Based on Machine Learning and Its Regional and Drought Adaptability Analysis. Agronomy, 15(5), 1237. https://doi.org/10.3390/agronomy15051237








