Research on the Precise Regulation of Korla Fragrant Pear Quality Based on Sensitivity Analysis and Artificial Neural Network Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of the Experimental Site
2.2. Data Collection
2.3. Measurement of Soil Indicators
2.4. Leaf Index Indicators
2.5. Fruit Quality Indicators
2.6. Outlier Removal Using Mahalanobis Distance Method
2.7. Statistical Analysis
3. Results and Analysis
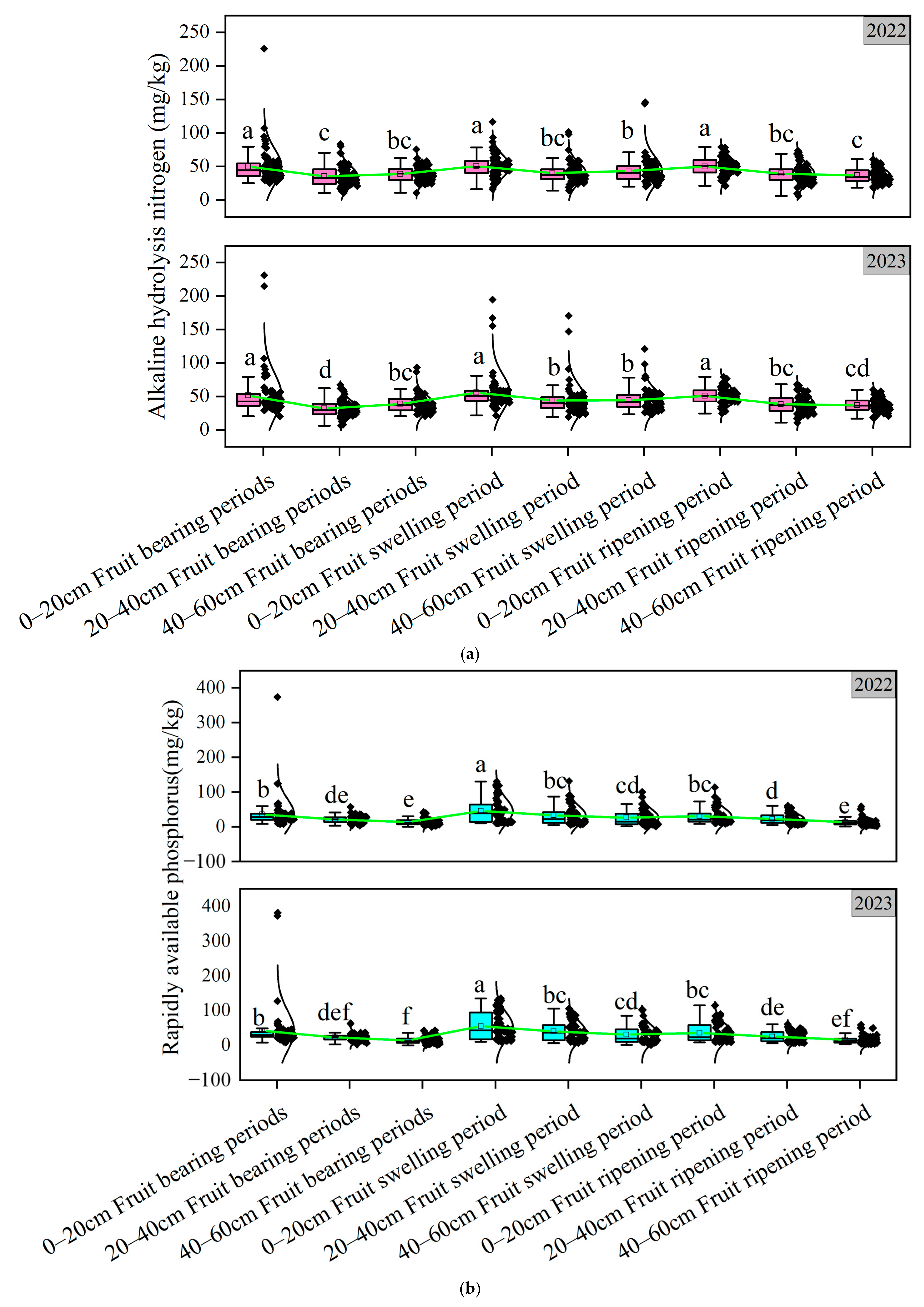
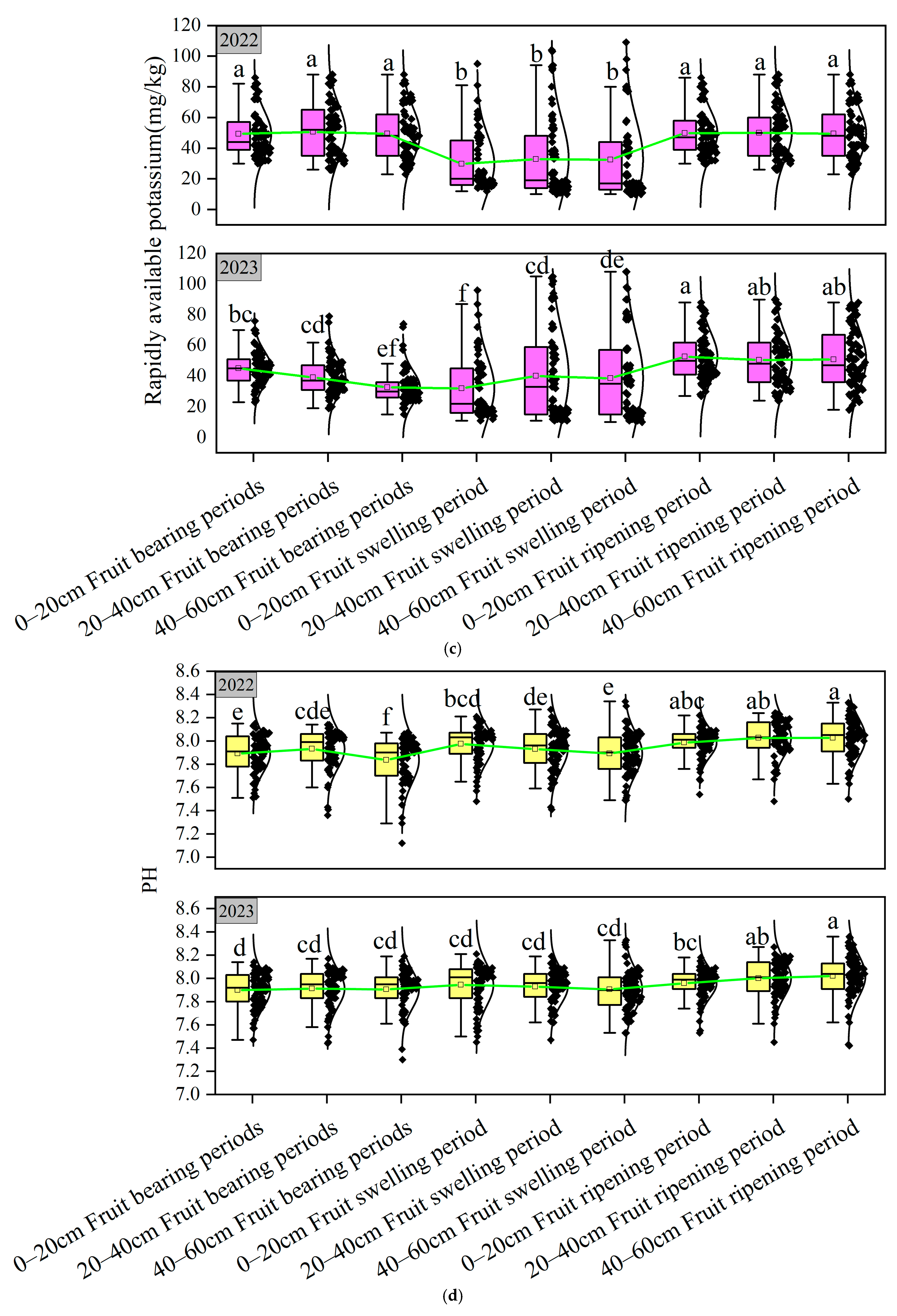
3.1. Soil Nutrient Analysis
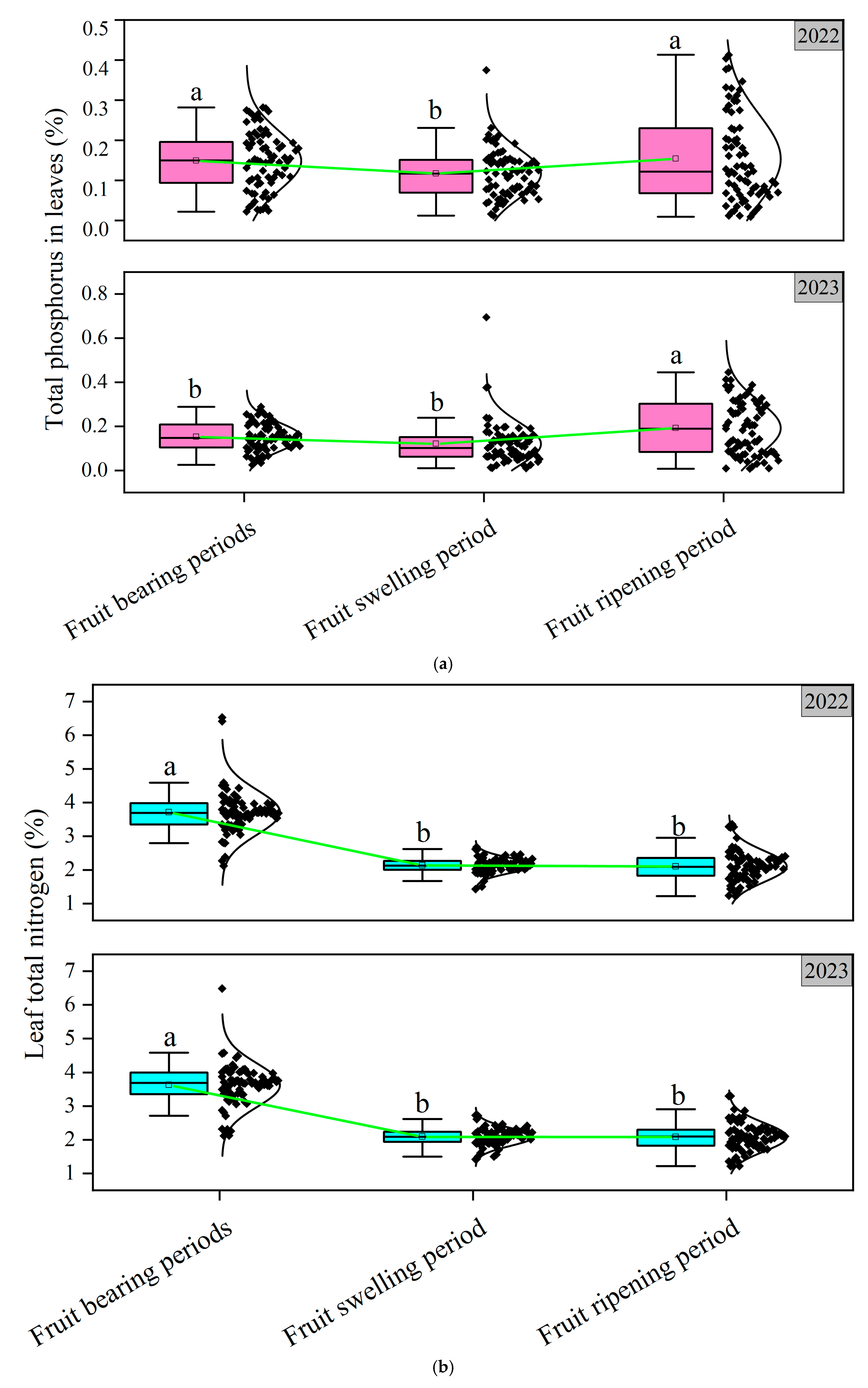
3.2. Analysis of Leaf Physiological Indicators
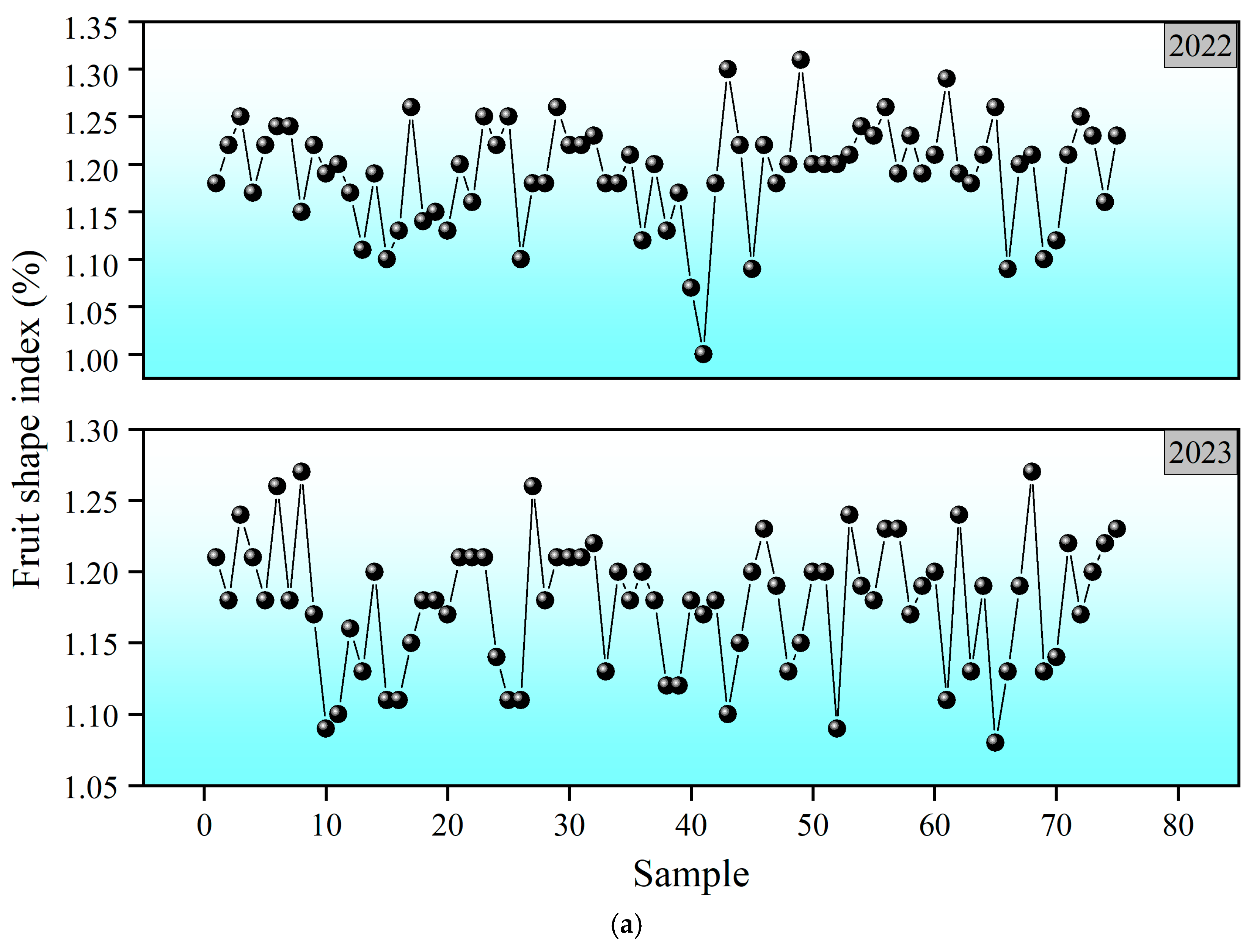
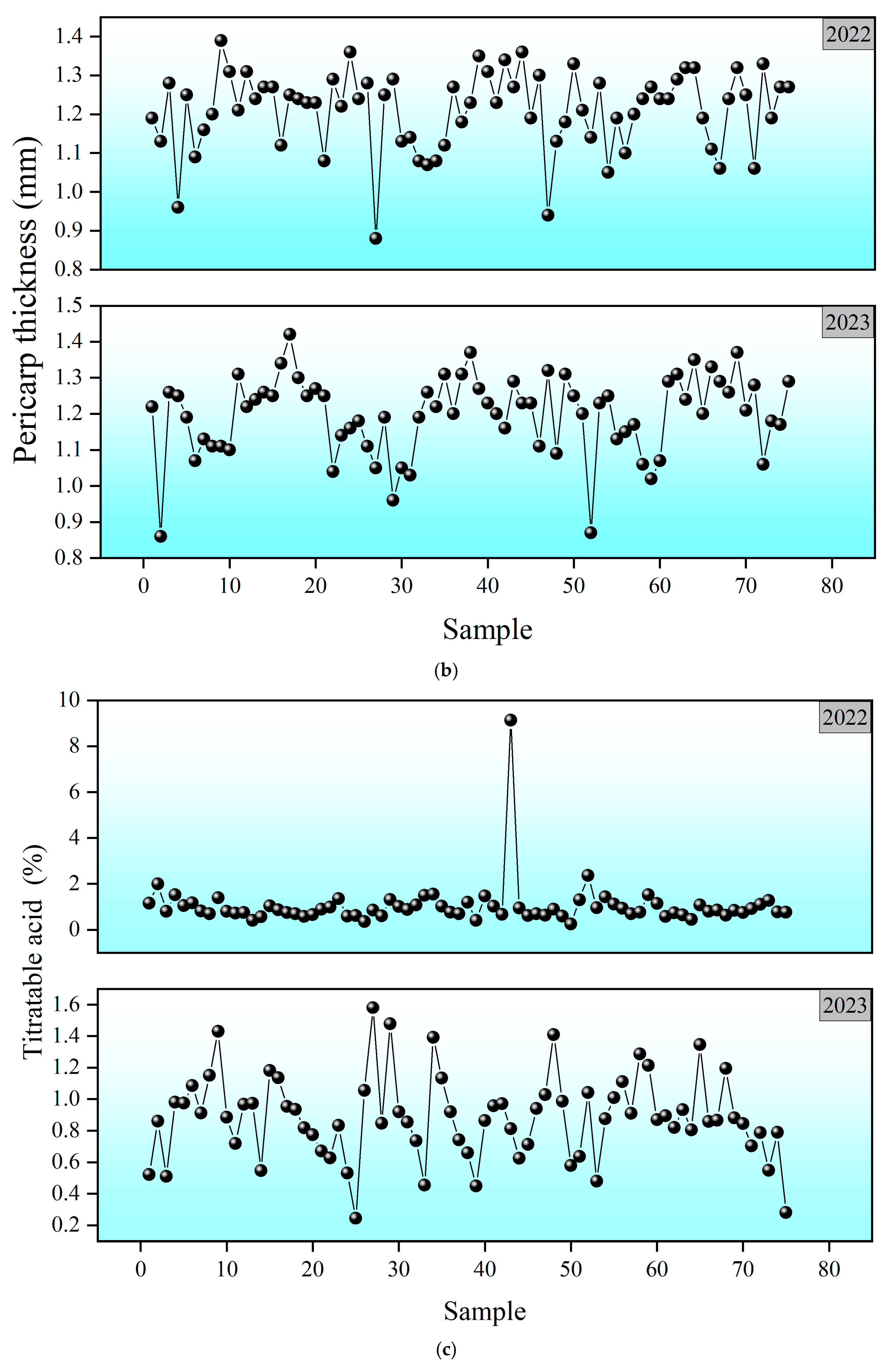
3.3. Visualization of Fruit Quality
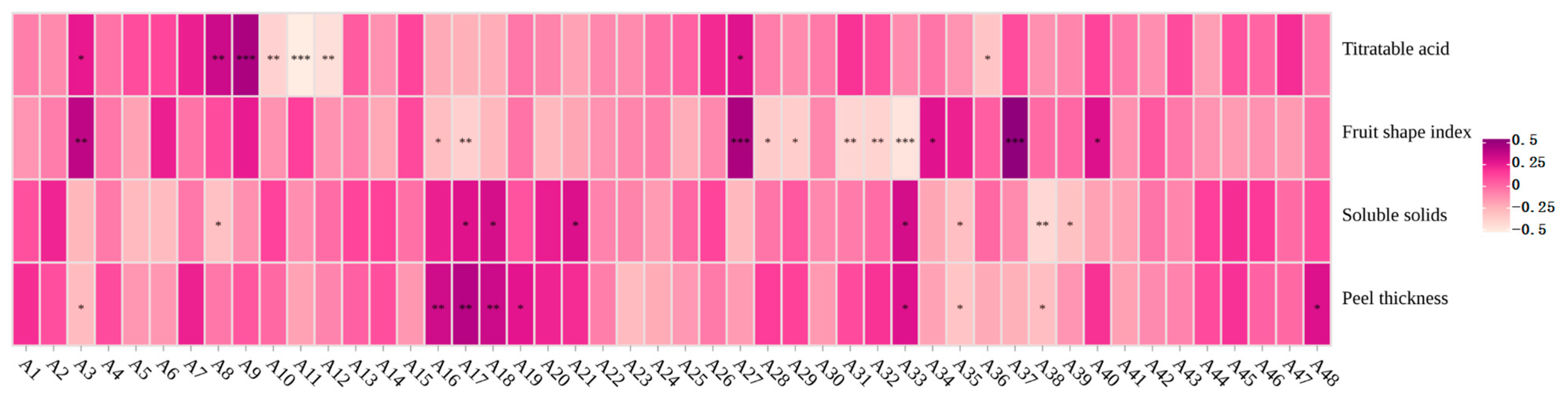
3.4. Feature Index Selection
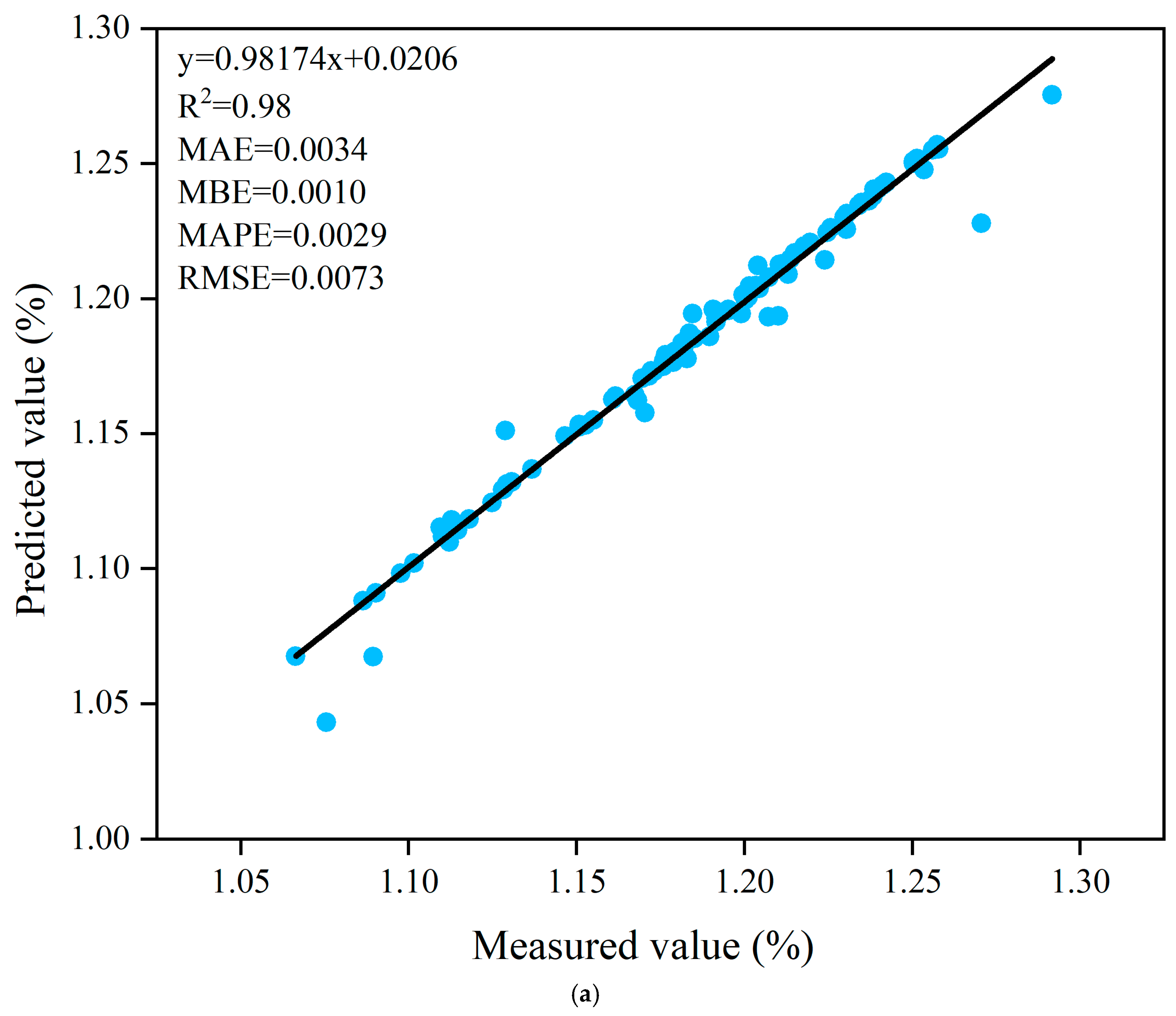
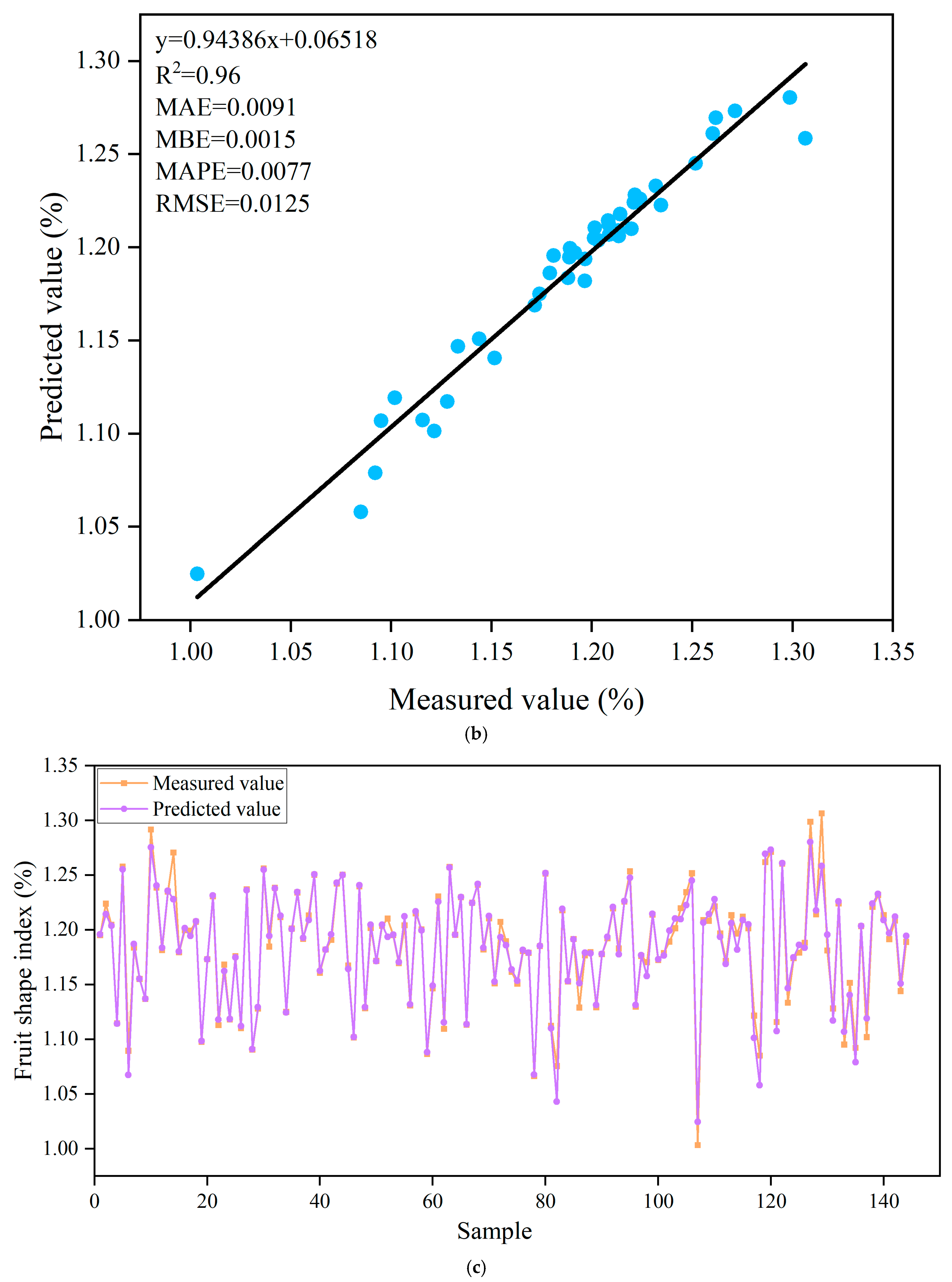
3.5. Prediction of Fruit Shape Index Based on ANN Algorithm
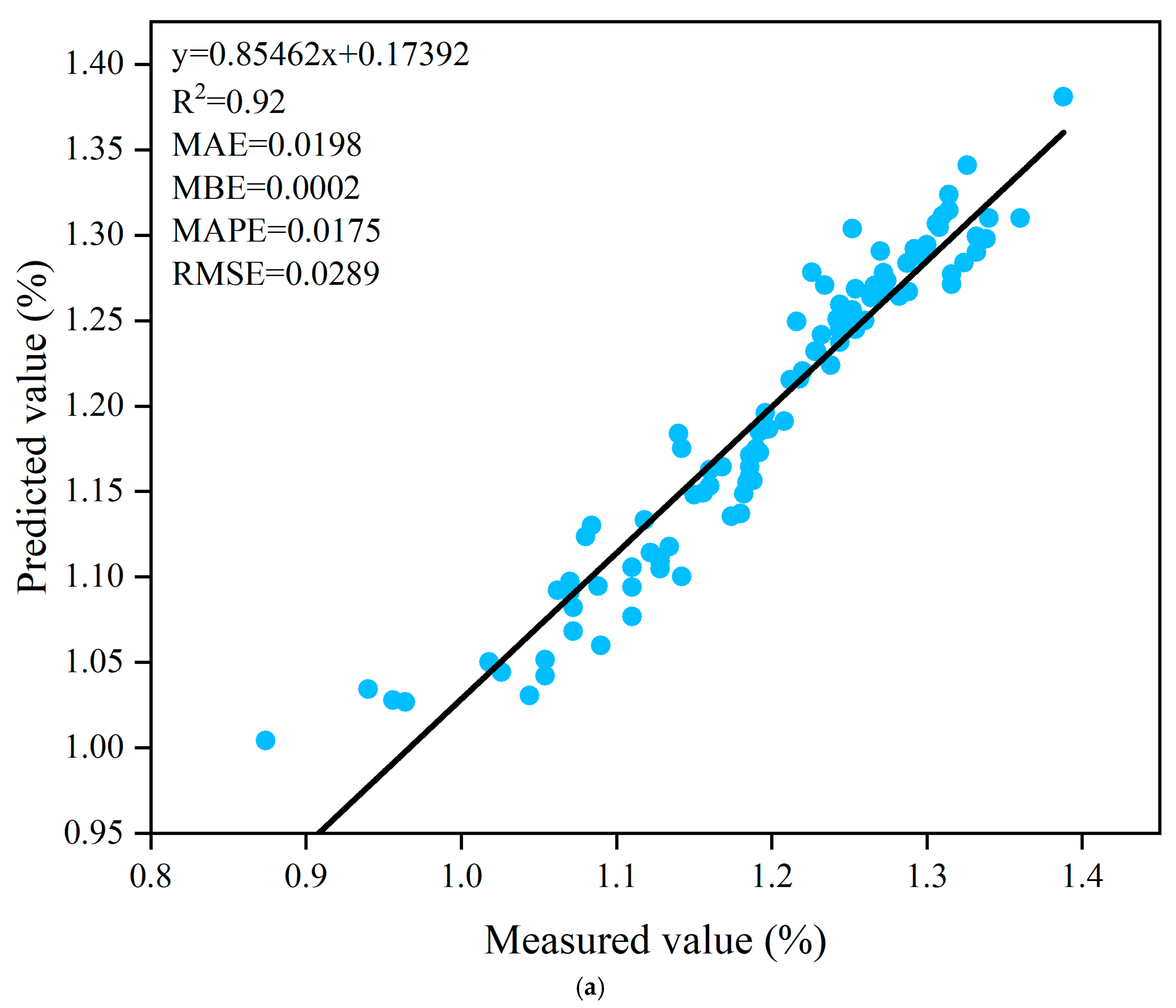
3.6. Prediction of Fruit Peel Thickness Based on ANN Algorithm
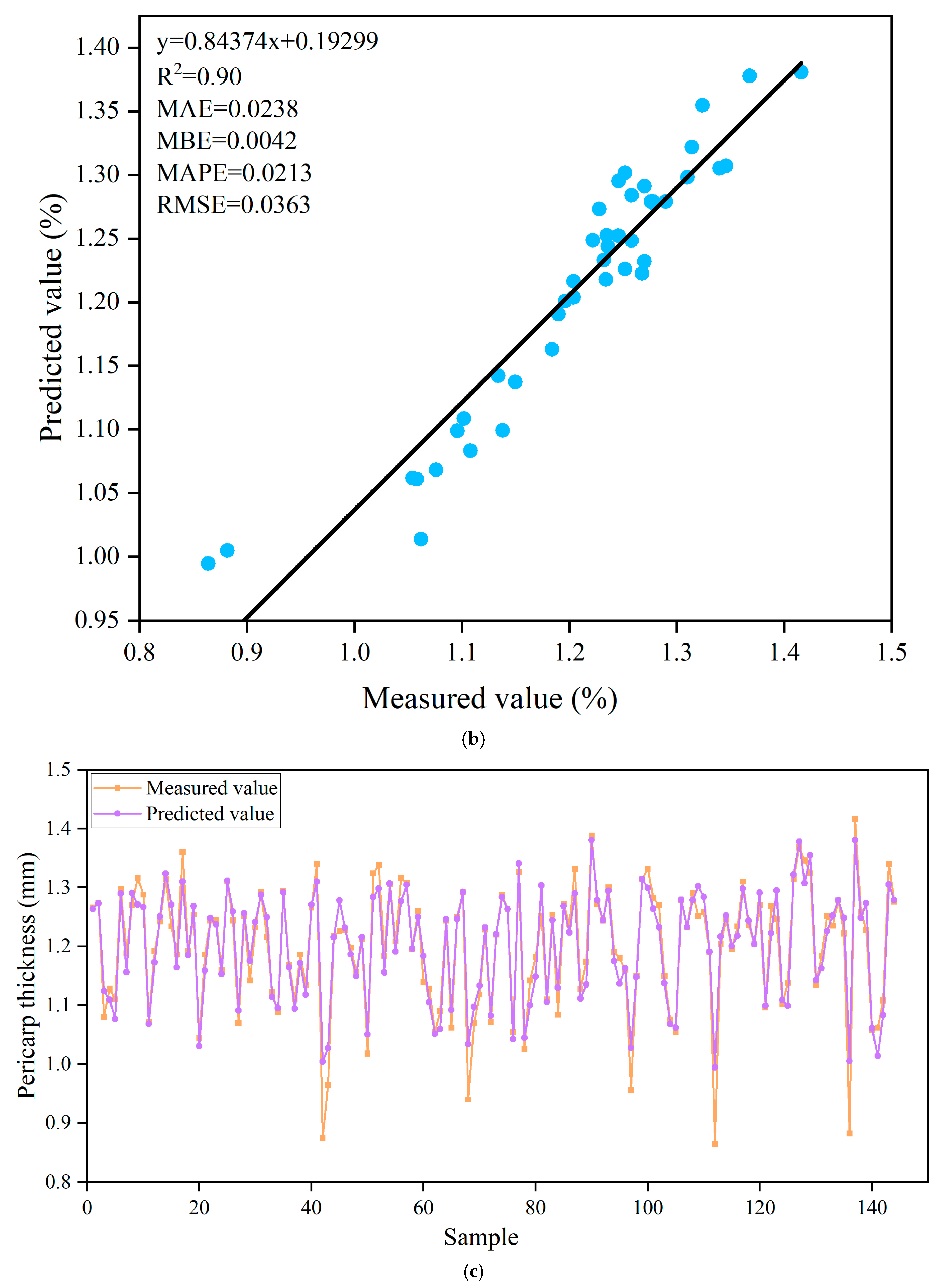
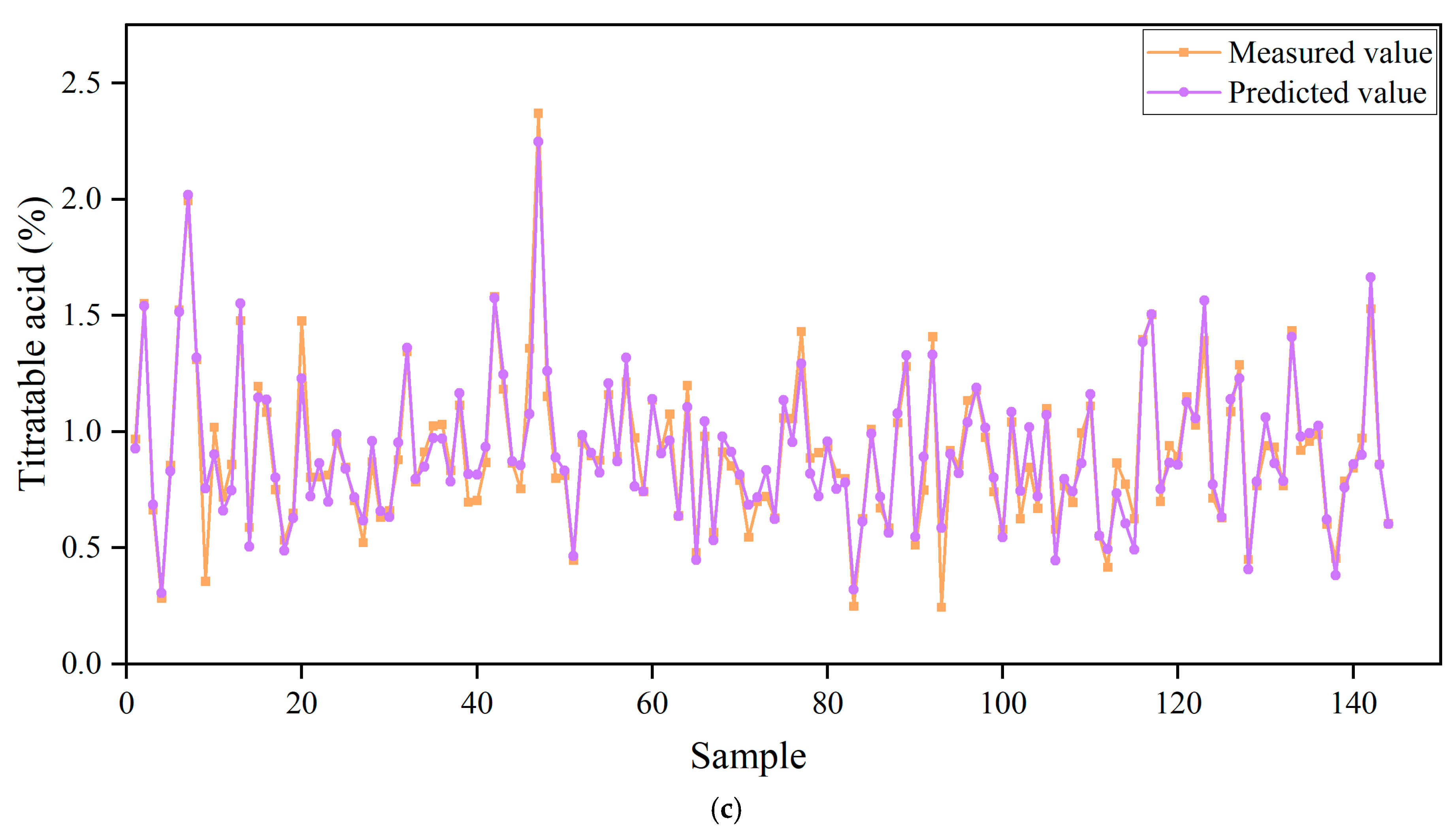
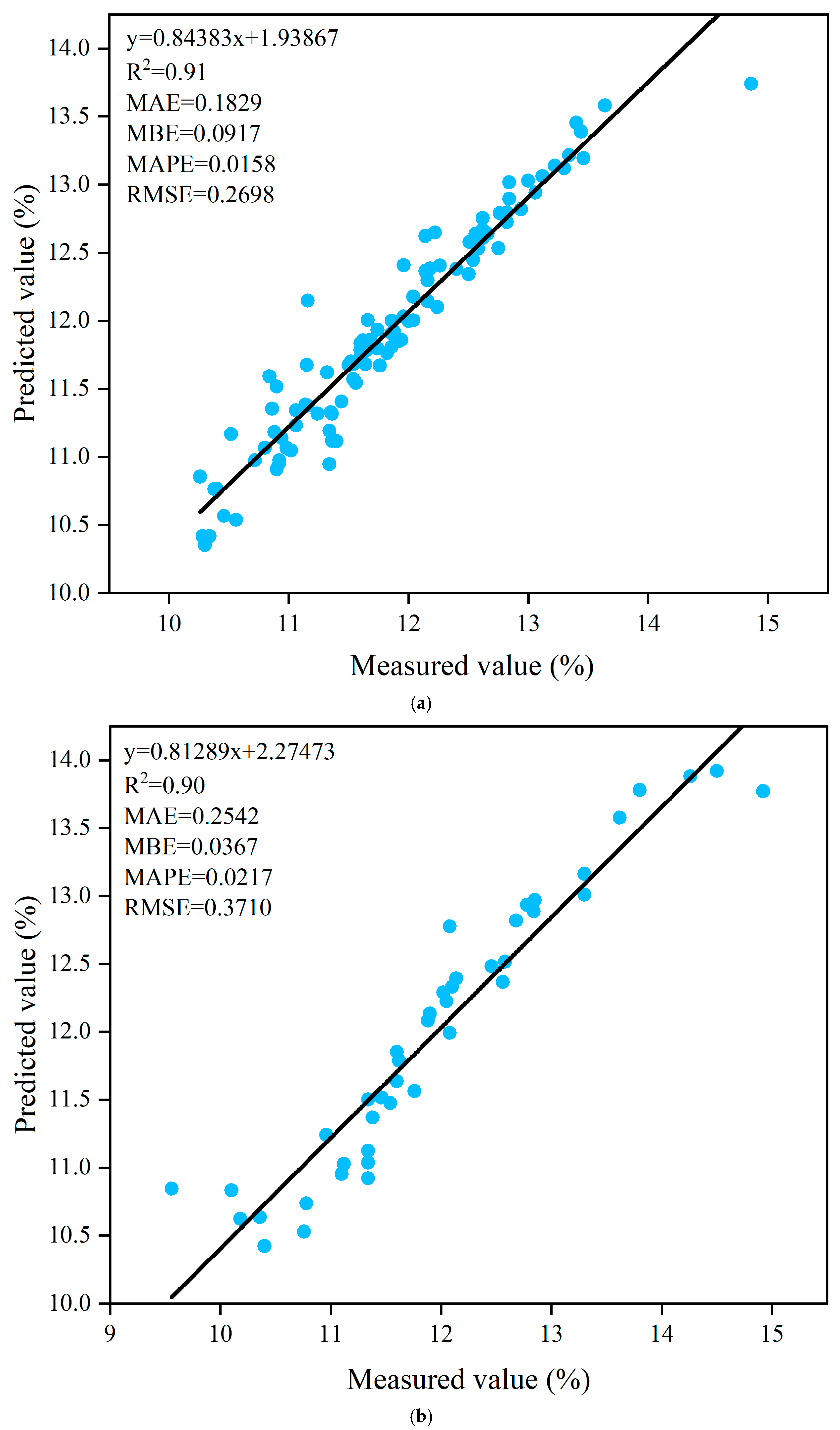
3.7. Prediction of Titratable Acids Based on ANN Algorithm
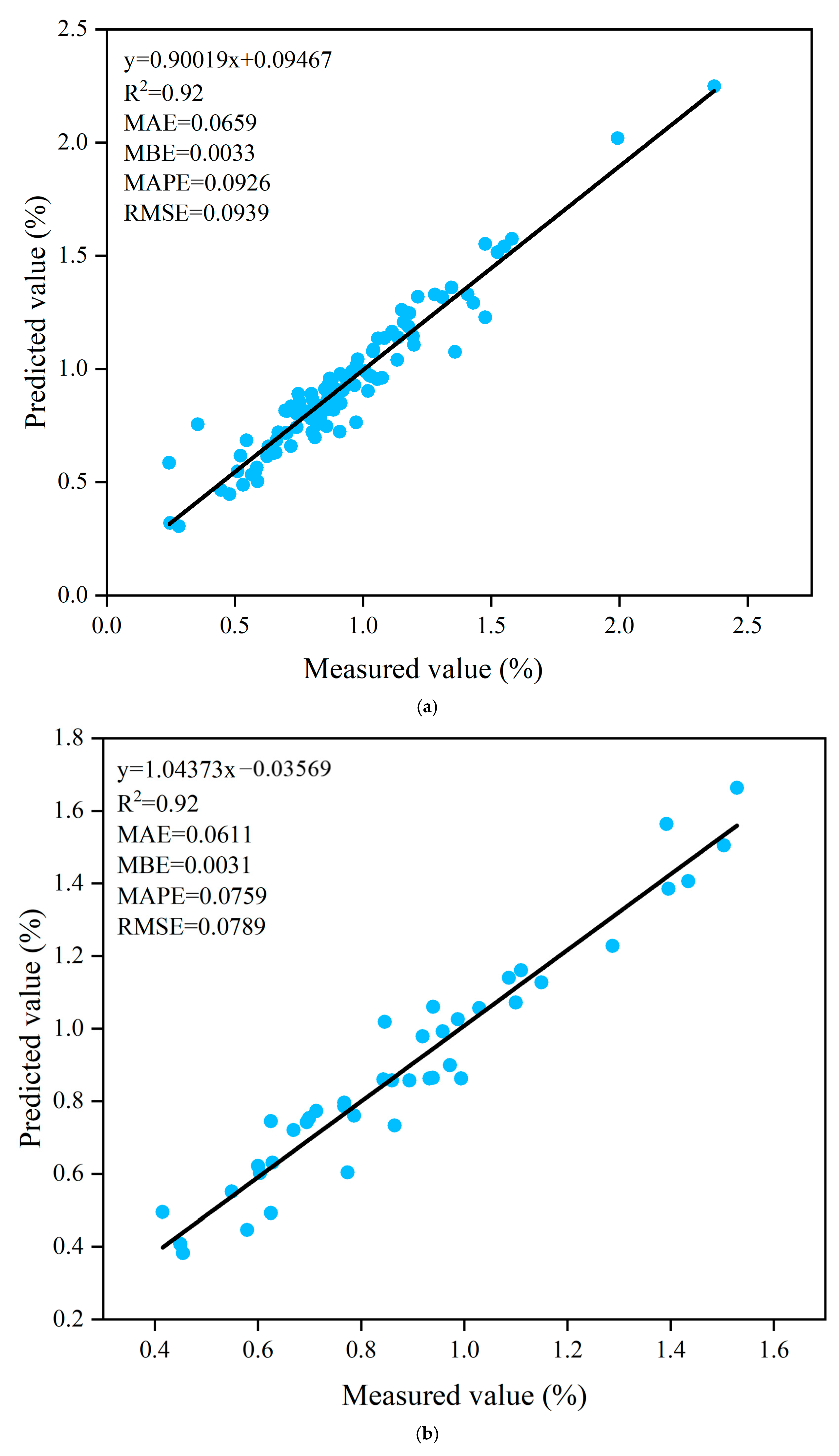
3.8. Prediction of Soluble Solid Content Based on ANN Algorithm
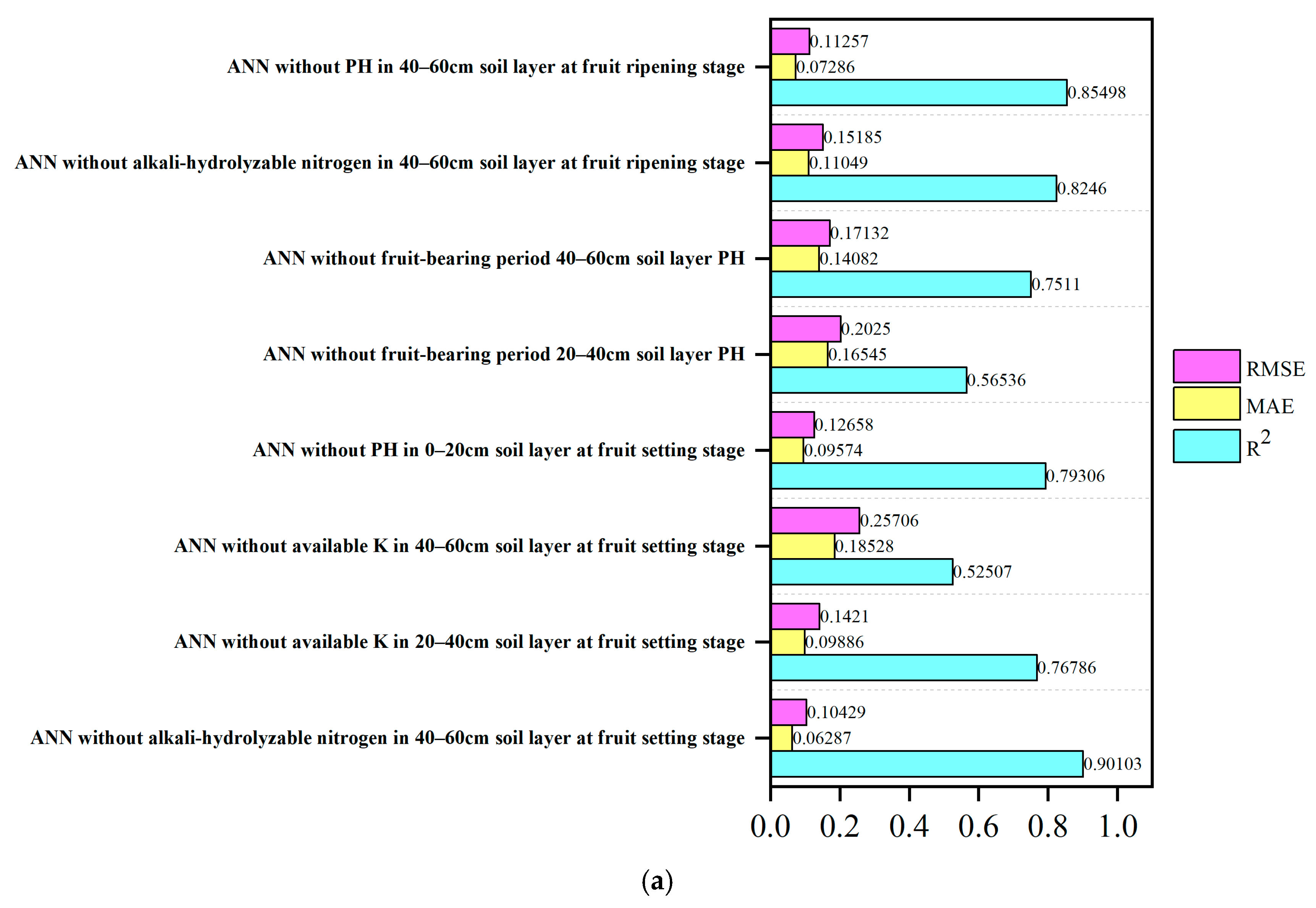
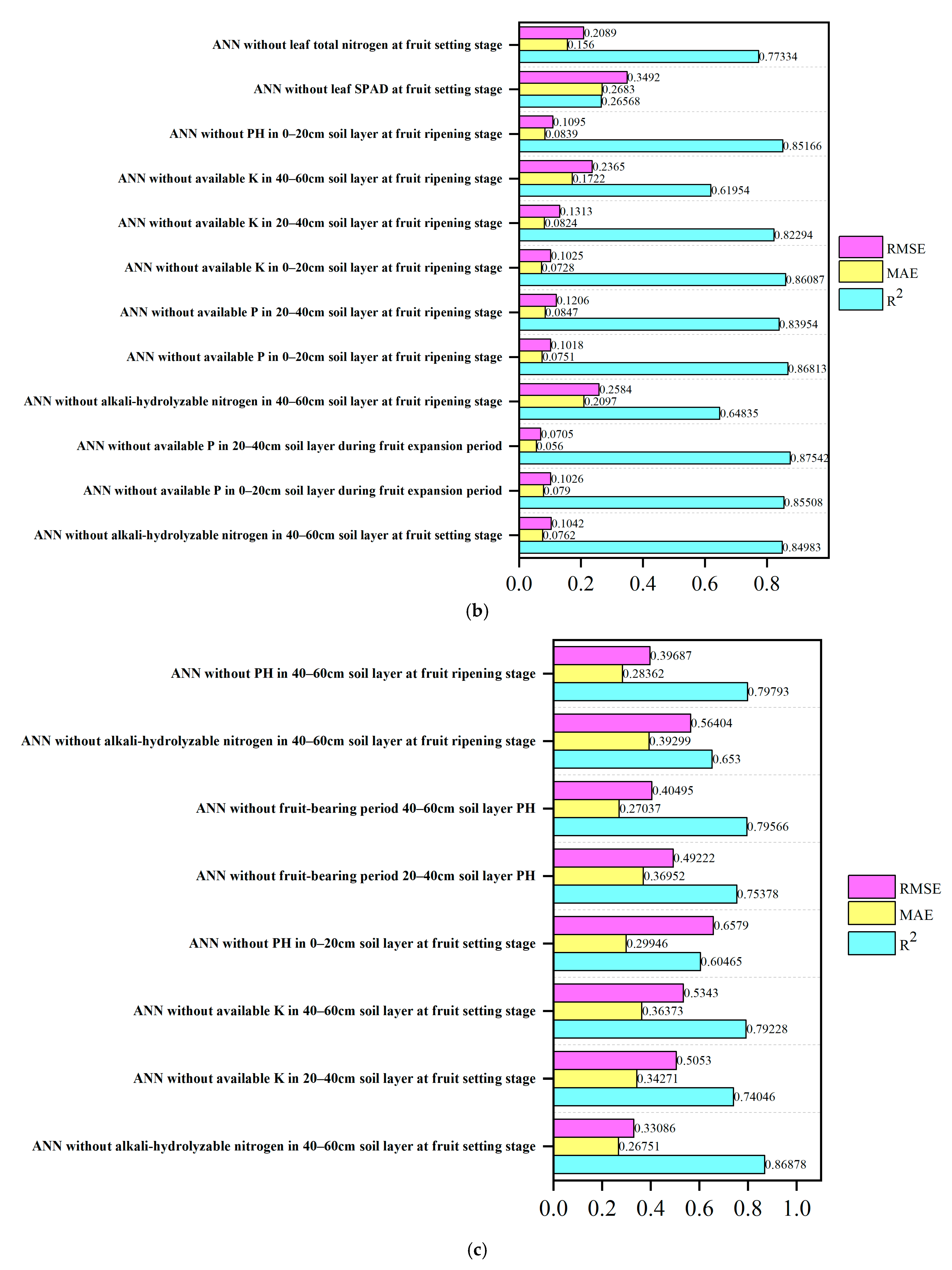
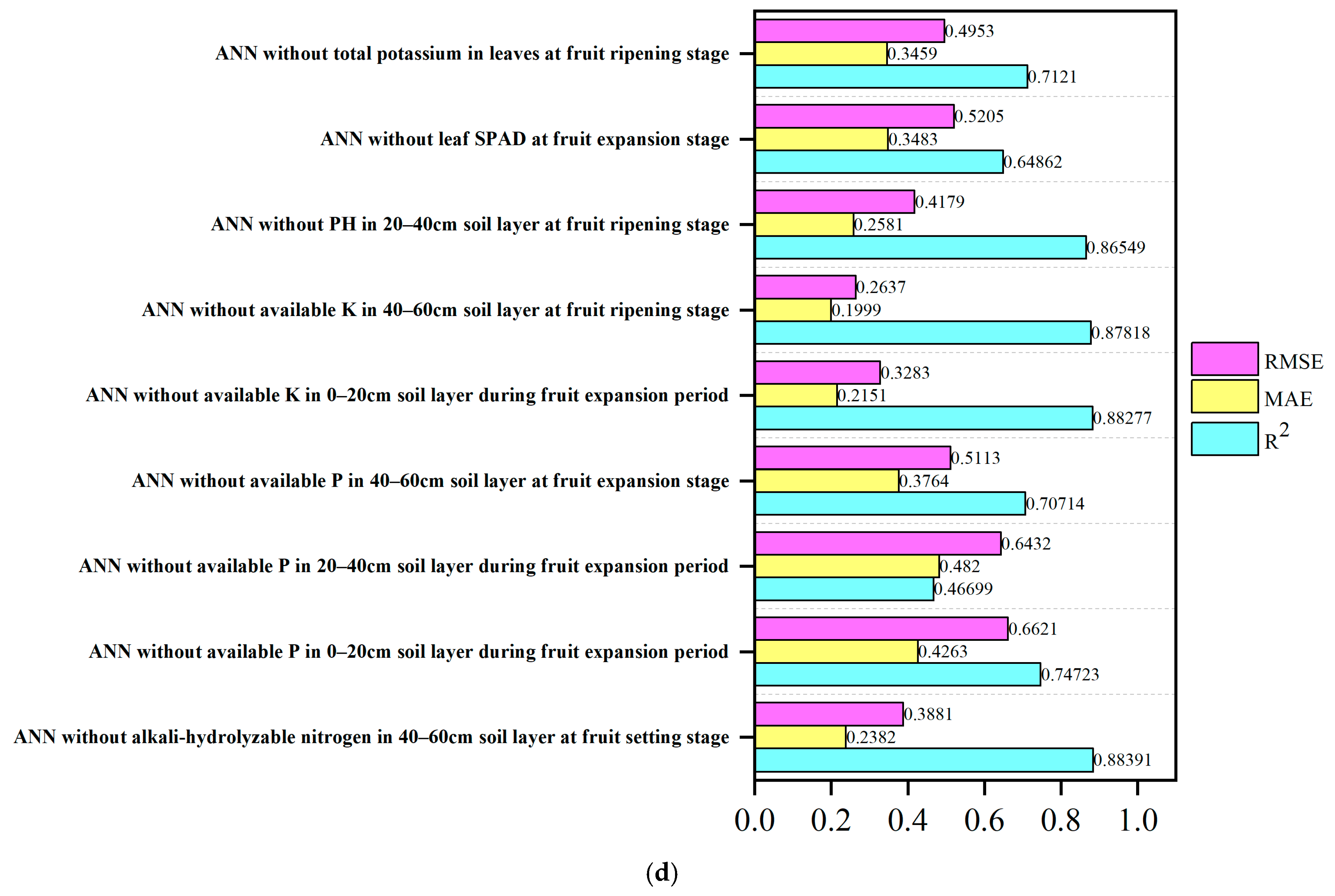
3.9. Desensitization Analysis
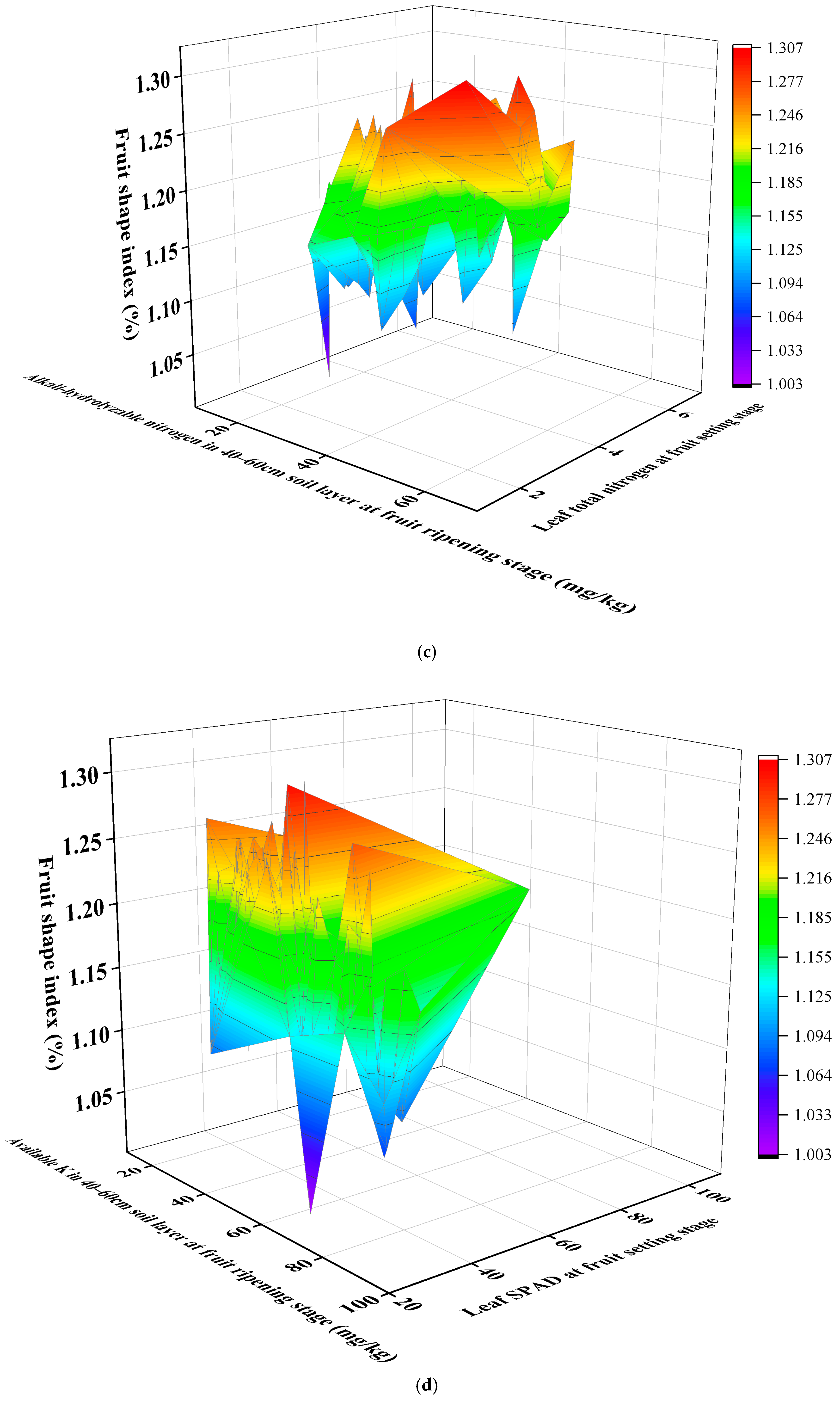
3.10. Response Surface Methodology Analysis
4. Discussion
4.1. The Relationship Between Soil Indicators and Fruit Quality
4.2. The Correlation Between Leaf Indicators and Fruit Quality
4.3. The Application and Significance of ANN Model in Fruit Quality Prediction
4.4. Implications of Sensitivity Analysis and Response Surface Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SPAD | Soil and Plant Analysis Development |
| ANN | Artificial Neural Network |
| R2 | Coefficient of Determination |
| MAE | Mean Absolute Error |
| MBE | Mean Bias Error |
| MAPE | Mean Absolute Percentage Error |
| RMSE | Root Mean Square Error |
References
- Lan, H.; Wang, Z.; Niu, H.; Zhang, H.; Zhang, Y.; Tang, Y.; Liu, Y. A nondestructive testing method for soluble solid content in Korla fragrant pears based on electrical properties and artificial neural network. Food Sci. Nutr. 2020, 8, 5172–5181. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Shi, L.; Li, Y.; Liang, Y.; Zhang, Z. Research progress on pear fruit quality and its influencing factors. J. Zhejiang Agric. Sci. 2022, 63, 330–333. [Google Scholar] [CrossRef]
- Penzel, M.; Lakso, A.; Tsoulias, N.; Zude-Sasse, M. Carbon consumption of developing fruit and the fruit bearing capacity of individual RoHo 3615 and Pinova apple trees. Int. Agrophys. 2020, 34, 409–423. [Google Scholar] [CrossRef]
- Lu, Y.; Xiao, Q.; Wu, S.; Yuan, H.; Gao, T.; Cai, T.; Wu, X.; Ma, Y.; Liao, X. Partial Substitution of Nitrogen Fertilizer with Biogas Slurry Increases Rice Yield and Fertilizer Utilization Efficiency, Enhancing Soil Fertility in the Chaohu Lake Basin. Plants 2024, 13, 2024. [Google Scholar] [CrossRef]
- Bai, Z.; Ma, L.; Jin, S.; Ma, W.; Velthof, G.L.; Oenema, O.; Liu, L.; Chadwick, D.; Zhang, F. Nitrogen, Phosphorus, and Potassium Flows Through the Manure Management Chain in China. Environ. Sci. Technol. 2016, 50, 13409–13418. [Google Scholar] [CrossRef] [PubMed]
- Tziolas, N.; Tsakiridis, N.; Chabrillat, S.; Demattê, J.A.M.; Ben-Dor, E.; Gholizadeh, A.; Zalidis, G.; van Wesemael, B. Earth Observation Data-Driven Cropland Soil Monitoring: A Review. Remote Sens. 2021, 13, 4439. [Google Scholar] [CrossRef]
- Sahbeni, G.; Ngabire, M.; Musyimi, P.K.; Székely, B. Challenges and Opportunities in Remote Sensing for Soil Salinization Mapping and Monitoring: A Review. Remote Sens. 2023, 15, 2540. [Google Scholar] [CrossRef]
- Liu, X.; Kang, F.; Hu, C.; Wang, L.; Xu, Z.; Zheng, D.; Gong, W.; Lu, Y.; Ma, Y.; Wang, J. A genetically encoded photosensitizer protein facilitates the rational design of a miniature photocatalytic CO2-reducing enzyme. Nat. Chem. 2018, 10, 1201–1206. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, Z.; Zhao, F.; Cheng, X.; Zhao, P.; Liu, S. Response of Pear Trees’ (Pyrus bretschneideri ‘Sinkiangensis’) Fine Roots to a Soil Water Regime of Regulated Deficit Irrigation. Agronomy 2021, 11, 2316. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, M.; Chen, H.; Fu, X.; Wang, L.; Wang, R. Soil moisture and salinity dynamics of drip irrigation in saline-alkali soil of Yellow River basin. Front. Environ. Sci. 2023, 11, 1130455. [Google Scholar] [CrossRef]
- Siatwiinda, S.M.; Ros, G.H.; Yerokun, O.A.; de Vries, W. Options to reduce ranges in critical soil nutrient levels used in fertilizer recommendations by accounting for site conditions and methodology: A review. Agron. Sustain. Dev. 2024, 44, 9. [Google Scholar] [CrossRef]
- Matsuoka, K. Methods for Nutrient Diagnosis of Fruit Trees Early in the Growing Season by Using Simultaneous Multi-Element Analysis. Hortic. J. 2020, 89, 197–207. [Google Scholar] [CrossRef]
- Batista, P.V.G.; Evans, D.L.; Cândido, B.M.; Fiener, P. Does soil thinning change soil erodibility? An exploration of long-term erosion feedback systems. Soil 2023, 9, 71–88. [Google Scholar] [CrossRef]
- Lykhovyd, P. Prediction of sweet corn yield depending on cultivation technology parameters by using linear regression and artificial neural network methods. Biosyst. Divers. 2018, 26, 11–15. [Google Scholar] [CrossRef]
- Vawda, M.I.; Lottering, R.; Mutanga, O.; Peerbhay, K.; Sibanda, M. Comparing the Utility of Artificial Neural Networks (ANN) and Convolutional Neural Networks (CNN) on Sentinel-2 MSI to Estimate Dry Season Aboveground Grass Biomass. Sustainability 2024, 16, 1051. [Google Scholar] [CrossRef]
- Jiang, H.B.; Zhao, J.W.; Zhang, N.W.; Wang, H.; Dong, C.X.; Xu, Y.C. Effects of different soil surface management ondistribution characteristics of pear roots. J. Plant Nutr. Fertil. 2014, 20, 164–171. [Google Scholar] [CrossRef]
- Xu, G.; Li, C.; Qin, S.; Xiao, W.; Fu, X.; Chen, X.; Li, L.; Li, D. Changes in Sucrose and Sorbitol Metabolism Cause Differences in the Intrinsic Quality of Peach Fruits Cultivated in Field and Greenhouse Environments. Agronomy 2022, 12, 2877. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, X.; Ni, W.; Liu, C.; Qin, H.; Guan, Y.; Liu, J.; Feng, Z.; Xing, Y.; Tian, G.; et al. Nitrogen–potassium balance improves leaf photosynthetic capacity by regulating leaf nitrogen allocation in apple. Hortic. Res. 2024, 11, uhad253. [Google Scholar] [CrossRef]
- Vishwakarma, M.; Tagore, G.; Kulhare, P. Estimation of Chlorophyll Using SPAD. Int. J. Environ. Clim. Change 2023, 13, 1901–1912. [Google Scholar] [CrossRef]
- Han, S.; Zhao, J.; Liu, Y.; Xi, L.; Liao, J.; Liu, X.; Su, G. Effects of green manure planting mode on the quality of Korla fragrant pears (Pyrus sinkiangensis Yu). Front. Plant Sci. 2022, 13, 1027595. [Google Scholar] [CrossRef]
- Yang, J.; Lin, N.; Zhang, K.; Jia, L.; Zhang, D.; Li, G.; Zhang, J. A Parametric Study of MPSO-ANN Techniques in Gas-Bearing Distribution Prediction Using Multicomponent Seismic Data. Remote Sens. 2023, 15, 3987. [Google Scholar] [CrossRef]
- Chavlis, S.; Poirazi, P. Dendrites endow artificial neural networks with accurate, robust and parameter-efficient learning. Nat. Commun. 2025, 16, 943. [Google Scholar] [CrossRef] [PubMed]
- Castillo-Girones, S.; Munera, S.; Martínez-Sober, M.; Blasco, J.; Cubero, S.; Gómez-Sanchis, J. Artificial Neural Networks in Agriculture, the Core of Artificial Intelligence: What, When, and Why. Comput. Electron. Agric. 2025, 230, 109938. [Google Scholar] [CrossRef]
- Pandey, A.; Jain, K. An intelligent system for crop identification and classification from UAV images using conjugated dense convolutional neural network. Comput. Electron. Agric. 2022, 192, 106543. [Google Scholar] [CrossRef]
- Kulisz, M.; Duisenbekova, A.; Kujawska, J.; Kaldybayeva, D.; Issayeva, B.; Lichograj, P.; Cel, W. Implications of Neural Network as a Decision-Making Tool in Managing Kazakhstan’s Agricultural Economy. Appl. Comput. Sci. 2024, 19, 121–135. [Google Scholar] [CrossRef]
- Sun, H.; Huang, X.; Chen, T.; Zhou, P.; Huang, X.; Jin, W.; Liu, D.; Zhang, H.; Zhou, J.; Wang, Z.; et al. Fruit quality prediction based on soil mineral element content in peach orchard. Food Sci. Nutr. 2022, 10, 1756–1767. [Google Scholar] [CrossRef]
- Huang, X.; Wang, H.; Qu, S.; Luo, W.; Gao, Z. Using artificial neural network in predicting the key fruit quality of loquat. Food Sci. Nutr. 2021, 9, 1780–1791. [Google Scholar] [CrossRef]
- Liu, X.; Arif, M.; Zheng, J.; Wu, Y.; Chen, Y.; Gao, J.; Liu, J.; Changxiao, L. Assessing leaf physiological traits in response to flooding among dominant riparian herbs along the Three Gorges Dam in China. Ecol. Evol. 2024, 14, e11533. [Google Scholar] [CrossRef]
- Guo, Z.; Li, X.; Ren, Y.; Qian, S.; Shao, Y. Research on regional soil moisture dynamics based on hyperspectral remote sensing technology. Int. J. Low-Carbon Technol. 2023, 18, 737–749. [Google Scholar] [CrossRef]
- Qiang, R.; Wang, M.; Li, Q.; Li, Y.; Sun, H.; Liang, W.; Li, C.; Zhang, J.; Liu, H. Response of Soil Nitrogen Components and nirK- and nirS-Type Denitrifying Bacterial Community Structures to Drip Irrigation Systems in the Semi-Arid Area of Northeast China. Agronomy 2024, 14, 577. [Google Scholar] [CrossRef]
- Yang, K.; Li, S.; Sun, Y.; Cartmill, A.D.; López, I.F.; Ma, C.; Zhang, Q. Effects of combined nitrogen and phosphorus application on soil phosphorus fractions in alfalfa (Medicago sativa L.) production in China. Front. Plant Sci. 2024, 15, 1380738. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhang, Y.; Zhang, X.; Wu, W.; Liu, H. The Spatiotemporal Variability of Soil Available Phosphorus and Potassium in Karst Region: The Crucial Role of Socio-Geographical Factors. Land 2024, 13, 882. [Google Scholar] [CrossRef]
- Abdulraheem, M.I.; Zhang, W.; Li, S.; Moshayedi, A.J.; Farooque, A.A.; Hu, J. Advancement of Remote Sensing for Soil Measurements and Applications: A Comprehensive Review. Sustainability 2023, 15, 15444. [Google Scholar] [CrossRef]
- Lu, Q.; Liu, Z.; Zeng, S.; Song, A.; Li, Z.; Zhang, S.; Zhang, S.; Lan, M. Determination of Hydrolysable Nitrogen in Soil Samples by Alkaline Hydrolysis Diffusion Separation Acid-Base Titration Based on a Polypropylene Diffusion Dish. ROCK Miner. Anal. 2023, 42, 156–166. [Google Scholar] [CrossRef]
- Fei, T.; Liqiong, F.; Xiaofeng, J. Improvement of determination method of hydrolyzable nitrogen in soil. Geol. Yunnan 2022, 41, 131–135. [Google Scholar] [CrossRef]
- Jiaxin, R.; Wenna, Y.; Zhongyi, L.; Yanyan, H. Influence of matrix effect on determination accuracy of potassium content in soil and plantsamples by flame photometer. Acta Agric. Zhejiangensis 2019, 31, 955–962. [Google Scholar] [CrossRef]
- Yan, X.; Wang, D.-J.; Zhang, G.; Bo, L.-J.; Peng, X.-L. Soil phosphorous accumulation in long-term P fertilization paddy field and its environmental effects. Chin. J. Eco-Agric. 2013, 21, 393–400. [Google Scholar] [CrossRef]
- Yu, M.; Bai, X.; Bao, J.; Wang, Z.; Tang, Z.; Zheng, Q.; Zhi, J. The Prediction Model of Total Nitrogen Content in Leaves of Korla Fragrant Pear Was Established Based on Near Infrared Spectroscopy. Agronomy 2024, 14, 1284. [Google Scholar] [CrossRef]
- Liu, J.; Zhong, J.; Liu, J.; Luo, S.; Wang, M.; Fan, J.; Jia, L. Stoichiometric characteristics of soil and leaves in Sapindus mukorossi plantation at an early fruiting stage. J. Nanjing For. Univ. Nat. Sci. Ed. 2021, 45, 67–75. [Google Scholar] [CrossRef]
- Villegas-VeláZquez, I.; Zavaleta-Mancera, H.A.; Arévalo-Galarza, M.L.; Suarez-Espinosa, J.; Garcia-Osorio, C.; Padilla-Chacon, D.; Galvan-Escobedo, I.G.; Jimenez-Bremont, J.F. Chlorophyll measurements in Alstroemeria sp. using SPAD-502 meter and the color space CIE L*a*b*, and its validation in foliar senescence. Photosynthetica 2022, 60, 230–239. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, R.; Yin, Z.; Wang, H. Comprehensive quality evaluation of highbush blueberry cultivars based on principal component analysis. Trans. Chin. Soc. Agric. Eng. 2022, 38, 262–269. [Google Scholar] [CrossRef]
- Adou, M.; Adjouman, Y.D.; Kouadio, K.O.; Tetchi, A.F.; Amani, N.G.G. Improvement of Cashew Apple Juice (Anacardium occidentale L.) by Association with Passion Fruit Juice (Passiflora edulis). Food Nutr. Sci. 2021, 12, 787–804. [Google Scholar] [CrossRef]
- Wang, G.; Meng, J.; Xu, W.; Chen, C.; Liu, S.; Lv, Y. Analysis of Nutritional Components and Flavor Substances of Different Varieties of Mangoes. Sci. Technol. Food Ind. 2022, 43, 71–79. [Google Scholar] [CrossRef]
- Xin, Z.; Yongxiang, J.; Xibin, L.; Shefeng, L.; Xiaolei, N. Research on the Trajectory Consistency based on Mahalanobis distance method. J. Phys. Conf. Ser. 2023, 2478, 112039. [Google Scholar] [CrossRef]
- Shabani, A.; Ghaffary, K.A.; Sepaskhah, A.R.; Kamgar-Haghighi, A.A. Using the artificial neural network to estimate leaf area. Sci. Hortic. 2017, 216, 103–110. [Google Scholar] [CrossRef]
- Xiaoyong, L.; Jing, R.; Fen, K.; Fujun, H.; Hai, P.; Jianming, L.; Qiang, L.; Junping, J.; Youfu, W. Effects of nitrogen regulation on fruit quality of long-termsand-covered apple orchard in Jingning, Gansu Province. Agric. Res. Arid. Areas 2022, 40, 124–134. [Google Scholar] [CrossRef]
- Wei, L.; Wenge, X.; Xiyu, Z.; Leia, F.; Qiaoa, X.; Zhongping, C. Effect of nitrogen fertilization on soil nutrients, root biomass, yield andquality in Korla Fragrant Pear orchard. Non-Wood For. Res. 2023, 41, 235–243. [Google Scholar] [CrossRef]
- Chen, G.; Wang, L.; Fabrice, M.R.; Tian, Y.; Qi, K.; Chen, Q.; Cao, P.; Wang, P.; Zhang, S.; Wu, J.; et al. Physiological and Nutritional Responses of Pear Seedlings to Nitrate Concentrations. Front. Plant Sci. 2018, 9, 1679. [Google Scholar] [CrossRef]
- Liu, Y.-W.; Guo, X.-H.; Yang, K.; Xu, H.-H.; Sun, X.-H.; Ma, J.-J.; Lei, T.; He, Q.-Q. Effects of Different Ratios of Phosphorus and Potassium Fertilizers on Apple Quality under Drip Irrigation and Comprehensive Evaluation. Water Sav. Irrig. 2020, 6, 33–37. [Google Scholar] [CrossRef]
- Wu, H.; Wang, L.; Kang, L.; Liu, C.; Li, M. Study on the effect of planting pattern adjustment on the growth of kiwifruit inter-root microorganisms and fruit quality. Turk. J. Agric. For. 2023, 47, 263–272. [Google Scholar] [CrossRef]
- Corrêa, V.; Gonçalves, J.; Costa, K.; Oliveira, I.; Santos, J.; Oliveira, S.; Ferreira, M.; Lima, R.; Araújo, W.; Nunes-Nesi, A. The Role of Phosphate Fertilization on Physiological Responses of the Young Bertholletia excelsa Plants Grown in a P-Deficient Amazon Ferralsol. Plants 2022, 11, 2955. [Google Scholar] [CrossRef]
- Zhao, Z.-P.; Tong, Y.-A.; Liu, F.; Wang, X.-Y.; Zeng, Y.-J. Assessment of current conditions of household fertilization of apples in Weibei Plateau. Chin. J. Eco-Agric. 2012, 20, 1003–1009. [Google Scholar] [CrossRef]
- Gao, Y.-M.; Tong, Y.-A.; Lu, Y.-L.; Ma, H.-Y. Effect of long -term application of nitrogen, phosphorus and potassiumon apple yield and soil nutrient accumulation and distribution in orchardsoil of Loess Plateau. J. Fruit Sci. 2012, 29, 322–327. [Google Scholar] [CrossRef]
- Liu, Z.X.; Liu, Y.J.; Peng, S.G.; Shan, X.H.; Xie, P.F.; Li, H.G. Vertical Distribution Characteristics of Soil Available Nutrients in Tobacco-Rice Rotation Area Based on Long-Term Shallow Tillage. Chin. Tob. Sci. 2020, 41, 28–35. [Google Scholar] [CrossRef]
- Wu, K.; Hu, C.; Liao, P.; Hu, Y.; Sun, X.; Tan, Q.; Pan, Z.; Xu, S.; Dong, Z.; Wu, S. Potassium stimulates fruit sugar accumulation by increasing carbon flow in Citrus sinensis. Hortic. Res. 2024, 11, uhae240. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.C.; Xia, L.H.; Xiong, X.Y.; Li, D.Z. Effects of applying potassium on kiwifruit eating quality and storage life. J. Fruit Sci. 2006, 23, 200–204. [Google Scholar] [CrossRef]
- Liu, G.; Hanlon, E. Soil pH Range for Optimum Commercial Vegetable Production: HS1207/HS1207, 10/2012. EDIS 2012, 2012. [Google Scholar] [CrossRef]
- Yanni, L.; Yanan, T.; Chen, M.; Bomei, W.; Xinyue, Z. Present situation and adjustment measures of orchard soil pH in Shaanxi area. Shaanxi J. Agric. Sci. 2019, 65, 58–61. [Google Scholar]
- Zhang, H.-Y.; Hu, B.; Bao, W.-K.; Li, G.-L.; Pan, H.-B.; Du, B. Current status and change tendency of soil pH in mango orchards in Panzhihua City. Chin. J. Appl. Environ. Biol. 2020, 26, 63–73. [Google Scholar] [CrossRef]
- Shuai, Y.; Liang, S.; Zhenjie, L.; Fuchun, Z.; Kai, X.; Jicun, Y.; Shaoyu, Z.; Deying, Z. Correlation analysis of leaf and fruit mineral nutrition and fruit quality of Nanguo pear. China Fruits 2022, 33–36. [Google Scholar] [CrossRef]
- Szűcs, E.; Kállay, T. Interaction of nutrient supply and crop load of apple trees (Malus domestica Borkh.). Int. J. Hortic. Sci. 2008, 14, 33–35. [Google Scholar] [CrossRef]
- Maity, A.; Marathe, R.A.; Sarkar, A.; Basak, B.B. Phosphorus and potassium supplementing bio-mineral fertilizer augments soil fertility and improves fruit yield and quality of pomegranate. Sci. Hortic. 2022, 303, 111234. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, J.-B.; Ren, F.; Wang, S.-D.; Wang, Z.; Li, X.-Y.; Zheng, Z.-Q.; Zheng, S.-Q.; Jiang, Q.; Guo, J.-Y. Yield and quality response of nectarine to different nitrogen topdressing amounts at fruit expanding stage. J. Plant Nutr. Fertil. 2020, 26, 581–586. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, Q.; Ling, Q.; Wei, Y.; Ning, Q.; Kong, F.; Zhang, Y.; Shi, X.; Wang, J. Adjusted nitrogen application using non-destructive monitoring model of citrus leaf functional nitrogen content. Trans. Chin. Soc. Agric. Eng. 2023, 39, 167–175. [Google Scholar] [CrossRef]
- Mengqing, S.; Jiali, Y.; Yijian, L.; Shiwen, W.; Lina, Y.; Xiping, D. Relationship between drought adaptability and potassium nutrient characteristics in different potato varieties. Agric. Res. Arid. Areas 2024, 42, 51. [Google Scholar] [CrossRef]
- Wu, X.; Shen, C.-W.; Ding, Y.-F.; Wu, C.-C.; Dong, C.-X.; Xu, Y.-C. Potassium accumulation in ‘Huangguan’ pear fruits and leaves and theirresponse to different potassium application. J. Plant Nutr. Fertil. 2016, 22, 1425–1432. [Google Scholar] [CrossRef]
- Zhao, X.; Xiao, W.; Guo, J.; Gao, D.; Fu, X.; Li, D. Effects of supplementary blue light on photosynthetic performance and sugar and acid accumulation of nectarine in protected cultivation. Chin. Bull. Bot. 2018, 53, 227–237. [Google Scholar] [CrossRef]
- Yan, J.; Liu, J.; Yang, S.; Jiang, C.; Liu, Y.; Zhang, N.; Sun, X.; Zhang, Y.; Zhu, K.; Peng, Y.; et al. Light quality regulates plant biomass and fruit quality through a photoreceptor-dependent HY5-LHC/CYCB module in tomato. Hortic. Res. 2023, 10, uhad219. [Google Scholar] [CrossRef]
- Al-Saif, A.M.; Abdel-Sattar, M.; Aboukarima, A.M.; Eshra, D.H.; Górnik, K. Physico-Chemical Properties Prediction of Flame Seedless Grape Berries Using an Artificial Neural Network Model. Foods 2022, 11, 2766. [Google Scholar] [CrossRef]
- Amoriello, T.; Ciccoritti, R.; Ferrante, P. Prediction of Strawberries’ Quality Parameters Using Artificial Neural Networks. Agronomy 2022, 12, 963. [Google Scholar] [CrossRef]
- AlKandari, M.; Ahmad, I. Solar power generation forecasting using ensemble approach based on deep learning and statistical methods. Appl. Comput. Inform. 2020, 20, 231–250. [Google Scholar] [CrossRef]
- Al-Saif, A.M.; Abdel-Sattar, M.; Eshra, D.H.; Sas-Paszt, L.; Mattar, M.A. Predicting the Chemical Attributes of Fresh Citrus Fruits Using Artificial Neural Network and Linear Regression Models. Horticulturae 2022, 8, 1016. [Google Scholar] [CrossRef]
- Hassan-Esfahani, L.; Torres-Rua, A.; Jensen, A.; McKee, M. Assessment of Surface Soil Moisture Using High-Resolution Multi-Spectral Imagery and Artificial Neural Networks. Remote Sens. 2015, 7, 2627–2646. [Google Scholar] [CrossRef]
- Göçmen Polat, E.; Kuvvetli, Y. Prediction of Citrus Fruits Production using Artificial Neural Networks and Linear Regression Analysis. Erzincan Üniversitesi Fen. Bilim. Enstitüsü Derg. 2020, 13, 972–983. [Google Scholar] [CrossRef]
- Ahmed, A.R.; Aleid, S.M.; Mohammed, M. Impact of Modified Atmosphere Packaging Conditions on Quality of Dates: Experimental Study and Predictive Analysis Using Artificial Neural Networks. Foods 2023, 12, 3811. [Google Scholar] [CrossRef]
- Qian, J.; Xing, B.; Wu, X.; Chen, M.; Wang, Y.A. A smartphone-based apple yield estimation application using imaging features and the ANN method in mature period. Sci. Agric. 2018, 75, 273–280. [Google Scholar] [CrossRef]
- Fang, S.; Hou, X.; Liang, X. Response Mechanisms of Plants Under Saline-Alkali Stress. Front. Plant Sci. 2021, 12, 667458. [Google Scholar] [CrossRef]
- Jing, S.; Zhenlong, B.; Yuebo, L.; Xueming, Z.; Xiaoguang, Q.; Bingbing, Z. Research Progress on Salt-alkali Tolerance Mechanism of Apple Plants. Mol. Plant Breedin 2024, 22, 3961–3969. [Google Scholar] [CrossRef]
- Xie, B.; An, X.-H.; Chen, Y.-H.; Cheng, C.-G.; Zhao, D.-Y.; Kang, G.-D.; Zhou, J.-T.; Li, Z.; Zhang, Y.-Z.; Yang, A.; et al. Response and Adaptability Evaluation of Apple Rootstocks to Low Nitrogen Stress. J. Plant Nutr. Fertil. 2022, 28, 1092–1103. [Google Scholar] [CrossRef]
- Hamza, D.; Sefan, R.; El-Boray, M. Effect of Potassium Nano Fertilizer on Yield and Berry Qualities of ‘Flame Seedless’ Grapevines. J. Plant Prod. 2019, 10, 929–934. [Google Scholar] [CrossRef]
- Dahro, B.; Li, C.; Liu, J.-H. Overlapping responses to multiple abiotic stresses in citrus: From mechanism understanding to genetic improvement. Hortic. Adv. 2023, 1, 4. [Google Scholar] [CrossRef]
- Wei, L. Practice and Application of Precision Agriculture Technology in Fruit Tree Planting. China Fruit Ind. Inf. 2024, 41, 37–39. [Google Scholar] [CrossRef]
- Xin, Y.; Yue, W.; Yuxin, Y.; Yuanpeng, D. Evaluation of composite saline-alkali tolerance of grape rootstocks ‘SA15’ and ‘SA17’. Chin. Foreign Grapes Wine 2019, 34–38. [Google Scholar] [CrossRef]

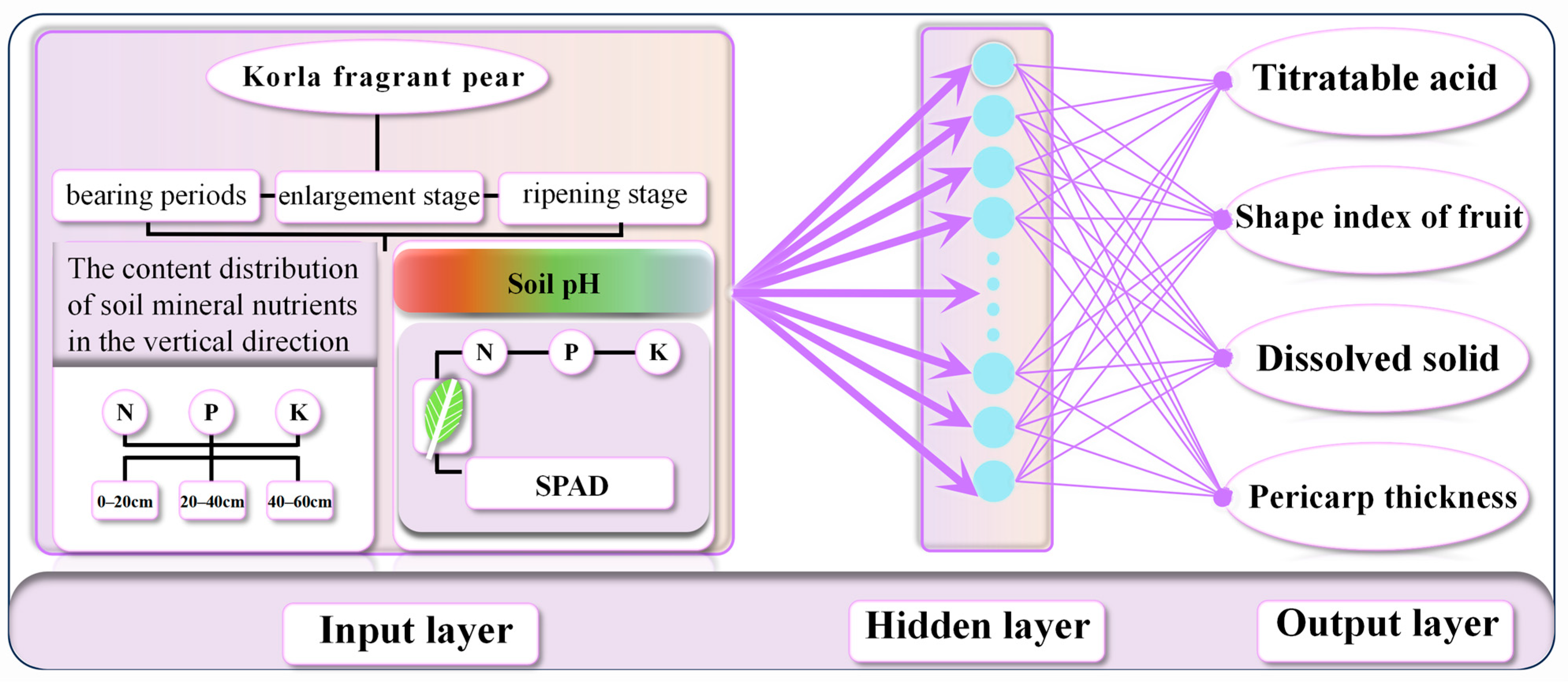






| Output Layer | Input Layer |
|---|---|
| Titratable acid | A3, A8, A9, A10, A11, A12, A27, A36 |
| Fruit shape index | A3, A16, A17, A27, A28, A29, A31, A32, A33, A34, A37, A40 |
| Soluble solids | A8, A17, A18, A21, A33, A35, A38, A39 |
| Peel thickness | A3, A16, A17, A18, A19, A33, A35, A38, A48 |
| Training Function | Transfer Function | Best Model | Training Set | Validation Set | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | MAE | MBE | MAPE | RMSE | R2 | MAE | MBE | MAPE | RMSE | |||
| Trainlm | Tansig-Purelin | 12-10-1 | 0.98 | 0.0034 | 0.0010 | 0.0029 | 0.0073 | 0.96 | 0.0091 | 0.0015 | 0.0077 | 0.0125 |
| logsig- Purelin | 12-8-1 | 0.97 | 0.0032 | 0.0014 | 0.0028 | 0.0083 | 0.96 | 0.0080 | 0.0003 | 0.0068 | 0.0104 | |
| Traingd | Tansig-Purelin | 12-9-1 | 0.66 | 0.0216 | 0.0029 | 0.1818 | 0.0277 | 0.68 | 0.0280 | 0.0029 | 0.0240 | 0.0350 |
| logsig- Purelin | 12-10-1 | 0.46 | 0.0301 | 0.0030 | 0.0256 | 0.0389 | 0.32 | 0.0317 | 0.0033 | 0.0268 | 0.0401 | |
| Traingdm | Tansig-Purelin | 12-12-1 | 0.64 | 0.0229 | 0.0292 | 0.0194 | 0.0283 | 0.69 | 0.0268 | 0.0079 | 0.0225 | 0.0336 |
| logsig- Purelin | 12-11-1 | 0.57 | 0.0294 | 0.0041 | 0.0249 | 0.0356 | 0.52 | 0.0253 | 0.0044 | 0.0213 | 0.0308 | |
| Training Function | Transfer Function | Best Model | Training Set | Validation Set | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | MAE | MBE | MAPE | RMSE | R2 | MAE | MBE | MAPE | RMSE | |||
| Trainlm | Tansig- Purelin | 9-9-1 | 0.92 | 0.0198 | 0.0002 | 0.0175 | 0.0289 | 0.90 | 0.0238 | 0.0042 | 0.0213 | 0.0363 |
| logsig- Purelin | 9-9-1 | 0.90 | 0.0193 | 0.0038 | 0.0174 | 0.0324 | 0.84 | 0.0247 | 0.0073 | 0.2335 | 0.0434 | |
| Traingd | Tansig- Purelin | 9-9-1 | 0.54 | 0.0587 | 0.0075 | 0.0510 | 0.0717 | 0.53 | 0.0484 | 0.0040 | 0.0415 | 0.0673 |
| logsig- Purelin | 9-12-1 | 0.45 | 0.0560 | 0.0005 | 0.0476 | 0.6070 | 0.37 | 0.0665 | 0.0250 | 0.0629 | 0.0961 | |
| Traingdm | Tansig- Purelin | 9-11-1 | 0.64 | 0.0501 | 0.0037 | 0.0429 | 0.0626 | 0.59 | 0.0532 | 0.0182 | 0.0441 | 0.0671 |
| logsig- Purelin | 9-12-1 | 0.48 | 0.0529 | 0.0086 | 0.0452 | 0.0685 | 0.52 | 0.0617 | 0.0118 | 0.0560 | 0.0859 | |
| Training Function | Transfer Function | Best Model | Training Set | Validation Set | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | MAE | MBE | MAPE | RMSE | R2 | MAE | MBE | MAPE | RMSE | |||
| Trainlm | Tansig-Purelin | 8-12-1 | 0.92 | 0.0659 | 0.0033 | 0.0926 | 0.0939 | 0.92 | 0.0611 | 0.0031 | 0.0759 | 0.0789 |
| logsig- Purelin | 8-11-1 | 0.86 | 0.0152 | 0.0078 | 0.0131 | 0.0192 | 0.83 | 0.0164 | 0.0109 | 0.0142 | 0.0196 | |
| Traingd | Tansig-Purelin | 8-8-1 | 0.41 | 0.1835 | 0.0159 | 0.2355 | 0.2339 | 0.57 | 0.1761 | 0.0491 | 0.2080 | 0.2339 |
| logsig- Purelin | 8-10-1 | 0.27 | 0.2111 | 0.0408 | 0.2669 | 0.2730 | 0.20 | 0.2308 | 0.0604 | 0.2669 | 0.2865 | |
| Traingdm | Tansig-Purelin | 8-8-1 | 0.34 | 0.1962 | 0.0029 | 0.7228 | 0.2648 | 0.56 | 0.1605 | 0.0029 | 0.1815 | 0.2012 |
| logsig- Purelin | 8-10-1 | 0.44 | 0.1879 | 0.0025 | 0.2350 | 0.2313 | 0.51 | 0.1735 | 0.0297 | 0.1987 | 0.2404 | |
| Training Function | Transfer Function | Best Model | TRAINING SET | Validation Set | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | MAE | MBE | MAPE | RMSE | R2 | MAE | MBE | MAPE | RMSE | |||
| Trainlm | Tansig-Purelin | 8-9-1 | 0.91 | 0.1829 | 0.0917 | 0.0158 | 0.2698 | 0.90 | 0.2542 | 0.0367 | 0.0217 | 0.3710 |
| logsig- Purelin | 8-9-1 | 0.93 | 0.1760 | 0.0220 | 0.0151 | 0.2699 | 0.78 | 0.2969 | 0.0851 | 0.0260 | 0.4222 | |
| Traingd | Tansig-Purelin | 8-10-1 | 0.77 | 0.3821 | 0.0183 | 0.0320 | 0.4888 | 0.59 | 0.4241 | 0.0165 | 0.0371 | 0.5608 |
| logsig- Purelin | 8-11-1 | 0.47 | 0.5724 | 0.0300 | 0.0481 | 0.6919 | 0.29 | 0.6626 | 0.1079 | 0.0549 | 0.8767 | |
| Traingdm | Tansig-Purelin | 8-9-1 | 0.52 | 0.5005 | 0.0354 | 0.0422 | 0.6557 | 0.46 | 0.6199 | 0.0102 | 0.0526 | 0.7835 |
| logsig- Purelin | 8-11-1 | 0.20 | 0.7061 | 0.0215 | 0.0603 | 0.8979 | 0.12 | 0.7021 | 0.1672 | 0.0584 | 0.8906 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, M.; Li, Y.; Wang, L.; Fan, W.; Wang, Z.; Wang, H.; Guo, K.; Fu, L.; Bao, J. Research on the Precise Regulation of Korla Fragrant Pear Quality Based on Sensitivity Analysis and Artificial Neural Network Model. Agronomy 2025, 15, 1236. https://doi.org/10.3390/agronomy15051236
Yu M, Li Y, Wang L, Fan W, Wang Z, Wang H, Guo K, Fu L, Bao J. Research on the Precise Regulation of Korla Fragrant Pear Quality Based on Sensitivity Analysis and Artificial Neural Network Model. Agronomy. 2025; 15(5):1236. https://doi.org/10.3390/agronomy15051236
Chicago/Turabian StyleYu, Mingyang, Yang Li, Lanfei Wang, Weifan Fan, Zengheng Wang, Hao Wang, Kailu Guo, Liang Fu, and Jianping Bao. 2025. "Research on the Precise Regulation of Korla Fragrant Pear Quality Based on Sensitivity Analysis and Artificial Neural Network Model" Agronomy 15, no. 5: 1236. https://doi.org/10.3390/agronomy15051236
APA StyleYu, M., Li, Y., Wang, L., Fan, W., Wang, Z., Wang, H., Guo, K., Fu, L., & Bao, J. (2025). Research on the Precise Regulation of Korla Fragrant Pear Quality Based on Sensitivity Analysis and Artificial Neural Network Model. Agronomy, 15(5), 1236. https://doi.org/10.3390/agronomy15051236





