Numerical Simulation of Dry and Wet Rice Seeds in an Air-Suction Seed Metering Device
Abstract
1. Introduction
2. Materials and Methods
2.1. Measurement of Seed Physical Characteristics
2.1.1. Rice Seeds
2.1.2. Size, Thousand-Grain Weight, and Density
2.1.3. Contact Parameters
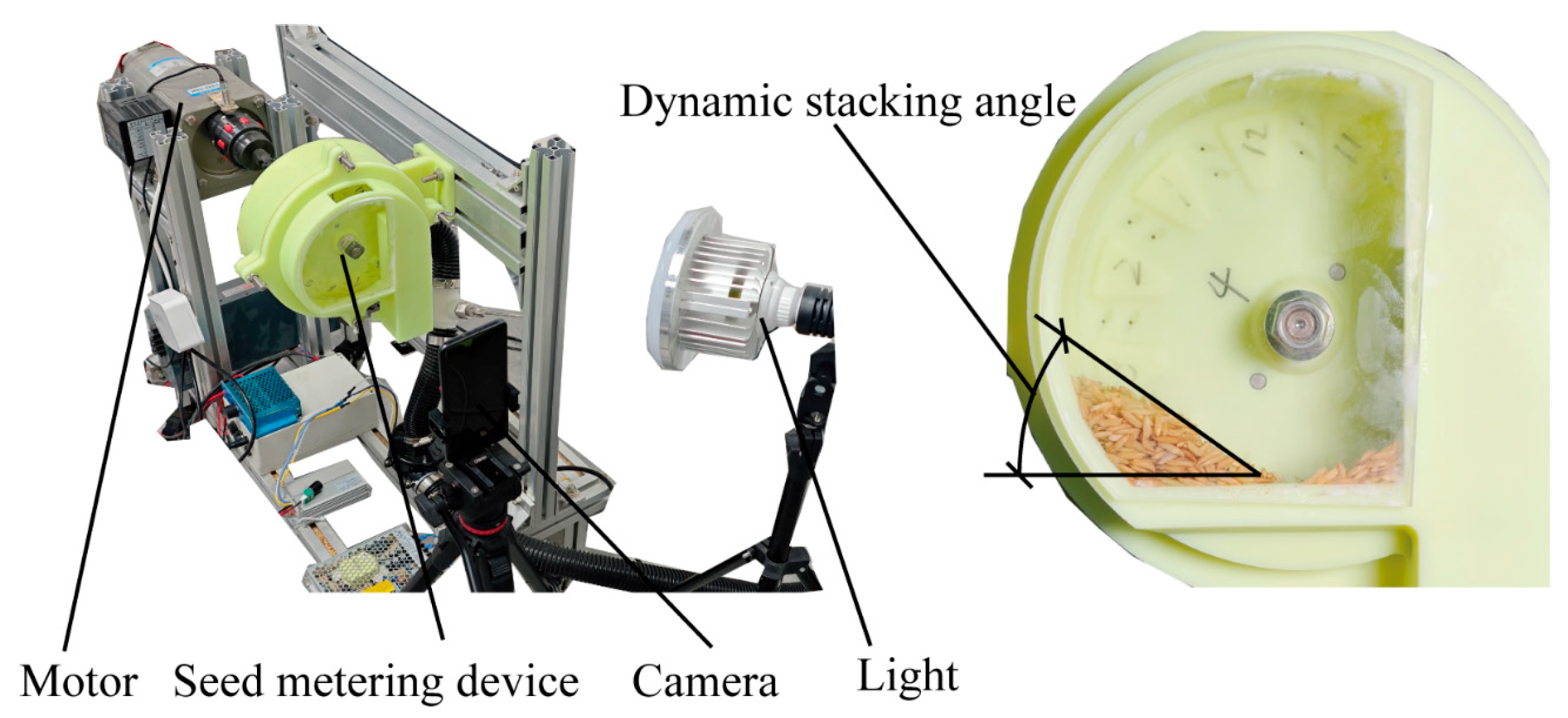
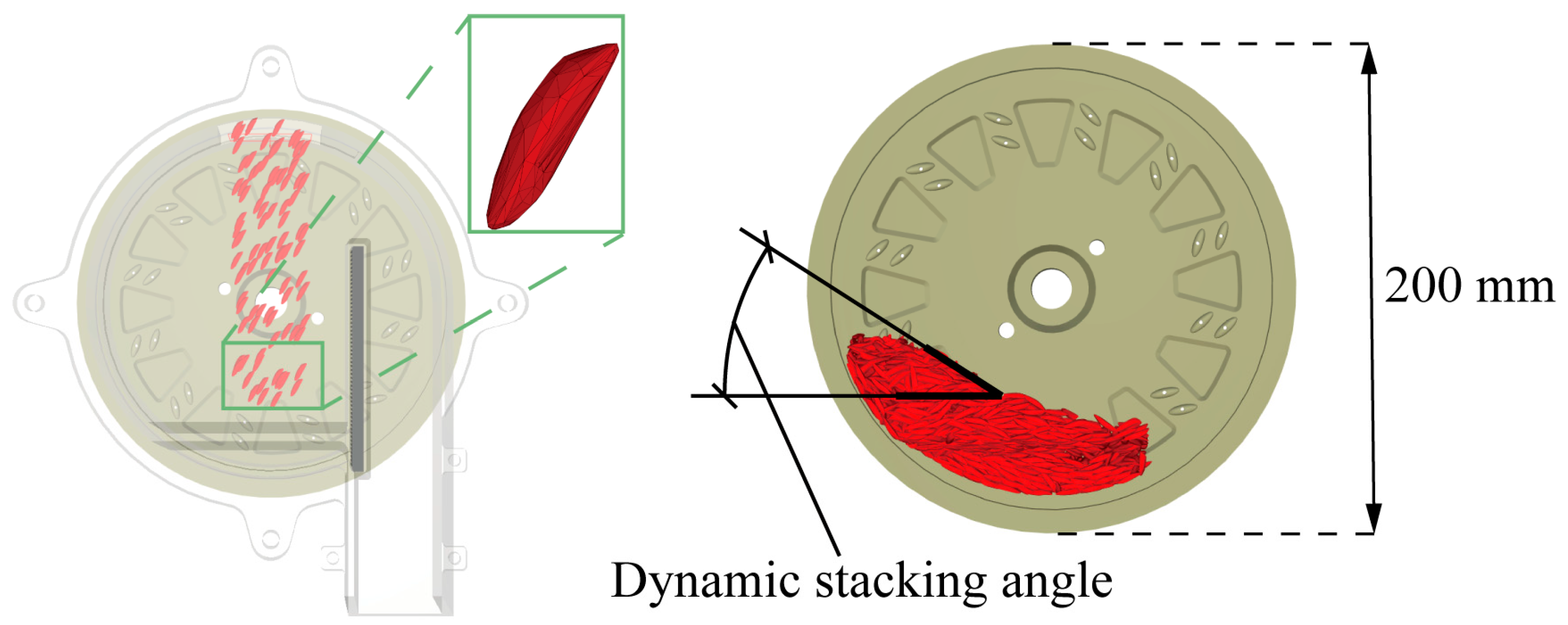
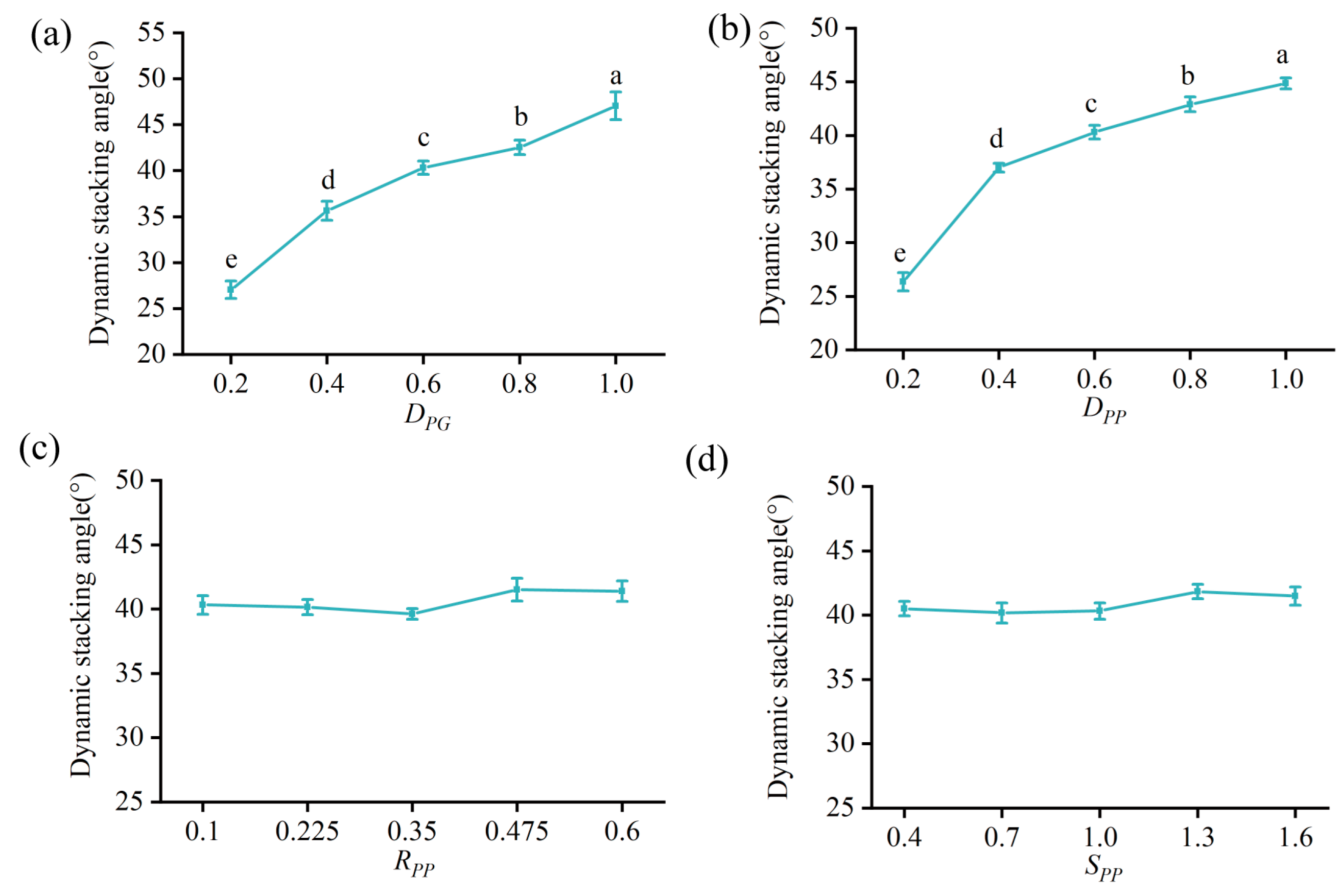
2.1.4. Dynamic Stacking Angle
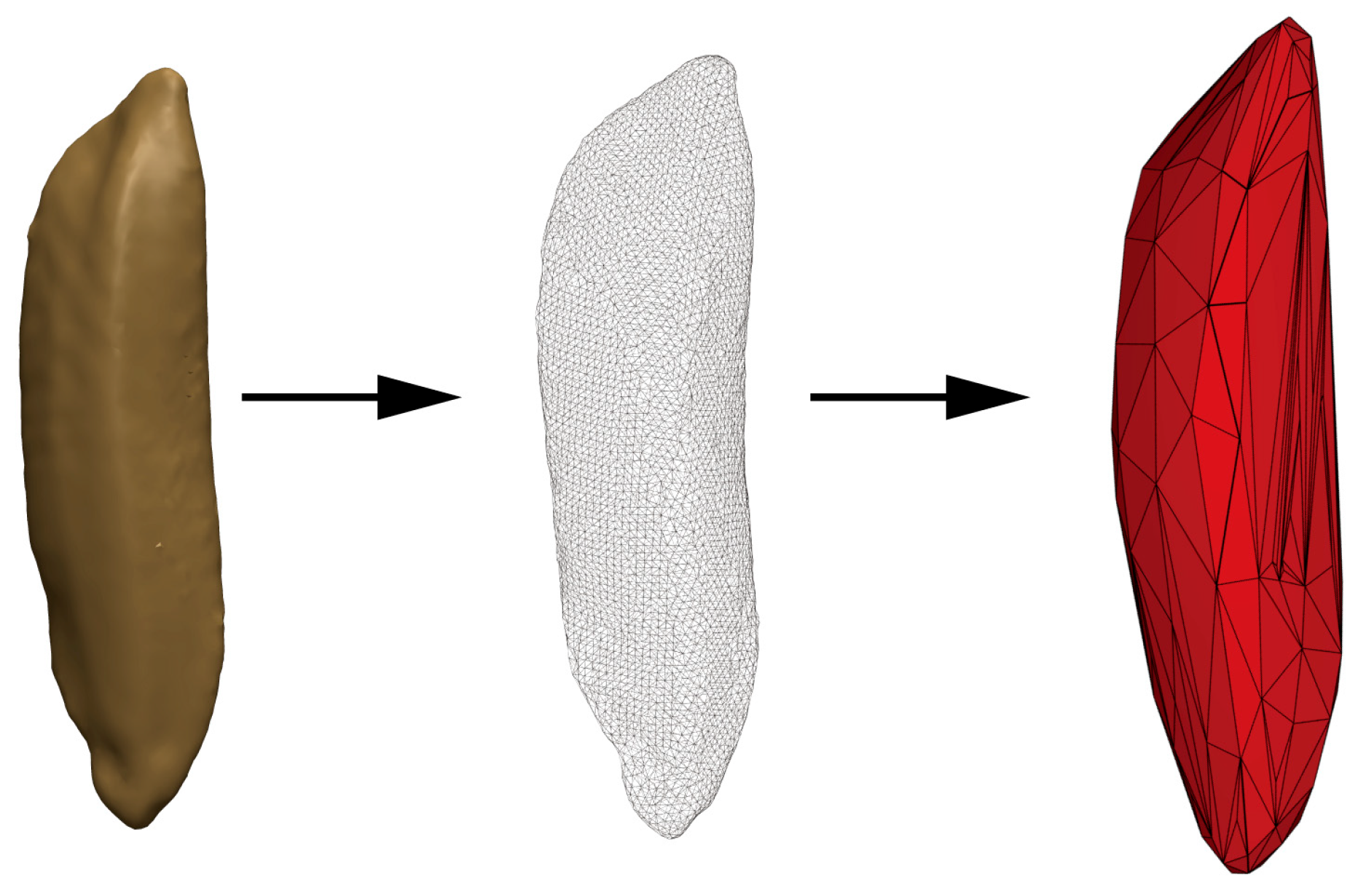
2.2. Parameter Calibration of the Discrete Elemental Model of Rice Seed
2.2.1. Modeling Methods
2.2.2. Experimental Design
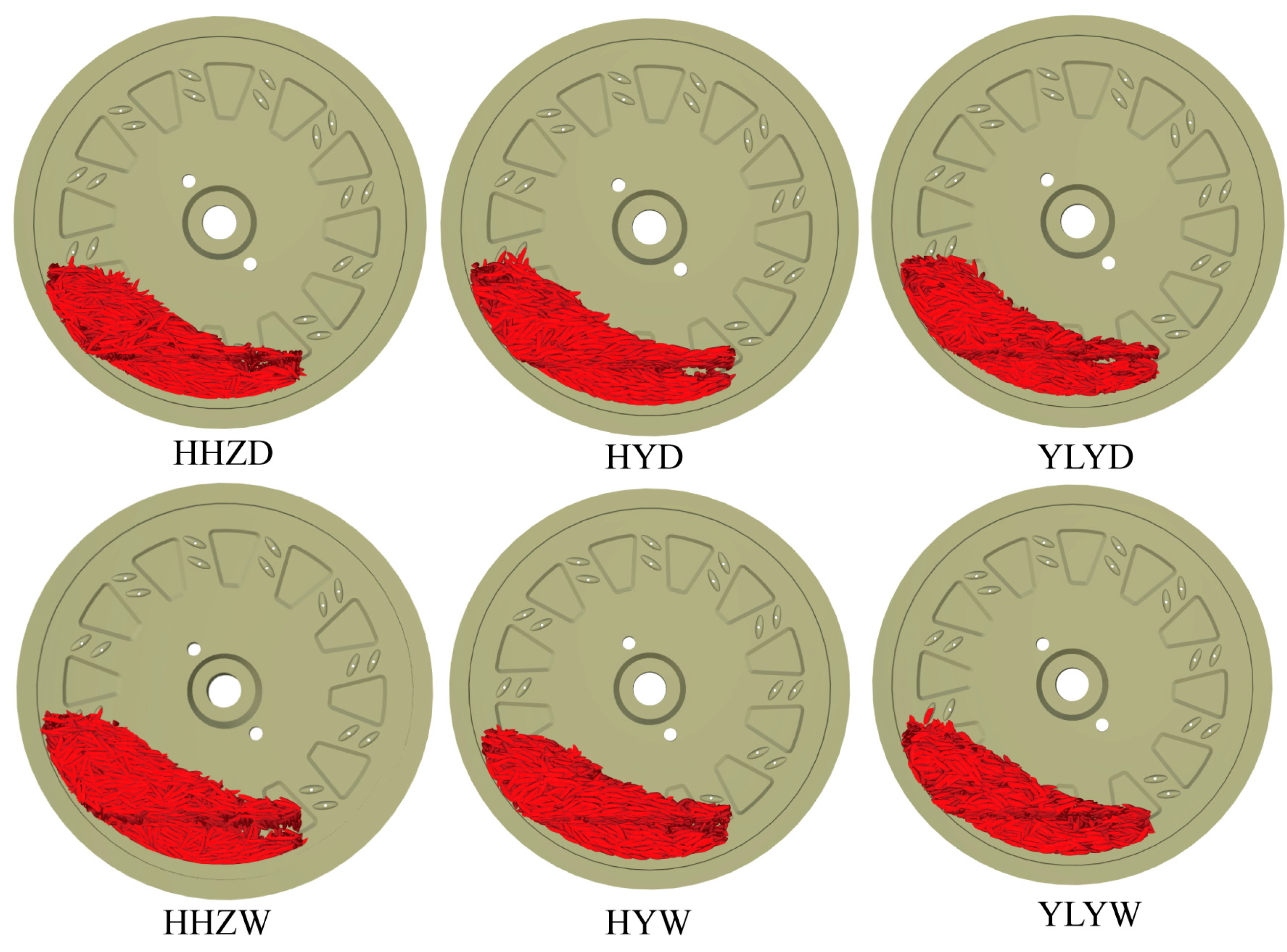
2.3. Seeding Accuracy Test
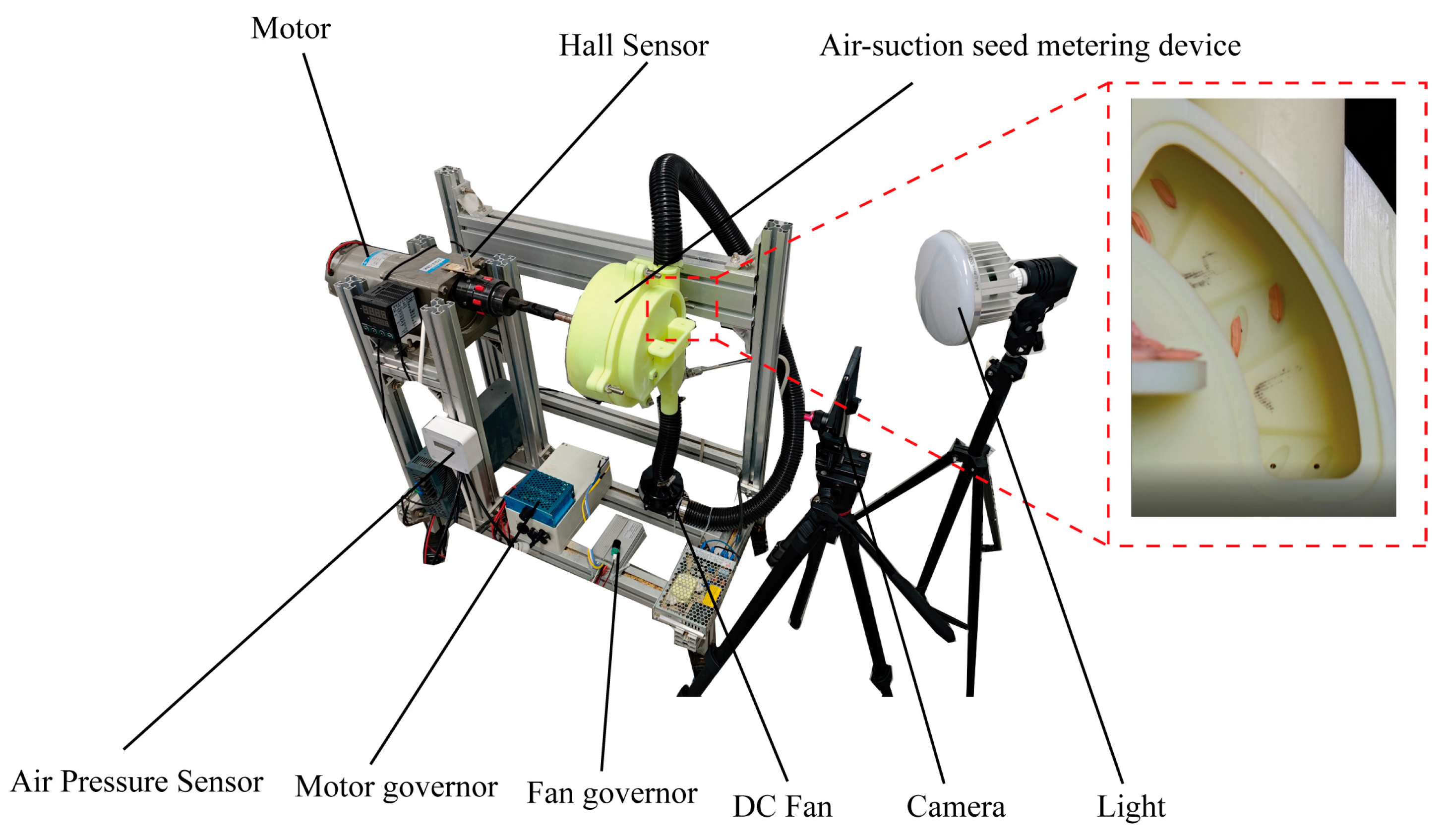
2.4. CFD-DEM Two-Way Coupled Numerical Simulation
2.4.1. Theoretical Equations of CFD-DEM
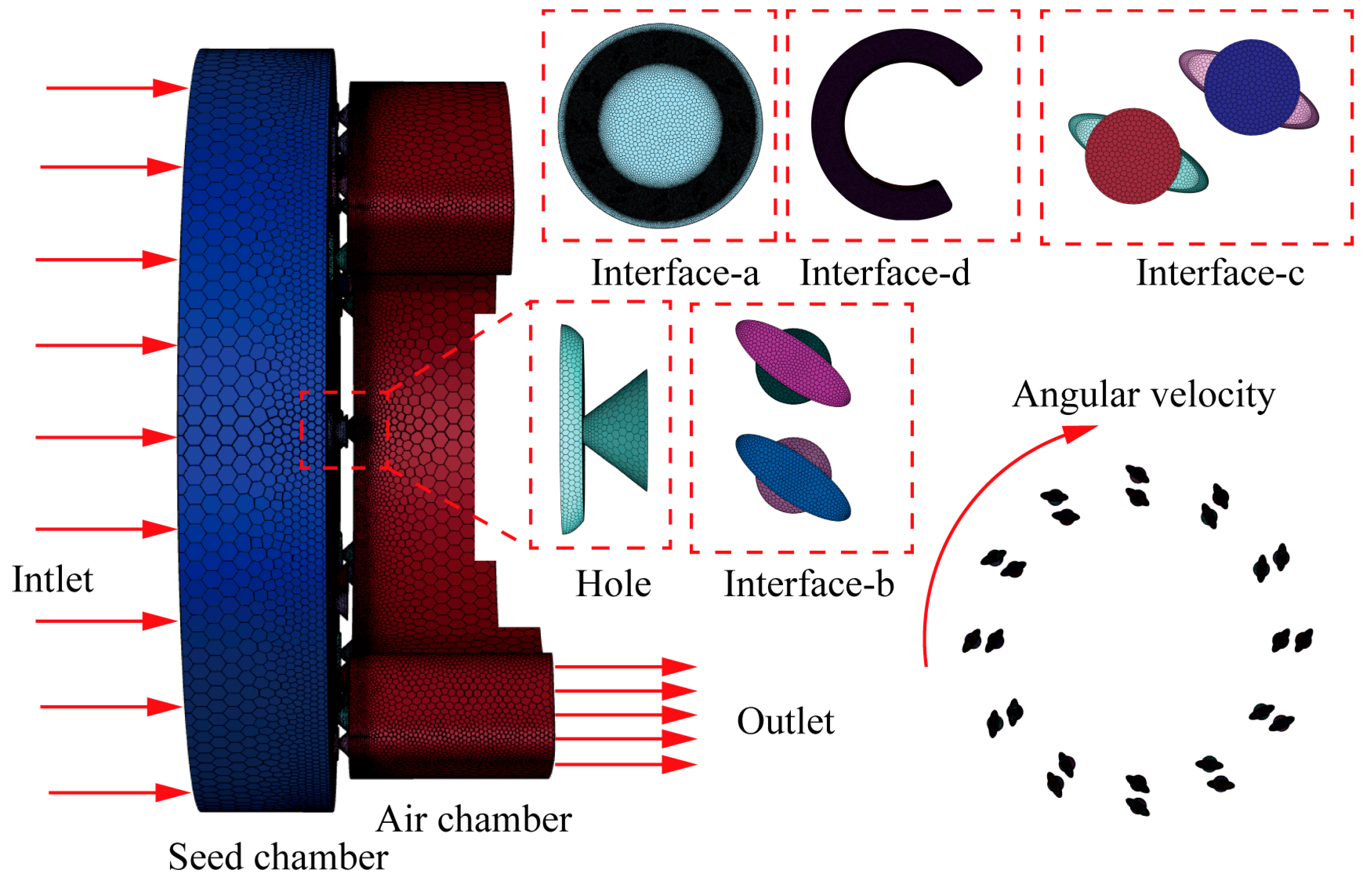
2.4.2. Fluid Domain Meshing
2.4.3. Data Processing
3. Results
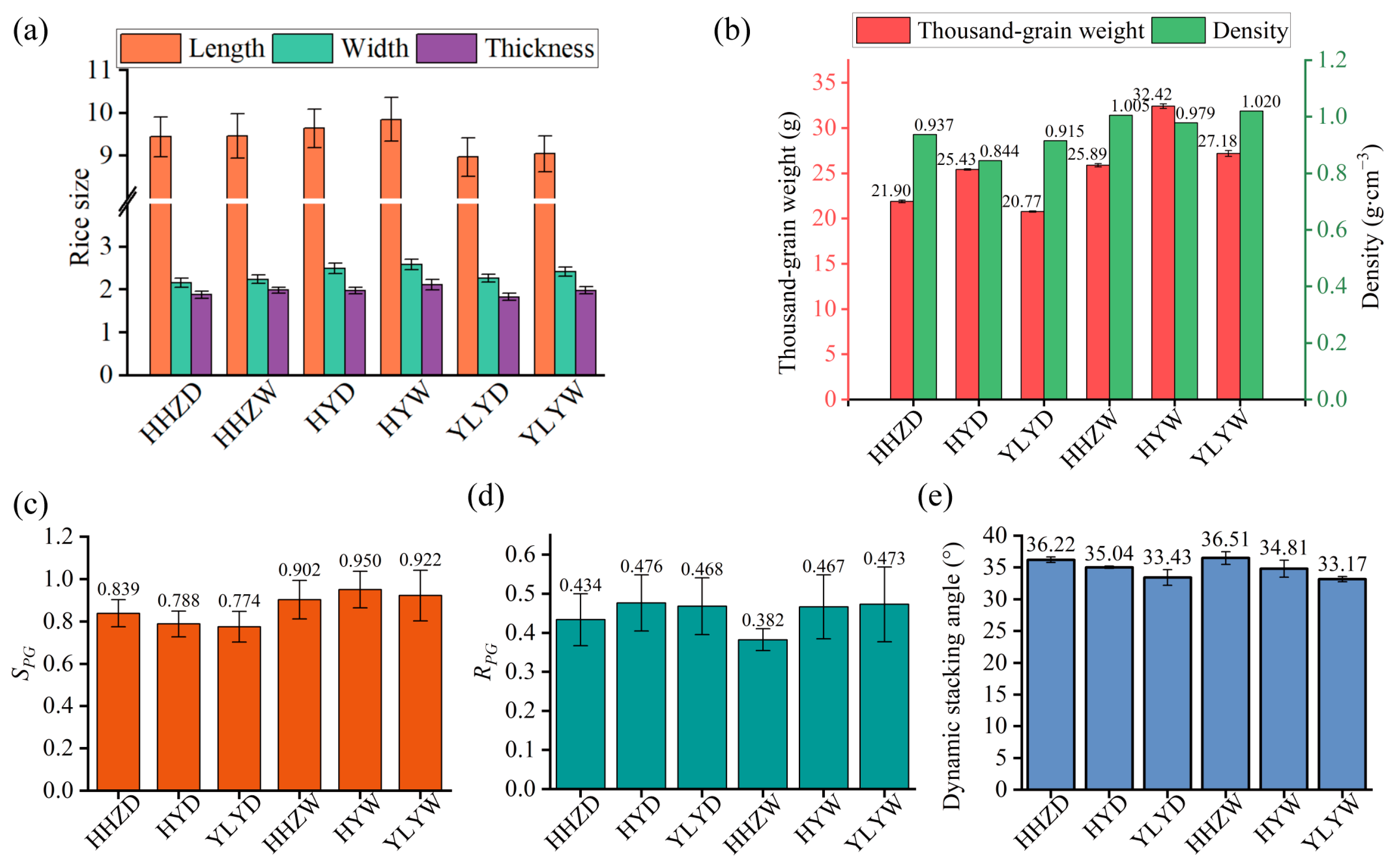
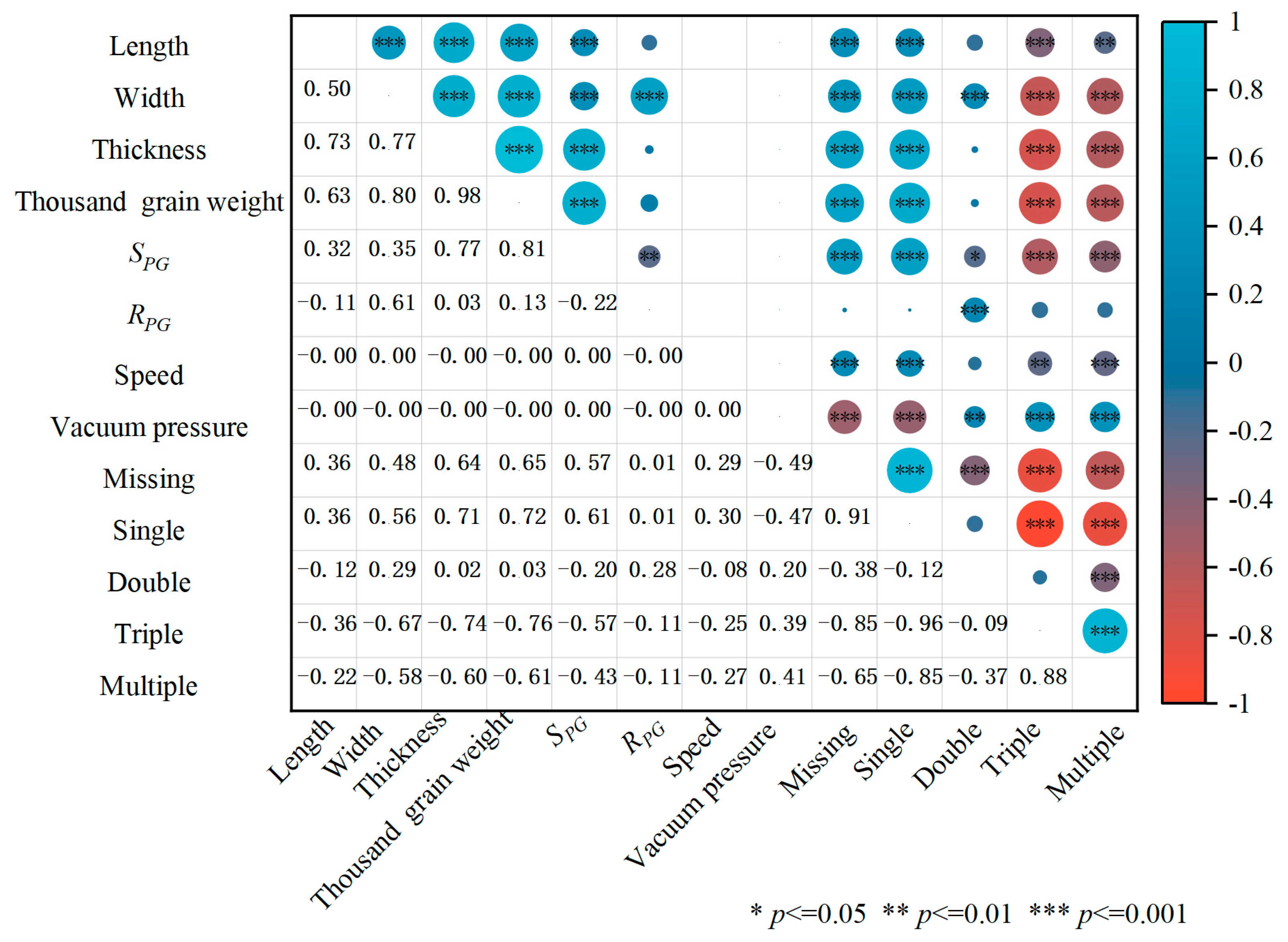
3.1. Seed Physical Characteristics
3.2. Discrete Elemental Model of Rice Seed
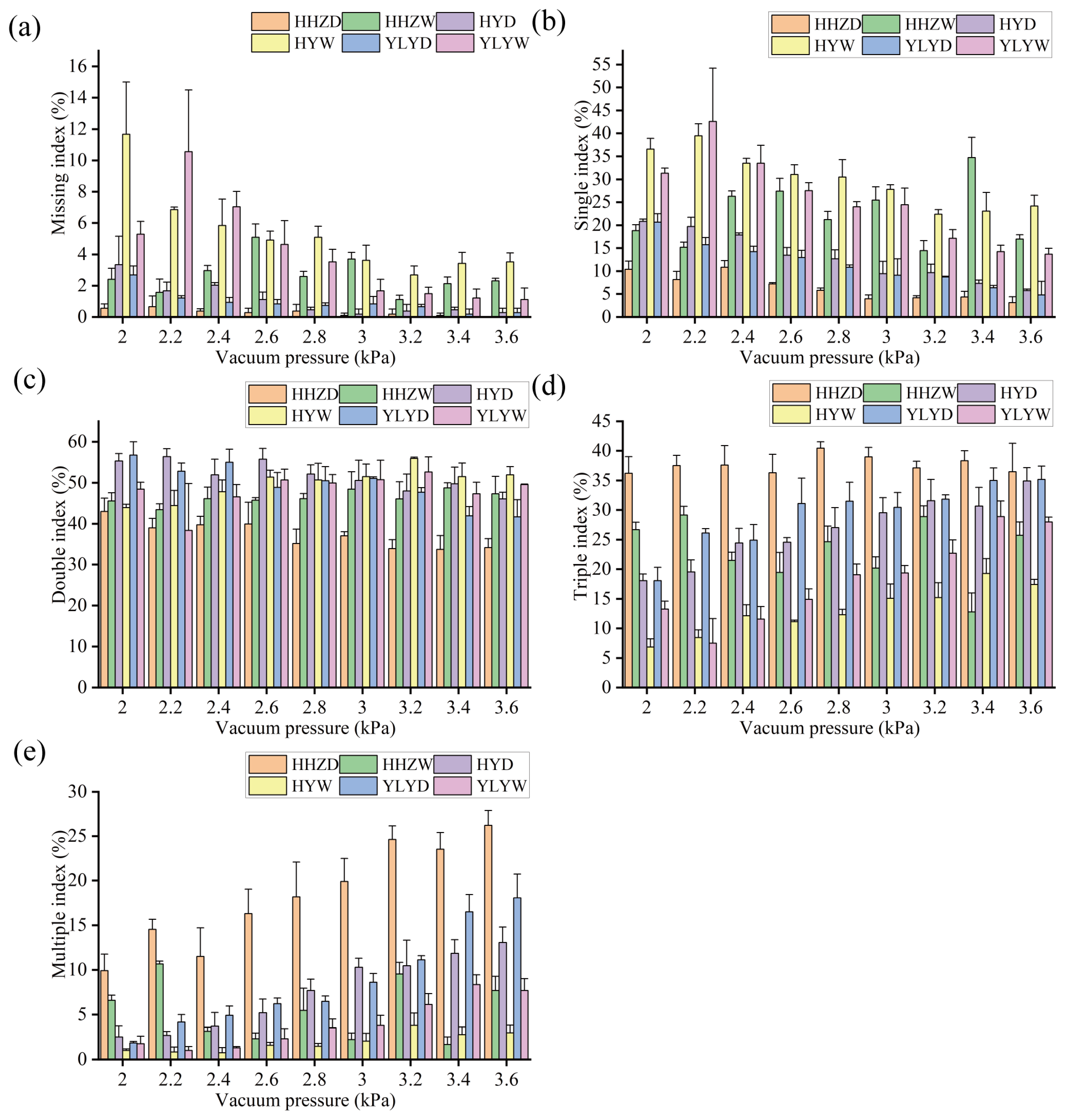
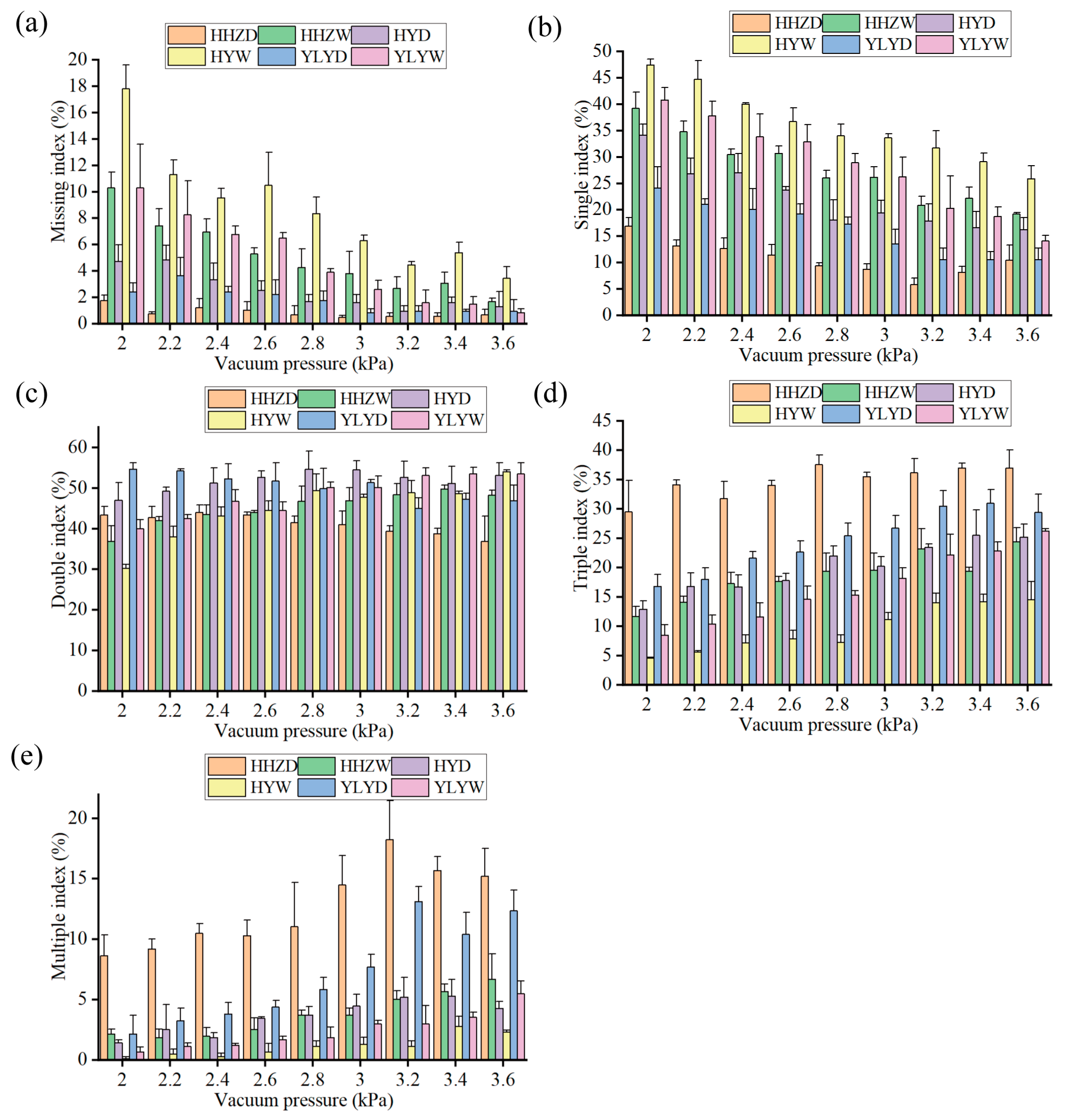
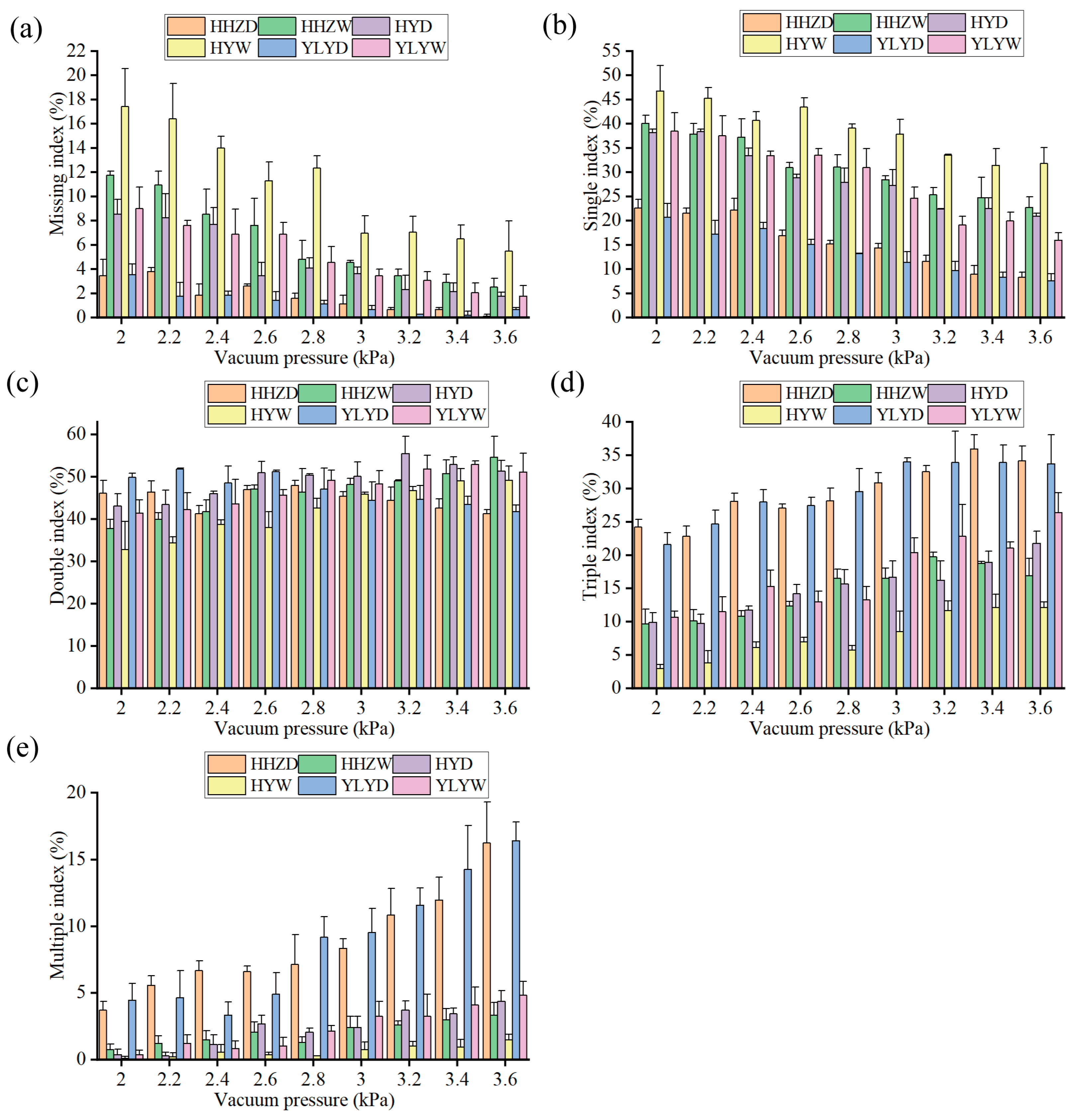
3.3. Seeding Accuracy
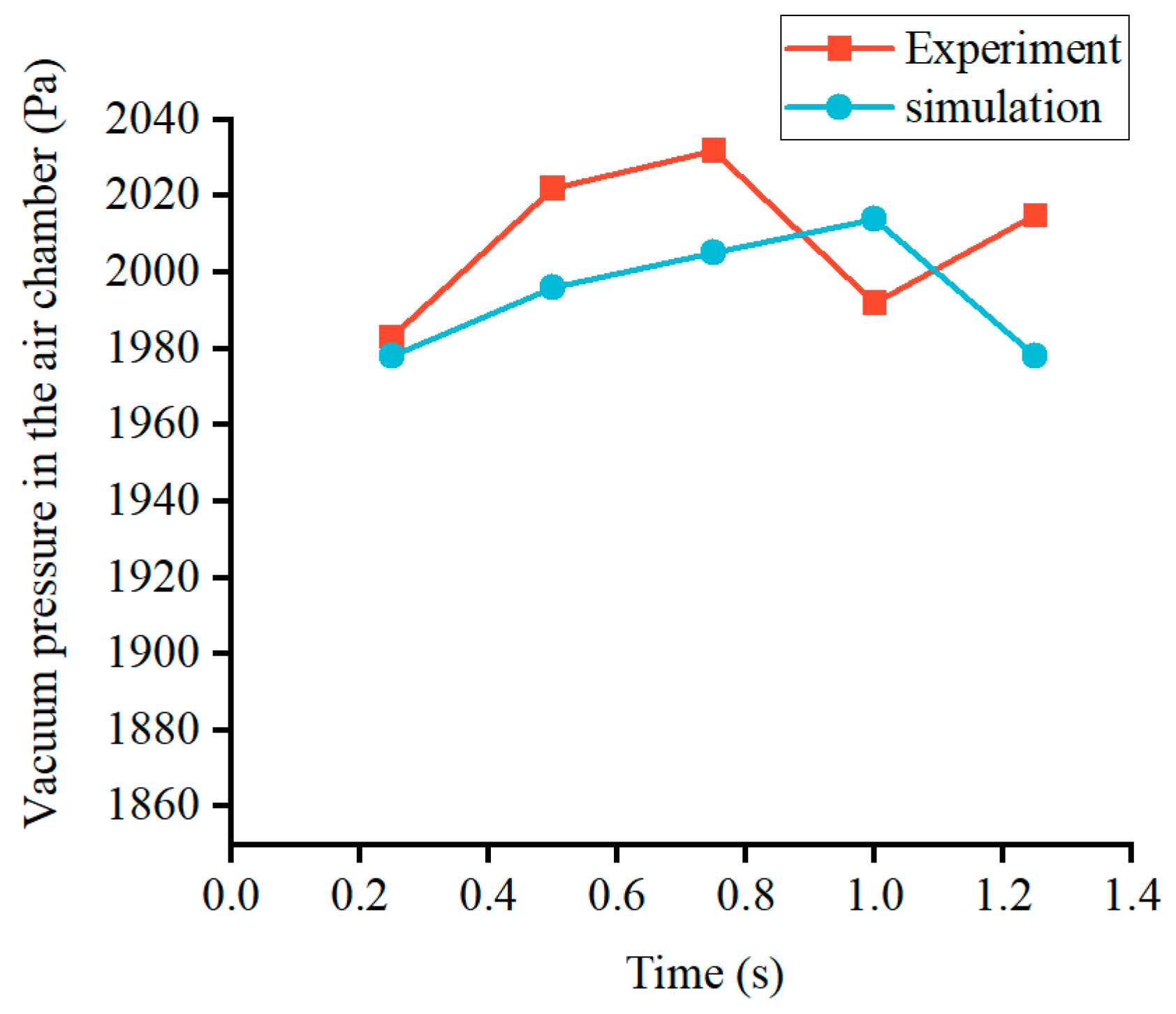
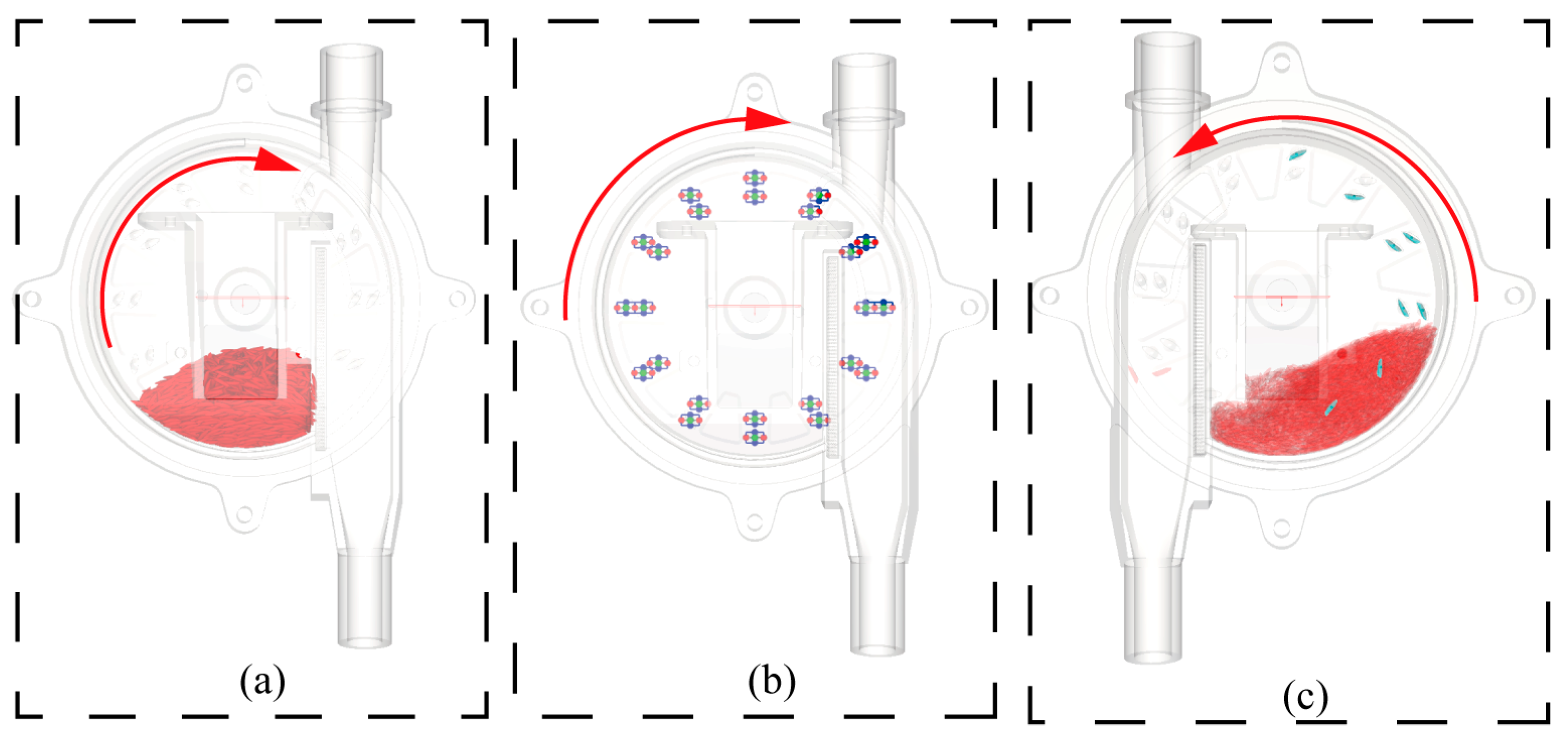
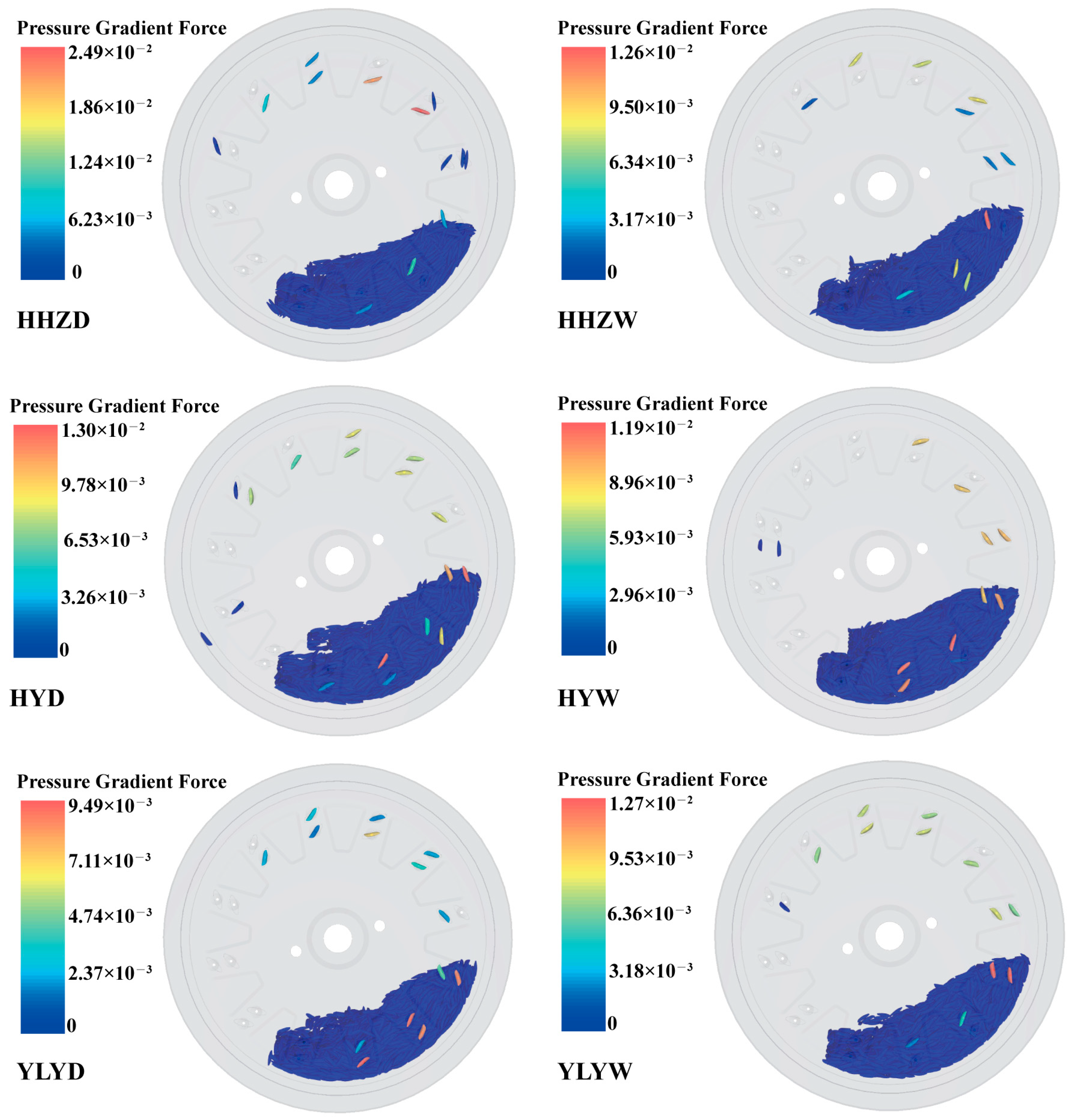
3.4. CFD-DEM Simulation
4. Discussion
5. Conclusions
- (1)
- Rice seeds subjected to pre-germination treatment exhibited greater triaxial dimensions, thousand-grain weight, density, and coefficient of static friction between the seeds and the seed discharger than dry rice seeds. The effects of RPP and SPP on the dynamic stacking angle were found to be insignificant (p > 0.05), whereas the effects of DPG and DPP on the dynamic stacking angle were significant (p < 0.05). The difference between the calibrated seeds’ simulated and physical dynamic stacking angles was minimal, indicating that the polyhedral method is reliable for constructing the discrete elements of rice seeds;
- (2)
- For the same variety of seeds, the missing index and single index of wet rice seeds were higher than those of dry rice seeds, while the triple index and multiple index of dry rice seeds were higher than those of wet rice seeds. No significant difference was observed in the double index between dry and wet rice seeds. Additionally, there were differences in the missing index, single index, triple index, and multiple index for the same treatment across different rice seed varieties;
- (3)
- For the same variety of rice seeds, the normal and tangential forces on wet rice seeds during seed filling were higher than those on dry rice seeds. Additionally, for the same treatment, the greater the action force between the seeds, the higher the missing index and single index. The differences in seeding accuracy between dry and wet rice seeds of the same variety were primarily attributed to the thousand-grain weight, the coefficient of static friction between the air-suction seed metering device and the seed, and the action force between the seeds.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational fluid dynamics |
| DEM | Discrete element method |
| SPG | Static friction coefficient between the seed meter and the seed |
| RPG | Restitution coefficient of the collision between the seed and the seed metering device |
| DPG | Dynamic friction coefficient between the seed and the metering device |
| DPP | Dynamic friction coefficient between seeds and seeds |
| RPP | Restitution coefficient between seeds and seeds |
| SPP | Static friction coefficient between seeds and seeds |
| DSA | Dynamic stacking angle |
References
- Lv, Y.S.; Shao, G.N.; Jiao, G.A.; Sheng, Z.H.; Xie, L.H.; Hu, S.K.; Tang, S.Q.; Wei, X.J.; Hu, P.S. Targeted mutagenesis of that negatively regulates mesocotyl elongation enables the generation of direct-seeding rice with improved grain yield. Mol. Plant 2021, 14, 344–351. [Google Scholar] [CrossRef] [PubMed]
- Ma, P.; Zhou, L.; Liao, X.H.; Zhang, K.Y.; Aer, L.; Yang, E.L.; Deng, J.; Zhang, R.P. Effects of Low Light after Heading on the Yield of Direct Seeding Rice and Its Physiological Response Mechanism. Plants 2023, 12, 4077. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.H.; Mo, Z.W.; Liao, J.; Pan, S.G.; Chen, X.F.; Zheng, L.; Luo, X.W.; Wang, Z.M. Lodging Resistance Related to Root Traits for Mechanized Wet-Seeding of Two Super Rice Cultivars. Rice Sci. 2021, 28, 200–208. [Google Scholar] [CrossRef]
- Kargbo, M.B.; Pan, S.G.; Mo, Z.W.; Wang, Z.M.; Luo, X.W.; Tian, H.; Hossain, M.F.; Ashraf, U.; Tang, X.R. Physiological Basis of Improved Performance of Super Rice to Deep Placed Fertilizer with Precision Hill-drilling Machine. Int. J. Agric. Biol. 2016, 18, 797–804. [Google Scholar] [CrossRef]
- Zhang, M.H.; Wang, Z.M.; Luo, X.W.; Zang, Y.; Yang, W.W.; Xing, H.; Wang, B.L.; Dai, Y.Z. Review of precision rice hill-drop drilling technology and machine for paddy. Int. J. Agric. Biol. Eng. 2018, 11, 1–11. [Google Scholar] [CrossRef]
- Qian, C.; He, S.Y.; Qin, W.; Jiang, Y.C.; Huang, Z.S.; Zhang, M.L.; Zhang, M.H.; Yang, W.W.; Zang, Y. Influence of Shaped Hole and Seed Disturbance on the Precision of Bunch Planting with the Double-Hole Rice Vacuum Seed Meter. Agronomy 2024, 14, 768. [Google Scholar] [CrossRef]
- Farooq, M.; Barsa, S.M.A.; Wahid, A. Priming of field-sown rice seed enhances germination, seedling establishment, allometry and yield. Plant Growth Regul. 2006, 49, 285–294. [Google Scholar] [CrossRef]
- Tang, H.; Guan, T.; Xu, F.; Xu, C.; Wang, J. Test on adsorption posture and seeding performance of the high-speed precision dual-chamber maize metering device based on the seed characteristics. Comput. Electron. Agric. 2024, 216, 108471. [Google Scholar] [CrossRef]
- Van Loon, J.; Krupnik, T.J.; López-Gómez, J.A.; Timsina, J.; Govaerts, B. A Standard Methodology for Evaluation of Mechanical Maize Seed Meters for Smallholder Farmers Comparing Devices from Latin America, Sub-Saharan Africa, and Asia. Agronomy 2020, 10, 1091. [Google Scholar] [CrossRef]
- Zhong, W.D.; Zhao, X.; Liu, F.; Bai, H.B.; Dong, W.X.; Hu, H.T.; Kong, X. Design and Experiment of Precision Seed Metering Device for Flow Adsorption of Quinoa Seeds. Agriculture 2024, 14, 434. [Google Scholar] [CrossRef]
- Cai, Y.Q.; Luo, X.; Hu, B.; Mao, Z.B.; Li, J.W.; Guo, M.Y.; Wang, J. Theoretical and experimental analyses of high-speed seed filling in limited gear-shaped side space of cotton precision dibbler. Comput. Electron. Agric. 2022, 200, 107202. [Google Scholar] [CrossRef]
- St Jack, D.; Hesterman, D.C.; Guzzomi, A.L. Precision metering of Santalum spicatum (Australian Sandalwood) seeds. Biosyst. Eng. 2013, 115, 171–183. [Google Scholar] [CrossRef]
- Jia, X.; Zhu, J.Y.; Guo, G.; Huang, Y.X.; Gao, X.J.; Zhang, C.Q. Design and test of a novel converging groove-guided seed tube for precision seeding of maize. Biosyst. Eng. 2024, 245, 36–55. [Google Scholar] [CrossRef]
- Li, Y.F.; Zhou, W.Q.; Ma, C.C.; Feng, Z.H.; Wang, J.W.; Yi, S.J.; Wang, S. Design and optimization of the seed conveying system for belt-type high-speed corn seed guiding device. Int. J. Agric. Biol. Eng. 2024, 17, 123–131. [Google Scholar] [CrossRef]
- Deng, S.D.; Feng, Y.M.; Cheng, X.P.; Wang, X.L.; Zhang, X.C.; Wei, Z.C. Disturbance analysis and seeding performance evaluation of a pneumatic-seed spoon interactive precision maize seed-metering device for plot planting. Biosyst. Eng. 2024, 247, 221–240. [Google Scholar] [CrossRef]
- Sun, Y.H.; Guo, J.H.; Shi, L.R. Design and parameter optimization of air-suction wheel type of seed-metering device with elastic pad for maize. Int. J. Agric. Biol. Eng. 2024, 17, 116–127. [Google Scholar] [CrossRef]
- Wang, Y.B.; Li, H.W.; Hu, H.N.; He, J.; Wang, Q.J.; Lu, C.Y.; Liu, P.; Yang, Q.L.; He, D.; Jiang, S.; et al. A noncontact self-suction wheat shooting device for sustainable agriculture: A preliminary research. Comput. Electron. Agric. 2022, 197, 106927. [Google Scholar] [CrossRef]
- Anantachar, M.; Kumar, P.G.V.; Guruswamy, T. Neural network prediction of performance parameters of an inclined plate seed metering device and its reverse mapping for the determination of optimum design and operational parameters. Comput. Electron. Agric. 2010, 72, 87–98. [Google Scholar] [CrossRef]
- Karayel, D.; Güngör, O.; Sarauskis, E. Estimation of optimum vacuum pressure of air-suction seed-metering device of precision seeders using artificial neural network models. Agronomy 2022, 12, 1600. [Google Scholar] [CrossRef]
- Weng, W.; Wang, C.; Zhu, G.; Gu, Z.; Tang, H.; Wang, J.; Wang, J. Optimization of and experiment on simulation parameters for rotary hole filling corn precision metering device. Agriculture 2023, 13, 1093. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, R.; Liu, F.; Bai, H.; Dong, W. Research on the Cluster Hole Effect and Performance Testing of Air-Suction Quinoa Seed Metering Device. Agriculture 2024, 14, 1391. [Google Scholar] [CrossRef]
- Ding, L.; Yuan, Y.C.; Dou, Y.F.; Li, C.X.; He, Z.; Guo, G.M.; Zhang, Y.; Chen, B.J.; Li, H. Design and Experiment of Air-Suction Maize Seed-Metering Device with Auxiliary Guide. Agriculture 2024, 14, 169. [Google Scholar] [CrossRef]
- Zhao, P.; Gao, X.; Su, Y.; Xu, Y.; Huang, Y. Investigation of seeding performance of a novel high-speed precision seed metering device based on numerical simulation and high-speed camera. Comput. Electron. Agric. 2024, 217, 108563. [Google Scholar] [CrossRef]
- Xu, J.; Sun, S.L.; He, Z.K.; Wang, X.M.; Zeng, Z.H.; Li, J.; Wu, W.B. Design and optimisation of seed-metering plate of air-suction vegetable seed-metering device based on DEM-CFD. Biosyst. Eng. 2023, 230, 277–300. [Google Scholar] [CrossRef]
- Du, X.; Liu, C.L. Design and testing of the filling-plate of inner- filling positive pressure high-speed seed-metering device for maize. Biosyst. Eng. 2023, 228, 1–17. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhou, L.; Bai, L.; Wang, B.; Agarwal, R. Recent Advances and Perspectives of CFD–DEM Simulation in Fluidized Bed. Arch. Comput. 2023, 31, 871–918. [Google Scholar] [CrossRef]
- Lavrinec, A.; Orozovic, O.; Rajabnia, H.; Williams, K.; Jones, M.G.; Klinzing, G. Velocity and porosity relationships within dense phase pneumatic conveying as studied using coupled CFD-DEM. Powder Technol. 2020, 375, 89–100. [Google Scholar] [CrossRef]
- El-Emam, M.A.; Zhou, L.; Shi, W.D.; Han, C. True shape modeling of bio-particulate matter flow in an aero-cyclone separator using CFD-DEM simulation. Comput. Part. Mech. 2021, 8, 955–971. [Google Scholar] [CrossRef]
- Ma, H.Q.; Zhou, L.Y.; Liu, Z.H.; Chen, M.Y.; Xia, X.H.; Zhao, Y.Z. A review of recent development for the CFD-DEM investigations of non-spherical particles. Powder Technol. 2022, 412, 117972. [Google Scholar] [CrossRef]
- Chen, Z.R.; Yu, J.Q.; Xue, D.M.; Wang, Y.; Zhang, Q.; Ren, L.Q. An approach to and validation of maize-seed-assembly modelling based on the discrete element method. Powder Technol. 2018, 328, 167–183. [Google Scholar] [CrossRef]
- Yan, D.X.; Yu, J.Q.; Wang, Y.; Zhou, L.; Yu, Y.J. A general modelling method for soybean seeds based on the discrete element method. Powder Technol. 2020, 372, 212–226. [Google Scholar] [CrossRef]
- Sun, K.; Yu, J.Q.; Liang, L.S.; Wang, Y.; Yan, D.X.; Zhou, L.; Yu, Y.J. A DEM-based general modelling method and experimental verification for wheat seeds. Powder Technol. 2022, 401, 117353. [Google Scholar] [CrossRef]
- Chiaravalle, A.G.; Cotabarren, I.M.; Pina, J. DEM breakage calibration for single particle fracture of maize kernels under a particle replacement approach. Chem. Eng. Res. Des. 2023, 195, 151–165. [Google Scholar] [CrossRef]
- Chiaravalle, A.G.; Pina, J.; Cotabarren, I.M. DEM simulation of maize milling in a hammer mill. Powder Technol. 2025, 457, 120892. [Google Scholar] [CrossRef]
- Wang, X.; Zhai, Q.; Zhang, S.; Li, Q.; Zhou, H. Efficient and accurate calibration of discrete element method parameters for black beans. Agronomy 2024, 14, 2803. [Google Scholar] [CrossRef]
- Hu, M.; Xia, J.; Zhou, Y.; Luo, C.; Zhou, M.; Liu, Z. Measurement and calibration of the discrete element parameters of coated delinted cotton seeds. Agriculture 2022, 12, 286. [Google Scholar] [CrossRef]
- Li, A.; Jia, F.; Shen, S.; Han, Y.; Chen, P.; Wang, Y.; Zhang, J.; Feng, W.; Fei, J.; Hao, X. Numerical simulation approach for predicting rice milling performance under different convex rib helix angle based on discrete element method. Innov. Food Sci. Emerg. Technol. 2023, 83, 103257. [Google Scholar] [CrossRef]
- Hao, X.Z.; Han, Y.L.; Shen, S.H.; Li, A.Q.; Chen, P.Y.; Zhang, J.C.; Wang, Y.L.; Feng, W.Y.; Fei, J.M.; Jia, F.G. Study on radial segregation of whole and broken rice in an indented cylinder separator. Powder Technol. 2023, 422, 118499. [Google Scholar] [CrossRef]
- Zhang, S.; Tekeste, M.Z.; Li, Y.; Gaul, A.; Zhu, D.Q.; Liao, J. Scaled-up rice grain modelling for DEM calibration and the validation of hopper flow. Biosyst. Eng. 2020, 194, 196–212. [Google Scholar] [CrossRef]
- Tang, H.; Xu, C.; Guo, F.; Yao, Z.; Jiang, Y.; Guan, R.; Sun, X.; Wang, J. Analysis and Experiment on the Seed Metering Mechanism of Multi-Grain Cluster Air Suction Type Rice (Oryza sativa L.) Hill Direct Seed Metering Device. Agriculture 2022, 12, 1094. [Google Scholar] [CrossRef]
- He, S.; Qian, C.; Jiang, Y.; Qin, W.; Huang, Z.; Huang, D.; Wang, Z.; Zang, Y. Design and optimization of the seed feeding device with DEM-CFD coupling approach for rice and wheat. Comput. Electron. Agric. 2024, 219, 108814. [Google Scholar] [CrossRef]
- Yue, Y.; Zhang, Q.; Dong, B.; Li, J. Application of Discrete Element Method to Potato Harvesting Machinery: A Review. Agriculture 2025, 15, 315. [Google Scholar] [CrossRef]
- Xing, H.; Cao, X.M.; Zhong, P.; Wan, Y.K.; Lin, J.J.; Zang, Y.; Zhang, G.Z. DEM-CFD coupling simulation and optimisation of rice seed particles seeding a hill in double cavity pneumatic seed metering device. Comput. Electron. Agric. 2024, 224, 109075. [Google Scholar] [CrossRef]






| Materials | Poisson’s Ratio | Young’s Modulus (MPa) | Density (g/cm3) |
|---|---|---|---|
| Rice | 0.25 | 70 | Test results |
| Metering device | 0.4 | 2500 | 1.15 |
| Parameters | Value |
|---|---|
| Dynamic friction coefficient between the seed and the metering device (DPG) | 0.2~1.0 |
| Dynamic friction coefficient between seeds and seeds (DPP) | 0.2~1.0 |
| Restitution coefficient between seeds and seeds (RPP) | 0.2~0.6 |
| Static friction coefficient between seeds and seeds (SPP) | 0.4~1.6 |
| Coefficient of static friction between the seed and the seed metering device (SPG) | Test results |
| Restitution coefficient of the collision between the seed and the seed metering device (RPG) | Test results |
| Indicator | Rice Seed | |||||
|---|---|---|---|---|---|---|
| HHZD | HHZW | HYD | HYW | YLYD | YLYW | |
| DPP | 0.40 | 0.60 | 0.40 | 0.50 | 0.50 | 0.40 |
| DPG | 0.32 | 0.38 | 0.42 | 0.26 | 0.36 | 0.32 |
| DSA (°) | 36.17 ± 0.34 | 35.38 ± 0.68 | 34.56 ± 0.40 | 32.33 ± 0.32 | 32.83 ± 0.19 | 31.41 ± 0.59 |
| DPG | 0.34 | 0.40 | 0.44 | 0.28 | 0.38 | 0.34 |
| DSA (°) | 36.31 ± 0.53 | 36.23 ± 0.51 | 35.30 ± 0.37 | 34.61 ± 0.74 | 33.64 ± 0.17 | 32.64 ± 0.81 |
| DPG | 0.36 | 0.42 | 0.46 | 0.30 | 0.40 | 0.36 |
| DSA (°) | 36.83 ± 0.19 | 37.3 ± 0.53 | 35.97± | 35.13 ± 0.85 | 33.72 ± 0.96 | 33.58 ± 0.76 |
| DPG | 0.38 | 0.44 | 0.48 | 0.32 | 0.42 | 0.38 |
| DSA (°) | 37.31 ± 0.18 | 39.41 ± 0.28 | 36.41± | 35.77 ± 0.51 | 34.91 ± 0.63 | 34.18 ± 0.97 |
| Process | Location | Seed | Drag Force (×10−3N) | Pressure Gradient Force (×10−3N) | Sum (×10−3N) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Rotational Speed (rpm) | |||||||||||
| 20 | 40 | 60 | 20 | 40 | 60 | 20 | 40 | 60 | |||
| Filling | Inside | HHZD | 4.19 | 3.80 | 3.83 | 8.75 | 9.19 | 8.76 | 12.94 | 12.99 | 12.59 |
| HHZW | 3.53 | 3.00 | 2.82 | 8.97 | 8.43 | 8.13 | 12.5 | 11.43 | 10.95 | ||
| HYD | 2.48 | 2.25 | 2.42 | 9.61 | 8.67 | 9.64 | 12.09 | 10.92 | 12.06 | ||
| HYW | 2.52 | 2.41 | 2.37 | 10.03 | 9.70 | 9.37 | 12.55 | 12.11 | 11.74 | ||
| YLYD | 3.37 | 2.92 | 2.97 | 7.57 | 6.74 | 6.70 | 10.94 | 9.66 | 9.67 | ||
| YLYW | 2.64 | 2.42 | 2.37 | 10.72 | 9.75 | 9.86 | 13.36 | 12.17 | 12.23 | ||
| Outside | HHZD | 3.78 | 3.70 | 3.80 | 8.74 | 7.89 | 7.83 | 12.52 | 11.59 | 11.63 | |
| HHZW | 3.40 | 2.88 | 2.72 | 7.96 | 8.62 | 6.72 | 11.36 | 11.5 | 9.44 | ||
| HYD | 2.47 | 2.39 | 2.25 | 9.63 | 9.57 | 8.98 | 12.1 | 11.96 | 11.23 | ||
| HYW | 2.51 | 2.23 | 2.17 | 10.16 | 8.72 | 8.77 | 12.67 | 10.95 | 10.94 | ||
| YLYD | 3.26 | 2.82 | 2.78 | 7.25 | 6.59 | 6.81 | 10.51 | 9.41 | 9.59 | ||
| YLYW | 2.57 | 2.21 | 2.24 | 10.48 | 8.93 | 9.33 | 13.05 | 11.14 | 11.57 | ||
| Carrying | Inside | HHZD | 2.96 | 3.24 | 3.02 | 3.44 | 6.22 | 4.89 | 6.4 | 9.46 | 7.91 |
| HHZW | 2.54 | 2.32 | 2.46 | 5.85 | 6.09 | 6.27 | 8.39 | 8.41 | 8.73 | ||
| HYD | 1.91 | 1.87 | 1.77 | 8.14 | 7.92 | 7.45 | 10.05 | 9.79 | 9.22 | ||
| HYW | 1.96 | 1.98 | 1.80 | 8.46 | 8.60 | 7.75 | 10.42 | 10.58 | 9.55 | ||
| YLYD | 2.51 | 2.42 | 2.24 | 4.03 | 3.78 | 4.72 | 6.54 | 6.2 | 6.96 | ||
| YLYW | 1.88 | 1.86 | 1.79 | 7.94 | 7.83 | 7.55 | 9.82 | 9.69 | 9.34 | ||
| Outside | HHZD | 2.98 | 3.40 | 2.97 | 3.73 | 6.83 | 4.22 | 6.71 | 10.23 | 7.19 | |
| HHZW | 2.54 | 2.23 | 2.45 | 5.44 | 6.50 | 5.28 | 7.98 | 8.73 | 7.73 | ||
| HYD | 1.88 | 1.90 | 1.77 | 7.95 | 8.11 | 7.61 | 9.83 | 10.01 | 9.38 | ||
| HYW | 1.96 | 1.96 | 1.86 | 8.49 | 8.48 | 8.10 | 10.45 | 10.44 | 9.96 | ||
| YLYD | 2.46 | 2.38 | 2.21 | 3.64 | 4.03 | 4.58 | 6.1 | 6.41 | 6.79 | ||
| YLYW | 1.82 | 1.82 | 1.81 | 7.63 | 7.64 | 7.64 | 9.45 | 9.46 | 9.45 | ||
| Process | Location | Indicators | Factors | df | F | p |
|---|---|---|---|---|---|---|
| Filling | Inside | Drag force | Seed | 5 | 72.16 | <0.01 |
| Rotational speed | 2 | 13.76 | <0.01 | |||
| Pressure gradient force | Seed | 5 | 29.16 | <0.01 | ||
| Rotational speed | 2 | 4.54 | 0.04 | |||
| Sum | Seed | 5 | 17.43 | <0.01 | ||
| Rotational speed | 2 | 8.87 | <0.01 | |||
| Outside | Drag force | Seed | 5 | 58.94 | <0.01 | |
| Rotational speed | 2 | 12.23 | <0.01 | |||
| Pressure gradient force | Seed | 5 | 13.29 | <0.01 | ||
| Rotational speed | 2 | 5.58 | 0.02 | |||
| Sum | Seed | 5 | 7.13 | <0.01 | ||
| Rotational speed | 2 | 9.35 | <0.01 | |||
| Carrying | Inside | Drag force | Seed | 5 | 75.01 | <0.01 |
| Rotational speed | 2 | 2.49 | 0.13 | |||
| Pressure gradient force | Seed | 5 | 19.41 | <0.01 | ||
| Rotational speed | 2 | 0.64 | 0.55 | |||
| Sum | Seed | 5 | 10.09 | <0.01 | ||
| Rotational speed | 2 | 0.62 | 0.56 | |||
| Outside | Drag force | Seed | 5 | 41.05 | <0.01 | |
| Rotational speed | 2 | 1.09 | 0.37 | |||
| Pressure gradient force | Seed | 5 | 19.04 | <0.01 | ||
| Rotational speed | 2 | 2.26 | 0.16 | |||
| Sum | Seed | 5 | 10.19 | <0.01 | ||
| Rotational speed | 2 | 2.14 | 0.17 |
| Process | Location | Seed | Normal Force (×10−3N) | Tangential Force (×10−3N) | ||||
|---|---|---|---|---|---|---|---|---|
| Rotational Speed (rpm) | ||||||||
| 20 | 40 | 60 | 20 | 40 | 60 | |||
| Filling | Inside | HHZD | 22.18 | 21.74 | 20.51 | 6.60 | 6.41 | 6.32 |
| HHZW | 24.31 | 24.17 | 23.33 | 8.60 | 9.24 | 9.28 | ||
| HYD | 28.67 | 25.18 | 27.86 | 9.93 | 9.19 | 10.15 | ||
| HYW | 36.02 | 37.69 | 30.36 | 11.91 | 12.47 | 10.03 | ||
| YLYD | 22.12 | 18.40 | 17.27 | 7.76 | 6.67 | 6.45 | ||
| YLYW | 30.29 | 26.96 | 22.56 | 9.67 | 9.14 | 7.77 | ||
| Outside | HHZD | 29.19 | 24.44 | 22.10 | 8.62 | 7.57 | 6.78 | |
| HHZW | 32.27 | 27.23 | 27.43 | 11.93 | 10.45 | 11.64 | ||
| HYD | 37.68 | 35.11 | 31.37 | 13.29 | 12.50 | 11.59 | ||
| HYW | 46.96 | 51.24 | 41.43 | 15.73 | 17.79 | 13.70 | ||
| YLYD | 26.02 | 23.91 | 20.40 | 9.19 | 11.45 | 7.68 | ||
| YLYW | 39.04 | 41.55 | 25.80 | 12.65 | 14.22 | 8.89 | ||
| Carrying | Inside | HHZD | 5.81 | 9.00 | 6.43 | 1.52 | 2.01 | 1.54 |
| HHZW | 7.59 | 7.64 | 8.22 | 2.10 | 2.10 | 2.35 | ||
| HYD | 9.86 | 9.53 | 8.82 | 2.89 | 2.69 | 2.65 | ||
| HYW | 10.21 | 10.31 | 9.06 | 2.66 | 2.48 | 2.49 | ||
| YLYD | 5.82 | 5.16 | 5.90 | 1.58 | 1.49 | 1.67 | ||
| YLYW | 9.66 | 9.36 | 8.96 | 2.21 | 2.31 | 2.34 | ||
| Outside | HHZD | 7.06 | 9.15 | 5.77 | 1.83 | 1.89 | 1.51 | |
| HHZW | 7.24 | 8.08 | 6.31 | 2.10 | 2.10 | 1.91 | ||
| HYD | 9.76 | 9.70 | 12.25 | 2.71 | 2.94 | 3.92 | ||
| HYW | 10.26 | 10.14 | 9.40 | 2.56 | 2.65 | 2.43 | ||
| YLYD | 5.21 | 5.05 | 5.55 | 1.40 | 1.97 | 1.58 | ||
| YLYW | 9.28 | 9.08 | 9.03 | 2.21 | 2.46 | 2.24 | ||
| Process | Location | Indicators | Factors | df | F | p |
|---|---|---|---|---|---|---|
| Filling | Inside | Normal force | Seed | 5 | 21.03 | <0.01 |
| Rotational speed | 2 | 4.73 | 0.04 | |||
| Tangential force | Seed | 5 | 19.43 | <0.01 | ||
| Rotational speed | 2 | 1.67 | 0.24 | |||
| Outside | Normal force | Seed | 5 | 29.16 | <0.01 | |
| Rotational speed | 2 | 21.88 | <0.01 | |||
| Tangential force | Seed | 5 | 13.23 | <0.01 | ||
| Rotational speed | 2 | 5.13 | 0.03 | |||
| Carrying | Inside | Normal force | Seed | 5 | 11.60 | <0.01 |
| Rotational speed | 2 | 0.78 | 0.48 | |||
| Tangential force | Seed | 5 | 23.29 | <0.01 | ||
| Rotational speed | 2 | 0.02 | 0.98 | |||
| Outside | Normal force | Seed | 5 | 10.40 | <0.01 | |
| Rotational speed | 2 | 0.35 | 0.71 | |||
| Tangential force | Seed | 5 | 9.43 | <0.01 | ||
| Rotational speed | 2 | 0.59 | 0.57 |
| Process | Seed | Normal Action Force (×10−3N) | Tangential Action Force (×10−3N) | ||||
|---|---|---|---|---|---|---|---|
| Rotational Speed (rpm) | |||||||
| 20 | 40 | 60 | 20 | 40 | 60 | ||
| Inside | HHZD | 16.37 | 12.74 | 14.08 | 5.08 | 4.53 | 4.78 |
| HHZW | 16.72 | 16.53 | 15.11 | 6.49 | 7.14 | 6.93 | |
| HYD | 18.81 | 15.65 | 19.05 | 7.04 | 6.5 | 7.51 | |
| HYW | 25.81 | 27.38 | 21.30 | 9.25 | 9.99 | 7.54 | |
| YLYD | 16.30 | 13.24 | 11.38 | 6.18 | 5.18 | 4.77 | |
| YLYW | 20.63 | 17.6 | 13.61 | 7.45 | 6.83 | 5.43 | |
| Outside | HHZD | 22.13 | 15.29 | 16.32 | 6.79 | 5.68 | 5.27 |
| HHZW | 25.03 | 19.15 | 21.13 | 9.83 | 8.35 | 9.73 | |
| HYD | 27.92 | 25.41 | 19.13 | 10.57 | 9.56 | 7.67 | |
| HYW | 36.71 | 41.1 | 32.03 | 13.17 | 15.14 | 11.26 | |
| YLYD | 20.81 | 18.86 | 14.85 | 7.79 | 9.48 | 6.10 | |
| YLYW | 29.76 | 32.47 | 16.77 | 10.44 | 11.76 | 6.66 | |
| Location | Indicators | Factors | df | F | p |
|---|---|---|---|---|---|
| Inside | Drag force | Seed | 5 | 12.46 | <0.01 |
| Rotational speed | 2 | 4.39 | 0.04 | ||
| Tangential force | Seed | 5 | 11.50 | <0.01 | |
| Rotational speed | 2 | 1.67 | 0.24 | ||
| Outside | Drag force | Seed | 5 | 11.52 | <0.01 |
| Rotational speed | 2 | 6.44 | 0.02 | ||
| Tangential force | Seed | 5 | 10.56 | <0.01 | |
| Rotational speed | 2 | 5.41 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, C.; Fan, Z.; Yan, D.; Qin, W.; Jiang, Y.; Huang, Z.; Xing, H.; Wang, Z.; Zang, Y. Numerical Simulation of Dry and Wet Rice Seeds in an Air-Suction Seed Metering Device. Agronomy 2025, 15, 1145. https://doi.org/10.3390/agronomy15051145
Qian C, Fan Z, Yan D, Qin W, Jiang Y, Huang Z, Xing H, Wang Z, Zang Y. Numerical Simulation of Dry and Wet Rice Seeds in an Air-Suction Seed Metering Device. Agronomy. 2025; 15(5):1145. https://doi.org/10.3390/agronomy15051145
Chicago/Turabian StyleQian, Cheng, Zhuorong Fan, Daoqing Yan, Wei Qin, Youcong Jiang, Zishun Huang, He Xing, Zaiman Wang, and Ying Zang. 2025. "Numerical Simulation of Dry and Wet Rice Seeds in an Air-Suction Seed Metering Device" Agronomy 15, no. 5: 1145. https://doi.org/10.3390/agronomy15051145
APA StyleQian, C., Fan, Z., Yan, D., Qin, W., Jiang, Y., Huang, Z., Xing, H., Wang, Z., & Zang, Y. (2025). Numerical Simulation of Dry and Wet Rice Seeds in an Air-Suction Seed Metering Device. Agronomy, 15(5), 1145. https://doi.org/10.3390/agronomy15051145





