Simulating Pasture Yield Under Alternative Environments and Grazing Management in Wisconsin, USA
Abstract
1. Introduction
2. Materials and Methods
2.1. SSURGO-Based Pasture Yield Model
2.1.1. Representative Yields
2.1.2. Soil Properties
2.1.3. Model Development of Yield Predicted by Soil Properties
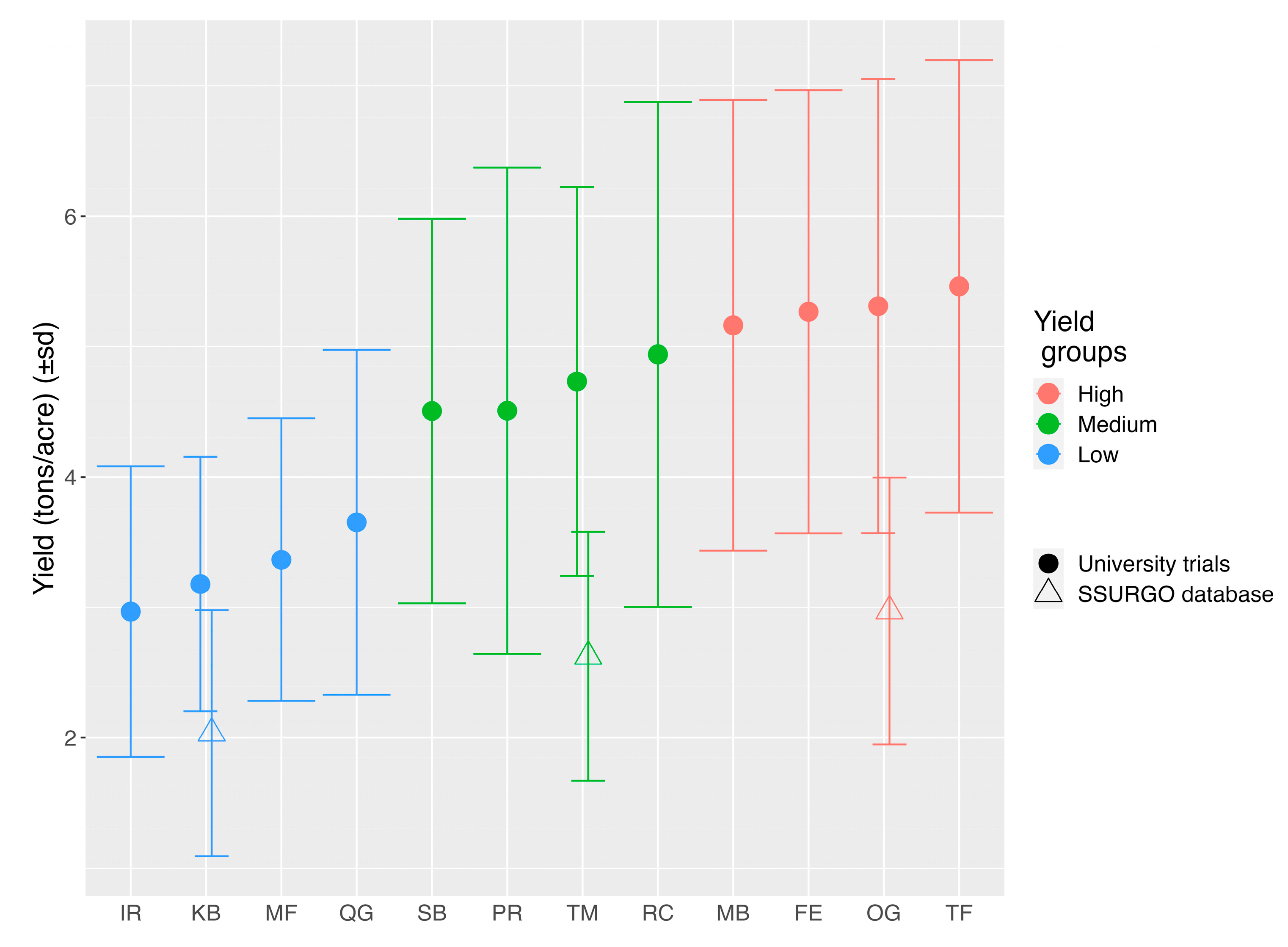
2.2. Grass Species Yield Groups
2.3. Effect of Grazing Management on Pasture Yield
3. Results and Discussion
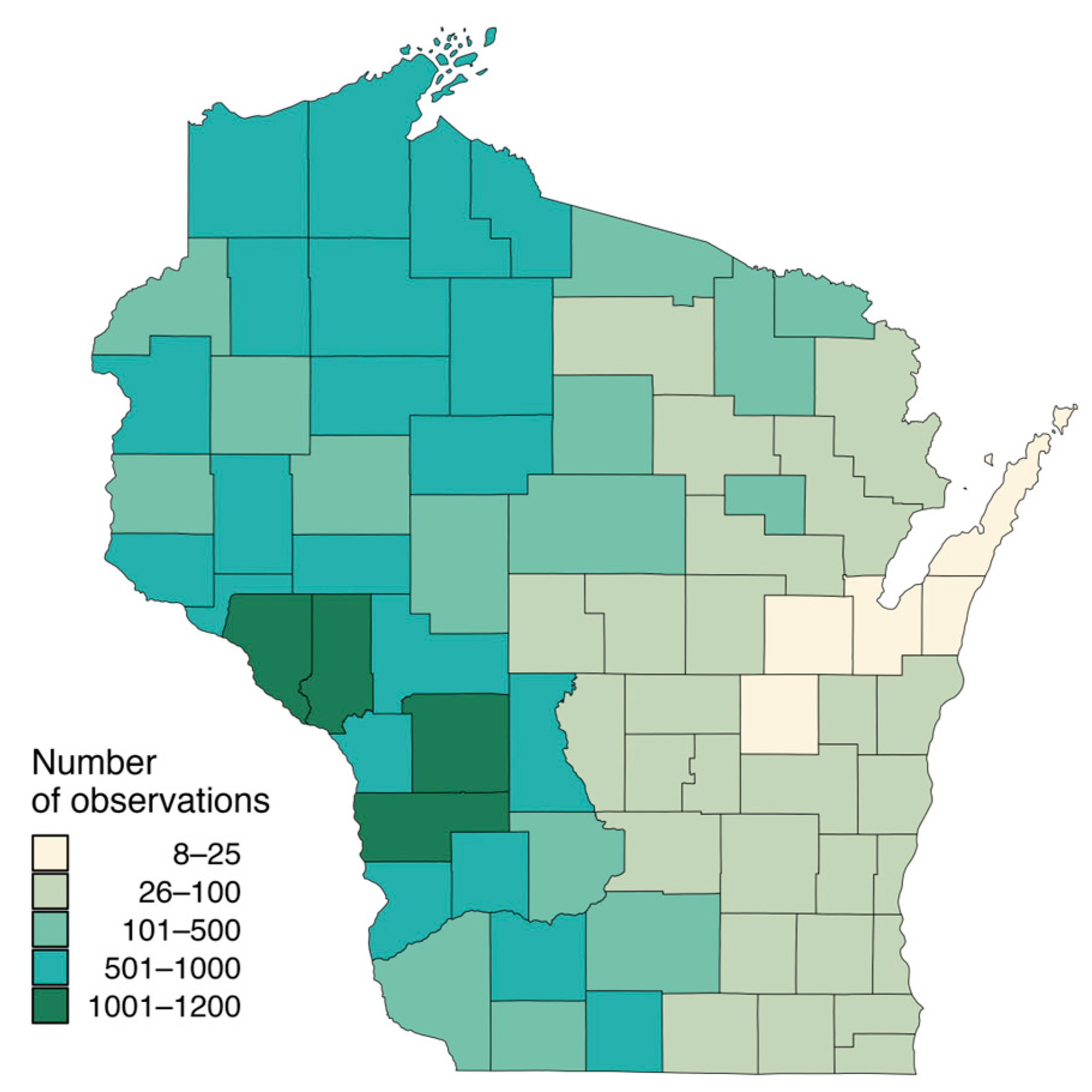
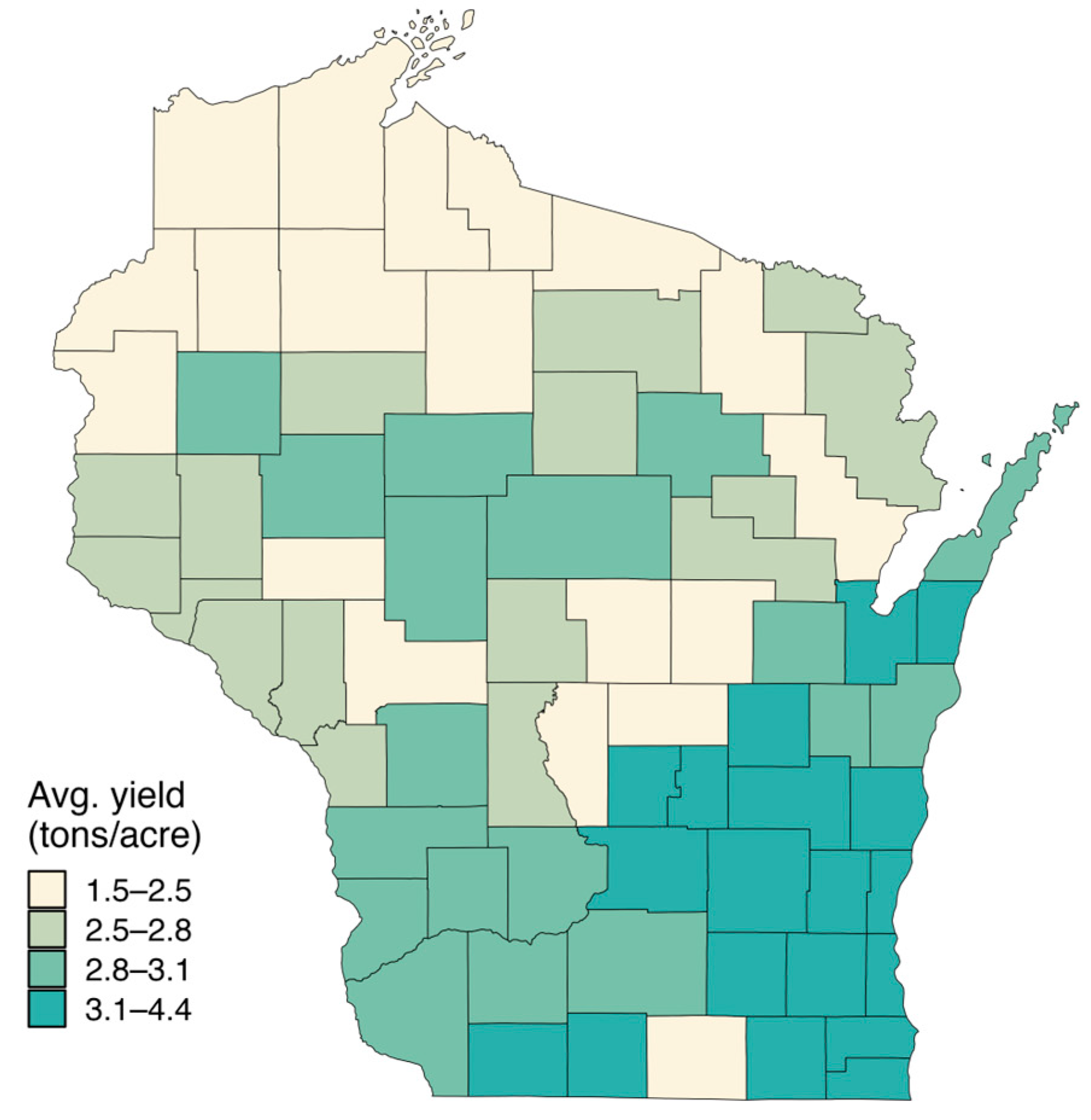
3.1. SSURGO Summary Statistics
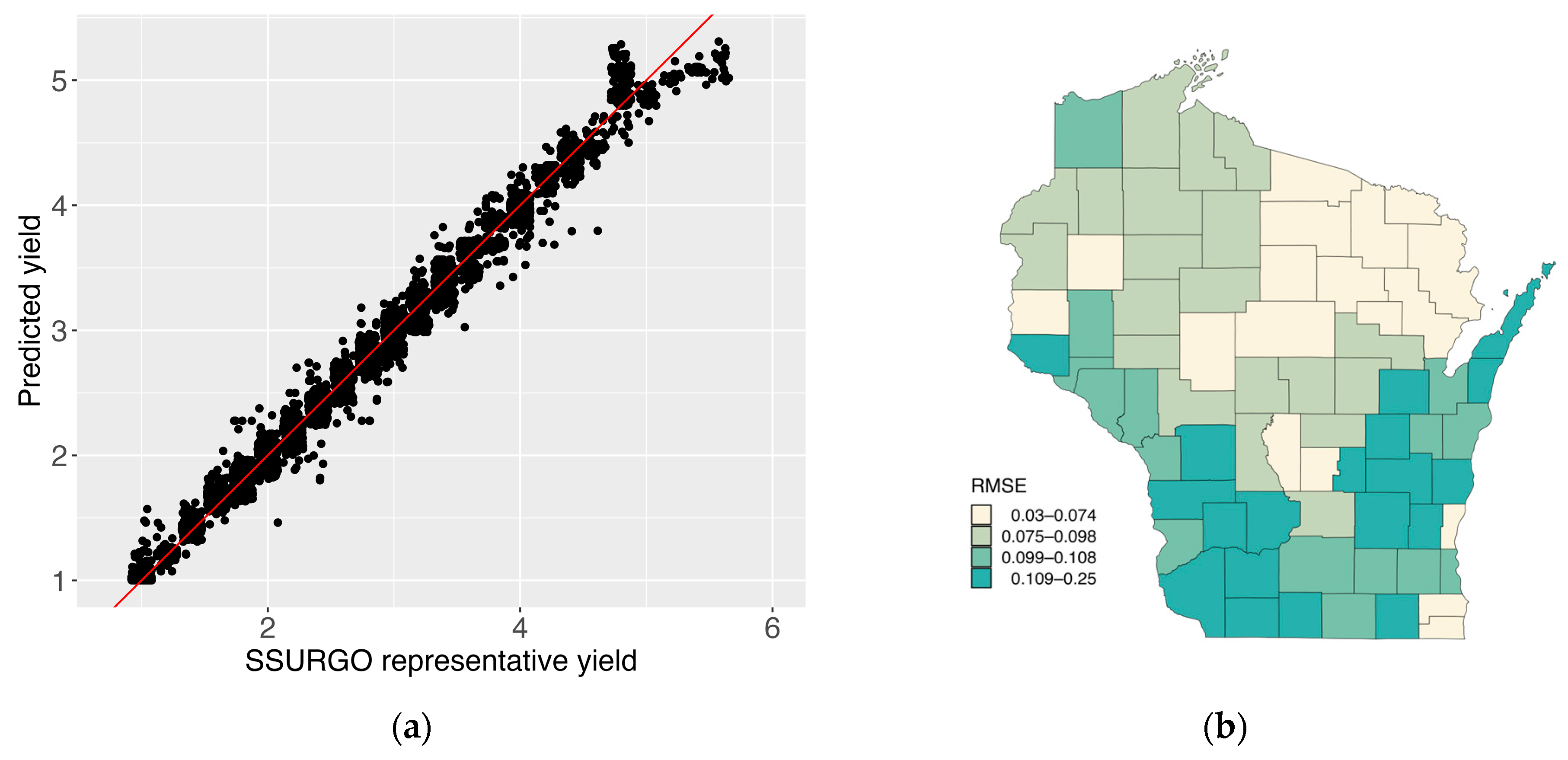
3.2. Random Forest Model Results and Assessment
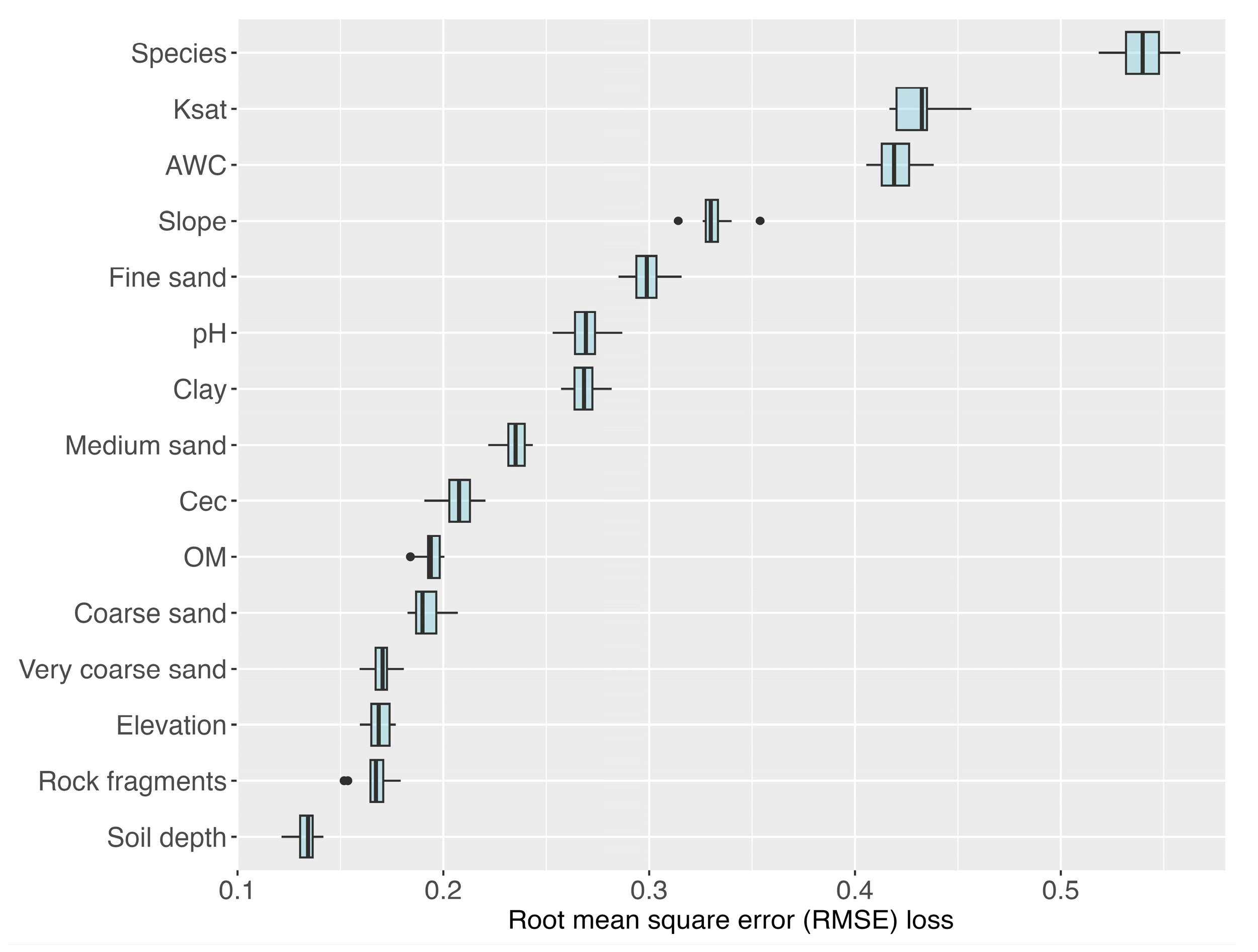
3.3. Effect of Soil Properties on Pasture Yield
3.4. Grass Species
3.5. Effect of Grazing Management on Pasture Yield
3.6. Model Limitations
3.7. Pasture Prediction Web-App Tool
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dartt, B.A. A Comparison of Management-Intensive Grazing and Conventionally Managed Michigan Dairies: Profitability, Economic Efficiencies, Quality of Life, and Management Priorities. Master’s Thesis, Michigan State University, East Lansing, MI, USA, 1998. [Google Scholar]
- Kriegl, T. Major Cost Items on Wisconsin Organic, Grazing and Confinement (Average of All Sizes) Dairy Farms. Center for Dairy Profitability, University of Wisconsin—Madison, UWEX. February 2008, p. 6. Available online: https://cias.wisc.edu/directory/tom-kriegl/ (accessed on 10 February 2025).
- Undersander, D.; Albert, B.; Cosgrove, D.; Johnson, D.; Peterson, P. Pastures for Profit: A Guide to Rotational Grazing; Cooperative Extension Publications, University of Wisconsin-Extension: Madison, WI, USA, 2014; p. A3529. [Google Scholar]
- Winsten, J.R.; Kerchner, C.D.; Richardson, A.; Lichau, A.; Hyman, J.M. Trends in the Northeast Dairy Industry: Large-Scale Modern Confinement Feeding and Management-Intensive Grazing. J. Dairy Sci. 2010, 93, 1759–1769. [Google Scholar] [CrossRef] [PubMed]
- Winsten, J.R.; Richardson, A.; Kerchner, C.D.; Lichau, A.; Hyman, J.M. Barriers to the Adoption of Management-Intensive Grazing among Dairy Farmers in the Northeastern United States. Renew. Agric. Food Syst. 2011, 26, 104–113. [Google Scholar] [CrossRef]
- Johnson, I.R.; Chapman, D.F.; Snow, V.O.; Eckard, R.J.; Parsons, A.J.; Lambert, M.G.; Cullen, B.R. DairyMod and EcoMod: Biophysical Pasture-Simulation. Aust. J. Exp. Agric. 2008, 48, 621–631. [Google Scholar] [CrossRef]
- Baldinger, L.; Vaillant, J.; Zollitsch, W.; Rinne, M. Making a Decision-Support System for Dairy Farmers Usable throughout Europe: The Challenge of Feed Evaluation. Adv. Anim. Biosci. 2015, 6, 3–5. [Google Scholar] [CrossRef]
- Hurtado-Uria, C.; Hennessy, D.; Shalloo, L.; Schulte, R.P.O.; Delaby, L.; O’connor, D. Evaluation of Three Grass Growth Models to Predict Grass Growth in Ireland. J. Agric. Sci. 2013, 151, 91–104. [Google Scholar] [CrossRef]
- Keating, B.A.; Carberry, P.S.; Hammer, G.L.; Probert, M.E.; Robertson, M.J.; Holzworth, D.; Huth, N.I.; Hargreaves, J.N.G.; Meinke, H.; Hochman, Z.; et al. An Overview of APSIM, a Model Designed for Farming Systems Simulation. Eur. J. Agron. 2003, 18, 267–288. [Google Scholar] [CrossRef]
- Cohen, R.D.H.; Stevens, J.P.; Moore, A.D.; Donnelly, J.R. Validating and Using the GrassGro Decision Support Tool for a Mixed Grass/Alfalfa Pasture in Western Canada. Can. J. Anim. Sci. 2003, 83, 171–182. [Google Scholar] [CrossRef]
- Jeong, J.H.; Resop, J.P.; Mueller, N.D.; Fleisher, D.H.; Yun, K.; Butler, E.E.; Timlin, D.J.; Shim, K.-M.; Gerber, J.S.; Reddy, V.R.; et al. Random Forests for Global and Regional Crop Yield Predictions. PLoS ONE 2016, 11, e0156571. [Google Scholar] [CrossRef]
- Kravchenko, A.N.; Bullock, D.G. Correlation of Corn and Soybean Grain Yield with Topography and Soil Properties. Agron. J. 2000, 92, 75–83. [Google Scholar] [CrossRef]
- Lark, T.J.; Spawn, S.A.; Bougie, M.; Gibbs, H.K. Cropland Expansion in the United States Produces Marginal Yields at High Costs to Wildlife. Nat. Commun. 2020, 11, 4295. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Thelen, K.D. Effect of Soil and Topographic Properties on Crop Yield in a North-Central Corn–Soybean Cropping System. Agron. J. 2004, 96, 252–258. [Google Scholar] [CrossRef]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine Learning in Agriculture: A Review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [PubMed]
- van Klompenburg, T.; Kassahun, A.; Catal, C. Crop Yield Prediction Using Machine Learning: A Systematic Literature Review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Sollenberger, L.E.; Agouridis, C.T.; Vanzant, E.S.; Franzluebbers, A.J.; Owens, L.B. Prescribed Grazing on Pasturelands. In Conservation Outcomes from Pastureland and Hayland Practices: Assessment, Recommendations, and Knowledge Gaps; Allen Press: Lawrence, KS, USA, 2012; pp. 111–204. [Google Scholar]
- Oates, L.G.; Undersander, D.J.; Gratton, C.; Bell, M.M.; Jackson, R.D. Management-Intensive Rotational Grazing Enhances Forage Production and Quality of Subhumid Cool-Season Pastures. Crop Sci. 2011, 51, 892–901. [Google Scholar] [CrossRef]
- Paine, L.K.; Undersander, D.; Casler, M.D. Pasture Growth, Production, and Quality under Rotational and Continuous Grazing Management. J. Prod. Agric. 1999, 12, 569–577. [Google Scholar] [CrossRef]
- Bertelsen, B.S.; Faulkner, D.B.; Buskirk, D.D.; Castree, J.W. Beef Cattle Performance and Forage Characteristics of Continuous, 6-Paddock, and 11-Paddock Grazing Systems. J. Anim. Sci. 1993, 71, 1381–1389. [Google Scholar] [CrossRef]
- Gurda, A. Mob Grazing, from People to Pastures: Weed Biology, Pasture Productivity, and Farmer Perception and Adoption. Master’s Thesis, University of Wisconsin, Madison, WI, USA, 2014. [Google Scholar]
- Soil Survey Staff Soil Survey Geographic (SSURGO) Database. Available online: https://sdmdataaccess.sc.egov.usda.gov (accessed on 1 December 2023).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Bocinsky, R. FedData: Functions to Automate Downloading Geospatial Data Available from Several Federated Data Sources; R Package Version 401; 2023. Available online: https://CRAN.R-project.org/package=FedData (accessed on 10 February 2025).
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the Tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Kuhn, M.; Wickhan, H. Tidymodels: A Collection of Packages for Modeling and Machine Learning Using Tidyverse Principles; 2020. Available online: https://www.tidymodels.org/ (accessed on 10 February 2025).
- Wright, M.N.; Ziegler, A. Ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef]
- Gregorutti, B.; Michel, B.; Saint-Pierre, P. Correlation and Variable Importance in Random Forests. Stat. Comput. 2017, 27, 659–678. [Google Scholar] [CrossRef]
- Biecek, P. DALEX: Explainers for Complex Predictive Models in R. J. Mach. Learn. Res. 2018, 19, 5. [Google Scholar]
- USDA Soil Survey Geographic (SSURGO) Database. Available online: https://www.fsl.orst.edu/pnwerc/wrb/metadata/soils/ssurgo.pdf (accessed on 1 December 2023).
- Jackson, R.B.; Canadell, J.; Ehleringer, J.R.; Mooney, H.A.; Sala, O.E.; Schulze, E.D. A global Analysis of Root Distributions for Terrestrial Biomes. Oecologia 1996, 108, 389–411. [Google Scholar] [CrossRef]
- Grömping, U. Variable Importance Assessment in Regression: Linear Regression Versus Random Forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- Oldfield, E.E.; Bradford, M.A.; Wood, S.A. Global Meta-Analysis of the Relationship between Soil Organic Matter and Crop Yields. SOIL 2019, 5, 15–32. [Google Scholar] [CrossRef]
- Fisher, A.; Rudin, C.; Dominici, F. All Models are Wrong, but Many are Useful: Learning a Variable’s Importance by Studying an Entire Class of Prediction Models Simultaneously. J. Mach. Learn. Res. 2019, 20, 1–81. [Google Scholar]
- Undersander, D.; Bertram, M.; Breuer, J.; Cavadini, J.; Crooks, A. Forage Variety Update for Wisconsin; University of Wisconsin—Extension: Madison, WI, USA, 2017; p. A1525. [Google Scholar]
- NRCS Forage Animal Balance Worksheet. Available online: https://efotg.sc.egov.usda.gov/#/state/WI/documents/section=3&folder=65188 (accessed on 13 January 2025).
- NRCS Soil Quality Indicators. Available online: https://www.nrcs.usda.gov/sites/default/files/2022-10/nrcs142p2_051590.pdf (accessed on 1 June 2023).
- Taiz, L. Plant Physiology, 5th ed.; Sinauer Associates: Sunderland, MA, USA, 2010. [Google Scholar]
- Greenwood, K.L.; McKenzie, B.M. Grazing Effects on Soil Physical Properties and the Consequences for Pastures: A Review. Aust. J. Exp. Agric. 2001, 41, 1231. [Google Scholar] [CrossRef]
- Meehan, T.D.; Gratton, C.; Diehl, E.; Hunt, N.D.; Mooney, D.F.; Ventura, S.J.; Barham, B.L.; Jackson, R.D. Ecosystem-Service Tradeoffs Associated with Switching from Annual to Perennial Energy Crops in Riparian Zones of the US Midwest. PLoS ONE 2013, 8, e80093. [Google Scholar] [CrossRef]


| Soil Property | Citation | Final Model? |
|---|---|---|
| Available water capacity (AWC) | Yes | |
| Cation exchange capacity (CEC) | Yes | |
| Clay (%) | [14] | Yes |
| Coarse sand (%) | [14] | Yes |
| Coarse silt (%) | No—Too many NAs | |
| Depth to bedrock | Yes | |
| Electrical conductivity | No—No variance | |
| Elevation | [12] | Yes |
| Fine sand (%) | [14] | Yes |
| Fine silt (%) | No—Too many NAs | |
| Medium sand (%) | Yes | |
| Organic matter (%) | [33] | Yes |
| pH | [14] | Yes |
| Particle density | No—Too many NAs | |
| Rock fragments (3–10 in) | Yes | |
| Rock fragments (>10 in) | No—No variance | |
| Sand (%) | [14] | No—Highly correlated |
| Saturated hydraulic conductivity (Ksat) | Yes | |
| Silt (%) | No—Highly correlated | |
| Slope | [12,14] | Yes |
| Very coarse sand | Yes |
| Occupancy (Days) | Low-Yielding Species | Medium-Yielding Species | High-Yielding Species |
|---|---|---|---|
| Yield (Tons/Acre) | |||
| Continuous | 1.49 | 1.84 | 1.95 |
| 7 | 1.72 | 2.12 | 2.25 |
| 3 | 2.17 | 2.69 | 2.84 |
| 1 | 2.29 | 2.83 | 2.99 |
| <1 | 2.74 | 3.39 | 3.59 |
| Rotation Frequency (Days) | NRCS Yield Adjustment | Final Yield Adjustment 1 |
|---|---|---|
| <1 | NA | 1.2 2 |
| 1 | NA | 1.0 2 |
| 2 | NA | 1.0 3 |
| 3 | NA | 0.95 3 |
| 4 | 0.92 | 0.92 3 |
| 5 | 0.85 | 0.85 3,4 |
| 6 | 0.78 | 0.78 3 |
| 7 | 0.72 | 0.72 3 |
| Continuous | NA | 0.65 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chasen, E.; Booth, E.; Gratton, C. Simulating Pasture Yield Under Alternative Environments and Grazing Management in Wisconsin, USA. Agronomy 2025, 15, 437. https://doi.org/10.3390/agronomy15020437
Chasen E, Booth E, Gratton C. Simulating Pasture Yield Under Alternative Environments and Grazing Management in Wisconsin, USA. Agronomy. 2025; 15(2):437. https://doi.org/10.3390/agronomy15020437
Chicago/Turabian StyleChasen, Elissa, Eric Booth, and Claudio Gratton. 2025. "Simulating Pasture Yield Under Alternative Environments and Grazing Management in Wisconsin, USA" Agronomy 15, no. 2: 437. https://doi.org/10.3390/agronomy15020437
APA StyleChasen, E., Booth, E., & Gratton, C. (2025). Simulating Pasture Yield Under Alternative Environments and Grazing Management in Wisconsin, USA. Agronomy, 15(2), 437. https://doi.org/10.3390/agronomy15020437






