Probabilistic Assessment of Crop Yield Loss Under Drought and Global Warming in the Canadian Prairies
Abstract
1. Introduction
2. Materials and Methods
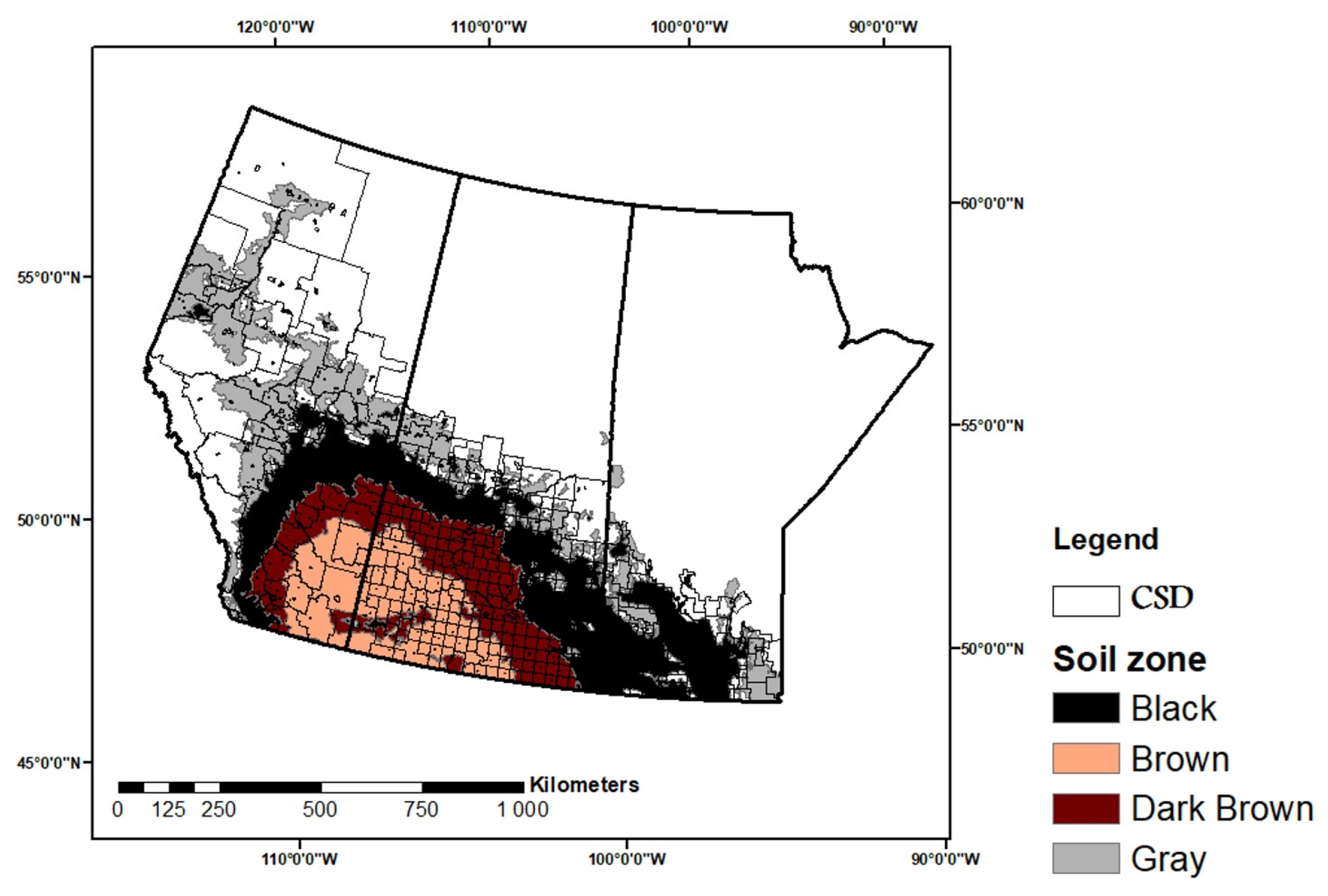
2.1. Study Area
2.2. Decision Support System for Agrotechnology Transfer
2.3. NEX-GDDP-CMIP6
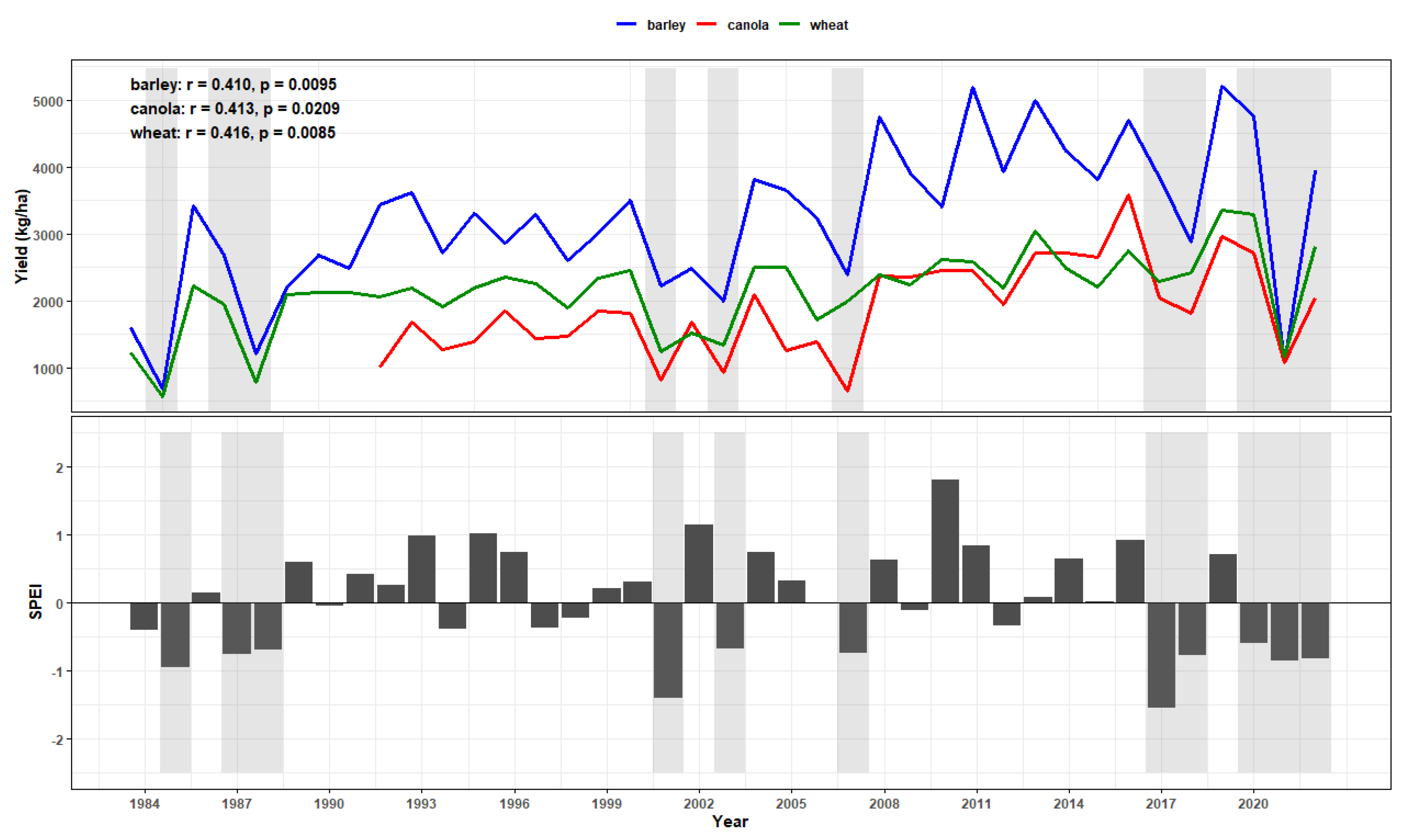
2.4. Drought Indices
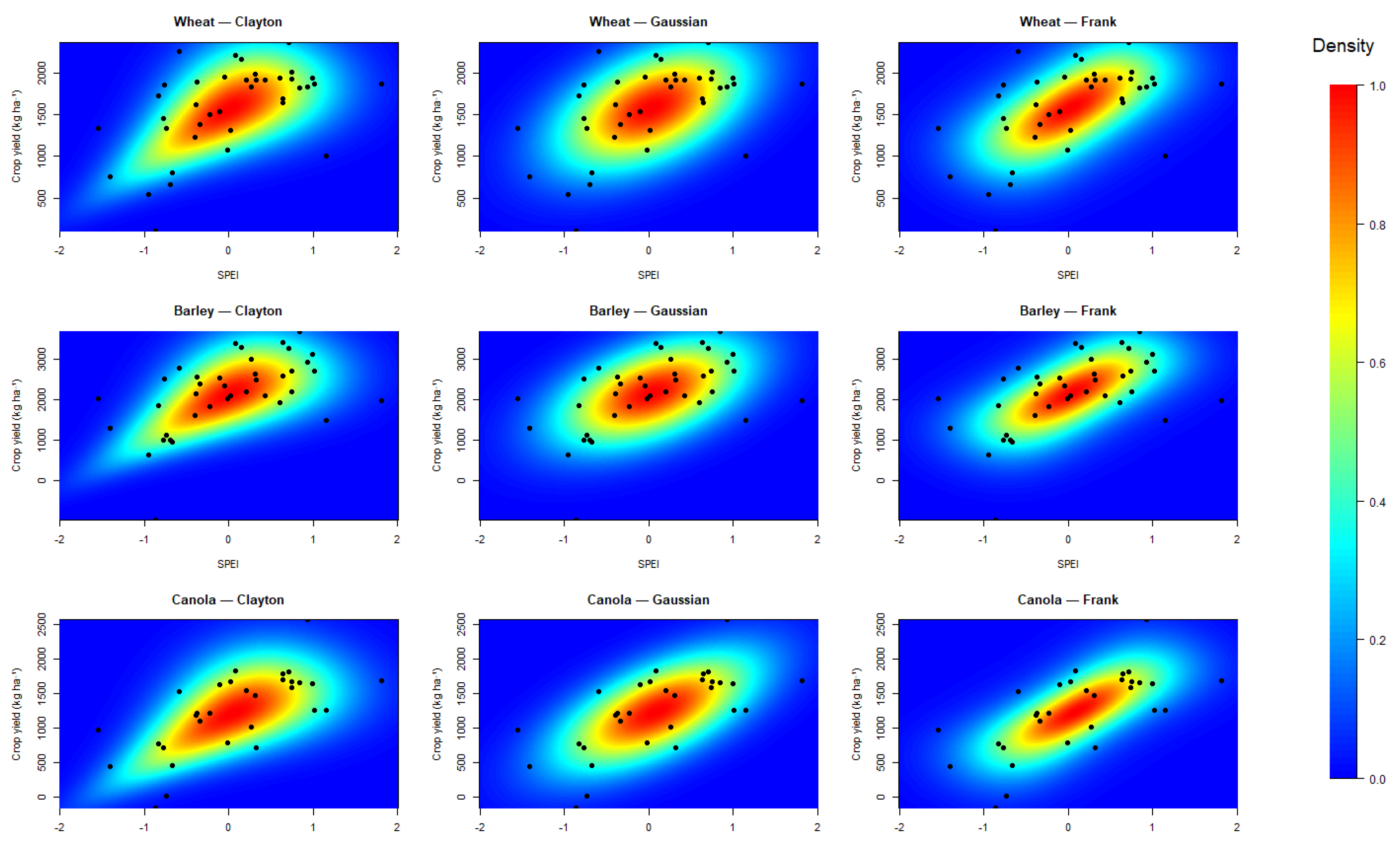
2.5. Copula-Based Model
- For any
- if, wheremeans thatfor all
- is-increasing, i.e., for any boxwith non-empty volume,
3. Results
3.1. DSSAT Model Calibration and Validation
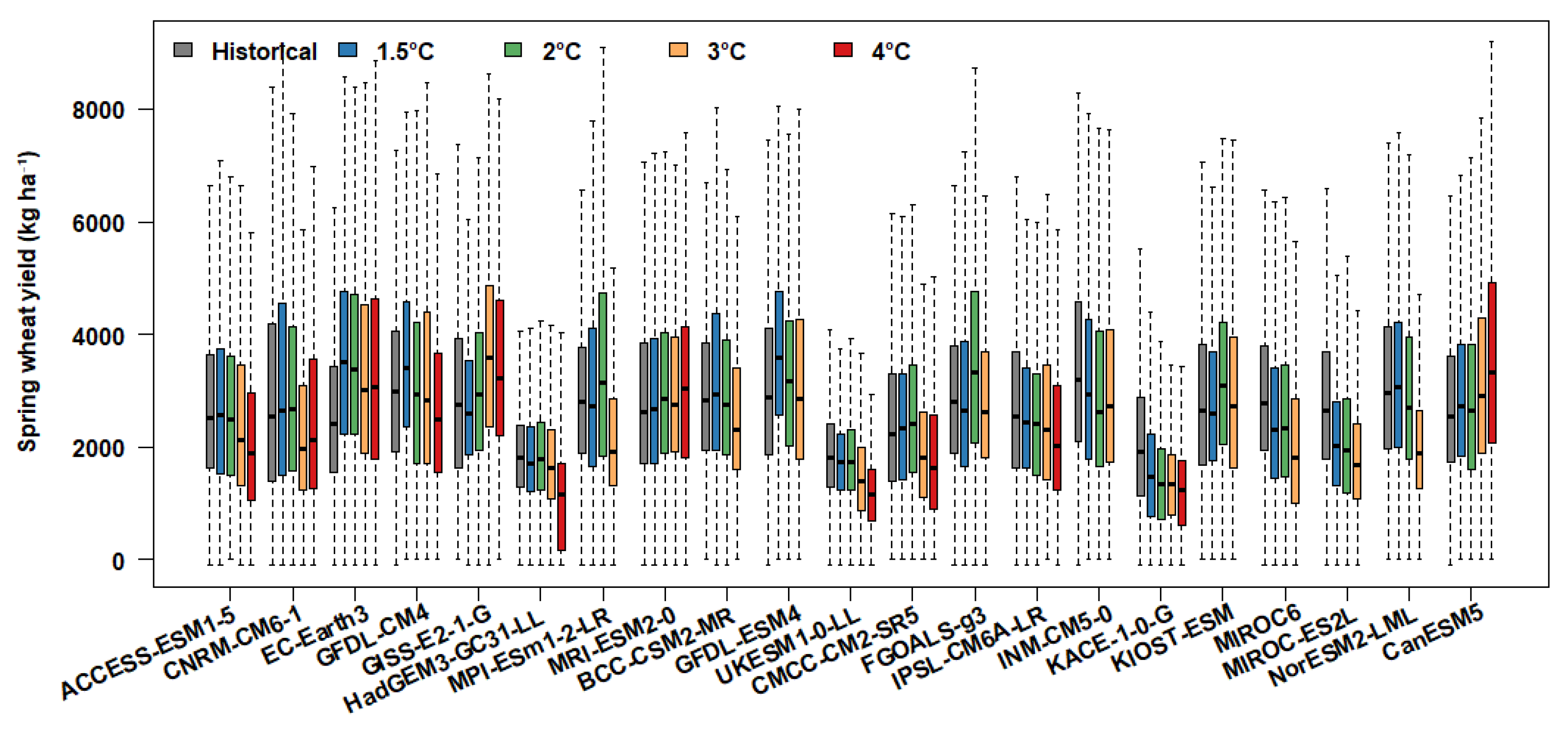
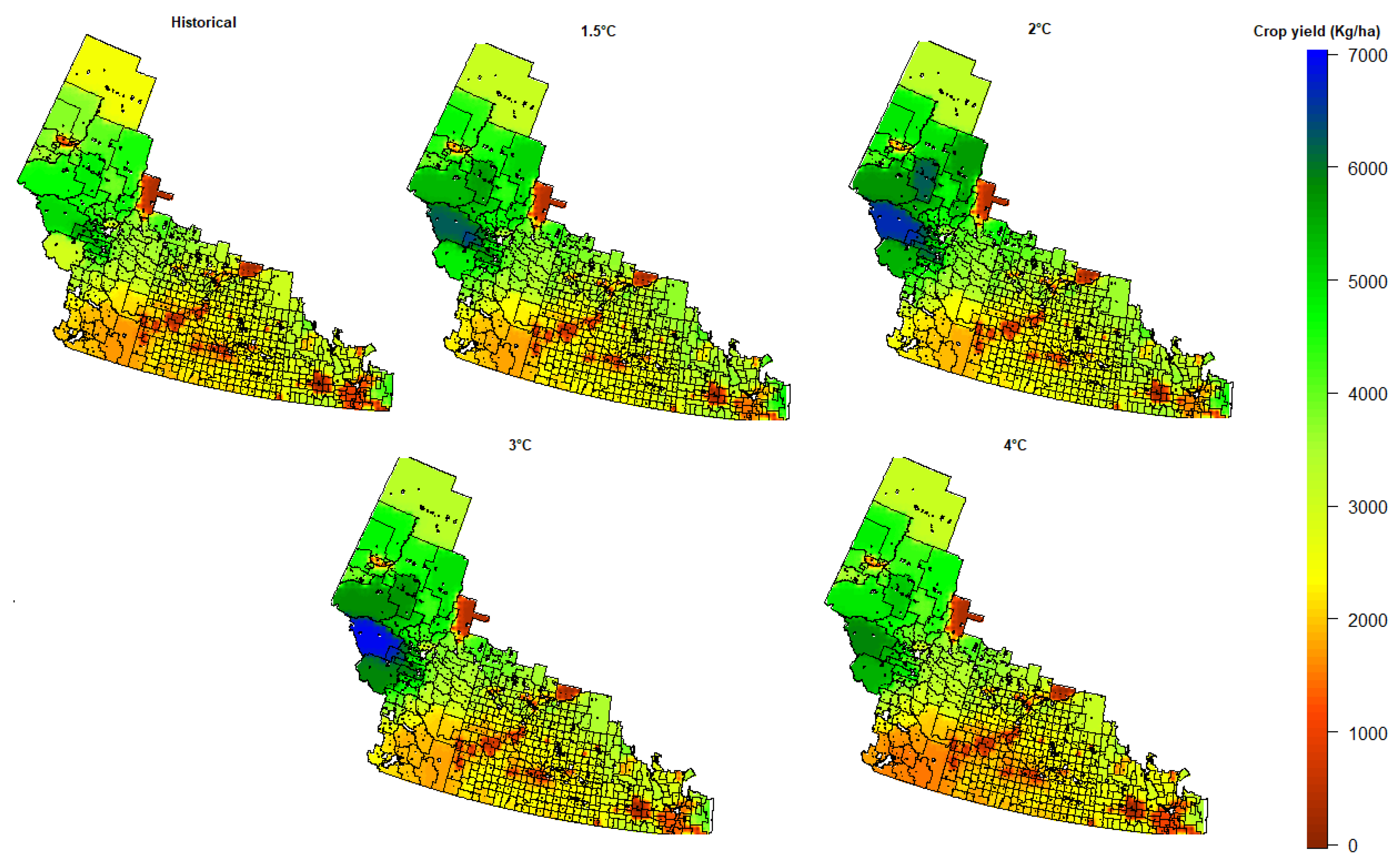
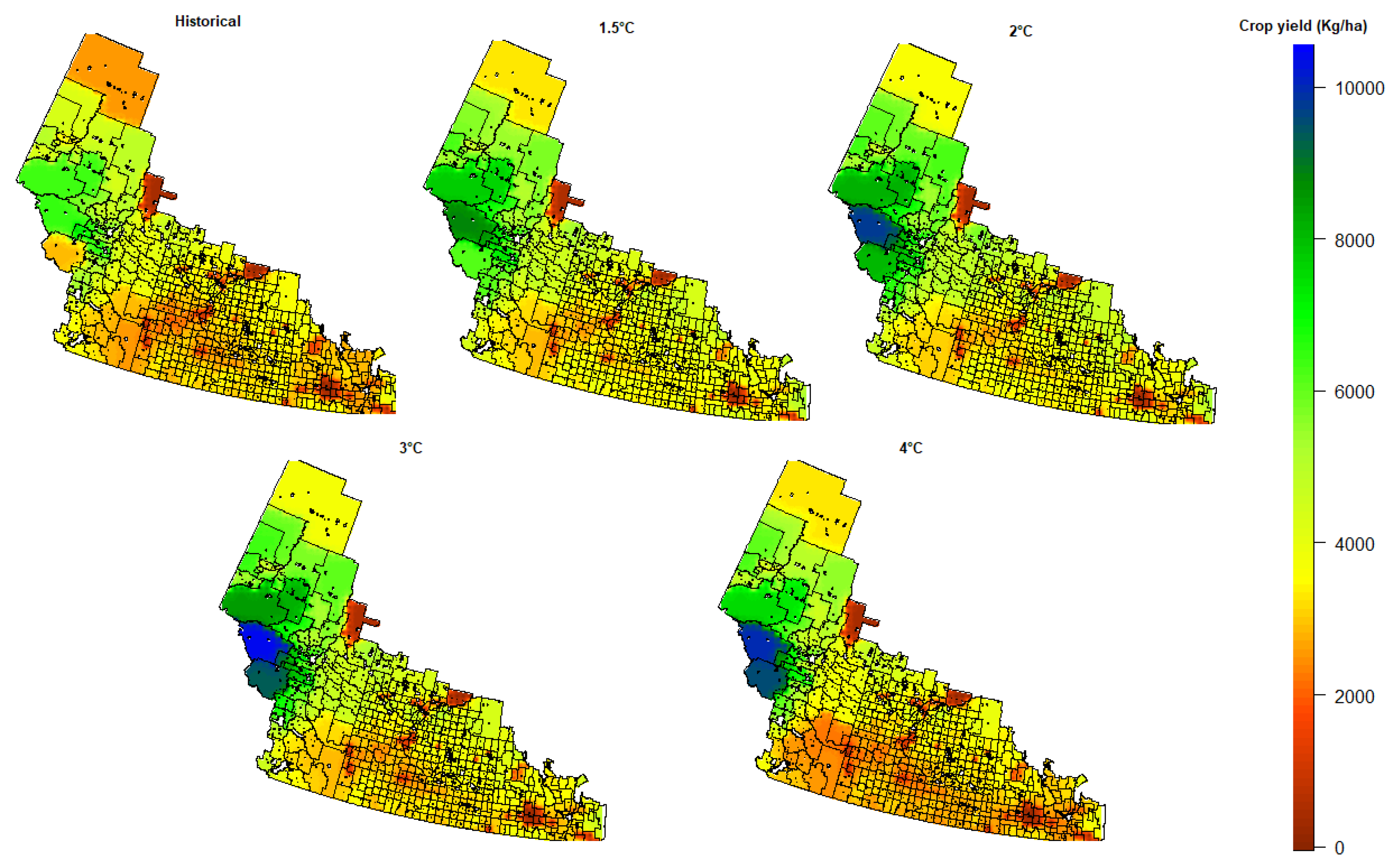
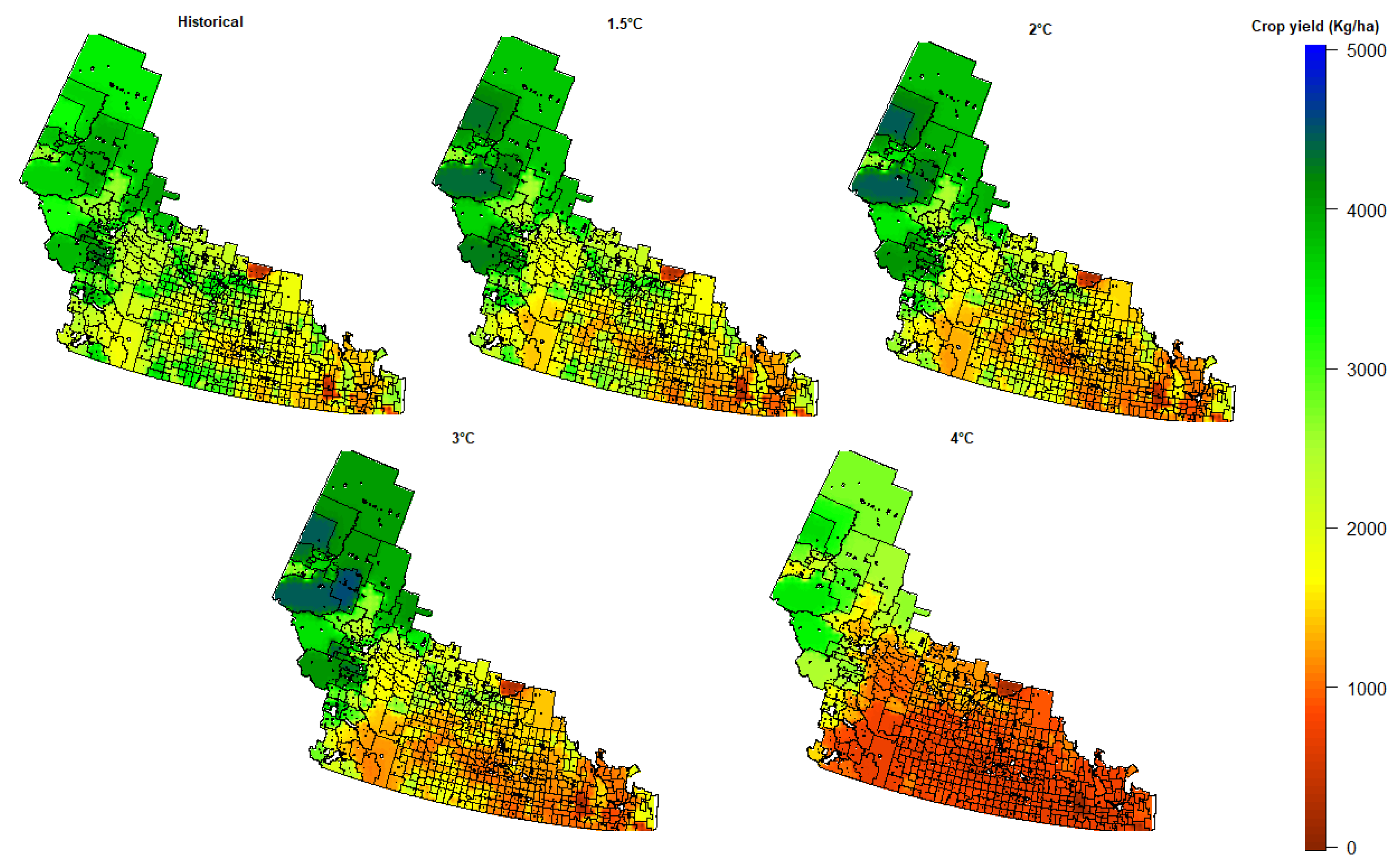
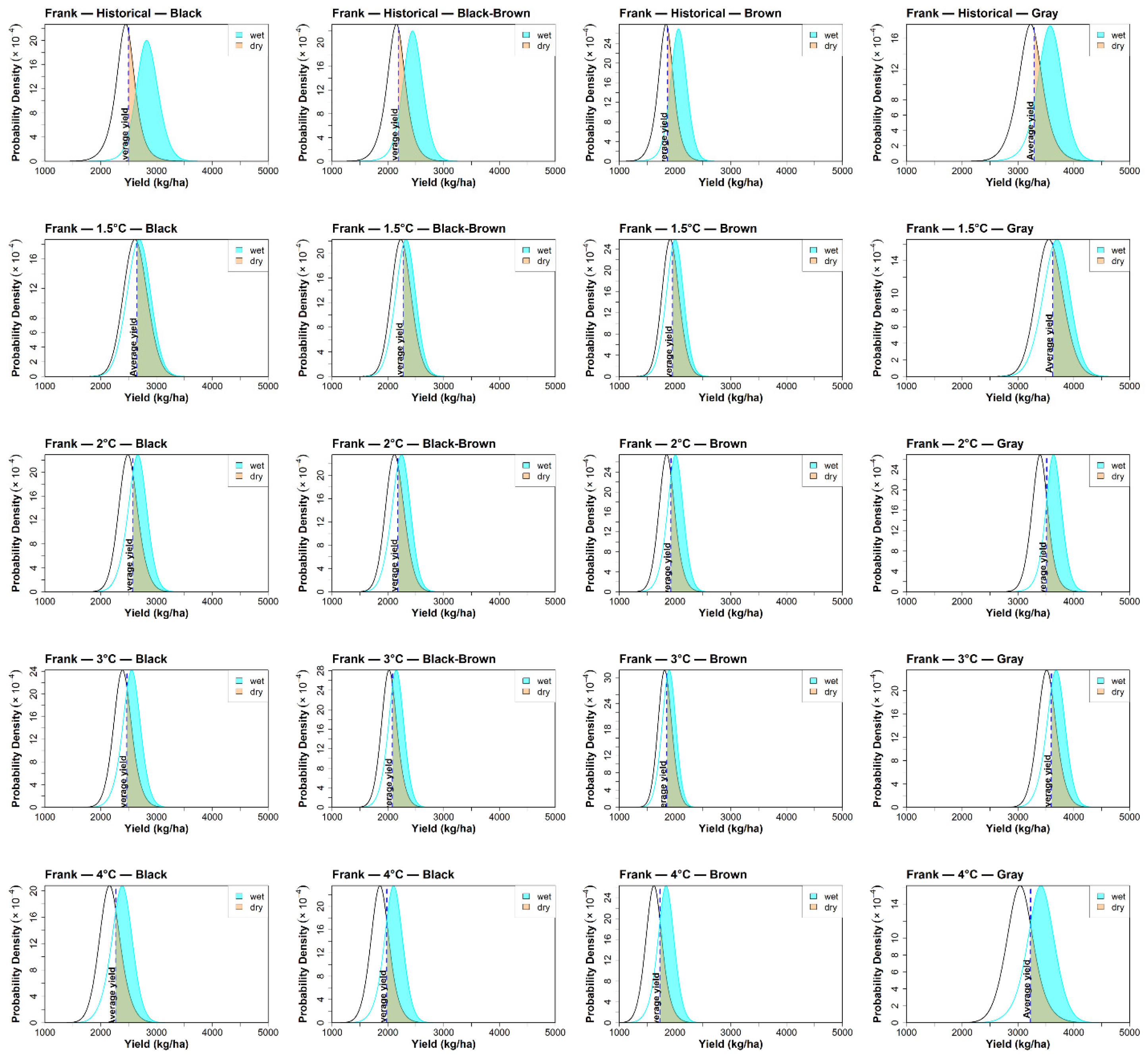
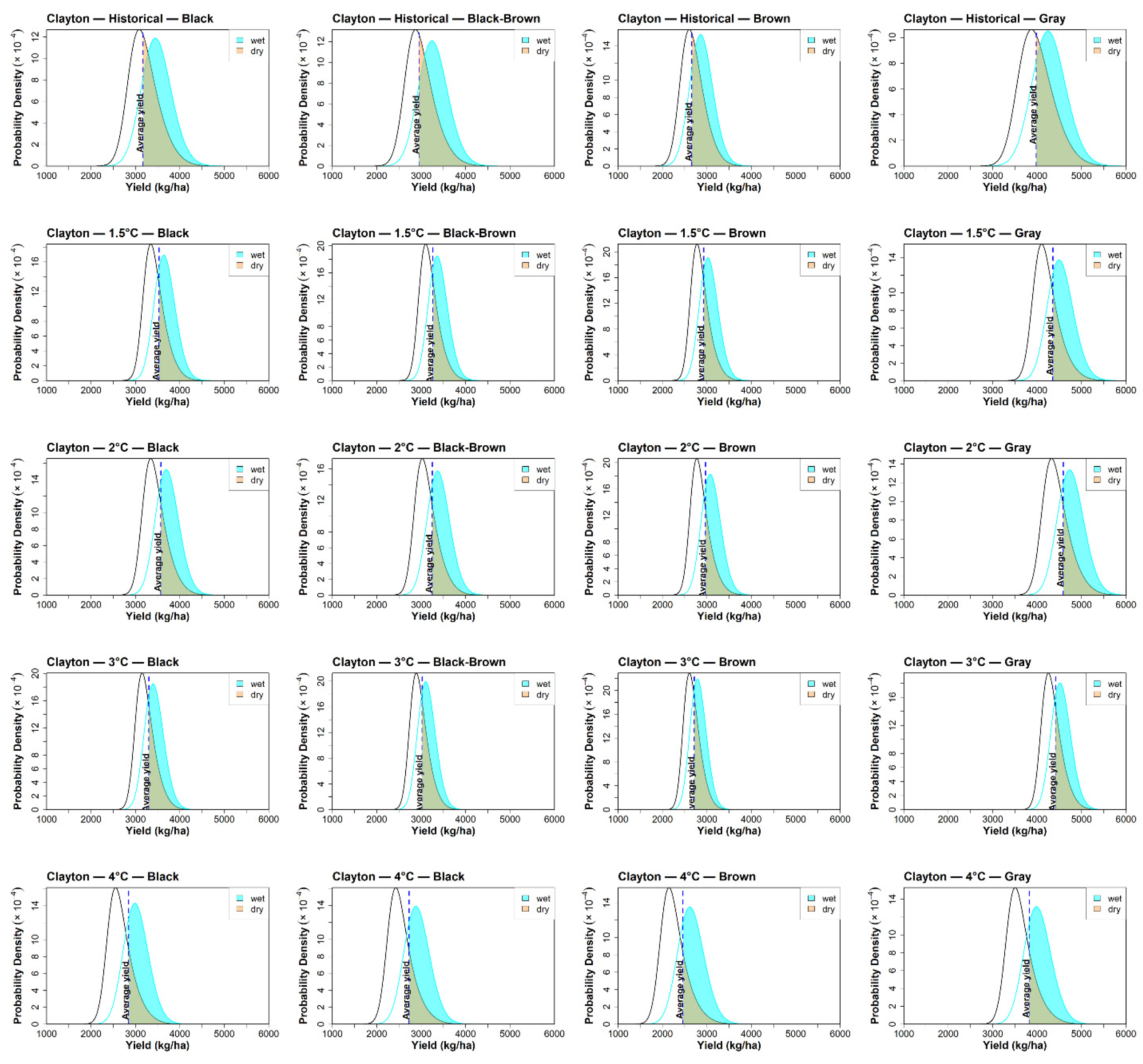
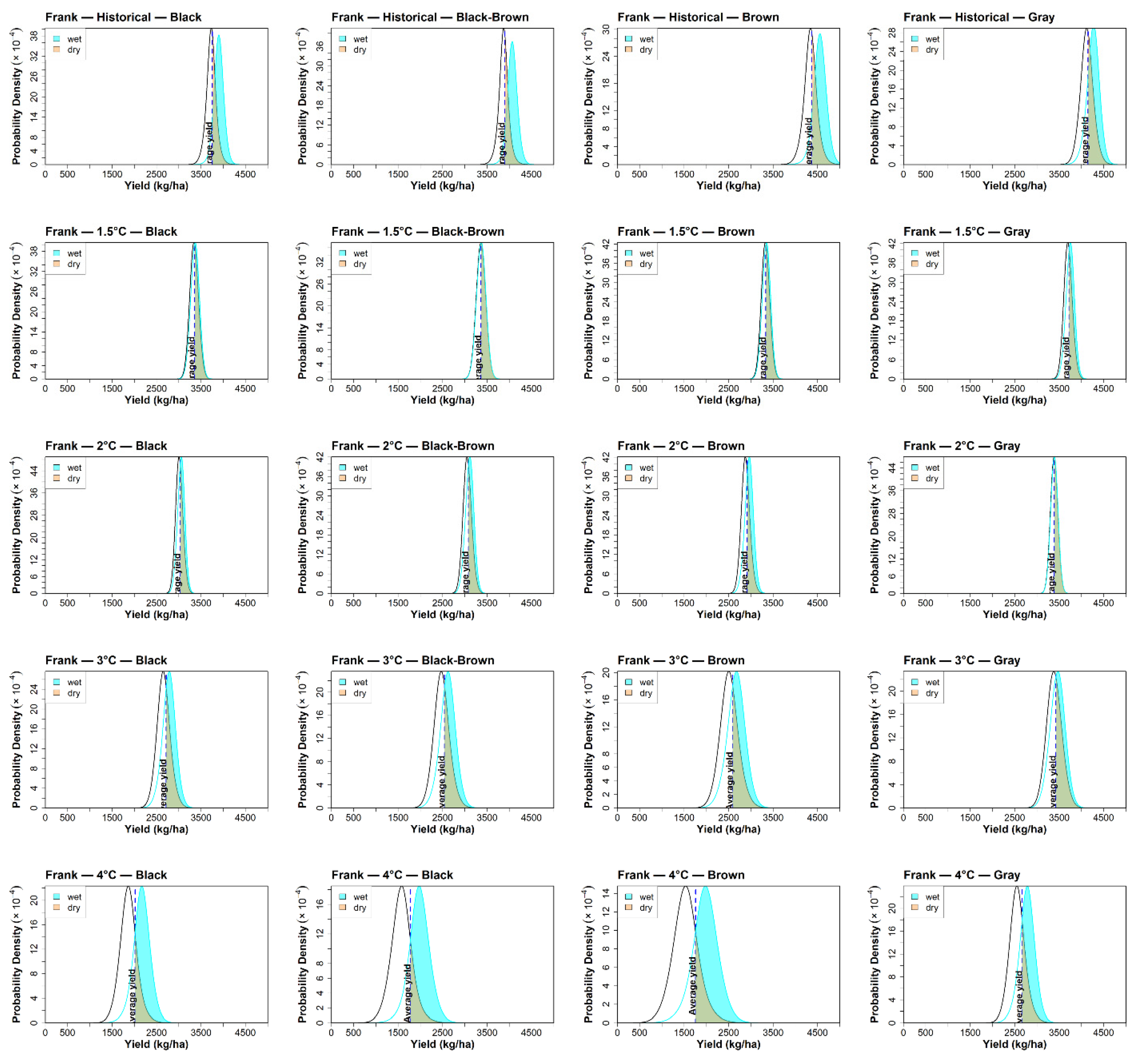
3.2. Impacts of Future Climate Change on Crop Yield
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aadhar, S.; Mishra, V. High-resolution near real-time drought monitoring in South Asia. Sci. Data 2017, 4, 170145. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Farahmand, A.; Melton, F.S.; Teixeira, J.; Anderson, M.C.; Wardlow, B.D.; Hain, C.R. Remote sensing of drought: Progress, challenges and opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Canadian Canola Growers Association. Canola: Growing Canadian Prosperity. Available online: https://www.ccga.ca/advocacy/priorities (accessed on 19 April 2022).
- Zhang, X.; Flato, G.; Cannon, A.; Wan, H.; Wang, X.; Rong, R.; Fyfe, J.; Li, G.; Kharin, V.V. Changes in Temperature and Precipitation Across Canada; Chapter 4; Canada’s Changing Climate Report; Government of Canada: Ottawa, ON, Canada, 2019; Available online: https://natural-resources.canada.ca/ (accessed on 20 October 2025).
- Agriculture and Agri-Food Canada. Statistical Overview of the Canadian Agriculture Industry 2021; Agriculture and Agri-Food Canada: Ottawa, ON, Canada, 2021; Available online: https://agriculture.canada.ca/ (accessed on 20 October 2025).
- Heim, R.R., Jr. A review of twentieth-century drought indices used in the United States. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1166. [Google Scholar] [CrossRef]
- Li, Y.; Ye, W.; Wang, M.; Yan, X. Climate change and drought: A risk assessment of crop production in China. Agric. Ecosyst. Environ. 2009, 134, 341–347. [Google Scholar] [CrossRef]
- Wakatsuki, H.; Ju, H.; Nelson, G.C.; Farrell, A.D.; Deryng, D.; Meza, F.; Hasegawa, T. Research trends and gaps in climate change impacts and adaptation potentials in major crops. Curr. Opin. Environ. Sustain. 2023, 61, 101249. [Google Scholar] [CrossRef]
- Leng, G.; Hall, J. Crop yield sensitivity of global major agricultural countries to droughts and the projected changes in the future. Sci. Total Environ. 2019, 654, 811–821. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, A.F.S.; Russo, A.; Gouveia, C.M.; Páscoa, P. Copula-based agricultural drought risk of rainfed cropping systems. Agric. Water Manag. 2019, 223, 105689. [Google Scholar] [CrossRef]
- Li, P.; Huang, Q.; Huang, S.; Leng, G.; Peng, J.; Wang, H.; Fang, W. Various maize yield losses and their dynamics triggered by drought thresholds based on Copula-Bayesian conditional probabilities. Agric. Water Manag. 2022, 261, 107391. [Google Scholar] [CrossRef]
- Wu, H.; Su, X.; Singh, V.P.; Feng, K.; Niu, J. Agricultural drought prediction based on conditional distributions of vine copulas. Water Resour. Res. 2021, 57, e2021WR029562. [Google Scholar] [CrossRef]
- Madadgar, S.; AghaKouchak, A.; Farahmand, A.; Davis, S.J. Probabilistic estimates of drought impacts on agricultural production. Geophys. Res. Lett. 2017, 44, 7799–7807. [Google Scholar] [CrossRef]
- Zare, M.; Sauchyn, D.; Noorisameleh, Z. Barley, Canola and Spring Wheat Yield Throughout the Canadian Prairies under the Effect of Climate Change. Climate 2025, 13, 179. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- El-Mahroug, S.E.; Suleiman, A.A.; Zoubi, M.M.; Al-Omari, S.; Abu-Afifeh, Q.Y.; Al-Jawaldeh, H.F.; Alta’any, Y.A.; Al-Nawaiseh, T.M.F.; Obeidat, N.; Alsoud, S.H.; et al. Predictive modeling of climate-driven crop yield variability using DSSAT towards sustainable agriculture. AgriEngineering 2025, 7, 156. [Google Scholar] [CrossRef]
- Hanesiak, J.M.; Stewart, R.E.; Bonsal, B.R.; Harder, P. Characterization and summary of the 1999–2005 Canadian Prairie drought. Atmos.–Ocean 2011, 49, 421–452. [Google Scholar] [CrossRef]
- McGinn, S.M. Weather and climate patterns in Canada’s prairie grasslands. Arthropods Can. Grassl. 2010, 1, 105–119. [Google Scholar]
- Bailey, W.G.; Oke, T.R.; Rouse, W.R. The Surface Climates of Canada; McGill–Queen’s University Press: Montreal-Kingston, QC, Canada, 1997; Available online: https://www.mqup.ca/ (accessed on 20 October 2025).
- Gregorich, E.G.; Anderson, D.W. Effects of cultivation and erosion on soils of four toposequences in the Canadian prairies. Geoderma 1985, 36, 343–354. [Google Scholar] [CrossRef]
- Statistics Canada. Estimated Areas, Yield, Production, Average Farm Price and Total Farm Value of Principal Field Crops, in Metric and Imperial Units; Table 32-10-0359-01; Statistics Canada: Ottawa, ON, Canada, 2019; Available online: https://www150.statcan.gc.ca/ (accessed on 12 June 2024).
- Wheaton, E.; Kulshreshtha, S.; Wittrock, V.; Koshida, G. Dry times: Hard lessons from the Canadian drought of 2001 and 2002. Can. Geogr. 2008, 52, 241–262. [Google Scholar] [CrossRef]
- Mardian, J.; Champagne, C.; Bonsal, B.; Daneshfar, B.; Berg, A. From drought hazard to risk: A spring wheat vulnerability assessment in the Canadian Prairies. Agric. For. Meteorol. 2024, 353, 110056. [Google Scholar] [CrossRef]
- Sattar, F. Spring wheat cultivar coefficients: GenCalc vs GLUE. Asian J. Emerg. Res. 2020, 2, 17–18. [Google Scholar] [CrossRef]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Loague, K.; Freeze, R.A. A comparison of rainfall–runoff modeling techniques: Event-based simulation using measured parameter values. Water Resour. Res. 1985, 21, 229–248. [Google Scholar] [CrossRef]
- Cinkus, G.; Mazzilli, N.; Jourde, H.; Wunsch, A.; Liesch, T.; Ravbar, N.; Chen, Z.; Goldscheider, N. When best is the enemy of good—Critical evaluation of performance criteria in hydrological models. Hydrol. Earth Syst. Sci. 2023, 27, 2397–2411. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Kriegler, E.; Riahi, K.; Ebi, K.L.; Hallegatte, S.; Carter, T.R.; Mathur, R.; van Vuuren, D.P. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- Thrasher, B.; Maurer, E.P.; McKellar, C.; Duffy, P.B. Bias correcting climate model simulated daily temperature extremes with quantile mapping. Hydrol. Earth Syst. Sci. 2012, 16, 3309–3314. [Google Scholar] [CrossRef]
- Thrasher, B.; Wang, W.; Michaelis, A.; Melton, F.; Lee, T.; Nemani, R. NASA global daily downscaled projections, CMIP6. Sci. Data 2022, 9, 262. [Google Scholar] [CrossRef]
- Hauser, M.; Engelbrecht, F.; Fischer, E.M. Transient Global Warming Levels for CMIP5 and CMIP6; Zenodo: Geneva, Switzerland, 2021; Available online: https://zenodo.org/records/7390473 (accessed on 20 October 2025).
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index (SPEI). J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Penman, H.L. Natural Evaporation from Open Water, Bare Soil and Grass. Proc. R. Soc. Lond. A Math. Phys. Sci. 1948, 193, 120–145. Available online: https://www.jstor.org/stable/98151 (accessed on 20 October 2025).
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain. Eng. 1982, 108, 223–230. [Google Scholar] [CrossRef]
- Byakatonda, J.; Parida, B.P.; Kenabatho, P.K.; Moalafhi, D.B. Modeling dryness severity using artificial neural network at the Okavango Delta, Botswana. Glob. Nest J. 2016, 18, 463–481. [Google Scholar] [CrossRef]
- Paulo, A.A.; Rosa, R.D.; Pereira, L.S. Climate trends and behaviour of drought indices based on precipitation and evapotranspiration in Portugal. Nat. Hazards Earth Syst. Sci. 2012, 12, 1481–1491. [Google Scholar] [CrossRef]
- Xu, K.; Yang, D.; Yang, H.; Li, Z.; Qin, Y.; Shen, Y. Spatio-temporal variation of drought in China during 1961–2012: A climatic perspective. J. Hydrol. 2015, 526, 253–264. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions de répartition à n dimensions et leurs marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Madadgar, S.; Moradkhani, H. A Bayesian framework for probabilistic seasonal drought forecasting. J. Hydrol. 2013, 14, 1685–1705. [Google Scholar] [CrossRef]
- Mazdiyasni, O.; AghaKouchak, A. Substantial increase in concurrent droughts and heatwaves in the United States. Proc. Natl. Acad. Sci. USA 2015, 112, 11484–11489. [Google Scholar] [CrossRef]
- Genest, C.; Rémillard, B. Validity of the parametric bootstrap for goodness-of-fit testing in semiparametric models. Ann. Inst. Stat. Math. 2008, 60, 1–23. [Google Scholar] [CrossRef]
- Sadegh, M.; Ragno, E.; AghaKouchak, A. Multivariate Copula Analysis Toolbox (MvCAT): Describing dependence and underlying uncertainty using a Bayesian framework. Water Resour. Res. 2017, 53, 5166–5183. [Google Scholar] [CrossRef]
- Huffman, T.; Qian, B.; De Jong, R.; Liu, J.; Wang, H.; McConkey, B.; Brierley, T.; Yang, J. Upscaling modelled crop yields to regional scale: A case study using DSSAT for spring wheat on the Canadian Prairies. Can. J. Soil Sci. 2015, 95, 49–61. [Google Scholar] [CrossRef]
- Hoogenboom, G.; Tsuji, G.Y.; Hoogenboom, G.; Hunt, L.A.; Thornton, P.K.; Wilkens, P.W.; Imamura, D.T.; Bowen, W.T.; Singh, U. Decision Support System for Agrotechnology Transfer (DSSAT) Version 4.7.5; DSSAT Foundation: Gainesville, FL, USA, 2019; Available online: https://DSSAT.net (accessed on 20 October 2025).
- Ewert, F.; Rötter, R.P.; Bindi, M.; Webber, H.; Trnka, M.; Kersebaum, K.C.; Olesen, J.; van Ittersum, M.; Janssen, S.; Rivington, M.; et al. Crop modelling for integrated assessment of risk to food production from climate change. Environ. Model. Softw. 2015, 72, 287–303. [Google Scholar] [CrossRef]
- Qian, B.; He, J.; Song, C.; Wang, H.; Jing, Q.; Hoogenboom, G.; Drury, C.; Yang, J.; He, P.; Zhou, W. Simulated canola yield responses to climate change and adaptation in Canada. Agron. J. 2018, 110, 1331–1344. [Google Scholar] [CrossRef]
- Qian, B.; De Jong, R.; Huffman, T.; Wang, H.; Yang, J. Projecting yield changes of spring wheat under future climate scenarios on the Canadian Prairies. Theor. Appl. Climatol. 2016, 123, 651–669. [Google Scholar] [CrossRef]
- Mohamed, I.; Najafi, M.R.; Joe, P.; Brimelow, J. Multivariate analysis of compound hail, wind and rainfall extremes in Alberta’s hail alley. Weather Clim. Extremes 2024, 46, 100718. [Google Scholar] [CrossRef]
- Khaledi-Alamdari, M.; Majnooni-Heris, A.; Fakheri-Fard, A.; Russo, A. Probabilistic climate risk assessment in rainfed wheat yield: Copula approach using water requirement satisfaction index. Agric. Water Manag. 2023, 289, 108542. [Google Scholar] [CrossRef]
- Schmitt, J.; Offermann, F.; Ribeiro, A.F.S.; Finger, R. Drought risk management in agriculture: A copula perspective on crop diversification. Agric. Econ. 2024, 55, 823–847. [Google Scholar] [CrossRef]
- Li, M.; Wang, G.; Zong, S.; Chai, X. Copula-based assessment and regionalization of drought risk in China. Int. J. Environ. Res. Public Health 2023, 20, 4074. [Google Scholar] [CrossRef]
- Lychuk, T.E.; Moulin, A.P.; Lemke, R.L.; Izaurralde, R.C.; Johnson, E.N.; Olfert, O.O.; Brandt, S.A. Modelling the effects of climate change, agricultural inputs, cropping diversity, and soil on wheat and canola yields at a long-term Prairie site. Agric. Syst. 2021, 252, 106850. [Google Scholar] [CrossRef]


| No. | Model | Institution/Country |
|---|---|---|
| 1 | ACCESS-ESM1-5 | CSIRO, Australia |
| 2 | BCC-CSM2-MR | Beijing Climate Center, China |
| 3 | CanESM5 | Canadian Centre for Climate Modelling, Canada |
| 4 | CNRM-CM6-1 | National Center of Meteorological Research, France |
| 5 | CMCC-CM2-SR5 | Euro-Mediterranean Centre, Italy |
| 6 | EC-Earth3 | EC-Earth Consortium, Sweden |
| 7 | FGOALS-g3 | Chinese Academy of Sciences, China |
| 8 | GFDL-CM4 | NOAA Geophysical Fluid Dynamics Lab, USA |
| 9 | GFDL-ESM4 | NOAA Geophysical Fluid Dynamics Lab, USA |
| 10 | GISS-E2-1-G | Goddard Institute for Space Studies, USA |
| 11 | HadGEM3-GC31-LL | Met Office, Hadley Centre, UK |
| 12 | INM-CM5-0 | Institute for Numerical Mathematics, Russia |
| 13 | IPSL-CM6A-LR | Institute Pierre-Simon Laplace, France |
| 14 | KACE-1-0-G | Korea Meteorological Administration, South Korea |
| 15 | KIOST-ESM | Korea Institute of Ocean Science & Technology, South Korea |
| 16 | MIROC6 | JAMSTEC, Japan |
| 17 | MIROC-ES2L | JAMSTEC, Japan |
| 18 | MPI-ESM1-2-LR | Max Planck Institute for Meteorology, Germany |
| 19 | MRI-ESM2-0 | Meteorological Research Institute, Japan |
| 20 | NorESM2-LM | Norwegian Climate Centre, Norway |
| 21 | UKESM1-0-LL | Met Office, Hadley Centre, UK |
| GCMs Model | 1.5 °C | 2.0 °C | 3.0 °C | 4.0 °C |
|---|---|---|---|---|
| ACCESS-ESM1-5 | 2018–2037 | 2030–2049 | 2051–2070 | 2069–2088 |
| BCC-CSM2-MR | 2021–2040 | 2034–2053 | 2056–2075 | |
| CanESM5 | 2003–2022 | 2013–2032 | 2031–2050 | 2045–2064 |
| CNRM-CM6-1 | 2019–2038 | 2031–2050 | 2049–2068 | 2063–2082 |
| CMCC-CM2-SR5 | 2012–2031 | 2024–2043 | 2043–2062 | 2060–2079 |
| EC-Earth3 | 2015–2034 | 2026–2045 | 2048–2067 | 2064–2083 |
| FGOALS-g3 | 2020–2039 | 2038–2057 | 2065–2084 | |
| GFDL-CM4 | 2020–2039 | 2032–2051 | 2050–2069 | 2070–2089 |
| GFDL-ESM4 | 2030–2049 | 2043–2062 | 2066–2085 | |
| GISS-E2-1-G | 2012–2031 | 2020–2039 | 2047–2066 | 2069–2088 |
| HadGEM3-GC31-LL | 2011–2030 | 2021–2040 | 2038–2057 | 2054–2073 |
| INM-CM5-0 | 2021–2040 | 2037–2056 | 2065–2084 | |
| IPSL-CM6A-LR | 2009–2028 | 2025–2044 | 2041–2060 | 2057–2076 |
| KACE-1-0-G | 2005–2024 | 2014–2033 | 2034–2053 | 2053–2072 |
| KIOST-ESM | 2008–2027 | 2029–2048 | 2055–2074 | |
| MIROC6 | 2031–2050 | 2044–2063 | 2067–2086 | |
| MIROC-ES2L | 2025–2044 | 2038–2057 | 2061–2080 | |
| MPI-ESM1-2-LR | 2025–2044 | 2039–2058 | 2062–2081 | |
| MRI-ESM2-0 | 2017–2036 | 2029–2048 | 2055–2074 | 2074–2093 |
| NorESM2-LM | 2033–2052 | 2047–2066 | 2068–2087 | |
| UKESM1-0-LL | 2014–2033 | 2022–2041 | 2037–2056 | 2051–2070 |
| SPEI Value | Class |
|---|---|
| Greater than 2.00 | Extremely wet |
| 1.50 to 1.99 | Severely wet |
| 1.00 to 1.49 | Moderately wet |
| 0.50 to 0.99 | Slightly wet |
| −0.49 to 0.49 | Near normal |
| −0.99 to −0.50 | Mild dry |
| −1.49 to −1.00 | Moderately dry |
| −1.99 to −1.5 | Severely dry |
| Less than −2.00 | Extremely dry |
| Copula | Mathematical Description | Parameter Range |
|---|---|---|
| Gaussian | : Linear correlation coefficient : Standard normal cumulative distribution function | |
| Clayton | : Measure of dependency betweenand | |
| Frank | : Measure of dependency betweenand |
| Crop | Period | Year | Statistical Performance | ||||
|---|---|---|---|---|---|---|---|
| Observation | Simulation | d | EF | nRMSE | |||
| Wheat CERES | Calibration | 1992–2010 | 2089 | 2316 | 0.73 | 0.17 | 20.15 |
| Validation | 2011–2022 | 2548 | 2573 | 0.85 | 0.3 | 18.5 | |
| Barley | Calibration | 2000–2011 | 3009 | 3358 | 0.77 | 0.25 | 19.9 |
| Validation | 2012–2019 | 3504 | 3546 | 0.85 | 0.57 | 7.2 | |
| Canola | Calibration | 1992–2010 | 1980 | 2098 | 0.8 | 0.03 | 13.6 |
| Validation | 2011–2022 | 2564 | 2309 | 0.81 | 0.1 | 14.1 | |
| Crop | Copula | S | p-Value |
|---|---|---|---|
| Wheat | Clayton | 0.036 | 0.89 |
| Gaussian | 0.428 | 0.321 | |
| Frank | 0.002 | 0.95 | |
| Barley | Clayton | 0.013 | 0.878 |
| Gaussian | 0.919 | 0.169 | |
| Frank | 0.247 | 0.569 | |
| Canola | Clayton | 0.049 | 0.83 |
| Gaussian | 0.487 | 0.447 | |
| Frank | 0.001 | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zare, M.; Sauchyn, D.; Roshani, A.; Noorisameleh, Z. Probabilistic Assessment of Crop Yield Loss Under Drought and Global Warming in the Canadian Prairies. Agronomy 2025, 15, 2484. https://doi.org/10.3390/agronomy15112484
Zare M, Sauchyn D, Roshani A, Noorisameleh Z. Probabilistic Assessment of Crop Yield Loss Under Drought and Global Warming in the Canadian Prairies. Agronomy. 2025; 15(11):2484. https://doi.org/10.3390/agronomy15112484
Chicago/Turabian StyleZare, Mohammad, David Sauchyn, Amin Roshani, and Zahra Noorisameleh. 2025. "Probabilistic Assessment of Crop Yield Loss Under Drought and Global Warming in the Canadian Prairies" Agronomy 15, no. 11: 2484. https://doi.org/10.3390/agronomy15112484
APA StyleZare, M., Sauchyn, D., Roshani, A., & Noorisameleh, Z. (2025). Probabilistic Assessment of Crop Yield Loss Under Drought and Global Warming in the Canadian Prairies. Agronomy, 15(11), 2484. https://doi.org/10.3390/agronomy15112484









