Quantifying Field Soil Moisture, Temperature, and Heat Flux Using an Informer–LSTM Deep Learning Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Field Data
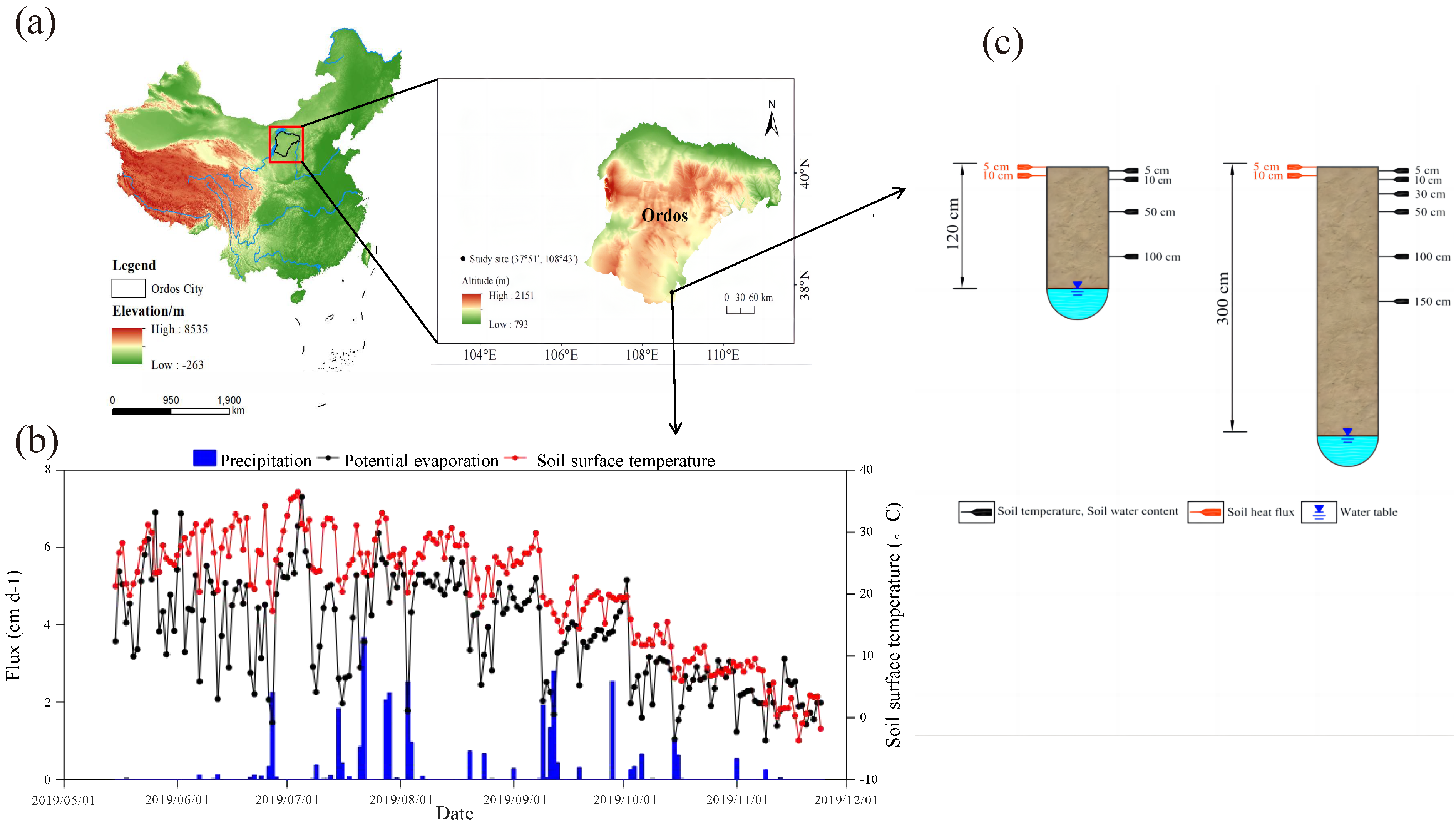
2.1.1. Study Area
2.1.2. Meteorological Data
2.2. Method
2.2.1. Random Forest
2.2.2. Informer–LSTM
2.2.3. Architecture of the Deep Learning
- Step 1. Initial Screening and Empirical Setting
- Step 2. Validation Set Optimization
- Step 3. Tuning and Training Strategy
- Step 4. Final Verification
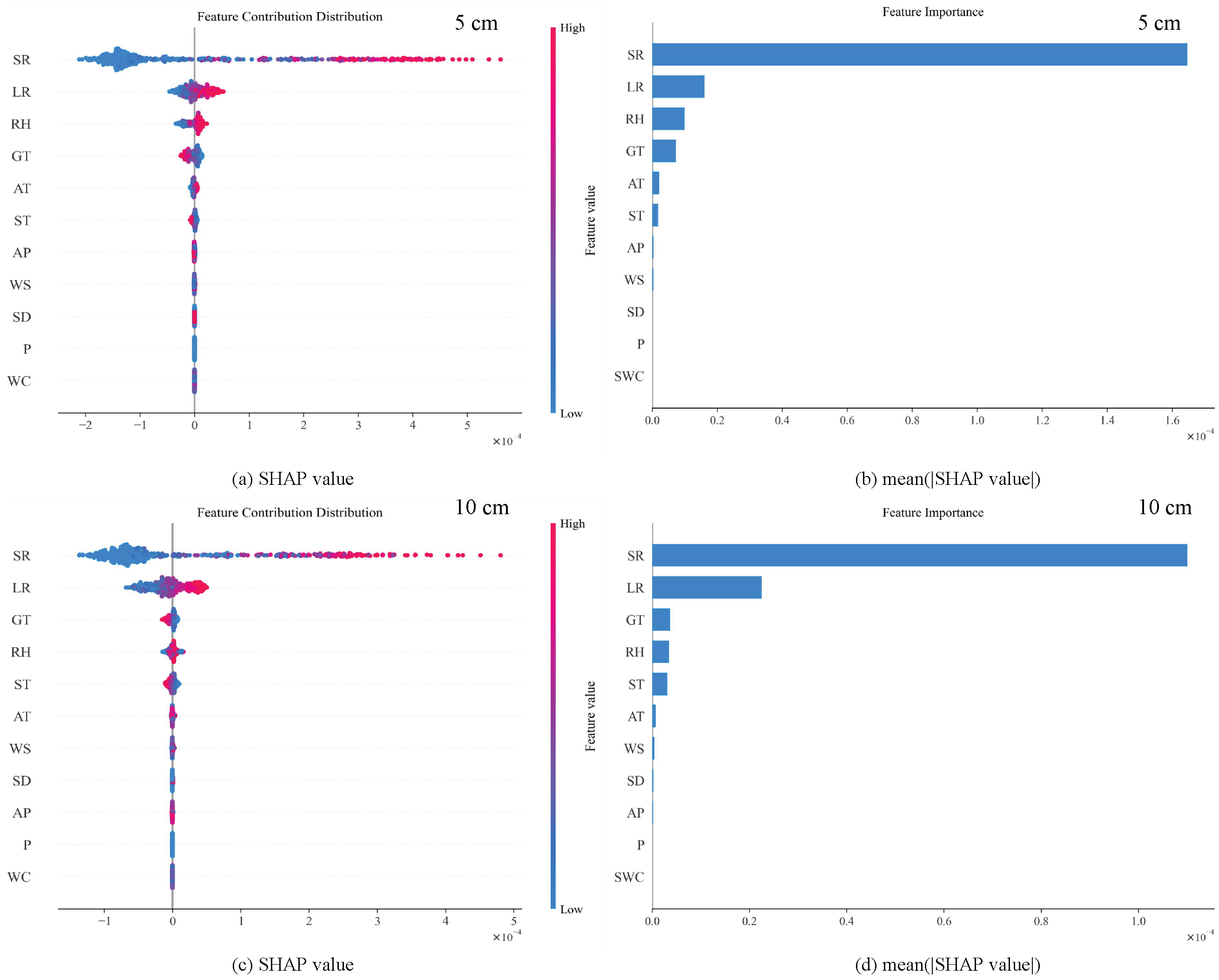
2.2.4. Deep Learning Interpretability: SHapley Additive exPlanations (SHAP)
2.3. Metrics
3. Results and Discussions
3.1. Impact of Meteorological Factors on Soil Temperature and Moisture
3.2. Simulation of Water Content at Different Soil Depths Using Informer–LSTM
3.3. Simulation of Soil Temperature at Different Depths Using Informer–LSTM
3.4. Simulation of Soil Heat Flux at Different Depths Using Informer–LSTM
3.5. Model Explainability
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hopmans, J.; Van Genuchten, M. Vadose zone: Hydrological process. In Encyclopedia of Soils in the Environment; Elsevier: Oxford, UK, 2005; pp. 209–216. [Google Scholar]
- Arora, B.; Dwivedi, D.; Faybishenko, B.; Jana, R.B.; Wainwright, H.M. Understanding and predicting vadose zone processes. Rev. Mineral. Geochem. 2019, 85, 303–328. [Google Scholar] [CrossRef]
- Vereecken, H.; Amelung, W.; Bauke, S.L.; Bogena, H.; Brüggemann, N.; Montzka, C.; Vanderborght, J.; Bechtold, M.; Blöschl, G.; Carminati, A.; et al. Soil hydrology in the Earth system. Nat. Rev. Earth Environ. 2022, 3, 573–587. [Google Scholar] [CrossRef]
- Heinse, R.; Link, T.E. Vadose zone processes: A compendium for teaching interdisciplinary modeling. J. Contemp. Water Res. Educ. 2013, 152, 22–31. [Google Scholar] [CrossRef]
- Vanderborght, J.; Fetzer, T.; Mosthaf, K.; Smits, K.M.; Helmig, R. Heat and water transport in soils and across the soil-atmosphere interface: 1. Theory and different model concepts. Water Resour. Res. 2017, 53, 1057–1079. [Google Scholar] [CrossRef]
- Saito, H.; Šimunek, J.; Mohanty, B.P. Numerical analysis of coupled water, vapor, and heat transport in the vadose zone. Vadose Zone J. 2006, 5, 784–800. [Google Scholar] [CrossRef]
- Garcia Gonzalez, R.; Verhoef, A.; Luigi Vidale, P.; Braud, I. Incorporation of water vapor transfer in the JULES land surface model: Implications for key soil variables and land surface fluxes. Water Resour. Res. 2012, 48, W05538. [Google Scholar] [CrossRef]
- Deb, S.K.; Shukla, M.K.; Sharma, P.; Mexal, J.G. Coupled liquid water, water vapor, and heat transport simulations in an unsaturated zone of a sandy loam field. Soil Sci. 2011, 176, 387–398. [Google Scholar] [CrossRef]
- Scharnagl, B.; Vrugt, J.; Vereecken, H.; Herbst, M. Inverse modelling of in situ soil water dynamics: Investigating the effect of different prior distributions of the soil hydraulic parameters. Hydrol. Earth Syst. Sci. 2011, 15, 3043–3059. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, W.Z. Evolution of soil-water states in the vadose zone of a desert soil after an extreme rainfall event and its impact on the ecosystem. Hydrogeol. J. 2021, 29, 2127–2147. [Google Scholar] [CrossRef]
- Lu, T.; Zheng, C.; Zhou, B.; Wu, J.; Wang, X.; Zhao, Y.; Liu, X.; Yuan, W. Response of Liquid Water and Vapor Flow to Rainfall Events in Sandy Soil of Arid and Semi-Arid Regions. Agronomy 2023, 13, 2424. [Google Scholar] [CrossRef]
- Gao, W.; Liu, X.; Zheng, C.; Lu, Y.; He, J.; He, Y. Comparison of the soil water, vapor, and heat dynamics between summer maize and bare fields in arid and semi-arid areas. Agronomy 2023, 13, 1171. [Google Scholar] [CrossRef]
- Zhang, M.; Wen, Z.; Xue, K.; Chen, L.; Li, D. A coupled model for liquid water, water vapor and heat transport of saturated–unsaturated soil in cold regions: Model formulation and verification. Environ. Earth Sci. 2016, 75, 701. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, L.; Hu, Y.; Hu, X.; Song, W.; Wang, L. A comprehensive study of deep learning for soil moisture prediction. Hydrol. Earth Syst. Sci. 2023, 28, 917–943. [Google Scholar] [CrossRef]
- Mohammadi, B. A review on the applications of machine learning for runoff modeling. Sustain. Water Resour. Manag. 2021, 7, 98. [Google Scholar] [CrossRef]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Liang, F. Machine learning for hydrologic sciences: An introductory overview. Wiley Interdiscip. Rev. Water 2021, 8, e1533. [Google Scholar] [CrossRef]
- Li, X.; Nieber, J.L.; Kumar, V. Machine learning applications in vadose zone hydrology: A review. Vadose Zone J. 2024, 23, e20361. [Google Scholar] [CrossRef]
- Minasny, B.; Bandai, T.; Ghezzehei, T.A.; Huang, Y.C.; Ma, Y.; McBratney, A.B.; Ng, W.; Norouzi, S.; Padarian, J.; Sharififar, A.; et al. Soil Science-Informed Machine Learning. Geoderma 2024, 452, 117094. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Fang, K.; Pan, M.; Shen, C. The value of SMAP for long-term soil moisture estimation with the help of deep learning. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2221–2233. [Google Scholar] [CrossRef]
- Yu, J.; Tang, S.; Zhangzhong, L.; Zheng, W.; Wang, L.; Wong, A.; Xu, L. A deep learning approach for multi-depth soil water content prediction in summer maize growth period. IEEE Access 2020, 8, 199097–199110. [Google Scholar] [CrossRef]
- Li, Q.; Shi, G.; Shangguan, W.; Nourani, V.; Li, J.; Li, L.; Huang, F.; Zhang, Y.; Wang, C.; Wang, D.; et al. A 1 km daily soil moisture dataset over China using in situ measurement and machine learning. Earth Syst. Sci. Data 2022, 14, 5267–5286. [Google Scholar] [CrossRef]
- Alibabaei, K.; Gaspar, P.D.; Lima, T.M. Modeling soil water content and reference evapotranspiration from climate data using deep learning method. Appl. Sci. 2021, 11, 5029. [Google Scholar] [CrossRef]
- Orth, R. Global soil moisture data derived through machine learning trained with in-situ measurements. Sci. Data 2021, 8, 170. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Ma, Z.; Zhao, M.; Li, W.; Hou, X.; Li, J.; Ye, F.; Ma, W. A deep learning approach based on physical constraints for predicting soil moisture in unsaturated zones. Water Resour. Res. 2023, 59, e2023WR035194. [Google Scholar] [CrossRef]
- Kara, A.; Pekel, E.; Ozcetin, E.; Yıldız, G.B. Genetic algorithm optimized a deep learning method with attention mechanism for soil moisture prediction. Neural Comput. Appl. 2024, 36, 1761–1772. [Google Scholar] [CrossRef]
- Bakhshian, S.; Zarepakzad, N.; Nevermann, H.; Hohenegger, C.; Or, D.; Shokri, N. Field-scale soil moisture dynamics predicted by deep learning. Adv. Water Resour. 2025, 201, 104976. [Google Scholar] [CrossRef]
- Alizamir, M.; Kisi, O.; Ahmed, A.N.; Mert, C.; Fai, C.M.; Kim, S.; Kim, N.W.; El-Shafie, A. Advanced machine learning model for better prediction accuracy of soil temperature at different depths. PLoS ONE 2020, 15, e0231055. [Google Scholar] [CrossRef] [PubMed]
- Farhangmehr, V.; Cobo, J.H.; Mohammadian, A.; Payeur, P.; Shirkhani, H.; Imanian, H. A convolutional neural network model for soil temperature prediction under ordinary and hot weather conditions: Comparison with a multilayer perceptron model. Sustainability 2023, 15, 7897. [Google Scholar] [CrossRef]
- Hou, J.; Wang, Y.; Zhou, J.; Tian, Q. Prediction of hourly air temperature based on CNN–LSTM. Geomat. Nat. Hazards Risk 2022, 13, 1962–1986. [Google Scholar] [CrossRef]
- Imanian, H.; Mohammadian, A.; Farhangmehr, V.; Payeur, P.; Goodarzi, D.; Hiedra Cobo, J.; Shirkhani, H. A comparative analysis of deep learning models for soil temperature prediction in cold climates. Theor. Appl. Climatol. 2024, 155, 2571–2587. [Google Scholar] [CrossRef]
- Didem, G. Estimation of soil temperatures with machine learning algorithms—Giresun and Bayburt stations in Turkey. Theor. Appl. Climatol. 2022, 147, 109–125. [Google Scholar]
- Taheri, M.; Schreiner, H.K.; Mohammadian, A.; Shirkhani, H.; Payeur, P.; Imanian, H.; Cobo, J.H. A review of machine learning approaches to soil temperature estimation. Sustainability 2023, 15, 7677. [Google Scholar] [CrossRef]
- Asadzadeh, F.; Emami, S.; Elbeltagi, A.; Akiner, M.E.; Rezaverdinejad, V.; Taran, F.; Salem, A. Investigating the impact of meteorological parameters on daily soil temperature changes using machine learning models. Sci. Rep. 2025, 15, 19988. [Google Scholar] [CrossRef]
- Bonsoms, J.; Boulet, G. Ensemble machine learning outperforms empirical equations for the ground heat flux estimation with remote sensing data. Remote Sens. 2022, 14, 1788. [Google Scholar] [CrossRef]
- Zheng, C.; Jia, L. Evaluation of different methods for soil heat flux estimation at large scales using remote sensing observations. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 6081–6084. [Google Scholar]
- Cross, J.F.; Drewry, D.T. Ensemble machine learning for interpretable soil heat flux estimation. Ecol. Inform. 2024, 82, 102697. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, X.; Xu, L.; Dong, J.; Zhangzhong, L. A hybrid CNN-GRU model for predicting soil moisture in maize root zone. Agric. Water Manag. 2021, 245, 106649. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence 2021, Virtual, 2–9 February 2021; pp. 11106–11115. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Chow, F.K.; Kollet, S.J. The groundwater–land-surface–atmosphere connection: Soil moisture effects on the atmospheric boundary layer in fully-coupled simulations. Adv. Water Resour. 2007, 30, 2447–2466. [Google Scholar] [CrossRef]
- Sauer, T.J.; Horton, R. Soil heat flux. Micrometeorol. Agric. Syst. 2005, 47, 131–154. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Ma, W.W.; Zhang, Z. Assessing bare-soil evaporation from different water-table depths using lysimeters and a numerical model in the Ordos Basin. China 2019, 27, 2707–2718. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Salman, H.A.; Kalakech, A.; Steiti, A. Random forest algorithm overview. Babylon. J. Mach. Learn. 2024, 2024, 69–79. [Google Scholar] [CrossRef] [PubMed]









| Meteorological Factor | Unit | Max | Min | Mean | SD | CV |
|---|---|---|---|---|---|---|
| LR (longwave radiation) | W/m2 | 1185.43 | −15.84 | 223.77 | 315.82 | 1.41 |
| SR (shortwave radiation) | W/m2 | 3.95 | −165.74 | −59.85 | 37.20 | 0.62 |
| WS (average wind speed) | m/s | 23.20 | 0.00 | 2.49 | 1.59 | 0.64 |
| AP (average air pressure) | hPa | 892.30 | 71.10 | 874.41 | 31.05 | 0.04 |
| AT (air temperature) | °C | 34.80 | −6.70 | 18.15 | 7.24 | 0.40 |
| GT (ground temperature) | °C | 67.60 | −5.30 | 23.67 | 13.90 | 0.59 |
| RH (relative humidity) | % | 99.00 | 6.00 | 62.93 | 26.50 | 0.42 |
| SD (sunshine duration) | hour | 1.00 | 0 | 0.36 | 0.45 | 0.23 |
| P (precipitation) | cm | 1.94 | 0 | 0.0078 | 0.0656 | 8.33 |
| Step 1: Input and Initialization |
|---|
| Historical input sequence , label sequence , and prediction length . |
| Goal: Predict soil variables (soil temperature, soil moisture, or soil heat flux). |
| Step 2: Embedding Stage |
| Embed input and label sequences with positional and value encoding: |
| Step 3: Informer Encoder |
| For each encoder layer: |
|
| Step 4: Informer Decoder |
| For each decoder layer: |
|
| Output encoded-decoded sequence: |
| Step 5: LSTM Integration |
| Feed Informer output into LSTM pipeline: |
| Step 6: Post-processing and Output |
| Aggregate prediction results along feature dimension: |
| Return predicted soil variables |
| Hyperparameter | Value |
|---|---|
| Sequence length | 3 |
| Label length | 3 |
| Dropout rate | 0.05 |
| Training epochs | 20 |
| Patience | 3 |
| Learning rate | 0.00064 |
| Batch size | 64 |
| Number of attention heads | Increase by one with the number of feature inputs |
| Attention factor | 5 |
| Model dimension | 512 |
| Soil Depth (cm) | Inputs | Evaluation Indicators | |||
|---|---|---|---|---|---|
| (−) | RMSE (cm3/cm3) | MAPE (%) | MAE (cm3/cm3) | ||
| 5 | MFC | 0.8513 | 0.0086 | 0.0224 | 0.0033 |
| ST | 0.8759 | 0.0078 | 0.0190 | 0.0026 | |
| GWL | 0.8732 | 0.0079 | 0.0183 | 0.0026 | |
| ST, GWL | 0.8553 | 0.0084 | 0.0259 | 0.0036 | |
| MFC, ST | 0.8381 | 0.0089 | 0.0251 | 0.0037 | |
| MFC, GWL | 0.8474 | 0.0086 | 0.0233 | 0.0034 | |
| MFC, GWL, ST | 0.8452 | 0.0087 | 0.0251 | 0.0036 | |
| 10 | MFC | 0.9097 | 0.0039 | 0.0132 | 0.0015 |
| ST | 0.9252 | 0.0036 | 0.0111 | 0.0012 | |
| GWL | 0.9242 | 0.0036 | 0.0115 | 0.0013 | |
| ST, GWL | 0.9052 | 0.0040 | 0.0162 | 0.0018 | |
| MFC, ST | 0.8914 | 0.0043 | 0.0174 | 0.0020 | |
| MFC, GWL | 0.9089 | 0.0039 | 0.0140 | 0.0016 | |
| MFC, GWL, ST | 0.9020 | 0.0041 | 0.0157 | 0.0018 | |
| 30 | MFC | 0.9574 | 0.0034 | 0.0112 | 0.0017 |
| ST | 0.9628 | 0.0032 | 0.0089 | 0.0014 | |
| GWL | 0.9649 | 0.0031 | 0.0076 | 0.0012 | |
| ST, GWL | 0.8954 | 0.0053 | 0.0235 | 0.0036 | |
| MFC, ST | 0.9427 | 0.0039 | 0.0156 | 0.0024 | |
| MFC, GWL | 0.9511 | 0.0036 | 0.0122 | 0.0019 | |
| MFC, GWL, ST | 0.9322 | 0.0043 | 0.0169 | 0.0025 | |
| 50 | MFC | 0.9636 | 0.0015 | 0.0086 | 0.0012 |
| ST | 0.9826 | 0.0008 | 0.0038 | 0.0005 | |
| GWL | 0.9833 | 0.0007 | 0.0037 | 0.0005 | |
| ST, GWL | 0.8869 | 0.0019 | 0.0118 | 0.0016 | |
| MFC, ST | 0.8874 | 0.0026 | 0.0148 | 0.0021 | |
| MFC, GWL | 0.9524 | 0.0013 | 0.0072 | 0.0010 | |
| MFC, GWL, ST | 0.9256 | 0.0017 | 0.0100 | 0.0014 | |
| 100 | MFC | 0.8072 | 0.0006 | 0.0045 | 0.0005 |
| ST | 0.9434 | 0.0003 | 0.0021 | 0.0002 | |
| GWL | 0.9465 | 0.0003 | 0.0021 | 0.0002 | |
| ST, GWL | −2.9085 | 0.0028 | 0.0239 | 0.0026 | |
| MFC, ST | −1.6135 | 0.0023 | 0.0185 | 0.0020 | |
| MFC, GWL | −0.9983 | 0.0020 | 0.0171 | 0.0018 | |
| MFC, GWL, ST | −0.9381 | 0.0020 | 0.0162 | 0.0017 | |
| 150 | MFC | 0.8658 | 0.0013 | 0.0065 | 0.0010 |
| ST | 0.9645 | 0.0006 | 0.0038 | 0.0006 | |
| GWL | 0.9785 | 0.0005 | 0.0025 | 0.0004 | |
| ST, GWL | −4.6870 | 0.0082 | 0.0534 | 0.0080 | |
| MFC, ST | −0.8933 | 0.0047 | 0.0285 | 0.0043 | |
| MFC, GWL | 0.7561 | 0.0017 | 0.0098 | 0.0015 | |
| MFC, GWL, ST | −0.8505 | 0.0047 | 0.0292 | 0.0044 | |
| Soil Depth (cm) | Input | Evaluation Indicators | |||
|---|---|---|---|---|---|
| (−) | RMSE (℃) | MAPE (%) | MAE (℃) | ||
| 5 | MFC | 0.9030 | 1.6531 | 12.41 | 1.1508 |
| SWC | 0.8252 | 2.2191 | 16.80 | 1.5711 | |
| GWL | 0.8112 | 2.3060 | 17.35 | 1.7013 | |
| SWC, GWL | 0.8134 | 2.2930 | 16.13 | 1.5967 | |
| MFC, SWC | 0.9109 | 1.5836 | 11.66 | 1.1197 | |
| MFC, GWL | 0.8932 | 1.7342 | 13.05 | 1.2335 | |
| MFC, GWL, SM | 0.9114 | 1.5797 | 11.64 | 1.1622 | |
| 10 | MFC | 0.9197 | 1.2072 | 7.830 | 0.8173 |
| SWC | 0.8316 | 1.7482 | 11.65 | 1.269 | |
| GWL | 0.838 | 1.7145 | 10.98 | 1.2149 | |
| SWC, GWL | 0.8075 | 1.8696 | 12.75 | 1.3680 | |
| MFC, SWC | 0.9287 | 1.1373 | 7.340 | 0.7712 | |
| MFC, GWL | 0.9049 | 1.3136 | 8.440 | 0.8451 | |
| MFC, GWL, SM | 0.9253 | 1.1645 | 7.700 | 0.8162 | |
| 30 | MFC | 0.8841 | 0.9682 | 5.050 | 0.5986 |
| SWC | 0.8819 | 0.9772 | 5.320 | 0.6456 | |
| GWL | 0.88 | 0.9849 | 5.460 | 0.6697 | |
| SWC, GWL | 0.8230 | 1.1965 | 6.790 | 0.8438 | |
| MFC, SWC | 0.8806 | 0.9825 | 5.240 | 0.6212 | |
| MFC, GWL | 0.9056 | 0.8737 | 4.400 | 0.5157 | |
| MFC, GWL, SM | 0.8386 | 1.1422 | 6.330 | 0.758 | |
| 50 | MFC | 0.9003 | 0.7291 | 3.540 | 0.4712 |
| SWC | 0.9542 | 0.4943 | 2.500 | 0.3479 | |
| GWL | 0.9338 | 0.594 | 2.750 | 0.3628 | |
| SWC, GWL | 0.9164 | 0.6680 | 3.520 | 0.4817 | |
| MFC, SWC | 0.912 | 0.6851 | 3.150 | 0.4149 | |
| MFC, GWL | 0.8971 | 0.7408 | 3.650 | 0.486 | |
| MFC, GWL, SM | 0.9166 | 0.6669 | 3.300 | 0.4421 | |
| 100 | MFC | 0.9885 | 0.1672 | 0.800 | 0.1278 |
| SWC | 0.9952 | 0.1276 | 0.630 | 0.0984 | |
| GWL | 0.9984 | 0.0618 | 0.300 | 0.05 | |
| SWC, GWL | 0.7517 | 0.7754 | 4.190 | 0.6840 | |
| MFC, SWC | 0.9951 | 0.1078 | 0.500 | 0.0810 | |
| MFC, GWL | 0.8441 | 0.6142 | 2.800 | 0.4284 | |
| MFC, GWL, SM | 0.9687 | 0.275 | 1.380 | 0.2141 | |
| 150 | MFC | 0.9819 | 0.1364 | 0.670 | 0.1133 |
| SWC | 0.9912 | 0.1451 | 0.770 | 0.1245 | |
| GWL | 0.9961 | 0.0629 | 0.290 | 0.0493 | |
| SWC, GWL | −0.8793 | 1.3916 | 7.360 | 1.2255 | |
| MFC, SWC | 0.7924 | 0.4625 | 2.500 | 0.4256 | |
| MFC, GWL | 0.9461 | 0.2356 | 1.160 | 0.1973 | |
| MFC, GWL, SM | 0.9533 | 0.2191 | 1.080 | 0.1811 | |
| Soil Column | Soil Depth (cm) | Inputs | Evaluation Indicators | |||
|---|---|---|---|---|---|---|
| (−) | RMSE (MJ/m2/d) | MAPE (%) | MAE (MJ/m2/d) | |||
| 1.2 m | 5 | MFC | 0.9160 | 8.4537 | 2.7621 | 5.3601 |
| SM, ST | 0.8892 | 9.7082 | 6.4036 | 6.4940 | ||
| MFC, SM, ST | 0.9152 | 8.4940 | 3.0813 | 5.4764 | ||
| 10 | MFC | 0.9537 | 2.9748 | 1.0605 | 2.0450 | |
| SM, ST | 0.9180 | 3.9578 | 1.6930 | 2.5730 | ||
| MFC, SM, ST | 0.9237 | 8.0563 | 2.2297 | 5.2154 | ||
| 1.2 m | 5 | MFC | 0.7985 | 22.2681 | 0.7862 | 15.2318 |
| SM, ST | 0.7244 | 26.0425 | 0.8984 | 18.8354 | ||
| MFC, SM, ST | 0.7835 | 23.0791 | 0.8236 | 15.6490 | ||
| 10 | MFC | 0.8976 | 10.8302 | 0.5522 | 7.1323 | |
| SM, ST | 0.8649 | 12.4403 | 0.6949 | 8.1077 | ||
| MFC, SM, ST | 0.8823 | 11.6096 | 0.6358 | 7.8982 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Sun, X.; Wang, P.; Wang, W.; Ma, Z. Quantifying Field Soil Moisture, Temperature, and Heat Flux Using an Informer–LSTM Deep Learning Model. Agronomy 2025, 15, 2453. https://doi.org/10.3390/agronomy15112453
Li N, Sun X, Wang P, Wang W, Ma Z. Quantifying Field Soil Moisture, Temperature, and Heat Flux Using an Informer–LSTM Deep Learning Model. Agronomy. 2025; 15(11):2453. https://doi.org/10.3390/agronomy15112453
Chicago/Turabian StyleLi, Na, Xiaoxiao Sun, Peng Wang, Wenke Wang, and Zhitong Ma. 2025. "Quantifying Field Soil Moisture, Temperature, and Heat Flux Using an Informer–LSTM Deep Learning Model" Agronomy 15, no. 11: 2453. https://doi.org/10.3390/agronomy15112453
APA StyleLi, N., Sun, X., Wang, P., Wang, W., & Ma, Z. (2025). Quantifying Field Soil Moisture, Temperature, and Heat Flux Using an Informer–LSTM Deep Learning Model. Agronomy, 15(11), 2453. https://doi.org/10.3390/agronomy15112453








