Prediction of Winter Wheat Cultivar Performance Using Mixed Models and Environmental Mean Regression from Multi-Environment Trials for Cultivar Recommendation to Reduce Yield Gap in Poland
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Source and Trial Design
2.2. Development of Model
2.2.1. Data Preprocessing
2.2.2. Mixed Model Analysis
× L × Y)gij + (G × M)gk + εijkgm
2.2.3. Cultivar Specific Regression Modelling
2.2.4. Simplified Reference Model for Yield Prediction
2.2.5. Model Validation
2.3. Application of Model for Cultivar Recommendation
2.3.1. Evaluation of Cultivar Adaptability Across Diverse Environmental Conditions
2.3.2. Recommendation Scenarios Based on Cultivar Responsiveness
3. Results and Discussion
3.1. Yield Range and Representativeness of Trial Environments
3.2. Data Preparation
- Outlier removal based on environment-specific standardized residuals.
- Exclusion of cultivars with fewer than 30 observations across the 2015–2023 period.
3.3. Statistical Models
3.3.1. Performance of the Linear Mixed Model
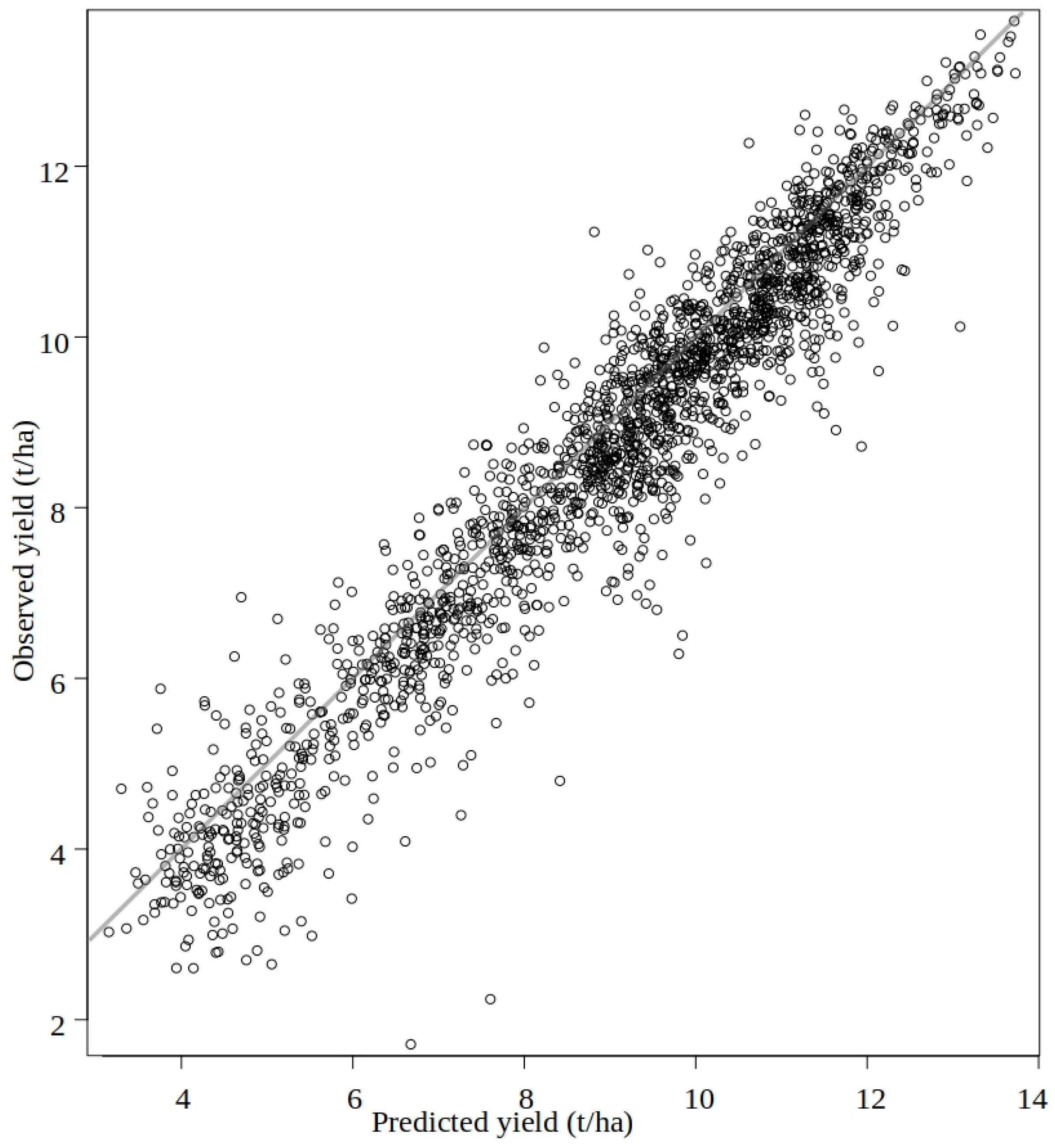
3.3.2. Performance and Prediction Accuracy of Cultivar-Specific Regression Models
Model Fit and Predictive Accuracy
Cultivar Responsiveness and Model Robustness
3.3.3. Comparative Validation of Predictive Accuracy Using 2024 Data
Validation of Specific-Cultivar Regression Models Using 2024 Data
3.3.4. Cultivar Adaptation to Diverse Environmental Productivity
3.3.5. Implications for Cultivar Recommendation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMMI | Additive Main Effects and Multiplicative Interaction (analysis method) |
| COBORU | Centralny Ośrodek Badania Odmian Roślin Uprawnych (Research Centre for Cultivar Testing, Poland) |
| IHAR-PIB | Instytut Hodowli i AKlimatyzacji Roślin—Państwowy Instytut badawczy (Institute of Plant Breeding and Acclimatization—National Research Institute, Poland) |
| IUNG-PIB | Instytut Uprawy Nawożenia i Gleboznawstwa—Państwowy Instytut Badawczy Institute of Soil Science and Plant Cultivation—State Research Institute, Poland) |
| GGE | Genotype + Genotype × Environment (biplot analysis method) |
| G×E | Genotype-by-environment (interaction) |
| L × Y × M | Location × Year × Management (combined trial factors) |
| MIM | Management intensity (treatment factor in trials) |
| RMSE | Root mean square error |
| SD | Standard deviation |
| R2 | Coefficient of determination |
| RMSE/SD | Ratio of prediction error to standard deviation |
References
- Federizzi, L.C.; Carbonell, S.A.M.; Pacheco, M.T.; Nava, I.C. Breeders’ Work after Cultivar Development: The Stage of Recommendation. Crop Breed. Appl. Biotechnol. 2012, 12, 67–74. [Google Scholar] [CrossRef]
- Qian, J.; Zhao, Z. Estimating the Contribution of New Seed Cultivars to Increases in Crop Yields: A Case Study for Corn. Sustainability 2017, 9, 1282. [Google Scholar] [CrossRef]
- FAOSTAT. Statistical Database. Food and Agriculture Organization of the United Nations. 2023. Available online: https://www.fao.org/faostat/ (accessed on 5 August 2025).
- Dziechciarz, M.; Kaczmarek, J.; Rolbiecki, R. Production and Economic Importance of Winter Wheat in Poland. Sci. J. Warsaw Univ. Life Sci. Probl. World Agric. 2020, 20, 55–63, (Original work published in Polish). [Google Scholar]
- Shiferaw, B.; Smale, M.; Braun, H.-J.; Duveiller, E.; Reynolds, M.; Muricho, G. Crops That Feed the World 10: Past Successes and Future Challenges to the Role Played by Wheat in Global Food Security. Food Secur. 2013, 5, 291–317. [Google Scholar] [CrossRef]
- Wójcik-Gront, E.; Iwańska, M.; Wnuk, A.; Oleksiak, T. The Analysis of Wheat Yield Variability Based on Experimental Data from 2008–2018 to Understand the Yield Gap. Agriculture 2022, 12, 32. [Google Scholar] [CrossRef]
- Yan, W.; Tinker, N.A. Biplot Analysis of Multi-Environment Trial Data: Principles and Applications. Can. J. Plant Sci. 2006, 86, 623–645. [Google Scholar] [CrossRef]
- van Eeuwijk, F.A.; Bustos-Korts, D.V.; Malosetti, M. What Should Students in Plant Breeding Know about the Statistical Aspects of Genotype × Environment Interactions? Crop Sci. 2016, 56, 2119–2140. [Google Scholar] [CrossRef]
- Li, X.; Bai, G.; Carver, B.; Chao, S. Genotype-by-Environment Interaction and Stability Analysis in Multi-Environment Trials of Wheat. Field Crops Res. 2020, 255, 107866. [Google Scholar] [CrossRef]
- Finlay, K.W.; Wilkinson, G.N. The Analysis of Adaptation in a Plant-Breeding Programme. Aust. J. Agric. Res. 1963, 14, 742–754. [Google Scholar] [CrossRef]
- Becker, H.C.; Leon, J. Stability Analysis in Plant Breeding. Plant Breed. 1988, 101, 1–23. [Google Scholar] [CrossRef]
- Gauch, H.G. Statistical Analysis of Yield Trials by AMMI and GGE. Crop Sci. 2006, 46, 1488–1500. [Google Scholar] [CrossRef]
- Yan, W.; Holland, J.B. A Heritability-Adjusted GGE Biplot for Test Environment Evaluation. Euphytica 2010, 171, 355–369. [Google Scholar] [CrossRef]
- Piepho, H.P.; Büchse, A.; Emrich, K. A Stage-Wise Approach for the Analysis of Multi-Environment Trials. Biometr. J. 2014, 56, 761–777. [Google Scholar] [CrossRef]
- Smith, A.; Cullis, B.; Thompson, R. The Analysis of Crop Cultivar Breeding and Evaluation Trials: An Overview of Current Mixed Model Approaches. J. Agric. Sci. 2005, 143, 449–462. [Google Scholar] [CrossRef]
- Crossa, J.; Pérez-Rodríguez, P.; Cuevas, J.; Montesinos-López, O.; Jarquín, D.; de Los Campos, G.; Burgueño, J.; González-Camacho, J.M.; Pérez-Elizalde, S.; Beyene, Y.; et al. Genomic Selection in Plant Breeding: Methods, Models, and Perspectives. Trends Plant Sci. 2017, 22, 961–975. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: https://www.R-project.org/ (accessed on 5 August 2025).
- Iwańska, M.; Paderewski, J.; Stępień, M.; Rodrigues, P.C. Winter Wheat Cultivar Recommendation Based on Expected Environment Productivity. Agriculture 2021, 11, 522. [Google Scholar] [CrossRef]
- COBORU. Results of Winter Wheat Cultivar Trials 2015–2024; Centralny Ośrodek Badania Odmian Roślin Uprawnych (COBORU): Słupia Wielka, Poland, 2024.
- Iwańska, M.; Paderewski, J.; Žukovskis, J.; Wnuk, A.; Oleksiak, T.; Rodrigues, P.C. Evaluating Cultivar Intensity and Dataset Size for Reliable Cultivar Recommendation in Winter Wheat: A Systematic Research of Environmental and Genotype Factors. Crop Sci. 2024, 64, 1666–1677. [Google Scholar] [CrossRef]
- Piepho, H.P.; Möhring, J.; Melchinger, A.E.; Büchse, A. BLUP for Phenotypic Selection in Plant Breeding and Variety Testing. Euphytica 2003, 161, 209–228. [Google Scholar] [CrossRef]
- Bates, D.; Maechler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Kuznetsova, A.; Brockhoff, P.B.; Christensen, R.H.B. lmerTest Package: Tests in Linear Mixed Effects Models. J. Stat. Softw. 2017, 82, 1–26. [Google Scholar] [CrossRef]
- Technow, F.; Messina, C.D.; Totir, L.R.; Cooper, M. Integrating Crop Growth Models with Whole Genome Prediction through Approximate Bayesian Computation. PLoS ONE 2015, 10, e0130855. [Google Scholar] [CrossRef] [PubMed]
- Heslot, N.; Yang, H.-P.; Sorrells, M.E.; Jannink, J.-L. Genomic Selection in Plant Breeding: A Comparison of Models. Crop Sci. 2014, 54, 89–106. [Google Scholar] [CrossRef]
- Leśniowska, K.; Wanic, M. Procedures for the Evaluation of Cereal Cultivars in Poland—Criteria and Intensity of Recommendation Selection. Biul. COBORU 2019. [Google Scholar]
- Gozdowski, D.; Stępień, M.; Samborski, S.; Dobers, E.S.; Szatyłowicz, J.; Chormański, J. Determination of the Most Relevant Soil Properties for the Delineation of Management Zones in Production Fields. Commun. Soil Sci. Plant Anal. 2014, 45, 2289–2304. [Google Scholar] [CrossRef]
- Gozdowski, D.; Leszczyńska, E.; Stępień, M.; Rozbicki, J.; Samborski, S. Within-Field Variability of Winter Wheat Yield and Grain Quality versus Soil Properties. Commun. Soil Sci. Plant Anal. 2017, 48, 1029–1041. [Google Scholar] [CrossRef]
- Panek, E.; Gozdowski, D.; Stępień, M.; Samborski, S.; Ruciński, D.; Buszke, B. Within-Field Relationships between Satellite-Derived Vegetation Indices, Grain Yield and Spike Number of Winter Wheat and Triticale. Agronomy 2020, 10, 1842. [Google Scholar] [CrossRef]
- IUNG-PIB. Characteristics of Arable Soils in Poland; IUNG-PIB: Puławy, Poland, 2021. [Google Scholar]
- Czarnowski, F.; Truszkowska, R. Commentary on the Soil Classification Table for the Evaluation of Arable Land in Plains, Highlands, and Lowlands, Including Regional Instructions for Mountainous Areas and Commentary on the Evaluation of Grassland and Forest Soils for Soil Classifiers and Cartographers; Institute of Soil Science and Plant Cultivation IUNG-PIB: Puławy, Poland, 1963. (In Polish) [Google Scholar]
- UTKG. Official Table of Land Classes; Attachment to a Regulation of the Council of Ministers on Soil Classification, Poland. 2012. Available online: https://eli.gov.pl/eli/DU/2012/1246/ogl (accessed on 7 August 2025). (In Polish)
- GUS. Statistical Yearbook of Agriculture 2024; Statistics Poland: Warsaw, Poland, 2024.
- Lobell, D.B.; Cassman, K.G.; Field, C.B. Crop Yield Gaps: Their Importance, Magnitudes, and Causes. Annu. Rev. Environ. Resour. 2009, 34, 179–204. [Google Scholar] [CrossRef]
- van Ittersum, M.K.; Cassman, K.G.; Grassini, P.; Wolf, J.; Tittonell, P.A.; Hochman, Z. Yield Gap Analysis with Local to Global Relevance—A Review. Field Crops Res. 2013, 143, 4–17. [Google Scholar] [CrossRef]

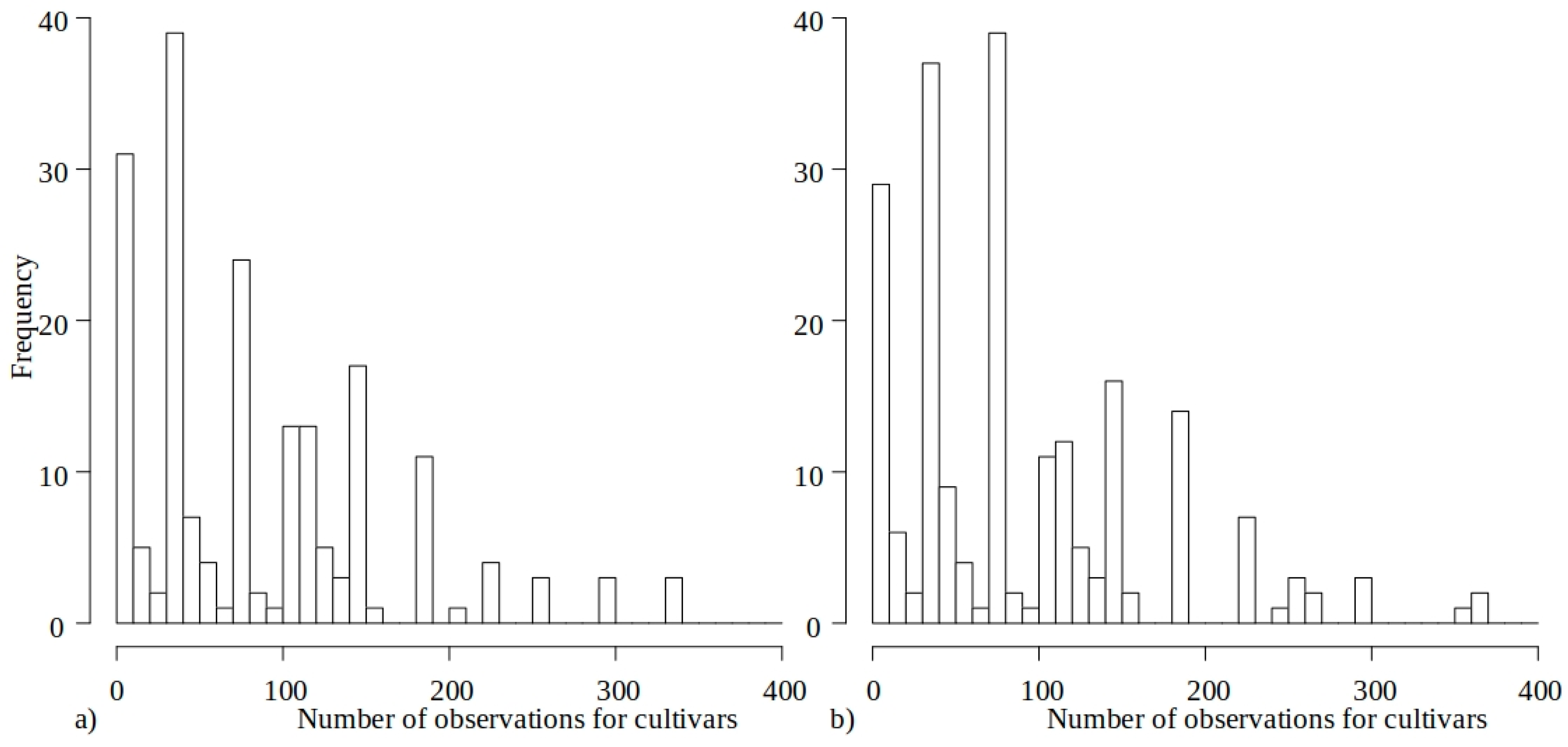
| Location | Period | Soil Quality Class | Land Suitability Group | Land Suitable Mainly for | Mean ± SD Yield (t/ha) |
|---|---|---|---|---|---|
| Cicibór Duży | 2015–2023 | IIIb | 4 | rye and wheat | 7.99 ± 1.69 |
| 2024 | IIIb | 4 | rye and wheat | 6.50 ± 0.54 | |
| Czesławice | 2015–2023 | IIIa | 2 | wheat | 9.53 ± 1.40 |
| 2024 | IIIa | 2 | wheat | 11.57 ± 0.74 | |
| Głębokie | 2015–2023 | IIIa | 2 | wheat | 7.98 ± 2.25 |
| 2024 | IIIa | 2 | wheat | 7.71 ± 0.53 | |
| Głubczyce | 2015–2023 | II | 1 | wheat | 10.93 ± 1.16 |
| 2024 | II | 1 | wheat | 10.54 ± 1.34 | |
| Krościna Mała | 2015–2023 | IIIa. IIIb. IVa. IVb | 2 and 4 | wheat. rye and wheat | 9.36 ± 1.54 |
| 2024 | IIIa | 2 | wheat | 9.68 ± 1.09 | |
| Marianowo | 2015–2023 | IIIb. IVa. IVb | 4 and 5 | rye and wheat. rye | 9.24 ± 1.91 |
| 2024 | IIIb | 4 | rye and wheat | 10.54 ± 0.65 | |
| Masłowice | 2015–2023 | IIIb. IVb | 4 and 5 | rye and wheat. rye | 9.25 ± 1.51 |
| 2024 | IIIb | 4 | rye and wheat | 9.12 ± 0.95 | |
| Nowa Wieś Ujska | 2015–2023 | IIIa. IIIb. IVa | 2 and 4 | wheat. rye and wheat | 7.22 ± 1.77 |
| 2024 | IVa | 4 | rye and wheat | 7.32 ± 1.27 | |
| Pawłowice | 2015–2023 | IIIb | 2 | wheat | 8.80 ± 2.28 |
| 2024 | IIIb | 2 | wheat | 9.02 ± 0.72 | |
| Radostowo | 2015–2023 | II | 1 | wheat | 10.28 ± 2.82 |
| 2024 | II | 1 | wheat | 10.46 ± 0.89 | |
| Rarwino | 2015–2023 | IIIb. IVa. IVb | 4 and 5 | rye and wheat. rye | 9.03 ± 1.61 |
| 2024 | IVa | 5 | rye | 9.95 ± 0.93 | |
| Rychliki | 2015–2023 | IIIb. IVa | 2 | wheat | 9.79 ± 1.58 |
| 2024 | IIIb | 2 | wheat | 9.78 ± 0.93 | |
| Seroczyn | 2015–2023 | IIIb. IVa | 4 and 5 | rye and wheat. rye | 8.42 ± 1.74 |
| 2024 | IIIb | 4 | rye and wheat | 9.64 ± 0.81 | |
| Skołoszów | 2015–2023 | II | 1 | wheat | 9.43 ± 1.82 |
| 2024 | II | 1 | wheat | 10.98 ± 1.29 | |
| Słupia | 2015–2023 | IIIa | 2 | wheat | 10.83 ± 1.85 |
| 2024 | IIIa | 2 | wheat | 4.42 ± 0.98 | |
| Tomaszów Bol. | 2015–2023 | IVa. IVb | 3 and 5 | wheat. rye | 6.30 ± 1.46 |
| 2024 | IVb | 5 | rye | 4.23 ± 0.56 | |
| Węgrzce | 2015–2023 | II | 1 | wheat | 9.40 ± 1.34 |
| 2024 | II | 1 | wheat | 7.89 ± 0.99 | |
| Zybiszów | 2015–2023 | II. IIIa | 1 and 2 | wheat | 10.23 ± 1.53 |
| 2024 | IIIa | 2 | wheat | 11.92 ± 0.99 | |
| Świebodzin | 2015–2023 | IIIa. IIIb. IVa | 2. 3 and 4 | wheat. rye and wheat | 9.23 ± 3.07 |
| 2024 | IIIa | 4 | rye and wheat | 5.73 ± 0.85 |
| Location | Training Dataset | Testing Dataset | Sum | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 | 2024 | 2015–2024 | |
| Cicibór Duży | 102 | 98 | 108 | 68 | 82 | 100 | 110 | 108 | 130 | 144 | 1050 |
| Czesławice | 102 | 98 | 108 | 68 | 82 | 100 | 110 | 108 | 130 | 144 | 105- |
| Głębokie | 98 | 96 | 106 | 70 | 86 | 108 | 110 | 108 | 130 | 144 | 1056 |
| Głubczyce | 106 | 106 | 106 | 72 | 86 | 138 | 110 | 108 | 130 | 144 | 1106 |
| Marianowo | 98 | 0 | 100 | 64 | 82 | 106 | 110 | 108 | 130 | 144 | 942 |
| Nowa Wieś Ujska | 104 | 100 | 104 | 74 | 90 | 107 | 110 | - | 130 | 144 | 963 |
| Pawłowice | 98 | 98 | 112 | 78 | 84 | 98 | 110 | 108 | 130 | 144 | 1060 |
| Radostowo | 105 | 100 | 106 | 76 | 90 | 102 | 110 | 108 | 130 | 144 | 1071 |
| Rarwino | 104 | - | 120 | 68 | 86 | 100 | 110 | 108 | 130 | 144 | 970 |
| Rychliki | 100 | 96 | 102 | 68 | 84 | 100 | 110 | 108 | 130 | 144 | 1042 |
| Seroczyn | 98 | 94 | 100 | 70 | 86 | 107 | 110 | 108 | 130 | 144 | 1047 |
| Skołoszów | 96 | 94 | 104 | 66 | 84 | 100 | 110 | 108 | 130 | 144 | 1036 |
| Słupia | 98 | 96 | 106 | 72 | 94 | 134 | 110 | 108 | 130 | 144 | 1090 |
| Świebodzin | 96 | 98 | - | 66 | 82 | 100 | 110 | 130 | 144 | 826 | |
| Węgrzce | 98 | 94 | 106 | 74 | 84 | 132 | 110 | 108 | 130 | 144 | 1076 |
| Zybiszów | 102 | 96 | 108 | 76 | 94 | 106 | 110 | 108 | 130 | 144 | 1074 |
| Krościna Mała | 98 | 96 | 108 | 76 | 94 | 106 | 110 | 108 | 130 | 144 | 1070 |
| Masłowice | 100 | 94 | 100 | 70 | 84 | 1–2 | 110 | 108 | 130 | 144 | 1–42 |
| Tomaszów Bol. | 98 | 96 | 108 | 76 | 94 | 106 | 110 | 108 | 130 | 144 | 1070 |
| Sum | 1901 | 1650 | 1912 | 1352 | 1642 | 2052 | 2090 | 1836 | 2470 | 2736 | 19,641 |
| Source | SS | MS | NumDF | DenDF | F | p-Value |
|---|---|---|---|---|---|---|
| Location | 3582 | 199 | 18 | 7977 | 1717 | <0.001 |
| Management Intensity (MIM) | 1088 | 1088 | 1 | 135 | 9386 | <0.001 |
| Year | 1170 | 146 | 8 | 7728 | 1263 | <0.001 |
| Location × MIM | 428 | 24 | 18 | 7973 | 205 | <0.001 |
| Location × Year | 3226 | 23 | 139 | 7976 | 200 | <0.001 |
| MIM × Year | 87 | 11 | 8 | 3820 | 94 | <0.001 |
| Location × MIM × Year | 769 | 6 | 139 | 7965 | 48 | <0.001 |
| Metric | Full Model (Regression-Based) | Simplified Reference Model |
|---|---|---|
| Pearson correlation (r) | 0.958 | 0.502 |
| RMSE [t/ha] | 0.45 | 2.08 |
| Cultivar-specific effects | ✓ Yes | ✗ No |
| G×E interactions modeled | ✓ Yes | ✗ No |
| Data used for prediction | Cultivar × environment (2015–2023) | Location × management (2015–2023) |
| Suitability for recommendations | High (individualized) | Low (aggregated) |
| Rank | Cultivar | Yield (t/ha) | Rank at (t/ha) | Group | RMSE (t/ha) | SD (t/ha) | RMSE/SD | R2 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 9 | 11 | 7 | 9 | 11 | |||||||
| 1 | SU Banatus | 7.36 | 9.50 | 11.64 | 24 | 13 | 12 | Top Prediction Accuracy | 0.39 | 2.31 | 0.17 | 0.95 |
| 2 | Comandor | 6.88 | 8.94 | 11.00 | 99 | 94 | 85 | 0.42 | 2.42 | 0.17 | 0.95 | |
| 3 | Symetria | 7.16 | 9.21 | 11.27 | 51 | 45 | 42 | 0.42 | 2.41 | 0.17 | 0.88 | |
| 4 | Chevignon | 7.61 | 9.72 | 11.84 | 9 | 4 | 3 | 0.45 | 2.55 | 0.18 | 0.95 | |
| 5 | Callistus | 7.28 | 9.22 | 11.16 | 37 | 44 | 60 | 0.49 | 2.40 | 0.20 | 0.94 | |
| 6 | Asory | 6.94 | 9.11 | 11.28 | 90 | 59 | 39 | 0.53 | 2.49 | 0.21 | 0.94 | |
| 7 | RGT Bilanz | 7.245 | 9.28 | 11.32 | 40 | 37 | 34 | 0.52 | 2.43 | 0.22 | 0.94 | |
| 8 | Bulldozer | 8.11 | 9.92 | 11.74 | 1 | 2 | 8 | 0.50 | 2.25 | 0.22 | 0.80 | |
| 9 | Revolver | 7.49 | 9.61 | 11.72 | 16 | 9 | 9 | 0.54 | 2.40 | 0.23 | 0.94 | |
| 10 | Knut | 7.44 | 9.49 | 11.54 | 20 | 17 | 17 | 0.55 | 2.36 | 0.23 | 0.93 | |
| Rank | Cultivar | Yield (t/ha) | Rank at (t/ha) | Group | RMSE (t/ha) | SD (t/ha) | RMSE/SD | R2 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 9 | 11 | 7 | 9 | 11 | |||||||
| 1 | LG Nida | 6.79 | 9.00 | 11.20 | 118 | 73 | 51 | Lowest Prediction Accuracy | 1.93 | 2.76 | 0.70 | 0.92 |
| 2 | KWS Donovan | 7.62 | 9.69 | 11.76 | 8 | 7 | 6 | 1.43 | 2.47 | 0.58 | 0.92 | |
| 3 | Bosporus | 7.01 | 9.10 | 11.18 | 78 | 64 | 57 | 1.14 | 2.18 | 0.52 | 0.91 | |
| 4 | SU Mangold | 6.82 | 9.18 | 11.54 | 113 | 48 | 16 | 1.11 | 2.55 | 0.44 | 0.94 | |
| 5 | Bright | 7.66 | 9.54 | 11.42 | 6 | 11 | 26 | 0.99 | 2.23 | 0.44 | 0.90 | |
| 6 | Adrenalin | 7.51 | 9.46 | 11.41 | 14 | 20 | 28 | 0.85 | 2.40 | 0.35 | 0.94 | |
| 7 | Arevus | 7.41 | 9.51 | 11.61 | 21 | 12 | 14 | 0.75 | 2.12 | 0.35 | 0.93 | |
| 8 | Tonnage | 7.18 | 9.47 | 11.76 | 48 | 19 | 5 | 0.76 | 2.17 | 0.35 | 0.90 | |
| 9 | LG Keramik | 7.55 | 9.55 | 11.56 | 10 | 10 | 15 | 0.88 | 2.44 | 0.36 | 0.90 | |
| 10 | SU Willem | 7.00 | 9.20 | 11.40 | 82 | 46 | 29 | 0.88 | 2.24 | 0.39 | 0.86 | |
| Cultivar | Rank at 7 t/ha | Rank at 9 t/ha | Rank at 11 t/ha | Sum of Ranks | Intercept | Slope | R2 | Recommendation |
|---|---|---|---|---|---|---|---|---|
| Bulldozer | 1 | 2 | 8 | 11 | 1.75 | 0.91 | 0.80 | Low-productivity environments |
| SY Cellist | 7 | 3 | 2 | 12 | 0.10 | 1.08 | 0.95 | High-productivity environments |
| Chevignon | 9 | 4 | 3 | 16 | 0.20 | 1.06 | 0.95 | High-productivity environments |
| LG Mondial | 3 | 5 | 11 | 19 | 1.00 | 0.97 | 0.91 | Consistently top-performing |
| SU Tarroca | 19 | 1 | 1 | 21 | −1.53 | 1.28 | 0.93 | High-productivity environments |
| KWS Donovan | 8 | 7 | 6 | 21 | 0.37 | 1.03 | 0.92 | Consistently top-performing |
| Hyvega | 5 | 6 | 10 | 21 | 0.89 | 0.98 | 0.88 | Consistently top-performing |
| Revolver | 16 | 9 | 9 | 34 | 0.10 | 1.06 | 0.94 | Consistently top-performing |
| RGT Ritter | 2 | 8 | 24 | 34 | 1.59 | 0.90 | 0.85 | Consistently top-performing |
| LG Keramik | 10 | 10 | 15 | 35 | 0.52 | 1.00 | 0.90 | Consistently top-performing |
| Bright | 6 | 11 | 26 | 43 | 1.08 | 0.94 | 0.90 | Consistently top-performing |
| Arevus | 21 | 12 | 14 | 47 | 0.06 | 1.05 | 0.93 | consistently top-performing |
| Venecja | 13 | 14 | 21 | 48 | 0.62 | 0.99 | 0.93 | Consistently top-performing |
| SU Banatus | 24 | 13 | 12 | 49 | −0.13 | 1.07 | 0.95 | Consistently top-performing |
| Knut | 20 | 17 | 17 | 54 | 0.26 | 1.03 | 0.93 | Consistently top-performing |
| Adrenalin | 14 | 20 | 28 | 62 | 0.69 | 0.97 | 0.94 | Consistently top-performing |
| SU Geometry | 44 | 15 | 4 | 63 | −0.78 | 1.14 | 0.96 | Consistently top-performing |
| LG Egmont | 33 | 18 | 13 | 64 | −0.28 | 1.08 | 0.97 | Consistently top-performing |
| LG Mocca | 41 | 16 | 7 | 64 | −0.66 | 1.13 | 0.86 | Consistently top-performing |
| Elektra | 25 | 21 | 19 | 65 | 0.13 | 1.03 | 0.91 | Consistently top-performing |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iwańska, M.; Paderewski, J.; Stępień, M. Prediction of Winter Wheat Cultivar Performance Using Mixed Models and Environmental Mean Regression from Multi-Environment Trials for Cultivar Recommendation to Reduce Yield Gap in Poland. Agronomy 2025, 15, 2309. https://doi.org/10.3390/agronomy15102309
Iwańska M, Paderewski J, Stępień M. Prediction of Winter Wheat Cultivar Performance Using Mixed Models and Environmental Mean Regression from Multi-Environment Trials for Cultivar Recommendation to Reduce Yield Gap in Poland. Agronomy. 2025; 15(10):2309. https://doi.org/10.3390/agronomy15102309
Chicago/Turabian StyleIwańska, Marzena, Jakub Paderewski, and Michał Stępień. 2025. "Prediction of Winter Wheat Cultivar Performance Using Mixed Models and Environmental Mean Regression from Multi-Environment Trials for Cultivar Recommendation to Reduce Yield Gap in Poland" Agronomy 15, no. 10: 2309. https://doi.org/10.3390/agronomy15102309
APA StyleIwańska, M., Paderewski, J., & Stępień, M. (2025). Prediction of Winter Wheat Cultivar Performance Using Mixed Models and Environmental Mean Regression from Multi-Environment Trials for Cultivar Recommendation to Reduce Yield Gap in Poland. Agronomy, 15(10), 2309. https://doi.org/10.3390/agronomy15102309






