Designing an Economical Water Harvesting System Using a Tank with Numerical Simulation Model WASH_2D
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Model, WASH_2D
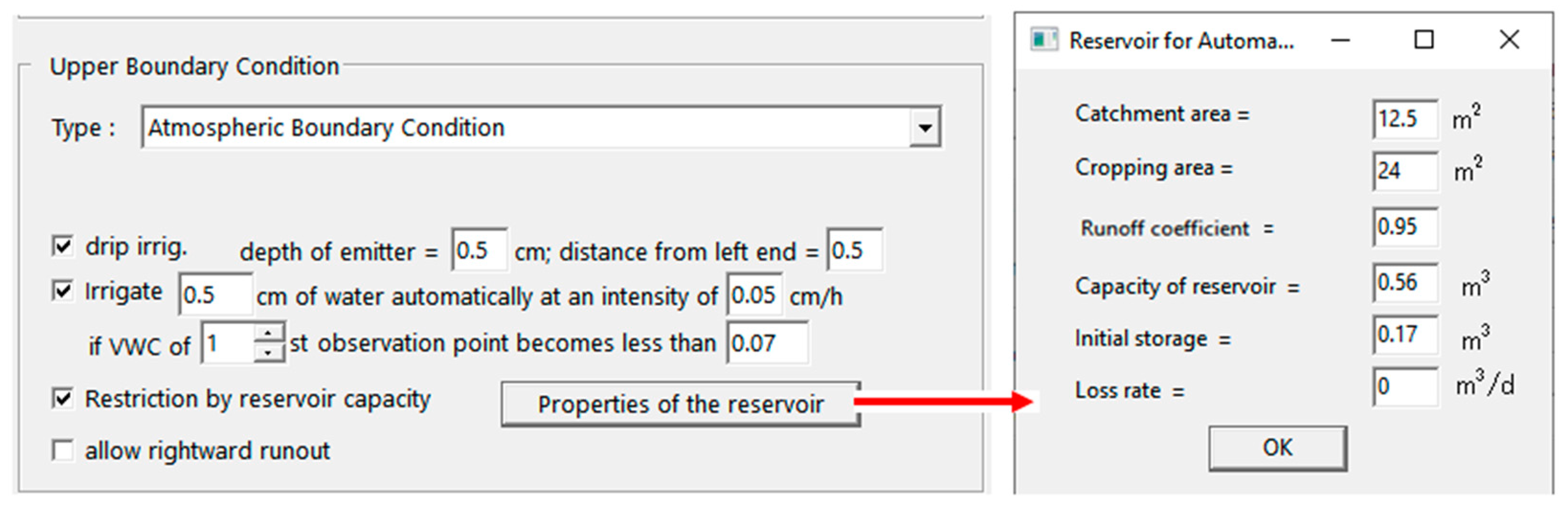
2.2. Simulation of RWHS in WASH_2D
2.3. Optimization of Tank Capacity in RWHS
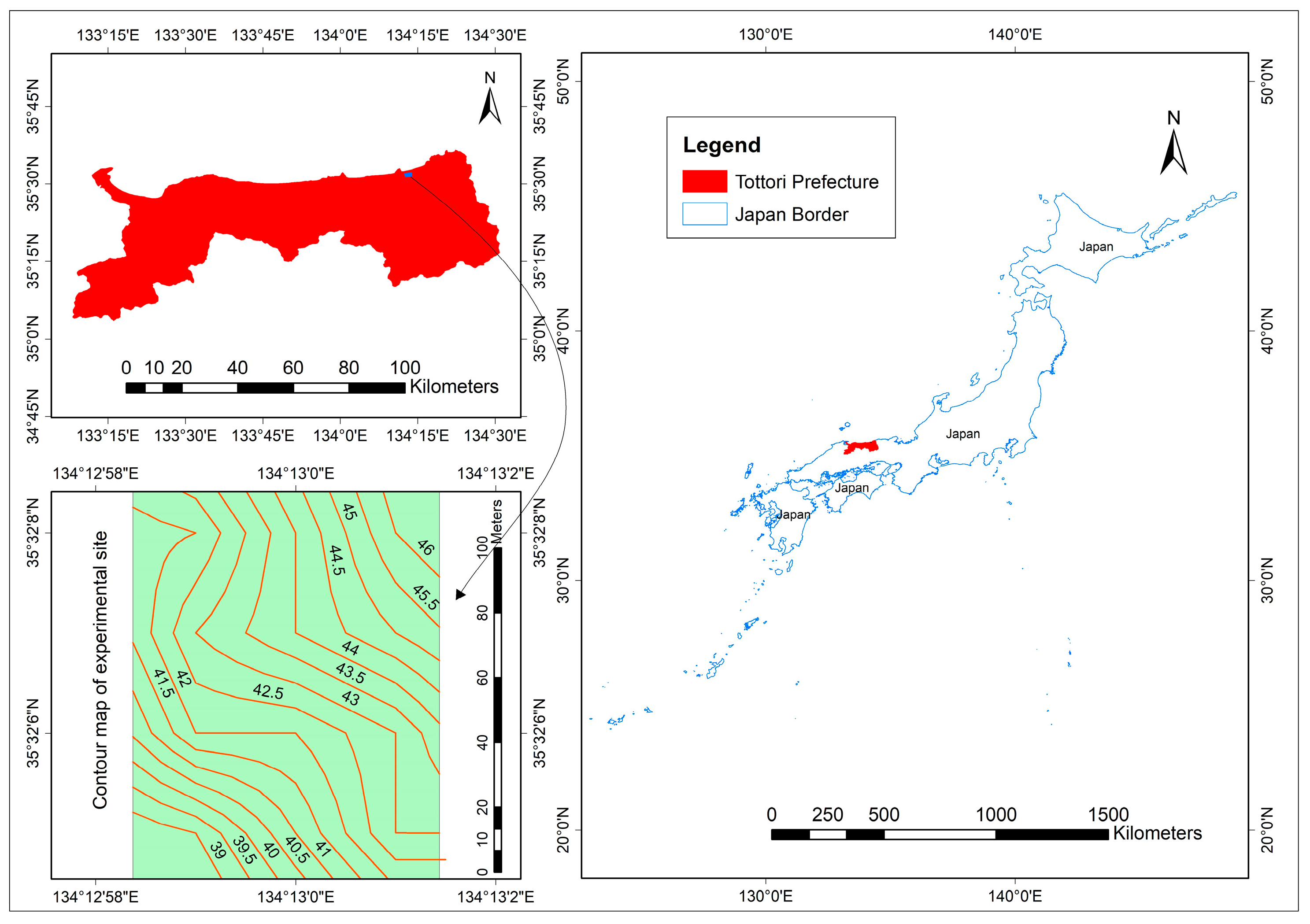
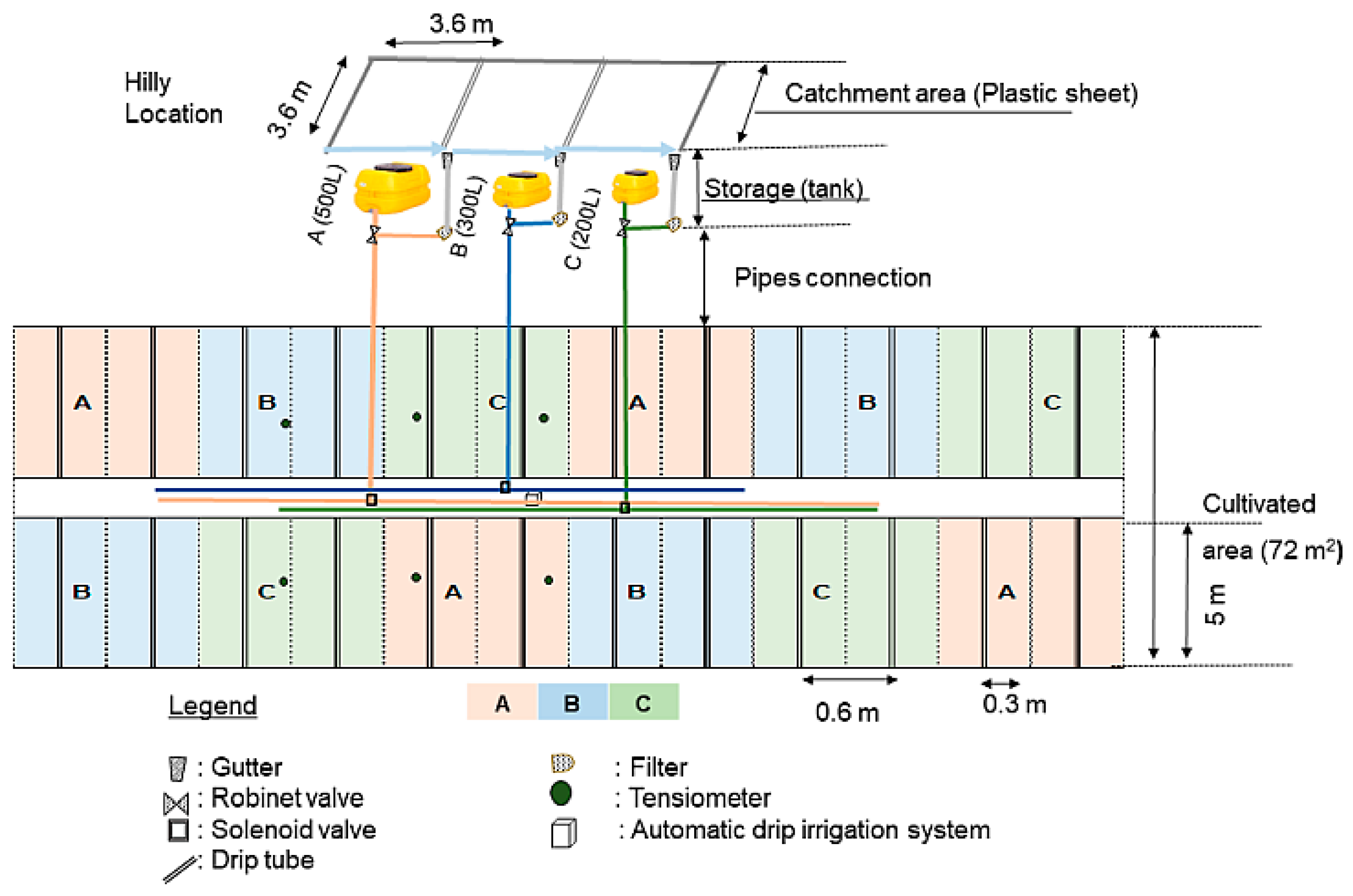
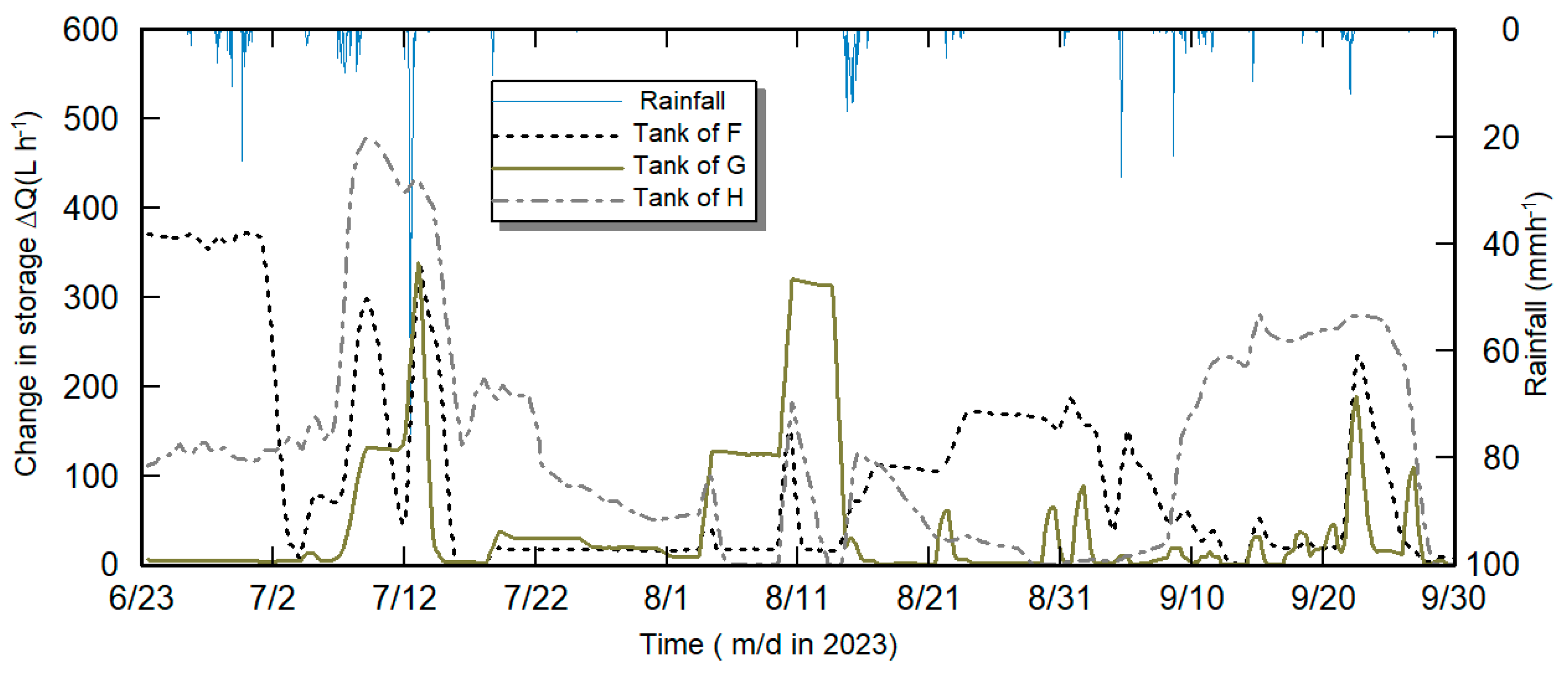
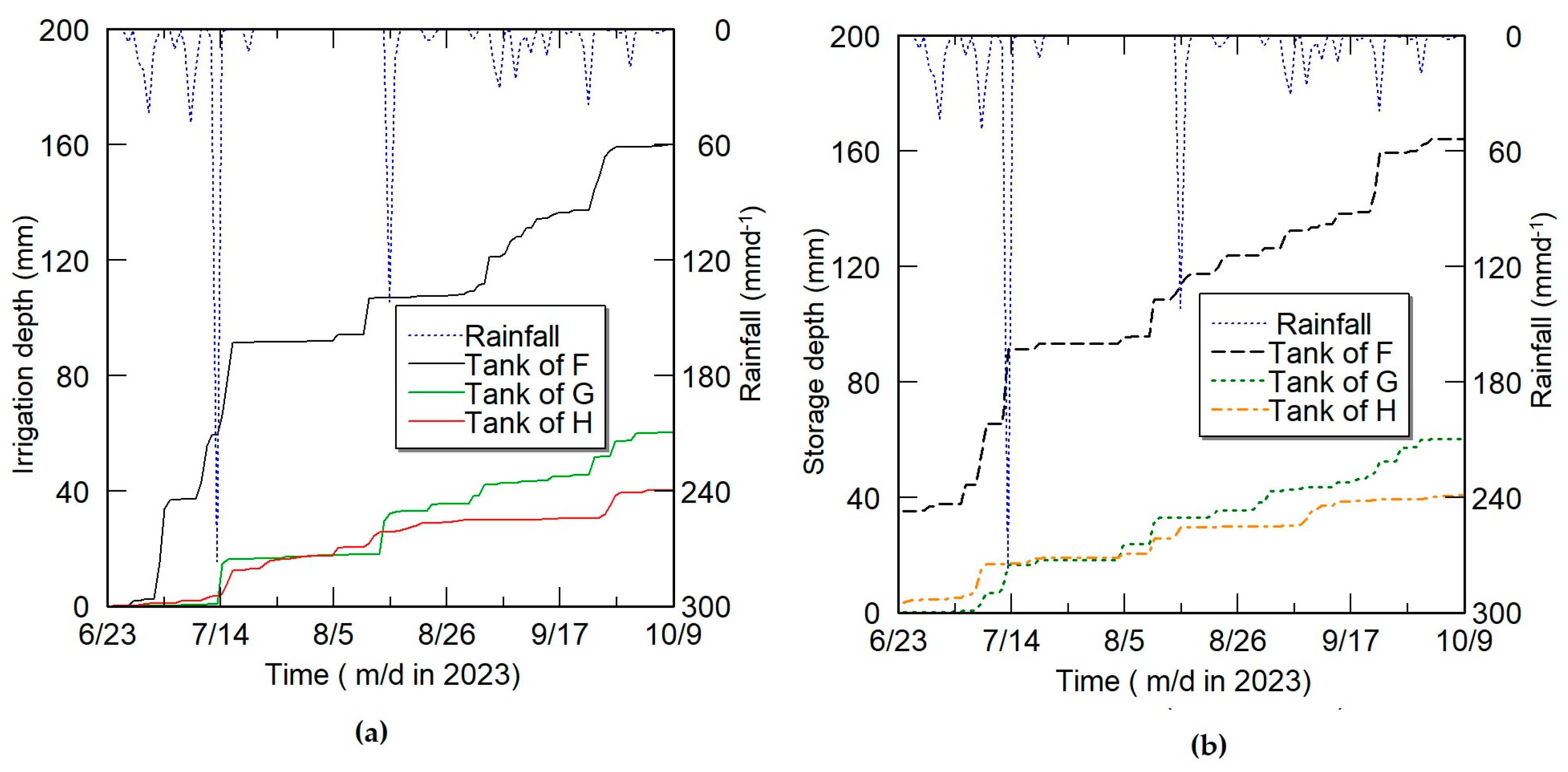
2.3.1. Field Experiment 1
2.3.2. Procedure of Numerical Optimization of Tank Capacity
2.4. Net Income for RWHS with Different Cultivated Areas
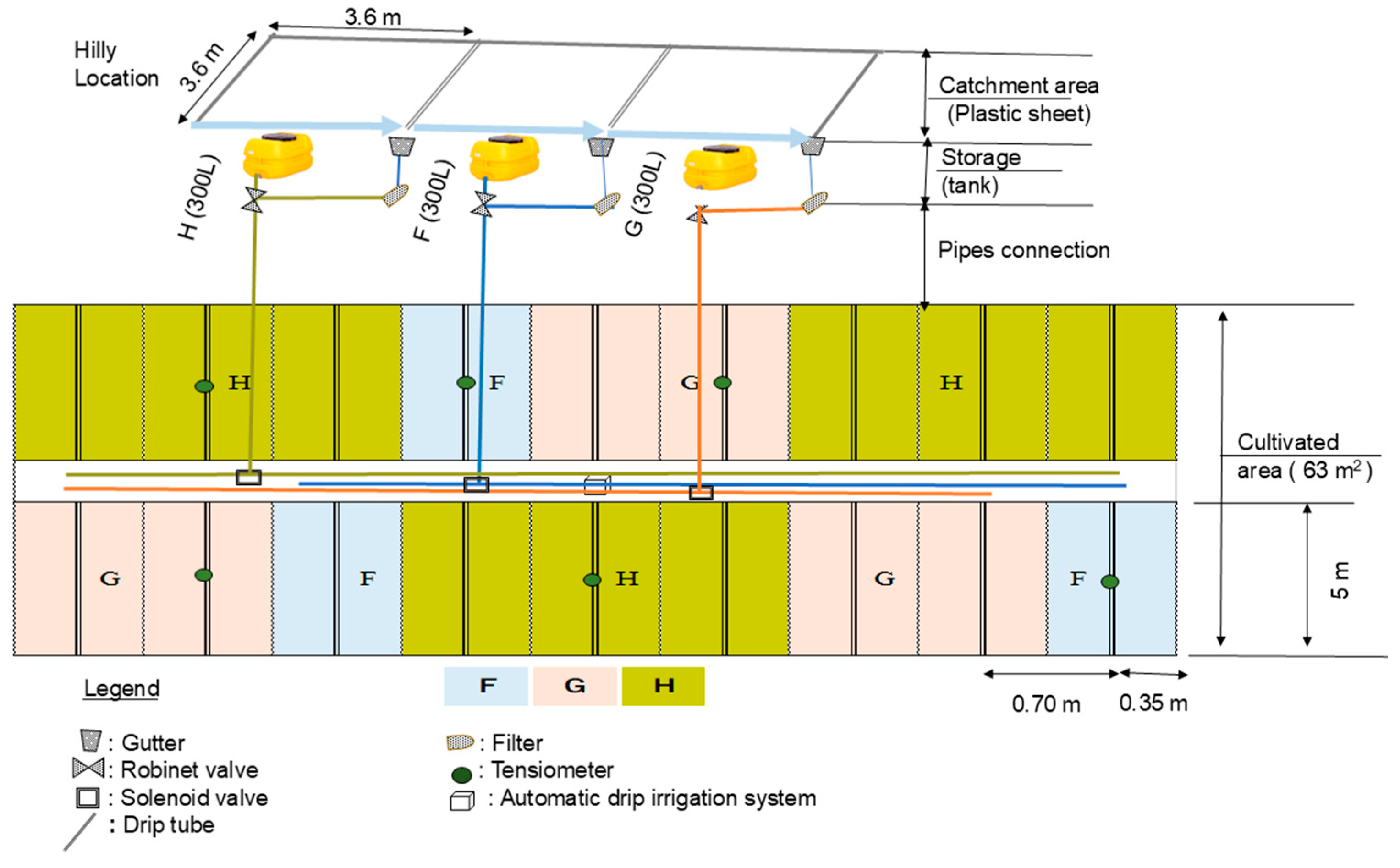
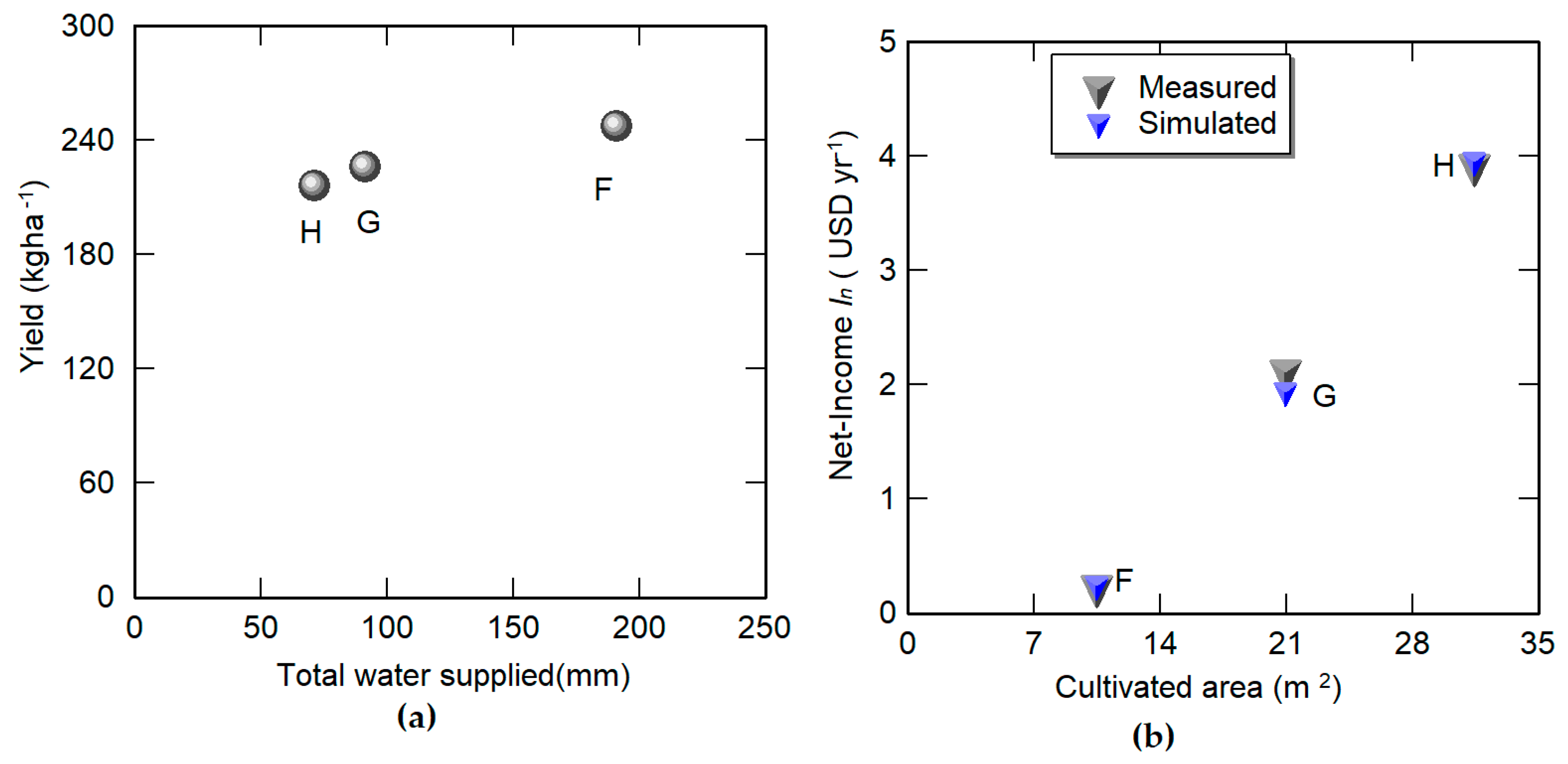
2.4.1. Field Experiment 2
2.4.2. Numerical Prediction of Net Income for the Experiment 2
3. Results and Discussion
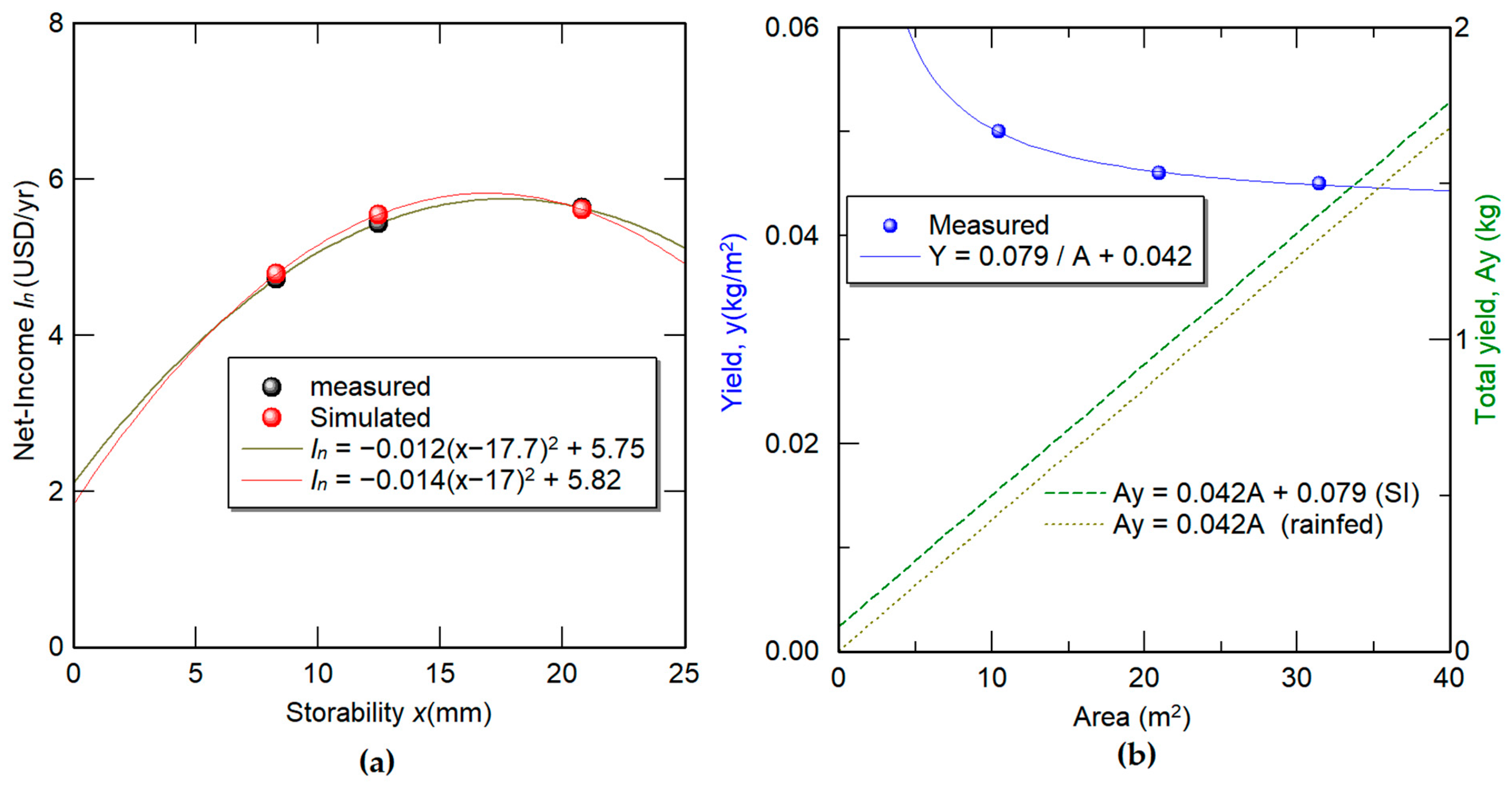
3.1. Optimization of Tank Capacity in Terms of
3.2. Assessment of for Different Cultivated Areas
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fox, P.; Rockström, J. Supplemental Irrigation for Dry-Spell Mitigation of Rainfed Agriculture in the Sahel. Agric. Water Manag. 2003, 61, 29–50. [Google Scholar] [CrossRef]
- Ngigi, S.N.; Savenije, H.H.G.; Rockström, J.; Gachene, C.K. Hydro-Economic Evaluation of Rainwater Harvesting and Management Technologies: Farmers’ Investment Options and Risks in Semi-Arid Laikipia District of Kenya. Phys. Chem. Earth 2005, 30, 772–782. [Google Scholar] [CrossRef]
- Zongo, B.; Barbier, B.; Diarra, A.; Zorom, M.; Atewamba, C.; Combary, O.S.; Ouédraogo, S.; Toé, P.; Hamma, Y.; Dogot, T. Economic Analysis and Food Security Contribution of Supplemental Irrigation and Farm Ponds: Evidence from Northern Burkina Faso. Agric. Food Secur. 2022, 11, 4. [Google Scholar] [CrossRef]
- Uwizeyimana, D.; Mureithi, S.M.; Karuku, G.; Kironchi, G. Effect of Water Conservation Measures on Soil Moisture and Maize Yield under Drought Prone Agro-Ecological Zones in Rwanda. Int. Soil Water Conserv. Res. 2018, 6, 214–221. [Google Scholar] [CrossRef]
- Odhiambo, K.O.; Iro Ong’Or, B.T.; Kanda, E.K. Optimization of Rainwater Harvesting System Design for Smallholder Irrigation Farmers in Kenya: A Review. J. Water Supply Res. Technol. Aqua. 2021, 70, 483–492. [Google Scholar] [CrossRef]
- Reddy, K.S.; Ricart, S.; Maruthi, V.; Pankaj, P.K.; Krishna, T.S.; Reddy, A.A. Economic Assessment of Water Harvesting Plus Supplemental Irrigation for Improving Water Productivity of a Pulse–Cotton Based Integrated Farming System in Telangana, India†. Irrig. Drain. 2020, 69, 25–37. [Google Scholar] [CrossRef]
- Nangia, V.; Oweis, T. Supplemental Irrigation: A Promising Climate-Resilience Practice for Sustainable Dryland Agriculture. In Innovations in Dryland Agriculture; Farooq, M., Siddique, K., Eds.; Springer: Cham, Switzerland, 2016; pp. 549–564. [Google Scholar]
- He, X.F.; Cao, H.; Li, F.M. Econometric Analysis of the Determinants of Adoption of Rainwater Harvesting and Supplementary Irrigation Technology (RHSIT) in the Semiarid Loess Plateau of China. Agric. Water Manag. 2007, 89, 243–250. [Google Scholar] [CrossRef]
- Ngigi, S.N.; Savenije, H.H.G.; Thome, J.N.; Rockström, J.; De Vries, F.W.T.P. Agro-Hydrological Evaluation of on-Farm Rainwater Storage Systems for Supplemental Irrigation in Laikipia District, Kenya. Agric. Water Manag. 2005, 73, 21–41. [Google Scholar] [CrossRef]
- Roy, D.; Panda, S.N.; Panigrahi, B. Water Balance Simulation Model for Optimal Sizing of On-Farm Reservoir in Rainfed Farming System. Comput. Electron. Agric. 2009, 65, 114–124. [Google Scholar] [CrossRef]
- Rozaki, Z.; Senge, M.; Ito, K.; Priyo Ariyanto, D. Komariah Evaluation on Rainwater Harvesting Suitability in Indonesia. J. Rainwater Catchment Syst. 2017, 22, 19–24. [Google Scholar] [CrossRef]
- Amos, C.; Rahman, A.; Gathenya, J.; Friedler, E.; Karim, F.; Renzaho, A. Roof-Harvested Rainwater Use in Household Agriculture: Contributions to the Sustainable Development Goals. Water 2020, 12, 332. [Google Scholar] [CrossRef]
- Nana, J.B.; Abd El Baki, H.M.; Erukudi, A.C.; Fujimaki, H. Optimization of the Capacity of Tank in Water Harvesting Using Plastic Sheet and Tank in a Sandy Field 2024. J. Arid. Land Stud. 2024, 34-S, 79–82. [Google Scholar] [CrossRef]
- Sample, D.J.; Liu, J. Optimizing Rainwater Harvesting Systems for the Dual Purposes of Water Supply and Runoff Capture. J. Clean. Prod. 2014, 75, 174–194. [Google Scholar] [CrossRef]
- Woltersdorf, L.; Liehr, S.; Döll, P. Rainwater Harvesting for Small-Holder Horticulture in Namibia: Design of Garden Variants and Assessment of Climate Change Impacts and Adaptation. Water 2015, 7, 1402–1421. [Google Scholar] [CrossRef]
- Mishra, A.; Adhikary, A.K.; Panda, S.N. Optimal Size of Auxiliary Storage Reservoir for Rain Water Harvesting and Better Crop Planning in a Minor Irrigation Project. Water Resour. Manag. 2009, 23, 265–288. [Google Scholar] [CrossRef]
- Liang, X.; van Dijk, M.P. Identification of Decisive Factors Determining the Continued Use of Rainwater Harvesting Systems for Agriculture Irrigation in Beijing. Water 2016, 8, 7. [Google Scholar] [CrossRef]
- Velasco-Muñoz, J.F.; Aznar-Sánchez, J.A.; Batlles-delaFuente, A.; Fidelibus, M.D. Rainwater Harvesting for Agricultural Irrigation: An Analysis of Global Research. Water 2019, 11, 1320. [Google Scholar] [CrossRef]
- Srivastava, R.C. Methodology for Design of Water Harvesting System for High Rainfall Areas. Agric. Water Manag. 2001, 47, 37–53. [Google Scholar] [CrossRef]
- Panigrahi, B.; Panda, S.N. Optimal Sizing of On-Farm Reservoirs for Supplemental Irrigation. J. Irrig. Drain. Eng. 2003, 129, 117–128. [Google Scholar] [CrossRef]
- Verma, H.N.; Sarma, P.B.S. Design of Storage Tanks for Water Harvesting in Rainfed Areas. Agric. Water Manag. 1990, 18, 195–207. [Google Scholar] [CrossRef]
- Al-Ansari, N.; Ezz-Aldeen, M.; Knutsson, S.; Zakaria, S. Water Harvesting and Reservoir Optimization in Selected Areas of South Sinjar Mountain, Iraq. J. Hydrol. Eng. 2013, 18, 1607–1616. [Google Scholar] [CrossRef]
- Shinde, M.; Smout, I.; Gorantiwal, S. Algorithms for Sizing Reservoirs for Rainwater Harvesting and Supplementary Irrigation. Hydrol. Sci. Pract. 21st Century 2004, II, 480–486. [Google Scholar]
- Traore, S.; Wang, Y.-M. On-Farm Rainwater Reservoir System Optimal Sizing for Increasing Rainfed Production in the Semiarid Region of Africa. Afr. J. Agric. Res. 2011, 6, 4711–4720. [Google Scholar] [CrossRef]
- Vico, G.; Tamburino, L.; Rigby, J.R. Designing On-Farm Irrigation Ponds for High and Stable Yield for Different Climates and Risk-Coping Attitudes. J. Hydrol. 2020, 584, 124634. [Google Scholar] [CrossRef]
- Pandey, P.K.; Panda, S.N.; Panigrahi, B. Sizing On-Farm Reservoirs for Crop-Fish Integration in Rainfed Farming Systems in Eastern India. Biosyst. Eng. 2006, 93, 475–489. [Google Scholar] [CrossRef]
- Šimůnek, J.; Hopmans, J.W. Modeling Compensated Root Water and Nutrient Uptake. Ecol. Model. 2009, 220, 505–521. [Google Scholar] [CrossRef]
- Van Dam, J.C.; Huygen, J.; Wesseling, J.G.; Feddes, R.A.; Kabat, P.; Van Walsum, P.E.V.; Groenendijk, P.; van Diepen, C.A. Theory of SWAP, Version 2.0: Simulation of Water Flow, Solute Transport and Plant Growth in the Soil-Water-Atmosphere-Plant Environment; DLO Winand Staring Centre: Wageningen, The Netherlands, 1997; p. 71. [Google Scholar]
- Fujimaki, H.; Tokumoto, I.; Saito, T.; Inoue, M.; Shibata, M.; Okazaki, T.; El-Mokh, F. Determination of Irrigation Depths Using a Numerical Model and Quantitative Weather Forecasts and Comparison with an Experiment. R Laj Ed Pract. Appl. Agric. Syst. Models Optim. Use Ltd. Water Adv. Agric. Syst. Model. 2014, 5, 209–235. [Google Scholar] [CrossRef]
- Homaee, M.; Feddes, R.A.; Dirksen, C. A Macroscopic Water Extraction Model for Nonuniform Transient Salinity and Water Stress. Soil Sci. Soc. Am. J. 2002, 66, 1764–1772. [Google Scholar] [CrossRef]
- Yanagawa, A.; Fujimaki, H. Tolerance of Canola to Drought and Salinity Stresses in Terms of Root Water Uptake Model Parameters. J. Hydrol. Hydromech. 2013, 61, 73–80. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements. FAO Irrig. Drain. Pap. No 56 Food Agric. Organ. U. N. Rome 1998, 300, D05109. [Google Scholar]
- Nana, J.B.; Abd El Baki, H.M.; Fujimaki, H. Determining Drought and Salinity Stress Response Function for Garlic. Soil Syst. 2024, 8, 59. [Google Scholar] [CrossRef]
- Abd El Baki, H.M.; Liang, S.; Fujimaki, H. Simulation-Based Schemes to Determine Economical Irrigation Depths Considering Volumetric Water Price and Weather Forecasts. J. Water Resour. Plan. Manag. 2023, 149, 1–13. [Google Scholar] [CrossRef]

| Parameter | Garlic | Mung-Bean | ||
|---|---|---|---|---|
| Value | Remarks | |||
| h50 | −50 | [33] | −150 | Equation (3) |
| ho50 | −4821 | −3300 | ||
| p | 27.5 | 2 | ||
| b | 1 | Equation (4) | 0.02 | Equation (4) |
| grt | 20 | 30 | ||
| zr0 | 1 | 1 | ||
| adrt | 40 | 45 | ||
| bdrt | −0.5 | −0.5 | ||
| cdrt | 5 | Equations (5) and (6) | 5 | Equations (5) and (6) |
| akc | 0.87 | 1 | ||
| bkc | −0.21 | −0.15 | ||
| ckc | 0.15 | 0.1 | ||
| tlate | 200 | 78 | ||
| tend | 230 | 97 | ||
| kcb | 0.6 | 0.6 | ||
| aLAI | 2 | 2 | ||
| bLAI | −0.02 | −0.1 | ||
| Parameter | Value |
|---|---|
| θsat (cm3 cm−3) | 0.42 |
| θr (cm3 cm−3) | 0.03 |
| αv (cm−1) | 0.018 |
| n | 4 |
| 0.0061 | |
| 0.0032 | |
| 22.6 | |
| 0.00152 | |
| 1.46 | |
| 0.224 | |
| 0.159 | |
| 8 | |
| 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nana, J.B.; Abd El Baki, H.M.; Fujimaki, H. Designing an Economical Water Harvesting System Using a Tank with Numerical Simulation Model WASH_2D. Agronomy 2024, 14, 2466. https://doi.org/10.3390/agronomy14112466
Nana JB, Abd El Baki HM, Fujimaki H. Designing an Economical Water Harvesting System Using a Tank with Numerical Simulation Model WASH_2D. Agronomy. 2024; 14(11):2466. https://doi.org/10.3390/agronomy14112466
Chicago/Turabian StyleNana, Jean Bosco, Hassan M. Abd El Baki, and Haruyuki Fujimaki. 2024. "Designing an Economical Water Harvesting System Using a Tank with Numerical Simulation Model WASH_2D" Agronomy 14, no. 11: 2466. https://doi.org/10.3390/agronomy14112466
APA StyleNana, J. B., Abd El Baki, H. M., & Fujimaki, H. (2024). Designing an Economical Water Harvesting System Using a Tank with Numerical Simulation Model WASH_2D. Agronomy, 14(11), 2466. https://doi.org/10.3390/agronomy14112466







