A Novel Approach for Predicting Heavy Metal Contamination Based on Adaptive Neuro-Fuzzy Inference System and GIS in an Arid Ecosystem
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Zone
2.2. Field Survey Sample Collection
2.3. Sample Preparation and Laboratory Analysis
2.4. Heavy Metal Properties’ Spatial Variability Maps
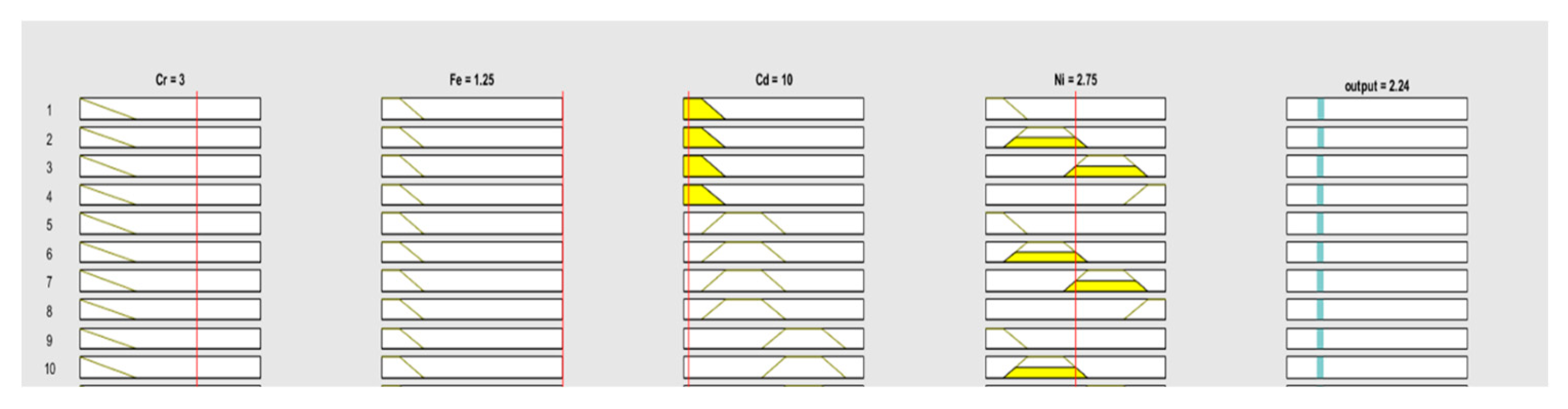
2.5. Soil Contamination Predication Using ANFIS
2.5.1. Modified Degree of Contamination (mCd)
- CF is contamination factor;
- n is number of samples.
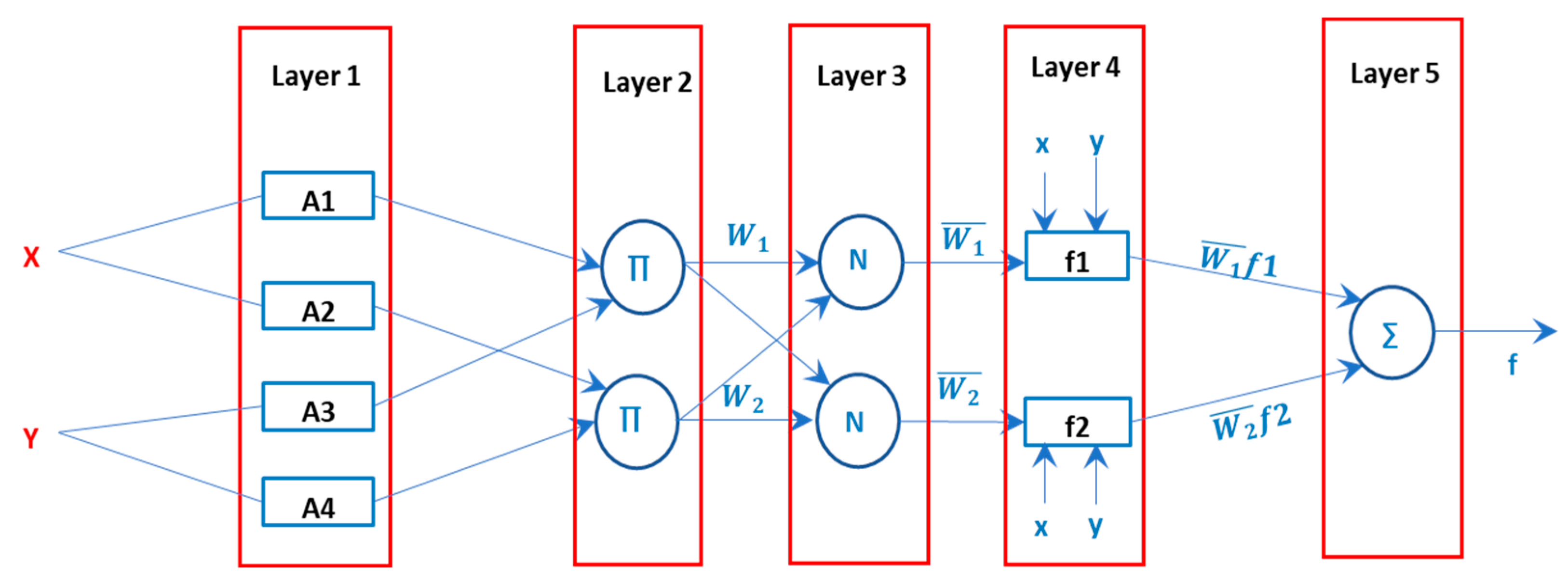
2.5.2. ANFIS Modeling
- k: The number of rules;
- Ai and Bi: The n fuzzy membership function denoted by µ in the antecedent part of the rule Rk;
- pk, qk, and rk: The linear parameters of the consequent part of the kth rule.
- -
- First layer: Fuzzification; in this layer, each node “” is a node on which the membership function of the next node is most dependent. So, it is called an adaptive node:There are many fuzzy membership functions, i.e., Gaussian, triangular, trapezoidal, etc., that can be used; in this work, trapezoidal shape MF was used.
- -
- Second layer: Product layer calculates the rule firing strength via product ∏ operation.
- -
- Third layer: Normalized; in this layer, the normalized release force of a previous layer’s base is computed as follows:
- -
- Fourth layer: Defuzzification; each node indicates a distinct component of the fuzzy rule. The linear coefficients resulting from the rule are trainable.where pk, qk, and rk are the linear parameters.
- -
- Fifth layer: Output layer; Layer 5 nodes defuzzified the consequent part of the rules by summing the outputs of all the rules.
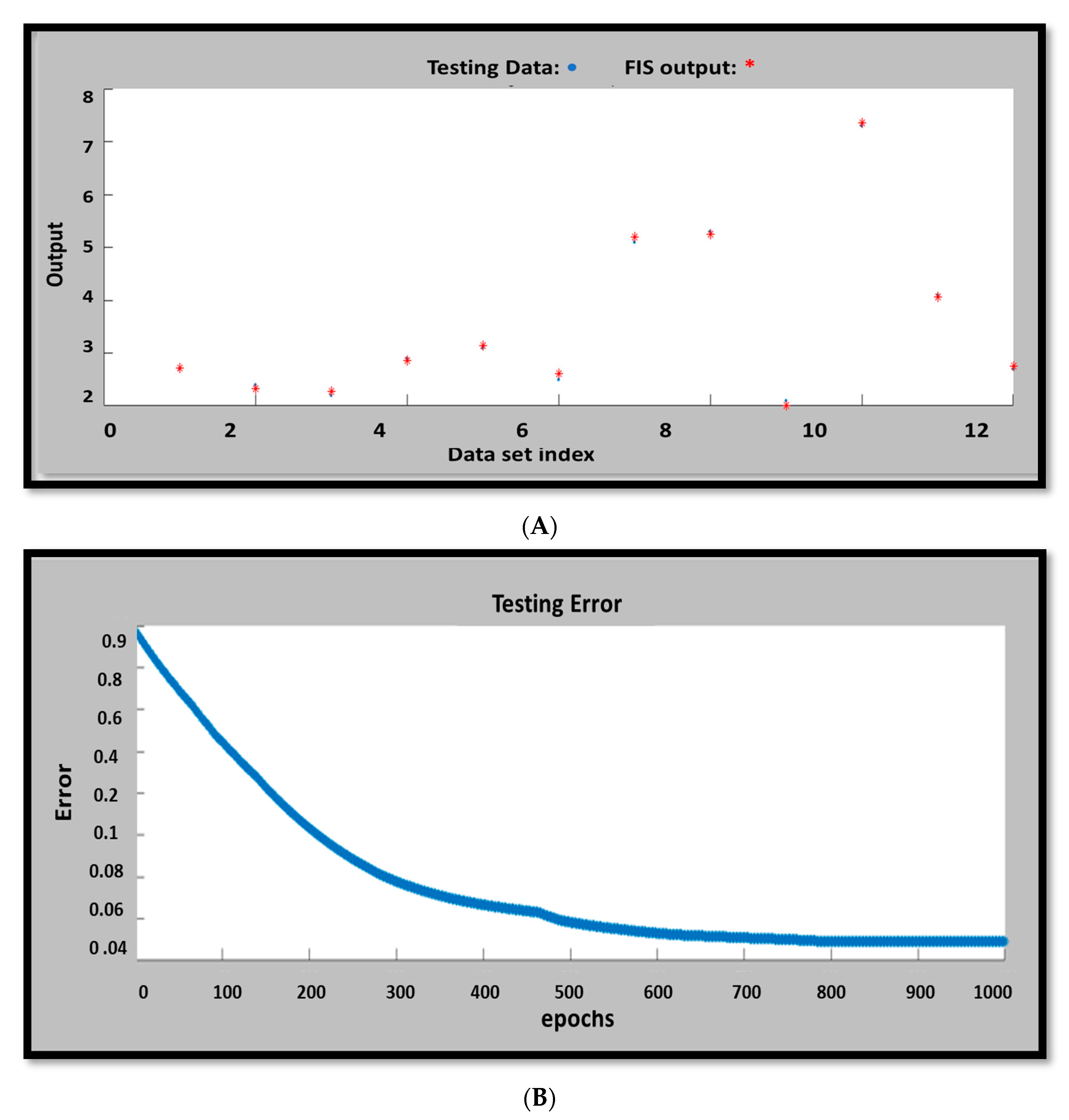
2.5.3. Model Performance
3. Results and Discussion
3.1. Concentration of Heavy Metals in Investigated Area
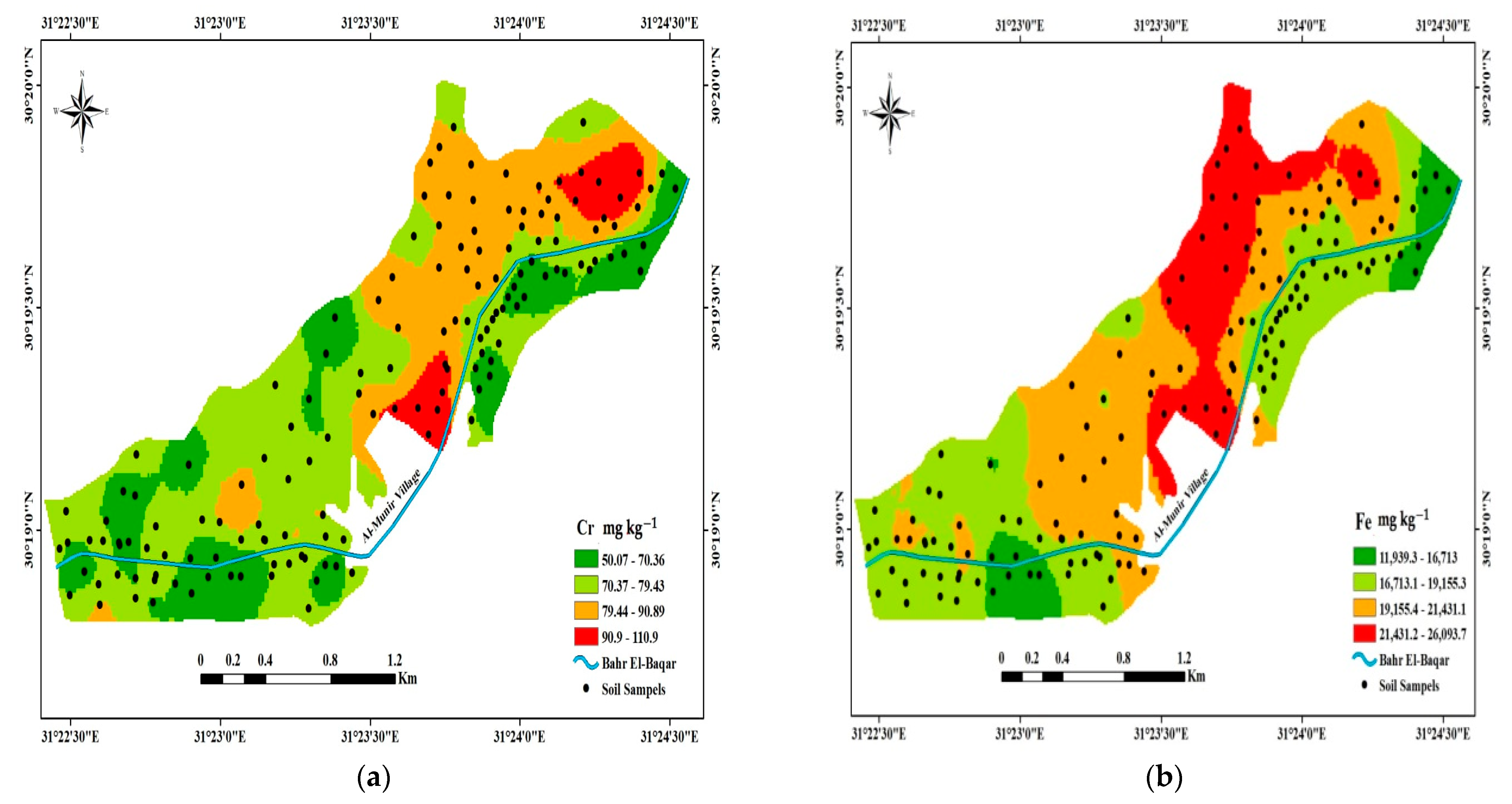
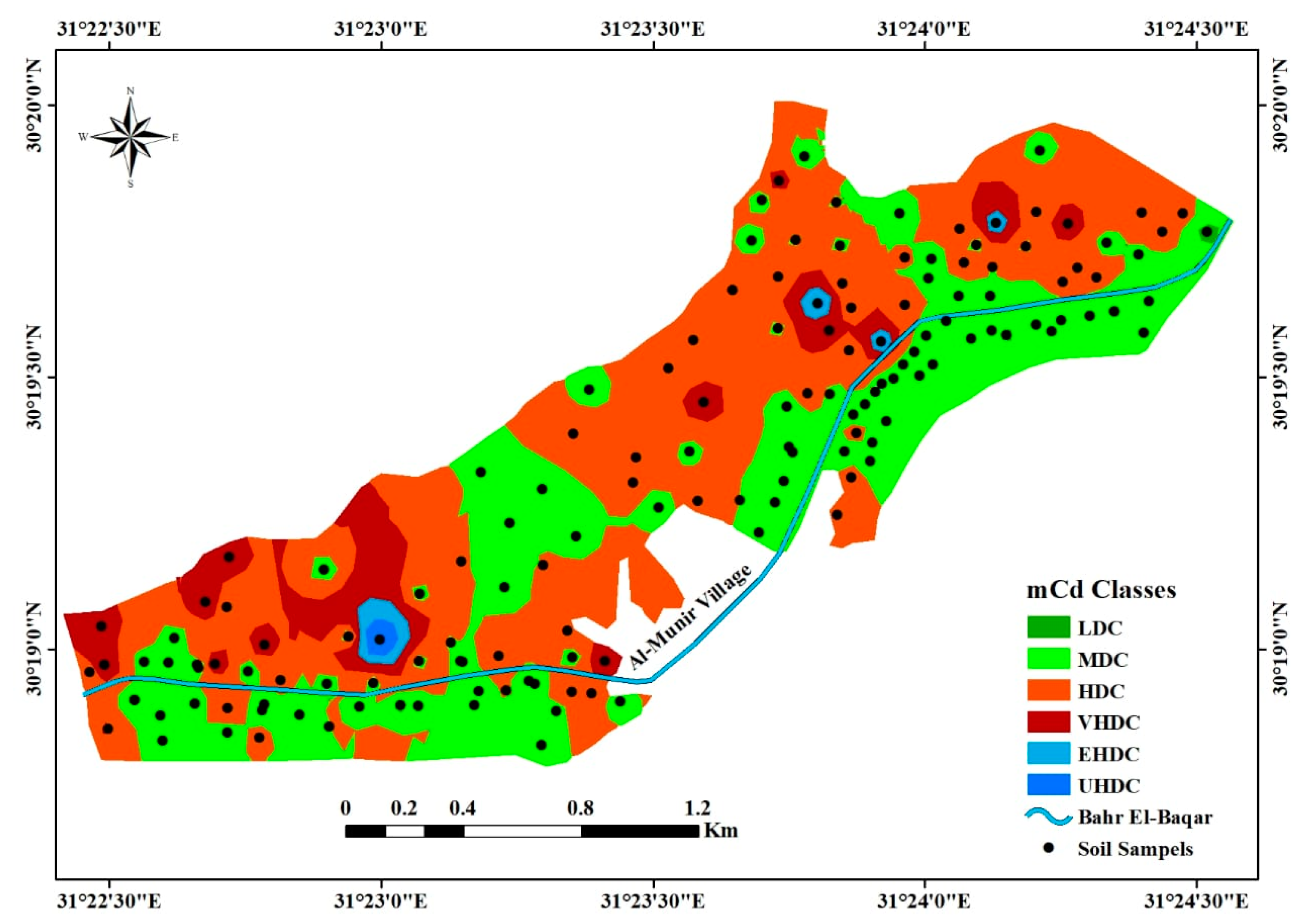
3.2. Mapping and Geostatistical Analysis
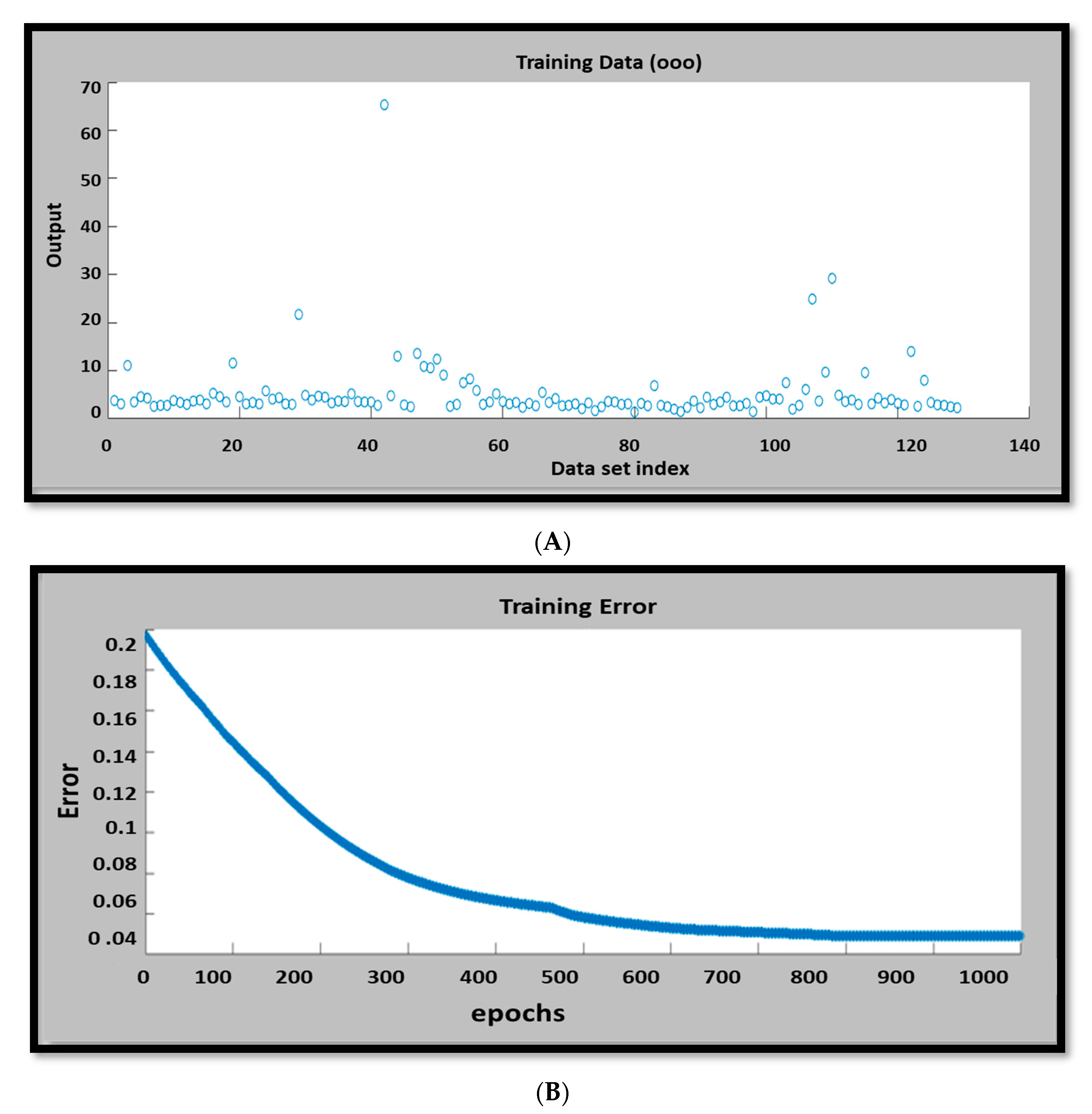
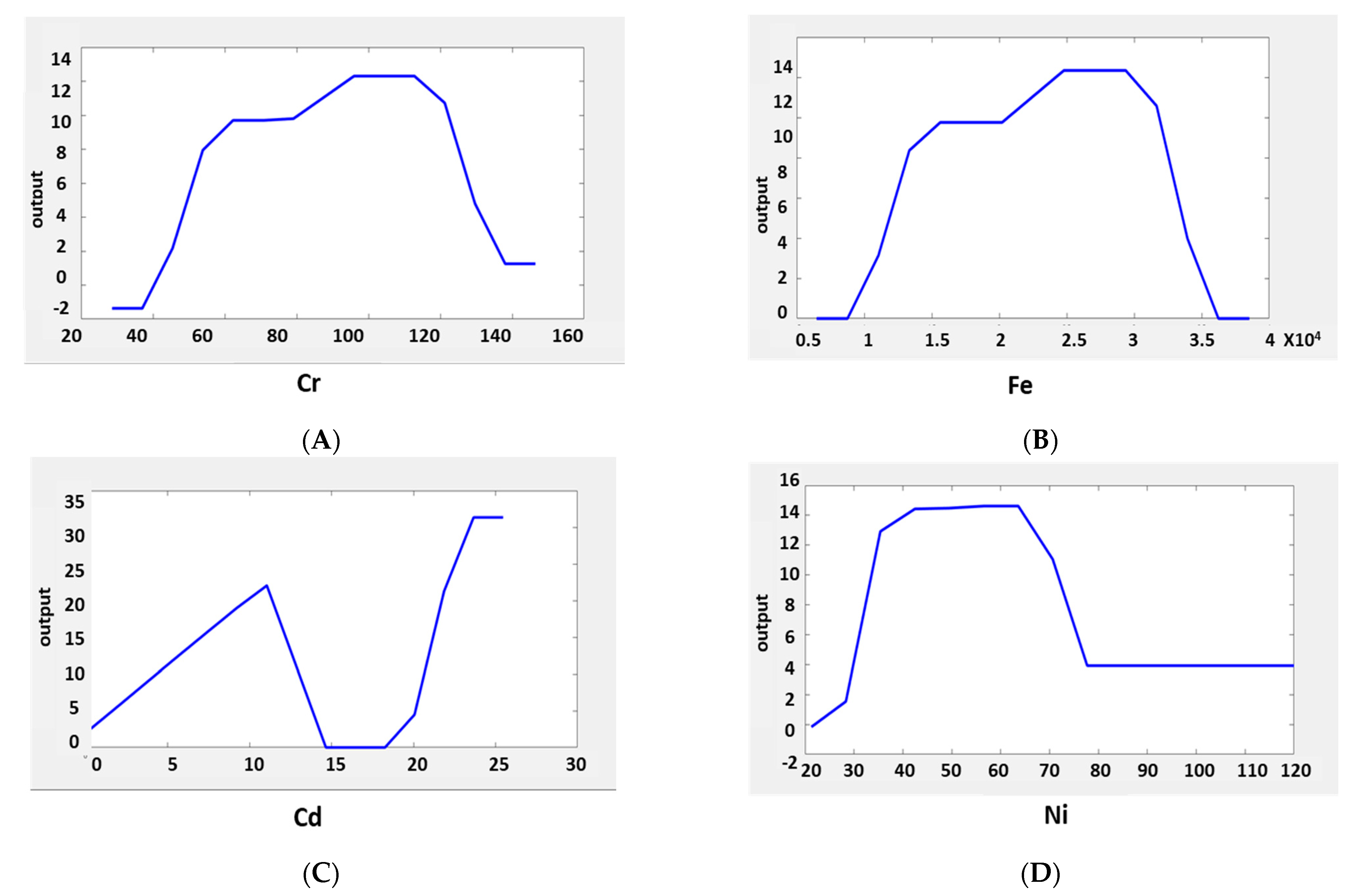
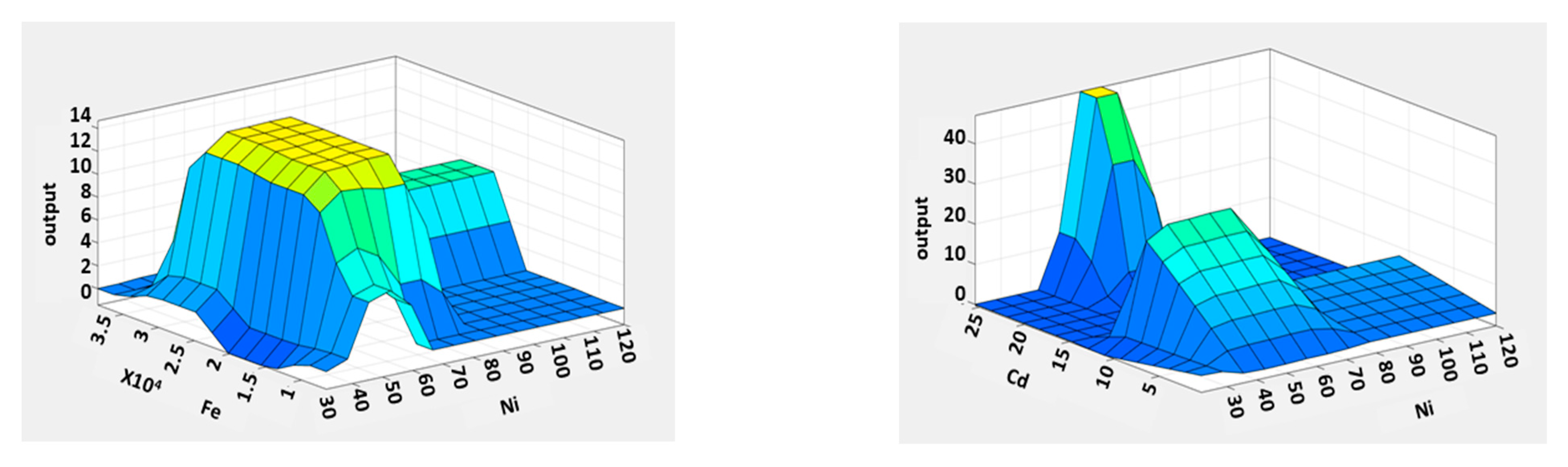
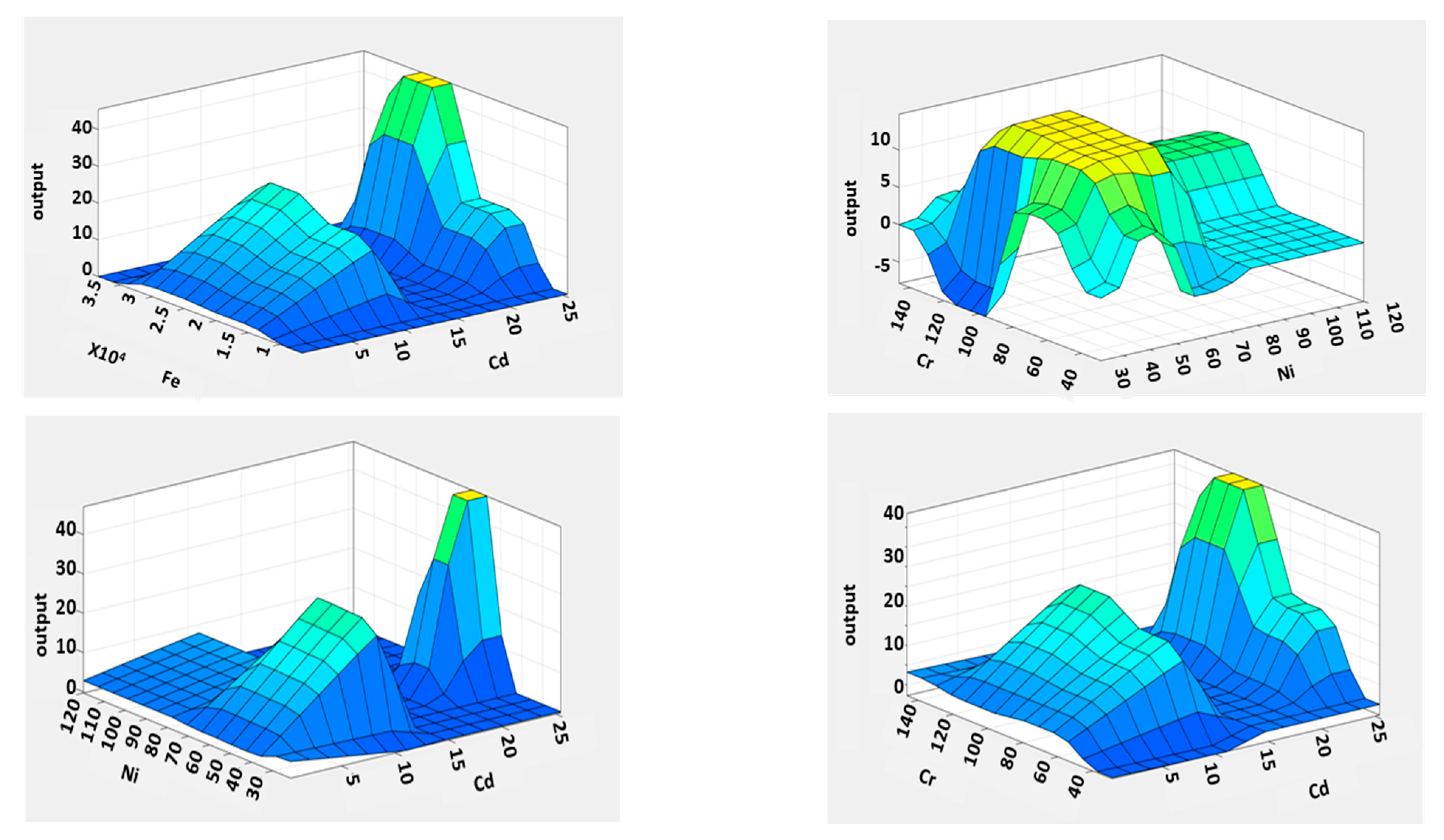
3.3. ANFIS Modeling
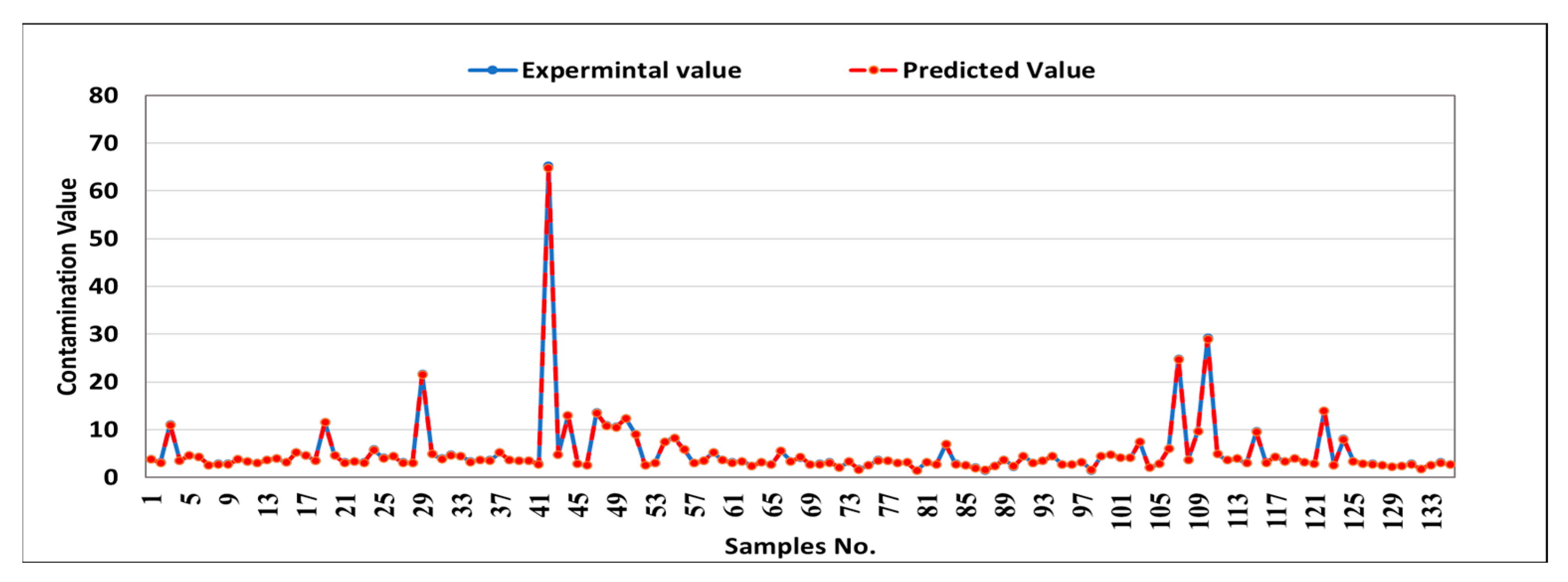
3.4. Predictive Model
3.5. Modified Degree of Contamination (mCd)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ismail, A.; Hettiarachchi, H. Environmental damage caused by wastewater discharge into the Lake Manzala in Egypt. Am. J. Biosci. Bioeng. 2017, 5, 141–150. [Google Scholar] [CrossRef]
- Aitta, A.; El-Ramady, H.; Alshaal, T.; El-Henawy, A.; Shams, M.; Talha, N.; Elbehiry, F.; Brevik, E.C. Seasonal and spatial distribution of soil trace elements around Kitchener drain in the northern Nile Delta, Egypt. Agriculture 2019, 9, 152. [Google Scholar] [CrossRef]
- Abd-Elaty, I.; Pugliese, L.; Zelenakova, M.; Mesaros, P.; Shinawi, A.E. Simulation-based solutions reducing soil and groundwater contamination from fertilizers in arid and semi-arid regions: Case study the Eastern Nile Delta, Egypt. Int. J. Environ. Res. Public Health 2020, 17, 9373. [Google Scholar] [CrossRef]
- He, Z.L.; Yang, X.E.; Stoffella, P.J. Trace elements in agroecosystems and impacts on the environment. J. Trace Elem. Med. Biol. 2005, 19, 125–140. [Google Scholar] [CrossRef]
- Abd-Elaty, I.; Zelenakova, M.; Straface, S.; Vranayová, Z.; Abu-hashim, M. Integrated modelling for groundwater contamination from polluted streams using new protection process techniques. Water 2019, 11, 2321. [Google Scholar] [CrossRef]
- Abdel-Shafy, H.I.; Aly, R.O. Water issue in Egypt: Resources, pollution and protection endeavors. Cent. Eur. J. Occup. Environ. Med. 2002, 8, 3–21. [Google Scholar]
- Saad, A. Environmental Hydrogeologic Impacts of Ground Water Withdrawal in the Eastern Nile Delta Region with Emphasis on Ground-Water Pollution Potential. Ph.D. Thesis, Ain Shams University, Cairo, Egypt, 1997. [Google Scholar]
- Zahran, M.A.E.-K.; El-Amier, Y.A.; Elnaggar, A.A.; Mohamed, H.A.E.-A.; El-Alfy, M.A.E.-H. Assessment and distribution of heavy metals pollutants in Manzala Lake, Egypt. J. Geosci. Environ. Prot. 2015, 3, 107. [Google Scholar] [CrossRef]
- Omran, E.; Abd El Razek, A.A. Mapping and screening risk assessment of heavy metals concentrations in soils of the Bahr El-Baker Region, Egypt. J Soil Sci Env. Manag. 2012, 6, 182–195. [Google Scholar]
- Soliman, R.M.; Othman, B.A.; Shoman, S.A.; Gado, M.M.; Azzam, M.I. Assessment of Bahr El-Baqar Drain and its Environmental Impact on Manzala Lake in Egypt. J. Ecol. Nat. Resour. 2022, 6, 2578–4994. [Google Scholar]
- El Behairy, R.A.; El Baroudy, A.A.; Ibrahim, M.M.; Kheir, A.M.; Shokr, M.S. Modelling and assessment of irrigation water quality index using GIS in semi-arid region for sustainable agriculture. Water Air Soil Pollut. 2021, 232, 352. [Google Scholar] [CrossRef]
- El Behairy, R.A.; El Baroudy, A.A.; Ibrahim, M.M.; Mohamed, E.S.; Kucher, D.E.; Shokr, M.S. Assessment of soil capability and crop suitability using integrated multivariate and GIS approaches toward agricultural sustainability. Land 2022, 11, 1027. [Google Scholar] [CrossRef]
- Galil Hussein, I.A.E. Desertification process in Egypt. In Coping with Global Environmental Change, Disasters and Security: Threats, Challenges, Vulnerabilities and Risks; Springer: Berlin/Heidelberg, Germany, 2011; pp. 863–874. [Google Scholar]
- Abdelhak, M. Soil improvement in arid and semiarid regions for sustainable development. In Natural Resources Conservation and Advances for Sustainability; Elsevier: Amsterdam, The Netherlands, 2022; pp. 73–90. [Google Scholar]
- Hendawy, E.; Belal, A.; Mohamed, E.; Elfadaly, A.; Murgante, B.; Aldosari, A.A.; Lasaponara, R. The prediction and assessment of the impacts of soil sealing on agricultural land in the North Nile Delta (Egypt) using satellite data and GIS modeling. Sustainability 2019, 11, 4662. [Google Scholar] [CrossRef]
- El Behairy, R.A.; El Baroudy, A.A.; Ibrahim, M.M.; Mohamed, E.S.; Rebouh, N.Y.; Shokr, M.S. Combination of GIS and Multivariate Analysis to Assess the Soil Heavy Metal Contamination in Some Arid Zones. Agronomy 2022, 12, 2871. [Google Scholar] [CrossRef]
- Shokr, M.S.; Abdellatif, M.A.; El Behairy, R.A.; Abdelhameed, H.H.; El Baroudy, A.A.; Mohamed, E.S.; Rebouh, N.Y.; Ding, Z.; Abuzaid, A.S. Assessment of Potential Heavy Metal Contamination Hazards Based on GIS and Multivariate Analysis in Some Mediterranean Zones. Agronomy 2022, 12, 3220. [Google Scholar] [CrossRef]
- Abuzaid, A.S.; Jahin, H.S.; Shokr, M.S.; El Baroudy, A.A.; Mohamed, E.S.; Rebouh, N.Y.; Bassouny, M.A. A Novel Regional-Scale Assessment of Soil Metal Pollution in Arid Agroecosystems. Agronomy 2023, 13, 161. [Google Scholar] [CrossRef]
- Omran, E.-S.E. Environmental modelling of heavy metals using pollution indices and multivariate techniques in the soils of Bahr El Baqar, Egypt. Model. Earth Syst. Environ. 2016, 2, 119. [Google Scholar] [CrossRef]
- Mohamed, E.; Ali, A.; El Shirbeny, M.; Abd El Razek, A.A.; Savin, I.Y. Near infrared spectroscopy techniques for soil contamination assessment in the Nile Delta. Eurasian Soil Sci. 2016, 49, 632–639. [Google Scholar] [CrossRef]
- Hammam, A.A.; Mohamed, W.S.; Sayed, S.E.-E.; Kucher, D.E.; Mohamed, E.S. Assessment of soil contamination using gis and multi-variate analysis: A case study in El-Minia Governorate, Egypt. Agronomy 2022, 12, 1197. [Google Scholar] [CrossRef]
- Uchimiya, M.; Bannon, D.; Nakanishi, H.; McBride, M.B.; Williams, M.A.; Yoshihara, T. Chemical speciation, plant uptake, and toxicity of heavy metals in agricultural soils. J. Agric. Food Chem. 2020, 68, 12856–12869. [Google Scholar] [CrossRef]
- Gautam, K.; Sharma, P.; Dwivedi, S.; Singh, A.; Gaur, V.K.; Varjani, S.; Srivastava, J.K.; Pandey, A.; Chang, J.-S.; Ngo, H.H. A review on control and abatement of soil pollution by heavy metals: Emphasis on artificial intelligence in recovery of contaminated soil. Environ. Res. 2023, 225, 115592. [Google Scholar] [CrossRef]
- El Behairy, R.A.; El Arwash, H.M.; El Baroudy, A.A.; Ibrahim, M.M.; Mohamed, E.S.; Rebouh, N.Y.; Shokr, M.S. Artificial Intelligence Integrated GIS for Land Suitability Assessment of Wheat Crop Growth in Arid Zones to Sustain Food Security. Agronomy 2023, 13, 1281. [Google Scholar] [CrossRef]
- Jang, J. ANFIS: Adaptive-Network Based Fuzzy Inference Systems. IEEE Trans Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Hooda, N.; Malik, M. Review on neuro-fuzzy system. In Available at SSRN 4033495; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Salleh, M.N.M.; Talpur, N.; Hussain, K. Adaptive neuro-fuzzy inference system: Overview, strengths, limitations, and solutions. In Proceedings of the Data Mining and Big Data: Second International Conference, DMBD 2017, Fukuoka, Japan, 27 July–1 August 2017; pp. 527–535. [Google Scholar]
- Al-Hamed, S.; Wahby, M.; Al-Sulaiman, M.; Aboukarima, A. Prediction of soil fractions (sand, silt and clay) in surface layer based on natural radionuclides concentration in the soil using adaptive neuro fuzzy inference system. Open J. Soil Sci. 2014, 4, 215. [Google Scholar] [CrossRef]
- Aboukarima, A.; El-Marazky, M.; Ghoneim, A.; Ebid, A. Modelling of Sodium Adsorption Ratio of the Soil Using Adaptive Neuro Fuzzy Inference System. J. Exp. Agric. Int. 2016, 14, 1–12. [Google Scholar] [CrossRef]
- Sonmez, A.Y.; Kale, S.; Ozdemir, R.C.; Kadak, A.E. An adaptive neuro-fuzzy inference system (ANFIS) to predict of cadmium (Cd) concentrations in the Filyos River, Turkey. Turk. J. Fish. Aquat. Sci. 2018, 18, 1333–1343. [Google Scholar] [CrossRef] [PubMed]
- Rezaei, A.; Hassani, H.; Fard Mousavi, S.B.; Hassani, S.; Jabbari, N. Assessment of heavy metals contamination in surface soils in Meiduk copper mine area, SE Iran. Earth Sci. Malays. 2019, 3, 01–08. [Google Scholar] [CrossRef]
- Ucun Ozel, H.; Gemici, B.T.; Gemici, E.; Ozel, H.B.; Cetin, M.; Sevik, H. Application of artificial neural networks to predict the heavy metal contamination in the Bartin River. Environ. Sci. Pollut. Res. 2020, 27, 42495–42512. [Google Scholar] [CrossRef]
- Wong, Y.J.; Arumugasamy, S.K.; Chung, C.H.; Selvarajoo, A.; Sethu, V. Comparative study of artificial neural network (ANN), adaptive neuro-fuzzy inference system (ANFIS) and multiple linear regression (MLR) for modeling of Cu (II) adsorption from aqueous solution using biochar derived from rambutan (Nephelium lappaceum) peel. Environ. Monit. Assess. 2020, 192, 439. [Google Scholar] [CrossRef]
- Agbaogun, B.K.; Olu-Owolabi, B.I.; Buddenbaum, H.; Fischer, K. Adaptive neuro-fuzzy inference system (ANFIS) and multiple linear regression (MLR) modelling of Cu, Cd, and Pb adsorption onto tropical soils. Environ. Sci. Pollut. Res. 2023, 30, 31085–31101. [Google Scholar] [CrossRef]
- Page, A.; Miller, R.; Keeney, D. Methods of soil analysis. Part 2. American Society of Agronomy. Soil Sci. Soc. Am. Madison WI USA 1982, 4, 167–179. [Google Scholar]
- Isaaks, E.H.; Srivastava, R.M. Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989; Volume 561. [Google Scholar]
- Templeton, G.F. A two-step approach for transforming continuous variables to normal: Implications and recommendations for IS research. Commun. Assoc. Inf. Syst. 2011, 28, 4. [Google Scholar] [CrossRef]
- Johnston, K.; Ver Hoef, J.M.; Krivoruchko, K.; Lucas, N. Using ArcGIS Geostatistical Analyst; Esri Redlands: Redlands, CA, USA, 2001; Volume 380. [Google Scholar]
- Gundogdu, K.S.; Guney, I. Spatial analyses of groundwater levels using universal kriging. J. Earth Syst. Sci. 2007, 116, 49–55. [Google Scholar] [CrossRef]
- Cambardella, C.; Elliott, E. Carbon and nitrogen dynamics of soil organic matter fractions from cultivated grassland soils. Soil Sci. Soc. Am. J. 1994, 58, 123–130. [Google Scholar] [CrossRef]
- Abrahim, G.; Parker, R. Assessment of heavy metal enrichment factors and the degree of contamination in marine sediments from Tamaki Estuary, Auckland, New Zealand. Environ. Monit. Assess. 2008, 136, 227–238. [Google Scholar] [CrossRef]
- Cheng, Q.; Wang, R.; Huang, W.; Wang, W.; Li, X. Assessment of heavy metal contamination in the sediments from the Yellow River Wetland National Nature Reserve (the Sanmenxia section), China. Environ. Sci. Pollut. Res. 2015, 22, 8586–8593. [Google Scholar] [CrossRef]
- Wedepohl, K.H. The composition of the continental crust. Geochim. Cosmochim. Acta 1995, 59, 1217–1232. [Google Scholar] [CrossRef]
- Rahman, S.H.; Khanam, D.; Adyel, T.M.; Islam, M.S.; Ahsan, M.A.; Akbor, M.A. Assessment of heavy metal contamination of agricultural soil around Dhaka Export Processing Zone (DEPZ), Bangladesh: Implication of seasonal variation and indices. Appl. Sci. 2012, 2, 584–601. [Google Scholar] [CrossRef]
- Soroush, E.; Mesbah, M.; Hajilary, N.; Rezakazemi, M. ANFIS modeling for prediction of CO2 solubility in potassium and sodium based amino acid Salt solutions. J. Environ. Chem. Eng. 2019, 7, 102925. [Google Scholar] [CrossRef]
- Najafi, B.; Ardabili, S.F. Application of ANFIS, ANN, and logistic methods in estimating biogas production from spent mushroom compost (SMC). Resour. Conserv. Recycl. 2018, 133, 169–178. [Google Scholar] [CrossRef]
- Hesami, M.; Naderi, R.; Tohidfar, M.; Yoosefzadeh-Najafabadi, M. Application of adaptive neuro-fuzzy inference system-non-dominated sorting genetic Algorithm-II (ANFIS-NSGAII) for modeling and optimizing somatic embryogenesis of Chrysanthemum. Front. Plant Sci. 2019, 10, 869. [Google Scholar] [CrossRef]
- Ani, K.A.; Agu, C.M.; Menkiti, M.C. Preliminary investigation and neural network modeling of palm oil mill effluent as a potential bio-stimulating organic co-substrate in hydrocarbon degradation. Environ. Chall. 2021, 5, 100216. [Google Scholar] [CrossRef]
- Sislian, R.; da Silva, F.V.; Coghi, M.A.; Gedraite, R. Neuro-fuzzy model-based simulation of a laboratory scale clean-in-place system: A study of the rinsing process. Environ. Chall. 2021, 4, 100098. [Google Scholar] [CrossRef]
- El-Bady, M.S. Spatial distribution of some important heavy metals in the soils south of Manzala Lake in Bahr El-Baqar region, Egypt. Nova J. Eng. Appl. Sci. 2014, 3, 1–12. [Google Scholar]
- Department of Environmental Affairs. National Norms and Standards for the Remediation of Contaminated Land and Soil Quality in the Republic of South Africa; Department of Environmental Affairs (DEA), National Environmental Management: Pretoria, South Africa, 2013.
- Alloway, B. Soil processes and the behaviour of metals. Heavy Met. Soils 1995, 13, 3488. [Google Scholar]
- Janardhana, K.; Sridhar, S.; Dixit, C.K.; Deivakani, M.; Tamilselvi, S.; Kaladgi, A.R.; Afzal, A.; Baig, M.A.A. ANFIS modeling of biodiesels’ physical and engine characteristics: A review. Heat Transf. 2021, 50, 8052–8079. [Google Scholar] [CrossRef]
- Noori, R.; Hoshyaripour, G.; Ashrafi, K.; Araabi, B.N. Uncertainty analysis of developed ANN and ANFIS models in prediction of carbon monoxide daily concentration. Atmos. Environ. 2010, 44, 476–482. [Google Scholar] [CrossRef]
- Perendeci, A.; Arslan, S.; Çelebi, S.S.; Tanyolaç, A. Prediction of effluent quality of an anaerobic treatment plant under unsteady state through ANFIS modeling with on-line input variables. Chem. Eng. J. 2008, 145, 78–85. [Google Scholar] [CrossRef]
- Amirkhani, S.; Nasirivatan, S.; Kasaeian, A.; Hajinezhad, A. ANN and ANFIS models to predict the performance of solar chimney power plants. Renew. Energy 2015, 83, 597–607. [Google Scholar] [CrossRef]
- Sayyad Amin, J.; Rajabi Kuyakhi, H.; Kashiwao, T.; Bahadori, A. Development of ANFIS models for polycyclic aromatic hydrocarbons (PAHs) formation in sea sediment. Pet. Sci. Technol. 2019, 37, 679–686. [Google Scholar] [CrossRef]



| Variable | Min | Max | Mean | SD | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| Cr (mg kg−1) | 28.62 | 146.45 | 77.29 | 18.49 | 0.46 | 0.98 |
| Fe (mg kg−1) | 6468.17 | 38,526.6 | 19,565.15 | 4735.40 | 0.48 | 1.37 |
| Cd (mg kg−1) | 0.24 | 25.47 | 1.48 | 2.52 | 6.79 | 58.31 |
| Ni (mg kg−1) | 21.30 | 82.14 | 45.39 | 10.01 | 0.88 | 1.46 |
| Variable | Model | Nugget | Partial | Sill | Nugget/Sill | SDC | MSE | ASE | RMSSE | ASE |
|---|---|---|---|---|---|---|---|---|---|---|
| (C0) | Sill | (C0 + C) | ||||||||
| Cr (mg kg−1) | Spherical | 0.028 | 0.03 | 0.025 | 0.48 | Moderate | 0.014 | 0.005 | 0.975 | 0.45 |
| Fe (mg kg−1) | Exponential | 0.035 | 0.034 | 0.069 | 0.5 | Moderate | 0.026 | 0.009 | 1.04 | 0.47 |
| Cd (mg kg−1) | Stable | 0.14 | 0.46 | 0.60 | 0.23 | strong | 0.024 | 0.021 | 0.99 | 0.52 |
| Ni (mg kg−1) | Exponential | 0.028 | 0.026 | 0.54 | 0.48 | Moderate | 0.021 | 0.02 | 1.07 | 0.59 |
| Parameters | Description/Values |
|---|---|
| FIS type | Sugeno |
| Generated FIS | Grid partition |
| Membership Function type | Trapezoidal (Trapmf) |
| O/p Membership Function | linear |
| I/Ps No. | 4 |
| O/Ps No. | 1 |
| Nodes No. | 551 |
| Linear parameters No. | 256 |
| Nonlinear parameters No. | 64 |
| Training data pairs No. | 136 |
| Parameters total No. | 320 |
| Checking data pairs No. | 2 |
| Testing data pairs No. | 14 |
| Fuzzy rules No. | 256 |
| Parameters | Training | Test |
|---|---|---|
| Network type optimization | Hybrid | Hybrid |
| RMSE | 0.04859 | 0.06450 |
| MSE | 0.00236 | 0.00416 |
| SSE | 0.31637 | 0.05824 |
| R2 | 0.99254 | 0.92857 |
| mCd Classes | Cr | Fe | Cd | Ni | Acer | % | Significantly of Different Classes |
|---|---|---|---|---|---|---|---|
| LDC | 50.46 ± 13.2 | 12,991.58 ± 4884 | 0.31 ± 0.05 | 30.43 ± 6.79 | 1.28 | 0.2 | F |
| MDC | 76.03 ± 17.9 | 19,205.25 ± 4471.8 | 0.69 ± 0.17 | 44.86 ± 8.57 | 273.05 | 37.5 | E |
| HDC | 82.86 ± 15.5 | 20,963.84 ± 4447.8 | 1.46 ± 0.42 | 48.71 ± 11.88 | 375.45 | 51.6 | D |
| VHDC | 82.41 ± 22.96 | 19,604.31 ± 3735.7 | 3.91 ± 0.83 | 49.4 ± 21.22 | 68.27 | 9.3 | C |
| EHDC | 84.72 ± 34.70 | 22,286.91 ± 7490.5 | 7.23 ± 4.58 | 56.26 ± 8.21 | 7.76 | 1.1 | B |
| UHDC | 90.6 | 23,464.7 | 25.46 | 58.12 | 2.31 | 0.3 | A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, E.S.; Jalhoum, M.E.M.; Belal, A.A.; Hendawy, E.; Azab, Y.F.A.; Kucher, D.E.; Shokr, M.S.; El Behairy, R.A.; El Arwash, H.M. A Novel Approach for Predicting Heavy Metal Contamination Based on Adaptive Neuro-Fuzzy Inference System and GIS in an Arid Ecosystem. Agronomy 2023, 13, 1873. https://doi.org/10.3390/agronomy13071873
Mohamed ES, Jalhoum MEM, Belal AA, Hendawy E, Azab YFA, Kucher DE, Shokr MS, El Behairy RA, El Arwash HM. A Novel Approach for Predicting Heavy Metal Contamination Based on Adaptive Neuro-Fuzzy Inference System and GIS in an Arid Ecosystem. Agronomy. 2023; 13(7):1873. https://doi.org/10.3390/agronomy13071873
Chicago/Turabian StyleMohamed, Elsayed Said, Mohamed E. M. Jalhoum, Abdelaziz A. Belal, Ehab Hendawy, Yara F. A. Azab, Dmitry E. Kucher, Mohamed. S. Shokr, Radwa A. El Behairy, and Hasnaa M. El Arwash. 2023. "A Novel Approach for Predicting Heavy Metal Contamination Based on Adaptive Neuro-Fuzzy Inference System and GIS in an Arid Ecosystem" Agronomy 13, no. 7: 1873. https://doi.org/10.3390/agronomy13071873
APA StyleMohamed, E. S., Jalhoum, M. E. M., Belal, A. A., Hendawy, E., Azab, Y. F. A., Kucher, D. E., Shokr, M. S., El Behairy, R. A., & El Arwash, H. M. (2023). A Novel Approach for Predicting Heavy Metal Contamination Based on Adaptive Neuro-Fuzzy Inference System and GIS in an Arid Ecosystem. Agronomy, 13(7), 1873. https://doi.org/10.3390/agronomy13071873










