Advanced Hybrid Metaheuristic Machine Learning Models Application for Reference Crop Evapotranspiration Prediction
Abstract
1. Introduction
2. Case Study and Data Description
2.1. Case Study Area
2.2. Data Sources and Quality Control
2.3. FAO56 Penman–Monteith Model (FAO56-PM Model)
3. Methods
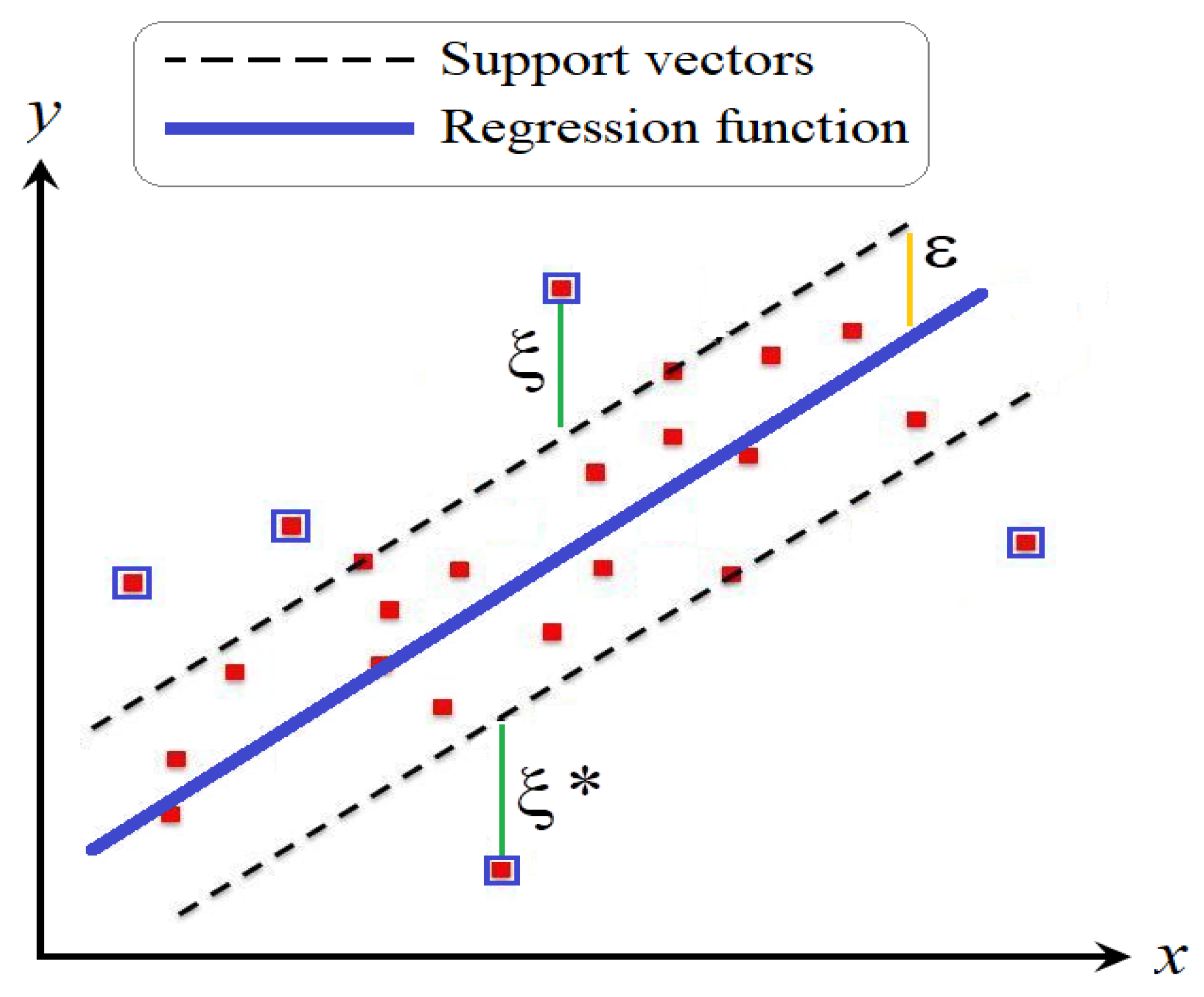
3.1. Machine Learning Model (SVR)
3.2. Heuristic Optimization Methods (PSO, GWO, and GSA)
- (i)
- Tracking, chasing, and approaching the prey;
- (ii)
- Pursuing, encircling, and harassing the prey;
- (iii)
- And finally, getting close to the prey and attacking.
3.3. Hybrid Optimization Methods (PSOGWO and PSOGSA)
- -
- PSOGWO
| Algorithm 1. PSOGWO |
| • Setting up parameters Epoch: the number of iterations (either set by the user or reached according to the other types of stopping criteria) SP: Initial swarm population number (particles in the PSO algorithm) prob: possibility rate (set by the user) • Hybrid procedure Initializing particles in the solution space FOR i = 1 to Epoch FOR j = 1 to SP Run PSO (updating the x and v vectors) Evaluating the fitness values Updating Pg (memorizing the best values of the swarm) IF rand (0,1) < prob then (to avoid trapping in local minima) THEN Run GWO Evaluating the fitness of all wolves Updating the positions of the Alpha, Beta, and delta wolves Calculating the mean of the position of three best (α, β, δ) wolves Returning updated values for the particles in the PSO algorithm END IF END FOR END FOR |
- -
- PSOGSA
| Algorithm 2. PSOGSA |
| • Setting up initial values and parameters Epoch: the number of iterations; SP: Initial swarm population number; prob: possi bility rate • Hybrid procedure Initializing particles in the solution space FOR i = 1 to Epoch FOR j = 1 to SP Run PSO Evaluating the fitness values of the particles updating Pg IF rand(0,1) < prob then (to avoid trapping in local minima) THEN Run GSA Computing the resultant force (F) and the acceleration (a) Updating values for the velocity and positions (Pi) Returning updated values for the particles in the PSO algorithm END IF END FOR END FOR |
3.4. Performance Evaluation
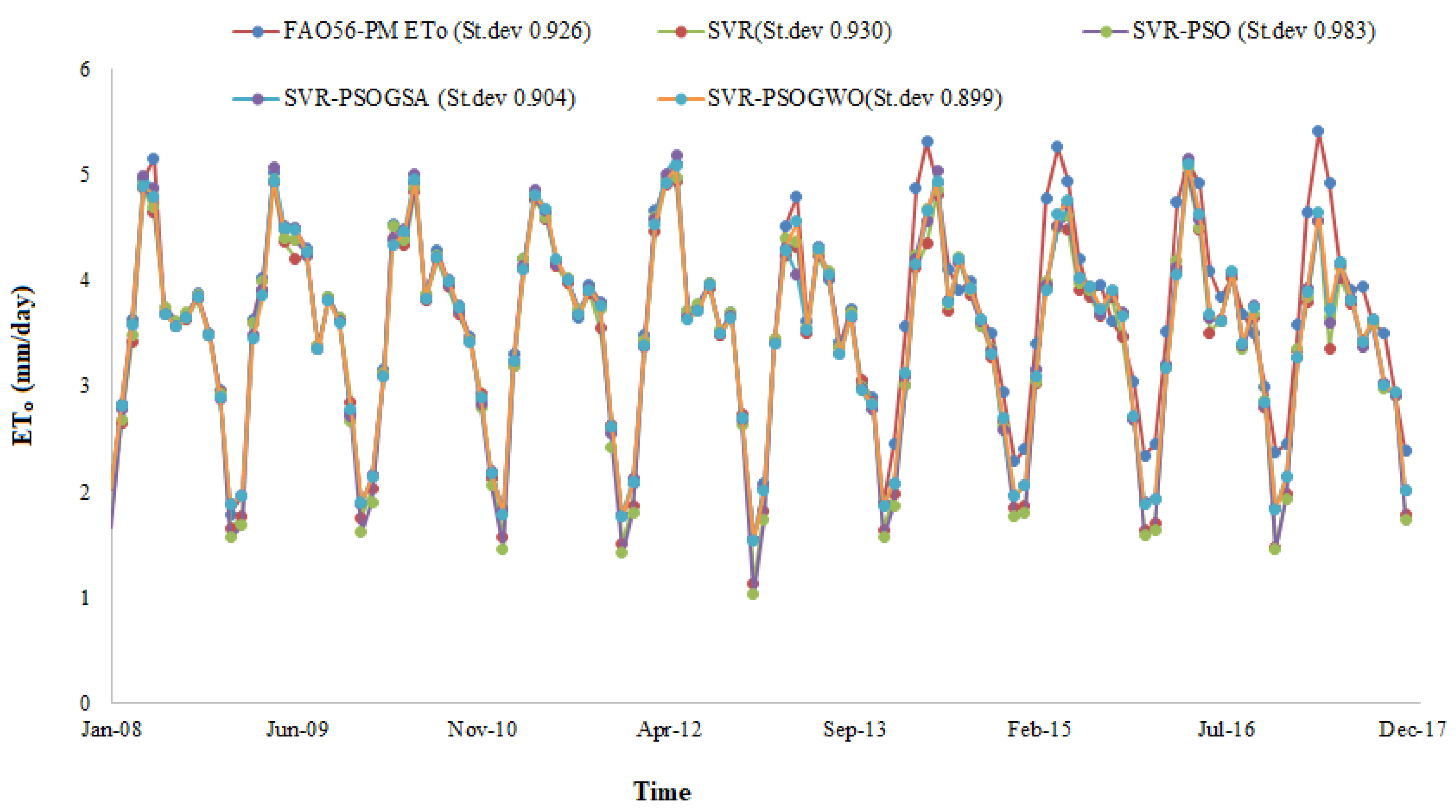
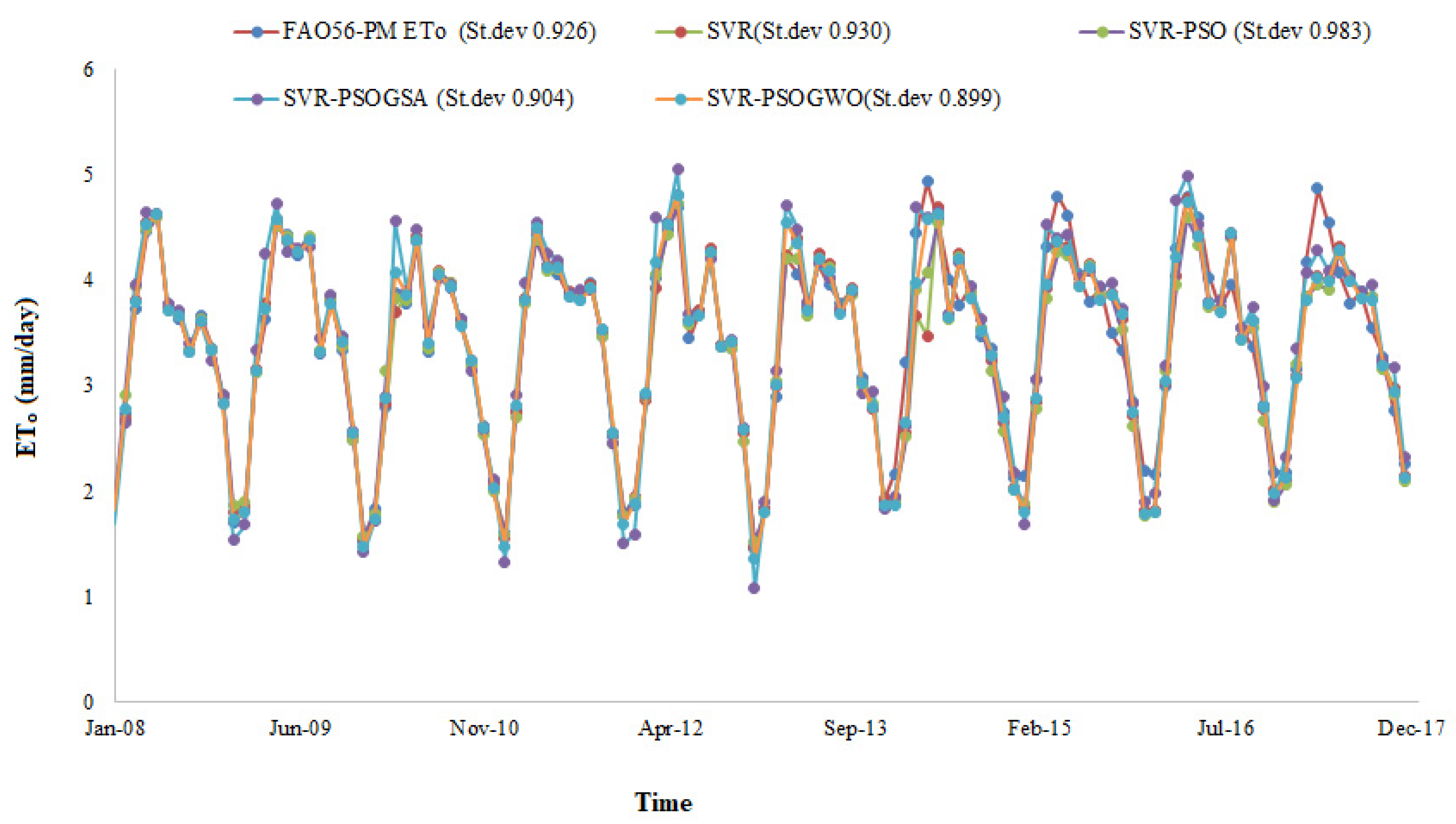
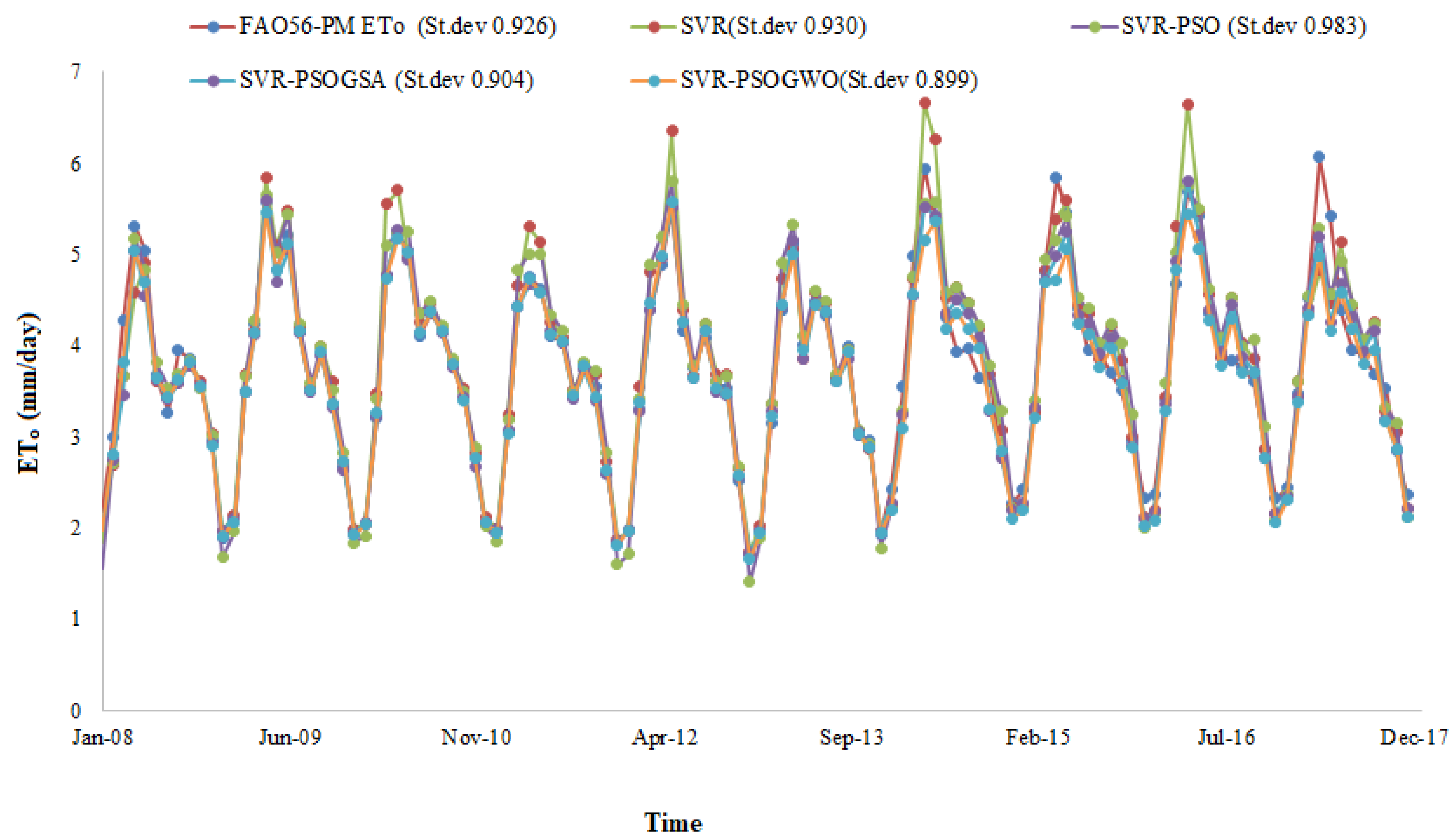
4. Results and Discussion
5. Conclusions
- (i)
- Monthly discharge, Tmin, Tmax, Ra, Rs, U2, and HR data from three stations were used for assessing the above-mentioned methods. Based on the root mean square error, mean absolute error, Nash–Sutcliffe efficiency and determination coefficient and graphical methods, the SVR–PSOGWO was superior to the other methods, followed by the SVR–PSOGSA, SVR–PSO, and SVR. This implies the necessity of hybrid metaheuristic algorithms in SVR training.
- (ii)
- It was observed that the input combination involving whole climatic data generally produced the best accuracy. The SVR–PSOGWO with Tmin, Tmax, Ra, Rs, and U2 inputs improved the accuracy of single SVR by 27%, 32%, and 23% for Bogra, Rajshahi, and Rangpur stations with respect to root mean square errors in the testing stage, respectively. The second input combination comprising Tmin, Tmax, and Ra also provided good accuracy (NSE ranges from 0.808 to 0.897). The models with this input combination can be a good alternative when other climatic data are unavailable. The viability of the presented hybrid metaheuristic algorithms can be assessed for improving other machine learning methods such as extreme leaning machine, neural networks, or neuro-fuzzy systems in future studies.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bozkurt Çolak, Y.; Yazar, A.; Alghory, A.; Tekin, S. Evaluation of crop water stress index and leaf water potential for differentially irrigated quinoa with surface and subsurface drip systems. Irrig. Sci. 2021, 39, 81–100. [Google Scholar] [CrossRef]
- Huang, D.; Wang, J.; Khayatnezhad, M. Estimation of Actual Evapotranspiration Using Soil Moisture Balance and Remote Sensing. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 45, 2779–2786. [Google Scholar] [CrossRef]
- Ghiat, I.; Mackey, H.R.; Al-Ansari, T. A Review of Evapotranspiration Measurement Models, Techniques and Methods for Open and Closed Agricultural Field Applications. Water 2021, 13, 2523. [Google Scholar] [CrossRef]
- Lugato, E.; Lavallee, J.M.; Haddix, M.L.; Panagos, P.; Cotrufo, M.F. Different climate sensitivity of particulate and mineral-associated soil organic matter. Nat. Geosci. 2021, 14, 295–300. [Google Scholar] [CrossRef]
- Shah, S.; Duan, Z.; Song, X.; Li, R.; Mao, H.; Liu, J.; Ma, T.; Wang, M. Evaluating the added value of multi-variable calibration of SWAT with remotely sensed evapotranspiration data for improving hydrological modeling. J. Hydrol. 2021, 603, 127046. [Google Scholar] [CrossRef]
- Fan, G.; Sarabandi, A.; Yaghoobzadeh, M. Evaluating the climate change effects on temperature, precipitation and evapotranspiration in eastern Iran using CMPI5. Water Supply 2021, 21, 4316–4327. [Google Scholar] [CrossRef]
- Machakaire, A.T.B.; Steyn, J.M.; Franke, A.C. Assessing evapotranspiration and crop coefficients of potato in a semi-arid climate using Eddy Covariance techniques. Agric. Water Manag. 2021, 255, 107029. [Google Scholar] [CrossRef]
- Makwana, J.J.; Tiwari, M.K.; Deora, B.S. Development and comparison of artificial intelligence models for estimating daily reference evapotranspiration from limited input variables. Smart Agric. Technol. 2023, 3, 100115. [Google Scholar] [CrossRef]
- Rodrigues, G.C.; Braga, R.P. Estimation of Reference Evapotranspiration during the Irrigation Season Using Nine Temperature-Based Methods in a Hot-Summer Mediterranean Climate. Agriculture 2021, 11, 124. [Google Scholar] [CrossRef]
- Samadi, S.Z. Assessing the sensitivity of SWAT physical parameters to potential evapotranspiration estimation methods over a coastal plain watershed in the southeastern United States. Hydrol. Res. 2016, 48, 395–415. [Google Scholar] [CrossRef]
- Gisolo, D.; Previati, M.; Bevilacqua, I.; Canone, D.; Boetti, M.; Dematteis, N.; Balocco, J.; Ferrari, S.; Gentile, A.; N’Sassila, M.; et al. A calibration free radiation driven model for estimating actual evapotranspiration of mountain grasslands (CLIME-MG). J. Hydrol. 2022, 610, 127948. [Google Scholar] [CrossRef]
- Abeysiriwardana, H.D.; Muttil, N.; Rathnayake, U. A Comparative Study of Potential Evapotranspiration Estimation by Three Methods with FAO Penman–Monteith Method across Sri Lanka. Hydrology 2022, 9, 206. [Google Scholar] [CrossRef]
- Wanniarachchi, S.; Sarukkalige, R. A Review on Evapotranspiration Estimation in Agricultural Water Management: Past, Present, and Future. Hydrology 2022, 9, 123. [Google Scholar] [CrossRef]
- Tejada, A.T.; Ella, V.B.; Lampayan, R.M.; Reaño, C.E. Modeling Reference Crop Evapotranspiration Using Support Vector Machine (SVM) and Extreme Learning Machine (ELM) in Region IV-A, Philippines. Water 2022, 14, 754. [Google Scholar] [CrossRef]
- Abedi-Koupai, J.; Dorafshan, M.-M.; Javadi, A.; Ostad-Ali-Askari, K. Estimating potential reference evapotranspiration using time series models (case study: Synoptic station of Tabriz in northwestern Iran). Appl. Water Sci. 2022, 12, 212. [Google Scholar] [CrossRef]
- Chia, M.Y.; Huang, Y.F.; Koo, C.H. Improving reference evapotranspiration estimation using novel inter-model ensemble approaches. Comput. Electron. Agric. 2021, 187, 106227. [Google Scholar] [CrossRef]
- Dou, X.; Yang, Y. Evapotranspiration estimation using four different machine learning approaches in different terrestrial ecosystems. Comput. Electron. Agric. 2018, 148, 95–106. [Google Scholar] [CrossRef]
- Nourani, V.; Elkiran, G.; Abdullahi, J. Multi-station artificial intelligence based ensemble modeling of reference evapotranspiration using pan evaporation measurements. J. Hydrol. 2019, 577, 123958. [Google Scholar] [CrossRef]
- Antonopoulos, V.Z.; Antonopoulos, A.V. Daily reference evapotranspiration estimates by artificial neural networks technique and empirical equations using limited input climate variables. Comput. Electron. Agric. 2017, 132, 86–96. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, B.; Zhu, T.; Zhou, A.; Zhou, W. Visual privacy attacks and defenses in deep learning: A survey. Artif. Intell. Rev. 2022, 55, 4347–4401. [Google Scholar] [CrossRef]
- Emadi, A.; Zamanzad-Ghavidel, S.; Fazeli, S.; Zarei, S.; Rashid-Niaghi, A. Multivariate modeling of pan evaporation in monthly temporal resolution using a hybrid evolutionary data-driven method (case study: Urmia Lake and Gavkhouni basins). Environ. Monit. Assess. 2021, 193, 355. [Google Scholar] [CrossRef] [PubMed]
- Mehdizadeh, S. Estimation of daily reference evapotranspiration (ETo) using artificial intelligence methods: Offering a new approach for lagged ETo data-based modeling. J. Hydrol. 2018, 559, 794–812. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Malik, A.; Souag-Gamane, D.; Kisi, O. Artificial intelligence models versus empirical equations for modeling monthly reference evapotranspiration. Environ. Sci. Pollut. Res. 2020, 27, 30001–30019. [Google Scholar] [CrossRef] [PubMed]
- Tikhamarine, Y.; Malik, A.; Kumar, A.; Souag-Gamane, D.; Kisi, O. Estimation of monthly reference evapotranspiration using novel hybrid machine learning approaches. Hydrol. Sci. J. 2019, 64, 1824–1842. [Google Scholar] [CrossRef]
- Seifi, A.; Riahi, H. Estimating daily reference evapotranspiration using hybrid gamma test-least square support vector machine, gamma test-ANN, and gamma test-ANFIS models in an arid area of Iran. J. Water Clim. Chang. 2018, 11, 217–240. [Google Scholar] [CrossRef]
- Hossain, M.A.; Rahman, M.M.; Hasan, S.S. Application of combined drought index to assess meteorological drought in the south western region of Bangladesh. Phys. Chem. Earth Parts A/B/C 2020, 120, 102946. [Google Scholar] [CrossRef]
- Mojid, M.A.; Aktar, S.; Mainuddin, M. Rainfall-induced recharge-dynamics of heavily exploited aquifers—A case study in the North-West region of Bangladesh. Groundw. Sustain. Dev. 2021, 15, 100665. [Google Scholar] [CrossRef]
- Sumon, K.A.; Rashid, H.; Peeters, E.T.H.M.; Bosma, R.H.; Van den Brink, P.J. Environmental monitoring and risk assessment of organophosphate pesticides in aquatic ecosystems of north-west Bangladesh. Chemosphere 2018, 206, 92–100. [Google Scholar] [CrossRef]
- Jamal, M.R.; Kristiansen, P.; Kabir, M.J.; Kumar, L.; Lobry de Bruyn, L. Trajectories of cropping system intensification under changing environment in south-west coastal Bangladesh. Int. J. Agric. Sustain. 2022, 20, 722–742. [Google Scholar] [CrossRef]
- Dewan, A.; Shahid, S.; Bhuian, M.H.; Hossain, S.M.J.; Nashwan, M.S.; Chung, E.-S.; Hassan, Q.K.; Asaduzzaman, M. Developing a high-resolution gridded rainfall product for Bangladesh during 1901–2018. Sci. Data 2022, 9, 471. [Google Scholar] [CrossRef]
- Salehie, O.; Ismail, T.; Shahid, S.; Ahmed, K.; Adarsh, S.; Asaduzzaman, M.; Dewan, A. Ranking of gridded precipitation datasets by merging compromise programming and global performance index: A case study of the Amu Darya basin. Theor. Appl. Climatol. 2021, 144, 985–999. [Google Scholar] [CrossRef]
- Pour, S.H.; Shahid, S.; Chung, E.-S.; Wang, X.-J. Model output statistics downscaling using support vector machine for the projection of spatial and temporal changes in rainfall of Bangladesh. Atmos. Res. 2018, 213, 149–162. [Google Scholar] [CrossRef]
- Wahiduzzaman, M.; Luo, J.-J. A statistical analysis on the contribution of El Niño–Southern Oscillation to the rainfall and temperature over Bangladesh. Meteorol. Atmos. Phys. 2021, 133, 55–68. [Google Scholar] [CrossRef]
- Rouf, M.A.; Uddin, M.K.; Debsarma, S.K.; Rahman, M.M. Climate of Bangladesh: An Analysis of Northwestern and Southwestern Part Using High Resolution Atmosphere-Ocean General Circulation Model (AOGCM). Agriculturists 2012, 9, 143–154. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Islam, A.R.M.T.; Kisi, O.; Kuriqi, A.; Heddam, S. Estimating reference evapotranspiration using hybrid adaptive fuzzy inferencing coupled with heuristic algorithms. Comput. Electron. Agric. 2021, 191, 106541. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Salam, R.; Islam, A.R.M.T. Potential of RT, Bagging and RS ensemble learning algorithms for reference evapotranspiration prediction using climatic data-limited humid region in Bangladesh. J. Hydrol. 2020, 590, 125241. [Google Scholar] [CrossRef]
- Salam, R.; Islam, A.R.M.T.; Pham, Q.B.; Dehghani, M.; Al Ansari, N.; Linh, N.T.T. The optimal alternative for quantifying reference evapotranspiration in climatic sub-regions of Bangladesh. Sci. Rep. 2020, 10, 20171. [Google Scholar] [CrossRef]
- Dabral, P.P.; Mor, N.; Jhajharia, D. Time series modelling of monthly reference evapotranspiration for Bikaner, Rajasthan (India). Indian J. Soil Conserv. 2018, 46, 42–51. [Google Scholar]
- Aliku, O.; Oshunsanya, S.O.; Aiyelari, E.A. Estimation of crop evapotranspiration of Okra using drainage Lysimeters under dry season conditions. Sci. Afr. 2022, 16, e01189. [Google Scholar] [CrossRef]
- Moazenzadeh, R.; Mohammadi, B.; Shamshirband, S.; Chau, K.-W. Coupling a firefly algorithm with support vector regression to predict evaporation in northern Iran. Eng. Appl. Comput. Fluid Mech. 2018, 12, 584–597. [Google Scholar] [CrossRef]
- Adnan, R.M.; Kisi, O.; Mostafa, R.R.; Ahmed, A.N.; El-Shafie, A. The potential of a novel support vector machine trained with modified mayfly optimization algorithm for streamflow prediction. Hydrol. Sci. J. 2022, 67, 161–174. [Google Scholar] [CrossRef]
- Sreedhara, B.M.; Rao, M.; Mandal, S. Application of an evolutionary technique (PSO–SVM) and ANFIS in clear-water scour depth prediction around bridge piers. Neural Comput. Appl. 2019, 31, 7335–7349. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Dai, H.-L.; Ewees, A.A.; Shiri, J.; Kisi, O.; Zounemat-Kermani, M. Application of improved version of multi verse optimizer algorithm for modeling solar radiation. Energy Rep. 2022, 8, 12063–12080. [Google Scholar] [CrossRef]
- Meng, E.; Huang, S.; Huang, Q.; Fang, W.; Wang, H.; Leng, G.; Wang, L.; Liang, H. A Hybrid VMD-SVM Model for Practical Streamflow Prediction Using an Innovative Input Selection Framework. Water Resour. Manag. 2021, 35, 1321–1337. [Google Scholar] [CrossRef]
- Huang, W.; Liu, H.; Zhang, Y.; Mi, R.; Tong, C.; Xiao, W.; Shuai, B. Railway dangerous goods transportation system risk identification: Comparisons among SVM, PSO-SVM, GA-SVM and GS-SVM. Appl. Soft Comput. 2021, 109, 107541. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mittal, H.; Tripathi, A.; Pandey, A.C.; Pal, R. Gravitational search algorithm: A comprehensive analysis of recent variants. Multimed. Tools Appl. 2021, 80, 7581–7608. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Şenel, F.A.; Gökçe, F.; Yüksel, A.S.; Yiğit, T. A novel hybrid PSO–GWO algorithm for optimization problems. Eng. Comput. 2019, 35, 1359–1373. [Google Scholar] [CrossRef]
- Song, B.; Wang, Z.; Zou, L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Appl. Soft Comput. 2021, 100, 106960. [Google Scholar] [CrossRef]
- Eappen, G.; Shankar, T. Hybrid PSO-GSA for energy efficient spectrum sensing in cognitive radio network. Phys. Commun. 2020, 40, 101091. [Google Scholar] [CrossRef]
- Song, B.; Xiao, Y.; Xu, L. Design of fuzzy PI controller for brushless DC motor based on PSO–GSA algorithm. Syst. Sci. Control Eng. 2020, 8, 67–77. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration evaluation models based on machine learning algorithms—A comparative study. Agric. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
- Shiri, J. Improving the performance of the mass transfer-based reference evapotranspiration estimation approaches through a coupled wavelet-random forest methodology. J. Hydrol. 2018, 561, 737–750. [Google Scholar] [CrossRef]
- Huang, G.; Wu, L.; Ma, X.; Zhang, W.; Fan, J.; Yu, X.; Zeng, W.; Zhou, H. Evaluation of CatBoost method for prediction of reference evapotranspiration in humid regions. J. Hydrol. 2019, 574, 1029–1041. [Google Scholar] [CrossRef]
- Khosravi, K.; Daggupati, P.; Alami, M.T.; Awadh, S.M.; Ghareb, M.I.; Panahi, M.; Pham, B.T.; Rezaie, F.; Qi, C.; Yaseen, Z.M. Meteorological data mining and hybrid data-intelligence models for reference evaporation simulation: A case study in Iraq. Comput. Electron. Agric. 2019, 167, 105041. [Google Scholar] [CrossRef]
- Khosravi, K.; Mao, L.; Kisi, O.; Yaseen, Z.M.; Shahid, S. Quantifying hourly suspended sediment load using data mining models: Case study of a glacierized Andean catchment in Chile. J. Hydrol. 2018, 567, 165–179. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Kisi, O.; Piri, J.; Mahdavi-Meymand, A. Assessment of artificial intelligence–based models and metaheuristic algorithms in modeling evaporation. J. Hydrol. Eng. 2019, 24, 04019033. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Heddam, S.; Zounemat-Kermani, M.; Kisi, O.; Li, B. Least square support vector machine and multivariate adaptive regression splines for streamflow prediction in mountainous basin using hydro-meteorological data as inputs. J. Hydrol. 2020, 586, 124371. [Google Scholar] [CrossRef]
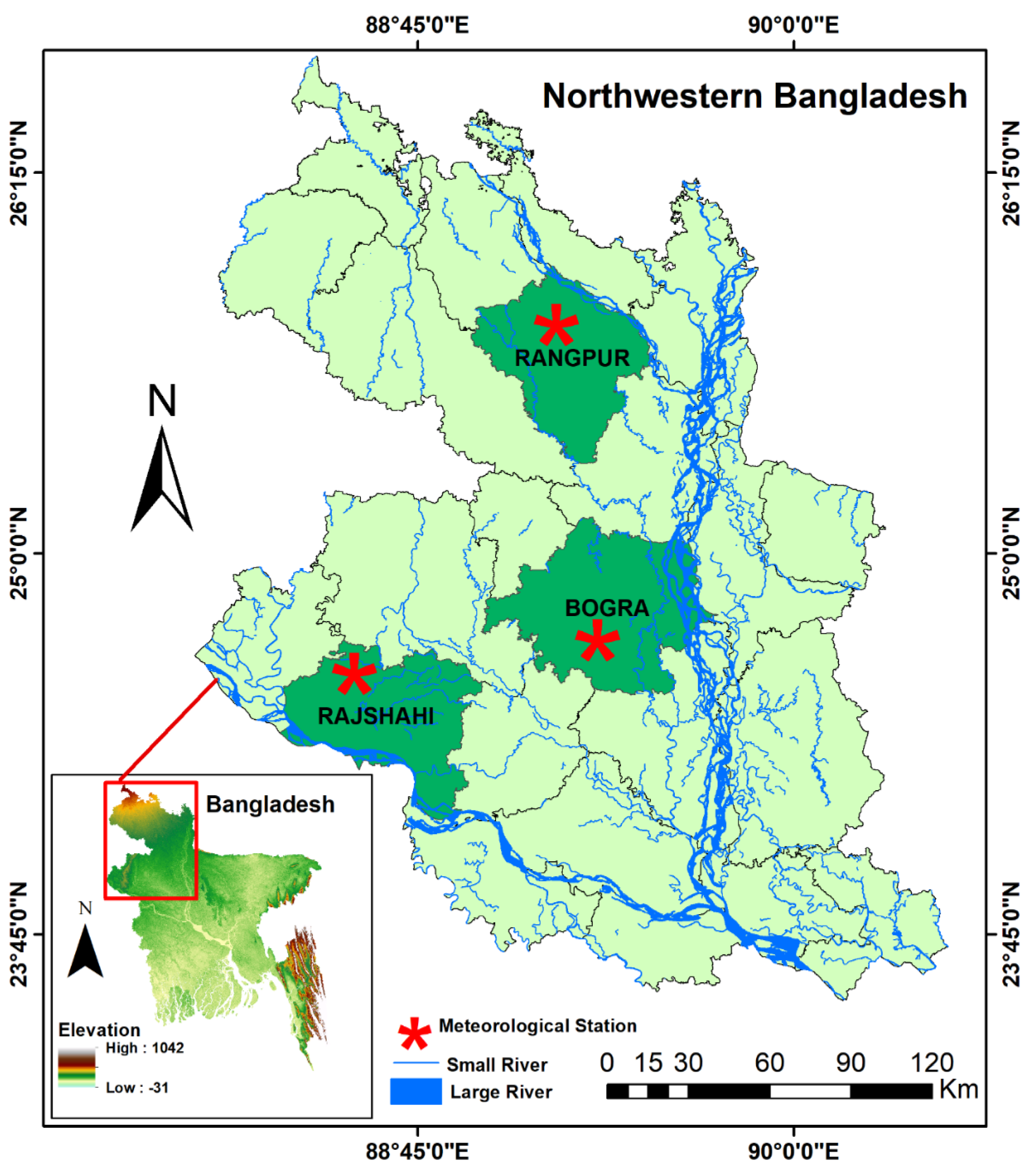
| Stations | Latitude (N) | Longitude (E) | Altitude (m) | Tmax (°C) | Tmin (°C) | Rs (MJm−2d−1) | Ra (MJm−2d−1) | U2 (ms−1) | Hr (%) | ETo (mmd−1) |
|---|---|---|---|---|---|---|---|---|---|---|
| Bogura | 24.85 | 89.37 | 17.90 | 29.91 | 21.04 | 16.69 | 32.84 | 1.06 | 78.14 | 3.69 |
| Rajshahi | 24.37 | 88.7 | 19.50 | 30.11 | 20.56 | 17.25 | 32.97 | 1.00 | 78.18 | 3.78 |
| Rangpur | 25.73 | 89.27 | 32.61 | 28.96 | 20.25 | 16.60 | 32.63 | 1.03 | 80.26 | 3.53 |
| SVR | 10 | |
| 0.1 | ||
| 0.01 | ||
| Kernel type | Radial bias function (RBF) | |
| PSO | Cognitive component () | 2 |
| Social component () | 2 | |
| Inertia weight | 0.2–0.9 | |
| GWO | decreased from 2 to 0 | |
| GSA | Initial gravitational constant | 100 |
| Search parameter | 20 | |
| PSOGWO | As in both PSO and GWO | |
| PSOGSA | As in both PSO and GSA | |
| All algorithms | Population | 25 |
| Number of iterations | 100 | |
| Number of runs for each algorithm | 8 |
| Input Combinations | Variables |
|---|---|
| (i) | Tmin, Tmax |
| (ii) | Tmin, Tmax, Ra |
| (iii) | Tmin, Tmax, Rs |
| (iv) | Tmin, Tmax, U2 |
| (v) | Tmin, Tmax, Ra, Rs |
| (vi) | Tmin, Tmax, Rs, U2 |
| (vii) | Tmin, Tmax, Ra, U2 |
| (viii) | Tmin, Tmax, Ra, Rs, U2 |
| (ix) | Tmin, Tmax, Ra, Rs, U2, HR |
| Models | Input Combinations | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | NSE | R2 | RMSE | MAE | NSE | R2 | ||
| SVR | I | 0.508 | 0.403 | 0.682 | 0.682 | 0.597 | 0.511 | 0.584 | 0.692 |
| II | 0.396 | 0.310 | 0.807 | 0.807 | 0.390 | 0.324 | 0.823 | 0.834 | |
| III | 0.209 | 0.154 | 0.946 | 0.946 | 0.432 | 0.316 | 0.782 | 0.875 | |
| IV | 0.395 | 0.307 | 0.808 | 0.821 | 0.470 | 0.332 | 0.743 | 0.749 | |
| V | 0.190 | 0.136 | 0.955 | 0.955 | 0.326 | 0.198 | 0.876 | 0.898 | |
| VI | 0.172 | 0.128 | 0.963 | 0.963 | 0.441 | 0.306 | 0.773 | 0.866 | |
| VII | 0.311 | 0.240 | 0.881 | 0.881 | 0.379 | 0.269 | 0.833 | 0.863 | |
| VIII | 0.147 | 0.107 | 0.974 | 0.974 | 0.373 | 0.250 | 0.838 | 0.891 | |
| IX | 0.100 | 0.073 | 0.988 | 0.988 | 0.352 | 0.232 | 0.856 | 0.912 | |
| SVR-PSO | I | 0.411 | 0.338 | 0.792 | 0.803 | 0.498 | 0.419 | 0.710 | 0.743 |
| II | 0.308 | 0.232 | 0.883 | 0.884 | 0.364 | 0.305 | 0.845 | 0.871 | |
| III | 0.182 | 0.133 | 0.959 | 0.960 | 0.398 | 0.290 | 0.815 | 0.888 | |
| IV | 0.317 | 0.240 | 0.877 | 0.877 | 0.430 | 0.312 | 0.784 | 0.792 | |
| V | 0.153 | 0.109 | 0.971 | 0.971 | 0.353 | 0.244 | 0.855 | 0.909 | |
| VI | 0.152 | 0.112 | 0.972 | 0.972 | 0.426 | 0.296 | 0.788 | 0.876 | |
| VII | 0.241 | 0.190 | 0.929 | 0.929 | 0.346 | 0.263 | 0.860 | 0.883 | |
| VIII | 0.127 | 0.096 | 0.980 | 0.980 | 0.420 | 0.318 | 0.794 | 0.905 | |
| IX | 0.097 | 0.071 | 0.988 | 0.989 | 0.335 | 0.222 | 0.869 | 0.923 | |
| SVR- PSOGSA | I | 0.369 | 0.293 | 0.832 | 0.833 | 0.490 | 0.391 | 0.720 | 0.761 |
| II | 0.238 | 0.183 | 0.930 | 0.930 | 0.368 | 0.291 | 0.842 | 0.916 | |
| III | 0.131 | 0.098 | 0.979 | 0.979 | 0.309 | 0.213 | 0.888 | 0.901 | |
| IV | 0.281 | 0.221 | 0.903 | 0.903 | 0.420 | 0.305 | 0.794 | 0.805 | |
| V | 0.127 | 0.093 | 0.980 | 0.980 | 0.283 | 0.181 | 0.907 | 0.919 | |
| VI | 0.118 | 0.083 | 0.983 | 0.983 | 0.472 | 0.367 | 0.740 | 0.890 | |
| VII | 0.215 | 0.170 | 0.943 | 0.943 | 0.304 | 0.216 | 0.892 | 0.893 | |
| VIII | 0.109 | 0.076 | 0.985 | 0.985 | 0.369 | 0.247 | 0.841 | 0.897 | |
| IX | 0.061 | 0.043 | 0.995 | 0.995 | 0.292 | 0.178 | 0.900 | 0.927 | |
| SVR- PSOGWO | I | 0.316 | 0.247 | 0.877 | 0.877 | 0.512 | 0.388 | 0.694 | 0.782 |
| II | 0.233 | 0.177 | 0.933 | 0.933 | 0.298 | 0.241 | 0.897 | 0.931 | |
| III | 0.148 | 0.109 | 0.973 | 0.973 | 0.330 | 0.219 | 0.873 | 0.898 | |
| IV | 0.283 | 0.222 | 0.902 | 0.902 | 0.390 | 0.278 | 0.823 | 0.832 | |
| V | 0.106 | 0.078 | 0.986 | 0.986 | 0.306 | 0.208 | 0.891 | 0.927 | |
| VI | 0.122 | 0.086 | 0.982 | 0.982 | 0.446 | 0.343 | 0.768 | 0.892 | |
| VII | 0.215 | 0.168 | 0.943 | 0.943 | 0.305 | 0.233 | 0.892 | 0.922 | |
| VIII | 0.113 | 0.082 | 0.984 | 0.984 | 0.301 | 0.212 | 0.894 | 0.929 | |
| IX | 0.061 | 0.042 | 0.995 | 0.995 | 0.277 | 0.167 | 0.911 | 0.933 | |
| Models | Input Combinations | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | NSE | R2 | RMSE | MAE | NSE | R2 | ||
| SVR | I | 0.345 | 0.266 | 0.892 | 0.892 | 0.550 | 0.414 | 0.717 | 0.856 |
| II | 0.307 | 0.231 | 0.914 | 0.914 | 0.454 | 0.320 | 0.807 | 0.883 | |
| III | 0.250 | 0.176 | 0.943 | 0.943 | 0.358 | 0.286 | 0.880 | 0.908 | |
| IV | 0.281 | 0.225 | 0.928 | 0.928 | 0.395 | 0.315 | 0.854 | 0.873 | |
| V | 0.213 | 0.144 | 0.959 | 0.959 | 0.319 | 0.226 | 0.909 | 0.919 | |
| VI | 0.324 | 0.258 | 0.905 | 0.905 | 0.454 | 0.363 | 0.807 | 0.843 | |
| VII | 0.293 | 0.236 | 0.922 | 0.922 | 0.393 | 0.318 | 0.855 | 0.864 | |
| VIII | 0.261 | 0.201 | 0.938 | 0.947 | 0.366 | 0.277 | 0.875 | 0.903 | |
| IX | 0.323 | 0.228 | 0.905 | 0.921 | 0.327 | 0.239 | 0.906 | 0.913 | |
| SVR-PSO | I | 0.306 | 0.231 | 0.915 | 0.915 | 0.527 | 0.400 | 0.740 | 0.872 |
| II | 0.260 | 0.191 | 0.939 | 0.939 | 0.431 | 0.336 | 0.826 | 0.906 | |
| III | 0.226 | 0.151 | 0.954 | 0.955 | 0.346 | 0.271 | 0.888 | 0.918 | |
| IV | 0.254 | 0.199 | 0.941 | 0.942 | 0.392 | 0.293 | 0.857 | 0.881 | |
| V | 0.208 | 0.143 | 0.961 | 0.961 | 0.290 | 0.226 | 0.921 | 0.936 | |
| VI | 0.182 | 0.138 | 0.970 | 0.970 | 0.315 | 0.246 | 0.907 | 0.920 | |
| VII | 0.266 | 0.209 | 0.936 | 0.936 | 0.345 | 0.261 | 0.889 | 0.911 | |
| VIII | 0.206 | 0.152 | 0.961 | 0.962 | 0.315 | 0.247 | 0.907 | 0.922 | |
| IX | 0.227 | 0.173 | 0.953 | 0.953 | 0.298 | 0.230 | 0.917 | 0.929 | |
| SVR- PSOGSA | I | 0.276 | 0.206 | 0.931 | 0.931 | 0.525 | 0.412 | 0.742 | 0.875 |
| II | 0.245 | 0.182 | 0.946 | 0.946 | 0.379 | 0.305 | 0.865 | 0.928 | |
| III | 0.186 | 0.121 | 0.969 | 0.969 | 0.302 | 0.210 | 0.915 | 0.932 | |
| IV | 0.223 | 0.175 | 0.955 | 0.955 | 0.377 | 0.279 | 0.867 | 0.893 | |
| V | 0.192 | 0.121 | 0.967 | 0.967 | 0.271 | 0.199 | 0.931 | 0.945 | |
| VI | 0.153 | 0.111 | 0.979 | 0.979 | 0.302 | 0.219 | 0.915 | 0.928 | |
| VII | 0.218 | 0.166 | 0.957 | 0.957 | 0.316 | 0.235 | 0.907 | 0.920 | |
| VIII | 0.134 | 0.096 | 0.984 | 0.984 | 0.241 | 0.144 | 0.946 | 0.947 | |
| IX | 0.092 | 0.052 | 0.992 | 0.992 | 0.252 | 0.147 | 0.941 | 0.944 | |
| SVR- PSOGWO | I | 0.264 | 0.197 | 0.937 | 0.937 | 0.496 | 0.385 | 0.770 | 0.884 |
| II | 0.243 | 0.177 | 0.946 | 0.946 | 0.389 | 0.316 | 0.859 | 0.939 | |
| III | 0.194 | 0.127 | 0.966 | 0.966 | 0.312 | 0.233 | 0.909 | 0.931 | |
| IV | 0.199 | 0.152 | 0.964 | 0.964 | 0.317 | 0.249 | 0.906 | 0.916 | |
| V | 0.180 | 0.112 | 0.971 | 0.971 | 0.255 | 0.188 | 0.939 | 0.943 | |
| VI | 0.130 | 0.088 | 0.985 | 0.985 | 0.274 | 0.184 | 0.930 | 0.936 | |
| VII | 0.199 | 0.148 | 0.964 | 0.964 | 0.298 | 0.228 | 0.917 | 0.933 | |
| VIII | 0.111 | 0.071 | 0.989 | 0.989 | 0.270 | 0.191 | 0.932 | 0.936 | |
| IX | 0.082 | 0.047 | 0.994 | 0.994 | 0.248 | 0.145 | 0.943 | 0.950 | |
| Models | Input Combinations | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | NSE | R2 | RMSE | MAE | NSE | R2 | ||
| SVR | I | 0.369 | 0.276 | 0.831 | 0.831 | 0.516 | 0.412 | 0.651 | 0.773 |
| II | 0.281 | 0.180 | 0.902 | 0.902 | 0.390 | 0.316 | 0.800 | 0.887 | |
| III | 0.240 | 0.169 | 0.929 | 0.929 | 0.352 | 0.230 | 0.838 | 0.878 | |
| IV | 0.348 | 0.254 | 0.850 | 0.850 | 0.446 | 0.331 | 0.739 | 0.787 | |
| V | 0.205 | 0.133 | 0.948 | 0.948 | 0.392 | 0.264 | 0.798 | 0.879 | |
| VI | 0.206 | 0.149 | 0.948 | 0.948 | 0.339 | 0.222 | 0.850 | 0.882 | |
| VII | 0.297 | 0.193 | 0.890 | 0.890 | 0.323 | 0.251 | 0.863 | 0.876 | |
| VIII | 0.171 | 0.111 | 0.964 | 0.964 | 0.306 | 0.179 | 0.877 | 0.890 | |
| IX | 0.139 | 0.086 | 0.976 | 0.976 | 0.246 | 0.143 | 0.920 | 0.923 | |
| SVR-PSO | I | 0.345 | 0.256 | 0.852 | 0.853 | 0.518 | 0.413 | 0.649 | 0.773 |
| II | 0.250 | 0.195 | 0.922 | 0.924 | 0.383 | 0.306 | 0.808 | 0.885 | |
| III | 0.228 | 0.159 | 0.936 | 0.938 | 0.320 | 0.231 | 0.866 | 0.896 | |
| IV | 0.286 | 0.234 | 0.898 | 0.905 | 0.416 | 0.325 | 0.773 | 0.793 | |
| V | 0.152 | 0.109 | 0.971 | 0.971 | 0.317 | 0.211 | 0.868 | 0.899 | |
| VI | 0.167 | 0.113 | 0.966 | 0.966 | 0.323 | 0.217 | 0.863 | 0.884 | |
| VII | 0.234 | 0.166 | 0.932 | 0.932 | 0.318 | 0.245 | 0.868 | 0.891 | |
| VIII | 0.135 | 0.100 | 0.977 | 0.977 | 0.299 | 0.184 | 0.883 | 0.909 | |
| IX | 0.099 | 0.064 | 0.988 | 0.988 | 0.228 | 0.145 | 0.932 | 0.936 | |
| SVR- PSOGSA | I | 0.253 | 0.198 | 0.921 | 0.921 | 0.490 | 0.383 | 0.685 | 0.793 |
| II | 0.235 | 0.183 | 0.932 | 0.932 | 0.389 | 0.316 | 0.802 | 0.888 | |
| III | 0.163 | 0.120 | 0.967 | 0.967 | 0.290 | 0.209 | 0.889 | 0.909 | |
| IV | 0.255 | 0.198 | 0.919 | 0.919 | 0.397 | 0.309 | 0.793 | 0.804 | |
| V | 0.089 | 0.062 | 0.990 | 0.990 | 0.238 | 0.169 | 0.926 | 0.945 | |
| VI | 0.106 | 0.078 | 0.986 | 0.986 | 0.296 | 0.192 | 0.885 | 0.904 | |
| VII | 0.149 | 0.109 | 0.973 | 0.973 | 0.323 | 0.251 | 0.863 | 0.895 | |
| VIII | 0.122 | 0.084 | 0.981 | 0.981 | 0.262 | 0.188 | 0.910 | 0.942 | |
| IX | 0.098 | 0.072 | 0.988 | 0.988 | 0.242 | 0.177 | 0.923 | 0.943 | |
| SVR- PSOGWO | I | 0.234 | 0.178 | 0.932 | 0.932 | 0.524 | 0.407 | 0.640 | 0.795 |
| II | 0.179 | 0.138 | 0.960 | 0.960 | 0.385 | 0.314 | 0.805 | 0.890 | |
| III | 0.150 | 0.109 | 0.972 | 0.972 | 0.294 | 0.210 | 0.886 | 0.918 | |
| IV | 0.204 | 0.157 | 0.948 | 0.948 | 0.391 | 0.295 | 0.800 | 0.825 | |
| V | 0.086 | 0.059 | 0.991 | 0.991 | 0.243 | 0.184 | 0.922 | 0.939 | |
| VI | 0.100 | 0.071 | 0.988 | 0.988 | 0.342 | 0.237 | 0.847 | 0.898 | |
| VII | 0.172 | 0.128 | 0.963 | 0.963 | 0.325 | 0.247 | 0.861 | 0.905 | |
| VIII | 0.106 | 0.070 | 0.986 | 0.986 | 0.278 | 0.203 | 0.899 | 0.939 | |
| IX | 0.041 | 0.029 | 0.998 | 0.998 | 0.200 | 0.132 | 0.948 | 0.951 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ikram, R.M.A.; Mostafa, R.R.; Chen, Z.; Islam, A.R.M.T.; Kisi, O.; Kuriqi, A.; Zounemat-Kermani, M. Advanced Hybrid Metaheuristic Machine Learning Models Application for Reference Crop Evapotranspiration Prediction. Agronomy 2023, 13, 98. https://doi.org/10.3390/agronomy13010098
Ikram RMA, Mostafa RR, Chen Z, Islam ARMT, Kisi O, Kuriqi A, Zounemat-Kermani M. Advanced Hybrid Metaheuristic Machine Learning Models Application for Reference Crop Evapotranspiration Prediction. Agronomy. 2023; 13(1):98. https://doi.org/10.3390/agronomy13010098
Chicago/Turabian StyleIkram, Rana Muhammad Adnan, Reham R. Mostafa, Zhihuan Chen, Abu Reza Md. Towfiqul Islam, Ozgur Kisi, Alban Kuriqi, and Mohammad Zounemat-Kermani. 2023. "Advanced Hybrid Metaheuristic Machine Learning Models Application for Reference Crop Evapotranspiration Prediction" Agronomy 13, no. 1: 98. https://doi.org/10.3390/agronomy13010098
APA StyleIkram, R. M. A., Mostafa, R. R., Chen, Z., Islam, A. R. M. T., Kisi, O., Kuriqi, A., & Zounemat-Kermani, M. (2023). Advanced Hybrid Metaheuristic Machine Learning Models Application for Reference Crop Evapotranspiration Prediction. Agronomy, 13(1), 98. https://doi.org/10.3390/agronomy13010098












