Abstract
Globally, croplands represent a significant contributor to climate change, through both greenhouse gas emissions and land use changes associated with cropland expansion. They also represent locations with significant potential to contribute to mitigating climate change through alternative land use management practices that lead to increased soil carbon sequestration. In spite of their global importance, there is a relative paucity of tools available to support field- or farm-level crop land decision making that could inform more effective climate mitigation practices. In recognition of this shortcoming, the Simple Algorithm for Yield Estimate (SAFY) model was developed to estimate crop growth, biomass, and yield at a range of scales from field to region. While the original SAFY model was developed and evaluated for winter wheat in Morocco, a key advantage to utilizing SAFY is that it presents a modular architecture which can be readily adapted. This has led to numerous modifications and alterations of specific modules which enable the model to be refined for new crops and locations. Here, we adapted the SAFY model for use with spring barley, winter wheat and winter oilseed rape at selected sites in Ireland. These crops were chosen as they represent the dominant crop types grown in Ireland. We modified the soil–water balance and carbon modules in SAFY to simulate components of water and carbon budgets in addition to crop growth and production. Results from the modified model were evaluated against available in situ data collected from previous studies. Spring barley biomass was estimated with high accuracy (R2 = 0.97, RMSE = 95.8 g·m−2, RRMSE = 11.7%) in comparison to GAI (R2 = 0.73, RMSE = 0.44 m2·m−2, RRMSE = 10.6%), across the three years for which the in situ data was available (2011–2013). The winter wheat module was evaluated against measured biomass and yield data obtained for the period 2013–2015 and from three sites located across Ireland. While the model was found to be capable of simulating winter wheat biomass (R2 = 0.71, RMSE = 1.81 t·ha−1, RRMSE = 8.0%), the model was found to be less capable of reproducing the associated yields (R2 = 0.09, RMSE = 2.3 t·ha−1, RRMSE = 18.6%). In spite of the low R2 obtained for yield, the simulated crop growth stage 61 (GS61) closely matched those observed in field data. Finally, winter oilseed rape (WOSR) was evaluated against a single growing season for which in situ data was available. WOSR biomass was also simulated with high accuracy (R2 = 0.99 and RMSE = 0.52 t·ha−1) in comparison to GAI (R2 = 0.3 and RMSE = 0.98 m2·m−2). In terms of the carbon fluxes, the model was found to be capable of estimating heterotrophic respiration (R2 = 0.52 and RMSE = 0.28 g·C·m−2·day−1), but less so the ecosystem respiration (R2 = 0.18 and RMSE = 1.01 g·C·m−2·day−1). Overall, the results indicate that the modified model can simulate GAI and biomass, for the chosen crops for which data were available, and yield, for winter wheat. However, the simulations of the carbon budgets and water budgets need to be further evaluated—a key limitation here was the lack of available in situ data. Another challenge is how to address the issue of parameter specification; in spite of the fact that the model has only six variable crop-related parameters, these need to be calibrated prior to application (e.g., date of emergence, effective light use efficiency etc.). While existing published values can be readily employed in the model, the availability of regionally derived values would likely lead to model improvements. This limitation could be overcome through the integration of available remote sensing data using a data assimilation procedure within the model to update the initial parameter values and adjust model estimates during the simulation.
1. Introduction
In Ireland, the dominant agricultural land use is grasslands (91%) with croplands representing less than 10% of the agriculture land [1]. The predominance of grassland is largely due to the near year-round conditions favorable for grass growth, associated with the mild maritime climate experienced here, which results in lower input costs for dairy production over other agricultural systems. Consequently, crop production is typically confined to the lighter soils and warmer and drier conditions associated with the east and south-east of Ireland. The main tillage area is dominated by cereal crops Spring Barley (Hordeum vulgare L.; hereafter referred to as SB) and Winter wheat (Triticum aestivum L.; WW). SB provides a valuable source for animal feed and the malting industries with a land area of 128,720 ha and an average yield of 7.2 t·ha−1 [2] and WW is the most economically viable crop grown here with an area of 60,400 ha and an average yield of 9.5 t·ha−1 [3]. Winter oilseed rape (Brassica napus L.; WOSR) is a more marginal crop, covering approximately 8500 hectares, with an average yield of 4.0 t·ha−1, and is typically grown as a break crop for WW. While the dominant contribution from agriculture to Ireland’s natural greenhouse gas emissions (GHG) comes from the dairy sector, reflecting its dominance in terms of area and economic activity, croplands represent a relatively small GHG source, mainly due to activities associated with cultivation and fertilizer use [4,5]. In spite of the relatively small impact to the overall national emissions, this sector has potential to make an important contribution to reducing agricultural emissions.
While process-based crop models are potentially useful tools for quantifying both production and carbon budgets [6,7,8,9], and how these relate to weather, climate and environmental conditions, there are challenges related to the application of these models at the regional level. These challenges are further compounded by a lack of readily available in situ data in order calibrate and evaluate these models. A number of crop models have been developed, which vary in terms of their driving mechanisms and complexity [10]. For example, GECROS [11] and SUCROS [12] are illustrative of carbon-focused models; radiation-based models include SAFY [13], SAFY-WB [14], STICS [15], CERES [16], and water focused models include AqYield [17] and Aquacrop [18]. This list is not exhaustive but represents some of the main crop models currently available for use, depending on application. In addition, these models are generally employed as research tools and require a level of expertise in order to employ them.
Models can be further classified depending on whether they simulate a crop using a generic approach or those that are specific to certain crops. For example, Aquacrop is a generic crop growth model that utilizes crop specific parameters. In contrast, SuMoToRI [19] and LINTUL-BRASNAP [20] are specific to a single crop type, namely WOSR. While the more general crop models, such as STICS and Aquacrop, have found widespread use they are relatively complex models and require a number of parameters to be calibrated prior to application; therefore their suitability for use at the regional level or in potentially data sparse regions is challenging [21,22]. As an alternative, simple semi-empirical models, such as the Simple Algorithm for Yield Estimate (SAFY) model [14], which require a reduced number of inputs and parameters, offer potential for more widespread use and application, can be readily applied, and are potentially suitable for scaling to the regional level. However, similar to all models, they require appropriate testing and evaluation. While a number of empirical and semi-empirical based models have been developed for specific crop types [23,24,25,26], the development of a ‘common’ model framework which is readily adaptable has been missing, therefore limiting their widespread use in new locations and/or for different crop types.
The SAFY crop model was originally developed by [13] and the model was initially evaluated on WW fields in dry land areas in Morocco. The basic version of the model simulated crop growth as green area index (GAI), dry above-ground matter (biomass) and dry grain matter (yield). Due to the simple model architecture, which is modular in design, the SAFY model has been widely adapted by the research community and applied in different environments and crops [24,27,28,29,30,31]. Refs. [14,24] added a soil–water balance module to simulate the effect of the water stress on the crop growth and production. Refs. [25,32] added a module to simulate the carbon budgets in addition to a soil–water balance module. Additional modifications have focussed on GAI, an important biophysical variable that can describe the crop growth and a state variable in the SAFY model. GAI can be measured on the ground by different sensors [33], collected by destructive sampling methods [33] or, can be retrieved from remote sensing data using empirical or process-based/hybrid methods [21,34,35]. For example, Refs. [29,31] integrated remote sensing data into the SAFY model to update the crop-state variable GAI during the assimilation process, leading to improved model estimates.
For the research presented here, we sought to evaluate the use of the SAFY model [13], with modified soil–water balance module [24,31] and carbon fluxes module [25,32] to simulate crop growth, biomass, grain yield and components of the water and carbon fluxes for the main crop types grown in Ireland and for which we had access to published or available in situ data. The decision to employ the specific model was based around the model architecture, which can be readily modified and adapted, and the limited number of parameters required to run the model. Given the model’s simplistic modelling approach, it has been successfully applied for estimation of crop growth, above ground biomass and grain yield using limited computational resources which is usually a challenge at spatial level application of complex crop models and makes it even more attractive for practical applications. In addition, the model offers the potential to use and deploy in an operational capacity, with limited user intervention. We also sought to contribute to the model development, through the addition of a new water stress function and modifications of components in the energy and carbon flux modules. The soil–water balance module, specifically the water stress function, is detailed in the methods section and latent heat is derived from the actual evapotranspiration in the context of the Irish soils that have been comparatively less studied. The modified model was then evaluated on three maincrop types in Ireland, namely WW, SB and WOSR. Thus, the objective of the work was to adapt a previously developed model, enhancing its capacity to be deployed in a broader range of applications, and evaluate the model for use in a maritime climate regime.
2. Materials and Methods
The input datasets, management data and model are described in the following sections.
2.1. Context
The island of Ireland experiences a mild maritime temperate climate associated with the westerly moisture-laden airflow off the North Atlantic [36]. Based on the daily mean climatology (1981–2010), the maximum temperature across the region is between 18 °C and 20 °C in summer, and winters are generally mild, around 8 °C; only occasionally do temperatures drop below 0 °C. Mean annual rainfall is approximately 1200 mm, distributed throughout the year. The higher rainfall amounts of 1000–1400 mm mainly occur in the west, associated with proximity to the ocean, and may exceed 2000 mm in the upland areas due to influence of topography. In contrast, the east experiences lower rainfall amounts of between 750–1000 mm. More details on the background climate of Ireland are provided in [37]. In the context of general soil information, the main tillage area in Ireland, located in the south-east, is characterized as mostly freely draining sandy soils, while the midlands and south are dominated by limestone rich soils, with peat soils dominate on the hills, mountains and the western fringes of the country [38].
2.2. Study Locations
In situ data, collated from previously published, and unpublished, studies, was available for five locations, representing SB, WW and WOSR. With the exception of the northern-most site located in Crossnacreevy, Co. Down, all sites are located in the main tillage growing areas along the east and south-east of Ireland (Figure 1). Field data for the SB site located in Duncormick County Wexford, included GAI and biomass for the period 2011–2013. For WW, yield data for the period 2013–2015 were available for three sites, located in Oakpark, County Carlow, Killeagh County Cork and Crossnacreevy, County Down (Northern Ireland), respectively. The WOSR experimental site, located in Gowran Co. Kilkenny, had measurements of GAI, biomass, and respiration data for the period 2015–2016. Table 1 outlines the main crop events for the selected study sites.
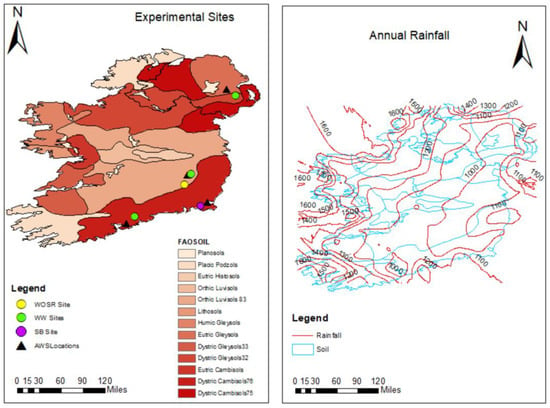
Figure 1.
Location of meteorological stations (AWS) and crop sites (WOSR, WW, SB) for which in situ data was available. Soil map (FAO-UNESCO) and annual precipitation isohyetal are presented in the background).

Table 1.
Crop, year, experimental sites, dates on sowing, emergence, harvest and senescence, and weather stations.
2.3. Evaluation Data: In Situ
The available in situ data, used to evaluate the model, were obtained from previous studies. For SB, measured GAI and biomass data for three years 2011–2013 was obtained for Duncormick, Co. Wexford, with an average yield of 8.5 t·ha−1 (850 g·m−2) [39]. Observed WW yield data and sowing dates were taken from [23]. These were used to evaluate the simulated biomass and yield data for WW for three sites (Table 2; Figure 1), WW growth stage GS61, which refers to stage of the start of flowering (first anthers visible) [3] in presented in Table 2. Evaluation data for WOSR at Gowran site were obtained from a previously published study [40].

Table 2.
Observed yield (Y), biomass (B), sowing dates and date of growth stage 61 (GS61) for the selected WW study sites and years and model estimated yield, biomass and GS61.
2.4. Site Soil Information
Soils in Ireland are comparatively young and very heterogeneous, are less studied and lack detailed information on soil properties, including water content, and soil profile information. Consequently, model-derived soil information was obtained from the global SoilGrids (https://soilgrids.org) (accessed on 17 November 2022) database [41]. SoilGrids produces global maps of soil properties using different machine learning approaches, trained on soil observation from 240,000 locations worldwide [42]. It contains estimates of soil textural properties (sand, silt, clay and bulk density) for six different depth intervals (to 100 cm) in addition to information on soil–water content at field capacity (FC), saturation (SAT) and permanent wilting point (PWP) [43,44,45], derived using pedo-transfer functions and the data are available at 1 km and 250 m. We obtained the soil texture information and soil–water parameters at 250 m for each available depth. For the purposes of the subsequent modelling and in the absence of site-specific soil information, we only consider the bulk soil properties. Therefore, we aggregated the available layers, using a weighted average, to derive a mean depth profile value for FC, SAT and PWP.
2.5. Meteorlogical Data
Daily meteorological data was obtained from Met Éireann, the Irish national meteorological service, for Ireland and from the UK Met Office Integrated Data Archive System (MIDAS) for Aldergrove, located in Northern Ireland. Daily maximum and minimum temperature, global radiation and precipitation were obtained for the years 2011–2013 for JC, 2013–2016 OP and 2013–2015 for AG, RP (Table 1). Reference evapotranspiration was derived based on the FAO-Penman Monteith equation.
2.6. Model Overview
A schematic overview of the model is presented in Figure 2. All the simulated components and related equations of the flowchart are described in the following sections.
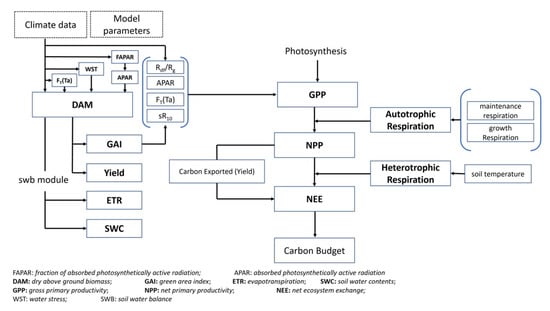
Figure 2.
Model Overview—Simulated fluxes are highlighted in bold.
The model framework used in this work was originally developed by [13] and was initially tested for WW. The original model is based on the Monteith light use efficiency (LUE) theory [46] and its relationship to biomass. Within the model, biomass is separated into leaf and non-leaf components using a partitioning function and specific leaf area is used to simulate crop growth. Grain yield is simulated using a rate of grain-filling parameter. The model simulates GAI, biomass, and yield on a daily time step, consistent with the driving meteorological inputs. The basic equations for simulating crop biomass and yield are shown in Equations (1)–(5). Equation (4a,c) shows the temperature stress function.
where, DAM is the daily accumulated biomass, APAR is the Absorbed photosynthetically active radiation computed as a product of the global radiation, climatic efficiency parameter and the fractional absorbed photosynthetic active radiation (FAPAR), calculated using Beer’s law. Equations (2) and (3) show the calculations for APAR and the use of Beer’s law. FT(Ta) is a temperature stress function (Equation (4a–4c), Ta is the mean air temperature, and WST is the water stress coefficient (Equation (11)) computed from the soil–water balance module. WST is not in the basic version of the SAFY model, it is added here to take water stress into account when estimating crop biomass.
where, Rg is the global radiation in Mj.m−2 and ϵc is a climatic efficiency parameter.
where, kext is the light extinction coefficient.
where, Topt is the optimal temperature for the crop, Tmin and Tmax are the minimum and maximum temperature thresholds beyond which crop growth ceases. Ta is the mean air temperature and β is the degree of the polynomial.
where, ΔYield is the daily change in yield and Py is a grain filling factor.
The soil–water balance module (SAFY-SW), adapted from [24,29], utilizes a simple ‘leaky bucket’ model to simulate soil–water balance and includes inputs in the form of precipitation, and losses, in the form of runoff, evapotranspiration (ETR) and deep percolation or drainage. The water balance model assumes no unsaturated flow, and capillary or upward flow only occurs as a result of soil evaporation. A root-growth sub-module was adapted for SAFY to aid the simulation of root water uptake, which is used to compute the plant transpiration [24,31]. Because of the availability of field specific soil information, Refs. [24,29,31] implemented the soil–water balance module for a 5-layer soil profile. We adapted the same architecture for estimating water movement in the soil and water stress during the growing season but utilizing the bulk soil information and a mean soil profile, due to the absence of site specific soil information. Equations (6)–(11) shows the equations in the soil–water balance module.
Potential evapotranspiration (PET) is computed as 1.1 times the equilibrium evaporation rate (EET), following [47] and EET is calculated using the Priestly-Taylor equilibrium equation, using albedo (α), global radiation (Rg) and daily mean temperature (Tavg). The Priestly–Taylor equation only requires a limited number of meteorological inputs.
PE is potential evaporation, PT is potential transpiration, and is computed based on the daily estimated GAI. Potential root water uptake (PRWU) is derived using Equation (10).
SW is the soil–water content, WP is water availability at wilting point and RLV is the root length density. The actual evapotranspiration (AET) is equal to PT, if PRWU is greater than or equal to PT, i.e., no water stress condition. Where PRWU is less then PT crop transpiration demand is not satisfied and the crop is considered to be experiencing water stress (WST), computed as the ratio of AET to PT.
An equation is also added to translate AET (in mm.day−1) to a latent heat (LH) flux in Watts/m2 Equation (12). This should enable the model to be compared to equivalent measurements obtained from a flux tower or similar instrument, if available at a site and is an important component of the energy balance.
A carbon flux module was previously implemented within the SAFY model. The approach estimates the Gross Primary Productivity (GPP) similar to Equation (1) with a modification to the ELUE parameter and inclusion of sR10, to account for the fraction of the green tissues in the senescence stage. Here, we replaced ELUE by fELUE, a product of ELUE and radiation use efficiency (RUE). RUE takes into account the diffuse fraction of radiation that is not usually considered in crop models, but studies have shown that RUE can be significant in the estimation of productivity; ignoring the parameter may lead to an inaccurate estimation of the fluxes. Equations (13)–(16) outline the equations used to derive GPP [25,32].
Rdf/Rg is highly correlated with the Rg/Ra where Rdf is the diffuse fraction of the radiation, Ra is the extra-terrestrial radiation and Rg is the global radiation downwards. Rdf/Rg is computed using the equations as suggested by [48].
Net Primary Productivity (NPP) is calculated as the difference between GPP and autotrophic respiration (Ra) [13], estimated following [49]. This approach separates Ra into two components—maintenance (Rm) and growth (Rg) respiration as shown in Equations (17)–(20) [25,32].
Net ecosystem exchange (NEE) is computed as the difference between NPP and heterotrophic respiration (Rh), calculated as follows
Ecosystem respiration (Reco) is calculated as the sum of autotrophic (Ra) and heterotrophic (Rh) respiration.
The list of all parameters employed in the model are outlined in the Supplementary Material Tables S1 and S2.
2.7. Model Evaluation
In order to determine if the model was capable of reproducing the available observations at the study locations, we employed a range of statistical measures. We used the R2, root mean square error (RMSE) and relative RMSE (RRMSE%) metrics to quantify the accuracy of the simulated variables with respect to the observed variables. The statistical metrics were computed in Python 3.6.5 environment. Observed/measured quantities are typically plotted on the x-axis, except where time (DOY) appears on the x-axis; simulated/estimated variables are plotted on the y-axis for figures provided in the results.
3. Results
3.1. Sping Barley
For the SB crop, there was close agreement between the simulated and measured GAI (R2 = 0.74–0.96, RMSE = 0.27–1.02 m2·m−2 and RRMSE = 6.5–24.9%) and biomass (R2 = 0.97–0.98, RMSE = 70.9–115.6 g·m−2 and RRMSE = 8.6–13.9%) over the three years (Figure 3a–f). The model performed best for GAI in 2011 and biomass in 2012. Mean model estimates of GAI and biomass were R2 = 0.73,RMSE = 0.44 m2·m−2 and RRMSE = 10.6% (Figure 4a) and R2 = 0.97, RMSE = 95.8 g·m−2 and RRMSE = 11.7% (Figure 4b), respectively.
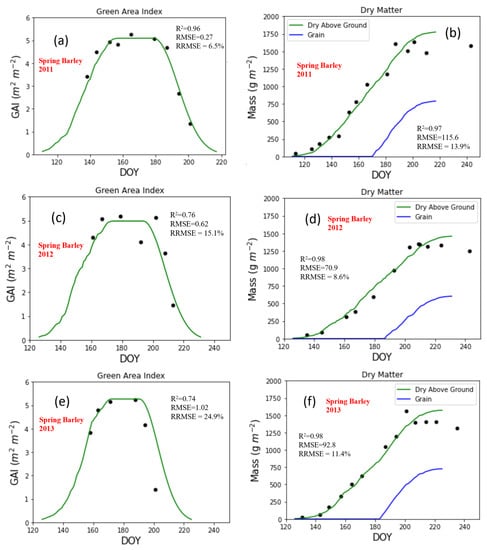
Figure 3.
Measured (black dots) and simulated (colored lines) for GAI (a,c,e), biomass & yield (b,d,f) for SB for 2011 (a,b), 2012 (c,d) and 2013 (e,f). DOY indicates day of year. Grain yield is plotted for illustrative purposes, no in situ data was available for this variable.
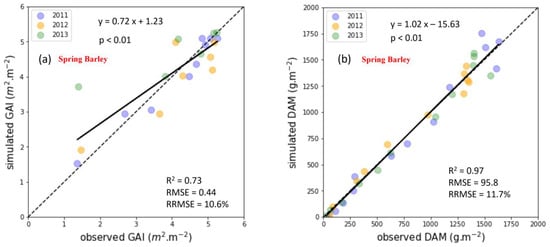
Figure 4.
Simulated and observed (a) GAI and (b) biomass for SB from selected sites for all years.
3.2. Winter Wheat
For WW, the model generates reasonable estimates of biomass accumulation (R2 = 0.71, RMSE = 1.81 t·ha−1 and RRMSE = 8.0%). In contrast, the model did not predict grain yield with any degree of accuracy (R2 = 0.09, RMSE = 2.33 t·ha−1 and RRMSE = 18.6%), with estimated values showing wide variation between years (Figure 5a,b biomass and grain yield). If two anomalous observations from Crossnacreevy and Carlow are removed, the model fit for yield becomes statistically significant (R2 = 0.85, p < 0.004). However, as we do not have access to the raw data it is not possible to exclude these values just to improve the model fit. The model estimated date for growth stage GS61, along with the observed date, is presented in Table 2. The model estimated date for growth stage GS61 ranges from between 0.5% to 12% difference, relative to the observed dates.
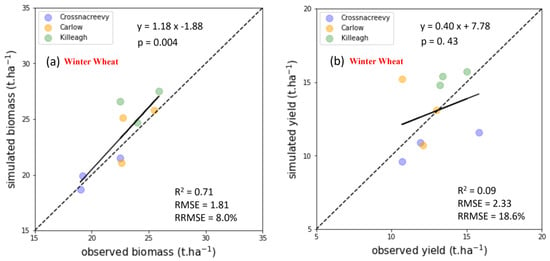
Figure 5.
(a) Simulated and measured biomass; and (b) simulated and observed yield for WW crop. Different sizes indicate different years smallest size indicate 2013 and the largest point represents 2015 year. Different counties are represented with different colors as outlined in the legend.
3.3. Winter Oilseed Rape
For WOSR, there was close agreement between the observed and simulated biomass (R2 = 0.99 and RMSE = 0.52 t·ha−1) but the model performed less well for predicting GAI (Figure 6a) (R2 = 0.30 and RMSE = 0.98 m2·m−2) (Figure 6b). As there were limited available measurements of respiration for this crop and site, we were able to undertake a preliminary evaluation of the model for these variables. The comparisons between observed and simulated ecosystem respiration (Reco) and soil respiration (Rh) are shown in Figure 7a,b, respectively. The model was found to systematically overestimate Reco and resulted in a spread in model estimated values, relative to the observations, which is reflected in the poor evaluation metric scores (R2 = 0.18 and RMSE = 1.01 g·C·m−2·day−1). However, good agreement was found between the measured and estimated Rh (R2 = 0.52 and RMSE = 0.28 g·C·m−2·day−1) over the six-month period in 2016 for which observations were available. The simulated Reco and observed Rh showed similar ranges from January to March, however, simulated Reco values exceeded Rh values by up to 3-fold from April to June.
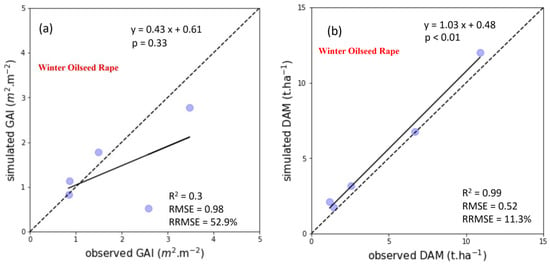
Figure 6.
Simulated and observed (a) GAI, (b) biomass.
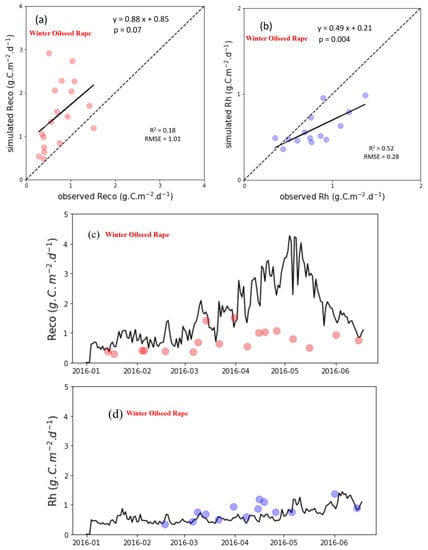
Figure 7.
(a) Simulated and observed ecosystem respiration (Reco); and (b) simulated and observed heterotrophic respiration (Rh). In (c), the black line represents the dynamics of the ecosystem respiration (Reco) and red points observed values; in (d) the black line shows the simulated heterotrophic respiration (Rh) values and blue points represents observed heterotrophic respiration.
4. Discussion
Here, the original SAFY model framework was adapted to include a modified soil–water balance and carbon fluxes module to simulate crop growth, biomass and yield, and components of the water, energy and carbon budgets. The soil–water balance module adapted in this work was modified to a single layer soil profile to represent mean soil profile in the absence of the site specific information- while this represents a simplification, it is unlikely that many potential study locations would have access to detailed soil profile information and thus represents a pragmatic approach. The modified model was applied to selected locations in Ireland for which there was previously published crop data available, specifically for SB, WW and WOSR. The crop model was subsequently evaluated against the available measurements obtained from these sources and studies [23,39,40].
4.1. Spring Barley (SB)
The model simulates the crop growth, biomass, and yield from the day of emergence to the day of complete senescence (Figure 3a–3f). The performances for simulating the above ground biomass and GAI are within the range of those of other studies. [50] implemented the SAFY model to estimate barley yield in a semi-arid region in Central Tunisia and obtain a good correlation between the measured and simulated yield with R2 = 0.77. The model fit was attributed to the integration of the in-season SPOT/HRV remote sensing data and the local calibration of the most sensitive model parameters. In the study [51] barley biomass was estimated with an R2 ranging from 0.39 to 0.68 and RMSE ranging from 0.42 kg·m−2–0.83 kg·m−2 (420 g·m−2–830 g·m−2) using the crop surface models—generated by (a) mosaicking of collected UAV images (b) point cloud generation (c) digital surface model (DSM) export, the main limiting factors were attributed to the four lodging cultivars 10,11,12,14. Ref. [52] employed the Sirius wheat model to estimate SB biomass and yield; their model simulated biomass with an RMSE = 1.4 t·ha−1 (140 g·m−2) and yield with an RMSE = 1.3 t·ha−1(130 g·m−2). The model was also able to simulate the differences in barley growth due to its mechanistic treatment of canopy development. Ref. [53] assessed the performance of nine different process-based crop models during 44 growing seasons of barley in northern and central Europe. Large uncertainties were found in estimating barley yield across sites and years, while the mean predictions from the nine models agreed well with the observations, the uncertainties were attributed to limited calibration of the models. In terms of simulated total above-ground biomass, models followed a slightly different order compared to the simulation of grain yields. Ref. [54] estimated biomass with median R2 = 0.62; RMSE = 1.63 t·ha−1 (163 g·m−2); nRMSE = 14.9% and LAI with median R2 = 0.92; RMSE = 0.3 m2·m−2; nRMSE = 7.1% for barley crop at three sites in Germany using the remote sensing and random forest modeling approach, LAI could be predicted with high accuracy because of the strong correlation of reflectance in the visible spectrum and leaf pigments per area.
Our modeling approach was found to be statistically significant (p < 0.01) for simulating biomass and GAI (Figure 4a,b); there are a few parameters that are variable and need to be manually fixed before its application, the date of sowing is one of them. Date of sowing SB in 2011 was 25 March and 3 April in 2012 and 2013. As illustrated in Figure 3a–f the simulated date of emergence is DOY 100, which represents 10 April. The simulated date of emergence for 2012 and 2013 is DOY 125 or 25 April, calibrating this parameter is important as the model starts simulating fluxes from the day of emergence. Where the actual date of sowing can be specified within the model, the model is clearly capable of simulating GAI and biomass (e.g., Figure 3) for SB. Biomass was simulated with high accuracy for all three years of available data; however the accuracy was somewhat compromised in estimating GAI. GAI is estimated using the leaf partitioning coefficients (Pla and Plb) on biomass. This indicates that the sensitive parameters need to be calibrated locally or inferred from remote sensing data. Error may also have been introduced in obtaining the measurements of GAI on the ground, specifically for the year 2012, where the unusual measurement is clearly visible (Figure 3c). In comparison to studies [51,52,53,54,55] the model adapted in this work was found to perform reasonably in simulating biomass during all the crop growth stages (Figure 3a–f). Simulated grain yield was estimated to between 6–8 t·ha−1 (600–800 g·m−2); the average reported yield from the field experiments for the period for which data was available is 8.5 t·ha−1 (850 g·m−2). The model simulated grain yield is close to the observed grain yield. In our study we used a constant value of 0.6 to estimate the grain yield from the above ground biomass. Calibrated values of this parameter would likely result in improved model estimates.
4.2. Winter Wheat (WW)
The model was subsequently applied to WW crop for three sites over the period 2013–2015—including Crossnacreevy, Carlow and Kileagh. Grain yield is derived by multiplying the daily biomass with the grain filling factor which is assumed to be a constant 0.6 for this study. In our validation for WW crop there are two observations of the grain yield that cause high errors, and if these two observations are removed, then our model shows high correlation with the observed values and becomes statistically significant (R2 = 0.85, p < 0.01), As we do not have access to the ground collected raw data, we could not assess the quality of these data points and so cannot simply remove the observation to improve the model accuracy. There are two other possibilities for the low accuracy achieved in estimating grain yield through this approach, first the grain filing factor constant value may not be representative and requires further investigation; the other possible reason may be the lack of available data to more robustly evaluate the model. [23] developed a winter wheat yield potential model (WWYPM) for different sites in Ireland and evaluated against WW crop yield. They obtained an R2 = 0.37 for biomass and R2 = 0.19 for yield. The model adapted in this work represents an improvement for biomass, but with a lower R2 for yield, which was also poorly estimated in [23]. It is clear that the model estimate for WW yield specifically needs to be investigated further and evaluated, subject to alternative in situ data becoming available. In spite of the poorer model performance for yield, the estimated timing of GS61 closely matched the available observations (Table 2). The % differential ranges from 0.5–12% with respect to the GS61 stage of WW (data not shown). [21] calibrated the Aquacrop model parameters for wheat using the canopy cover derived from the Venµs satellite images for the crop season 2017–2018 and found R2 = 0.51; RMSE = 683 g·m−2; RRMSE = 68.45% for biomass and R2 = 0.11; RMSE = 151 g·m−2 RRMSE = 26.9% for grain yield on validating Aquacrop model for 2018–2019 year on wheat fields in Maccarse, Italy. Ref. [31] estimated wheat yield with R2 = 0.66 by integrating crop model with the Sentinel-2 remote sensing data. Ref. [13] applied the basic SAFY model to the WW crop in Haouz plain, Marrakech city and found that the model underestimated yield by almost 0.5–0.9 t·ha−1 when compared to field measurements, which they attributed to differences in growing conditions between the plots used for calibration and evaluation. Ref. [30] integrated in-season remote sensing data into the SAFY model to improve the GAI, biomass and yield estimates. The model was applied to three different years 2013–2015 for WW crop in China, the study found 20%, 17%, and 15% RRMSE on validation with measured yield estimates, averaging to 18% over the three years studied, which is similar to what we found in our work (18.6%).
4.3. Winter Oil Seed Rape (WOSR)
In situ data were also available for WOSR at Gowran, Co. Kilkenny. The crop was sown in September 2015 and harvested the following year in August 2016 [40]. A benefit of this site was the availability of both ecosystem and heterotrophic respiration. Ref. [56] assimilated optical and SAR data into the SAFY model for the estimation of GAI and biomass for rapeseed over three years in France, the model making use of the in-season remote sensing data derived GAI from Sentinel-1, Sentinel-2 and Landsat-8 simulated GAI with R2 ranging from 0.84–0.92 and RRMSE from 28–41%. Our modeling approach represents an improvement in simulating biomass but not GAI, the reason maybe as described above, local calibration of partitioning coefficients (Supplementary Materials, Table S2) that partitions biomass into leaf and non-leaf biomass. Daily GAI growth and senescence is derived by multiplying daily biomass with the leaf partitioning coefficients (PLa and PLb) and specific leaf area parameter. In the assimilation approach these parameters and the other variable parameters (Supplementary Material) can be optimized with in-season remote sensing data. Ref. [57] estimated rapeseed LAI using the empirical equations on UAV multispectral images at different growth stages, the study concludes that LAI estimation at seedling and flowering stages have high errors in comparison to the elongation stage and it may also be a probable reason for the underestimation of GAI single point observation in our work (Figure 6a). The carbon fluxes module of the model simulated the components of the carbon budgets. Due to lack of observed data, we have compared the modelled simulated ecosystem respiration that includes aboveground autotrophic and soil respiration with the observed ecosystem soil respiration. The soil chambers used in the study were inserted into the interrow spacing between the plants but did not include plants, therefore CO2 flux consisted predominantly of heterotrophic respiration with a minor contribution of autotrophic root respiration. The large difference in CO2 emissions between the modelled respiration and measured soil respiration values thus can be attributed to the aboveground autotrophic respiration not captured by the soil chambers (Figure 7a,c). Soil respiration was also measured in bare soil without vegetation to quantify CO2 emissions only of heterotrophic origin. In contrast, the model simulated heterotrophic respiration was compared with the observed heterotrophic respiration and a low error with improved correlation was found compared to the ecosystem respiration model (Figure 7b,d). Ref. [25] simulated the components of the carbon budget for sunflower in France, the study shows ecosystem respiration was simulated with R2 = 0.83 and RMSE = 0.96 g·C·m2·day−1, higher than that found in this study. Additional evaluation data are required to confirm if the model is capable of producing more reliable estimates of ecosystem respiration. In a previous study [58], the CERES model was evaluated at several European flux sites, the model estimated components of carbon budget with RMSE = 30 g·C·m2·day−1. In the present study, heterotrophic respiration is somewhat underestimated in comparison to the observed heterotrophic respiration as it will be limited by temperature, moisture and C substrate (Figure 7b).
Overall, the model was found to estimate biomass across all crops and sites. Biomass is a function of APAR, ELUE and is constrained by both temperature (FTTa) and water (WST) stress. However, there are some uncertainties in simulating GAI and yield. For the simulation of GAI, the best model estimates were associated with SB, likely due to the availability of an optimal suite of model parameters for this crop. However, for WW and WOSR the parameter information was insufficient or not available and consequently lead to some uncertainties in simulating GAI. For yield, the harvest index or grain filling factor needs to be calibrated based on available data.
In this work, we found that the model effectively simulates the crop growth, biomass, yield and components of the carbon budgets. However, there are some challenges related to the calibration of the model sensitive parameters. More validation data is required to test the model for different crops and years. In the case of the non-availability of the calibration data and upscaling the model, multi-source remote sensing data can be included into the model, such as [24,29,30,31]. There are available a few generic crop models that allows simulating growth, biomass and yield for multiple crops, example Aquacrop [18], STICS [15] etc., but are computationally expensive and requires calibration for a large number of parameters, which is usually not possible. In comparison, the model in our work has a limited number of required parameters, is not computationally expensive to run and can be readily adapted as a common tool and deployed in a larger application for simulating crop components, water and carbon fluxes for multiple crops and geographical locations. The model is modular in nature and existing modules can be modified, new modules can be added further enhancing the capabilities of the model, For example, the adapted model can be integrated with the biogeochemical DNDC model to estimate the carbon stocks or the model can be applied to grasslands and forestry applications with some modifications to simulate the canopy gas exchange in the forest ecosystems.
5. Conclusions
In this work, we applied the simple crop model SAFY to both spring and winter crops in Ireland. We modified the soil–water balance and CO2 fluxes modules to estimate the water, energy, and carbon budgets along with the crop growth, biomass, and yield at selected study sites. The modified model was evaluated against available in situ data for spring barley, winter wheat and winter oilseed rape. Overall, we found that the model was capable of simulating crop growth (GAI) and biomass. While the model also simulates components of the water, energy, and carbon budgets, we could not validate these at the study sites due to lack of observations. We do intend to evaluate the energy, water, and CO2 components at available flux tower sites as part of future work.
The model was found to perform poorly in simulating grain yield; there may be two main reasons for this, the lack of validation data and the constant value employed for the grain-filling factor–ideally this should be calibrated from the ground values. There are a limited number of model parameters that require calibration prior to application: date of emergence and effective light use efficiency are two of them. In the absence of measured values, the use of remote sensing data obtained during the crop season can be employed, which removes the need to manually set the parameters, as these can be optimized using data assimilation techniques. As part of the continued development of the model, we aim to integrate remote sensing data-derived information into the model for the spatial application of the model.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/agronomy12112900/s1, Table S1: fix crop model parameters; Table S2: variable crop model parameters.
Author Contributions
Conceptualization, D.U. and R.F.; methodology, D.U. and R.F.; software, D.U.; validation, D.U. and M.O.; formal analysis, D.U.; investigation, D.U.; resources, D.U. and R.F.; data curation, D.U.; writing—draft preparation and review, D.U. and R.F.; writing contributions, K.I. and M.O.; visualization, D.U.; supervision, R.F.; project administration, R.F. and T.M.; funding acquisition, R.F. and T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This material is based upon works supported by Terrain-AI (SFI 20/SPP/3705) which is funded under the Science Foundation Ireland Strategic Partnership Programme.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
The meteorological data used in this study was downloaded from Met Eireann Ireland (https://www.met.ie/climate/available-data/historical-data) (accessed on 17 November 2022). This data is freely accessible. The model parameters are provided in the Supplementary Materials. For validation data, interested user is recommended to contact related researchers on their published studies. For the modelling work and source code, a request can be made to the authors (deepak.upreti@mu.ie).
Acknowledgments
We thank Met Eireann, Ireland and MIDAS, UK for providing the required meteorological data to run the model simulations. We thank Shane Kennedy for measurements of GAI and Biomass for Spring Barley crop for the years 2011–2013. We also thank Teagasc for having information on the winter wheat yield for the years 2013–2015.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zimmermann, J.; Lydon, K.; Packham, I.; Smith, G.; Green, S. The Irish Land-Parcels Identification System (LPIS)–Experiences in Ongoing and Recent Environmental Research and Land Cover Mapping. R. Ir. Acad. 2016, 116, 53–62. [Google Scholar] [CrossRef]
- Spink, J.; Hennessy, M.; Lynch, J.; O’Donovan, T.; Forristal, D.; Hackett, R.; Kildea, S.; Glynn, L.; Hickey, C.; Kennedy, S.; et al. The Spring Barley Guide; Teagasc Agriculture and Food Development Authority: Carlow, Ireland, 2018; Available online: https://www.teagasc.ie/publications/2015/the-spring-barley-guide.php (accessed on 17 November 2022).
- Lynch, J.; Spink, J.; Doyle, D.; Hackett, R.; Phelan, S.; Forristal, D.; Kildea, S.; Glynn, L.; Plunkett, M.; Wall, D.; et al. The Winter Wheat Guide; Teagasc Agriculture and Food Development Authority: Carlow, Ireland, 2016; p. 40. Available online: https://www.teagasc.ie/publications/2016/the-winter-wheat-guide.php (accessed on 17 November 2022).
- Emmet-Booth, J.P.; Dekker, S.; O’Brien, P. Climate Change Mitigation and the Irish Agriculture and Land Use Sector; Working Paper on Climate Change Advisory Council: Dublin, Ireland, 2019. [Google Scholar]
- Ciais, P.; Gervois, S.; Vuichard, N.; Piao, S.; Viovy, N. Effects of Land Use Change and Management on the European Cropland Carbon Balance. Glob. Change Biol. 2011, 17, 320–338. [Google Scholar] [CrossRef]
- Brilli, L.; Bechini, L.; Bindi, M.; Carozzi, M.; Cavalli, D.; Conant, R.; Dorich, C.D.; Doro, L.; Ehrhardt, F.; Farina, R. Review and Analysis of Strengths and Weaknesses of Agro-Ecosystem Models for Simulating C and N Fluxes. Sci. Total Environ. 2017, 598, 445–470. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Yu, Y.; Zhang, W.; Sun, W.; Liu, S.; Jiang, J.; Wu, J.; Yu, W.; Wang, Y.; Yang, Z. Agro-C: A Biogeophysical Model for Simulating the Carbon Budget of Agroecosystems. Agric. For. Meteorol. 2009, 149, 106–129. [Google Scholar] [CrossRef]
- Wattenbach, M.; Sus, O.; Vuichard, N.; Lehuger, S.; Gottschalk, P.; Li, L.; Leip, A.; Williams, M.; Tomelleri, E.; Kutsch, W.L. The Carbon Balance of European Croplands: A Cross-Site Comparison of Simulation Models. Agric. Ecosyst. Environ. 2010, 139, 419–453. [Google Scholar] [CrossRef]
- Zhang, X.; Izaurralde, R.C.; Manowitz, D.H.; Sahajpal, R.; West, T.O.; Thomson, A.M.; Xu, M.; Zhao, K.; LeDuc, S.D.; Williams, J.R. Regional Scale Cropland Carbon Budgets: Evaluating a Geospatial Agricultural Modeling System Using Inventory Data. Environ. Model. Softw. 2015, 63, 199–216. [Google Scholar] [CrossRef]
- Rauff, K.O.; Bello, R. A Review of Crop Growth Simulation Models as Tools for Agricultural Meteorology. Agric. Sci. 2015, 6, 1098. [Google Scholar] [CrossRef]
- Xinyou, Y.; Van Laar, H. Crop Systems Dynamics: An Ecophysiological Simulation Model of Genotype-by-Environment Interactions; Wageningen Academic Publishers: Wageningen, The Netherlands, 2005; ISBN 90-76998-55-8. [Google Scholar]
- Van Laar, H.H. Simulation of Crop Growth for Potential and Water-Limited Production Situations: As Applied to Spring Wheat. 1992. Available online: https://library.wur.nl/WebQuery/wurpubs/fulltext/359573 (accessed on 17 November 2022).
- Duchemin, B.; Maisongrande, P.; Boulet, G.; Benhadj, I. A Simple Algorithm for Yield Estimates: Evaluation for Semi-Arid Irrigated Winter Wheat Monitored with Green Leaf Area Index. Environ. Model. Softw. 2008, 23, 876–892. [Google Scholar] [CrossRef]
- Duchemin, B.; Fieuzal, R.; Rivera, M.A.; Ezzahar, J.; Jarlan, L.; Rodriguez, J.C.; Hagolle, O.; Watts, C. Impact of Sowing Date on Yield and Water Use Efficiency of Wheat Analyzed through Spatial Modeling and FORMOSAT-2 Images. Remote Sens. 2015, 7, 5951–5979. [Google Scholar] [CrossRef]
- Brisson, N.; Gary, C.; Justes, E.; Roche, R.; Mary, B.; Ripoche, D.; Zimmer, D.; Sierra, J.; Bertuzzi, P.; Burger, P. An Overview of the Crop Model STICS. Eur. J. Agron. 2003, 18, 309–332. [Google Scholar] [CrossRef]
- Mackinnon, J.C. CERES-Maize: A Simulation Model of Maize Growth and Development: C.A. Jones and J.R. Kiniry (Editors). Texas A&M University Press, College Station, TX, 1986. 194 Pp., US$33.50. ISBN 0-89096-269-3. Comput. Electron. Agric. 1987, 2, 171–172. [Google Scholar] [CrossRef]
- Constantin, J.; Willaume, M.; Murgue, C.; Lacroix, B.; Therond, O. The Soil-Crop Models STICS and AqYield Predict Yield and Soil–water Content for Irrigated Crops Equally Well with Limited Data. Agric. For. Meteorol. 2015, 206, 55–68. [Google Scholar] [CrossRef]
- Steduto, P.; Hsiao, T.C.; Raes, D.; Fereres, E. AquaCrop—The FAO Crop Model to Simulate Yield Response to Water: I. Concepts and Underlying Principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef]
- Brunel-Muguet, S.; Mollier, A.; Kauffmann, F.; Avice, J.-C.; Goudier, D.; Sénécal, E.; Etienne, P. SuMoToRI, an Ecophysiological Model to Predict Growth and Sulfur Allocation and Partitioning in Oilseed Rape (Brassica napus L.) until the Onset of Pod Formation. Front. Plant Sci. 2015, 6, 993. [Google Scholar] [CrossRef] [PubMed]
- Habekotte, B. Evaluation of Seed Yield Determining Factors of Winter Oilseed Rape (Brassica napus L.) by Means of Crop Growth Modelling. Field Crops Res. 1997, 54, 137–151. [Google Scholar] [CrossRef]
- Upreti, D.; Pignatti, S.; Pascucci, S.; Tolomio, M.; Huang, W.; Casa, R. Bayesian Calibration of the Aquacrop-OS Model for Durum Wheat by Assimilation of Canopy Cover Retrieved from VENµS Satellite Data. Remote Sens. 2020, 12, 2666. [Google Scholar] [CrossRef]
- Upreti, D.; Pignatti, S.; Pascucci, S.; Tolomio, M.; Li, Z.; Huang, W.; Casa, R. A Comparison of Moment-Independent and Variance-Based Global Sensitivity Analysis Approaches for Wheat Yield Estimation with the Aquacrop-OS Model. Agronomy 2020, 10, 607. [Google Scholar] [CrossRef]
- Lynch, J.; Fealy, R.; Doyle, D.; Black, L.; Spink, J. Assessment of Water-Limited Winter Wheat Yield Potential at Spatially Contrasting Sites in Ireland Using a Simple Growth and Development Model. Ir. J. Agric. Food Res. 2017, 56, 65–76. [Google Scholar] [CrossRef]
- Kang, Y.; Özdoğan, M. Field-Level Crop Yield Mapping with Landsat Using a Hierarchical Data Assimilation Approach. Remote Sens. Environ. 2019, 228, 144–163. [Google Scholar] [CrossRef]
- Pique, G.; Fieuzal, R.; Debaeke, P.; Al Bitar, A.; Tallec, T.; Ceschia, E. Combining High-Resolution Remote Sensing Products with a Crop Model to Estimate Carbon and Water Budget Components: Application to Sunflower. Remote Sens. 2020, 12, 2967. [Google Scholar] [CrossRef]
- Shirley, R.; Pope, E.; Bartlett, M.; Oliver, S.; Quadrianto, N.; Hurley, P.; Duivenvoorden, S.; Rooney, P.; Barrett, A.B.; Kent, C. An Empirical, Bayesian Approach to Modelling Crop Yield: Maize in USA. Environ. Res. Commun. 2020, 2, 025002. [Google Scholar] [CrossRef]
- Claverie, M.; Demarez, V.; Duchemin, B.; Hagolle, O.; Ducrot, D.; Marais-Sicre, C.; Dejoux, J.-F.; Huc, M.; Keravec, P.; Béziat, P. Maize and Sunflower Biomass Estimation in Southwest France Using High Spatial and Temporal Resolution Remote Sensing Data. Remote Sens. Environ. 2012, 124, 844–857. [Google Scholar] [CrossRef]
- Silvestro, P.C.; Pignatti, S.; Yang, H.; Yang, G.; Pascucci, S.; Castaldi, F.; Casa, R. Sensitivity Analysis of the Aquacrop and SAFYE Crop Models for the Assessment of Water Limited Winter Wheat Yield in Regional Scale Applications. PLoS ONE 2017, 12, e0187485. [Google Scholar] [CrossRef] [PubMed]
- Silvestro, P.C.; Casa, R.; Hanuš, J.; Koetz, B.; Rascher, U.; Schuettemeyer, D.; Siegmann, B.; Skokovic, D.; Sobrino, J.; Tudoroiu, M. Synergistic Use of Multispectral Data and Crop Growth Modelling for Spatial and Temporal Evapotranspiration Estimations. Remote Sens. 2021, 13, 2138. [Google Scholar] [CrossRef]
- Silvestro, P.; Pignatti, S.; Pascucci, S.; Yang, H.; Li, Z.; Yang, G.; Huang, W.; Casa, R. Estimating Wheat Yield in China at the Field and District Scale from the Assimilation of Satellite Data into the Aquacrop and Simple Algorithm for Yield (SAFY) Models. Remote Sens. 2017, 9, 509. [Google Scholar] [CrossRef]
- Pignatti, S.; Casa, R.; Laneve, G.; Li, Z.; Liu, L.; Marzialetti, P.; Mzid, N.; Pascucci, S.; Silvestro, P.C.; Tolomio, M. Sino–EU Earth Observation Data to Support the Monitoring and Management of Agricultural Resources. Remote Sens. 2021, 13, 2889. [Google Scholar] [CrossRef]
- Pique, G.; Fieuzal, R.; Al Bitar, A.; Veloso, A.; Tallec, T.; Brut, A.; Ferlicoq, M.; Zawilski, B.; Dejoux, J.-F.; Gibrin, H. Estimation of Daily CO2 Fluxes and of the Components of the Carbon Budget for Winter Wheat by the Assimilation of Sentinel 2-like Remote Sensing Data into a Crop Model. Geoderma 2020, 376, 114428. [Google Scholar] [CrossRef]
- Casa, R.; Upreti, D.; Pelosi, F. Measurement and Estimation of Leaf Area Index (LAI) Using Commercial Instruments and Smartphone-Based Systems; IOP Publishing: Bristol, UK, 2019; Volume 275, p. 012006. [Google Scholar] [CrossRef]
- Upreti, D.; Huang, W.; Kong, W.; Pascucci, S.; Pignatti, S.; Zhou, X.; Ye, H.; Casa, R. A Comparison of Hybrid Machine Learning Algorithms for the Retrieval of Wheat Biophysical Variables from Sentinel-2. Remote Sens. 2019, 11, 481. [Google Scholar] [CrossRef]
- Casa, R.; Upreti, D.; Palombo, A.; Pascucci, S.; Yang, H.; Yang, G.; Huang, W.; Pignatti, S. Evaluation and Exploitation of Retrieval Algorithms for Estimating Biophysical Crop Variables Using Sentinel-2, Venus, and PRISMA Satellite Data. J. Geod. Geoinf. Sci. 2021, 3, 79–88. [Google Scholar]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated World Map of the Köppen-Geiger Climate Classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Éireann, M. A Summary of Climate Averages for Ireland 1981–2010; Met Éireann, Glasnevin Hill: Dublin, Ireland, 2012. [Google Scholar]
- Irish Soil Information System. Available online: https://www.teagasc.ie/environment/soil/irish-soil-information-system/ (accessed on 17 November 2022).
- Kennedy, S. Identifying Constraints to Increasing Yield Potential of Spring Barley; The University of Edinburgh: Edinburgh, UK, 2015. [Google Scholar]
- O’Neill, M.; Lanigan, G.J.; Forristal, P.D.; Osborne, B.A. Greenhouse Gas Emissions and Crop Yields from Winter Oilseed Rape Cropping Systems Are Unaffected by Management Practices. Front. Environ. Sci. 2021, 9, 377. [Google Scholar] [CrossRef]
- Hengl, T.; Mendes de Jesus, J.; Heuvelink, G.B.; Ruiperez Gonzalez, M.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B. SoilGrids250m: Global Gridded Soil Information Based on Machine Learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [PubMed]
- Poggio, L.; De Sousa, L.M.; Batjes, N.H.; Heuvelink, G.; Kempen, B.; Ribeiro, E.; Rossiter, D. SoilGrids 2.0: Producing Soil Information for the Globe with Quantified Spatial Uncertainty. Soil 2021, 7, 217–240. [Google Scholar] [CrossRef]
- Pollacco, J.A.P. A Generally Applicable Pedotransfer Function That Estimates Field Capacity and Permanent Wilting Point from Soil Texture and Bulk Density. Can. J. Soil Sci. 2008, 88, 761–774. [Google Scholar] [CrossRef]
- Santra, P.; Kumar, M.; Kumawat, R.; Painuli, D.; Hati, K.; Heuvelink, G.; Batjes, N. Pedotransfer Functions to Estimate Soil–water Content at Field Capacity and Permanent Wilting Point in Hot Arid Western India. J. Earth Syst. Sci. 2018, 127, 1–16. [Google Scholar] [CrossRef]
- Wu, X.; Lu, G.; Wu, Z.; He, H.; Zhou, J.; Liu, Z. An Integration Approach for Mapping Field Capacity of China Based on Multi-Source Soil Datasets. Water 2018, 10, 728. [Google Scholar] [CrossRef]
- Monteith, J.L. Climate and the Efficiency of Crop Production in Britain. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1977, 281, 277–294. [Google Scholar] [CrossRef]
- Wallach, D.; Makowski, D.; Jones, J.W.; Brun, F. Working with Dynamic Crop Models: Methods, Tools and Examples for Agriculture and Environment; Academic Press: Cambridge, MA, USA, 2018; ISBN 0-12-811757-5. [Google Scholar]
- De Jong, R.; Shaykewich, C.; Reimer, A. The Net Radiation Flux and Its Prediction at Pinawa, Manitoba. Argic. Meteorol. 1980, 22, 217–225. [Google Scholar] [CrossRef]
- McCree, K. Equations for the Rate of Dark Respiration of White Clover and Grain Sorghum, as Functions of Dry Weight, Photosynthetic Rate, and Temperature 1. Crop Sci. 1974, 14, 509–514. [Google Scholar] [CrossRef]
- Chahbi Bellakanji, A.; Zribi, M.; Lili-Chabaane, Z.; Mougenot, B. Forecasting of Cereal Yields in a Semi-Arid Area Using the Simple Algorithm for Yield Estimation (SAFY) Agro-Meteorological Model Combined with Optical SPOT/HRV Images. Sensors 2018, 18, 2138. [Google Scholar] [CrossRef]
- Bendig, J.; Bolten, A.; Bennertz, S.; Broscheit, J.; Eichfuss, S.; Bareth, G. Estimating Biomass of Barley Using Crop Surface Models (CSMs) Derived from UAV-Based RGB Imaging. Remote Sens. 2014, 6, 10395–10412. [Google Scholar] [CrossRef]
- Fletcher, A.; Martin, R.; de Ruiter, J.; Jamieson, P.; Zyskowski, R. Simulating Biomass and Grain Yields of Barley and Oat Crops with the Sirius Wheat Model. In Crop Modeling and Decision Support; Springer: Berlin/Heidelberg, Germany, 2009; pp. 192–202. [Google Scholar] [CrossRef]
- Rötter, R.P.; Palosuo, T.; Kersebaum, K.C.; Angulo, C.; Bindi, M.; Ewert, F.; Ferrise, R.; Hlavinka, P.; Moriondo, M.; Nendel, C. Simulation of Spring Barley Yield in Different Climatic Zones of Northern and Central Europe: A Comparison of Nine Crop Models. Field Crops Res. 2012, 133, 23–36. [Google Scholar] [CrossRef]
- Wengert, M.; Piepho, H.-P.; Astor, T.; Graß, R.; Wijesingha, J.; Wachendorf, M. Assessing Spatial Variability of Barley Whole Crop Biomass Yield and Leaf Area Index in Silvoarable Agroforestry Systems Using UAV-Borne Remote Sensing. Remote Sens. 2021, 13, 2751. [Google Scholar] [CrossRef]
- Khan, A.; Stöckle, C.O.; Nelson, R.L.; Peters, T.; Adam, J.C.; Lamb, B.; Chi, J.; Waldo, S. Estimating Biomass and Yield Using Metric Evapotranspiration and Simple Growth Algorithms. Agron. J. 2019, 111, 536–544. [Google Scholar] [CrossRef]
- Allies, A.; Roumiguié, A.; Fieuzal, R.; Dejoux, J.-F.; Jacquin, A.; Veloso, A.; Champolivier, L.; Baup, F. Assimilation of Multisensor Optical and Multiorbital SAR Satellite Data in a Simplified Agrometeorological Model for Rapeseed Crops Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 15, 1123–1138. [Google Scholar] [CrossRef]
- Hussain, S.; Gao, K.; Din, M.; Gao, Y.; Shi, Z.; Wang, S. Assessment of UAV-Onboard Multispectral Sensor for Non-Destructive Site-Specific Rapeseed Crop Phenotype Variable at Different Phenological Stages and Resolutions. Remote Sens. 2020, 12, 397. [Google Scholar] [CrossRef]
- Lehuger, S.; Gabrielle, B.; Cellier, P.; Loubet, B.; Roche, R.; Béziat, P.; Ceschia, E.; Wattenbach, M. Predicting the Net Carbon Exchanges of Crop Rotations in Europe with an Agro-Ecosystem Model. Agric. Ecosyst. Environ. 2010, 139, 384–395. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).