Comparison of Frequentist and Bayesian Meta-Analysis Models for Assessing the Efficacy of Decision Support Systems in Reducing Fungal Disease Incidence
Abstract
1. Introduction
2. Material and Methods
2.1. Literature Search and Data
2.2. Meta-Analysis
Statistical Modelling
2.3. Parameter Estimation: Frequentist vs. Bayesian Approach
2.4. Treatment Effects: Disease Incidence, Odds Ratio, Incidence Ratio and Predictive Distribution of the Odds Ratio
2.4.1. Disease Incidence
2.4.2. Odds Ratio
2.4.3. Incidence Ratio
2.4.4. Predictive Distribution of the Odds Ratio
3. Results
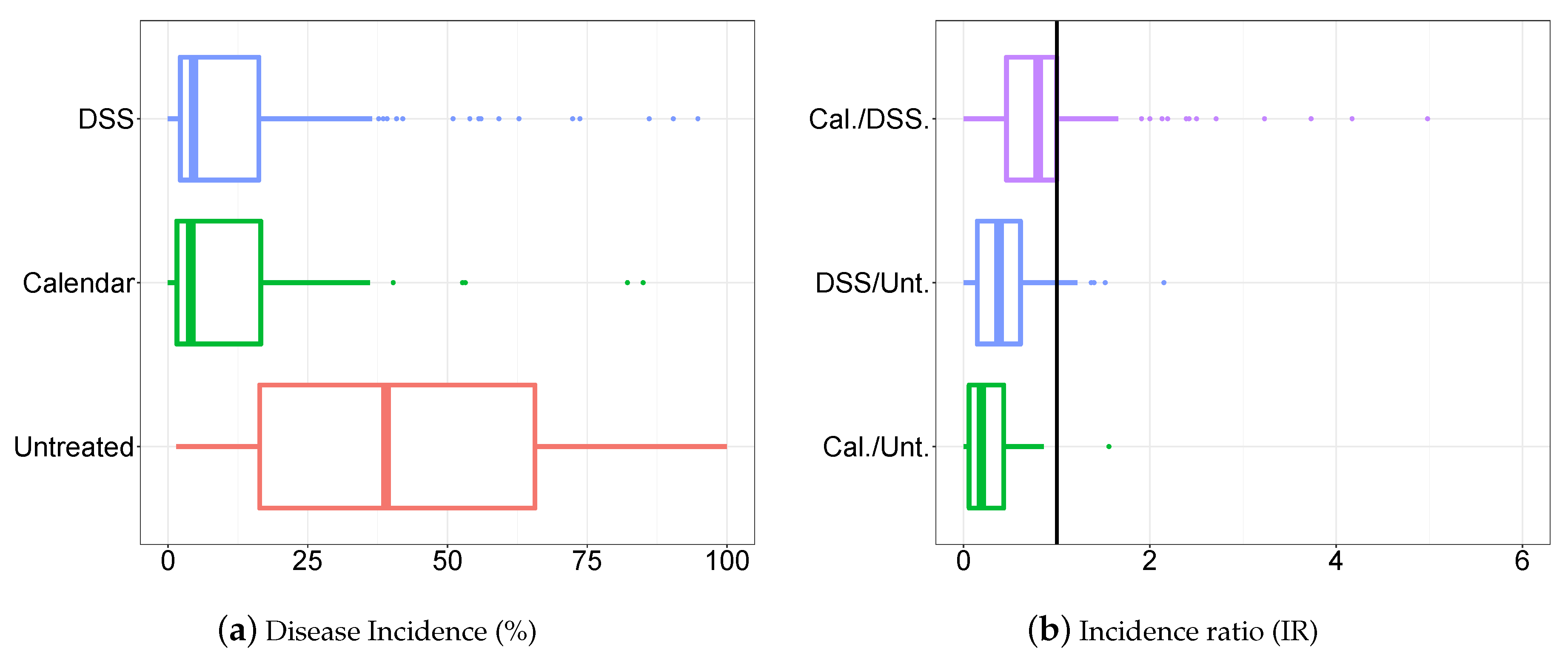
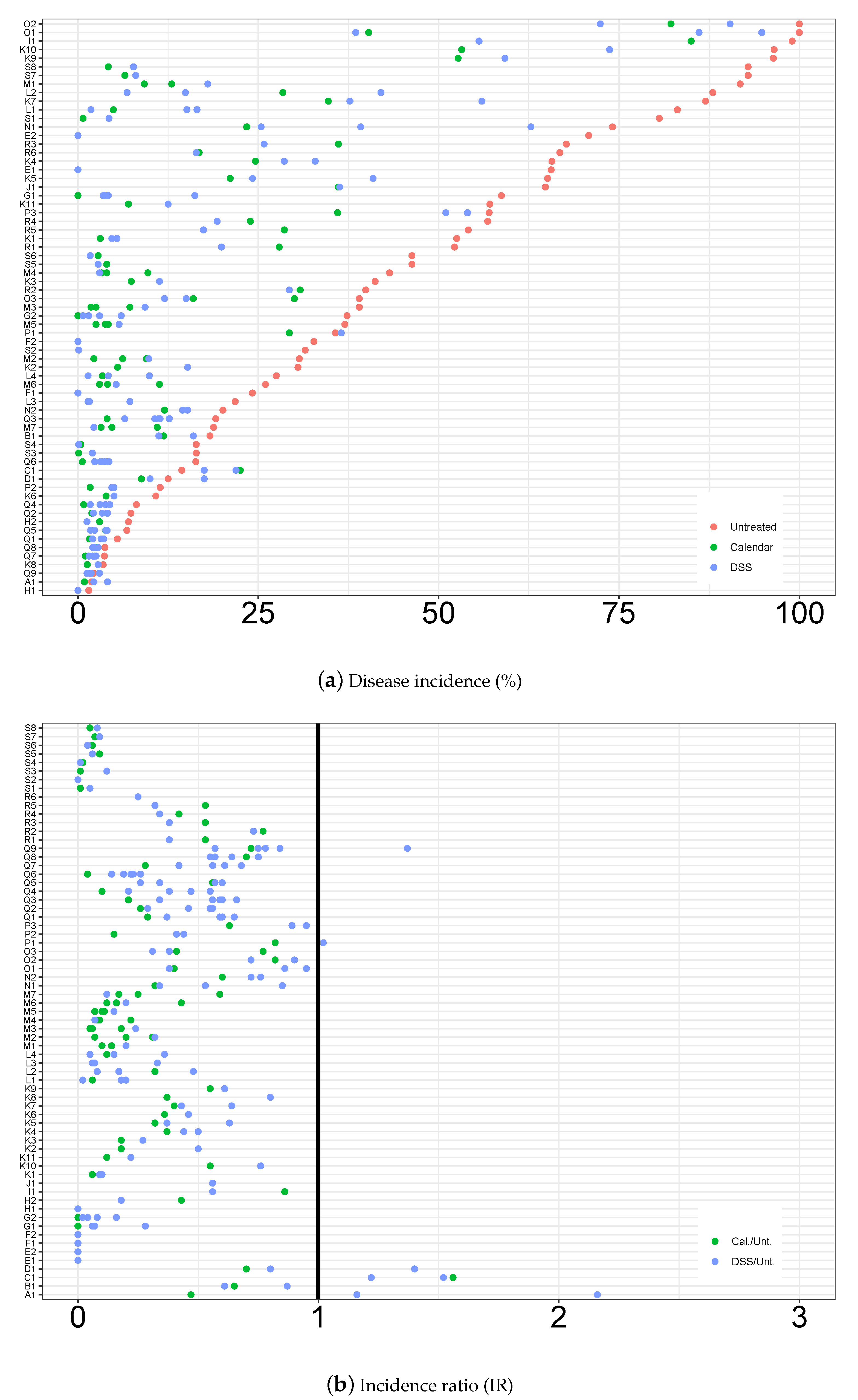
3.1. Descriptive Analysis of the Database
3.2. Statistical Modelling Evaluation
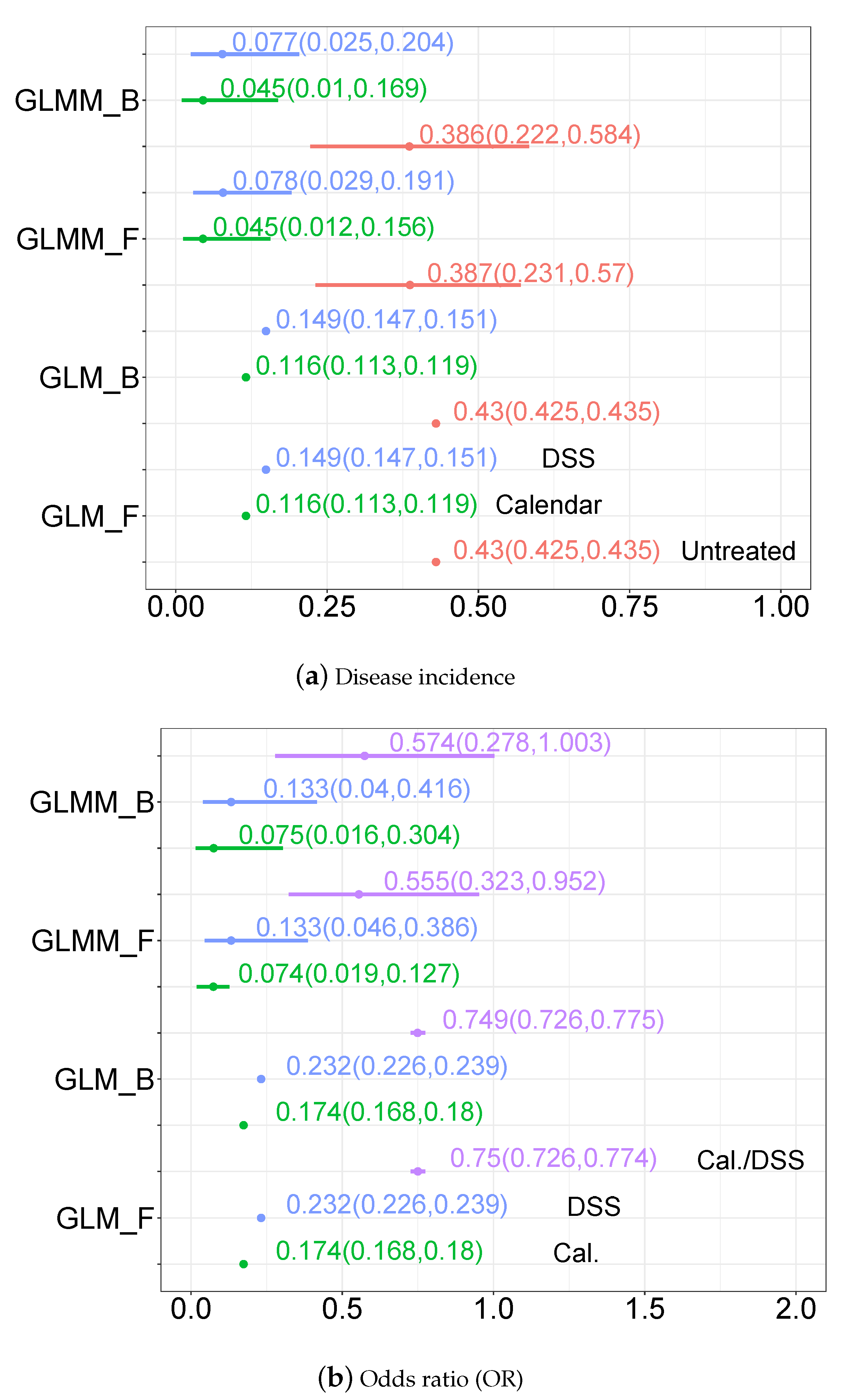
3.3. Statistical Modelling Inference Results
3.3.1. Parameter Estimates
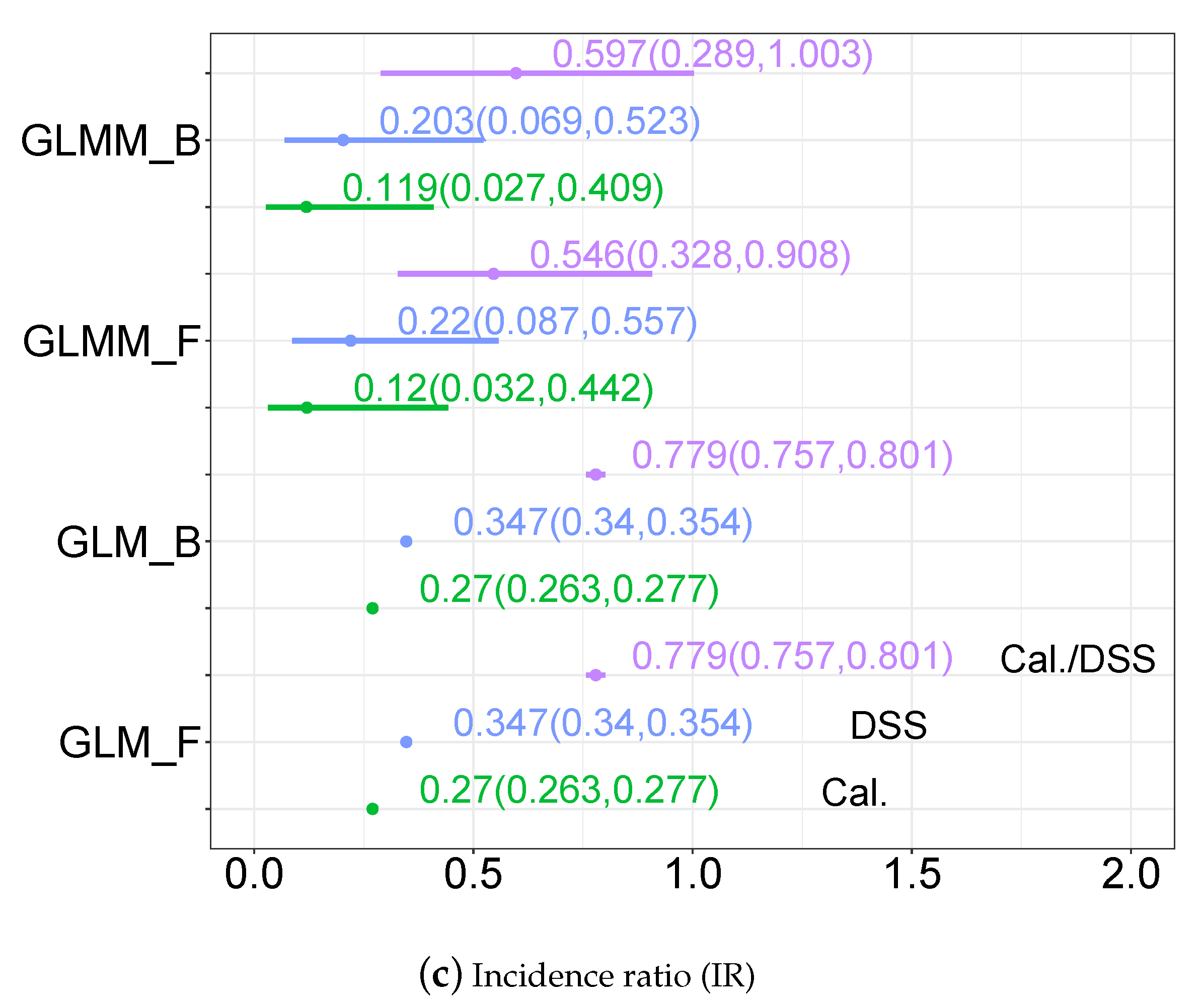
3.3.2. Disease Incidence, Odds Ratio and Incidence Ratio Estimates
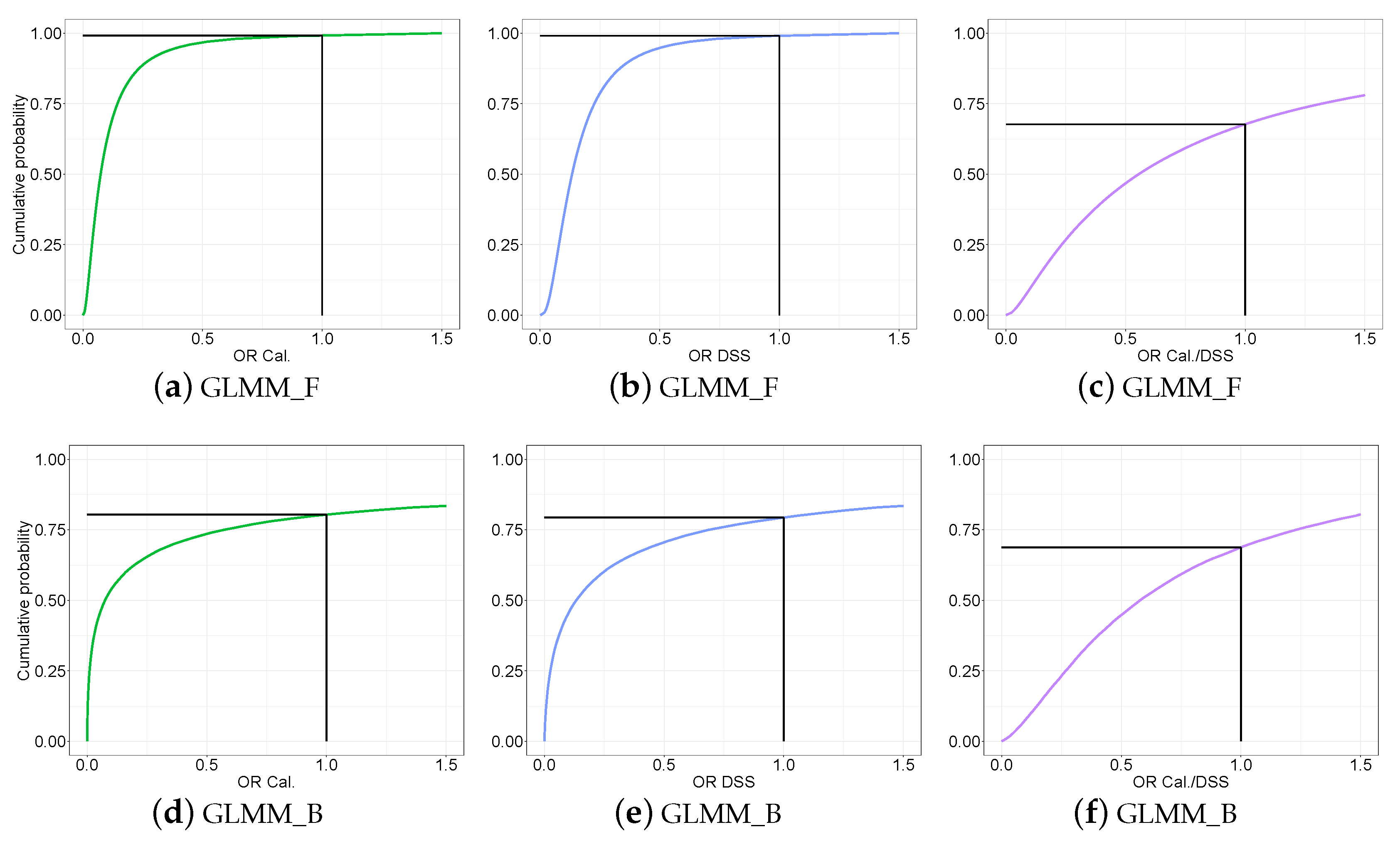
3.3.3. Predictive Distribution of the Odds Ratio
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AIC | Akaike Information Criterion |
| DIC | Deviance Information Criterion |
| DSS | Decision Support System |
| F&N Tests | Fungicide and Nematicide Tests |
| GLM | Generalized Linear Model |
| GLMM | Generalized Linear Mixed Model |
| IR | Incidence Ratio |
| OR | Odds Ratio |
| SE | Standard Error |
| WOS | Web of Science |
Appendix A
| Paper | Source | Search String |
|---|---|---|
| Brown-Rytlewski et al. [44] | F & N Tests | Forecasting |
| Brown-Rytlewski et al. [45] | F & N Tests | Forecasting |
| Brown-Rytlewski et al. [46] | F & N Tests | Forecasting |
| Brown-Rytlewski et al. [47] | F & N Tests | Forecasting |
| Babadoost [48] | F & N Tests | Warning |
| Babadoost [49] | F & N Tests | Warning |
| Gleason et al. [50] | F & N Tests | Warning |
| Hovius and McDonald [51] | F & N Tests | Forecasting |
| McDonald et al. [52] | F & N Tests | Forecasting |
| Averre et al. [53] | F & N Tests | Hard copies |
| Llorente et al. [54] | WOS | Other references |
| Bhatia et al. [55] | WOS | Other references |
| Byrne et al. [56] | WOS | Other references |
| Montesinos et al. [57] | WOS | Other references |
| Peres and Timmer [58] | WOS | Other references |
| Wu et al. [59] | WOS | (crop OR plant) AND disease AND (fungus OR fungi OR fungal OR fungicide) |
| AND (forecasting OR warning OR prediction OR predictive) | ||
| AND (decision-support OR decision OR support OR treatment OR model OR system) | ||
| AND (weekly OR calendar OR daily) AND (Comparison) | ||
| Louws et al. [60] | WOS | (crop OR plant) AND disease AND (fungus OR fungi OR fungal OR fungicide) |
| AND (forecasting OR warning OR prediction OR predictive) | ||
| AND (decision-support OR decision OR support OR treatment) | ||
| AND (weekly OR calendar OR daily) AND(model OR system) | ||
| Rasiukevivciute et al. [61] | WOS | (crop OR plant) AND disease AND (fungus OR fungi OR fungal OR fungicide) |
| AND (forecasting OR warning OR prediction OR predictive) | ||
| AND (decision-support OR decision OR support OR treatment) | ||
| AND(model OR system) | ||
| Rosli et al. [62] | WOS | (crop OR plant) AND (disease) AND (fungal OR fungi OR fun- gus) |
| AND (forecasting OR warning OR prediction) AND decision-support |
Appendix B
| Paper | Experiment | |||
|---|---|---|---|---|
| Reference | Id | Location | Crop | Disease * |
| Brown-Rytlewski et al. [44] | A1 | Ohio, US | Wheat | Fusarium head blight |
| Brown-Rytlewski et al. [45] | B1 | Michigan, US | Wheat | Fusarium head blight |
| Brown-Rytlewski et al. [46] | C1 | Michigan, US | Wheat | Fusarium head blight |
| Brown-Rytlewski et al. [47] | D1 | Michigan, US | Wheat | Fusarium head blight |
| Babadoost [48] | E1 | California, US | Apple | Sooty blotch complex |
| E2 | California, US | Apple | Flyspeck | |
| Babadoost [49] | F1 | California, US | Apple | Sooty blotch complex |
| F2 | California, US | Apple | Flyspeck | |
| Gleason et al. [50] | G1 | Iowa, US | Apple | Sooty blotch complex |
| G2 | Iowa, US | Apple | Flyspeck | |
| Hovius and McDonald [51] | H1 | Ontario, CA | Lettuce | Downy mildew |
| H2 | Ontario, CA | Lettuce | Downy mildew | |
| Mcdonald et al. [52] | I1 | Ontario, CA | Lettuce | Downy mildew |
| Averre et al. [53] | J1 | North Carolina, US | Asparagus | Cercospora blight |
| Llorente et al. [54] | K1 | Emilia-Romagna, IT | Pear | Brown spot |
| K2 | Girona, ES | Pear | Brown spot | |
| K3 | Emilia-Romagna, IT | Pear | Brown spot | |
| K4 | Girona, ES | Pear | Brown spot | |
| K5 | Girona, ES | Pear | Brown spot | |
| K6 | Emilia-Romagna, IT | Pear | Brown spot | |
| K7 | Girona, ES | Pear | Brown spot | |
| K8 | Girona, ES | Pear | Brown spot | |
| K9 | Girona, ES | Pear | Brown spot | |
| K10 | Girona, ES | Pear | Brown spot | |
| K11 | Emilia-Romagna, IT | Pear | Brown spot | |
| Bhatia et al. [55] | L1 | Florida, US | Mandarin | Alternaria brown spot |
| L2 | Florida, US | Mandarin | Alternaria brown spot | |
| L3 | Florida, US | Mandarin | Alternaria brown spot | |
| L4 | Florida, US | Mandarin | Alternaria brown spot | |
| Byrne et al. [56] | M1 | Michigan, US | Tomato | Anthracnose |
| M2 | Michigan, US | Tomato | Anthracnose | |
| M3 | Indiana, US | Tomato | Anthracnose | |
| M4 | Michigan, US | Tomato | Anthracnose | |
| M5 | Michigan, US | Tomato | Anthracnose | |
| M6 | Indiana, US | Tomato | Anthracnose | |
| M7 | Indiana, US | Tomato | Anthracnose | |
| Montesinos et al. [57] | N1 | Girona, ES | Pear | Brown spot |
| N2 | Girona, ES | Pear | Brown spot | |
| Peres and Timmer [58] | O1 | São Paulo, BR | Mandarin | Alternaria brown spot |
| O2 | São Paulo, BR | Mandarin | Alternaria brown spot | |
| O3 | São Paulo, BR | Mandarin | Alternaria brown spot | |
| Wu et al. [59] | P1 | California, US | Lettuce | Downy mildew |
| P2 | California, US | Lettuce | Downy mildew | |
| P3 | California, US | Lettuce | Downy mildew | |
| Louws et al. [60] | Q1 | Michigan, US | Tomato | Early blight |
| Q2 | Michigan, US | Tomato | Early blight | |
| Q3 | Michigan, US | Tomato | Early blight | |
| Q4 | Michigan, US | Tomato | Anthracnose | |
| Q5 | Michigan, US | Tomato | Anthracnose | |
| Q6 | Michigan, US | Tomato | Anthracnose | |
| Q7 | Michigan, US | Tomato | Rhizoctonia fruit rot | |
| Q8 | Michigan, US | Tomato | Rhizoctonia fruit rot | |
| Q9 | Michigan, US | Tomato | Rhizoctonia fruit rot | |
| Rasiukevivciute et al. [61] | R1 | Kaunas, LT | Strawberry | Gray mold |
| R2 | Kaunas, LT | Strawberry | Gray mold | |
| R3 | Kaunas, LT | Strawberry | Gray mold | |
| R4 | Kaunas, LT | Strawberry | Gray mold | |
| R5 | Kaunas, LT | Strawberry | Gray mold | |
| R6 | Kaunas, LT | Strawberry | Gray mold | |
| Rosli et al. [62] | S1 | Iowa, US | Apple | Sooty blotch complex /Flyspeck |
| S2 | Iowa, US | Apple | Sooty blotch complex /Flyspeck | |
| S3 | Iowa, US | Apple | Sooty blotch complex /Flyspeck | |
| S4 | Iowa, US | Apple | Sooty blotch complex /Flyspeck | |
| S5 | Iowa, US | Apple | Sooty blotch complex /Flyspeck | |
| S6 | Iowa, US | Apple | Sooty blotch complex /Flyspeck | |
| S7 | Iowa, US | Apple | Sooty blotch complex /Flyspeck | |
| S8 | Iowa, US | Apple | Sooty blotch complex /Flyspeck | |
| Paper | Experiment | Sub-Experiments | |||
|---|---|---|---|---|---|
| Reference | Id | Id | Untreated | Calendar | DSS |
| Brown-Rytlewski et al. [44] | A | A1 | 1 | 1 | 2 |
| Brown-Rytlewski et al. [45] | B | B1 | 1 | 1 | 2 |
| Brown-Rytlewski et al. [46] | C | C1 | 1 | 1 | 2 |
| Brown-Rytlewski et al. [47] | D | D1 | 1 | 1 | 2 |
| Babadoost [48] | E | E1 | 1 | 2 | 2 |
| E2 | 1 | 2 | 2 | ||
| Babadoost [49] | F | F1 | 1 | 2 | 2 |
| F2 | 1 | 2 | 2 | ||
| Gleason et al. [50] | G | G1 | 1 | 1 | 4 |
| G2 | 1 | 1 | 4 | ||
| Hovius and McDonald [51] | H | H1 | 1 | 1 | 1 |
| H2 | 1 | 1 | 1 | ||
| McDonald et al. [52] | I | I1 | 1 | 1 | 1 |
| Averre et al. [53] | J | J1 | 1 | 1 | 1 |
| K | K1 | 1 | 1 | 2 | |
| K2 | 1 | 1 | 1 | ||
| K3 | 1 | 1 | 1 | ||
| K4 | 1 | 1 | 2 | ||
| K5 | 1 | 1 | 2 | ||
| Llorente et al. [54] | K6 | 1 | 1 | 1 | |
| K7 | 1 | 1 | 2 | ||
| K8 | 1 | 1 | 1 | ||
| K9 | 1 | 1 | 1 | ||
| K10 | 1 | 1 | 1 | ||
| K11 | 1 | 1 | 1 | ||
| Bhatia et al. [55] | L | L1 | 1 | 1 | 3 |
| L2 | 1 | 1 | 3 | ||
| L3 | 1 | 1 | 3 | ||
| L4 | 1 | 1 | 3 | ||
| M | M1 | 1 | 3 | 1 | |
| M2 | 1 | 3 | 1 | ||
| M3 | 1 | 3 | 1 | ||
| Byrne et al. [56] | M4 | 1 | 3 | 1 | |
| M5 | 1 | 3 | 1 | ||
| M6 | 1 | 3 | 1 | ||
| M7 | 1 | 3 | 1 | ||
| Montesinos et al. [57] | N | N1 | 1 | 1 | 3 |
| N2 | 1 | 1 | 2 | ||
| O | O1 | 1 | 1 | 3 | |
| Peres and Timmer [58] | O2 | 1 | 1 | 2 | |
| O3 | 1 | 2 | 2 | ||
| P | P1 | 1 | 1 | 1 | |
| Wu et al. [59] | P2 | 1 | 1 | 2 | |
| P3 | 1 | 1 | 2 | ||
| Q | Q1 | 1 | 1 | 4 | |
| Q2 | 1 | 1 | 4 | ||
| Q3 | 1 | 1 | 5 | ||
| Q4 | 1 | 1 | 4 | ||
| Louws et al. [60] | Q5 | 1 | 1 | 4 | |
| Q6 | 1 | 1 | 5 | ||
| Q7 | 1 | 1 | 4 | ||
| Q8 | 1 | 1 | 4 | ||
| Q9 | 1 | 1 | 5 | ||
| Rasiukevivciute et al. [61] | R | R1 | 1 | 1 | 1 |
| R2 | 1 | 1 | 1 | ||
| R3 | 1 | 1 | 1 | ||
| R4 | 1 | 1 | 1 | ||
| R5 | 1 | 1 | 1 | ||
| R6 | 1 | 1 | 1 | ||
| Rosli et al. [62] | S | S1 | 1 | 1 | 1 |
| S2 | 1 | 1 | 1 | ||
| S3 | 1 | 1 | 1 | ||
| S4 | 1 | 1 | 1 | ||
| S5 | 1 | 1 | 1 | ||
| S6 | 1 | 1 | 1 | ||
| S7 | 1 | 1 | 1 | ||
| S8 | 1 | 1 | 1 | ||
| TOTAL | 67 | 86 | 132 | ||
References
- Higgins, J.P.; Thompson, S.G.; Spiegelhalter, D.J. A re-evaluation of random-effects meta-analysis. J. R. Stat. Soc. A Stat. 2009, 172, 137–159. [Google Scholar] [CrossRef] [PubMed]
- Rosenberg, M.; Garrett, K.; Su, Z.; Bowden, R. Meta-analysis in plant pathology: synthesizing research results. Phytopathology 2004, 94, 1013–1017. [Google Scholar] [CrossRef] [PubMed]
- Ngugi, H.K.; Esker, P.D.; Scherm, H. Meta-analysis to determine the effects of plant disease management measures: review and case studies on soybean and apple. Phytopathology 2011, 101, 31–41. [Google Scholar] [CrossRef] [PubMed]
- Madden, L.; Paul, P. Meta-analysis for evidence synthesis in plant pathology: An overview. Phytopathology 2011, 101, 16–30. [Google Scholar] [CrossRef]
- Makowski, D.; Vicent, A.; Pautasso, M.; Stancanelli, G.; Rafoss, T. Comparison of statistical models in a meta-analysis of fungicide treatments for the control of citrus black spot caused by Phyllosticta citricarpa. Eur. J. Plant Pathol. 2014, 139, 79–94. [Google Scholar] [CrossRef]
- Sutton, A.J.; Abrams, K.R.; Jones, D.R.; Jones, D.R.; Sheldon, T.A.; Song, F. Methods for Meta-Analysis in Medical Research; John Wiley & Sons: Hoboken, NJ, USA, 2000; Volume 348. [Google Scholar]
- Philibert, A.; Loyce, C.; Makowski, D. Assessment of the quality of meta-analysis in agronomy. Agric. Ecosyst. Environ. 2012, 148, 72–82. [Google Scholar] [CrossRef]
- Borenstein, M.; Hedges, L.V.; Higgins, J.P.; Rothstein, H.R. Introduction to Meta-Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Rice, K.; Higgins, J.P.; Lumley, T. A re-evaluation of fixed effect (s) meta-analysis. J. R. Stat. Soc. A Stat. 2018, 181, 205–227. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J. Generalized Linear Models, 2nd ed.; Chapman and Hall/CRC Monographs on Statistics and Applied Probability Series; Chapman & Hall: Boca Raton, FL, USA, 1989. [Google Scholar]
- Magarey, R.; Travis, J.; Russo, J.; Seem, R.; Magarey, P. Decision support systems: Quenching the thirst. Plant Dis. 2002, 86, 4–14. [Google Scholar] [CrossRef]
- De Wolf, E.D.; Isard, S.A. Disease cycle approach to plant disease prediction. Annu. Rev. Phytopathol. 2007, 45, 203–220. [Google Scholar] [CrossRef]
- Shtienberg, D. Will decision-support systems be widely used for the management of plant diseases? Annu. Rev. Phytopathol. 2013, 51, 1–16. [Google Scholar] [CrossRef]
- Warn, D.E.; Thompson, S.; Spiegelhalter, D.J. Bayesian random effects meta-analysis of trials with binary outcomes: methods for the absolute risk difference and relative risk scales. Stat. Med. 2002, 21, 1601–1623. [Google Scholar] [CrossRef] [PubMed]
- Jackson, D.; White, I.R. When should meta-analysis avoid making hidden normality assumptions? Biom. J. 2018, 60, 1040–1058. [Google Scholar] [CrossRef] [PubMed]
- Hoyer, A.; Kuss, O. Meta-analysis for the comparison of two diagnostic tests to a common gold standard: A generalized linear mixed model approach. Stat. Methods Med. Res. 2018, 27, 1410–1421. [Google Scholar] [CrossRef] [PubMed]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Sakamoto, Y.; Ishiguro, M.; Kitagawa, G. Akaike Information Criterion Statistics; Taylor & Francis: Abingdon, UK, 1986. [Google Scholar]
- Burnham, K.P.; Anderson, D.R. Multimodel inference: Understanding AIC and BIC in model selection. Sociol. Method. Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Lázaro, E.; Armero, C.; Roselló, J.; Serra, J.; Muñoz, M.; Canet, R.; Galipienso, L.; Rubio, L. Comparison of viral infection risk between organic and conventional crops of tomato in Spain. Eur. J. Plant Pathol. 2019, 155, 1145–1154. [Google Scholar] [CrossRef]
- Chen, M.H.; Shao, Q.M. Monte Carlo estimation of Bayesian credible and HPD intervals. J. Comput. Graph. Stat. 1999, 8, 69–92. [Google Scholar]
- Gelman, A.; Jakulin, A.; Pittau, M.G.; Su, Y.S. A weakly informative default prior distribution for logistic and other regression models. Ann. Appl. Stat. 2008, 2, 1360–1383. [Google Scholar] [CrossRef]
- Su, Y.S.; Yajima, M. R2jags: Using R to run ‘JAGS’. R package version 0.5-7 2015, 34. Available online: https://cran.r-project.org/web/packages/R2jags/index.html (accessed on 10 March 2020).
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van Der Linde, A. The deviance information criterion: 12 years on. J. R. Stat. Soc. B Met. 2014, 76, 485–493. [Google Scholar] [CrossRef]
- Carlin, B.P.; Louis, T.A. Bayesian Methods for Data Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Engels, E.A.; Schmid, C.H.; Terrin, N.; Olkin, I.; Lau, J. Heterogeneity and statistical significance in meta-analysis: an empirical study of 125 meta-analyses. Stat. Med. 2000, 19, 1707–1728. [Google Scholar] [CrossRef]
- Deeks, J.J. Issues in the selection of a summary statistic for meta-analysis of clinical trials with binary outcomes. Stat. Med. 2002, 21, 1575–1600. [Google Scholar] [CrossRef] [PubMed]
- Held, L.; Bové, D.S. Frequentist Properties of the Likelihood. In Applied Statistical Inference; Springer: Berlin/Heidelberg, Germany, 2014; pp. 79–122. [Google Scholar]
- Schwarzer, G.; Carpenter, J.R.; Rücker, G. Meta-Analysis with Binary Outcomes. In Meta-Analysis with R; Springer: Berlin/Heidelberg, Germany, 2015; pp. 55–83. [Google Scholar]
- Spiegelhalter, D.J.; Abrams, K.R.; Myles, J.P. Bayesian Approaches to Clinical Trials and Health-Care Evaluation; John Wiley & Sons: Hoboken, NJ, USA, 2004; Volume 13. [Google Scholar]
- Graham, P.L.; Moran, J.L. Robust meta-analytic conclusions mandate the provision of prediction intervals in meta-analysis summaries. J. Clin. Epidemiol. 2012, 65, 503–510. [Google Scholar] [CrossRef]
- Riley, R.D.; Higgins, J.P.; Deeks, J.J. Interpretation of random effects meta-analyses. BMJ 2011, 342, d549. [Google Scholar] [CrossRef]
- Hamaguchi, Y.; Noma, H.; Nagashima, K.; Yamada, T.; Furukawa, T.A. Frequentist performances of Bayesian prediction intervals for random-effects meta-analysis. arXiv 2019, arXiv:1907.00345. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Hong, H.; Carlin, B.P.; Shamliyan, T.A.; Wyman, J.F.; Ramakrishnan, R.; Sainfort, F.; Kane, R.L. Comparing Bayesian and frequentist approaches for multiple outcome mixed treatment comparisons. Med. Decis. Mak. 2013, 33, 702–714. [Google Scholar] [CrossRef]
- Ntzoufras, I. Bayesian Modeling Using WinBUGS; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 698. [Google Scholar]
- Plummer, M. Rjags: Bayesian Graphical Models using MCMC. R package version 4-6 2016. Available online: https://www.rdocumentation.org/packages/rjags/versions/4-6 (accessed on 10 March 2020).
- Rue, H.; Riebler, A.; Sørbye, S.H.; Illian, J.B.; Simpson, D.P.; Lindgren, F.K. Bayesian computing with INLA: A review. Annu. Rev. Stat. Appl. 2017, 4, 395–421. [Google Scholar] [CrossRef]
- Bürkner, P.C. brms: An R package for Bayesian multilevel models using Stan. J. Stat. Softw. 2017, 80, 1–28. [Google Scholar] [CrossRef]
- Lázaro, E.; Armero, C.; Rubio, L. Bayesian correlated models for assessing the prevalence of viruses in organic and non-organic agroecosystems. SORT-Stat. Oper. Res. T. 2017, 1, 93–116. [Google Scholar]
- Gent, D.H.; De Wolf, E.; Pethybridge, S.J. Perceptions of risk, risk aversion, and barriers to adoption of decision support systems and integrated pest management: an introduction. Phytopathology 2011, 101, 640–643. [Google Scholar] [CrossRef]
- Brown-Rytlewski, W.W.; Schafer, R.; Berry, D. Evaluation of fungicides for control of Fusarium head scab of winter wheat at Sandusky, MI, 2006. Plant Dis. Manag. Rep. 2007, 1, CF017. [Google Scholar]
- Brown-Rytlewski, W.W.; Schafer, R.; Berry, D. Evaluation of fungicides for control of Fusarium head scab of winter wheat at Williamston MI, 2006. Plant Dis. Manag. Rep. 2007, 1, CF016. [Google Scholar]
- Brown-Rytlewski, W.W.; Schafer, R.; Berry, D. Evaluation of fungicides for control of Fusarium head scab of winter wheat at East Lansing, MI, 2006. Plant Dis. Manag. Rep. 2007, 1, CF018. [Google Scholar]
- Brown-Rytlewski, W.W.; Schafer, R.; Berry, D. Evaluation of fungicides for control of Fusarium head scab of winter wheat at Saginaw, MI, 2006. Plant Dis. Manag. Rep. 2007, 1, CF019. [Google Scholar]
- Babadoost, M. Performance of reduced-risk fungicides and a wetness-based warning system for control of sooty blotch and flyspeck of apple, 2006. Plant Dis. Manag. Rep. 2007, 1, PF001. [Google Scholar]
- Babadoost, M. Evaluating effectiveness of reduced-risk fungicides and a wetness-based warning system for control of sooty blotch and flyspeck of apple, 2007. Plant Dis. Manag. Rep. 2008, 1, PF050. [Google Scholar]
- Gleason, M.L.; Massman, J.M.; Sisson, A.J.; Mueller, T.A.; S, M.D. Evaluation of fungicides sprayed according to different disease warning systems for control of sooty blotch and flyspeck, 2004. Fungic. Nematic. Tests 2005, 60, PF020. [Google Scholar]
- Hovius, M.H.Y.; McDonald, M.R. Field evaluation of forecasting systems to optimize fungicide applications for downy mildew of lettuce. Fungic. Nematic. Tests 2000, 54, 146–147. [Google Scholar]
- McDonald, M.R.; Vander-Kooi, L.; Roberts, L. Field evaluation of Bremcast: a forecasting system for downy mildew of lettuce. Fungic. Nematic. Tests 2001, 56, V21. [Google Scholar]
- Averre, C.W.; Jenkins, S.F.; Cooperman, C. Evaluation of various spray schedules for control of Cercospora leaf spot on asparagus, 1983. Fungic. Nematic. Tests 1984, 39, 103. [Google Scholar]
- Llorente, I.; Vilardell, P.; Bugiani, R.; Gherardi, I.; Montesinos, E. Evaluation of BSPcast disease warning system in reduced fungicide use programs for management of brown spot of pear. Plant Dis. 2000, 84, 631–637. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bhatia, A.; Roberts, P.; Timmer, L. Evaluation of the Alter-Rater model for timing of fungicide applications for control of Alternaria brown spot of citrus. Plant Dis. 2003, 87, 1089–1093. [Google Scholar] [CrossRef] [PubMed]
- Byrne, J.; Hausbeck, M.; Latin, R. Efficacy and economics of management strategies to control anthracnose fruit rot in processing tomatoes in the Midwest. Plant Dis. 1997, 81, 1167–1172. [Google Scholar] [CrossRef][Green Version]
- Montesinos, E.; Vilardell, P. Evaluation of FAST as a forecasting system for scheduling fungicide sprays for control of Stemphylium vesicarium on pear. Plant Dis. 1992, 76, 1221–1226. [Google Scholar] [CrossRef]
- Peres, N.; Timmer, L. Evaluation of the Alter-Rater model for spray timing for control of Alternaria brown spot on Murcott tangor in Brazil. Crop Prot. 2006, 25, 454–460. [Google Scholar] [CrossRef]
- Wu, B.; Subbarao, K.; Van Bruggen, A.; Koike, S. Comparison of three fungicide spray advisories for lettuce downy mildew. Plant Dis. 2001, 85, 895–900. [Google Scholar] [CrossRef][Green Version]
- Louws, F.J.; Hausbeck, M.K.; Stephens, C. Impact of reduced fungicide and tillage on foliar blight, fruit rot, and yield of processing tomatoes. Plant Dis. 1996, 80, 1251–1256. [Google Scholar] [CrossRef]
- Rasiukevičiūtė, N.; Uselis, N.; Valiuškaitė, A. The use of forecasting model iMETOS® for strawberry grey mould management. Zemdirbyste 2019, 106, 143–150. [Google Scholar] [CrossRef]
- Rosli, H.; Mayfield, D.A.; Batzer, J.C.; Dixon, P.M.; Zhang, W.; Gleason, M.L. Evaluating the performance of a relative humidity-based warning system for sooty blotch and flyspeck in Iowa. Plant Dis. 2017, 101, 1721–1728. [Google Scholar] [CrossRef] [PubMed]
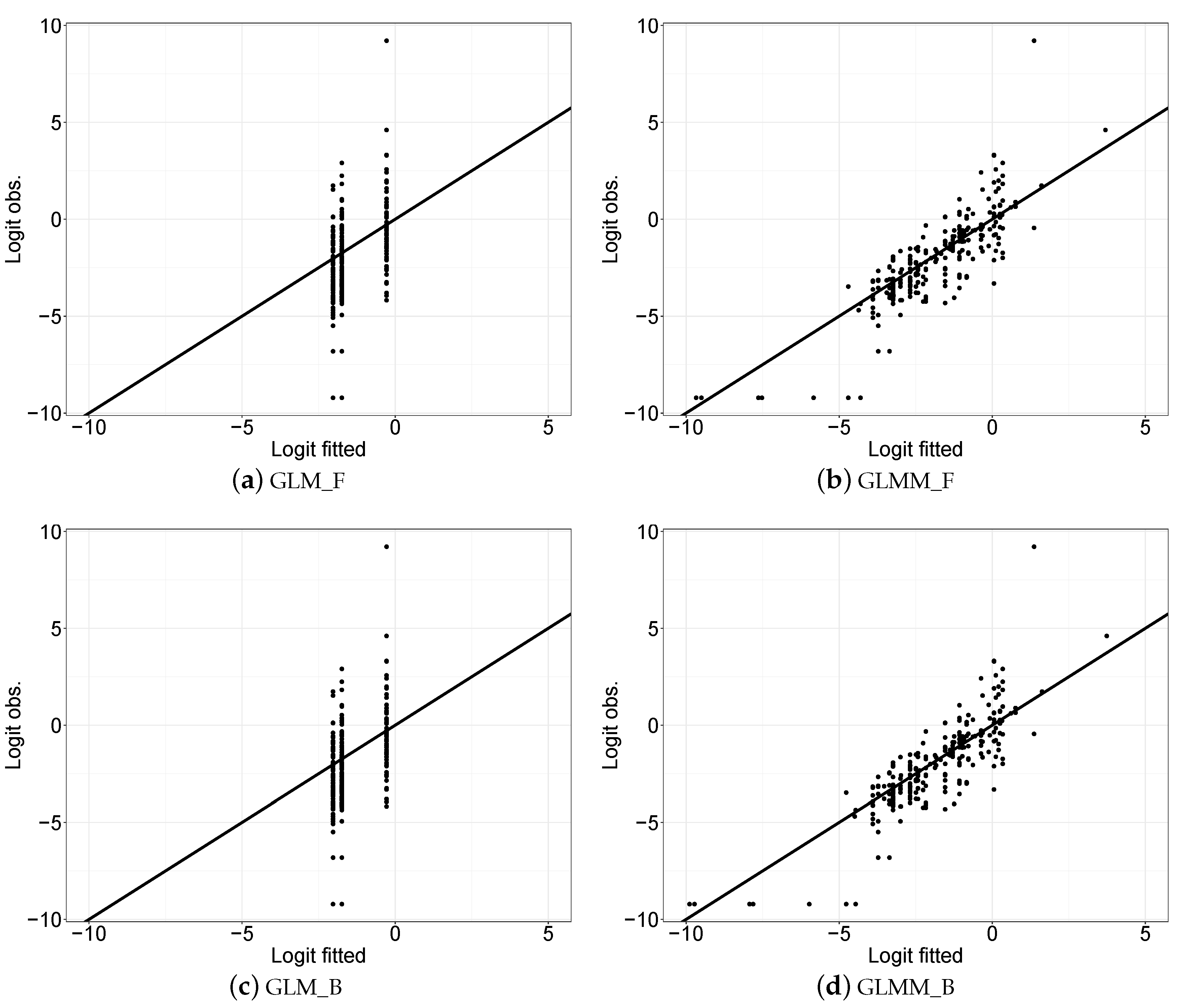
| GLM_F | GLMM_F | ||||
|---|---|---|---|---|---|
| * | |||||
| * | * | ||||
| * | * | ||||
| 2.677 | |||||
| 8.369 | |||||
| 5.387 | |||||
| −1.066 | |||||
| −1.453 | |||||
| 6.387 | |||||
| AIC | 64,189.000 | 26,098.962 | |||
| GLM_B | GLMM_B | ||||
|---|---|---|---|---|---|
| * | |||||
| * | * | ||||
| * | * | ||||
| 2.778 | |||||
| 8.717 | |||||
| 5.726 | |||||
| −1.061 | |||||
| −1.433 | |||||
| 6.614 | |||||
| DIC | 64,188.970 | 25,860.42 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lázaro, E.; Makowski, D.; Martínez-Minaya, J.; Vicent, A. Comparison of Frequentist and Bayesian Meta-Analysis Models for Assessing the Efficacy of Decision Support Systems in Reducing Fungal Disease Incidence. Agronomy 2020, 10, 560. https://doi.org/10.3390/agronomy10040560
Lázaro E, Makowski D, Martínez-Minaya J, Vicent A. Comparison of Frequentist and Bayesian Meta-Analysis Models for Assessing the Efficacy of Decision Support Systems in Reducing Fungal Disease Incidence. Agronomy. 2020; 10(4):560. https://doi.org/10.3390/agronomy10040560
Chicago/Turabian StyleLázaro, Elena, David Makowski, Joaquín Martínez-Minaya, and Antonio Vicent. 2020. "Comparison of Frequentist and Bayesian Meta-Analysis Models for Assessing the Efficacy of Decision Support Systems in Reducing Fungal Disease Incidence" Agronomy 10, no. 4: 560. https://doi.org/10.3390/agronomy10040560
APA StyleLázaro, E., Makowski, D., Martínez-Minaya, J., & Vicent, A. (2020). Comparison of Frequentist and Bayesian Meta-Analysis Models for Assessing the Efficacy of Decision Support Systems in Reducing Fungal Disease Incidence. Agronomy, 10(4), 560. https://doi.org/10.3390/agronomy10040560





