Semiflexible Chains at Surfaces: Worm-Like Chains and beyond
Abstract
:1. Introduction
2. The WLC Model: Some Results in 3D and 2D
2.1. Single Chain Properties
2.2. Melt of Worm-Like Chains
2.2.1. Simulations of WLC Melts and Lattice Artifacts
Generalities
Caveats
2.2.2. Two-Dimensional Polymer Melts: Isotropic-Nematic Phase Transition
Flexible Chains
Weak Persistence Length Effects
Strong Persistence Length Effects
2.2.3. Three-Dimensional Polymer Melts: Corrections to Chain Ideality
3. Adsorption of WLC
3.1. Loop and Tail Partition Function
3.2. Reversible Adsorption of an Ideal WLC from Dilute Solution
3.3. Irreversible Chemisorption of a WLC from Dilute Solution
4. Filaments in 2D beyond WLC
4.1. The Helical Filament Squeezed in 2D
4.1.1. A Bit of Mechanics
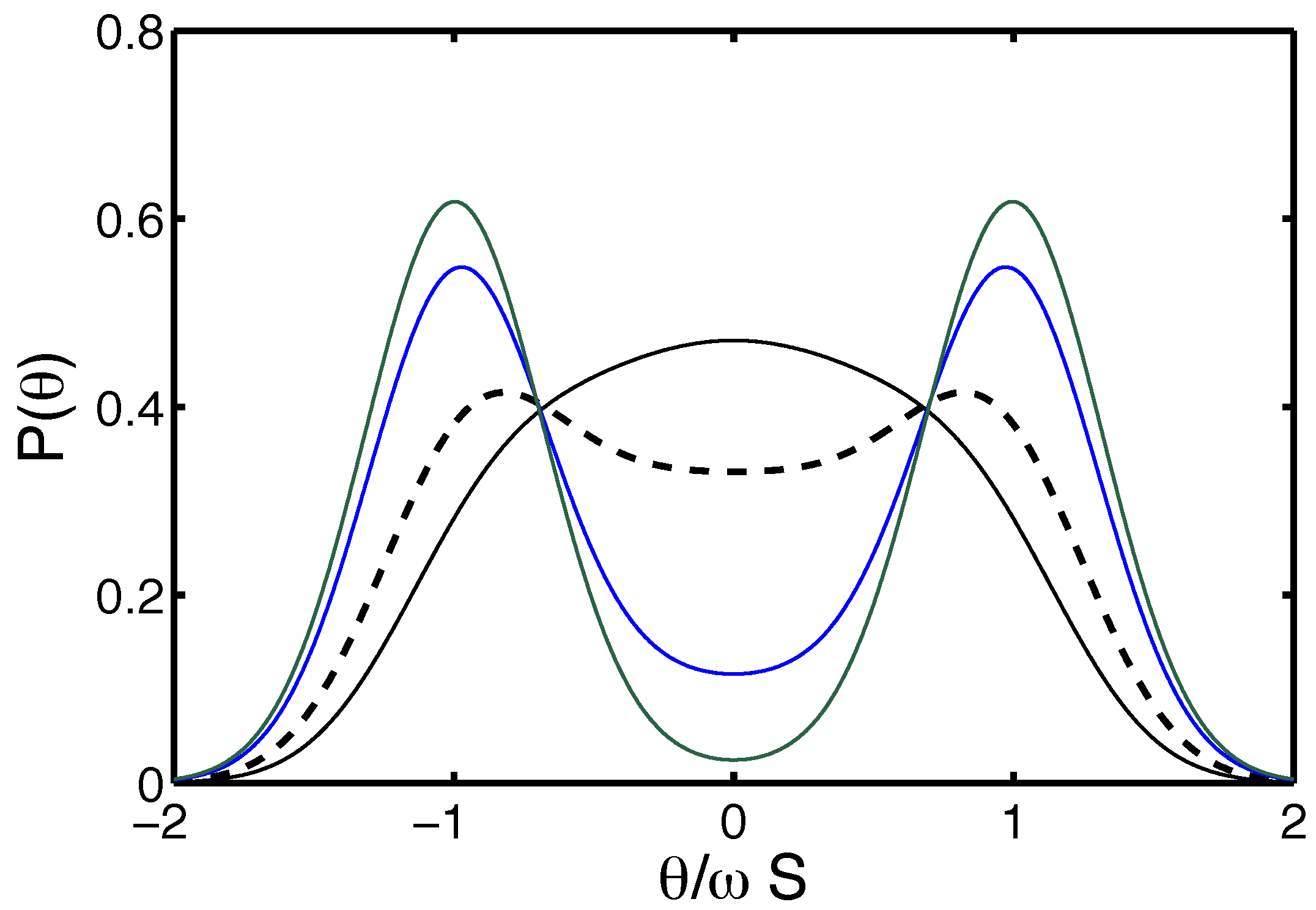
4.1.2. Thermally-Injected Twist-Kinks and Hyper Flexibility: The Arc/Arc Toy Model
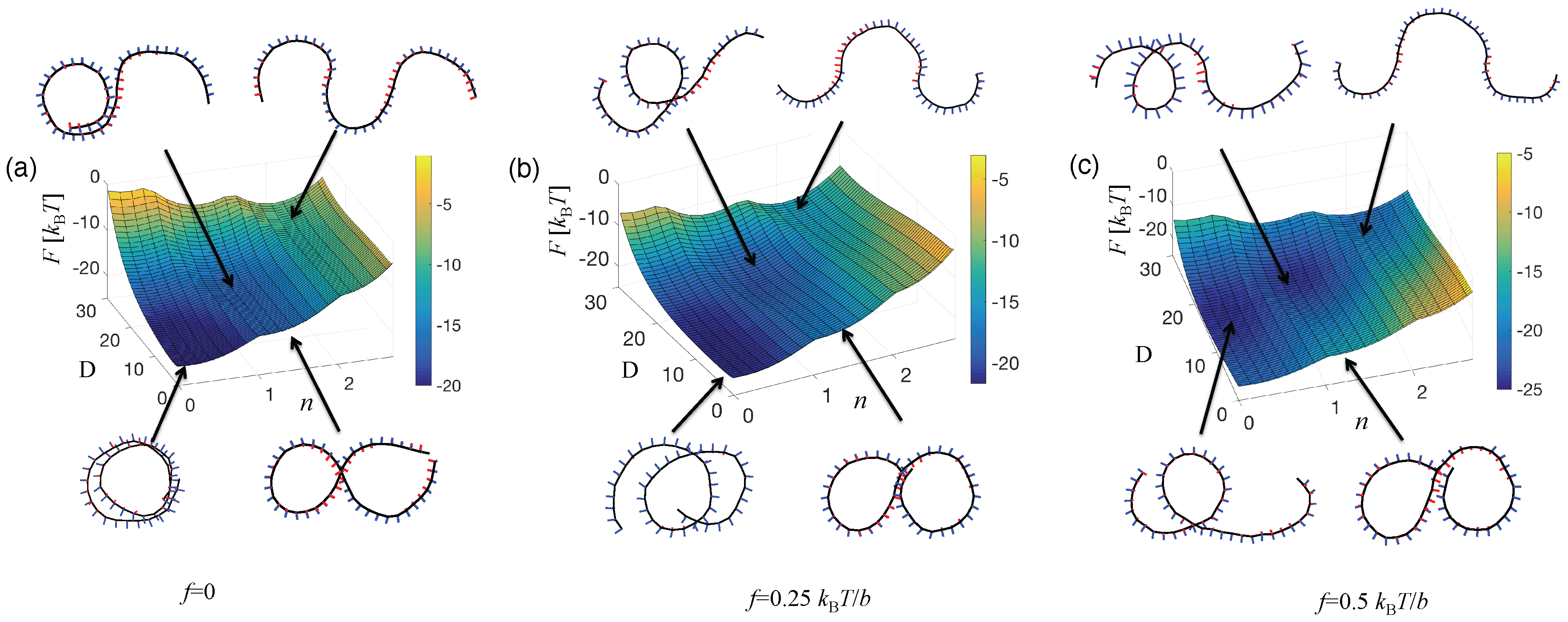
4.1.3. The Free Energy Map
4.2. Emergence of Bistability
4.2.1. Long Range Elasticity and Switchability
4.2.2. Bistability and Cooperativity
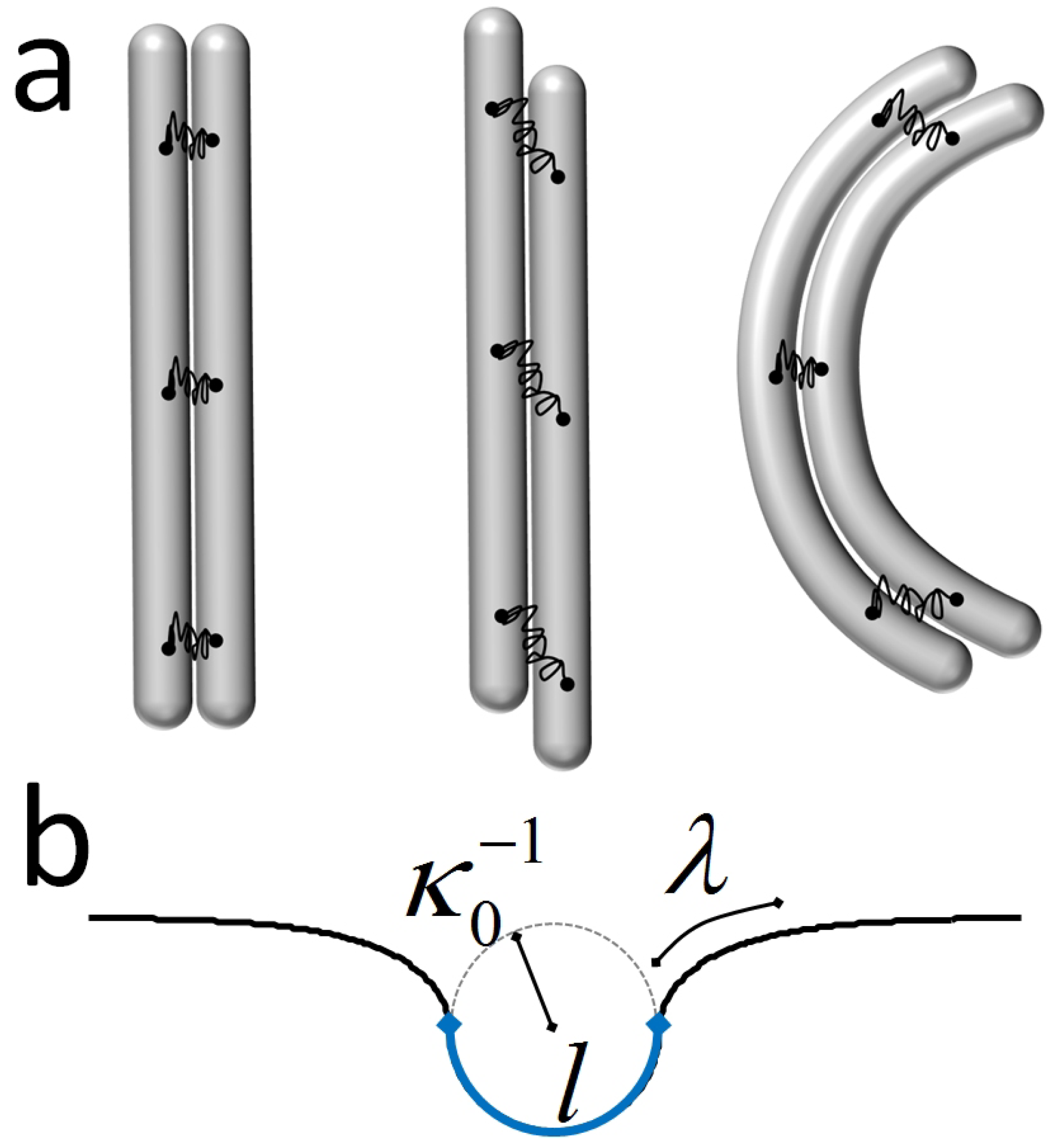
4.3. Polymorphic Model of Microtubules
5. Miscellaneous Topics and Outlook
- We restricted our study to adsorption from dilute solution and mentioned that nematic order is expected in very dense solutions or melts. Even if the nematic order is not thermodynamically stable in the bulk, there may be a thin layer of thickness ℓ closest to the wall where orientational order prevails as described in work by Milner [144]. Strong adsorption of WLC in the melt has been simulated recently [145] with a focus on the distribution of loops and tails, layering effects closest to the wall and local mobility.
- We only considered adsorption on undeformable planar surfaces. Biofilaments can deform soft surfaces like membranes to optimize their surface binding [146]; for example, when the orientation for adsorption is not compatible with the in-plane orientation of the preferred curvature. WLCs have to adapt to the curvature of undeformable shells to adsorb, and this can lead to special arrangements as found in [147]. Surfaces bearing fixed obstacles alter the 2D dynamics of a WLC [148,149].
- Another way to fix polymers on a surface is end-grafting, earlier mentioned in the latest stage of irreversible adsorption. One recent simulation work compares single end graft and middle graft WLC in great detail [153], which is related to the distributions of loops and tails discussed above (Section 3.1). The role of stiffness in densely-grafted brushes was considered early by Pickett and Witten [154]. More recently, simulations in the Binder group discuss grafted WLC in the brush regime and the crossover to the dilute surface regime (so-called mushrooms) [155].
- Anisotropic filaments (tapes) with two flexural moduli [156,157] do occur; examples are synthetic ladder polymers or short (rigid) associated polypeptides. Helical polypeptide tapes [158] can reassemble in a hierarchy of structures. Similar associations play a role in amyloid diseases [158]. Mesini and coworkers studied a family of organogelators and report various self-assembled structures, including microtubes [159]. Recently, the adsorption of helical tapes on rigid surfaces was considered by Quint [160].
- It is sometimes argued that the reptation tube can be represented by some transverse (in a first approximation harmonic) potential [161]. The motion of a WLC confined to an effective tube by a transverse harmonic potential was considered by several authors [21,162]. The loosely-related topic of polymers in random media was considered in [163].
- Some larger scale man-made chains can be considered as semiflexible. The mechanics of semiflexible chains formed by poly(ethylene glycol)-linked paramagnetic particles was studied by Gast and coworkers [164] as a function of the length of the poly(ethylene glycol) spacer.
- Concerning the helical filaments squeezed in 2D discussed in Section 4.1, many open questions remain in the specific biological contexts. Open questions pertain also to the nonequilibrium behavior of squeelices: e.g., when they are transported along molecular motor-covered substrates, where they display circular, spiraling or wavy trajectories [165] that are also observed experimentally [112,166].
- The investigation of cooperativity and switchability discussed in Section 4.2 and Section 4.3 has only just began. For instance, there are indications for cooperative binding of molecular motors on microtubules [167], for which cooperative conformational changes in the tubulins may be responsible [131]. The polymorphic switching model discussed in Section 4.3 has so far only been employed to taxol-stabilized microtubules, for which there is the most experimental evidence (as taxol is the main microtubule stabilizer preventing further polymerization/depolymerization). In fact, many other molecules, especially microtubule-associated proteins, may also induce conformational changes of tubulin upon binding with different associated energy gains . This subject deserves further study as a new route for microtubule regulation that goes beyond the regulation of spatial distribution and length (as typically discussed in biology) towards a regulation of their mechanical behavior and response.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Rubinstein, M.; Colby, R. Polymer Physics; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Howard, J. Mechanics of Motor Proteins and the Cytoskeleton; Sinauer: Sunderland, MA, USA, 2001. [Google Scholar]
- Amos, L.A.; Amos, W.G. Molecules of the Cytoskeleton; Guilford Press: New York, NY, USA, 1991. [Google Scholar]
- Kulic, I.M.; Brown, A.E.X.; Kim, H.; Kural, C.; Blehm, B.; Selvin, P.R.; Nelson, P.C.; Gelfand, V.I. The role of microtubule movement in bidirectional organelle transport. Proc. Natl. Acad. Sci. USA 2008, 105, 10011. [Google Scholar] [CrossRef] [PubMed]
- Kruse, K.; Joanny, J.F.; Jülicher, F.; Prost, J.; Sekimoto, K. Asters, Vortices, and Rotating Spirals in Active Gels of Polar Filaments. Phys. Rev. Lett. 2004, 92, 078101. [Google Scholar] [CrossRef] [PubMed]
- Grosberg, A.Y.; Khokhlov, A.R. Statistical Physics of Macromolecules; AIP: New York, NY, USA, 1994. [Google Scholar]
- Hsu, H.P.; Paul, W.; Binder, K. Breakdown of the Kratky-Porod wormlike chain model for semiflexible polymers in two dimensions. EPL 2011, 95, 68004. [Google Scholar] [CrossRef]
- Flory, P.J. Statistical Mechanics of Chain Molecules; Oxford University Press: New York, NY, USA, 1988. [Google Scholar]
- Wittmer, J.P.; Beckrich, P.; Meyer, H.; Cavallo, A.; Johner, A.; Baschnagel, J. Intramolecular long-range correlations in polymer melts: The segmental size distribution and its moments. Phys. Rev. E 2007, 76, 011803. [Google Scholar] [CrossRef] [PubMed]
- Wittmer, J.P.; Cavallo, A.; Xu, H.; Zabel, J.; Polińska, P.; Schulmann, N.; Meyer, H.; Farago, J.; Johner, A.; Obukhov, S.; et al. Scale-free static and dynamical correlations in melts of monodisperse and Flory distributed homopolymers: A review of recent bond-fluctuation model studies. J. Stat. Phys. 2011, 145, 1017–1126. [Google Scholar] [CrossRef]
- Odijk, T. Polyelectrolytes near the rod limit. J. Polym. Sci. 1977, 15, 477. [Google Scholar] [CrossRef]
- Skolnick, J.; Fixman, M. Electrostatic Persistence Length of a Wormlike Polyelectrolyte. Macromolecules 1977, 10, 944. [Google Scholar] [CrossRef]
- Odijk, T. The statistics and dynamics of confined or entangled stiff polymers. Macromolecules 1983, 16, 1340. [Google Scholar] [CrossRef]
- Khokhlov, A.R.; Katchaturian, K.A. On the theory of weakly charged polyelectrolytes. Polymer 1982, 23, 1742. [Google Scholar] [CrossRef]
- Barrat, J.L.; Joanny, J.F. Theory of Polyelectrolyte Solutions. Adv. Chem. Phys. 1996, 94, 1. [Google Scholar]
- Ha, B.Y.; Thirumalai, D. Persistence length of flexible polyelectrolyte chains. J. Chem. Phys. 1999, 110, 7533. [Google Scholar] [CrossRef]
- Manghi, M.; Netz, R.R. Variational theory for a single polyelectrolyte chain revisited. Eur. Phys. J. E 2004, 14, 67. [Google Scholar] [CrossRef] [PubMed]
- Everaers, R.; Milchev, A.; Yamakov, V. The electrostatic persistence length of polymers beyond the OSF limit. Eur. Phys. J. E 2002, 8, 3. [Google Scholar] [CrossRef] [PubMed]
- Fleck, C.; Netz, R.R.; von Gruenberg, H.H. Poisson-Boltzmann theory for membranes with mobile charged lipids and the pH dependent interaction of a DNA molecule with a membrane. Biophys. J. 2002, 82, 76. [Google Scholar] [CrossRef]
- Lee, N.K.; Schmatko, T.; Muller, P.; Maaloum, M.; Johner, A. Shape of adsorbed supercoiled plasmids: An equilibrium description. Phys. Rev. E 2012, 85, 051804. [Google Scholar] [CrossRef] [PubMed]
- Samaj, L.; Trizac, E. Counterions at Highly Charged Interfaces: From One Plate to Like-Charge Attraction. Phys. Rev. Lett. 2011, 106, 078301. [Google Scholar] [CrossRef] [PubMed]
- Winkler, R.G. Semiflexible Polymers in Shear Flow. Phys. Rev. Lett. 2006, 97, 128301. [Google Scholar] [CrossRef] [PubMed]
- Harasim, M.; Wunderlich, B.; Preleg, O.; Kröger, M.; Bausch, A.R. Direct Observation of the Dynamics of Semiflexible Polymers in Shear Flow. Phys. Rev. Lett. 2013, 110, 108302. [Google Scholar] [CrossRef] [PubMed]
- Winkler, R. Dynamics of semiflexible polymers. Polymers 2016. under review.
- Nam, G.M.; Johner, A.; Lee, N.K. Drift and diffusion of a confined semiflexible chain. Eur. Phys. J. E 2010, 32, 119. [Google Scholar] [CrossRef] [PubMed]
- Nyrkova, I.; Semenov, A.N. Dynamic scattering of semirigid macromolecules. Phys. Rev. E 2007, 76, 011802. [Google Scholar] [CrossRef] [PubMed]
- Everaers, R.; Jülicher, F.; Ajdari, A.; Maggs, A.C. Dynamic Fluctuations of Semiflexible Filaments. Phys. Rev. Lett. 1999, 82, 3717. [Google Scholar] [CrossRef]
- Thüroff, F.; Obermayer, B.; Frey, E. Longitudinal response of confined semiflexible polymers. Phys. Rev. E 2011, 83, 021802. [Google Scholar] [CrossRef] [PubMed]
- Carlier, M.F.; Pantaloni, D. Control of Actin Assembly Dynamics in Cell Motility. Minirev. J. Biol. Chem. 2007, 282, 23005. [Google Scholar] [CrossRef] [PubMed]
- Desai, A.; Mitchison, T.J. Microtubule Polymerization Dynamics. Annu. Rev. Cell Dev. Biol. 1997, 13, 83. [Google Scholar] [CrossRef] [PubMed]
- Padinhateeri, R.; Kolomeisky, A.; Lacoste, D. Random Hydrolysis Controls the Dynamic Instability of Microtubules. Biophys. J. 2012, 102, 1274. [Google Scholar] [CrossRef] [PubMed]
- Hamprecht, B.; Janke, W.; Kleinert, H. End-to-end distribution function of two-dimensional stiff polymers for all persistence lengths. Phys. Lett. A 2004, 330, 254–259. [Google Scholar] [CrossRef]
- Cardy, J.L.; Saleur, H. Universal distance ratios for two-dimensional polymers. J. Phys. A: Math. Gen. 1989, 22, L601–L604. [Google Scholar] [CrossRef]
- Zierenberg, J.; Marenz, M.; Janke, W. Dilute Semiflexible Polymers with Attraction: Collapse, Folding and Aggregation. Polymers 2016. under review.
- Duplantier, B.; Saleur, H. Exact Tricritical Exponents for Polymers at the theta Point in Two Dimensions. Phys. Rev. Lett. 1987, 59, 537. [Google Scholar] [CrossRef] [PubMed]
- Blöte, H.W.J.; Nienhuis, B. Critical behaviour and conformal anomaly of the O(n) model on the square lattice. J. Phys. A Math. Gen. 1989, 22, 1415–1438. [Google Scholar] [CrossRef]
- Vernier, E.; Jacobsen, J.L.; Saleur, H. A new look at the collapse of two-dimensional polymers. J. Stat. Mech. 2015, 2015, P09001. [Google Scholar] [CrossRef]
- Baumgärtner, A.; Yoon, D. Phase transition of lattice polymer systems. J. Chem. Phys. 1983, 79, 521. [Google Scholar] [CrossRef]
- Wittmer, J.P.; Paul, W.; Binder, K. Rouse and Reptation Dynamics at Finite Temperatures: A Monte Carlo Simulation. Macromolecules 1992, 25, 7211–7216. [Google Scholar] [CrossRef]
- Wittmer, J.P. Untersuchung des Einflusses der Kettensteifigkeit auf die Dynamik von Polymeren in der Schmelze mittels Monte-Carlo-Simulation. Master’s Thesis, Diplomarbeit, Johannes-Gutenberg Universität, Mainz, Germany, 1991. [Google Scholar]
- Milchev, A.; Landau, D. Monte-Carlo study of semiflexible living polymers. Phys. Rev. E 1995, 52, 6431. [Google Scholar] [CrossRef]
- Baschnagel, J.; Wittmer, J.P.; Meyer, H. Monte Carlo Simulation of Polymers: Coarse-Grained Models. In Computational Soft Matter: From Synthetic Polymers to Proteins; Attig, N., Ed.; NIC Series: Jülich, Germany, 2004; Volume 23, pp. 83–140. [Google Scholar]
- Vanderzande, C. Lattice Models of Polymers; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Jacobsen, J.; Kondev, J. Continuous melting of compact polymers. Phys. Rev. Lett. 2004, 92, 210601. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, J.; Kondev, J. Conformal field theory of the Flory model of polymer melting. Phys. Rev. E 2004, 69, 066108. [Google Scholar] [CrossRef] [PubMed]
- Hsu, H.P.; Binder, K. Effect of Chain Stiffness on the Adsorption Transition of Polymers. Macromolecules 2013, 46, 2496. [Google Scholar] [CrossRef]
- Allen, M.; Tildesley, D. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation—From Algorithms to Applications, 2nd ed.; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Binder, K.; Herrmann, D. Monte Carlo Simulation in Statistical Physics: An Introduction, Fifth ed.; Springer: Heidelberg, Germany, 2002. [Google Scholar]
- Landau, D.P.; Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Carmesin, I.; Kremer, K. The bond fluctuation method: A new effective algorithm for the dynamics of polymers in all spatial dimensions. Macromolecules 1988, 21, 2819. [Google Scholar] [CrossRef]
- Carmesin, I.; Kremer, K. Static and dynamic properties of 2-dimensional polymer melts. J. Phys. 1990, 51, 915. [Google Scholar] [CrossRef]
- Deutsch, H.; Binder, K. Interdiffusion and self-diffusion in polymer mixtures: A Monte Carlo study. J. Chem. Phys. 1991, 94, 2294. [Google Scholar] [CrossRef]
- Grest, G.S.; Kremer, K. Molecular-dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 1986, 33, 3628. [Google Scholar] [CrossRef]
- Plimpton, S.J. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Gerroff, I.; Milchev, A.; Binder, K.; Paul, W. A new off-lattice Monte-Carlo model for polymers—A comparison of static and dynamic properties with the bond-fluctuation model and application to random-media. J. Chem. Phys. 1993, 98, 6526. [Google Scholar] [CrossRef]
- Milchev, A.; Paul, W.; Binder, K. Off-lattice Monte-Carlo simulation of dilute and concentrated polymer-solutions under theta conditions. J. Chem. Phys. 1993, 99, 4786. [Google Scholar] [CrossRef]
- Milchev, A.; Binder, K. Anomalous diffusion and relaxation of collapsed polymer-chains. Euro. Phys. Lett. 1994, 26, 671. [Google Scholar] [CrossRef]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Duplantier, B. Exact contact critical exponents of a self-avoiding polymer chain in two dimensions. Phys. Rev. B 1987, 35, 5290–5293. [Google Scholar] [CrossRef]
- Duplantier, B. Statistical Mechanics of Polymer Networks of Any Topology. J. Stat. Phys. 1989, 54, 581. [Google Scholar] [CrossRef]
- Semenov, A.N.; Johner, A. Theoretical notes on dense polymers in two dimensions. Eur. Phys. J. E 2003, 12, 469. [Google Scholar] [CrossRef] [PubMed]
- Nelson, P.H.; Hatton, T.A.; Rutledge, G. General reptation and scaling of 2d athermal polymers on close-packed lattices. J. Chem. Phys. 1997, 107, 1269. [Google Scholar] [CrossRef]
- Yethiraj, A. Computer simulation study of two-dimensional polymer solutions. Macromolecules 2003, 36, 5854. [Google Scholar] [CrossRef]
- Meyer, H.; Kreer, T.; Aichele, M.; Cavallo, A.; Johner, A.; Baschnagel, J.; Wittmer, J.P. Perimeter length and form factor in two-dimensional polymer melts. Phys. Rev. E 2009, 79, 050802. [Google Scholar] [CrossRef] [PubMed]
- Meyer, H.; Wittmer, J.P.; Kreer, T.; Johner, A.; Baschnagel, J. Static properties of polymer melts in two dimensions. J. Chem. Phys. 2010, 132, 184904. [Google Scholar] [CrossRef]
- Schulmann, N.; Meyer, H.; Kreer, T.; Cavallo, A.; Johner, A.; Baschnagel, J.; Wittmer, J.P. Strictly two-dimensional self-avoiding walks: Density crossover scaling. Polym. Sci. Ser. C 2013, 55, 990–1020. [Google Scholar] [CrossRef]
- Maier, B.; Rädler, J.O. Conformation and self-diffusion of single DNA molecules confined to two dimensions. Phys. Rev. Lett. 1999, 82, 1911. [Google Scholar] [CrossRef]
- Maier, B.; Rädler, J.O. DNA on fluid membranes: A model polymer in two dimensions. Macromolecules 2000, 33, 7185. [Google Scholar] [CrossRef]
- Sun, F.; Dobrynin, A.; Shirvanyants, D.; Lee, H.; Matyjaszewski, K.; Rubinstein, G.; Rubinstein, M.; Sheiko, S. Flory theorem for structurally asymmetric mixtures. Phys. Rev. Lett. 2007, 99, 137801. [Google Scholar] [CrossRef] [PubMed]
- Nikomarov, E.; Obukhov, S. Extended description of a solution of linear polymers based on a polymer-magnet analogy. Sov. Phys. JETP 1981, 53, 328–335. [Google Scholar]
- Cavallo, A.; Müller, M.; Binder, K. Anomalous Scaling of the Critical Temperature of Unmixing with Chain Length for Two-Dimensional Polymer Blends. Europhys. Lett. 2003, 61, 214–220. [Google Scholar] [CrossRef]
- Maier, B.; Rädler, J.O. Shape of self-avoiding walks in two dimension. Macromolecules 2001, 34, 5723. [Google Scholar] [CrossRef]
- Cavallo, A.; Müller, M.; Binder, K. Unmixing of Polymer Blends Confined in Ultrathin Films: Crossover between Two-Dimensional and Three-Dimensional Behavior. J. Phys. Chem. B 2005, 109, 6544. [Google Scholar] [CrossRef] [PubMed]
- Schulmann, N.; Meyer, H.; Wittmer, J.P.; Johner, A.; Baschnagel, J. Interchain monomer contact probability in two-dimensional polymer solutions. Macromolecules 2012, 45, 1646. [Google Scholar] [CrossRef]
- Gallyamov, M.; Tartsch, B.; Potemkin, I.; Börner, H.; Matyjaszewski, K.; Khokhlov, A.; Möller, M. Individual brush molecules in dense 2D layers restoring high degree of extension after collapse-decollapse cycle: Directly measured scaling exponents. Eur. Phys. J. E 2009, 29, 73–85. [Google Scholar] [CrossRef] [PubMed]
- Arriaga, L.R.; Monroy, F.; Langevin, D. Influence of backbond rigidity on the surface rheology of acrylic Langmuir polymer films. Soft Matter 2011, 7, 7754. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G. Dynamics of entangled linear polymer melts: A molecular dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Schulmann, N.; Xu, H.; Meyer, H.; Polińska, P.; Baschnagel, J.; Wittmer, J.P. Strictly two-dimensional self-avoiding walks: Thermodynamic properties revisited. Eur. Phys. J. E 2012, 35, 93. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, J.L.; Alet, F. Semiflexible Fully Packed Loop Model and Interacting Rhombus Tilings. Phys. Rev. Lett. 2009, 102, 145702. [Google Scholar] [CrossRef] [PubMed]
- Semenov, A.N.; Obukhov, S.P. Fluctuation-induced long-range interactions in polymer systems. J. Phys.: Cond. Matt. 2005, 17, S1747. [Google Scholar] [CrossRef]
- Hsu, H.P.; Kremer, K. Static and dynamic properties of large polymer melts in equilibrium. J. Chem. Phys. 2016, 144, 154907. [Google Scholar] [CrossRef] [PubMed]
- Janke, W. Computer Simulation Studies of Polymer Adsorption and Aggregation—From Flexible to Stiff. Phys. Procedia 2015, 68, 69–79. [Google Scholar] [CrossRef]
- Linse, P.; Kallrot, N. Polymer Adsorption from Bulk Solution onto Planar Surfaces: Effect of Polymer Flexibility and Surface Attraction in Good Solvent. Macromolecules 2010, 43, 2054. [Google Scholar] [CrossRef]
- De Gennes, P.G. Polymers at an interface; a simplified view. Adv. Colloid Interface Sci. 1987, 27, 189. [Google Scholar] [CrossRef]
- Semenov, A.N.; Bonet-Avalos, J.; Johner, A.; Joanny, J.F. Adsorption of Polymer Solutions onto a Flat Surface. Macromolecules 1996, 29, 2179. [Google Scholar] [CrossRef]
- Konstadinidis, K.; Prager, S.; Tirrell, M. Monte Carlo simulation of irreversible polymer adsorption: Single chains. J. Chem. Phys. 1992, 97, 7777. [Google Scholar] [CrossRef]
- Konstadinidis, K.; Thakkar, B.; Chakraborty, A.; Potts, L.W.; Tannenbaum, R.; Tirrell, M.; Evans, J.F. Segment level chemistry and chain conformation in the reactive adsorption of poly(methyl methacrylate) on aluminum oxide surfaces. Langmuir 1992, 8, 1307. [Google Scholar] [CrossRef]
- Fleer, G.; Stuart, M.A.; Scheutjens, J.M.H.M.; Cosgrove, T.; Vincent, B. Polymers at Interfaces; Chapman and Hall: London, UK, 1993. [Google Scholar]
- Semenov, A.N.; Joanny, J.F. Structure of Adsorbed Polymer Layers: Loops and Tails. Europhys. Lett. 1995, 29, 279. [Google Scholar] [CrossRef]
- Semenov, A.N. Adsorption of a semiflexible wormlike chain. Eur. Phys. J. E 2002, 9, 353. [Google Scholar] [CrossRef] [PubMed]
- Lee, N.K.; Jung, Y.K.; Johner, A. Irreversible Adsorption of Worm-Like Chains. Macromolecules 2015, 48, 7681. [Google Scholar] [CrossRef]
- De Gennes, P.G. Polymer solutions near an interface. Adsorption and depletion layers. Macromolecules 1981, 14, 1637. [Google Scholar] [CrossRef]
- Maggs, A.C.; Huse, D.A.; Leibler, S. Unbinding Transitions of Semi-flexible Polymers. Europhys. Lett. 1989, 8, 615. [Google Scholar] [CrossRef]
- Kuznetsov, D.V.; Sung, W. A Greenś function perturbation theory for nonuniform semiflexible polymers: Phases and their transitions near attracting surfaces. J. Chem. Phys. 1997, 107, 4729. [Google Scholar] [CrossRef]
- Kuznetsov, D.V.; Sung, W. Semiflexible Polymers near Attracting Surfaces. Macromolecules 1998, 31, 2679. [Google Scholar] [CrossRef]
- Kuznetsov, D.V.; Sung, W. A New Scaling Theory of Semiflexible Polymer Phases Near Attracting Surfaces. J. Phys. II 1997, 7, 1287. [Google Scholar] [CrossRef]
- Deng, M.; Jiang, Y.; Liang, H.; Chen, J.Z.Y. Adsorption of a wormlike polymer in a potential well near a hard wall: Crossover between two scaling regimes. J. Chem. Phys. 2010, 133, 034902. [Google Scholar] [CrossRef] [PubMed]
- O’Shaughnessy, B.; Vavylonis, D. Irreversibility and Polymer Adsorption. Phys. Rev. Lett. 2003, 2, 056103. [Google Scholar] [CrossRef] [PubMed]
- O’Shaughnessy, B.; Vavylonis, D. Irreversible adsorption from dilute polymer solutions. Eur. Phys. J. E 2003, 11, 213. [Google Scholar] [CrossRef] [PubMed]
- O’Shaughnessy, B.; Vavylonis, D. The slowly formed Guiselin brush. EPL 2003, 63, 895. [Google Scholar] [CrossRef]
- O’Shaughnessy, B.; Vavylonis, D. Non-Equilibrium in Adsorbed Polymer Layers. J. Phys.: Condens. Matter 2005, 17, R63–R99. [Google Scholar] [CrossRef]
- Tarjus, G.; Viot, P. Asymptotic results for the random sequential addition of unoriented objects. Phys. Rev. Lett. 1991, 67, 1875. [Google Scholar] [CrossRef] [PubMed]
- Viot, P.; Tarjus, G.; Ricci, S.; Talbot, J. Random sequential adsorption of anisotropic particles. I. Jamming limit and asymptotic behavior. J. Chem. Phys. 1992, 97, 5212. [Google Scholar] [CrossRef]
- Lee, N.K.; Jung, Y.K.; Johner, A. Crossing and alignment of irreversibly adsorbed Worm-Like-Chains. (in Preparation)
- Sanchez, T.; Kulić, I.M.; Dogic, Z. Circularization, Photomechanical Switching, and a Supercoiling Transition of Actin Filaments. Phys. Rev. Lett. 2010, 104, 098103. [Google Scholar] [CrossRef] [PubMed]
- Pampaloni, F.; Lattanzi, G.; Jonas, A.; Surrey, T.; Frey, E.; Florin, E.L. Thermal fluctuations of grafted microtubules provide evidence of a length-dependent persistence length. Proc. Natl. Acad. Sci. USA 2006, 103, 10248. [Google Scholar] [CrossRef] [PubMed]
- Taute, K.M.; Pampaloni, F.; Frey, E.; Florin, E.L. Microtubule Dynamics Depart from the Wormlike Chain Model. Phys. Rev. Lett. 2008, 100, 028102. [Google Scholar] [CrossRef] [PubMed]
- Roos, J.; Hummel, T.; Ng, N.; Klämbt, C.; Davis, G.W. Drosophila Futsch Regulates Synaptic Microtubule Organization and Is Necessary for Synaptic Growth. Neuron 2000, 26, 371. [Google Scholar] [CrossRef]
- Conde, C.; Cáceres, A. Microtubule assembly, organization and dynamics in axons and dendrites. Nat. Rev. Neurosci. 2009, 10, 319. [Google Scholar] [CrossRef] [PubMed]
- Amos, L.A.; Amos, W.B. The bending of sliding microtubules imaged by confocal light microscopy and negative stain electron microscopy. J. Cell Sci. Suppl. 1991, 14, 95. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Tüzel, E.; Ross, J.L. Loop formation in microtubules during gliding at high density. J. Phys. Condens. Matter 2011, 23, 374104. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Reedy, M.; Erickson, H.P. Straight and Curved Conformations of FtsZ Are Regulated by GTP Hydrolysis. J. Bacteriol. 2000, 182, 164. [Google Scholar] [CrossRef] [PubMed]
- Van den Ent, F.; Amos, L.; Löwe, J. Prokaryotic origin of the actin cytoskeleton. Nature 2001, 413, 39. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, E.; Kamiya, R.; Asakura, S. Thermal transition in helical forms of Salmonella flagella. J. Mol. Biol. 1982, 160, 609. [Google Scholar] [CrossRef]
- Li, X.E.; Holmes, K.C.; Lehman, W.; Jung, H.; Fischer, S. The shape and flexibility of tropomyosin coiled coils: Implications for actin filament assembly and regulation. J. Mol. Biol. 2010, 395, 327. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, H.; Aebi, U. Intermediate filaments: Molecular structure, assembly mechanism, and integration into functionally distinct intracellular Scaffolds. Annu. Rev. Biochem. 2004, 73, 749. [Google Scholar] [CrossRef] [PubMed]
- Li, L.S.; Jiang, H.; Messmore, B.W.; Bull, S.R.; Stupp, S.I. A torsional strain mechanism to tune pitch in supramolecular helices. Angew. Chem. Int. Ed. 2007, 46, 5873. [Google Scholar] [CrossRef] [PubMed]
- Wolgemuth, C.W.; Inclan, Y.F.; Quan, J.; Mukherjee, S.; Oster, G.; Koehl, M.A.R. How to make a spiral bacterium. Phys. Biol. 2005, 2, 189. [Google Scholar] [CrossRef] [PubMed]
- Bouzar, L.; Müller, M.M.; Gosselin, P.; Kulic, I.M.; Mohrbach, H. Squeezed Helical Elastica. 2016; arXiv 1606.03611. [Google Scholar]
- Kamien, R.D. The geometry of soft materials: A primer. Rev. Mod. Phys. 2002, 74, 953. [Google Scholar] [CrossRef]
- Chouaieb, N.; Goriely, A.; Maddocks, J.H. Helices. Proc. Natl. Acad. Sci. USA 2006, 103, 9398. [Google Scholar] [CrossRef] [PubMed]
- Nam, G.M.; Lee, N.-K.; Mohrbach, H.; Johner, A.; Kulić, I. Helices at interfaces. EPL 2012, 100, 28001. [Google Scholar] [CrossRef]
- Lee, N.-K.; Johner, A. Defects on semiflexible filaments: Kinks and twist kinks. JKPS 2016, 68, 923. [Google Scholar] [CrossRef]
- Fierling, J.; Mohrbach, H.; Kulić, I.K.; Lee, N.K.; Johner, A. Biofilaments as annealed semi-flexible copolymers. EPL 2014, 106, 58006. [Google Scholar] [CrossRef]
- Wang, F.; Landau, D.P. Efficient, Multiple-Range Random Walk Algorithm to Calculate the Density of States. Phys. Rev. Lett. 2001, 86, 2050. [Google Scholar] [CrossRef] [PubMed]
- Everaers, R.; Bundschuh, R.; Kremer, K. Fluctuations and Stiffness of Double-Stranded Polymers: Railway-Track Model. EPL 1995, 29, 263. [Google Scholar] [CrossRef]
- Mohrbach, H.; Kulić, I. Motor Driven Microtubule Shape Fluctuations: Force from within the Lattice. Phys. Rev. Lett. 2007, 99, 218102. [Google Scholar] [CrossRef] [PubMed]
- Heussinger, C.; Bathe, M.; Frey, E. Statistical Mechanics of Semiflexible Bundles of Wormlike Polymer Chains. Phys. Rev. Lett. 2007, 99, 048101. [Google Scholar] [CrossRef] [PubMed]
- Sekimoto, K.; Prost, J. Elastic Anisotropy Scenario for Cooperative Binding of Kinesin-Coated Beads on Microtubules. J. Phys. Chem. B 2016, 120, 5953. [Google Scholar] [CrossRef] [PubMed]
- Mohrbach, H.; Johner, A.; Kulić, I. Cooperative lattice dynamics and anomalous fluctuations of microtubules. Eur. Biophys. J . 2012, 41, 217. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, B.; Lavery, R. DNA structural forms. Q. Rev. Biophys. 1996, 29, 309. [Google Scholar] [CrossRef] [PubMed]
- Son, A.; Kwon, A.Y.; Johner, A.; Hong, S.C.; Lee, N.K. Underwound DNA under tension: L-DNA vs. plectoneme. Europhys. Lett. 2014, 105, 48002. [Google Scholar] [CrossRef]
- Egelman, E.H. Actin allostery again? Nat. Struc. Biol. 2001, 8, 735. [Google Scholar] [CrossRef] [PubMed]
- Fierling, J.; Müller, M.M.; Mohrbach, H.; Johner, A.; Kulić, I.K. Crunching biofilament rings. EPL 2014, 107, 68002. [Google Scholar] [CrossRef]
- Italiano, J.E.; Lecine, P.; Shivdasani, R.A.; Hartwig, J.H. Blood Platelets Are Assembled Principally at the Ends of Proplatelet Processes Produced by Differentiated Megakaryocytes. J. Cell Biol. 1999, 147, 1299. [Google Scholar] [CrossRef] [PubMed]
- Müller-Reichert, T.; Chrétien, D.; Severin, F.; Hyman, A.A. Structural changes at microtubule ends accompanying GTP hydrolysis: Information from a slowly hydrolyzable analogue of GTP, guanylyl (alpha, beta)methylenediphosphonate. Proc. Natl. Acad. Sci. USA 1998, 95, 3661. [Google Scholar] [CrossRef] [PubMed]
- Elie-Caille, C.; Severin, F.; Helenius, J.; Howard, J.; Muller, D.J.; Hyman, A.A. Straight GDP-tubulin protofilaments form in the presence of taxol. Curr. Biol. 2007, 17, 1765. [Google Scholar] [CrossRef] [PubMed]
- Arnal, I.; Wade, R.H. How does taxol stabilize microtubules? Curr. Biol. 1995, 5, 900. [Google Scholar] [CrossRef]
- Ziebert, F.; Mohrbach, H.; Kulić, I.M. Why Microtubules Run in Circles: Mechanical Hysteresis of the Tubulin Lattice. Phys. Rev. Lett. 2015, 114, 148101. [Google Scholar] [CrossRef] [PubMed]
- Mohrbach, H.; Johner, A.; Kulić, I.M. Tubulin Bistability and Polymorphic Dynamics of Microtubules. Phys. Rev. Lett. 2010, 105, 268102. [Google Scholar] [CrossRef] [PubMed]
- Nödig, B.; Köster, S. Intermediate Filaments in Small Configuration Spaces. Phys. Rev. Lett. 2012, 108, 088101. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Gomez, E.D.; Milner, S.T. Surface-Induced Chain Alignment of Semiflexible Polymers. Macromolecules 2016, 49, 963. [Google Scholar] [CrossRef]
- Carrillo, J.M.Y.; Cheng, S.; Kumar, R.; Goswami, M.; Sokolov, A.P.; Sumpter, B.G. Untangling the Effects of Chain Rigidity on the Structure and Dynamics of Strongly Adsorbed Polymer Melts. Macromolecules 2015, 48, 4207. [Google Scholar] [CrossRef]
- Fierling, J.; Johner, A.; Kulić, I.M.; Mohrbach, H.; Müller, M.M. How Bio-Filaments Twist Membranes. Soft Matter 2016, 12, 5747. [Google Scholar] [CrossRef] [PubMed]
- Zhan, D.; Chai, A.; Wen, X.; He, L.; Zhang, L.; Liang, H. Ordered regular pentagons for semiflexible polymers on soft elastic shells. Soft Matter 2012, 8, 2152. [Google Scholar] [CrossRef]
- Nam, G.; Johner, A.; Lee, N.K. Reptation of a semiflexible polymer through porous media. J. Chem. Phys. 2010, 133, 044908. [Google Scholar] [CrossRef] [PubMed]
- Milchev, A. Single-polymer dynamics under constraints: Scaling theory and computer experiment. J. Phys.-Condens. Mat. 2011, 23, 103101. [Google Scholar] [CrossRef] [PubMed]
- Lam, P.M.; Zhen, Y. A wormlike chain model of forced desorption of a polymer adsorbed on an attractive wall. J. Stat. Mech. 2014, 4, P04020. [Google Scholar] [CrossRef]
- Kulic, I.M.; Schiessel, H. DNA Spools under Tension. Phys. Rev. Lett. 2004, 92, 228101. [Google Scholar] [CrossRef] [PubMed]
- Kunze, K.K.; Netz, R.R. Complexes of semiflexible polyelectrolytes and charged spheres as models for salt-modulated nucleosomal structures. Phys. Rev. E 2002, 66, 011918. [Google Scholar] [CrossRef] [PubMed]
- Waters, J.T.; Kim, H.D. Equilibrium Statistics of a Surface-Pinned Semiflexible Polymer. Macromolecules 2013, 46, 6659. [Google Scholar] [CrossRef]
- Pickett, G.T.; Witten, T.A. End-grafted polymer melt with nematic interaction. Macromolecules 1992, 25, 4569. [Google Scholar] [CrossRef]
- Egorov, S.A.; Hsu, H.P.; Milchev, A.; Binder, K. Semiflexible polymer brushes and the brush-mushroom crossover. Soft Matter 2015, 11, 2604. [Google Scholar] [CrossRef] [PubMed]
- Nyrkova, I.; Semenov, A.; Joanny, J.F.; Khokhlov, A. Highly Anisotropic Rigidity of “Ribbon-like” Polymers: I. Chain Conformation in Dilute Solutions. J. Phys. II 1996, 6, 1411. [Google Scholar] [CrossRef]
- Nyrkova, I.; Semenov, A.; Joanny, J.F. Highly Anisotropic Rigidity of “Ribbon-Like” Polymers: II. Nematic Phases in Systems between Two and Three Dimensions. J. Phys. II (Paris) 1997, 7, 625. [Google Scholar] [CrossRef]
- Davies, R.P.W.; Aggeli, A.; Beevers, A.J.; Boden, N.; Carrick, L.M.; Fishwick, C.W.G. Self-assembling beta-sheet tape forming peptides. Supramol. Chem. 2006, 18, 435–443. [Google Scholar] [CrossRef]
- Simon, F.X.; T.Nguyen, T.T.; Diaz, N.; Schmutz, M.; Demé, B.; Jestin, J.; Combet, J.; Mésini, P.J. Self-assembling properties of a series of homologous ester-diamides: From ribbons to nanotubes. Soft Matter 2013, 9, 8483. [Google Scholar] [CrossRef]
- Quint, D.A.; Gopinathan, A.; Grason, G.M. Conformational collapse of surface-bound helical filaments. Soft Matter 2012, 8, 9460. [Google Scholar] [CrossRef]
- Sussman, D.M.; Schweitzer, K.S. Microscopic Theory of Entangled Polymer Melt Dynamics: Flexible Chains as Primitive-Path Random Walks and Supercoarse Grained Needles. Phys. Rev. Lett. 2012, 109, 168306. [Google Scholar] [CrossRef] [PubMed]
- Granek, R. From Semi-Flexible Polymers to Membranes: Anomalous Diffusion and Reptation. J. Phys. II 1997, 7, 1761. [Google Scholar] [CrossRef]
- Fricke, N.; Sturm, S.; Lämmel, M.; Schöbl, S.; Kroy, K.; Janke, W. Polymers in disordered environments. Diffus. Fundam. 2015, 23, 7. [Google Scholar]
- Biswal, S.L.; Gast, A.P. Mechanics of semiflexible chains formed by poly(ethylene glycol)-linked paramagnetic particles. Phys. Rev. E 2003, 68, 021402. [Google Scholar] [CrossRef] [PubMed]
- Gosselin, P.; Mohrbach, H.; Kulic, I.M.; Ziebert, F. On complex, curved trajectories in microtubule gliding. Phys. D-Nonlinear Phenom. 2016, 318–319, 105. [Google Scholar] [CrossRef]
- Böhm, K.J.; Stracke, R.; Vater, W.; Unger, E. Inhibition of kinesin-driven microtubule motility by polyhydroxy compounds. In Micro- and Nanostructures of Biological Systems; Hein, H.J., Bischoff, G., Eds.; Shaker Verlag: Aachen, Germany, 2001; pp. 153–165. [Google Scholar]
- Muto, E.; Sakai, H.; Kaseda, K. Long-range Cooperative Binding of Kinesin to a Microtubule in the Presence of ATP. J. Cell Biol. 2005, 168, 691. [Google Scholar] [CrossRef] [PubMed]

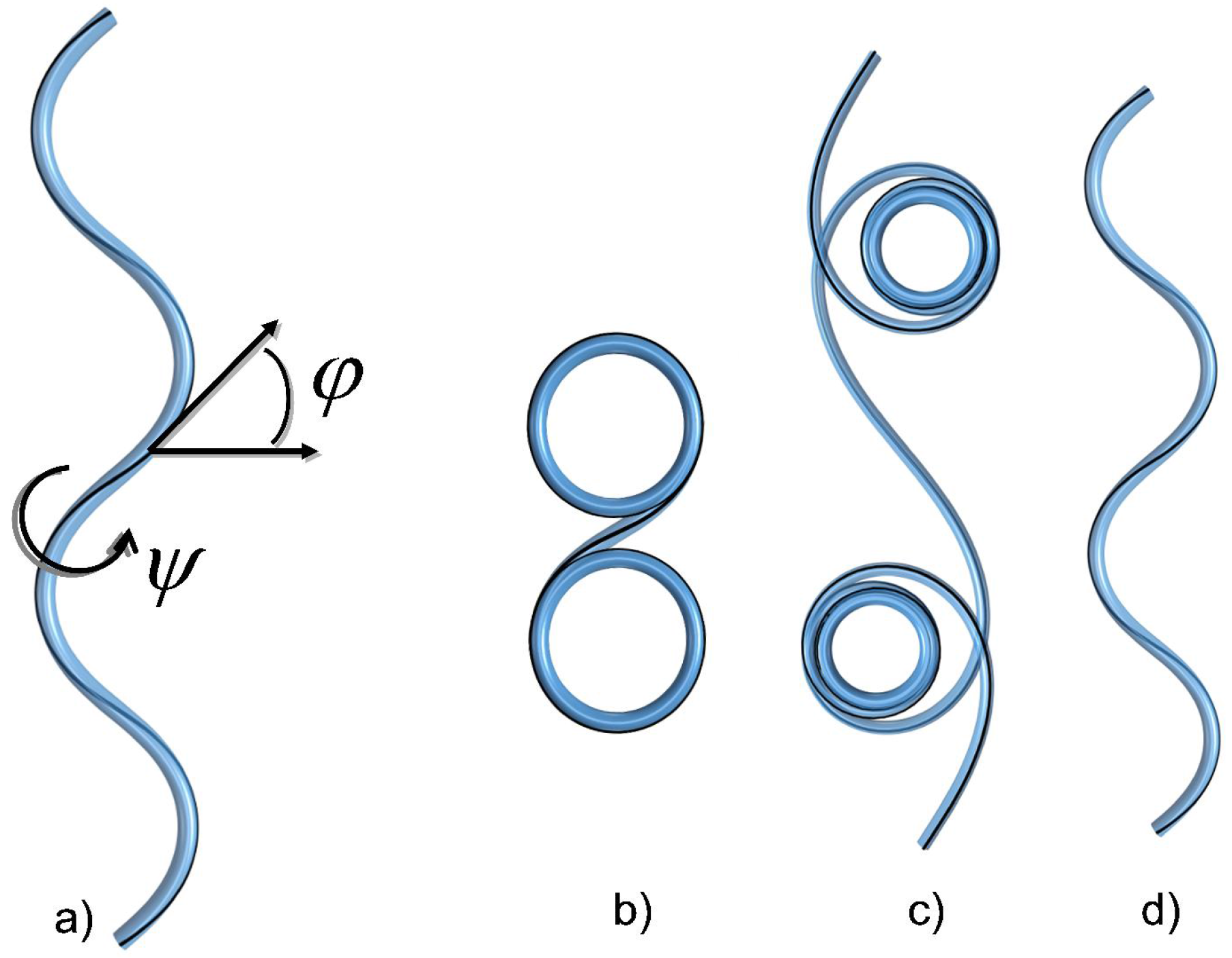

| ℓ (nm) | b (nm) | ||
|---|---|---|---|
| PE (Dodecanol1) | 0.59 | 0.13 | 4.5 |
| PIB (Benzene) | 0.59 | 0.26 | 2.3 |
| PS (Cyclohexane) | 0.86 | 0.26 | 3.3 |
| PDMS (Hexane) | 0.57 | 0.29 | 2 |
| NaPSS (high salt) | 1.0 | 0.25 | 4 |
| PDADMAC (high salt) | 3.0 | 0.47 | 5.3 |
| HA (high salt) | 4–5; 7–10 | 1.0 | 4–5; 7–10 |
| d-DNA | 50 | 0.34 | 150 |
| IF | 10 | ∼10 | ∼100 |
| F-actin | 17 × 10 | 5 | 3400 |
| ℓ (nm) | b (nm) | (nm) | (nm) | |
|---|---|---|---|---|
| PE (dodecanol1) | 0.59 | 0.13 | 0.21 | 1.6 |
| PIB (benzene) | 0.59 | 0.26 | 0.34 | 1 |
| PS (cyclohexane) | 0.86 | 0.26 | 0.38 | 1.9 |
| PDMS (hexane) | 0.57 | 0.29 | 0.36 | 0.90 |
| NAPSS (high salt) | 1.0 | 0.25 | 0.39 | 2.5 |
| PDADMAC (high salt) | 3.0 | 0.47 | 0.80 | 7.6 |
| HA (high salt) | 4–5; 7–10 | 1.0 | 1.6–2 | 12–35 |
| d-DNA | 50 | 0.34 | ∼1.8 | ∼ 1.4 × 10 |
| IF | 10 | ∼ 10 | ∼46 | ∼ 2 × 10 |
| F-actin | 17 × 10 | 5 | ∼75 | 3 × 10 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baschnagel, J.; Meyer, H.; Wittmer, J.; Kulić, I.; Mohrbach, H.; Ziebert, F.; Nam, G.-M.; Lee, N.-K.; Johner, A. Semiflexible Chains at Surfaces: Worm-Like Chains and beyond. Polymers 2016, 8, 286. https://doi.org/10.3390/polym8080286
Baschnagel J, Meyer H, Wittmer J, Kulić I, Mohrbach H, Ziebert F, Nam G-M, Lee N-K, Johner A. Semiflexible Chains at Surfaces: Worm-Like Chains and beyond. Polymers. 2016; 8(8):286. https://doi.org/10.3390/polym8080286
Chicago/Turabian StyleBaschnagel, Jörg, Hendrik Meyer, Joachim Wittmer, Igor Kulić, Hervé Mohrbach, Falko Ziebert, Gi-Moon Nam, Nam-Kyung Lee, and Albert Johner. 2016. "Semiflexible Chains at Surfaces: Worm-Like Chains and beyond" Polymers 8, no. 8: 286. https://doi.org/10.3390/polym8080286
APA StyleBaschnagel, J., Meyer, H., Wittmer, J., Kulić, I., Mohrbach, H., Ziebert, F., Nam, G.-M., Lee, N.-K., & Johner, A. (2016). Semiflexible Chains at Surfaces: Worm-Like Chains and beyond. Polymers, 8(8), 286. https://doi.org/10.3390/polym8080286







