The Connection between Biaxial Orientation and Shear Thinning for Quasi-Ideal Rods
Abstract
:1. Introduction
2. Theory
2.1. Smoluchowski Theory
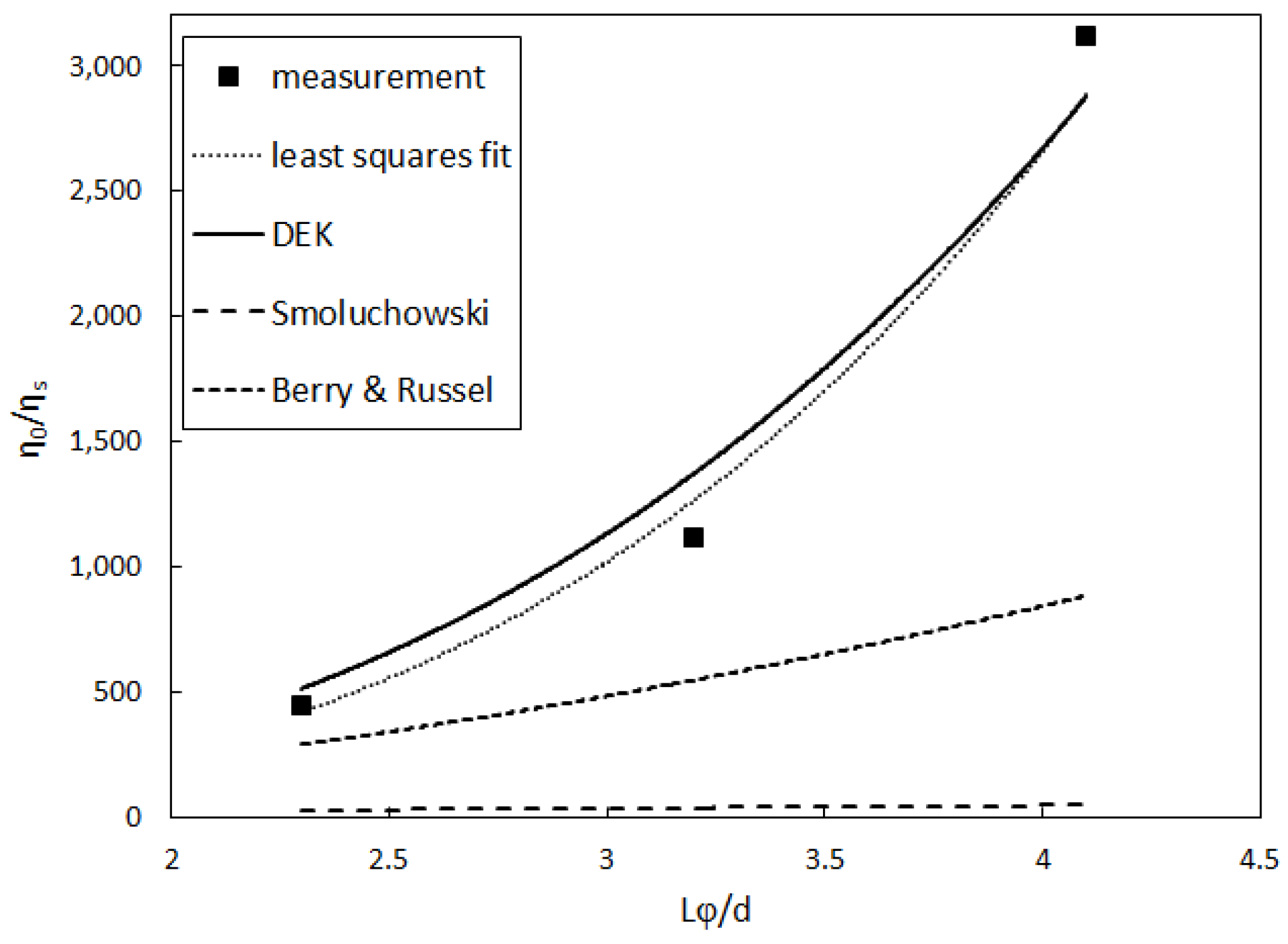
2.2. Doi–Edwards–Kuzuu (DEK) Theory
2.3. Scaling
3. Experiments, Materials and Methods
3.1. Measurements and Materials
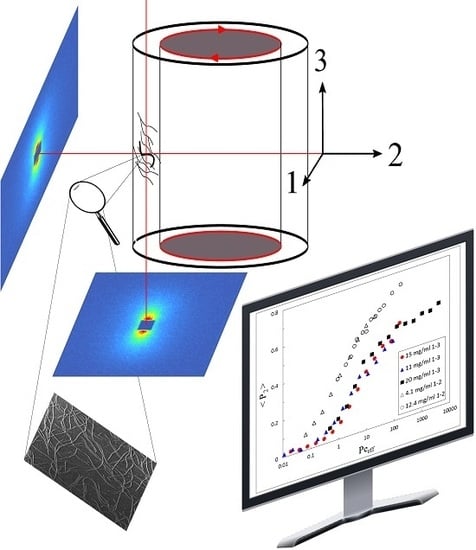
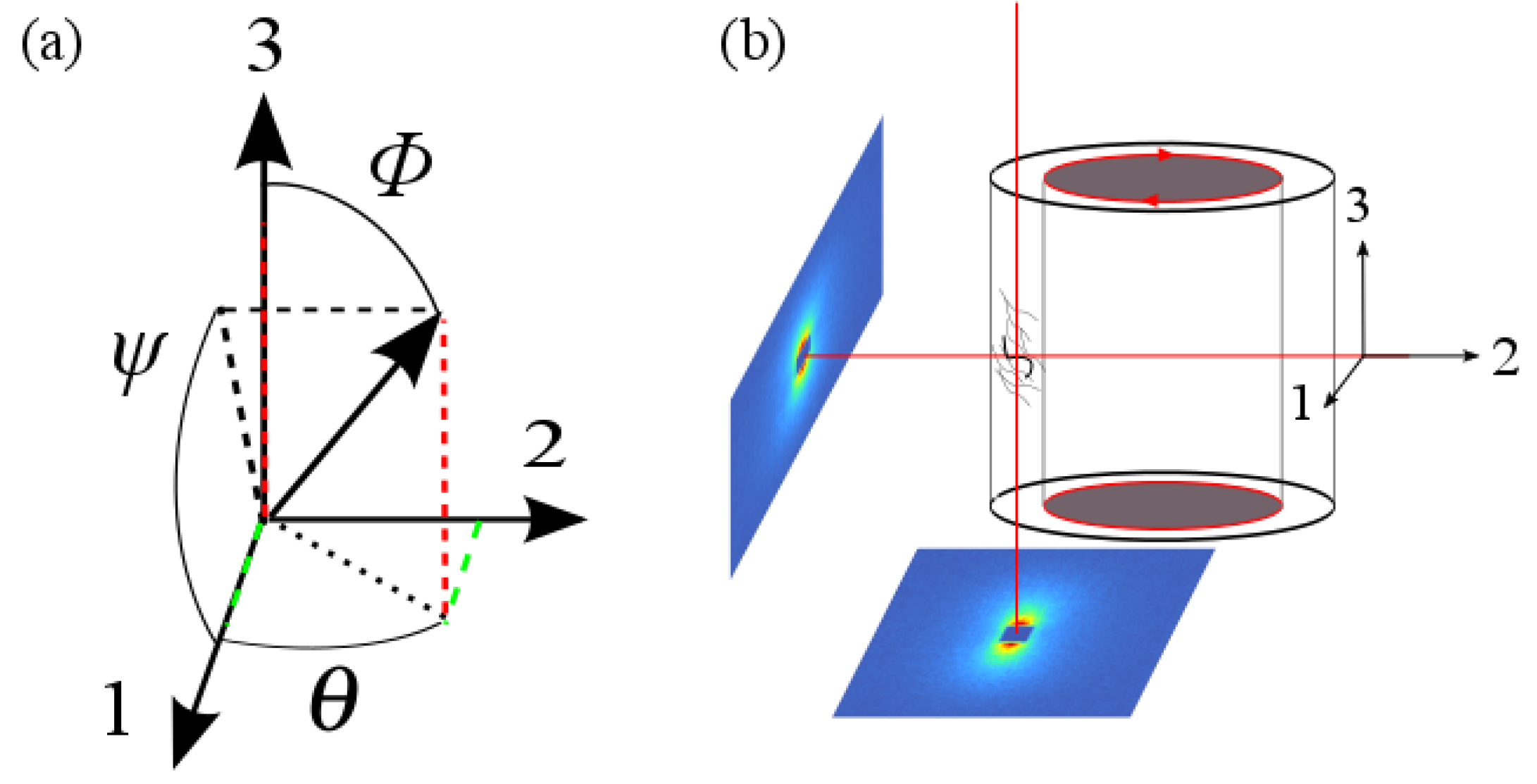
3.2. Obtaining the Full Orientation Tensor and the Biaxiality
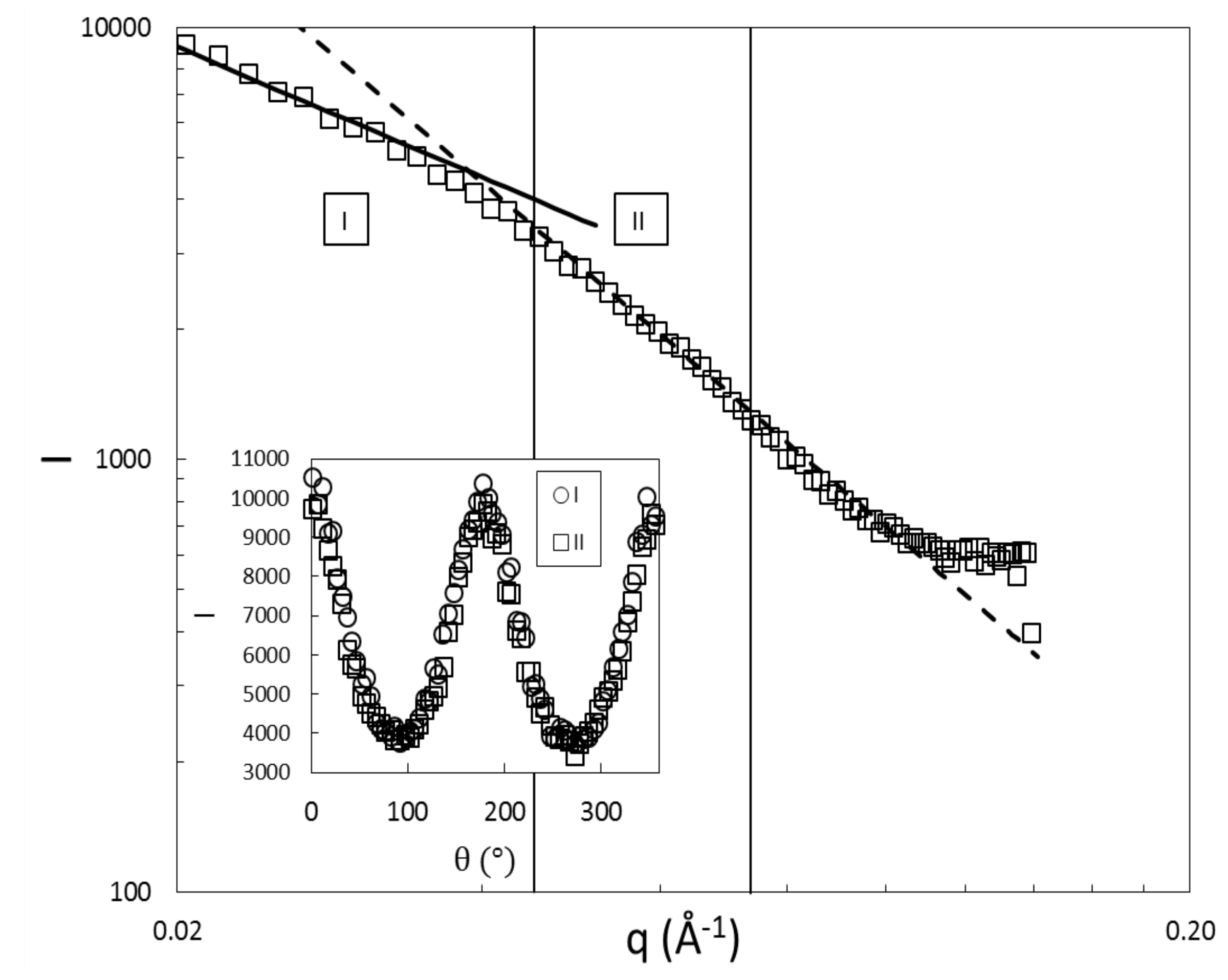
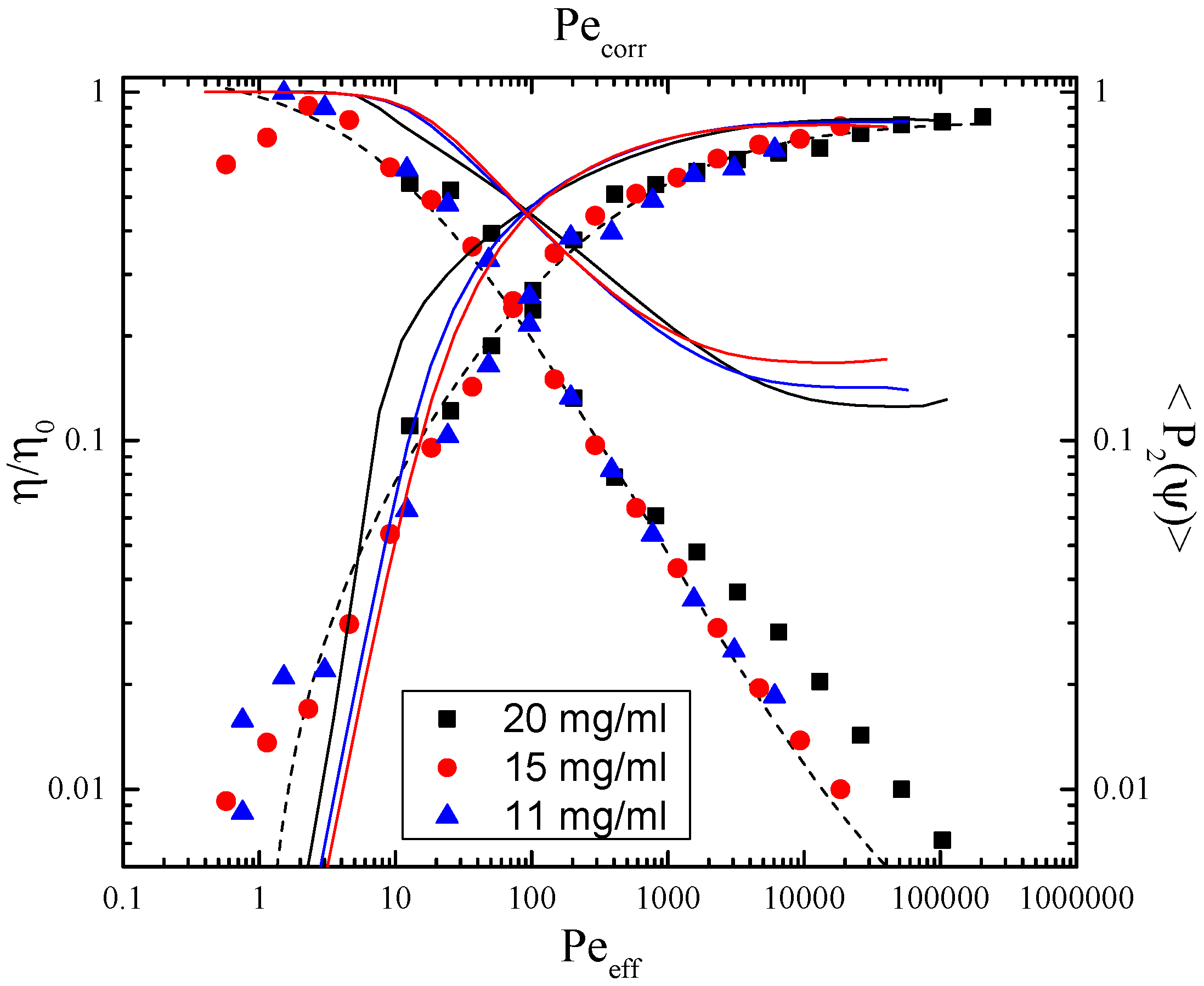
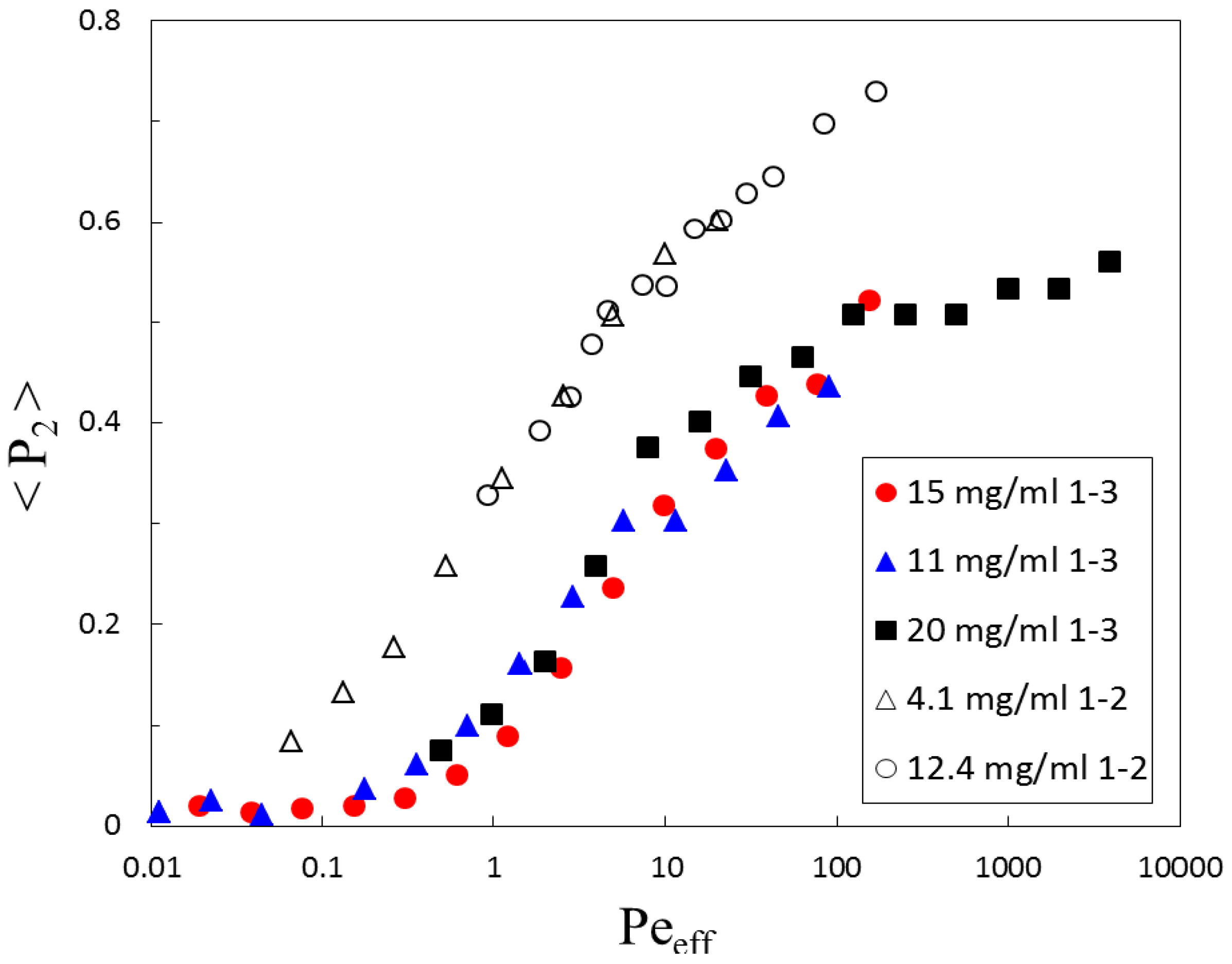
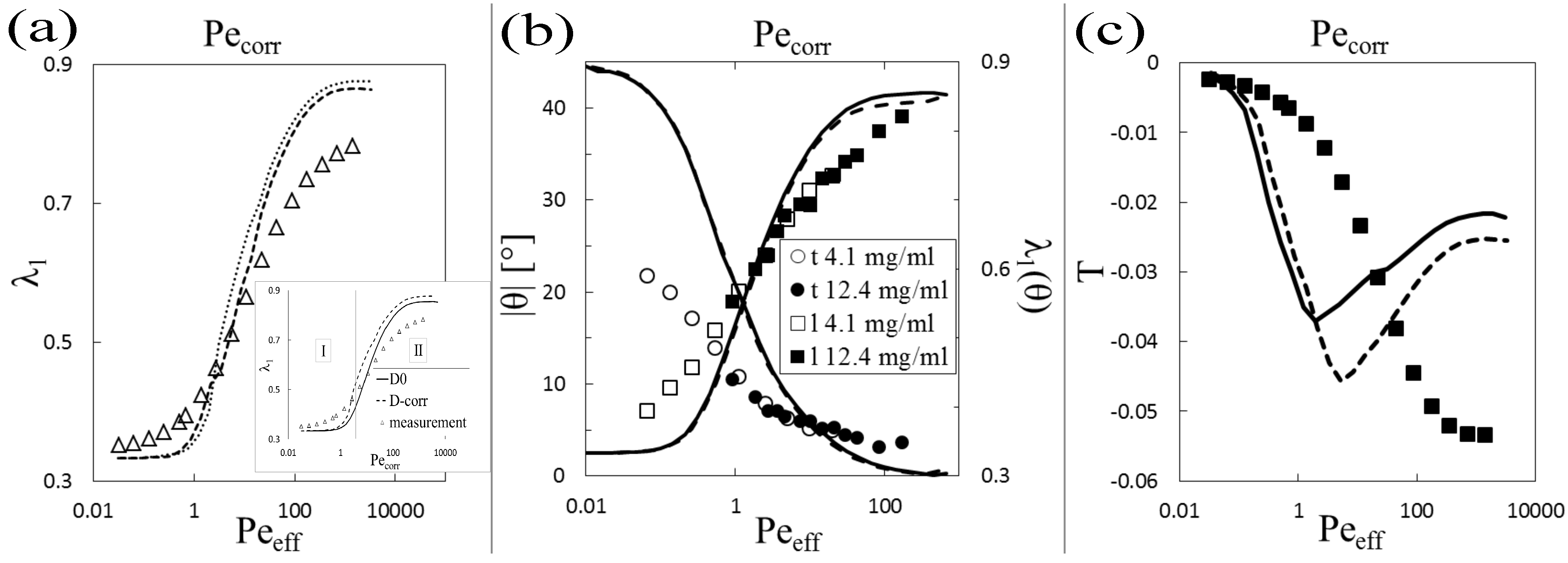
4. Results
5. Discussion
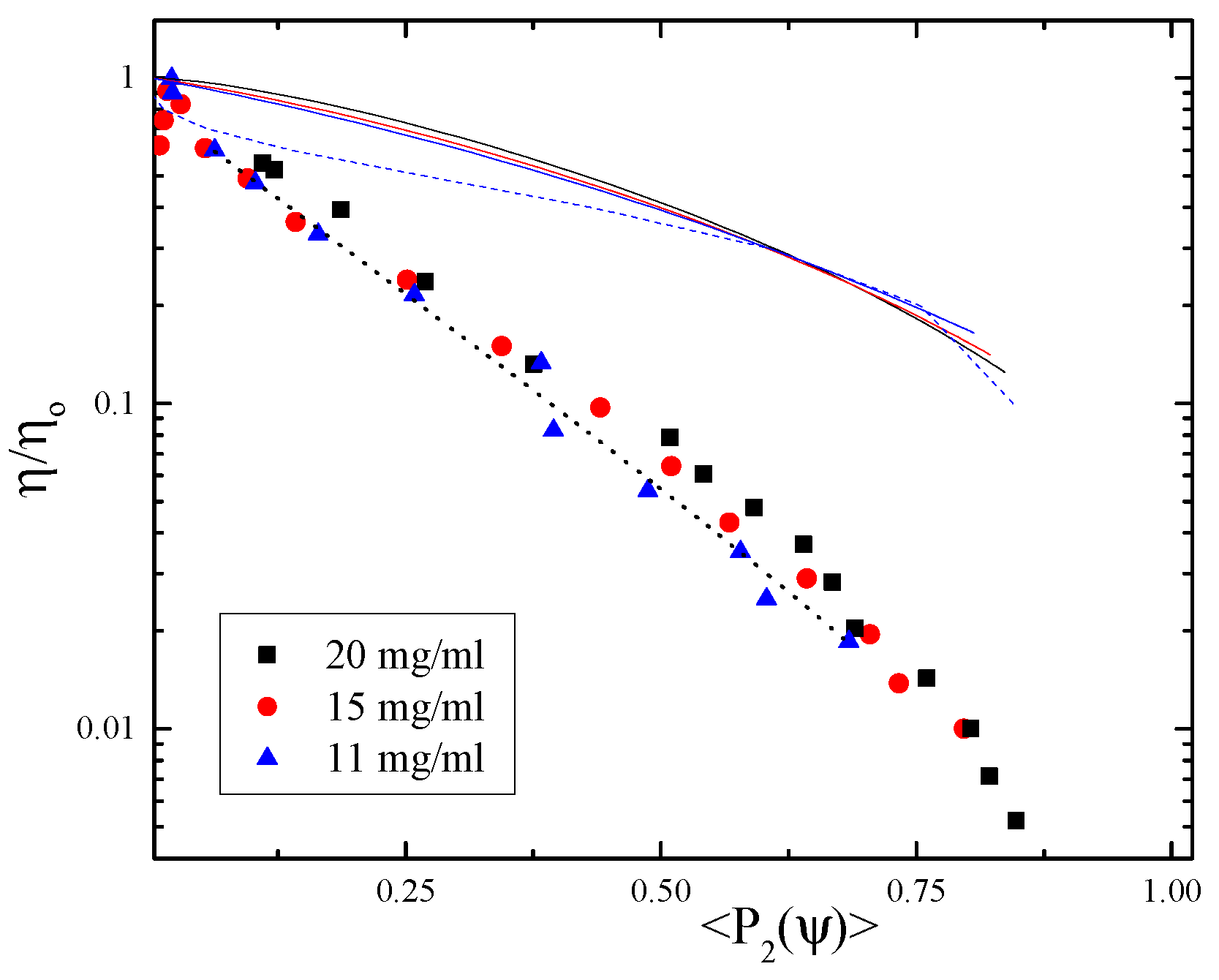
5.1. Shear Thinning
5.2. Biaxiality
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ODF | orientational distribution function |
| DEK | Doi–Edwards–Kuzuu |
| SANS | small angle neutron scattering |
References
- Baus, M.; Rull, S.F.; Ryckaert, J.-P. Observation, Prediction and Simulation of Phase Transitions in Complex Fluids; Springer Science and Business: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Gompper, G.; Schick, M. Soft Matter; Wiley-VCH: Weinheim, Germany, 2002; Volume 2. [Google Scholar]
- Dogic, Z.; Fraden, S. Ordered phases of filamentous viruses. Curr. Opin. Colloid Interface Sci. 2006, 11, 47–55. [Google Scholar] [CrossRef]
- Grelet, E. Hard-rod behavior in dense mesophases of semiflexible and rigid charged viruses. Phys. Rev. X 2014, 4. [Google Scholar] [CrossRef]
- Graf, C.; Kramer, H.; Deggelmann, M.; Hagenbüchle, M.; Johner, C.; Martin, C.; Weber, R. Rheological properties of suspensions of interacting rodlike fd-virus particles. J. Chem. Phys. 1992, 98, 4920. [Google Scholar] [CrossRef]
- Ripoll, M.; Holmquist, P.; Winkler, R.G.; Gompper, G.; Dhont, J.K.G.; Lettinga, M.P. Attractive colloidal rods in shear flow. Phys. Rev. Lett. 2008, 101. [Google Scholar] [CrossRef] [PubMed]
- Lenstra, T.A.J.; Dhont, J.K.G. Flow dichroism in critical colloidal fluids. Phys. Rev. E 2001, 63. [Google Scholar] [CrossRef] [PubMed]
- Lettinga, M.P.; Dhont, J.K.G. Non-equilibrium phase behaviour of rod-like viruses under shear flow. J. Phys. Condens. Matter 2004, 16, 3929. [Google Scholar] [CrossRef]
- Tang, J.; Fraden, S. Isotropic-cholesteric phase transition in colloidal suspensions of filamentous bacteriophage fd. Liq. Cryst. 1995, 19, 459–467. [Google Scholar] [CrossRef]
- Hess, S. Pre- and post-transitional behavior of the flow alignment and flow-induced phase transition in liquid crystals. Z. Naturforsch. A 1976, 31, 1507–1513. [Google Scholar] [CrossRef]
- Hess, S.; Kröger, M. Regular and chaotic orientational and rheological behaviour of liquid crystals. J. Phys. Condens. Matter 2004, 16, 3835–3859. [Google Scholar] [CrossRef]
- Klapp, S.H.L.; Hess, S. Shear-stress-controlled dynamics of nematic complex fluids. Phys. Rev. E 2010, 81. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.-G.; denOtter, W.K.; Dhont, J.K.G.; Briels, W.J. Isotropic-nematic spinodals of rigid long thin rodlike colloids by event-driven Brownian dynamics simulations. J. Chem. Phys. 2006, 124. [Google Scholar] [CrossRef] [PubMed]
- Lettinga, M.P.; Dogic, Z.; Wang, H.; Vermant, J. Flow behavior of colloidal rodlike viruses in the nematic phase. Langmuir 2005, 21, 8048–8060. [Google Scholar] [CrossRef] [PubMed]
- Dhont, J.K.G.; Briels, W.J. Viscoelasticity of suspensions of long, rigid rods. Colloids Surf. A 2003, 213, 131–156. [Google Scholar] [CrossRef]
- Olmsted, P.D.; Lu, C.Y.D. Phase separation of rigid-rod suspensions in shear flow. Phys. Rev. E 1999, 60, 4397. [Google Scholar] [CrossRef]
- Frank, H.; Day, L.A. Electron microscopic observations on fd bacteriophage, its alkali denaturation products and its DNA. Virology 1970, 42, 144–154. [Google Scholar] [CrossRef]
- Schlagberger, X.; Netz, R.R. Orientation of elastic rods in homogeneous Stokes flow. Europhys. Lett. 2005, 70, 129. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford: New York, NY, USA, 1986. [Google Scholar]
- Doi, M. Molecular dynamics and rheological properties of concentrated solutions of rodlike polymers in isotropic and liquid crystalline phases. J. Polym. Sci. Polym. Phys. 1981, 19, 229–243. [Google Scholar] [CrossRef]
- Kuzuu, N.; Doi, M. Constitutive equation for nematic liquid crystals under weak velocity gradient derived from a molecular kinetic equation. J. Phys. Soc. Jpn. 1983, 52, 3486–3494. [Google Scholar] [CrossRef]
- Onsager, L. Theories of concentrated electrolytes. Chem. Rev. 1933, 13, 73–89. [Google Scholar] [CrossRef]
- Andrews, N.C.; Edwards, B.J.; McHugh, A.J. Continuum dynamic behavior of homogeneous liquid-crystalline polymers under the imposition of shear and magnetic fields. J. Rheol. 1995, 39, 1161–1181. [Google Scholar] [CrossRef]
- Pelletier, O.; Bourgaux, C.; Diat, O.; Davidson, P.; Livage, J. A biaxial nematic gel phase in aqueous vanadium pentoxide suspensions. Eur. Phys. J. B 1999, 12, 541–546. [Google Scholar] [CrossRef]
- Kirchenbüchler, I.; Guu, D.; Kurniawan, N.A.; Koenderik, G.H.; Lettinga, M.P. Direct visualization of flow-induced conformational transitions of single actin filaments in entangled solutions. Nat. Commun. 2014, 5, 5060. [Google Scholar] [CrossRef] [PubMed]
- Huber, B.; Harasim, M.; Wunderlich, B.; Kröger, M.; Bausch, A.R. Microscopic origin of the non-newtonian viscosity of semiflexible polymer solutions in the semidilute regime. ACS Macro Lett. 2014, 3, 136–140. [Google Scholar] [CrossRef]
- Harasim, M.; Wunderlich, B.; Peleg, O.; Kröger, M.; Bausch, A. Direct observation of the dynamics of semiflexible polymers in shear flow. Phys. Rev. Lett. 2013, 110. [Google Scholar] [CrossRef] [PubMed]
- Lindner, P.; Hess, S. Analysis of structural anisotropy from SANS multidetector data. Phys. B 1989, 156–157, 512–514. [Google Scholar] [CrossRef]
- Liberatore, M.W.; Nettesheim, F.; Wagner, N.J.; Porcar, L. Spatially resolved small-angle neutron scattering in the 1-2 plane: A study of shear-induced phase-separating worm-like micelles. Phys. Rev. E 2006, 73. [Google Scholar] [CrossRef] [PubMed]
- Liberatore, M.W.; Nettesheim, F.; Vasquez, P.A.; Helgeson, M.E.; Wagner, N.J.; Kaler, E.W.; Cook, L.P.; Porcar, L.; Hu, Y.T. Microstructure and shear rheology of entangled worm-like micelles in solution. J. Rheol. 2009, 53, 441. [Google Scholar] [CrossRef]
- Berry, D.H.; Russel, W.B. The rheology of dilute suspensions of slender rods in weak flows. J. Fluid Mech. 1987, 180, 475–494. [Google Scholar] [CrossRef]
- Förster, S.; Konrad, M.; Lindner, P. Shear thinning and orientational ordering of worm-like micelles. Phys. Rev. Lett. 2005, 94. [Google Scholar] [CrossRef] [PubMed]
- Kirchhoff, T.; Loewen, H.; Klein, R. Dynamical correlations in suspensions of charged rodlike macromolecules. Phys. Rev. E 1996, 53, 5011. [Google Scholar] [CrossRef]
- Sambrook, J.; Russel, D.W. Molecular Cloning; Cold Spring Harbor: New York, NY, USA, 2001. [Google Scholar]
- Berret, J.-F.; Roux, D.C.; Lindner, P. Structure and rheology of concentrated worm-like micelles at the shear-induced isotropic-to-nematic transition. Eur. Phys. J. B 1998, 5, 67–77. [Google Scholar] [CrossRef]
- Bihannic, I.; Baravian, C.; Duval, J.F.L.; Paineau, E.; Meneau, F.; Levitz, P.; de Silva, J.P.; Davidson, P.; Michot, L.J. Orientational order of colloidal disk-shaped particles under shear-flow conditions: A rheological-small-angle X-ray scattering study. J. Phys. Chem. B 2010, 114, 16347–16355. [Google Scholar] [CrossRef] [PubMed]
- Hongladarom, K.; Ugaz, V.M.; Cinader, D.K.; Burghardt, W.R.; Quintana, J.P. Birefringence, X-ray scattering and neutron scattering measurements of molecular orientation in sheared liquid crystal polymer solutions. Macromolecules 1996, 29, 5346–5355. [Google Scholar] [CrossRef]
- Purdy, K.R.; Dogic, Z.; Fraden, S.; Rühm, A.; Lurio, L.; Mochrie, S.G.J. Measuring the nematic order of suspensions of colloidal fd virus by X-ray diffraction and optical birefringence. Phys. Rev. E 2003, 67. [Google Scholar] [CrossRef] [PubMed]
- Lonetti, B.; Kohlbrecher, J.; Willner, L.; Dhont, J.K.G.; Lettinga, M.P. Dynamic response of block copolymer worm-like micelles to shear flow. J. Phys. Condens. Matter 2008, 20. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341. [Google Scholar] [CrossRef]
- Magda, J.J.; Davis, H.T.; Tirrell, M. The transport properties of rod-like particles via molecular dynamics. I. Bulk fluid. J. Chem. Phys. 1986, 85, 6674. [Google Scholar] [CrossRef]
- Kröger, M.; Ammar, A.; Chinesta, F. Consistent closure schemes for statistical models of anisotropic fluids. J. Non-Newton. Fluid Mech. 2008, 149, 40–55. [Google Scholar] [CrossRef]
- Winkler, R.G.; Mussawisade, K.; Ripoll, M.; Gompper, G. Rod-like colloids and polymers in shear flow: A multi-particle-collision dynamics study. J. Phys. Condens. Matter 2004, 16, 3941–3954. [Google Scholar] [CrossRef]
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, C.; Kohlbrecher, J.; Porcar, L.; Lettinga, M.P. The Connection between Biaxial Orientation and Shear Thinning for Quasi-Ideal Rods. Polymers 2016, 8, 291. https://doi.org/10.3390/polym8080291
Lang C, Kohlbrecher J, Porcar L, Lettinga MP. The Connection between Biaxial Orientation and Shear Thinning for Quasi-Ideal Rods. Polymers. 2016; 8(8):291. https://doi.org/10.3390/polym8080291
Chicago/Turabian StyleLang, Christian, Joachim Kohlbrecher, Lionel Porcar, and Minne Paul Lettinga. 2016. "The Connection between Biaxial Orientation and Shear Thinning for Quasi-Ideal Rods" Polymers 8, no. 8: 291. https://doi.org/10.3390/polym8080291
APA StyleLang, C., Kohlbrecher, J., Porcar, L., & Lettinga, M. P. (2016). The Connection between Biaxial Orientation and Shear Thinning for Quasi-Ideal Rods. Polymers, 8(8), 291. https://doi.org/10.3390/polym8080291