Predictive Analysis of the Mechanical Properties of Biopolymer–Fiber-Reinforced Composite-Stabilized Soil Based on Genetic Algorithm-Optimized Back Propagation Neural Networks
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Design
2.3. Test Methods
2.3.1. Mechanical Properties Test
2.3.2. Micro Properties Tests
2.4. Analysis Methods
2.4.1. Determine the Coding Method
2.4.2. Generation of the Initial Population
2.4.3. Selection, Crossover, and Mutation
3. Predictive Model Construction
3.1. Data Selection and Normalization
3.2. Setting the Optimization Parameters
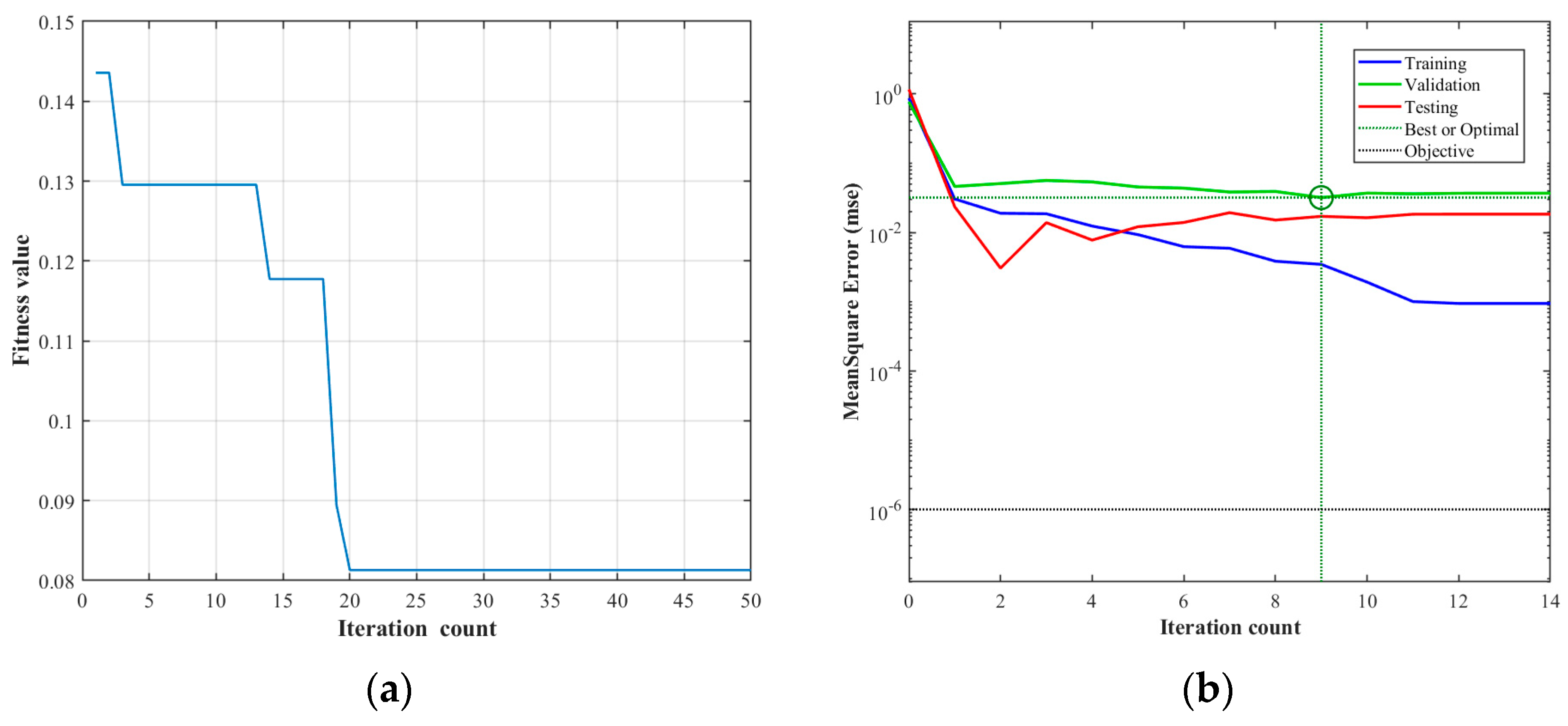
3.3. Genetic Algorithm Implementation
4. Analysis and Discussion
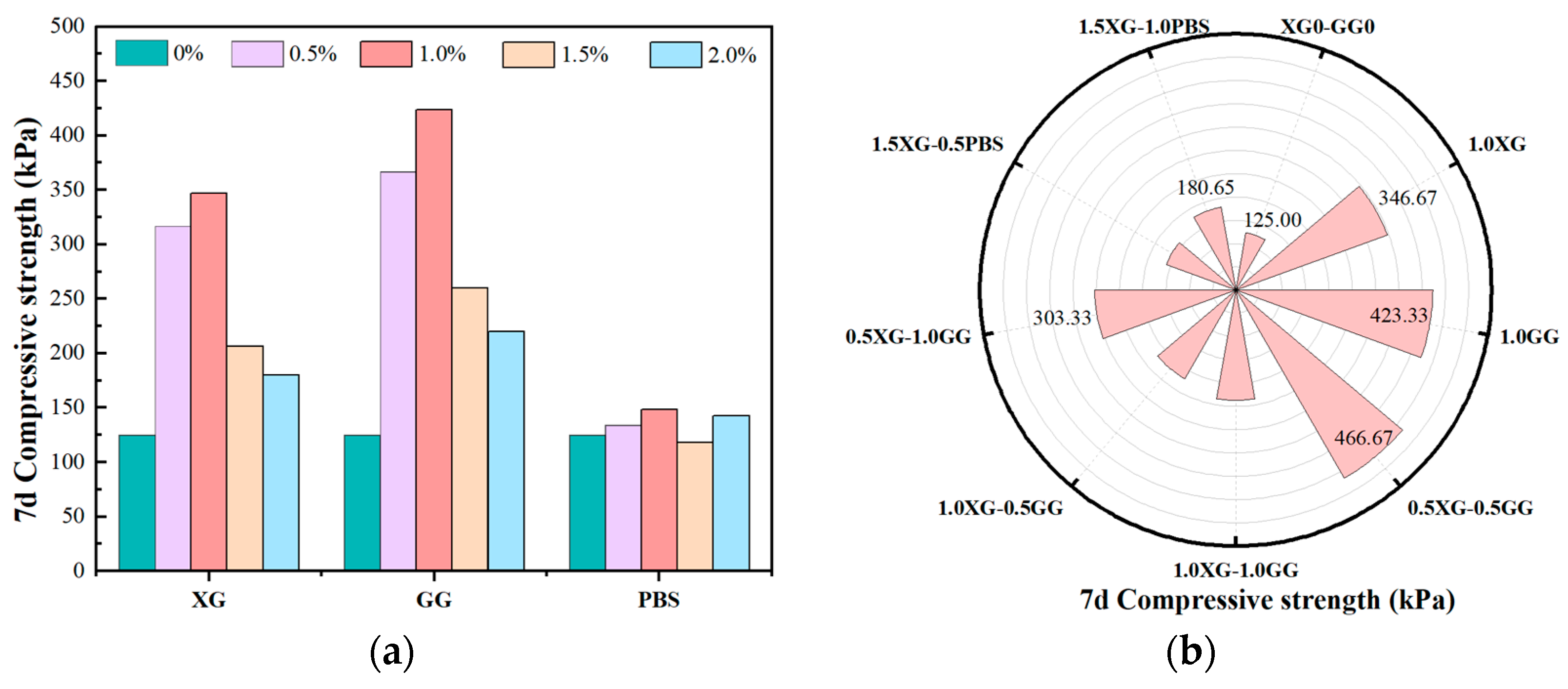
4.1. Mechanical Properties
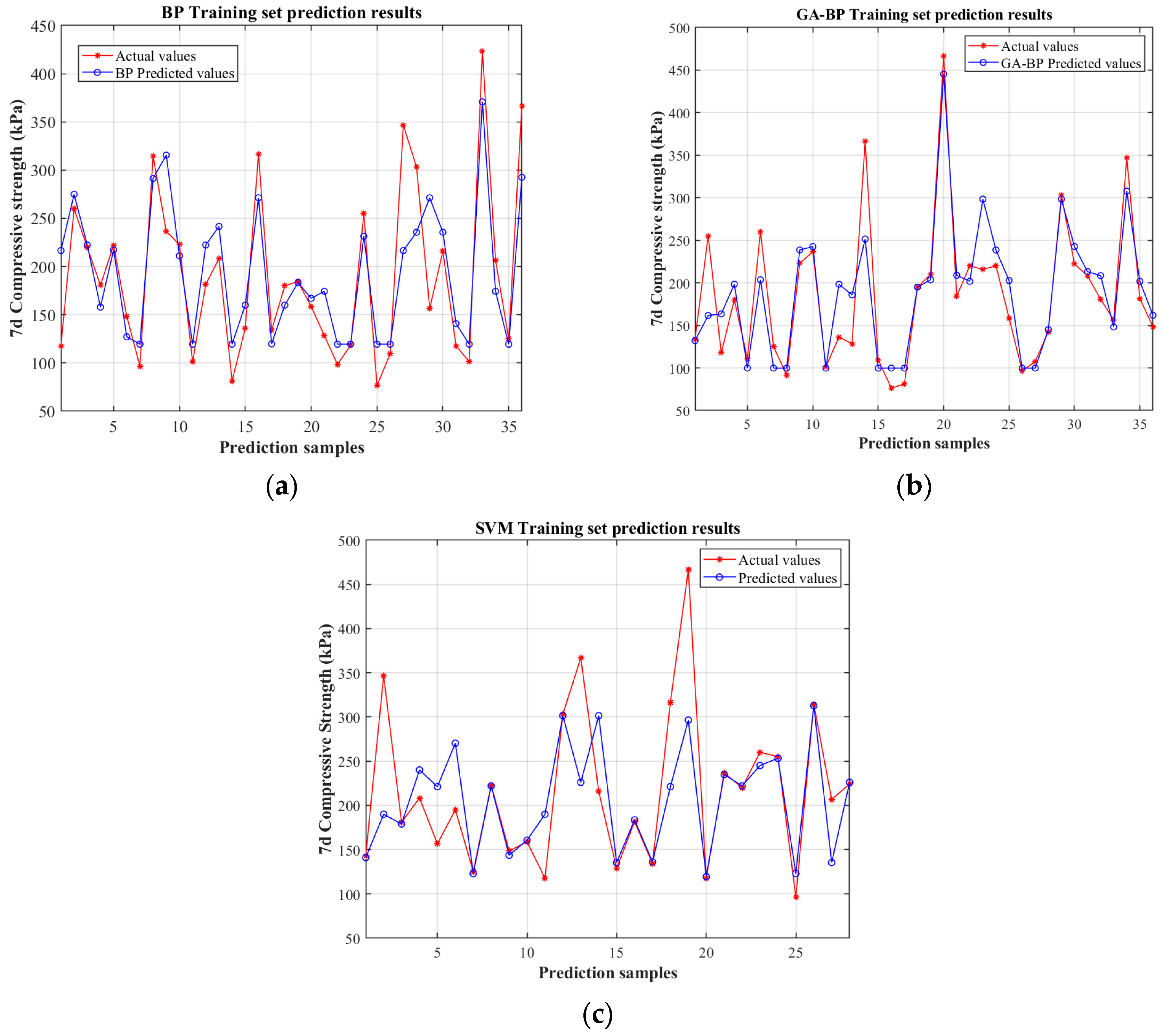
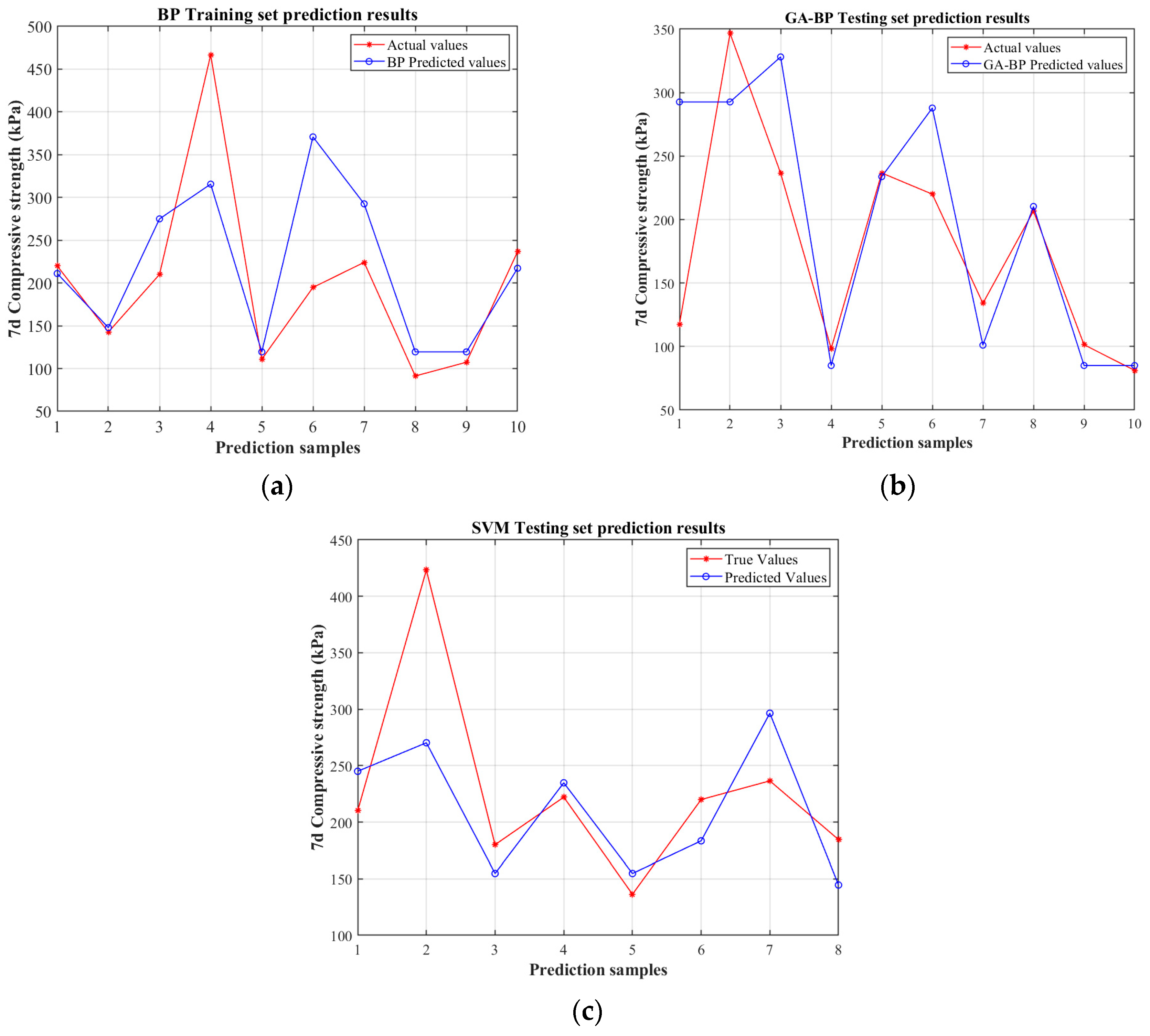
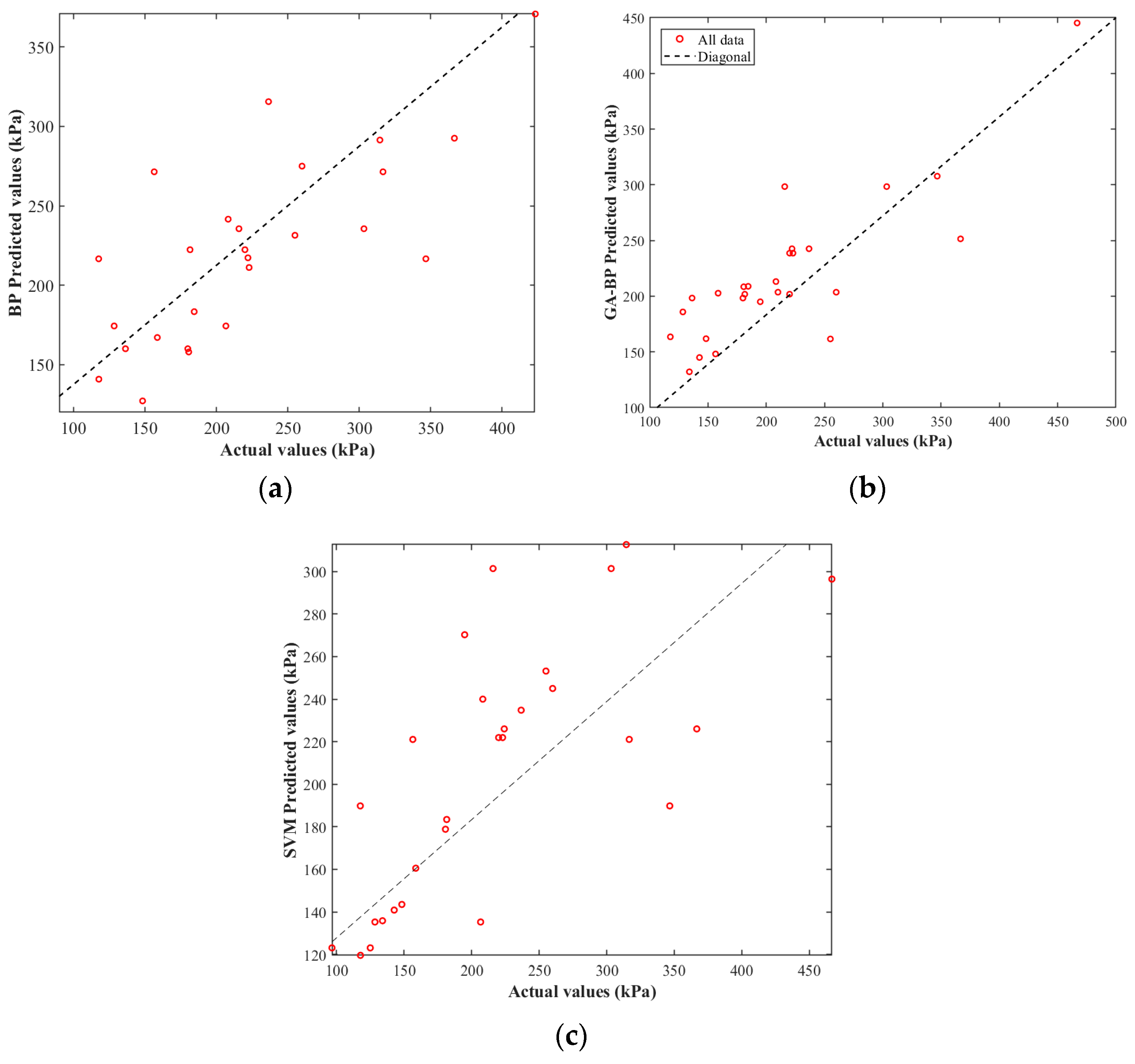
4.2. Comparative Analysis of BP, GA-BP Neural Networks, and SVM Model for Predicting Mechanical Properties
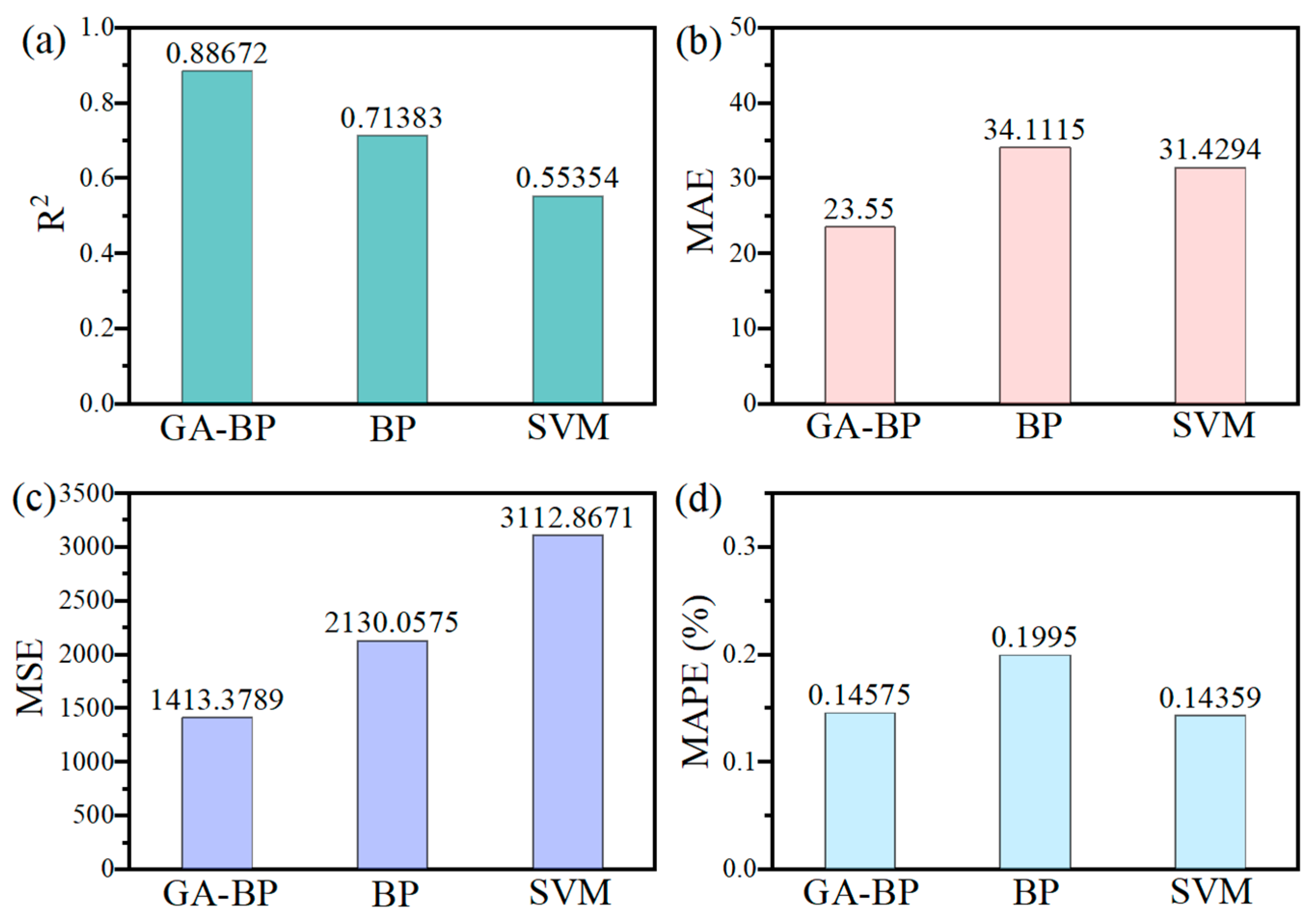
4.3. Predictive Indicator Analysis
4.4. Microscopic Mechanism Analysis
5. Conclusions
- (1)
- The optimal dosage range of biopolymers for fiber-reinforced composite stabilized soil is approximately 0.5–1.0%. The combined doping of 0.5XG-0.5GG achieves the highest compressive strength of 466.67 kPa, a 273% enhancement, meeting the sub-base intensity criterion for secondary and lower-grade highways.
- (2)
- Compared to the traditional BP neural network and SVM, the GA-BP model—with an R2 of 0.8867, an MAE of 23.55, an MSE of 1413.38, and a MAPE of 0.14575—demonstrates significantly improved accuracy and stability. The integration of genetic algorithm optimization for initial weights and convergence has enhanced the model’s predictive performance, outperforming BP by approximately 30–34% in errors and showing better results than SVM. This confirms that GA-BP is the most reliable and precise approach for predicting the uniaxial compressive strength.
- (3)
- The strength mechanism of biopolymer-stabilized soils is attributed to the further enhancement of the spatial crosslinking density within the polymer three-dimensional network, achieved through interchain hydrogen bonding and electrostatic interactions in the reinforced skeletal framework based on straw fibers. Soil stabilization is realized through the formation of a film-like hardened coating that encapsulates soil particles.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, L.; Wang, D.; Miao, Y. A review of two-dimensional image-based technologies for size and shape characterization of coarse-grained granular soils. Powder Technol. 2024, 445, 120115. [Google Scholar] [CrossRef]
- Shin, H.; Santamarina, J.C. Role of Particle Angularity on the Mechanical Behavior of Granular Mixtures. J. Geotech. Geoenvironmental Eng. 2013, 139, 353–355. [Google Scholar] [CrossRef]
- Chang, Z.; Huang, F.; Huang, J.; Jiang, S.-H.; Zhou, C.; Zhu, L. Experimental study of the failure mode and mechanism of loess fill slopes induced by rainfall. Eng. Geol. 2021, 280, 105941. [Google Scholar] [CrossRef]
- Li, J.; Cameron, D.A.; Ren, G. Case study and back analysis of a residential building damaged by expansive soils. Comput. Geotech. 2014, 56, 89–99. [Google Scholar] [CrossRef]
- Ikeagwuani, C.C.; Nwonu, D.C. Emerging trends in expansive soil stabilisation: A review. J. Rock Mech. Geotech. Eng. 2019, 11, 423–440. [Google Scholar] [CrossRef]
- Armistead, S.J.; Rawlings, A.E.; Smith, C.C.; Staniland, S.S. Biopolymer Stabilization/Solidification of Soils: A Rapid, Micro-Macro, Cross-Disciplinary Approach. Environ. Sci. Technol. 2020, 54, 13963–13972. [Google Scholar] [CrossRef] [PubMed]
- Zhu, M.; Leo, C.; Zeng, Q.; Fanna, D.J.; Hsi, J.; Karimi, R.; Fabbri, A.; Liyanapathirana, S.; Hu, P.; Alzghool, H. Efficacy of expansive soil stabilisation using un-calcinated Kaolinite-Based Alkali-Activated binders. Clean. Mater. 2025, 16, 100315. [Google Scholar] [CrossRef]
- Biju, M.S.; Arnepalli, D.N. Effect of biopolymers on permeability of sand-bentonite mixtures. J. Rock Mech. Geotech. Eng. 2020, 12, 1093–1102. [Google Scholar] [CrossRef]
- Rosalam, S.; England, R. Review of xanthan gum production from unmodified starches by Xanthomonas comprestris sp. Enzym. Microb. Technol. 2006, 39, 197–207. [Google Scholar] [CrossRef]
- Sujatha, E.R.; Saisree, S. Geotechnical behaviour of guar gum-treated soil. Soils Found. 2019, 59, 2155–2166. [Google Scholar] [CrossRef]
- Sulaiman, H.; Taha, M.R.; Abd Rahman, N.; Mohd Taib, A. Performance of soil stabilized with biopolymer materials—xanthan gum and guar gum. Phys. Chem. Earth Parts A/B/C 2022, 128, 103276. [Google Scholar] [CrossRef]
- Ayeldeen, M.; Negm, A.; El-Sawwaf, M.; Kitazume, M. Enhancing mechanical behaviors of collapsible soil using two biopolymers. J. Rock Mech. Geotech. Eng. 2017, 9, 329–339. [Google Scholar] [CrossRef]
- Chang, I.; Cho, G.-C. Strengthening of Korean residual soil with β-1,3/1,6-glucan biopolymer. Constr. Build. Mater. 2012, 30, 30–35. [Google Scholar] [CrossRef]
- Chang, I.; Im, J.; Prasidhi, A.K.; Cho, G.-C. Effects of Xanthan gum biopolymer on soil strengthening. Constr. Build. Mater. 2015, 74, 65–72. [Google Scholar] [CrossRef]
- Bao, H.; Liu, C.; Lan, H.; Yan, C.; Li, L.; Zheng, H.; Dong, Z. Time-dependency deterioration of polypropylene fiber reinforced soil and guar gum mixed soil in loess cut-slope protecting. Eng. Geol. 2022, 311, 106895. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Y.; Tian, H.; Sun, S.; Zhang, L.; Zhou, R.; Han, C. Mechanical properties and toughening effect of rice straw fiber-reinforced soil. Case Stud. Constr. Mater. 2024, 21, e03511. [Google Scholar] [CrossRef]
- Galán-Marín, C.; Rivera-Gómez, C.; Petric, J. Clay-based composite stabilized with natural polymer and fibre. Constr. Build. Mater. 2010, 24, 1462–1468. [Google Scholar] [CrossRef]
- Kidari, R.; Tilioua, A. Investigation of the thermomechanical characteristics of compressed earth bricks reinforced with cement and corn straw waste fibers. Clean. Waste Syst. 2024, 9, 100160. [Google Scholar] [CrossRef]
- Xiao, F.; Zhao, Z.; Chen, H. A simplified model for predicting grout flow in fracture channels. Tunn. Undergr. Space Technol. 2017, 70, 11–18. [Google Scholar] [CrossRef]
- Zhang, D.M.; Huang, Z.K.; Yin, Z.Y.; Ran, L.Z.; Huang, H.W. Predicting the grouting effect on leakage-induced tunnels and ground response in saturated soils. Tunn. Undergr. Space Technol. 2017, 65, 76–90. [Google Scholar] [CrossRef]
- Ozkaynak, M.I.; Yilmaz, Y. Prediction of resilient modulus with pre-post experimental data of undisturbed subgrade soils using machine learning algorithms. Transp. Geotech. 2024, 49, 101396. [Google Scholar] [CrossRef]
- Wang, Z.-F.; Cheng, W.-C. Predicting jet-grout column diameter to mitigate the environmental impact using an artificial intelligence algorithm. Undergr. Space 2021, 6, 267–280. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, X.; Zhang, X.; Wang, H.; He, P.; Luo, L.; Xu, C. Prediction of high-performance concrete compressive strength using Decision Tree-Guided Artificial Neural Network Pretraining approach. Eng. Appl. Artif. Intell. 2025, 156, 110828. [Google Scholar] [CrossRef]
- Mohammed, A.; Burhan, L.; Ghafor, K.; Sarwar, W.; Mahmood, W. Artificial neural network (ANN), M5P-tree, and regression analyses to predict the early age compression strength of concrete modified with DBC-21 and VK-98 polymers. Neural Comput. Appl. 2021, 33, 7851–7873. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Mohammed, A.S.; Mohammed, A.A. Proposing several model techniques including ANN and M5P-tree to predict the compressive strength of geopolymer concretes incorporated with nano-silica. Environ. Sci. Pollut. Res. 2022, 29, 71232–71256. [Google Scholar] [CrossRef]
- Bishnoi, S.; Singh, S.; Ravinder, R.; Bauchy, M.; Gosvami, N.N.; Kodamana, H.; Krishnan, N.M.A. Predicting Young’s modulus of oxide glasses with sparse datasets using machine learning. J. Non-Cryst. Solids 2019, 524, 119643. [Google Scholar] [CrossRef]
- Jyothi Swaroop, C.; Vutukuri, S.G.; Dabade, A. Effect of ultrasound treatment on the physicochemical and functional properties of Guar gum. Food Humanit. 2025, 4, 100505. [Google Scholar] [CrossRef]
- Risica, D.; Dentini, M.; Crescenzi, V. Guar gum methyl ethers. Part I. Synthesis and macromolecular characterization. Polymer 2005, 46, 12247–12255. [Google Scholar] [CrossRef]
- Garcıa-Ochoa, F.; Santos, V.E.; Casas, J.A.; Gómez, E. Xanthan gum: Production, recovery, and properties. Biotechnol. Adv. 2000, 18, 549–579. [Google Scholar] [CrossRef]
- Jalal, F.E.; Iqbal, M.; Bao, X.; Abbas Jaffar, S.T.; Chen, X. Compressive strength of biopolymer-stabilized residual granitic soil using polybutylene succinate and xanthan gum: A mechanical-microstructural study. J. Rock Mech. Geotech. Eng. 2025. [Google Scholar] [CrossRef]
- Tipu, R.K.; Batra, V.; Suman; Pandya, K.S.; Panchal, V.R. Efficient compressive strength prediction of concrete incorporating recycled coarse aggregate using Newton’s boosted backpropagation neural network (NB-BPNN). Structures 2023, 58, 105559. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, D.; Liu, S.; Jin, Z.; Chowwanonthapunya, T.; Gao, J.; Li, X. Prediction of polycarbonate degradation in natural atmospheric environment of China based on BP-ANN model with screened environmental factors. Chem. Eng. J. 2020, 399, 125878. [Google Scholar] [CrossRef]
- Wang, F.; Xie, H.; Li, C.; Li, M.; Long, X.; Shan, K.; Wang, Z. Hydraulic properties of stressed granite fractures with heat-induced void alteration. Eng. Geol. 2024, 333, 107476. [Google Scholar] [CrossRef]
- Ray, S.; Haque, M.; Rahman, M.M.; Sakib, M.N.; Al Rakib, K. Experimental investigation and SVM-based prediction of compressive and splitting tensile strength of ceramic waste aggregate concrete. J. King Saud Univ.-Eng. Sci. 2024, 36, 112–121. [Google Scholar] [CrossRef]
- Ray, S.; Rahman, M.M.; Haque, M.; Hasan, M.W.; Alam, M.M. Performance evaluation of SVM and GBM in predicting compressive and splitting tensile strength of concrete prepared with ceramic waste and nylon fiber. J. King Saud Univ.-Eng. Sci. 2023, 35, 92–100. [Google Scholar] [CrossRef]
- Abd, A.M.; Abd, S.M. Modelling the strength of lightweight foamed concrete using support vector machine (SVM). Case Stud. Constr. Mater. 2017, 6, 8–15. [Google Scholar] [CrossRef]
- Bill, J.; Cox, B.A.; Champagne, L. A comparison of quaternion neural network backpropagation algorithms. Expert Syst. Appl. 2023, 232, 120448. [Google Scholar] [CrossRef]
- Feng, D.; Liang, B.; He, X.; Yi, F.; Xue, J.; Wan, Y.; Xue, Q. Mechanical properties of dredged soil reinforced by xanthan gum and fibers. J. Rock Mech. Geotech. Eng. 2023, 15, 2147–2157. [Google Scholar] [CrossRef]
- Kwon, Y.-M.; Moon, J.-H.; Cho, G.-C.; Kim, Y.-U.; Chang, I. Xanthan gum biopolymer-based soil treatment as a construction material to mitigate internal erosion of earthen embankment: A field-scale. Constr. Build. Mater. 2023, 389, 131716. [Google Scholar] [CrossRef]
- Abbasi, F.; Janalizadeh Choobbasti, A.; Roushan, K. Advanced stabilization of clayey sand using xanthan gum: Insights from multiscale evaluation and ultrasonic pulse velocity analysis. Results Eng. 2025, 25, 104419. [Google Scholar] [CrossRef]
- Katzbauer, B. Properties and applications of xanthan gum. Polym. Degrad. Stab. 1998, 59, 81–84. [Google Scholar] [CrossRef]
- Bozyigit, I.; Javadi, A.; Altun, S. Strength properties of xanthan gum and guar gum treated kaolin at different water contents. J. Rock Mech. Geotech. Eng. 2021, 13, 1160–1172. [Google Scholar] [CrossRef]
- Dwari, R.K.; Mishra, B.K. Evaluation of flocculation characteristics of kaolinite dispersion system using guar gum: A green flocculant. Int. J. Min. Sci. Technol. 2019, 29, 745–755. [Google Scholar] [CrossRef]
- Eichler, S.; Ramon, O.; Ladyzhinski, I.; Cohen, Y.; Mizrahi, S. Collapse processes in shrinkage of hydrophilic gels during dehydration. Food Res. Int. 1997, 30, 719–726. [Google Scholar] [CrossRef]
- Wang, L.; Liu, R.; Hu, Y.; Sun, W. pH effects on adsorption behavior and self-aggregation of dodecylamine at muscovite/aqueous interfaces. J. Mol. Graph. Model. 2016, 67, 62–68. [Google Scholar] [CrossRef]
- Khosravi, H.; Bahram, M. Prediction of geopolymer concrete compressive strength using artificial neural network and genetic algorithm. Results Eng. 2025, 27, 105537. [Google Scholar] [CrossRef]
- Chang, I.; Lee, M.; Tran, A.T.P.; Lee, S.; Kwon, Y.-M.; Im, J.; Cho, G.-C. Review on biopolymer-based soil treatment (BPST) technology in geotechnical engineering practices. Transp. Geotech. 2020, 24, 100385. [Google Scholar] [CrossRef]
- DeJong, J.T.; Mortensen, B.M.; Martinez, B.C.; Nelson, D.C. Bio-mediated soil improvement. Ecol. Eng. 2010, 36, 197–210. [Google Scholar] [CrossRef]
- Orts, W.J.; Sojka, R.E.; Glenn, G.M. Biopolymer additives to reduce erosion-induced soil losses during irrigation. Ind. Crops Prod. 2000, 11, 19–29. [Google Scholar] [CrossRef]
- Chang, I.; Prasidhi, A.K.; Im, J.; Shin, H.-D.; Cho, G.-C. Soil treatment using microbial biopolymers for anti-desertification purposes. Geoderma 2015, 253–254, 39–47. [Google Scholar] [CrossRef]
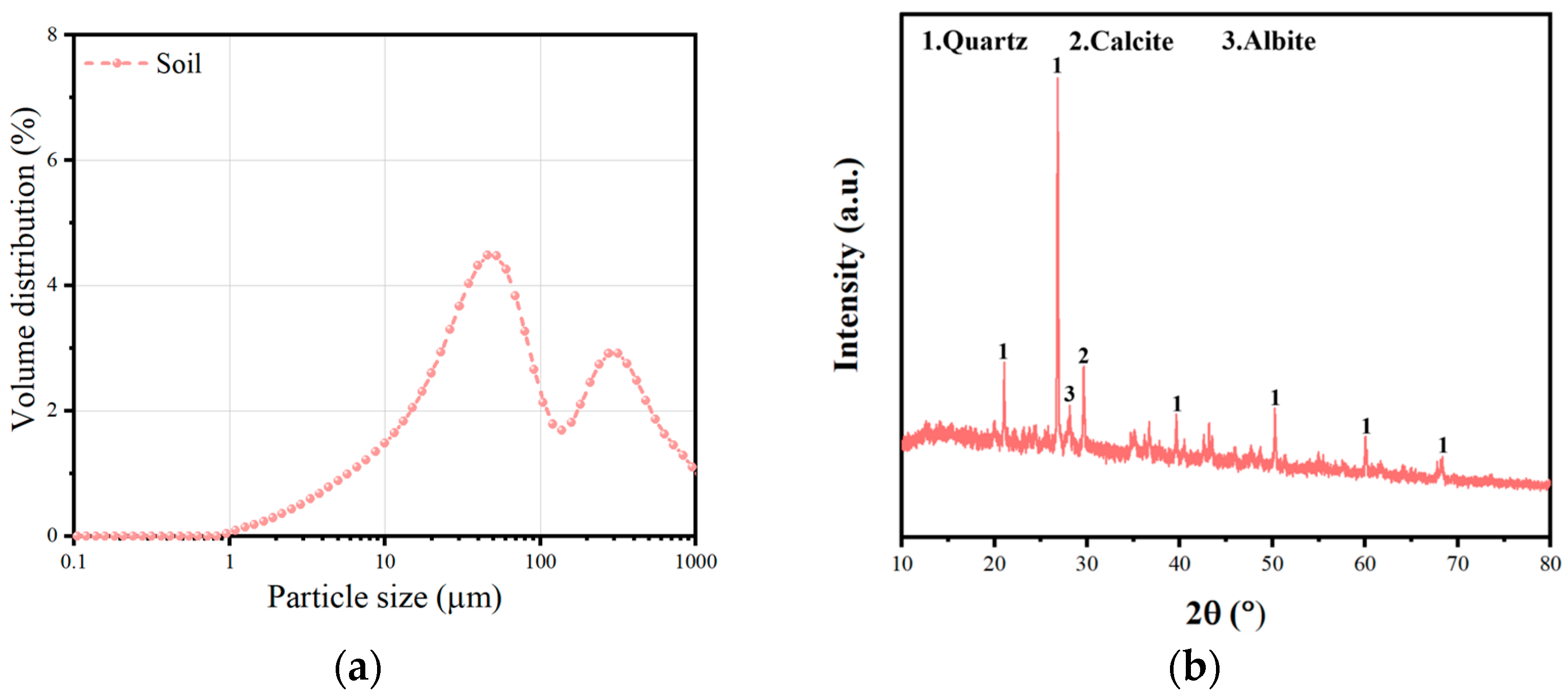

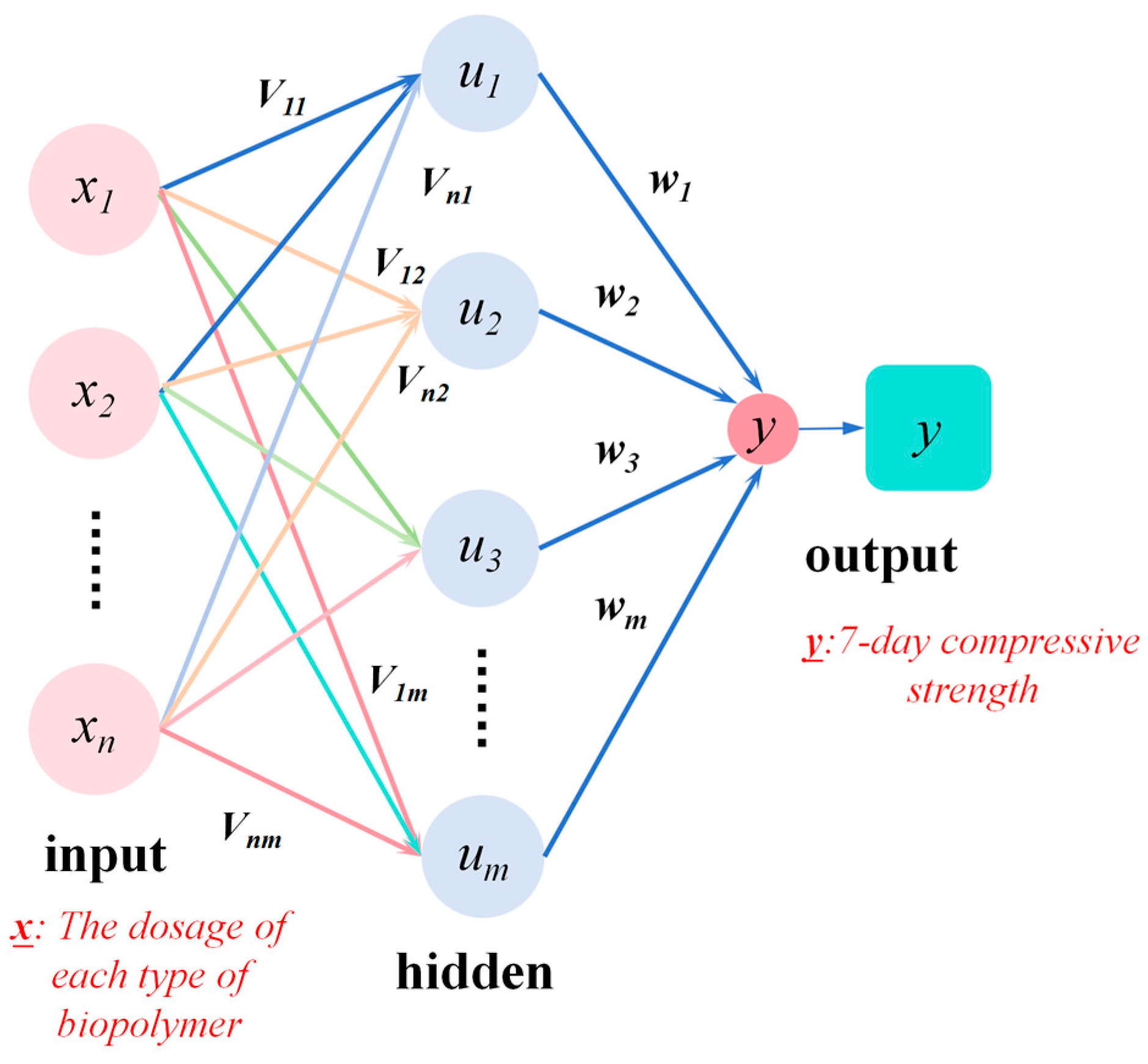

| Material | CaO | SiO2 | Al2O3 | Fe2O3 | SO3 | MgO | K2O | TiO2 | Other |
|---|---|---|---|---|---|---|---|---|---|
| Soil | 12.472 | 60.315 | 15.219 | 5.382 | 0.07 | 2.478 | 3.033 | 0.787 | 0.244 |
| Material | Natural Moisture Content (%) | Plastic Limit (%) | Liquid Limit (%) | Plasticity Index (Ip) | Maximum Dry Density (g/cm3) | Optimum Water Content (wop) |
|---|---|---|---|---|---|---|
| Soil | 10.12 | 7.22 | 24.57 | 17.35 | 1.861 | 13.58% |
| Material | Molecular Mass (g/mol) | Viscosity (mPa.s) | pH | Grain Size | Form |
|---|---|---|---|---|---|
| XG | 268.5 | 1680 | 7.8 | 80 mesh | Powder |
| GG | 522.6 | 5368 | 6.2 | 100 mesh | Powder |
| Sample | XG (%) | GG (%) | PBS (%) | Straw Fiber (%) | Sample | XG (%) | GG (%) | PBS (%) | Straw Fiber (%) |
|---|---|---|---|---|---|---|---|---|---|
| XG-GG-0 | 0 | 0 | 0 | 0.4% | PBS-1.0 | 0 | 0 | 1.0 | 0.4% |
| XG-0.5 | 0.5 | 0 | 0 | PBS-1.5 | 0 | 0 | 1.5 | ||
| XG-1.0 | 1.0 | 0 | 0 | PBS-2.0 | 0 | 0 | 2.0 | ||
| XG-1.5 | 1.5 | 0 | 0 | 0.5XG-0.5GG | 0.5 | 0.5 | 0 | ||
| XG-2.0 | 2.0 | 0 | 0 | 1.0XG-1.0GG | 1.0 | 1.0 | 0 | ||
| GG-0.5 | 0 | 0.5 | 0 | 0.5XG-1.0GG | 0.5 | 1.0 | 0 | ||
| GG-1.0 | 6 | 1.0 | 0 | 1.0GG-0.5XG | 1.0 | 0.5 | 0 | ||
| GG-1.5 | 0 | 1.5 | 0 | 1.5XG-0.5PBS | 0 | 1.5 | 0.5 | ||
| GG-2.0 | 0 | 2.0 | 0 | 1.5XG-1.0PBS | 0 | 1.5 | 1.0 | ||
| PBS-0.5 | 0 | 0 | 0.5 | - | |||||
| Model Parameters | Maximum Number of Iterations | Convergence Error | Learning Rate | Connection Weights Between Input Layer and Hidden Layer | Hidden Layer Threshold | Connection Weights Between Hidden Layer and Output Layer | Output Layer Threshold |
|---|---|---|---|---|---|---|---|
| Value | 1000 | 1 × 10−6 | 0.005 | 15 | 10 | 10 | 5 |
| Model Parameters | Kernel Type (-t) | Penalty Parameter (C) | RBF Kernel Parameter (Gamma) | Task Type (-s) | Epsilon Value of Insensitivity Loss Function |
|---|---|---|---|---|---|
| Value | 2 (RBF kernel) | 4.0 | 0.7 | 3 | 0.01 |
| Population Size | Genetic Generations | Selection Function Parameters | Crossover Function Parameters | Mutation Function Parameters |
|---|---|---|---|---|
| 80 | 10 | 0.08 | 2 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, G.; Wang, Z.; Cao, X.; Wen, J. Predictive Analysis of the Mechanical Properties of Biopolymer–Fiber-Reinforced Composite-Stabilized Soil Based on Genetic Algorithm-Optimized Back Propagation Neural Networks. Polymers 2025, 17, 2176. https://doi.org/10.3390/polym17162176
Wei G, Wang Z, Cao X, Wen J. Predictive Analysis of the Mechanical Properties of Biopolymer–Fiber-Reinforced Composite-Stabilized Soil Based on Genetic Algorithm-Optimized Back Propagation Neural Networks. Polymers. 2025; 17(16):2176. https://doi.org/10.3390/polym17162176
Chicago/Turabian StyleWei, Guotao, Zhaoping Wang, Xuanhao Cao, and Jiuran Wen. 2025. "Predictive Analysis of the Mechanical Properties of Biopolymer–Fiber-Reinforced Composite-Stabilized Soil Based on Genetic Algorithm-Optimized Back Propagation Neural Networks" Polymers 17, no. 16: 2176. https://doi.org/10.3390/polym17162176
APA StyleWei, G., Wang, Z., Cao, X., & Wen, J. (2025). Predictive Analysis of the Mechanical Properties of Biopolymer–Fiber-Reinforced Composite-Stabilized Soil Based on Genetic Algorithm-Optimized Back Propagation Neural Networks. Polymers, 17(16), 2176. https://doi.org/10.3390/polym17162176





