A Contact Mechanics Model for Surface Wear Prediction of Parallel-Axis Polymer Gears
Abstract
1. Introduction
2. Materials and Methods
2.1. Wear Formulation
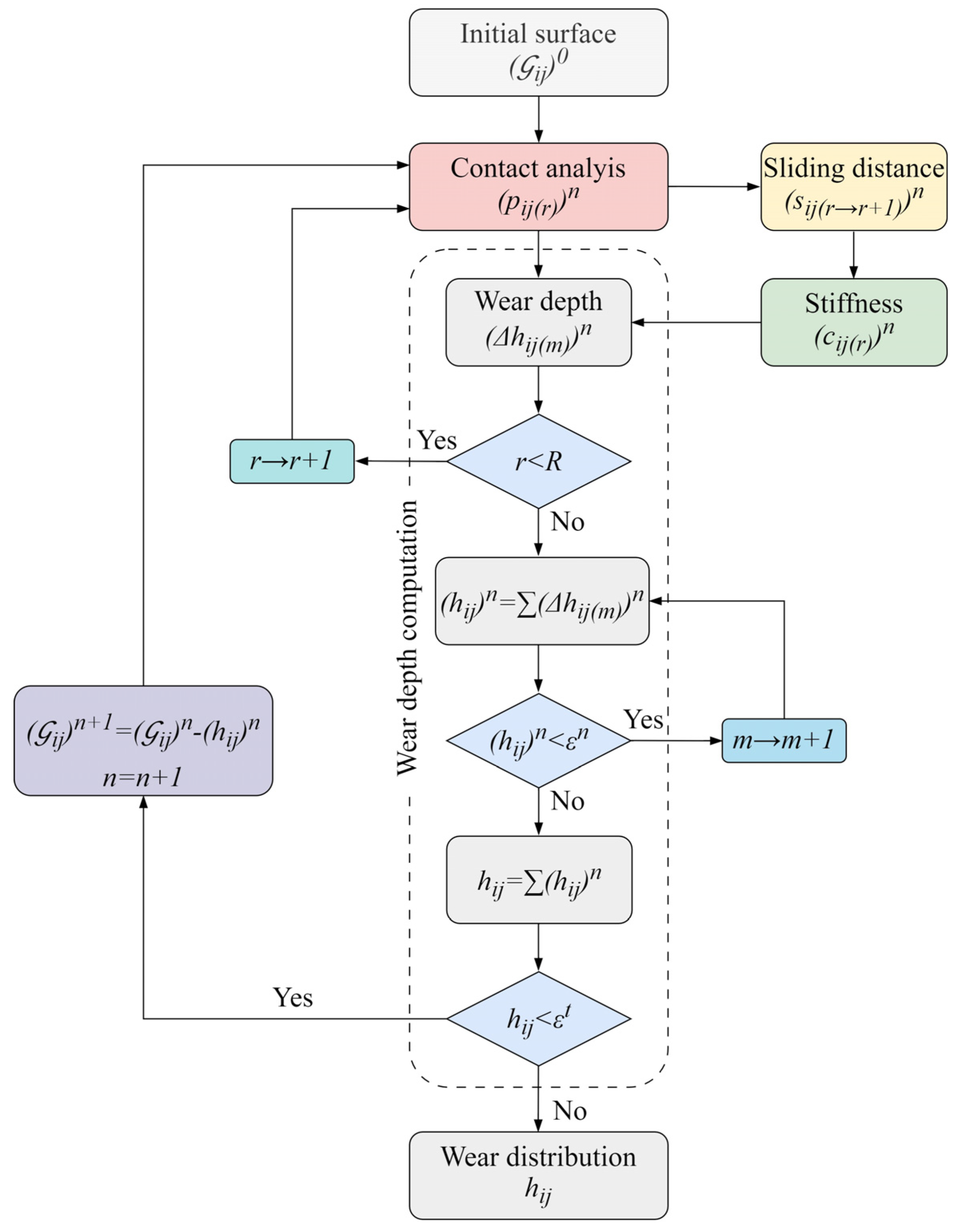
2.1.1. Computational Modeling of the Wear Depth
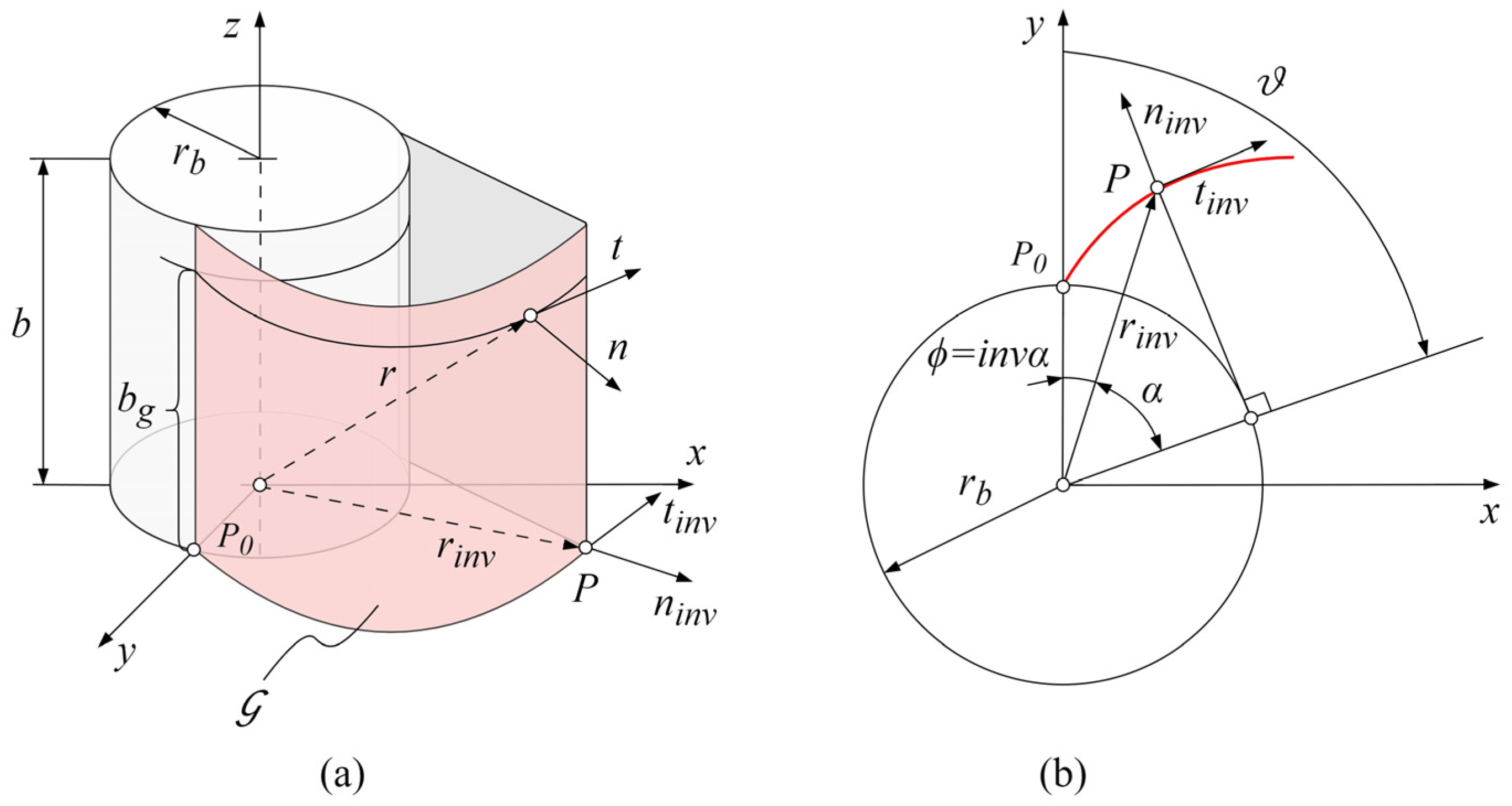
2.1.2. Geometric Description of Tooth Flank Surface
2.2. Contact Pressure Distribution
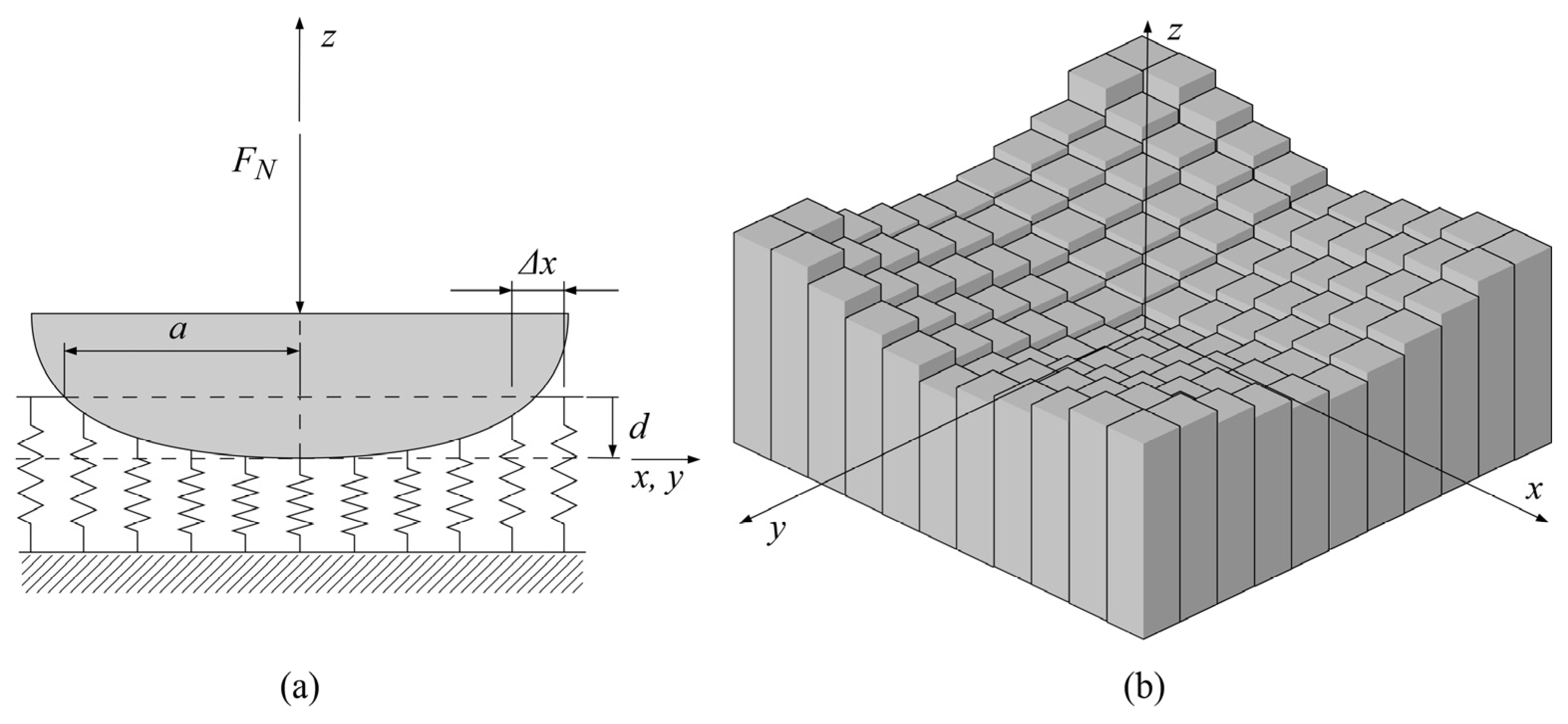
2.2.1. Winkler’s Surface Model
2.2.2. Winkler’s Modulus
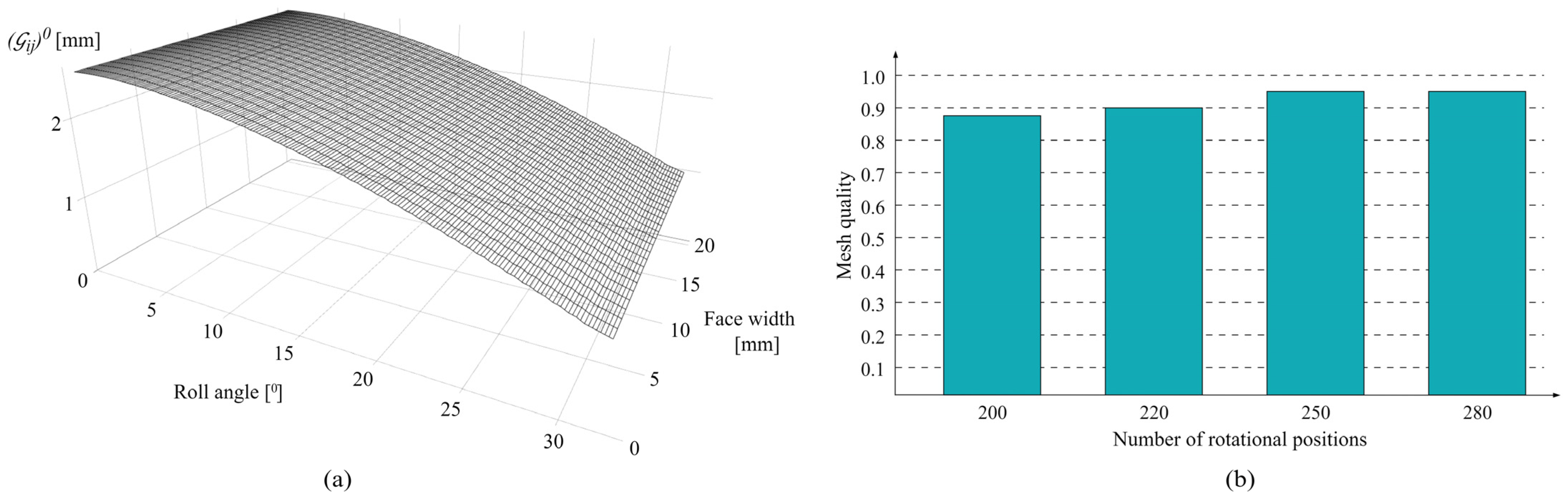
2.2.3. Algorithm for the Computation of Contact Pressure Distribution
| Algorithm 1 Contact pressure distribution |
| Initialize f(0), d(0), and p(0) |
| 1 Calculation of wear depth (hij)n |
| 2 Profile update f(n) = f(n−1) + (hij)n |
| 3 Calculation of new indentation depth d(n) |
| 4 Calculation of new contact pressure distribution p(n) |
| 5 if |f(n+1) − f(n)| < tolerance go to step 6 else go to step 1 |
| 6 Limiting profile p(n) = const. |
| end |
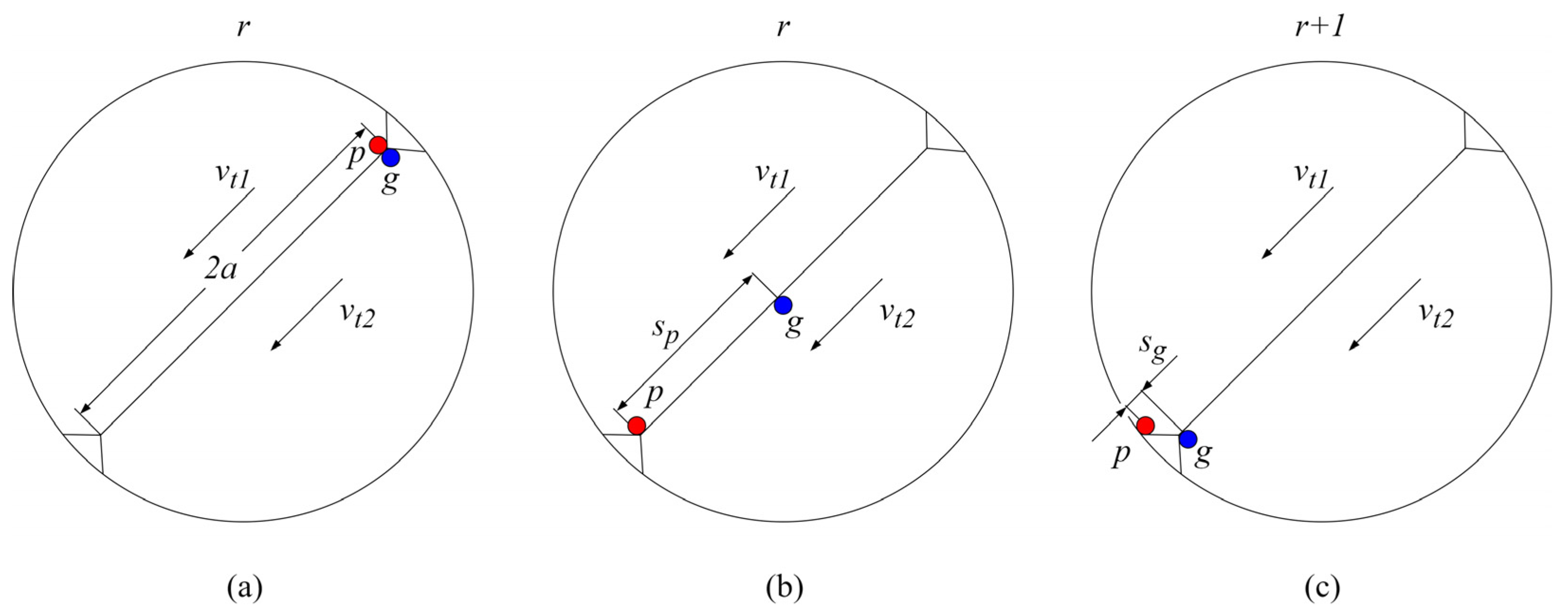
2.3. Sliding Distance
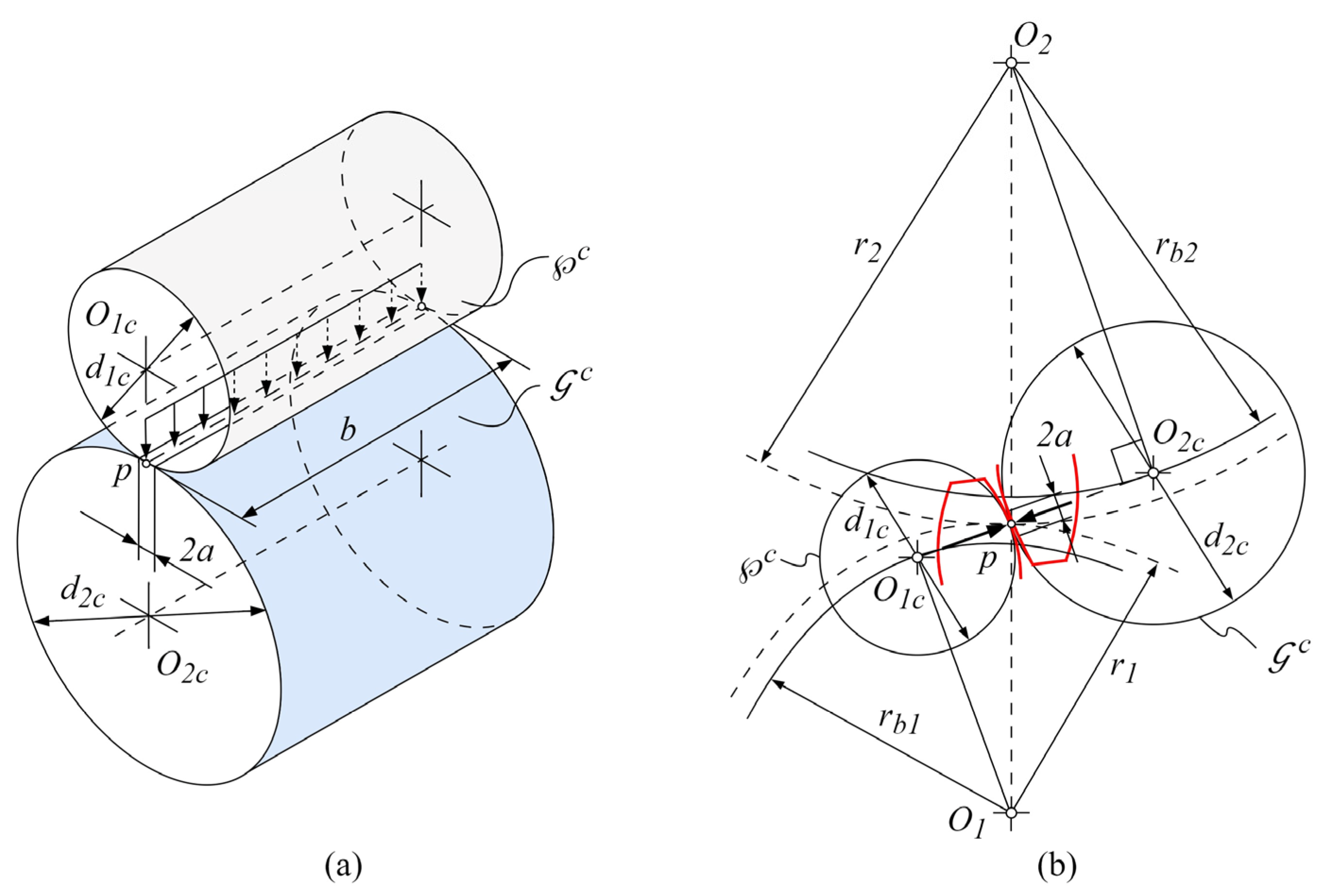
2.4. Meshing Stiffness
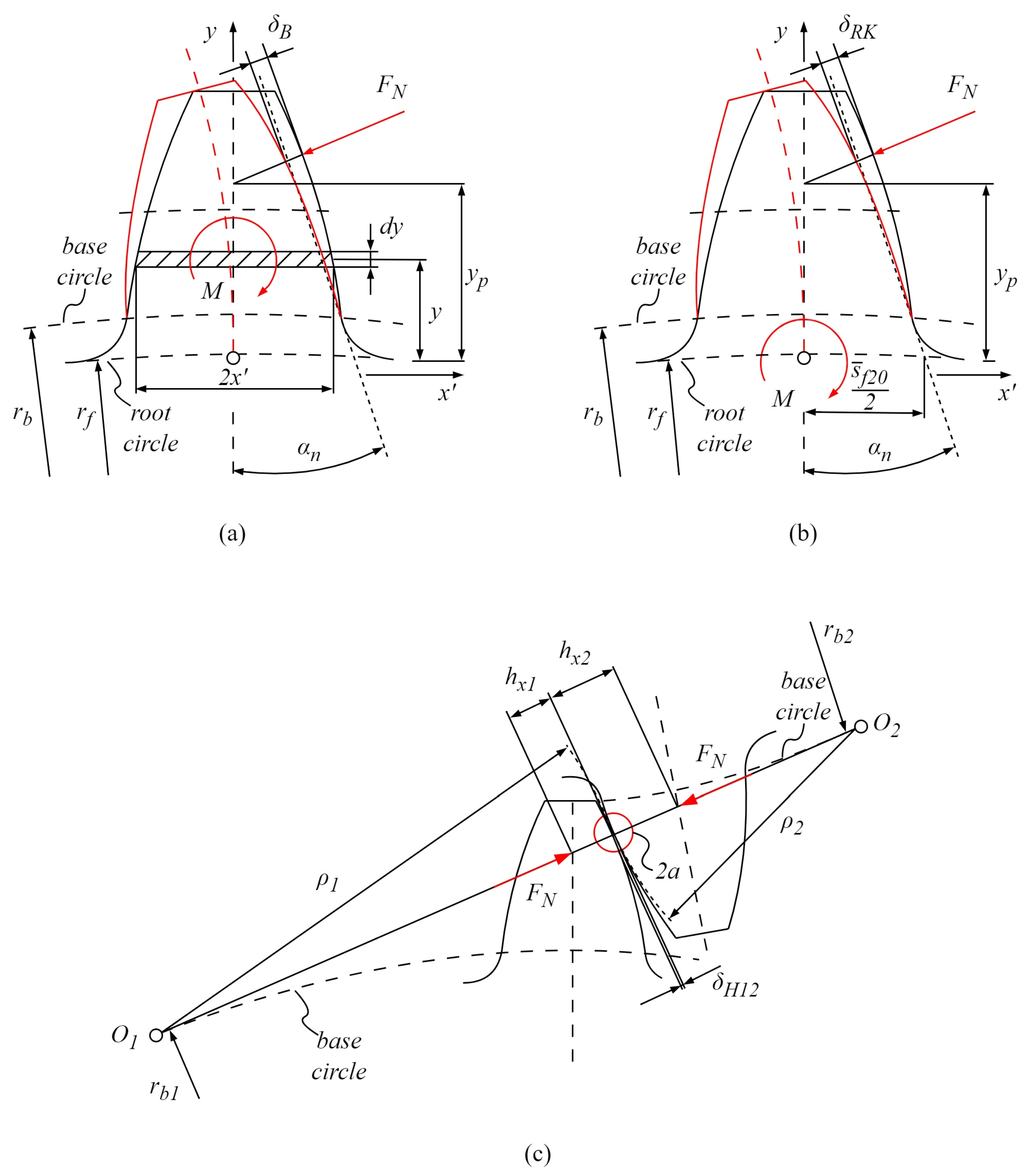
2.4.1. Weber’s Stiffness Model
2.4.2. Load-Sharing Factor
2.4.3. Algorithm for the Computation of Meshing Stiffness and Normal Load Distribution
| Algorithm 2 Meshing stiffness and load-sharing factors |
| Initialize ()0, (pij(r))0, and (sij(r→r+1))0 |
| 1 Calculation of deformations (δBp)n, (δRKp)n, (δBg)n, (δRKg)n, and (δH)n |
| 2 Calculation of stiffnesses (csp)n, (c1)n, and (c2)n |
| 3 Calculation of load-sharing factors (ξ1)n and (ξ2)n |
| 4 Calculation of normal load distribution FN = (ξ1FN)n+(ξ2FN)n |
| 5 if n < stopping criteria update ()n, (pij(r))n, and (sij(r→r+1))n and go to step 1 else go to step 6 |
| 6 return (csp)n and FN |
| end |
2.5. Computation of Wear Depth
2.6. Development of Surface Model
2.7. Wear Coefficient Assessment
2.7.1. Data on Polymer Gears
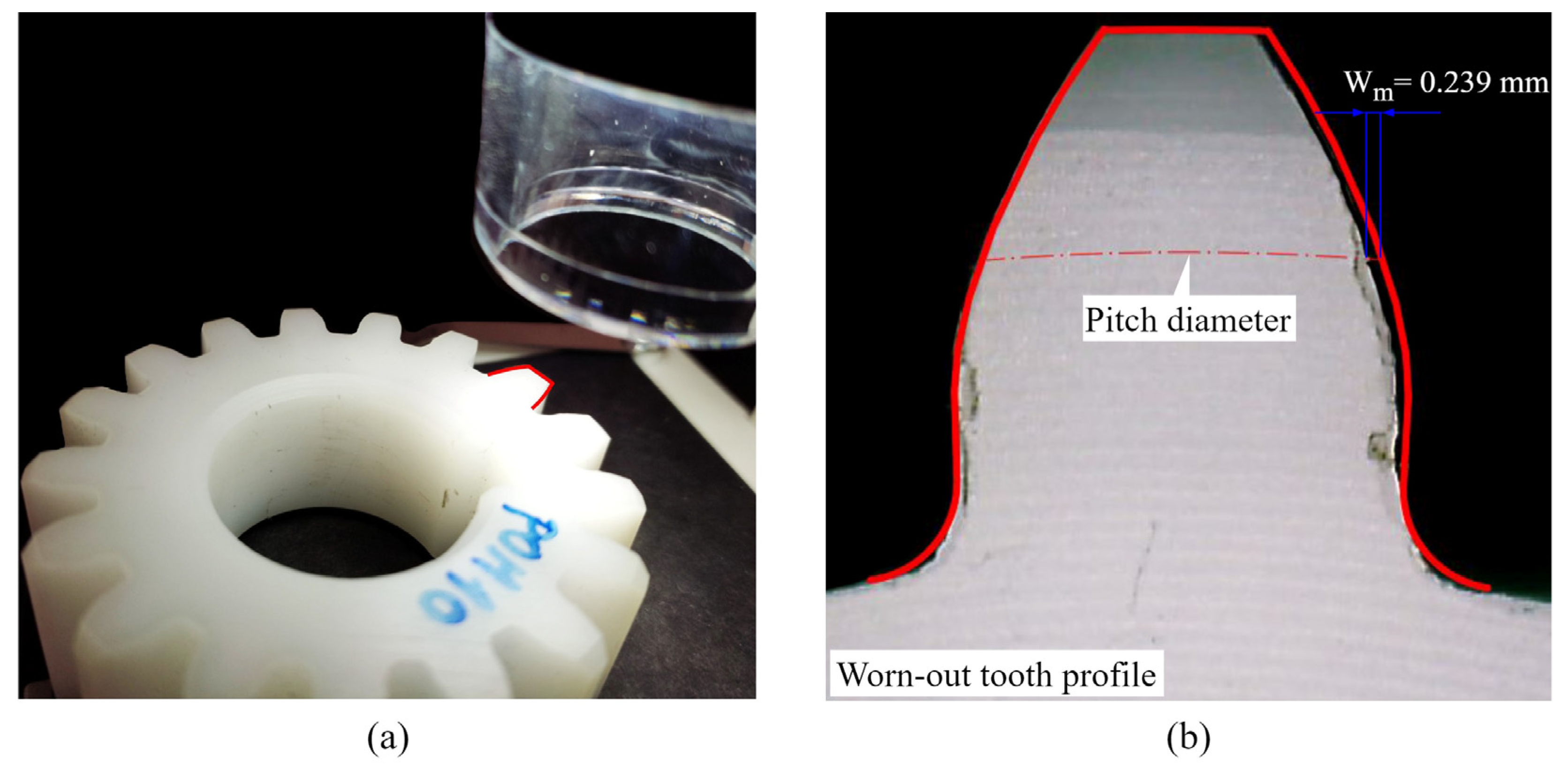
2.7.2. Experimental Setup
2.7.3. Wear Analysis
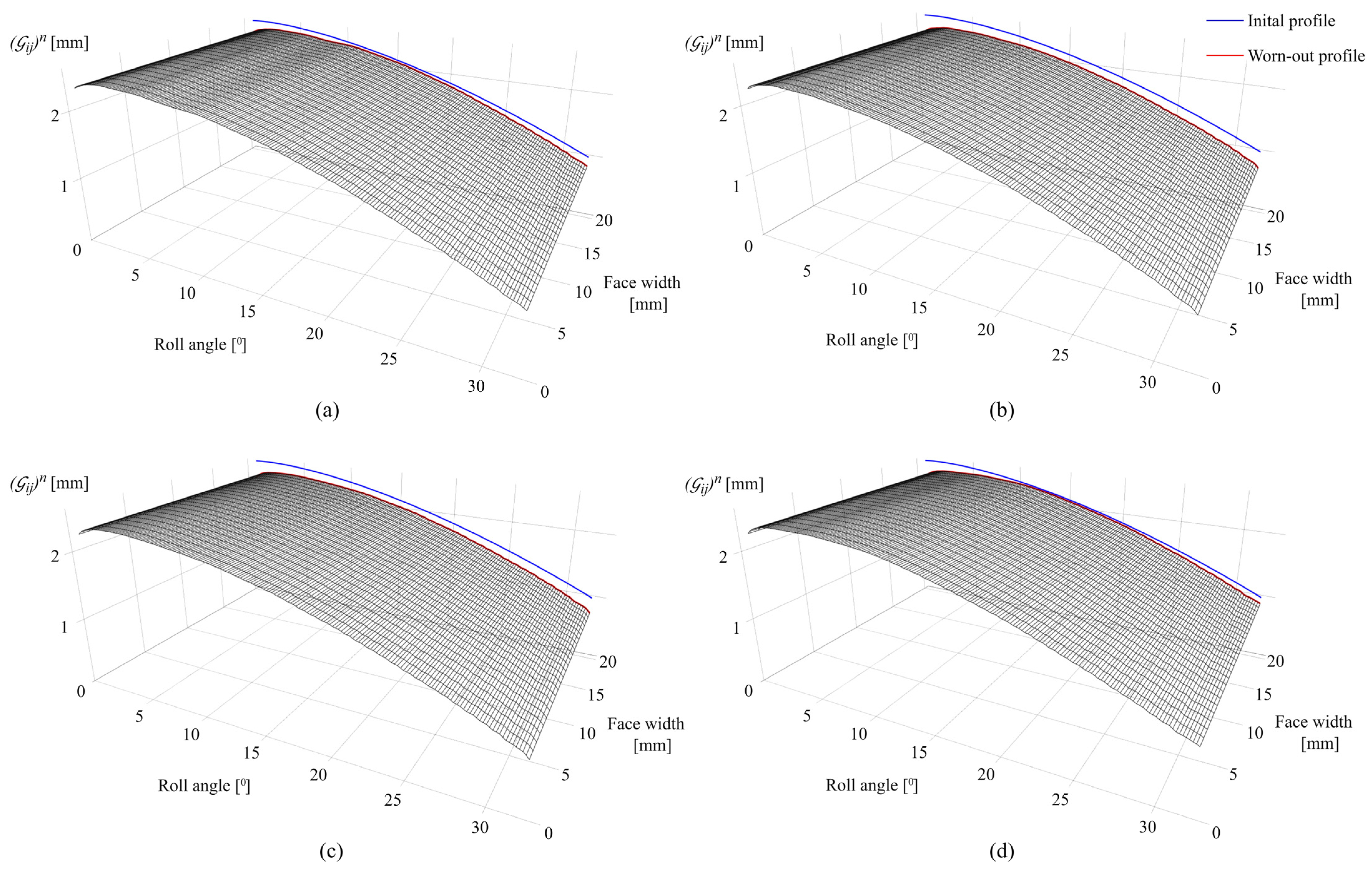
3. Results
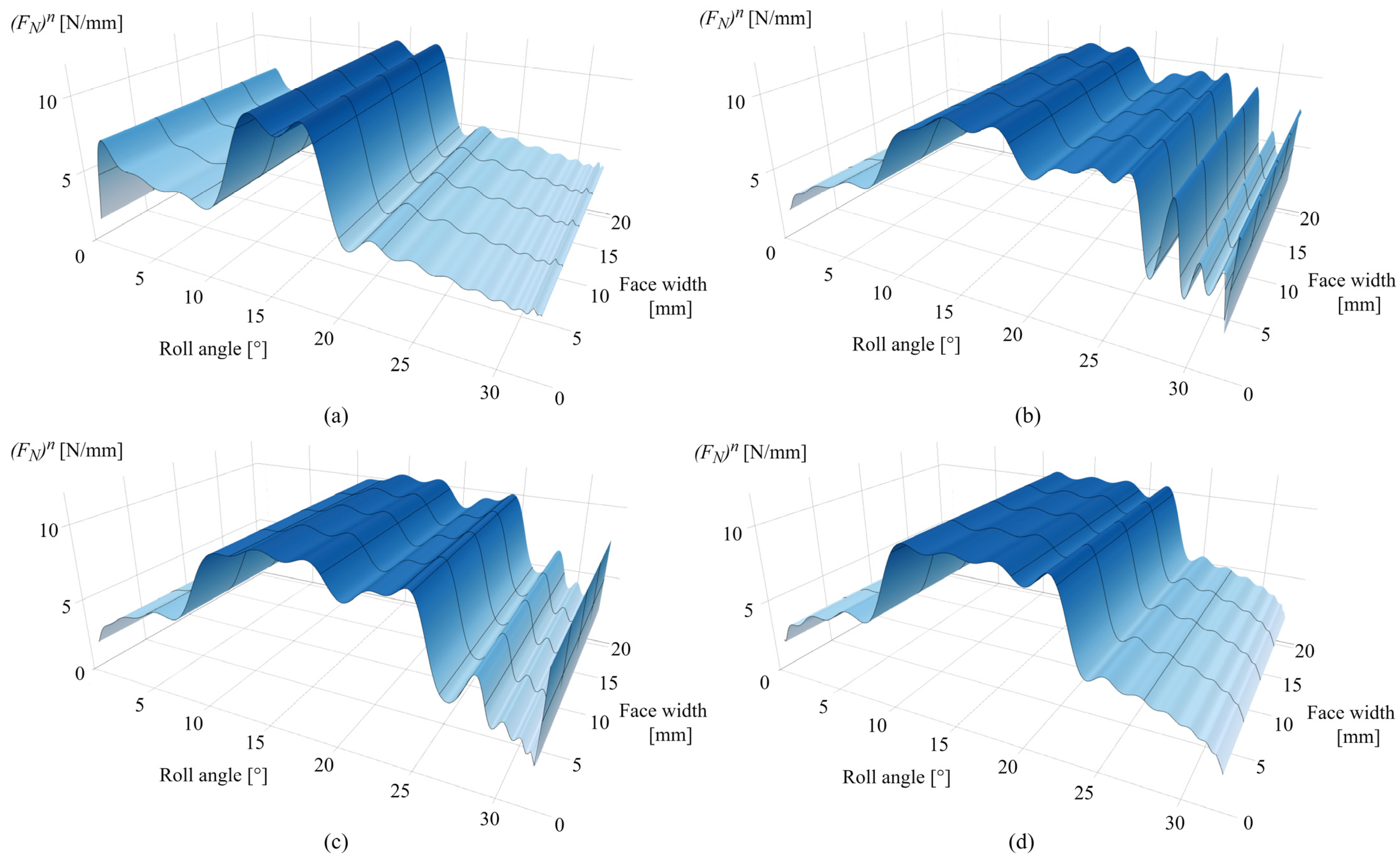
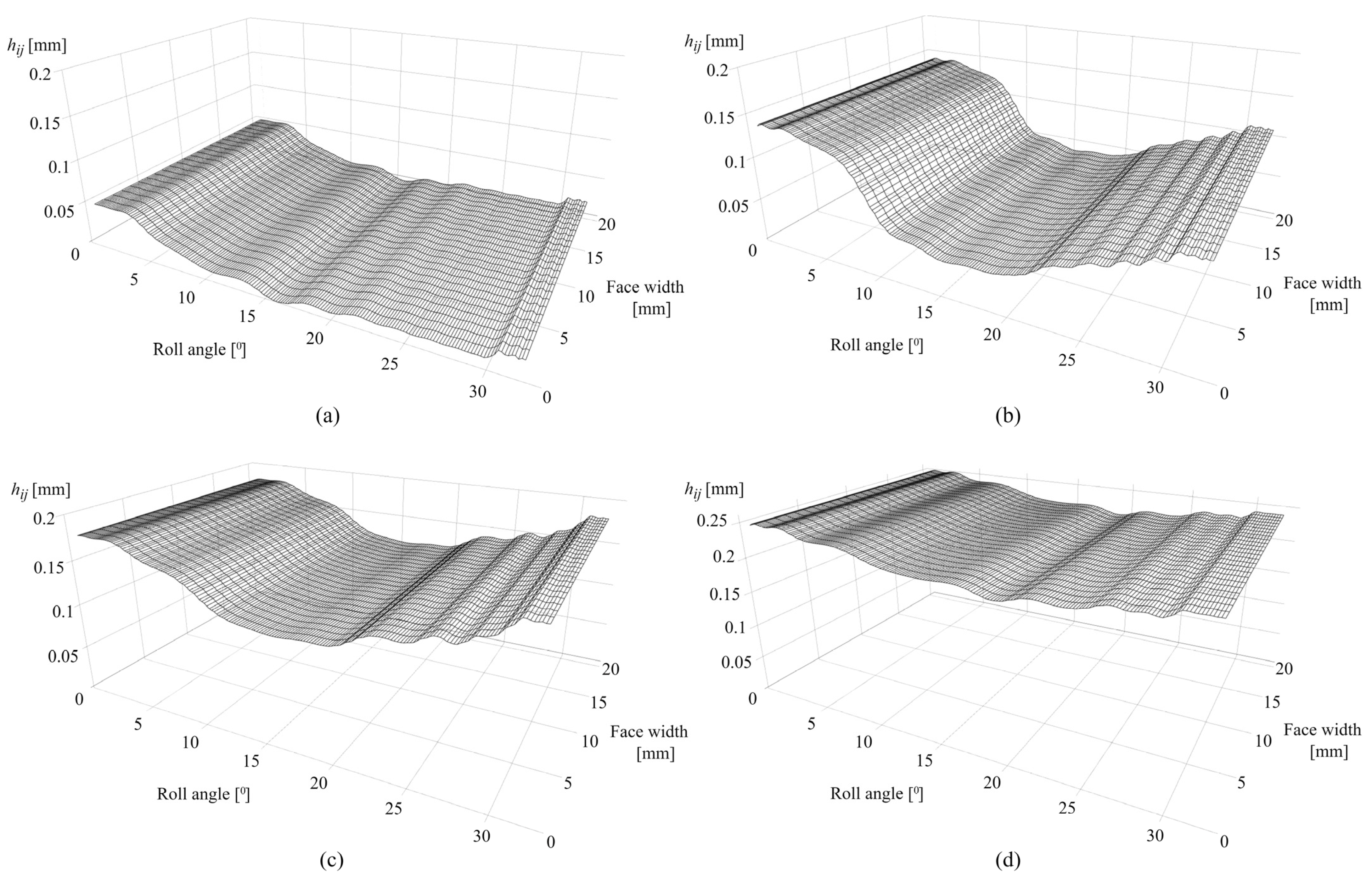
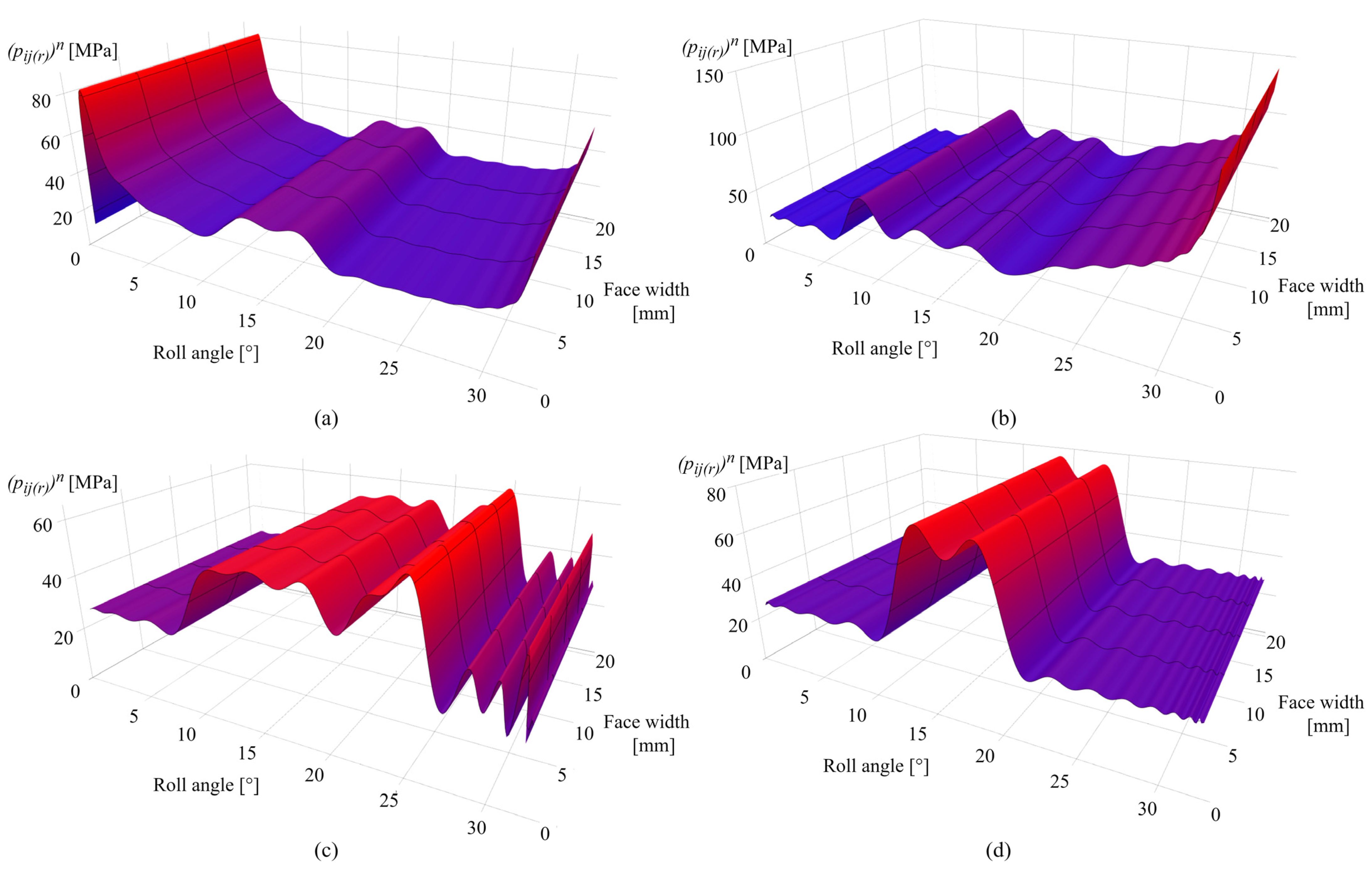
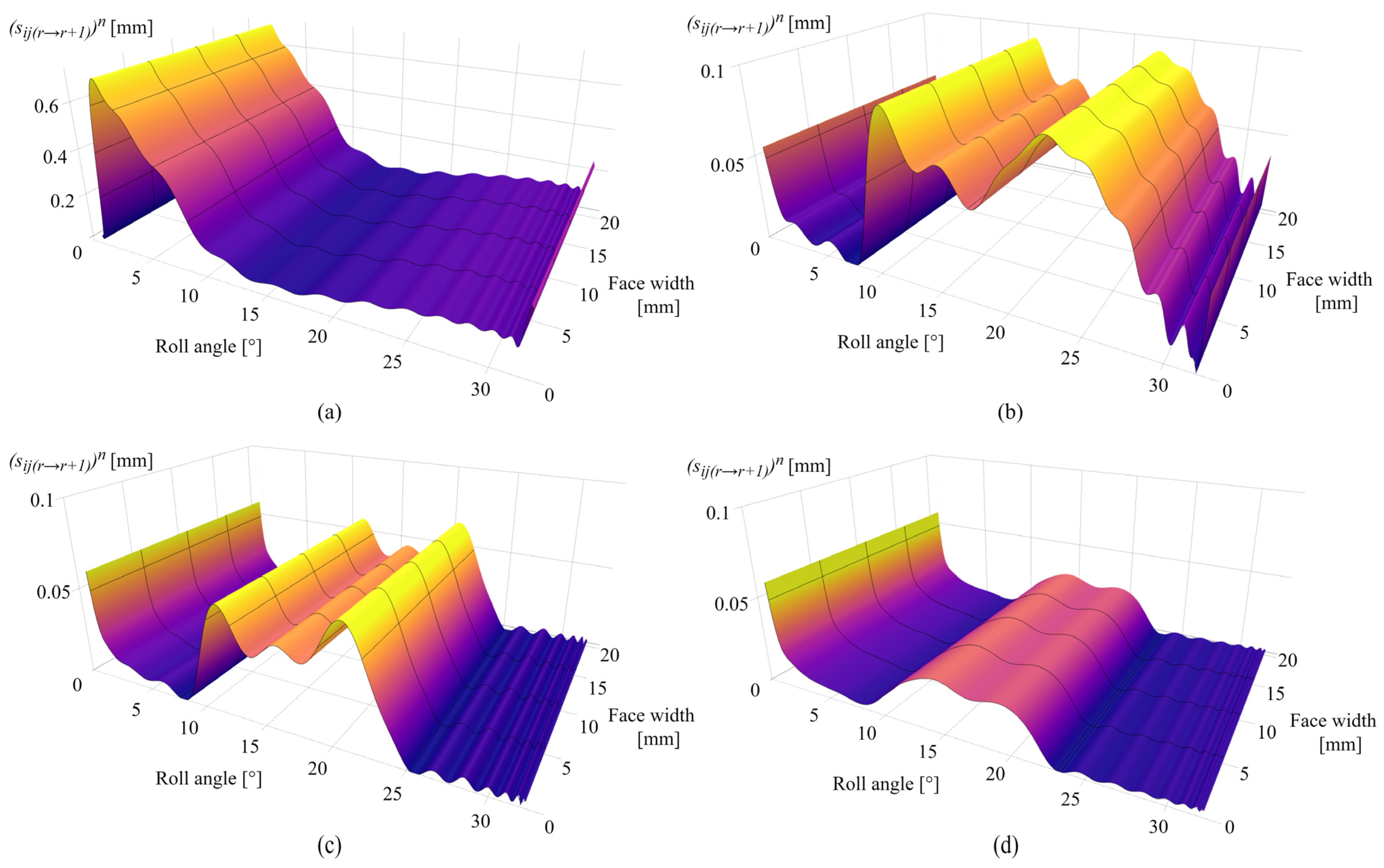
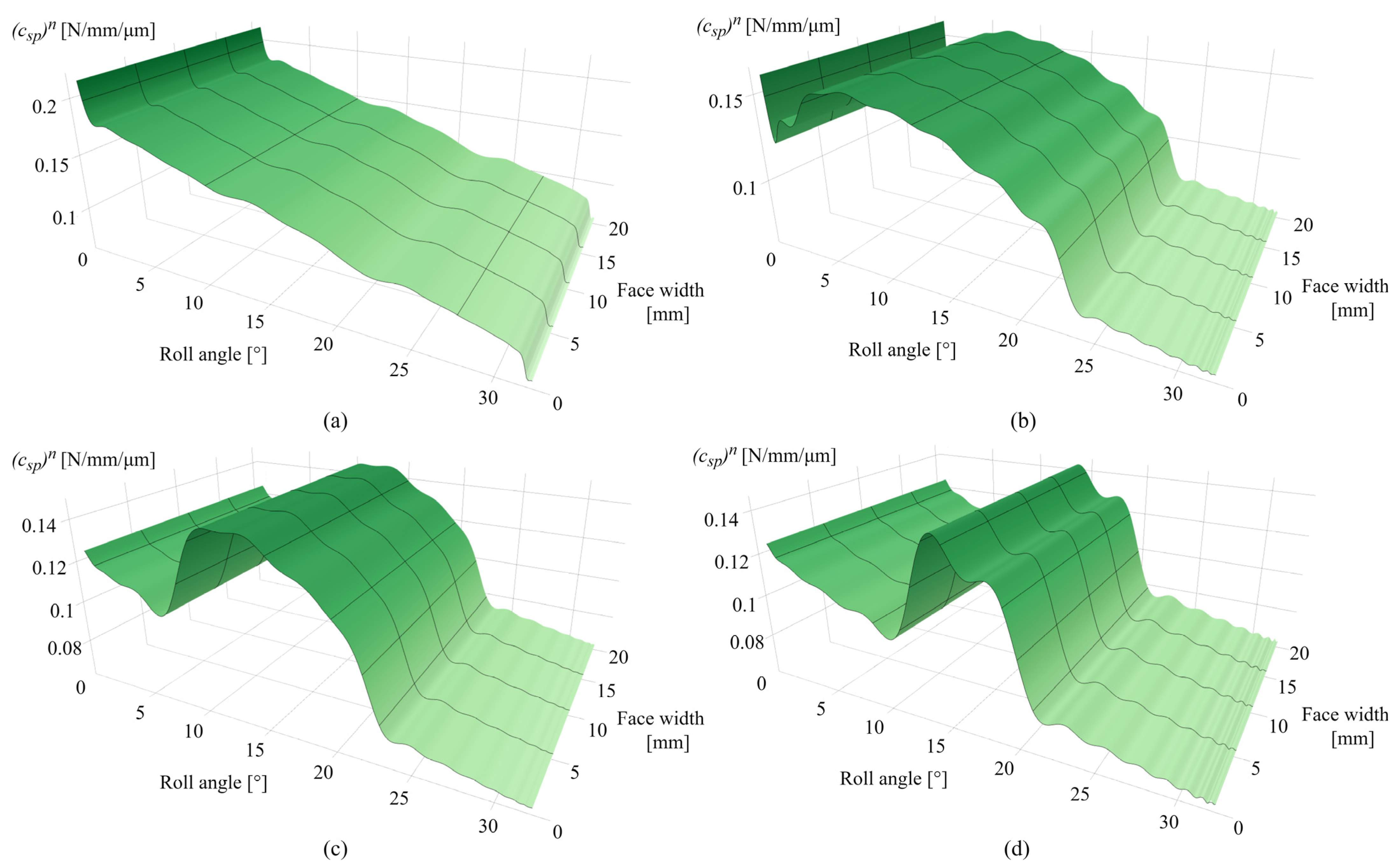
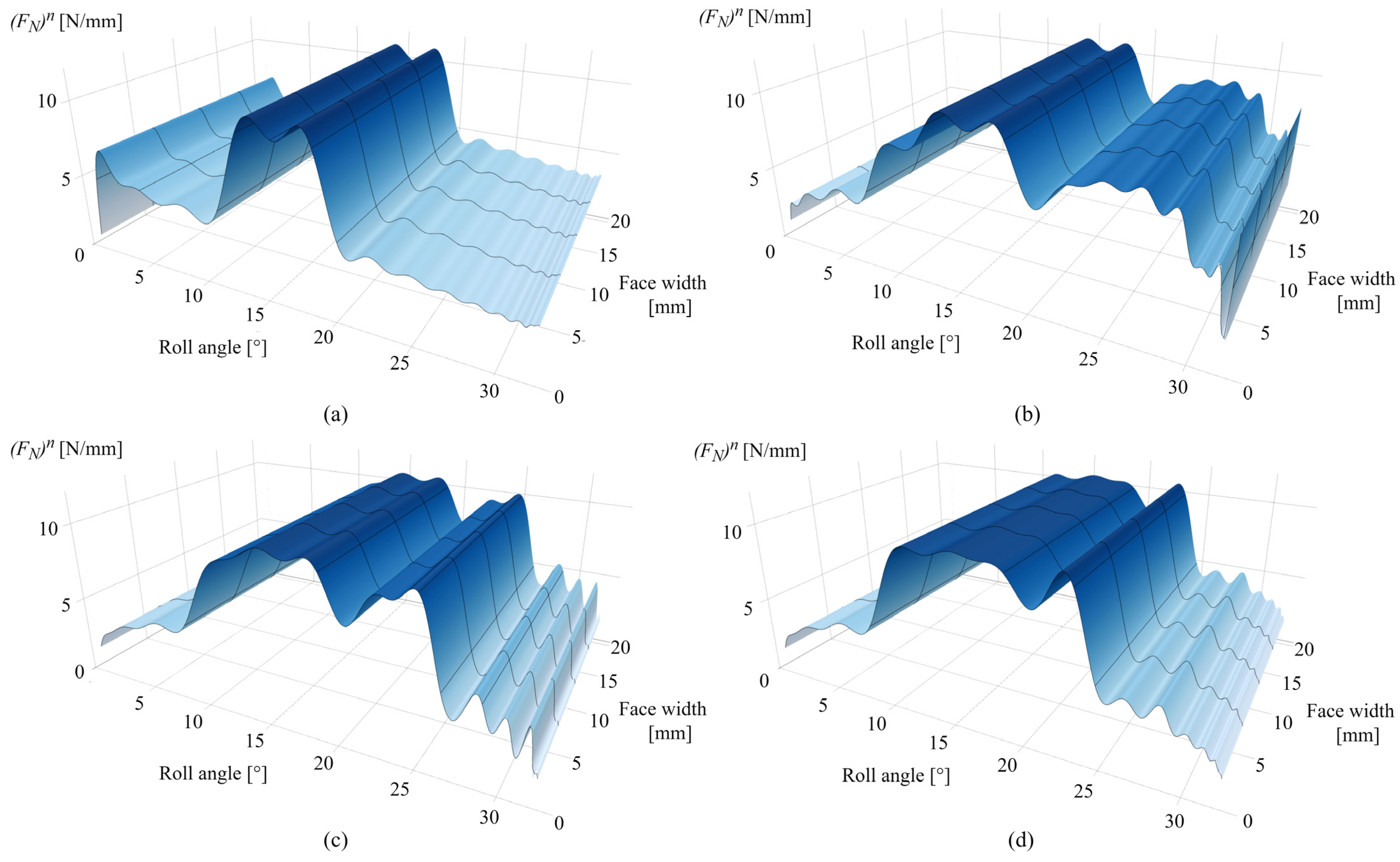
3.1. Contact Mechanics Model Predictions for POM Gears
3.2. Contact Mechanics Model Predictions for PVDF Gears
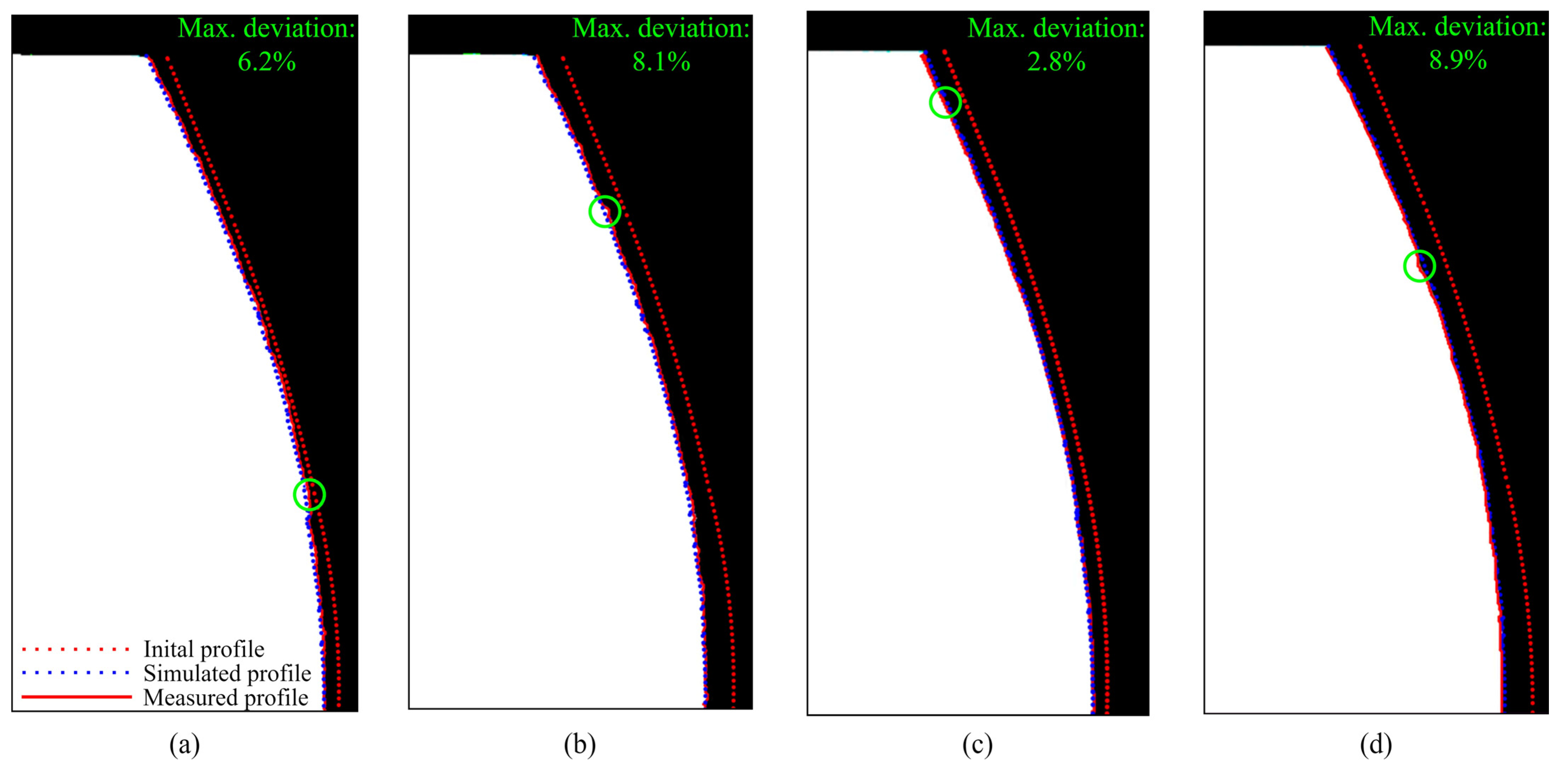
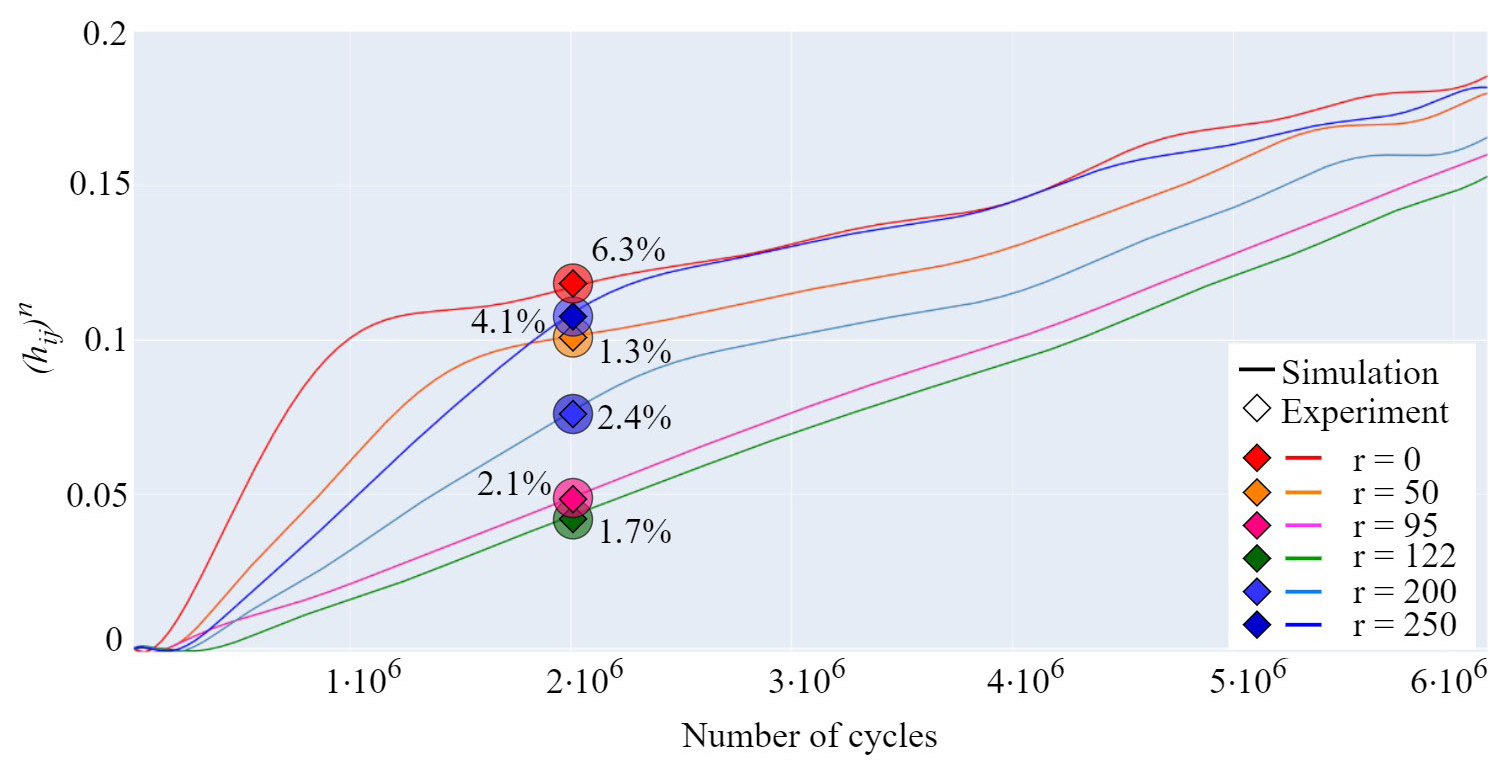
3.3. Model Validation
4. Discussion
5. Conclusions
- As the proposed contact mechanics model for wear prediction and experimentally obtained data are in good agreement, the presented model can be used for the wear prediction of parallel-axis polymer gears.
- The model allows for the visualization and assessment of numerous contact parameters at different phases of engagement, i.e., number of load cycles under different load conditions, which can be very useful in the polymer gear design process and can reduce the need for time-consuming experimental tests.
- The changes in contact parameters are altered with the changes in contact topography due to wear, with the maximum contact pressures and most severe sliding conditions at the most heavily worn areas of the tooth profile.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Radzevich, S.P. Dudley’s Handbook of Practical Gear Design and Manufacture; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Zorko, D.; Štiglic, J.; Černe, B.; Vukašinović, N. The Effect of Center Distance Error on the Service Life of Polymer Gears. Polym. Test. 2023, 123, 108033. [Google Scholar] [CrossRef]
- Zorko, D.; Kulovec, S.; Duhovnik, J.; Tavčar, J. Durability and Design Parameters of a Steel/PEEK Gear Pair. Mech. Mach. Theory 2019, 140, 825–846. [Google Scholar] [CrossRef]
- Zhong, B.; Zhang, R.; Wei, P.; Liu, H.; Li, J.; Lu, Z. The Durability Performance of Polyketone Gears under Various Lubrication Conditions. J. Tribol. 2022, 144, 091203. [Google Scholar] [CrossRef]
- Muratović, E.; Muminović, A.; Delić, M.; Pervan, N.; Muminović, A.J.; Šarić, I. Potential and Design Parameters of Polyvinylidene Fluoride in Gear Applications. Polymers 2023, 15, 4275. [Google Scholar] [CrossRef]
- Zhong, B.; Song, H.; Liu, H.; Wei, P.; Lu, Z. Loading Capacity of POM Gear under Oil Lubrication. J. Adv. Mech. Des. Syst. Manuf. 2022, 16, JAMDSM0006. [Google Scholar] [CrossRef]
- Hribersek, M.; Erjavec, M.; Hlebanja, G.; Kulovec, S. Durability Testing and Characterization of POM Gears. Eng. Fail. Anal. 2021, 124, 105377. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, H.; Zhu, C.; Song, H.; Yu, G. Identification of Failure Modes of a PEEK-Steel Gear Pair under Lubrication. Int. J. Fatigue 2019, 125, 342–348. [Google Scholar] [CrossRef]
- Tavčar, J.; Cerne, B.; Duhovnik, J.; Zorko, D. A Multicriteria Function for Polymer Gear Design Optimization. J. Comput. Des. Eng. 2021, 8, 581–599. [Google Scholar] [CrossRef]
- Zorko, D.; Demšar, I.; Tavčar, J. An Investigation on the Potential of Bio-Based Polymers for Use in Polymer Gear Transmissions. Polym. Test. 2021, 93, 106994. [Google Scholar] [CrossRef]
- Tavcar, J.; Grkman, G.; Duhovnik, J. Accelerated Lifetime Testing of Reinforced Polymer Gears. J. Adv. Mech. Des. Syst. Manuf. 2018, 12, JAMDSM0006. [Google Scholar] [CrossRef]
- Singh, A.K.; Siddhartha; Singh, P.K. Polymer Spur Gears Behaviors under Different Loading Conditions: A Review. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2018, 232, 210–228. [Google Scholar] [CrossRef]
- Černe, B.; Petkovšek, M.; Duhovnik, J.; Tavčar, J. Thermo-Mechanical Modeling of Polymer Spur Gears with Experimental Validation Using High-Speed Infrared Thermography. Mech. Mach. Theory 2020, 146, 103734. [Google Scholar] [CrossRef]
- Evans, S.M.; Keogh, P.S. Wear Mechanisms in Polyoxymethylene Spur Gears. Wear 2019, 428–429, 356–365. [Google Scholar] [CrossRef]
- Kumar Singh, A. Siddhartha Thermal and Wear Behavior of Glass Fiber-Filled Functionally Graded Material-Based Polyamide 66 Spur Gears Manufactured by a Novel Technique. J. Tribol. 2018, 140, 021601. [Google Scholar] [CrossRef]
- Matkovič, S.; Pogačnik, A.; Kalin, M. Wear-Coefficient Analyses for Polymer-Gear Life-Time Predictions: A Critical Appraisal of Methodologies. Wear 2021, 480–481, 203944. [Google Scholar] [CrossRef]
- Mao, K.; Chetwynd, D.G.; Millson, M. A New Method for Testing Polymer Gear Wear Rate and Performance. Polym. Test. 2020, 82, 106323. [Google Scholar] [CrossRef]
- Polanec, B.; Glodež, S.; Belšak, A. Noise Evaluation of Coated Polymer Gears. Polymers 2023, 15, 783. [Google Scholar] [CrossRef]
- Trobentar, B.; Hriberšek, M.; Kulovec, S.; Glodež, S.; Belšak, A. Noise Evaluation of S-Polymer Gears. Polymers 2022, 14, 438. [Google Scholar] [CrossRef]
- Alharbi, K.A.M. Wear and Mechanical Contact Behavior of Polymer Gears. J. Tribol. 2019, 141, 011101. [Google Scholar] [CrossRef]
- Rohrmoser, A.; Bode, C.; Schleich, B.; Hagenah, H.; Wartzack, S.; Merklein, M. Influence of Metal Gear Tooth Geometry on Load and Wear within Metal-Polymer Gear Pairs. Appl. Sci. 2022, 12, 270. [Google Scholar] [CrossRef]
- Kahraman, A.; Ding, H. Wear in Gears. In Encyclopedia of Tribology; Springer: Boston, MA, USA, 2013; pp. 3993–4001. [Google Scholar]
- VDI 2736 Part 1; Thermoplastic Gear Wheels—Materials, Material Selection, Production Methods, Production Tolerances, Form Design. Verein Deutscher Ingenieure: Harzgerode, Germany, 2016.
- VDI 2736 Part 2; Thermoplastic Gear Wheels—Cylindrical Gears—Calculation of the Load—Carrying Capacity. Verein Deutscher Ingenieure: Harzgerode, Germany, 2016.
- VDI 2736 Part 3; Thermoplastic Gear Wheels—Crossed Helical Gears—Mating Cylindrical Worm with Helical Gear—Calculation of the Load Carrying Capacity. Deutscher Ingenieure: Harzgerode, Germany, 2016.
- VDI 2736 Part 4; Thermoplastic Gear Wheels—Determination of Strength Parameters on Gears. Deutscher Ingenieure: Harzgerode, Germany, 2016.
- Xu, X.; Gao, F.; Valle, A.L.; Makenji, K.; Nedolisa, C.; Zhao, Y.; Goodship, V.; Mao, K. Wear Performance of Commercial Polyoxymethylene Copolymer and Homopolymer Injection Moulded Gears. Tribol. Ind. 2021, 43, 561–573. [Google Scholar] [CrossRef]
- Matkovič, S.; Pogačnik, A.; Kalin, M. Comparison between VDI 2736 Wear Calculation and Experimentally Obtained Results. In International Conference on Gears 2019; Deutscher Ingenieure: Harzgerode, Germany, 2019; pp. 1311–1322. [Google Scholar]
- Černe, B.; Vukašinović, N.; Zorko, D. In-Situ Experimental Methods for Measuring Tooth Meshing Displacements and Wear during Polymer Gear Tests Using a High-Speed Camera with Microscopy Optics. VDI Berichte 2023, 2023. [Google Scholar] [CrossRef]
- Kahraman, A.; Ding, H. A Methodology to Predict Surface Wear of Planetary Gears under Dynamic Conditions. Mech. Based Des. Struct. Mach. 2010, 38, 493–515. [Google Scholar] [CrossRef]
- Choudhry, J.; Larsson, R.; Almqvist, A. A Stress-State-Dependent Thermo-Mechanical Wear Model for Micro-Scale Contacts. Lubricants 2022, 10, 223. [Google Scholar] [CrossRef]
- Li, Q.; Forsbach, F.; Schuster, M.; Pielsticker, D.; Popov, V.L. Wear Analysis of a Heterogeneous Annular Cylinder. Lubricants 2018, 6, 28. [Google Scholar] [CrossRef]
- Katsikadelis, J.T. The Boundary Element Method for Engineers and Scientists: Theory and Applications, 2nd ed.; Academic Press: Cambridge, MA, USA, 2016; ISBN 9780128044933. [Google Scholar]
- Xi, Y.; Li, B.; Almqvist, A. Semi-Analytical Model for 3D Multilayered Rolling Contact Problems with Different Creepage Combinations. J. Tribol. 2024, 146, 044103. [Google Scholar] [CrossRef]
- Pérez-Ràfols, F.; Almqvist, A. Generating Randomly Rough Surfaces with given Height Probability Distribution and Power Spectrum. Tribol. Int. 2019, 131, 591–604. [Google Scholar] [CrossRef]
- Marian, M.; Almqvist, A.; Rosenkranz, A.; Fillon, M. Numerical Micro-Texture Optimization for Lubricated Contacts—A Critical Discussion. Friction 2022, 10, 1772–1809. [Google Scholar] [CrossRef]
- Liu, Z.; Xiao, X.; Zhou, W.; Wang, Z.; Zhang, H.; Zhou, J. Wear Analysis of Hot Extrusion Punch for Large Fan Shaft Based on Archard Wear Theory. In Lecture Notes in Mechanical Engineering; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
- Yan, Y.; Helmons, R.; Carr, M.; Wheeler, C.; Schott, D. Modelling of Material Removal Due to Sliding Wear Caused by Bulk Material. Powder Technol. 2023, 415, 118109. [Google Scholar] [CrossRef]
- Di Puccio, F.; Mattei, L. Further Validation of a Simple Mathematical Description of Wear and Contact Pressure Evolution in Sliding Contacts. Lubricants 2023, 11, 230. [Google Scholar] [CrossRef]
- Zhao, Q.; Xing, Z.; Yuan, J.; Zhang, Z.; Zhu, J.; Jiang, H. An Improved Modeling and Numerical Analysis Method for Tooth Surface Wear of Double-Arc Harmonic Gears. Materials 2022, 15, 8869. [Google Scholar] [CrossRef] [PubMed]
- Winkler, A.; Bartz, M.; Wartzack, S. Numerical Wear Modeling in the Mixed and Boundary Lubrication Regime. Lubricants 2022, 10, 334. [Google Scholar] [CrossRef]
- Winkler, A.; Marian, M.; Tremmel, S.; Wartzack, S. Numerical Modeling of Wear in a Thrust Roller Bearing under Mixed Elastohydrodynamic Lubrication. Lubricants 2020, 8, 58. [Google Scholar] [CrossRef]
- Kong, Y.; Bennett, C.J.; Hyde, C.J. A Computationally Efficient Method for the Prediction of Fretting Wear in Practical Engineering Applications. Tribol. Int. 2022, 165, 107317. [Google Scholar] [CrossRef]
- Popov, V. Generalized Archard Law of Wear Based on Rabinowicz Criterion of Wear Particle Formation. Facta Univ. Ser. Mech. Eng. 2019, 17, 39–45. [Google Scholar] [CrossRef]
- Choudhry, J.; Almqvist, A.; Prakash, B.; Larsson, R. A Stress-State-Dependent Sliding Wear Model for Micro-Scale Contacts. J. Tribol. 2023, 145, 111702. [Google Scholar] [CrossRef]
- Vakis, A.I.; Yastrebov, V.A.; Scheibert, J.; Nicola, L.; Dini, D.; Minfray, C.; Almqvist, A.; Paggi, M.; Lee, S.; Limbert, G.; et al. Modeling and Simulation in Tribology across Scales: An Overview. Tribol. Int. 2018, 125, 169. [Google Scholar] [CrossRef]
- Pérez-Ràfols, F. A Two-Scale Stochastic Model for the Contact Mechanics of Rough Surfaces Including a Wide Span of Length Scales. Tribol. Int. 2023, 185, 108502. [Google Scholar] [CrossRef]
- Xi, Y.; Björling, M.; Almqvist, A. A Numerical Model for Solving Three-Dimensional Rolling Contact Problems with Elastic Coating Layers. Tribol. Lett. 2021, 69, 139. [Google Scholar] [CrossRef]
- Garcin, S.; Baydoun, S.; Arnaud, P.; Fouvry, S. Fretting Wear Modeling of 3D and 2D Hertzian Contacts with a Third-Body Layer Using a Winkler Elastic Foundation Model. Tribol. Int. 2022, 170, 107493. [Google Scholar] [CrossRef]
- Menga, N.; Ciavarella, M. A Winkler Solution for the Axisymmetric Hertzian Contact Problem with Wear and Finite Element Method Comparison. J. Strain Anal. Eng. Des. 2015, 50, 156–162. [Google Scholar] [CrossRef]
- Popov, V.L.; Heß, M.; Willert, E. Handbook of Contact Mechanics: Exact Solutions of Axisymmetric Contact Problems; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Popov, V.L.; Willert, E.; Heß, M. Method of Dimensionality Reduction in Contact Mechanics and Friction: A User’s Handbook. Iii. Viscoelastic Contacts. Facta Univ. Ser. Mech. Eng. 2018, 16, 99–113. [Google Scholar] [CrossRef]
- Argatov, I.I.; Chai, Y.S. A Self-Similar Model for Fretting Wear Contact with the Third Body in Gross Slip. Wear 2021, 466–467, 203562. [Google Scholar] [CrossRef]
- Heß, M.; Forsbach, F. An Analytical Model for Almost Conformal Spherical Contact Problems: Application to Total Hip Arthroplasty with Uhmwpe Liner. Appl. Sci. 2021, 11, 1170. [Google Scholar] [CrossRef]
- Sánchez, M.B.; Pleguezuelos, M.; Pedrero, J.I. Influence of Profile Modification on the Transmission Error of Spur Gears under Surface Wear. Mech. Mach. Theory 2024, 191, 105473. [Google Scholar] [CrossRef]
- Mao, H.; Fu, L.; Yu, G.; Tupolev, V.; Liu, W. Numerical Calculation of Meshing Stiffness for Beveloid Gear with Profile Modification. Jisuanji Jicheng Zhizao Xitong/Comput. Integr. Manuf. Syst. CIMS 2022, 28, 526. [Google Scholar] [CrossRef]
- Cao, Z.; Chen, Z.; Jiang, H. Nonlinear Dynamics of a Spur Gear Pair with Force-Dependent Mesh Stiffness. Nonlinear Dyn. 2020, 99, 1227–1241. [Google Scholar] [CrossRef]
- Sánchez, M.B.; Pleguezuelos, M.; Pedrero, J.I. Approximate Equations for the Meshing Stiffness and the Load Sharing Ratio of Spur Gears Including Hertzian Effects. Mech. Mach. Theory 2017, 109, 231–249. [Google Scholar] [CrossRef]
- Pedrero, J.I.; Pleguezuelos, M.; Sánchez, M.B. Analytical Model for Meshing Stiffness, Load Sharing, and Transmission Error for Helical Gears with Profile Modification. Mech. Mach. Theory 2023, 185, 105340. [Google Scholar] [CrossRef]
- Chen, W.; Lei, Y.; Fu, Y.; Hou, L. A Study of Effects of Tooth Surface Wear on Time-Varying Mesh Stiffness of External Spur Gear Considering Wear Evolution Process. Mech. Mach. Theory 2021, 155, 104055. [Google Scholar] [CrossRef]
- ISO 1183; Plastics—Methods for Determining the Density of Non-Cellular Plastics - Part 1: Immersion Method, Liquid Pycnometer Method and Titration Method. ISO: Geneva, Switzerland, 2019.
- ISO 527-2; Plastics—Determination of Tensile Properties—Part 2: Test Conditions for Moulding and Extrusion Plastics. ISO: Geneva, Switzerland, 2012.
- ISO 11359; Plastics—Thermomechanical Analysis (TMA)—Part 2: Determination of Coefficient of Linear Thermal Expansion and Glass Transition Temperature. ISO: Geneva, Switzerland, 2021.
- ISO 22007-4; Plastics—Determination of Thermal Conductivity and Thermal Diffusivity—Part 4: Laser Flash Method. ISO: Geneva, Switzerland, 2008.
- DIN 53765; Testing of Plastics and Elastomeres; Thermal Analysis; DSC-Method. German Institute for Standardization: Berlin, Germany, 1994.
- ISO 11357; Plastics—Differential Scanning Calorimetry (DSC)-Part 1: General Principles. ISO: Geneva, Switzerland, 2023.
- ISO 11357; Plastics—Determination of Hardness-Part 1: Ball Indentation Method. ISO: Geneva, Switzerland, 2023.
- DIN 52612; Tesing of Thermal Insulating Materials; Determination of Thermal Conductivity by Means of the Guarded Hot Plate Apparatus; Conversion of the Measured Values for Building Applications. German Institute for Standardization: Berlin, Germany, 1984.
- ISO 3146; Plastics—Determination of Melting Behaviour (Melting Temperature or Melting Range) of Semi-Crystalline Polymers by Capillary Tube and Polarizing-Microscope Methods. ISO: Geneva, Switzerland, 2022.

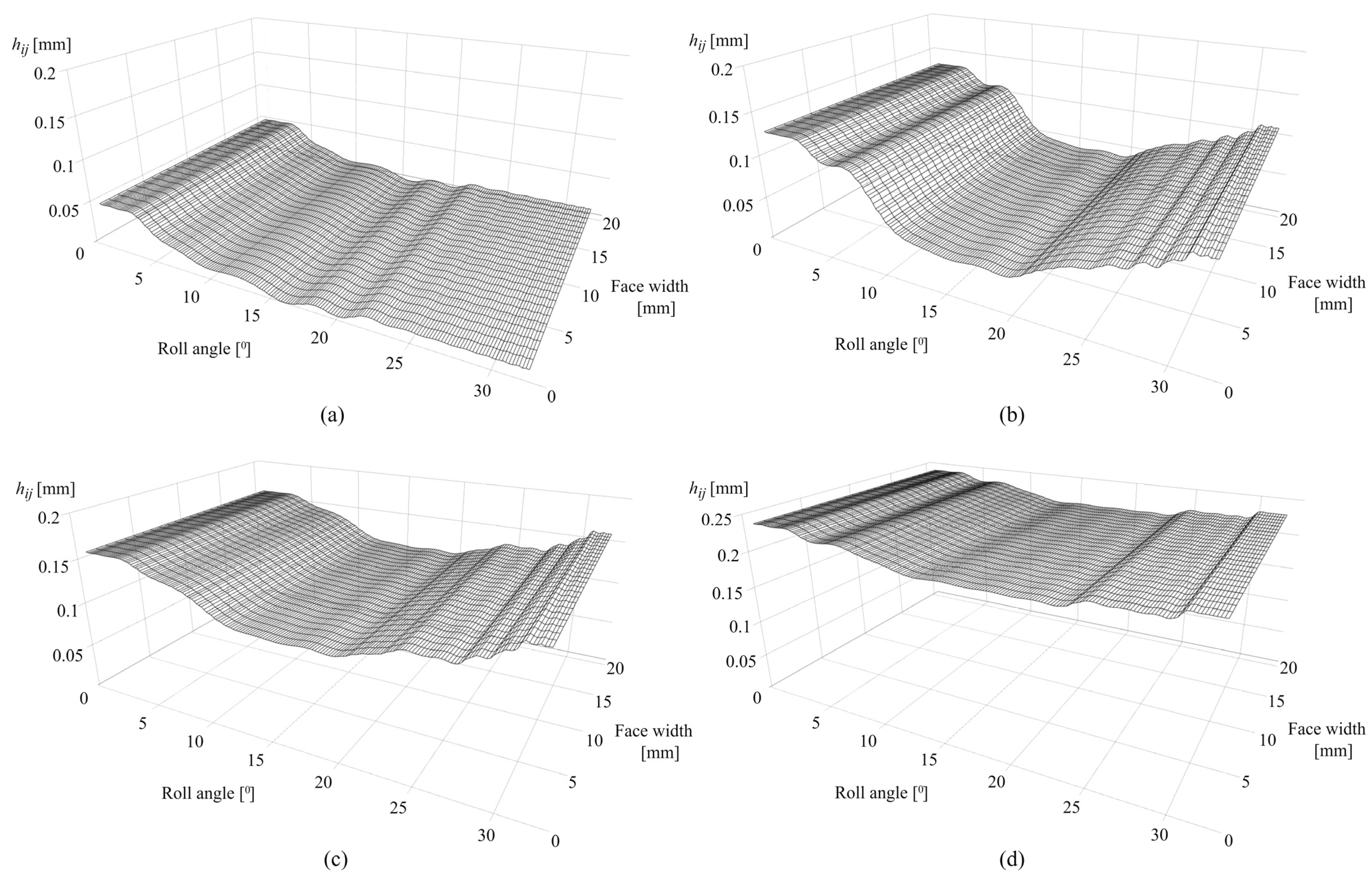
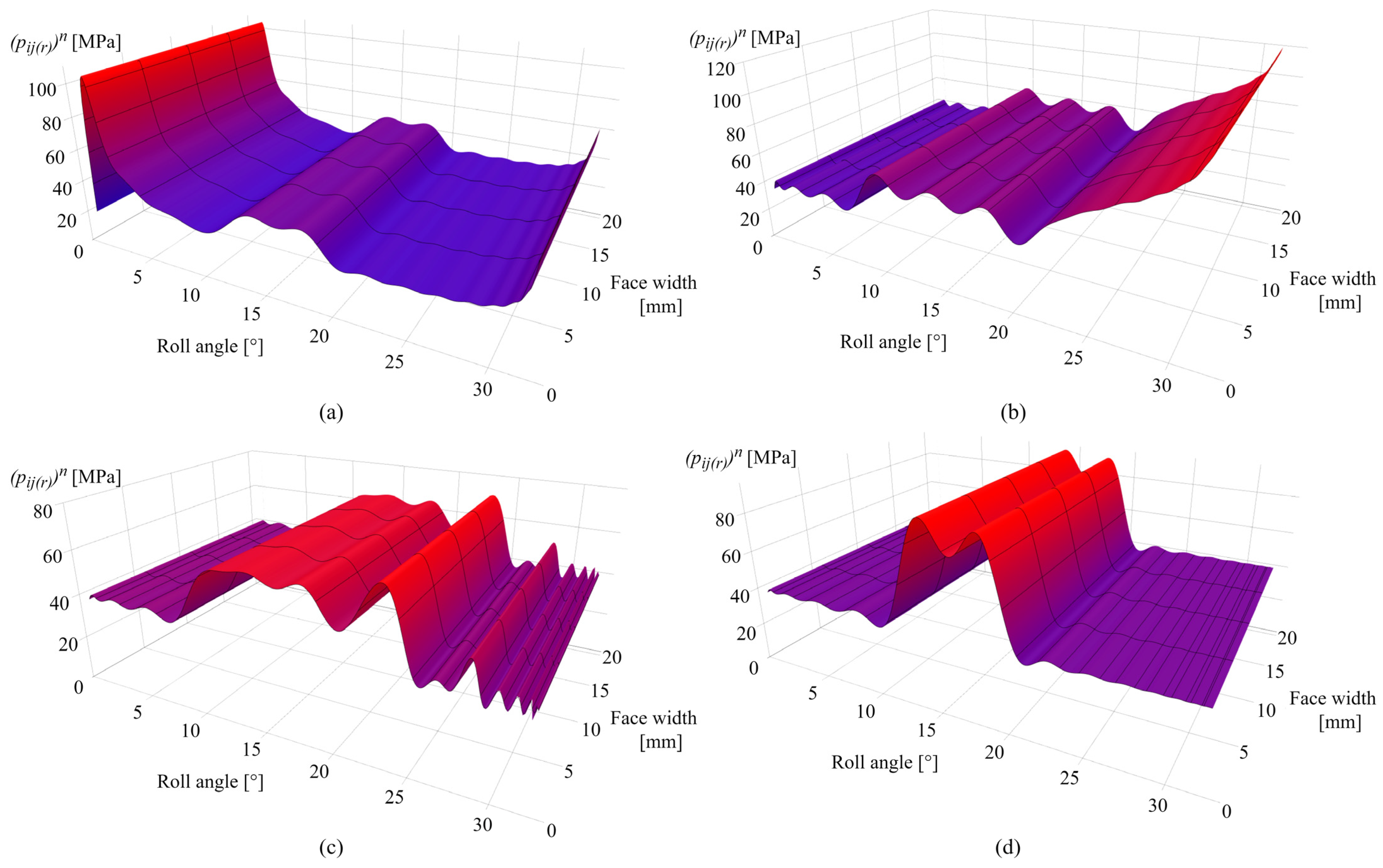
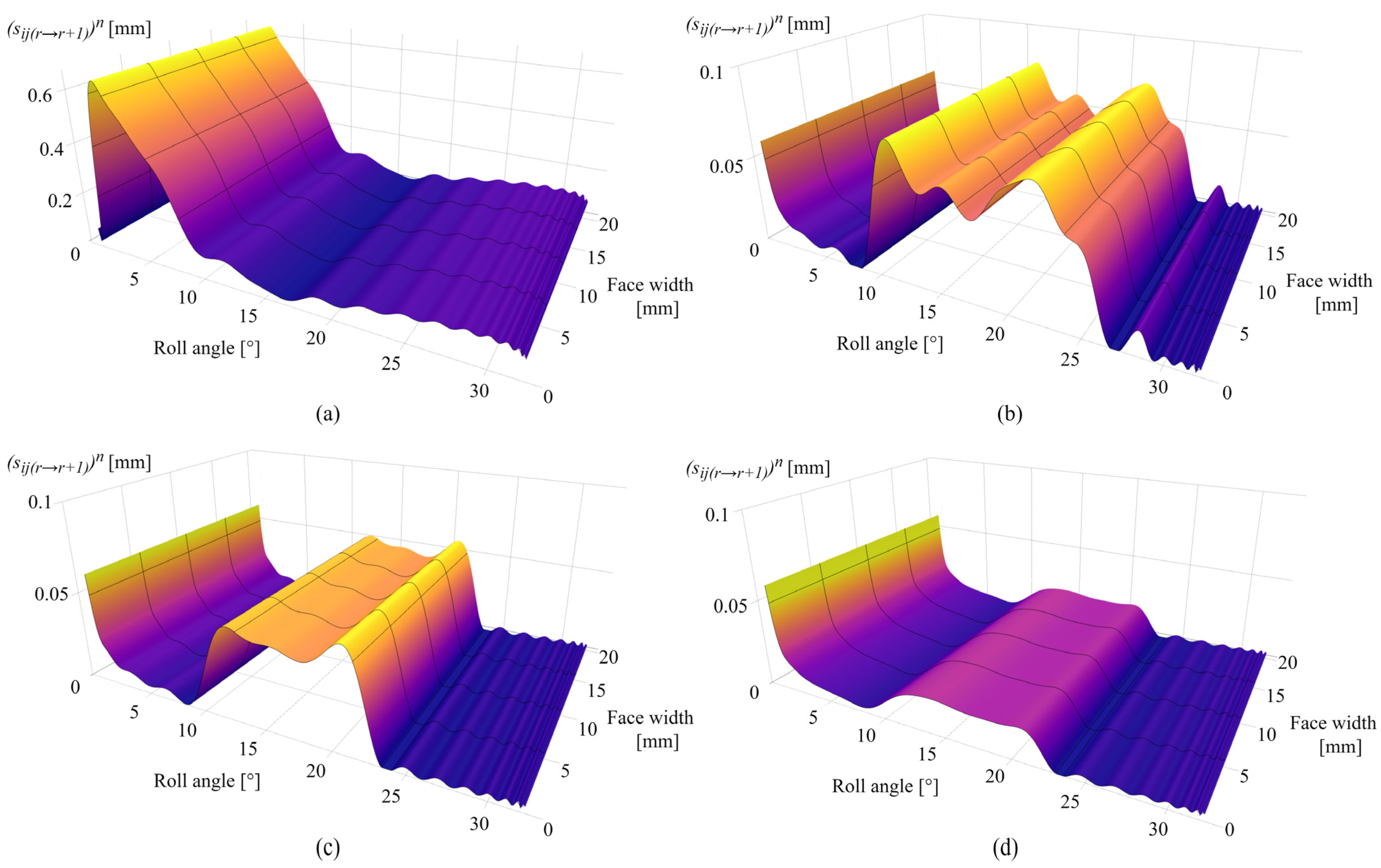
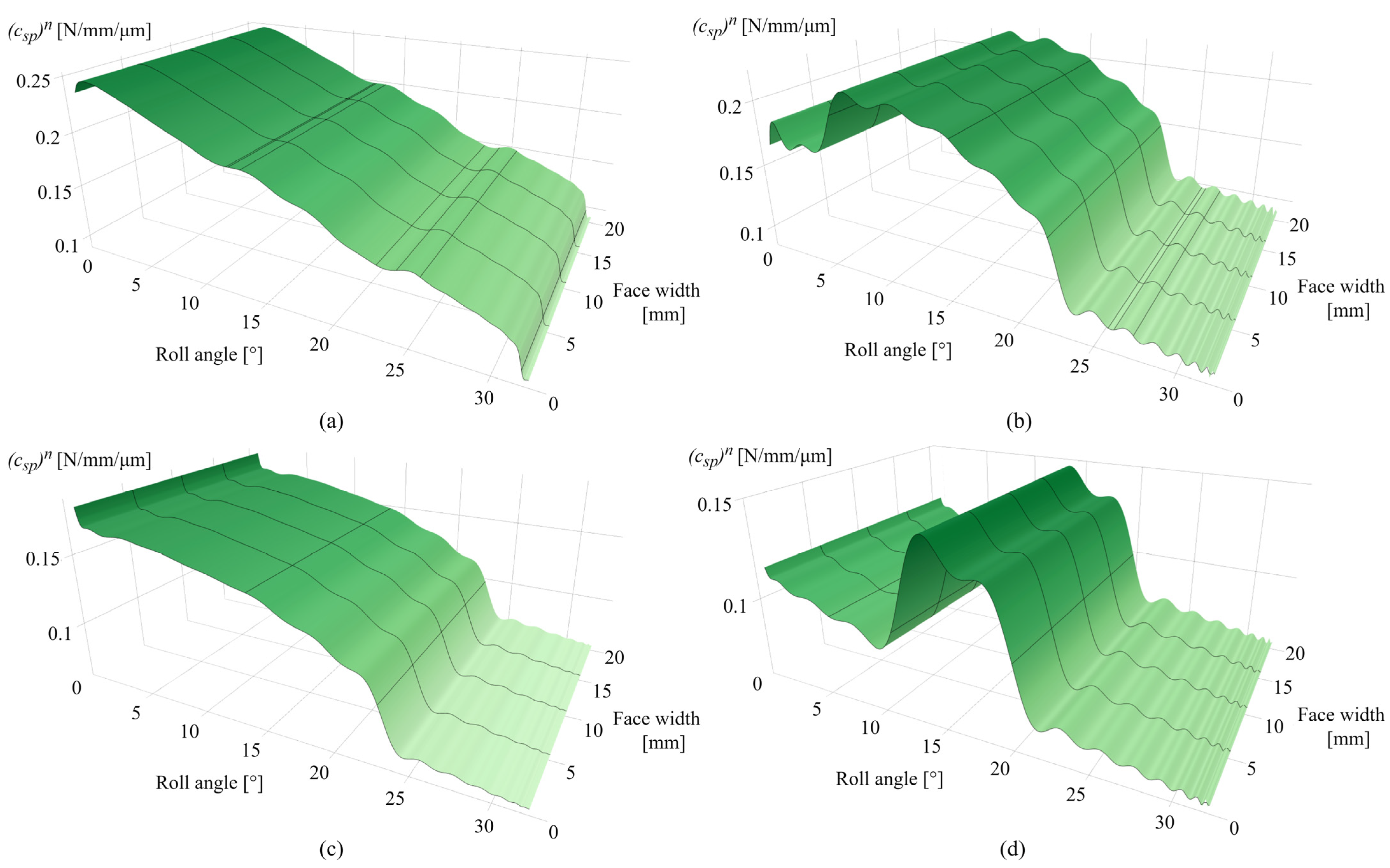
| Parameter | Value |
|---|---|
| Module | 3 mm |
| Number of teeth | 17 |
| Pressure angle | 20° |
| Face width | 20 mm |
| Parameter | Value | Test Method |
|---|---|---|
| Density | 1.41 g/cm3 | ISO 1183 [61] |
| Tensile modulus | 2800 MPa | ISO 527-2 [62] |
| Tensile strength | 67 MPa | ISO 527-2 |
| Coefficient of linear expansion | 1.4 × 10−4 K−1 | ISO 11359 [63] |
| Thermal conductivity | 0.39 W/(K⋅m) | ISO 22007-4 [64] |
| Melting temperature | 166 °C | DIN 53765 [65] |
| Glass transition temperature | −85° | ISO 11375-1 [66] |
| Hardness (Brinell) | 145 MPa | ISO 2039-1 [67] |
| Parameter | Value | Test Method |
|---|---|---|
| Density | 1.78 g/cm3 | ISO 1183 |
| Tensile modulus | 2000 MPa | ISO 527-2 |
| Tensile strength | 50 MPa | ISO 527-2 |
| Coefficient of linear expansion | 1.2 × 10−4 K−1 | ISO 11359 |
| Thermal conductivity | 0.19 W/(K⋅m) | DIN 52612 [68] |
| Melting temperature | 169 °C | ISO 3146 [69] |
| Glass transition temperature | −40° | DIN 53765 |
| Hardness (Brinell) | 90 MPa | ISO 2039-1 |
| Engagement | Torque Level (Nm) | ||
|---|---|---|---|
| 4 | 5 | 6 | |
| C45/POM | Wear coefficient, (10−6 mm3/(Nm)) | ||
| 5.58 | 9.77 | 12.96 | |
| C45/PVDF | Wear coefficient, (10−6 mm3/(Nm)) | ||
| 7.72 | 10.98 | 12.62 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muratović, E.; Pervan, N.; Muminović, A.; Delić, M. A Contact Mechanics Model for Surface Wear Prediction of Parallel-Axis Polymer Gears. Polymers 2024, 16, 2858. https://doi.org/10.3390/polym16202858
Muratović E, Pervan N, Muminović A, Delić M. A Contact Mechanics Model for Surface Wear Prediction of Parallel-Axis Polymer Gears. Polymers. 2024; 16(20):2858. https://doi.org/10.3390/polym16202858
Chicago/Turabian StyleMuratović, Enis, Nedim Pervan, Adil Muminović, and Muamer Delić. 2024. "A Contact Mechanics Model for Surface Wear Prediction of Parallel-Axis Polymer Gears" Polymers 16, no. 20: 2858. https://doi.org/10.3390/polym16202858
APA StyleMuratović, E., Pervan, N., Muminović, A., & Delić, M. (2024). A Contact Mechanics Model for Surface Wear Prediction of Parallel-Axis Polymer Gears. Polymers, 16(20), 2858. https://doi.org/10.3390/polym16202858








