Applications of Long Short-Term Memory (LSTM) Networks in Polymeric Sciences: A Review
Abstract
1. Introduction
1.1. Purpose of the Review
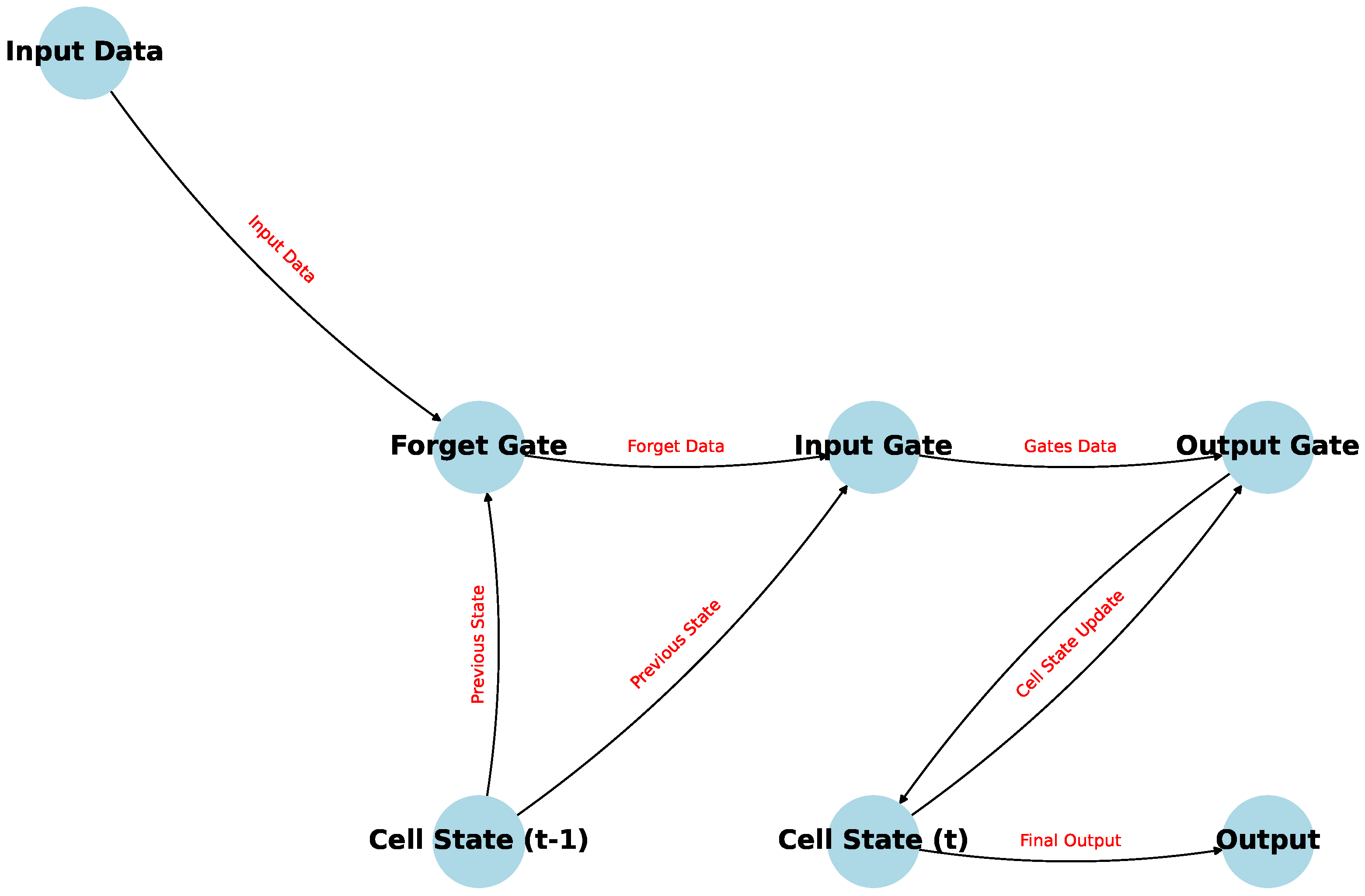
1.2. LSTM Overview
- The cell state acts as the memory of the LSTM unit [21], carrying information across time steps [22]. It can retain information over long periods, enabling the network to remember past data for future predictions. The cell state is updated based on the interactions between the gates, allowing it to accumulate or forget information as needed [23].
- The input gate controls how much of the new information [24] (i.e., the candidate cell state) should be added to the cell state. This gate decides what portion of the incoming data at the current time step t, combined with the previous hidden state , should be considered and stored in the cell [25]. Mathematically, it is defined aswhere is the sigmoid function, represents the weight matrix, is the previous hidden state, is the current input, and is the bias.
- The forget gate [26] determines how much of the previous cell state should be retained in the current cell state . This gate is crucial for deciding which information is no longer relevant and can be “forgotten.” The forget gate’s operation is given byA value of close to 0 means that the corresponding information in the cell state will be mostly discarded, while a value close to 1 means the information will be largely retained [27].
- The output gate [28] controls what information from the cell state should be passed on to the next time step or used as the output of the current LSTM unit. It decides what part of the cell state’s information contributes to the hidden state , which in turn influences the network’s predictions [29]. The output gate is calculated asThe final hidden state [30] is then computed by combining the output gate’s result with the cell state, passed through a nonlinearity:
1.3. Variants of LSTM Networks
1.3.1. Bidirectional LSTM
- Forward LSTM: processes the sequence in the original order [46].
- Backward LSTM: processes the sequence in reverse order [47].
- Final output: concatenates the forward and backward hidden states.
1.3.2. Stacked LSTM
- Layer 1 LSTM [53]: processes the input sequence.
- Layer 2 LSTM [54]: takes the output of Layer 1 as input.
- Final output [55]: can be taken from the last layer’s hidden state.
1.3.3. Peephole LSTM
- Peephole forget gate:
- Peephole input gate:
- Peephole output gate:
1.3.4. Attention-Based LSTM
- Context vector [66]:
- Final output: combines the context vector with the LSTM output.
2. Applications of LSTM in Polymeric Sciences
2.1. Tim- Series Analysis in Polymer Systems
2.2. Diagnostics and Monitoring of Polymer Materials
2.3. Managing the Condition and Performance of Polymer Products
2.4. Predicting Aging and Degradation of Polymers
2.5. Sensor Technologies and LSTM-Based Modeling for Polymer Composites
3. Challenges and Limitations
3.1. Data Availability
3.2. Interpretability
- Hidden and memory states:
- Gates:
- is the sigmoid function.
- are the weights for the merging probability.
- are the adaptive gates that measure the influence of nodes i and j based on their states.
- is the probability of transitioning from graph back to .
- is the probability of transitioning from graph to .
- is the posterior probability of graph given the model parameters and input data.
- is the posterior probability of graph given the model parameters and input data.
- and are the transition probabilities between graphs.
- is the product of merging probabilities for all edges that are removed in .
- Merging probability () helps in deciding whether to merge two nodes based on their mutual influence.
- Transition probability () is used to select the new graph, considering structural improvements.
- Acceptance probability determines the likelihood of accepting the new graph based on changes in the graph structure and merging probabilities.
4. Future Directions
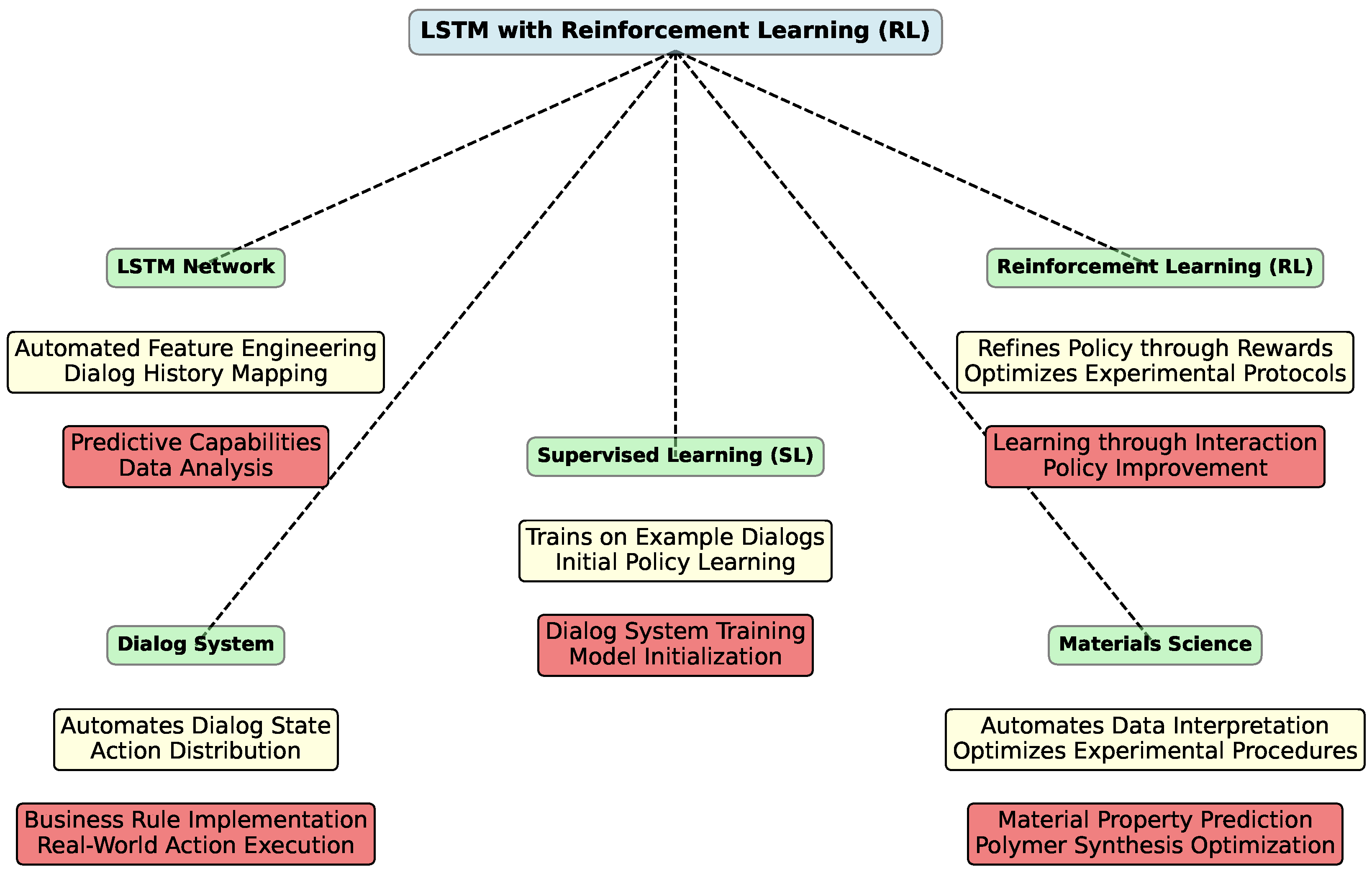
4.1. Integration with Reinforcement Learning (RL)
- Action Mask [225]: A small constant is added to action probabilities to avoid undefined logarithms.
- Momentum [226]: AdaDelta optimization accelerates convergence.
- Policy Reconstruction [227]: After each RL update, the policy is checked against the training set, with SL applied if necessary to ensure it reconstructs the training dialogs.
4.2. Integration with Heuristic Algorithms
4.3. Real-Time Applications
5. Conclusions
5.1. Improvement in Performance and Efficiency with LSTM Integration
5.2. Elementary Data Components for Effective LSTM Analysis
5.3. Challenges in LSTM Application
5.3.1. Feature Engineering
5.3.2. Model Complexity and Computational Cost
5.3.3. Interpretability and Explainability
5.3.4. Real-Time Monitoring and Control Systems
5.4. Itemized Key Findings
- LSTM networks have been effectively utilized to predict various properties of polymers, such as mechanical strength, degradation rates, and thermal behavior. Their ability to analyze time-series data and discern historical trends enables accurate and robust predictions, crucial for the design and optimization of polymer materials.
- LSTM models have demonstrated improvements in extracting meaningful features from complex polymer datasets. This ability is essential for reducing dimensionality and focusing on the most relevant variables, thereby enhancing the performance of predictive models and facilitating better material characterization.
- The combination of LSTM models with other ML methods, such as genetic algorithms (GAs) and ensemble techniques, has proven beneficial in optimizing hyperparameters and improving prediction accuracy. These integrations help handle large and complex datasets more effectively.
- Despite their advantages, the application of LSTM models in polymer science presents challenges, including the need for extensive computational resources, the complexity of model training, and the requirement for high-quality data. Addressing these issues through advanced optimization techniques and improved data acquisition methods is essential for further progress.
- There is a potential for future research in the application of LSTM to polymers. Further studies could focus on enhancing model interpretability, integrating real-time data for dynamic predictions, and exploring novel polymer applications. Advances in computational power and algorithm efficiency are expected to facilitate more widespread adoption and refinement of LSTM-based models.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Machine learning (ML) | A field of artificial intelligence focused on developing algorithms that enable computers to learn from data. |
| Long Short-Term Memory (LSTM) | A type of recurrent neural network capable of remembering long-term dependencies in data. |
| Artificial neural network (ANN) | A mathematical model inspired by the neural network of the brain, used for data processing and decision making. |
| Charge-Coupled Device (CCD) | An electronic device used for capturing images in digital cameras and telescopes. |
| Facial recognition (Facial Recog.) | Technology for identifying or verifying a person’s identity based on their facial image. |
| Object tracking (Obj. Tracking) | The process of following the movement of an object in a sequence of images or video. |
| Chemical sensor arrays (Chem. Sensor Arrays) | A system of multiple sensors used for detecting and analyzing chemical substances. |
| Temperature response (Temp. Resp.) | The change in system parameters in response to a change in temperature. |
| Neural architecture (Neural Arch.) | The structure and organization of a neural network. |
| Chemical awareness (Chem. Awareness) | The ability of a system to detect and identify chemical substances. |
| Dynamic environments (Dyn. Envs.) | Changing or unstable conditions in which a system operates. |
| Carbon black | A black carbon powder used as a filler in rubber and plastics. |
| Organic polymers (Org. Polymers) | Polymers made of carbon compounds, widely used in various fields. |
| Poly(4-vinyl phenol) (P(4-vinyl phenol)) | A polymer used in electronics manufacturing and coatings. |
| Poly(styrene-co-allyl alcohol) (P(styrene-co-allyl alcohol)) | A copolymer used in plastics and coatings. |
| Poly(ethylene oxide) (P(ethylene oxide)) | A polymer used in medicine, cosmetics, and the textile industry. |
| Classification tasks (Class. Tasks) | Tasks related to categorizing data into classes or groups. |
| Traffic sign recognition (Traffic Sign Recog.) | Technology for recognizing traffic signs for use in automated driving systems. |
| Olfactory signal classification (Olf. Signal Class.) | The process of classifying smells based on signals obtained from olfactory sensors. |
| Temperature dynamics (Temp. Dyn.) | The study of temperature change in a system over time. |
| Olfactory sensing systems (Olf. Sensing Sys.) | Systems that use sensors to detect and analyze odors. |
| Extended Kalman Filter (EKF) | A filtering algorithm used for state estimation in nonlinear dynamic systems. |
| State-of-charge estimation (SOC Est.) | The estimation of a battery’s charge level based on measured data. |
| Lithium polymer batteries (Li-poly Batteries) | A type of battery with a polymer electrolyte, known for high energy density. |
| Battery management system (BMS) | A system that monitors and optimizes battery performance. |
| Carbon fiber-reinforced polymer (CFRP) | A composite material made from carbon fiber, known for high strength and low weight. |
| Laser infrared thermography (Laser IR Thermography) | A diagnostic method using infrared laser for temperature measurement in materials. |
| Defect depth assessment (Def. Depth Assess.) | Determining the depth of defects in materials or structures. |
| Traffic sign recognition (TSR) | The process of automatically recognizing traffic signs. |
| Generative DL (Generative DL) | A branch of DL focused on generating new data based on a trained model. |
| Ultraviolet–visible spectra (UV-vis Spectra) | Absorption and reflection spectra in the ultraviolet and visible range, used for substance analysis. |
| Coarse-grained models | Models that simplify complex systems while retaining essential characteristics. |
| Cable-driven robots | Robots controlled by a system of cables or wires. |
| Nonlinear characteristics (Nonlinear Char.) | Properties of a system or material that do not follow linear laws. |
| Real-time control | The control of processes in real time. |
| Hierarchical recurrent neural network (H-RNN) | A variant of recurrent neural network with a hierarchical structure. |
| Composite damage (Comp. Damage) | Damage to composite materials under various factors. |
| Finite element model (FE Model) | A numerical model used for solving problems in solid mechanics using the finite element method. |
| Twisted-coiled actuators | Actuators made of twisted and coiled fibers that change shape in response to temperature or electrical current. |
| Model Predictive Control (Model Predict. Control) | A control algorithm that uses predictive models to optimize system performance. |
| Organic photovoltaic materials (OPV Materials) | Organic materials used for making solar cells. |
| Simplified Molecular Input Line Entry System Fingerprints (SMILES Fingerprints) | A string-based encoding of chemical structures used for molecular analysis and comparison. |
| Polymer repeat units | The basic structural elements that make up polymers. |
| Glass fiber-reinforced polymer (GFRP) | A composite material reinforced with glass fiber, used in construction and engineering. |
| Terahertz time-domain spectroscopy (Terahertz Time-Domain Spec.) | A method for studying materials using terahertz radiation. |
| Dielectric electroactive polymer actuators (DEAP Actuators) | Actuators based on dielectric electroactive polymers that change shape when an electric field is applied. |
| Hysteresis | A phenomenon where the state of a system depends on its previous states despite identical current conditions. |
| Empirical mode decomposition (EMD) | A method for signal analysis that decomposes signals into component frequencies. |
| Battery state-of-charge estimation (Battery SOC Est.) | Estimation of a battery’s state of charge. |
| Plastic recycling | The process of recycling plastics for reuse. |
| Hyperspectral imaging | A method of acquiring and analyzing images that include spectral information across a wide range of wavelengths. |
| Polymer insulation resistance (Polymer Ins. Resist.) | A polymer’s ability to resist electrical leakage. |
| Melt index | A measure of the flow rate of a polymer when melted under specific conditions. |
| Polymerization processes | Chemical processes in which monomers combine to form polymers. |
| Acoustic behavior | The characteristics of a system related to the generation, transmission, and absorption of sound waves. |
| Muffler design | The design and construction of mufflers to reduce noise. |
| Soft sensor | A software tool for estimating system parameters based on indirect measurements. |
| Dielectric electroactive polymer actuation (DEAP Act.) | The actuation process of a device based on dielectric electroactive polymers. |
| Proportional–integral–derivative controller (PID Controller) | A control algorithm using three components: proportional, integral, and derivative. |
| Ethyl acetate solution (Ethyl Acetate Sol.) | A solution of ethyl acetate, used in various chemical processes. |
| Hybrid sensor | A sensor that combines multiple technologies to enhance accuracy and functionality. |
| Motor tics recognition (Motor Tics Recog.) | A system for recognizing motor tics in individuals based on movement analysis. |
| Polymethyl methacrylate (PMMA) | A transparent thermoplastic widely used in construction and medicine. |
| Heat transfer | The process of transferring heat from one object to another. |
| High-temperature proton exchange membrane fuel cell (High-Temp PEMFC) | A fuel cell with a proton exchange membrane operating at high temperatures. |
| Hydrogen starvation (H2 Starvation) | A condition where a fuel cell receives insufficient hydrogen. |
| Nafion membranes | Proton-conducting polymer membranes used in fuel cells. |
| Flooding and drying | Phenomena occurring in fuel cells due to excess moisture or drying of the membrane. |
| Tool wear prediction (Tool Wear Pred.) | Predicting tool wear using data analysis and modeling. |
| Polybutadiene-urethane | A polymer used as an elastomer or coating. |
| Motion detection | Technology for detecting movement in space using sensors or cameras. |
| Knot identification (Knot Ident.) | The process of recognizing knots in a rope or cord. |
| Structural health monitoring (SHM) | Monitoring the condition of structures to detect defects or damage. |
| Lamb wave | A type of elastic wave that propagates in solid materials and is used for diagnostics. |
| Variational mode decomposition (VMD) | A signal decomposition method for analyzing various modes of a signal. |
References
- Pilania, G. Machine learning in materials science: From explainable predictions to autonomous design. Comput. Mater. Sci. 2021, 193, 110360. [Google Scholar] [CrossRef]
- Mishin, Y. Machine-learning interatomic potentials for materials science. Acta Mater. 2021, 214, 116980. [Google Scholar] [CrossRef]
- Morgan, D.; Jacobs, R. Opportunities and challenges for machine learning in materials science. Annu. Rev. Mater. Res. 2020, 50, 71–103. [Google Scholar] [CrossRef]
- Gogineni, A.; Rout, M.D.; Shubham, K. Evaluating machine learning algorithms for predicting compressive strength of concrete with mineral admixture using long short-term memory (LSTM) Technique. Asian J. Civ. Eng. 2024, 25, 1921–1933. [Google Scholar] [CrossRef]
- Dai, Y.; Wei, J.; Qin, F. Recurrent neural network (RNN) and long short-term memory neural network (LSTM) based data-driven methods for identifying cohesive zone law parameters of nickel-modified carbon nanotube reinforced sintered nano-silver adhesives. Mater. Today Commun. 2024, 39, 108991. [Google Scholar] [CrossRef]
- Mendeley. Search Results for “LSTM Polymers”. 2024. Available online: https://www.mendeley.com/search/?page=1&query=LSTM%20polymers&sortBy=relevance (accessed on 17 August 2024).
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef]
- Landi, F.; Baraldi, L.; Cornia, M.; Cucchiara, R. Working memory connections for LSTM. Neural Netw. 2021, 144, 334–341. [Google Scholar] [CrossRef]
- Candan, M.; Çubukçu, M. Implementation of Caputo type fractional derivative chain rule on back propagation algorithm. Appl. Soft Comput. 2024, 155, 111475. [Google Scholar] [CrossRef]
- Rahman, L.; Mohammed, N.; Al Azad, A.K. A new LSTM model by introducing biological cell state. In Proceedings of the 2016 3rd International Conference on Electrical Engineering and Information Communication Technology (ICEEICT), Dhaka, Bangladesh, 22–24 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Duan, J.; Zhang, P.F.; Qiu, R.; Huang, Z. Long short-term enhanced memory for sequential recommendation. World Wide Web 2023, 26, 561–583. [Google Scholar] [CrossRef]
- Choudhary, K.; DeCost, B.; Chen, C.; Jain, A.; Tavazza, F.; Cohn, R.; Park, C.W.; Choudhary, A.; Agrawal, A.; Billinge, S.J.; et al. Recent advances and applications of deep learning methods in materials science. NPJ Comput. Mater. 2022, 8, 59. [Google Scholar] [CrossRef]
- Danoun, A.; Prulière, E.; Chemisky, Y. FE-LSTM: A hybrid approach to accelerate multiscale simulations of architectured materials using Recurrent Neural Networks and Finite Element Analysis. Comput. Methods Appl. Mech. Eng. 2024, 429, 117192. [Google Scholar] [CrossRef]
- Yadav, H.; Thakkar, A. NOA-LSTM: An efficient LSTM cell architecture for time series forecasting. Expert Syst. Appl. 2024, 238, 122333. [Google Scholar] [CrossRef]
- Baruah, R.D.; Organero, M.M. Explicit Context Integrated Recurrent Neural Network for applications in smart environments. Expert Syst. Appl. 2024, 255, 124752. [Google Scholar] [CrossRef]
- Xu, S.; Xiong, J.; Zhang, T.Y. Translating strain to stress: A single-layer Bi-LSTM approach to predicting stress-strain curves in alloys during hot deformation. Mater. Res. Express 2024, 11, 076526. [Google Scholar] [CrossRef]
- Kamrava, S.; Tahmasebi, P.; Sahimi, M.; Arbabi, S. Phase transitions, percolation, fracture of materials, and deep learning. Phys. Rev. E 2020, 102, 011001. [Google Scholar] [CrossRef]
- Martinez, Q.; Chen, C.; Xia, J.; Bahai, H. Sequence-to-sequence change-point detection in single-particle trajectories via recurrent neural network for measuring self-diffusion. Transp. Porous Med. 2023, 147, 679–701. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Gunnarsson, B.R.; vanden Broucke, S.; De Weerdt, J. A direct data aware LSTM neural network architecture for complete remaining trace and runtime prediction. IEEE Trans. Serv. Comput. 2023, 16, 2330–2342. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, Z.; Li, C.; Xu, R.; Yang, D.; Sun, L. Van der Waals materials-based floating gate memory for neuromorphic computing. Chip 2023, 2, 100059. [Google Scholar] [CrossRef]
- Li, H.; Shen, Y.; Zhu, Y. Stock price prediction using attention-based multi-input LSTM. In Proceedings of the Asian Conference on Machine Learning, PMLR, Beijing, China, 14–16 November2018; pp. 454–469. [Google Scholar]
- Zaheer, S.; Anjum, N.; Hussain, S.; Algarni, A.D.; Iqbal, J.; Bourouis, S.; Ullah, S.S. A multi parameter forecasting for stock time series data using LSTM and deep learning model. Mathematics 2023, 11, 590. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Xue, K.; Yang, J.; Yang, M.; Wang, D. An improved generic hybrid prognostic method for RUL prediction based on PF-LSTM learning. IEEE Trans. Instrum. Meas. 2023, 72, 3509121. [Google Scholar] [CrossRef]
- Pulver, A.; Lyu, S. LSTM with working memory. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 845–851. [Google Scholar]
- tu Zahra, F.; Bostanci, Y.S.; Soyturk, M. LSTM-Based Jamming Detection and Forecasting Model using Transport and Application Layer Parameters in Wi-Fi Based IoT Systems. IEEE Access 2024, 12, 32944–32958. [Google Scholar] [CrossRef]
- Strobelt, H.; Gehrmann, S.; Pfister, H.; Rush, A.M. Lstmvis: A tool for visual analysis of hidden state dynamics in recurrent neural networks. IEEE Trans. Vis. Comput. Graph. 2017, 24, 667–676. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, J.; Zuo, W.; Xu, G.; Yuan, C.; Wang, L.; Du, Z.; Lu, Y.; She, W. Prediction of Time-dependent Concrete Mechanical Properties Based on Advanced Deep Learning Models Considering Complex Variables. Case Stud. Constr. Mater. 2024, 21, e03629. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, Z.; Dong, Y.; Tu, J. An interpretable LSTM deep learning model predicts the time-dependent swelling behavior in CERCER composite fuels. Mater. Today Commun. 2023, 37, 106998. [Google Scholar] [CrossRef]
- Heng, F.; Gao, J.; Xu, R.; Yang, H.; Cheng, Q.; Liu, Y. Multiaxial fatigue life prediction for various metallic materials based on the hybrid CNN-LSTM neural network. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 1979–1996. [Google Scholar] [CrossRef]
- Long, X.; Ding, X.; Li, J.; Dong, R.; Su, Y.; Chang, C. Indentation reverse algorithm of mechanical response for elastoplastic coatings based on LSTM deep Learning. Materials 2023, 16, 2617. [Google Scholar] [CrossRef]
- Tanhadoust, A.; Yang, T.; Dabbaghi, F.; Chai, H.K.; Mohseni, M.; Emadi, S.; Nasrollahpour, S. Predicting stress-strain behavior of normal weight and lightweight aggregate concrete exposed to high temperature using LSTM recurrent neural network. Constr. Build. Mater. 2023, 362, 129703. [Google Scholar] [CrossRef]
- Anooj, G.V.S.; Marri, G.K.; Balaji, C. A machine learning methodology for the diagnosis of phase change material-based thermal management systems. Appl. Therm. Eng. 2023, 222, 119864. [Google Scholar] [CrossRef]
- Zhao, Y. Understanding and design of metallic alloys guided by phase-field simulations. NPJ Comput. Mater. 2023, 9, 94. [Google Scholar] [CrossRef]
- Bhatt, P.; Kumar, Y.; Soulaïmani, A. Deep convolutional architectures for extrapolative forecasts in time-dependent flow problems. Adv. Model. Simul. Eng. Sci. 2023, 10, 17. [Google Scholar] [CrossRef]
- Asem, M. DiffusionNet: Accelerating the solution of Time-Dependent partial differential equations using deep learning. arXiv 2020, arXiv:2011.10015. [Google Scholar]
- Dash, S.; Li, Y.; Sung, W.L. A Hybrid 1D-CNN-LSTM Technique for WKF-Induced Variability of Multi-Channel GAA NS-and NF-FETs. IEEE Access 2023, 11, 56619–56633. [Google Scholar] [CrossRef]
- Zheng, R.; Bao, Y.; Zhao, L.; Xing, L. Method to predict alloy yield based on multiple raw material conditions and a PSO-LSTM network. J. Mater. Res. Technol. 2023, 27, 3310–3322. [Google Scholar] [CrossRef]
- Liu, G.; Guo, J. Bidirectional LSTM with attention mechanism and convolutional layer for text classification. Neurocomputing 2019, 337, 325–338. [Google Scholar] [CrossRef]
- Yu, L.; Qu, J.; Gao, F.; Tian, Y. A novel hierarchical algorithm for bearing fault diagnosis based on stacked LSTM. Shock Vib. 2019, 2019, 2756284. [Google Scholar] [CrossRef]
- Joshi, A.; Deshmukh, P.K.; Lohokare, J. Comparative analysis of Vanilla LSTM and Peephole LSTM for stock market price prediction. In Proceedings of the 2022 International Conference on Computing, Communication, Security and Intelligent Systems (IC3SIS), Kochi, India, 23–25 June 2015; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Wang, Y.; Huang, M.; Zhu, X.; Zhao, L. Attention-based LSTM for aspect-level sentiment classification. In Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, Austin, TX, USA, 1–5 November 2016; pp. 606–615. [Google Scholar]
- Pavlatos, C.; Makris, E.; Fotis, G.; Vita, V.; Mladenov, V. Enhancing Electrical Load Prediction Using a Bidirectional LSTM Neural Network. Electronics 2023, 12, 4652. [Google Scholar] [CrossRef]
- Naheliya, B.; Redhu, P.; Kumar, K. MFOA-Bi-LSTM: An optimized bidirectional long short-term memory model for short-term traffic flow prediction. Phys. A Stat. Mech. Its Appl. 2024, 634, 129448. [Google Scholar] [CrossRef]
- Cui, Z.; Ke, R.; Pu, Z.; Wang, Y. Stacked bidirectional and unidirectional LSTM recurrent neural network for forecasting network-wide traffic state with missing values. Transp. Res. Part C Emerg. Technol. 2020, 118, 102674. [Google Scholar] [CrossRef]
- Pradhan, A.; Yajnik, A. Parts-of-speech tagging of Nepali texts with Bidirectional LSTM, Conditional Random Fields and HMM. Multimed. Tools Appl. 2024, 83, 9893–9909. [Google Scholar] [CrossRef]
- Sabzalian, M.H.; Kharajinezhadian, F.; Tajally, A.; Reihanisaransari, R.; Alkhazaleh, H.A.; Bokov, D. New bidirectional recurrent neural network optimized by improved Ebola search optimization algorithm for lung cancer diagnosis. Biomed. Signal Process. Control. 2023, 84, 104965. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, X.; Wang, J. Lightweight bidirectional long short-term memory based on automated model pruning with application to bearing remaining useful life prediction. Eng. Appl. Artif. Intell. 2023, 118, 105662. [Google Scholar] [CrossRef]
- Guo, F.; Mo, H.; Wu, J.; Pan, L.; Zhou, H.; Zhang, Z.; Li, L.; Huang, F. A Hybrid Stacking Model for Enhanced Short-Term Load Forecasting. Electronics 2024, 13, 2719. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, R.; Gao, F. A network structure for industrial process fault diagnosis based on hyper feature extraction and stacked LSTM. Chem. Eng. Sci. 2024, 287, 119745. [Google Scholar] [CrossRef]
- Maharatha, A.; Das, R.; Mishra, J.; Nayak, S.R.; Aluvala, S. Employing Sequence-to-Sequence Stacked LSTM Autoencoder Architecture to Forecast Indian Weather. Procedia Comput. Sci. 2024, 235, 2258–2268. [Google Scholar] [CrossRef]
- Alghamdi, M.A.; Abdullah, S.; Ragab, M. Predicting Energy Consumption Using Stacked LSTM Snapshot Ensemble. Big Data Min. Anal. 2024, 7, 247–270. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, M.; Li, X.; Xie, L.; Chen, Z. Multivariate Time-Series Representation Learning via Hierarchical Correlation Pooling Boosted Graph Neural Network. IEEE Trans. Artif. Intell. 2023, 5, 321–333. [Google Scholar] [CrossRef]
- Alabdulkreem, E.; Alruwais, N.; Mahgoub, H.; Dutta, A.K.; Khalid, M.; Marzouk, R.; Motwakel, A.; Drar, S. Sustainable groundwater management using stacked LSTM with deep neural network. Urban Clim. 2023, 49, 101469. [Google Scholar] [CrossRef]
- Kumar, V.; Paul, K.; Chowdhary, M. Long Short Term Memory (LSTM)-based Cuffless Continuous Blood Pressure Monitoring. In Proceedings of the 2024 37th International Conference on VLSI Design and 2024 23rd International Conference on Embedded Systems (VLSID), Kolkata, India, 6–10 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 330–335. [Google Scholar]
- Essai Ali, M.H.; Abdellah, A.R.; Atallah, H.A.; Ahmed, G.S.; Muthanna, A.; Koucheryavy, A. Deep learning peephole LSTM neural network-based channel state estimators for OFDM 5G and beyond networks. Mathematics 2023, 11, 3386. [Google Scholar] [CrossRef]
- Zhu, D.; Dai, X.; Liu, Y.; Wang, F.; Luo, X.; Chen, D.; Ye, Z. Deep learning approach of drilling decision for subhorizontal drain geosteering based on APC-LSTM model. SPE Drill. Complet. 2023, 38, 1–17. [Google Scholar] [CrossRef]
- Pilataxi, J.I.; Zambrano, J.E.; Perez, C.A.; Bowyer, K.W. Improved Search in Neuroevolution Using a Neural Architecture Classifier With the CNN Architecture Encoding as Feature Vector. IEEE Access 2024, 12, 11987–12000. [Google Scholar] [CrossRef]
- Mienye, I.D.; Swart, T.G.; Obaido, G. Recurrent Neural Networks: A Comprehensive Review of Architectures, Variants, and Applications. Information 2024, 15, 517. [Google Scholar] [CrossRef]
- Dai, Z.; Zhang, M.; Nedjah, N.; Xu, D.; Ye, F. A hydrological data prediction model based on lstm with attention mechanism. Water 2023, 15, 670. [Google Scholar] [CrossRef]
- Lei, X. A Photovoltaic Prediction Model with Integrated Attention Mechanism. Mathematics 2024, 12, 2103. [Google Scholar] [CrossRef]
- Shi, J.; Zhong, J.; Zhang, Y.; Xiao, B.; Xiao, L.; Zheng, Y. A dual attention LSTM lightweight model based on exponential smoothing for remaining useful life prediction. Reliab. Eng. Syst. Saf. 2024, 243, 109821. [Google Scholar] [CrossRef]
- Kumar, C.; Kumar, M. Session-based recommendations with sequential context using attention-driven LSTM. Comput. Electr. Eng. 2024, 115, 109138. [Google Scholar] [CrossRef]
- Griffis, E.J.; Patil, O.S.; Bell, Z.I.; Dixon, W.E. Lyapunov-based long short-term memory (Lb-LSTM) neural network-based control. IEEE Control. Syst. Lett. 2023, 7, 2976–2981. [Google Scholar] [CrossRef]
- Kim, T.; Ahn, D.; Lee, D.; Kim, J.J. V-LSTM: An efficient LSTM accelerator using fixed nonzero-ratio viterbi-based pruning. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2023, 42, 3327–3337. [Google Scholar] [CrossRef]
- Aburass, S.; Dorgham, O.; Al Shaqsi, J. A hybrid machine learning model for classifying gene mutations in cancer using LSTM, BiLSTM, CNN, GRU, and GloVe. Syst. Soft Comput. 2024, 6, 200110. [Google Scholar] [CrossRef]
- Laitsos, V.; Vontzos, G.; Bargiotas, D.; Daskalopulu, A.; Tsoukalas, L.H. Data-Driven Techniques for Short-Term Electricity Price Forecasting through Novel Deep Learning Approaches with Attention Mechanisms. Energies 2024, 17, 1625. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, W.; Wang, C.; Song, Q.; Zhang, T.; Dong, Q.; Li, X. An electricity load forecasting model based on multilayer dilated LSTM network and attention mechanism. Front. Energy Res. 2023, 11, 1116465. [Google Scholar] [CrossRef]
- Wen, X.; Li, W. Time series prediction based on LSTM-attention-LSTM model. IEEE Access 2023, 11, 48322–48331. [Google Scholar] [CrossRef]
- Agarwal, H.; Mahajan, G.; Shrotriya, A.; Shekhawat, D. Predictive Data Analysis: Leveraging RNN and LSTM Techniques for Time Series Dataset. Procedia Comput. Sci. 2024, 235, 979–989. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, L.; Tang, T. Image Stabilization of A Model-following Dual-Stage System with Charge-Coupled Device Measurement. IEEE Photonics J. 2024. [Google Scholar] [CrossRef]
- Shukla, A.K.; Shukla, A.; Singh, R. Automatic attendance system based on CNN–LSTM and face recognition. Int. J. Inf. Technol. 2024, 16, 1293–1301. [Google Scholar] [CrossRef]
- Hassan, S.; Mujtaba, G.; Rajput, A.; Fatima, N. Multi-object tracking: A systematic literature review. Multimed. Tools Appl. 2024, 83, 43439–43492. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, D.; Yang, L.; Chen, Y. A Multibranch LSTM-Attention Ensemble Classification Network for Sensor Drift Compensation. IEEE Sens. J. 2024, 24, 25830–25841. [Google Scholar] [CrossRef]
- Sung, S.H.; Suh, J.M.; Hwang, Y.J.; Jang, H.W.; Park, J.G.; Jun, S.C. Data-centric artificial olfactory system based on the eigengraph. Nat. Commun. 2024, 15, 1211. [Google Scholar] [CrossRef] [PubMed]
- Ryman, S.K.; Bruce, N.D.; Freund, M.S. Temporal responses of chemically diverse sensor arrays for machine olfaction using artificial intelligence. Sens. Actuators B Chem. 2016, 231, 666–674. [Google Scholar] [CrossRef]
- Kim, T.; Yoon, J.H.; Seo, M.; Kim, S.Y. Synthesis and self-assembly of poly (4-vinylphenol)-b-poly (vinyl alcohol) diblock copolymer for invertible core-shell nanoparticles. Polymer 2024, 307, 127293. [Google Scholar] [CrossRef]
- Nayak, G.; Maroliya, M.; Qadeer, M.; Midhun, V.; Saha, S.K.; Subramaniam, C. Development and Characterization of a Solid-Solid-Phase Change Material for Low-Temperature Applications. In Proceedings of the 27th National and 5th International ISHMT-ASTFE Heat and Mass Transfer Conference, Bihar, India, 14–17 December 2023; Begel House Inc.: Danbury, CT, USA, 2024. [Google Scholar]
- Su, X.; Xu, X.P.; Ji, Z.Q.; Wu, J.; Ma, F.; Fan, L.Z. Polyethylene Oxide-Based Composite Solid Electrolytes for Lithium Batteries: Current Progress, Low-Temperature and High-Voltage Limitations, and Prospects. Electrochem. Energy Rev. 2024, 7, 2. [Google Scholar] [CrossRef]
- Waziry, S.; Rasheed, J.; Ghabban, F.M.; Alsubai, S.; Elkiran, H.; Alqahtani, A. Unveiling Interpretability: Analyzing Transfer Learning in Deep Learning Models for Traffic Sign Recognition. SN Comput. Sci. 2024, 5, 682. [Google Scholar] [CrossRef]
- Kausar, R.; Zayer, F.; Viegas, J.; Dias, J. Efficient Hybrid Neuromorphic-Bayesian Model for Olfaction Sensing: Detection and Classification. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 2089–2095. [Google Scholar]
- Wang, C.; Wang, R.; Zhang, C.; Yu, Q. Coupling effect of state of charge and loading rate on internal short circuit of lithium-ion batteries induced by mechanical abuse. Appl. Energy 2024, 375, 124138. [Google Scholar] [CrossRef]
- Tamarozzi, T.; Jiránek, P.; De Gregoriis, D. A differential-algebraic extended Kalman filter with exact constraint satisfaction. Mech. Syst. Signal Process. 2024, 206, 110901. [Google Scholar] [CrossRef]
- Shin, D.; Yoon, B.; Yoo, S. Compensation method for estimating the state of charge of li-polymer batteries using multiple long short-term memory networks based on the extended kalman filter. Energies 2021, 14, 349. [Google Scholar] [CrossRef]
- Andrews, J.; Gkountouna, O.; Blaisten-Barojas, E. Forecasting molecular dynamics energetics of polymers in solution from supervised machine learning. Chem. Sci. 2022, 13, 7021–7033. [Google Scholar] [CrossRef]
- Singh, A.; Gupta, S.; Goel, L.; Agarwal, A.K.; Dargar, S.K. Archimedes optimization-based Elman Recurrent Neural Network for detection of post-traumatic stress disorder. Biomed. Signal Process. Control. 2024, 90, 105806. [Google Scholar] [CrossRef]
- Moctezuma, L.A.; Suzuki, Y.; Furuki, J.; Molinas, M.; Abe, T. GRU-powered sleep stage classification with permutation-based EEG channel selection. Sci. Rep. 2024, 14, 17952. [Google Scholar] [CrossRef]
- Chountoulesi, M.; Pippa, N.; Forys, A.; Trzebicka, B.; Pispas, S. Structure-Based Evaluation of Hybrid Lipid–Polymer Nanoparticles: The Role of the Polymeric Guest. Polymers 2024, 16, 290. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Chen, C.C.; Shie, C.Y.; Li, T.T.; Fuh, Y.K. A hybrid sensor for motor tics recognition based on piezoelectric and triboelectric design and fabrication. Sens. Actuators A Phys. 2022, 342, 113622. [Google Scholar] [CrossRef]
- Lewin, A.B.; Murphy, T.K.; Mink, J.W.; Small, B.J.; Adams, H.R.; Brennan, E.; Augustine, E.F.; Vermilion, J.; Vierhile, A.; Collins, A.; et al. Brief youth self-report screener for tics: Can a subscale of the Motor tic, Obsession and compulsion, and Vocal tic Evaluation Survey (MOVES) identify tic disorders in youth? Evid.-Based Pract. Child Adolesc. Ment. Health 2024, 9, 181–191. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Mishra, T.T.; Parashar, C.K.; Murmu, K.; Chakraborty, M. Effect of Poling on β-Phase Structure of Electrospun PVDF-TrFE Nanofiber Film. J. Mater. Eng. Perform. 2024, 33, 5439–5445. [Google Scholar] [CrossRef]
- Lenka, A.; Jankovic, J. An update on the pharmacological management of Tourette syndrome and emerging treatment paradigms. Expert Rev. Neurother. 2024, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Yezerska, K.; Dushina, A.; Sarabakha, A.; Wagner, P.; Dyck, A.; Wark, M. Model-based degradation prediction on impedance data and artificial neural network for high-temperature polymer electrolyte membrane fuel cells after hydrogen starvation. Int. J. Hydrogen Energy 2022, 47, 29495–29504. [Google Scholar] [CrossRef]
- Heinritz, A.; Leidinger, P.; Buhk, B.; Herranz, J.; Schmidt, T. A High-Potential Trapped State Upon H2-Starvation of a Platinum Electrode in Aqueous Electrolyte. J. Electrochem. Soc. 2024, 171, 014503. [Google Scholar] [CrossRef]
- Solangi, N.H.; Mubarak, N.M.; Karri, R.R.; Mazari, S.A.; Koduru, J.R. Recent development of graphene and MXene-based nanomaterials for proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2024, 73, 905–931. [Google Scholar] [CrossRef]
- Asghar, M.R.; Xu, Q. A review of advancements in commercial and non-commercial Nafion-based proton exchange membranes for direct methanol fuel cells. J. Polym. Res. 2024, 31, 125. [Google Scholar] [CrossRef]
- Benhaddouch, T.E.; Marcial, J.; Metler, C.; Bhansali, S.; Dong, D. Real-Time Continuous Monitoring of Fuel Cell Ionomer Degradation with Electrochemical Inline Micro Sensor Arrays. In Proceedings of the Electrochemical Society Meeting Abstracts 242, Atlanta, GA, USA, 9–13 October 2022; The Electrochemical Society, Inc.: Pennington, NJ, USA, 2022. Number 61. p. 2256. [Google Scholar]
- Nussbaum, R.; Nonis, A.; Jeanneret, S.; Cherubini, T.; Bakker, E. Ultrasensitive sensing of pH and fluoride with enhanced constant potential coulometry at membrane electrodes. Sens. Actuators B Chem. 2023, 392, 134101. [Google Scholar] [CrossRef]
- Sharma, R.; Morgen, P.; Larsen, M.J.; Roda-Serrat, M.C.; Lund, P.B.; Grahl-Madsen, L.; Andersen, S.M. Recovery, Regeneration, and Reapplication of PFSA Polymer from End-of-Life PEMFC MEAs. ACS Appl. Mater. Interfaces 2023, 15, 48705–48715. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Huo, W.; Li, F.; Zhou, H. Classification of liquid ingress in GFRP honeycomb based on one-dimension sequential model using THz-TDS. Sensors 2023, 23, 1149. [Google Scholar] [CrossRef] [PubMed]
- Shubham, K.; Metya, S.; Sinha, A.K.; Gobinath, R. One-Dimensional-Convolutional Neural Network (1D-CNN) Based Reliability Analysis of Foundation Over Cavity Incorporating the Effect of Simulated Noise. Adv. Civ. Eng. 2024, 2024, 9981433. [Google Scholar] [CrossRef]
- Song, M.J.; Kim, S.; Oh, S.H.; Jo, P.S.; Lee, J.M. Soft Sensor for Melt Index Prediction Based on Long Short-Term Memory Network. IFAC-PapersOnLine 2022, 55, 857–862. [Google Scholar] [CrossRef]
- da Silveira, P.H.P.M.; da Conceição, M.d.N.; de Pina, D.N.; de Moraes Paes, P.A.; Monteiro, S.N.; Tapanes, N.d.L.C.O.; da Conceição Ribeiro, R.C.; Bastos, D.C. Impact of Different Mineral Reinforcements on HDPE Composites: Effects of Melt Flow Index and Particle Size on Physical and Mechanical Properties. Polymers 2024, 16, 2063. [Google Scholar] [CrossRef]
- Liu, M.; Tang, Q.; Liu, B.; Zhang, M. Preparation of poly (butyl acrylate)-grafted-poly (styrene-co-acrylonitrile) particles for toughening poly (styrene-co-acrylonitrile) resin. Polym. Eng. Sci. 2024, 64, 4298–4308. [Google Scholar] [CrossRef]
- Song, Z.; Feng, Y.; Lu, C.; Liu, J.; Pan, W. Self-constructed strategy-based reinforcement LSTM approach for fiber-reinforced polymer non-linear degradation performance analysis. Compos. Sci. Technol. 2024, 248, 110414. [Google Scholar] [CrossRef]
- Qiu, W.; Xu, X.; Dong, K.; Wang, Y.; Xiong, Y. Recent advances in 4D printing of fiber-reinforced polymer composites: A review and outlook. Compos. Part B Eng. 2024, 283, 111645. [Google Scholar] [CrossRef]
- Goswami, S.; Ghosh, R.; Neog, A.; Das, B. Deep learning based approach for prediction of glass transition temperature in polymers. Mater. Today Proc. 2021, 46, 5838–5843. [Google Scholar] [CrossRef]
- Loretz, R.; Loretz, T. Corrections to theoretical glass transition temperature models and interpretations with application examples to chalcogenide glass. J. Non-Cryst. Solids 2024, 628, 122845. [Google Scholar] [CrossRef]
- Srivastava, M.; MR, A.K.; Zaghib, K. Binders for Li-Ion Battery Technologies and Beyond: A Comprehensive Review. Batteries 2024, 10, 268. [Google Scholar] [CrossRef]
- Kim, K.; Kim, J.; Choi, H.; Kwon, O.; Jang, Y.; Ryu, S.; Lee, H.; Shim, K.; Park, T.; Cha, S.W. Pre-diagnosis of flooding and drying in proton exchange membrane fuel cells by bagging ensemble deep learning models using long short-term memory and convolutional neural networks. Energy 2023, 266, 126441. [Google Scholar] [CrossRef]
- Oyedeji, O.A.; Khan, S.; Erkoyuncu, J.A. Application of CNN for Multiple Phase Corrosion Identification and Region Detection. Appl. Soft Comput. 2024, 164, 112008. [Google Scholar]
- Zizaan, A.; Idri, A. Evaluating and comparing bagging and boosting of hybrid learning for breast cancer screening. Sci. Afr. 2024, 23, e01989. [Google Scholar] [CrossRef]
- Ramachandran, V.P.; Pranavam, V.; Sreedharan, P. Life Prediction of Underwater Electroacoustic Sensor Using Data-Driven Approach. In Proceedings of the International Conference on Artificial Intelligence and Data Science, Medan, Indonesia, 11–12 November 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 465–475. [Google Scholar]
- Gao, Z.; Hu, B.; Ye, W.; Cao, T.; Chen, L.; Li, H.; Guo, C.Y.; Wang, C. Water-Resistant and Thermal Insulation Aerogels Based on Polymers toward a Room-Temperature Phosphorescent Sensor. ACS Appl. Opt. Mater. 2024, 2, 1159–1171. [Google Scholar] [CrossRef]
- Ge, X.; Fan, F.; Given, M.J.; Stewart, B.G. Insulation resistance degradation models of extruded power cables under thermal ageing. Energies 2024, 17, 1062. [Google Scholar] [CrossRef]
- Lee, J.; Lee, N.; Son, J.; Shin, D. An LSTM model with optimal feature selection for predictions of tensile behavior and tensile failure of polymer matrix composites. Korean J. Chem. Eng. 2023, 40, 2091–2101. [Google Scholar] [CrossRef]
- Coccato, A.; Caggiani, M.C. An overview of Principal Components Analysis approaches in Raman studies of cultural heritage materials. J. Raman Spectrosc. 2024, 55, 125–147. [Google Scholar] [CrossRef]
- Kumar, M. Early detection of chronic kidney disease using recursive feature elimination and cross-validated XGBoost model. Int. J. Comput. Mater. Sci. Eng. 2024, 13. [Google Scholar] [CrossRef]
- Tian, Q.; Guo, L.; Zhang, Y.; Gao, H.; Li, Z. Multi-angle property analysis and stress–strain curve prediction of cementitious sand gravel based on triaxial test. Sci. Rep. 2024, 14, 16400. [Google Scholar] [CrossRef]
- Yang, B.; Liang, B.; Qian, Y.; Zheng, R.; Su, S.; Guo, Z.; Jiang, L. Parameter identification of PEMFC via feedforward neural network-pelican optimization algorithm. Appl. Energy 2024, 361, 122857. [Google Scholar] [CrossRef]
- Chistyakova, T.B.; Damrin, A.; Grishchenkov, N.D. The Software Complex for the Selection and Analysis of Algorithms Predicting Key Quality Indicators of Polymer Film Materials of Industrial Production. In Proceedings of the 2023 5th International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA), Lipetsk, Russia, 8–10 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 799–801. [Google Scholar]
- Koinig, G.; Kuhn, N.; Fink, T.; Grath, E.; Tischberger-Aldrian, A. Inline classification of polymer films using Machine learning methods. Waste Manag. 2024, 174, 290–299. [Google Scholar] [CrossRef]
- Xing, H.J.; Liu, W.T.; Wang, X.Z. Bounded exponential loss function based AdaBoost ensemble of OCSVMs. Pattern Recognit. 2024, 148, 110191. [Google Scholar] [CrossRef]
- Shakouri Mahmoudabadi, N.; Bahrami, A.; Saghir, S.; Ahmad, A.; Iqbal, M.; Elchalakani, M.; Özkılıç, Y.O. Effects of eccentric loading on performance of concrete columns reinforced with glass fiber-reinforced polymer bars. Sci. Rep. 2024, 14, 1890. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, K.; Bao, R. Machine learning models to predict the residual tensile strength of glass fiber reinforced polymer bars in strong alkaline environments: A comparative study. J. Build. Eng. 2023, 73, 106817. [Google Scholar] [CrossRef]
- Machello, C.; Bazli, M.; Santos, J.; Rajabipour, A.; Arashpour, M.; Hassanli, R. Tensile strength retention of fibre-reinforced polymer composites exposed to elevated temperatures: A meta-analysis review. Constr. Build. Mater. 2024, 438, 137150. [Google Scholar] [CrossRef]
- Niazkar, M.; Menapace, A.; Brentan, B.; Piraei, R.; Jimenez, D.; Dhawan, P.; Righetti, M. Applications of XGBoost in water resources engineering: A systematic literature review (Dec 2018–May 2023). Environ. Model. Softw. 2024, 174, 105971. [Google Scholar] [CrossRef]
- Yoon, B.; Yoo, S.; Seong, S. Compensation Method of EKF Based on LSTM for Estimating State of Charge of Li-polymer Battery. Trans. KSAE 2019, 27, 501–507. [Google Scholar] [CrossRef]
- Guo, K.; Li, S.; Wang, J.; Shi, Z.; Wang, Y.; Xue, Z. In situ orthogonal polymerization for constructing fast-charging and long-lifespan Li metal batteries with topological copolymer electrolytes. ACS Energy Lett. 2024, 9, 843–852. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Wu, J.; Su, C.Y. Inverse Compensation-based Global Fast Terminal Integral Sliding Mode Control with Lumped Uncertainty Fuzzy Estimation for Dielectric Electro-active Polymer Actuator. IEEE Trans. Fuzzy Syst. 2024. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, Y.; Wang, Q. Modeling of the dynamic hysteresis in DEAP actuator using an empirical mode decomposition based long-short term memory network. J. Intell. Mater. Syst. Struct. 2021, 32, 2108–2123. [Google Scholar] [CrossRef]
- Shi, J.; Teh, J. Load forecasting for regional integrated energy system based on complementary ensemble empirical mode decomposition and multi-model fusion. Appl. Energy 2024, 353, 122146. [Google Scholar] [CrossRef]
- Wang, S.; Mei, H.; Liu, J.; Chen, D.; Wang, L. A terahertz identification method for internal interface structures of polymers based on the long short-term memory classification network. Polymers 2022, 14, 2611. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Lu, Z.; Jin, X.; Zhao, L. Tool wear prediction in milling CFRP with different fiber orientations based on multi-channel 1DCNN-LSTM. J. Intell. Manuf. 2024, 35, 2547–2566. [Google Scholar] [CrossRef]
- Binbusayyis, A. Hybrid VGG19 and 2D-CNN for intrusion detection in the FOG-cloud environment. Expert Syst. Appl. 2024, 238, 121758. [Google Scholar] [CrossRef]
- Hantono, B.S.; Cahyadi, A.I.; Pratama, G.N.P. LSTM for state of charge estimation of lithium polymer battery on Jetson nano. In Proceedings of the 2021 13th International Conference on Information Technology and Electrical Engineering (ICITEE), Chiang Mai, Thailand, 14–15 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 80–85. [Google Scholar]
- Dehghan Manshadi, M.; Alafchi, N.; Tat, A.; Mousavi, M.; Mosavi, A. Comparative analysis of machine learning and numerical modeling for combined heat transfer in Polymethylmethacrylate. Polymers 2022, 14, 1996. [Google Scholar] [CrossRef]
- Luong, T.; Kim, K.; Seo, S.; Jeon, J.; Park, C.; Doh, M.; Koo, J.C.; Choi, H.R.; Moon, H. Long short term memory model based position-stiffness control of antagonistically driven twisted-coiled polymer actuators using model predictive control. IEEE Robot. Autom. Lett. 2021, 6, 4141–4148. [Google Scholar] [CrossRef]
- Köhler, J.; Müller, M.A.; Allgöwer, F. Analysis and design of model predictive control frameworks for dynamic operation—An overview. Annu. Rev. Control. 2024, 57, 100929. [Google Scholar] [CrossRef]
- Dong, C.; Jiang, C.; Gao, S.; Wang, X.; Bo, C.; Li, J.; Jin, X. Hybrid-modeling for PTFE polymerization reaction with deep learning-based reaction rate model. Int. J. Chem. React. Eng. 2023, 21, 1389–1401. [Google Scholar] [CrossRef]
- Ok, S.; Steinhart, M.; Scheler, U.; Améduri, B. TFE Terpolymers: Once Promising–Are There Still Perspectives in the 21st Century: Synthesis, Characterization, and Properties—Part I. Macromol. Rapid Commun. 2024, 2400294. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, L.; Yu, C.; Xie, G.; Li, Y.; Wu, X.; Li, X.; Guo, D. Surface modification of polytetrafluoroethylene (PTFE) fibers through methyl methacrylate (MMA) polymerization for self-lubricating composites. Appl. Surf. Sci. 2024, 660, 159992. [Google Scholar] [CrossRef]
- Bi, J.; Zhang, P.; Zhang, J.; Wang, M.; Zhao, C. Data-Driven Prediction of Polymer Intrinsic Viscosity with Incomplete Time Series Data. In Proceedings of the 2023 28th International Conference on Automation and Computing (ICAC), Birmingham, UK, 30 August–1 September 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Ma, Z.; Sun, Y.; Ji, H.; Li, S.; Nie, S.; Yin, F. A CNN-BiLSTM-Attention approach for EHA degradation prediction based on time-series generative adversarial network. Mech. Syst. Signal Process. 2024, 215, 111443. [Google Scholar] [CrossRef]
- Rahman, M.M.; Farahani, M.A.; Wuest, T. Multivariate time-series classification of critical events from industrial drying hopper operations: A deep learning approach. J. Manuf. Mater. Process. 2023, 7, 164. [Google Scholar] [CrossRef]
- Lee, Z.; Lindgren, T.; Papapetrou, P. Z-Time: Efficient and effective interpretable multivariate time series classification. Data Min. Knowl. Discov. 2024, 38, 206–236. [Google Scholar] [CrossRef]
- Gao, Z.; Chang, L.; Ren, B.; Han, J.; Li, J. Enhanced braille recognition based on piezoresistive and piezoelectric dual-mode tactile sensors. Sens. Actuators A Phys. 2024, 366, 115000. [Google Scholar] [CrossRef]
- Simine, L.; Allen, T.C.; Rossky, P.J. Predicting optical spectra for optoelectronic polymers using coarse-grained models and recurrent neural networks. Proc. Natl. Acad. Sci. USA 2020, 117, 13945–13948. [Google Scholar] [CrossRef]
- Braghetto, A.; Kundu, S.; Baiesi, M.; Orlandini, E. Machine learning understands knotted polymers. Macromolecules 2023, 56, 2899–2909. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, X.M.; Hao, Z.; Cai, Y.; Rong, H.; Zhang, F.; Chen, W.; Zhang, C.; Lin, J.; Zhao, Y.; et al. On the topological surface states of the intrinsic magnetic topological insulator Mn-Bi-Te family. Natl. Sci. Rev. 2024, 11, nwad066. [Google Scholar] [CrossRef] [PubMed]
- Benrabia, I.; Söffker, D. Modeling and Evaluation of Dynamical Properties of Different Energy Storage Systems Using Machine Learning Methods. In Proceedings of the 2023 IEEE Vehicle Power and Propulsion Conference (VPPC), Milan, Italy, 24–27 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Khan, T.A.; Chaudhary, N.I.; Khan, Z.A.; Mehmood, K.; Hsu, C.C.; Raja, M.A.Z. Design of Runge-Kutta optimization for fractional input nonlinear autoregressive exogenous system identification with key-term separation. Chaos Solitons Fractals 2024, 182, 114723. [Google Scholar] [CrossRef]
- Altabey, W.A.; Noori, M.; Wu, Z.; Al-Moghazy, M.A.; Kouritem, S.A. Studying acoustic behavior of BFRP laminated composite in dual-chamber muffler application using deep learning algorithm. Materials 2022, 15, 8071. [Google Scholar] [CrossRef]
- Hassan, B.R.; Yousif, A.R. Shear behavior of reinforced beams with basalt fiber reinforced polymer bars: Review, comparative analysis, and experimental validation. Structures 2024, 59, 105730. [Google Scholar] [CrossRef]
- Rüther, C.; Rieck, J. A Bayesian Optimization Approach for Tuning a Grouping Genetic Algorithm for Solving Practically Oriented Pickup and Delivery Problems. Logistics 2024, 8, 14. [Google Scholar] [CrossRef]
- Fu, T.; Rao, E.; Rabczuk, T. Sound transmission loss and energy absorbing performance of stiffened doubly-curved shells with corrugated-honeycomb hybrid cores. Eur. J. Mech. A/Solids 2024, 107, 105386. [Google Scholar] [CrossRef]
- Liu, Z.; Yin, X.; Yin, X.; Lu, Q.; Qiao, J.; Wang, Y. A Dice similarity coefficient-based pilot protection method for 500kV transmission lines of large-scale integrated photovoltaic power supply. Electr. Power Syst. Res. 2024, 226, 109918. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Q.; Xia, R.; Zhang, P.; Zhou, H.; Zhao, B.; Li, G. Automatic defect prediction in glass fiber reinforced polymer based on THz-TDS signal analysis with neural networks. Infrared Phys. Technol. 2021, 115, 103673. [Google Scholar] [CrossRef]
- Rehra, J.; Jungbluth, J.; Katri, B.; Schmeer, S.; Gurka, M.; Balle, F.; Breuer, U.P. Damage and failure mechanisms of hybrid carbon fiber and steel fiber reinforced polymer composites. Compos. Part A Appl. Sci. Manuf. 2024, 185, 108366. [Google Scholar] [CrossRef]
- Bérot, O.S.; Canot, H.; Durand, P.; Hassoune-Rhabbour, B.; Acheritobehere, H.; Laforet, C.; Nassiet, V. Choice of Parameters of an LSTM Network, based on a Small Experimental Dataset. Eng. Lett. 2024, 32, 59–71. [Google Scholar]
- Sukur, E.F.; Elimsa, S.; Eskizeybek, V.; Avci, A. Damage tolerance of basalt fiber reinforced multiscale composites: Effect of nanoparticle morphology and hygrothermal aging. Compos. Part B Eng. 2024, 273, 111234. [Google Scholar] [CrossRef]
- Oudah, F.; Alhashmi, A.E. Time-dependent reliability analysis of degrading structural elements using stochastic fe and lstm learning. In Proceedings of the Canadian Society of Civil Engineering Annual Conference, Whistler, BC, Canada, 25–28 May 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 131–140. [Google Scholar]
- Oh, H.S.; Kim, J.M.; Chang, C.Y. A Study on LSTM-Based Lithium Battery SoH Estimation in Urban Railway Vehicle Operating Environments. J. Electr. Eng. Technol. 2024, 19, 2817–2829. [Google Scholar] [CrossRef]
- Wang, X.; Hu, B.; Su, X.; Xu, L.; Zhu, D. State of health estimation for lithium-ion batteries using random forest and gated recurrent unit. J. Energy Storage 2024, 76, 109796. [Google Scholar] [CrossRef]
- Karaburun, N.N.; Hatipoğlu, S.A.; Konar, M. SOC Estimation of Li-Po Battery Using Machine Learning and Deep Learning Methods. J. Aviat. 2024, 8, 26–31. [Google Scholar] [CrossRef]
- Al-lQubaydhi, N.; Alenezi, A.; Alanazi, T.; Senyor, A.; Alanezi, N.; Alotaibi, B.; Alotaibi, M.; Razaque, A.; Hariri, S. Deep learning for unmanned aerial vehicles detection: A review. Comput. Sci. Rev. 2024, 51, 100614. [Google Scholar] [CrossRef]
- Yong, S.L.S.; Ng, J.L.; Huang, Y.F.; Ang, C.K.; Ahmad Kamal, N.; Mirzaei, M.; Najah Ahmed, A. Enhanced daily reference evapotranspiration estimation using optimized hybrid support vector regression models. Water Resour. Manag. 2024, 28, 4213–4241. [Google Scholar] [CrossRef]
- Iranzad, R.; Liu, X. A review of random forest-based feature selection methods for data science education and applications. Int. J. Data Sci. Anal. 2024, 2, 927312. [Google Scholar] [CrossRef]
- Tripathi, K.; Hamza, M.H.; Chattopadhyay, A.; Henry, T.C.; Hall, A. Impact of buckypaper on the mechanical properties and failure modes of composites. In Proceedings of the 38th Technical Conference of the American Society for Composites, ASC 2023, Tucson, AZ, USA, 19–21 September 2023; DEStech Publications: Lancaster, PA, USA, 2023; pp. 2281–2297. [Google Scholar]
- Kim, M.; Goerzen, D.; Jena, P.V.; Zeng, E.; Pasquali, M.; Meidl, R.A.; Heller, D.A. Human and environmental safety of carbon nanotubes across their life cycle. Nat. Rev. Mater. 2024, 9, 63–81. [Google Scholar] [CrossRef]
- Nath, D.; Ankit; Neog, D.R.; Gautam, S.S. Application of machine learning and deep learning in finite element analysis: A comprehensive review. Arch. Comput. Methods Eng. 2024, 31, 2945–2984. [Google Scholar] [CrossRef]
- Xiao, S.; Cunningham, W.J.; Kondabolu, K.; Lowet, E.; Moya, M.V.; Mount, R.A.; Ravasio, C.; Bortz, E.; Shaw, D.; Economo, M.N.; et al. Large-scale deep tissue voltage imaging with targeted-illumination confocal microscopy. Nat. Methods 2024, 21, 1094–1102. [Google Scholar] [CrossRef]
- Reiner, J.; Vaziri, R.; Zobeiry, N. Machine learning assisted characterisation and simulation of compressive damage in composite laminates. Compos. Struct. 2021, 273, 114290. [Google Scholar] [CrossRef]
- Najjar, I.; Sadoun, A.; Abd Elaziz, M.; Abdallah, A.; Fathy, A.; Elsheikh, A.H. Predicting kerf quality characteristics in laser cutting of basalt fibers reinforced polymer composites using neural network and chimp optimization. Alex. Eng. J. 2022, 61, 11005–11018. [Google Scholar] [CrossRef]
- Du, N.; Zhou, Y.; Luo, Q.; Jiang, M.; Deng, W. Multi-strategy chimp optimization algorithm for global optimization and minimum spanning tree. Soft Comput. 2024, 28, 2055–2082. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Mishra, D.R. Characterisation of basalt/glass/kevlar-29 hybrid fibre-reinforced plastic composite material through Nd: YAG laser drilling and optimisation using stochastic methods. J. Mech. Sci. Technol. 2024, 38, 4321–4331. [Google Scholar] [CrossRef]
- Ahmed, F.R.; Alsenany, S.A.; Abdelaliem, S.M.F.; Deif, M.A. Development of a hybrid LSTM with chimp optimization algorithm for the pressure ventilator prediction. Sci. Rep. 2023, 13, 20927. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Li, Y.; Wang, Q. Intelligent feedforward hysteresis compensation and tracking control of dielectric electro-active polymer actuator. Sens. Actuators A Phys. 2022, 341, 113581. [Google Scholar] [CrossRef]
- Khodadoost, S.; Saraee, M.; Talatahari, S.; Sareh, P. Optimal design of fractional-order proportional integral derivative controllers for structural vibration suppression. Sci. Rep. 2024, 14, 17207. [Google Scholar] [CrossRef] [PubMed]
- Munshi, J.; Chen, W.; Chien, T.; Balasubramanian, G. Transfer learned designer polymers for organic solar cells. J. Chem. Inf. Model. 2021, 61, 134–142. [Google Scholar] [CrossRef]
- Reza, M.S.; Reza, M.S.; Ghosh, A.; Rahman, M.F.; Rajabathar, J.R.; Ahmed, F.; Sajid, M.; Buian, M.F.I.; Bhandari, J.; Islam, M.A.; et al. New highly efficient perovskite solar cell with power conversion efficiency of 31% based on Ca3NI3 and an effective charge transport layer. Opt. Commun. 2024, 561, 130511. [Google Scholar] [CrossRef]
- Luong, T.; Seo, S.; Kim, K.; Jeon, J.; Koo, J.C.; Choi, H.R.; Moon, H. Hysteresis modeling of twisted-coiled polymer actuators using long short term memory networks. In Proceedings of the IFToMM Asian Conference on Mechanism and Machine Science, Hanoi, Vietnam, 15–18 December 2024; Springer: Berlin/Heidelberg, Germany, 2021; pp. 590–599. [Google Scholar]
- Luong, T.; Seo, S.; Hudoklin, J.; Koo, J.C.; Choi, H.R.; Moon, H. Variable stiffness robotic hand driven by twisted-coiled polymer actuators. IEEE Robot. Autom. Lett. 2022, 7, 3178–3185. [Google Scholar] [CrossRef]
- Kumar, A.; Parey, A.; Kankar, P.K. A new hybrid LSTM-GRU model for fault diagnosis of polymer gears using vibration signals. J. Vib. Eng. Technol. 2024, 12, 2729–2741. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, W. Complete Ensemble Empirical Mode Decomposition with Adaptive Noise to Extract Deep Information of Bearing Fault in Steam Turbines via Deep Belief Network. Int. J. High Speed Electron. Syst. 2024, 2440079. [Google Scholar] [CrossRef]
- Shunhu, H.; Feng, M.; Qingshan, G.; Hua, Z. Efficient low-carbon manufacturing for CFRP composite machining based on deep networks. Int. J. Prod. Res. 2024, 1–12. [Google Scholar] [CrossRef]
- Aklouche, B.; Benkedjouh, T.; Habbouche, H.; Rechak, S. Damage assessment of composite material based on variational mode decomposition and BiLSTM. Int. J. Adv. Manuf. Technol. 2023, 129, 1801–1815. [Google Scholar] [CrossRef]
- Lu, H.; Chandran, B.; Wu, W.; Ninic, J.; Gryllias, K.; Chronopoulos, D. Damage features for structural health monitoring based on ultrasonic Lamb waves: Evaluation criteria, survey of recent work and outlook. Measurement 2024, 232, 114666. [Google Scholar] [CrossRef]
- Ali, L.; Isleem, H.F.; Bahrami, A.; Jha, I.; Zou, G.; Kumar, R.; Sadeq, A.M.; Jahami, A. Integrated behavioural analysis of FRP-confined circular columns using FEM and machine learning. Compos. Part C Open Access 2024, 13, 100444. [Google Scholar] [CrossRef]
- Deng, X.; Yang, F. Energy absorption characteristics of a double-filled sinusoidal corrugated filled tube under axial impact. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 364. [Google Scholar] [CrossRef]
- Li, B.F.; Wang, X.T.; Xie, C.D.; Yan, X.F.; Wang, S. Compressive behaviour and design of tapered lightweight concrete-filled double-skin stiffened steel tubular short columns with large hollow ratio. Structures 2024, 64, 106527. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Q.; Xia, R.; Li, G.; Gao, J.; Zhou, H.; Zhao, B. Defect depth determination in laser infrared thermography based on LSTM-RNN. IEEE Access 2020, 8, 153385–153393. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Z.; Yin, W.; Zhou, G.; Wang, L.; Li, Y.; Zhao, C.; Wang, C. Shape characterization and depth recognition of metal cracks based on laser infrared thermography and machine learning. Expert Syst. Appl. 2024, 238, 122083. [Google Scholar] [CrossRef]
- Gahleitner, L.; Mayr, G.; Burgholzer, P.; Cakmak, U. Efficient defect reconstruction from temporal non-uniform pulsed thermography data using the virtual wave concept. NDT E Int. 2024, 147, 103200. [Google Scholar]
- Kang, J.M.; Choi, S.H.; Park, J.w.; Park, K.S. Position error prediction using hybrid recurrent neural network algorithm for improvement of pose accuracy of cable driven parallel robots. Microsyst. Technol. 2020, 26, 209–218. [Google Scholar] [CrossRef]
- Kolemen, E.; Egrioglu, E.; Bas, E.; Turkmen, M. A new deep recurrent hybrid artificial neural network of gated recurrent units and simple seasonal exponential smoothing. Granul. Comput. 2024, 9, 7. [Google Scholar] [CrossRef]
- Chan, A.N.F.; Cheng, W.; Lau, D. Deformable Open-Frame Cable-Driven Parallel Robots: Modeling, Analysis and Control. IEEE Trans. Robot. 2024, 40, 3465–3480. [Google Scholar] [CrossRef]
- Lin, T.; Hu, L.; Wisely, W.; Gu, X.; Cai, J.; Litster, S.; Kara, L.B. Prediction of high frequency resistance in polymer electrolyte membrane fuel cells using long short term memory based model. Energy AI 2021, 3, 100045. [Google Scholar] [CrossRef]
- Lorenzo-Navarro, J.; Serranti, S.; Bonifazi, G.; Capobianco, G. Performance evaluation of classical classifiers and deep learning approaches for polymers classification based on hyperspectral images. In Proceedings of the Advances in Computational Intelligence: 16th International Work-Conference on Artificial Neural Networks, IWANN 2021, Virtual Event, 16–18 June 2021; Proceedings, Part II 16. Springer: Berlin/Heidelberg, Germany, 2021; pp. 281–292. [Google Scholar]
- Choi, S.B.; Shin, H.S.; Kim, J.W. Convolution Neural Networks for Motion Detection with Electrospun Reversibly-Cross-linkable Polymers and Encapsulated Ag Nanowires. ACS Appl. Mater. Interfaces 2023, 15, 47591–47603. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Wang, Q.; Jiang, J.; Xiang, X.; Ye, P.; Wang, Y.; Qin, Y.; Chen, Y.; Lai, W.; Zhang, X. Highly Stable Silver Nanowire Plasmonic Electrodes for Flexible Polymer Light-Emitting Devices. ACS Appl. Mater. Interfaces 2024, 16, 31419–31427. [Google Scholar] [CrossRef]
- Xu, J.; Chen, W.; Liu, L.; Jiang, S.; Wang, H.; Zhang, J.; Gan, X.; Zhou, X.; Guo, T.; Wu, C.; et al. Intelligent recognition of human motion using an ingenious electronic skin based on metal fabric and natural triboelectrification. Sci. China Mater. 2024, 67, 887–897. [Google Scholar] [CrossRef]
- Tan, D.; Wang, K.; Zhou, J.; Peng, J.; Wang, Q. A brief review of nonlinear triboelectric nanogenerator. Int. J. Dyn. Control. 2024, 12, 2072–2092. [Google Scholar] [CrossRef]
- Jiang, W.; Zhou, Q.; He, J.; Habibi, M.A.; Melnyk, S.; El-Absi, M.; Han, B.; Di Renzo, M.; Schotten, H.D.; Luo, F.L.; et al. Terahertz communications and sensing for 6G and beyond: A comprehensive review. IEEE Commun. Surv. Tutor. 2024. [Google Scholar] [CrossRef]
- Kadhafi, M.; Park, J.; Kang, D.; Koo, B. Thermal characteristics of multilayer sandwich Nomex honeycomb core composite with heating elements for railways wall panels. Adv. Compos. Mater. 2024, 1–19. [Google Scholar] [CrossRef]
- Badour, Y.; Pedros, M.; Gaudon, M.; Danto, S. Hybrid organic–inorganic PMMA optical fibers functionalized with photochromic active WO3 nanoparticles: From materials design to photochromic fabrics. Adv. Opt. Mater. 2024, 12, 2301717. [Google Scholar] [CrossRef]
- Ntonti, E.; Sotiriadou, S.; Assael, M.J.; Huber, M.L.; Wilthan, B.; Watanabe, M. Reference Correlations for the Density and Thermal Conductivity, and Review of the Viscosity Measurements, of Liquid Titanium, Zirconium, Hafnium, Vanadium, Niobium, Tantalum, Chromium, Molybdenum, and Tungsten. Int. J. Thermophys. 2024, 45, 18. [Google Scholar] [CrossRef]
- Molinié, P. Trap Spectroscopy from the Dielectric Isothermal Step Response: Theory and Simulations. In Proceedings of the 2024 IEEE 5th International Conference on Dielectrics (ICD), Toulouse, France, 30 June–10 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–4. [Google Scholar]
- Li, S.; Ma, S.; Wang, F. A combined NOx emission prediction model based on semi-empirical model and black box models. Energy 2023, 264, 126130. [Google Scholar] [CrossRef]
- Guo, T.; Lin, T.; Antulov-Fantulin, N. Exploring interpretable LSTM neural networks over multi-variable data. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 2494–2504. [Google Scholar]
- Seddik, S.; Routaib, H.; Elhaddadi, A. Multi-variable time series decoding with long short-term memory and mixture attention. Acadlore Trans. Mach. Learn. Res. 2023, 2, 154–169. [Google Scholar] [CrossRef]
- Liang, X.; Lin, L.; Shen, X.; Feng, J.; Yan, S.; Xing, E.P. Interpretable structure-evolving LSTM. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1010–1019. [Google Scholar]
- Wu, J.M.T.; Li, Z.; Herencsar, N.; Vo, B.; Lin, J.C.W. A graph-based CNN-LSTM stock price prediction algorithm with leading indicators. Multimed. Syst. 2023, 29, 1751–1770. [Google Scholar] [CrossRef]
- Tang, H.; Wu, S.; Xu, G.; Li, Q. Dynamic graph evolution learning for recommendation. In Proceedings of the 46th international ACM Sigir Conference on Research and Development in Information Retrieval, Taipei, Taiwan, 23–27 July 2023; pp. 1589–1598. [Google Scholar]
- Ye, Q.; Li, Y.; Niu, B. Risk Propagation Mechanism and Prediction Model for the Highway Merging Area. Appl. Sci. 2023, 13, 8014. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, C.; Wu, T.; Zhang, M. A novel spatio-temporal cellular automata model coupling partitioning with CNN-LSTM to urban land change simulation. Ecol. Model. 2023, 482, 110394. [Google Scholar] [CrossRef]
- Su, H.; Tretyakov, M.; Newton, D.P. Deep learning of transition probability densities for stochastic asset models with applications in option pricing. Manag. Sci. 2024. [Google Scholar] [CrossRef]
- Yang, D.; Liu, T.; Zhang, X.; Zeng, X.; Song, D. Construction of high-precision driving cycle based on Metropolis-Hastings sampling and genetic algorithm. Transp. Res. Part D Transp. Environ. 2023, 118, 103715. [Google Scholar] [CrossRef]
- Oyewola, D.O.; Akinwunmi, S.A.; Omotehinwa, T.O. Deep LSTM and LSTM-Attention Q-learning based reinforcement learning in oil and gas sector prediction. Knowl.-Based Syst. 2024, 284, 111290. [Google Scholar] [CrossRef]
- Williams, J.D.; Zweig, G. End-to-end LSTM-based dialog control optimized with supervised and reinforcement learning. arXiv 2016, arXiv:1606.01269. [Google Scholar]
- Igual, L.; Seguí, S. Supervised learning. In Introduction to Data Science: A Python Approach to Concepts, Techniques and Applications; Springer: Berlin/Heidelberg, Germany, 2024; pp. 67–97. [Google Scholar]
- Zhong, D.; Yang, Y.; Zhao, Q. No Prior Mask: Eliminate Redundant Action for Deep Reinforcement Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Kragujevac, Serbia, 23–24 May 2024; Volume 38, pp. 17078–17086. [Google Scholar]
- Wang, H.; He, S.; Zhang, Z.; Miao, F.; Anderson, J. Momentum for the Win: Collaborative Federated Reinforcement Learning across Heterogeneous Environments. arXiv 2024, arXiv:2405.19499. [Google Scholar]
- Brandonisio, A.; Capra, L.; Lavagna, M. Deep reinforcement learning spacecraft guidance with state uncertainty for autonomous shape reconstruction of uncooperative target. Adv. Space Res. 2024, 73, 5741–5755. [Google Scholar] [CrossRef]
- Yi, Z.; Ouyang, J.; Liu, Y.; Liao, T.; Xu, Z.; Shen, Y. A Survey on Recent Advances in LLM-Based Multi-turn Dialogue Systems. arXiv 2024, arXiv:2402.18013. [Google Scholar]
- Elakkiya, R.; Subramaniyaswamy, V. Cognitive Analytics and Reinforcement Learning: Theories, Techniques and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar]
- Liu, S.; Yuan, H.; Hu, M.; Li, Y.; Chen, Y.; Liu, S.; Lu, Z.; Jia, J. RL-GPT: Integrating Reinforcement Learning and Code-as-policy. arXiv 2024, arXiv:2402.19299. [Google Scholar]
- Gueldner, P.H.; Darvish, C.J.; Chickanosky, I.K.; Ahlgren, E.E.; Fortunato, R.; Chung, T.K.; Rajagopal, K.; Benjamin, C.C.; Maiti, S.; Rajagopal, K.R.; et al. Aortic tissue stiffness and tensile strength are correlated with density changes following proteolytic treatment. J. Biomech. 2024, 172, 112226. [Google Scholar] [CrossRef] [PubMed]
- Kalinin, S.V.; Ziatdinov, M.; Ahmadi, M.; Ghosh, A.; Roccapriore, K.; Liu, Y.; Vasudevan, R.K. Designing workflows for materials characterization. Appl. Phys. Rev. 2024, 11, 011314. [Google Scholar] [CrossRef]
- Zhao, Z.; Tang, D.; Zhu, H.; Zhang, Z.; Chen, K.; Liu, C.; Ji, Y. A Large Language Model-based multi-agent manufacturing system for intelligent shopfloor. arXiv 2024, arXiv:2405.16887. [Google Scholar]
- Jhong, Y.D.; Chen, C.S.; Jhong, B.C.; Tsai, C.H.; Yang, S.Y. Optimization of LSTM parameters for flash flood forecasting using genetic algorithm. Water Resour. Manag. 2024, 38, 1141–1164. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Z.; Li, T.; Si, X. A review on physics-informed data-driven remaining useful life prediction: Challenges and opportunities. Mech. Syst. Signal Process. 2024, 209, 111120. [Google Scholar] [CrossRef]
- Chui, K.T.; Gupta, B.B.; Vasant, P. A genetic algorithm optimized RNN-LSTM model for remaining useful life prediction of turbofan engine. Electronics 2021, 10, 285. [Google Scholar] [CrossRef]
- Frusque, G.; Fink, O. Robust time series denoising with learnable wavelet packet transform. Adv. Eng. Inform. 2024, 62, 102669. [Google Scholar] [CrossRef]
- Sha, X. Time Series Stock Price Forecasting Based on Genetic Algorithm (GA)-Long Short-Term Memory Network (LSTM) Optimization. arXiv 2024, arXiv:2405.03151. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, H. An Automatic Analysis Approach of Bridge Life Based on Engineering Mathematics and LSTM. In Proceedings of the 2024 19th Annual System of Systems Engineering Conference (SoSE), Tacoma, WA, USA, 23–26 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 308–313. [Google Scholar]
- Jung, S.G.; Jung, G.; Cole, J.M. Automatic Prediction of Band Gaps of Inorganic Materials Using a Gradient Boosted and Statistical Feature Selection Workflow. J. Chem. Inf. Model. 2024, 64, 1187–1200. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Sun, C.; Pu, J.; Li, J.; Li, Y.; Xie, Q.; Li, K.; Chen, H. Efficiency optimization of fuel cell systems with energy recovery: An integrated approach based on modeling, machine learning, and genetic algorithm. J. Power Sources 2024, 615, 235077. [Google Scholar] [CrossRef]
- Cui, X.; Chipusu, K.; Ashraf, M.A.; Riaz, M.; Xiahou, J.; Huang, J. Symmetry-Enhanced LSTM-Based Recurrent Neural Network for Oscillation Minimization of Overhead Crane Systems during Material Transportation. Symmetry 2024, 16, 920. [Google Scholar] [CrossRef]
- Sharma, S.; Sen, S. Real-time structural damage assessment using LSTM networks: Regression and classification approaches. Neural Comput. Appl. 2023, 35, 557–572. [Google Scholar] [CrossRef]
- Gu, M.; Xu, A.; Wang, H.; Wang, Z. Real-time dynamic carbon content prediction model for second blowing stage in BOF based on CBR and LSTM. Processes 2021, 9, 1987. [Google Scholar] [CrossRef]
- Wolf, T.N.; Bongratz, F.; Rickmann, A.M.; Pölsterl, S.; Wachinger, C. Keep the faith: Faithful explanations in convolutional neural networks for case-based reasoning. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 5921–5929. [Google Scholar]
- Ghazimoghadam, S.; Hosseinzadeh, S. A novel unsupervised deep learning approach for vibration-based damage diagnosis using a multi-head self-attention LSTM autoencoder. Measurement 2024, 229, 114410. [Google Scholar] [CrossRef]
- Tien, T.B.; Quang, T.V.; Ngoc, L.N.; Ngoc, H.T. Time series data recovery in SHM of large-scale bridges: Leveraging GAN and Bi-LSTM networks. Structures 2024, 63, 106368. [Google Scholar] [CrossRef]
- Gupta, A.; Kumar, N.; Sachdeva, A. Factors affecting the ageing of polymer composite: A state of art. Polym. Degrad. Stab. 2024, 221, 110670. [Google Scholar] [CrossRef]
- Xu, B.; Blok, R.; Teuffel, P.; Lucas, S.; Moonen, F. Effect of Moisture in Flax Fiber on Viscoelastic Properties of the Manufactured Flax Fiber Reinforced Polymer by Fractional-Order Viscoelastic Model. Mater. Today Commun. 2024, 40, 110138. [Google Scholar] [CrossRef]
- Singh, S.J.; Ahlawat, N.; Panwar, V. Computational analysis of viscoelastic properties in polymer composites. In Dynamic Mechanical and Creep-Recovery Behavior of Polymer-Based Composites; Elsevier: Amsterdam, The Netherlands, 2024; pp. 291–309. [Google Scholar]
- Senapati, S.; Banerjee, A.; Rajesh, R. Acoustic emission data based modelling of fracture of glassy polymer. Eng. Fract. Mech. 2024, 304, 110154. [Google Scholar] [CrossRef]
- Schilling, M.; Marschall, N.; Niebergall, U.; Wachtendorf, V.; Böhning, M. Characteristics of Environmental Stress Cracking of PE-HD induced by Biodiesel and Diesel Fuels. Polym. Test. 2024, 138, 108547. [Google Scholar] [CrossRef]
- Aydonat, S.; Hergesell, A.H.; Seitzinger, C.L.; Lennarz, R.; Chang, G.; Sievers, C.; Meisner, J.; Vollmer, I.; Göstl, R. Leveraging mechanochemistry for sustainable polymer degradation. Polym. J. 2024, 56, 249–268. [Google Scholar] [CrossRef]
- Singh, S.K.; Soman, R.N.; Malinowski, P.H. A novel multi-damage localization method for polymers and composites based on electromechanical impedance. Mech. Syst. Signal Process. 2024, 216, 111508. [Google Scholar] [CrossRef]
- Li, Y.; Feng, T.; Wang, Y.; Zhu, Z.; Peng, H.X.; Xu, P.; Qin, F. Real-time evaluating temperature-dependent interfacial shear strength of thermoplastic composites based on stress impedance effect of magnetic fibers. Compos. Part A Appl. Sci. Manuf. 2024, 176, 107874. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, X.; Chen, J.; Chen, H.; Pak, R.Y. Effect of cyclic loading level on mechanical response and microcracking behavior of saturated sandstones: Correlation with water weakening phenomenon. Eng. Geol. 2024, 340, 107667. [Google Scholar] [CrossRef]
- Jia, D.; Hao, Z.; Peng, Y.; Yan, S.; Hu, W. Experimental Study on the Localized Deformation and Damage Behavior of Polymer-Bonded Explosive Simulant under Cyclic Compression. Materials 2024, 17, 919. [Google Scholar] [CrossRef]
- Li, J.; Wu, G.; Zhang, Y.; Shi, W. Optimizing flood predictions by integrating LSTM and physical-based models with mixed historical and simulated data. Heliyon 2024, 10, e33669. [Google Scholar] [CrossRef]
- Meng, Y.; Yun, S.; Zhao, Z.; Guo, J.; Li, X.; Ye, D.; Jia, L.; Yang, L. Short-term electricity load forecasting based on a novel data preprocessing system and data reconstruction strategy. J. Build. Eng. 2023, 77, 107432. [Google Scholar] [CrossRef]
- Zhou, Y.; Aryal, S.; Bouadjenek, M.R. Review for Handling Missing Data with special missing mechanism. arXiv 2024, arXiv:2404.04905. [Google Scholar]




| Reference | Focus | Applied Model | Limitations | Data Information | Metrics |
|---|---|---|---|---|---|
| Ryman et al. [79] | Development of sensors using organic polymers for chemical detection | LSTM | Limited research into the neural architectures for chemical awareness in dynamic environments | Sensor data from organic polymers | N/A |
| Shin et al. [87] | Enhancing state-of-charge (SOC) estimation in batteries | LSTM combined with EKF | Potential uncertainties in battery models and varying conditions | Battery charge and discharge data | RMSE (<1%) |
| Andrews et al. [88] | Predicting the energetics of ethyl acetate solution with polymer–lipid aggregate | ERNN, LSTM, GRU | Struggles with accurate short- and long-term forecasts | Energetics data from polymer–lipid solutions | RMSE (0.1) |
| Wang et al. [92] | Recognition of motor tics using a hybrid sensor | LSTM | Potential limitations in recognition accuracy and self-powered operation | Motor tic sensor data | Signal recognition rate (88.1%) |
| Yezerska et al. [96] | Predicting starvation effects in fuel cells | LSTM | Recommendations are based on simulations, which may have limitations in real-world applicability | Fuel cell performance data | N/A |
| Benhaddouch et al. [100] | Real-time monitoring of radical-induced degradation in PEMFCs | LSTM | Limited to predictive diagnostics, may not address all degradation mechanisms | PEMFC degradation data | N/A |
| Xu et al. [103] | Classification of substances within GFRP structures using THz-TDS | LSTM, 1D-CNN | LSTM excels with time-domain but struggles with frequency-domain signals compared to improved 1D-CNN | THz-TDS data from GFRP structures | (0.88–0.91) |
| Song et al. [105] | Predicting melt index (MI) in polymerization processes | LSTM | Challenges with nonlinearity and complex temporal correlations | Polymerization process data | (≈0.8) |
| Song et al. [108] | Predicting nonlinear performance degradation of FRP | Reinforcement LSTM (SCRLA) | Potential complexity in model generalization and integration of Bayesian algorithms | FRP performance data | (≈0.9) |
| Goswami et al. [110] | Predicting Glass Transition Temperature (Tg) in polymers | LSTM based on SMILES | Model performance and practical application may need further validation | Polymer SMILES data | N/A |
| Reference | Focus | Applied Model | Limitations | Data Information | Metrics |
|---|---|---|---|---|---|
| Kim et al. [113] | DL-based prediagnosis system for PEMFCs | LSTM, CNN combined with bagging ensemble method | Focused on specific failure modes (flooding, drying); may require validation in broader conditions | PEMFC performance data | Recall (83–93%), precision (73–98%) |
| Ramachandran et al. [116] | Predicting end of life of underwater electroacoustic sensors by modeling polymer insulation degradation | LSTM | Model predictions based on resistance measurements; real-time applicability may vary | Resistance measurements from polymer insulation | N/A |
| Lee et al. [119] | Predicting tensile behavior of polymer matrix composites (PMCs) | LSTM, FNN, PCA, RFECV | Accuracy may depend on the quality of feature selection and input data | Tensile test data from PMC | (0.92) |
| Chistyakova et al. [124] | Predictive models for quality indicators in polymer film materials | AdaBoost, LSTM | Performance depends on specific production data characteristics; generalization may be limited | Production data from polymer films | N/A |
| Zhang et al. [128] | Predicting tensile strength retention (TSR) in GFRPs under alkaline conditions | LSTM, XGBoost | Sensitive to variations in pH and temperature; may need adaptation for different environmental conditions | Tensile strength data from GFRPs | Accuracy (85%) |
| Yoon et al. [131] | Enhancing EKF for SOC estimation in Li-polymer batteries | LSTM combined with EKF | Inaccuracies in SOC estimation under dynamic conditions still possible | Battery charge/discharge data | RMSE (≈0.24) |
| Jiang et al. [134] | Modeling hysteresis in DEAP actuators for robotics | LSTM with EMD | Hybrid model complexity may affect real-time implementation | Hysteresis data from DEAP actuators | MAE (≈0.02), MRE (≈0.01) |
| Wang et al. [136] | Classifying internal interfaces in polymers using THz waveform data | LSTM | Effectiveness depends on the quality of THz data; sensitivity to noise may limit use in some applications | THz waveform data from polymers | Accuracy (≈0.95) |
| Li et al. [137] | Predicting tool wear in milling CFRP by analyzing cutting force signals | Multichannel 1D CNN with LSTM | Performance may vary with different tool materials and cutting conditions | Cutting force signal data | (95.04%), MAE (2.94) |
| Hantono et al. [139] | Estimating SOC of lithium polymer batteries | LSTM | Computation limited by hardware (Jetson Nano); may not scale easily to larger models | Battery charge, discharge data | RMSE (≈1.8) |
| Reference | Focus | Applied Model | Limitations | Data Information | Metrics |
|---|---|---|---|---|---|
| Dehghan et al. [140] | Predicting conductive and radiative heat transfer in PMMA | LSTM networks | May require further validation across diverse conditions | Heat transfer data from PMMA | RMSE (16.4) |
| Luong et al. [141] | Predicting behavior of an antagonistic joint driven by twisted-coiled polymer actuators | LSTM with Model Predictive Control (MPC) | Performance may be sensitive to actuator material variations | Actuator performance data | RMSE (0.21) |
| Dong et al. [143] | Hybrid modeling for TFE polymerization process | LSTM combined with kinetic and thermodynamic models | Effectiveness depends on accurate kinetic parameter estimation | Polymerization process data | N/A |
| Bi et al. [146] | Predicting polymer intrinsic viscosity for polyester fiber quality | TSDGAN, Attention LSTM, CNN | Sensitivity to the rate of missing data may limit generalizability | Intrinsic viscosity data | N/A |
| Rahman et al. [148] | Predictive maintenance for industrial drying hopper | CNN for Multivariate Time-Series (MTS) classification | Imbalanced data handling might require additional techniques | Drying hopper performance data | Accuracy (98%) |
| Gao et al. [150] | Enhancing tactile perception with dual-mode tactile sensor | CNN-LSTM model | Performance may degrade under varying tactile conditions | Tactile sensor data | Recognition rate (77–90%) |
| Simine et al. [151] | Predicting UV-vis spectra of conjugated polymers | LSTM-RNN | Applicability might be limited to specific polymer types | UV-vis spectra data | N/A |
| Braghetto et al. [152] | Analyzing configurations of flexible knotted rings within spherical cavities | LSTM neural networks | Misclassification within the same topological family indicates model limitations | Configuration data of knotted rings | Accuracy (0.2–0.80) |
| Benrabia et al. [154] | Modeling energy storage systems under varying external states | NARX and LSTM models | NARX is more effective for batteries, LSTM for fuel cells; each model has application-specific strengths | Energy storage system data | N/A |
| Altabey et al. [156] | Predicting acoustic behavior of BFRP composite mufflers | RNN-LSTM, CNN optimized with Bayesian genetic algorithms | Generalization may be limited to specific muffler designs | Acoustic behavior data | Accuracy (>90%) |
| Wang et al. [161] | Detecting internal defects in GFRP using terahertz spectroscopy | 1D CNN, LSTM-RNN, Bidirectional LSTM-RNN | Best results with 1D CNN; other models might need further refinement | Terahertz spectroscopy data | F1 score (0.91) |
| Reference | Focus | Applied Model | Limitations | Data Information | Metrics |
|---|---|---|---|---|---|
| Berot et al. [163] | Predicting polymer aging in epoxy adhesives under hygrothermal aging | LSTM with single hidden layer, 150 units, hyperbolic tangent activation | Requires precise tuning of network parameters for stability and accuracy | Aging data from epoxy adhesives | MSE (<0.01) |
| Oudan et al. [165] | Assessing time-dependent reliability of degrading structural systems | Hybrid FE simulation with LSTM networks | Validation needed across different structural materials and conditions | Structural degradation data | N/A |
| Oh et al. [166] | Estimating state of health (SoH) of lithium polymer batteries in railway fleets | LSTM models for SoH analysis over 500 charge/discharge cycles | Performance may vary under different operational environments | Battery SoH data | N/A |
| Karaburun et al. [168] | State-of-charge (SOC) estimation for lithium polymer batteries in UAVs | LSTM, SVR, Random Forest | Requires comparison with real-time applications in UAVs for further validation | Battery SOC data | RMSE (0.3) |
| Tripathi et al. [172] | Predicting mechanical response of CFRP laminates with BP/CNT interleaves | LSTM model trained on FEA and experimental data | Model accuracy depends on quality and quantity of FEA and experimental data | Mechanical response data from CFRP laminates | N/A |
| Reiner et al. [176] | Characterizing strain-softening in laminated composites under compression | LSTM-based recurrent neural network | High computational cost due to the need for extensive FE simulations | Strain-softening data from laminated composites | N/A |
| Najjar et al. [177] | Predicting kerf quality in laser cutting of basalt fiber-reinforced polymers | LSTM combined with Chimp Optimization Algorithm (CHOA) | Generalizability to different composite materials requires further exploration | Kerf quality data from laser cutting | RMSE (27–60%) |
| Jiang et al. [181] | Addressing hysteresis and creep in DEAP actuators | Hybrid LSTM with EMD and PID control | Application limited to DEAP actuators; may not extend to other actuator types | Hysteresis and creep data from DEAP actuators | N/A |
| Munshi et al. [183] | Discovering new polymer chemistries for OPV materials using transfer learning | LSTM model using SMILES molecular fingerprints | Model trained on a small dataset; larger datasets needed for broader application | Polymer chemistry data | N/A |
| Reference | Focus | Applied Model | Limitations | Data Information | Metrics |
|---|---|---|---|---|---|
| Luong et al. [185] | Predicting nonlinear behavior of an antagonistic joint driven by hybrid TCA bundle | LSTM network for joint angle prediction | Specific to TCA-driven systems; may require adaptation for other actuation systems | Joint angle data from TCA-driven systems | Working range of 30% of the TCA |
| Kumar et al. [187] | Detecting faults in polymer gears | Hybrid LSTM-GRU model with CEEMDAN preprocessing | Model performance needs validation in different operational environments | Fault detection data from polymer gears | Accuracy (99%) |
| Shunhu et al. [189] | Optimizing drilling quality and energy efficiency in CFRP components | CNN-LSTM network correlating process parameters with outcomes | Applicability to other drilling processes and materials needs further testing | Drilling process data from CFRP components | N/A |
| Aklouche et al. [190] | Estimating damage severity in CFRP using LW data | Bidirectional LSTM (BiLSTM) with VMD for preprocessing | Limited to composite materials like CFRP; may not generalize to other material types | Damage severity data from CFRP | N/A |
| Ali et al. [192] | Comparing structural behavior of DSDFT and DSHT columns | LSTM and BiLSTM models for predicting axial load capacity | Predictions specific to column types studied; generalization needs further exploration | Axial load capacity data from columns | RMSE (0.065) |
| Wang et al. [195] | Assessing defect depth in CFRP sheets using LIT | LSTM-RNN combined with TSR for noise reduction | Model effectiveness might vary with different defect types and depths | Defect depth data from CFRP sheets | (0.78–93) |
| Kang et al. [198] | Addressing nonlinear issues in CDPRs with polymer cables | Hybrid RNN (H-RNN) combining LSTM and basic RNN for position error prediction | Model complexity may limit its application to simpler systems | Position error data from CDPRs | N/A |
| Lin et al. [201] | Real-time prediction of HFR in PEMFCs | LSTM model using current and past sensor data | Model effectiveness may decrease with changes in PEMFC operational conditions | HFR data from PEMFCs | MAPE (2.82%) |
| Lorenzo et al. [202] | Classifying plastics using hyperspectral images | 1D CNN and SVM+RBF models | Requires extensive hyperspectral data; may be limited to specific plastic types | Hyperspectral image data from plastics | Accuracy (99.41%) |
| Choi et al. [203] | Enhancing mechanical stability and motion detection in PBU/AgNW/PBU sensors | 1D CNN and LSTM models for motion detection | Limited testing in real-world applications; further validation required | Motion detection data from sensors | Accuracy (98%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malashin, I.; Tynchenko, V.; Gantimurov, A.; Nelyub, V.; Borodulin, A. Applications of Long Short-Term Memory (LSTM) Networks in Polymeric Sciences: A Review. Polymers 2024, 16, 2607. https://doi.org/10.3390/polym16182607
Malashin I, Tynchenko V, Gantimurov A, Nelyub V, Borodulin A. Applications of Long Short-Term Memory (LSTM) Networks in Polymeric Sciences: A Review. Polymers. 2024; 16(18):2607. https://doi.org/10.3390/polym16182607
Chicago/Turabian StyleMalashin, Ivan, Vadim Tynchenko, Andrei Gantimurov, Vladimir Nelyub, and Aleksei Borodulin. 2024. "Applications of Long Short-Term Memory (LSTM) Networks in Polymeric Sciences: A Review" Polymers 16, no. 18: 2607. https://doi.org/10.3390/polym16182607
APA StyleMalashin, I., Tynchenko, V., Gantimurov, A., Nelyub, V., & Borodulin, A. (2024). Applications of Long Short-Term Memory (LSTM) Networks in Polymeric Sciences: A Review. Polymers, 16(18), 2607. https://doi.org/10.3390/polym16182607









